三维沉积盆地对地震动的放大效应间接边界元法模拟

刘中宪; 尚策; 王小燕; 王冬

doi:10.11939/jass.2017.01.010

三维沉积盆地对地震动的放大效应间接边界元法模拟

刘中宪^1,2, ,,
尚策¹,
王小燕³,
王冬⁴

1.
中国天津 300384 天津城建大学天津市土木建筑结构防护与加固重点实验室
2.
中国天津 300074 天津市地震工程研究所
3.
中国天津 300401 河北工业大学土木与交通学院
4.
中国石家庄 050021 河北建研科技有限公司

基金项目:

国家自然科学基金项目 51678390

国家自然科学基金项目(51678390)和天津市应用基础与前沿研究计划重点项目(15JCZDJC39900)共同资助

天津市应用基础与前沿研究计划重点项目 15JCZDJC39900

详细信息

通讯作者:
刘中宪: e-mail: zhongxian1212@163.com

中图分类号: P315.9
计量
- 文章访问数: 822
- HTML全文浏览量: 324
- PDF下载量: 27
出版历程
- 收稿日期: 2016-05-04
- 修回日期: 2016-07-06
- 发布日期: 2016-12-31

Simulation on the amplification effect of a three-dimensional alluvial basin on the earthquake ground motion using the indirect boundary element method

1.
Tianjin Key Laboratory of Civil Structure Protection and Reinforcement， Tianjin Chengjian University， Tianjin 300384， China
2.
Earthquake Engineering Research Institute of Tianjin City， Tianjin 300074， China
3.
School of Civil Engineering and Transportation, Hebei University of Technology，Tianjin 300401， China
4.
Hebei Construction Technology Co.， Ltd， Shijiazhuang 050021， China

摘要

摘要: 基于一种高精度间接边界元法(IBEM)，实现了沉积盆地三维地震响应的频域、时域精细求解，并以半空间中椭球形沉积盆地对平面P波和SV波的散射为例，着重探讨了入射角度、入射波型、入射频率、盆地长宽比和深宽比对沉积盆地地震动放大效应的影响规律．结果表明：盆地形状对地震波的放大效应和空间分布状态具有显著影响，且具体规律受控于入射波频段． ① 随着盆地深度增大，盆地边缘面波发育更为充分，在较宽频段内均会出现显著的地震动放大效应，且深盆地的放大区域集中于盆地中部． ② 圆形盆地对地震波的汇聚效应最为显著，而狭长盆地对地震波的汇聚作用相对较弱，高频情况下可在盆地内部形成多个聚焦区域． ③ 不同波型入射下，盆地对地震动放大效应的机制有所差异： P波入射下，竖向位移放大主要是由于盆地边缘面波由四周向中部汇聚所致； SV波入射下，边缘面波汇聚效应相对较弱，而当盆地较深时，底部透射体波和边缘面波易形成同相干涉从而显著放大地震动．按盆地内外介质波速比为1/2， P波和SV波垂直入射下频域最大放大倍数分别为25和15，时域放大倍数约为4.0和3.7(雷克子波)． ④ 低频波入射下，位移从盆地中部向边缘逐渐减小，且浅层沉积盆地对地表位移幅值的放大作用不明显． ⑤ P波和SV波的入射角度对盆地地震动放大幅值及空间分布特征也具有显著影响．
- 盆地边缘效应 /
- 地震波 /
- 散射 /
- 间接边界元法(IBEM) /
- 聚焦效应
Abstract: Based on the indirect boundary element method (IBEM) with high precision, this paper solves the seismic response of a three-dimensional sedimentary basins both in the frequency domain and time domain. Taking the scattering of plane P and SV waves around an semi-ellipsoidal three-dimensional sedimentary basin as an example, the amplification effects of incident angle, wave type, incident frequency, length-width ratio and depth-width ratio of the basin on the ground motion are investigated in detail. The numerical results show that the basin shape has a significant impact on the amplification effect of seismic waves and the spatial distribution characteristics, and the detail effect also strongly depends on the frequency band of incident wave. In particular, as the basin depth increases, edge-generated surface waves become dominant, significant ground motion amplification effect can be observed for a wider band, and amplification area is mainly located in the middle of basin. The seismic wave focusing effect within the circular basin seems most significant, while that within long-narrow basin seems relatively weak, and multiple wave-focused areas appear within the basin for incident high-frequency waves. The amplification mechanism of basin effect on ground motion is different for different types of waves: for incident P waves, significant amplification of vertical displacement in the middle of basin can be mainly attributed to the focusing of surface waves generated from the basin edge; as for SV wave incidence, the surface wave focusing effect is relatively weak, but when the basin is deep, constructive interference of transmitted body waves and edge surface waves tend to result in a considerable amplification effect. For the wave-velocity ratio 1/2 between the alluvial basin and the bedrock, amplification factors of P and SV waves can reach up to 25, 15, respectively in frequency domain, and to 4.0, 3.7, respectively in time domain (Ricker waves). As for the low frequency waves, the displacement amplitude decreases from the basin center to basin edge, and the amplification is not obvious for the shallow basin. In addition, the angle of incidence also has significant impact on the amplitude and spatial distribution characteristics of ground motion.
- basin-edge effect /
- seismic wave /
- scattering /
- indirect boundary element method (IBEM) /
- focusing effect

HTML全文

引言

面波勘探也称为弹性波频率探测，是二十世纪末发展起来的一种浅层地震勘探方法，主要是对地震波到达弹性、速度或密度不同的界面时所产生的沿表面传播的界面波进行探测（刘庆华等，2015），其中瑞雷波在面波中能量最强、振幅最大、频率最低，容易识别且易于测量，因此一般被当作面波勘探的主要有效信号。Rayleigh （1885）最早通过研究P波与SV波在自由表面的相互作用证明了瑞雷波的存在，此外还发现瑞雷波振幅在水平向随距离增加的衰减慢于体波，垂向上随深度增加而呈指数衰减，并且具有波速小于体波、传播时引起表面质点逆时椭圆运动的特点。通过对探测到的瑞雷波提取频散曲线可反演地下结构，从而获得地下介质物性参数（Haskell，1953），因此瑞雷波勘探被广泛应用于地球结构探测（李白基等，1989；冯梅等，2008；陈浩朋等，2012）、工程勘察（沈玉松，康英，2014）及各种无损检测（Chai et al，2010）。

瑞雷波勘探方法按瑞雷波信号来源的不同分为主动源法和被动源法。主动源法中，发震时间、地震波频率、波动能量等参数需人为控制，起震方式要求较为严格，成本也相对较高；被动源法则利用天然地震或噪声进行勘探，因其对起震方式要求更为宽泛，勘探成本较低，现逐步成为常用的勘探方法。基于主动源和被动源发展而来的分析方法众多（Aki，1957；Jones，1958；Capon，1970；Park，Miller，2008；房立华等，2013；王小龙等，2013），其中多道瞬态面波分析方法（multi-channel analysis of surface waves，缩写为MASW）因其排列简单、抗干扰能力强而被广泛应用，并且由于该方法处理主动源和被动源数据的技术壁垒逐渐被打破，其在作业成本、施工难度、数据处理等方面具有技术优势（夏江海等，2015），在工程应用中的前景也变得更为广阔。

通常，MASW方法多利用地表震源激发的地震信号或背景噪声来获取地下介质信息，其观测系统中的最小偏移距（震中与第一个检波器之间的距离）是控制近场效应的关键参数，它直接决定着勘探数据质量，进而影响频散图像的分辨率、探测深度和反演结果的可信度（刘康等，2018）。以往的大多数研究均基于水平地层进行，对于倾斜地层地下震源产生瑞雷波的地表最小偏移距的研究尚不够广泛和深入。例如：Stokoe等（1994）初步建议水平地层最佳偏移距约为瑞雷波波长的1.5倍；Zhang等（2004）根据相速度范围和场地界面深度的关系绘制了频散图像，并通过评价不同采集参数下频散图像的一致性和可靠性提出了水平地层最近和最远接收点的偏移距公式；Xu等（2006）对双层介质中震源与接收偏移距的关系进行理论分析，建立了地表震源水平层状弹性模型的偏移距定量计算公式；Dikmen等（2010）通过评估最小偏移距和检波器配置对MASW方法中频散图像分辨率的影响确定了最小偏移距应为三四倍道间距或三分之一排列长度；席超强（2017）对倾斜地层地表震源激发面波中排列参数与面波频散能量团收敛程度的研究也为复杂地形瑞雷波勘探的偏移距选择提供了参考；Dai等（2019）通过研究检波器布设参数对瑞雷波能量的显著性和频散分辨率的影响程度，提出了水平地层埋置震源的地表瑞雷波接收最小偏移距公式。

上述关于MASW方法排列参数的研究多基于地表震源且对象多为水平层状介质，而倾斜地层形成的边坡作为人类工程活动中最基本的地质环境之一，目前研究较少。随着我国地下能源探测及开采的不断深入，以浅表采矿为例，掘进机、破碎机、运输机等机械进行施工作业的同时也可作为地下震源产生向地表传播的地震波，其携带的下部介质的剪切波速、基频和介质泊松比等信息可为浅地表的工程开发提供选址参考。这种利用已有条件进行的瑞雷面波探测可以降低勘探作业的难度和成本，具有较大的应用价值。然而目前关于瑞雷波在边坡中的传播规律以及倾斜边坡多道面波分析中最小偏移距的确定方法鲜见可参考的公开资料。鉴于此，本文拟通过分析地下震源产生瑞雷波的机制，提出倾斜边坡多道面波分析中最小偏移距的估计公式，并通过数值模拟对其进行验证，以探讨该方法的有效性，进一步拓展MASW方法的应用场景。

1. 边坡地层波传规律分析

1.1 边坡地形

自然界中，地下介质总体呈层状叠加的形态，为便于研究，通常将其简化为水平层状的理想介质。地下岩层受到地质作用和人类活动的改造，逐渐形成形态多样的边坡。本文重点考虑多道面波分析方法在倾斜边坡地形中的应用，分两种情况讨论倾斜边坡上瑞雷波最小偏移距估计方法：如图1所示，以向右为正方向，第一类为地层沿正向上倾，第二类为地层沿正向下倾。

图 1 倾斜边坡示意图

（a）上倾边坡；（b）下倾边坡

Figure 1. Schematic diagram of slopes

（a） Updip slope；（b） Downdip slope

下载: 全尺寸图片幻灯片

1.2 地下震源产生的地震波传播

由波动地震学可知，当SV波沿介质传播至地表满足sinα＝v_S/v_P （α为入射角）时会发生全反射并出现波型转换，其中沿自由界面传播的非均匀P波与反射SV波相互作用形成瑞雷波（Ewing et al，1957；Lay，Wallace，1995）。此时地表入射点可作为瑞雷波最先形成的位置（即最小偏移距），在此处布设第一个检波器即可检测到瑞雷波。

1.2.1 上倾边坡情形下的瑞雷波最小偏移距

分别建立单层上倾边坡和多层上倾边坡模型（图2），采用波场高阶近似的射线理论对瑞雷波的传播进行研究。根据几何地震学进行以下推导：

图 2 单层（a）与多层（b）上倾边坡示意图

Figure 2. Schematic diagram of single-layer （a） and multi-layer （b） updip slopes

下载: 全尺寸图片幻灯片

对于单层上倾边坡（图2a），在△ABC中，

$${\text{∠}} BAC ＝ \pi － \left(\frac{\pi }{2} - \alpha \right) － \left(\frac{\pi }{2} ＋ \beta \right) ＝ \alpha － \beta ， $$

(1)

由正弦定理可知

$$ \frac{h}{{\sin \left(\dfrac{\pi }{2} － \alpha \right)}} ＝ \frac{d}{{\sin （\alpha － \beta ）}} ，$$

(2)

由此可得

$$ d ＝ h\frac{{\sin （\alpha － \beta ）}}{{\cos \alpha }} ＝ h（\tan \alpha \cos \beta － \sin \beta ）， $$

(3)

式中d为最小偏移距，h为震源埋深，α为地表入射临界角，β为地层倾斜角。

多层上倾边坡（图2b）的偏移距可由多个单层上倾边坡偏移距叠加而得，即

$$ \begin{split} d ＝& h_1\frac{{\sin （{\alpha _1} －\beta ）}}{{\cos {\alpha _1}}} ＋ h_2\frac{{\sin （{\alpha _2} －\beta ）}}{{\cos {\alpha _2}}} ＋ \cdots ＋ h_i \frac{{\sin （{\alpha _i} － \beta ）}}{{\cos {\alpha _i}}} ＋ \cdots ＋ \\&\qquad h_n \frac{{\sin （{\alpha _n} － \beta ）}}{{\cos {\alpha _n}}} ＝\sum\limits_{i ＝ 1}^n {{h_i}}（\tan {\alpha _i}\cos \beta － \sin \beta ）， \end{split}$$

(4)

式中d为最小偏移距，h_i为第i层介质厚度，α_i为第i层地层上表入射角，β为地层倾斜角。

由式（4）可知最小偏移距与下覆地层厚度、地层倾斜角和入射角有关。在下覆地层中以S波速度v_S为桥梁，结合地表产生瑞雷波的条件（sinα＝v_S/v_P）和斯奈尔（Snell）定律可将式（4）改写为

$$ d ＝ \sum\limits_{i ＝ 1}^n {{h_i}} \left(\frac{{{v_{{\rm{S}}i}}}}{{\sqrt {v_{\rm{P}}^2 － v_{{\rm{S}}i}^2} }} \cos \beta － \sin \beta \right) ， $$

(5)

式中v_Si为第i层介质S波波速，v_P为第一层介质P波波速。

1.2.2 下倾边坡情形下的瑞雷波最小偏移距

同理，对于单层下倾边坡（图3a），在△ABC中，

图 3 单层（a）与多层（b）下倾边坡示意图

Figure 3. Schematic diagram of a single-layer （a） and multi-layer （b） downdip slopes

下载: 全尺寸图片幻灯片

$$ {\text{∠}} BAC ＝ \alpha ＋ \beta ， $$

(6)

由正弦定理可得

$$ d ＝ h\frac{{\sin （\alpha ＋ \beta ）}}{{\cos \alpha }} ＝ h（\tan \alpha \cos \beta ＋ \sin \beta ）， $$

(7)

对单层下倾边坡的最小偏移距累加可得多层下倾边坡（图3b）的最小偏移距为

$$ d ＝ \sum\limits_{i ＝ 1}^n {{h_i}} \left(\frac{{{v_{{\rm{S}}i}}}}{{\sqrt {v_{{\rm{P}}i}^2 － v_{{\rm{S}}i}^2} }}\cos \beta ＋ \sin \beta \right) {\text{.}} $$

(8)

综上，对于上倾边坡和下倾边坡，瑞雷波最小偏移距公式进行整合得到

$$ d ＝ \sum\limits_{i ＝ 1}^n {{h_i}} \left(\frac{{{v_{{\rm{S}}i}}}}{{\sqrt {v_{{\rm{P}}i}^2 － v_{{\rm{S}}i}^2} }}\cos \beta \mp \sin \beta \right) \qquad（上倾取－，下倾取＋） {\text{.}} $$

(9)

Dai等（2019）曾提出多层水平地层瑞雷波最小偏移距为

$$ d ＝ \sum\limits_{i ＝ 1}^n {\frac{{{h_i}{v_{{\rm{S}}i}}}}{{\sqrt {v_{{\rm{P}}1}^2 － v_{{\rm{S}}i}^2} }}} ，$$

(10)

当倾斜度β＝0时式（9）即化简为式（10），表明本文推导的最小偏移距公式涵盖水平地层和倾斜地层，具有应用的一般性。

同时，弹性波中v_S，v_P与泊松比σ的关系（刘康等，2018）为

$$ \frac{{{v_{\text{S}}}}}{{{v_{\text{P}}}}} = \sqrt {\frac{{2 - 2\sigma }}{{1 - 2\sigma }}} \text{，} $$

(11)

因此式（9）可改写为

$$ d {\text{≈}} h\Biggr(\dfrac{1}{{\sqrt{\dfrac{{2 － 2{\sigma _1}}}{{1 － 2{\sigma _1}}}\cdot \dfrac{1}{{\kappa _n^2}} － 1} }} \cos \beta {\mp} \sin \beta \Biggr) ， $$

(12)

式中，σ₁为第一层介质的泊松比，κ_n为S波波速比v_Sn/v_S1，h为震源深度。对于浅表地层，介质泊松比σ的取值区间多为0.35—0.45，分别以5 m和25 m深度处地层的剪切波速作为v_S1和v_Sn，则剪切波速比κ_n的取值区间多在1.22—1.72之间（刘康等，2018）。对两者取平均值，即σ₁＝0.4，κ_n＝1.47，将其代入式（12），则

$$ d {\text{≈}} 1.25h\sin \left( \mp \beta ＋ \frac{\pi }{5}\right) \qquad （上倾取－，下倾取＋）{\text{.}} $$

(13)

由式（13）可知，给定地下震源深度与地层倾斜角即可估算地下震源在倾斜边坡地表产生瑞雷波的位置。如果地层中存在断层、不整合面、采空区等，会造成地震波的绕射，利用上式计算结果会存在较大偏差，但在实际工程勘察中仍可作为最小偏移距的近似估计来指导检波器的布设，由此在该偏移距附近或更远处获得能量占比可观的面波数据。

2. 数值模拟

目前尚未提出瑞雷波在浅层复杂介质中的解析解，因此本文采用数值模拟对其进行研究。常用的数值模拟方法为有限差分法（Isaacs，1941）、有限单元法（Malavika et al，2021）和谱单元法（Komatitsch et al，2012；Cristini，Komatitsch，2012）等。因为有限差分法原理简单、便于建模，因此本文利用该方法建立边坡模型进行验算，从数值模拟的角度探讨倾斜边坡瑞雷波形成及传播机制，以验证上文提出的最小偏移距估算公式。

分别建立水平、上倾、下倾地层模型，相关参数列于表1，模型左右为吸收边界以避免边界反射所造成的影响。震源位于地下25 m处，与左边界相距50 m，采用雷克子波单炮激发，频率为30 Hz。

表 1 本文所用模型的地层参数

Table 1. Stratum parameters of the models used in this study

层位	厚度/m	v_P/（m·s⁻¹）	v_S/（m·s⁻¹）
①	4	480	200
②	6	600	247
③	半无限空间	750	294
注：地层③因倾斜角度从左至右厚度变化，不作统计。

下载: 导出CSV

| 显示表格

2.1 水平地层模型验证

在水平地层模型（图4a）地表布设接收道集获得初至波共炮点（common shot point，缩写为CSP）记录（图4b）。

图 4 多层水平地层示意图（a）及其共炮点记录（b）

Figure 4. Schematic diagram of a multi-layer horizontal strata （a） and its common shot point gathers （b）

下载: 全尺寸图片幻灯片

假定土层为层状连续介质，选取地下震源对应的地表位置为零偏移点，将地层参数带入式（9）可得理论最小偏移距d＝17.03 m。为接收到更有效的瑞雷波信号，最小偏移距应大于该理论值，因此对其取整为18 m。

对上述150道共炮点数据进行抽道选排，提取零偏移距右侧不同偏移距对应质点运动轨迹组成偏振图，如图5所示。可见：偏移距小于12 m时质点为不规则运动；当偏移距为18 m时质点轨迹呈初步椭圆化，表明瑞雷波开始发育，与理论值吻合；当偏移距继续增大时，质点轨迹椭圆化趋于稳定，表明瑞雷波已较为发育。利用式（13）计算最小偏移距估计值并取整可得d≈19 m。

图 5 不同偏移距d下水平地层地表的质点偏振图

Figure 5. Polarization map of surface particles in horizontal strata with different offset d

下载: 全尺寸图片幻灯片

利用f-k法（Capon，1970）选取不同偏移距范围内的地震道数据计算得到其频散结果（图6），以期通过对比频散分辨率来分析最小偏移距对勘探数据的影响。由图6可知：当偏移距为0—12 m时，频散图的分辨率很差，未形成提取频散曲线（ f-v）的能量团；当偏移距为19 m时，频散开始出现，与估计值吻合；随着偏移距增大，频散分辨率逐步提高。由于偏移距大于40 m之后瑞雷波较为发育，以偏移距为49—65 m的稳定频散为参照，偏移距处于0—35 m之间的频散与稳定频散特征相差较大，而19—35 m范围的频散已开始接近稳定频散，表明偏移距小于19 m的地震数据对面波频散的贡献微弱，因此通过式（13）来计算偏移距的估计方法可以应用。此外，对比图6上行的三个子图可知，排列起点相同时，随着排列长度的增加，频散分辨率逐渐提高；对比图6下行的三个子图可知，一定范围内当排列长度相同时，随着偏移距的增大，体波的近场效应逐渐减弱，因此瑞雷波的频散特征趋于稳定。

图 6 不同偏移距d范围内的水平地层频散计算图

Figure 6. Dispersion calculation diagram of horizontal strata with different offset d

下载: 全尺寸图片幻灯片

2.2 上倾边坡验证

同理建立上倾边坡模型（图7a），其地层速度参数与水平地层相同，地层倾斜角取为π/18，以相同震源激发获得地表初至波共炮点记录（图7b）。利用式（9）可得上倾边坡最小偏移距理论值，取整得d≈13 m。绘制不同偏移距质点运动轨迹偏振图，如图8所示。

图 7 多层上倾边坡示意图（a）及其共炮点记录（b）

Figure 7. Schematic diagram of a multi-layer updip slope （a） and its common shot point gathers （b）

下载: 全尺寸图片幻灯片

图 8 不同偏移距d范围内上倾边坡地表质点偏振图

Figure 8. Polarization map of surface particles on updip slope with different offset d

下载: 全尺寸图片幻灯片

对偏振图（图8）进行分析可得：当偏移距d为6 m时，偏振图表示的质点运动轨迹不规则；当偏移距增至13 m后，椭圆偏振初步形成，表明瑞雷波在此处已经发育，与理论值吻合；随着偏移距继续增大，质点轨迹总体呈椭圆，表明瑞雷波已较为发育。利用式（13）计算上倾边坡最小偏移距估计值并取整得d≈14 m。

对共炮点记录进行频散分析（图9）可知：当偏移距d为0—8 m时几乎未呈频散特征；偏移距为14 m时出现频散特征，与估计值吻合；进一步增大偏移距可看到频散分辨率提高，表明瑞雷波更为发育。以偏移距为40—60 m的频散为参考，偏移距为0—30 m的频散特征与稳定频散的差异相对较大，而偏移距为14—30 m的频散特征与稳定频散已较为接近，证明了估计值的可靠性，同时可见上倾边坡瑞雷波检测中的最小偏移距相较水平地层有所减小。

图 9 不同偏移距d范围内的上倾边坡频散计算图

Figure 9. Dispersion calculation diagram of updip slope with different offset d

下载: 全尺寸图片幻灯片

2.3 下倾边坡验证

采用相同的地层参数建立下倾边坡（图10a），地层倾斜角为π/18，同时获得地表初至波CSP记录（图10b）。采用式（9）计算下倾边坡最小偏移距的理论值并取整得d≈21 m。提取地表质点运动轨迹得到偏振图，如图11所示。可见：当偏移距小于21 m时，质点轨迹椭圆化现象不明显；当偏移距增至21 m后可看到椭圆偏振形成，表明瑞雷波已在此发育。

图 10 多层下倾边坡示意图（a）及其共炮点记录（b）

Figure 10. Schematic diagram of a multi-layer downdip slope （a） and its common shot point gathers （b）

下载: 全尺寸图片幻灯片

图 11 不同偏移距d范围内下倾边坡地表质点偏振图

Figure 11. Polarization map of surface particles on downdip slope with different offset d

下载: 全尺寸图片幻灯片

利用式（13）计算下倾边坡最小偏移距的估计值并取整得d≈23 m。同理对共炮点记录进行频散分析，结果如图12所示，可见：当偏移距与估计值相差较大时频散分辨率很差；当偏移距等于或大于估计值时频散分辨率较高且频散能量集中。这证明了最小偏移距估计方法的可靠性，同时发现下倾边坡瑞雷波检测中的最小偏移距相较于水平地层有所增大。

图 12 不同偏移距d范围内的下倾边坡频散计算图

Figure 12. Dispersion calculation diagram of downdip slope with different offset d

下载: 全尺寸图片幻灯片

综上所述，本文推导的地下震源在倾斜边坡地表产生瑞雷波的最小偏移距估计公式兼容了前人建立的水平地层瑞雷波最小偏移距估计公式，其可靠性通过数值模拟也得以验证，实现了常见地层形态下面波最小偏移距的估算。

3. 讨论与结论

本文基于瑞雷波最小偏移距的研究，推导了地下震源在倾斜边坡地表产生瑞雷波的最小偏移距经验公式，建立了三种常见形态的地层模型，对获得的模拟共炮点记录进行了质点运动轨迹分析和频散计算，得到的结论如下：

1）对比地表质点运动轨迹绘制的偏振图、频散计算结果与理论值和经验估计值可知，四者相对偏差在3 m以内，吻合较好，从而验证了本文经验公式的可靠性。

2）相比于水平地层，上倾边坡的最小偏移距减小，下倾边坡的最小偏移距增大，表明地层形态对瑞雷波最小偏移距具有一定程度的影响。

3）对于瑞雷波的频散计算，排列起点相同时，排列长度越大，瑞雷波数据的频散分辨率越高；在一定范围内，排列长度相同时，偏移距越大，体波近场效应影响越小，瑞雷波频散特征稳定程度越高。

通过本文的研究将前人水平地层面波分析中最小偏移距的经验估计方法拓展至层状倾斜边坡中，进一步扩大了工程应用场景，为野外面波实测中检波器的布设提供了理论支撑和实际指导。此外，由于地下工况的复杂性，对更复杂地形下多道面波分析中最小偏移距的估计方法尚待进一步研究。

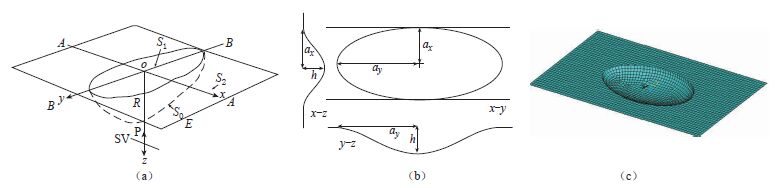
图 1 三维沉积盆地计算模型

(a)三维视图，图中R为沉积盆地域，E为半空间域，S₀为沉积域与基岩半空间域的交界面，S₁为沉积内部地表，S₂为外部半空间地表；(b)平面投影和竖向剖面；(c)单元网格离散

Figure 1. Calculation model for a three-dimensional alluvial basin

(a)Three-dimensional view. R is the sedimentary basin domain，E is a half-space domain，S₀ is the interface between the sedimentary basin domain and bedrock half-space domain，S₁ is the surface of sedimentary basin interior，and S₂ is the surface of outer half-space;(b)Planar projection and vertical section;(c)Element discretization

下载: 全尺寸图片幻灯片

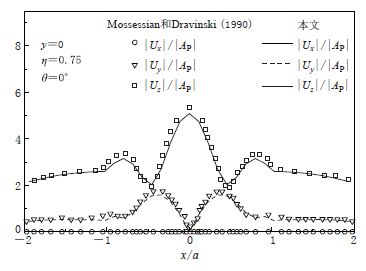
图 2 本文结果与Mossessian和Dravinski(1990)所得地表位移幅值的对比

Figure 2. Surface displacement amplitudes of a hemisphere alluvial valley in half-space for P wave incidence in this paper compared with the results of Mossessian and Dravinski(1990)

下载: 全尺寸图片幻灯片

图 3 半球形沉积盆地时域结果

Figure 3. The time domain results for a semi-spherical alluvial basin

下载: 全尺寸图片幻灯片

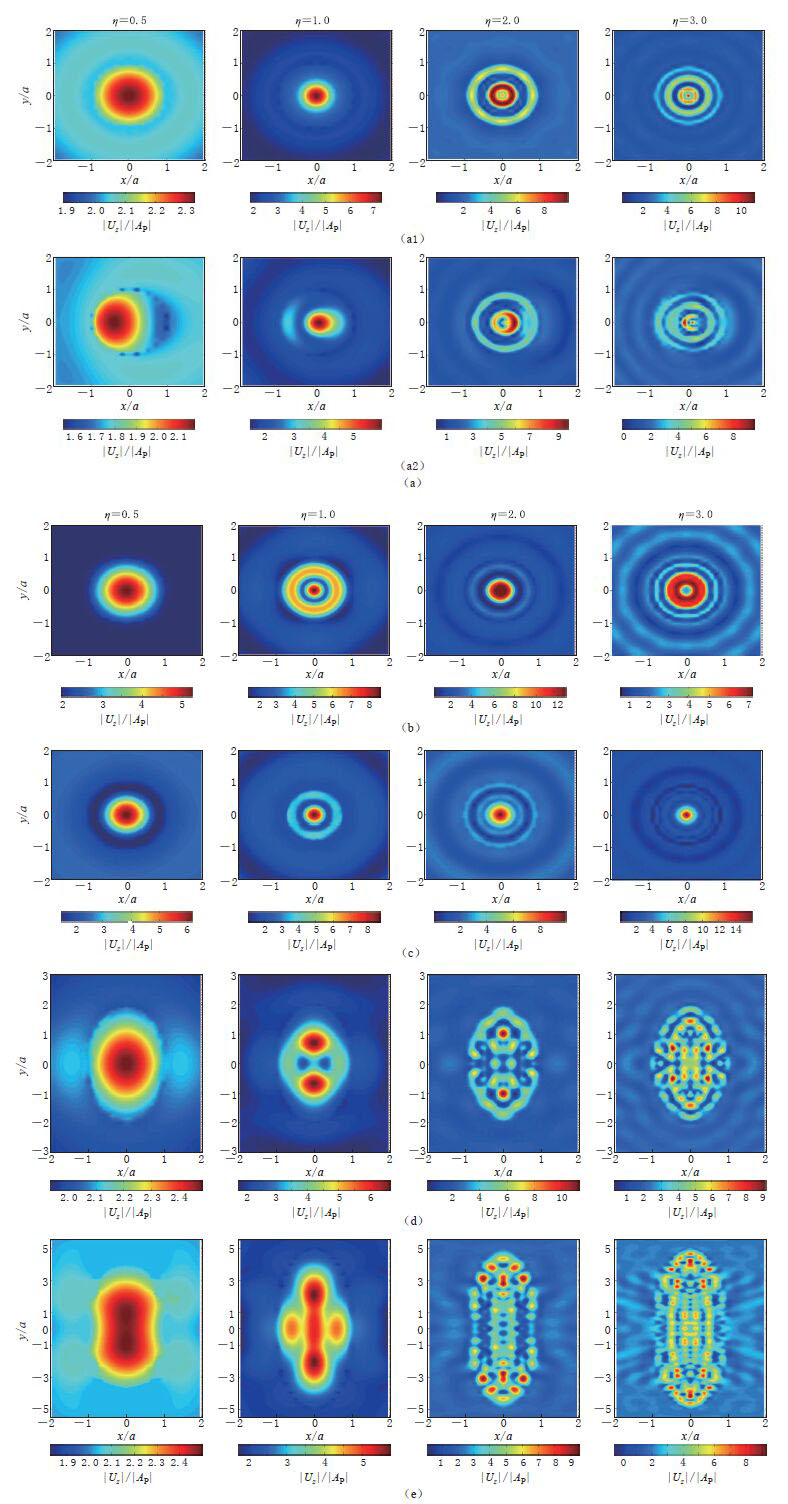
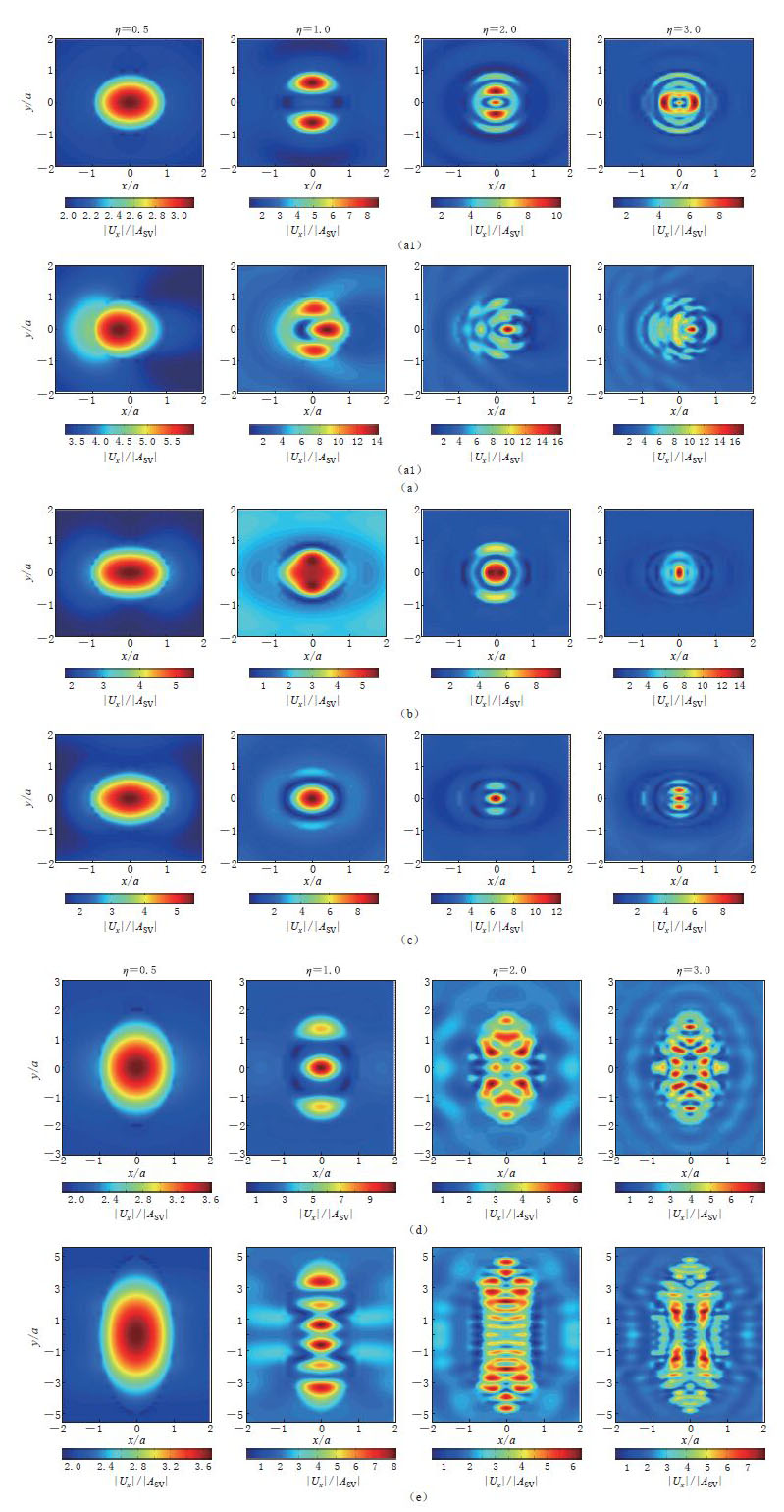
图 4 P波入射下不同深宽比S、长宽比D沉积盆地的地表位移幅值云图

(a)D=1.0，S=0.5，a_z/a_x=0.5(浅椭球盆地)：(a1)垂直入射(θ=90°)，(a2)斜入射(θ=60°)(b)D=1.0，S=1.0，a_z/a_x=1.0(半球沉积盆地);(c)D=1.0，S=2.0，a_z/a_x=2.0(深椭球盆地); (d)D=2.0，S=0.5，a_y/a_x=2.0(较狭长盆地);(e)D=5.0，S=0.5，a_y/a_x=5.0(狭长盆地)

Figure 4. The surface displacement amplitude cloud images in alluvial basin with different depth-width ratios S and length-width ratios D for incident P waves

(a)D=1.0，S=0.5，a_z/a_x=0.5(shallow ellipsoid basin)： (a1)Vertical incidence(θ=90°)，(a2)Oblique incidence(θ=60°)(b)D=1.0，S=1.0，a_z/a_x=1.0(hemispheric sedimentary basin);(c)D=1.0，S=2.0，a_z/a_x=2.0(deep ellipsoid basin);(d)D=2.0，S=0.5，a_y/a_x=2.0(narrower basin);(e)D=5.0，S=0.5，a_y/a_x=5.0(narrow basin)

下载: 全尺寸图片幻灯片

图 5 SV波入射下不同深宽比S、长宽比D沉积盆地的地表位移幅值云图

(a)D=1.0，S=0.5，a_z/a_x=0.5(浅椭球盆地):(a1)垂直入射(θ=90°)，(a2)斜入射(θ=60°); (b)D=1.0，S=1.0，a_z/a_x=1.0(半球沉积盆地);(c)D=1.0，S=2.0，a_z/a_x=2.0(深椭球盆地); (d)D=2.0，S=0.5，a_y/a_x=2.0(较狭长盆地);(e)D=5.0，S=0.5，a_y/a_x=5.0(狭长盆地)

Figure 5. The surface displacement amplitude cloud images in alluvial basin with different depth-width ratios S and length-width ratios D for incident SV waves

(a)D=1.0，S=0.5，a_z/a_x=0.5(shallow ellipsoid basin):(a1)Vertical incidence(θ=90°)，(a2)Oblique incidence(θ=60°);(b)D=1.0，S=1.0，a_z/a_x=1.0(hemispheric sedimentary basin);(c)D=1.0，S=2.0，a_z/a_x=2.0(deep ellipsoid basin)(d)D=2.0，S=0.5，a_y/a_x=2.0(narrower basin);(e)D=5.0，S=0.5，a_y/a_x=5.0(narrow basin)

下载: 全尺寸图片幻灯片

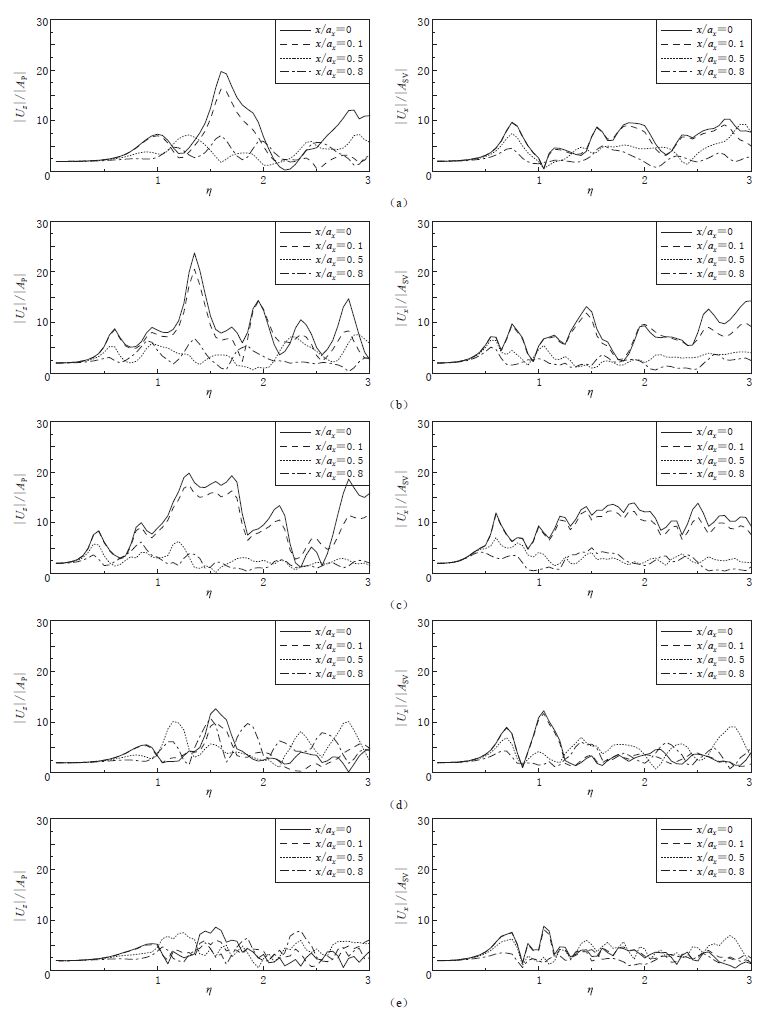
图 6 P波(左)和SV波(右)入射下不同深宽比S、长宽比D沉积盆地地表x轴上(y=0)的位移幅值谱

(a)D=1.0，S=0.5(浅椭球盆地)；(b)D=1.0，S=1.0(半球沉积盆地)；(c)D=1.0，S=2.0(深椭球盆地)；(d)D=2.0，S=0.5(较狭长盆地)；(e)D=5.0，S=0.5(狭长盆地)

Figure 6. The displacement amplitude spectrum along x-axis(y=0)in alluvial basins with different depth-width S and length-width ratios D for incident P(left panels)and SV(right panels)waves

(a)D=1.0，S=0.5(shallow ellipsoid basin);(b)D=1.0，S=1.0(hemispheric sedimentary basin);(c)D=1.0，S=2.0(deep ellipsoid basin);(d)D=2.0，S=0.5(narrower basin);(e)D=5.0，S=0.5(narrow basin)

下载: 全尺寸图片幻灯片

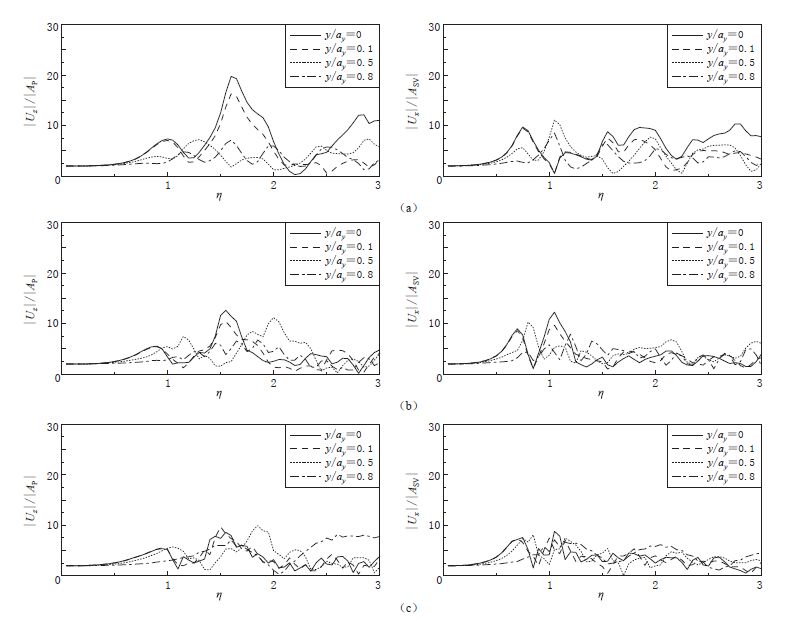
图 7 P波(左)和SV波(右)入射下深宽比S=0.5时不同长宽比D沉积盆地地表y轴(x=0)上的位移幅值谱

(a)D=1.0(浅椭球盆地)；(b)D=2.0(较狭长盆地)；(c)D=5.0(狭长盆地)

Figure 7. The displacement amplitude spectrum along y-axis(x=0)in alluvial basins with depth-width ratio S=0.5 and different length-width ratios D for incident P(left panels)and SV(right panels)waves

(a)D=1.0(shallow ellipsoid basin);(b)D=2.0(narrower basin);(c)D=5.0(narrow basin)

下载: 全尺寸图片幻灯片

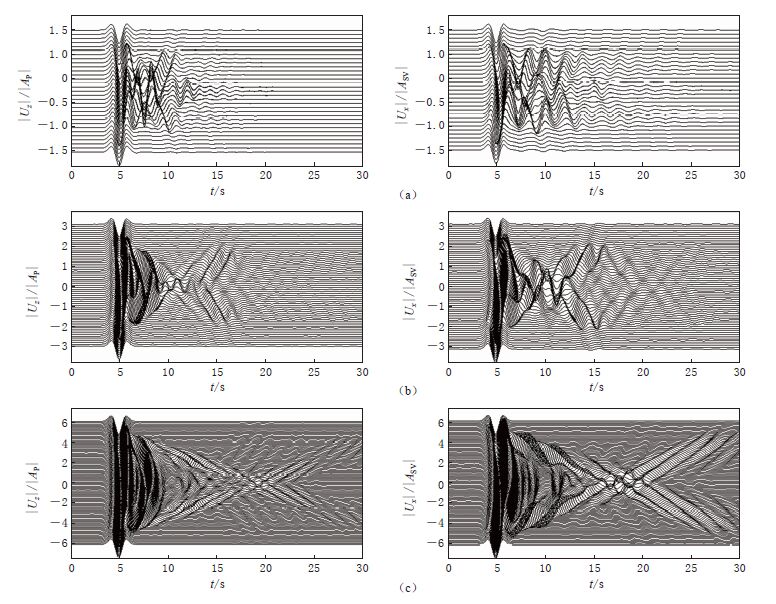
图 8 P波(左)和SV波(右)入射下不同深宽比S、长宽比D沉积盆地地表在x轴上(y=0)的位移时程(雷克子波型脉冲)

(a)D=1.0，S=0.5(浅椭球盆地)；(b)D=1.0，S=1.0(半球沉积盆地);(c)D=1.0，S=2.0(深椭球盆地);(d)D=2.0，S=0.5(较狭长盆地);(e)D=5.0，S=0.5(狭长盆地)

Figure 8. The surface displacement time history along x-axis(y=0)in alluvial basins with different depth-width ratios S and length-width ratios D for incident P(left panels)and SV waves(right panels)(Ricker pulse)

(a)D=1.0，S=0.5(shallow ellipsoid basin);(b)D=1.0，S=1.0(hemispheric sedimentary basin);(c)D=1.0，S=2.0(deep ellipsoid basin);(d)D=2.0，S=0.5(narrower basin);(e)D=5.0，S=0.5(narrow basin)

下载: 全尺寸图片幻灯片

图 9 P波(左)、 SV波(右)入射下，深宽比S=0.5、不同长宽比D沉积盆地地表y轴上(x=0)的位移时程(雷克型脉冲)

(a)D=1.0(浅椭球盆地)；(b)D=2.0(较狭长盆地);(c)D=5.0(狭长盆地)

Figure 9. The surface displacement time history along y-axis(x=0)in alluvial basins with depth-width ratios S=0.5 and different length-width ratios D for incident P wave (left panels)and SV wave(right panels)(Ricker pulse)

(a)D=1.0(shallow ellipsoid basin);(b)D=2.0(narrower basin);(c)D=5.0(narrow basin)

下载: 全尺寸图片幻灯片

图 10 Tar-Tarzana波加速度时程

Figure 10. Acceleration time history of Tar-Tarzana wave

下载: 全尺寸图片幻灯片

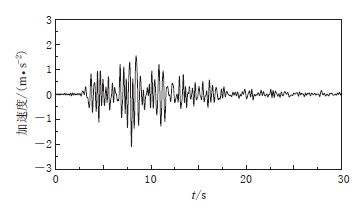
图 11 Tar-Tarzana波(SV波)垂直入射下不同深宽比S、长宽比D三维沉积盆地内部典型点位水平向(y=0)加速度反应谱

Figure 11. Acceleration response spectrum in horizontal direction(y=0)of typical points within the 3D alluvial basins with different depth-width ratio S and length-width ratio D for incident Tar-Tarzana waves with θ=90°

(a)S=0.5，D=1.0;(b)S=1.0，D=1.0;(c)S=0.5，D=2.0

下载: 全尺寸图片幻灯片

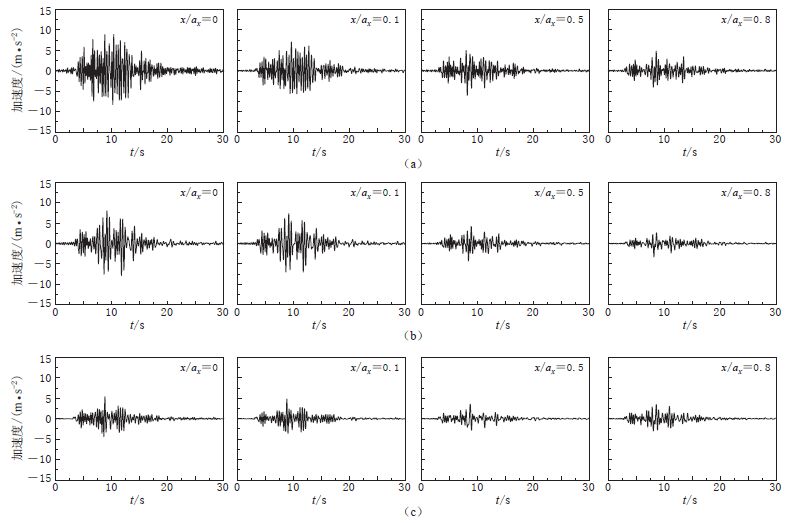
图 12 SV波入射下沉积盆地地表(y=0)加速度时程(输入Tar-Tarzana地震波)

(a)S=0.5，D=1.0(浅椭球盆地)；(b)S=1.0，D=1.0(半球沉积盆地); (c)S=0.5，D=2.0(较狭长盆地)

Figure 12. The acceleration time histories along x-axis within the alluvial basin for incident SV waves(Tar-Tarzana wave)

(a)S=0.5，D=1.0(shallow ellipsoid basin);(b)S=1.0，D=1.0(hemispheric sedimentary basin);(c)S=0.5，D=2.0(narrower basin)

下载: 全尺寸图片幻灯片

参考文献(40)

陈学良, 高孟潭, 李铁飞. 2011. Rayleigh面波作用下盆地场地响应特性研究[J]. 土木建筑与环境工程, 33(S2): 29-33. http://www.cnki.com.cn/Article/CJFDTOTAL-JIAN2011S2008.htm

Chen X L, Gao M T, Li T F. 2011. Study on response characteristics of basin site under the action of Rayleigh surface wave[J]. Journal of Civil, Architectural & Environmental Engineering, 33(S2): 29-33 (in Chinese).

高孟潭, 俞言祥, 张晓梅, 吴健, 胡平, 丁彦慧. 2002. 北京地区地震动的三维有限差分模拟[J]. 中国地震, 18(4): 356-364. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD200204004.htm

Gao M T, Yu Y X, Zhang X M, Wu J, Hu P, Ding Y H. 2002. Three-dimensional finite-difference simulations of ground motions in the Beijing area[J]. Earthquake Research in China, 18(4): 356-364 (in Chinese).

景立平, 卓旭炀, 王祥建. 2005. 复杂场地对地震波传播的影响[J]. 地震工程与工程振动, 25(6): 16-23. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200506003.htm

Jing L P, Zhuo X Y, Wang X J. 2005. Effect of complex site on seismic wave propagation[J]. Earthquake Engineering and Engineering Vibration, 25(6): 16-23 (in Chinese). http://www.baidu.com/link?url=-fnDdqs84uD6IXgyf-VoKt6SHHlz5TfA9m-RedQFTyBbTYD7gA4UDlgzdlyEfJ18sepuI2jogbswlmREy3ZALcrONhLILAPc_X5qEW_aBC3sCLao52vvIFPICHTdAA83CzNXy-0WMiSs0BkCOMoktEraghGBDA43Wo8xAoNvn1vXSRbpI4SAQoq5Avk1U81D5ycK5lpetA43yx2Cd89IpGbwMPA8ZlYf7mOXy8uw13LMEpBauNKpm0c7KC_9QY2MDvYq1IOzsS7xljRiSooCqCF7IyPdwEpILRkUO1-pRY_NZRlY5HgUF6vRcmgZeOod&wd=&eqid=b49ead330002ecb60000000558808a8e

李铁飞, 陈学良, 高孟潭. 2013. 盆地场地效应的三维数值模拟研究进展及沉积环境对盆地场地的影响[J]. 世界地震工程, 29(3): 128-138. http://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201303020.htm

Li T F, Chen X L, Gao M T. 2013. Research progress of basin site effect based on 3D numerical simulation and influence of sedimentary environment on basin site[J]. World Earthquake Engineering, 29(3): 128-138 (in Chinese). http://www.baidu.com/link?url=3EcAiUVd01sANMUSRcf8RiczFP7JUtMzcky8YTyvjdkfRhHeT5iX3kfsuJ93ncfAzmuDAF35W-LANnME_GwnU1gaMPNw85trtwiUx0s0QK-EvLH7Oy76CX91TUyXQP1oJcu_NvraPvgZdQNouo6cy18Hxm3k3Ts_nf5zBFFbOPSEwZ3DjxKLF7tXEBOuIioYSvpCj9HVmMpXMFZoQ-iB_3LR4uCffro3t6MC0jr559ubZDHyn_1EgepbabZlo8fAtjf5IC9d7FMDgv7_xz3JVMhshS63UhgNgDq0D31ApPp7tYeEF7pWYCj686tNYrFMMNmWbVs2IBYqGL22xfMtd2tQ1TivUmTuWUrs3yOWDpjGaofNFc_yodoS0UEXOTDAEjHTtHm1WRVEGF1uY65ZvpkMJEE3BZG-QwDuj_zrrlm&ie=utf-8&f=8&tn=30009039_2_pg&wd=Research%20progress%20of%20basin%20site%20effect%20based%20on%203D%20numerical%20simulation%20and%20influence%20of%20sedimentary%20environment%20on%20basin%20site&oq=Research%20progress%20of%20basin%20site%20effect%20based%20on%203D%20numerical%20simulation%20and&rqlang=cn&inputT=611

梁建文, 张郁山, 顾晓鲁. 2003. 圆弧形层状凹陷地形对平面SH波的散射[J]. 振动工程学报, 16(2): 158-165. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC200302005.htm

Liang J W, Zhang Y S, Gu X L. 2003. Scattering of plane SH waves by a circular-arc layered canyon[J]. Journal of Vibration Engineering, 16(2): 158-165 (in Chinese). http://www.baidu.com/link?url=mnlHjGB9K4e0RNHABTTEwZYv-mLbi8XWRibt1lwfIS88x_cPg56OcNB7t3kc0OYb8z30mQ5Vrt-2CQfruhk6CmHt5ySrAswggI3UbAYb9WSl0QoS-4aj5_CgsAQFearS7TrlfkL1boIGsvop-mHo94-j436J-Sct_uYv9VC37I7DsRjcFhm0JgmE4PquvDmRdj0aUrGXzRW4xj5VorylDuJR5xA9A0-3lNEg_DMsj9O1I_3pOQeT4gZbArl4WUDEi6PQK4KjYGArSLWSuk0z1EruGZhsI22NZ4X-4aeoa5FPyo5NcQE8L03R9Le7rR7mT3J1_M5M8QFnjnoQ08iYBK&wd=&eqid=b9a78b590002ced50000000558808aba

梁建文, 巴振宁. 2007. 弹性层状半空间中沉积谷地对入射平面SH波的放大作用[J]. 地震工程与工程振动, 27(3): 1-9. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200703000.htm

Liang J W, Ba Z N. 2007. Surface motion of an alluvial valley in layered half-space for incident plane SH waves[J]. Journal of Earthquake Engineering and Engineering Vibration, 27(3): 1-9 (in Chinese).

刘启方, 李雪强, 孙平善. 2013a. 施甸盆地三维速度结构模型研究[J]. 地震工程与工程振动, 33(3): 88-94. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201303014.htm

Liu Q F, Li X Q, Sun P S. 2013a. Study on the 3-D velocity model of Shidian basin[J]. Journal of Earthquake Engineering and Engineering Vibration, 33(3): 88-94 (in Chinese). http://www.baidu.com/link?url=vAdaxqMpGDIar8CsLQVxM5HurhfVmJnX2gSZ73wNgWV290dlRxoW2xx_gndkOk_XjJ5PoXkG1KBOf-WLXD_ZjFa8QjSN72BJH2AmKUH1_a6mvK8kC_gn8izmQ87InZ-yIf3OWVNRYNTJ3Yzf_PjV-WAZtR1_FnEoXzMwEVhqTvvVY7aa764BSiE_q7il3pa1Klwr-1TQsVFG9l91b7rogNthiNul7hc6BiZ_9ObA9nuWJkgW6QlnBq7XTWfgLoEPfD7xNInxGm4tudioDFbFInogreyLbqH5ACb4-fLbNUnTQ6FjpC0GOHcTVOuJTl10&wd=&eqid=b49ead330002f7250000000558808ae6

刘启方, 于彦彦, 章旭斌. 2013b. 施甸盆地三维地震动研究[J]. 地震工程与工程振动, 33(4): 54-60. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201304007.htm

Liu Q F, Yu Y Y, Zhang X B. 2013b. Three-dimensional ground motion simulation for Shidian basin[J]. Journal of Earthquake Engineering and Engineering Vibration, 33(4): 54-60 (in Chinese). http://www.baidu.com/link?url=P8XhvBc2JQtEWISTyG1fepKDryxVqlHnSSjluX4lRe4s_PRIFywWwuZOuM1n-7FWVvmEernHs4qi_SpKTCK1qqTgOERdE0IxeCRtRKi_A15mpw0HoSp3DqJL1BHha5-_RQAnCO3YBRB7kTVm9yZ4EMHsx5GeZcbb8lxGGMItal5_Y88LSRYKhvsWCxVg45veww1ySZln8TT8uWUs_yC7Q2oXKY8HSTNvZK5OuTzJaeYnbDFm9fTr5i1Vdh9ewzHK7maWtzJdP6BDDWOHHKCfew5ws7-yeqDMkj3umOLVqaPARAH_dbOGvPAs85_lv3DnbdghT_PNDIRsbrRvH1-iqq&wd=&eqid=bd9058f400034ecf0000000558808af9

王海云. 2011. 渭河盆地中土层场地对地震动的放大作用[J]. 地球物理学报, 54(1): 137-150. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201101014.htm

Wang H Y. 2011. Amplification effects of soil sites on ground motion in the Weihe basin[J]. Chinese Journal of Geophysics, 54(1): 137-150 (in Chinese). http://cn.bing.com/academic/profile?id=d2244bd52a56ea57277f5913951321cf&encoded=0&v=paper_preview&mkt=zh-cn

王建龙, 陈学良, 高孟潭, 李宗超, 鄢兆伦, 李铁飞. 2014. 地震动峰值放大与盆地深度关系的初步数值模拟[J]. 地震工程与工程振动, 34(S): 167-172. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC2014S1026.htm

Wang J L, Chen X L, Gao M T, Li Z C, Yan Z L, Li T F. 2014. Preliminary numerical simulation of the dependence of the peak ground motion amplification on the basin depth[J]. Earthquake Engineering and Engineering Dynamics, 34(S): 167-172 (in Chinese). http://www.baidu.com/link?url=RojWol9vZKra1wxZBYAbGpuhPUFqkt_z09oDUgzU4Zaf_4Mp49GPbJ5pof9Bafhb4SwV-XsZ1Jya0JC7X7Oook9tKuf3Xrn-6B9CNBiX_3T_dvxDmVIFTQS8d3Rd7ImfRBJBVnme8trRJBH3TR_9tvp7lN0Jso5Keed1xz9ixrJSyOn4UxLVHbMYS_NsFXKqz9YRcpXXPIuHjIyfQ9krVbPmL6OBi8QoHXXkIy8O404v74l0pxUv986Npp8LRzzdxlEZ0UPRu10mYUGr3OPY5uEkDmna91TTao5GuPLm9ZKimL8etEeb4qBeFUNVKZr6E2faO9Jl2zNJGaYW2BumTJXN9U6xAeRaiKJrmV9FeEiUoZGTXrQeerLsfWOehuE7Bg_3FhWuwpis4jP74JJ_4a&wd=&eqid=b49ead330002ff260000000558808b1a

张冬丽, 徐锡伟, 赵伯明, 陈桂华, 解廷伟. 2007. 强地面运动数值模拟中三维物理模型的建立方法：以昆明盆地为例[J]. 地震学报, 29(2): 187-196. http://www.dzxb.org/Magazine/Show?id=26410

Zhang D L, Xu X W, Zhao B M, Chen G H, Xie T W. 2007. 3-D physical model in strong ground motion numerical simulation: A case study of Kunming basin[J]. Acta Seismologica Sinica, 29(2): 187-196 (in Chinese).

赵成刚, 韩铮. 2007. 半球形饱和土沉积谷场地对入射平面Rayleigh波的三维散射问题的解析解[J]. 地球物理学报, 50(3): 905-914. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200703031.htm

Zhao C G, Han Z. 2007. Three-dimensional scattering and diffraction of plane Rayleigh-waves by a hemispherical alluvial valley with saturated soil deposit[J]. Chinese Journal of Geophysics, 50(3): 905-914 (in Chinese). http://www.baidu.com/link?url=gy1iPB03p3i1oNIvISb___aBqqU8yfcfQylKm8aWLDTa_Eyh_0_htxTDTzw1vQ-j8_wa0sFA31JmA5sAJmteVPq_7V6axAIwqUhYxrtu1tVAxNqtKeCoZGvg-Jx1GEsdhPKz92Vf91tzg-TKLlMNv6y5_4YYkp61nxCXA6Ti6P4qWUVW4QU3tRcdizYQppTL-2FfoKsNaU6kEmeppCtYNx4G-jfX7RbP-ygwhGZ3p48Jms3f3EloXHtA4QI6UuUoeI7_6eKPYDJ59fGFGn-mkt-wd0CGHZqReS_7wOzxvQkN-uAY8HjpyWGIvrAAiWXMh_chvEM_lYMMwCRDZspYJxriHaSHw_CEtF6B6oXxR0eyqlxjcsBjr_D14Z9NsTAfL2e3HnItF29JrBId4aW57eAuxgrz_fSVySO7OU1KaAf4Yeynr2iKeOxD5WuYI4P8nibdJUH7p91d05QCeTN2kIqJw4ePku650jTQ_YbHipjBR9TJd15zZ7u0dF0OwxWf6rvEXa5eqZ7o-QgfYHielJHZjLUdjGPqEuO7TWSHlFDDwVIdW81B5xE4Lm0_jITe&wd=&eqid=b9a78b590002e2a20000000558808b75

Anderson J G, Bodin P, Brune J N, Prince J, Singh S K, Quaas R, Onate M. 1986. Strong ground motion from the Michoacan, Mexico, earthquake[J]. Science, 233(4768): 1043-1049. doi: 10.1126/science.233.4768.1043

Bouchon M. 1973. Effect of topography on surface motion[J]. Bull Seismol Soc Am, 63(2): 615-632. http://cn.bing.com/academic/profile?id=d9373c9a23dd7d71558faeb34b765631&encoded=0&v=paper_preview&mkt=zh-cn

Chaillat S, Bonnet M, Semblat J F. 2009. A new fast multi-domain BEM to model seismic wave propagation and amplification in 3-D geological structures[J]. Geophys J Int, 177(2): 509-531. doi: 10.1111/gji.2009.177.issue-2

Chen G X, Jin D D, Zhu J, Shi J, Li X J. 2015. Nonlinear analysis on seismic site response of Fuzhou basin, China[J]. Bull Seismol Soc Am, 105(2A): 928-949. doi: 10.1785/0120140085

Kamalian M, Gatmiri B, Sohrabi-Bidar A, Khalaj A. 2007. Amplification pattern of 2D semi-sine-shaped valleys subjected to vertically propagating incident waves[J]. Int J Numer Meth Biomed Eng, 23(9): 871-887. http://cn.bing.com/academic/profile?id=073be94e87d5dd28a86116ee3fe4f32f&encoded=0&v=paper_preview&mkt=zh-cn

Kawase H, Aki K. 1989. A study on the response of a soft basin for incident S, P, and Rayleigh waves with special reference to the long duration observed in Mexico city[J]. Bull Seismol Soc Am, 79(5): 1361-1382. http://cn.bing.com/academic/profile?id=6189dfc639602d642c86762a026f9059&encoded=0&v=paper_preview&mkt=zh-cn

Lee S J, Chen H W, Liu Q, Komatitsch D, Huang B S, Tromp J. 2008. Three-dimensional simulations of seismic wave propagation in the Taipei basin with realistic topography based upon the spectral element method[J]. Bull Seismol Soc Am, 98(1): 253-264. doi: 10.1785/0120070033

Lee V W. 1984. Three-dimensional diffraction of plane P, SV & SH waves by a hemispherical alluvial valley[J]. Soil Dyn Earthquake Eng, 3(3): 133-144. doi: 10.1016/0261-7277(84)90043-3

Luzón F, Sánchez-Sesma F J, Pérez-Ruiz J A, Ramírez-Guzmán L, Pech A. 2009. In-plane seismic response of inhomogeneous alluvial valleys with vertical gradients of velocities and constant Poisson ratio[J]. Soil Dyn Earthquake Eng, 29(6): 994-1004. doi: 10.1016/j.soildyn.2008.11.007

Mossessian T K, Dravinski M. 1990. Amplification of elastic waves by a three dimensional valley. Part 1: Steady state response[J]. Earthquake Eng Struct Dyn, 19(5): 667-680. doi: 10.1002/(ISSN)1096-9845

Olsen K B. 2000. Site amplification in the Los Angeles basin from three dimensional modeling of ground motion[J]. Bull Seismol Soc Am, 90(6B): S77-S94. doi: 10.1785/0120000506

Sánchez-Sesma F J, Luzón F. 1995. Seismic response of three-dimensional alluvial valleys for incident P, S, and Rayleigh waves[J]. Bull Seismol Soc Am, 85(1): 269-284. http://cn.bing.com/academic/profile?id=6d42a691cfe7b18b9ebef9995baae35c&encoded=0&v=paper_preview&mkt=zh-cn

Sánchez-Sesma F J, Palencia V J, Luzón F. 2002. Estimation of local site effects during earthquakes: An overview[J]. ISET J Earthq Techn, 39(3): 167-193. http://www.baidu.com/link?url=O5OAIRCUkZuxusGoIoA_P8tIYGf_eu8m21Sfsni1f4YXo1UxzJT5Aa5tiOJvuWG0y_-U6vpc7D_t99Jdvyf04RWNo8p_NN4AwPeLBwSU51YXS-lyd0jBxRb-wn8OWzO6QSCtQOhTNcBU3x9VLFS7KUpqVZr9KAxCL4DvHwrdpzkZeYuistP2Ug_MkxywJqVaTYn02Ynm5majNlBoNfeF4viE4mmvyziOkspE_yzdCg9hQ47aXq_HC1Jr2f7J62v9O90EzOLgEvlz7uIlW1BmKm06Hna7bvaxHSQpfDWauTVQYlx_Fd5N38PNUPYZpO5DQesZE-frHcFeDpohoU_KUK&wd=&eqid=b9f0b3c4000302820000000558808bac

Trifunac M D. 1971. Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves[J]. Bull Seismol Soc Am, 61(6): 1755-1770. http://www.baidu.com/link?url=7JNFyJ8mbqDgd1YwIkxt2_S1WxlB67536rCQ5vq3isg6SDPiqgFcaEHvO2rn4PRLMUdmIWEwCsTgeUMkLaxCdOJhlv9nrmmQyDK1JoNUr_GZjBs6aRdgys0t6g57PE_m5wdx8NYoR0Xa6ycjbo5GBmo2xhZ36iWtcS1TTX4LFz5g9Nj6fiYzDn3nfjEM8BQ3REsR1FYBFsmtm1XVBZB6W1dJqrBjWkjfJGpnVjSYOWNJIfbz4IGvh_YJboNCmUW3PC-JVt58Lb2MDKCkqwC0zMIVpBiyTeNk-zh7TuCOoEQw8FhYgB0NQ65nzSQ1MfXlaQLA_H290wY6XNsz7eUG43AFzjB9OI1Sz1YZjAcH_-G&wd=&eqid=c231334e0002c8fa0000000558808bc0

Yuan XM, Liao Z P. 1995. Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section[J]. Earthquake Eng Struct Dyn, 24(10): 1303-1313. doi: 10.1002/(ISSN)1096-9845

Zhao C B, Valliappan S. 1993. Incident P and SV wave scattering effects under different canyon topographic and geo-logical conditions[J]. Int J Numer Anal Meth Geomech, 17(2): 73-94. doi: 10.1002/(ISSN)1096-9853