A seismic data denoising method based on complete ensemble empirical mode decomposition with adaptive noise and Hurst exponent
-
摘要: 在地震观测中,地震数据中普遍包含有噪声信号。由于噪声信号的干扰,地震分析的效率会受到不同程度的影响。传统的去噪方法通常需要噪声的先验知识,并且滤波时会造成部分有效信号丢失。针对这一问题,本文提出一种将自适应噪声完全集合经验模态分解(CEEMDAN)算法与Hurst指数相结合的地震数据去噪方法。首先通过CEEMDAN方法将信号分解为一系列本征模函数(IMF),然后利用Hurst指数对滤波后的IMF分量进行识别,最后对地震数据IMF分量进行重构,从而实现数据去噪。与传统方法的去噪效果对比表明,本文方法可将低信噪比波形的去噪效果提高32%,将高信噪比波形的去噪效果提高6倍。同时对地磁数据的去噪结果表明,本文方法能够较完整地将地铁噪声从地磁信号波形中滤除。
-
关键词:
- 地震数据去噪 /
- 地磁数据去噪 /
- 自适应噪声完全集合经验模态分解 /
- Hurst指数
Abstract: In seismic observation, seismic data generally contain ambient noise, which reducesthe efficiency of seismic analysis. Traditional denoising methods usually need a priori knowledge of noise, and some effective data will be lost when filtering. To solve this problem, this paper proposes a seismic data denoising method based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and Hurst exponent. Firstly, the signal is decomposed into a series intrinsic mode functions (IMF) by CEEMDAN method. Secondly, the Hurst exponent is used to identify the filtered IMF component. Finally, the IMF component of seismic data is reconstructed to realize data denoising. Compared with the denoising effect of traditional methods, the filtering ability of this method for low SNR waveforms is improved by 32%, and the filtering ability for high SNR waveforms is 6 times higher. At the same time, as shown in the denoising results of geomagnetic data, this method can completely filter subway noise from geomagnetic signal waveform. -
引言
建筑场地划分反映了不同场地条件对基岩地震动的综合放大效应,场地分类对应着不同的抗震设计要求。根据 《建筑抗震设计规范》 (GB50011—2010)(以下简称 《规范》 ),我国用场地覆盖层厚度以及岩石的剪切波速或者土的等效剪切波速vS20作为建筑场地类别的判断依据(中华人民共和国住房和城乡建设部,2010)。
根据 《规范》 对场地划分的要求,当土层覆盖层厚度较大时,土层的等效剪切波速vS20就成为场地类别的主要判断依据,例如:当土层厚度>80 m时,若等效剪切波速为150 m/s,则场地类别为Ⅳ类;若等效剪切波速为151 m/s,则场地类别为Ⅲ类,即等效剪切波速的细微差别就会导致划分场地类别时产生Ⅲ类场地与Ⅳ类场地之间的类别变化。然而由于受到场地试验环境、测试仪器种类、现场人员经验等因素的影响,剪切波速的读取误差是不可避免的。因此,通过现有手段来解决这类因单一或少量的特征值细微变化即引起场地类别变化的问题对未来工程的开展十分关键。
针对上述问题,学者们多从两个角度着手解决,其一为增加用于判断的特征值,其二为进一步细化场地类别的划分。迟明杰等(2021)通过结合场地软硬程度对场地类别进行扩展,但由于不同场地类别对应着不同的抗震设计要求,仅扩展新的场地类别而不设置对应的抗震设计要求则难以使用;也有学者考虑到剪切波速在土层深度20—30 m时依然具有较强的变异性,建议将 《规范》 中的判断依据—20 m等效剪切波速vS20延伸至30 m等效剪切波速vS30 (战吉艳等,2012;林凤仙等,2020);或如陈国兴等(2020)引入场地基本周期Ts值作为判断依据,在不改变 《规范》 所设场地类别的情况下利用三个指标对场地进行分类。尽管学者们针对场地类别的划分提出了许多可行的方案,但由于场地类别变化问题的关键在于明确界限,因此上述研究均未解决这一问题。
近年来,随着机器学习方法在岩土工程领域的应用,之前工程中大量的实测数据得以二次利用(Calderón-Macías et al,2000;王昊等,2020)。但随着基础建设的不断完善,能够利用的最新实测数据不断减少(Ching,2020),且现场测试难度高、消耗大,这意味着新建工程利用空间相关性,即在相关风险评价时参考工程周围的最新实测数据,再难实现。因此,以数据驱动的岩土工程成为当前解决这一问题的新方法(Zhang,Phoon,2022;Phoon,Zhang,2023)。
目前,已有一些学者使用成熟的机器学习方法来解决岩土工程领域中的各类问题,例如:在实际工程中由人为判断或理想化假设所导致的风险评估误差问题;区域数据有限或部分缺失的问题。Zhang等(2021a)讨论了机器学习方法在基于广泛有限元分析结果下建立预测模型的可行性;姬建等(2021)通过加权均匀模拟(weighted uniform simulation,缩写为WUS)算法改进了蒙特卡洛模拟(Monte Carlo simulation,缩写为MCS)算法在进行边坡可靠度分析时需要大量样本的缺点;Xiao等(2021)通过建立层级贝叶斯模型(hierarchical Bayesian model,缩写为HBM)解决了特定区域剪切波速vS稀缺的问题;Zhang等(2021b)对我国液化判断中的部分理想化假设进行了合理性评估;黄鑫怀等(2023)利用随机森林算法和K近邻算法基于化学元素指标对特定花岗岩的成矿潜力进行了评价。上述研究成果证明了合理运用机器学习方法可以有效地解决岩土工程领域中因受限于数据数量和精度导致的问题,也为文本提出的问题提供了新思路。
综上所述,使用多个特征值,并利用机器学习方法可解决这一问题,即可有效避免因单一或少量的特征值细微变化而引起场地类别变化的问题,同时又能使特征值的边界判断模糊化,从而弱化上述不可避免的误差所造成的问题。为此,本文从江苏省盐城地区收集了大量相关试验数据,拟利用机器学习方法对所收集的数据进行训练建模,为厚覆盖土层场地类别的判断提供可靠的方式,进而对上述特定情况下场地类别出现变化的问题进行深入研究,以期为工程上类似的情况提供一种用于二次判断的模型。
1. 数据与方法
1.1 数据集
《规范》 中使用场地覆盖层厚度以及岩石的剪切波速或者土的等效剪切波速vS20作为建筑场地类别的判断依据,这使得非特定情况下的场地类别判断结果十分可靠,且充分考虑了整个钻孔的一体性。因此,本文所建模型仍然保留剪切波速这一特征值,并同时收集其它特征值作为判断依据,以此避免因单一或少量的特征值细微变化即引起场地类别变化的问题。
标准贯入试验(standard penetration test,缩写为SPT)是现场测定砂性土或黏性土地基承载力的方法,用标准贯入击数N作为计数方式。已有学者就标准贯入值与剪切波速之间的关系进行研究,并得到一些标准贯入值与剪切波速间的预测模型和替换公式(Bajaj,Anbazhagan,2019;Zhang et al,2021b;刘益平等,2022),证明了标准贯入值作为反映土体性能的特征值具有良好的实用性。与剪切波速不同,标准贯入击数的计数方式更明确,读数更准确。
考虑到标准贯入试验以测定砂性土地基承载力为主,其现场测试数据较多,本文从收集砂性土的标准贯入值入手,从盐城地区收集了1 293组砂性土的标准贯入值,并同时收集了与之对应的相关土层信息:标准贯入处的中点深度和剪切波速,将其作为用于建立机器学习模型的特征值。
1.2 相关性分析
各特征值之间具有一定相关性是常见的,但如果特征值之间存在强相关性则可能会使得预测结果出现偏差,尤其是如随机森林算法这样的对特征值之间相关性的敏感度较高的算法(Altmann et al,2010)。皮尔逊(Pearson)相关系数法通过计算两个变量之间的协方差和标准差的商来描述两个特征值之间的相关性:
$$ \rho_{x\text{,} y}=\frac{\mathrm{cov} ( x\text{,} y) }{\sigma_x\sigma_y}=\frac{E [ ( x-\mu_x) ( y-\mu_y) ] }{\sigma_x\sigma_y}\text{,} $$ (1) $$ r=\frac{\displaystyle\sum\limits_{i=1}^n ( x_i-\overline{x} ) ( y_i-\overline{y}) }{\sqrt{\displaystyle\sum\limits_{i=1}^n ( x_i-\overline{x} ) ^2}\sqrt{\displaystyle\sum\limits_{i=1}^n ( y_i-\overline{y} ) ^2}}\text{,} $$ (2) 式中,$\rho_{x\text{,} y} $为特征值x与y的相关系数,cov为协方差,E为均值,σ为标准差,μ为均值,r为皮尔逊相关系数,$\overline x \,\,$与$\,\, \overline y \,\,$分别为xi与yi的均值。
本文利用皮尔逊相关系数法验证剪切波速与标准贯入值之间的相关性。结果显示,两者间相关系数的绝对值<0.6,即两个特征值间具有的相关性不会使模型的预测结果出现过偏的问题(Chelgani et al,2016)。
1.3 建模流程与评价方法
本文所用厚覆盖土层相关试验数据中所有的土层厚度均>80 m,即本文所研究的场地类别变化的问题只在Ⅲ类场地与Ⅳ类场地之间,因此本文将146—154 m/s作为容易影响场地类别判断的误差区间,从1 293组样本中挑选出处于上述临界状态的75组样本,将其作为“临界样本”利用所建成模型对其进行判断。其余1 218组数据作为样本集,选出70%作为训练集,30%作为验证集,用于建立模型所需。
首先使用各机器学习方法对样本集进行学习与建模,并进行可行性分析,为厚覆盖土层场地类别的判断提供可靠的方式;进而将优选出的最优模型用于上述区间进行研究,为工程上类似的情况提供一种用于二次判断的模型,具体流程如图1所示。
为了避免训练模型时出现过拟合的问题,通过逻辑回归(logistics regression)算法和支持向量机(support vector machine,缩写为SVM)算法建模时使用十折交叉验证法;随机森林模型自身在进行bootstrap抽样时会留下部分袋外数据用于内部误差估计。本文采用上述方式以尽可能减少最终用于预测“临界样本”的模型的精度受到除算法本身以外的影响因素。
本模型用于二分类问题,通过正确率(精度)、召回率以及AUC (area under curve)值来评价模型的分类效果。正确率也称真阳率(true positive rate,缩写为TPR)、召回率也称假阳率(false positive rate,缩写为FPR)。具体计算公式如下:
$$ \mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP+FN}}\text{,} $$ (3) $$ \mathrm{FPR}=\mathrm{\frac{FP}{FP+TN}}\text{,} $$ (4) 式中,TP (true positive)为被模型正确预测为正类的正样本,FP (false positive)为被模型错误预测为正类的负样本,TN (true negative)为被模型正确预测为负类的负样本,FN (false negative)为被模型错误预测为负类的正样本。
正确率可以描述模型对阴性样本的判别能力,正确率越高,则模型对阴性样本的判别能力越强;召回率可以描述模型对阳性样本的判别能力,召回率越高,则模型对阳性样本的判别能力越强。正确率和召回率是一对矛盾关系的参数,当两者相近时,模型具有相对较好的平衡性。AUC值为受试者工作特征(receiver operating characteristic,缩写为ROC)曲线下方x轴与y轴所形成的面积,可以描述模型的分类性能,AUC值越接近1,说明模型的分类性能越强。
2. 算法描述与可行性分析
2.1 逻辑回归算法
逻辑回归算法因其原理简单且可以较好地解决因子间相互依赖的问题而常被用于危险性评价(许冲,徐锡伟,2012;罗路广等,2021)。结合所收集的数据,逻辑回归同样是本文的首选算法。
本文可行性分析试验所建逻辑回归模型对样本集分类所得到的ROC曲线和混淆矩阵如图2所示。逻辑回归模型对823个Ⅲ类场地进行预测,结果正确预测了其中的742个;对395个Ⅳ类场地进行预测,结果正确预测了其中的220个。逻辑回归模型的正确率为0.809,召回率为0.902,AUC值为0.85。
综上所述,尽管逻辑回归算法因其易用性而被广泛使用,但受限于其本身容易欠拟合、精度普遍低等问题,其分类性能与泛化能力有限。因此,必须使用分类性能更好、泛化能力更强的模型来进一步研究。
2.2 支持向量机算法
支持向量机常被认为是优越的分类器(Bhavsar,Panchal,2012;刘方园等,2018)。其原理为寻求一种满足分类要求的最优分类超平面,使其在确保分类精度的同时最大化超平面两侧的空白区域。因此,支持向量机算法非常适用于线性可分的二分类问题(张学工,2000)。
但实际样本往往不是线性可分的,或原始样本空间中无法找到一个可以正确划分样本的超平面,这同样也是逻辑回归算法难以得到高精度模型的一大原因。为了解决这一类常见的问题,提出了核函数方法。核函数通过将原始空间的样本映射到更高维的特征空间使其能够在新的特征空间中线性可分,利用核函数展开结合最优分类超平面理论形成的支持向量机模型解决了其只能处理线性可分样本的弊端,两者结合形成当前使用的支持向量机算法(Liu et al,2005)。
本文可行性分析试验选用高斯核函数来建立支持向量机模型,最终得到的支持向量机模型对样本集分类所得到的ROC曲线和混淆矩阵如图3所示。支持向量机模型对823个Ⅲ类场地进行预测,结果正确预测了其中的801个;对395个Ⅳ类场地进行预测,结果正确预测了其中的343个。支持向量机模型的正确率为0.939,召回率为0.973,AUC值为0.96。
针对当前数据的最优分类器需结合当前样本进行比选(赖成光等,2015),且在使用支持向量机算法时还需要考虑以下问题:随着原特征值数据的补充以及新特征值的引入,支持向量机对此进行训练的可行性存疑(Martens et al,2007);支持向量机算法解释性不足也导致模型无法明确各特征值在模型中的相对权值;实际使用中对支持向量机模型进行调整的难度比较大。因此,本文提出解释性更强、更易操作的随机森林算法作为比选方案,并将其结果与支持向量机模型进行对比。
2.3 随机森林算法
随机森林(random forest)算法是一种基于决策树的组合分类器(黄衍,查伟雄,2012),它通过bootstrap抽样,在训练集中有放回地、可重复地随机选择样本并组成新的训练集,再使用决策树算法对其进行训练,重复上述过程产生多棵决策树,最后便组成随机森林,随机森林的分类结果就是多决策树的投票结果(Tesfamariam,Liu,2010)。
得益于这样的结果输出机制,随机森林算法具有良好的解释性,即可以通过调整抽样方式给出每一个特征值在分类中的重要程度(Breiman,2001)。此外,随机森林算法对样本进行bootstrap抽样训练时都会留下部分袋外数据用于内部误差估计。Breiman (2001)通过试验证明了这种利用袋外数据的误差估计是类似于交叉验证的无偏估计,因此无需额外对模型进行交叉验证。
本文可行性分析试验使用500棵决策树来建立随机森林模型,最终得到的随机森林模型对样本集分类所得到的结果如图4所示。利用此随机森林模型对261个Ⅲ类场地进行预测,结果正确预测了其中的251个;对107个Ⅳ类场地进行预测,结果正确预测了其中的94个。随机森林模型的正确率为0.951,召回率为0.962,AUC值为0.98。
综上所述,支持向量机模型、随机森林模型的分类正确率分别达到93.9%和92.9%,远高于逻辑回归模型80.9%的分类正确率。
2.4 等效变异系数
尽管在可行性分析中,支持向量机模型和随机森林模型优于逻辑回归模型,但其分类精度仍不够高,以至于还需对其进行优选用于对临界样本的二次判断。本文通过加入等效变异系数提高模型的精度,同时便于在支持向量机模型和随机森林模型中比选出最优模型。
20 m等效剪切波速vS20通过20 m以浅各土类的剪切波速计算获得,能够表示场地土的刚性和土层对地震动的响应。但由于剪切波速在测试中的不确定性较大,且直接使用等效剪切波速作为特征值可能导致模型在大量数据的支持下得到与 《规范》 中规定数值相近的界限。因此,为了尽可能考虑整个钻孔的一体性,同时避免在模型中出现上述情况,本文参考陈卓识等(2019)引入一个各钻孔统一的无量纲参数作为新的特征值。该参数的具体计算方式为:将20 m等效剪切波速vS20作为等效平均值,将1—20 m深度范围内的剪切波速作为变量,最终计算得到等效变异系数,具体表达式为
$$ \mathrm{COV}=\frac{\sqrt{\displaystyle\sum\limits_{i=1}^{20} ( v_{\mathrm{S}i}-v_{\mathrm{S}20} ) ^2}}{v_{\mathrm{S}20}}. $$ (5) 等效变异系数作为一组具有整个钻孔特点的特征值,能提高模型精度,同时能够使模型对同一钻孔内的信息判断更一致。
3. 结果与分析
3.1 模型建立与对比
建立支持向量机模型时需要确定分类核函数,本文通过比较不同核函数情况下的模型精度来进行比选。进行比选的核函数分别为:线性核、多项式核(核数d=2,3)、高斯核,结果如表1所示。
表 1 不同核函数的模型精度Table 1. Accuracy of the models with different kernel functions核函数 精度 线性核 83.6% 多项式核 (d=2) 91.2% 多项式核 (d=3) 93.7% 高斯核 95.1% 显然,使用高斯核的模型精度在一众核函数中具有绝对优势,因此本文建立支持向量机模型选用高斯核函数,最终得到的支持向量机模型对样本集分类所得到的结果如图5所示,可见:支持向量机模型对823个Ⅲ类场地的预测结果中,正确预测了其中的808个;对395个Ⅳ类场地的预测结果中,正确预测了其中的353个。支持向量机模型的正确率为0.951,召回率为0.982,AUC值为0.98。
建立随机森林算法时,需给出合理的分类器数量,以平衡模型运算速度与输出结果精度。本文通过设置不同决策树数量的方式对模型进行分类性能测试,不同数量决策树的情况下各测试100次并取其均值,结果如图6所示。结果表明:当选用150棵决策树时精度最高,且150棵决策树并不会在模型建立的过程中造成过大的计算量,因此本文决定使用150棵决策树来建立随机森林模型。利用随机森林模型对样本集分类,结果如图7所示,可见:随机森林模型对263个Ⅲ类场地的预测结果中,正确预测了其中的256个;对105个Ⅳ类场地的预测结果中,正确预测了其中的99个。支持向量机模型的正确率为0.977,召回率为0.973,AUC值为0.98。这一结果与决策树数分类性能测试的结果基本一致。
支持向量机模型和随机森林模型的正确率分别为95.1%和97.7%,召回率分别为98.2%和97.3%,两者的AUC值同为0.98。因此随机森林模型在分类性能不弱于支持向量机模型的同时与样本数据的适配度更高,且随机森林模型的召回率与正确率相近,即模型对样本总体的判断更平衡。综上所述,上述随机森林模型是解决本文所研究问题的最优模型,能够为厚覆盖土层场地类别的判断提供可靠的依据。
3.2 试验结果
使用上述随机森林模型对本研究临界样本中的75组数据进行场地类别判断,分类所得结果(图8)显示:模型对该样本75组数据的判断中,有61组与勘探报告的判断结果一致,14组与勘探报告的判断结果不同,且模型对Ⅲ类场地的判断与勘探报告完全一致。
从同一钻孔中可以收集到多组砂性土的标贯试验数据,如果模型对同一钻孔内多组数据的判断产生矛盾的结果,则会严重影响模型判断结果的有效性。为了确保模型在实际工程中的有效性,将模型的判断结果依次输出,并按照原有钻孔信息整理核对,具体结果列于表2。可见,模型对10个钻孔场地类别的判断中,8个与勘探报告的结果一致。验证结果证明了模型对于同一钻孔中收集到的多组数据作出了一致判断,即模型有效。
表 2 随机森林模型输出结果与现场结果对比Table 2. Comparison between the output results of random forest model and on-site results钻孔序号 现场判断结果 模型判断结果 1 Ⅳ类 Ⅲ类 2 Ⅳ类 Ⅲ类 3 Ⅳ类 Ⅳ类 4 Ⅲ类 Ⅲ类 5 Ⅲ类 Ⅲ类 6 Ⅲ类 Ⅲ类 7 Ⅲ类 Ⅲ类 8 Ⅲ类 Ⅲ类 9 Ⅲ类 Ⅲ类 10 Ⅲ类 Ⅲ类 3.3 试验结果分析
随机森林模型对Ⅲ类场地的判断与勘探报告完全一致,且判断结果与勘探报告结果多数一致,证明该模型不仅在非临界情况下具有极好的判断能力,当其用于解决临界情况的问题时依然保有良好的判断能力。因此,该模型可以针对工程上的类似问题进行二次判断,并提供有效的参考依据。
在对临界样本的判断中,模型有两个钻孔的场地类别判断与勘探报告的判断不同,且都是报告中认为Ⅳ类场地的钻孔在模型中被判断为Ⅲ类场地。在实际工程中,出于安全考虑,在现场作出的判断往往偏保守,而这样的判断方式在边界附近的分类结果则被放大成两种不同的场地类别,这可以解释模型与勘探报告对Ⅳ类场地的判断分歧较大的情况。因此,本文认为,当遇到文中所述的临界情况时,该模型可以为工程现场避免过于保守的判断提供可靠的依据。
4. 讨论与结论
本文收集了盐城地区1293组厚覆盖土层情况下的相关现场试验数据,并将等效剪切波速146—154 m/s作为各误差容易影响场地类别判断的区间,利用逻辑回归、支持向量机、随机森林等三种算法进行训练建模,为厚覆盖土层场地类别的判断提供可靠的方式,进而优化并选出随机森林模型对临界样本进行二次判断,将结果与勘探报告进行对比分析。主要结论如下:
1) 利用支持向量机与随机森林算法建立的模型分类正确率分别可达93.9%和92.9%,远高于逻辑回归模型80.9%的分类正确率。通过对模型的验证与分析证明了在现有数据的情况下,支持向量机模型和随机森林模型具有良好的可行性。
2) 通过加入等效变异系数,随机森林模型的分类正确率达到97.7%,且对同一钻孔内的信息判断更一致,使模型具有更强的有效性,为厚覆盖土层场地类别的判断提供了一种新的方式。
3) 使用随机森林模型对临界样本进行二次判断,判断结果证明了该模型可用于解决工程上类似的厚覆盖土层场地类别划分问题。本模型为避免实际工程对具有争议的情况作出偏保守判断提供了可靠的依据。
本文建立了随机森林模型用于场地类别划分,并得到了良好的结果,但在实际工程中场地类别的划分以及用于这类问题的机器学习方法等方面仍有许多不足之处:
1) 由于收集的数据有限,本文用于模型建立的样本集只包含了砂性土的相关参数,但这并不意味其它岩性的土类在场地类别的判断中不重要,尤其是浅表层土。但不同土类间的标准贯入值及其相关数据的差别明显,在建模时难以混合使用,因此如何合理优化算法,使更多的数据能够在建模过程中加入样本集作为特征值,也需要在未来深入研究。
2) 本文用于模型建立的样本集来自江苏盐城,而用于模型验证的数据也来自江苏盐城,因此该模型在其它地区的泛化能力还有待研究,可以考虑通过构建多层次的模型使其在用于多地区时能够保持良好的泛化能力。
-
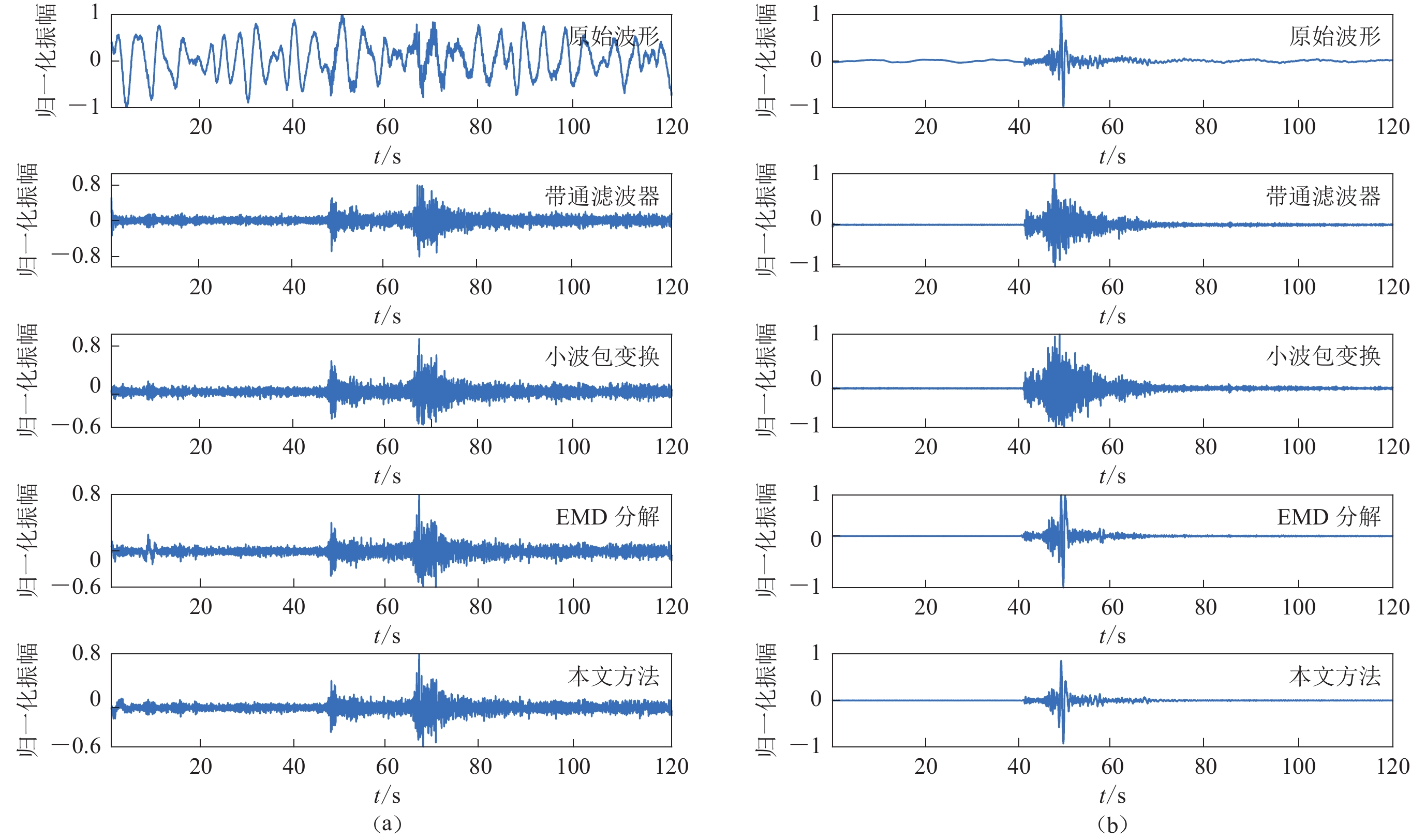
图 4 使用本文方法所得四个事件的去噪结果
左侧为原始波形,右侧为去噪后波形。(a) 百色地震波形;(b) 灵川地震波形;(c) 南宁爆破事件波形;(d) 桂林坍塌事件波形
Figure 4. Denoising results of the four events by the method proposed in this paper
The left column stands for original waveforms and the right column stands for denoising waveforms. (a) Baise earthquake waveform;(b) Lingchuan earthquake waveform;(c) Nanning blasting waveform;(d) Guilin collapse waveform
表 1 本文所选事件的信息
Table 1 The information of events selected in this paper
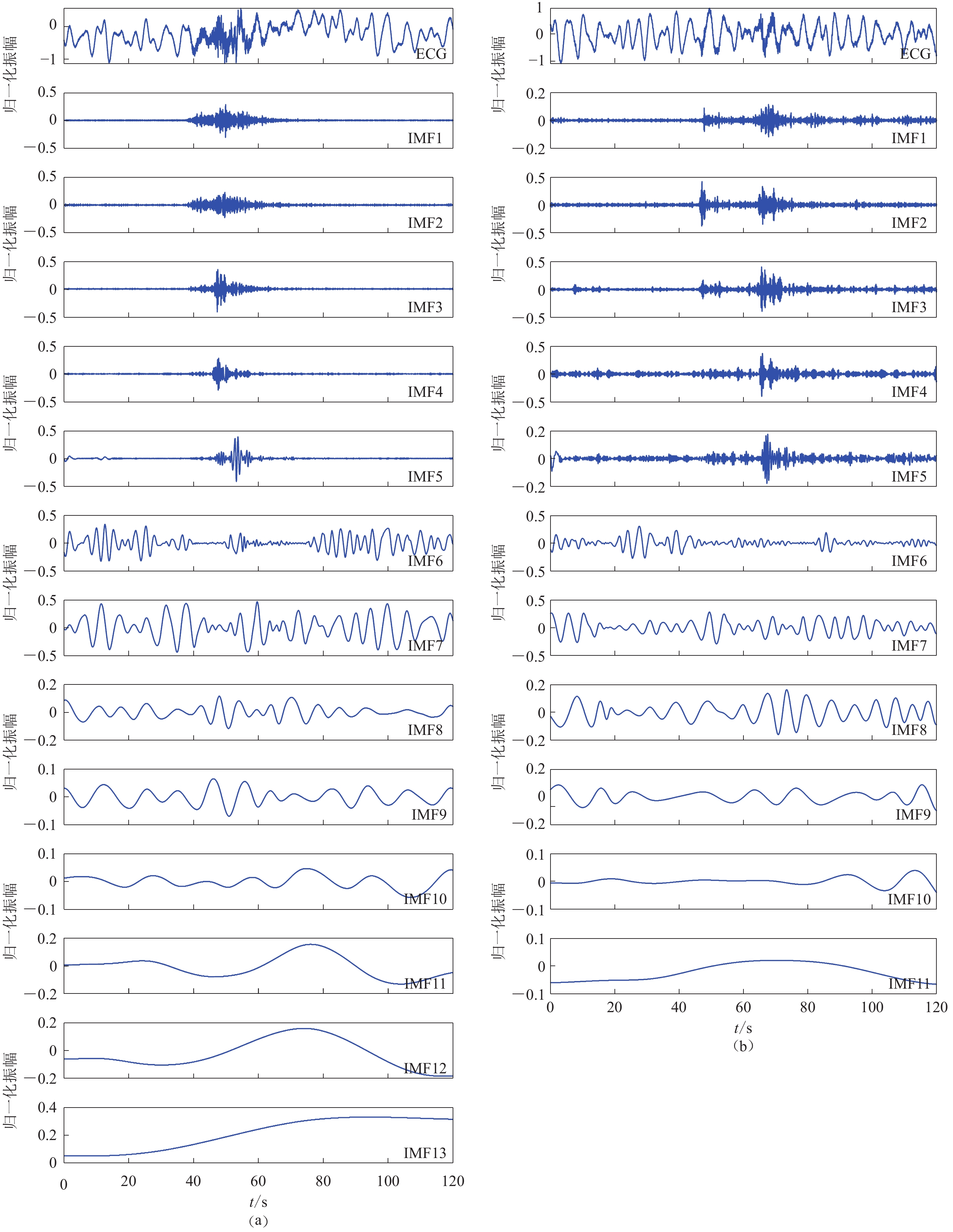
事件序号 事件类型 发震日期 震中位置 记录台站 震中距/km ML a 天然地震 2021-04-28 广西百色 FUN 73 1.3 b 天然地震 2017-11-25 广西灵川 YOF 148 1.9 c 人工爆破 2021-04-04 广西南宁 DAQ 88 2.0 d 山体坍塌 2020-06-23 广西桂林 GUL 36 2.3 表 2 表1中四个事件的IMF分量的Hurst指数
Table 2 The Hurst exponents of different IMF components for four events in Table 1
分量序号 事件a 事件b 事件c 事件d IMF1 0.302 5 0.294 6 0.258 9 0.359 4 IMF2 0.322 6 0.407 5 0.425 5 0.325 4 IMF3 0.307 0 0.287 5 0.356 1 0.466 3 IMF4 0.418 9 0.333 7 0.306 3 0.487 1 IMF5 0.483 8 0.384 6 0.515 9 0.361 1 IMF6 0.655 8 0.640 8 0.612 2 0.647 8 IMF7 0.686 0 0.686 2 0.658 9 0.683 1 IMF8 0.763 8 0.792 9 0.796 6 0.653 0 IMF9 0.806 2 0.877 7 0.870 9 0.864 5 IMF10 0.969 3 0.916 5 0.992 9 0.908 0 IMF11 0.973 3 0.966 8 1.007 0 0.955 1 IMF12 0.985 1 1.009 2 1.004 0 IMF13 0.994 9 表 3 不同去噪方法的质量因子Q值和均方根误差RMSE
Table 3 Quality factor Q and root-mean-square error RMSE of different denoising methods
去噪方法 灵川地震事件 桂林坍塌事件 Q值 RMSE Q值 RMSE 带通滤波器 0.723 9 0.380 1 1.360 1 0.076 1 小波包变换 0.718 5 0.375 6 1.193 9 0.073 3 EMD方法 0.854 9 0.374 7 7.344 2 0.040 0 本文方法 0.955 9 0.373 9 9.606 9 0.025 7 表 4 地磁数据IMF分量的Hurst指数
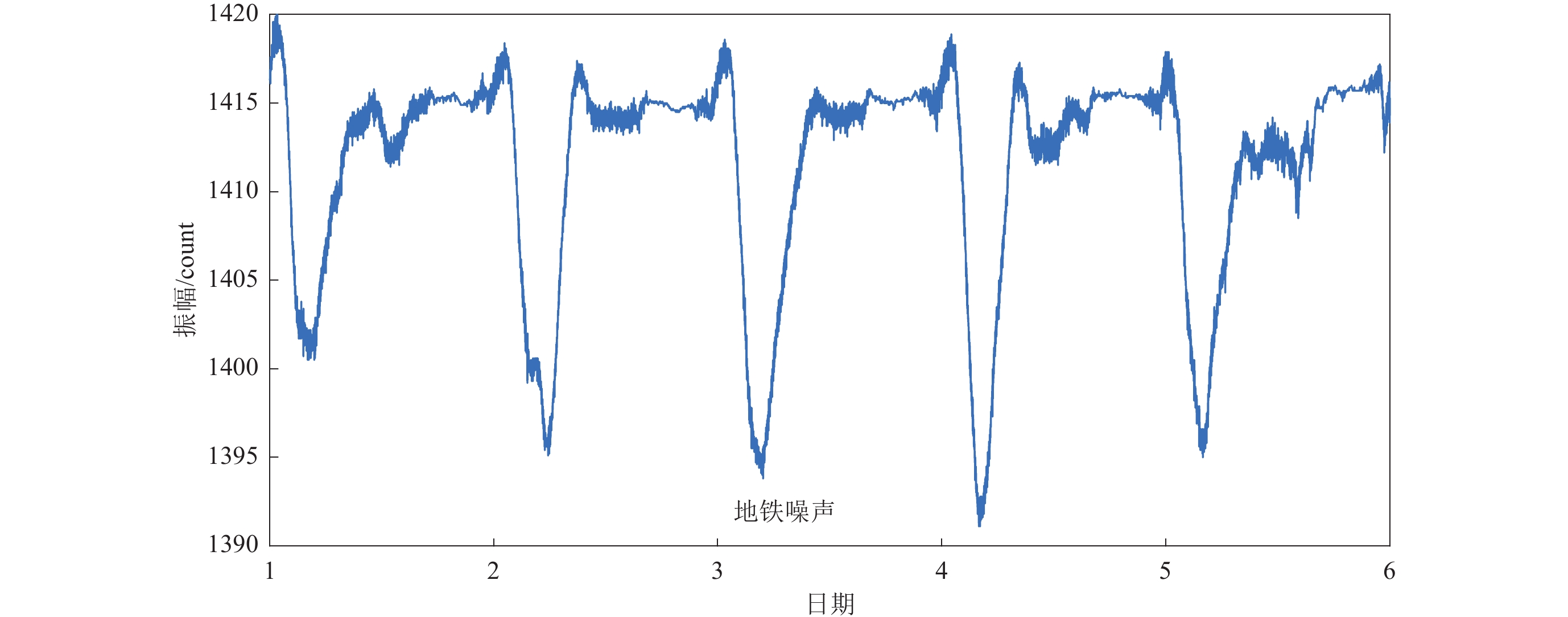
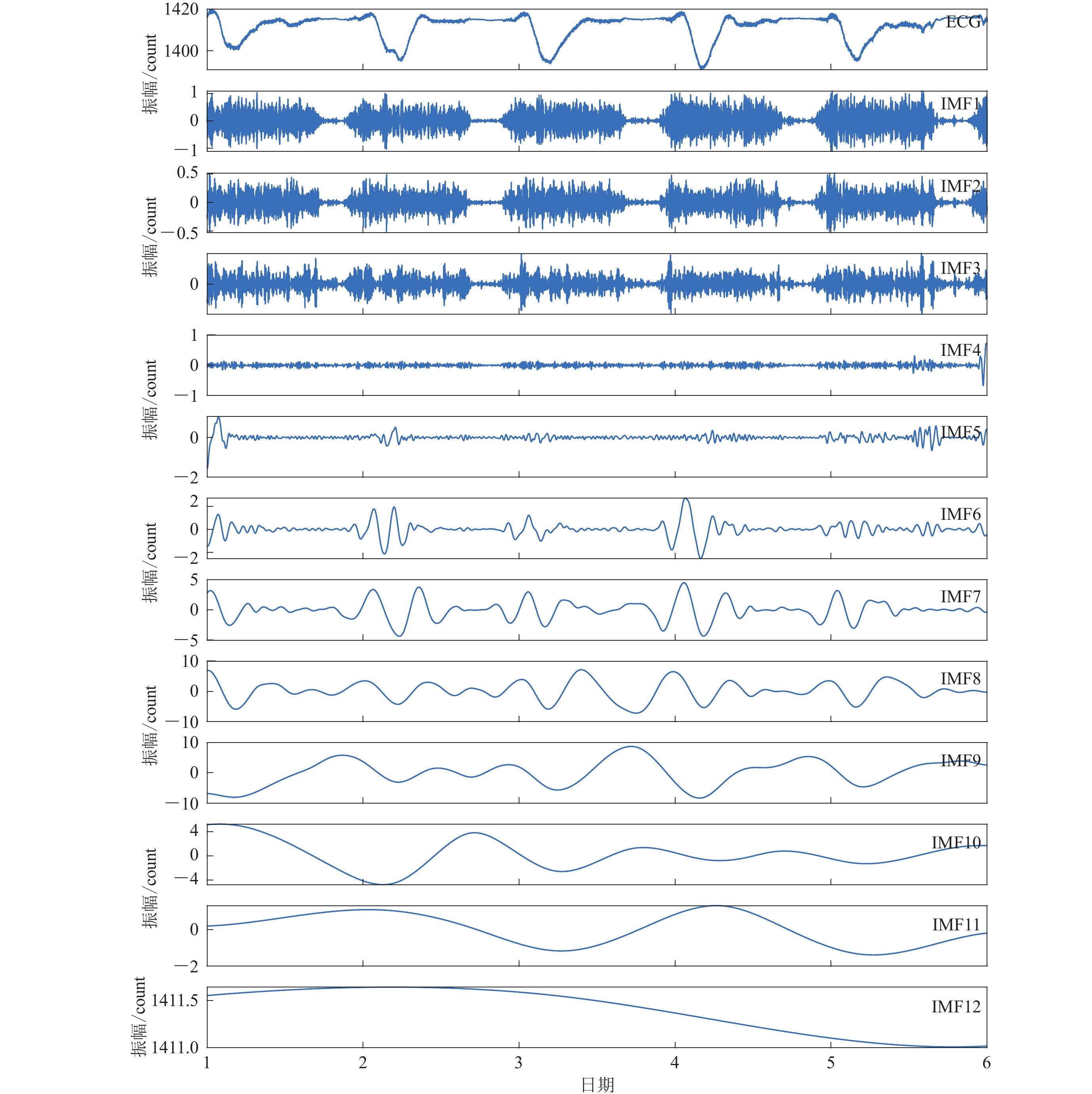
Table 4 The Hurst exponent of different IMFs from geomagnetic data
序号 Hurst指数 序号 Hurst指数 序号 Hurst指数 IMF1 0.284 6 IMF5 0.497 9 IMF9 0.954 7 IMF2 0.323 2 IMF6 0.583 0 IMF10 0.989 9 IMF3 0.208 0 IMF7 0.702 9 IMF11 0.997 1 IMF4 0.352 4 IMF8 0.861 3 IMF12 1.006 3 -
蔡剑华,肖晓. 2015. 基于小波自适应阈值去噪的MT信号处理方法[J]. 地球物理学进展,30(6):2433–2439. doi: 10.6038/pg20150601 Cai J H,Xiao X. 2015. Method of processing magnetotelluric signal based on the adaptive threshold wavelet[J]. Progress in Geophysics,30(6):2433–2439 (in Chinese).
陈学华,贺振华,黄德济. 2008. 广义S变换及其时频滤波[J]. 信号处理,24(1):28–31. doi: 10.3969/j.issn.1003-0530.2008.01.007 Chen X H,He Z H,Huang D J. 2008. Generalized S transform and its time-frequency filtering[J]. Signal Processing,24(1):28–31 (in Chinese).
韩卫雪,周亚同,池越. 2018. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探,57(6):862–869. doi: 10.3969/j.issn.1000-1441.2018.06.008 Han W X,Zhou Y T,Chi Y. 2018. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum,57(6):862–869 (in Chinese).
牛永效. 2017. 基于频率及f-k域联合应用的地震波去噪技术研究[J]. 铁道标准设计,61(2):47–49. Niu Y X. 2017. Research on seismic data noise reduction based on combined application of frequency and f-k domain filter[J]. Railway Standard Design,61(2):47–49 (in Chinese).
孙月. 2012. 基于广义S变换和阈值函数的地震信号去噪研究[D]. 长春: 吉林大学: 19–26. Sun Y. 2012. Seismic Signal Denoising Research Based on Generalized S Transformation and Threshold Function[D]. Changchun: Jilin University: 19–26 (in Chinese).
万光南. 2014. f-k滤波在压制面波噪声中的应用[J]. 中州煤炭,(2):99–101. Wan G N. 2014. Application of f-k filtering in noise suppression of surface wave[J]. Zhongzhou Coal,(2):99–101 (in Chinese).
杨凯,刘伟. 2012. 基于改进EMD的地震信号去噪[J]. 西南石油大学学报(自然科学版),34(4):75–82. Yang K,Liu W. 2012. Random noise attenuation of seismic signal based on improved EMD[J]. Journal of Southwest Petroleum University (Science &Technology Edition),34(4):75–82 (in Chinese).
张杏莉,卢新明,贾瑞生,阚淑婷. 2018. 基于变分模态分解及能量熵的微震信号降噪方法[J]. 煤炭学报,43(2):356–363. doi: 10.13225/j.cnki.jccs.2017.4153 Zhang X L,Lu X M,Jia R S,Kan S T. 2018. Micro-seismic signal denoising method based on variational mode decomposition and energy entropy[J]. Journal of China Coal Society,43(2):356–363 (in Chinese).
Chen K,Sacchi M D. 2015. Robust reduced-rank filtering for erratic seismic noise attenuation[J]. Geophysics,80(1):V1–V11.
Hurst H E. 1951. Long-term storage capacity of reservoirs[J]. Trans Am Soc Civ Eng,116(1):770–799. doi: 10.1061/TACEAT.0006518
Liu W,Cao S Y,Chen Y K. 2016. Seismic time-frequency analysis via empirical wavelet transform[J]. IEEE Geosci Remote Sens Lett,13(1):28–32. doi: 10.1109/LGRS.2015.2493198
Lu Y,Huang Y M,Xue W,Zhang G B. 2019. Seismic data processing method based on wavelet transform for denoising[J]. Cluster Comput,22(3):6609–6620.
Torres M E, Colominas M A, Schlotthauer G, Flandrin P. 2011. A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Prague: IEEE: 4144–4147.
Wang Y Q, Peng Z M, He Y M. 2016. Time-frequency representation for seismic data using sparse S transform[C]//2016 2nd IEEE International Conference on Computer and Communications (ICCC). Chengdu: IEEE: 1923–1926.
Zhang C,Li Y,Lin H B,Yang B J. 2015. Signal preserving and seismic random noise attenuation by Hurst exponent based time-frequency peak filtering[J]. Geophys J Int,203(2):901–909. doi: 10.1093/gji/ggv340
-
期刊类型引用(2)
1. 刘琦,刘培兵,邵晓鹏,李永红,淮刚. 基于数字孪生的复杂环境下钢结构施工技术优化研究. 建筑技术. 2025(01): 13-17 .  百度学术
百度学术
2. 赵贵武,丁建刚. 机器学习算法在海洋石油支持船智能视频图像危险识别与预警系统中的应用与性能比较. 大数据时代. 2024(09): 41-45 .  百度学术
百度学术
其他类型引用(1)





 下载:
下载: