High-order finite-difference seismic forward modeling method for fluid-solid boundary coupling media
-
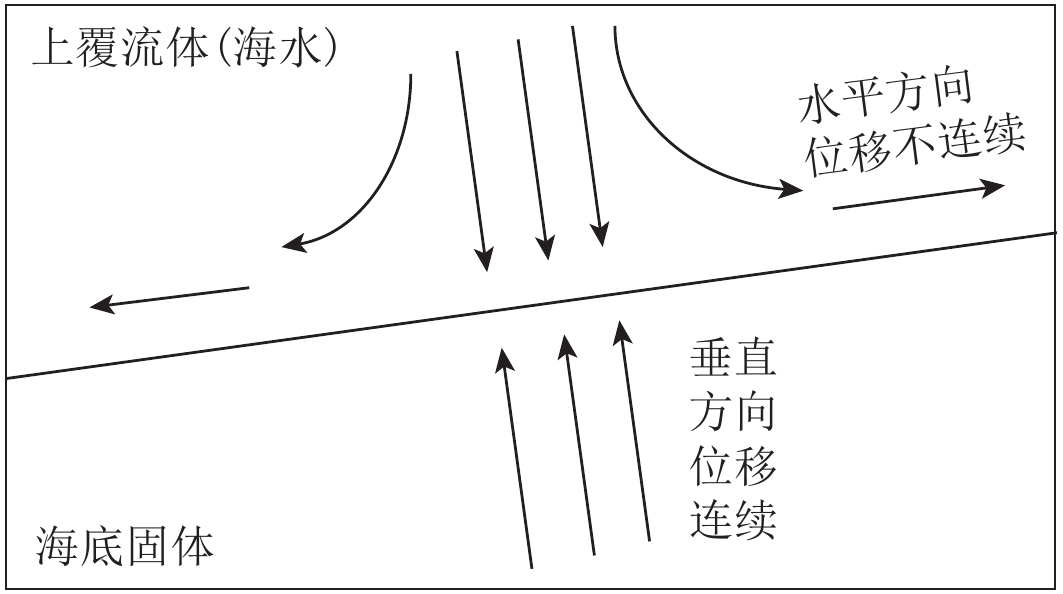
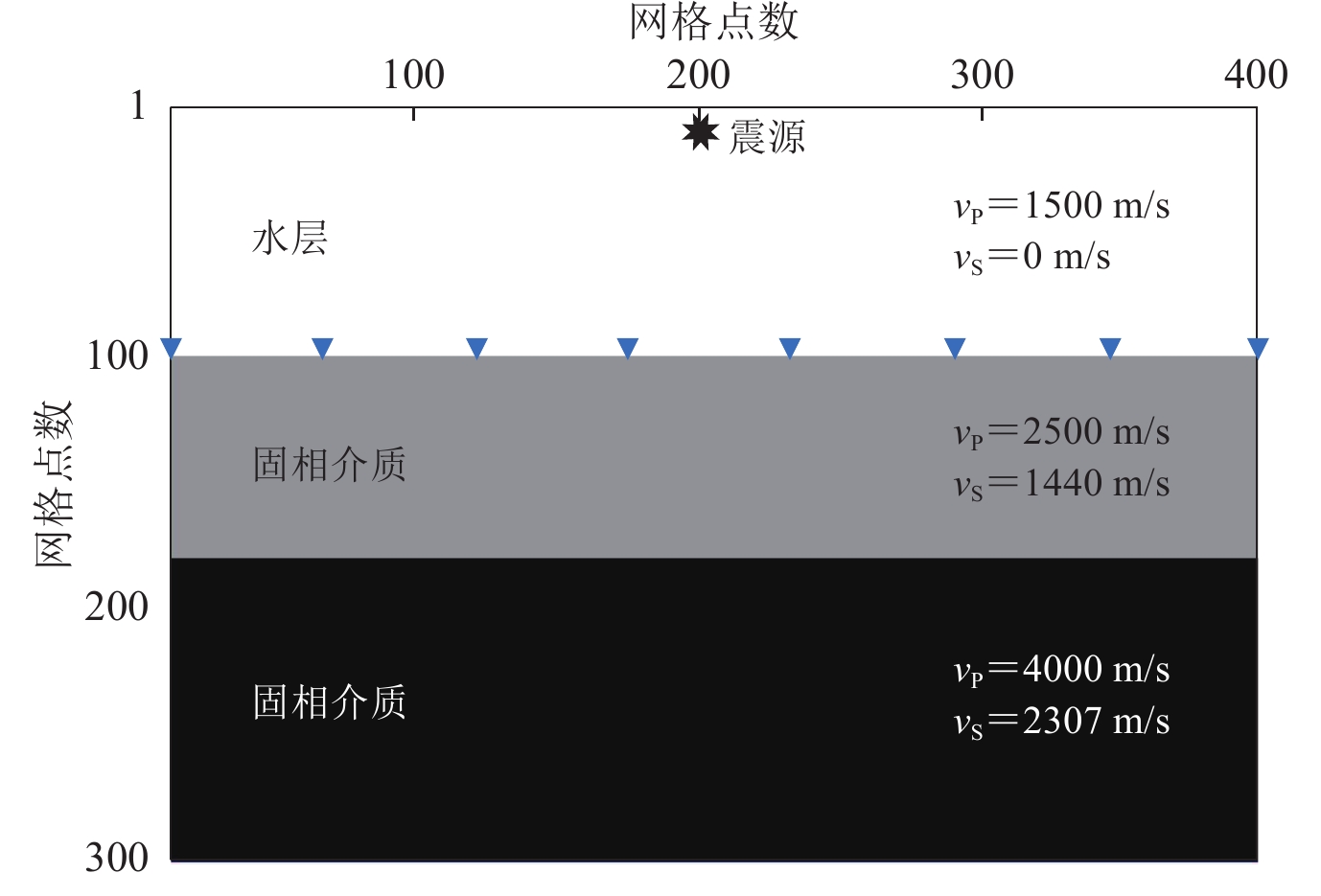
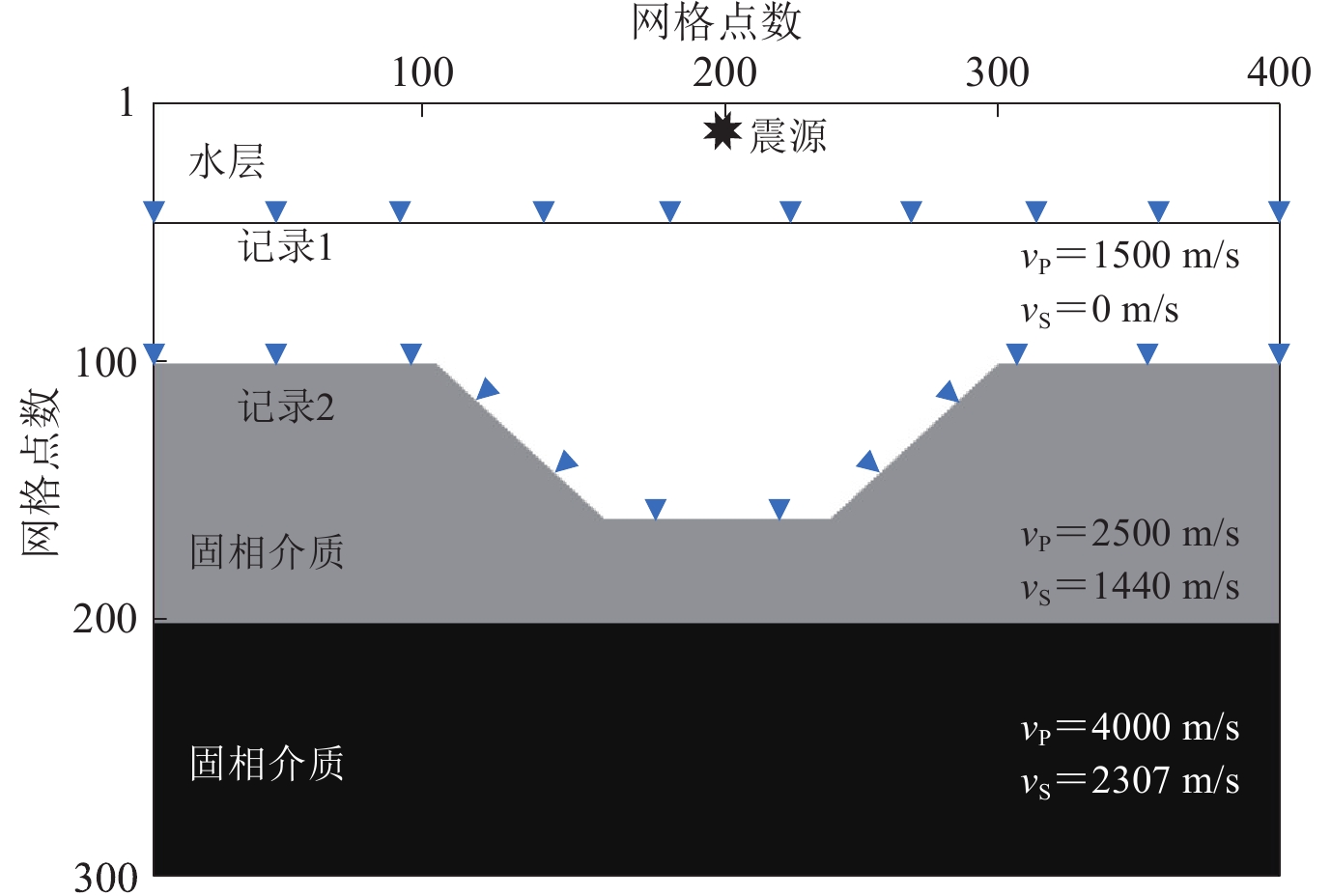
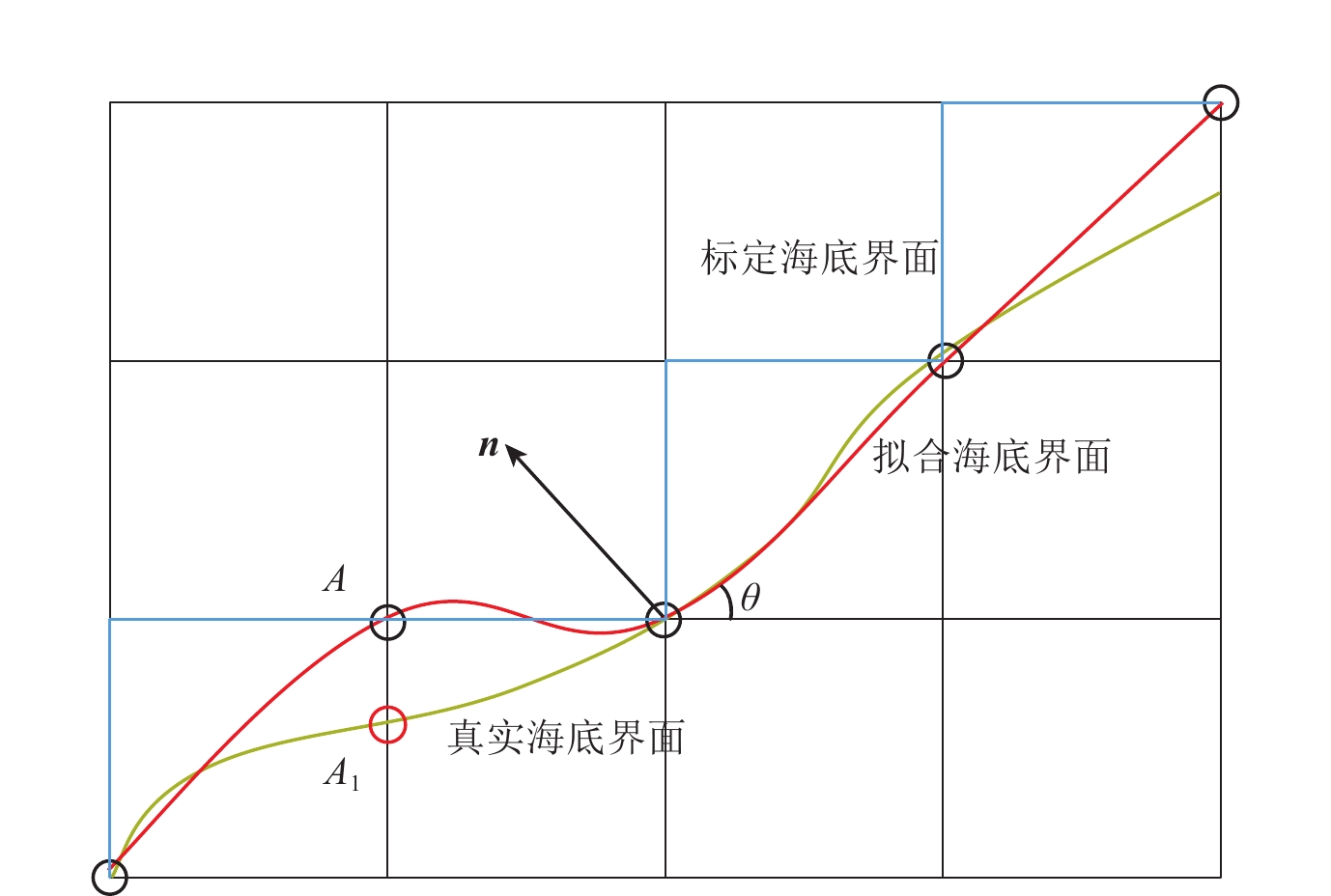
摘要: 本文针对流固边界耦合介质提出了一种高效、稳定的正演数值模拟方法. 首先，从一阶位移-应力弹性波方程出发，基于海底流固边界的位移和应力的连续性条件，采用三次样条海底界面定量表征方法，推导出不规则海底界面下流固边界耦合介质中的地震波波动方程；其次，通过空间微分的高阶差分格式提高数值模拟的空间精度，并结合已推导的地震波波动方程，将四阶时间微分转换至高阶空间微分，进一步提高了数值模拟的时间精度；最后，在与标量波波动方程数值模拟结果对比分析的基础上，分别利用简单的水平层状模型和复杂海底模型，验证和讨论了本文提出的流固边界耦合介质高阶有限差分地震波正演模拟方法的有效性和准确性.Abstract: This paper proposes a novel and stable forward modeling method, which can describe the wave propagation through fluid-solid coupled media. Firstly, we deduce the seismic wave equations of fluid-solid coupled media with irregular interface of seabed utilizing the cubic-spline quantitative method based on the continuity of stress and displacement of the interface. And then, the high-order differential scheme for spatial differentiation is introduced into the method above, which can improve the spatial accuracy of numerical simulation. Furthermore, we also suppress the time discretization that reduces the numerical dispersion by transforming the fourth-order time differential into higher-order spatial differential method. Finally, comparing with results of the scalar wave equation and numerical simulation, we analyze the numerical results of the method proposed in this paper for a simple horizontal layered model and a complex one. The numerical simulation of wave propagation in the fluid-solid coupled media indicates that the method proposed in this paper is convenient and accurate.
-
Keywords:
- seismic forward /
- finite difference /
- scalar wave /
- elastic wave /
- fluid-solid boundary
-
-
![]()
图 1 流固耦合界面正应力连续
${n_x}, \ {n_y}, \ {n_z}$ 表示n与3个坐标轴夹角的余弦Figure 1. Fluid-solid coupling normal stress continuous in interface
${n_x}, \ {n_y}, \ {n_z}$ represents the cosine of the angle between the n and axis![]()
图 2 流固耦合分界面法向位移连续
Figure 2. Displacement continuous in normal direction at the fluid-solid coupling interface
![]()
图 3 时间二阶精度（a）和四阶精度（b）模拟的频散特性对比
Figure 3. Comparison of the dispersion properties of the second-order （a） and the fourth-order （b） time accuracy
![]()
图 5 水平层介质模型的共炮点地震记录
（a） 纯声波记录；（b） 水平分量记录；（c） 垂直分量记录
Figure 5. Common shot point seismic records based on horizontal layered medium model
（a） Pure acoustic records；（b） Horizontal component records；（c） Vertical component records
![]()
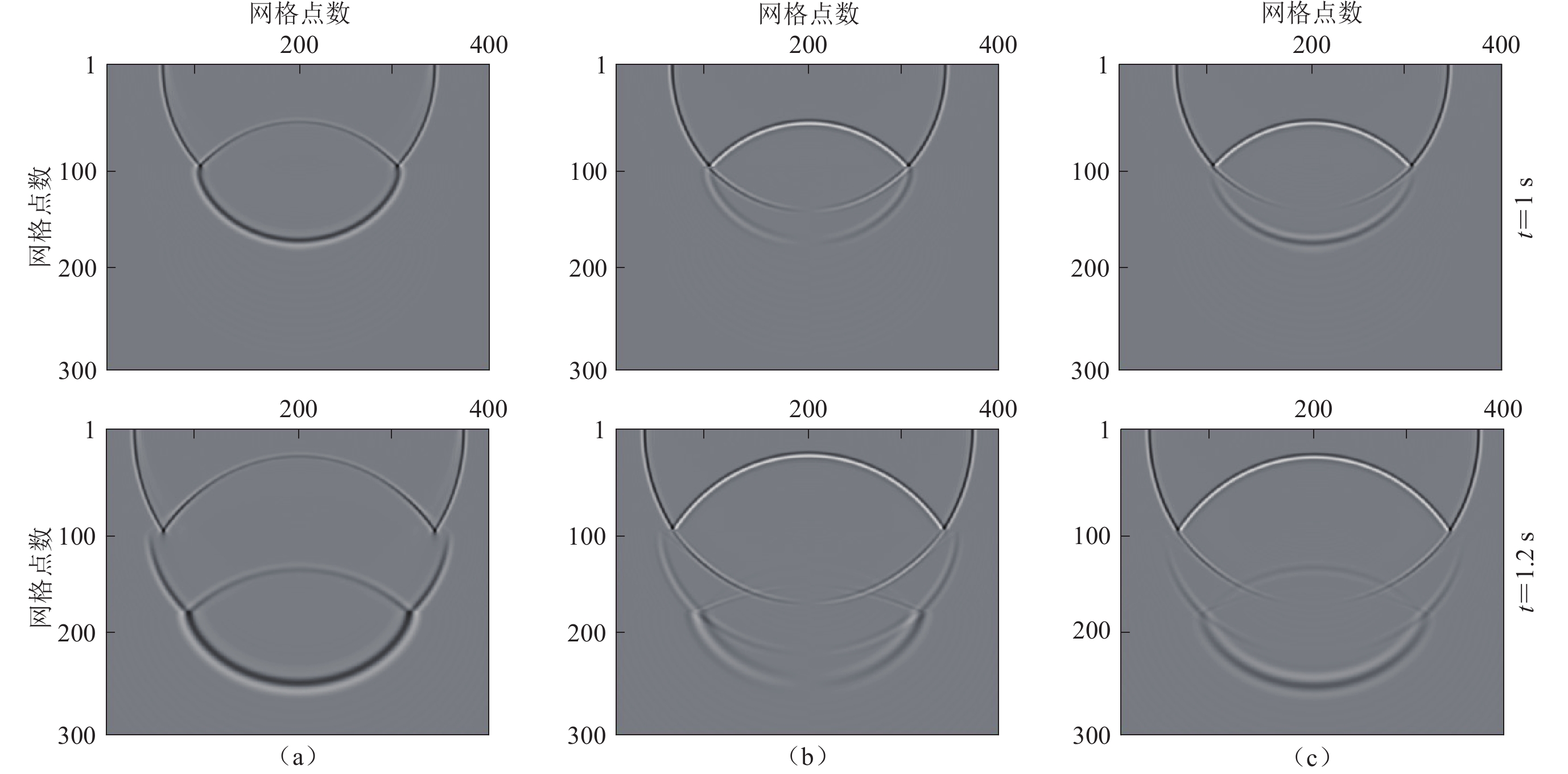
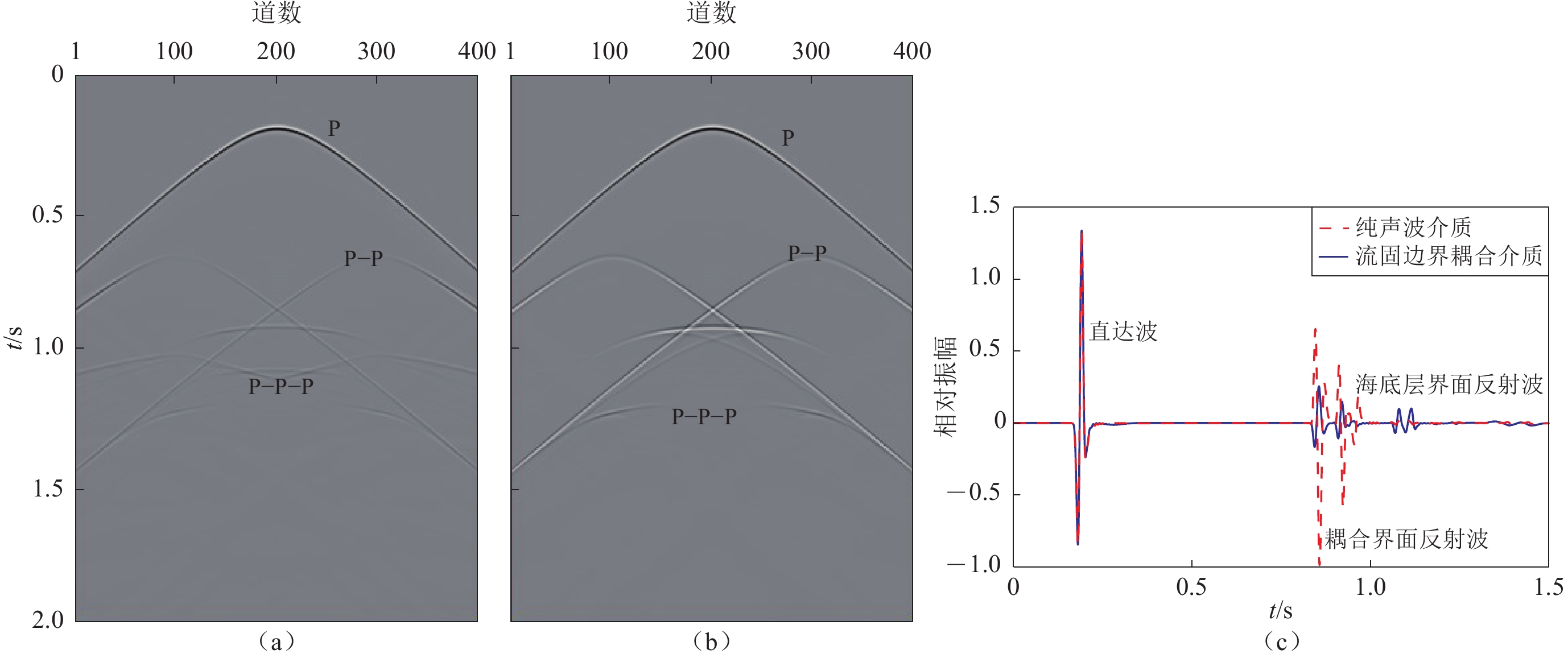
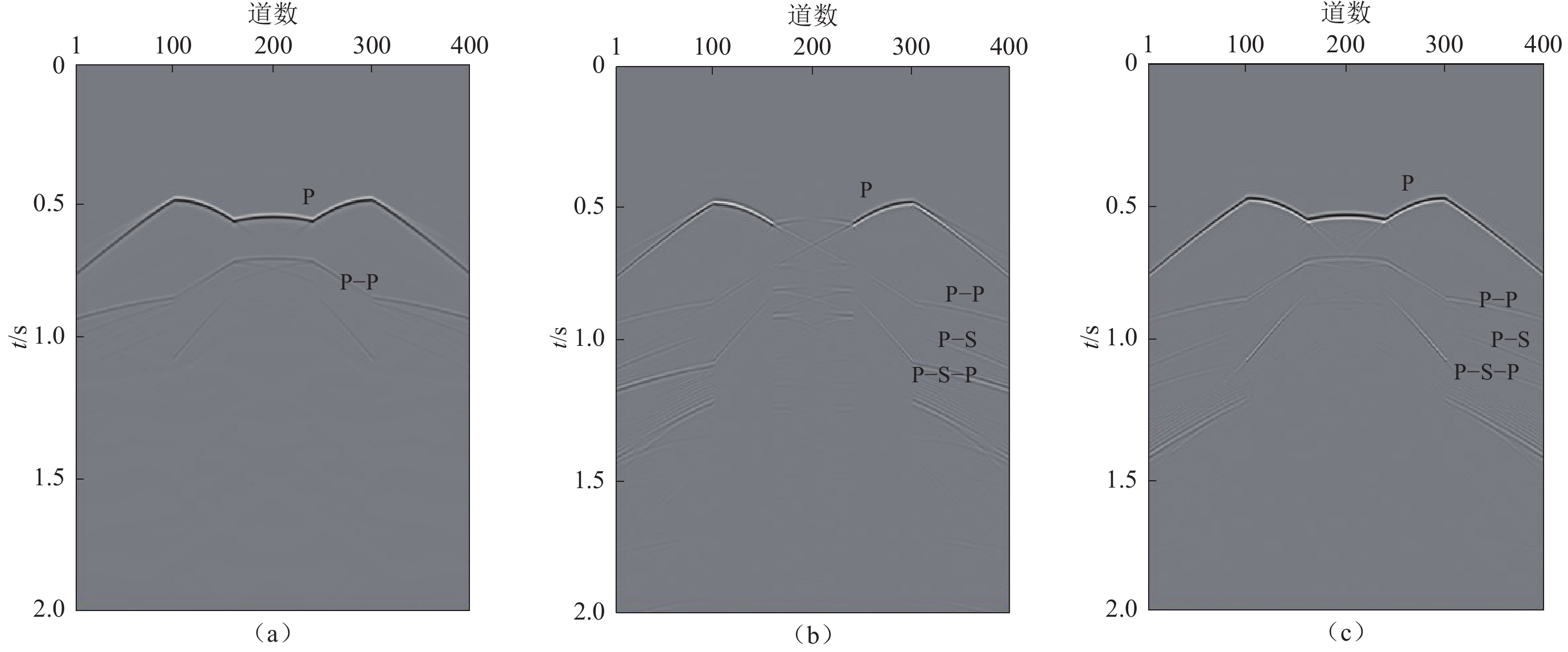
图 6 1 s (上)和1.2 s （下）时的水平层状介质模型波场
（a） 纯声波波场；（b） 应力-位移场中的水平位移分量；（c） 应力-位移场中的垂直位移分量
Figure 6. Snapshots of wavefields based on the horizontal layered medium model at the moment 1 s (upper panels) and 1.2 s (lower panels)
（a） Pure acoustic wavefield；（b） Horizontal displacement component of stress-displacement wavefield；（c） Vertical displacement component of stress-displacement wavefield
![]()
图 8 海底耦合边界的变角度处理
Figure 8. Angle processing strategy of coupled boundary of the seabed
![]()
图 9 凹陷模型拖缆接收共炮点记录
（a） 纯声波记录；（b） 流固边界耦合记录；（c） 图（a）与图（b）中第200道记录的波形对比
Figure 9. Common shot point records received by the streamer based on the sag model
（a） Pure acoustic records；（b） Fluid-solid boundary coupled records；（c） Comparison of the 200th track records in Figs. (a) and (b)
![]()
图 11 纯声波介质与流固边界耦合介质多分量第150道记录对比曲线
Figure 11. Comparison of the 150th record in pure-acoustic wave medium with that of multi-component records in fluid-solid coupled medium
![]()
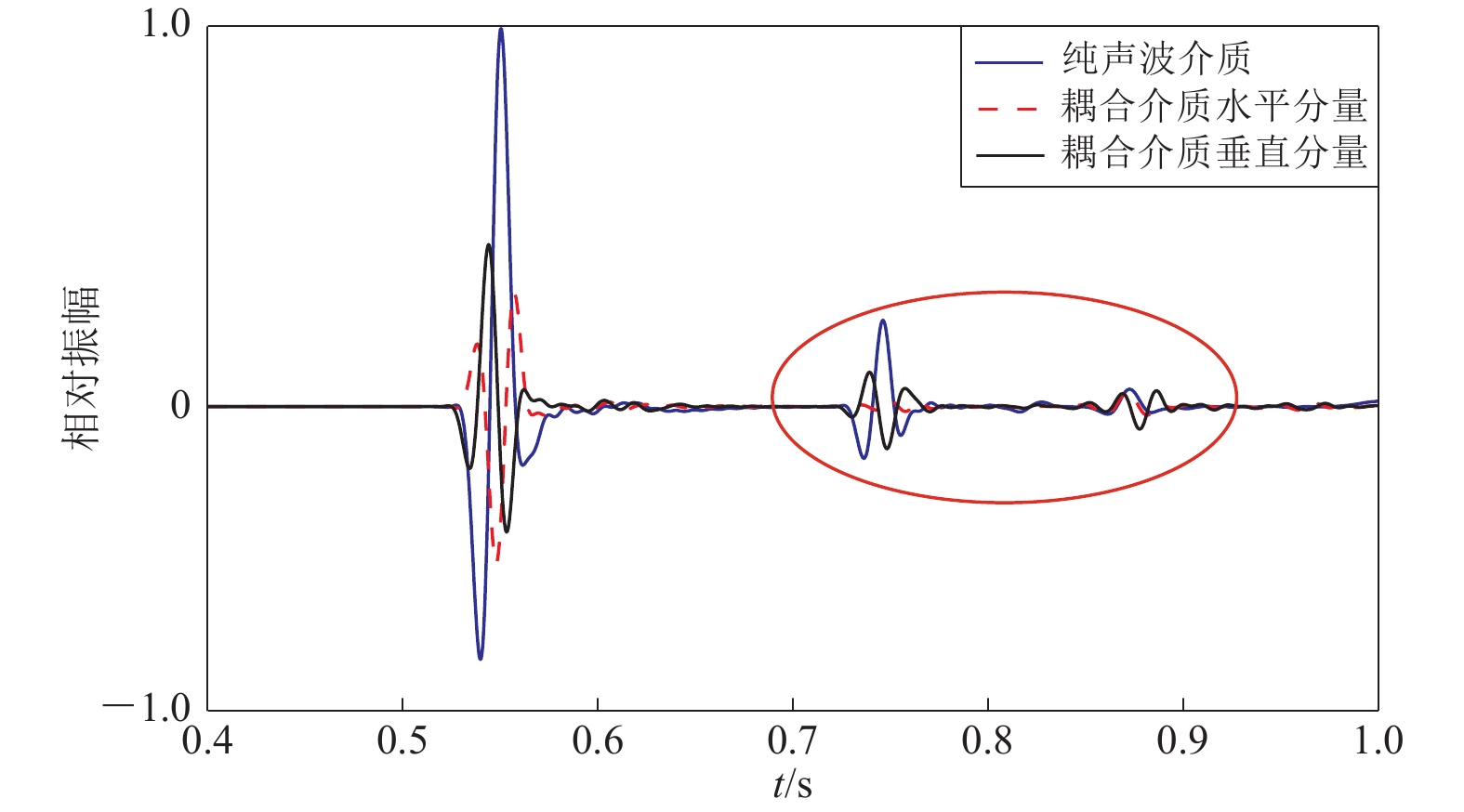
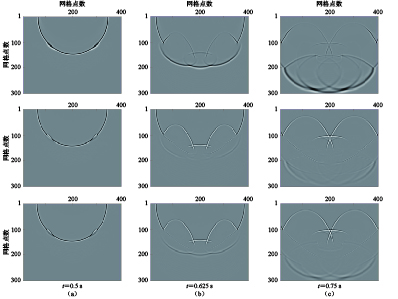
图 12 凹陷模型波场快照
（a） 0.5 s时的纯声波波场；（b） 0.625 s时的应力-位移波场中的水平分量；（c） 0.75 s时的应力-位移波场中的垂直分量
Figure 12. Snapshots of wavefield based on the sag model
（a） Pure acoustic wavefield at the moment 0.5 s；（b） The horizontal component of stress-displacement wavefield at the moment 0.625 s；（c） The vertical component of stress-displacement wavefield at the moment 0.75 s
-
何燕. 2008. 正交各向异性弹性波高阶有限差分正演模拟研究[D]. 青岛: 中国石油大学（华东）: 10–100. He Y. 2008. High-order Finite-Difference Forward Modeling of Elastic-Wave in Orthorhombic Aniostropic Media[D]. Qingdao: China University of Petroleum: 10–100 （in Chinese）.
刘庆敏. 2007. 高阶差分数值模拟方法研究[D]. 青岛: 中国石油大学（华东）: 6–15. Liu Q M. 2007. Method Study of High-Order Finite-Difference Numerical Modeling[D]. Qingdao: China University of Petroleum: 6–15 （in Chinese）.
刘洋, 李承楚, 牟永光. 1998. 任意偶数阶精度有限差分法数值模拟[J]. 石油地球物理勘探, 33（1）: 1–10. Liu Y, Li C C, Mou Y G. 1998. Finite-difference numerical modeling of any even-over accuracy[J]. Oil Geophysical Prospecting, 33（1）: 1–10 （in Chinese）.
吴国忱, 王华忠. 2005. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展, 20（1）: 58–65. Wu G C, Wang H Z. 2005. Analysis of numerical dispersion in wave-field simulation[J]. Progress in Geophysics, 20（1）: 58–65 （in Chinese）.
赵茂强. 2010. 多分量VSP/RVSP正演模拟方法研究[D]. 青岛: 中国石油大学（华东）: 7–48. Zhao M Q. 2010. The Study of Multi-Component VSP/RVSP Seismic Forward Modeling[D]. Qingdao: China University of Petroleum: 7–48 （in Chinese）.
Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves[J]. J Comput Phys, 114（2）: 185–200.
Cho Y, Ha W, Kim Y, Shin C, Singh S, Park E. 2016. Laplace–Fourier–domain full waveform inversion of deep-sea seismic data acquired with limited offsets[J]. Pure Appl Geophys, 173（3）: 749–773.
Choi Y, Min D J, Shin C. 2008. Two-dimensional waveform inversion of multi-component data in acoustic-elastic coupled media[J]. Geophys Prospect, 56（6）: 863-881.
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 51（1）: 54–66.
Higdon R L. 1991. Absorbing boundary conditions for elastic waves[J]. Siam Journal on Numerical Analysis, 1991, 56（2）: 231–241.
Levander A R. 1988. Fourth-order finite-difference P–SV seismograms[J]. Geophysics, 53（11）: 1425–1436.
Lee H Y, Lim S C, Min D J, Kwon B D, Park M. 2009. 2D time-domain acoustic-elastic coupled modeling: A cell-based finite-difference method[J]. Geosci J, 13（4）: 407–414.
Madariaga R. 1976. Dynamics of an expanding circular fault[J]. Bull Seismol Soc Am, 66（3）: 639–666.
Reynolds A C. 1978. Boundary conditions for the numerical solution of wave propagation problems[J]. Geophysics, 43（6）: 1099–1110.
Virieux J. 1986. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 51（4）: 889–901.
Yu P F, Geng J H, Li X B, Wang C L. 2016. Acoustic-elastic coupled equation for ocean bottom seismic data elastic reverse time migration[J] Geophysics, 81（5）: S333–S345.
Zhang J F. 2004. Wave propagation across fluid–solid interfaces: A grid method approach[J]. Geophys J Int, 159（1）: 240–252.
下载:
计量
- 文章访问数: 1517
- HTML全文浏览量: 950
- PDF下载量: 78
