Northern gravity gradient changes of the Nepal MS8.1 earthquake derived from GRACE data
-
摘要: 利用德克萨斯大学空间研究中心发布的GRACE RL05月重力场模型数据，采用300 km扇形滤波，得到2015年尼泊尔MS8.1地震北向重力梯度的时空分布，之后利用最小二乘拟合方法分析尼泊尔及其邻近区域北向重力梯度的长期变化趋势及研究区内6个特征点的北向重力梯度月变化时间序列，并结合黏弹性分层位错理论对GRACE检测尼泊尔MS8.1地震北向重力梯度同震变化的可能性进行分析. 研究结果表明：在尼泊尔MS8.1地震发生前北向重力梯度表现出比较明显的正负异常变化，而该地震即发生在北向重力梯度正负变化的零值线附近；研究区北向重力梯度年变率在印度板块边界及其垂直方向所形成的四象限呈正负相间分布，6个特征点的北向重力梯度在2012年4月出现比较明显的跳变. 由此推断，北向重力梯度的动态变化过程反映了震前区域物质迁移和震后壳幔物质黏滞性调整等问题.
-
关键词:
- GRACE /
- 北向重力梯度 /
- 尼泊尔MS8.1地震 /
- 时间序列 /
- 同震变化
Abstract: Based on the RL05 monthly gravity field model released by Center for Space Research, University of Texas at Austin (UTCSR), the spatio-temporal distribution of northern gravity gradient of the Nepal MS8.1 earthquake is successfully obtained by using 300 km Fan filter. Then we analyzed both the long term change tendency in Nepal and its vicinity areas and monthly time series at six feature points of the northern gravity gradient by the least-squares fitting method. Furthermore, the possibility of the detection on coseismic change of the northern gravity gradient in the Nepal MS8.1 earthquake by GRACE is discussed combined with the viscoelastic-gravitational dislocation theory as well. The results show that, the positive and negative anomaly of the northern gravity gradient is obvious before the Nepal MS8.1 earthquake, which occurred in the vicinity of the zero line; the annual change rate of the northern gravity gradient presents positive and negative distribution in the four quadrants along the Indian Plate boundary and its vertical direction in the studied area, and the northern gravity gradient at the six feature points shows obvious jump in April 2012. Therefore, it is deduced that the dynamic change process of northern gravity gradient reflects mass migration before the earthquake and viscosity adjustment of crust and mantle after the earthquake in Nepal and its vicinity areas.-
Keywords:
- GRACE /
- northern gravity gradient /
- the Nepal MS8.1 earthquake /
- time series /
- coseismic change
-
引言
依据Reid （1910）提出的弹性回跳理论，断层源上强震的复发满足准周期性模型。我国的海原断裂带、可可托海—二台断裂带、鲜水河断裂带、小江断裂带的古地震和历史地震资料均显示出强震的周期性复发行为，因此特征地震的复发行为是普遍的（宋方敏等，1998）。特征地震具有原地复发、震级相近、位错和破裂尺度大致相同的特点（Schwartz，Coppersmith，1984）。现如今特征地震和准周期复发模型是活动断裂强震危险性评价的重要理论基础。然而，大多数活动断裂上地震的复发间隔并不满足准周期性，而是表现为复发间隔的变化。从本文搜集到的45条活动断层古地震复发间隔的统计来看，经无量纲标准化处理（间隔/均值）的复发间隔分布在0.26—2.95之间，具有较大的不确定性，但是复发间隔数据的分布又大致满足正态分布（图1）。这一统计结果与前人的统计结果是一致的（Nishenko，Buland，1987）。可见，大型活动断裂上强震的复发行为介于完美周期性与完全随机性之间，为此，概率方法被用于当前活动断裂未来强震危险性的评价，诸如正态分布、对数正态分布、伽玛（Gamma）分布、韦伯（Weibell）分布等多种概率分布模型被用于表达强震复发间隔的概率分布特征，其中，考虑随机扰动的布朗过程时间（Brownian passage time，简写为BPT）模型是Ellsworth等（1999）和Matthews等（2002）在弹性回跳理论基础上提出的具有一定内在物理基础的强震复发模型，该模型随着美国加州地震概率工作组（Working Group on California Earthquake Proba-bilities，简写为WGCEP）在对加州地区未来30年强震发生概率评价工作中的使用（WGCEP，1999）逐步得到广泛重视；WGCEP （2003， 2007）在其后续工作中时间相关的地震复发模型更是只采用BPT模型，而放弃了其它模型，BPT模型因而成为用于断层强震复发概率评估最重要的模型。
![]()
图 1 古地震复发间隔T/Tave直方图Figure 1. The T/Tave histogram of the recurrence interval for paleo-earthquake events强震概率危险性评估假定某条大型活动断裂复发间隔的概率密度分布函数为f （t），前一次地震发生至今的时间为离逝时间Te，则该断裂上未来时段ΔT内发生强震的概率P随着Te而变化，表示为（Wesnousky，1986）
$P\left({{T_{\rm{e}}}, \Delta T} \right) \text{＝} \frac{{\int_{{T_{\rm{e}}}}^{{T_{\rm{e}}} + \Delta T} {f\left(t \right){\rm{d}}t} }}{{1 - \int_0^{{T_{\rm{e}}}} {f\left(t \right){\rm{d}}t} }}\text{.}$
(1) BPT模型认为断层构造应力（或地震矩）在加载过程中会受到一些随机事件的干扰，整个过程表现为一种稳定加载附加布朗扰动的随机过程。复发间隔数据服从双参数的逆高斯分布，其概率密度函数为
$f\left(t \right) \text{＝} \sqrt {\frac{\mu }{{2{\rm{\pi }}{\alpha ^3}{t^3}}}} \exp \left[ { - \frac{{{{\left({t - \mu } \right)}^2}}}{{2{\alpha ^2}\mu t}}} \right]{\text{，}}$
(2) 式中：μ为断层上强震的平均复发间隔；α为平均复发间隔变异系数，即α越大表示随机干扰对复发间隔的周期性影响越大，α越小表示随机干扰越少，周期性越明显。一个完全没有随机干扰的规则地震序列的复发间隔变异系数α为0。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
然而Ellsworth等（1999）的研究在合成地震序列的过程中并未考虑实测地震序列的α值与其地震事件数目的对应关系，针对这一问题，郭星和潘华（2015）利用蒙特卡洛方法对地震序列中不同样本量统计得到的α值与真实值的偏差进行了定量化研究，最终也得到一个通用的变异系数值α=0.34。该值考虑了不同复发间隔数据序列样本量的多寡对于统计可靠性的影响差异。
通用变异系数值较好地解决了单条断层样本量不足无法得到变异系数值的问题，但是所有活动断层选择一个通用的变异系数值，尽管能够满足单条断层强震复发概率模型的构建需求，但却无法体现断裂复发行为的差异性。实际上，断裂复发行为呈现如此大的不确定性，正是断裂活动的差异性所致，不同断裂活动的运动学和动力学特性往往具有很大差异，不同活动断裂的地震构造条件及其与周边活动断层的交互影响也大不相同。忽略这些具体构造条件，无疑会对强震概率危险性评价的合理性产生影响。
为此，本文拟针对通用变异系数在具体断裂复发间隔概率分布模型中的合理应用进行研究和探讨，以期在联合断裂样本解决通用变异系数统计问题的同时，寻找更为合理地应用通用变异系数解决具体断裂构造复发行为差异表述的可行途径，改进断裂强震危险性概率评价。
1. 复发间隔变异系数的计算
1.1 数据选择
在复发间隔变异系数的估算过程中，若某条断层上的历史地震（或古地震）数据很多，则可以利用统计方法得到该条断层的变异系数；但实际上，在地震序列的选择过程中，地震序列中地震事件的数目往往都比较少，一般来说，对于包含3个或3个以上的地震事件的地震序列，我们才可以同时估计其复发间隔均值和变异系数。Ellsworth等（1999）选取了震级范围为M0.7—9.2的37个地震序列，其中包含一些中小震级的地震。郭星和潘华（2015）的研究则剔除了Ellsworth等（1999）样本集中的小震序列，同时还增加了一些我国的板内强震序列。
为减少地震序列之间的差异，同时考虑到中小地震受周围地震活动的影响较大，本文选取了我国45个板内强震序列，每个序列的地震事件均不少于3个，具体资料列于表1。
1.2 统计计算
根据最大似然估计法，平均复发间隔μ和相邻地震事件间隔的变异系数α为
$\mu \text{＝} E\left[ {{{{T}}_i}} \right], $
(3) $\alpha _i^2 \text{＝} \mu E\left[ {\frac{1}{{{{{T}}_i}}}} \right] \text{－} 1, $
(4) 式中，Ti为每个地震序列中相邻地震事件的时间间隔，大部分相邻古地震事件的时间间隔均会有一些不确定性。表1 中所有断层源的Ti取值为复发间隔不确定性的中值。利用上式计算得到地震序列的αi值处于0.12—0.79的范围内，如图2所示。
![]()
图 2 复发间隔变异系数α的频率直方图Figure 2. Frequency histogram for aperiodicity parameter α of the recurrence interval首先按样本量对不同地震序列的αi进行分组，然后进行均值标准化处理得到αj，标准差为0.16，最后对具有相同样本量的不同地震序列的样本数Nj统计加权平均，即可得到通用的变异系数值αc，
$\alpha _{\rm c}^2 \text{＝} \frac{{\alpha _1^2 {N_1} \text{＋} \alpha _2^2 {N_2} \text{＋} \cdots \text{＋} \alpha _j^2 {N_j}}}{{{N_1} \text{＋} {N_2} \text{＋} \cdots \text{＋} {N_j}}}. $
(5) 通过搜集到的我国大陆内45条断裂上的古地震序列，由上式计算得到一个通用的变异系数αc约为0.37，该值接近于郭星和潘华（2015）所得的通用变异系数值0.34，而小于Ellsworth等（1999）所取的0.5，这说明去掉小地震序列，只分析强震序列时的变异系数偏小，即强震的特征性和周期性更明显。
表 1 45条活动断裂带的古地震数据资料及其变异系数Table 1. Paleo-earthquake data of 45 active faults and corresponding aperiodicitiy parameters编号 断层分段 平均复发
间隔μ归一化
Ti/μ变异系数αi 断层长
度/km滑移速率
/（mm·a−1）断层类型 参考文献 F1 西秦岭北缘断裂鸳凤段 3 922 1.274 9 0.30 75 1.89 左旋走滑 滕瑞增等（1994），张波（2012） 0.637 4 1.087 7 F2 西秦岭北缘断裂黄香沟段 2 463 1.457 3 0.26 72 2.3 左旋走滑 1.165 1 0.759 9 0.860 5 0.757 1 F3 海原断裂带南、西华山段 1 06 0 0.754 7 0.43 73 4.74 左旋走滑 张培震等（2003） 0.669 8 0.575 5 1.707 5 1.292 5 F4 海原断裂带哈思山—
马厂山段（西段）1 927 1.131 5 0.13 100 5.00 左旋走滑 1.043 3 0.8253 F5 榆木山北缘断裂西段 2 177 0.643 2 0.37 50 1.50 逆断层 陈柏林等（2007），金卿等（2011） 1.516 1 0.840 7 F6 榆木山东缘断裂上龙王段 3 350 0.567 2 0.48 25 1.10 逆断层 邹谨敞等（1993） 1.432 8 F7 皇城—双塔断裂上寺段 3 808 1.129 2 0.13 36 2.10 逆断层 王永成和刘百篪（2001） 0.871 1 F8 昌马断裂 3 101 1.260 9 0.23 60 2.71 左旋走滑 康来迅（1986），罗浩等（2013） 0.722 3 1.016 4 F9 肃南断层中段 750 0.693 3 0.32 80 3.00 逆断层 刘百篪等（2008） 1.306 7 F10 冷龙岭断裂西段 1 364 1.375 4 0.21 69 4.09 左旋走滑 李正芳等（2012） 0.843 1 0.982 4 0.799 1 F11 鄂拉山断裂 2 475 1.010 1 0.37 207 2.23 右旋走滑 袁道阳等（2004） 1.616 2 0.767 7 0.606 1 F12 罗山东麓断裂 2 584 1.238 4 0.28 60 右旋走滑 闵伟等（1993） 0.657 9 1.103 3 F13 老虎山毛毛山断裂
（老虎山段）1 150 1.321 8 0.24 78 4.82 左旋走滑 刘小凤等（1994） 0.852 1 0.826 1 1.043 5 0.913 0 1.043 5 2. 变异系数与断层参数的相关性
变异系数反映的是强震复发间隔的非周期性，其产生原因主要是地震孕育过程中所受到的各种随机干扰。不同断层源的地震构造条件以及所受到的随机干扰并不相同，其强震复发间隔变异系数也应该不同。但囿于缺乏数据，统计确定每条断层的复发间隔变异系数不可能实现，因此，本文探讨是否可以将断裂进行适当的划分，并基于此考察变异系数是否存在变化的趋势与规律，据此改善断裂复发间隔概率分布模型。
鉴于本文所搜集到的45条断层上发生的地震序列的断层源参数之间差异很大，下面将讨论变异系数α与活动断层参数（长度、类型、滑动速率）之间的关系，其中断层长度被认为与发震断层的厚度有关，而断层类型和滑动速率与断层破裂过程中的运动形式有关。
引入皮尔逊（Pearson）相关系数来表述变量之间的相关性，皮尔逊相关系数由两个变量的协方差除以两个变量的标准差得到。由协方差和标准差的定义可知，皮尔逊系数介于−1与1之间，当两个变量的线性关系增强时，相关系数趋于1或−1；当一个变量增大，另一个变量也增大时，表明二者之间是正相关，相关系数大于0；当一个变量增大，另一个变量却减小，表明二者之间是负相关，相关系数小于0；若相关系数等于0，表明它们之间不存在线性相关关系。
变异系数α与对应断层源长度l之间的皮尔逊相关系数rαl为
${r_{\alpha l}} \text{＝} \frac{{\sum\limits_{i \text{＝} 1}^n {\left( {{\alpha _i} \text{－} \bar \alpha } \right)( {{l_i} \text{－} \bar l } \, )} }}{{\sqrt {\sum\limits_{i\text{＝}1}^n {{{\left( {{\alpha _i} \text{－} \bar \alpha } \right)}^2}} } \sqrt {\sum\limits_{i\text{＝}1}^n {{{( {{l_i} \text{－} \bar l } \, )}^2}} } }},$
(6) 式中，n为α和l的样本量。为了避免可能存在的异常值对统计结果的影响，本文对n个数据的原始数据重新采样，n次采样每次取n－1个子样本，这样对子样本的统计学处理结果比从完整的数据集计算得到的统计学参数（平均值、标准差、相关系数）能更好地反映数据集的总体特征信息。本文对数据进行1 000次重采样的结果显示，重采样数据的皮尔逊相关系数呈明显的高斯分布，取其平均值得到变异系数α与断层长度l的皮尔逊相关系数，其有效估计仅为0.251 6，即对本文搜集到的我国大陆内45条断裂上的古地震序列进行分析的结果是变异系数α与断层长度之间无明显的相关关系（图3），同样可能由于不同断层类型的数据偏少，断层类型与变异系数α之间也未呈明显的相关性，如图4所示。
![]()
图 3 断层长度l与变异系数α 之间的关系Figure 3. Relation between fault length l and aperiodicity parameter α![]()
图 4 断层类型与变异系数α 之间的关系Figure 4. Relation between fault type and aperiodicity parameter α为了更加准确地评估α与断层参数之间的相关关系，本文对我国大陆内45条断裂上的古地震序列分析可知，其中30条断层的长度集中在100 km以内。由于本文所统计的断层长度侧重于表示活动断层可以孕育大地震的发震断层，而非大地震发生后断层破裂的整体长度，且长度大于100 km的活动断层数据量较少；再考虑到活动断层的研究程度，本文按照上述方法对断层的长度集中于100 km以内的地震序列作相同的相关性检验，得到变异系数α与断层长度l的皮尔逊相关系数的有效估计为−0.418 2，显示为负相关，为中等程度相关（图5）。同理可得到变异系数α与断层滑移速率v的皮尔逊相关系数的有效估计为−0.4736，显示为负相关，也为中等程度相关（图6），这表明随着断层滑移速率和长度的增大，变异系数α有减小的趋势，这也符合Wesnousky （1986）的断层演化模型：长距离和高滑移速率的活动断层，其断层线比较平滑，即活动断层的“成熟程度”较高，强震复发的特征性和周期性较稳定。
![]()
图 5 断层长度（≤100 km）与变异系数α 之间的关系Figure 5. Relation between fault length （≤100 km） and aperiodicity parameter α![]()
图 6 断层滑移速率与变异系数α 之间的关系Figure 6. Relation between horizontal sliding rate and aperiodicity parameter α为解决单个断层源上重复发生地震的历史数据稀少的问题而假定所有断层源上的强震复发间隔具有一个相同的变异系数，显然缺乏可靠的科学依据，所以加州概率工作组（WGCEP，2003）在使用Ellsworth等（1999）统计得到的变异系数通用值（α＝0.5）时，采用对不同α进行加权平均，即α （权值）为0.3 （0.2），0.5 （0.5），0.7 （0.3）；但由于该办法没有明确的物理意义，其效果实际上与取通用值（α＝0.5）几乎没有差别。根据本文的上述分析，考虑在对活动断层作概率地震危险性评估时，对变异系数进行适当的调整。本文提出利用上述计算得到变异系数αj的标准差，对通用变异系数αc＝0.37作一倍标准差（0.16）运算，将其应用于具有巨大差异的地震序列。具体而言，当活动断层的“成熟程度”较高，即强震复发的特征性和周期性较稳定时，选择对αc少一倍标准差（0.37－0.16＝0.21）作为通用变异系数；当活动断层的“成熟程度”相对较高，即强震复发的特征性和周期性相对较稳定时，选择αc＝0.37作为通用变异系数；当活动断层的“成熟程度”不高，即强震复发的特征性和周期性一般时，选择对αc多一倍标准差（0.37＋0.16＝0.53）作为通用变异系数。
3. 讨论与结论
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
根据上述结论，本文利用经均值标准化的变异系数αj，对通用变异系数（αc＝0.37）作一倍标准差运算，并提出以下建议：① 若所评估断层的特征性很明显，断层活动受外界干扰很小，可以选择αc少一倍标准差（αc＝0.21）作为通用变异系数；② 若所评估断层的特征性相对明显，断层受周边地质构造影响不是很清楚，可以选择αc＝0.37作为通用变异系数；③ 若所评估断层的特征性一般，周边有其它多条活动断层及其它外界干扰，可以选择αc多一倍标准差（αc＝0.53）作为通用变异系数。 但实际应用中对活动断层的分类以及变异系数的选择，还需要进一步研究。
-
![]()
图 1 尼泊尔及其邻近区域地形及2008—2015年MS≥7.0地震分布
Figure 1. Topography and distribution of MS≥7.0 earthquakes in Nepal and its vicinity areas from 2008 to 2015
![]()
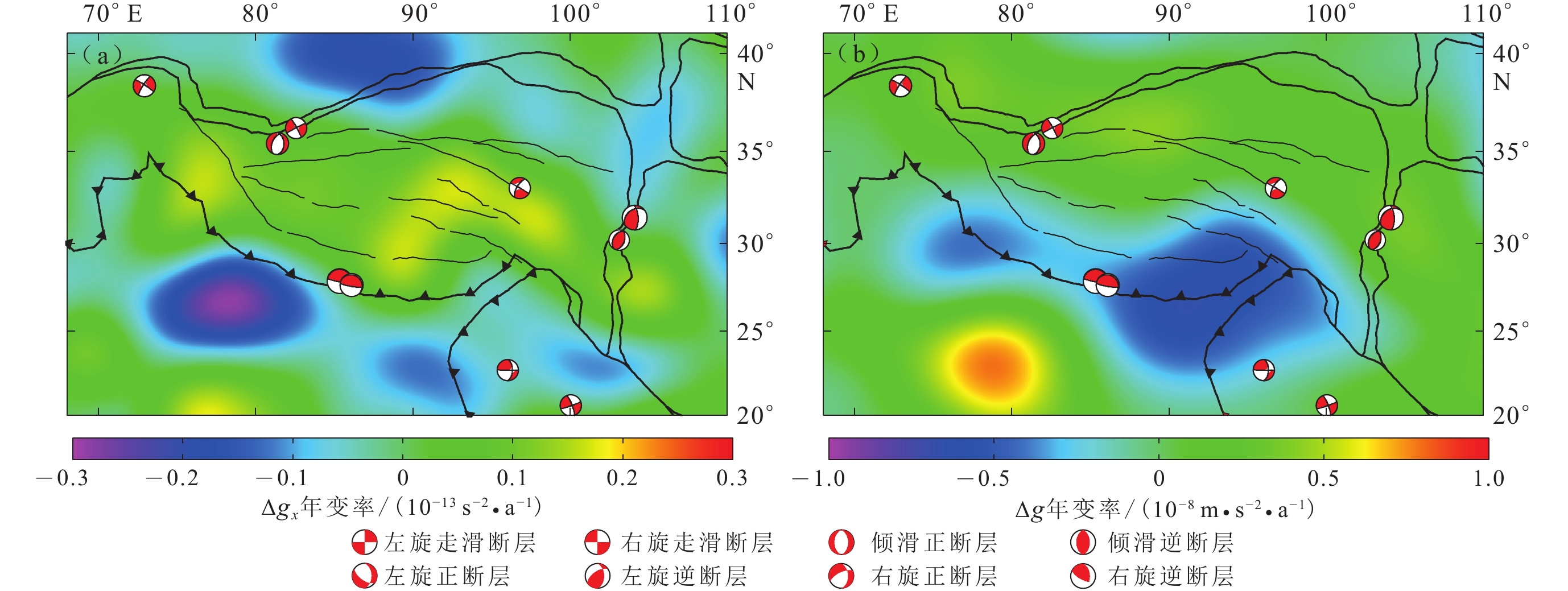
图 2 与2012—2014年月平均重力场差分后得到的2015年9月全球重力变化Δg分布（a）及北向Δgx （b）、东向Δgy （c）和垂向Δgz （d）重力梯度变化分布
Figure 2. The difference of global gravity change Δg （a） and gravity gradient change of north Δgx（b），east Δgy （c），and vertical Δgz （d） components from GRACE monthly data between September 2015 and the mean field from 2012 to 2014
![]()
图 3 尼泊尔及其邻近区域2008—2015年年度累积北向重力梯度
Figure 3. Annual northern gravity gradient from 2008 to 2015 in Nepal and its vicinity areas
（a） 2008；（b） 2009；（c） 2010；（d） 2011；（e） 2012；（f） 2013；（g） 2014；（h） 2015
![]()
图 4 特征点A—F北向重力梯度变化Δgx的时间序列，红色虚线表示北向重力梯度发生跳变的时间，下同
Figure 4. Time series of the northern gravity gradient changes Δgx for feature points A−F，the red dashed line denotes the time when the northern gravity gradient jumped，the same below
（a） A； （b） B；（c） C；（d） D；（e） E；（f） F
![]()
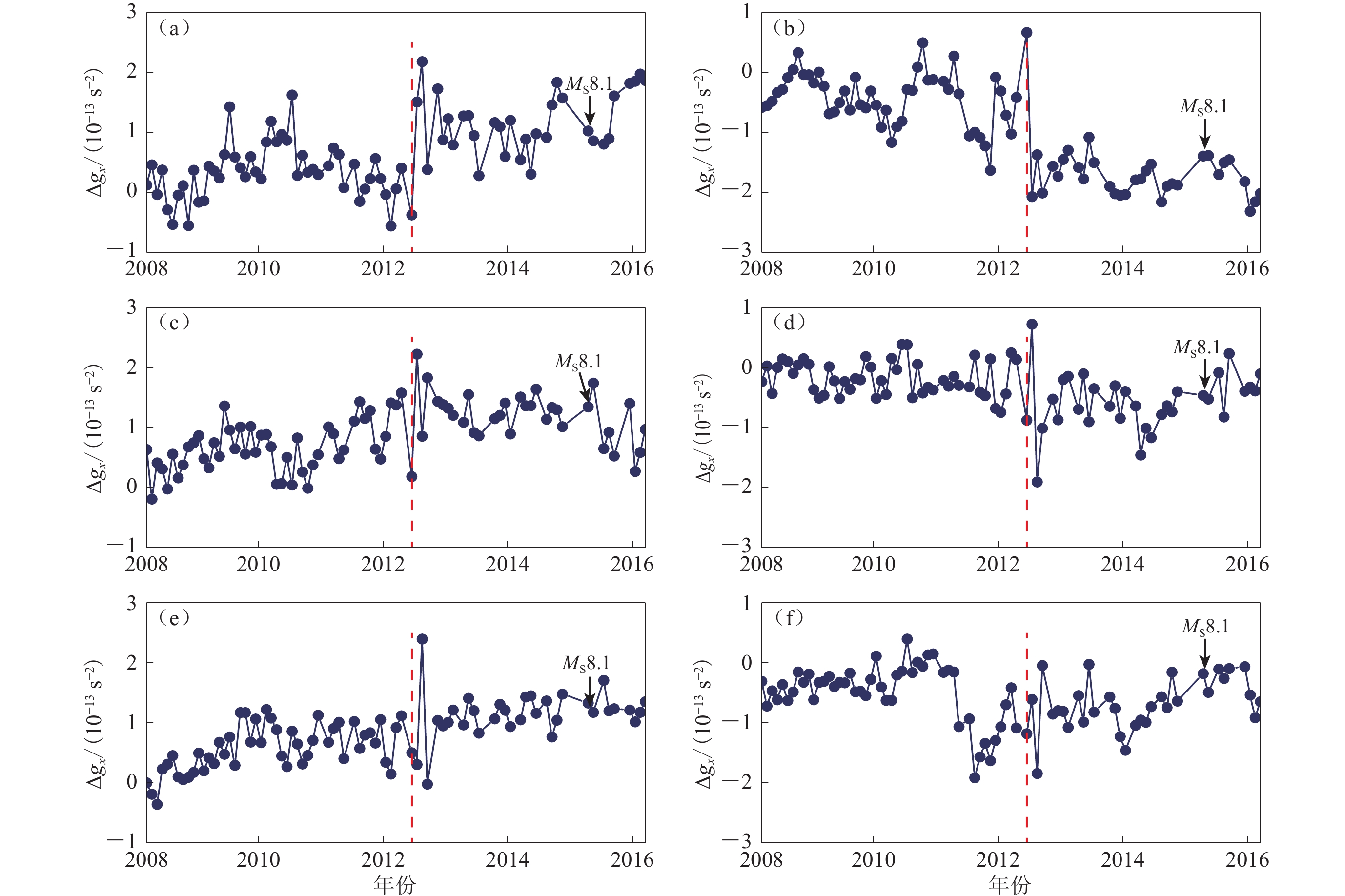
图 5 喜马拉雅断裂带两侧北向重力梯度Δgx的相对变化
（a） 印度板块上点B相对于青藏地块上点C的变化； （b） 印度板块上点D相对于青藏地块上点C的变化
Figure 5. The northern gravity gradient relative change Δgx series of the points in bilateral sides of Himalayan orogenic belt
（a） The relative change of point B on Indian Plate to point C on Tibetan Plateau; （b） The relative change of point D on Indian Plate to point C on Tibetan Plateau
![]()
图 6 尼泊尔及其邻近区域北向重力梯度Δgx年变率（a）及重力Δg年变率（b）
Figure 6. Annual change rate of northern gravity gradient Δgx （a） and gravity Δg （b） in Nepal and its vicinity areas
![]()
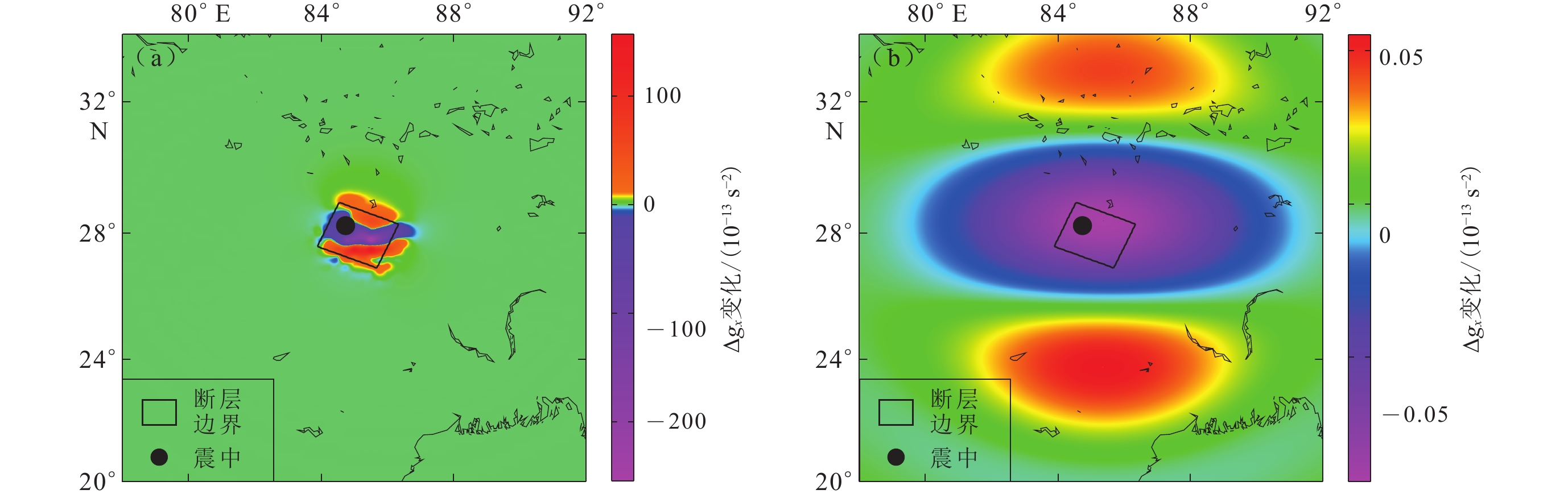
图 7 尼泊尔MS8.1地震的理论北向重力梯度Δgx同震变化
（a） 空间固定点的北向重力梯度变化； （b） 平滑处理后的北向重力梯度变化
Figure 7. Theoretically coseismic northern gravity gradient Δgx change of the Nepal MS8.1 earthquake calculated by PSGRN/PSCMP
（a） Northern gravity gradient change on the space-fixed points; （b） Northern gravity gradient change after filtering
![]()
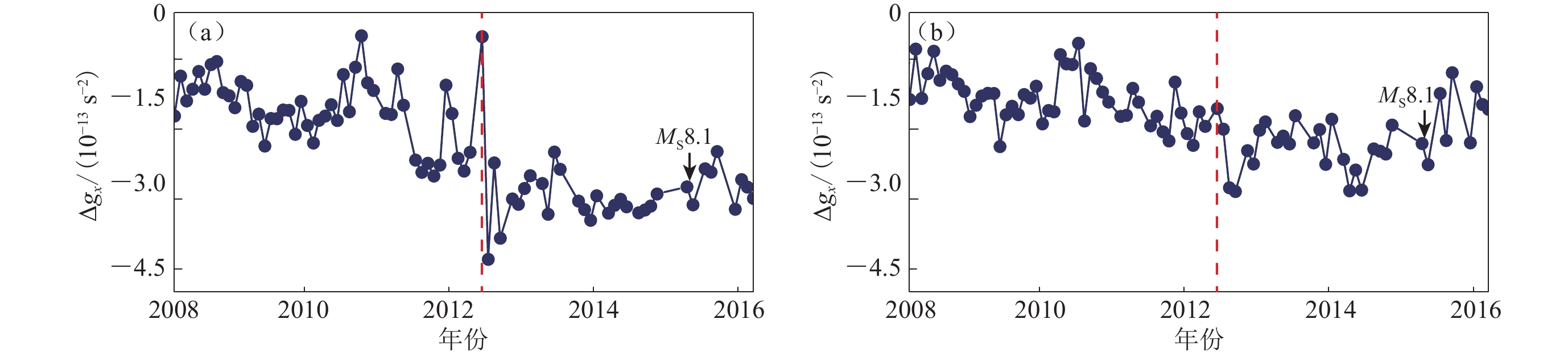
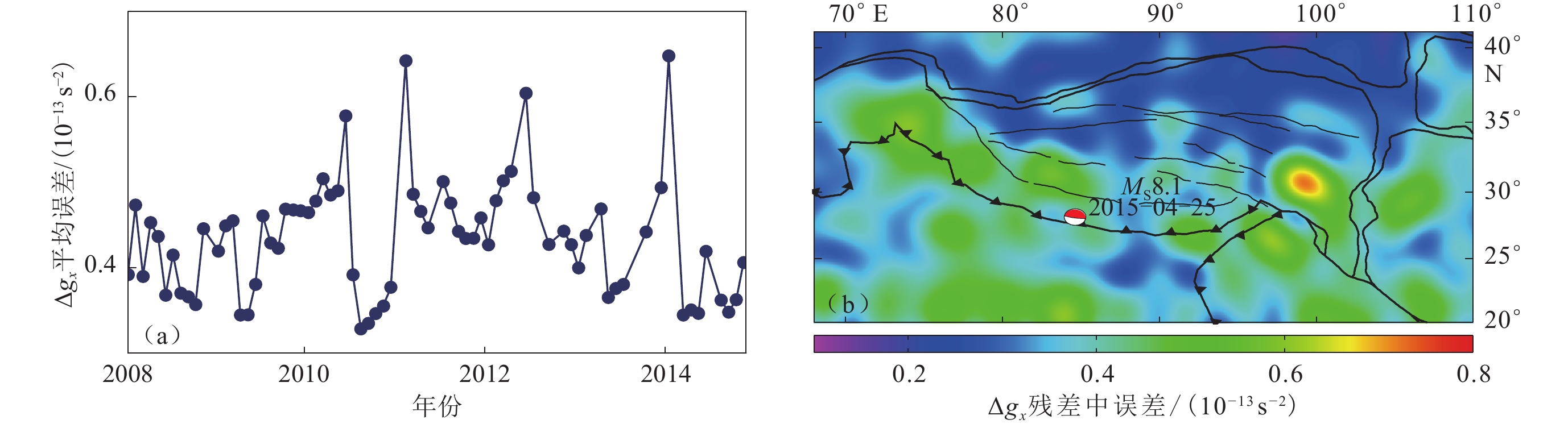
图 8 尼泊尔及其邻近区域北向重力梯度Δgx误差
（a） 2008—2014 Δgx年平均误差时间序列；（b） 拟合所得北向重力梯度残差中误差的空间分布
Figure 8. Errors of northern gravity gradient Δgx in Nepal and its vicinity areas
（a） The regional average errors change series from 2008 to 2014; （b） The root mean square errors of the northern gravity gradient residuals by using least squares fitting
表 1 尼泊尔MS8.1地震的4层地球模型
Table 1 The four layer model of Nepal MS8.1 earthquake from Crust1.0
深度/km 密度/(103 kg·m−3) vP/(km·s−1) vS/(km·s−1) 0—23.65 2.72 6.00 3.52 23.65—36.73 2.79 6.30 3.68 36.73—50.90 2.85 6.60 3.82 50.90—∞ 3.45 8.44 4.68 
下载: 导出CSV
-
邓起东, 程绍平, 马冀, 杜鹏. 2014. 青藏高原地震活动特征及当前地震活动形势[J]. 地球物理学报, 57（7）: 2025-2042. Deng Q D, Cheng S P, Ma J, Du P. 2014. Seismic activities and earthquake potential in the Tibetan Plateau[J]. Chinese Journal of Geophysics, 57（7）: 2025-2042（in Chinese）.
高春春, 陆洋, 张子占, 史红岭, 朱传东.2015. GRACE重力卫星探测南极冰盖质量平衡及其不确定性[J]. 地球物理学报, 58(3):780-792. Gao C C, Lu Y, Zhang Z Z, Shi H L, Zhu C D.2015. Ice Sheet mass balance in Antarctica measured by GRACE and its uncertainty [J]. Chinese Journal of Geophysics, 58(3):780-792. （in Chinese）
徐锡伟, 闻学泽, 叶建青, 马保起, 陈杰, 周荣军, 何宏林, 田勤俭, 何玉林, 王志才, 孙昭民, 冯希杰, 于贵华, 陈立春, 陈桂华, 于慎鄂, 冉勇康, 李细光, 李陈侠, 安艳芬. 2008. 汶川Ms8.0地震地表破裂带及其发震构造[J]. 地震地质, 30（3）: 597-629. Xu X W, Wen X Z, Ye J Q, Ma B Q, Chen J, Zhou R J, He H L, Tian Q J, He Y L, Wang Z C, Sun Z M, Feng X J, Yu G H, Chen L C, Chen G H, Yu S E, Ran Y K, Li X G, Li C X, An Y F. 2008. The Ms8.0 Wenchuan earthquake surface ruptures and its seismogenic structure[J]. Seismology and Geology, 30（3）: 597-629（in Chinese）.
杨晓平, 吴果, 陈立春, 李传友, 陈晓莉. 2016. 青藏高原南缘2015年尼泊尔Mw7.8地震发震构造[J]. 地球物理学报, 59（7）: 2528-2538. Yang X P, Wu G, Chen L C, Li C Y, Chen X L. 2016. The seismogentic structure of the April 25, 2015 Mw7.8 Nepal earthquake in the southern margin of Qinghai-Tibetan Plateau[J]. Chinese Journal of Geophysics, 59（7）: 2528-2538（in Chinese）.
周新, 孙文科, 付广裕. 2011. 重力卫星GRACE检测出2010年智利Mw8.8地震的同震重力变化[J]. 地球物理学报, 54（7）: 1745-1749. Zhou X, Sun W K, Fu G Y. 2011. Gravity satellite GRACE detects coseismic gravity changes caused by 2010 Chile Mw8.8 earthquake[J]. Chinese Journal of Geophysics, 54（7）: 1745-1749（in Chinese）.
祝意青, 徐云马, 吕弋培, 李铁明. 2009. 龙门山断裂带重力变化与汶川8.0级地震关系研究[J]. 地球物理学报, 52（10）: 2538-2546. Zhu Y Q, Xu Y M, Lü Y P, Li T M. 2009. Relations between gravity variation of Longmenshan fault zone and Wenchuan Ms8.0 earthquake[J]. Chinese Journal of Geophysics, 52（10）: 2538-2546（in Chinese）.
祝意青, 赵云峰, 李铁明, 梁伟锋, 徐云马, 郭树松. 2014. 2013年甘肃岷县漳县6.6级地震前后重力场动态变化[J]. 地震地质, 36（3）: 667-676. Zhu Y Q, Zhao Y F, Li T M, Liang W F, Xu Y M, Guo S S. 2014. Dynamic variation of gravity field before and after the Minxian-Zhangxian Ms6.6 earthquake on July 22, 2013, Gansu, China[J]. Seismology and Geology, 36（3）: 667-676（in Chinese）.
邹正波, 罗志才, 吴海波, 申重阳, 李辉. 2012. 日本MW9.0地震前GRACE卫星重力变化[J]. 测绘学报, 41（2）: 171-176. Zou Z B, Luo Z C, Wu H B, Shen C Y, Li H. 2012. Gravity changes observed by GRACE before the Japan Mw9.0 earthquake[J]. Acta Geodaetica et Cartographica Sinica, 41（2）: 171-176（in Chinese）.
邹正波, 李辉, 吴云龙, 吴桂桔, 康开轩. 2015. 尼泊尔M8.1地震震前卫星重力场时变特征[J]. 大地测量与地球动力学, 35（4）: 547-551. Zou Z B, Li H, Wu Y L, Wu G J, Kang K X. 2015. Characteristics of satellite time-variable gravity field before M8.1 Nepal earthquake[J]. Journal of Geodesy and Geodynamics, 35（4）: 547-551（in Chinese）.
Chen J L, Rodell M, Wilson C R, Famiglietti J S. 2005. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment（GRACE）water storage estimates[J]. Geophys Res Lett, 32（14）: L14405.
De Linage C, Rivera L, Hinderer J, Boy J, Rogister Y, Lambotte S, Biancale R. 2009. Separation of coseismic and postseismic gravity changes for the 2004 Sumatra-Andaman earthquake from 4.6 yr of GRACE observations and modelling of the coseismic change by normal-modes summation[J]. Geophys J Int, 176（3）: 695-714.
Eshagh M. 2009. On Satellite Gravity Gradiometry[D]. Sweden: Royal Institute of Technology: 8–16.
Gross R S, Chao B F. 2001. The gravitational signature of earthquakes[G]//Gravity, Geoid and Geodynamics 2000. Heidelberg: Springer: 205–210.
Han S C, Shum C K, Bevis M, Ji C, Kuo C Y. 2006. Crustal dilatation observed by GRACE after the 2004 Sumatra-Andaman earthquake[J]. Science, 313（5787）: 658-662.
Imanishi Y, Sato T, Higashi T, Sun W K, Okubo S. 2004. A network of superconducting gravimeters detects submicrogal coseismic gravity changes[J]. Science, 306（5695）: 476-478.
Li J, Shen W B. 2011. Investigation of the co-seismic gravity field variations caused by the 2004 Sumatra-Andaman earthquake using monthly GRACE data[J]. J Earth Sci, 22（2）: 280-291.
Matsuo K, Heki K. 2011. Coseismic gravity changes of the 2011 Tohoku-Oki Earthquake from satellite gravimetry[J]. Geophys Res Lett, 38（7）: L00G12.
Mikhailov V, Tikhotsky S, Diament M, Panet I, Ballu V. 2004. Can tectonic processes be recovered from new gravity satellite data?[J]. Earth Planet Sci Lett, 228（3/4）: 281-297.
Mittal H, Kumar A. 2015. Stochastic finite-fault modeling of MW 5.4 earthquake along Uttarakhand-Nepal border[J]. Nat Hazards, 75（2）: 1145-1166.
Prajapati S K, Kumar A, Chopra S, Bansal B K. Intensity map of Mw 6.9 2011 Sikkim–Nepal border earthquake and its relationships with PGA: distance and magnitude[J]. Nat Hazards, 69（3）: 1781-1801.
Rodell M, Velicogna I, Famiglietti J S. 2009. Satellite-based estimates of groundwater depletion in India[J]. Nature, 460（7258）: 999-1002.
Shah A A. 2013. Two great historical earthquake ruptures revealed in Nepal[J]. Curr Sci, 104（8）: 994.
Sun W K, Okubo S. 2004. Coseismic deformations detectable by satellite gravity missions: a case study of Alaska（1964, 2002）and Hokkaido（2003）earthquakes in the spectral domain[J]. J Geophys Res, 109（B4）: B04405.
Sun W K, Okubo S, Fu G Y, Akito A. 2009. General formulations of global co-seismic deformations caused by an arbitrary dislocation in a spherically symmetric earth model-applicable to deformed earth surface and space-fixed point[J]. Geophys J Int, 177（3）: 817-833.
Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data[J]. Geophysical Research Letters, 33（8）: 2006-2009.
United States Geological Survey. 2015. Updated finite fault results for the Apr 25, 2015 MS8.1 35 km E of Lamjung, Nepal earthquake( Version 2) [EB/OL]. [2015-05-16]．https://earthquake.usgs.gov/earthquakes/eventpage/us20002926#executive.
Wahr J, Swenson S, Zlotnicki V, Velicogna I. 2004. Time-variable gravity from GRACE: first results[J]. Geophys Res Lett, 31（11）: L11501.
Wahr J, Swenson S, Velicogna I. 2006. Accuracy of GRACE mass estimates[J]. Geophys Res Lett, 33（6）: L06401.
Wang L, Shum C K, Jekeli C. 2012. Gravitational gradient changes following the 2004 December 26 Sumatra–Andaman earthquake inferred from GRACE[J]. Geophys J Int, 191（3）: 1109-1118.
Wang R J, Lorenzo-Martín F, Roth F. 2006. PSGRN/PSCMP—a new code for calculating co- and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory[J]. Comput Geosci, 32（4）: 527-541.
Yagi Y, Okuwaki R.2015. Integrated seismic source model of the 2015 Gorkha, Nepal, earthquake[J]. Geophysical Research Letters, 42(15):6229-6235.
Yi S, Sun W K. 2014. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models[J]. J Geophys Res, 119（3）: 2504-2517.
Zhang Z Z, Chao B F, Lu Y, Hsu H T. 2009. An effective filtering for GRACE time-variable gravity: fan filter[J]. Geophysi Res Lett, 36（17）: L17311.
Zhong M, Duan J B, Xu H Z, Peng P, Yan H M, Zhu Y Z. 2009. Trend of China land water storage redistribution at medi- and large-spatial scales in recent five years by satellite gravity observations[J]. Chin Sci Bull, 54（5）: 816-821.
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 2056
- HTML全文浏览量: 1319
- PDF下载量: 63
- 被引次数: 1
