A method for identifying the baseline drift of strong-motion records based on L1-norm regularization
-
摘要: 本文提出了一种基于L1范数正则化的基线校正新方法，即以拟合速度时程误差最小为目标，以基线漂移本身尽可能小为约束条件，经过凸优化多次迭代自动求解出满足条件的基线漂移，避免了人为选取基线漂移分段次数和基线漂移起止时刻的主观干扰；随后利用该方法对多组加入了基线漂移噪声模型的强震动加速度记录进行验证。结果表明：本文方法对于识别和处理单段式、两段式和多段式的基线漂移噪声具有普适性，能敏锐地捕捉到速度时程发生漂移的趋势（斜率变化），无需预先设定加速度基线漂移模型也可有效地识别出多种基线漂移噪声的起止位置和漂移程度；地震记录事前部分对本文方法处理结果影响较大，当记录事前部分足够长时（如20 s），识别基线漂移噪声的准确性较高，位移时程可以较好地与原始位移匹配；而对于发生漂移的速度时程，本文方法可以不受地震事前部分长短的干扰，甚至在加速度记录出现明显丢头现象时，也能很好地实现峰值速度和整个速度时程的恢复。Abstract: To identify the accurate baseline drift in ground acceleration, velocity, and displacement time series is one of the basic and challenge problems in the research of strong ground motion. This study proposes a new baseline-correction method based on L1-norm regularization. It aims at minimizing the error of fitting velocity trace subject to let the sum of absolute values of acceleration baseline drift be small. As the baseline-offset is figured out by the convexity-optimized tool automatically in this L1-norm regularization based baseline-correction method, the subjective interferences can be well avoided such as selecting segmentation times and the start and end moments. And then representative noise models of acceleration baseline offset are added respectively to typical strong-motion records in order to test and verify the new method. The results shows that our method is universal for identifying and processing single-, double-, and multi-stage baseline drift noises. It can sensitively capture the trend （slope） change of the velocity trace while it’s no need to set segmentation times and positions of piecewise linear fitting in advance. The pre-event interval of strong-motion record has a great influence on the processing results of this method. If the pre-event interval is long enough （e.g. 20 seconds） in a record, the identification of the baseline drift noise will be much more accurate, and the recovered displacement trace will match better with the real one. Additionally, this method shows good performance to recover peak ground velocity and the whole velocity time series even if the record almost has no pre-event portion.
-
引言
强震动观测是地震工程和工程地震研究中的重要环节。大量有价值的强震动记录，可为震源机制、地震动衰减规律、场地和活断层对地震动的影响、土与结构的相互作用、典型结构的地震反应特性等方面的研究提供可靠的基础资料（彭小波等，2010，2011）。而强震动加速度记录中往往会存在基线漂移（Iwan et al，1985 ；Boore，2001；周宝峰等，2013），Chiu（1997）指出微小的加速度漂移会导致积分得到的速度和位移产生巨大的数值误差，例如0.01 cm/s2加速度漂移在持时为60 s时，积分得到的速度会有0.6 cm/s的误差，得到的最终位移误差可达到18 cm，而速度时程和位移时程对于地震近断层地面运动规律和极震区抗震设计等的深入研究具有重要作用（于海英等，2009）。
合理判断强震记录中基线漂移的位置及漂移程度并提供合理可行的校正方法，是强震动数据处理的基本问题之一（周宝峰等，2013）。模拟式记录仪的强震动记录，由于缺少事前部分等原因，判断零线复杂且不准确，研究人员普遍认为模拟式记录仪得到的加速度记录难以用来估算位移（Housner，1947；Hershberger，1955；Trifunac，1970；Trifunac，Lee，1974）。20世纪70年代逐渐发展起来的数字强震仪，具有高精度、宽频带和预存储特性（Boore，2005），有效地克服了模拟式记录仪的缺点。此后，研究人员通过对帕克菲尔德地震、集集地震和汶川地震等一系列重大地震的数字强震动记录的研究（Iwan et al，1985 ；Boore，2001；Wang et al，2003 ；Wu，Wu，2007；Chao et al，2010 ；Wang et al，2011a ，2013），认为数字强震仪的加速度记录积分得到的位移包含长周期信息，对于近断层大震所产生的地面永久位移，在一定条件下可以通过高质量的加速度记录积分得到，然而加速度记录中普遍存在的基线漂移对最终位移影响较大。周宝峰等（2013）指出为防止永久位移信息的损失或畸变，客观地获得地震动永久位移，采用基线校正的方法进行强震动记录以避免滤波。但是由于加速度时程中基线漂移的复杂性，很难从加速度记录中直观地、准确地判断基线漂移的起始和结束位置以及漂移的程度。因此，通常选择速度时程为切入点进行分析，从而识别永久位移。彭小波等（2011）将获取近断层同震位移的基线处理方法总体概括为基于分段拟合和基于小波分析两大类，而在选择合适的分段拟合方法时可以将加速度噪音模型分为单段式、多段式和脉冲式；同时也指出真实的加速度噪声形式可能更为复杂，使用几种模型联合分析或开发新模型来进行评估很有必要，这些方法应注意平衡主观经验和客观判断条件。Wang等（2011a）在总结前人研究的几种基线校正方法后认为，基于阈值方法确定基线漂移时刻的方法往往会导致对真实基线偏移的评估不准确，因为基线漂移不一定伴随着最强烈的地面震动，而其它校正方法虽然可以通过手动调整参数来校准改善，但参数选择都是由研究人员主观决定的，基于此其提出一种改进的可自动化的经验基线校正方法。
现今通用的基线校正方法中，一般假设加速度在某个给定的时间段内发生基线漂移，且给定了基线漂移的次数。这些参数往往是凭借主观经验给定的。通常根据对原始记录积分得到速度时程的漂移情况进行判断，然后运用分段线性拟合速度的方法，获得加速度时程的基线漂移。但在分段拟合时如何确定分段次数和分段点位置，即加速度在什么时间段内发生偏移，往往需要人为进行选择。这导致了该类基线校正程序的主观性太强，不容易标准化和自动化（周宝峰等，2013）。
当地震发生以后，不同震级和频率特性的地震波传播到不同距离和场地条件的台站，强震仪采集到的加速度记录中发生基线漂移的随机性很强。以基线漂移初始时刻的选取为例，最为常用的有两种方式：一是认为基线漂移主要受强震仪的仪器响应影响，发生在加速度大于50 cm/s2的初始时刻；二是认为基线漂移主要受到地面初始震动影响，发生在地震波P波到达的初始时刻。导致加速度漂移的因素繁多且随机性强，不仅会产生低频误差（包括仪器噪声、背景噪声、初始值等），还会因地面扭转和倾斜导致仪器倾斜，因此很难清楚地确定加速度漂移所发生的具体时刻。无论是选择强震仪记录的加速度幅值达到事先确定的某个阈值的时刻，还是选择强震仪所在位置的地面初始震动时刻，都是基于研究人员对强震动数据已有认识的一种经验判断。对集集地震和汶川地震中大量强震动记录进行基线校正，得出主观干预选择基线漂移分段起止点的位置，这对基线校正处理后得到的位移结果有很大的影响（Boore ，2001；Wang et al，2003 ；王国权，周锡元，2004；周宝峰等，2013）。
为此，本文拟运用凸优化中的L1范数正则化方法，求得满足条件的加速度基线漂移最优解，即以分段线性拟合速度时程的方差与求解的基线漂移的绝对值之和最小为目标，不再人为选取基线漂移的起止时刻点，尝试获得一种适用性更为广泛的基线校正方法；并通过对人工加入加速度基线漂移噪声的识别，检验该方法在进行基线校正处理时识别基线漂移的准确性和精度。
1. L1范数正则化
范数是用于衡量某个向量空间（或矩阵）中的每个向量长度或大小的量。L1范数则表示某个向量中所有元素绝对值的和，它可以有效地实现稀疏表示（sparse representations），防止数据过拟合，有利于特征选取，通过不断迭代优化去掉数据中无效信息的特征，把这些特征对应的权重置为零；此外其模型结构也相对简单，更具有“可解释性”。因L1范数具有较好的优化求解特性（可以解决非确定性多项式问题，即NP-hard问题）被广泛应用。
L1范数正则化是双准则式（即保证拟合残差Ax －b较小的同时，也使得向量x尽可能小），残差用Euclid范数（||Ax －b||2）度量，而正则化用L1范数（||x||1）进行（Boyd，Vandenberghe，2004）。L1范数正则化可以用作求取稀疏解的启发式算法，可以较好地解决下式求解最小值的优化问题：
$ \mathop {\min }\limits_x f\left( x \right) {\text{＝}} {\left| {\left| {{{A}}x {\text{－}} b} \right|} \right|_2} {\text{＋}} \lambda {\left| {\left| x \right|} \right|_1}{\text{，}} $
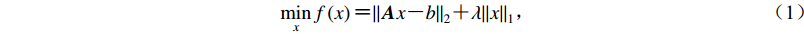
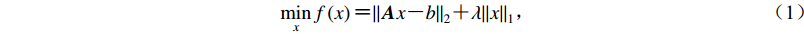
(1) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
由于基线漂移受多种因素的综合影响，本文认为：① 加速度基线发生漂移是随机的、预先无法确定漂移次数的；② 某一时刻基线发生漂移后会保持不变，在另一时刻发生突变后一段时间内继续保持不变，即加速度漂移是时间的分段线性函数（阶梯函数）；③ 地震动结束后速度尽量为零。在以上假设基础上，基于常用的最小二乘分段线性拟合速度时程，以找到加速度基线漂移的思路，结合L1范数的稀疏性特点，本文提出运用L1范数正则化方法来求解最优化的基线漂移，以在拟合漂移的速度时程时方差最小为目标，并同时使得所求的基线漂移本身也尽可能小。即在式（1）中设b为待拟合的速度，x为所需求解的基线漂移。然后运用MATLAB中CVX凸优化工具包来求解x。根据Schmidt （2005）对参数λ取值方法的总结和Tibshirani （1996）给出的示例，本文设置正则化参数λ为1，即拟合误差项和L1范数正则化项对求解目标函数最小值具有同等重要的贡献。
2. 地震加速度数据与基线漂移噪声模型的选取
本文设计了一组试验来验证提出的基于L1范数正则化方法识别基线漂移位置和漂移程度的可靠性和精确性。首先，选择合适的地震动加速度记录作为原始记录，加入已知的人工基线漂移噪声；其次，用本文方法对加完噪声后的数据进行处理以计算出加速度基线漂移，将其求解得到的基线漂移与人工加入的已知基线漂移噪声进行对比，以此来测试新方法对加速度时程中的基线漂移有效识别的程度；最后，通过原始数据与加入噪声处理后的速度和位移的比较，检验新方法对于速度和位移时程的恢复效果。
本文选用Akkar和Boore （2009）在讨论基于蒙特卡罗方法识别典型基线漂移噪声模型的基线校正方案中所采用的地震记录，以及工程应用上最为常用的El Centro波，作为测试基于L1范数正则化基线校正方法识别人工基线漂移噪声的原始地震记录。相应的数据从美国太平洋地震工程研究中心（Pacific Earthquake Engineering Research Center，简写为PEER）强震数据库下载，这些记录已进行了仪器校准、基线校正和滤波处理。限于篇幅，本文仅以1999年中国台湾集集地震TCU129台南北分量，1999年土耳其迪兹杰（Duzce）地震Bolu台东西分量和1940年美国帝王谷（Imperial Valley）地震的El Centro Array #9台的南北分量（即El Centro波）为例，具体信息列于表1，其中，事前部分（地震波P波到时）采用Allen （1978，1982）提出的P波捡拾方法—长短时平均算法（STA/LTA）计算得出，其余信息来自PEER （2013）的NGA-West2中的地震元数据。
表 1 本文所列地震记录信息（PEER，2013）Table 1. Information about digital accelerograms shown in this study （PEER，2013）发震年 地震 MW P波到时/s 持时/s 分量方向 台站名称 场地类型* 震中距/km 1940 帝王谷地震 6.95 0.04 40 NS El Centro Array#9 D 12.99 1999 迪兹杰地震 7.14 5.39 56 EW Bolu D 41.27 1999 集集地震 7.62 20.65 90 NS TCU129 C 14.16 注：场地类型采用美国地震减灾计划（National Earthquake Hazards Reduction Program，NEHRP）给出的A，B，C，D和E等5类场地条件划分类型（ Huang et al，2010 ）.对于加速度基线漂移噪声模型，根据Akkar和Boore （2009）提出的典型加速度基线漂移噪声可概括为4类：单段式、两段式、多段式和斜线式。Wang等（2011a）、彭小波等（2011）和荣棉水等（2014）在对现有基线校正方法总结后认为，相对于简单的单段式和复杂的多段式，两段式是基线校正方法中最为普遍采用的基线漂移模型。在两段式加速度基线漂移校正方法中，广为使用的是Iwan等（1985）提出的两段式校正方法及其改进方法（于海英等，2009；Wang et al，2011a ，2013）、修正方法（Boore，2001，2005；Wu，Wu，2007；Chaoet al，2010 ；荣棉水等，2014；Jones et al，2017 ）。考虑到基线漂移的常见形式，以及L1范数正则化所求解出来的基线漂移形式是分段线性函数（由L1范数的稀疏性决定），本文选择单段式、两段式和多段式的加速度基线漂移噪声模型，如图1所示。
![]()
图 1 本文采用的典型加速度基线漂移噪声模型（修改自Akkar，Boore，2009）tb和te分别为加速度记录的起、止时刻，t1和t2分别为加速度绝对值在第一次和最后一次大于50 m/s2时刻，t3为[t1，t2]中间时刻，am1和am2分别为加速度在强烈震动时段的加速度漂移幅值，af为加速度最终保持的漂移幅值Figure 1. Representative sketches of acceleration baseline-offset noise models （modified from Akkar，Boore，2009）tb and te are respectively the beginning and ending of the recording， the time t1 and t2 represent the first and last time that the recording’s absolute values are larger than 50 m/s2， t3 is the medium time between t1 and t2，am1 and am2 mean the two consecutive constant offsets during the strong ground shaking，af is the final offsetIwan等（1985）认为加速度记录在第一次和最后一次大于50 m/s2时刻（分别记为t1，t2）的强烈震动区间[t1，t2]最有可能发生基线漂移，而从加速度记录的最初时刻tb到第一次大于50 m/s2时刻t1一般不发生漂移，而漂移发生后会持续到记录最终时刻te。本文在具体设置基线漂移噪声模型参数时，参考Akkar和Boore （2009）提出的典型加速度基线漂移模型，但对其幅值进行了适当调整。其中，单段式噪声模型在加速度记录的[t1，te]区间漂移量af保持为5 m/s2；两段式噪声模型在加速度记录的[t1，t2]区间漂移量am1保持为5 m/s2，在[t2，te]区间漂移量af保持为−2 m/s2；多段式（三段）噪声模型在加速度记录的[t1，（t1＋t2）/2]和[（t1＋t2）/2，t2]区间的漂移量am1，am2分别为2 m/s2和−2 m/s2，在[t2，te]区间的漂移量af保持为5 m/s2。
3. 结果和分析
3.1 两段式
图2给出了本文方法对于两段式基线噪声模型的识别和处理结果，可以看出在对集集地震TCU129台站南北向记录、迪兹杰地震Bolu台站东西向记录和帝王谷地震El Centro台站南北向记录加入两段式基线漂移噪声后，加速度时程的变化并不明显（图2a），但通过加速度积分得到的速度时程出现了明显漂移（图2b），对速度时程再次积分得到的位移时程漂移会更大。而速度时程和位移时程，特别是位移时程，对于近场地面运动破坏、中长周期结构对地震动响应等研究有着十分重要的作用。整体而言，本文方法在识别两段式基线噪声模型时，分段线性拟合速度时程和恢复位移时程表现较好。
![]()
图 2 L1范数正则化方法对于两段式基线漂移噪声模型的识别和处理结果（a） 地震加速度时程；（b） 速度时程；（c） 加速度基线；（d） 位移时程Figure 2. The results of identifying and processing double-stage baseline-offset noise model based on the L1-norm regularization method（a） Acceleration time history；（b） Velocity time history；（c） Acceleration baseline-offset；（d） Displacement time history从识别出的加速度基线漂移与加入的两段式基线噪声模型的两次漂移位置和漂移程度的对比结果（图2c）可以看出：对于TCU129台南北向记录，利用本文方法处理得到的基线漂移几乎与加入的已知噪声模型完全吻合；Bolu台东西向记录处理得到结果在基线两次发生漂移的时刻点都吻合得很好，基线漂移程度在一段很短的时段有−1.1 m/s2的偏差；而El Centro台南北向记录处理得到的结果略有偏差，在基线第一次发生漂移的起始位置大约滞后了0.5 s，基线漂移程度最大偏差为＋1.3 m/s2，但在第二次漂移时，位置和漂移程度均能准确吻合。本文方法在对基线漂移识别时，处理后的TCU129台南北向记录结果优于Bolu台东西向记录，远优于El Centro台南北向记录。其原因在于，这几条记录的事前部分存在明显差异（见表1中的“P波到时”），其中TCU129台南北向记录事前部分足够长（20.65 s），Bolu台东西向记录事前部分较短（5.39 s），而El Centro台南北向记录存在明显的丢头现象。如图3所示，从PEER下载的El Centro台南北向记录明显缺乏事前部分，且其初始记录部分并不为零（如黑线所示，前0.8 s内均值为5.8 m/s2，前2 s均值为8.3 m/s2）。而使用本文方法处理时，得到该初始部分的基线漂移为2.4 m/s2 （图3中红线），即本文方法在处理缺乏足够事前部分且其初始记录部分不为零的加速度记录时，会造成地震记录的事前部分尽量靠近零线（图3的绿线）。这说明地震记录的事前部分越充分，越有利于识别基线漂移的准确位置和大小，由此也就更有利于恢复速度时程和位移时程。
位移时程的处理结果受加速度基线漂移识别的准确程度影响很明显（图2d），TCU129台南北向记录处理后的效果要远远好于El Centro台南北向记录，而Bolu台东西向记录处理后的效果处在两者之间。对于El Centro台南北向记录，在使用本文方法处理后得到的位移时程最初时刻到基线第二次漂移这段时间内（0—30 s），处理后的位移与原始数据的位移有明显偏差。其原因是该时间段内本文方法识别的El Centro台南北向加速度的基线漂移与已知的基线漂移噪声模型在漂移时刻和漂移程度上存在偏差。为进一步探讨基线识别偏差引起的位移时程变化，对本文方法识别出来的基线漂移与已知的基线漂移噪声模型差值（即处理后的加速度减去加入噪声的加速度）进行分析处理，将差值积分后得到速度差值，然后再积分得到位移差值，结果如图4所示，由于加速度基线差值是不规则的分段函数，其分段的大小和持续时间不同，经过两次积分得到位移的差值与加速度差值的正负关系不完全相匹配，具有一定的“滞后”性。
![]()
图 4 本文方法所识别的El Centro台南北向记录与加入两段式噪声模型后的基线漂移噪声差值Figure 4. The difference between baseline-offset identified by this paper and added two-stage noise model for El Centro NS component3.2 单段式和多段式
本文方法在识别单段式基线噪声模型时，拟合速度时程和恢复位移时程表现较好（图5）。用本文方法处理TCU129台南北向记录和Bolu台东西向记录后，所得基线漂移结果与已知的单段式加速度基线噪声的漂移位置和漂移程度均吻合较好，所得的位移时程也能很好地与原始数据位移时程相匹配。而对于El Centro台南北向记录，本文方法在识别其加速度基线发生漂移的起始时刻大约滞后了0.5 s，基线漂移程度最大偏差为＋1.4 m/s2，其原因也是El Centro台南北向记录事前部分的缺失，且初始记录部分的加速度值不为零（图3）。
![]()
图 3 El Centro台南北向初始部分记录处理结果Figure 3. Comparison of the original record with the results processed by the new method in the pre-event portion of El Centro NS components record![]()
图 5 基于L1范数正则化方法对单段式基线漂移噪声模型的识别和处理结果（a） 地震加速度时程；（b） 速度时程；（c） 加速度基线；（d） 位移时程Figure 5. The results of identifying and processing on records added single-stage baseline-offset noise model based on the L1-norm regularization method（a） Acceleration time history；（b） Velocity time history；（c） Acceleration baseline-offset；（d） Displacement time history多段式是加速度基线漂移模型中较为复杂的模式，本文方法能敏锐地捕捉到速度时程发生漂移的趋势（斜率变化），其表现为速度拟合分段次数更多，如图6c所示，每两条灰色虚线之间即为一次分段拟合，更准确地拟合出发生漂移的速度时程。而由于加速度基线漂移由分段线性拟合的速度所间接求得，因此得到的加速度基线漂移段数也会更多（图6d）。由于人工判读识别往往会忽略小的变化趋势，本文所提出的基于L1范数正则化的基线校正方法运用凸优化工具不断迭代优化求解，能自动计算出拟合误差尽量小、分段数量合适的速度时程拟合线段，对速度时程的漂移更加“敏感”，可更有效地识别出速度漂移现象（即速度整体漂移的趋势变化）。对于TCU129台南北向记录和Bolu台东西向记录，本文方法处理后位移时程与原始位移时程能够很好地匹配吻合；而对于缺少事前部分的El Centro台南北向记录，本文方法恢复的位移时程与原始位移时程存在一定的偏差。
![]()
图 6 基于L1范数正则化方法对于多段式基线漂移噪声模型的识别和处理结果（a） 地震加速度时程；（b） 速度时程；（c） 加速度基线；（d） 位移时程Figure 6. The results of identifying and processing on records added multi-stage baseline-offset noise model based on the L1-norm regularization method（a） Acceleration time history；（b） Velocity time history；（c） Acceleration baseline-offset；（d） Displacement time history本文方法通过对分别加入单段式、两段式和多段式加速度基线漂移噪声的地震动记录进行处理，可以较好地拟合出漂移的速度记录，由此可以有效地识别加速度基线漂移位置和漂移程度。经过本文方法基线校正处理后，加入噪声的TCU129台南北向记录和Bolu台东西向记录经过两次积分得到的位移可以很好地与最初的原始数据位移时程进行匹配。而针对缺少事前部分（记录丢头现象）的El Centro台南北向记录，本文方法处理后的位移时程与最初的位移时程存在一定的偏差，但处理后的速度时程在各个噪声模型下都能很好的与最初的速度时程相吻合，如图7所示。El Centro台南北向原始记录积分得到的PGV为−29.66 cm/s，本文方法在处理加入单段式、两段式和多段式加速度基线漂移噪声模型后的数据得到的PGV分别为−30.66，−30.66和−30.53 cm/s。
![]()
图 7 利用本文方法对加入不同噪声模型后的El Centro台NS向记录进行恢复的结果（a） 单段式基线漂移噪声；（b） 两段式基线漂移噪声；（c） 多段式基线漂移噪声Figure 7. Velocity trace recovered from El Centro NS component records with different noise models by the method proposed in this paper（a） Single-stage baseline drift noises； （b） Double-baseline drift noises； （c） Multi-stage baseline drift noises4. 讨论与结论
相比于Iwan等（1985）提出的两段式方法和Boore （2001）提出的υ0方法及其改进方法，本文所提出的基于L1范数正则化的加速度基线漂移识别方法，运用加入L1范数正则化的最优化思想，以拟合速度误差尽可能小为目标并以加速度基线漂移稀疏为约束条件，通过凸优化技术多次迭代求解，自动计算出合适的加速度基线漂移分段数量，并计算其漂移时刻和漂移程度，因而减少了加速度基线校正中人为干预选择的主观性，拓展了基线校正方法的通用性。通过对不同地震动记录分别加入不同类型的基线漂移噪声模型，本文方法对其基线校正后得出了以下主要结论：
1） 地震加速度记录保留足够长的事前部分（pre-event portion）是十分重要的，事前部分越长越有利于准确识别基线漂移的位置和基线漂移程度。通常符合标准要求的地震记录会留有大约20 s的事前部分，经过对不同长短事前部分的地震记录进行处理后，本文方法所得结果再次证明了具有充分事前部分的地震记录是必要的，其事前部分越充分，越能得到更为准确的基线漂移结果。这一结论对于单段式、两段式和多段式的加速度基线漂移同样适用。而当地震加速度记录事前部分过短（明显的丢头现象）且不为零时，本文方法会把加速度往零线“拉拢”，这在一定程度上会造成恢复后的位移略微偏小。
2） 本文所采用的加速度基线校正方法适用于单段式、两段式和多段式的加速度基线漂移，不用预先设定基线漂移模型即可自动识别基线漂移类型。由于地震发生时，强震台采集到的加速度记录受多种因素干扰，真实的基线漂移情况通常较为复杂，而本文方法可以更为敏锐地察觉速度漂移的趋势（斜率）变化，从而有效捕捉到人工判断中容易被忽视的速度漂移变化，特别是在多段式基线漂移噪声中，对速度拟合的分段次数会更多，由此得到的基线漂移次数也会随之增加。但是由于本文方法采用了L1范数正则化，其稀疏性特征可以很好地控制基线漂移的次数和大小。
3） 本文方法可以较好地恢复加速度基线漂移后的速度时程和位移时程。无论地震加速度记录是否有足够的事前部分，本方法都可以很好地恢复峰值速度值，且对于整个速度时程也有很好的恢复效果。地震记录事前部分越长，本文方法对其位移时程恢复效果也越好；反之，则会出现较大偏差。
通过对几种典型的基线漂移噪声模型进行识别和对比，本文方法所得结果一定程度上可以证明基于L1范数正则化的基线校正方法对未知加速度漂移的实际强震动记录也应该具备适用性。正则化参数λ是一个模型相关的超参数，不同的λ取值会直接影响凸优化求解的基线漂移结果，但如何获取合适的超参数值一直是个难题和挑战。后续工作将运用本文方法对更多的实际强震动数据进行处理，并对正则化参数λ的取值进行研究。
审稿专家对文章提出宝贵建议，作者在此表示感谢。
-
![]()
图 1 本文采用的典型加速度基线漂移噪声模型（修改自Akkar，Boore，2009）
tb和te分别为加速度记录的起、止时刻，t1和t2分别为加速度绝对值在第一次和最后一次大于50 m/s2时刻，t3为[t1，t2]中间时刻，am1和am2分别为加速度在强烈震动时段的加速度漂移幅值，af为加速度最终保持的漂移幅值
Figure 1. Representative sketches of acceleration baseline-offset noise models （modified from Akkar，Boore，2009）
tb and te are respectively the beginning and ending of the recording， the time t1 and t2 represent the first and last time that the recording’s absolute values are larger than 50 m/s2， t3 is the medium time between t1 and t2，am1 and am2 mean the two consecutive constant offsets during the strong ground shaking，af is the final offset
![]()
图 2 L1范数正则化方法对于两段式基线漂移噪声模型的识别和处理结果
（a） 地震加速度时程；（b） 速度时程；（c） 加速度基线；（d） 位移时程
Figure 2. The results of identifying and processing double-stage baseline-offset noise model based on the L1-norm regularization method
（a） Acceleration time history；（b） Velocity time history；（c） Acceleration baseline-offset；（d） Displacement time history
![]()
图 4 本文方法所识别的El Centro台南北向记录与加入两段式噪声模型后的基线漂移噪声差值
Figure 4. The difference between baseline-offset identified by this paper and added two-stage noise model for El Centro NS component
![]()
图 3 El Centro台南北向初始部分记录处理结果
Figure 3. Comparison of the original record with the results processed by the new method in the pre-event portion of El Centro NS components record
![]()
图 5 基于L1范数正则化方法对单段式基线漂移噪声模型的识别和处理结果
（a） 地震加速度时程；（b） 速度时程；（c） 加速度基线；（d） 位移时程
Figure 5. The results of identifying and processing on records added single-stage baseline-offset noise model based on the L1-norm regularization method
（a） Acceleration time history；（b） Velocity time history；（c） Acceleration baseline-offset；（d） Displacement time history
![]()
图 6 基于L1范数正则化方法对于多段式基线漂移噪声模型的识别和处理结果
（a） 地震加速度时程；（b） 速度时程；（c） 加速度基线；（d） 位移时程
Figure 6. The results of identifying and processing on records added multi-stage baseline-offset noise model based on the L1-norm regularization method
（a） Acceleration time history；（b） Velocity time history；（c） Acceleration baseline-offset；（d） Displacement time history
![]()
图 7 利用本文方法对加入不同噪声模型后的El Centro台NS向记录进行恢复的结果
（a） 单段式基线漂移噪声；（b） 两段式基线漂移噪声；（c） 多段式基线漂移噪声
Figure 7. Velocity trace recovered from El Centro NS component records with different noise models by the method proposed in this paper
（a） Single-stage baseline drift noises； （b） Double-baseline drift noises； （c） Multi-stage baseline drift noises
表 1 本文所列地震记录信息（PEER，2013）
Table 1 Information about digital accelerograms shown in this study （PEER，2013）
发震年 地震 MW P波到时/s 持时/s 分量方向 台站名称 场地类型* 震中距/km 1940 帝王谷地震 6.95 0.04 40 NS El Centro Array#9 D 12.99 1999 迪兹杰地震 7.14 5.39 56 EW Bolu D 41.27 1999 集集地震 7.62 20.65 90 NS TCU129 C 14.16 注：场地类型采用美国地震减灾计划（National Earthquake Hazards Reduction Program，NEHRP）给出的A，B，C，D和E等5类场地条件划分类型（ Huang et al，2010 ）.
下载: 导出CSV
-
符伟,刘财. 2015. 基于L1正则化的地震谱反演方法[J]. 世界地质,34(2):505–510 doi: 10.3969/j.issn.1004-5589.2015.02.028 Fu W,Liu C. 2015. Seismic spectral-inversion technique based on L1-norm regulation method[J]. Global Geology,34(2):505–510 (in Chinese)
李欣,杨婷,孙文博,王贝贝. 2018. 一种基于光滑L1范数的地震数据插值方法[J]. 石油地球物理勘探,53(2):251–256 Li X,Yang T,Sun W B,Wang B B. 2018. A gradient projection method for smooth L1 norm regularization based seismic data sparse interpolation[J]. Oil Geophysical Prospecting,53(2):251–256 (in Chinese)
彭小波,李小军,刘泉. 2010. 数字加速度记录基线校正相关问题的初步研究[J]. 世界地震工程,26(增刊1):142–147 Peng X B,Li X J,Liu Q. 2010. Preliminary study on baseline correction of digital acceleration records[J]. World Earthquake Engineering,26(S1):142–147 (in Chinese)
彭小波,李小军,刘启方. 2011. 基于强震记录估算同震位移的研究进展及方法[J]. 世界地震工程,27(3):73–80 Peng X B,Li X J,Liu Q F. 2011. Advances and methods for the recovery of coseismic displacements from strong-motion accelero-grams[J]. World Earthquake Engineering,27(3):73–80 (in Chinese)
荣棉水,彭艳菊,喻畑,杨宇. 2014. 近断层强震观测记录基线校正的优化方法[J]. 土木工程学报,47(增刊2):308–314 Rong M S,Peng Y J,Yu T,Yang Y. 2014. Optimized baseline correction method for the near-fault observation strong motion records[J]. China Civil Engineering Journal,47(S2):308–314 (in Chinese)
王国权,周锡元. 2004. 9·21台湾集集地震近断层强震记录的基线校正[J]. 地震地质,26(1):1–14 doi: 10.3969/j.issn.0253-4967.2004.01.001 Wang G Q,Zhou X Y. 2004. Baseline correction of near fault ground motion recordings of the 1999 Chi-Chi,Taiwan earth-quake[J]. Seismology and Geology,26(1):1–14 (in Chinese)
于海英,江汶乡,解全才,杨永强,程翔,杨剑. 2009. 近场数字强震仪记录误差分析与零线校正方法[J]. 地震工程与工程振动,29(6):1–12 Yu H Y,Jiang W X,Xie Q C,Yang Y Q,Cheng X,Yang J. 2009. Baseline correction of digital strong-motion records in near-field[J]. Journal of Earthquake Engineering and Engineering Vibration,29(6):1–12 (in Chinese)
周宝峰,于海英,温瑞智,谢礼立. 2013. 一种识别永久位移的新方法[J]. 土木工程学报,46(增刊2):135–140 Zhou B F,Yu H Y,Wen R Z,Xie L L. 2013. A new way of permanent displacement identification[J]. China Civil Engineering Journal,46(S2):135–140 (in Chinese)
周巍. 2013. L1范数最小化算法及应用[D]. 广州: 华南理工大学: 14–23. Zhou W. 2013. L1-Norm Minimization Algorithms and Its Applications[D]. Guangzhou: South China University of Technology: 14–23（in Chinese）.
Akkar S,Boore D M. 2009. On baseline corrections and uncertainty in response spectra for baseline variations commonly encountered in digital accelerograph records[J]. Bull Seismol Soc Am,99(3):1671–1690 doi: 10.1785/0120080206
Allen R V. 1978. Automatic earthquake recognition and timing from single traces[J]. Bull Seismol Soc Am,68(5):1521–1532
Allen R V. 1982. Automatic phase pickers:Their present use and future prospects[J]. Bull Seismol Soc Am,72(6B):S225–S242
Boore D M. 2001. Effect of baseline corrections on displacements and response spectra for several recordings of the 1999 Chi-Chi,Taiwan,earthquake[J]. Bull Seismol Soc Am,91(5):1199–1211
Boore D M. 2005. On pads and filters:Processing strong-motion data[J]. Bull Seismol Soc Am,95(2):745–750 doi: 10.1785/0120040160
Boyd S P, Vandenberghe L. 2004. Convex Optimization[M]. New York: Cambridge University Press: 291–311.
Chao W A,Wu Y M,Zhao L. 2010. An automatic scheme for baseline correction of strong-motion records in coseismic deformation determination[J]. J Seismol,14(3):495–504 doi: 10.1007/s10950-009-9178-7
Chiu H C. 1997. Stable baseline correction of digital strong-motion data[J]. Bull Seismol Soc Am,87(4):932–944
Dai Z J,Li X J,Hou C L. 2014. An optimization method for the generation of ground motions compatible with multi-damping design spectra[J]. Soil Dyn Earthq Eng,66:199–205 doi: 10.1016/j.soildyn.2014.06.032
Donoho D L,Tsaig Y. 2008. Fast solution of L1-norm minimization problems when the solution may be sparse[J]. IEEE Trans Inf Theory,54(11):4789–4812 doi: 10.1109/TIT.2008.929958
Efron B,Hastie T,Johnstone I,Tibshirani R. 2004. Least angle regression[J]. Ann Statist,32(2):407–499 doi: 10.1214/009053604000000067
Huang Y N,Whittaker A S,Luco N. 2010. NEHRP site amplification factors and the NGA relationships[J]. Earthquake Spectra,26(2):583–593
Hershberger J. 1955. Recent developments in strong-motion analysis[J]. Bull Seismol Soc Am,45(1):11–21
Housner G W. 1947. Ground displacement computed from strong-motion accelerograms[J]. Bull Seismol Soc Am,37(4):299–305
Iwan W D,Moser M A,Peng C Y. 1985. Some observations on strong-motion earthquake measurement using a digital accelerograph[J]. Bull Seismol Soc Am,75(5):1225–1246
Jones J, Kalkan E, Stephens C. 2017. Processing and Review Interface for Strong Motion Data （PRISM） Software, Version 1.0.0: Methodology and Automated Processing[R].Reston: U S Geological Survey : 3–20.
Mallat S G,Zhang Z F. 1993. Matching pursuits with time-frequency dictionaries[J]. IEEE Trans Signal Process,41(12):3397–3415 doi: 10.1109/78.258082
PEER. 2013. PEER NGA-West2 ground motion database[EB/OL]. [2017–10–02]. https://peer.berkeley.edu/research/nga-west-2.
Schmidt M. 2005. Least Squares Optimization With L1-Norm Regularization[R]. Vancouver: Univercity of British Clumbia: 3–6.
Tibshirani R. 1996. Regression shrinkage and selection via the lasso[J]. J Roy Statist Soc Ser B,58(1):267–288
Trifunac M D. 1970. Low Frequency Digitization Errors and A New Method for Zero Baseline Correction of Strong-Motion Accelerograms[R]. Pasadena: Earthquake Engineering Research Laboratory: 7–24.
Trifunac M D,Lee V W. 1974. A note on the accuracy of computed ground displacements from strong-motion accelerograms[J]. Bull Seismol Soc Am,64(4):1209–1219
Wang G Q,Boore D M,Igel H,Zhou X Y. 2003. Some observations on colocated and closely spaced strong ground-motion records of the 1999 Chi-Chi,Taiwan,earthquake[J]. Bull Seismol Soc Am,93(2):674–693 doi: 10.1785/0120020045
Wang R J,Schurr B,Milkereit C,Shao Z G,Jin M P. 2011a. An improved automatic scheme for empirical baseline correction of digital strong-motion records[J]. Bull Seismol Soc Am,101(5):2029–2044 doi: 10.1785/0120110039
Wang R J,Parolai S,Ge M R,Jin M P,Walter T R,Zschau J. 2013. The 2011 MW9.0 Tohoku earthquake:Comparison of GPS and strong-motion data[J]. Bull Seismol Soc Am,103(2B):1336–1347 doi: 10.1785/0120110264
Wang Y F,Cao J J,Yang C C. 2011b. Recovery of seismic wavefields based on compressive sensing by an L1-norm constrained trust region method and the piecewise random subsampling[J]. Geophys J Int,187(1):199–213 doi: 10.1111/gji.2011.187.issue-1
Wu Y M,Wu C F. 2007. Approximate recovery of coseismic deformation from Taiwan strong-motion records[J]. J Seismol,11(2):159–170 doi: 10.1007/s10950-006-9043-x
计量
- 文章访问数: 1266
- HTML全文浏览量: 873
- PDF下载量: 80
