Test methods for nonlinear parameters of seismic data recorders and their effect analyses
-
摘要: 为了分析总谐波失真度和互调失真度这两个非线性指标的测试方法、输入信号幅值等变化对其测试结果的影响，本文从总谐波失真信号、互调失真信号的产生原理出发，详细地给出了两种指标的测试方法、数据处理方法及相关影响分析，并通过实际应用中不同类型的输入信号进行了总谐波失真度和互调失真度试验。测试结果表明：信号模式和信号幅值对总谐波失真度的影响显著；输入信号幅值对互调失真度的影响较大；输入信号的频率变化对两指标的测试结果无影响。本研究进一步细化了地震数据采集器性能指标的标准化测试方法，该方法可广泛应用于地震数据采集器的非线性指标测试。Abstract: Total harmonic distortion （THD） and intermodulation distortion （IMD） characteris-tics are two important nonlinear parameters of seismic data recorders. Input signal mode and peak value of sine-wave can affect the test results of these two characteristics. In order to deter-mine these effects, the basic principles on THD and IMD were introduced in this paper, and then test methods, data processing methods and effect analyses on THD and IMD were fully presented. Finally, some different kinds of sine-waves were input into the seismic data recorder to test THD and IMD. The test results show that the two signals with the same peak value but different input-mode have great impact on THD, and those with the same frequency but different peak value of sine-wave have great impact on IMD. However, signal frequency variation has no impact on THD and IMD. The research in this paper is of great value for quality test of seismic data recorder, which can be applied to test THD and IMD of seismic data recorders.
-
引言
为了保证地震监测获得数据的质量，须对直接获取地震数据的地震仪器进行全面的质量检测。从地震监测网络建设伊始，中国地震局就开展了针对各种地震仪器各项性能指标的测试工作；而从中国地震监测网络多年的运行管理来看，如何对在网运行的地震仪器进行在线质量检测的工作变得更加迫切。中国地震局监测预报司（2016）已发布了 《地震数据采集器质量检测技术规程》 ，本文将在其基础上开展一系列地震数据采集器的质量检测工作。
非线性指标是地震数据采集器的重要指标之一，它反映了地震数据采集器在地震信号采集和记录过程中的保真能力，谐波失真度和互调失真度是采集器非线性指标中两种典型的失真指标。传统上使用失真度分析仪对一般电子仪器进行非线性指标测试，大部分失真度分析仪采用模拟信号输入-模拟信号输出的方式进行测试，而地震数据采集器采用数字信号输出，因此采用失真度分析仪对地震采集器进行非线性指标测试几乎不可能。对高精度地震数据采集器的非线性指标测试，一般采用高精度的模拟信号源输入低失真度信号，然后对数据采集器的数字输出信号进行频谱分析，计算得出采集器的非线性指标结果。为了对多通道地震数据采集器进行谐波畸变测试，刘益成等（2006）采用所有谐波功率之和与基波功率之比判定谐波失真度，采用在特殊频率点具有低失真度的信号源对地震数据采集器进行谐波失真度测试，并进一步采用离散傅里叶算法（discrete Fourier transform，简写为DFT）在频域内计算输出信号各频率分量的频谱，从而计算出采集器各个通道的谐波失真度。张永学等（2008）从总谐波失真度的计算公式和快速傅里叶变换（fast Fourier transform，简写为FFT）的运算结构出发，提出了测试多达万道的地震数据采集器系统总谐波失真度的剪切FFT算法，该算法只计算对目标输出有贡献的运算节点，提高计算速度的同时达到与标准算法相同的运算精度，适用于大道数地震数据采集系统总谐波失真度的野外或室内测试。以上是部分谐波失真度测试的相关研究，但互调失真度测试少有提及。为此，本文拟基于现有研究成果（Christian，1994；刘益成等，2006；张永学等，2008；李彩华等，2014），开展地震数据采集器的谐波失真度和互调失真度测试方法研究及影响分析，以期达到进一步细化地震数据采集器的非线性指标测试方法的目的。
1. 地震数据采集系统非线性分析
理论上，任何数据采集系统的输出信号与输入信号的频率应该是相同的，但是由于系统中各部分的非线性特性，数据采集器的输出信号中总会包含输入信号中不存在的频率成分，从而造成了系统的非线性失真。实际的系统都是非线性的，但在实际应用中会忽略一些次级效应，将其等效为线性系统。对于地震数据采集系统而言，假设系统的输入为x（t），输出为y（t），系统增益为k，则有
$y(t) {\text{＝}} k\, x(t){\text{.}} $
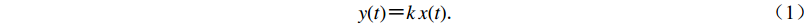
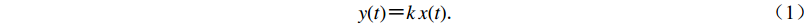
(1) 对于理想的线性系统，若式（1）中k值不随输入改变，则输出信号所含频率成分与输入信号一致，也不会产生其它频率成分信号；当系统存在非线性时，k值将是输入信号的函数（刘亮，2014；杨健，2014；何芹，2015），可以表示为
$ k {\text{＝}} k(x){\text{，}} $
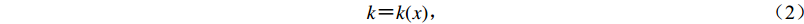
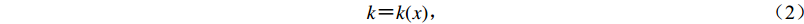
(2) 对其进行泰勒展开，可得
$ k {\text{＝}} {k_0} {\text{＋}} {k_1}x(t) {\text{＋}} {k_2}{x^2}(t) {\text{＋}} {k_3}{x^3}(t) {\text{＋}} \cdots{\text{＋}}k_n x^n(n){\text{＋}}\cdots {\text{，}} $
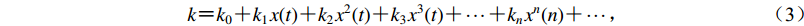
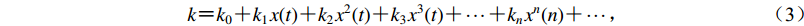
(3) 式中
$ {k_n} {\text{＝}} \frac{1}{{n!}}\frac{{{{\rm{d}}^n}[k(x)]}}{{{\rm{d}}{x^n}}}{\text{.}} $
$ y(t) {\text{＝}} {k_0}x(t) {\text{＋}} {k_1}{x^2}(t) {\text{＋}} {k_2}{x^3}(t) {\text{＋}} {k_3}{x^4}(t){\text{＋}} \cdots{\text{＋}}k_n x^{n{\text{＋}}1}(x){\text{＋}}\cdots {\text{，}} $
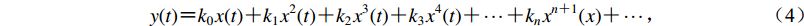
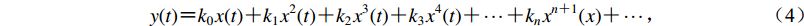
(4) 此即为非线性系统的输入与输出关系。
由于地震数据采集器的传递函数也可以用式（4）来描述，因此单一频率信号经过式（4）的运算后必定会产生一定比例的其它频率信号（Offelli，Petri，1991；Alegria，Da Silva，2012），这些其它频率信号的产生被称之为采集器的非线性失真。这是由于输入信号经过地震数据采集器中有源或无源非线性器件所组成的非线性系统后，在输出信号中产生了原信号中所不存在的新频率分量，从而引起信号波形的失真。这些新的频率分量若为原信号的各次谐波分量，则由此引起的失真为非线性谐波失真，简称为谐波失真，这一类失真是各类非线性失真中应用最广的一种，也是对仪器性能影响最大的一种。当输入双频率信号时，由于采集器的非线性，两种不同频率信号互相调制产生诸如2阶交调、3阶交调等其它频率信号，使得采集器中测量信号产生互调失真，这种失真信号对正确测量输出信号也会产生一定影响。下面本文将就地震数据采集器的非线性特性所引起的谐波失真、互调失真测试的原理及方法予以分析。
1.1 总谐波失真产生原理
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {x^2}(t) {\text{＝}} A_0^2{\sin ^2}\omega t {\text{＝}} \frac{{A_0^2}}{2}(1 {\text{－}} \cos 2\omega t){\text{，}} $
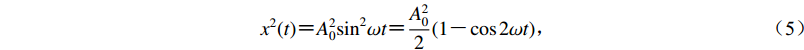
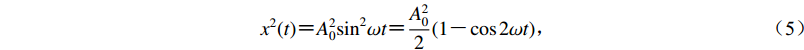
(5) $ {x^3}(t) {\text{＝}} A_0^3{\sin ^3}\omega t {\text{＝}} \frac{{A_0^3}}{4}(3\sin \omega t {\text{－}} \sin 3\omega t) {\text{，}} $
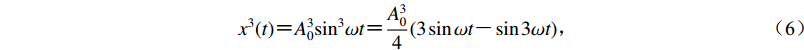
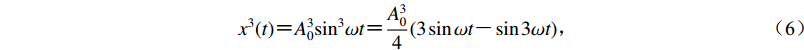
(6) 将式（5）和式（6）代入式（4）中并忽略高次项，则地震数据采集器的输出信号可以表示为
$ y(t){\text{＝}} \frac{1}{2}{k_1}A_0^2 {\text{＋}} ({k_0}{A_0} {\text{＋}} \frac{3}{4}{k_2}A_0^3)\sin \omega t {\text{－}} \frac{{{k_1}}}{2}A_0^2\cos 2\omega t {\text{－}} \frac{{{k_2}}}{4}A_0^3\sin 3\omega t {\text{＋}} \cdots . $
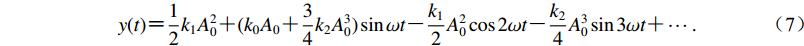
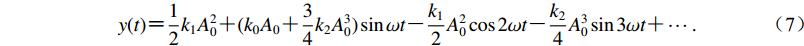
(7) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
1.2 互调失真信号产生原理
由于非线性的存在，数据采集电路输出信号与输入信号之间并不是简单的线性关系，通常可用式（4）的幂级数形式来表示，式中kn为第n阶幂级系数，其阶数n越大，kn数值越小，因此电路分析中一般只取前3阶，即
$ y(t) {\text{＝}} \sum\limits_{n {\text{＝}}1}^{\infty } {{k_{n{\text{－}}1}}{x^n}(t)} {\text{＝}} {k_0}x(t) {\text{＋}} {k_1}{x^2}(t) {\text{＋}} {k_2}{x^3}(t){\text{.}} $
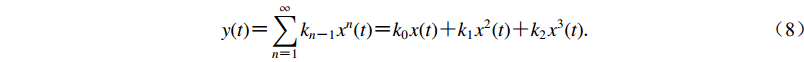
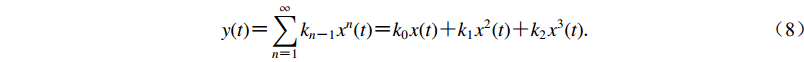
(8) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ y(t) {\text{＝}}{k_0}A(\cos {\omega _1}t {\text{＋}} \cos {\omega _2}t) {\text{＋}} {k_1}{A^2}{(\cos {\omega _1}t {\text{＋}} \cos {\omega _2}t)^2} {\text{＋}} {k_2}{A^3}{(\cos {\omega _1}t {\text{＋}} \cos {\omega _2}t)^3}{\text{.}} $
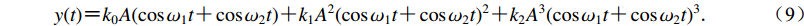
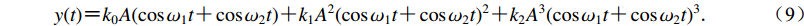
(9) 将式（9）展开后可以看到，输出信号中不仅包含输入信号中的频率成分，还包含其它频率成分，且各频率成分信号的幅值分别为
$ \left\{ \begin{aligned} & {{\omega _1}, \;\;{\omega _2} {\text{：}}{k_1}A {\text{＋}} \frac{9}{4}{k_3}{A^3}}{\text{，}}\\ & {{\omega _1} {\text{±}}{\omega _2} {\text{：}}{k_2}{A^2}}{\text{，}} \\ & {2{\omega _1} {\text{±}} {\omega _2},\;\; 2{\omega _2} {\text{±}}{\omega _1} {\text{：}}{\frac{{3}}{4}} }{k_3}{A^3}{\text{，}} \end{aligned} \right. $
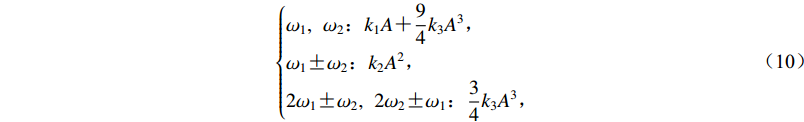
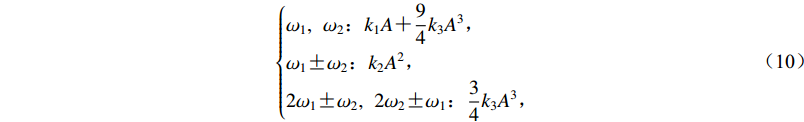
(10) 并将由2阶系数产生的频率分量ω1±ω2称为2阶交调，而由3阶系数产生的频率分量2ω1±ω2和2ω2±ω1称为3阶交调。从式（10）可以看出，2阶交调分量的强度与输入信号强度的平方成正比，3阶交调分量强度与输入信号强度的立方成正比，见图 1。
地震数据采集器电路设计的不完全线性特性，使得采集器输入双音信号时，输出信号中存在2阶交调、3阶交调等信号，这种非线性失真即为互调失真。当输入信号为双音信号且两种频率信号的幅值较大时，地震数据采集器所产生的2阶、3阶调制信号的幅值为输入信号幅值的指数倍，从而影响地震数据质量，因此对于数据采集器电路的互调失真测试很有必要。
2. 数据采集系统非线性指标测试
本文选用一款国内常用的地震数据采集器和安捷伦信号发生器分别进行相应的测试工作，其中测试方法参考中国地震局监测预报司（2016）关于总谐波失真度、互调失真度的测试方法及对应数据处理方法。
2.1 总谐波失真度测试方法及数据处理方法
进行采集器的总谐波失真度测试时，测试信号选取频率为5 Hz的正弦波，信号幅值为满量程的90%或其它幅值，将数据采集器的采样率设置为100 Hz （或相近采样率）。从连续记录数据中截取1万个样点的数据，经谱分析后求出其基波及各次谐波的幅值，按照
${\rm THD} {\text{＝}} 10\lg \sum\limits_{i {\text{＝}} 2}^N {V_i^2} {\text{－}} 10\lg \sum\limits_{i {\text{＝}} 1}^N {V_i^2} $
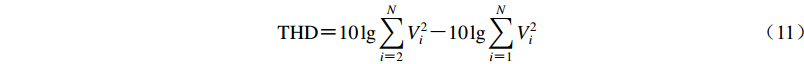
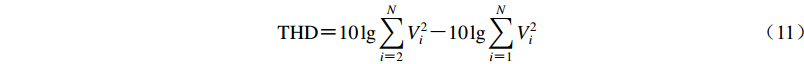
(11) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
2.2 互调失真度测试方法及数据处理方法
进行采集器的互调失真度测试时选用双音信号源，取输入信号S1的频率为1 Hz （或其它频率），幅值为3 V，输入信号S2的频率为1.1 Hz （或其它频率），幅值为2 V，记录长度不少于1万个样点。对采集器测量数据进行谱分析获得频谱图，根据频谱计算即可读出相应各调制信号频率所对应的幅值，由
$ \frac{{\sqrt {{{({b_5} {\text{＋}} {b_5}^{\!\!\!\!\prime})}^2} {\text{＋}} {{({b_3} {\text{＋}} {b_3}^{\!\!\!\!\prime})}^2} {\text{＋}} {{({b_1} {\text{＋}} {b_1}^{\!\!\!\!\prime})}^2}} }}{{a {\text{＋}} b}} \times 100\% $
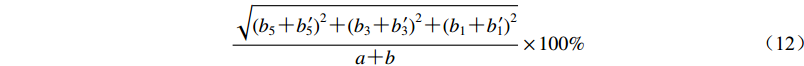
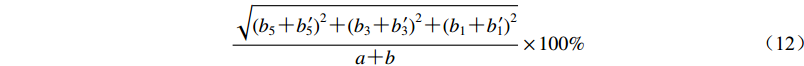
(12) 和
$ {\rm IMD} {\text{＝}} 20\lg \frac{{\sqrt {{{({b_5} {\text{＋}} {b_5}^{\!\!\!\!\prime})}^2} {\text{＋}} {{({b_3} {\text{＋}} {b_3}^{\!\!\!\!\prime})}^2} {\text{＋}} {{({b_1} {\text{＋}} {b_1}^{\!\!\!\!\prime})}^2}} }}{{a {\text{＋}} b}} $
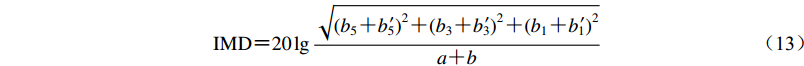
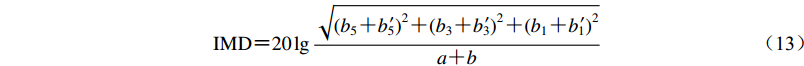
(13) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
3. 总谐波失真度和互调失真度测试及数据分析
本文选用一台型号为Basalt的地震采集器、高精度标准信号源（0.001% THD）及相关辅助设备，采用本文所列测试方法对该地震数据采集器1—3通道的多项技术指标进行测试，并分别编写相应的测试数据处理程序，计算各项技术指标的测试结果。此处仅介绍有关采集器非线性特性指标—总谐波失真度、互调失真度的测试结果。
首先进行不同输入方式、不同幅值信号和不同频率信号下的地震数据采集器总谐波失真度的测试，主要按以下步骤进行：
1） 分别以差动输入方式、单端输入方式对5 Hz幅值、幅值满量程的45%正弦波信号（图 2）进行地震数据采集器总谐波失真度测试。对两种测试信号分别依据2.1节方法进行数据分析计算，得到表 1所示的总谐波失真度测试结果。
![]()
图 2 差动输入模式（a）和单端输入模式（b）Figure 2. Differential input mode （a） and single end input mode （b）2） 分别对采集器输入相同频率、不同幅值的正弦波进行总谐波失真度测试，得到对应测试条件下的采集器总谐波失真度结果，见表 2。
3） 分别对采集器输入相同幅值、不同频率的正弦波进行总谐波失真度测试，得到对应测试条件下的采集器总谐波失真度结果，见表 3。
可以看出：在单端输入情况下，测得的采集器总谐波失真度较差动输入情况下的总谐波失真度高约20 dB （表 1），这是由于差动输入模式下的一部分谐波信号因为幅值相同、方向相反而被抵消所致；在差动输入模式下，低信号幅值下测得的采集器总谐波失真度与高信号幅值下测得的结果相差约15 dB （表 2），这说明信号幅值变化对采集器THD指标测试具有影响，建议一般情况下输入信号幅值高于采集器满量程的一半；5 Hz和10 Hz两种不同信号频率、两种不同幅值信号下，所测得的采集器THD值均优于−90 dB （表 3），说明信号频率变化对采集器THD指标测试无影响。
表 3 不同信号频率下总谐波失真度THD测试结果Table 3. Test result of total harmonic distortion THD with different signal frequencies通道号 THD/dB 信号频率5 Hz 信号频率10 Hz 18Vpp 36Vpp 18Vpp 36Vpp 1 −96.924 0 −91.407 2 −93.976 4 −94.200 1 2 −96.829 8 −91.262 9 −93.913 6 −93.873 7 3 −96.116 8 −91.764 5 −91.830 8 −93.511 5 表 1 总谐波失真度THD测试结果Table 1. Test result of total harmonic distortion THD通道号 THD/dB 单端输入 差动输入 1 −73.973 3 −96.924 0 2 −74.731 4 −96.829 8 3 −74.726 2 −96.116 8 表 2 差动输入下的总谐波失真度THD测试结果Table 2. Test result of total harmonic distortion THD with differential input通道号 THD/dB 4Vpp 9Vpp 18Vpp 36Vpp 1 −78.006 6 −95.814 0 −96.924 0 −91.407 2 2 −78.008 4 −94.114 1 −96.829 8 −91.262 9 3 −78.006 2 −95. 411 1 −96.116 8 −91.764 5 注：Vpp代表信号幅值为峰峰值，下同。 采用同一台型号为Basalt的数据采集器，对该采集器的通道1—3进行不同量程、不同输入信号幅值下的互调失真度测试，以100 Hz采样率下的测试结果为例。表 4给出了采样率为100 Hz时5 V、20 V量程下的互调失真度的测试结果；表 5为100 Hz采样率、20 V量程下不同输入信号幅值下的互调失真度测试结果；表 6为100 Hz采样率、5 V量程下不同输入信号频率下的互调失真度的测试结果；表 7为100 Hz采样率、5 V量程下互调失真度的实际测试结果与仿真计算结果的比较。从以上4种情况下的测试结果可以看出：相同测试条件下，小量程采集器的互调失真度较好；相同测试条件下，输入信号峰值小，则采集器的互调失真度较好，输入信号峰值大，则采集器互调失真度变差；仿真分析结果证明，理想线性采集器的互调失真度可以达到−150 dB，高于实际采集器互调失真度约65 dB，从而也证明了采集器具有一定的非线性。
表 4 互调失真度IMD测试结果（采样率为100 Hz）Table 4. Test result of intermodulation distortion IMD （sample rate is 100 Hz）量程/V 互调失真系数 IMD/dB 通道1 通道2 通道3 通道1 通道2 通道3 5 0.004 6% 0.004 1% 0.003 6% −86.68 −87.70 −88.82 20 0.029 0% 0.085 8% 0.045 0% −70.81 −67.55 −66.90 表 5 互调失真度IMD测试结果（采样率为100 Hz，量程为20 V）Table 5. Test result of intermodulation distortion IMD （sample rate is 100 Hz，range is 20 V）幅值/V 互调失真系数 IMD/dB 通道1 通道2 通道3 通道1 通道2 通道3 0.75 0.009 5% 0.009 5% 0.009 6% −80.39 −80.39 −80.34 3 0.041 0% 0.089 0% 0.145 0% −67.73 −61.32 −56.79 表 6 互调失真度IMD测试结果（采样率为100 Hz，量程为5 V）Table 6. Test result of intermodulation distortion IMD （sample rate is 100 Hz，range is 5 V）信号频率/Hz IMD/dB 通道1 通道2 通道3 1，1.1 −86.68 −87.70 −88.82 5，5.1 −85.74 −86.16 −86.26 表 7 互调失真度IMD仿真结果与实际测试结果比较（采样率为100 Hz，量程为5 V）Table 7. Comparison between simulation result and actual test result of intermodulation distortion IMD （sample rate is 100 Hz，range is 5 V）通道号 互调失真系数 IMD/dB 实际测量 仿真测试 实际测量 仿真测试 1 0.004 6% 0.000 002% −86.68 −153.84 2 0.004 1% 0.000 002% −87.70 −154.28 3 0.003 6% 0.000 002% −88.82 −153.37 4. 讨论与结论
总谐波失真度和互调失真度是地震数据采集器的重要性能指标。本文从这两种指标的产生原理出发，通过对总谐波失真、互调失真的理论分析和实际测试计算，得出以下结论和建议：
信号频率对地震数据采集器的总谐波失真度、互调失真度测试结果无影响，这符合地震数据采集器的特征。但当输入信号幅值较大时，采集器总谐波失真度测试结果较好；而当输入信号幅值较小时，互调失真度测试结果较好；而随着输入信号幅值的增大，互调失真度测试结果下降约20 dB。这种规律是否符合采集器特点，是否由信号源自身性能变化引起，尚需进一步开展相关研究来解释。
由于地震数据采集器的总谐波失真度、互调失真度测试结果受测试信号源稳定性、计算方法等因素影响，故建议采集器制造商及仪器质量检测人员在进行相关技术指标测试及研究时，公开相关仪器指标及算法，使得各种不同仪器及不同测试仪器的测试结果具有可比性。
本研究是地震数据采集器质量检测规范的有益补充，可用于地震台网中各种地震数据采集器设备的非线性指标测试。
-
![]()
图 2 差动输入模式（a）和单端输入模式（b）
Figure 2. Differential input mode （a） and single end input mode （b）
表 3 不同信号频率下总谐波失真度THD测试结果
Table 3 Test result of total harmonic distortion THD with different signal frequencies
通道号 THD/dB 信号频率5 Hz 信号频率10 Hz 18Vpp 36Vpp 18Vpp 36Vpp 1 −96.924 0 −91.407 2 −93.976 4 −94.200 1 2 −96.829 8 −91.262 9 −93.913 6 −93.873 7 3 −96.116 8 −91.764 5 −91.830 8 −93.511 5 
下载: 导出CSV
表 1 总谐波失真度THD测试结果
Table 1 Test result of total harmonic distortion THD
通道号 THD/dB 单端输入 差动输入 1 −73.973 3 −96.924 0 2 −74.731 4 −96.829 8 3 −74.726 2 −96.116 8
下载: 导出CSV
表 2 差动输入下的总谐波失真度THD测试结果
Table 2 Test result of total harmonic distortion THD with differential input
通道号 THD/dB 4Vpp 9Vpp 18Vpp 36Vpp 1 −78.006 6 −95.814 0 −96.924 0 −91.407 2 2 −78.008 4 −94.114 1 −96.829 8 −91.262 9 3 −78.006 2 −95. 411 1 −96.116 8 −91.764 5 注：Vpp代表信号幅值为峰峰值，下同。
下载: 导出CSV
表 4 互调失真度IMD测试结果（采样率为100 Hz）
Table 4 Test result of intermodulation distortion IMD （sample rate is 100 Hz）
量程/V 互调失真系数 IMD/dB 通道1 通道2 通道3 通道1 通道2 通道3 5 0.004 6% 0.004 1% 0.003 6% −86.68 −87.70 −88.82 20 0.029 0% 0.085 8% 0.045 0% −70.81 −67.55 −66.90
下载: 导出CSV
表 5 互调失真度IMD测试结果（采样率为100 Hz，量程为20 V）
Table 5 Test result of intermodulation distortion IMD （sample rate is 100 Hz，range is 20 V）
幅值/V 互调失真系数 IMD/dB 通道1 通道2 通道3 通道1 通道2 通道3 0.75 0.009 5% 0.009 5% 0.009 6% −80.39 −80.39 −80.34 3 0.041 0% 0.089 0% 0.145 0% −67.73 −61.32 −56.79
下载: 导出CSV
表 6 互调失真度IMD测试结果（采样率为100 Hz，量程为5 V）
Table 6 Test result of intermodulation distortion IMD （sample rate is 100 Hz，range is 5 V）
信号频率/Hz IMD/dB 通道1 通道2 通道3 1，1.1 −86.68 −87.70 −88.82 5，5.1 −85.74 −86.16 −86.26
下载: 导出CSV
表 7 互调失真度IMD仿真结果与实际测试结果比较（采样率为100 Hz，量程为5 V）
Table 7 Comparison between simulation result and actual test result of intermodulation distortion IMD （sample rate is 100 Hz，range is 5 V）
通道号 互调失真系数 IMD/dB 实际测量 仿真测试 实际测量 仿真测试 1 0.004 6% 0.000 002% −86.68 −153.84 2 0.004 1% 0.000 002% −87.70 −154.28 3 0.003 6% 0.000 002% −88.82 −153.37
下载: 导出CSV
-
何芹. 2015. 高速高精度ADC频域特性测试方法研究[D]. 无锡: 江南大学: 7–15. He Q. 2015. Research on Frequency-Domain Characteristics Testing Methods for High Speed and High Precision ADCs[D]. Wuxi: Jiangnan University: 7–15 （in Chinese）.
李彩华,滕云田,张旸,胡星星. 2014. FFT和DFT在地震数据采集器幅频特性测试中的应用[J]. 地震学报,36(5):956–963 Li C H,Teng Y T,Zhang Y,Hu X X. 2014. Applications of FFT and DFT in amplitude-frequency characteristic test of seismic data recorders[J]. Acta Seismologica Sinica,36(5):956–963 (in Chinese)
刘亮. 2014. Sigma Delta数字加速度计中谐波失真分析及优化[D]. 哈尔滨: 哈尔滨工业大学: 21–24. Liu L. 2014. Analysis and Optimization for Harmonic Distortion of Sigma Delta Accelerometer[D]. Harbin: Harbin Institute of Technology: 21–24 （in Chinese）.
刘益成,易碧金,罗福龙. 2006. 地震数据采集系统谐波畸变测试方法研究[J]. 石油物探,45(4):431–434 doi: 10.3969/j.issn.1000-1441.2006.04.018 Liu Y C,Yi B J,Luo F L. 2006. Testing method for harmonic distortion of seismic data acquisition system[J]. Geophysical Prospecting for Petroleum,45(4):431–434 (in Chinese)
杨健. 2014. 四阶前馈Σ-ΔADC中噪声与谐波失真分析及验证[D]. 哈尔滨: 哈尔滨工业大学: 6–14. Yang J. 2014. Analysis and Verification of Noise and Harmonic Distortion of Fourth-Order Feed-Forward Sigma-Delta Modulator[D]. Harbin: Harbin Institute of Technology: 6–14 （in Chinese）.
张永学,印兴耀,宋建平,张在陆,薛会珍. 2008. 测试地震数据采集系统总谐波畸变的剪切FFT算法[J]. 石油地球物理勘探,43(3):252–256 doi: 10.3321/j.issn:1000-7210.2008.03.003 Zhang Y X,Yin X Y,Song J P,Zhang Z L,Xue H Z. 2008. An algorithm testing total harmonic distortion of seismic data acquisition system:FFT Pruning algorithm[J]. Oil Geophysical Prospecting,43(3):252–256 (in Chinese)
中国地震局监测预报司. 2016. 地震数据采集器质量检测技术规程[S]. 北京: 中国地震局: 7–8. Department of Earthquake Monitoring and Prediction, China Earthquake Administration. 2016. Technical Specification for Quality Inspection of Seismic Data Acquisition Unit[S]. Beijing: China Earthquake Administration: 7–8 （in Chinese）.
Alegria F C,Da Silva H P. 2012. Choosing between terminal and independently based gain and offset error in the ADC histogram test[J]. IEEE Trans Instrum Meas,61(1):9–16 doi: 10.1109/TIM.2011.2161014
Christian H. 1994. Intermodulation distortion （IMD）[EB/OL]. [2018-05-03]. http://www.ti.com/lit/an/sboa077/sboa077.pdf.
Offelli C,Petri D. 1991. Weighting effect on the discrete time Fourier transform of noisy signals[J]. IEEE Trans Instrum Meas,40(6):972–981 doi: 10.1109/19.119777
-
期刊类型引用(2)
1. 赵立军，李文一，唐荣，郑淑梅，邓董建. 用于数据采集器测试的时间脉冲插值分析方法. 电子器件. 2024(01): 111-115 . 
百度学术
2. 熊宇鹏，方如意，黄煜，陈炳权. 基于STM32的非线性失真放大器设计与测试分析. 电子设计工程. 2022(07): 53-57+62 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 1228
- HTML全文浏览量: 550
- PDF下载量: 44
- 被引次数: 4
