Seismic hazard parameters estimation based on strain energy accumulation in both sides of a fault：Taking the 1679 Sanhe-Pinggu M8.0 earthquake as an example
-
摘要: 本文基于断裂两侧应变能积累的概念，利用新夏垫断裂上探槽研究的古地震资料和1679年三河—平谷M8.0地震的历史资料，通过原地地震复发原则来评价指定断裂（段）在某一时段内的地震危险性，探讨其在未来一段时间内可能发生地震的最大潜在震级。由此说明现今应变能确定所面临的困难，而应用局部化应变（变形）与岩石-断裂系统局部失稳临界条件之间的联系，理论上可以由变形带的宽度减小率来预估未来地震的发生时间。Abstract: Based on the historical data of the 1679 Sanhe-Pinggu M8.0 earthquake and paleo-earthquake data revealed by trenching on the Xinxiadian fault, together with the principle for earthquake recurrence in-situ on a fault or a segment, the maximum potential magnitude in the future on some segments of Xinxiadian fault is evaluated by taking consideration of the concept that strain energy accumulates on both sides of a fault. This illustrates that due to difficulty in determining the strain and stress in deep crustal rocks, the accumulated strain energy cannot be determined accurately. On the other hand, when the strain （deformation） localization is combined with the local instability critical conditions of the rock-fault system, the decreasing rate of deformation belt could be used for prediction of earthquake occurrence.
-
引言
地震的孕育发生机制表明，持续的构造运动会导致断裂两侧岩体的应变能积累，当积累的应变能（或应变、应力）超过一定限度时，断裂将局部失稳并释放出巨大能量，这一过程表现为断裂的扩展和沿已有断裂突然发生滑动，以及弹性回跳产生振动向四周传播的地震波（Reid，1910；胡聿贤，2006）。
沿断裂及其两侧一定范围内构建一个力学分析模型，理论上可以分析该断裂的地震孕育机制和发生过程等细节，而获取其精确解的前提是：已知研究区的断裂几何模型、区域内每一点的现今应力状态和本构参数、加载条件、边界条件及远、近场动力扰动（赵纪生，周正华，2009），但由于地球深部的非触摸性，短期内得到这些参数的可能性很低。在几何、力学和加载条件等均未知的极端情况下，可以利用两个基本原则指导实践：一是历史重演原则，即历史上曾经发生过大地震的地区，将来还可能发生同样强度的地震，此原则可应用于未来一段时间内，在区域的几何、力学和加载条件均无较大变化的情形下对未来发震能力进行预测（Wallace et al，1984）；二是构造类比原则，即地质构造相同的地区可能发生同样大的地震，该原则是基于已发生大地震地区的地质构造特征来预测尚未发生大地震地区的发震能力（卢寿德，2006）。
实际上，随着地震（古、历史和现今）、地质构造调查（定性和定量）、地球物理和大地测量（传统方法和全球导航卫星系统（Global Navigation Satellite System，简写为GNSS）应用）等研究的进一步开展，关于历史重演原则的相关理解也有一定深入。例如应用断裂分段长度、同震位移、滑动速率、古地震期次和复发间隔以及发震断层错动面积等定量数据，分别单独选用或同时采用相应的经验关系，如破裂长度法、同震位移法、滑动速率法、破裂面积法、地震矩法以及历史地震法等，可以对活动断裂上发生地震的最大潜在震级进行估计，只是这些方法对震级的估计精度均有待提高。对于一个特征断层源来说，根据前人给出的各种震级-破裂面积和震级-破裂长度的经验关系式，可以计算出给定分段断层源上特征地震震级的不确定性，其上限与下限最多相差1.0 （郭星，潘华，2014）。
为了有效地估计地震危险性参数，本文拟基于断裂两侧应变能积累的概念，通过研究断裂上有限的历史地震资料，应用历史重演原则评价指定断裂（段）在某一时间段内的地震危险性，探讨其未来一段时间内可能发生地震的最大潜在震级。
1. 应变能、地震释放能量与地震矩
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ E {\text{＝}} \frac{1}{2}G{\left({\frac{{vt}}{b}} \right)^2}lbh {\text{，}} $
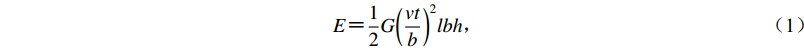
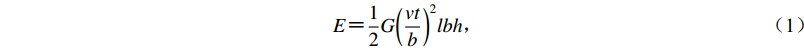
(1) 其中，E的单位为J，G为断裂两侧介质的剪切刚度，l和h分别为断裂面的长度和宽度，b为变形带宽度，v为断裂两侧的年活动速率，t为距上一次大地震的时长。
地震所释放的能量Es是震源错动引起的振动传播、错动过程中摩擦所产生的光与热以及错动前后的静力功等多种能量的综合表现，可由著名的古登堡-里克特震级能量关系（中国地震局监测预报司，2007）给出：
$ \lg {E_{\rm{s}}} {\text{＝}}\frac{3}{2}M_{\rm{S}} {\text{＋}} 4.8 {\text{，}} $
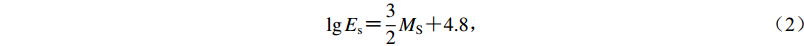
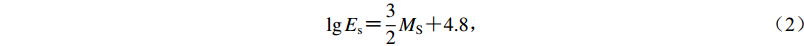
(2) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
Boatwright和Choy （1986）统计了全球397个震例，认为古登堡-里克特关系高估了地震能量Es，遂将式（2）的系数由4.8变化为4.4，推出新的震级能量关系式，其基本形式并未改变。
一次地震的地震矩定义为
$ {M_0} {\text{＝}} Gdlh {\text{，}} $
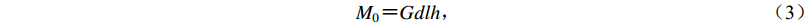
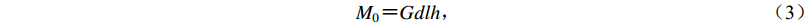
(3) 式中，M0的单位为J，d为一次地震的平均位错。
关于地震震级MS与地震矩M0统计关系的研究较多，我国大陆已有针对不同性质断裂的相应关系式（钟羽云等，2004），其中MS与M0的一般性关系为（陈运泰，刘瑞丰，2004）
$ \lg {M_{\rm{0}}} {\text{＝}}\frac{3}{2}M_{\rm{S}} {\text{＋}} 9.1{\text{，}} $
(4) $ {M_0}{\rm{ {\text{＝}} 2}} {\text{×}} {\rm{1}}{{\rm{0}}^{\rm{4}}}{E_{\rm{s}}}{\text{.}} $
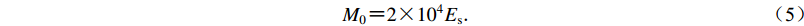
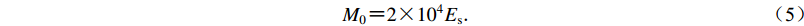
(5) 2. 历史地震和古地震震级的确定
历史地震和古地震的震级可由式（3）和式（4）或其它破裂尺度关系式确定，其结果均存在一定的不确定性。对于历史资料记载为7.0级以上的历史地震，其震源破裂面的长度l一般取Ⅸ度烈度圈的长轴尺度，也可取Ⅸ度与Ⅹ度烈度圈之间的某个长轴尺度（吕晓健，闻学泽，2014）；震源破裂面的宽度h和平均同震位移d则可由断裂陡坎或探槽测定，且分布于破裂面上的断裂陡坎或探槽的数量原则上不少于5个。
根据历史资料描述，1679年三河—平谷地震的概况为：“震之所及东至辽宁沈阳，西至甘肃岷县，南至安徽桐城，凡数千里，而三河、平谷最惨。远近荡然一空，了无障碍，山崩地陷，裂地涌水，土砾成丘，尸骸枕籍，官民死伤不计其数，有全家覆没者。 ”（郭增建，马宗晋，1988）；地震赈灾情况为：“三河、平谷、通县被灾最重，本年丁钱粮尽行蠲免；香河、武清、永清、宝坻稍次，蠲免赋额十之三；蓟县、固安又次之，免十之二。 ”（国家地震局震害防御司，1995）。可见该地震的震中烈度之大，地震波及面之广，震级应为M7.0以上。
对该地震引起的地表破裂或陡坎记载有：“三河县城西行30余里至柳河屯地脉中断、落2尺许，渐西北至东务里，则东南界落5尺许，又北至潘各庄，则正南界落1丈许；平谷县之四境，较低于旧时，或二尺或五尺一丈不等。 ”（国家地震局震害防御司，1995），表明该地震的破裂长度在60—70 km，极震区内的平均位错介于0.933—1.555 m （3—5尺，清代1尺相当于31.1 cm）之间。
向宏发等（1988）的研究表明，新夏垫断裂为三河—平谷地震的发震构造，断裂性质以倾滑为主，破裂表现为张扭性形变带，地表破裂长度约为20 km，Ⅸ度烈度圈的长轴长140 km （国家地震局震害防御司编，1995），折算平均位错为0.933 m （3尺）；他们还认为新夏垫断裂的最大位移在潘各庄一带，为3.16 m，东至东兴庄，西到东柳河屯，分别减小至0.5 m；江娃利等（2000）在齐心庄探槽的同震垂直位移为1.8 m；冉永康等（1997）应用钻探、探槽、陡坎量测给出了地震的位移量（表 1），平均位移量为0.873 m。
表 1 新夏垫断裂两次地表断错事件的参考位移量Table 1. The displacements associated with the last two events along the Xinxiadian fault剖面位置 综合推测的位移量/m 东柳河电东北1 1.00 东柳河电东北2 1.30 二里半 1.06 潘各庄西 1.74 大胡庄西南 1.17 大胡庄南1 1.25 齐心庄西南 1.00 齐心庄南1 0.97 齐心庄南2 0.96 齐心庄东南 0.58 本文将该地震的破裂长度假定为Ⅸ度烈度圈的长轴长度140 km，破裂宽度为30 km，平均位错采用历史记载（约0.933 m）、向宏发等（1988）（约1.0 m）和冉永康等（1997）（0.873 m）等3种结果，3种记录所对应的震级分别为M7.31，M7.33和M7.29，均与国家地震局震害防御司（1995）确定的震级M8.0有较大差距，说明1679年三河—平谷地震或许并未达到M8.0。
对于古地震预测所需的计算数据，通常断裂面的长度l由现场考察确定，地震的平均位错d由探槽资料确定，断裂面的宽度h则由现代仪器确定的小震震源深度来确定。由于发震震源所处断裂位置不确定，因此要求探槽数量尽量多，才可提高l和d的精度；古地震的发震年代，则需要借助于现代测年技术，且测年样品和测试手段力求多样化，以便多种方式的测年数据互相印证。
3. 未来地震震级的判断
3.1 应用历史地震和古地震资料确定未来地震的震级
应用历史地震和古地震资料确定未来地震震级的前提是：已知某断裂活动分段上特征地震的震级MS和复发周期T；假设上一次大地震后，断裂的活动特征无明显变化，断裂两侧积累的应变能的波动能量释放率无变化，且忽略两个特征地震之间所有地震能量的释放。
应用式（1）和式（2）及其平均比例关系，可以得到该断裂未来一段时间t内地震的最大潜在震级为
$ M_{\rm{S}}(t) {\text{＝}} M_{\rm{S}} {\text{－}} \frac{4}{3}\lg ({\frac{T}{t}} ){\text{.}} $
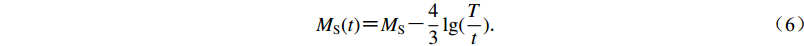
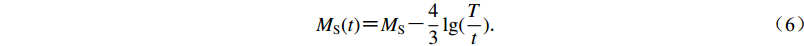
(6) 冉永康等（1997）沿三河—平谷地震的发震断层进行大探槽开挖和断层陡坎分析的结果揭示出，新夏垫断裂距今约2万年以来共发生了4次古地震事件，前两次由砂土液化判定，后两次则依据可见的直接断错；断层陡坎分析得到的1679年地震的最大垂直位移为1.75 m，1679年以前的古地震事件的最大垂直位移为1.41 m。冉永康等（1997）研究表明，4次古地震事件发生时间距今分别约20 000，13 000，7 500和317年，平均重复间隔为（6 561±691）年，表现出了准周期重复的特征。
尽管1679年三河—平谷地震的震级可能低于M8.0，本文出于安全性考虑，暂定其震级为MS8.0，离逝时间为338 （1679—2017）年，按照式（6）估算出未来100，200和300年新夏垫断裂上可能发生地震的最大震级分别为MS6.4—6.5，MS6.5—6.6和MS6.6—6.7，变化趋势如图 1所示。
![]()
图 1 新夏垫断裂上未来一段时间内可能发生地震的最大潜在震级Figure 1. The maximum potential magnitude of an earthquake on the Xinxiadian fault in a period in the future（a） 0—7 000 a；（b） 338—638 a3.2 利用断裂的现今活动速率判定未来地震震级
利用断裂的现今活动速率来判定未来地震震级，需要以下假定：已知断裂上发生过一次历史地震的震级MS和发生年代；上一次大地震后，断裂的活动特征没有明显变化；断裂两侧积累的应变能的波动能量释放率没有变化，且忽略两个特征地震之间所有的地震能量释放。
已知现今GPS测量出断裂的年活动速率v，应用式（1）和式（2）及其平均比例关系，可以得到该断裂未来一段时间内地震的最大潜在震级为
$ M_{\rm{S}}(t) {\text{＝}} \frac{4}{3}\lg v {\text{＋}} \frac{4}{3}\lg t{\text{＋}} C{\text{，}} $
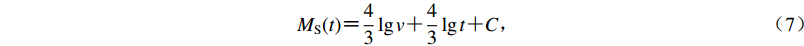
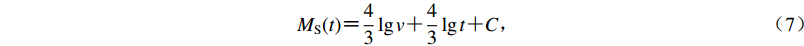
(7) 式中，C与断裂自身固有属性及地震背景有关。
应用现阶段的断裂滑动速率、历史地震发震构造上的同震位移，或应用Wells和Coppersmith （1994）的震级与破裂尺度之间的关系来确定地震的复发周期，进而确定C值，以此来判断该断裂在未来一段时间内所发生地震的最大潜在震级。对于新夏垫断裂而言，前2万年的滑动速率相对较小，为0.13—0.30 mm/a （万永魁等，2014），应用平均滑动速率和重复间隔时间确定的C值为7.8，按照式（7）估算出未来100，200和300年新夏垫断裂上可能发生地震的最大震级分别为MS6.1—6.6，MS6.3—6.7和MS6.4—6.8，变化趋势如图 2所示。
![]()
图 2 新夏垫断裂上未来一段时间内可能发生地震的最大潜在震级Figure 2. The maximum potential magnitude of an earthquake on the Xinxiadian fault in a period in the future（a） 0—7 000 a；（b） 338—638 a本文式（7）中的lgv和lgt系数为4/3，相较于沈军等（2004）的lgv和lgt系数（均为2或3）小，故本文计算所得的短期内预测震级偏低，可能更符合区域地震特征。
4. 断裂两侧应变能的积累过程
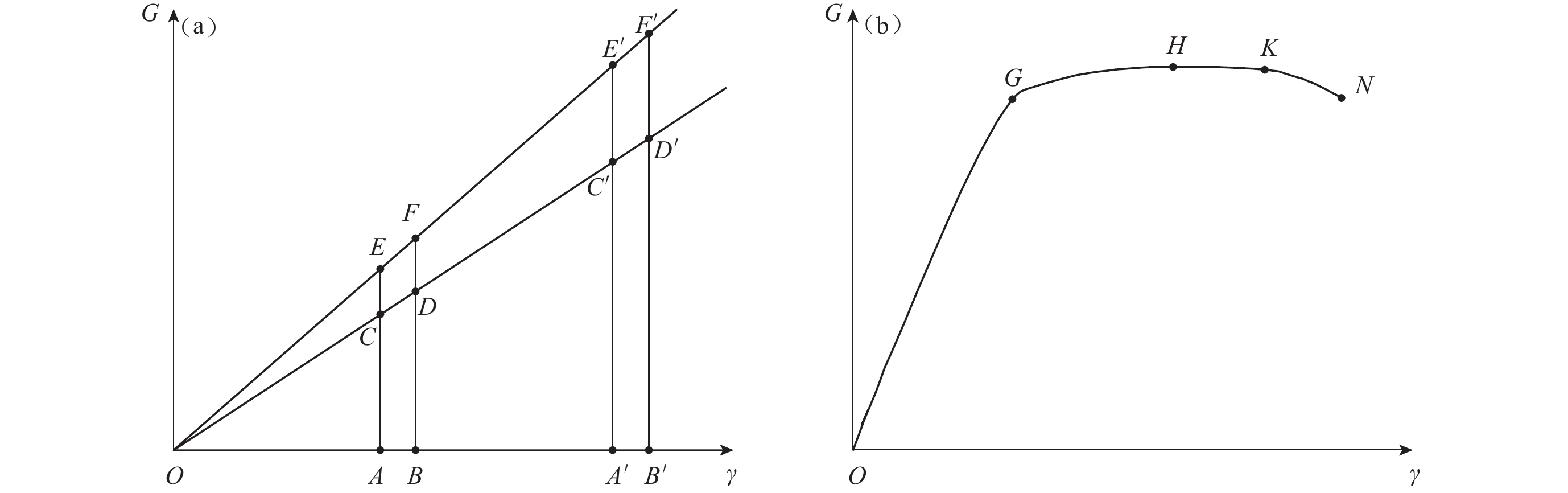
已知一条断裂（段）的长度l、宽度h、变形带宽度b、岩体剪切刚度G和现今年活动速率v，且认为其上一次地震时积累的能量已完全释放，则可计算上一次地震以来断裂两侧积累的应变能。假定应力与应变之间存在线性关系，设l，h，G，v为1，应变能单位为J，当b分别为1，0.5和0.25 m时，位移和应变的分布如图 3所示，可以看出：在一定的位错作用下，变形带越宽，位移和应变曲线越平缓，相应积累在断裂两侧的应变能的数量级偏小，但分布范围大，所面临的地震危险性则较小；相反，变形带越窄，其变形和应变进入局部化状态，所积累的应变能变大，地震危险性增大。
![]()
图 3 变形带宽度b为1 m （a），0.5 m （b）和0.25 m （c）时位移和应变的分布示意图Figure 3. Distribution of displacement and strain with deformation belt width of 1 m （a），0.5 m （b） and 0.25 m （c）断裂两侧变形带通常存在由宽变窄的过程，因此应变能积累会随着变形带变窄逐渐加速，断裂两侧的应变能随时间的变化如图 4所示，可以看出，若变形带在某一段时间内急剧变窄，应变能也会急剧上升，在图上表现为最下方的曲线在该时段内加速上升变为最上方曲线。
![]()
图 4 不同变形带宽度b所对应的断裂两侧的应变能积累曲线Figure 4. Strain energy accumulation curves in both sides of a fault with different width b of deformation belt实际上，构造地震的发生是断裂（段）局部失稳的过程，断裂两侧很薄的岩体的应力应变关系（界面本构关系）起控制界面作用（图 5b中K与M之间）；而应变积累是在断裂两侧较宽范围、较长时间内进行的过程，断裂两侧较薄的岩体并不会起到决定性作用。例如，1976年唐山MS7.8地震的发震断裂的原地复发重复间隔约为7 600年，孕震时间约为47—78年（李世愚等，2010），发震过程仅持续不到1分钟。
![]()
图 5 岩体（a）和界面（b）的剪应力G与剪应变γ关系示意图Figure 5. The relationship between shear stress G and shear strain γ on rock （a） and at interface （b）This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
5. 基于连续GPS数据预估未来地震发震时间
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ \Delta \varPi {\text{＝}} \delta \varPi {\text{＋}} \frac{1}{{2!}}{\delta ^2}\varPi {\text{＋}} \frac{1}{{{\rm{3}}!}}{\delta ^{\rm{3}}}\varPi {\text{＋}}\cdots{\text{，}} $
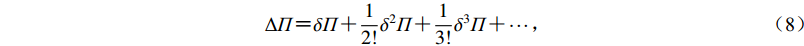
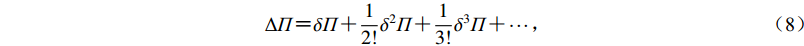
(8) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
应用式（8）和应力应变关系可得
$ {{{x}}_{ij}}{{{D}}_{ijkl}}{{{x}}_{kl}} {\text{＝}} {{0}}{\text{，}} $
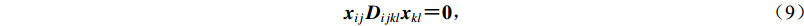
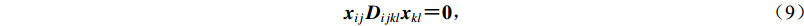
(9) 式中，D为弹塑性矩阵，x为某一向量。
若考虑一个特殊向量
$ {{{x}}_{ij}} {\text{＝}} \dfrac{1}{2}({{{g}}_i}{{{n}}_j} {\text{＋}} {{{g}}_j}{{{n}}_i}){\text{，}} \forall {{{g}}_i}{\text{≠}} {{0}}{\text{，}}{\forall }{{{n}}_i} \in \left({\left| {{n}} \right| {\text{＝}} 1} \right){\text{，}} $
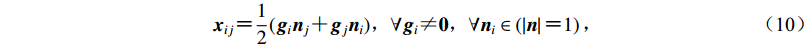
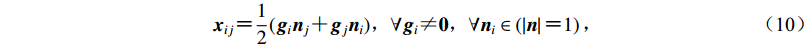
(10) 地震沿平面失稳的临界条件则为
$ ({{{n}}_j}{{{D}}_{ijkl}}{{{n}}_l}) {\text{·}} {{{g}}_i} {\text{＝}} {{0}}{\text{.}} $
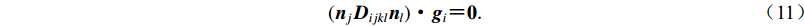
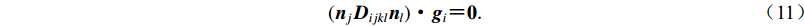
(11) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
赵纪生（2004）的研究结果表明：当岩石材料处于线弹性阶段、塑性硬化阶段时，式（11）不存在非零解；对于关联塑性模型，仅当塑性软化至一个限值时，材料才会失去稳定性，与马瑾（2010）关于地震触发工作的结论一致。
上述的数学描述可以进一步解释为，岩体-断裂系统在构造作用下进入非线性响应后，当应变能积累到某个时刻，系统刚度的降低导致应变逐渐集中在某一较窄的区域，形成应变局部化带，之后随着外部作用的持续或加剧，应变局部化带的宽度趋近为0，导致岩体-断裂系统处于局部失稳临界状态，此时地震将可能发生。如图 5所示，当界面剪应力-剪应变关系曲线达到K点时，岩体-断裂系统处于局部失稳临界状态，即地震将可能发生。
岩体-断裂系统局部失稳的临界条件与系统的刚度变化相关，刚度的变化导致变形带逐渐变窄，因此，若预估新夏垫断裂上未来大地震发震时间，利用目前的观测技术和分析水平，可能还存在一定差距。但是，随着断裂两侧GPS观测的空间密度和时间频度的增加，从积累的观测资料中，确定变形带宽度b的年变化率和月变化率的变化趋势，联合采用地球物理勘探反演技术，加强断裂两侧范围内深部岩石介质的波速变化率趋势以及地表变形前兆（断裂附近出现鼓包、裂缝和地陷现象）的观测，可能成为地震短（3个月）中（2年）期预报的主要依据。
6. 讨论与结论
本文以1679年三河—平谷M8.0地震和新夏垫断裂探槽开挖所揭示的古地震为基础，从断裂两侧应变能积累的概念出发，计算了该断裂在未来一段时间内可能发生地震的最大潜在震级；并应用变形（应变）局部化与岩石-断裂系统局部失稳临界条件之间的联系，理论上提出由变形带宽度减小率来预估未来地震的发生时间。
本文假定新夏垫断裂的活动特征没有明显变化，断裂两侧积累的应变能的波动能量释放率没有变化，且忽略两个特征地震之间所有地震能量的释放，新夏垫断裂的特征地震为M8，重复间隔为（6 561±691）年，离逝时间为338年，估计未来100，200和300年新夏垫断裂上可能发生地震的最大震级分别为MS6.4—6.5，MS6.5—6.6和MS6.6—6.7。
基于上述结论，新夏垫断裂上前20 000年以来的滑动速率相对较小（0.13—0.30 mm/a），估计未来100，200和300年内该断裂上可能发生地震的最大震级分别为MS6.1—6.6，MS6.3—6.7和MS6.4—6.8。
对构造作用下的岩体-断裂系统局部失稳临界条件进行了数学描述，表现为应变（变形）会逐渐集中在一很窄的区域形成应变局部化带。因此，加强新夏垫断裂两侧GPS观测和深部岩石介质波速探测，从观测资料中确定变形带宽度的年变化率、月变化率，从其变化趋势预估地震可能发生时间。预测的结果可能存在较大的误差，但随着观测资料的不断积累，以及成功经验和失败教训的总结，这种基于数学力学稳定描述的预测地震发生时间会成为可能。
-
![]()
图 1 新夏垫断裂上未来一段时间内可能发生地震的最大潜在震级
Figure 1. The maximum potential magnitude of an earthquake on the Xinxiadian fault in a period in the future
（a） 0—7 000 a；（b） 338—638 a
![]()
图 2 新夏垫断裂上未来一段时间内可能发生地震的最大潜在震级
Figure 2. The maximum potential magnitude of an earthquake on the Xinxiadian fault in a period in the future
（a） 0—7 000 a；（b） 338—638 a
![]()
图 3 变形带宽度b为1 m （a），0.5 m （b）和0.25 m （c）时位移和应变的分布示意图
Figure 3. Distribution of displacement and strain with deformation belt width of 1 m （a），0.5 m （b） and 0.25 m （c）
![]()
图 4 不同变形带宽度b所对应的断裂两侧的应变能积累曲线
Figure 4. Strain energy accumulation curves in both sides of a fault with different width b of deformation belt
![]()
图 5 岩体（a）和界面（b）的剪应力G与剪应变γ关系示意图
Figure 5. The relationship between shear stress G and shear strain γ on rock （a） and at interface （b）
表 1 新夏垫断裂两次地表断错事件的参考位移量
Table 1 The displacements associated with the last two events along the Xinxiadian fault
剖面位置 综合推测的位移量/m 东柳河电东北1 1.00 东柳河电东北2 1.30 二里半 1.06 潘各庄西 1.74 大胡庄西南 1.17 大胡庄南1 1.25 齐心庄西南 1.00 齐心庄南1 0.97 齐心庄南2 0.96 齐心庄东南 0.58 
下载: 导出CSV
-
陈运泰,刘瑞丰. 2004. 地震的震级[J]. 地震地磁观测与研究,25(6):1–12. Chen Y T,Liu R F. 2004. Earthquake magnitude[J]. Seismological and Geomagnetic Observation and Research,25(6):1–12 (in Chinese).
国家地震局震害防御司. 1995. 中国历史强震目录（公元前23世纪—公元1911年）[M]. 北京: 地震出版社: 1–514. Department of Earthquake Disaster Prevention, State Seismological Bureau. 1995. Catalogue of Historical Strong Earthquakes in China （23rd Century BC to 1911）[M]. Beijing: Seismological Press: 1–514 （in Chinese）.
郭星,潘华. 2014. 海原断裂带强震发生概率的评估方法[J]. 地震学报,36(6):1043–1053. Guo X,Pan H. 2014. Estimation methods for occurrence probability of large earthquakes in the Haiyuan fault zone in northwestern China[J]. Acta Seismologica Sinica,36(6):1043–1053 (in Chinese).
郭增建, 马宗晋. 1988. 中国特大地震研究（一）[M]. 北京: 地震出版社: 98–113. Guo Z J, Ma Z J. 1988. Mega Earthquake Research of China （ Ⅰ ）[M]. Beijing: Seismological Press: 98–113 （in Chinese）.
胡聿贤, 2006. 地震工程学[M]. 第二版. 北京: 地震出版社: 13. Hu Y X, 2006. Earthquake Engineering [M]. 2nd edition. Beijing: Seismological Press: 13 （in Chinese）.
江娃利,侯治华,肖振敏,谢新生. 2000. 北京平原夏垫断裂齐心庄探槽古地震事件分析[J]. 地震地质,22(4):413–422. Jiang W L,Hou Z H,Xiao Z M,Xie X S. 2000. Study on paleoearthquakes of Qixinzhuang trench at the Xiadian fault,Beijing plain[J]. Seismology and Geology,22(4):413–422 (in Chinese).
李世愚, 和泰名, 尹祥础. 2010. 岩石断裂力学导论[M]. 合肥: 中国科学技术大学出版社: 1–468. Li S Y, He T M, Yi X C. 2010. Introduction to Rock Fracture Mechanics[M]. Hefei: China University of Science and Technology Press: 1–468 （in Chinese）.
卢寿德. 2006. GB17741—2005《 工程场地地震安全性评价 》宣贯教材[M]. 北京: 中国标准出版社: 1–105. Lu S D. 2006. Teaching Book for GB17741−2005 Evaluation of Seismic Safety for Engineering Sites[M]. Beijing: Standards Press of China: 1–105 （in Chinese）.
吕晓健,闻学泽. 2014. 根据烈度分布确定华北历史地震破裂区的经验准则及其应用[J]. 地震地质,36(1):62–79. Lü X J,Wen X Z. 2014. Empirical criterions and their preliminary application to determine rupture zones of historical earthquakes in North China from seismic intensity distributions[J]. Seismology and Geology,36(1):62–79 (in Chinese).
马瑾. 2010. 地震机理与瞬间因素对地震的触发作用:兼论地震发生的不确定性[J]. 自然杂志,32(6):311–313. Ma J. 2010. Uncertainty of the earthquakes and earthquake mechanism and seismic triggering effect of instantaneous factors[J]. Chinese Journal of Nature,32(6):311–313 (in Chinese).
冉永康,邓起东,杨晓平,张晚霞,李如成,向宏发. 1997. 1679年三河—平谷8级地震发震断层的古地震及其重复间隔[J]. 地震地质,19(3):193–201. Ran Y K,Deng Q D,Yang X P,Zhang W X,Li R C,Xiang H F. 1997. Paleoearthquakes and recurrence interval on the seismogenic fault of 1679 Sanhe-Pinggu M8 earthquake,Hebei and Beijing[J]. Seismology and Geology,19(3):193–201 (in Chinese).
沈军,李莹甄,汪一鹏. 2004. 地震构造的能量积累和释放特征与新疆天山部分地区地震危险性分析[J]. 中国地震,20(3):229–237. Shen J,Li Y Z,Wang Y P. 2004. Preliminary study on accumulating and releasing characteristics of seismic tectonic energy and seismic risk of some seismogenic tectonics in Tianshan[J]. Earthquake Research in China,20(3):229–237 (in Chinese).
孙训方, 方孝淑, 关来泰. 2002. 材料力学（ Ⅰ ）[M]. 北京: 高等教育出版社: 1–360. Sun X F, Fang X S, Guan L T. 2002. Mechanics of Materials （ Ⅰ ）[M]. Beijing: Higher Education Press: 1–360 （in Chinese）.
万永魁,沈军,于晓辉,戴训也,王雷,邵博,李祥. 2014. 北京平原区夏垫活动断裂滑动速率及古地震复发间隔[J]. 防灾科技学院学报,16(3):38–45. Wan Y K,Shen J,Yu X H,Dai X Y,Wang L,Shao B,Li X. 2014. The slipping rates and ancient earthquake recurrence interval at Xiadian fault,Beijing plain[J]. Journal of Institute of Disaster Prevention,16(3):38–45 (in Chinese).
向宏发,方仲景,徐杰,李如成,贾三发,郝书俭,王景钵,张晚霞. 1988. 三河—平谷8级地震区的构造背景与大震重复性研究[J]. 地震地质,10(1):15–28. Xiang H F,Fang Z J,Xu J,Li R C,Jia S F,Hao S J,Wang J B,Zhang W X. 1988. Seismotectonic background and recurrence interval of great earthquakes in 1676 Sanhe-Pinggu M=8 earthquake area[J]. Seismology and Geology,10(1):15–28 (in Chinese).
赵纪生. 2004. 岩土材料破坏过程分析[R]. 哈尔滨: 哈尔滨工业大学: 20–31. Zhao J S. 2004. Analysis of the Failure Process of Geomaterials[R]. Harbin: Harbin Institute of Technology: 20–31 （in Chinese）.
赵纪生,周正华. 2009. 发震断层的永久位移概率评估方法[J]. 岩石力学与工程学报,28(增刊2):3349–3356. Zhao J S,Zhou Z H. 2009. A probabilistic approach to evaluate permanent displacement of causative faults[J]. Chinese Journal of Rock Mechanics and Engineering,28(S2):3349–3356 (in Chinese).
中国地震局监测预报司. 2007. 地震学与地震观测（试用本）[M]. 北京: 地震出版社: 1–270. Department of Earthquake Monitoring and Prediction, China Earthquake Administration. 2007. Seismology and Seismic Observation （Trial Edition）[M]. Beijing: Seismological Press: 1–270 （in Chinese）.
钟羽云,朱新运,张震峰. 2004. 不同类型地震的地震矩-震级标度关系研究[J]. 西北地震学报,26(1):57–61. Zhong Y Y,Zhu X Y,Zhang Z F. 2004. Study on relations between seismic moment and magnitude for various types of earthquake sequence[J]. Northwestern Seismological Journal,26(1):57–61 (in Chinese).
Boatwright J,Choy G L. 1986. Teleseismic estimates of the energy radiated by shallow earthquakes[J]. J Geophys Res,91(B2):2095–2112.
Reid H F. 1910. The Mechanics of the Earthquake, The California Earthquake of April 18, 1906[R]. Washington D C: State Earthquake Investigation Commission: 43–47.
Wallace R E,Davis J F,McNally K C. 1984. Terms for expressing earthquake potential,prediction and probability[J]. Bull Seismol Soc Am,74:1819–1825.
Wells D L,Coppersmith K J. 1994. New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J]. Bull Seismol Soc Am,84(4):974–1002.
-
期刊类型引用(2)
1. 巴振宁，赵靖轩，吴孟桃，梁建文. 基于CPU-GPU异构并行的复杂场地近断层地震动谱元法模拟. 地震学报. 2022(01): 182-193 . 
本站查看
2. 刘智荣，沈军，王昌盛. 河北三河上更新统-全新统磁化率变化旋回分析. 科学技术与工程. 2020(35): 14410-14416 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 1691
- HTML全文浏览量: 1206
- PDF下载量: 83
- 被引次数: 4
