The evaluation method for the accuracy of short-term earthquake prediction
-
摘要: 预测效果的科学评价是预测学科必须要解决的问题，对地震预测效果的评价一般分为两种，一种是对单次预测成败的评判，另一种是对方法或手段多次预测效果的统计评分。本文提出了针对单次有震预测是否准确的定量评价方法，即地震预测准确性A值评分法。针对我国地震预测现状，本文约定了准确性评分由预测与实际地震的对应情况（简称“对应度” ）和时、空、强预测窗口的精确程度（简称“精确度” ）综合决定，同时，还给出了对应度的计算方法和精确度的评价标准。通过对四川省地震局2013年2月上报的短期预测意见进行试算，结果表明该方法具有可行性，可用于短期地震预测意见统一管理的准确性评价。Abstract: Scientific evaluation of prediction effect is a problem that must be solved in prediction discipline. There are two kinds of evaluation of earthquake prediction effect, one is the evaluation of single prediction, the other is the statistical evaluation of multiple prediction effects of a method. This paper presents a quantitative evaluation method for the accuracy of single earthquake prediction, which is called accuracy score method （abbreviated as " A score” ）. In view of the present situation of earthquake prediction in China, this paper stipulates that the accuracy score is determined by the corresponding situation between prediction and actual earthquake （abbreviated as " correspondence score” ） and the exactitude of time, space and strong prediction window （abbreviated as" exactitude score” ）. This paper also shows the calculation method of correspondence score and exactitude score. The opinions and examples of the short-term prediction reported by Sichuan Earthquake Agency in February 2013 show that this method is scientific and reasonable, and can be used for the evaluation and unified management of short-term earthquake prediction.
-
引言
地震预测意见是对地震孕育发生过程的客观认识，其是否准确有效，必须经过科学的检验和验证。实证性是科学，特别是自然科学的一个基本的和显著的特性（杨玉辉，2003），自然科学的检验分为观测检验和实验检验两种，由于地震现象的复杂性，关于地震的认识和经验只能通过观测进行检验，即通过将地震发生的实际情况与地震预测情况进行对比，以二者相符合的程度来判定预测是否准确或有效。由于地震预测包括时间、地点和震级三要素的预测，当预测三要素中可能存在仅一个或两个要素比较准确，或者预测的要素与地震发生的实况有较小偏差时，建立一个客观、合理、定量的地震预测评价方法是非常重要的。一方面，由于目前对地震孕育过程认识的局限性，关于地震孕育发生的众多模型和理论假设是否真实，以及从各种地震和地球物理、化学观测数据中提取到的地震发生时间、地点及强度的技术指标是否科学合理，均需要通过地震实况进行检验；另一方面，建立客观合理的地震预测检验方法可使地震科学研究程序规范化和标准化。科学认识过程分为感性认识阶段、理性认识阶段和复归实践阶段。地震预测理论和技术方法最初均是从具体现象出发，通过积累形成感性的经验认识。在此基础上，形成统一、规范的检验评价标准是从感性认识阶段上升到理性认识阶段的必要过程，也是地震预测作为一门成熟学科的重要标志之一。
科学合理地评估地震预报的能力，首先需要寻找客观评价地震预报能力的方法，这项研究既具有很强的探索性，也是十分复杂的（朱令人等，1991；张国民等，2002）。例如，20世纪90年代中叶，国际学术界对希腊科学家采用的VAN方法（以Varotsos P，Alexopoulos K和Nomicos K姓氏的第一个字母简称）预报地震的有效性问题就有过非常激烈的辩论（Aceves et al，1996；Geller，1996；Kagan，1996，1997；Varotsos et al，1996）。我国自1966年河北邢台MS7.2强震群开始实践地震预测预报，而如何科学地检验和评价预测意见的问题很早就引起了广泛关注，一些研究人员在定量统计检验方面进行了探索，例如朱令人等（1991）提出地震预报必须是三要素预报，缺一或缺二就构不成有意义的预报，并提出分三个方面解决这个问题：① 一次有震综合预报的成败，即是否准确的判定，其标准是依据理论模型或预报现状约定的；② 一类预报与地震自然发生概率对比的有效性的统计检验；③ 单项预报方法或手段有效性的统计检验。许绍爕（1989）在对1972年提出的震兆鉴定方法总结的基础上，提出对上述第2类预报有效性检验的具体方法，即扣除随机概率的地震预报效能的R值评分方法，
$ R {\text{＝}} {\displaystyle\frac{{{\text{报对的地震次数}}}}{{{\text{应预报的地震总次数}}}} {\text{－}} \frac{{{\text{预报占用时间}}}}{{{\text{预报研究的总时间}}}}}{\text{，}} $
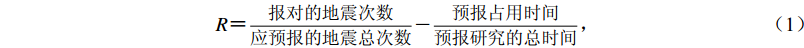
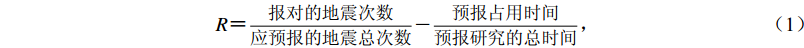
(1) 该方法已被中国地震学界和国际上一些研究人员所采纳（Keilis-Borok，Kossobokov，1990）。石耀霖等（2000）改进了R值计算方法，用虚报面积占全部无震面积代替预报时间窗口总和与总时长比例，并将该方法用于评价1990年至1998年间国家地震局年度地震危险区的预报效能，认为中国大陆地区年度危险区预测效果总体上好于随机预报。张国民等（2002）为了讨论地震能否预报和评价当时中国地震预报能力等问题，将中国大陆分为931个1°×1°的网格，以报有震网格数占总网格数比例与虚报网格数占总无震网格数比例为评分值，评价1990年至2000年年度危险区预报效果，认为虽然预报水平还相当低且不稳定，但年度危险区预测结果好于随机预测。马宏生等（2004）将中国大陆以107°E为界分为东部和西部，针对1990至2002年的年度地震危险区，计算东西部不同震级下限时的R值评分，结果表明，虽然年度危险区预测水平还很低且不稳定，但总体呈上升趋势。地震预报效能的R值评分方法已被用于每年年度危险区预报效果的评价和总结①—②③，该方法在优化改进年度危险区预测技术方法上发挥了重要的作用。
自2009年新修订的防震减灾法颁布实施以来，中国地震局每年会接收到几百份地震预测卡，其中多数为短期预测，因此亟需建立统一规范的定量评价方法，才能够从中筛选出准确性较高的预测，总结其中有效的预测思路和方法，进而促进地震预测的发展。但目前尚缺少对单次地震预报准确性的定量评价方法。中国地震预测分为十年尺度、年度、短期和临震等4种，其中3个月以内的短期预测是可以采取紧急应对措施减轻地震灾害的重要参考依据。本文提出了一种针对单次短期预测准确性的定量评价方法，即A值评分法。约定该评分是预测与地震活动实况的对应程度（以下简称 “对应度” ，即C值）及其预测窗口的精确程度（以下简称 “精确度” ，即E值）等两方面评价的综合结果，约定了对应度C值的计算方法，依据我国大陆地震活动特点确定了计算参数；参照中国地震局关于上报地震预测卡的规定，约定了精确度E值的评价标准。最后，进行了举例和实例试算，结果表明该方法能够基本客观合理地评价单次短期预测的预测效果。
1. A值评分法定义与算法
短期预测准确性评价是指，短期预测的时间、空间、震级窗口与实际地震对应程度及其精确程度。由该方法确定的准确性评价值称为A值，最高值为1.0，最低值为0，准确性越低数值越小。准确性评价值的计算方法为
$ A{\text{＝}}C \cdot E{\text{，}} $
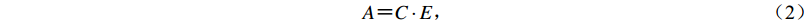
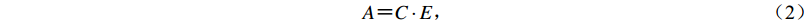
(2) 式中：A为准确性评价值，称为准确性评分；C为预测地震与实际地震对应程度的评价值，即对应度；E为预测的时间、空间、震级窗口的精确程度的评价值，即精确度。
上述用于评价预测准确性的实际发生的地震事件称为评价地震。评价地震一般为预测窗口内或其附近的最高震级的地震事件，其选取原则为能使预测获得最高的A值评分。
2. 对应度的设计原则及计算方法
2.1 对应度的设计原则
1） 预测意见与实际地震符合程度决定了对应度的大小。当评价地震的发生时间、震中、震级均位于预测窗口之内时对应度最高，为1.0，位于预测窗口之外时，对应度下降。
2） 评价地震偏离预测窗口时，对应度与偏离预测窗口距离的大小相关，越靠近预测窗口，对应度越大，越远离窗口对应度越小。
3） 不同预测窗口相比，预测窗口越小，评价地震偏离预测窗口时对应度下降速率越慢，反之，预测窗口越大，评价地震偏离预测窗口时对应度下降速率越快（图1）。
![]()
图 1 预测窗口尺度与对应度得分关系示意图（a） 预测窗口为中等尺度时；（b） 预测窗口为较小尺度时；（c） 预测窗口为较大尺度时Figure 1. Diagram of the relationship between different predicted window lengths and correspondence score（a） With medium scale prediction window length；（b） With small scale prediction window length；（c） With large scale prediction window length4） 对应度为时间、空间、震级3个要素对应度的乘积，即
$ C{\text{＝}}C_{\rm t} \cdot C_{\rm m} \cdot C_{\rm s}{\text{，}} $
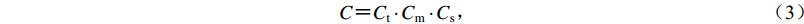
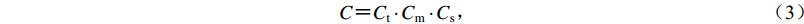
(3) 式中：Ct为预测时间的对应度评价值，简称时间对应度；Cm为预测震级的对应度评价值，简称震级对应度；Cs为预测空间的对应度评价值，简称空间对应度。
2.2 对应度的计算模型
在满足对应度计算原理的情况下，可构建对应度函数，即
$ C {\text{＝}} \exp\, \left[\alpha {\,(x {\text{－}} \mu)^2}\right]{\text{，}} $
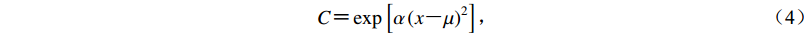
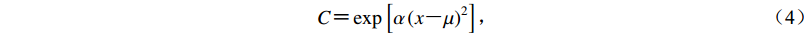
(4) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ C {\text{＝}} \exp \left[ {\frac{{\ln {C_0}}}{{{{({x_0} {\text{－}} \mu)}^2}}}{{(x - \mu)}^2}} \right]{\text{，}} $
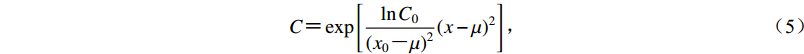
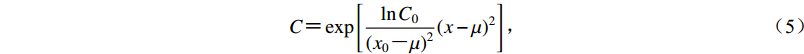
(5) 式中，x0为允许误差，C0为该允许误差下对应度的得分。
2.3 对应度的计算方法
2.3.1 时间对应度计算方法
假设时间预测窗口长度为T，地震短期预测时间范围为10天以上、3个月以内，即T取值为11天—3个月。由于不同预测意见的预测时间窗口T不同，统一设定3.5个月时的对应度得分为0.1，即评价地震距离预测窗口起点达到3.5个月时对应度为0.1。假设ΔTmax为预测窗口外的时间允许误差，即ΔTmax＝3.5－T，则允许误差将随预测时间窗口T的增加而减少（图2a）。
![]()
图 2 不同时间、空间和震级下的对应度计算结果（a） 预测时间为1个月、2个月、3个月；（b） 半径为40，100，150，200 km；（c） 震级为5.0，5.5，5.8和6.2Figure 2. Results of correspondence score of different time，space and magnitude ranges（a） Time length of one month，two months and three months；（b） Space range of 40，100，150 and 200 km；（c） Magni-tude of MS5.0，MS5.5，MS5.8 and MS6.2This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {C_{\rm t}} {\text{＝}} \exp \left[ {\frac{{\ln {C_{t_0}}}}{{{{\!\!{\text{（}}{t_0} {\text{－}} T{\text{）}}}\!\!\!\!^2}}}\!\!\!\!{{{\text{（}}{x_{\rm t}} - T{\text{）}}}\!\!\!\!^2}} \right]{\text{，}} $
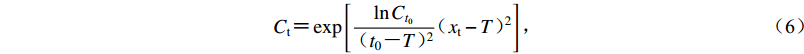
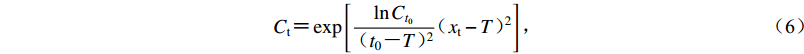
(6) 式中，xt为设定评价地震发生时间超出预测开始时间的长度。
2.3.2 空间对应度计算方法
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {C_{\rm s}} {\text{＝}} \exp \left({\frac{{\ln {C_{{s}_0}}}}{{\Delta {L_{\max }^2}}}{x_{\rm s}}^2} \right){\text{，}} $
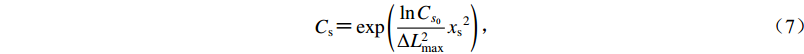
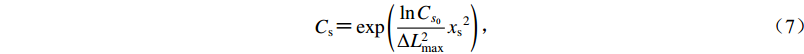
(7) 式中，xs为评价地震位于预测窗口以外、距离窗口边界的距离。当预测窗口为正方形、长方形或其它不规则形状、且评价地震震中位于窗口之外时，xs为距预测区域最短的距离，L为与预测窗口范围同等面积的圆的半径（图2b）。
2.3.3 震级对应度计算参数
设震级预测窗口为确定的震级范围，下限为M1，上限为M2，中值为M1，则有M1＝（M1＋M2）/2。当评价地震震级超出预测窗口时，或当评价地震震级小于M1和大于M2时，需要约定不同的计算参数（图2c）。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ C_{\rm m} {\text{＝}} \left\{ \begin{align} & {\exp \left({\displaystyle\frac{{\ln {C_{m_0}}}}{{{{({M_{\min }} {\text{－}} {M_1})}^2}}}{{\left({{x_{\rm m}} - {M_1}} \right)}^2}} \right)}{\text{，}}\quad\quad{{x_{\rm m}} {\text{＜}} {M_1}}{\text{，}} \\ & 1{\text{，}}\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\; {{M_1} {\text{≤}} {x_{\rm m}} {\text{≤}} {M_2}}{\text{，}}\\ & {\exp \left({\displaystyle\frac{{\ln {C_{m_0}}}}{{{{({M_{\max }} {\text{－}} {M_2})}^2}}}{{\left({{x_{\rm m}} - {M_2}} \right)}^2}} \right)}{\text{，}}\quad\quad\!{{x_{\rm m}} {\text{＞}} {M_2}{\text{，}}{M_1} {\text{＜}} 6.5}{\text{，}}\\ & 2{\text{，}}\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;{{x_{\rm m}} {\text{＞}} {M_2}{\text{，}}{M_1} {\text{≥}} 6.5}{\text{，}} \end{align}\right. $
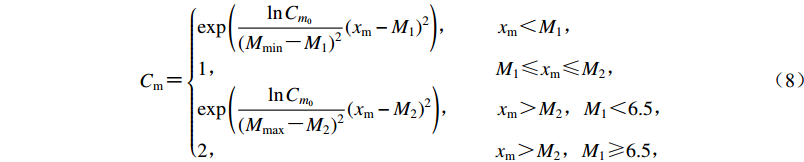
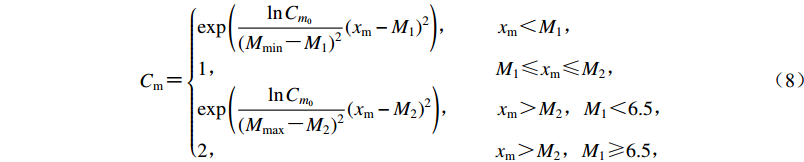
(7) 式中，xm为评价地震的震级。
3. 精确度的设计原则及计算方法
3.1 精确度的设计原则
精确度设计原则为：① 精确度的评价标准参照 《地震预报管理条例》 （中国地震局，1998）规定、取得减灾实效震例的预报尺度、中国地震局关于地震预测意见三要素预测窗口尺度规定等确定；② 预测范围在标准范围以内，精确度为1.0，超出标准范围时精确度线性减小；③ 精确度为时间、空间、震级三要素精确度的乘积，即
$ E{\text{＝}}E_{\rm t} \cdot E_{\rm m} \cdot E_{\rm s}{\text{，}} $
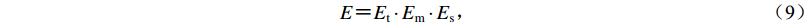
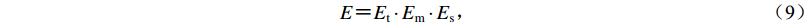
(8) 式中：E为预测精确度，最大值为1.0，精确程度越低值越小，精确度是对预测意见精确程度的描述，与地震实况之间的对应情况无关；Et为预测时间的精确程度评价值，简称时间精确度；Em为预测震级的精确程度评价值，简称震级精确度；Es为预测空间的精确程度评价值，简称空间精确度。
3.2 时间精确度的计算方法
按照 《地震预报管理条例》 （中国地震局，1998）的规定，地震短期预测意见的时间窗口为11天—3个月。为了引导预测者在经验和依据允许的情况下尽可能地缩小预测时间窗口，提高预测意见的精度，规定当预测时间窗口小于一个月时，时间精确度最高，为Et＝1.0，窗口越大时间精确度越低，当预测时间窗口为3个月时，时间精确度为Et＝0.8。当预测时间窗口介于11天与3个月之间时，通过线性内插取值（图3a）。
![]()
图 3 不同时间、空间和震级精确度取值（a） 不同预测时间窗口尺度的时间精确度取值；（b） 不同预测震级的空间精确度取值与预测区域半径之间的关系；（c） 不同预测震级范围时的震级精确度取值Figure 3. Exactitude score of different time，space and magnitude ranges（a） Time exactitude score of different time length；（b） Space exactitude score of different space ranges in each predicted magnitude；（c） Magnitude exactitude score of different magnitude ranges3.3 空间精确度的计算方法
按照 《地震预报管理条例》 （中国地震局，1998）的规定，M7以上地震的预测空间半径应小于200 km；M6 （6.0—6.9）地震的预测空间半径应小于150 km；M5 （5.0—5.9）地震的预测空间半径应小于100 km。本文以此作为评价短期预测意见空间精确度的标准，并规定，对于圆形预测区域：预测震级（取中值）为5.0—5.9，半径小于100 km时，Es＝1.0，半径为150 km时，Es＝0.6；预测震级（取中值）为6.0—6.9，半径小于150 km时，Es＝1.0，半径为200 km时，Es＝0.6；预测震级（取中值）≥7.0，半径小于200 km时，Es＝1.0，半径为250 km时，Es＝0.6。对于矩形区域或地震预测意见提出者定义的不规则形状，按照预测空间面积的等效圆处理（图3b）。
3.4 震级精确度的计算方法
本文参照地震震级测定误差来确定震级精确度的评价标准。目前中国地震台网测定的震级误差一般为0.3—0.5，因此认为预测震级误差在此范围内震级精确度最高，即预测震级M2－M1≤1.0时，Em＝1.0。震级误差范围增大时，精确度下降，设当震级预测窗口增大一倍时震级精确度为0.6，即M2－M1＝2.0时，Em＝0.6。当预测震级范围介于1.0和2.0之间时通过线性内插取值，大于2.0时则外推取值（图3c）。
4. 举例和实例试算
4.1 举例试算
举例1. 例如某预测意见为：未来1个月内，以A点为圆心、50 km为半径的范围内，将会发生M5.5—6.5地震。假设了4种地震实况，试算结果列于表1。
表 1 举例1试算参数及其准确性评价结果Table 1. The calculation parameters and its accuracy results of example one时间参数 空间参数 强度参数 精确度E 对应度C 准确度A 发震时间 时间对
应度Ct时间精
确度Et震中位置 空间对
应度Cs空间精
确度EsM 震级对
应度Cm震级精
确度Em实况1 第25天 1 1 圆形区内 1 1 6.0 1 1 1 1 1 实况2 超出窗
口3天1 1 窗口外
50 km0.91 1 5.3 0.86 1 1 0.78 0.78 实况3 超出窗
口9天0.97 1 窗口外
100 km0.69 1 5.1 0.57 1 1 0.38 0.38 实况4 超出窗
口33天0.65 1 窗口外
120 km0.44 1 4.3 0.04 1 1 0.011 0.011 举例2. 例如某预测意见为：未来3个月内，以B点为圆心、100 km为半径的范围内，将会发生M5.0—7.0地震。也假设4种地震实况，试算结果列于表2。
表 2 举例2试算参数及其准确性评价结果Table 2. The calculation parameters and its accuracy results of example two时间参数 空间参数 强度参数 精确度E 对应度C 准确度A 发震时间 时间对
应度Ct时间精
确度Et震中位置 空间对
应度Cs空间精
确度EsM 震级对
应度Cm震级精
确度Em实况1 第75天 1 0.8 圆形区内 1 1 6.0 1 0.6 0.48 1 0.48 实况2 超出窗
口3天0.91 0.8 窗口外
50 km0.7 1 4.8 0.49 0.6 0.48 0.31 0.15 实况3 超出窗
口9天0.44 0.8 窗口外
100 km0.23 1 4.6 0.35 0.6 0.48 0.035 0.017 实况4 超出窗
口25天0.001 0.8 窗口外
170 km0.04 1 4.4 0.05 0.6 0.48 0.000 002 0.000 000 96 分析例1和例2的试算结果可以看出：① 对比实况1的试算结果，例1较例2的预测窗口小而精确度高，精确度只由预测窗口大小决定，即一次预测的精确度只可能有一个值，而对应度依据与实际地震活动的对应情况可能有不同的值。准确性的最高评分是精确度，即预测与实际地震完全对应时的评分值。② 对比实况2和3的试算结果，当评价地震偏离预测窗口相同时间、距离和震级的情况下，例1的对应度和准确度均明显大于例2。③ 实况4的试算结果，当评价地震的震级及发生时间低于最大误差范围时，对应度和准确度的数值接近于0，可以认为实况4与预测意见基本不对应。
4.2 实例试算
2013年四川省地震局工程测绘院于2013年2月22日上报了短期预测卡（苏琴等，2014）（图4），预测2013年2月25日—2013年5月10日期间，以（101.65°E，29.33°N）为圆心，154 km为半径的区域，有可能发生M6.0—6.9地震。根据地震活动实况，评价地震为2013年4月20日四川芦山MS7.0地震（103.0°E，30.3°N）。利用A值评分算法计算该次预测的准确性，计算过程如图5所示。
![]()
图 4 2013年四川省地震局测绘工程院预报卡截图Figure 4. The screenshot of the prediction card in 2013 provided by the Institute of Surveying and Mapping Engineering，Sichuan Earthquake Agency![]()
图 5 四川地震局短期预测的对应度和精确度计算过程灰线为本文约定的计算规则，红色线条为本预测意见满足的评分规则，蓝色方框为本预测意见的具体得分Figure 5. Calculation process of correspondence score and exactitude score of prediction card provided by Sichuan Earthquake AgencyThe grey line is the calculation rule in this paper，the red line is the scoring rule satisfied by this prediction card，and the blue box is the score of this prediction card根据图5可知，该预测意见的准确性评价得分为：对应度：Ct＝1.00；Cm＝0.94；Cs＝1.00；C＝0.94；精确度：Et＝0.85；Em＝1.0；Es＝0.97；E＝0.82；准确性评分：A＝0.78。
如上所示，2013年芦山MS7.0地震发生在预测时间、空间窗口内，震级超出预测震级窗口0.1，对应效果较好，对应度为0.94。该次预测的时间窗口为2.5个月，时间精确度较低；震级窗口为0.9，震级精确度达到标准，为1.0；空间窗口相当于半径154 km的圆型区域，稍大于标准，空间精确度为0.97。总体看，该预测虽然对应效果较好，但时间、空间预测窗口较大，精确度较低。相比于1975年海城MS7.3地震等成功短临预报实例，该预测的准确性稍低（蒋凡，1978）。准确性评分计算结果为0.78，基本是合理的。
5. 讨论与结论
通过上述分析，本文初步得出如下结论：
1） 本文提出的针对短期地震预测准确性的定量评价方法是基本科学合理的，可用于短期地震预测的评价和地震预测意见的统一管理。
2） 中国的地震预报探索在国际上是最持久广泛的，且具鲜明的实践性特点，地震预测始终服务于防震减灾，为地震灾害风险应对决策提供参考。为此要求预测尽可能准确，即与实际地震相符，同时尽可能精确，即预测窗口尽可能小，以利于采取应急措施的同时尽可能地缩小影响范围，因此要求在有把握的情况下努力提高预测的精确性。应避免为了追求对应效果而扩大预测窗口，或者为了追求精确缩小窗口从而使得地震落在窗口以外的可能性增大，这两种情况均会使预测作为风险决策参考的价值下降。本文约定由对应度和精确度共同决定准确度的评分，旨在为了引导预测者在资料和经验允许的情况下尽可能缩小时间、空间和震级的预测窗口。
3） 为了更好地提供灾害风险决策，地震预测准确性评价标准应考虑地震灾害的区域特点。中国大陆具有地震活动西高东低的特点，西部（一般以107°E为界）地震频度和强度明显高于东部，而相同震级地震造成的灾害和影响则低于东部。因此，本文确定的震级精确度评价标准西部高于东部，是符合中国大陆地震国情的。时间和震级精确度评分标准的约定主要基于中国地震短期预测现状。未来随着短期预测水平的提高，评分标准也会作出相应调整。
4） 中国地震预报历经50年，现有地震预测按时间尺度分为长中短临等4种，即中长期（10年尺度）、中期（1年）、短期（3个月）和临震（10天以内），每一种都需要有单项预测的评价方法。本方法可用于短期预测的准确性评价，也可用于另外3种地震预测的准确性评价，以及预测所依据的方法和技术的预报效能的评估。
5） 目前地震预测总体水平较低，表现在准确性低和稳定性较差两个方面，某一次预测是否准确存在很大的不确定性，是否能够依据该预测采取应对措施，需要对该预测的准确性有一定的预先评估。利用本方法，可对之前类似预测的准确性进行评价，依据多次评分的平均值预估该次预测可能的预测效果，以供决策时参考。
-
![]()
图 1 预测窗口尺度与对应度得分关系示意图
（a） 预测窗口为中等尺度时；（b） 预测窗口为较小尺度时；（c） 预测窗口为较大尺度时
Figure 1. Diagram of the relationship between different predicted window lengths and correspondence score
（a） With medium scale prediction window length；（b） With small scale prediction window length；（c） With large scale prediction window length
![]()
图 2 不同时间、空间和震级下的对应度计算结果
（a） 预测时间为1个月、2个月、3个月；（b） 半径为40，100，150，200 km；（c） 震级为5.0，5.5，5.8和6.2
Figure 2. Results of correspondence score of different time，space and magnitude ranges
（a） Time length of one month，two months and three months；（b） Space range of 40，100，150 and 200 km；（c） Magni-tude of MS5.0，MS5.5，MS5.8 and MS6.2
![]()
图 3 不同时间、空间和震级精确度取值
（a） 不同预测时间窗口尺度的时间精确度取值；（b） 不同预测震级的空间精确度取值与预测区域半径之间的关系；（c） 不同预测震级范围时的震级精确度取值
Figure 3. Exactitude score of different time，space and magnitude ranges
（a） Time exactitude score of different time length；（b） Space exactitude score of different space ranges in each predicted magnitude；（c） Magnitude exactitude score of different magnitude ranges
![]()
图 4 2013年四川省地震局测绘工程院预报卡截图
Figure 4. The screenshot of the prediction card in 2013 provided by the Institute of Surveying and Mapping Engineering，Sichuan Earthquake Agency
![]()
图 5 四川地震局短期预测的对应度和精确度计算过程
灰线为本文约定的计算规则，红色线条为本预测意见满足的评分规则，蓝色方框为本预测意见的具体得分
Figure 5. Calculation process of correspondence score and exactitude score of prediction card provided by Sichuan Earthquake Agency
The grey line is the calculation rule in this paper，the red line is the scoring rule satisfied by this prediction card，and the blue box is the score of this prediction card
表 1 举例1试算参数及其准确性评价结果
Table 1 The calculation parameters and its accuracy results of example one
时间参数 空间参数 强度参数 精确度E 对应度C 准确度A 发震时间 时间对
应度Ct时间精
确度Et震中位置 空间对
应度Cs空间精
确度EsM 震级对
应度Cm震级精
确度Em实况1 第25天 1 1 圆形区内 1 1 6.0 1 1 1 1 1 实况2 超出窗
口3天1 1 窗口外
50 km0.91 1 5.3 0.86 1 1 0.78 0.78 实况3 超出窗
口9天0.97 1 窗口外
100 km0.69 1 5.1 0.57 1 1 0.38 0.38 实况4 超出窗
口33天0.65 1 窗口外
120 km0.44 1 4.3 0.04 1 1 0.011 0.011 
下载: 导出CSV
表 2 举例2试算参数及其准确性评价结果
Table 2 The calculation parameters and its accuracy results of example two
时间参数 空间参数 强度参数 精确度E 对应度C 准确度A 发震时间 时间对
应度Ct时间精
确度Et震中位置 空间对
应度Cs空间精
确度EsM 震级对
应度Cm震级精
确度Em实况1 第75天 1 0.8 圆形区内 1 1 6.0 1 0.6 0.48 1 0.48 实况2 超出窗
口3天0.91 0.8 窗口外
50 km0.7 1 4.8 0.49 0.6 0.48 0.31 0.15 实况3 超出窗
口9天0.44 0.8 窗口外
100 km0.23 1 4.6 0.35 0.6 0.48 0.035 0.017 实况4 超出窗
口25天0.001 0.8 窗口外
170 km0.04 1 4.4 0.05 0.6 0.48 0.000 002 0.000 000 96
下载: 导出CSV
-
蒋凡. 1978. 海城地震[M]. 北京: 地震出版社: 61−63. Jiang F. 1978. Hai Cheng Earthquake[M]. Beijing: Seismological Press: 61−63 （in Chinese）.
马宏生,刘杰,吴昊,李杰飞. 2004. 基于R值评分的年度地震预报能力评价[J]. 地震,24(2):31–37. doi: 10.3969/j.issn.1000-3274.2004.02.005 Ma H S,Liu J,Wu H,Li J F. 2004. Scientific evaluation of annual earthquake prediction efficiency based on R-value[J]. Earthquake,24(2):31–37 (in Chinese).
石耀霖,刘杰,张国民. 2000. 对我国90年代年度地震预报的评估[J]. 中国科学院研究生院学报,17(1):63–69. Shi Y L,Liu J,Zhang G M. 2000. The evaluation of Chinese annual earthquake prediction in the 90s[J]. Journal of Graduate School,Academia Sinica,17(1):63–69 (in Chinese).
苏琴,杨永林,郑兵,王双洪,李菲菲,刘冠中. 2014. 4·20芦山7.0级地震预测思路及过程回顾[J]. 地震地质,36(4):1076–1093. Su Q,Yang Y L,Zheng B,Wang S H,Li F F,Liu G Z. 2014. A review of the thinking and process about prediction of Lushan M7.0 earthquake on Apr.20,2013[J]. Seismology and Geology,36(4):1076–1093 (in Chinese).
许绍爕. 1989. 地震预报能力评分[G]//地震预报方法实用化研究文集地震学专辑. 北京: 地震出版社: 586−589. Xu S X. 1989. Earthquake prediction ability score[G]//Seismic Prediction Method Practical Research Collection: Seismological Album. Beijing: Seismological Press: 586−589 （in Chinese）.
杨玉辉. 2003. 现代自然辩证法原理[M]. 北京: 人民出版社: 220−221. Yang Y H. 2003. Principle of Modern Natural Dialectics[M]. Beijing: People’s Press: 220−221 (in Chinese).
张国民,刘杰,石耀霖. 2002. 年度地震预报能力的科学评价[J]. 地震学报,24(5):525–532. doi: 10.3321/j.issn:0253-3782.2002.05.010 Zhang G M,Liu J,Shi Y L. 2002. A scientific evaluation of annual earthquake prediction ability[J]. Acta Seismologica Sinica,24(5):525–532 (in Chinese).
中国地震局. 1998. 地震预报管理条例[S]. 北京: 地震出版社: 1−5. China Earthquake Administration. 1998. Regulations on Administration of Earthquake Dredictions[S]. Beijing: Seismological Press: 1−5 （in Chinese）. 朱令人, 朱成熹, 洪时中, 秦卫平, 郑兴树, 黄世奇. 1991. 地震预报效能评价[G]//中国地震预报方法研究: 实用化研究论文集. 北京: 地震出版社: 35−45. Zhu L R, Zhu C X, Hong S Z, Qin W P, Zheng X S, Huang S Q. 1991. Earthquake prediction effectiveness evaluation[G]//China Earthquake Prediction Method Research: Practical Research Papers. Beijing: Seismological Press: 35−45 （in Chinese）.
Aceves R L,Park S K,Straus D J. 1996. Statistical evaluation of the VAN method using the historic earthquake catalog in Greece[J]. Geophys Res Lett,23(11):1425–1428. doi: 10.1029/96GL01478
Geller R J. 1996. Debate on evaluation of the VAN method: Editor’s introduction[J]. Geophys Res Lett,23(11):1291–1293. doi: 10.1029/96GL00742
Kagan Y Y. 1996. VAN earthquake prediction:An attempt at statistical evaluation[J]. Geophys Res Lett,23(11):1315–1318. doi: 10.1029/95GL03417
Kagan Y Y. 1997. Statistical aspects of Parkfield earthquake sequence and Parkfield prediction experiment[J]. Tectonophysics,207(3/4):207–219.
Keilis-Borok V I,Kossobokov V G. 1990. Premonitory activation of earthquake flow: Algorithm M8[J]. Phys Earth Planet Inter,61(1/2):73–83.
Varotsos P,Eftaxias K,Vallianatos F,Lazaridou M. 1996. Basic principles for evaluating an earthquake prediction method[J]. Geophys Res Lett,23(11):1295–1298. doi: 10.1029/96GL00905
-
期刊类型引用(7)
1. 唐春呈，张仁鹏，焉恒琦，张帆，乔天罡. 双阳水管NS分量异常分析及其预报效能评估. 防灾减灾学报. 2024(02): 57-62 . 
百度学术
2. 苑争一，姜祥华，刘琦. 基于R值和统计分布检验的年度地震危险区个数评估. 中国地震. 2023(01): 88-97 . 百度学术
3. Jin Wei，Huining Huang，Ying Jiang，Ziwei Liu. Abnormal characteristics and effectiveness evaluation of the micro-seismic signal before the Debao M_S4.8 earthquake. Geodesy and Geodynamics. 2023(06): 605-613 . 必应学术
4. 关玉梅，王紫燕，杨锦玲，秦双龙. 华南地区定点形变预测指标建设. 华南地震. 2022(04): 34-40 . 百度学术
5. 杨红樱，于章棣，黄瑞滨，齐彬彬，裴东洋，王磊. 赤峰地震台定点形变2021年短期大幅变化分析. 地震地磁观测与研究. 2022(06): 159-165 . 百度学术
6. 苑争一，闫伟，牛安福，赵静，高歌. 定点形变破年变异常自动识别应用研究. 地震研究. 2020(02): 394-401 . 百度学术
7. 王婷，延军平，李双双，万佳，张玉凤. 帕米尔高原Mw≥6.6级地震时间韵律特征. 高原地震. 2020(04): 6-16 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 1789
- HTML全文浏览量: 1212
- PDF下载量: 117
- 被引次数: 8
