Statistical analysis of the February 2018 Hualien，Taiwan，China，earthquake sequence：The features of its foreshocks，mainshocks，and aftershocks
-
摘要:
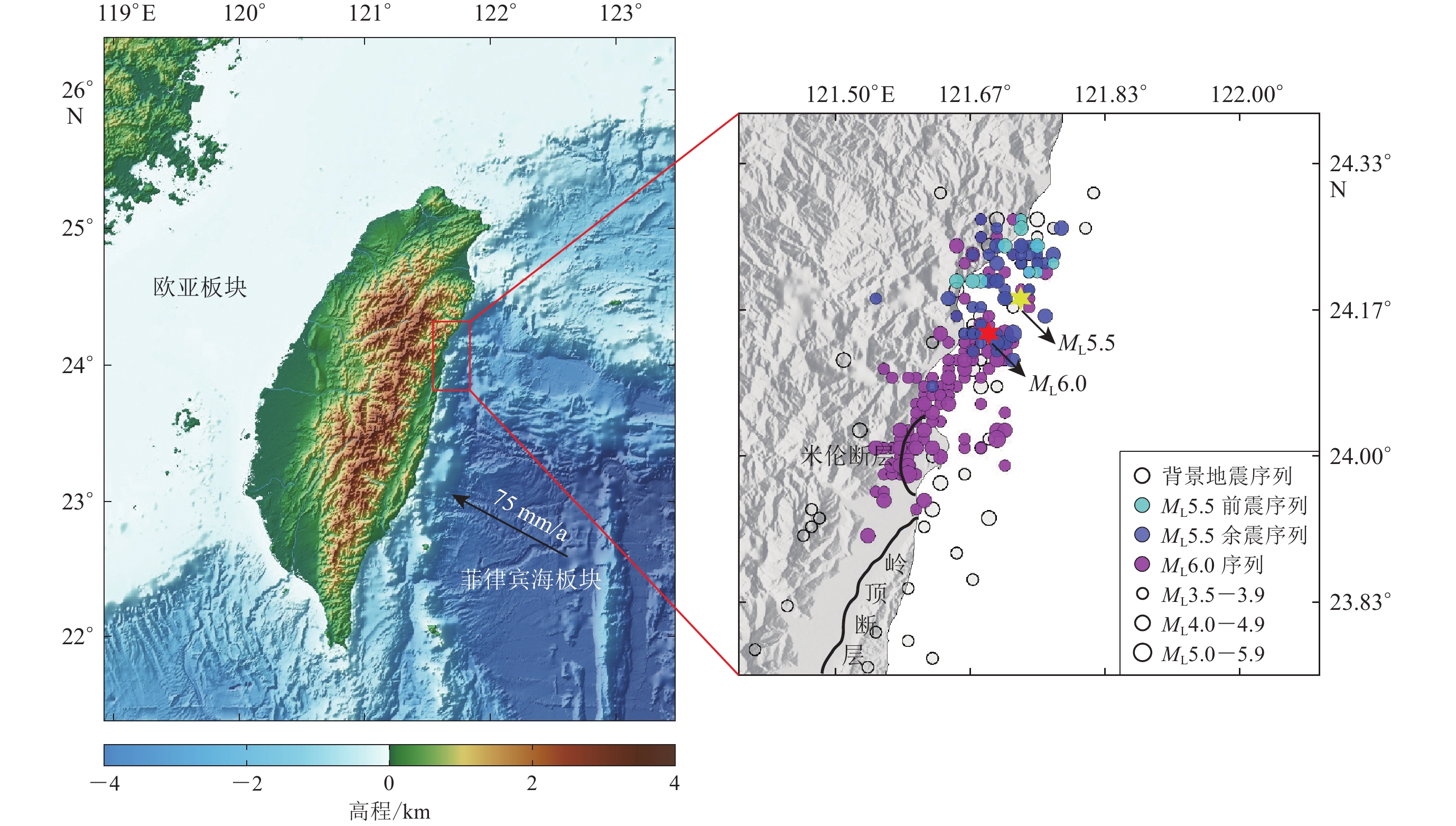
利用地震学的三个经典经验模型（古登堡-里克特定律、修正的大森定律和巴特定律）和描述前震活动的Dieterich前震模型对2018年2月中国台湾花莲地震序列的特征进行了分析。将该地震序列分为ML5.5前震序列、ML5.5余震序列和ML6.0余震序列等3段子序列进行研究，结果显示：利用古登堡-里克特定律得到的ML5.5余震序列和ML6.0余震序列的b值近似为1，ML5.5前震序列的b值近似为0.5；利用修正的大森定律得到的ML5.5余震序列和ML6.0余震序列的p值近似为0.9；利用修正的巴特定律得出ML5.5余震序列和ML6.0余震序列的推定最大余震震级分别为ML5.0和ML5.5，与实际数据相比，其误差值约为0.1。通过拟合ML5.5前震的发生率，分析可得ML5.5前震序列的地震发生率
$\dot {N}$ 正比于1/（tm−t），其中$t\ ({t}{\text{＜}} {t_{\rm{m}}})$ 为前震发生时刻，${t_{\rm{m}}}$ 为ML5.5地震发生时间，与Dieterich前震模型对前震现象的描述一致，表明其成因机制可能为主震成核过程中区域断层的次级断裂。-
关键词:
- 花莲地震 /
- b值 /
- p值 /
- 巴特定律 /
- Dieterich模型
Abstract:As we know, the statistical properties of an earthquake sequence are associated with three important empirical laws in seismology: Gutenberg-Richter law for the frequency-magnitude distribution, Båth law for the magnitude of the largest aftershock, and the modified Omori’s law for the temporal decay of aftershocks. In this paper these three laws are combined to study the February 2018 Hualien, Taiwan, China, earthquake sequence. In addition, a physics-based model proposed by Dieterich is used to describe the foreshock activities. The Hualien aftershock sequence is divided as three major sequences compounding with the ML5.5 foreshock sequence, the ML5.5 aftershock sequence and the ML6.0 sequence. The results indicate that the b values associated with Gutenberg-Richter law for the ML5.5 aftershock sequence and the ML6.0 aftershock sequence are approximately 1, respectively. And b value of the ML5.5 foreshock sequence are approximately 0.5. The p values with associated modified Omori’s law for the ML5.5 and ML6.0 aftershock sequences are both approximately 0.9, respectively. The estimated maximum aftershock magnitudes based on the modified form of Båth law are about ML5.0 and ML5.5, respectively, for ML5.5 and ML6.0 aftershock sequences, and the magnitude error is within
$\Delta M$ ＝0.1 with a comparison to the recorded events. We also find that, for the ML5.5 foreshock sequence, the seismicity rate${\dot N}$ increases as a function of 1/（tm−t）, where t （$t {\text{＜}} {t_{\rm{m}}}$ ） is the time of the foreshock and${t_{\rm{m}}}$ is the time when the ML5.5 earthquake occurred, respectively, which is consistent with the Dieterich earthquake triggering model, suggesting that the foreshock sequence may be related with mainshock nucleation process.-
Keywords:
- Hualien earthquake /
- b-value /
- p-value /
- Båth law /
- Dieterich model
-
-
![]()
图 1 花莲地区 M-t图
（a） 2016年6月1日至2018年3月30日；（b） 2018年2月3日至10日；（c） 2018年2月4日21时0分至22时18分
Figure 1. M-t diagram of Hualian area
（a） From June 1，2016 to March 30，2018；（b） From 3 to 10 February，2018；（c） From 21： 00 to 22： 18 on February 4，2018
![]()
图 2 2016年6月1日至2018年2月10日花莲地区地震空间分布图
Figure 2. The spatial distribution of Hualian earthquakes from June 1，2016 to February 10，2018
![]()
图 3 花莲地震序列发生后不同地震序列的地震目录的震级-频度图
（a） 背景地震序列；（b） ML5.5前震序列；（c） ML5.5余震序列；（d） ML6.0序列
Figure 3. The magnitude-frequency plot for the catalog of Hualian earthquakes with different time spans
（a） Background earthquake sequence；（b） ML5.5 foreshock sequence；（c） ML5.5 aftershock sequence；（d） ML6.0 earthquake sequence
![]()
图 4 不同时段内修正的大森定律拟合的曲线图
（a） 自2018年2月4日地震后至2月10日花莲地区地震累计次数随时间的变化；（b） 利用修正的大森定律拟合ML5.5余震序列图；（c） 利用修正的大森定律拟合2天内ML6.0余震序列
Figure 4. Curves fitted by the modified Omori’s law with different time spans
（a） The cumulative number of events in Hualian area from February 4 to February 10；（b） Fitting ML5.5 aftershock sequence；（c） Fitting ML6.0 aftershock sequence in two days
![]()
图 5 ML5.5地震发生前120分钟内的地震发生率
Figure 5. Seismicity rate within 120 minutes before the ML5.5 earthquake
表 1 通过古登堡-里克特定律拟合得到的不同时间尺度下的a值与b值
Table 1 Fitting a-value and b-value by the Gutenberg-Richter law with different time scales
地震序列 起始时间 持续时间/d a 值 b 值 年-月-日 时:分:秒 背景地震序列 2016-06-01 00:00:00 610 5.327 1.016±0.015 ML5.5前震序列 2018-02-04 03:30:00 0.75 3.080 0.548±0.147 ML5.5余震序列 2018-02-04 22:13:00 2 5.656 1.128±0.037 ML6.0序列 2018-02-06 23:53:00 2 5.657 1.028±0.079 
下载: 导出CSV
表 2 通过修正的大森定律拟合得到的不同时间段的参数值
Table 2 Fitting parameters by the modified Omori’s law with different time spans
地震序列 起始时间 持续时间/d K c（M） p 年-月-日 时∶分∶秒 ML5.5余震序列 2018-02-04 22∶16∶00 2 13.75 0.79 0.88 ML6.0序列 2018-02-06 23∶53∶00 2 19.23 1.80 0.92
下载: 导出CSV
表 3 通过S-T方法计算得到的不同时间段的推定最大余震震级
Table 3 The estimated maximum aftershock magnitude by S-T method with different time spans
地震序列 起始时间 持续时间/d 推定最大余震
震级$ { M_{\max }^{\rm a}} $年-月-日 时:分:秒 ML5.5余震序列 2018-02-04 22:16:00 2 5.0 ML6.0序列 2018-02-06 23:53:00 2 5.5
下载: 导出CSV
-
毛春长. 1989. 利用B值截距法估计强余震震级[J]. 山西地震,(3):41–42. Mao C C. 1989. Estimating strong aftershock magnitude by B-value intercept method[J]. Earthquake Research in Shanxi,(3):41–42 (in Chinese).
台湾气象局. 2018. 地震测报中心[EB/OL]. [2018−04−03]. http://www.cwb.gov.tw/V7/index.htm. Taiwan Weather Bureau. 2018. Earthquake monitoring and reporting center[EB/OL]. [2018−04−03]. http://www.cwb.gov.tw/V7/index.htm.
吴开统,焦远碧,王志东. 1984. 华北地区的晚期强余震特征[J]. 西北地震学报,6(2):35–43. Wu K T,Jiao Y B,Wang Z D. 1984. Certain characteristics of late strong aftershocks of North China[J]. Northwestern Seismological Journal,6(2):35–43 (in Chinese).
解孟雨,孟令媛,申文豪,史保平. 2017. 基于Gutenberg-Richter定律快速估算最大余震震级:以2017年九寨沟MS7.0地震为例[J]. 中国地震,33(4):493–502. doi: 10.3969/j.issn.1001-4683.2017.04.005 Xie M Y,Meng L Y,Shen W H,Shi B P. 2017. Fast estimating of the largest aftershock’s magnitude based on the Gutenberg-Richter law:A case study of the 2017 Jiuzhaigou MS7.0 earthquake sequence[J]. Earthquake Research in China,33(4):493–502 (in Chinese).
张智,吴开统,焦远碧,张天润. 1989. 用b值横截距预报强余震震级的方法探讨[J]. 中国地震,5(4):59–69. Zhang Z,Wu K T,Jiao Y B,Zhang T R. 1989. Discussion on the prediction method for magnitude of strong aftershock with the crosscut way of b-value[J]. Earthquake Research in China,5(4):59–69 (in Chinese).
Chan C H,Ma K F,Lee Y T,Wang Y J. 2019. Rethinking seismic source model of probabilistic hazard assessment in Taiwan after the 2018 Hualien,Taiwan,earthquake sequence[J]. Seismol Res Lett,90(1):88–96. doi: 10.1785/0220180225
Dieterich J H,Linker M F. 1992. Fault stability under conditions of variable normal stress[J]. Geophys Res Lett,19(16):1691–1694. doi: 10.1029/92GL01821
Dieterich J H. 1994. A constitutive law for rate of earthquake production and its application to earthquake clustering[J]. J Geophys Res,99(B2):2601–2618. doi: 10.1029/93JB02581
Dieterich J H,Kilgore B. 1996. Implications of fault constitutive properties for earthquake prediction[J]. Proc Natl Acad Sci USA,93(9):3787–3794. doi: 10.1073/pnas.93.9.3787
Dieterich J H. 2007. Applications of rate- and state-dependent friction to models of fault slip and earthquake occurrence[G]//Treatise on Geophysics. Boston: Elsevier: 107−129.
Hamdache M,Peláez J A,Kijko A,Smit A. 2017. Energetic and spatial characterization of seismicity in the Algeria-Morocco region[J]. Nat Hazards,86(S2):273–293. doi: 10.1007/s11069-016-2514-7
Helmstetter A,Sornette D,Grasso J R. 2003. Mainshocks are aftershocks of conditional foreshocks:How do foreshock statisti-cal properties emerge from aftershock laws[J]. J Geophys Res,108(B1):2046.
Jian P R,Hung S H,Meng L S. 2018. Rupture behavior and interaction of the 2018 Hualien earthquake sequence and its tectonic implication[J]. Seismol Res Lett,90(1):68–77.
Jones L M. 1985. Foreshocks and time-dependent earthquake hazard assessment in southern California[J]. Bull Seismol Soc Am,75(6):1667–1679.
Kisslinger C,Jones L M. 1991. Properties of aftershock sequences in southern California[J]. J Geophys Res,96(B7):11947–11958. doi: 10.1029/91JB01200
Kuo Y T,Wang Y,Hollingsworth J,Huang S Y,Chuang R Y,Lu C H,Hsu Y C,Tung H,Yen J Y,Chang C P. 2018. Shallow fault rupture of the milun fault in the 2018 MW6.4 Hualien earthquake:A high-resolution approach from optical correlation of Pléiades satellite imagery[J]. Seismol Res Lett,90(1):97–107.
Lin C M,Kuo C H,Huang J Y,Chao S H,Hsu T Y,Wen K L. 2018. Strong ground motion and pulse-like velocity observations in the near-fault region of the 2018 MW6.4 Hualien,Taiwan,earthquake[J]. Seismol Res Lett,90(1):40–50.
Ma K F,Wu Y M. 2018. Preface to the focus section on the 6 February 2018 MW6.4 Hualien,Taiwan,earthquake[J]. Seismol Res Lett,90(1):15–18.
Marzocchi W,Sandri L. 2003. A review and new insights on the estimation of the b-value and its uncertainty[J]. Ann Geophys,46(6):1271–1282.
Pollitz F F,Johnston M J S. 2006. Direct test of static stress versus dynamic stress triggering of aftershocks[J]. Geophys Res Lett,33(15):L15318. doi: 10.1029/2006GL026764
Popov V L. 2009. Contact Mechanics and Friction[M]. Berlin: Springer: 323−342.
Sandri L,Marzocchi W. 2007. A technical note on the bias in the estimation of the b-value and its uncertainty through the least squares technique[J]. Ann Geophys,50(3):329–339.
Scholz C H. 2002. The Mechanics of Earthquakes and Faulting[M]. New York: Cambridge University Press: 358−380.
Shcherbakov R,Turcotte D L. 2004. A modified form of Ba °th’s law[J]. Bull Seismol Soc Am,94(5):1968–1975. doi: 10.1785/012003162
USGS. 2018. Earthquake hazards program[EB/OL]. [2018−04−03]. https://earthquake.usgs.gov/.
Utsu T. 1961. A statistical study on the occurrence of aftershocks[J]. Geophys Mag,30:521–605.
Utsu T,Ogata Y,Ritsuko S,Matsu′ ura. 1995. The centenary of the Omori formula for a decay law of aftershock activity[J]. J Phys Earth,43(1):1–33. doi: 10.4294/jpe1952.43.1
Wiemer S,Wyss M. 2000. Minimum magnitude of completeness in earthquake catalogs:Examples from Alaska,the western United States,and Japan[J]. Bull Seismol Soc Am,90(4):859–869. doi: 10.1785/0119990114
Zúñiga F R,Wyss M. 1995. Inadvertent changes in magnitude reported in earthquake catalogs:Their evaluation through b-value estimates[J]. Bull Seismol Soc Am,85(6):1858–1866.
计量
- 文章访问数: 2164
- HTML全文浏览量: 825
- PDF下载量: 94
