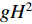Correlation between shear wave velocity and buried depth of common soils in Liuzhou city of Guangxi region
-
摘要:
基于广西柳州地区地震安全性评价中实测所获的钻孔资料，利用线性模型、幂函数模型和二次函数模型分别对该地区土层剪切波速与埋深之间的相关性进行了拟合分析，通过对比发现幂函数模型为二者间相关性拟合的最优选择，同时探讨了土体状态对二者相关性的影响。结果表明：除人工填土外，柳州地区内常见土层剪切波速与埋深之间具有较强的相关性，区域性对其相关性也具有影响。最后以实测钻孔为例，验证了本文模型的预测精度和可靠性，而且模型的预测精度可以通过区分土体状态得到明显提高。
Abstract:Based on the measured borehole data in the earthquake safety assessment of Liuzhou region, Guangxi, three models （linear, power function, quadratic function models） were used to fit and analyze the correlation between shear wave velocity of soil layer and burial depth in this area. And then the power function model was selected to analyze the correlation between the depth of the soil layer and corresponding shear wave velocity in the area, and the influence of the soil state on the correlation between the two parameters was also discussed, and finally the actual drilling was taken as an example to verify the accuracy and reliability of the model. The obtained results are as follows: ① except artificial filling, there is a strong correlation between the shear wave velocity and the buried depth of common soils in the area, and the correlation can be affected by the region where it is; ② the soil state can significantly improve the prediction accuracy of the model.
-
Keywords:
- shear wave velocity /
- buried depth /
- soil state /
- regression model /
- correlation
-
引言
剪切波速是土体重要的物理参数之一，在场地划分、土层地震反应分析等方面都起到了重要的作用（汪闻韶，1994；兰景岩等，2007）。土层的剪切波速一般是通过现场钻孔波速测试给出，其影响因素包括土层成因、土的类型、结构、埋深和地下水等，其中土层埋深与剪切波速具有较强的相关性。Ohta和Goto （1978）认为，将标准贯入击数、深度、土的类型和地质年代一起考虑即可给出剪切波速的最佳回归关系。Lee （1990）指出根据土的类型和沉积年代，建立标准贯入击数与剪切波速的关系并不是最优选择，并提出建立埋深与剪切波速的关系式。程祖峰等（1997）收集深圳地区25个建筑场地的48个测试孔资料，给出了该地区内各类土体剪切波速与土层埋深的经验公式。陈国兴等（1998）收集了南京地区13个地段的土体资料，利用单孔法分析埋深与波速的关系，并给出了二者之间的关系式，其结果表明：线性和隐线性关系式精度相差较小，但当浅层土较软时，隐线性关系式表现较好，反之，则宜选用线性关系式。蔡宗文（2003）在统计相关工程勘探资料和大量波速测试的基础上，给出了福建沿海地区相应土类剪切波速与土层密度、标准贯入击数以及土层埋深之间的关系。刘红帅等（2010）基于所收集的大量地区的地震安全性评价资料，给出了区分场地类型和不区分场地类型两种情形下常规土类剪切波速与埋深之间的关系式。邱志刚等（2011）收集了黑龙江地区大量的实测钻孔资料，利用线性、多项式和指数等三类模型拟合，并通过对比给出了该地区不同土类、不同状态下拟合模型的最优选择。此外，针对不同地区的相关研究也给出了相应地区土层剪切波速与埋深之间相关性的关系式（丁国瑜，卢演俦，1983；李帅等，2012；齐鑫，丁浩，2012；王强等，2014；贺为民等，2016；张龙飞等，2018）。针对某些地区缺少剪切波速经验公式的情况， 《构筑物抗震设计规范》 （GB50191—1993）根据土体软硬程度和密实度，给出了常规土类剪切波速与埋深之间的经验公式（国家技术监督局，中华人民共和国建设部，1995）。刘华贵和蒋文宇（2015）收集整理了广西壮族自治区柳州市官塘地区的硬塑状红黏土的钻孔数据，给出了该地区内硬塑状红黏土与埋深之间的回归模型。综上所述，相同地区不同土类以及不同地区土层的剪切波速之间均存在较大差别，故土层剪切波速与埋深之间的经验公式存在一定的区域性。
为此，本文收集广西柳州地区的地震安全性报告，从中提取实测钻孔资料，拟通过统计分析，给出柳州地区覆盖土层剪切波速与埋深之间的关系，同时探讨不同状态下各类土体剪切波速与埋深间关系是否存在差异，并以柳州市柳东新区花岭片区场地工程和河西工业区工程为实例对本文模型进行验证，以期为柳州地区的实际工程提供参考。
引言
剪切波速是土体重要的物理参数之一，在场地划分、土层地震反应分析等方面都起到了重要的作用（汪闻韶，1994；兰景岩等，2007）。土层的剪切波速一般是通过现场钻孔波速测试给出，其影响因素包括土层成因、土的类型、结构、埋深和地下水等，其中土层埋深与剪切波速具有较强的相关性。Ohta和Goto （1978）认为，将标准贯入击数、深度、土的类型和地质年代一起考虑即可给出剪切波速的最佳回归关系。Lee （1990）指出根据土的类型和沉积年代，建立标准贯入击数与剪切波速的关系并不是最优选择，并提出建立埋深与剪切波速的关系式。程祖峰等（1997）收集深圳地区25个建筑场地的48个测试孔资料，给出了该地区内各类土体剪切波速与土层埋深的经验公式。陈国兴等（1998）收集了南京地区13个地段的土体资料，利用单孔法分析埋深与波速的关系，并给出了二者之间的关系式，其结果表明：线性和隐线性关系式精度相差较小，但当浅层土较软时，隐线性关系式表现较好，反之，则宜选用线性关系式。蔡宗文（2003）在统计相关工程勘探资料和大量波速测试的基础上，给出了福建沿海地区相应土类剪切波速与土层密度、标准贯入击数以及土层埋深之间的关系。刘红帅等（2010）基于所收集的大量地区的地震安全性评价资料，给出了区分场地类型和不区分场地类型两种情形下常规土类剪切波速与埋深之间的关系式。邱志刚等（2011）收集了黑龙江地区大量的实测钻孔资料，利用线性、多项式和指数等三类模型拟合，并通过对比给出了该地区不同土类、不同状态下拟合模型的最优选择。此外，针对不同地区的相关研究也给出了相应地区土层剪切波速与埋深之间相关性的关系式（丁国瑜，卢演俦，1983；李帅等，2012；齐鑫，丁浩，2012；王强等，2014；贺为民等，2016；张龙飞等，2018）。针对某些地区缺少剪切波速经验公式的情况， 《构筑物抗震设计规范》 （GB50191—1993）根据土体软硬程度和密实度，给出了常规土类剪切波速与埋深之间的经验公式（国家技术监督局，中华人民共和国建设部，1995）。刘华贵和蒋文宇（2015）收集整理了广西壮族自治区柳州市官塘地区的硬塑状红黏土的钻孔数据，给出了该地区内硬塑状红黏土与埋深之间的回归模型。综上所述，相同地区不同土类以及不同地区土层的剪切波速之间均存在较大差别，故土层剪切波速与埋深之间的经验公式存在一定的区域性。
为此，本文收集广西柳州地区的地震安全性报告，从中提取实测钻孔资料，拟通过统计分析，给出柳州地区覆盖土层剪切波速与埋深之间的关系，同时探讨不同状态下各类土体剪切波速与埋深间关系是否存在差异，并以柳州市柳东新区花岭片区场地工程和河西工业区工程为实例对本文模型进行验证，以期为柳州地区的实际工程提供参考。
1. 数据
本文共收集到柳州地区的地震安评报告99份，去除其中缺少钻孔柱状图和非实测剪切波速资料的报告，最终得到66份报告，共计346个实测钻孔数据。需要说明的是，柳州地区的场地类型为 Ⅰ 类和 Ⅱ 类场地，其中 Ⅰ 类场地样本较少，故本文仅针对柳州地区 Ⅱ 类场地进行描述分析。表1为柳州地区Ⅱ类场地各类土体的埋深范围，其中由于该区域内杂填土、耕耘土和素填土数据较少，故本文将其统称为人工填土，本文所选数据均来源于剪切波速小于500 m/s的土层。
表 1 柳州地区Ⅱ类场地常规土类的埋深范围Table 1. Conventional soil depth range for the class Ⅱ sites in Liuzhou region岩土类型 埋深范围/m 人工填土 0.2—12.2 红黏土 1.0—31.0 粉质黏土 0.8—25.0 黏土 3.8—25.7 土层剪切波速vS与埋深H之间的关系可以用线性函数、幂函数及二次函数分别表示为vS＝a＋bH，vS＝cHd和vS＝e＋fH＋
$gH^2 $ ，式中a，b，c，d，e，f，g均为拟合参数。回归方程与实测数据之间的拟合程度选用拟合优度R2 （0＜R2＜1）进行检验，R2越趋近于1，回归方程的拟合效果越与实际相符合。1. 数据
本文共收集到柳州地区的地震安评报告99份，去除其中缺少钻孔柱状图和非实测剪切波速资料的报告，最终得到66份报告，共计346个实测钻孔数据。需要说明的是，柳州地区的场地类型为 Ⅰ 类和 Ⅱ 类场地，其中 Ⅰ 类场地样本较少，故本文仅针对柳州地区 Ⅱ 类场地进行描述分析。表1为柳州地区Ⅱ类场地各类土体的埋深范围，其中由于该区域内杂填土、耕耘土和素填土数据较少，故本文将其统称为人工填土，本文所选数据均来源于剪切波速小于500 m/s的土层。
表 1 柳州地区Ⅱ类场地常规土类的埋深范围Table 1. Conventional soil depth range for the class Ⅱ sites in Liuzhou region岩土类型 埋深范围/m 人工填土 0.2—12.2 红黏土 1.0—31.0 粉质黏土 0.8—25.0 黏土 3.8—25.7 This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
2. 土层剪切波速与埋深之间的变化规律
通过整理分析收集到的钻孔资料，绘制出柳州地区Ⅱ类场地的土层剪切波速与埋深之间的散点图，如图1所示，可见，柳州地区Ⅱ类场地覆盖土层剪切波速与埋深具有一定相关性，且随埋深不断增大，其离散程度也随之增大。
![]()
图 1 柳州地区Ⅱ类场地土层剪切波速与埋深之间的散点图Figure 1. Shear wave velocity versus depth of soils for the class Ⅱ sites in Liuzhou region图2给出了广西柳州地区人工填土剪切波速与埋深之间的散点图，可知，人工填土的剪切波速主要介于100—300 m/s之间，埋藏深度主要在10 m以内，且二者之间未呈明显的相关性联系，这可能与人工填土的成分、含水量等存在较大差异有关。
![]()
图 2 柳州地区人工填土剪切波速与埋深间的散点图Figure 2. Shear wave velocity versus depth of artificial filled soils in Liuzhou region2. 土层剪切波速与埋深之间的变化规律
通过整理分析收集到的钻孔资料，绘制出柳州地区Ⅱ类场地的土层剪切波速与埋深之间的散点图，如图1所示，可见，柳州地区Ⅱ类场地覆盖土层剪切波速与埋深具有一定相关性，且随埋深不断增大，其离散程度也随之增大。
![]()
图 1 柳州地区Ⅱ类场地土层剪切波速与埋深之间的散点图Figure 1. Shear wave velocity versus depth of soils for the class Ⅱ sites in Liuzhou region图2给出了广西柳州地区人工填土剪切波速与埋深之间的散点图，可知，人工填土的剪切波速主要介于100—300 m/s之间，埋藏深度主要在10 m以内，且二者之间未呈明显的相关性联系，这可能与人工填土的成分、含水量等存在较大差异有关。
![]()
图 2 柳州地区人工填土剪切波速与埋深间的散点图Figure 2. Shear wave velocity versus depth of artificial filled soils in Liuzhou region2.1 不同土类剪切波速与埋深间的关系
为了能够探究柳州地区覆盖土层剪切波速与埋深之间的关系，建立二者之间的经验公式，本文利用收集到的钻孔数据，绘制出该地区内Ⅱ类场地常规土类剪切波速随埋深变化的散点图，如图3所示。
![]()
图 3 不同土类剪切波速与埋深间关系散点图（a） 红黏土；（b） 粉质黏土；（c） 黏土Figure 3. Shear wave velocity versus buried depth for different soils（a） Red clay；（b） Silty clay；（c） Clay为了进一步分析图3所示三种土类的剪切波速与埋深之间的相关性，本文利用三种函数模型分别对图3中的数据进行回归拟合，得到该地区三种土类回归模型的拟合参数及拟合优度R2，详见表2。由表2可见，三种回归模型中幂函数的拟合效果最优，故选取幂函数为本文的回归模型。
表 2 柳州地区常规土类回归模型的拟合参数及拟合优度R2Table 2. Fitting parameters and goodness R2 for three regressive models of conventional soils in Liuzhou region岩土类型 线性模型 幂函数模型 二次函数模型 a b R2 c d R2 e f g R2 红黏土 243.80 4.237 3 0.803 2 215.93 0.129 7 0.813 1 240.02 5.059 4 −0.033 7 0.804 8 粉质黏土 224.22 6.325 4 0.772 4 201.86 0.149 6 0.824 2 223.02 5.777 0 −0.012 1 0.822 5 黏土 247.72 5.504 6 0.835 9 205.28 0.188 0 0.841 8 238.19 8.240 7 −0.077 8 0.840 3 2.1 不同土类剪切波速与埋深间的关系
为了能够探究柳州地区覆盖土层剪切波速与埋深之间的关系，建立二者之间的经验公式，本文利用收集到的钻孔数据，绘制出该地区内Ⅱ类场地常规土类剪切波速随埋深变化的散点图，如图3所示。
![]()
图 3 不同土类剪切波速与埋深间关系散点图（a） 红黏土；（b） 粉质黏土；（c） 黏土Figure 3. Shear wave velocity versus buried depth for different soils（a） Red clay；（b） Silty clay；（c） Clay为了进一步分析图3所示三种土类的剪切波速与埋深之间的相关性，本文利用三种函数模型分别对图3中的数据进行回归拟合，得到该地区三种土类回归模型的拟合参数及拟合优度R2，详见表2。由表2可见，三种回归模型中幂函数的拟合效果最优，故选取幂函数为本文的回归模型。
表 2 柳州地区常规土类回归模型的拟合参数及拟合优度R2Table 2. Fitting parameters and goodness R2 for three regressive models of conventional soils in Liuzhou region岩土类型 线性模型 幂函数模型 二次函数模型 a b R2 c d R2 e f g R2 红黏土 243.80 4.237 3 0.803 2 215.93 0.129 7 0.813 1 240.02 5.059 4 −0.033 7 0.804 8 粉质黏土 224.22 6.325 4 0.772 4 201.86 0.149 6 0.824 2 223.02 5.777 0 −0.012 1 0.822 5 黏土 247.72 5.504 6 0.835 9 205.28 0.188 0 0.841 8 238.19 8.240 7 −0.077 8 0.840 3 2.2 不同土体状态下剪切波速与埋深之间的关系
上文对不同土类剪切波速与埋深间的关系进行了分析，为了进一步探究覆盖土层剪切波速与埋深之间的关系，本文对柳州地区常见土类按土体状态进行细分。根据 《 铁路工程岩土分类标准 》 （TB10077—2001）（中华人民共和国铁道部，2001），黏性土的塑性状态按液性指数IL进行划分。由于地区内黏土均属于可塑状态，故不作重复描述，图4给出了该地区内红黏土和粉质黏土在硬塑（0<IL≤0.5）和可塑（0.5<IL≤1）状态下土层剪切波速与埋深之间的散点图。
![]()
图 4 柳州地区红黏土（a）和粉质黏土（b）在不同土体状态下剪切波速与埋深间的散点图Figure 4. Shear wave velocity versus depth of soils for red clay （a） and silty clay （b） with different soil states in Liuzhou region由图4可见：相同土类、不同土体状态下，其剪切波速与土层埋深仍具有相关性，离散程度随埋深的增大而增大，其中硬塑状态下土体的平均剪切波速高于可塑状态下的。
利用幂函数模型对图4数据进行回归拟合，得到该地区红黏土和粉质黏土在不同土体塑性状态下的回归模型的拟合参数c，d及拟合优度R2，详见表3。对比表2中的数据可以看出，土体状态对幂函数模型的拟合优度存在较为显著的影响。
表 3 不同土体状态下红黏土和粉质黏土的幂函数模型拟合参数及拟合优度R2Table 3. Fitting parameters and goodness R2 of power function model for red clay and silty clay with different plastic states回归模型 c d R2 可塑状态 硬塑状态 可塑状态 硬塑状态 可塑状态 硬塑状态 红黏土 195.35 205.35 0.145 2 0.131 9 0.742 9 0.714 2 粉质黏土 192.30 207.14 0.168 2 0.155 5 0.748 4 0.763 8 图5给出了红黏土和粉质黏土在区分土体状态条件下剪切波速随埋深变化的预测曲线，可见：红黏土和粉质黏土在同一埋藏深度下，剪切波速随塑性状态的增强而增大；随着埋深的增加，红黏土硬塑状态下的剪切波速的递增率小于可塑状态，当埋深达到30 m左右时，二者趋于重合。
![]()
图 5 柳州地区红黏土（a）和粉质黏土（b）不同土体状态下剪切波速预测曲线Figure 5. Prediction curves of shear wave velocity in red clay （a） and silty clay （b） with different soil states in Liuzhou region3. 实例验证
3. 实例验证
3.1 不同土体状态下土层剪切波速与埋深间相关性研究的对比分析
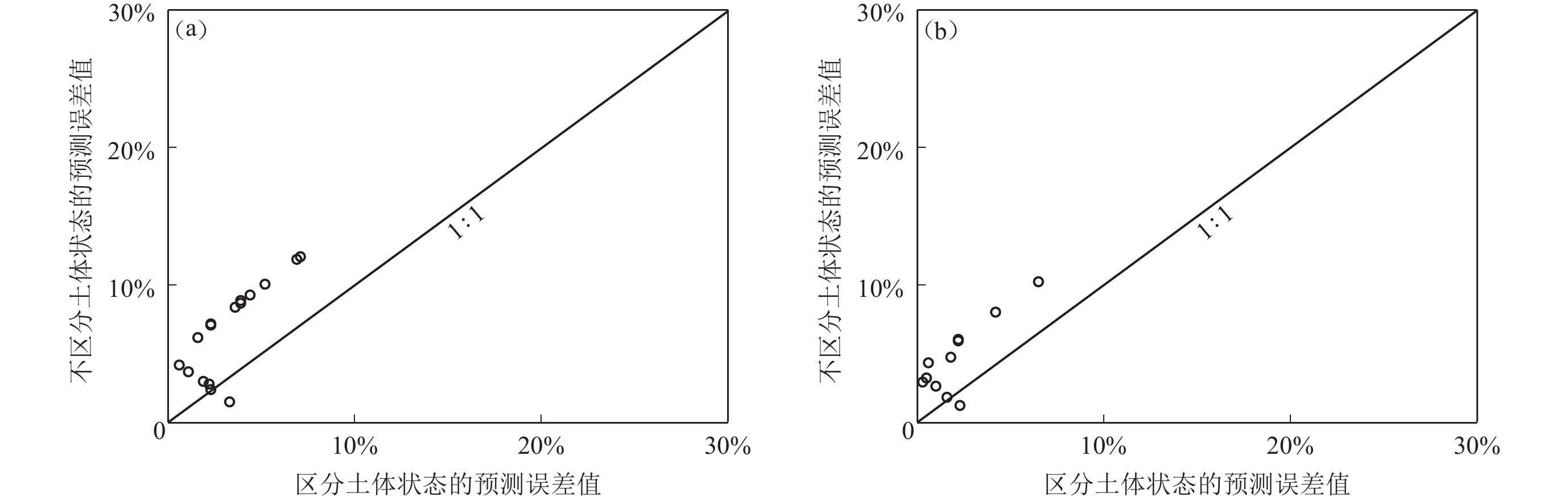
为探讨土体状态是否对回归模型预测结果的精度存在影响，本文从66份报告中的柳州市柳东新区花岭片区场地工程地震安全性评价报告中选取HK5号和HK19号钻孔的实测剪切波速为例，对比红黏土（HK5号）与粉质黏土（HK19号）在区分土体状态和不区分土体状态下由回归模型所得到的剪切波速预测值，并给出各自对应的相对误差，结果如表4和表5以及图6和图7所示，可见区分土体状态下回归模型给出的剪切波速预测值相对于不区分土体状态下回归模型给出的剪切波速预测值更加接近实测值，这说明土体状态对于土层剪切波速与埋深间关系的模型预测精度存在一定影响。
表 4 红黏土在不同土体状态下由回归模型按土体埋深所得剪切波速vS的预测值Table 4. The predicted shear wave velocity vS from the regression model of red clay with plastic state according to the buried depth of soils埋深/m 土体名称 土体状态 vS实测值
/（m·s−1）区分土体状态 不区分土体状态 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.70 杂填土 − 228 − − − − 2.00 红黏土 硬塑 230 225 2.2% 236 2.7% 3.00 红黏土 硬塑 242 237 1.9% 249 2.9% 4.00 红黏土 硬塑 255 247 3.3% 258 1.4% 5.00 红黏土 硬塑 260 254 2.3% 266 2.3% 6.00 红黏土 硬塑 263 260 1.1% 272 3.6% 7.00 红黏土 硬塑 267 265 0.6% 278 4.1% 8.00 红黏土 硬塑 264 270 2.3% 283 7.1% 9.00 红黏土 硬塑 264 274 3.9% 287 8.8% 10.00 红黏土 硬塑 272 278 2.3% 291 7.0% 11.00 红黏土 硬塑 272 282 3.6% 295 8.3% 12.00 红黏土 硬塑 273 285 4.4% 298 9.2% 13.00 红黏土 硬塑 269 288 7.1% 301 12.0% 14.00 红黏土 硬塑 272 291 6.9% 304 11.8% 15.00 红黏土 硬塑 279 294 5.2% 307 10.0% 16.50 红黏土 硬塑 286 297 3.9% 311 8.6% 18.00 红黏土 硬塑 296 301 1.6% 314 6.1% 表 5 粉质黏土在不同土体状态下由回归模型按土体埋深所得剪切波速vS及视剪切波速预测值Table 5. The shear wave velocity vS and predicted apparent shear wave velocity from the regression model of silty clay with plastic state according to the buried depth of soils埋深/m 土体名称 土体状态 vS实测值
/（m·s−1）区分土体状态 不区分土体状态 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.40 耕植土 174 − − − − 2.00 粉质黏土 硬塑 235 231 1.8% 224 4.7% 3.00 粉质黏土 硬塑 245 246 0.3% 238 2.9% 4.00 粉质黏土 硬塑 253 257 1.6% 248 1.8% 5.00 粉质黏土 硬塑 260 266 2.3% 257 1.2% 6.00 粉质黏土 硬塑 271 274 1.0% 264 2.6% 7.00 粉质黏土 硬塑 279 280 0.5% 270 3.2% 8.00 粉质黏土 硬塑 288 286 0.6% 276 4.3% 9.00 粉质黏土 硬塑 298 292 2.2% 280 5.9% 10.00 粉质黏土 硬塑 303 296 2.2% 285 6.0% 11.00 粉质黏土 硬塑 314 301 4.2% 289 8.0% 12.50 粉质黏土 硬塑 328 307 6.5% 295 10.2% ![]()
图 6 红黏土（a）和粉质黏土（b）不同土体状态下剪切波速与实测数据的对比Figure 6. Comparison of shear wave velocity with measured data of red clay （a） and silty clay （b） in different soil states![]()
图 7 红黏土（a）和粉质黏土（b）土体状态对模型预测误差的影响Figure 7. Influence of soil state on the predicted error from the model of red clay （a） and silty clay （b）3.1 不同土体状态下土层剪切波速与埋深间相关性研究的对比分析
为探讨土体状态是否对回归模型预测结果的精度存在影响，本文从66份报告中的柳州市柳东新区花岭片区场地工程地震安全性评价报告中选取HK5号和HK19号钻孔的实测剪切波速为例，对比红黏土（HK5号）与粉质黏土（HK19号）在区分土体状态和不区分土体状态下由回归模型所得到的剪切波速预测值，并给出各自对应的相对误差，结果如表4和表5以及图6和图7所示，可见区分土体状态下回归模型给出的剪切波速预测值相对于不区分土体状态下回归模型给出的剪切波速预测值更加接近实测值，这说明土体状态对于土层剪切波速与埋深间关系的模型预测精度存在一定影响。
表 4 红黏土在不同土体状态下由回归模型按土体埋深所得剪切波速vS的预测值Table 4. The predicted shear wave velocity vS from the regression model of red clay with plastic state according to the buried depth of soils埋深/m 土体名称 土体状态 vS实测值
/（m·s−1）区分土体状态 不区分土体状态 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.70 杂填土 − 228 − − − − 2.00 红黏土 硬塑 230 225 2.2% 236 2.7% 3.00 红黏土 硬塑 242 237 1.9% 249 2.9% 4.00 红黏土 硬塑 255 247 3.3% 258 1.4% 5.00 红黏土 硬塑 260 254 2.3% 266 2.3% 6.00 红黏土 硬塑 263 260 1.1% 272 3.6% 7.00 红黏土 硬塑 267 265 0.6% 278 4.1% 8.00 红黏土 硬塑 264 270 2.3% 283 7.1% 9.00 红黏土 硬塑 264 274 3.9% 287 8.8% 10.00 红黏土 硬塑 272 278 2.3% 291 7.0% 11.00 红黏土 硬塑 272 282 3.6% 295 8.3% 12.00 红黏土 硬塑 273 285 4.4% 298 9.2% 13.00 红黏土 硬塑 269 288 7.1% 301 12.0% 14.00 红黏土 硬塑 272 291 6.9% 304 11.8% 15.00 红黏土 硬塑 279 294 5.2% 307 10.0% 16.50 红黏土 硬塑 286 297 3.9% 311 8.6% 18.00 红黏土 硬塑 296 301 1.6% 314 6.1% 表 5 粉质黏土在不同土体状态下由回归模型按土体埋深所得剪切波速vS及视剪切波速预测值Table 5. The shear wave velocity vS and predicted apparent shear wave velocity from the regression model of silty clay with plastic state according to the buried depth of soils埋深/m 土体名称 土体状态 vS实测值
/（m·s−1）区分土体状态 不区分土体状态 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.40 耕植土 174 − − − − 2.00 粉质黏土 硬塑 235 231 1.8% 224 4.7% 3.00 粉质黏土 硬塑 245 246 0.3% 238 2.9% 4.00 粉质黏土 硬塑 253 257 1.6% 248 1.8% 5.00 粉质黏土 硬塑 260 266 2.3% 257 1.2% 6.00 粉质黏土 硬塑 271 274 1.0% 264 2.6% 7.00 粉质黏土 硬塑 279 280 0.5% 270 3.2% 8.00 粉质黏土 硬塑 288 286 0.6% 276 4.3% 9.00 粉质黏土 硬塑 298 292 2.2% 280 5.9% 10.00 粉质黏土 硬塑 303 296 2.2% 285 6.0% 11.00 粉质黏土 硬塑 314 301 4.2% 289 8.0% 12.50 粉质黏土 硬塑 328 307 6.5% 295 10.2% ![]()
图 6 红黏土（a）和粉质黏土（b）不同土体状态下剪切波速与实测数据的对比Figure 6. Comparison of shear wave velocity with measured data of red clay （a） and silty clay （b） in different soil states![]()
图 7 红黏土（a）和粉质黏土（b）土体状态对模型预测误差的影响Figure 7. Influence of soil state on the predicted error from the model of red clay （a） and silty clay （b）3.2 常规土类对比分析
为了验证本文各类土体回归模型对剪切波速预测结果的可靠性和精度，本文以柳州市河西工业区工程地震安全性评价报告中XK21号钻孔的实测剪切波速为实例，并与刘红帅等（2010）针对全国范围内常规土类剪切波速与埋深间的回归模型进行对比。需要说明的是，刘红帅等（2010）并未给出红黏土与埋深间的回归模型，故就红黏土部分本文将与刘华贵和蒋文宇（2015）给出的关于柳州市官塘地区硬塑红黏土的回归模型（下文统称 “刘模型” ）进行对比；同时本文还将与 《 构筑物抗震设计规范》 （GB50191—1993）中估算硬塑状黏土剪切波速的经验公式vS＝130H0.300 （下文统称 “规范模型” ）进行对比分析，并给出各层相应的相对误差，结果如表6及图8和图9所示。可见：对于硬塑状红黏土，由本文给出的回归模型与刘华贵和蒋文宇（2015）给出的回归模型所得到的预测剪切波速相接近，与实测波速值的误差在4%以内；对于粉质黏土和黏土，本文所给出的回归模型均优于刘红帅等（2010）给出的回归模型，且预测误差均控制在10%以内；从整体上看，本文模型所得预测结果与实测数值较为接近，且均优于规范数值。综上所述，说明区域性对土层剪切波速与埋深间关系的模型预测存在较为明显的影响。
表 6 基于本文模型、刘模型和规范回归模型按土体埋深所得剪切波速预测值Table 6. The predicted shear wave velocity vS based on the three models according to the buried depth of soils埋深/m 土的名称 土的状态 vS实测值
/（m·s−1）本文模型 刘模型 规范模型 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.80 素填土 200 − − − − 2.00 红黏土 硬塑 233 225 3.3% 221 5.0% 160 31.3% 3.00 红黏土 硬塑 236 238 0.7% 234 0.6% 181 23.4% 4.00 红黏土 硬塑 243 247 1.6% 244 0.6% 197 18.9% 5.00 红黏土 硬塑 253 254 0.4% 252 0.3% 211 16.7% 6.00 红黏土 硬塑 260 260 0.1% 259 0.4% 223 14.4% 7.00 红黏土 硬塑 264 266 0.6% 265 0.3% 233 11.7% 8.00 红黏土 硬塑 270 270 0.1% 270 0.1% 243 10.2% 9.00 红黏土 硬塑 279 275 1.6% 274 1.7% 251 9.9% 10.00 红黏土 硬塑 281 278 0.9% 279 0.9% 259 7.7% 11.00 红黏土 硬塑 280 282 0.7% 282 0.8% 267 4.7% 12.00 粉质黏土 硬塑 305 305 0.1% 260 14.6% 274 10.2% 13.00 粉质黏土 硬塑 303 309 1.9% 267 11.9% 281 7.4% 14.00 粉质黏土 硬塑 304 312 2.7% 273 10.3% 287 5.6% 15.00 粉质黏土 硬塑 326 316 3.2% 279 14.6% 293 10.1% 16.00 粉质黏土 硬塑 319 319 0.1% 284 11.0% 299 6.4% 17.00 粉质黏土 硬塑 319 322 0.9% 289 9.3% 304 4.7% 18.00 粉质黏土 硬塑 332 325 2.2% 294 11.4% 309 6.8% 19.00 粉质黏土 硬塑 351 327 6.7% 299 14.8% 314 10.4% 20.00 粉质黏土 硬塑 351 330 6.0% 304 13.5% 319 9.0% 21.00 粉质黏土 硬塑 359 333 7.4% 308 14.1% 324 9.7% 22.00 粉质黏土 硬塑 351 335 4.6% 313 10.9% 329 6.4% 23.00 粉质黏土 硬塑 369 337 8.6% 317 14.1% 333 9.8% 24.00 粉质黏土 硬塑 362 340 6.2% 321 11.4% 337 6.8% 25.00 粉质黏土 硬塑 368 342 7.1% 325 11.7% 341 7.2% 25.70 粉质黏土 硬塑 392 378 3.6% 336 14.2% 344 12.2% 注：刘模型引自刘红帅等（2010）以及刘华贵和蒋文宇（2015），规范模型引自中国人民共和国铁道部（2001）。 ![]()
图 8 本文模型与刘模型和规范模型所得剪切波速的对比Figure 8. Comparison of shear wave velocties from the model of this study with those from Liu model and the normative model![]()
图 9 本文模型与刘模型和规范模型预测误差对比Figure 9. Comparison of prediction errors from the model of this study with those from Liu model and normative model3.2 常规土类对比分析
为了验证本文各类土体回归模型对剪切波速预测结果的可靠性和精度，本文以柳州市河西工业区工程地震安全性评价报告中XK21号钻孔的实测剪切波速为实例，并与刘红帅等（2010）针对全国范围内常规土类剪切波速与埋深间的回归模型进行对比。需要说明的是，刘红帅等（2010）并未给出红黏土与埋深间的回归模型，故就红黏土部分本文将与刘华贵和蒋文宇（2015）给出的关于柳州市官塘地区硬塑红黏土的回归模型（下文统称 “刘模型” ）进行对比；同时本文还将与 《 构筑物抗震设计规范》 （GB50191—1993）中估算硬塑状黏土剪切波速的经验公式vS＝130H0.300 （下文统称 “规范模型” ）进行对比分析，并给出各层相应的相对误差，结果如表6及图8和图9所示。可见：对于硬塑状红黏土，由本文给出的回归模型与刘华贵和蒋文宇（2015）给出的回归模型所得到的预测剪切波速相接近，与实测波速值的误差在4%以内；对于粉质黏土和黏土，本文所给出的回归模型均优于刘红帅等（2010）给出的回归模型，且预测误差均控制在10%以内；从整体上看，本文模型所得预测结果与实测数值较为接近，且均优于规范数值。综上所述，说明区域性对土层剪切波速与埋深间关系的模型预测存在较为明显的影响。
表 6 基于本文模型、刘模型和规范回归模型按土体埋深所得剪切波速预测值Table 6. The predicted shear wave velocity vS based on the three models according to the buried depth of soils埋深/m 土的名称 土的状态 vS实测值
/（m·s−1）本文模型 刘模型 规范模型 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.80 素填土 200 − − − − 2.00 红黏土 硬塑 233 225 3.3% 221 5.0% 160 31.3% 3.00 红黏土 硬塑 236 238 0.7% 234 0.6% 181 23.4% 4.00 红黏土 硬塑 243 247 1.6% 244 0.6% 197 18.9% 5.00 红黏土 硬塑 253 254 0.4% 252 0.3% 211 16.7% 6.00 红黏土 硬塑 260 260 0.1% 259 0.4% 223 14.4% 7.00 红黏土 硬塑 264 266 0.6% 265 0.3% 233 11.7% 8.00 红黏土 硬塑 270 270 0.1% 270 0.1% 243 10.2% 9.00 红黏土 硬塑 279 275 1.6% 274 1.7% 251 9.9% 10.00 红黏土 硬塑 281 278 0.9% 279 0.9% 259 7.7% 11.00 红黏土 硬塑 280 282 0.7% 282 0.8% 267 4.7% 12.00 粉质黏土 硬塑 305 305 0.1% 260 14.6% 274 10.2% 13.00 粉质黏土 硬塑 303 309 1.9% 267 11.9% 281 7.4% 14.00 粉质黏土 硬塑 304 312 2.7% 273 10.3% 287 5.6% 15.00 粉质黏土 硬塑 326 316 3.2% 279 14.6% 293 10.1% 16.00 粉质黏土 硬塑 319 319 0.1% 284 11.0% 299 6.4% 17.00 粉质黏土 硬塑 319 322 0.9% 289 9.3% 304 4.7% 18.00 粉质黏土 硬塑 332 325 2.2% 294 11.4% 309 6.8% 19.00 粉质黏土 硬塑 351 327 6.7% 299 14.8% 314 10.4% 20.00 粉质黏土 硬塑 351 330 6.0% 304 13.5% 319 9.0% 21.00 粉质黏土 硬塑 359 333 7.4% 308 14.1% 324 9.7% 22.00 粉质黏土 硬塑 351 335 4.6% 313 10.9% 329 6.4% 23.00 粉质黏土 硬塑 369 337 8.6% 317 14.1% 333 9.8% 24.00 粉质黏土 硬塑 362 340 6.2% 321 11.4% 337 6.8% 25.00 粉质黏土 硬塑 368 342 7.1% 325 11.7% 341 7.2% 25.70 粉质黏土 硬塑 392 378 3.6% 336 14.2% 344 12.2% 注：刘模型引自刘红帅等（2010）以及刘华贵和蒋文宇（2015），规范模型引自中国人民共和国铁道部（2001）。 ![]()
图 8 本文模型与刘模型和规范模型所得剪切波速的对比Figure 8. Comparison of shear wave velocties from the model of this study with those from Liu model and the normative model![]()
图 9 本文模型与刘模型和规范模型预测误差对比Figure 9. Comparison of prediction errors from the model of this study with those from Liu model and normative model4. 讨论与结论
基于广西柳州地区地震安评报告中的实测钻孔数据资料，利用幂函数模型，整理分析给出了常见土类剪切波速与埋深的回归模型，并给出了区分和不区分土体状态情况下红黏土和粉质黏土剪切波速与埋深的经验公式，并与刘华贵和蒋文宇（2015）给出的柳州官塘地区硬塑状红黏土回归模型、刘红帅等（2010）给出的全国范围内常规土类回归模型以及 《 铁路工程岩土分类标准 》 规范推荐模型进行对比，验证了本文模型的可靠性，最后以柳州市河西工业区工程地震安全性评价报告中XK21号钻孔的实测剪切波速为例，验证了本文模型的精度，以确保本文结果可供该地区内无剪切波速测试场地使用。本文主要结论如下：
1） 柳州地区覆盖土层（除人工填土外）的剪切波速与埋深间存在一定相关性，且随埋藏深度的不断增大，其离散程度也随之增大；
2） 随着土体埋深的不断增大，红黏土和粉质黏土的剪切波速随塑性状态的增强而增大，其中，红黏土硬塑状态下剪切波速的递增率小于可塑状态，埋深达到30 m左右，二者趋于重合；
3） 相同土类（红黏土和粉质黏土）、不同土体状态对模型拟合效果会产生明显的影响，考虑土体状态可以较为明显地提高回归模型的预测精度。
4） 区域性对剪切波速与埋深间的经验公式存在较大影响，主要表现在预测精度方面。
影响土层剪切波速的因素有很多，包括土体成因、埋深、标准贯入技术、土体状态等，本文仅考虑了土类、埋深、土体状态的影响，并未考虑其它因素的影响，而且也未分析土层剪切波速与土体其余物理力学参数之间的相关性。建议该地区建立常规土类物理力学参数数据库，以土类为依据，细化各项指标间的相关性研究，使统计结果更加可靠。这一工作能够为该地区的岩土工程研究提供较为详实的数据基础，从而更好地为该地区岩土工程施工提供服务。
4. 讨论与结论
基于广西柳州地区地震安评报告中的实测钻孔数据资料，利用幂函数模型，整理分析给出了常见土类剪切波速与埋深的回归模型，并给出了区分和不区分土体状态情况下红黏土和粉质黏土剪切波速与埋深的经验公式，并与刘华贵和蒋文宇（2015）给出的柳州官塘地区硬塑状红黏土回归模型、刘红帅等（2010）给出的全国范围内常规土类回归模型以及 《 铁路工程岩土分类标准 》 规范推荐模型进行对比，验证了本文模型的可靠性，最后以柳州市河西工业区工程地震安全性评价报告中XK21号钻孔的实测剪切波速为例，验证了本文模型的精度，以确保本文结果可供该地区内无剪切波速测试场地使用。本文主要结论如下：
1） 柳州地区覆盖土层（除人工填土外）的剪切波速与埋深间存在一定相关性，且随埋藏深度的不断增大，其离散程度也随之增大；
2） 随着土体埋深的不断增大，红黏土和粉质黏土的剪切波速随塑性状态的增强而增大，其中，红黏土硬塑状态下剪切波速的递增率小于可塑状态，埋深达到30 m左右，二者趋于重合；
3） 相同土类（红黏土和粉质黏土）、不同土体状态对模型拟合效果会产生明显的影响，考虑土体状态可以较为明显地提高回归模型的预测精度。
4） 区域性对剪切波速与埋深间的经验公式存在较大影响，主要表现在预测精度方面。
影响土层剪切波速的因素有很多，包括土体成因、埋深、标准贯入技术、土体状态等，本文仅考虑了土类、埋深、土体状态的影响，并未考虑其它因素的影响，而且也未分析土层剪切波速与土体其余物理力学参数之间的相关性。建议该地区建立常规土类物理力学参数数据库，以土类为依据，细化各项指标间的相关性研究，使统计结果更加可靠。这一工作能够为该地区的岩土工程研究提供较为详实的数据基础，从而更好地为该地区岩土工程施工提供服务。
-
![]()
图 1 柳州地区Ⅱ类场地土层剪切波速与埋深之间的散点图
Figure 1. Shear wave velocity versus depth of soils for the class Ⅱ sites in Liuzhou region
![]()
图 2 柳州地区人工填土剪切波速与埋深间的散点图
Figure 2. Shear wave velocity versus depth of artificial filled soils in Liuzhou region
![]()
图 3 不同土类剪切波速与埋深间关系散点图
（a） 红黏土；（b） 粉质黏土；（c） 黏土
Figure 3. Shear wave velocity versus buried depth for different soils
（a） Red clay；（b） Silty clay；（c） Clay
![]()
图 4 柳州地区红黏土（a）和粉质黏土（b）在不同土体状态下剪切波速与埋深间的散点图
Figure 4. Shear wave velocity versus depth of soils for red clay （a） and silty clay （b） with different soil states in Liuzhou region
![]()
图 5 柳州地区红黏土（a）和粉质黏土（b）不同土体状态下剪切波速预测曲线
Figure 5. Prediction curves of shear wave velocity in red clay （a） and silty clay （b） with different soil states in Liuzhou region
![]()
图 6 红黏土（a）和粉质黏土（b）不同土体状态下剪切波速与实测数据的对比
Figure 6. Comparison of shear wave velocity with measured data of red clay （a） and silty clay （b） in different soil states
![]()
图 7 红黏土（a）和粉质黏土（b）土体状态对模型预测误差的影响
Figure 7. Influence of soil state on the predicted error from the model of red clay （a） and silty clay （b）
![]()
图 8 本文模型与刘模型和规范模型所得剪切波速的对比
Figure 8. Comparison of shear wave velocties from the model of this study with those from Liu model and the normative model
![]()
图 9 本文模型与刘模型和规范模型预测误差对比
Figure 9. Comparison of prediction errors from the model of this study with those from Liu model and normative model
表 1 柳州地区Ⅱ类场地常规土类的埋深范围
Table 1 Conventional soil depth range for the class Ⅱ sites in Liuzhou region
岩土类型 埋深范围/m 人工填土 0.2—12.2 红黏土 1.0—31.0 粉质黏土 0.8—25.0 黏土 3.8—25.7 
下载: 导出CSV
表 2 柳州地区常规土类回归模型的拟合参数及拟合优度R2
Table 2 Fitting parameters and goodness R2 for three regressive models of conventional soils in Liuzhou region
岩土类型 线性模型 幂函数模型 二次函数模型 a b R2 c d R2 e f g R2 红黏土 243.80 4.237 3 0.803 2 215.93 0.129 7 0.813 1 240.02 5.059 4 −0.033 7 0.804 8 粉质黏土 224.22 6.325 4 0.772 4 201.86 0.149 6 0.824 2 223.02 5.777 0 −0.012 1 0.822 5 黏土 247.72 5.504 6 0.835 9 205.28 0.188 0 0.841 8 238.19 8.240 7 −0.077 8 0.840 3
下载: 导出CSV
表 3 不同土体状态下红黏土和粉质黏土的幂函数模型拟合参数及拟合优度R2
Table 3 Fitting parameters and goodness R2 of power function model for red clay and silty clay with different plastic states
回归模型 c d R2 可塑状态 硬塑状态 可塑状态 硬塑状态 可塑状态 硬塑状态 红黏土 195.35 205.35 0.145 2 0.131 9 0.742 9 0.714 2 粉质黏土 192.30 207.14 0.168 2 0.155 5 0.748 4 0.763 8
下载: 导出CSV
表 4 红黏土在不同土体状态下由回归模型按土体埋深所得剪切波速vS的预测值
Table 4 The predicted shear wave velocity vS from the regression model of red clay with plastic state according to the buried depth of soils
埋深/m 土体名称 土体状态 vS实测值
/（m·s−1）区分土体状态 不区分土体状态 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.70 杂填土 − 228 − − − − 2.00 红黏土 硬塑 230 225 2.2% 236 2.7% 3.00 红黏土 硬塑 242 237 1.9% 249 2.9% 4.00 红黏土 硬塑 255 247 3.3% 258 1.4% 5.00 红黏土 硬塑 260 254 2.3% 266 2.3% 6.00 红黏土 硬塑 263 260 1.1% 272 3.6% 7.00 红黏土 硬塑 267 265 0.6% 278 4.1% 8.00 红黏土 硬塑 264 270 2.3% 283 7.1% 9.00 红黏土 硬塑 264 274 3.9% 287 8.8% 10.00 红黏土 硬塑 272 278 2.3% 291 7.0% 11.00 红黏土 硬塑 272 282 3.6% 295 8.3% 12.00 红黏土 硬塑 273 285 4.4% 298 9.2% 13.00 红黏土 硬塑 269 288 7.1% 301 12.0% 14.00 红黏土 硬塑 272 291 6.9% 304 11.8% 15.00 红黏土 硬塑 279 294 5.2% 307 10.0% 16.50 红黏土 硬塑 286 297 3.9% 311 8.6% 18.00 红黏土 硬塑 296 301 1.6% 314 6.1%
下载: 导出CSV
表 5 粉质黏土在不同土体状态下由回归模型按土体埋深所得剪切波速vS及视剪切波速预测值
Table 5 The shear wave velocity vS and predicted apparent shear wave velocity from the regression model of silty clay with plastic state according to the buried depth of soils
埋深/m 土体名称 土体状态 vS实测值
/（m·s−1）区分土体状态 不区分土体状态 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.40 耕植土 174 − − − − 2.00 粉质黏土 硬塑 235 231 1.8% 224 4.7% 3.00 粉质黏土 硬塑 245 246 0.3% 238 2.9% 4.00 粉质黏土 硬塑 253 257 1.6% 248 1.8% 5.00 粉质黏土 硬塑 260 266 2.3% 257 1.2% 6.00 粉质黏土 硬塑 271 274 1.0% 264 2.6% 7.00 粉质黏土 硬塑 279 280 0.5% 270 3.2% 8.00 粉质黏土 硬塑 288 286 0.6% 276 4.3% 9.00 粉质黏土 硬塑 298 292 2.2% 280 5.9% 10.00 粉质黏土 硬塑 303 296 2.2% 285 6.0% 11.00 粉质黏土 硬塑 314 301 4.2% 289 8.0% 12.50 粉质黏土 硬塑 328 307 6.5% 295 10.2%
下载: 导出CSV
表 6 基于本文模型、刘模型和规范回归模型按土体埋深所得剪切波速预测值
Table 6 The predicted shear wave velocity vS based on the three models according to the buried depth of soils
埋深/m 土的名称 土的状态 vS实测值
/（m·s−1）本文模型 刘模型 规范模型 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 vS计算值/（m·s−1） 误差 0.80 素填土 200 − − − − 2.00 红黏土 硬塑 233 225 3.3% 221 5.0% 160 31.3% 3.00 红黏土 硬塑 236 238 0.7% 234 0.6% 181 23.4% 4.00 红黏土 硬塑 243 247 1.6% 244 0.6% 197 18.9% 5.00 红黏土 硬塑 253 254 0.4% 252 0.3% 211 16.7% 6.00 红黏土 硬塑 260 260 0.1% 259 0.4% 223 14.4% 7.00 红黏土 硬塑 264 266 0.6% 265 0.3% 233 11.7% 8.00 红黏土 硬塑 270 270 0.1% 270 0.1% 243 10.2% 9.00 红黏土 硬塑 279 275 1.6% 274 1.7% 251 9.9% 10.00 红黏土 硬塑 281 278 0.9% 279 0.9% 259 7.7% 11.00 红黏土 硬塑 280 282 0.7% 282 0.8% 267 4.7% 12.00 粉质黏土 硬塑 305 305 0.1% 260 14.6% 274 10.2% 13.00 粉质黏土 硬塑 303 309 1.9% 267 11.9% 281 7.4% 14.00 粉质黏土 硬塑 304 312 2.7% 273 10.3% 287 5.6% 15.00 粉质黏土 硬塑 326 316 3.2% 279 14.6% 293 10.1% 16.00 粉质黏土 硬塑 319 319 0.1% 284 11.0% 299 6.4% 17.00 粉质黏土 硬塑 319 322 0.9% 289 9.3% 304 4.7% 18.00 粉质黏土 硬塑 332 325 2.2% 294 11.4% 309 6.8% 19.00 粉质黏土 硬塑 351 327 6.7% 299 14.8% 314 10.4% 20.00 粉质黏土 硬塑 351 330 6.0% 304 13.5% 319 9.0% 21.00 粉质黏土 硬塑 359 333 7.4% 308 14.1% 324 9.7% 22.00 粉质黏土 硬塑 351 335 4.6% 313 10.9% 329 6.4% 23.00 粉质黏土 硬塑 369 337 8.6% 317 14.1% 333 9.8% 24.00 粉质黏土 硬塑 362 340 6.2% 321 11.4% 337 6.8% 25.00 粉质黏土 硬塑 368 342 7.1% 325 11.7% 341 7.2% 25.70 粉质黏土 硬塑 392 378 3.6% 336 14.2% 344 12.2% 注：刘模型引自刘红帅等（2010）以及刘华贵和蒋文宇（2015），规范模型引自中国人民共和国铁道部（2001）。
下载: 导出CSV
-
蔡宗文. 2003. 福建沿海剪切波速与土层参数定量关系研究[J]. 华南地震,23(3):76–80. doi: 10.3969/j.issn.1001-8662.2003.03.011 Cai Z W. 2003. The quantitative analysis between shear wave velocity and soil-layer parameters in Fujian coastal areas[J]. South China Journal of Seismology,23(3):76–80 (in Chinese).
陈国兴,徐建龙,袁灿勤. 1998. 南京城区岩土体剪切波速与土层深度的关系[J]. 南京建筑工程学院学报,45(2):32–37. Chen G X,Xu J L,Yuan C Q. 1998. Relation between depth and shear wave velocity of soil and bedrock in Nanjing city[J]. Journal of Nanjing Architectural and Civil Engineering Institute,45(2):32–37 (in Chinese).
程祖锋,李萍,李燕,张桂珍. 1997. 深圳地区部分岩土类型剪切波速与深度的关系分析[J]. 工程地质学报,5(2):161–168. Cheng Z F,Li P,Li Y,Zhang G Z. 1997. Analysis of relationship between shear wave velocity and depth of some types of soil and rock in Shenzhen region[J]. Journal of Engineering Geology,5(2):161–168 (in Chinese).
丁国瑜,卢演俦. 1983. 华北地块新构造变形基本特点的讨论[J]. 华北地震科学,1(2):1–9. Ding G Y,Lu Y C. 1983. Discussion on the basic characteristics of new tectonic deformation in North China block[J]. North China Earthquake Sciences,1(2):1–9 (in Chinese).
国家技术监督局, 中华人民共和国建设部. 1995. GB 50191—1993 构筑物抗震设计规范[S]. 北京: 中国计划出版社: 11−13. State Bureau of Technology Supervision, Ministry of Housing and Urban-Rural Development of the People’s Republic of China. 1995. GB 50191−1993 Design Code for Antiseismic of Special Structures[S]. Beijing: China Planning Press: 11−13 （in Chinese）.
贺为民,刘明军,杨杰. 2016. 土层剪切波速与埋深关系统计分析和应用[J]. 地震地质,38(4):937–949. doi: 10.3969/j.issn.0253-4967.2016.04.011 He W M,Liu M J,Yang J. 2016. Application and statistical analysis of relationship between shear wave velocity and depth of soil-layers[J]. Seismology and Geology,38(4):937–949 (in Chinese).
兰景岩,薄景山,吕悦军. 2007. 剪切波速对设计反应谱的影响研究[J]. 震灾防御技术,2(1):19–24. doi: 10.3969/j.issn.1673-5722.2007.01.003 Lan J Y,Bo J S,Lü Y J. 2007. Study on the effect of shear wave velocity on the design spectrum[J]. Technology for Earthquake Disaster Prevention,2(1):19–24 (in Chinese).
李帅,赵纯青,唐丽华. 2012. 剪切波速在判定石河子市某建设场地类别中的应用[J]. 内陆地震,26(2):180–186. doi: 10.3969/j.issn.1001-8956.2012.02.009 Li S,Zhao C Q,Tang L H. 2012. Application on judgment of construction site classification in Shihezi with shear wave velocity[J]. Inland Earthquake,26(2):180–186 (in Chinese).
刘华贵,蒋文宇. 2015. 柳州官塘片区红粘土剪切波速与埋深的相关性分析[J]. 地震研究,38(2):280–284. Liu H G,Jiang W Y. 2015. Correlative analysis between shear wave velocity and depth of red clay in Liuzhou Guantang region[J]. Journal of Seismological Research,38(2):280–284 (in Chinese).
刘红帅,郑桐,齐文浩,兰景岩. 2010. 常规土类剪切波速与埋深的关系分析[J]. 岩土工程学报,32(7):1142–1149. Liu H S,Zheng T,Qi W H,Lan J Y. 2010. Relationship between shear wave velocity and depth of conventional soils[J]. Chinese Journal of Geotechnical Engineering,32(7):1142–1149 (in Chinese).
齐鑫,丁浩. 2012. 下辽河平原区剪切波速与土层埋深关系分析[J]. 世界地震工程,28(3):151–156. doi: 10.3969/j.issn.1007-6069.2012.03.027 Qi X,Ding H. 2012. Analysis of relationship between shear wave velocity and depth of soil layers in downstream Liaohe River plain[J]. World Earthquake Engineering,28(3):151–156 (in Chinese).
邱志刚,薄景山,罗奇峰. 2011. 土壤剪切波速与埋深关系的统计分析[J]. 世界地震工程,27(3):81–88. Qiu Z G,Bo J S,Luo Q F. 2011. Statistical analysis of relationship between shear wave velocity and depth of soil[J]. World Earthquake Engineering,27(3):81–88 (in Chinese).
王强,王兰民,吴志坚,王平. 2014. 天水市岩土体剪切波速与埋深的变化关系[J]. 地震工程与工程振动,34(增刊1):247–252. Wang Q,Wang L M,Wu Z J,Wang P. 2014. Relationship between shear wave velocity and depth of soils and rocks in Tianshui city[J]. Earthquake Engineering and Engineering Dynamics,34(S1):247–252 (in Chinese).
汪闻韶. 1994. 土工地震减灾工程中的一个重要参量:剪切波速[J]. 水利学报,25(3):80–84. doi: 10.3321/j.issn:0559-9350.1994.03.012 Wang W S. 1994. An important parameter in geotechnical engineering for earthquake disaster mitigation:Shear wave velocity[J]. Journal of Hydraulic Engineering,25(3):80–84 (in Chinese).
张龙飞,董斌,史双双,韩晓飞. 2018. 朔州市区土层剪切波速与埋深的统计关系[J]. 华北地震科学,36(2):28–37. doi: 10.3969/j.issn.1003-1375.2018.02.005 Zhang L F,Dong B,Shi S S,Han X F. 2018. Shear wave velocity and depth of soil layer in Shuozhou city of Datong basin[J]. North China Earthquake Sciences,36(2):28–37 (in Chinese).
中华人民共和国铁道部. 2001. TB 10077—2001 铁路工程岩土分类标准[S]. 北京: 中国铁路出版社: 12−16. Ministry of Railways of the People’s Republic of China. 2001. TB 10077−2001 Code for Rock and Soil Classification of Railway Engineering[S]. Beijing: China Railway Publishing House: 12−16 （in Chinese）.
Lee S H H. 1990. Regression models of shear wave velocities in Taipei basin[J]. Journal of Chinese Institute of Engineering,13(5):519–532. doi: 10.1080/02533839.1990.9677284
Ohta Y,Goto N. 1978. Empirical shear wave velocity equations in terms of characteristic soil indexes[J]. Earthq Eng Struct Dyn,6(2):167–187.
-
期刊类型引用(6)
1. 刘文玉，程正璞，年秀清，陈闫，胡钰铃，覃祖建，邵明正. 基于三维剩余密度结构的松原地震成因. 地震地质. 2024(02): 462-476 . 
百度学术
2. 张仁鹏，雷焕珍，陈聪，陈琳荣，冯靖乔. 2019年松原M_S5.1地震烈度评定及震害特征简析. 防灾减灾学报. 2023(01): 34-40 . 百度学术
3. 于晨，卢军，解滔，刘长生. 2017—2019年松原地区4次中强地震前绥化台地电阻率异常分析. 中国地震. 2023(02): 314-324 . 百度学术
4. 张仁鹏，冯靖乔，雷焕珍，于宏伟，马飞，王佳蕾. 松原市5.7级和5.1级地震房屋震害特征分析与启示. 防灾科技学院学报. 2022(03): 80-87 . 百度学术
5. 李梦莹，张志宏，焦明若，方禹心. 2018-05-28松原M_S5.7地震地电场变化特征研究. 大地测量与地球动力学. 2022(12): 1276-1280+1299 . 百度学术
6. 李梦莹，杨士超，张志宏，孔祥瑞，孙庆山. 2018年松原M_S 5.7地震地电场变化特征. 地震地磁观测与研究. 2022(S1): 120-122 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 1865
- HTML全文浏览量: 596
- PDF下载量: 70
- 被引次数: 7
