Probabilistic earthquake location in three-dimensional velocity models applied in Tengchong
-
摘要:
本文利用中国数字测震台网和流动台站的地震资料，基于参数优化的AICD自动拾取算法和质量评估方案得到了高质量的震相到时，并在此基础上使用一维、三维定位方法对腾冲地区的799次地震事件进行了重新定位。定位结果显示：水平方向上，一维、三维重定位结果相差较小；深度方向上，三维定位的震源成丛分布比一维定位结果更加密集，地震主要位于地壳内低速层之上。分别利用一维、三维定位方法对典型地震、人工震源进行定位，结果表明，三维定位的精度明显优于一维定位，其在水平、深度方向上的平均绝对定位误差分别为0.7 km和1.3 km。
Abstract:The accuracy of earthquake location strongly depends on quality and consistency of available traveltime data. We obtained accurate automatic picks by employing optimized AICD automatic pickers and quality assessment scheme at temporary and permanent seismic networks surrounding Tengchong volcanic area. Based on those high-quality first-arrivals, we relocated 799 earthquakes with 1D （Hypomat） and 3D （probabilistic earthquake location） location algorithms. The comparison of 799 hypocenter relocations obtained by 1D location method （Hypomat） to those relocated in 3D velocity model using a probabilistic approach reveals no systematic shifts in epicenter locations but does exhibit large vertical shifts. 3D relocations are usually at the top of low velocity layers in crust and more clustered than 1D relocations. The events relocated with the 1D model seem often deeper than the events relocated with the 3D model. Relocating artificial sources and typical seismic sequences using 1D and 3D methods confirms that probabilistic earthquake location combined with 3D velocity model yields more precise hypocenter locations for Tengchong and has mean absolute errors of 0.7 km horizontally and 1.3 km vertically.
-
引言
云南腾冲火山区地处青藏高原东南缘，是中国大陆最年轻的火山区之一，该区地热和地震活动均很强烈，长期被国内外地球科学研究人员所关注（楼海等，2002；Socquet，Pubellier，2005；Wang et al，2007；杨晓涛等，2011）。对该区地震进行精确定位，可为地球内部结构、地震活动构造等地震学研究提供重要的基础参数（Xu et al，2012；张广伟，雷建设，2015）。
地震定位的精度和不确定性受多种因素制约，包括震相到时的拾取精度和测量误差、地壳速度结构的精细程度、地震台网分布情况及可用于地震定位的震相数量和类型等（Lomax et al，2001；Hausmann et al，2010）。因此，如果可以改善震相到时的拾取精度，并利用能够反映出研究区地壳结构变化的精细地壳速度模型进行地震定位，地震定位的精度将会得到极大提高。
研究人员采用接收函数、人工地震测深等方法开展的相关研究表明：青藏高原东南缘（图1）地壳厚度变化剧烈，莫霍界面分布总趋势呈东南浅、西北深；在云南西北部的中甸、丽江地区，地壳厚度可达54—56 km；云南南部的景洪、思茅和沧源地区，地壳厚度仅为32—36 km；南华板块的大部分地区地壳厚度介于36—44 km之间；以红河断裂为界，其西南部地壳厚度变化较东北部更为剧烈（陈立华等，1992；阚荣举，赵晋明，1994；王椿镛等，2000；Li et al，2008，2014a；王夫运等，2014；潘素珍等，2015；郑晨等，2016）。目前有关云南地区地震定位的相关研究基本采用一维速度模型（He et al，2015；Xie et al，2015），但由于一维速度模型与研究区复杂的地壳结构存在明显偏差，会造成地震定位的精度较低。
![]()
图 1 云南地区断裂分布（修改自马丽芳等，2002）F1：怒江断裂；F2：澜沧江断裂；F3：红河断裂；F4：金沙江断裂；F5：哀牢山断裂；F6：小金河断裂；F7：小江断裂；F8：弥勒断裂；F9：则木河断裂；F10：绿汁江断裂；F11：楚雄—通海断裂Figure 1. The distribution of faults in Yunnan area （after Ma et al，2002）F1：Nujiang fault；F2：Lancangjiang fault；F3：Honghe fault；F4：Jinshajiang fault；F5：Ailaoshan fault；F6：Xiaojinhe fault；F7：Xiaojiang fault；F8：Mile fault；F9：Zemuhe fault；F10：Lüzhijiang fault；F11：Chuxiong-Tonghai fault本文收集了云南腾冲火山区固定台站、火山台站、流动台站共计64套宽频带地震仪记录到的波形资料，拟经近震震相到时自动拾取和质量评估得到高质量的P、S波初至走时，并基于研究区最优一维P、S波速度模型和腾冲地区已有的三维S波速度模型（郑晨等，2016）分别开展重定位研究，对比分析不同定位结果准确性和可靠性，对新的地震定位结果与已有地质构造的关系进行探讨。
引言
云南腾冲火山区地处青藏高原东南缘，是中国大陆最年轻的火山区之一，该区地热和地震活动均很强烈，长期被国内外地球科学研究人员所关注（楼海等，2002；Socquet，Pubellier，2005；Wang et al，2007；杨晓涛等，2011）。对该区地震进行精确定位，可为地球内部结构、地震活动构造等地震学研究提供重要的基础参数（Xu et al，2012；张广伟，雷建设，2015）。
地震定位的精度和不确定性受多种因素制约，包括震相到时的拾取精度和测量误差、地壳速度结构的精细程度、地震台网分布情况及可用于地震定位的震相数量和类型等（Lomax et al，2001；Hausmann et al，2010）。因此，如果可以改善震相到时的拾取精度，并利用能够反映出研究区地壳结构变化的精细地壳速度模型进行地震定位，地震定位的精度将会得到极大提高。
研究人员采用接收函数、人工地震测深等方法开展的相关研究表明：青藏高原东南缘（图1）地壳厚度变化剧烈，莫霍界面分布总趋势呈东南浅、西北深；在云南西北部的中甸、丽江地区，地壳厚度可达54—56 km；云南南部的景洪、思茅和沧源地区，地壳厚度仅为32—36 km；南华板块的大部分地区地壳厚度介于36—44 km之间；以红河断裂为界，其西南部地壳厚度变化较东北部更为剧烈（陈立华等，1992；阚荣举，赵晋明，1994；王椿镛等，2000；Li et al，2008，2014a；王夫运等，2014；潘素珍等，2015；郑晨等，2016）。目前有关云南地区地震定位的相关研究基本采用一维速度模型（He et al，2015；Xie et al，2015），但由于一维速度模型与研究区复杂的地壳结构存在明显偏差，会造成地震定位的精度较低。
![]()
图 1 云南地区断裂分布（修改自马丽芳等，2002）F1：怒江断裂；F2：澜沧江断裂；F3：红河断裂；F4：金沙江断裂；F5：哀牢山断裂；F6：小金河断裂；F7：小江断裂；F8：弥勒断裂；F9：则木河断裂；F10：绿汁江断裂；F11：楚雄—通海断裂Figure 1. The distribution of faults in Yunnan area （after Ma et al，2002）F1：Nujiang fault；F2：Lancangjiang fault；F3：Honghe fault；F4：Jinshajiang fault；F5：Ailaoshan fault；F6：Xiaojinhe fault；F7：Xiaojiang fault；F8：Mile fault；F9：Zemuhe fault；F10：Lüzhijiang fault；F11：Chuxiong-Tonghai fault本文收集了云南腾冲火山区固定台站、火山台站、流动台站共计64套宽频带地震仪记录到的波形资料，拟经近震震相到时自动拾取和质量评估得到高质量的P、S波初至走时，并基于研究区最优一维P、S波速度模型和腾冲地区已有的三维S波速度模型（郑晨等，2016）分别开展重定位研究，对比分析不同定位结果准确性和可靠性，对新的地震定位结果与已有地质构造的关系进行探讨。
1. 数据和速度模型
1. 数据和速度模型
1.1 台网及数据
本研究使用了中国地震科学台阵探测项目 Ⅰ 期在腾冲火山区43个流动地震台站于2011年6月到2013年6月期间观测到的地震波形记录（中国地震科学台阵，2006）和中国地震局地球物理研究所在腾冲地区布设的5套流动地震台站于2015年1月至12月记录的地震波形资料，以及腾冲地区8个火山台站和8个中国地震台网台站于上述观测周期内记录的地震波形资料（国家测震台网数据备份中心，2007；郑秀芬等，2009）。这些地震仪器记录的原始波形采样率均为100 Hz。
根据中国地震编目系统提供的地震目录，选取震中位于（23°N—26°N，97°E—100°E）范围内、震级ML≥1.5的3 849次地震事件，其分布如图2所示。截取震前30 s至震后210 s的三分量波形记录用于P、S波初至拾取。
![]()
图 2 研究区台站和中国地震编目系统提供的地震震中分布Figure 2. Distributions of seismic stations and epicenters provided by the unified national cataloging system1.2 震相到时自动拾取拾取和质量评估
高质量的地震走时与地震走时信息的一致性是地震精确定位工作的前提和保证（刘劲松等，2013）。为此，本文统一采用自动拾取的到时信息进行地震定位研究。到时拾取过程中，先通过对部分数据的测试得到各台站最佳拾取参数、筛选窗口常数值、权重分隔区间，再应用于全部波形的到时拾取。通过质量评估方案对自动拾取结果进行等级评判，评级为Class 0—3的自动拾取结果所对应的误差区间依次为[0，0.1），[0.1，0.2），[0.2，0.4），[0.4，2），相关原理及具体方法参见杨旭等（2019）。通过对各台站2011年11月至2012年1月、2015年5至8月的波形数据反复测试后得到了64个台站基于AICD拾取算法的最佳拾取参数，再将其运用到全部波形的到时拾取工作中，仅保留质量评估方案中得到的高质量到时（Class 0和Class 1），共计得到P波到时31 410条、S波到时29 136条。
1.2 震相到时自动拾取拾取和质量评估
高质量的地震走时与地震走时信息的一致性是地震精确定位工作的前提和保证（刘劲松等，2013）。为此，本文统一采用自动拾取的到时信息进行地震定位研究。到时拾取过程中，先通过对部分数据的测试得到各台站最佳拾取参数、筛选窗口常数值、权重分隔区间，再应用于全部波形的到时拾取。通过质量评估方案对自动拾取结果进行等级评判，评级为Class 0—3的自动拾取结果所对应的误差区间依次为[0，0.1），[0.1，0.2），[0.2，0.4），[0.4，2），相关原理及具体方法参见杨旭等（2019）。通过对各台站2011年11月至2012年1月、2015年5至8月的波形数据反复测试后得到了64个台站基于AICD拾取算法的最佳拾取参数，再将其运用到全部波形的到时拾取工作中，仅保留质量评估方案中得到的高质量到时（Class 0和Class 1），共计得到P波到时31 410条、S波到时29 136条。
1.3 速度模型
1.3 速度模型
1.3.1 最优一维P、S波速度模型
本文使用VELEST算法（Kissling et al，1994），以3个研究区一维P波速度模型HJ0 （Huang et al，2012），WCY0 （王椿镛等，2000）和GJY0 （高家乙等，2016）为初始参考模型，联合反演震源位置和一维速度模型来获取研究区最优一维速度模型HJ1，WCY1和GJY1。首先，基于这3个一维P波速度模型，通过Brocher （2005）一文中的公式（6）获得各自相应S波速度模型。然后，挑选P波到时和S波到时均有5个以上（等级为Class 0）、台站方位角GAP＜180°的事件共计826次，采用VELEST算法反演得到了3组最优一维P、S波速度模型。将这3组最优一维速度模型进行平均得到平均一维模型 ，再次通过VELEST算法反演得到最终最优一维P、S波速度模型（图3）。反演过程中，发震时刻、坐标和台站修正项的阻尼因子均为0.01。利用3组初始参考模型计算的走时与实际观测走时的平均残差均方根、平均方差分别为0.60 s和0.57 s2，而使用最终一维最优速度模型计算的走时与实际观测走时的残差均方根和方差分别降至0.24 s和0.07 s2。为了检验最优一维P、S波速度模型的稳定性，进行定位恢复试验，将该模型作为初始模型并在地震事件的纬度、经度和深度上随机改变−5—5 km，试验结果显示恢复后的震源坐标在纬度、经度和深度上的平均误差分别为0.38 km，0.38 km和0.88 km，表明该最终最优模型是可靠的（图4）。
![]()
图 3 一维速度模型和地震定位结果（a） P波和S波初始速度模型；（b） P波和S波最优一维速度模型，其中HJ1，WCY1 和GJY1基于图（a）中的初始模型得到，HJ1，WCY1 和GJY1的平均值为平均一维模型，基于平均一维模型得到最终最优速度模型；（c） 本文 一维定位使用的最终最优速度模型和基于该模型反演得到的震源深度分布图Figure 3. The P-wave and S-wave velocity models and relocating results（a） Initial P-wave and S-wave velocity structures；（b） The best P-wave and S-wave velocity models obtained from the VELEST inversion based on different initial models shown in Fig. （a）；（c） The final minimum 1D P-wave and S-wave velocity models used to 1D location and histogram of the events distributionin depth obtained by VELEST inversion based on the final minimum model，where the final minimum 1D P-wave and S-wave velocity models are obtained based on the average of three velocity models resulting from three different initial velocity models![]()
图 4 VELEST定位稳定性试验黑色圆点为地震事件在纬度（a）、经度（b）、深度（c）上的随机扰动量，红色圆点为定位恢复试验后震源坐标的误差Figure 4. Test of VELEST location stabilityBlack dots represent the amount of shift along latitude （a），longitude （b） and depth （c） with respect to the reference locations，the inversion is then repeated，and the retrieved location shifts are shown as red dots1.3.2 三维速度模型
本文三维定位研究中采用了郑晨等（2016）的三维S波速度模型，通过Brocher （2005）公式（9）获得了与该模型相一致的三维P波速度模型，用于后续的三维重定位工作。该三维S波速度结构源自面波群速度、相速度频散与接收函数波形资料联合反演结果，其中：用于反演的接收函数源自中国地震科学台阵探测项目 Ⅰ 期的350个流动台站记录的远震波形资料，其台站间距介于30—50 km之间；而面波频散则利用中国地震科学台阵探测项目 Ⅰ 期流动地震台站记录的远震波形资料，采用远震双台方法获得，其分辨率介于50—100 km之间（Li et al，2014b；潘佳铁等，2015）。
2. 地震重定位
目前关于云南地区地震定位的相关研究基本采用一维速度模型（He et al，2015；Xie et al，2015）。如果能在地壳结构复杂的地区采用三维地震定位方法开展定位研究，将会明显改善地震定位的精度（Lomax et al，2001；Béthoux et al，2016）。
2. 地震重定位
目前关于云南地区地震定位的相关研究基本采用一维速度模型（He et al，2015；Xie et al，2015）。如果能在地壳结构复杂的地区采用三维地震定位方法开展定位研究，将会明显改善地震定位的精度（Lomax et al，2001；Béthoux et al，2016）。
2.1 参与重定位的地震事件
基于前述自动拾取的到时，按以下条件来选取参与重定位的地震事件：① 记录台站数至少3个，每个台站同时具有P、S波初至到时；② 自动拾取初至到时的等级为Class 0或Class 1；③ 台站方位角GAP＜180°。最后共得到799个符合上述要求的地震事件。
2.1 参与重定位的地震事件
基于前述自动拾取的到时，按以下条件来选取参与重定位的地震事件：① 记录台站数至少3个，每个台站同时具有P、S波初至到时；② 自动拾取初至到时的等级为Class 0或Class 1；③ 台站方位角GAP＜180°。最后共得到799个符合上述要求的地震事件。
2.2 Hypomat精定位
为方便比较，本文首先采用Hypomat一维定位方法（牟磊育等，2006）对上述地震事件进行重定位。Hypomat是牟磊育等（2006）在Matlab下研发的一种近震定位程序，该程序实现了Inglada和Geiger地震定位算法的联合使用，先利用Inglada方法初步求解地震发生的经度、纬度、深度和发震时刻的估计解，再用Geiger方法在多层速度模型下对估计解进行迭代校正，以取得精确的地震定位结果。特别是在各台站采用精确的速度模型后，可明显提高定位精度。
2.2 Hypomat精定位
为方便比较，本文首先采用Hypomat一维定位方法（牟磊育等，2006）对上述地震事件进行重定位。Hypomat是牟磊育等（2006）在Matlab下研发的一种近震定位程序，该程序实现了Inglada和Geiger地震定位算法的联合使用，先利用Inglada方法初步求解地震发生的经度、纬度、深度和发震时刻的估计解，再用Geiger方法在多层速度模型下对估计解进行迭代校正，以取得精确的地震定位结果。特别是在各台站采用精确的速度模型后，可明显提高定位精度。
2.3 三维地震定位
本研究采用NonLinLoc软件中基于Oct-Tree搜索算法的非线性地震定位方法（Lomax et al，2000；Lomax，Curtis，2001）进行重定位研究。该方法用后验概率密度函数（probability density function，缩写为PDF）的最大似然点表示震源最优解，PDF散点图的空间离散程度反映了定位不确定性的大小（Wittlinger et al，1993；Lomax et al，2001）。由于地壳结构与理论速度模型的实际偏差未知，因此这种不确定性并不能表示绝对定位误差，但其对于判断震源解的受约束程度等仍具有一定的指示意义（Lomax et al，2000）。
PDF求解过程不涉及偏导数的计算，因此可用于复杂的三维速度模型。假设待求模型参数空间与已知观测参数空间的先验信息是相互独立的，模型化和观测的不确定性都符合高斯分布，相应的协方差矩阵分别为CT和Ct，则后验概率密度函数σ（x）的表达式为（Tarantola，Valette，1982；Tarantola，1987）：
$\sigma \!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!{\text{＝}} K\rho \!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!\exp \left[ { {\text{－}} \frac{1}{2}g\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!} \right]{\text{，}} $
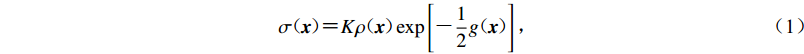
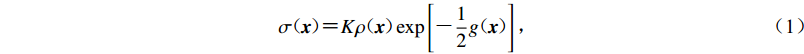
(1) $ g\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\! {\text{＝}} {[{ {{\hat{{t}}}_0}} {\text{－}} {\hat {{h}}}\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!]^{\rm{T}}}{\!\!\!\!{\text{（}}{{{{C}}_t} {\text{＋}} {{{C}}_T}}{\text{）}}\!\!\!\!^{ {\text{－}} 1}}[{ {{\hat{{t}}}_0}} {\text{－}} {\hat {{h}}}\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!]{\text{，}} $
(2) $ {{\omega _i} {\text{＝}} \displaystyle \sum\limits_j {{\omega _{ij}}} }{\text{，}} $
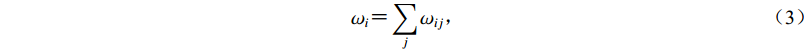
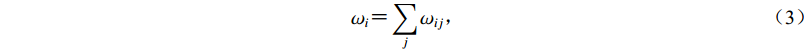
(3) ${{\omega _{ij}} {\text{＝}} {{\left[ \!\!\!\!\!{{{{\text{（}}{{{{C}}}_t {\text{＋}} {{{C}}}}_T \!{\text{）}}}\!\!\!\!^{{\text{－}}1}}} \right]}_{ij}}{\text{，}}} $
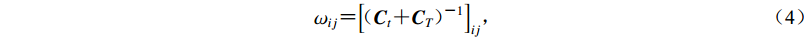
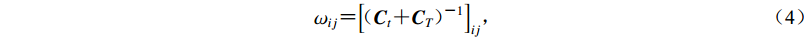
(4) $ {T\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}{\text{＝}} \frac{{\displaystyle\sum_i {\displaystyle\sum_j {{\omega _{ij}}} } \left[ {{{ t}_i} {\text{－}} {{ h}_i}\!\!\!\!{\text{（}}\!{ x}\!{\text{）}}} \!\!\!\!\right]}}{{\displaystyle\sum_i {{\displaystyle\sum _j}} {\omega _{ij}}}}{\text{，}}} $
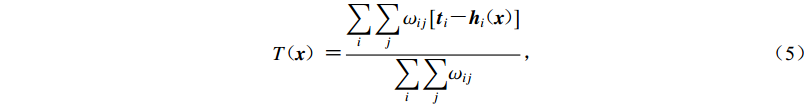
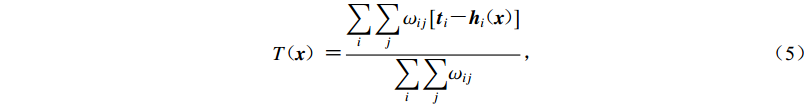
(5) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
本文使用Oct-Tree重要性采样算法搜索震源最优解，该算法在搜索空间内部寻找PDF值较高的节点，将其剖分成8个子节点并计算每个子节点的PDF值，锁定子节点中PDF值最高的节点，将其再次细分成8个子节点并计算子节点的PDF值，递归细分使得采样密度与空间节点的PDF值成正比，从而使搜索过程快速收敛至PDF的最小失配点（Lomax，Curtis，2001）。本研究中设置x，y和z坐标方向初始搜索节点个数分别为10，10和4，速度网格节点的边长为1 km，每次搜索中可容纳的子节点总数为20 000。
2.3 三维地震定位
本研究采用NonLinLoc软件中基于Oct-Tree搜索算法的非线性地震定位方法（Lomax et al，2000；Lomax，Curtis，2001）进行重定位研究。该方法用后验概率密度函数（probability density function，缩写为PDF）的最大似然点表示震源最优解，PDF散点图的空间离散程度反映了定位不确定性的大小（Wittlinger et al，1993；Lomax et al，2001）。由于地壳结构与理论速度模型的实际偏差未知，因此这种不确定性并不能表示绝对定位误差，但其对于判断震源解的受约束程度等仍具有一定的指示意义（Lomax et al，2000）。
PDF求解过程不涉及偏导数的计算，因此可用于复杂的三维速度模型。假设待求模型参数空间与已知观测参数空间的先验信息是相互独立的，模型化和观测的不确定性都符合高斯分布，相应的协方差矩阵分别为CT和Ct，则后验概率密度函数σ（x）的表达式为（Tarantola，Valette，1982；Tarantola，1987）：
$$\sigma \!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!{\text{＝}} K\rho \!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!\exp \left[ { {\text{－}} \frac{1}{2}g\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!} \right]{\text{，}} $$ (1) $$ g\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\! {\text{＝}} {[{ {{\hat{{t}}}_0}} {\text{－}} {\hat {{h}}}\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!]^{\rm{T}}}{\!\!\!\!{\text{（}}{{{{C}}_t} {\text{＋}} {{{C}}_T}}{\text{）}}\!\!\!\!^{ {\text{－}} 1}}[{ {{\hat{{t}}}_0}} {\text{－}} {\hat {{h}}}\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}\!\!\!\!]{\text{，}} $$ (2) $$ {{\omega _i} {\text{＝}} \displaystyle \sum\limits_j {{\omega _{ij}}} }{\text{，}} $$ (3) $${{\omega _{ij}} {\text{＝}} {{\left[ \!\!\!\!\!{{{{\text{（}}{{{{C}}}_t {\text{＋}} {{{C}}}}_T \!{\text{）}}}\!\!\!\!^{{\text{－}}1}}} \right]}_{ij}}{\text{，}}} $$ (4) $$ {T\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}{\text{＝}} \frac{{\displaystyle\sum_i {\displaystyle\sum_j {{\omega _{ij}}} } \left[ {{{ t}_i} {\text{－}} {{ h}_i}\!\!\!\!{\text{（}}\!{ x}\!{\text{）}}} \!\!\!\!\right]}}{{\displaystyle\sum_i {{\displaystyle\sum _j}} {\omega _{ij}}}}{\text{，}}} $$ (5) 式中，K是归一化因子，x＝（x，y，z）是震源空间坐标，T是发震时刻，t是震相到时，h是由三维空间的程函有限差分方程（Podvin，Lecomte，1991；Le Meur，1994；Le Meur et al，1997）计算得到的理论预测走时，ρ（x）是模型参数先验信息的概率密度函数，g（x）是失配函数，
${{\hat{{t}}}_0}$ 表示观测到时t减去其权重平均值，$\hat {{{{h}}}}\!\!\!\!{\text{（}}\!{{x}}\!{\text{）}}$ 表示理论预测走时h减去其权重平均值。由式（3）和（4）计算得到每条观测到时、理论走时的权重值，式中的i和j表示空间中的各个节点。本文使用Oct-Tree重要性采样算法搜索震源最优解，该算法在搜索空间内部寻找PDF值较高的节点，将其剖分成8个子节点并计算每个子节点的PDF值，锁定子节点中PDF值最高的节点，将其再次细分成8个子节点并计算子节点的PDF值，递归细分使得采样密度与空间节点的PDF值成正比，从而使搜索过程快速收敛至PDF的最小失配点（Lomax，Curtis，2001）。本研究中设置x，y和z坐标方向初始搜索节点个数分别为10，10和4，速度网格节点的边长为1 km，每次搜索中可容纳的子节点总数为20 000。
3. 重定位结果
基于腾冲火山区一维、三维速度模型，利用前述的两种定位方法，分别获得了799次地震的一维、三维重新定位结果，如图5所示。
![]()
图 5 腾冲火山区799次地震的的一维（a）和三维（b）重定位结果Figure 5. 1D Hypomat （a） and 3D NonLinLoc （b） relocations of 799 events located in Tengchong3. 重定位结果
基于腾冲火山区一维、三维速度模型，利用前述的两种定位方法，分别获得了799次地震的一维、三维重新定位结果，如图5所示。
![]()
图 5 腾冲火山区799次地震的的一维（a）和三维（b）重定位结果Figure 5. 1D Hypomat （a） and 3D NonLinLoc （b） relocations of 799 events located in Tengchong3.1 不同方法定位结果比较
一维重定位（Hypomat）后走时残差均方根（root mean square，缩写为RMS）的平均值为0.29 s，三维重定位（NonLinLoc，缩写为NLL）后RMS平均值降至0.14 s （图6），走时残差显著降低，表明由三维速度模型和NLL算法得到的理论走时比一维定位算得的更接近实际观测走时。
![]()
图 6 一维（a）和三维（b）重定位走时残差统计图Figure 6. Histograms of travel-time residual for 1D Hypomat （a） and 3D NonLinLoc （b） relocations将本文的799次地震事件重定位结果与中国地震台网中心（China Earthquake Networks Center，缩写为CENC）（2019）定位结果相比较（表1），一维和三维在水平方向上与中国地震台网中心定位差介于±3.5 km之内的事件占比分别为85.11%和83.10%，说明两者在水平方向上的定位结果相近且均与中国地震台网中心提供的震中位置相一致。两者在垂直方向上同中国地震台网中心的差别较为明显，主要是由于增加了流动台站的观测资料，以及使用了不同的速度模型、定位方法。
表 1 本文所得799次地震事件的一维、三维重定位结果与中国地震台网中心（CENC）定位结果的比较Table 1. Relative comparison of the 799 epicentre locations calculated by either this study or the CENC定位差 水平向定位差
平均值/km水平向定位差
最大值/km水平向定位差≤
3.5 km事件占比垂直向定位差
平均值/km垂直向定位差
最大值/km垂直向定位差≤
3.5 km事件占比NLL−CENC 2.31±1.64 12.96 85.11% 3.12±2.45 19.52 65.08% Hypomat−CENC 2.22±1.63 11.16 83.10% 3.21±2.68 21.00 64.83% NLL−Hypomat 1.69±1.44 14.52 92.12% 2.72±2.72 16.41 75.59% 对比本研究的一维、三维重定位结果，NLL和Hypomat在水平、垂直方向上定位差的平均值分别为1.69 m和2.72 m，产生这些定位差的主要原因是NLL和Hypomat使用了不同的速度模型、定位方法。个别事件的观测台站数目很少，台站离震源较远且台站方位角GAP超过160°，此类事件的一维、三维重定位结果相差很大（＞12.5 km），重定位结果与CENC的定位差也超过12.5 km，说明地震台网的几何分布、可用震相的数量同时制约一维、三维重定位结果。
3.1 不同方法定位结果比较
一维重定位（Hypomat）后走时残差均方根（root mean square，缩写为RMS）的平均值为0.29 s，三维重定位（NonLinLoc，缩写为NLL）后RMS平均值降至0.14 s （图6），走时残差显著降低，表明由三维速度模型和NLL算法得到的理论走时比一维定位算得的更接近实际观测走时。
![]()
图 6 一维（a）和三维（b）重定位走时残差统计图Figure 6. Histograms of travel-time residual for 1D Hypomat （a） and 3D NonLinLoc （b） relocations将本文的799次地震事件重定位结果与中国地震台网中心（China Earthquake Networks Center，缩写为CENC）（2019）定位结果相比较（表1），一维和三维在水平方向上与中国地震台网中心定位差介于±3.5 km之内的事件占比分别为85.11%和83.10%，说明两者在水平方向上的定位结果相近且均与中国地震台网中心提供的震中位置相一致。两者在垂直方向上同中国地震台网中心的差别较为明显，主要是由于增加了流动台站的观测资料，以及使用了不同的速度模型、定位方法。
表 1 本文所得799次地震事件的一维、三维重定位结果与中国地震台网中心（CENC）定位结果的比较Table 1. Relative comparison of the 799 epicentre locations calculated by either this study or the CENC定位差 水平向定位差
平均值/km水平向定位差
最大值/km水平向定位差≤
3.5 km事件占比垂直向定位差
平均值/km垂直向定位差
最大值/km垂直向定位差≤
3.5 km事件占比NLL−CENC 2.31±1.64 12.96 85.11% 3.12±2.45 19.52 65.08% Hypomat−CENC 2.22±1.63 11.16 83.10% 3.21±2.68 21.00 64.83% NLL−Hypomat 1.69±1.44 14.52 92.12% 2.72±2.72 16.41 75.59% 对比本研究的一维、三维重定位结果，NLL和Hypomat在水平、垂直方向上定位差的平均值分别为1.69 m和2.72 m，产生这些定位差的主要原因是NLL和Hypomat使用了不同的速度模型、定位方法。个别事件的观测台站数目很少，台站离震源较远且台站方位角GAP超过160°，此类事件的一维、三维重定位结果相差很大（＞12.5 km），重定位结果与CENC的定位差也超过12.5 km，说明地震台网的几何分布、可用震相的数量同时制约一维、三维重定位结果。
3.2 地震定位结果可靠性
3.2 地震定位结果可靠性
3.2.1 人工震源重定位
人工震源的激发时间和震源坐标是已知的，对人工震源进行重定位可以检验定位结果的绝对误差，但由于人工震源通常位于近地表，地震波射线容易受到近地表横向不均匀介质的影响，从而加大了人工震源重定位的难度，也使得在监测能力相同的前提下，人工震源定位误差会稍大于天然地震的定位误差（Husen et al，2003）。
为验证一维、三维定位方法和速度模型的准确性，本研究对中国地震局地球物理勘探中心于2012—2013年在腾冲及邻区激发的5个人工源地震事件进行了重定位（图7）。
![]()
图 7 人工震源的一维、三维重定位结果图（a）中右上角为人工震源重定位所用到的台站，图（b）为重定位结果在测线MN （图（a））上的投影Figure 7. The artificial sources （circles） relocated with 1D （squares） and 3D （stars） methods首先，人工拾取了喜马拉雅 Ⅰ 期密集台阵记录的P、S波震相到时，5次人工激发事件的震相到时（P波和S波）为22—44条，台站方位角GAP均小于180°。然后采用上述一维、三维定位方法对其进行定位工作。其中，位于台网西北侧的人工源属于网外地震，不参与重定位结果的评估。与其它4个网内实际人工震源相比，一维重定位在水平、垂直方向上的平均定位误差分别为1.4 km和4.3 km；三维重定位在水平、垂直方向上相应的误差均值分别为0.7 km和1.3 km。这进一步证实了三维定位结果较一维定位结果更准确。
一维、三维重定位结果显示，其中一个震源的最大深度误差分别高达9.8 km和4.9 km，其它震源的深度误差基本都小于5 km。深地震测深结果（潘素珍等，2015）表明跨越多个地质构造单元和重要断裂带的云南地区，其地下不同地质构造单元基底界面形态起伏变化剧烈，速度横向不均匀性明显。上地壳基底界面和速度的明显非均匀性在一定程度上会影响震源深度的测定，但这种较大的深度误差主要是由地震台站覆盖较差所致。
3.2.1 人工震源重定位
人工震源的激发时间和震源坐标是已知的，对人工震源进行重定位可以检验定位结果的绝对误差，但由于人工震源通常位于近地表，地震波射线容易受到近地表横向不均匀介质的影响，从而加大了人工震源重定位的难度，也使得在监测能力相同的前提下，人工震源定位误差会稍大于天然地震的定位误差（Husen et al，2003）。
为验证一维、三维定位方法和速度模型的准确性，本研究对中国地震局地球物理勘探中心于2012—2013年在腾冲及邻区激发的5个人工源地震事件进行了重定位（图7）。
![]()
图 7 人工震源的一维、三维重定位结果图（a）中右上角为人工震源重定位所用到的台站，图（b）为重定位结果在测线MN （图（a））上的投影Figure 7. The artificial sources （circles） relocated with 1D （squares） and 3D （stars） methods首先，人工拾取了喜马拉雅 Ⅰ 期密集台阵记录的P、S波震相到时，5次人工激发事件的震相到时（P波和S波）为22—44条，台站方位角GAP均小于180°。然后采用上述一维、三维定位方法对其进行定位工作。其中，位于台网西北侧的人工源属于网外地震，不参与重定位结果的评估。与其它4个网内实际人工震源相比，一维重定位在水平、垂直方向上的平均定位误差分别为1.4 km和4.3 km；三维重定位在水平、垂直方向上相应的误差均值分别为0.7 km和1.3 km。这进一步证实了三维定位结果较一维定位结果更准确。
一维、三维重定位结果显示，其中一个震源的最大深度误差分别高达9.8 km和4.9 km，其它震源的深度误差基本都小于5 km。深地震测深结果（潘素珍等，2015）表明跨越多个地质构造单元和重要断裂带的云南地区，其地下不同地质构造单元基底界面形态起伏变化剧烈，速度横向不均匀性明显。上地壳基底界面和速度的明显非均匀性在一定程度上会影响震源深度的测定，但这种较大的深度误差主要是由地震台站覆盖较差所致。
3.2.2 典型震例重定位
以2011年6月20日和8月9日发生在云南腾冲的MS5.2双震及其余震序列的震源参数为例，检验一维、三维定位深度的准确性。一维重定位得到的两次主震深度分别为10.2 km和13.8 km，余震深度分布在0—20 km之间（图8），比张广伟和雷建设（2015）利用双差定位得到的主震深度约深4.5 km。三维重定位得到的主震深度分别为7.1 km和8.1 km，余震序列的优势深度主要集中在2—12 km之间，与张广伟和雷建设（2015）采用双差定位法得到的主震、余震深度相一致。对比结果也体现了三维定位方法在求解震源深度时的准确性。
![]()
图 8 云南腾冲MS5.2双震及其余震序列在图5b中剖面AA-BB上的投影图中S波速度模型引自郑晨等（2016）Figure 8. The Tengchong MS5.2 double earthquakes and their aftershocks projected onto the cross section AA-BB of Fig. 5bS-wave velocity model refers from Zheng et al （2016）3.3 重定位震源深度分布
图9展示了一维、三维震源重定位深度。一维定位结果显示研究区地震多分布在20 km以浅。与之相比，三维定位结果给出的震源深度更浅，基本都集中在10 km以浅。三维重定位结果显示约72% （573次）的地震重定位深度小于10 km。在这573次浅源地震事件中，有212次震源集中分布在深度区间6.5—8.5 km。层析成像（Zhong et al，2000；Chen et al，2016）和地震测深（Zhang，Wang，2009）得到的结果表明滇西地区的岩石层结构为脆韧性的层架模式而非 “三明治” 式的岩石结构。结合本文的地震定位研究，可以认为腾冲火山区下方10 km以浅的上地壳是一个以脆性介质为主的薄皮构造，10 km以下的地壳部分含有一个高热流、低波速、低电阻率的软弱层，而9—10 km之间的区域是脆-韧性地壳过渡区。
![]()
图 9 重定位震源在各剖面（图5b）上的投影图中每次地震到剖面的垂直距离小于11 km，S波速度模型引自郑晨等（2016）Figure 9. Relocated earthquakes projected onto the cross-sections shown in Fig. 5bIn the fig. ，the distance of each earthquake from the section is smaller than 11 km，and the S-wave velocity model refers from Zheng et al （2016）天然地震、人工地震及大地电磁测深等研究表明，腾冲火山区下方中下地壳10—20 km深度范围内呈现出低速、高电导率和高泊松比等特征，被解释为壳内岩浆囊（楼海等，2002；Wang et al，2003；Lei et al，2009；胥颐等，2012；姜枚等，2016；于常青等，2017）。已有研究表明，脆性的中、上地壳部分更容易积累应力，腾冲火山区岩浆囊的存在可能对地震的发生起到了触发作用（叶建庆等，2003；张广伟，雷建设，2015）。本研究结果显示，三维重定位后震源主要集中于壳内低速层上方，分析认为腾冲地区的地震活动可能与火山下方的地壳岩浆活动密切相关，研究区的壳内低速层可能处于部分熔融或易于蠕变的状态，因此使其成为震源深度的下限。研究区震源深度的成簇分布现象可能与腾冲火山区地幔热物质上涌有关，地幔热物质的上涌导致地壳温度升高（胥颐等，2012），进而使得地壳介质强度降低。
4. 结论
本文利用云南腾冲火山区国家台、区域台、火山监测台网、流动台站记录的地震波形资料，使用基于参数优化的AICD自动拾取算法对这64个宽频带地震台站记录的波形数据开展了P、S波到时自动拾取，并通过拾取结果优化和质量评估对走时拾取质量进行了评估，结果表明该方法不仅能快速拾取走时，且具有较高的精度。
首先对高质量的到时数据进行反演得到了研究区最优一维速度模型，与已有一维速度模型（王椿镛等，2000；Huang et al，2012；高家乙等，2016）相比，该模型能更好地解释本研究拾取的地震到时；研究中还利用前述拾取到的地震到时数据，分别基于一维速度模型和三维速度模型开展了重定位研究。定位结果对比研究表明：三维重定位后平均走时残差比一维重定位后的平均走时残差减少了51.7%；一维、三维重定位结果在水平方向上相差不大，但在深度方向上，三维重定位结果整体较一维重定位结果更浅。本文通过对典型地震、人工震源开展的一维、三维重定位工作，验证了三维地震定位比一维定位更加精准、可靠。研究进一步显示，三维地震定位在水平、垂直方向上的平均绝对定位误差分别为0.7 km和1.3 km。
本文的三维定位结果显示，腾冲火山区震源成丛分布于10 km以浅的中上地壳，这与已有研究（Wang et al，2003；Lei et al，2009；楼海等，2002；胥颐等，2012；姜枚等，2016；于常青等，2017）所揭示的研究区10—20 km深度范围内存在岩浆囊的结论相符。
中国地震局地球物理研究所“中国地震科学探测台阵数据中心” （doi:10.12001/ChinArray.Data）、“国家测震台网数据备份中心”（doi:10.11998/SeisDmc/SN）为本研究提供了地震波形数据；中国地震局地球物理勘探中心潘素珍研究员提供了人工震源资料；中国地震局地球物理研究所牟磊育高级工程师提供了Hypomat定位软件；华中科技大学引力中心陈浩朋博士提供了云南地区断层数据；审稿专家为本文提出了宝贵的修改意见，作者在此一并表示感谢.
4. 结论
本文利用云南腾冲火山区国家台、区域台、火山监测台网、流动台站记录的地震波形资料，使用基于参数优化的AICD自动拾取算法对这64个宽频带地震台站记录的波形数据开展了P、S波到时自动拾取，并通过拾取结果优化和质量评估对走时拾取质量进行了评估，结果表明该方法不仅能快速拾取走时，且具有较高的精度。
首先对高质量的到时数据进行反演得到了研究区最优一维速度模型，与已有一维速度模型（王椿镛等，2000；Huang et al，2012；高家乙等，2016）相比，该模型能更好地解释本研究拾取的地震到时；研究中还利用前述拾取到的地震到时数据，分别基于一维速度模型和三维速度模型开展了重定位研究。定位结果对比研究表明：三维重定位后平均走时残差比一维重定位后的平均走时残差减少了51.7%；一维、三维重定位结果在水平方向上相差不大，但在深度方向上，三维重定位结果整体较一维重定位结果更浅。本文通过对典型地震、人工震源开展的一维、三维重定位工作，验证了三维地震定位比一维定位更加精准、可靠。研究进一步显示，三维地震定位在水平、垂直方向上的平均绝对定位误差分别为0.7 km和1.3 km。
本文的三维定位结果显示，腾冲火山区震源成丛分布于10 km以浅的中上地壳，这与已有研究（Wang et al，2003；Lei et al，2009；楼海等，2002；胥颐等，2012；姜枚等，2016；于常青等，2017）所揭示的研究区10—20 km深度范围内存在岩浆囊的结论相符。
中国地震局地球物理研究所“中国地震科学探测台阵数据中心” （doi:10.12001/ChinArray.Data）、“国家测震台网数据备份中心”（doi:10.11998/SeisDmc/SN）为本研究提供了地震波形数据；中国地震局地球物理勘探中心潘素珍研究员提供了人工震源资料；中国地震局地球物理研究所牟磊育高级工程师提供了Hypomat定位软件；华中科技大学引力中心陈浩朋博士提供了云南地区断层数据；审稿专家为本文提出了宝贵的修改意见，作者在此一并表示感谢.
-
![]()
图 5 腾冲火山区799次地震的的一维（a）和三维（b）重定位结果
Figure 5. 1D Hypomat （a） and 3D NonLinLoc （b） relocations of 799 events located in Tengchong
![]()
图 1 云南地区断裂分布（修改自马丽芳等，2002）
F1：怒江断裂；F2：澜沧江断裂；F3：红河断裂；F4：金沙江断裂；F5：哀牢山断裂；F6：小金河断裂；F7：小江断裂；F8：弥勒断裂；F9：则木河断裂；F10：绿汁江断裂；F11：楚雄—通海断裂
Figure 1. The distribution of faults in Yunnan area （after Ma et al，2002）
F1：Nujiang fault；F2：Lancangjiang fault；F3：Honghe fault；F4：Jinshajiang fault；F5：Ailaoshan fault；F6：Xiaojinhe fault；F7：Xiaojiang fault；F8：Mile fault；F9：Zemuhe fault；F10：Lüzhijiang fault；F11：Chuxiong-Tonghai fault
![]()
图 2 研究区台站和中国地震编目系统提供的地震震中分布
Figure 2. Distributions of seismic stations and epicenters provided by the unified national cataloging system
![]()
图 3 一维速度模型和地震定位结果
（a） P波和S波初始速度模型；（b） P波和S波最优一维速度模型，其中HJ1，WCY1 和GJY1基于图（a）中的初始模型得到，HJ1，WCY1 和GJY1的平均值为平均一维模型，基于平均一维模型得到最终最优速度模型；（c） 本文 一维定位使用的最终最优速度模型和基于该模型反演得到的震源深度分布图
Figure 3. The P-wave and S-wave velocity models and relocating results
（a） Initial P-wave and S-wave velocity structures；（b） The best P-wave and S-wave velocity models obtained from the VELEST inversion based on different initial models shown in Fig. （a）；（c） The final minimum 1D P-wave and S-wave velocity models used to 1D location and histogram of the events distributionin depth obtained by VELEST inversion based on the final minimum model，where the final minimum 1D P-wave and S-wave velocity models are obtained based on the average of three velocity models resulting from three different initial velocity models
![]()
图 4 VELEST定位稳定性试验
黑色圆点为地震事件在纬度（a）、经度（b）、深度（c）上的随机扰动量，红色圆点为定位恢复试验后震源坐标的误差
Figure 4. Test of VELEST location stability
Black dots represent the amount of shift along latitude （a），longitude （b） and depth （c） with respect to the reference locations，the inversion is then repeated，and the retrieved location shifts are shown as red dots
![]()
图 6 一维（a）和三维（b）重定位走时残差统计图
Figure 6. Histograms of travel-time residual for 1D Hypomat （a） and 3D NonLinLoc （b） relocations
![]()
图 7 人工震源的一维、三维重定位结果
图（a）中右上角为人工震源重定位所用到的台站，图（b）为重定位结果在测线MN （图（a））上的投影
Figure 7. The artificial sources （circles） relocated with 1D （squares） and 3D （stars） methods
The inset of Fig. （a） marks the seismic station distribution used to relocations，Fig. （b） shows relo-cations projected onto the cross section MN in Fig. （a）
![]()
图 8 云南腾冲MS5.2双震及其余震序列在图5b中剖面AA-BB上的投影
图中S波速度模型引自郑晨等（2016）
Figure 8. The Tengchong MS5.2 double earthquakes and their aftershocks projected onto the cross section AA-BB of Fig. 5b
S-wave velocity model refers from Zheng et al （2016）
![]()
图 9 重定位震源在各剖面（图5b）上的投影
图中每次地震到剖面的垂直距离小于11 km，S波速度模型引自郑晨等（2016）
Figure 9. Relocated earthquakes projected onto the cross-sections shown in Fig. 5b
In the fig. ，the distance of each earthquake from the section is smaller than 11 km，and the S-wave velocity model refers from Zheng et al （2016）
表 1 本文所得799次地震事件的一维、三维重定位结果与中国地震台网中心（CENC）定位结果的比较
Table 1 Relative comparison of the 799 epicentre locations calculated by either this study or the CENC
定位差 水平向定位差
平均值/km水平向定位差
最大值/km水平向定位差≤
3.5 km事件占比垂直向定位差
平均值/km垂直向定位差
最大值/km垂直向定位差≤
3.5 km事件占比NLL−CENC 2.31±1.64 12.96 85.11% 3.12±2.45 19.52 65.08% Hypomat−CENC 2.22±1.63 11.16 83.10% 3.21±2.68 21.00 64.83% NLL−Hypomat 1.69±1.44 14.52 92.12% 2.72±2.72 16.41 75.59% 
下载: 导出CSV
-
陈立华,宋仲和,安昌强,陈国英,庄真,傅竹武,胡家富,吕梓龄. 1992. 中国南北带地壳上地幔三维面波速度结构和各向异性[J]. 地球物理学报,35(5):574–583. doi: 10.3321/j.issn:0001-5733.1992.05.005 Chen L H,Song Z H,An C Q,Chen G Y,Zhuang Z,Fu Z W,Hu J F,Lü Z L. 1992. Three dimensional shear wave velocity and anisotropy of crust and upper mantle in the China north-south earthquake belt[J]. Acta Geophysica Sinica,35(5):574–583 (in Chinese).
高家乙,李永华,徐小明,张风雪. 2016. 云南地区地壳速度结构和地震活动性研究[J]. 地球物理学进展,31(2):508–516. doi: 10.6038/pg20160202 Gao J Y,Li Y H,Xu X M,Zhang F X. 2016. P-wave crustal velocity structure and seismicity in Yunnan area[J]. Progress in Geophysics,31(2):508–516 (in Chinese). doi: 10.6038/pg20160202
国家测震台网数据备份中心. 2007. 国家测震台网地震波形数据[DB/OL]. [2018−12−10]. 中国地震局地球物理研究所. doi: 10.11998/SeisDmc/SN. Data Management Centre of China National Seismic Network. 2007. Waveform data of China National Seismic Network[DB/OL]. [2018−12−10]. Institute of Geophysics, China Earthquake Administration. doi:10.11998/SeisDmc/SN （in Chinese）.
姜枚,谭捍东,彭淼,钱荣毅,张聿文,李庆庆,张立树,许乐红,郭帅. 2016. 腾冲火山构造区马站岩浆囊地球物理特征的再探讨[J]. 中国地质,43(5):1688–1696. Jiang M,Tan H D,Peng M,Qian R Y,Zhang Y W,Li Q Q,Zhang L S,Xu L H,Guo S. 2016. A further discussion on geophysical characteristics of Mazhan magma pocket in Tengchong volcano-tectonic zone[J]. Geology in China,43(5):1688–1696 (in Chinese).
阚荣举, 赵晋明. 1994. 腾冲火山地区的壳幔构造[G]//中国固体地球物理学进展. 北京: 海洋出版社: 23−30. Kan R J, Zhao J M. 1994. The crust-mantle structure of Tengchong volcanic area[G]//Chinese Solid Geophysics Progress. Beijing: Ocean Press: 23−30 （in Chinese）.
刘劲松,王赟,姚振兴. 2013. 微地震信号到时自动拾取方法[J]. 地球物理学报,56(5):1660–1666. doi: 10.6038/cjg20130523 Liu J S,Wang Y,Yao Z X. 2013. On micro-seismic first arrival identification:A case study[J]. Chinese Journal of Geophysics,56(5):1660–1666 (in Chinese). doi: 10.6038/cjg20130523
楼海,王椿镛,皇甫岗,秦嘉政. 2002. 云南腾冲火山区上部地壳三维地震速度层析成像[J]. 地震学报,24(3):243–251. doi: 10.3321/j.issn:0253-3782.2002.03.003 Lou H,Wang C Y,Huangfu G,Qin J Z. 2002. Three-demensional seismic velocity tomography of the upper crust in Tengchong volcanic area,Yunnan Province[J]. Acta Seismologica Sinica,24(3):243–251 (in Chinese).
马丽芳, 乔秀夫, 闵隆瑞, 范本闲, 丁孝忠. 2002. 中国地质图集[M]. 北京: 地质出版社: 293−300. Ma L F, Qiao X F, Min L R, Fan B X, Ding X Z. 2002. Geological Atlas of China[M]. Beijing: Geological Publishing House: 293−300 （in Chinese）.
牟磊育,赵仲和,张伟,王占英,马市振,徐晟涛,白永福. 2006. 用INGLADA与GEIGER方法实现近震精定位[J]. 中国地震,22(3):294–302. doi: 10.3969/j.issn.1001-4683.2006.03.010 Mu L Y,Zhao Z H,Zhang W,Wang Z Y,Ma S Z,Xu S T,Bai Y F. 2006. Using the INGLADA and GEIGER method to realize regional earthquake location accurately[J]. Earthquake Research in China,22(3):294–302 (in Chinese).
潘佳铁,李永华,吴庆举,丁志峰. 2015. 青藏高原东南部地区瑞雷波相速度层析成像[J]. 地球物理学报,58(11):3993–4006. doi: 10.6038/cjg20151109 Pan J T,Li Y H,Wu Q J,Ding Z F. 2015. Phase velocity maps of Rayleigh waves in the southeast Tibetan Plateau[J]. Chinese Journal of Geophysics,58(11):3993–4006 (in Chinese). doi: 10.6038/cjg20151109
潘素珍,王夫运,段永红,邓晓果,宋向辉,段玉玲,孙一男,张彩军,杨宇东,臧怡然. 2015. 滇南及临近地区基底结构:镇康—泸西深地震测深剖面结果[J]. 地球物理学报,58(11):3917–3927. doi: 10.6038/cjg20151103 Pan S Z,Wang F Y,Duan Y H,Deng X G,Song X H,Duan Y L,Sun Y N,Zhang C J,Yang Y D,Zang Y R. 2015. Basement structure of southern Yunnan and adjacent areas:The Zhenkang-Luxi deep seismic sounding profile[J]. Chinese Journal of Geophysics,58(11):3917–3927 (in Chinese). doi: 10.6038/cjg20151103
王椿镛,皇甫岗,万登堡,刘祖荫,秦嘉政,楼海,吴建平. 2000. 腾冲火山区地壳结构的人工地震探测[J]. 地震研究,23(2):148–156. doi: 10.3969/j.issn.1000-0666.2000.02.009 Wang C Y,Huangfu G,Wan D B,Liu Z Y,Qin J Z,Lou H,Wu J P. 2000. Deep seismic sounding of crustal structure in Tengchong volcanic area[J]. Journal of Seismological Research,23(2):148–156 (in Chinese).
王夫运,潘素珍,刘兰,刘宝峰,张建狮,邓晓果,马策军,张彩军. 2014. 玉溪—临沧剖面宽角地震探测:红河断裂带及滇南地壳结构研究[J]. 地球物理学报,57(10):3247–3258. doi: 10.6038/cjg20141013 Wang F Y,Pan S Z,Liu L,Liu B F,Zhang J S,Deng X G,Ma C J,Zhang C J. 2014. Wide angle seismic exploration of Yuxi-Lincang profile:The research of crustal structure of the Red River fault zone and southern Yunnan[J]. Chinese Journal of Geophysics,57(10):3247–3258 (in Chinese). doi: 10.6038/cjg20141013
胥颐,钟大赉,刘建华. 2012. 滇西地区壳幔解耦与腾冲火山区岩浆活动的深部构造研究[J]. 地球物理学进展,27(3):846–855. doi: 10.6038/j.issn.1004-2903.2012.03.003 Xu Y,Zhong D L,Liu J H. 2012. Constraints of deep structures on the crust-mantle decoupling in the western Yunnan and the magma activity in the Tengchong volcanic area[J]. Process in Geophysics,27(3):846–855 (in Chinese). doi: 10.6038/j.issn.1004-2903.2012.03.003
杨旭,李永华,苏伟,孙莲. 2019. 基于优化参数的地震P、S波震相到时自动拾取及质量评估[J]. 地球物理学报,62(11):4290–4299. doi: 10.6038/cjg2019M0059 Yang X,Li Y H,Su W,Sun L. 2019. Optimized automatic pickers and quality assessment:Application to identification of local and regional P and S wave phases[J]. Chinese Journal of Geophysics,62(11):4290–4299 (in Chinese). doi: 10.6038/cjg2019M0059
杨晓涛,胥颐,刘建华,李志伟. 2011. 腾冲火山区的地震层析成像及其构造意义[J]. 地球物理学报,54(8):2050–2059. doi: 10.3969/j.issn.0001-5733.2011.08.012 Yang X T,Xu Y,Liu J H,Li Z W. 2011. Seismic tomography in the Tengchong volcanic area and its tectonic implication[J]. Chinese Journal of Geophysics,54(8):2050–2059 (in Chinese). doi: 10.3969/j.issn.0001-5733.2011.08.012
叶建庆,蔡绍平,刘学军,王绍晋,蔡明军. 2003. 腾冲火山地震群的活动特征[J]. 地震地质,25(增刊1):128–137. Ye J Q,Cai S P,Liu X J,Wang S J,Cai M J. 2003. Characteristics of earthquake cluster activity in Tengchong volcanic area[J]. Seismology and Geology,25(S1):128–137 (in Chinese).
于常青,张刚,王绪本,罗威,李德伟,蔡学林,郭紫明. 2017. 滇西三江地区深部电性结构特征及其意义[J]. 地球物理学报,60(6):2385–2396. doi: 10.6038/cjg20170628 Yu C Q,Zhang G,Wang X B,Luo W,Li D W,Cai X L,Guo Z M. 2017. Deep electrical resistivity structure of Sanjiang area of west Yunnan and its significance[J]. Chinese Journal of Geophysics,60(6):2385–2396 (in Chinese). doi: 10.6038/cjg20170628
张广伟,雷建设. 2015. 2011年云南腾冲5.2级双震发震机理[J]. 地球物理学报,58(4):1194–1204. doi: 10.6038/cjg20150409 Zhang G W,Lei J S. 2015. Mechanism of the 2011 Tengchong,Yunnan,MS5.2 double earthquakes[J]. Chinese Journal of Geophysics,58(4):1194–1204 (in Chinese). doi: 10.6038/cjg20150409
郑晨,丁志峰,宋晓东. 2016. 利用面波频散与接收函数联合反演青藏高原东南缘地壳上地幔速度结构[J]. 地球物理学报,59(9):3223–3236. doi: 10.6038/cjg20160908 Zheng C,Ding Z F,Song X D. 2016. Joint inversion of surface wave dispersion and receiver functions for crustal and uppermost mantle structure in southeast Tibetan Plateau[J]. Chinese Journal of Geophysics,59(9):3233–3236 (in Chinese). doi: 10.6038/cjg20160908
郑秀芬,欧阳飚,张东宁,姚志祥,梁建宏,郑洁. 2009. “国家数字测震台网数据备份中心”技术系统建设及其对汶川大地震研究的数据支撑[J]. 地球物理学报,52(5):1412–1417. doi: 10.3969/j.issn.0001-5733.2009.05.031 Zheng X F,Ouyang B,Zhang D N,Yao Z X,Liang J H,Zheng J. 2009. Technical system construction of Data Backup Centre for China Seismograph Network and the data support to researches on the Wenchuan earthquake[J]. Chinese Journal of Geophysics,52(5):1412–1417 (in Chinese). doi: 10.3969/j.issn.0001-5733.2009.05.031
中国地震科学台阵. 2006. 中国地震科学探测台阵波形数据[DB/OL]. [2018-12-11]. 中国地震局. doi: 10.12001/ChinArray.Data. ChinArray. 2006. China Seismic Array waveform data[DB/OL]. [2018-12-10]. China Earthquake Administration. doi: 10.12001/China Array.Data （in Chinese）.
中国地震台网中心. 2019. 中国地震台网统一地震编目工作系统[EB/OL]. [2019-01-10]. http://10.5.160.18/console/index.action. China Earthquake Networks Center. 2019. Unified earthquake cataloging work system of the China Seismographic Network[EB/OL]. [2019-01-10]. http://10.5.160.18/console/index.action （in Chinese）. Béthoux N,Theunissen T,Beslier M O,Font Y,Thouvenot F,Dessa J X,Simon S,Courrioux G,Guillen A. 2016. Earthquake relocation using a 3D a-priori geological velocity model from the western Alps to Corsica:Implication for seismic hazard[J]. Tectonophysics,670:82–100. doi: 10.1016/j.tecto.2015.12.016
Brocher T M. 2005. Empirical relations between elastic wavespeeds and density in the Earth’s crust[J]. Bull Seismol Soc Am,95(6):2081–2092. doi: 10.1785/0120050077
Chen H P,Zhu L B,Su Y J. 2016. Low velocity crustal flow and crust-mantle coupling mechanism in Yunnan,SE Tibet,revealed by 3D S-wave velocity and azimuthal anisotropy[J]. Tectonophysics,685:8–20. doi: 10.1016/j.tecto.2016.07.007
Hausmann H,Hoyer S,Schurr B,Brückl E,Houseman G,Stuart G. 2010. New seismic data improve earthquake location in the Vienna basin area,Austria[J]. Austr J Earth Sci,103(2):2–14.
He X H,Ni S D,Liu J. 2015. Rupture directivity of the August 3rd,2014 Ludian earthquake (Yunan,China)[J]. Science China Earth Sciences,58(5):795–804. doi: 10.1007/s11430-015-5053-2
Huang J,Liu X J,Su Y J,Wang B S. 2012. Imaging 3-D crustal P-wave velocity structure of western Yunnan with bulletin data[J]. Earthquake Science,25(2):151–160. doi: 10.1007/s11589-012-0842-6
Husen S,Kissling E,Deichmann N,Wiemer S,Giardini D,Baer M. 2003. Probabilistic earthquake location in complex three-dimensional velocity models:Application to Switzerland[J]. J Geophys Res,108(B2):2077–2096. doi: 10.1029/2002JB001778
Kissling E,Ellsworth W L,Eberhart-Phillips D,Kradolfer U. 1994. Initial reference models in local earthquake tomography[J]. J Geophys Res,99(B10):19635–19646. doi: 10.1029/93JB03138
Le Meur H. 1994. Tomographie Tridimensionnelle A Partir Des Temps Des Premières Arrivées des Ondes P et S, Application a la Région de Patras （Grece）[D]. Paris: University Paris VII （in French）.
Le Meur H,Virieux J,Podvin P. 1997. Seismic tomography of the gulf of Corinth:A comparison of methods[J]. Ann Geofis,60(1):1–24.
Lei J S,Zhao D P,Su Y J. 2009. Insight into the origin of the Tengchong intraplate volcano and seismotectonics in southwest China from local and teleseismic data[J]. J Geophys Res,114(B5):B05302. doi: 10.1029/2008JB005881
Li Y H,Wu Q J,Zhang R Q,Tian X B,Zeng R S. 2008. The crust and upper mantle structure beneath Yunnan from joint inversion of receiver functions and Rayleigh wave dispersion data[J]. Phys Earth Planet Int,170(1/2):134–146.
Li Y H,Gao M T,Wu Q J. 2014a. Crustal thickness map of the Chinese mainland from teleseismic receiver functions[J]. Tectonophysics,611:51–60. doi: 10.1016/j.tecto.2013.11.019
Li Y H,Pan J T,Wu Q J,Ding Z F. 2014b. Crustal and uppermost mantle structure of SE Tibetan Plateau from Rayleigh-wave group-velocity measurements[J]. Earthquake Science,27(4):411–419. doi: 10.1007/s11589-014-0090-z
Lomax A, Virieux J, Volant P, Berge-Thierry C. 2000. Probabilistic earthquake location in 3D and layered models[G]//Advances in Seismic Event Location. Dordrecht: Springer: 101−134.
Lomax A,Curtis A. 2001. Fast,probabilistic earthquake location in 3D models using Oct-Tree importance sampling[J]. Geophys Res Abstr,3:955.
Lomax A,Zollo A,Capuano P,Virieux J. 2001. Precise,absolute earthquake location under Somma-Vesuvius volcano using a new three-dimensional velocity model[J]. Geophys J Int,146(2):313–331. doi: 10.1046/j.0956-540x.2001.01444.x
Podvin P,Lecomte I. 1991. Finite difference computation of traveltimes in very contrasted velocity models:A massively parallel approach and its associated tools[J]. Geophys J Int,105(1):271–284. doi: 10.1111/j.1365-246X.1991.tb03461.x
Socquet A,Pubellier M. 2005. Cenozoic deformation in western Yunnan (China-Myanmar border)[J]. J Asian Earth Sci,24(4):495–515. doi: 10.1016/j.jseaes.2004.03.006
Tarantola A,Valette B. 1982. Inverse problems = quest for information[J]. J Geophys,50(1):159–170.
Tarantola A. 1987. Inverse Problem Theory: Methods for Data Fitting and Model Parameter Estimation[M]. Amsterdam: Elsevier Publishing Company.
Wang C Y,Chan W W,Mooney W D. 2003. Three-dimensional velocity structure of crust and upper mantle in southwestern China and its tectonic implications[J]. J Geophys Res,108(B9):2442. doi: 10.1029/2002JB001973
Wang Y,Zhang X M,Jiang C S,Wei H Q,Wan J L. 2007. Tectonic controls on the Late Miocene-Holocence volcanic eruptions of the Tengchong volcanic field along the southeastern margin of the Tibetan Plateau[J]. J Asian Earth Sci,30(2):375–389. doi: 10.1016/j.jseaes.2006.11.005
Wittlinger G,Herquel G,Nakache T. 1993. Earthquake location in strongly heterogeneous media[J]. Geophys J Int,115(3):759–777. doi: 10.1111/j.1365-246X.1993.tb01491.x
Xie Z J,Zheng Y,Liu C L,Xiong X,Li Y D,Zheng X F. 2015. Source parameters of the 2014 MS6.5 Ludian earthquake sequence and their implications on the seismogenic structure[J]. Seismol Res Lett,86(6):1614–1621. doi: 10.1785/0220150085
Xu Y,Yang X T,Li Z W,Liu J H. 2012. Seismic structure of the Tengchong volcanic area southwest China from local earthquake tomography[J]. J Volcanol Geotherm Res,239/240:83–91. doi: 10.1016/j.jvolgeores.2012.06.017
Zhang X,Wang Y H. 2009. Crustal and upper mantle velocity structure in Yunnan,Southwest China[J]. Tectonophysics,471(3/4):171–185.
Zhong D L,Ding L,Liu F T,Liu J H,Zhang J J,Ji J Q,Chen H. 2000. Multi-oriented and layered structures of lithosphere in orogenic belt and their effects on Cenozoic magmatism:A case study of western Yunnan and Sichuan,China[J]. Science in China:Series D,43(S1):122–133. doi: 10.1007/BF02911938
-
期刊类型引用(3)
1. 闫小兵，梁瑞平，王伟君，郝雪景. 地脉动在系舟山北麓断裂次级断裂探测中的应用. 地震工程学报. 2023(02): 421-430 . 
百度学术
2. 李彩华，滕云田，周健超，胡星星，王喜珍，李小军，王玉石. 分布式地震数据采集器的高精度时间同步系统研制. 地震学报. 2022(06): 1111-1120 . 本站查看
3. 鲁兵，陈以伦. 基于GPS观测同震位移场的汶川地震矩震级计算. 兰州文理学院学报(自然科学版). 2020(01): 41-44 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 3683
- HTML全文浏览量: 1070
- PDF下载量: 190
- 被引次数: 3
