A new deep neural network for phase picking with balanced speed and accuracy
-
摘要: 深度神经网络虽然在震相拾取中取得了良好效果，但作为高复杂度的机器学习模型，深度神经网络在取得较高精度的同时需要付出较高的计算代价，而且试验研究表明震相拾取中并不需要过高的模型复杂度。为此，本文根据地震波形的特点设计了四种具有不同复杂度的深度神经网络改进模型，可以综合具体的精度和速度需求从中选取合适的模型。在此基础上，将改进模型与现有四种到时拾取的深度学习网络模型进行了对比，结果表明本文中的网络模型在到时拾取上具有较高的速度和精度。同时，本文的深度神经网络通过使用多种深度学习模型压缩手段可将震相拾取模型的大小压缩到2.0 MB以内，从而使得模型可以在低功耗设备上完成高速震相拾取的同时尽可能地减少精度损失。Abstract: The deep neural network （DNN） has achieved good results in phase picking. As a high complexity machine learning model, DNN suffers from high computational cost to achieve high accuracy. The experimental results show that there is no need to build a high complexity model for phase picking. So, we designed four network models with different complexity to improve speed and accuracy of phase picking based on characteristics of seismic waveforms, which offers a choice of accuracy and/or speed of the phase picking. And then we compared our results with those obtained from four existing DNN models, and verified the relative high speed and accuracy. More importantly, the DNN models can be compressed to within 2.0 MB after a variety of model compression methods, which allows the structure to perform high-speed phase picking with relatively high accuracy on low-power-consumption devices.
-
引言
随着深度神经网络的发展，越来越多的机器学习任务可以在深度学习算法框架内完成。深度学习模型由于具有较高的模型复杂度，可以完成多种类型的数据处理与分析任务。在地震震相拾取工作中使用深度神经网络算法可以直接以原始的三分量数据作为模型输入，这简化了震相拾取的数据预处理难度，并且可以对震相进行自动化拾取。现有可以用于震相拾取的深度神经网络结构包括全连接网络（fully connected network，缩写为FCN）、卷积神经网络（convolutional neural network，缩写为CNN）和循环神经网络（recurrent neural network，缩写为RNN）。
由多层全连接网络搭建的多层感知器（multi-layer perceptron，缩写为MLP）是最早用于震相拾取的神经网络模型。多层感知器模型缺乏信号处理结构，在不对波形进行预处理的情况下难以取得良好结果。Zhao和Takano （1999）设计的多级全连接网络可以拾取不同尺度震相的特征，该网络带有卷积神经网络的特点，在美国地震学研究联合会（Incorporated Research Institutions for Seismology，缩写为IRIS）数据中可以拾取95%的初至。卷积神经网络是波形处理的结构，因此可以简化使用卷积神经网络提取波形到时的过程。之后发展了一些融合卷积神经网络与全连接网络的算法（García et al，2016；于子叶等，2018；Ross et al，2018），Ross等（2018）对原始波形进行处理的分类精度高达95%。此外，使用卷积反卷积结构所搭建的编码解码模型（Zhu，Beroza，2018；赵明等，2019；Hu et al，2019）可实现点到点的输出，从而使到时提取精度得以提升。震相拾取工作中的编码解码模型使用了自稀疏编码器的结构，这使得编码解码模型对于噪声的鲁棒性更强。编码解码模型来源于图像分割领域所用的U形网络（U-Net）（Ronneberger et al，2015）。循环神经网络是为解决自然语言处理中的前后文问题而设计（Schuster，Paliwal，1997）。前后文指的是在分析某个字符的过程中综合考虑前后字符的信息。这与震相拾取相类似，在进行震相拾取的过程中需要综合其它震相进行判断，因此在处理原始信号的模型中可以使用融合卷积神经网络与循环神经网络的模型。一些研究人员使用了双向RNN单元来综合前后震相的信息进行拾取，这种融合结构在处理波形数据时与纯卷积神经网络模型的区别在于，卷积神经网络的感受野是有限的，而循环神经网络的感受野可以近似无限，因此可以处理更长时间的依赖，即可以综合更多的震相信息。Zhou等（2019）使用门控循环网络单元（gated recurrent unit，缩写为GRU），Cho等（2014）搭建了深度神经网络模型，其拾取P波和S波的精度分别达到（−0.03±0.48） s和（0.03±0.56） s。因此，双向循环神经网络结构解决了浅层CNN感受野不足的问题，因而在提取P和S等震相到时过程中可以兼顾其它震相。
现有的深度学习模型使用不同神经网络结构，在多种地震震相拾取过程中均取得了良好的效果，但现有震相拾取神经网络的设计大多源自于图像、文本处理中的深度学习模型。因此在网络构建中并未充分考虑地震波形尺度等问题，这导致了网络深度过深、关系依赖不完整等问题。与此同时，模型设计过程中也并未考虑计算速度的因素，这导致模型复杂度过高（Hinton et al，2015；Howard et al，2017；Sandler et al，2018），仅能在高性能计算设备上完成波形拾取，较高的模型复杂度限制了深度学习模型在震相拾取中的应用。
鉴于此，本文综合考虑模型的合理性、精度和速度，拟设计可用于不同场景的深度神经网络模型。在这些模型构建过程中综合考虑地震波形的特点，形成适用于不同精度场景的四个深度学习模型，并使用深度可分离卷积（Howard et al，2017）进行模型压缩，最终模型可以压缩至2.0 MB以内，使得模型可以在低功耗、低内存设备上以较快速度进行震相拾取。
1. 深度神经网络基本结构
在早期的神经网络结构设计中，研究人员一般将其作为仿生学模型（van der Baan，Jutten，2000），例如将神经网络看作神经细胞的突触和轴突。但以现代的神经网络模型来看，这种思路并不合理。模仿神经元的行为需要更加复杂的系统，这是以脉冲神经网络为代表的第三代神经网络所研究的内容（Maass，1997），目前还无法用于到时拾取之中。而深度神经网络可以对信号、文本直接进行处理是因为其结构中包含信号、文本处理的结构，即卷积神经网络和循环神经网络。因此用于震相拾取的深度学习算法更加接近信号处理算法。
现代的深度神经网络包含三种基本结构：全连接层、卷积网络层、循环网络层。全连接网络所构建的多层感知器（Rumelhart et al，1986）是最早的传统机器学习模型之一。由LeCun等（1998）提出的卷积神经网络则是信号处理的延伸。循环神经网络结构可以用于自然语言处理，由于其可以解决较长时间依赖问题，因此可以用于波形到时拾取中。本文将测试多种深度神经网络结构用于确定兼顾精度和速度的网络，在设计过程中主要考虑使用卷积神经网络和循环神经网络。
1.1 卷积神经网络
在震相拾取工作中卷积神经网络用于构建波形特征，其本质是滑动互相关算法，即：
$ \begin{array}{l} {{{h}}_{{t_2},{C_2}}} {\text{＝}} \displaystyle \mathop \sum \limits_{{k_1} {\text{＝}} 1}^K \displaystyle \mathop \sum \limits_{{c_{\rm{}}} {\text{＝}} 1}^{{C_1}} {{{x}}_{{t_1} {\text{＋}} {k_1},c}}{{{w}}_{{k_1},c,{C_2}}}{\text{＋}}{{{b}}_{{C_2}}}{\text{，}}{{t_1} {\text{＝}} {{t_2}S}{\text{，}} }\\ {}\left\{ {\begin{aligned} &{{T_2} {\text{＝}}\left[\dfrac{{{T_1} {\text{－}}K {\text{＋}} 1}}{S}\right]}\quad{\text{“}}\!\!{\text{补齐}}{\text{”}}\!\!\!{\text{，}}\\ &{{T_2} {\text{＝}} \left[\dfrac{{{T_1}}}{S}\right]} \qquad\qquad\;{\text{“}}\!{\text{不补齐}}{\text{”}}\!\!\!{\text{，}} \end{aligned}} \right. \end{array}$
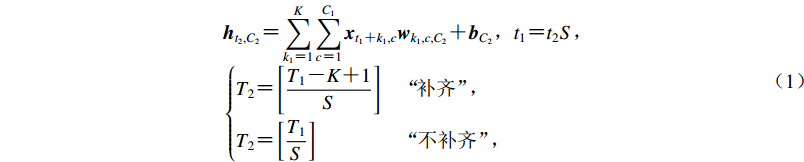
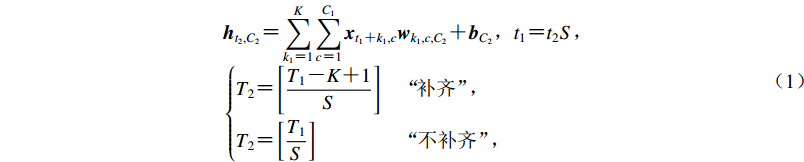
(1) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ \begin{array}{l} {{{h}}_{{t_2},{C_2}}} {\text{＝}} \displaystyle \mathop \sum \limits_{{k_1} {\text{＝}} 1}^K \displaystyle \mathop \sum \limits_{c {\text{＝}} 1}^{{C_1}} {{{x}}_{{t_1} {\text{＋}} {k_1} d,c}}{{{w}}_{{k_1},c,{C_2}}} {\text{＋}} {{{b}}_{{C_2}}}{\text{，}}{{t_1} {\text{＝}} \left[ {{t_2}S} \right] {\text{，}}}\\ \begin{array}{*{20}{c}} {\left\{ {\begin{aligned} &{{T_2} {\text{＝}} \left[ {\dfrac{{{T_1} {\text{－}} K {\text{＋}} 1}}{S}} \right]}\quad{\text{“}} {\text{补齐}} {\text{”}} \!\!\!{\text{，}}\\ &{{T_2} {\text{＝}} \left[ {\dfrac{{{T_1}}}{S}} \right]}\qquad\qquad\; {\text{“}} {\text{不补齐}} {\text{”}} \!\!\!{\text{，}} \end{aligned}} \right.} \end{array} \end{array}$
(2) 式中d为扩张率，其它参数与式（1）含义相同。与传统卷积、池化降采样不同，转置卷积是对图像进行上采样后再对上采样后的图像进行普通卷积，转置卷积会使得特征图变大，可以用于构建编码解码网络结构实现点到点的输出任务。
1.2 循环神经网络
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ p\!\!\!\!{\text{（}}{{{h}}_t}|{{{x}}_t}{\text{，}}\!\!\! \cdots{\text{，}}\!\!\!{{{x}}_2}{\text{，}} \ \!\!\!\!\!\!{{{x}}_1}\!{\text{）}}\xrightarrow{{\text{马尔可夫随机过程}}}p\!\!\!{\text{（}}\!{{{h}}_t}|{{{x}}_t}{\text{，}}\!\!\!{{{h}}_{t {\text{－}}1}}\!{\text{）}}\!\!\!\!{\text{.}} $
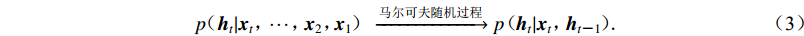
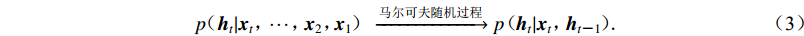
(3) 由于向量ht−1携带有ht−1，xt−1的信息，由此模型中某个时间的输出ht携带有所有输入{x1，x2，···，xt}的信息。本文使用循环神经网络的改进形式GRU （Cho et al，2014）作为基本的计算单元，GRU是LSTM （Hochreiter，Schmidhuber，1997）的改进结构，其计算方式为
$ \begin{split} {\hat {{x}} {\text{＝}} {\rm{concat}}\!\!\!\!{\text{（}}\!{{{{x}}_t}{\text{，}}\!\!\!{{{h}}_{t{\text{－}}1}}} \!{\text{）}}\!\!\!\!{\text{，}}\!\!\!} {{{{g}}_1} {\text{＝}} \sigma \!\!\!\!{\text{（}}\!{\hat {{x}} \cdot {{{w}}^1} {\text{＋}} {{{b}}^1}} \!{\text{）}}\!\!\!\!{\text{，}}\!\!\!} {{{{g}}_2} {\text{＝}} \sigma \!\!\!\!{\text{（}}\!{\hat {{x}} \cdot {{{w}}^2} {\text{＋}} {{{b}}^2}} \!{\text{）}}\!\!\!\!{\text{，}}\!\!\!} {{{c}} {\text{＝}} {{{h}}_{t{\text{－}}1}} \odot {{{g}}_1}{\text{，}}\!\!\!}\\ {\begin{array}{*{20}{c}} {\hat {{h}} {\text{＝}} \tanh [\!{{\rm{concat}}\!\!\!\!{\text{（}}\!{{{{x}}_t}{\text{，}}\!\!\!{{c}}} \!{\text{）}}\!\!\!\! \cdot {{{w}}^3} {\text{＋}} {{{b}}^3}}]\!{\text{，}}\!\!\!} {{{{h}}_t} {\text{＝}} \!\!\!\!{\text{（}}\!{1{\text{－}}{{{g}}_2}} \!{\text{）}}\!\!\!\! \odot {{{h}}_{{{t}}{\text{－}}1}} {\text{＋}} {{{g}}_2} \odot \hat {{h}}{\text{，}}\!\!\!} \end{array}} \end{split} $
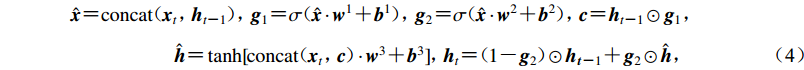
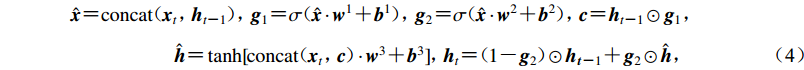
(4) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
1.3 批正则化层
在深度神经网络设计中，正则化被广泛地使用，从而避免网络训练过程中出现梯度消失问题。其中重要的正则化方式即为批正则化（batch normalization，缩写为BN）（Ioffe，Szegedy，2015）。批正则化改善了深度学习模型中的梯度消失问题，并可以避免过拟合提升网络精度。批正则化层对每层的输出均进行了归一化，其计算式为
$ {{{h}}} {\text{＝}} {{\gamma}} \frac{{{{x}}{\text{－}}{\overline{{ x}}}}}{{\sqrt {{\rm{var}}\!\!\!\!{\text{（}}\!{{x}} \!{\text{）}}\!\!\!\!} }} {\text{＋}} {{\beta}}{\text{，}} $
(5) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
2. 用于震相拾取的深度学习模型
2.1 到时拾取网络的设计与改进
一般认为地震波形的特征尺度较大，即完整波形具有较多采样点。人脸检测中典型的特征尺度为24×24 （Zhang et al，2016），因此在搭建卷积神经网络中，以卷积核心大小为3×3，在结合池化层降采样的情况下，搭建3—4层网络即可。以典型的100 Hz采样的地震波形数据为例，P和S等常见震相的特征尺度会比人脸识别中的特征尺度大1—2个数量级。因此，简单地模仿图形处理中的网络结构会产生特征拾取不完整的问题。于是一些研究人员将RNN用于解决长时间依赖问题，结果表明在一定程度上改善了这种问题，如图1所示。
![]()
图 1 卷积神经网络和循环神经网络用于震相拾取的关系示意Figure 1. The relationship between CNN and RNN used for phase picking图1用关系图的方式展示了这种关系：卷积神经网络在层数较少（浅层网络）的情况下，能处理的波形长度是有限的，且无法处理多个震相之间的关系。为了更加准确地拾取震相，需要结合更多的波形信息进行处理。此时需要一个较深的卷积神经网络或者使用RNN来处理多个震相之间关系，但是RNN的训练和推断速度均较慢，并且在采样点较多的情况下难以收敛。卷积神经网络处理过程中需要叠加多个层进行处理，这无疑会增加模型的复杂度。为了使用卷积神经网络完成波形处理，并尽可能地增加网络的感受野，本文使用WaveNet模型（van den Oord et al，2016）的方式，结合扩张卷积来处理感受野不足的问题，如图2所示。
由图2可知，在使用空洞卷积后，可以在不增加可训练参数的情况下增加感受野，使得纯CNN结构避免了速度较慢的RNN结构。在性能分析过程中，一般认为卷积神经网络的效率要优于循环神经网络。震相拾取中的WaveNet是一个纯卷积结构，这种结构可以完成实时拾取的工作。文本使用的模型中，卷积核心大小设置为5，相较人脸检测中的3×3更大，同时由于是一维数据处理，因此并不会显著增加模型复杂度。
另外，卷积神经网络的问题在于未对输入进行筛选，这可能导致网络容易受到噪声的影响，即神经网络无法对自身输出的幅值进行有效控制。因此在网络设计过程中使用了门控CNN单元（van den Oord et al，2016）。这种结构借鉴了GRU网络中门控单元的特点，可以对部分特征进行加权，即在重要的波形特征中门控单元给予接近1的输出值，反之则接近0。本质上讲，这种结构增加了网络的非线性，使得到时拾取对噪声的鲁棒性更强。为了提高训练的有效性，在CNN层中加入残差网络结构（He et al，2016）。残差网络即在门控单元输出之上加入本层输入的结果，可以提供训练过程中误差传播的支路，减轻梯度消失问题，从而加快训练过程。最终用于波形拾取的网络结构如图3所示。
考虑到不同震级的震相持续时间并不相同，简单地搭建多层神经网络的感受野较大，对于较小地震的震相拾取会出现较大误差。因此网络设计中将不同层的输出结果进行加和，即最终输出向量保留了多个感受野的卷积网络结果。这种建模方式更加符合不同震级震相拾取的需要。
现有到时拾取网络由于其设计过程中并未考虑计算效率的因素，在震相拾取过程中难以在低功耗设备上进行推断，为此本文将WaveNet模型简化为7层卷积神经网络。这样的网络依然是一个纯卷积结构，其结构如表1所示。
表 1 七层卷积神经网络Table 1. Seven-layer CNN层号 基础网络 核心 特征数量 扩张率 激活函数 正则化 1 卷积 3 32 1 LeakyReLU BN 2 卷积 3 64 1 LeakyReLU BN 3 卷积 3 128 1 LeakyReLU BN 4 卷积 3 128 1 LeakyReLU BN 5 卷积 3 128 2 LeakyReLU BN 6 卷积 3 128 4 LeakyReLU BN 7 卷积 3 128 8 LeakyReLU BN 8 全连接 3 无 无 This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {\rm{LeakyReLU}} {\text{＝}} {\rm{max}}\!\!\!\!{\text{（}}\!{0.25x{\text{，}}\!\!\!x} \!{\text{）}}\!\!\!\!{\text{.}} $
(6) 在一些设备上，单精度浮点计算与半精度浮点计算的效率不同，而且极端情况下，半精度浮点（FP16）的计算速度比单精度浮点计算要快一倍（Courbariaux et al，2014）。而深度学习中数值精度对于分类性能的影响较小，因此可以使用半精度代替单精度浮点用于震相拾取。在使用半精度浮点结合优化的7层卷积神经网络的情况下，模型大小可以控制在2 MB以内，这对于低功耗的场景下完成震相拾取是有利的。
2.2 其它用于到时拾取的深度学习模型
本文选择两种普通卷积神经网络和一种循环神经网络用于对比。传统卷积神经网络最早用于分类问题，这是最有效的卷积神经网络形式之一，Zhu和Beroza （2018）曾将这种网络用于波形识别，本文搭建3层网络用于波形到时的拾取。以神经网络依赖关系来看，形成的波形分类向量的每个时间步依然仅与感受野相关，因此与传统卷积神经网络并无区别。循环神经网络使用双向RNN并融合了卷积神经网络单元处理信号。
三层网络使用普通的卷积，在每层卷积中均使用批正则化，用于加快训练速度的同时提升模型精度。为尽可能地增加感受野，本文将卷积核心大小设置为5。神经网络结构列于表2。表2所示的神经网络结构较为简单，因此适合于快速检测场景。为了更好地进行震相拾取，本文搭建了稀疏编码模型作为对比。该模型包含多层卷积网络和用于降采样的池化层，同时包含多层转置卷积（Zeiler et al，2010），这可以将信号长度还原为原始信号长度，从而完成点到点的输出任务。每层中均使用批正则化作为正则化。稀疏编码模型列于表3。
表 2 三层卷积神经网络Table 2. Three-layer CNN层号 基础网络 卷积核心 特征数量 激活函数 正则化 1 卷积 5 32 LeakyReLU BN 2 卷积 5 64 LeakyReLU BN 3 卷积 5 128 LeakyReLU BN 4 全连接 3 无 无 表 3 编码解码模型（U-Net）Table 3. The encoder-decoder model （U-Net）层号 基础网络 核心 特征数量 降采样率 激活函数 正则化 1 卷积×2＋池化 3 32 2 LeakyReLU BN 2 卷积×2＋池化 3 64 2 LeakyReLU BN 3 卷积×2＋池化 3 128 2 LeakyReLU BN 4 卷积×2＋池化 3 256 2 LeakyReLU BN 5 转置卷积＋卷积×2 3 256，128 0.5 LeakyReLU BN 5 转置卷积＋卷积×2 3 128，64 0.5 LeakyReLU BN 6 转置卷积＋卷积×2 3 64，32 0.5 LeakyReLU BN 8 全连接 3 无 无 编码解码模型相比于传统分类问题的卷积网络更加复杂，该模型利用自稀疏编码器模型更加有效地提取特征并逐点输出类别，这样可以提升网络精度。为验证依赖关系对网络的影响，仿照Zhou等（2019）使用GRU搭建双向RNN网络。由于双向RNN难以处理原始波形，所以在双向RNN网络之前构建三层卷积神经网络用于处理原始波形。卷积网络中由于有循环神经网络处理时序信息，因此并不需要过大的感受野，其网络结构列于表4。
表 4 双向循环神经网络用于到时拾取Table 4. Bidirectional RNN used for phase picking层号 基础网络 核心 特征数量 激活函数 正则化 1 卷积 3 32 LeakyReLU BN 2 卷积 3 64 LeakyReLU BN 3 卷积 3 128 LeakyReLU BN 4 GRU （双向） − 128 tanh 无 5 GRU （双向） − 128 tanh 无 8 全连接 3 无 无 以上四种典型的深度神经网络模型均被用于震相拾取中。下文将对多种神经网络模型进行测试，并对其速度和精度予以分析。
3. 网络性能对比分析
3.1 训练和测试数据
本文使用波数法产生14万个地震数据用于训练，选取其中1 500个数据用于测试。测试数据来自于震中距处于20—470 km范围内的台站，台站为任意方位角；所选地震震源深度为4—19 km，震级MW3.0—6.0，其它震源参数是随机的。产生的单条数据采样点为1 024个，采样间隔为0.2 s。产生的数据不经过滤波，使用方差进行归一化。拾取到时为单一垂向分量波形，加入方差为0—0.2的噪声。测试数据的噪声方差为0.1和0.3。
在对波形进行标注的过程中，将正确到时前后两个采样点作为正样本，其它作为负样本。以分类问题来看，负样本过多，因此对正样本以及P波与S波之间的波形加入权值5，负样本加权值为0.1，由此所得训练数据如图4所示。
对于训练数据采取不同的加权，将P波与S波之间的数据加权设为5，这是因为在此区间的波形较难分类。标签数据使用独热编码（OneHot）对震相类型进行标注。
3.2 网络规模和推断速度测试
对于神经网络来说，网络的规模、深度直接影响内存大小。一般来说，内存需要越大，计算性能要求越高，同时完成相同任务需要的能量更多。本文对不同网络的可训练参数数量进行统计。对于不同的网络结构，在可训练参数规模相近的情况下，CNN一般比RNN更高效。本文对推断过程中的速度进行统计，测试中使用的CPU为E31225@3.3GHz，GPU为NVIDIA的K2200。将上述网络性能统计信息列于表5。
表 5 CPU和GPU上的网络性能统计Table 5. Performance statistics on CPU and GPU网络名称 可训练
参数个数CPU环境15个
样本推断时长/sGPU环境15个
样本推断时长/s3层CNN 52 195 0.12 0.008 8 7层CNN 229 283 0.51 0.025 编码解码结构 1 748 771 0.67 0.030 CNN＋RNN 476 195 1.2 1.0 WaveNet 2 715 651 4.5 0.17 7层CNN （RE） 78 758 0.19 0.021 7层CNN （RE，FP16） 78758 16 0.020 WaveNet （RE） 770692 2.4 0.17 注：RE代表深度可分离卷积优化，FP16代表16位浮点计算。 在GPU环境中，对于8个网络模型，震相拾取速度最慢的网络为卷积神经网络与RNN融合的深度学习结构，其推断时长达到1.0 s，这比纯卷积结构要慢。卷积结构计算速度与可训练参数数量呈正相关，其中三层卷积网络的推断时长比模型复杂度最高的WaveNet缩短了一个数量级，达到0.008 8 s，在样本采样率为100 Hz的情况下相当于每秒钟可以处理4小时数据，这对于大型数据集来说效率差尤为明显。在进行到时拾取等机器学习任务的过程中，搭建过于复杂的网络并不合理，因为这样会显著地增加推断负担，而神经网络应当具备简单高效的特点。使用深度敏感卷积优化的卷积神经网络，推断时间与普通卷积近似，但是可训练参数数量减少了66%。
而在CPU中所有计算速度均呈现出一定程度的降低，其中RNN速度降低最少，使用深度可分离卷积的网络则表现出比传统卷积更好的性能，CPU的缓存系统更适合处理深度敏感卷积。震相拾取过程中16位精度的计算达到16 s，这是因为Intel的CPU没有半精度计算单元，使得计算十分缓慢。因为GPU存在访存瓶颈，经过深度可分离卷积优化的网络速度并未得到明显提升。半精度计算适合于低功耗场景，而针对通过用场景设计的CPU和GPU难以发挥其高速性能。
3.3 分类性能测试
在分类性能测试中，选取非训练数据的1 500个样本进行测试，将到时拾取超过3个采样点的样本作为负样本，统计网络性能绘制成图5。
![]()
图 5 多个模型对于P波（a）和S波（b）拾取的受试者工作特征曲线（ROC）RE为使用深度可分离卷积代替传统卷积结构，FP16为网络计算中使用16位浮点Figure 5. ROC curves of picking P phase （a） and S phase （b） based on eight DNN modelsRE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing由图5可见：拾取结果中卷积神经网络与双向RNN融合模型和WaveNet结果最好，编码解码模型效果次之，3层神经网络与16位精度的7层卷积优化网络近似。这说明波形拾取过程中，网络复杂度与波形拾取结果优劣呈正相关。循环神经网络与WaveNet属于不同类型的网络，二者具有相近的性能，这说明在波形拾取过程中综合考虑多种波形可以获得更好的结果，这既可以通过RNN也可以通过增加感受野的方式达到。在满足依赖关系的情况下，多种网络结构均可以达到理想的结果。从受试者工作特征（receiver operating characteristic，缩写为ROC）曲线可以看出，不同网络对于S波提取的效果均好于P波，这是因为S波的振幅和持续时间相对较长，而P波由于振幅原因容易被噪声掩盖。对于到时提取误差，使用箱形图进行误差分析，结果如图6所示。
![]()
图 6 基于P波（a）和S波（b）的神经网络模型预测误差统计图RE为使用深度可分离卷积代替传统卷积结构，FP16为网络计算中使用16位浮点。箱型图矩形边界为上下四分位数，绿色线条为中位数，三角形为均值，黑色短线为数值边界。矩形上下四分位数越接近，且均值越接近0，效果越好Figure 6. The error staticstics of different DNN models on P phase （a） and S phase （b）RE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing. The box rectangle is the upper and lower quartiles，the green line is the median，the triangle symbol is the mean value，and the black short line is the boundary. The closer the upper and lower quartiles of the rectangle are and the closer the mean is to zero，the better可见：P波的到时误差相比于S波更小，这并非是因为P波在提取过程中误差较大的样本均作为负样本被剔除，但是这导致了较多P波未计入统计从而增加了正确提取到时的精度；八个网络中三层网络的精度最低，这与前面的分析类似；RNN融合模型与WaveNet的误差相差不大，经过卷积和浮点精度优化后的七层模型与三层模型的精度相近。
3.4 抗干扰测试
本文选择不同噪声水平对误差进行测试分析。定义信噪比SNR为地震波形的方差与噪声方差之比。首先选择体波振幅较大的近震波形进行测试，其网络输出概率如图7所示。
![]()
图 7 不同噪声对于模型预测的影响RE为使用深度可分离卷积代替传统卷积结构，FP16为网络计算中使用16位浮点（a） 近震波形分析；（b） 远震P波拾取失败分析Figure 7. Effect of different noises on model predictionRE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing（a） Analysis of near-shock waveforms；（b） Analysis of failures on tele-seismics由于近震波形中，体波振幅相对较大，不同网络对于到时预测均较为准确。三层网络由于感受野较小，受到噪声的影响相对更大。在近震波形拾取过程中三层网络受限于感受野，仅能覆盖一种波形，因此将面波部分也识别为S波，且无法综合其它波形判断。具有较大感受野的卷积神经网络和RNN模型对于这些错误则可以有效地避免。在远震波形测试中，P波所有概率均未超过0.25%，也就是均未拾取成功，这是因为体波相对较小，容易被噪声覆盖；而S波拾取相比于P波效果较好，这是因为S波不仅振幅相对较大，同时可以结合面波判断，此即为具有较大感受野的CNN模型和RNN模型的优势所在。RNN模型由于前后文更长（依赖更长），因此拾取P波相比于其它神经网络效果要好。我们测试750个波形并绘制ROC曲线进行更细致的分析，结果如图8所示。
![]()
图 8 八个测试模型在不同噪声情况下的ROC曲线ROC曲线下方面积越大效果越好。RE代表深度可分离卷积优化的网络，FP16代表16位浮点精度计算结果（a） P波拾取的ROC曲线；（b） S波拾取的ROC曲线Figure 8. ROC curves of eight DNN models with different signal to noise ratio （SNR）The bigger area under ROC，the better. RE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing （a） ROC curve of picking P phase；（b） ROC curve of picking S phase由图8可以看到：不同网络本身均受到了噪声的影响，不同网络对于P波拾取均劣于S波，其中三层网络受到噪声影响最大；RNN在拾取P波过程中则表现出了最好的性能，这与前面的分析类似；WaveNet优化模型的精度降低较少，这是因为原始模型可训练的参数数量较多；深度敏感卷积与传统卷积在性能上相差较小；16位精度的模型和32位精度的模型对于结果影响较小，因此在对于功耗敏感的场景，应当选择16位精度完成震相拾取。对于S波拾取，编码解码结构、RNN网络和WaveNet在具有大感受野的网络中均可以有效地识别，结果相差较小，三层卷积神经网络由于感受野不足对于S波拾取错误较多。
4. 讨论与结论
多种深度神经网络测试的结果表明WaveNet和RNN融合模型对于震相拾取的精度相近。RNN融合模型善于处理时间依赖问题，使得不同震相在拾取过程中可以互相参考；而WaveNet结构中既有与GRU相似的门结构用于特征加权，又具有较大的感受野能够处理多个震相，这是二者能够达到相似精度的原因。在速度对比上，虽然CPU场景下WaveNet速度较慢，但在GPU场景下WaveNet比RNN融合模型快了接近6倍，这使得在经过优化之后的硬件上速度差距会更加明显。在测试中发现七种CNN相比于RNN模型均有速度优势，因此在速度敏感型的场景下应当考虑使用卷积神经网络代替循环神经网络。文中出现的卷积神经网络模型均是纯卷积结构，这意味着网络均可以实时推断，而双向RNN由于需要反向输入，在实现实时检测的过程中会遇到问题。在不需要精度的场景下，我们给出了优化的七层卷积神经网络。这种网络模型参数较少，可使得半精度浮点情况下的模型大小压缩到2.0 MB以内，从而实现低功耗场景的推断工作，但这需要硬件设计的配合。
因此在性能和精度兼顾的网络设计过程中，首先应当考虑卷积神经网络模型，这是因为该模型在训练速度和推断速度上均具有较大优势。而实践中由于波形并非无限长，因此并无必要考虑无限长的前后文问题。而卷积神经网络中由于有深度可分离卷积的存在，可减少模型参数数量，并进一步减少计算量。同时，网络计算精度可以减少至半精度浮点。经过这种优化后，模型大小在卷积核心大小为3的情况下可以减少至原有的1/6。虽然会牺牲部分精度，但是在低功耗场景还是有利的。
本文的主要结论均是基于通用计算单元的CPU、GPU和合成地震波形数据上的测试，因此无法真正发挥所有优化模型的优势。在今后的工作中会考虑使用FPGA构建专用的计算硬件，用以加速深度神经网络拾取震相速度，并降低系统功耗。
文本所使用的网络均是基于单台震相拾取，可以看到现有网络结构中在满足感受野的情况下均可以获得相近的结果。这说明对于地震波形的复杂度而言，不需要使用过于复杂的神经网络结构，目前7层卷积神经网络即可满足需求。因此，今后工作中会融合传统的人工构建特征并联合拾取，这会加快网络拾取速度。再者，继续增加网络层数会增加计算代价，但并未带来精度的明显提升。鉴于单台检测无法综合其它台站的波形信息，未来需要结合其它台站预测结果进行震相关联，以提升单台拾取的精度，有利于远震震相识别。
-
![]()
图 1 卷积神经网络和循环神经网络用于震相拾取的关系示意
Figure 1. The relationship between CNN and RNN used for phase picking
![]()
图 5 多个模型对于P波（a）和S波（b）拾取的受试者工作特征曲线（ROC）
RE为使用深度可分离卷积代替传统卷积结构，FP16为网络计算中使用16位浮点
Figure 5. ROC curves of picking P phase （a） and S phase （b） based on eight DNN models
RE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing
![]()
图 6 基于P波（a）和S波（b）的神经网络模型预测误差统计图
RE为使用深度可分离卷积代替传统卷积结构，FP16为网络计算中使用16位浮点。箱型图矩形边界为上下四分位数，绿色线条为中位数，三角形为均值，黑色短线为数值边界。矩形上下四分位数越接近，且均值越接近0，效果越好
Figure 6. The error staticstics of different DNN models on P phase （a） and S phase （b）
RE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing. The box rectangle is the upper and lower quartiles，the green line is the median，the triangle symbol is the mean value，and the black short line is the boundary. The closer the upper and lower quartiles of the rectangle are and the closer the mean is to zero，the better
![]()
图 7 不同噪声对于模型预测的影响
RE为使用深度可分离卷积代替传统卷积结构，FP16为网络计算中使用16位浮点（a） 近震波形分析；（b） 远震P波拾取失败分析
Figure 7. Effect of different noises on model prediction
RE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing（a） Analysis of near-shock waveforms；（b） Analysis of failures on tele-seismics
![]()
图 8 八个测试模型在不同噪声情况下的ROC曲线
ROC曲线下方面积越大效果越好。RE代表深度可分离卷积优化的网络，FP16代表16位浮点精度计算结果（a） P波拾取的ROC曲线；（b） S波拾取的ROC曲线
Figure 8. ROC curves of eight DNN models with different signal to noise ratio （SNR）
The bigger area under ROC，the better. RE stands for separable CNN optimized network，FP16 stands for 16bit floating for computing （a） ROC curve of picking P phase；（b） ROC curve of picking S phase
表 1 七层卷积神经网络
Table 1 Seven-layer CNN
层号 基础网络 核心 特征数量 扩张率 激活函数 正则化 1 卷积 3 32 1 LeakyReLU BN 2 卷积 3 64 1 LeakyReLU BN 3 卷积 3 128 1 LeakyReLU BN 4 卷积 3 128 1 LeakyReLU BN 5 卷积 3 128 2 LeakyReLU BN 6 卷积 3 128 4 LeakyReLU BN 7 卷积 3 128 8 LeakyReLU BN 8 全连接 3 无 无 
下载: 导出CSV
表 2 三层卷积神经网络
Table 2 Three-layer CNN
层号 基础网络 卷积核心 特征数量 激活函数 正则化 1 卷积 5 32 LeakyReLU BN 2 卷积 5 64 LeakyReLU BN 3 卷积 5 128 LeakyReLU BN 4 全连接 3 无 无
下载: 导出CSV
表 3 编码解码模型（U-Net）
Table 3 The encoder-decoder model （U-Net）
层号 基础网络 核心 特征数量 降采样率 激活函数 正则化 1 卷积×2＋池化 3 32 2 LeakyReLU BN 2 卷积×2＋池化 3 64 2 LeakyReLU BN 3 卷积×2＋池化 3 128 2 LeakyReLU BN 4 卷积×2＋池化 3 256 2 LeakyReLU BN 5 转置卷积＋卷积×2 3 256，128 0.5 LeakyReLU BN 5 转置卷积＋卷积×2 3 128，64 0.5 LeakyReLU BN 6 转置卷积＋卷积×2 3 64，32 0.5 LeakyReLU BN 8 全连接 3 无 无
下载: 导出CSV
表 4 双向循环神经网络用于到时拾取
Table 4 Bidirectional RNN used for phase picking
层号 基础网络 核心 特征数量 激活函数 正则化 1 卷积 3 32 LeakyReLU BN 2 卷积 3 64 LeakyReLU BN 3 卷积 3 128 LeakyReLU BN 4 GRU （双向） − 128 tanh 无 5 GRU （双向） − 128 tanh 无 8 全连接 3 无 无
下载: 导出CSV
表 5 CPU和GPU上的网络性能统计
Table 5 Performance statistics on CPU and GPU
网络名称 可训练
参数个数CPU环境15个
样本推断时长/sGPU环境15个
样本推断时长/s3层CNN 52 195 0.12 0.008 8 7层CNN 229 283 0.51 0.025 编码解码结构 1 748 771 0.67 0.030 CNN＋RNN 476 195 1.2 1.0 WaveNet 2 715 651 4.5 0.17 7层CNN （RE） 78 758 0.19 0.021 7层CNN （RE，FP16） 78758 16 0.020 WaveNet （RE） 770692 2.4 0.17 注：RE代表深度可分离卷积优化，FP16代表16位浮点计算。
下载: 导出CSV
-
于子叶,储日升,盛敏汉. 2018. 深度神经网络拾取地震P和S波到时[J]. 地球物理学报,<bold>61</bold>(12):4873–4886. doi: 10.6038/cjg2018L0725 Yu Z Y,Chu R S,Sheng M H. 2018. Pick onset time of P and S phase by deep neural network[J]. <italic>Chinese Journal of Geophysics</italic>,<bold>61</bold>(12):4873–4886 (in Chinese). doi: 10.6038/cjg2018L0725（inChinese）
赵明,陈石,房立华,Yuen D A. 2019. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报,<bold>62</bold>(8):3034–3042. doi: 10.6038/cjg2019M0495 Zhao M,Chen S,Fang L H,Yuen D A. 2019. Earthquake phase arrival auto-picking based on U-shaped convolutional neural network[J]. <italic>Chinese Journal of Geophysics</italic>,<bold>62</bold>(8):3034–3042 (in Chinese). doi: 10.6038/cjg2019M0495
Cho K, van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, Bengio Y. 2014. Learning phrase representations using RNN encoder-decoder for statistical machine translation[Z]. arXiv preprint. arXiv: 1406.1078.
Courbariaux M, Bengio Y, David J P. 2014. Training deep neural networks with low precision multiplications[Z]. arXiv preprint. arXiv: 1412.7024.
García L,Álvarez I,Benítez C,Titos M,Titos M,Bueno Á,Mota S,De La Torre Á,Segura J C,Alguacil G,Díaz-Moreno A,Prudencio J,García-Yeguas A,Ibáñez J M,Zuccarello L,Cocina O,Patanè D. 2016. Advances on the automatic estimation of the P-wave onset time[J]. <italic>Ann Geophys</italic>,<bold>59</bold>(4):S0434.
He K M, Zhang X Y, Ren S Q, Sun J. 2016. Deep residual learning for image recognition[C]//Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA: IEEE: 770–778.
Hinton G, Vinyals O, Dean J. 2015. Distilling the knowledge in a neural network[Z]. arXiv preprint. arXiv: 1503.02531.
Hochreiter S,Schmidhuber J. 1997. Long short-term memory[J]. <italic>Neural Comput</italic>,<bold>9</bold>(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735
Howard A G, Zhu M L, Chen B, Kalenichenko D, Wang W J, Weyand T, Andreetto M, Adam H. 2017. Mobilenets: Efficient convolutional neural networks for mobile vision applications[Z]. arXiv preprint. arXiv: 1704.04861.
Hu L L,Zheng X D,Duan Y T,Yan X F,Hu Y,Zhang X L. 2019. First-arrival picking with a U-net convolutional network[J]. <italic>Geophysics</italic>,<bold>84</bold>(6):1–58. doi: 10.1190/geo2019-1029-tiogeo.1
Ioffe S, Szegedy C. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift[Z]. arXiv preprint. arXiv: 1502.03167.
LeCun Y,Bottou L,Bengio Y,Haffner P. 1998. Gradient-based learning applied to document recognition[J]. <italic>Proc IEEE</italic>,<bold>86</bold>(11):2278–2324. doi: 10.1109/5.726791
Maass W. 1997. Networks of spiking neurons:The third generation of neural network models[J]. <italic>Neu Networks</italic>,<bold>10</bold>(9):1659–1671. doi: 10.1016/S0893-6080(97)00011-7
Ronneberger O, Fischer P, Brox T. 2015. U-Net: Convolutional networks for biomedical image segmentation[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Munich, Germany: Springer: 234–241.
Ross Z E,Meier M A,Hauksson E. 2018. P wave arrival picking and first‐motion polarity determination with deep learning[J]. <italic>J Geophys Res</italic>:<italic>Solid Earth</italic>,<bold>123</bold>(6):5120–5129. doi: 10.1029/2017JB015251
Rumelhart D E,Hinton G E,Williams R J. 1986. Learning representations by back-propagating errors[J]. <italic>Nature</italic>,<bold>323</bold>(6088):533–536. doi: 10.1038/323533a0
Sandler M, Howard A, Zhu M L, Zhmoginov A, Chen L C. 2018. MobileNetV2: Inverted residuals and linear bottlenecks[C]//Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA: IEEE: 4510–4520.
Schuster M,Paliwal K K. 1997. Bidirectional recurrent neural networks[J]. <italic>IEEE Trans Signal Process</italic>,<bold>45</bold>(11):2673–2681. doi: 10.1109/78.650093
van der Baan M,Jutten C. 2000. Neural networks in geophysical applications[J]. <italic>Geophysics</italic>,<bold>65</bold>(4):1032–1047. doi: 10.1190/1.1444797
van den Oord A, Dieleman S, Zen H G, Simonyan K, Vinyals O, Graves A, Kalchbrenner N, Senior A, Kavukcuoglu K. 2016. WaveNet: A generative model for raw audio[Z]. arXiv preprint. arXiv: 1609.03499.
Zeiler M D, Krishnan D, Taylor G W, Fergus R. 2010. Deconvolutional networks[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, CA, USA: IEEE: 2528–2535.
Zhang K P,Zhang Z P,Li Z F,Qiao Y. 2016. Joint face detection and alignment using multitask cascaded convolutional networks[J]. <italic>IEEE Signal Process Lett</italic>,<bold>23</bold>(10):1499–1503. doi: 10.1109/LSP.2016.2603342
Zhao Y,Takano K. 1999. An artificial neural network approach for broadband seismic phase picking[J]. <italic>Bull Seismol Soc Am</italic>,<bold>89</bold>(3):670–680.
Zhou Y J,Yue H,Kong Q K,Zhou S Y. 2019. Hybrid event detection and phase‐picking algorithm using convolutional and recurrent neural networks[J]. <italic>Seismol Res Lett</italic>,<bold>90</bold>(3):1079–1087. doi: 10.1785/0220180319
Zhu W Q,Beroza G C. 2018. PhaseNet:A deep-neural-network-based seismic arrival-time picking method[J]. <italic>Geophys J Int</italic>,<bold>216</bold>(1):261–273.
-
期刊类型引用(3)
1. 申中寅，吴庆举. 卷积神经网络在远-近地震震相拾取中的应用及模型解释. 地震学报. 2022(06): 961-979 . 
本站查看
2. 廖诗荣，张红才，范莉苹，李珀任，黄玲珠，房立华，秦敏. 实时智能地震处理系统研发及其在2021年云南漾濞M_S6.4地震中的应用. 地球物理学报. 2021(10): 3632-3645 . 百度学术
3. Ziye Yu，Risheng Chu，Weitao Wang，Minhan Sheng. CRPN: A cascaded classification and regression DNN framework for seismic phase picking. Earthquake Science. 2020(02): 53-61 . 必应学术
其他类型引用(2)
计量
- 文章访问数: 943
- HTML全文浏览量: 408
- PDF下载量: 70
- 被引次数: 5
