Inversion method and application of seismic intensity attenuation parameters based on genetic algorithm
-
摘要: 收集郯庐断裂带中南段59次地震的等震线数据，运用遗传算法，将郯庐断裂带中南段按照断裂带东侧和西侧分区，分别反演其地震烈度衰减参数，反演时使目标函数的一范数最小，同时对烈度衰减曲线的远场施加约束，通过自助抽样（Bootstrap）技术多次重复反演以对反演结果的稳定性进行评价，并将断裂带东侧和西侧的烈度衰减曲线分别与第五代地震动参数区划图进行对比。结果表明：使用本文提出的方法进行反演可使烈度衰减曲线即使不进行近、远场补点，也能收敛；断裂带东侧和西侧的结果均与第五代地震动参数区划图的结果存在差异，且断裂带东侧与西侧的结果也不同。这种差异可能与断裂带两侧的介质速度结构及衰减效应等因素的差异有关。Abstract: Isoseismal lines of 59 earthquakes occurred in middle south segment of Tanlu fault zone are collected. Seismic intensity attenuation parameters in eastern and western part of Tanlu fault are inversed respectively by genetic algorithm. The one norm of misfit function is used and constraint on far field of seismic intensity attenuation curve is added during the inversion. A bootstrap technique is adopted to repeat the inversion process for several times to evaluate the stability of inversion. Results are compared with the fifth generation seismic ground motion parameter zonation map, it shows that seismic intensity attenuation curve can converge even no data are added in near and far filed by proposed inversion method in this paper. Seismic intensity attenuation of eastern and western part of Tanlu fault are different from those of fifth generation seismic ground motion parameter zonation map. Besides, the seismic intensity attenuation of eastern part and western part are different from each other. This difference may be related to the medium velocity structure and attenuation characteristic.
-
引言
地震动衰减关系的确定是地震安全性评价的重要一步，而地震烈度衰减关系是缺乏强震活动的观测地区地震动衰减关系确定的基础（胡聿贤，1999；俞言祥，汪素云，2006）。各省建立的应急指挥系统可以在地震后对震害进行快速评估，而震害快速评估的基础是本区的地震烈度衰减关系，无论是估计房屋破坏情况，还是经济损失等，首先都需要根据烈度衰减关系估算出地震的影响范围。
诸多研究者针对地震烈度随震源距和震源深度的变化给出了不同的公式（Gutenberg，Richter，1942；Ergin，1969；Brazee，1972）；Howell和Schultz （1975）对前人的工作进行了总结，从地震学的角度导出了烈度随震中距离的衰减关系模型，既椭圆烈度衰减模型；陈达生和刘汉兴（1989）对该模型进行了改进，提出了椭圆长短轴联合衰减模型，该模型可以保证烈度衰减曲线在近场收敛；而远场一般通过补点的方式使衰减曲线收敛，基于此，有研究人员提出了相应的改进模型（高德潜，1996；沙海军等，2004）。
传统的烈度衰减参数一般采用最小二乘法进行计算，即使得误差函数的二范数最小时所对应的反演参数的解。由于地震烈度值受诸多因素影响且烈度等震线的量取不可能十分精确，因此在烈度衰减参数的反演过程中常常存在异常点，而最小二乘法受异常点的影响较大，因此有研究人员提出使用稳健回归方法来反演烈度衰减参数（王晓军等，2012；刘军等，2014）。
郯庐断裂带自被发现起，一直是地学界研究的热点，其中南段（29°—38°N，115°—122°E）是整个断裂带中地震活动性最强的部分，1668年郯城M8.5地震就发生在这一范围内。何奕成等（2018）曾用稳健回归方法对这一区域的烈度衰减关系进行过研究。但是针对郯庐断裂带中南段的速度结构（黄耘等，2011；刘保金等，2015；熊振等，2016）及介质非均匀性（杨从杰等，2016；范小平等，2017）等相关的研究均表明，郯庐断裂带东侧与西侧的介质结构具有较大的差异，因此有必要对断裂带两侧的烈度衰减特性进行单独研究。
遗传算法是一种非线性全局搜索方法，它的优点是全局搜索，无需求导，不依赖于初始模型的选取等（万永革等，1997；王文萍，王庆良，1999；周都民等，1999；吴建平等，2001）。本文提出一种烈度衰减参数反演的新方法，即采用施加模型约束的遗传算法来分别反演郯庐断裂带两侧的地震烈度衰减参数。遗传算法作为一种全局最优化算法，较难对反演结果的稳定性进行评价，本文拟通过自助抽样（Bootstrap）技术多次重复反演过程，对反演结果的稳定性进行评价；此外，将本文结果与第五代地震动参数区划图中东部强震区烈度衰减关系的结果（以下简称“五代图结果”）进行比较，并将断裂带东侧与西侧的结果也进行比较，并分析产生这些差异的可能原因。
1. 数据与方法
1.1 等震线数据
本文沿用“江苏及邻区地震烈度衰减关系”（何奕成等，2018）一文中表1的等震线数据，按照震中位置在郯庐断裂带主断裂东侧或西侧将数据进行分区，其中在断裂带东侧收集到27次地震的54条等震线数据，在断裂带西侧收集到32次地震的66条等震线数据，此处不再给出具体的烈度与等震线数值，只给出断裂带两侧的地震震级和烈度分布，具体参数列于表1，图1给出了研究区参与反演的地震震中分布图。
表 1 郯庐断裂带东西两侧地震震级和烈度分布表Table 1. Distribution of earthquake magnitude and intensity in east and west sides of Tanlu fault zone震级范围 地震次数 烈度值≥Ⅳ的等震线条数 合计 主断裂东测 主断裂西测 东 西 Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ 东 西 MS3.0—3.9 8 10 6 6 0 0 0 0 0 9 7 0 0 0 0 0 12 16 MS4.0—4.9 15 14 9 15 5 0 0 0 0 7 14 4 0 0 0 0 29 25 MS5.0—5.9 2 5 1 1 2 2 0 0 0 1 4 5 3 0 0 0 6 13 MS6.0—6.9 2 1 2 2 1 1 1 0 0 0 0 1 1 0 0 0 7 2 MS7.0—7.9 0 2 0 0 0 0 0 0 0 0 1 2 2 2 2 1 0 10 合计 27 32 18 24 8 3 1 0 0 17 26 12 6 2 2 1 54 66 ![]()
图 1 研究区参与反演的地震震中分布图Figure 1. Epicenter location of earthquakes for inversion in the studied area1.2 烈度衰减参数反演方法
目前应用较为广泛的烈度衰减模型是陈达生和刘汉兴（1989）提出的椭圆长短轴联合衰减模型。本文沿用该衰减模型，其表达式为
$ \begin{split} I{\text{＝}}&a{\text{＋}}bM{\text{－}}{c}_{1}\mathrm{ln}\left({R}_{\mathrm{a}}{\text{＋}}{R}_{0\mathrm{a}}\right){\text{－}}\\ &{c}_{2}\mathrm{ln}\left({R}_{\mathrm{b}}{\text{＋}}{R}_{0\mathrm{b}}\right){\text{－}}{d}_{1}{R}_{\mathrm{a}}{\text{－}}{d}_{2}{R}_{\mathrm{b}}{\text{，}}\\ \end{split} $
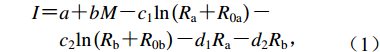
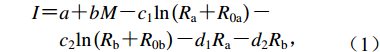
(1) 式中：I为地震烈度；M为震级；Ra和Rb分别为烈度为I的椭圆等震线的长半轴和短半轴的长度；R0a和R0b为近场饱和因子，一般可视为常数；a，b，c1，c2，d1，d2为需要求解的反演参数。令Rb＝0，导出长轴方向的衰减公式为
$ \begin{split} {I}_{{\rm{a}}}{\text{＝}}&a{\text{－}}{c}_{2}\mathrm{ln}{R}_{0\mathrm{b}}{\text{＋}}bM{\text{－}}\\&{c}_{1}\mathrm{ln}\left({R}_{\mathrm{a}}{\text{＋}}{R}_{0\mathrm{a}}\right){\text{－}}{d}_{1}{R}_{{\rm{a}}} {\text{；}} \end{split}$
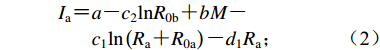
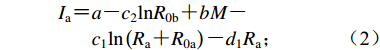
(2) 令Ra＝0，导出短轴方向的衰减公式为
$ {I}_{{\rm{b}}}{\text{＝}}a{\text{－}}{c}_{1}\mathrm{ln}{R}_{0\mathrm{a}}{\text{＋}}bM{\text{－}}{c}_{2}\mathrm{ln}\!\!\!\!{\text{（}}\!{R}_{\mathrm{b}}{\text{＋}}{R}_{0\mathrm{b}}\!{\text{）}}\!\!\!\!{\text{－}}{d}_{2}{R}_{\mathrm{b}}{\text{，}} $
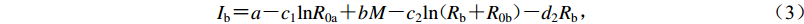
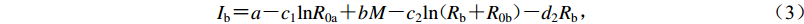
(3) 令式（2）中的Ra＝0，得到Ia＝a－c2lnR0b＋bM－c1lnR0a；令式（3）中的Rb＝0，得到Ib＝a－c1ln（R0a）＋bM－c2ln（R0b）。可以看出，在震中位置附近，Ia＝Ib，即椭圆长短轴联合衰减模型本身即能满足近场约束条件。
传统的烈度衰减关系一般采用最小二乘法来计算烈度衰减模型的参数，本文基于遗传算法，提出一种烈度衰减参数反演的新方法。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ \begin{aligned} { G} {\text{＝}} \left[ {\begin{array}{*{20}{c}} \!\!\!\!1&{{g_{11}}}&{{g_{12}}}&{{g_{13}}}&{{g_{14}}}&{{g_{15}}}\!\!\!\!\!\!\\ \!\!\!\!1&{{g_{21}}}&{{g_{22}}}&{{g_{23}}}&{{g_{24}}}&{{g_{25}}}\!\!\!\!\!\!\\ \!\!\!\!\vdots & \vdots & \vdots & \vdots & \vdots & \vdots \!\!\!\!\!\!\\ \!\!\!\!1&{{g_{N1}}}&{{g_{N2}}}&{{g_{N3}}}&{{g_{N4}}}&{{g_{N5}}}\!\!\!\!\!\! \end{array}} \right]{\text{，}} \end{aligned}$
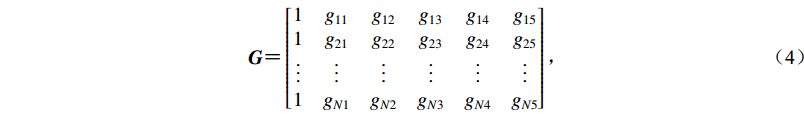
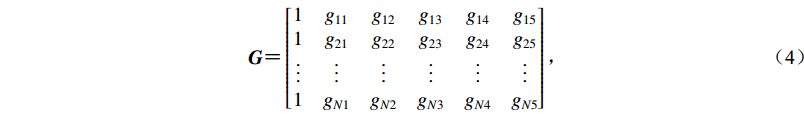
(4) 则式（1）可以表示为d＝Gm，即
$ \left[ {\begin{aligned} {{I_1}}\\ {{I_2}}\\ {{I_3}}\\ \vdots \;\\ {{I_N}} \end{aligned}} \right] {\text{＝}} \left[ {\begin{array}{*{20}{c}} {1}&{{g_{11}}}&{{g_{12}}}&{{g_{13}}}&{{g_{14}}}&{{g_{15}}}\\ {1}&{{g_{21}}}&{{g_{22}}}&{{g_{23}}}&{{g_{24}}}&{{g_{25}}}\\ { \vdots }&\vdots&\vdots&\vdots&\vdots&\vdots \\ {1}&{{g_{N1}}}&{{g_{N2}}}&{{g_{N3}}}&{{g_{N4}}}&{{g_{N5}}} \end{array}} \right]\left[ {\begin{aligned} {{m_1}}\\ {{m_2}}\\ {{m_3}}\\ {{m_4}}\\ {{m_5}}\\ {{m_6}} \end{aligned}} \right]{\text{，}}$
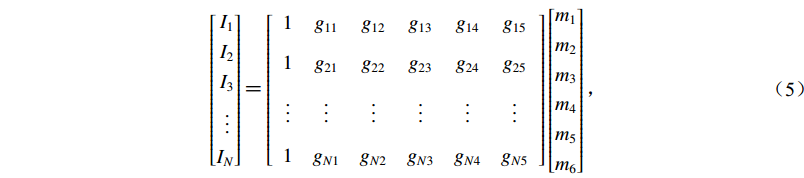
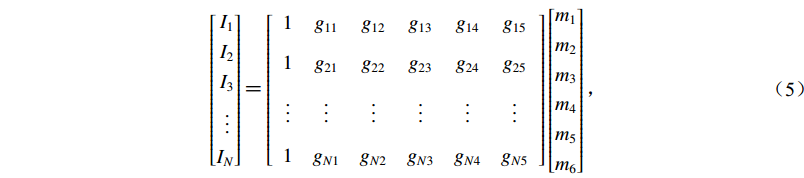
(5) $ {{\varPhi}} \left(m \right) {\text{＝}} \mathop \sum \limits_{i {\text{＝}} 1}^N \left| {{{d}} {\text{－}} {{Gm}}} \right| {\text{.}}$
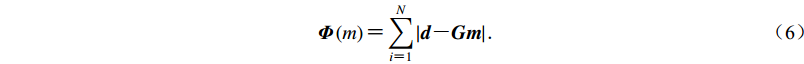
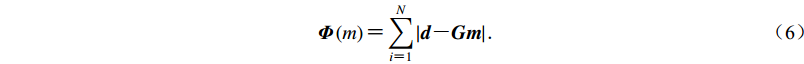
(6) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {I_{\rm{a}}}{\text{＝}} a {\text{－}} {c_2}\ln {{R_{0{\rm{b}}}}} {\text{＋}} bM {\text{－}} {c_1}{\rm{ln}}\left({{R_{0{\rm{a}}}} + 400} \right) {\text{－}} 400{d_1}{\text{，}} $
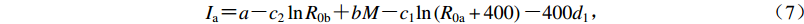
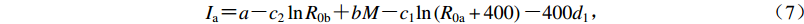
(7) $ {I_{\rm{b}}} {\text{＝}} a {\text{－}} {c_1}\ln {{R_{0{\rm{a}}}}} {\text{＋}} bM{\text{－}} {c_2}\ln \left({{R_{0{\rm{b}}}} {\text{＋}} 400} \right) {\text{－}} 400{d_2}{\text{.}} $
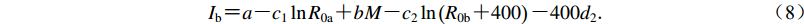
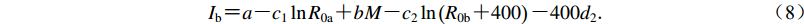
(8) 令Ia＝Ib，可以得到
$ {c}_{2}\mathrm{ln}{R}_{0\mathrm{b}}{\text{＋}}{c}_{1}\mathrm{ln}\left({R}_{0\mathrm{a}}{\text{＋}}400\right){\text{＋}}{400d}_{1}{\text{＝}}{c}_{1}\mathrm{ln}{R}_{0\mathrm{a}}{\text{＋}}{c}_{2}\mathrm{ln}\left({R}_{0\mathrm{b}}{\text{＋}}400\right){\text{＋}}{400d}_{2}{\text{，}} $
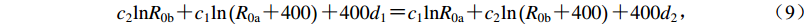
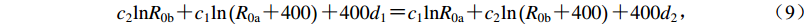
(9) 即
$ {m}_{4}\mathrm{ln}{R}_{0\mathrm{b}}{\text{＋}}{m}_{3}\mathrm{ln}\left({R}_{0\mathrm{a}}{\text{＋}}400\right){\text{＋}}400{m}_{5}{\text{＝}}{m}_{3}\mathrm{ln}{R}_{0\mathrm{a}}{\text{＋}}{m}_{4}\mathrm{ln}\left({R}_{0\mathrm{b}}{\text{＋}}400\right){\text{＋}}400{m}_{6}{\text{.}} $
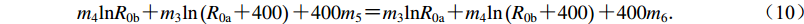
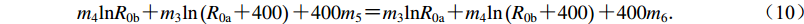
(10) 反演参数m3，m4，m5，m6还需要满足式（10），即在反演的过程中增加式（10），对反演参数施加模型约束。
一个完整的烈度衰减关系还需要给出反映反演结果不确定性的参数，通常用拟合标准差来表示，即
$ \sigma {\text{＝}} \sqrt {\frac{1}{N}\mathop \sum \limits_{i {\text{＝}} 1}^N {{\left({{{{d}}_{{\rm{obs}}}} {\text{－}} {{Gm}}{_{{\rm{ga}}}}} \right)}^2}{\rm{}}}{\text{，}}$
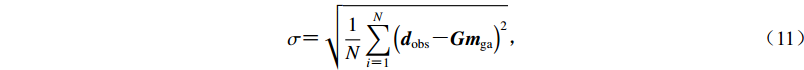
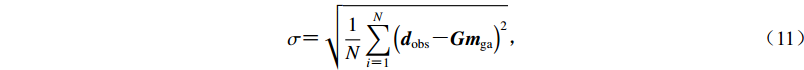
(11) 式中，dobs为观测数据，mga为反演得到的参数，N为总的观测数据个数。
1.3 反演的稳定性
本文用统计学上较为常用的自助抽样方法（bootstrap），随机从总的观测数据中抽取80%的数据进行反演，然后用余下的数据对反演结果进行检验，以检测反演方法的稳定性。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {\sigma _i} {\text{＝}} \sqrt {\frac{1}{{{N_{20\% }}}}\mathop \sum \limits_{k {\text{＝}} 1}^{{N_{20\% }}} {{\left({{{{d}}_{20\% }} {\text{－}} { {Gm}}{_{{\rm{ga}}{\text{，}}\!\!\!\!i}}} \right)}^2}}{\text{，}} $
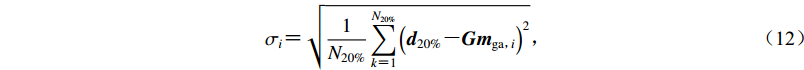
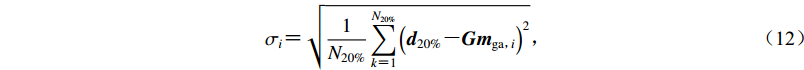
(12) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
2. 结果
2.1 烈度衰减参数反演结果
使用“江苏及邻区地震烈度衰减关系”一文（何奕成等，2018）表1中的数据，采用1.2节中介绍的反演方法计算郯庐断裂带中南段断裂带东侧和西侧的烈度衰减参数。近场饱和因子R0a和R0b通过回归搜索过程中使得衰减公式的标准差最小的原则来确定，按此原则，断裂带东侧取R0a＝11.5，R0b＝6.3；断裂带西侧取R0a＝11.1，R0b＝5.4。遗传算法交叉率取0.6，变异率取0.01，种群数目断裂带东侧取150，西侧取200，反演过程的拟合标准差σ通过式（11）计算得到。断裂带东侧烈度衰减参数反演结果为me＝[4.990 2，1.162 7，0.981 1，0.924 6，0.004 4，0.003 5]T，即
$ \begin{array}{*{20}{c}} I{\text{＝}}4.990\;2 {\text{＋}} 1.162\;7M {\text{－}} 0.981\;1\ln \left({{R_{\rm{a}}}{\text{＋}} 11.5} \right) {\text{－}} 0.924\;6 \ln \left({{R_{\rm{b}}}{\text{＋}} 6.3} \right){\text{－}}\\0.004\;4{R_{\rm{a}}} {\text{－}} 0.003\;5{R_{\rm{b}}}{\text{，}} \end{array} $
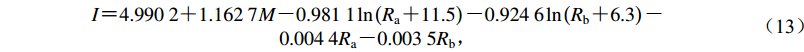
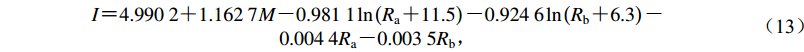
(13) 沿长轴和短轴方向的烈度衰减公式分别为
$ \left\{ {\begin{array}{*{20}{c}} {{\!\!\!\!I_{\rm{a}}}{\text{＝}} 3.288\;4 {\text{＋}} 1.162\;7M {\text{－}} 0.981\;1\ln \left({{R_{\rm{a}}} {\text{＋}} 11.5} \right) {\text{－}} 0.004\;4{R_{\rm{a}}}}{\text{，}}\\ {{\!\!\!\!\!\!\!\!\!\!I_{\rm{b}}} {\text{＝}} 2.594\;0{\text{＋}}1.1627M {\text{－}} 0.924\;6\ln \left({{R_{\rm{b}}} {\text{＋}} 6.3} \right) {\text{－}} 0.003\;5{R_{\rm{b}}}}{\text{，}} \end{array}\qquad \sigma {\text{＝}} 0.453} \right.{\text{，}} $
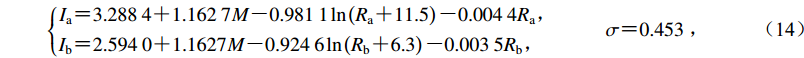
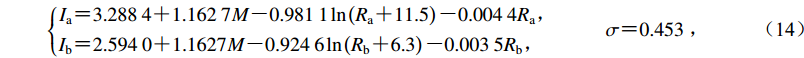
(14) 断裂带西侧烈度衰减参数反演结果为mw＝[4.247 1，1.315 1，1.017 8，0.885 6，0.004 2，0.003 8]T，即
$ \begin{array}{*{20}{c}} I{\text{＝}} 4.247\;1 {\text{＋}} 1.315\;1M {\text{－}} 1.017\;8\ln \left({{R_{\rm{a}}} {\text{＋}} 11.1} \right){\text{－}} 0.885\;6\ln \left({{R_{\rm{b}}} {\text{＋}} 5.4} \right) {\text{－}} \\0.004\;2{R_{\rm{a}}} {\text{－}} 0.003\;8{R_{\rm{b}}}{\text{，}} \end{array} $
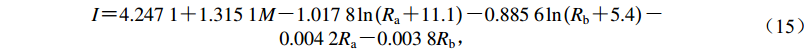
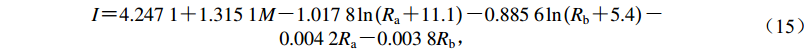
(15) 沿长轴和短轴方向的烈度衰减公式分别为
$ \left\{ {\begin{array}{*{20}{c}} {{\!\!\!\!I_{\rm{a}}} {\text{＝}} 2.753\;6 {\text{＋}} 1.315\;1M {\text{－}} 1.017\;8\ln \left({{R_{\rm{a}}} {\text{＋}}11.1} \right){\text{－}} 0.004\;2{R_{\rm{a}}}}{\text{，}}\\ {{\!\!\!\!\!\!\!I_{\rm{b}}} {\text{＝}} 1.797\;3 {\text{＋}} 1.315\;1M {\text{－}} 0.885\;6\ln \left({{R_{\rm{b}}} {\text{＋}} 5.4} \right) {\text{－}} 0.003\;8{R_{\rm{b}}}}{\text{，}} \end{array}} \right.\qquad \sigma {\text{＝}} 0.490{\text{.}} $
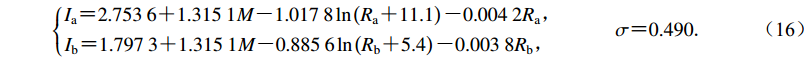
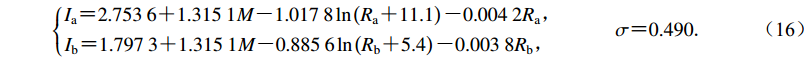
(16) 图2a和图2b分别给出了郯庐断裂带东、西两侧沿长轴和短轴方向的烈度衰减曲线。从图中可以看出，使用本文提出的方法，即使不进行近场补点和远场补点，烈度衰减曲线在近场和远场仍能收敛，说明本文提出的施加模型约束的反演方法是行之有效的。
![]()
图 2 研究区郯庐断裂带东侧（a）和西侧（b）烈度衰减曲线Figure 2. Seismic intensity attenuation curves in east side （a） and west side （b） of Tanlu fault zone in the studied area2.2 反演结果的稳定性
采用1.3节中介绍的方法，随机抽取80%的数据进行反演，用余下20%的数据进行检验，自助抽样试验重复1 000次。郯庐断裂带东西两侧1 000次自助抽样试验所得各参数结果的平均值分别为mebm=[4.906 9，1.143 7，0.950 4，0.907 7，0.003 8，0.002 9]T和mwbm=[4.419 7，1.271 8，1.002 6，0.894 4，0.003 8，0.003 2]T，此结果与2.1节中的反演结果相差不大。图3和图4给出了郯庐断裂带东侧和西侧1 000次自助抽样试验反演结果绘制而成的烈度衰减曲线，图中黑线为1 000次随机抽样试验反演结果绘制的烈度衰减曲线，绿线为1 000次随机抽样结果的平均值，红线为2.1节中的反演结果。从图中可以看出，郯庐断裂带无论是东侧还是西侧，随机抽样试验反演的平均结果（绿线）与所有数据的反演结果（红线）差异均不大，且对于M7.0以下的震级档，除去个别烈度衰减曲线出现一定的偏离，其余结果均相对集中，证明本文的反演方法是相对稳定的。
![]()
图 3 郯庐断裂带东侧长轴方向（a）和短轴方向（b）的自助抽样结果绘制的烈度衰减曲线Figure 3. Seismic intensity attenuation curves along major axis （a） and minor axis （b） in eastside of Tanlu fault zone by a bootstrapping process![]()
图 4 郯庐断裂带西侧长轴方向（a）和短轴方向（b）的自助抽样结果绘制的烈度衰减曲线Figure 4. Seismic intensity attenuation curves along major axis （a） and minor axis （b） in west side of Tanlu fault zone by a bootstrapping processThis page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
3. 结果对比
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
![]()
图 5 郯庐断裂带东侧烈度衰减曲线与五代图烈度衰减曲线对比（a） 长轴方向; （b） 短轴方向Figure 5. Comparison of seismic intensity attenuation curves between east side of Tanlu fault zone and fifth generation seismic ground motion parameter zonation map（a） Major-axis direction; （b） Minor-axis direction图6给出了本文反演的郯庐断裂带西侧结果与五代图东部强震区结果的对比，长轴方向和短轴方向的烈度衰减曲线对比结果分别如图6a和图6b所示。从图中可以看出，两者整体衰减趋势也基本一致，但断裂带西侧烈度衰减曲线在各个震级档均略高于五代图结果，但随着震级的增大两者的差距有略微变小的趋势。
![]()
图 6 郯庐断裂带西侧烈度衰减曲线与五代图烈度衰减曲线对比（a） 长轴方向；（b） 短轴方向Figure 6. Comparison of seismic intensity attenuation curves between west side of Tanlu fault zone and fifth generation seismic ground motion parameter zonation map（a） Major-axis direction; （b） Minor-axis direction图7给出了本文反演的郯庐断裂带东西两侧长轴方向（图7a）和短轴方向（图7b）烈度衰减曲线的对比结果。从两幅图中可以看出，断裂带两侧长短轴方向烈度衰减曲线的差异基本是一致的。当M＝3.0时，断裂带东侧的烈度衰减曲线略高于西侧；当M＝4.0时，两者很接近；当M＝5.0且震中距小于200 km时，断裂带西侧烈度衰减曲线略高于东侧，且距震中越近，这种趋势越明显；当M＝6.0时断裂带西侧烈度衰减曲线明显高于东侧，震中附近断裂带西侧的烈度衰减曲线比东侧高出约0.3度。
![]()
图 7 郯庐断裂带东侧与断裂带西侧烈度衰减曲线对比（a） 长轴方向；（b） 短轴方向Figure 7. Comparison of seismic intensity attenuation curves between east side and west side of Tanlu fault zone（a） Major-axis direction; （b） Minor-axis direction4. 讨论与结论
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
地震波的速度结构从不同角度反映了地下介质的状态，两者之间存在一定的联系，一般地震波速度越大，其衰减越弱。针对本研究区已有诸多介质三维速度结构的研究成果（黄耘等，2011；刘保金等，2015；熊振等，2016），这些结果表明，郯庐断裂带中南段东侧的地壳速度整体上低于西侧的地壳速度。地震波在地壳中传播的速度越快，表明介质越坚硬、致密，地震波在其中传播时衰减的能量越弱，反映在烈度上即为地震对该区域造成的烈度越强，烈度衰减的越慢。这可能也是本文之所以得出断裂带西侧的烈度衰减曲线大体上高于东侧的衰减曲线的原因。本文的主要结论如下：
1） 提出了一种施加模型约束的遗传算法来反演地震烈度衰减参数，通过令目标函数一范数最小的策略来使反演结果更加稳健，结果表明即使不进行近场和远场补点，烈度衰减曲线仍能收敛。之后，本文通过自助抽样方法对反演结果进行评价，1 000次自助抽样反演结果表明，在M≤7.0的震级档，本文结果是相对稳定的，此外，用自助抽样的反演结果能对未抽样的数据进行检验。
2） 郯庐断裂带两侧的烈度衰减特性存在差异，断裂带西侧整体上高于断裂带东侧，这与研究区衰减结构（Q值的分布）及速度结构是对应的，本质上还是与断裂带两侧本身的介质结构的差异有关。
3） 结合自助抽样结果和表1及图2的数据分布来看，本文反演的郯庐断裂带东侧和西侧的烈度衰减参数在M≤7.0，震中距小于300 km范围内相对可靠。但是应该指出的是，烈度值本身受诸多因素的影响，存在很强的不确定性，本文仅作为烈度衰减参数反演方法的学术探索，结果究竟是否合理，还有待实际数据的进一步检验和证明。
-
![]()
图 1 研究区参与反演的地震震中分布图
Figure 1. Epicenter location of earthquakes for inversion in the studied area
![]()
图 2 研究区郯庐断裂带东侧（a）和西侧（b）烈度衰减曲线
Figure 2. Seismic intensity attenuation curves in east side （a） and west side （b） of Tanlu fault zone in the studied area
![]()
图 3 郯庐断裂带东侧长轴方向（a）和短轴方向（b）的自助抽样结果绘制的烈度衰减曲线
Figure 3. Seismic intensity attenuation curves along major axis （a） and minor axis （b） in eastside of Tanlu fault zone by a bootstrapping process
![]()
图 4 郯庐断裂带西侧长轴方向（a）和短轴方向（b）的自助抽样结果绘制的烈度衰减曲线
Figure 4. Seismic intensity attenuation curves along major axis （a） and minor axis （b） in west side of Tanlu fault zone by a bootstrapping process
![]()
图 5 郯庐断裂带东侧烈度衰减曲线与五代图烈度衰减曲线对比
（a） 长轴方向; （b） 短轴方向
Figure 5. Comparison of seismic intensity attenuation curves between east side of Tanlu fault zone and fifth generation seismic ground motion parameter zonation map
（a） Major-axis direction; （b） Minor-axis direction
![]()
图 6 郯庐断裂带西侧烈度衰减曲线与五代图烈度衰减曲线对比
（a） 长轴方向；（b） 短轴方向
Figure 6. Comparison of seismic intensity attenuation curves between west side of Tanlu fault zone and fifth generation seismic ground motion parameter zonation map
（a） Major-axis direction; （b） Minor-axis direction
![]()
图 7 郯庐断裂带东侧与断裂带西侧烈度衰减曲线对比
（a） 长轴方向；（b） 短轴方向
Figure 7. Comparison of seismic intensity attenuation curves between east side and west side of Tanlu fault zone
（a） Major-axis direction; （b） Minor-axis direction
表 1 郯庐断裂带东西两侧地震震级和烈度分布表
Table 1 Distribution of earthquake magnitude and intensity in east and west sides of Tanlu fault zone
震级范围 地震次数 烈度值≥Ⅳ的等震线条数 合计 主断裂东测 主断裂西测 东 西 Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ 东 西 MS3.0—3.9 8 10 6 6 0 0 0 0 0 9 7 0 0 0 0 0 12 16 MS4.0—4.9 15 14 9 15 5 0 0 0 0 7 14 4 0 0 0 0 29 25 MS5.0—5.9 2 5 1 1 2 2 0 0 0 1 4 5 3 0 0 0 6 13 MS6.0—6.9 2 1 2 2 1 1 1 0 0 0 0 1 1 0 0 0 7 2 MS7.0—7.9 0 2 0 0 0 0 0 0 0 0 1 2 2 2 2 1 0 10 合计 27 32 18 24 8 3 1 0 0 17 26 12 6 2 2 1 54 66 
下载: 导出CSV
-
陈达生,刘汉兴. 1989. 地震烈度椭圆衰减关系[J]. 华北地震科学,7(3):31–42. Chen D S,Liu H X. 1989. Elliptical attenuation relationship of earthquake intensity[J]. North China Earthquake Science,7(3):31–42 (in Chinese).
范小平,何奕成,王俊菲,杨云. 2017. 郯庐断裂带中南段地壳介质散射强度[J]. 地球物理学报,60(5):1725–1734. doi: 10.6038/cjg20170510 Fan X P,He Y C,Wang J F,Yang Y. 2017. The crust seismic scattering strength below the middle-south segment of Tancheng–Lujiang fault zone[J]. Chinese Journal of Geophysics,60(5):1725–1734 (in Chinese).
高德潜. 1996. 地震烈度衰减关系统计方法的探讨[J]. 国际地震动态,3(4):6–10. Gao D Q. 1996. An approach to the statistical methods on relation of seismic intensity attenuation[J]. Recent Developments in World Seismology,3(4):6–10 (in Chinese).
高孟潭. 2015. GB18306—2015《中国地震动参数区划图》宣贯教材[M]. 北京: 中国质检出版社: 169–180. Gao M T. 2015. GB18306—2015, Publicity Materials for Seismic Ground Motion Parameter Zonation Map of China[M]. Beijing: Chinese Quality Inspection Publishing House: 169–180 （in Chinese）.
何奕成,徐年,吴珍云,郑黄海,王琛. 2018. 江苏及邻区地震烈度衰减关系[J]. 地震地磁观测与研究,39(1):60–66. doi: 10.3969/j.issn.1003-3246.2018.01.010 He Y C,Xu N,Wu Z Y,Zheng H H,Wang C. 2018. Study on seismic intensity attenuation law in Jiangsu and its adjacent areas[J]. Seismological and Geomagnetic Observation and Research,39(1):60–66 (in Chinese).
胡聿贤. 1999. 地震安全性评价技术教程[M]. 北京: 地震出版社: 288–292. Hu Y X. 1991. A Technical Course on Seismic Safety Evaluation[M]. Beijing: Seismological Press: 288–292 （in Chinese）.
黄耘,李清河,张元生,孙业君,毕雪梅,金淑梅,王俊. 2011. 郯庐断裂带鲁苏皖段及邻区地壳速度结构[J]. 地球物理学报,54(10):2549–2559. doi: 10.3969/j.issn.0001-5733.2011.10.012 Huang Y,Li Q H,Zhang Y S,Sun Y J,Bi X M,Jin S M,Wang J. 2011. Crustal velocity structure beneath the ShandongJiangsu-Anhui segment of the Tancheng-Lujiang fault zone and adjacent areas[J]. Chinese Journal of Geophysics,54(10):2549–2559 (in Chinese).
刘保金,酆少英,姬计法,石金虎,谭雅丽,李怡青. 2015. 郯庐断裂带中南段的岩石圈精细结构[J]. 地球物理学报,58(5):1610–1621. doi: 10.6038/cjg20150513 Liu B J,Feng S Y,Ji J F,Shi J H,Tan Y L,Li Y Q. 2015. Fine lithosphere structure beneath the middle-southern segment of the Tanlu fault zone[J]. Chinese Journal of Geophysics,58(5):1610–1621 (in Chinese).
刘军,吕红山,温和平,李志强,谭明. 2014. 稳健回归模型在地震烈度衰减关系中的应用[J]. 地震工程学报,36(1):114–119. doi: 10.3969/j.issn.1000-0844.2014.01.0114 Liu J,Lü H S,Wen H P,Li Z Q,Tan M. 2014. Application of robust regression model in seismic intensity attenuation relationship[J]. China Earthquake Engineering Journal,36(1):114–119 (in Chinese).
沙海军,吕悦军,彭燕菊,唐荣余,张晓波. 2004. 地震烈度椭圆衰减的限定模型及其在华北地区的应用[J]. 防灾减灾工程学报,24(1):28–36. Sha H J,Lü Y J,Peng Y J,Tang R Y,Zhang X B. 2004. A constrained model of elliptical attenuation of earthquake intensity and its application in North China[J]. Journal of Disaster Prevention and Mitigation Engineering,24(1):28–36 (in Chinese).
汪素云, 时振梁, 1993. 有感半径与震级的关系及其应用[G]//中国地震区划文集. 北京: 地震出版社: 179–184. Wang S Y, Shi Z L. 1993. The Relationship of Sensible Radius vs Magnitude and Its Applications[G]//The Collected Works on Seismic Zonation of China. Beijing: Seismological Press: 179–184 （in Chinese）.
汪素云,俞言祥,高阿甲,阎秀杰. 2000. 中国分区地震动衰减关系的确定[J]. 中国地震,16(2):99–106. doi: 10.3969/j.issn.1001-4683.2000.02.001 Wang S Y,Yu Y X,Gao A J,Yan X J. 2000. Development of attenuation relations for ground motion in China[J]. Earthquake Research in China,16(2):99–106 (in Chinese).
汪素云,裴顺平,Hearn T M,许忠淮,Ni J F,俞言祥. 2008. 利用ML振幅研究地壳横波Q值Ⅱ :Q横向变化特征[J]. 地球物理学报,51(7):133–139. Wang S Y,Pei S P,Hearn T M,Xu Z H,Ni J F,Yu Y X. 2008. Crustal S-wave Q estimated from ML amplitude Ⅱ :Q lateral variation in China[J]. Chinese Journal of Geophysics,51(7):133–139 (in Chinese).
王文萍,王庆良. 1999. 利用遗传算法和最小二乘联合反演共和地震位错参数[J]. 地震学报,21(3):285–290. doi: 10.3321/j.issn:0253-3782.1999.03.009 Wang W P,Wang Q L. 1999. Dislocation parameters of Gonghe earthquake jointly inferred by genetic algorithm and least squares method[J]. Acta Seismologica Sinica,21(3):285–290 (in Chinese).
王晓军,文毅,鲁权,邵辉成,聂大巍. 2012. 陕西分区烈度衰减关系研究[J]. 灾害学,27(4):98–102. doi: 10.3969/j.issn.1000-811X.2012.04.021 Wang X J,Wen Y,Lu Q,Shao H C,Nie D W. 2012. Research on intensity attenuation relations of different regions in Shaanxi Province[J]. Journal of Catastrophology,27(4):98–102 (in Chinese).
万永革,刘瑞丰,李鸿吉. 1997. 用遗传算法反演京津唐张地区的三维地壳结构和震源位置[J]. 地震学报,19(6):623–633. Wang Y G,Liu R F,Li H J. 1997. The inversion of 3D crustal structure and hypocenter location in the Beijing-Tianjin-Tangshan-Zhangjiakou area by genetic algorithm[J]. Acta Seismologica Sinica,19(6):623–633 (in Chinese).
吴建平,明跃红,曾融生. 2001. 遗传算法中的光滑约束反演及其在青藏高原面波研究中的应用[J]. 地震学报,23(1):45–53. doi: 10.3321/j.issn:0253-3782.2001.01.006 Wu J P,Ming Y H,Zeng R S. 2001. Smooth constraint inversion technique in genetic algorithms and its application to surface wave study in the Tibetan Plateau[J]. Acta Seismologica Sinica,23(1):45–53 (in Chinese).
熊振,李清河,张元生,毕雪梅,金淑梅. 2016. 郯庐断裂带鲁苏皖段地壳速度结构的分段特征及其地质意义[J]. 地球物理学报,59(7):2433–2443. doi: 10.6038/cjg20160710 Xiong Z,Li Q H,Zhang Y S,Bi X M,Jin S M. 2016. Segmentation of crustal velocity structure beneath the Shandong-Jiangsu-Anhui segment of the Tanlu fault zone and adjacent areas and its geological implications[J]. Chinese Journal of Geophysics,59(7):2433–2443 (in Chinese).
杨从杰,李清河,王俊,霍祝青. 2016. 郯庐断裂带中段中上地壳介质非均匀性[J]. 地震学报,38(1):29–40. doi: 10.11939/jass.2016.01.003 Yang C J,Li Q H,Wang J,Huo Z Q. 2016. Medium inhomogeneity of mid-upper crust beneath the middle segment of Tancheng-Lujiang fault zone[J]. Acta Seismologica Sinica,38(1):29–40 (in Chinese).
俞言祥,汪素云. 2006. 中国东部和西部地区水平向基岩加速度反应谱衰减关系[J]. 震灾防御计算,1(3):206–217. Yu Y X,Wang S Y. 2006. Attenuation relations for horizontal peak ground acceleration and response spectrum in eastern and western China[J]. Technology for Earthquake Disaster Prevention,1(3):206–217 (in Chinese).
周都民,张元生,张树勋. 1999. 遗传算法在地震定位中的应用[J]. 西北地震学报,19(2):167–171. Zhou D M,Zhang Y S,Zhang S X. 1999. Application of the genetic algorithm to seismic location[J]. Northwestern Seismological Journal,19(2):167–171 (in Chinese).
Brazee R J. 1972. Attenuation of modified mercalli intensities with distance for the United States East of 106°W[J]. Seismol Res Lett,43(1):41–52. doi: 10.1785/gssrl.43.1.41
Ergin K. 1969. Observed intensity-epicentral distance relations in earthquakes[J]. Bull Seismol Soc Am,59(3):1227–1238.
Gutenberg B,Richter C F. 1942. Earthquake magnitude,intensity,energy,and acceleration[J]. Bull Seismol Soc Am,32(3):163–191.
Howell B F Jr,Schultz T R. 1975. Attenuation of modified mercalli intensity with distance from the epicenter[J]. Bull Seismol Soc Am,65(3):651–665.
-
期刊类型引用(3)
1. 郑尔宗，张以晨，徐毓蔓. 基于改进遗传算法的地震应急物资配送路径规划. 华北地震科学. 2024(02): 25-29+72 . 
百度学术
2. 江昊琳，缪发军，李子烨，孙小航，何奕成. 国家地震烈度速报江苏子系统仪器烈度产出分析. 防灾减灾工程学报. 2024(03): 735-739 . 百度学术
3. 王冬辰，王琛，张婷，高飞. 江苏省地震应急专题图快速产出系统设计与实现. 地震地磁观测与研究. 2023(03): 185-191 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 1047
- HTML全文浏览量: 677
- PDF下载量: 74
- 被引次数: 5
