Influence of rupture velocity of the directly-beneath fault on the basin seismic effect
-
摘要: 首先基于有限断层破裂下的运动学震源模型，对比验证了三维谱元法对于近场地震动的模拟精度。 进而通过含盆地模型与不含盆地的一维水平成层模型的地震动强度之间和放大系数分布特征之间的对比，详细研究了直下型断层的破裂速度对盆地地震效应的影响。结果表明，盆地的存在会显著改变近断层地震动的分布特征，同时盆地内不同分量强地震动的分布特征变化较大。断层破裂速度对盆地地震效应影响显著，随破裂速度的增大盆地地震动强度逐渐增加，但不同分量上地震动强度的增加速率显著不同，受盆地效应的影响，放大系数表现出与强地震动不同的分布特征。盆地放大系数整体表现出随破裂速度的增加而减小的趋势，但不同分量放大系数所受影响程度差异明显。同时，盆地内地震动强烈放大区域的位置也受破裂速度的显著影响，但其总体上集中在断层两侧区域及垂直于破裂方向的盆地边缘附近。Abstract: Earthquakes caused by strike-slip fault often lead to serious earthquake damage to the cities above the basin when the fault rupture parameters have a significant effect on basin amplification. In this paper, the simulation accuracy of 3D spectral element method for near field vibration is contrasted under the kinematic source model based on the finite fault rupture. Then, by comparing the distribution characteristics of seismic intensity and amplification factor between the basin model and the one-dimensional horizontal layered model with no basin, the influence of the rupture velocity of the fault buried directly beneath the basin on the seismic effect of the basin is studied in detail. The results show that the existence of the basin will significantly change the distribution characteristics of near-fault ground motions, but the distribution characteristics of strong ground motions of different components in the basin will be significantly different. The amplification factor appears different distribution characteristics from strong ground motion with the influence of basin effect. The influence of fault rupture velocity on seismic effect of basin is significant. With the increase of rupture velocity, the ground motion intensity of the basin increases gradually, but the increase rate of different components is significantly different. The amplification factor of the basin overall shows a trend of decreasing with the rupture velocity increasement, but the influence degree for the amplification factor of different components is obviously different. Meanwhile, the location of the area with strong amplification in the basin is also significantly affected by the rupture velocity, but generally concentrated on both sides of the fault as well as near the basin edge perpendicular to the rupture direction.
-
引言
自1994年美国北岭MW6.7地震和1995年日本神户MW6.9地震之后，城市直下型断层发震对城市的强烈破坏作用逐渐引起研究者的重视。地壳浅部直下型断层由于距离地表较近，因此在其发震时地面运动表现出明显的近场地震效应，例如破裂的方向性效应、上盘效应、近场速度大脉冲等，常引起近场区域强烈的地面运动，进而对建造在其上的人口密集的城市系统造成非常严重的震害，典型实例如1976年唐山MS7.8大地震（刘启方，李雪强，2011）、1995年日本神户MW6.9地震（Furumura，Koketsu，1998）等。其中唐山地震的发震断层横穿唐山市区，造成重大人员伤亡和财产损失。而盆地对于地震动的放大作用已被大量的观测记录、震害调查及数值模拟结果所证实（郭恩，周锡元，2010；Bindi et al，2011；Yu et al，2017）。近场效应与盆地效应的耦合则会进一步加重震害的程度，例如1995年日本神户（Kobe） MW6.9地震中有限断层的破裂方向性效应和盆地边缘效应的共同作用所形成的较大幅值的地表速度是大阪盆地边缘强烈破坏带形成的主要原因（Pitarka et al，1998）。此外，城市活断层调查结果表明，位于盆地之上且下部区域存在发震断层的城市并非个例，许多城市范围之下经探明均有活断层存在，例如银川隐伏断层、成都龙泉山断裂、福州闽侯—南屿断裂等，地震危险性分析表明，这些活断层未来具备发生M6.0—6.5中强地震的可能性。因此，探究直下型断层发震对盆地地震放大效应的影响，以及近场地震效应与盆地地震效应的耦合对近场强地面运动的影响具有重要的现实意义。
既有研究已注意到有限断层的震源参数对盆地地震效应的重要影响。刘启方等（2008）探讨了设定直下型断层破裂下，断层埋深、破裂方式及破裂速度等对昆明盆地地震动模拟结果的影响。结果表明随破裂速度的增大，近场地震动的方向性效应增强，导致近场地震动幅值增大，但未对盆地地震效应的影响进行详细研究。Moschetti等（2017）的研究显示有限断层模型的震源参数（破裂速度、滑动速度、震源位置、位错分布等）对盐湖盆地的长周期地震动影响显著，并且将破裂速度的影响归因于方向性效应的变化。Graves等（2008）对圣安德列斯断层MW7.8设定地震作用下洛杉矶盆地的宽频带地震动模拟结果显示，盆地内地震动对断层的破裂速度非常敏感，破裂速度15%的变化可引起局部场点地面速度峰值变化2倍以上。刘中宪等（2017）研究了断层倾角变化对盆地内部地震动峰值的影响，得出当倾角在30°—90°范围内时，随着倾角的增大，盆地内PGA和PGV逐渐减小。Wirth等（2019）基于地震点源模型研究了盆地的放大特征与震源特性之间的关系，结果表明盆地地震动的放大系数很大程度上取决于震源的位置和深度，浅源地震更容易导致盆地长周期地震动的放大，且近震与远震所引起的盆地最大放大区域的位置相反。以往研究多集中于对盆地内地震动的影响上，对有限断层的破裂过程对盆地放大效应的影响关注不多，而其影响机理目前也并不十分清楚。同时，作为断层重要参数之一的破裂速度目前尚难以准确估计，多假定其与断层所在区域的地壳剪切波速之间的比值满足一定区间值（Beresnev，Atkinson，1997）。因此有必要开展破裂速度对盆地地震放大效应影响的研究。此外，当前在城市区划、结构抗震设计中考虑场地对地震动的影响时，多将其假定为一维水平成层模型，进而估计地表地震动的水平，而对于盆地等三维复杂地质结构的影响考虑不多，而不少研究表明这一简化方法会明显低估盆地内部分区域的地震动幅值（Horike et al，1990）。因此，有限断层破裂下，三维沉积盆地对于地表地震动的影响值得进一步研究。
本文拟采用谱元法（Patera，1984）模拟盆地直下型有限断层破裂辐射的地震波在地壳及盆地内的传播过程，探究断层破裂速度的变化对三维沉积盆地的地震动放大系数（定义为三维沉积盆地相比一维水平成层场地对应PGV的比值）及其空间分布特征的影响，并初步分析产生影响的机理，为考虑有限断层破裂过程的盆地区域近场地震动模拟提供参考。
1. 有限断层破裂下基于谱元法的近场地震动模拟精度验证
本文采用三维谱元法模拟近场有限断层破裂下地震波在盆地中的传播过程。Komatitsch和Tromp （1999）及廖树超等（2018）验证了三维谱元法在力源和矩张量点源作用下在近场地震动模拟中的高精度。本节通过对比相同断层破裂下，谱元程序与基于离散波数有限元法的COMPSYN程序（Spudich，Xu，2002）的模拟结果，以及与全空间条件下对应解析解（刘启方，2005）的差异来验证谱元程序在有限断层破裂下近场地震动模拟中的精度。
建立如图1所示的验证模型，即2 km×2 km×5 km的均匀半空间模型，压缩波速为5.196 km/s，剪切波速为3.0 km/s，密度为2.0 g/cm3。断层尺寸为100 m×200 m，倾角、走向、滑动角分别为90°，90°，0°。初始破裂点位于断层左端中心点，坐标为（0，0，−4 100） m，自左向右单侧破裂，破裂速度为2.7 km/s，上升时间为0.2 s，位错为0.2 m。采用6个点源近似该有限断层。观测点A的坐标为（−615，−630，−3 000） m。
首先将谱元程序与COMPSYN程序修改为相同的钟形震源时间函数，即
${\rm{s}}\!\!\!\!{\text{（}}t\!{\text{）}}\!\!\!\!{\text{＝}}\frac{{1{\text{－}} \cos \dfrac{{2{\rm{\pi }}t}}{T}}}{{2T}}{\text{，}}\;0{\text{≤}}t{\text{＜}}T{\text{，}}$
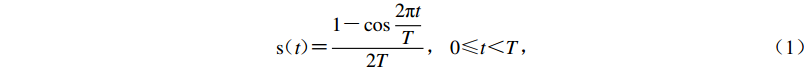
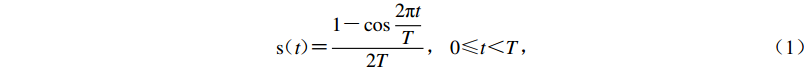
(1) 式中，T为上升时间，s（t）表示t时刻的滑动速率，其时程和傅里叶谱如图2所示。
![]()
图 2 震源钟形滑动速率时间函数的时程 （a）及其对应的傅里叶振幅谱 （b）Figure 2. Source bell-shaped slip-rate time history （a） and its Fourier spectrum （b）将上述震源破裂下谱元程序和COMPSYN程序模拟得到的观测点A的x分量的位移时程及频谱与全空间解析解的结果进行对比（图3）。从图3中可以看出，谱元程序的模拟结果无论在时域还是频域与COMPSYN程序及地表反射波到达前的全空间解析解的结果均较为吻合，表明谱元程序在有限断层破裂下对于近场地震动的模拟精度较高。
![]()
图 3 谱元程序和COMPSYN程序模拟得到的观测点A沿x向的结果与全空间解析解对比（a） 位移时程；（b） 位移时程对应的频谱Figure 3. Comparison of the simulated results of point A along the x direction obtained from the spectral element method and COMPSYN program and full-space analytical solution（a） Displacement time-history；（b） Corresponding spectrum2. 断层破裂速度对盆地地震效应的影响
2.1 计算模型
建立120 km×120 km×32 km的计算模型（图4），盆地形状为三维梯形，地表处长宽分别为13 km×6 km，盆地倾角为45°，深度为500 m。盆地覆盖层及外部基岩介质参数列于表1。取尺寸为49 km×17 km的垂直走滑断层为基本断层模型，断层滑动角为0°，顶面埋深为4 km。基于经验统计公式（Hanks，Kanamori，1979；Wells，Coppersimith，1994；Somerville et al，1999）确定基本断层的震源参数为：破裂速度为2.16 km/s，平均上升时间为1.1 s，平均位错为1.1 m。断层的破裂方式为单侧破裂，初始破裂点位于断层左端中心点，深度为12 km，破裂方向为x方向。取子断层尺寸为1 km×1 km，共计49×17个子断层。
表 1 盆地模型的介质参数Table 1. Medium parameters of basin model名称 vS/（km·s−1） vP/（km·s−1） ρ/（g·cm−3） 盆地外 2.4 5.2 2.4 盆地内 0.7 2.0 1.9 图5给出了观测点的具体分布情况。观测点均位于地表，共布置了950个，其中盆地内观测点为325个，测点间距为540 m；盆地外观测点为625个，测点间距为3 240 m。
![]()
图 5 模型观测点分布（a） 整个模型的地表区域；（b） 局部放大的盆地地表区域Figure 5. Distribution of observation points for the model（a） The surface area of the whole model； （b） The surface area of the enlarged basin单元网格尺寸划分：盆地外最大为810 m×810 m×810 m，盆地内约为90 m×90 m×30 m。为减小计算量，从盆地内到盆地外，单元尺寸由小到大进行两次过渡，其中盆地内较小的网格尺寸可以较好地模拟盆地边缘附近覆盖层厚度的变化。计算时取时间步长为0.3 ms，共模拟60 s的地震波传播过程。震源时间函数取高斯函数，其时间过程及频谱如图6所示。结合单元尺寸及模型介质波速分布情况，本文能模拟的地震动最高频率约为1 Hz。
![]()
图 6 震源滑动速率时间函数（a）及其对应的傅里叶振幅谱（b）Figure 6. Slip rate time function （a） and its Fourier spectrum （b） of the source2.2 有限断层破裂下盆地地震动及放大系数的分布特征
为研究盆地的放大效应，采用上、下两层介质构成的水平成层模型作为参考模型，其上层介质与盆地内的介质属性相同，下层介质与盆地外的介质属性相同。在上述基本断层模型作用下，水平成层模型和含盆地模型模拟得到了地表沿断层走向（FP）（图7）、垂直断层走向（FN）（图8）、垂直（UD）分量（图9）的地表速度峰值（peak ground velocity，缩写为PGV）以及放大系数的分布，其中放大系数定义为盆地模型地表的峰值速度与水平成层模型地表的峰值速度之比。从图7—9中可以看出：
![]()
图 7 FP分量的水平成层模型PGV （a）、含盆地模型PGV （b）、盆地内PGV （c）及盆地内PGV放大系数AF （d）的分布Figure 7. Distribution of PGV of horizontal stratification model （a）， PGV of basin model （b），PGV inside the basin （c） and amplification factor of PGV inside the basin （d） of FP component![]()
图 8 FN分量的水平成层模型PGV （a）、含盆地模型PGV （b）、盆地内PGV （c）及盆地内PGV放大系数AF （d）的分布Figure 8. Distribution of PGV of horizontal stratification model （a），PGV of basin model （b），PGV inside the basin （c） and amplification factor of PGV inside the basin （d） of FN component![]()
图 9 UD分量的水平成层模型PGV （a）、含盆地模型PGV （b）、盆地内PGV （c）及盆地内PGV放大系数AF （d） 的分布Figure 9. Distribution of PGV of horizontal stratification model （a），PGV of basin model （b），PGV inside the basin （c） and amplification factor of PGV inside the basin （d） of UD component1） 盆地的存在显著改变了近场地震动的分布特征。因盆地可捕获大部分的地震波能量，导致盆地区域的地震动幅值相比邻近区域强烈放大（图7b，8b，9b）。对于盆地外围区域，FP和FN分量的地震动峰值相比水平成层模型均显著减小（图7b，8b），但垂直分量的盆地外围PGV却有一定程度的放大，最大可达水平成层模型的2倍左右（图9b）。
2） 不同分量所对应的盆地内强地震动的分布特征差异明显。沿FP方向，最大地震动幅值位于盆地最右侧边缘区域（图7c）；沿FN方向，PGV最大值靠近盆地左侧边缘区域，并向右侧递减（图8c）；沿UD方向，强地震动位于紧靠断层地表迹线两侧及盆地南北两侧边缘的条带状区域内，而最大PGV位于盆地左上和左下角点附近的局部范围（图9c）。
3） 盆地内不同分量的地震动峰值大小与断层辐射方式有较强的相关性。盆地内PGV的最大值具有FN分量＞FP分量＞UD分量的特征，这与不含盆地的水平成层模型的规律相同。
4） 盆地内地震动放大系数的分布特征与强地震动的分布特征有类似之处，但也有明显区别。对于FP分量（图7d），强烈放大区域紧靠断层两侧呈条带状分布，最大放大系数（18左右）位于盆地右侧，且紧靠断层地表迹线，而盆地左侧边缘区域的放大系数相对较小（约为4）；对FN分量（图8d），其放大系数的分布与强地震动的分布基本一致，但最大放大系数（2左右）相比其余两分量小的多；垂直分量（图9d）的强烈放大区域亦集中在断层两侧，但与FP分量不同的是，其放大系数最大的区域并非发生在盆地边缘区域，而是呈较均匀的条带状展布在断层两侧，最大放大系数为20左右。
2.3 有限断层破裂速度对盆地地震效应的影响
大量的反演结果表明断层的平均破裂速度约为剪切波速的0.6—0.9倍（Beresnev，Atkinson，1997）。本节基于上述基本断层模型，分别取断层破裂速度（vr）为1.44，1.68，1.92，2.16 km/s，进而对比不同破裂速度下盆地内三分量的速度峰值分布和放大系数分布，对比结果如图10和图11所示。图12和图13分别给出了盆地内PGV的最大值及平均值、盆地内放大系数的最大值及平均值随破裂速度的变化趋势。图14为盆地内观测点B （−4 860，0，0）在不同破裂速度下FN分量的速度时程频谱。可以看出：
![]()
图 10 不同破裂速度vr下盆地内三分量的峰值速度PGV分布（a） 平行断层走向分量；（b） 垂直断层走向分量；（c） 竖向分量Figure 10. Distribution of PGV for three components in the basin under different rupture velocities vr（a） Fault-strike-parallel component； （b） Fault-strike-perpendicular component； （c） Vertical component![]()
图 11 不同破裂速度vr下盆地内三分量的放大系数AF分布（a） 平行断层走向分量；（b） 垂直断层走向分量；（c） 竖向分量Figure 11. Amplification factor distribution of three components in the basin under different rupture velocities vr（a） Fault-strike-parallel component； （b） Fault-strike-perpendicular component； （c） Vertical component![]()
图 12 不同破裂速度vr下盆地内三分量峰值速度PGV的最大值（a）及平均值（b）Figure 12. Maximum （a） and average （b） value of PGV for three components in the basin under different rupture velocities vr![]()
图 13 不同破裂速度vr下盆地内三分量峰值速度PGV的放大系数AF的最大值（a）及平均值（b）Figure 13. Maximum （a） and average （b） values of amplification factor for three components PGV in the basin under different rupture velocities vr![]()
图 14 破裂速度vr＝1.44 （a），1.68 （b），1.92 （c）和2.16 （d） km/s时观测点B模拟FN分量的速度时程频谱Figure 14. Spectrum of velocity time-history for FN component of point B when rupture velocities vr＝1.44 （a），1.68 （b），1.92 （c） and 2.16 （d） km/s，respectively1） 整体而言，随着破裂速度的增大，近场地震动方向性效应增强，盆地内三分量的地震动强度均逐渐增加（图10，12），这与刘启方等（2008）、Moschetti等（2017）的结论类似；但不同分量地震动强度的增大速率不同，其中FN分量的增长速率＞FP分量＞UD分量（图12）。此外，整体来看，三分量的最大或平均放大系数近似存在FP分量＞UD分量＞FN分量的特征（图13），表明FN分量主要受破裂方向性效应控制，受盆地效应的影响相对较小，而FP和UD分量受盆地放大效应的影响明显。
2） 随着破裂速度的增大，FP分量强烈放大区域的位置整体具有向右移动的趋势，且始终靠近盆地右侧边缘（图11a）。放大系数的大小起伏明显（图13），但整体表现出随破裂速度的增大而减小的趋势，较小破裂速度时的最大AF明显大于破裂速度较大时的最大AF，其中以破裂速度为1.44 km/s时最大。
3） 随着破裂速度的增加，FN分量最大放大系数逐渐减小（图13a），如vr＝2.16 km/s时的最大AF仅为vr＝1.44 km/s时的1/2左右，且最大放大系数的区域从盆地右侧边缘逐渐转移到盆地左侧边缘，但始终位于断层的地表迹线上（图11b）。随着破裂速度的增大，其平均放大系数接近于1 （图13b），表明该分量上由于盆地导致的放大效应越来越不明显。可能的原因是垂直断层走向分量上易出现速度大脉冲，断层破裂速度增大时，破裂方向性效应增强，形成周期更长、幅值更大的长周期大脉冲。这从图14中也可明显看出，即随着破裂速度的增大，盆地地面运动的频率成分逐渐从相对“高”频向低频移动。相比盆地有限的尺寸而言，盆地对此长周期大脉冲的放大效应可能并不明显，而放大效应主要受不同土层间的阻抗差异控制，导致放大系数减小。
4） 随着破裂速度的增大，垂直分量最大放大系数的变化无一致规律，当破裂速度与剪切波速的比值在0.6—0.8之间时，最大或平均放大系数随破裂速度的增加单调递减，但比值为0.9时最大或平均放大系数又突然急剧增加（图13）。最大放大系数出现在vr＝2.16 km/s的模型，而以vr＝1.92 km/s模型的放大系数最小。盆地效应与破裂方向性效应的耦合可能是产生上述现象的主要原因。此外，vr＝2.16 km/s时的强烈放大区域呈连续的条带状分布在断层两侧，而破裂速度较小时则呈散珠状分布（图11c），推测可能存在一临界破裂速度，当实际vr大于此值时才会出现条带状分布区域。
5） 基于本文模型及选定的破裂速度，三分量地震动的平均放大系数分别为5.43，1.72，5.42，表明忽略三维盆地的地震效应，而采用简化的一维水平成层模型可能导致地震动强度的明显低估，尤其是对于FP分量和UD分量。
2.4 盆地内外介质阻抗比的影响
本节对不同阻抗比（impedance contrast，缩写为IC）下模拟结果的差异进行讨论。在2.1节计算模型的基础上，保持断层破裂速度为剪切波速的0.9倍不变，仅增大盆地内外介质波阻抗的差异，具体介质参数列于表2。改变后的阻抗比为表1中所对应阻抗比的6倍左右。IC改变前后FN分量的PGV分布以及放大系数分布如图15，16所示。可以看出：首先，阻抗比的差异对盆地放大效应的影响很大。IC改变前后的最大峰值速度接近，但阻抗比较大时FN分量的放大系数是阻抗比较小时的2倍左右；其次，阻抗比的差异也显著影响盆地的强地震动及放大系数的分布特征。当IC＝4.33时，地震动最大值集中在靠近初始破裂点的盆地左侧边缘，当IC＝24.32时，地震动最大值则更加对称地分布在盆地的左右两侧边缘以及断层的地表迹线处，盆地地震动放大系数也有类似特征。
表 2 不同阻抗比模型的介质参数对比Table 2. Comparison of medium parameters for different impedance contrast modelvS/（km·s−1） ρ/（g·cm−3） 阻抗比IC
（盆地外/盆地内）盆地外 盆地内 盆地外 盆地内 改变前 2.4 0.7 2.4 1.9 4.33 改变后 3.0 0.256 4.15 2.0 24.32 ![]()
图 15 阻抗比IC分别为4.33 （a）和24.32 （b）时盆地内FN分量的PGV分布Figure 15. PGV distribution of FN component in the basin when impedance contrast IC is 4.33 （a） and 24.32 （b）![]()
图 16 阻抗比IC分别为4.33 （a）和24.32 （b）时盆地内FN分量的放大系数AF分布Figure 16. Amplification factor AF distribution of FN component in the basin when impedance contrast IC is 4.33 （a） and 24.32 （b）3. 讨论与结论
本文考虑有限断层破裂引起的近场地震效应与盆地放大效应的耦合作用，基于三维谱元法研究了盆地直下型断层的破裂速度对盆地放大效应的影响。结果显示：
1） 盆地内强地震动的分布特征受震源辐射方式的影响明显，是导致不同分量间最强烈地震动区域的位置不同的原因之一。相比一维水平成层模型，盆地对其内部地震动有显著的放大效应，最大放大系数可达20左右。受盆地影响，放大系数的分布特征与强地震动分布特征并不相同。放大区域主要分布在断层的地表投影两侧以及垂直破裂方向的盆地边缘区域。
2） 不同分量的放大系数分布特征差别显著，FP分量强烈放大区域靠近远离初始破裂点的盆地边缘且紧邻断层地表迹线，FN分量主要分布在断层的地表迹线上，UD分量集中在断层的地表投影线两侧。
3） 直下断层的破裂速度对盆地地震动的影响显著。破裂速度越大，盆地地表的反应就越强，其中盆地内PGV最大值的增大速率以FN分量最大，UD分量最小，但强烈地震动区域的范围受破裂速度的影响不敏感。
4） 盆地放大效应受破裂速度的影响强烈。除UD分量外，盆地最大和平均放大系数整体上随破裂速度的增加而减小，但不同分量放大系数值存在差异。其中FP分量最大，FN分量最小，主要受方向性效应控制。
5） 盆地内强烈放大区域的位置也受破裂速度的显著影响。随破裂速度的增加，FP分量的最大放大系数向右移动，FN分量从盆地右侧边缘转移到左侧边缘，垂直分量由散珠状分布转变为条带状分布。
此外，需要说明的是，本文结果是在设定盆地内外波速、密度的情况下获得的，而盆地内外介质阻抗比的差异对盆地地震效应的影响显著，有关不同阻抗比下破裂速度对盆地效应影响的差异性有必要开展更进一步的研究。
-
![]()
图 2 震源钟形滑动速率时间函数的时程 （a）及其对应的傅里叶振幅谱 （b）
Figure 2. Source bell-shaped slip-rate time history （a） and its Fourier spectrum （b）
![]()
图 3 谱元程序和COMPSYN程序模拟得到的观测点A沿x向的结果与全空间解析解对比
（a） 位移时程；（b） 位移时程对应的频谱
Figure 3. Comparison of the simulated results of point A along the x direction obtained from the spectral element method and COMPSYN program and full-space analytical solution
（a） Displacement time-history；（b） Corresponding spectrum
![]()
图 5 模型观测点分布
（a） 整个模型的地表区域；（b） 局部放大的盆地地表区域
Figure 5. Distribution of observation points for the model
（a） The surface area of the whole model； （b） The surface area of the enlarged basin
![]()
图 6 震源滑动速率时间函数（a）及其对应的傅里叶振幅谱（b）
Figure 6. Slip rate time function （a） and its Fourier spectrum （b） of the source
![]()
图 7 FP分量的水平成层模型PGV （a）、含盆地模型PGV （b）、盆地内PGV （c）及盆地内PGV放大系数AF （d）的分布
Figure 7. Distribution of PGV of horizontal stratification model （a）， PGV of basin model （b），PGV inside the basin （c） and amplification factor of PGV inside the basin （d） of FP component
![]()
图 8 FN分量的水平成层模型PGV （a）、含盆地模型PGV （b）、盆地内PGV （c）及盆地内PGV放大系数AF （d）的分布
Figure 8. Distribution of PGV of horizontal stratification model （a），PGV of basin model （b），PGV inside the basin （c） and amplification factor of PGV inside the basin （d） of FN component
![]()
图 9 UD分量的水平成层模型PGV （a）、含盆地模型PGV （b）、盆地内PGV （c）及盆地内PGV放大系数AF （d） 的分布
Figure 9. Distribution of PGV of horizontal stratification model （a），PGV of basin model （b），PGV inside the basin （c） and amplification factor of PGV inside the basin （d） of UD component
![]()
图 10 不同破裂速度vr下盆地内三分量的峰值速度PGV分布
（a） 平行断层走向分量；（b） 垂直断层走向分量；（c） 竖向分量
Figure 10. Distribution of PGV for three components in the basin under different rupture velocities vr
（a） Fault-strike-parallel component； （b） Fault-strike-perpendicular component； （c） Vertical component
![]()
图 11 不同破裂速度vr下盆地内三分量的放大系数AF分布
（a） 平行断层走向分量；（b） 垂直断层走向分量；（c） 竖向分量
Figure 11. Amplification factor distribution of three components in the basin under different rupture velocities vr
（a） Fault-strike-parallel component； （b） Fault-strike-perpendicular component； （c） Vertical component
![]()
图 12 不同破裂速度vr下盆地内三分量峰值速度PGV的最大值（a）及平均值（b）
Figure 12. Maximum （a） and average （b） value of PGV for three components in the basin under different rupture velocities vr
![]()
图 13 不同破裂速度vr下盆地内三分量峰值速度PGV的放大系数AF的最大值（a）及平均值（b）
Figure 13. Maximum （a） and average （b） values of amplification factor for three components PGV in the basin under different rupture velocities vr
![]()
图 14 破裂速度vr＝1.44 （a），1.68 （b），1.92 （c）和2.16 （d） km/s时观测点B模拟FN分量的速度时程频谱
Figure 14. Spectrum of velocity time-history for FN component of point B when rupture velocities vr＝1.44 （a），1.68 （b），1.92 （c） and 2.16 （d） km/s，respectively
![]()
图 15 阻抗比IC分别为4.33 （a）和24.32 （b）时盆地内FN分量的PGV分布
Figure 15. PGV distribution of FN component in the basin when impedance contrast IC is 4.33 （a） and 24.32 （b）
![]()
图 16 阻抗比IC分别为4.33 （a）和24.32 （b）时盆地内FN分量的放大系数AF分布
Figure 16. Amplification factor AF distribution of FN component in the basin when impedance contrast IC is 4.33 （a） and 24.32 （b）
表 1 盆地模型的介质参数
Table 1 Medium parameters of basin model
名称 vS/（km·s−1） vP/（km·s−1） ρ/（g·cm−3） 盆地外 2.4 5.2 2.4 盆地内 0.7 2.0 1.9 
下载: 导出CSV
表 2 不同阻抗比模型的介质参数对比
Table 2 Comparison of medium parameters for different impedance contrast model
vS/（km·s−1） ρ/（g·cm−3） 阻抗比IC
（盆地外/盆地内）盆地外 盆地内 盆地外 盆地内 改变前 2.4 0.7 2.4 1.9 4.33 改变后 3.0 0.256 4.15 2.0 24.32
下载: 导出CSV
-
郭恩,周锡元. 2010. 汶川地震盆地效应的思考与建议[J]. 防灾减灾工程学报,30(4):459–465. Guo E,Zhou X Y. 2010. Study on basin effects of Wenchuan earthquake[J]. Journal of Disaster Prevention and Mitigation Engineering,30(4):459–465 (in Chinese).
廖树超,于彦彦,丁海平. 2018. 基于Lamb问题的谱元法和有限元法模拟精度比较[J]. 世界地震工程,34(3):188–196. Liao S C,Yu Y Y,Ding H P. 2018. Comparison of simulation precision between spectral element method and finite element method based on lamb problem[J]. World Earthquake Engineering,34(3):188–196 (in Chinese).
刘启方. 2005. 基于运动学和动力学震源模型的近断层地震动研究[D]. 北京: 中国地震局工程力学研究所: 26–30. Liu Q F. 2005. Studies on Near-Fault Ground Motions Based on Kinematic and Dynamic Source Models[D]. Beijing: Institute of Engineering Mechanics, China Earthquake Administration : 26–30 （in Chinese）.
刘启方,金星,丁海平. 2008. 复杂场地条件下震源参数对断层附近长周期地震动的影响[J]. 地球物理学报,51(1):186–196. doi: 10.3321/j.issn:0001-5733.2008.01.023 Liu Q F,Jin X,Ding H P. 2008. Effects of the source parameters on long period near-fault ground motion in the case of complex site condition[J]. Chinese Journal of Geophysics,51(1):186–196 (in Chinese).
刘启方,李雪强. 2011. 唐山大地震近场宽频带地震动模拟[J]. 地震工程与工程振动,31(5):1–7. Liu Q F,Li X Q. 2011. Broad-band strong motion simulation of the great Tangshan earthquake[J]. Earthquake Engineering and Engineering Vibration,31(5):1–7 (in Chinese).
刘中宪,刘明珍,韩建斌. 2017. 近断层沉积盆地强地震动谱元模拟[J]. 世界地震工程,33(4):76–86. Liu Z X,Liu M Z,Han J B. 2017. Spectral-element simulation of strong ground motion in the near-fault alluvial basin[J]. World Earthquake Engineering,33(4):76–86 (in Chinese).
Beresnev I A,Atkinson G M. 1997. Modelling finite-fault radiation from the ω n spectrum[J]. Bull Seismol Soc Am,87(1):67–84.
Bindi D,Luzi L,Parolai S,Di Giacomo D,Monachesi G. 2011. Site effects observed in alluvial basins:The case of Norcia (Central Italy)[J]. Bull Earthq Eng,9(6):1941–1959. doi: 10.1007/s10518-011-9273-3
Furumura T,Koketsu K. 1998. Specific distribution of ground motion during the 1995 Kobe earthquake and its generation mechanism[J]. Geophys Res Lett,25(6):785–788. doi: 10.1029/98GL50418
Graves R W,Aagaard B T,Hudnut K W,Star L M,Stewart J P,Jordan T H. 2008. Broadband simulations for MW7.8 southern San Andreas earthquakes:Ground motion sensitivity to rupture speed[J]. Geophys Res: Lett,35(22):L22302. doi: 10.1029/2008GL035750
Hanks T C,Kanamori H. 1979. A moment magnitude scale[J]. J Geophys Res: Solid Earth,84(B5):2348–2350. doi: 10.1029/JB084iB05p02348
Horike M,Uebayashi H,Takeuchi Y. 1990. Seismic response in three-dimensional sedimentary basin due to plane S wave incidence[J]. J Phys Earth,38(4):261–284. doi: 10.4294/jpe1952.38.261
Komatitsch D,Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation[J]. Geophys J Int,139(3):806–822. doi: 10.1046/j.1365-246x.1999.00967.x
Moschetti M P,Hartzell S H,Ramirez-Guzman L,Frankel A D,Angster S J,Stephenson W J. 2017. 3D ground-motion simulations of MW7 earthquakes on the Salt Lake City segment of the Wasatch fault zone:Variability of long-period (T≥1 s) ground motions and sensitivity to kinematic rupture parameters[J]. Bull Seismol Soc Am,107(4):1704–1723.
Patera A T. 1984. A spectral element method for fluid dynamics:Laminar flow in a channel expansion[J]. J Computat phys,54(3):468–488. doi: 10.1016/0021-9991(84)90128-1
Pitarka A,Irikura K,Iwata T,Sekiguchi H. 1998. Three-dimensional simulation of the near-fault ground motion for the 1995 Hyogo-ken Nanbu (Kobe),Japan,earthquake[J]. Bull Seismol Soc Am,88(2):428–440.
Somerville P,Irikura K,Graves R,Sawada R,Wald D,Abrahamson N,Iwasaki Y,Kagawa T,Smith N,Kowada A. 1999. Characterizing crustal earthquake slip models for the prediction of strong ground motion[J]. Seismol Res Lett,70(1):59–80. doi: 10.1785/gssrl.70.1.59
Spudich P, Xu L S. 2002. Documentation of Software Package Compsyn sxv3. 11: Programs for Earthquake Ground Motion Calculation Using Complete 1-D Green’s Functions[M]. Pittsburgh: Academic Press: 26–64.
Wells D L,Coppersmith K J. 1994. New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J]. Bull Seismol Soc Am,84(4):974–1002.
Wirth E A,Vidale J E,Frankel A D,Pratt T L,Marafi N,Thompson M,Stephenson W J. 2019. Source-dependent amplification of earthquake ground motions in deep sedimentary basins[J]. Geophys Res Lett,46(12):6443–6450. doi: 10.1029/2019GL082474
Yu Y Y,Ding H P,Liu Q F. 2017. Three-dimensional simulations of strong ground motion in the Sichuan basin during the Wenchuan earthquake[J]. Bull Earthq Eng,15(11):4661–4679. doi: 10.1007/s10518-017-0154-2
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 1048
- HTML全文浏览量: 486
- PDF下载量: 41
- 被引次数: 1
