Influence of actual topography on the source dynamic rupture process and strong ground motion of the 2010 Yushu MS7.1 earthquake
-
摘要: 基于震源动力学模型,采用曲线网格有限差分法模拟了水平自由地表及实际地形条件下2010年玉树MS7.1地震的震源破裂过程及相应的地面地震动,获取了断层面上的破裂传播过程、最终滑移量分布及峰值地面速度分布,讨论了实际地形对玉树地震破裂过程及相应地震动的影响。基于本文设定的动力学模型,模拟结果显示:断层面上的高应力降是玉树地震出现超剪切破裂传播现象的主要原因;计算区域的实际地形阻碍了由自由地表引起的超剪切破裂的产生,对断层面滑移量的分布特征及滑动速率影响较大,进而在一定程度上降低了地震动峰值,同时对地震动的分布特征产生影响,且地震动平行断层面的水平分量相对受影响更大。Abstract: Based on the source dynamic models, the curved grid finite-difference method was implemented to simulate the dynamic rupture process and the resultant ground motions of the 2010 MS7.1 Yushu earthquake with horizontal free surface and actual topography respectively. Then the rupture propagation, final slip distribution and distribution of peak ground velocity were obtained to investigate the effect of actual topography on the dynamic rupture process of the Yushu earthquake and the resultant strong ground motions. Based on our models, the results show that the super-shear rupture occurred during the rupture propagation process, which was mainly induced by high stress drop on fault plane. The actual topography has prevented the generation of super-shear induced by free surface and has a great influence on the final slip distribution and slip rate on fault plane, then will affect the characteristics of ground motions as well as reduce the peak values of ground motions to a certain extent. The fault-parallel component of ground motion is relatively more affected. The investigation about the fault rupture dynamics will help us to understand well about the source rupture process and explain the characteristics of its strong ground motions, which is of great significance to more reasonably predict the ground motions of possible destructive earthquakes in the future.
-
引言
2010年青海玉树MS7.1地震发生于巴颜喀拉地块的边界,震中位于(33.2°N,96.6°E),震源深度为14 km,发震断层以左旋走滑为主。有研究表明此次地震的震源过程中出现了超剪切破裂传播现象(Wang,Mori,2012),而由超剪切破裂产生的马赫波会增加地震动的传播范围,能量也相对更高,导致相对更重的震害(Ben-Menahem,Shingh,1987;Andrews,2010)。因此,从应力场演化过程的角度出发,即基于震源动力学模型研究玉树地震的震源过程很有必要,特别是探讨破裂过程中出现的超剪切破裂现象及相应的地震动特征,能够为从物理机制上更合理地预测未来可能的破坏性大地震的地面地震动提供依据。
玉树地震发生之后,基于震源运动学的破裂过程反演工作大量展开(张勇等,2010;Li et al,2011),但关于动力学破裂过程的研究相对较少。张丽芬(2016)利用断层非均匀的应力分布与非平面断层几何之间的等效关系建立了平面断层模型,获取了玉树地震的震源过程。朱守彪等(2017)研究了玉树地震出现超剪切破裂的动力学机制,认为断层弯折有可能促进亚剪切向超剪切破裂转化,但实现这一转化需初始应力方位与断层间的夹角及断层走向变化的偏角处于某一特定关系。
超剪切破裂现象在震源动力学模型研究中一直备受关注,该现象有两种形成机制:一种是Andrews (1976)在Burridge (1973)研究的基础上进行数值计算时发现S波剪切应力峰值处的子裂纹成核可以使亚剪切破裂转换至超剪切破裂,这种源于断层面上高应力降的超剪切破裂称为Burridge-Andrews机制;另一种超剪切破裂的产生主要受到自由地表的影响(以下称自由地表超剪切),是由水平自由表面下放大的滑移量与SV波到衍射P波的相位转换所产生(Kaneko,Lapusta,2010)。玉树地震的破裂到达地表,而自由表面对浅源地震特别是破裂到达地表时的破裂传播过程有较大影响(Oglesby,Day,2001)。同时,有研究显示,震源破裂过程会受到起伏地形的影响(Ely et al,2010);一些数值模拟结果也表明起伏地形会阻滞自由地表超剪切的出现(Zhang et al,2014;Huang et al,2018)。那么,对于玉树地震而言,其超剪切破裂行为是否仅与断层本身相关,实际地形是否对超剪切破裂及地震动产生影响,这些问题都需要深入研究。
鉴于此,本文拟参考已有的理论模型模拟与实际反演结果,建立震源动力学模型,模拟玉树“设定”地震在水平自由地表及实际地形情况下的震源破裂过程及地震动,通过对比分析实际地形对震源破裂过程的影响,探讨玉树地震超剪切破裂现象的产生机制,以期更深入地理解震源破裂过程,进而为更合理地预测未来可能大地震的地震动提供参考。
1. 模拟方法与计算模型
1.1 曲线网格有限差分法
有限差分法经引入震源动力学模拟(Andrews,1976;Madariaga,1976)后,逐渐成为其中重要的方法之一(Day,1982;Zhang et al,2006,2010;Dalguer,Day,2007)。曲线网格有限差分法(张伟,2006)首先依据起伏地表生成贴体网格模拟实际地形,依此将计算区域离散化,然后求解曲线坐标系下的一阶速度-应力方程组,并使用牵引力镜像法处理自由地表条件,因而能够较好地处理地震波在起伏地形条件下的传播问题(Zhang et al,2012),近年来在动力学破裂模拟方面得到较好的应用(Zhang et al,2014)。作者基于曲线网格有限差分方法施加断层条件,实现了起伏地形条件下动力学破裂过程的数值模拟(王铭锋等,2018),可以用于本次地震破裂过程及地震动的模拟。
1.2 模型设定
1.2.1 断层几何及计算模型
震源运动学反演结果表明,此次玉树地震的发震断层为非平面断层(周慧芳等,2011;Li et al,2011)。胡峰(2014)建立了非平面断层几何形态与应力非均匀分布的平面断层之间的等效关系,使得两者在模拟中有相似的动力学破裂过程及地震动特征。因此,本文设定应力非均匀分布的平面断层为发震断层模型,这样可等效非平面断层几何形态的影响,同时兼顾地形条件的施加。
已有的震源机制参数研究结果表明,玉树地震的发震断层为近于直立的走滑断层(刘超等,2010;USGS,2014)。本文断层几何的设定主要参考张勇等(2010)的模型,设定破裂起始点位于(33.2°N,96.6°E),深度为14 km;考虑到发震断层破裂到达地表,设定断层上界深度为零,断层走向和倾角分别为119°和90°;断层面沿走向和倾向方向的长度分别为80 km和30 km。图1中黑色矩形框表示模拟计算范围,为100 km×50 km,水平自由地表模型中垂向长度为33 km。模拟计算中网格间距设为200 m,速度结构采用CRUST1.0模型,结合有限差分格式的稳定性要求,地震波的有效频率最高约为2.2 Hz。此外,时间步长为0.002 s。除自由地表外,模型其它边界均为吸收边界,以避免地震波在边界处反射而影响模拟结果。
为考察实际地形条件下的震源破裂过程,本文建立了计算区域的地形模型(图2),该模型采用相关区域90 m精度的航天飞机雷达地形测绘任务(Shuttle Radar Topography Mission,缩写为SRTM)高程数据。为便于描述,下文将水平自由地表模型称为模型Ⅰ ,考虑实际地形的模型称为模型Ⅱ 。为更好地分析实际地形的影响,除地形的差异外,模型Ⅱ 中采用的计算模型、断层模型及介质模型参数均与模型Ⅰ 一致。这意味着模型Ⅱ 中的断层上界并未到达实际地形的表面,而是在模拟区域地形高程最低处(3400 m)。这样的设置可以保证两个模型中断层几何的一致性,如果模型Ⅱ中断层几何形态因地形的起伏而出现不规则,那么模拟结果将是断层几何与地形耦合作用的共同结果,无法直观分辨出实际地形的影响。
1.2.2 背景应力分布
初始应力场分布是动力学自发破裂过程模拟的关键因素之一(Harris et al,2018),因此,合理地确定初始应力场分布尤为重要。作者已基于理论模型计算获取了初始应力、破裂强度及临界滑动弱化距离三者与破裂行为之间的定量关系(王铭锋,2018),本文主要依据运动学反演给出的滑移量分布结果及上述定量关系来确定背景应力参数。
张勇等(2010)通过反演远震P波获取了该次地震的滑移量分布,其结果表明该地震的破裂过程可分为两个子事件:破裂起始后0—5 s,主要分布于震中西北10 km到震中东南10 km范围内,其峰值对应的平均破裂速度为1.6 km/s,为亚剪切破裂,这是第一个子事件;破裂起始后5—16 s,分布于距离震中东南17—54 km范围内,为第二个子事件。后者可明显观测到地表破裂,其峰值对应的平均破裂速度为4.0 km/s,超过了震中的剪切波速,即出现了超剪切破裂现象。本文应力场参数的设定主要依据上述结果,同时参考合成孔径雷达干涉测量(interferometric synthetic aperture radar,缩写为InSAR)数据获取的滑移量分布结果(Li et al,2011),即断层面存在分段,滑移量较大的两个区域主要分布在震源附近(有一定深度)和地表附近。
根据上述滑动量分布特征,并考虑凹凸体面积占总破裂面积的比例(Somerville et al,1999),本文设置非均匀分布的背景应力场,主要是初始应力和屈服应力存在不均匀性,如图3和表1所示。图3中:破裂成核区(区域1)的中心点即破裂起始点;对应上述滑移量较大的两个区域设置高初始应力区2,3及4;破裂起始点上方地表附近和断层下界附近的滑动量空区分别设置高强度障碍体区域5和7,这两个区域无法发生破裂;不能破裂的障碍体区域6则对应发震断层分段的位置。各区域的残余应力σr均为零,其它应力参数详见表1,为简单表述各区域内应力的具体数值,表1内各应力值均为该应力具体数值与背景场的破裂强度σu之比值,σu取板内地震典型的应力降,即σu=10 MPa。
表 1 断层面上各区域应力参数Table 1. Stress parameters for the areas on fault plane区域 初始剪切
应力$ {\sigma }_{0} $ 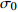
剪切破裂
强度${\sigma }_{{\rm{u}}}$ 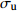
临界滑动弱化
距离Dc/m1 1.01 1.0 0 2 0.60 1.0 0.15 3 0.96 1.5 0.15 4 0.72 1.2 0.15 5 0.20 16.0 40.0 6 0.20 16.0 40.0 7 0.20 16.0 40.0 断层其它区域 0.49 1.0 0.15 断层外 0.20 200.0 40.0 1.2.3 摩擦准则
摩擦准则也是动力学自发破裂过程计算中的关键因素之一(Harris et al,2018),它主要控制着应力释放方式及破裂方式。本文参考前人研究的常用做法,采用滑动弱化摩擦准则(Ida,1972;Andrews,1976)。考虑到垂直断层情形下正应力不发生变化的特点,为简便起见,直接采用剪切应力的表述,即:
${\rm{\sigma }} {\text{=}} \left\{ {\begin{array}{*{20}{l}} \!\!\!{{\sigma _{\rm{u}}} {\text{-}} \left({{\sigma _{\rm{u}}} {\text{-}} {\sigma _{\rm{r}}}} \right)\dfrac{D}{{{D_{\rm{c}}}}}{\text{,}}}&{D {\text{>}} {D_{\rm{c}}}}{\text{,}}\\ \!\!\!{{\sigma _{\rm{r}}}{\text{,}}}&{D {\text{≥}} {D_{\rm{c}}}}{\text{,}} \end{array}} \right.$
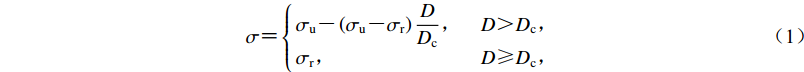
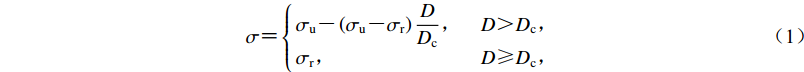
(1) 式中,σ为剪切应力,σu为破裂剪切强度,σr为残余应力,D为滑移量,Dc为临界滑动弱化距离。上述参数在模拟中的具体数值见表1。
2. 模拟结果
采用上述动力学参数,本文通过数值计算分别获取了模型 Ⅰ 和模型Ⅱ的震源破裂过程及相应的地震动分布。
2.1 断层面最终滑移量分布
模型 Ⅰ 和模型Ⅱ中断层面的最终滑移量分布如图4所示,为便于对比,两模型采用相同的色标。该结果显示两个模型的最终滑移量分布具有一些共同特征,即滑移量较大的区域有两个,一个位于破裂起始点附近,滑移量相对较小,另一个位于地表附近,滑移量相对较大。与相应的运动学反演结果(Li et al,2011;王洵等,2014)相比,虽然在滑移量数值及一些分布特征上有所差异,但上述主要分布特征较为一致,数值上的差异可能是由于本文预设应力场对应的应力降相对较大所致。该滑移量极值与朱守彪等(2017)的相关结果相近,表明本文获取的滑移量分布结果及预设模型具有其合理性。
模型 Ⅰ 与模型Ⅱ的滑移量分布也存在一定差异。就分布特征而言,模型 Ⅰ 中滑移量极值所在的滑移量高值区域位于自由地表附近,而模型Ⅱ中相应区域的位置则较断层上界有所下移,这表明滑移量分布特征会受到实际地形的影响。就滑移量而言,模型 Ⅰ 中滑移量的极值相比模型Ⅱ更大,这可能是由于模型 Ⅰ 中断层与自由地表的相互作用更为强烈,且该模型断层面上同时存在高应力降引起的超剪切和自由地表超剪切这两种超剪切破裂行为的原因。
2.2 震源破裂演化过程及破裂传播速度
为考察震源的破裂过程,本文给出了模型 Ⅰ 与模型Ⅱ断层面上滑动速率随时间的演化过程,如图5所示,同样地,两模型的滑动速率图像采用相同的色标。由图5a模型 Ⅰ 的演化过程可见:破裂自区域1成核后,以亚剪切波速自发向外传播;由于障碍体区域5和6无法破裂,破裂自断层下界上方绕过区域6,继续以亚剪切波速传播;当破裂传播至区域3并触发该区域破裂(12.2 s)后,该区域的高初始应力使更多的能量得以释放,破裂传播加快,即使破裂未传播至地表,已有较弱的超剪切破裂现象出现;由于区域3释放的能量持续增加,13.6 s时破裂传播速度明显超过剪切波速度,高应力降引起的超剪切破裂清晰可见;当超剪切破裂未传播至地表时(14.2—15.3 s),在以亚剪切波速传播的破裂前锋与自由地表的相互作用下自由地表附近出现了一个相对较弱的超剪切破裂前锋,本文认为该超剪切破裂前锋正是自由地表超剪切(此现象将在3.1节进行讨论);两种超剪切破裂前锋于15.6 s时在地表汇聚,该时刻的滑动速率达到最大值;15.6 s之后,破裂在两种超剪切破裂的共同作用下始终以超剪切波速扩展至整个断层面。
模型Ⅱ的断层破裂过程(图5b)与模型 Ⅰ 有所不同,两者的差异主要体现在破裂到达断层上界之后的过程中。当高应力降引起的超剪切破裂前锋未到达地表时(14.2—15.3 s),模型Ⅱ中断层上界并未出现相对较弱的超剪切破裂前锋,即未出现自由地表超剪切,其超剪切破裂前锋的位置相比模型 Ⅰ 而言距断层上界更远。在滑动速率数值上,模型 Ⅰ 中由于两种超剪切破裂行为的共同作用,其滑动速率极值大于模型Ⅱ中的极值。两个模型中滑动速率的差异主要集中在破裂起始点深度以上的范围内,破裂起始点深度以下的滑动速率差异很小。在15.6 s及之后的破裂过程中,模型Ⅱ的破裂传播速度略大于模型 Ⅰ 。本文提取了破裂起始点深度上沿走向方向破裂前锋的传播图像(图6)来考察两个模型的破裂传播速度,根据图6计算可知,模型 Ⅰ 和模型Ⅱ中超剪切破裂前锋的平均传播速度分别约为5.5 km/s和5.6 km/s,与Wang和Mori (2012)反演得到的破裂传播速度相符。从数值上看,模型Ⅱ的破裂传播速度确实略大于模型 Ⅰ 的值,但差异较小,这可能是由于复杂地形的形态改变了地震波的反射路径,一部分能量反射到断层面促使破裂传播速度略微增加所致。但是,本文认为这是在本文设定的模型下出现的现象,断层破裂与实际地形相对位置的较小变化可能会导致不同结果的出现,该现象是否具有一般性有待进一步的研究。对比图6a与图6b的滑动速率数值可知,在破裂起始点深度上,模型 Ⅰ 与模型Ⅱ破裂前锋的滑动速率值差异很小,这也表明实际地形影响滑动速率的范围主要集中在破裂起始点深度以上的区域内,这可能与实际地形的起伏高度、形态有关。Kyriakopoulos等(2017)对2010年El Mayor-Cucapah地震进行动力学模拟时考虑了实际地形的影响,认为山体内部未破裂的海拔较低(小于1 km)的库卡帕山影响了破裂前锋的花样及断层面滑动速率,且该影响在深度上可能达到5 km,同时也指出,对于西藏、四川等地形梯度很大的区域,地形影响的断层深度范围会更大,本文的滑动速率结果与此推论相符。
上述破裂演化过程表明,断层面上的高应力降是玉树地震出现超剪切破裂的主要因素,实际地形对自由地表超剪切的产生有阻碍作用,同时,实际起伏地形对断层面滑动速率的影响较大。
2.3 地震动特征
计算区域的地震动表现出与破裂传播过程相对应的特征,两个模型中地面质点振动速度平行于断层面的水平分量(以下简称y分量)在不同时刻的快照如图7所示。可见:自15 s起两个模型均呈现明显的马赫锥,这正是超剪切破裂对应的地震动的典型特征;模型 Ⅰ 中两种超剪切的破裂前锋在地表汇聚时(15.6 s),质点振动速度的y分量达到极值,这也是模型 Ⅰ 中振动速度y分量值大于模型Ⅱ中相应值的原因。
图8给出了两模型中峰值地面速度(peak ground velocity,缩写为PGV)三分量的分布,为便于对比,两者采用相同的色标。需要说明的是,两个模型的y分量的色标以模型Ⅱ中的y分量值为标准,以便于直观地考察模型Ⅱ中y分量的分布特征。根据设定的断层模型,玉树地震断层沿走向由西北向东南方向单侧破裂,在波传播方向上应有破裂方向性效应出现,沿西北向东南方向地震动幅值应逐渐增大,但图8中可见,由于受到初始应力场非均匀性和破裂过程的显著影响,PGV特征并未表现出明显的破裂方向性效应,这与王海云(2010)的模拟结果一致。PGV各分量的极值区域主要分布于对应应力降较高的区域3和4上方的地表附近区域,高强度障碍体区域5和6导致了震中东南方向的地面运动空区。
![]() 图 8 水平自由地表模型(模型Ⅰ,左侧)和实际地形模型(模型Ⅱ,右侧)中峰值地面速度三分量分布(a) 垂直于断层面的水平分量;(b) 平行于断层面的水平分量;(c) 垂向分量Figure 8. Three components of peak ground velocity distribution for horizontal free surface model (model Ⅰ ,left) and actual topography model (model Ⅱ ,right)(a) Fault-normal component;(b) Fault-parallel component;(c) Vertical component
图 8 水平自由地表模型(模型Ⅰ,左侧)和实际地形模型(模型Ⅱ,右侧)中峰值地面速度三分量分布(a) 垂直于断层面的水平分量;(b) 平行于断层面的水平分量;(c) 垂向分量Figure 8. Three components of peak ground velocity distribution for horizontal free surface model (model Ⅰ ,left) and actual topography model (model Ⅱ ,right)(a) Fault-normal component;(b) Fault-parallel component;(c) Vertical component除上述相似特征外,模型 Ⅰ 与模型Ⅱ的PGV特征存在较大差异。就分布特征而言,由于实际地形的影响,模型Ⅱ的PGV呈现了较为强烈的不对称性,特别是对于垂向分量,断层南侧存在一个极值区域,这应该是地形的放大效应所致。就PGV各分量峰值而言,模型Ⅱ中各分量峰值均比模型 Ⅰ 中相应的峰值稍小,模型 Ⅰ 中两种超剪切破裂的共同作用应该是模型 Ⅰ 中PGV各分量峰值相对更大的原因,而断层面的高应力降相对自由地表起主导作用则导致了两个模型峰值差异并不大。但对于y分量,两个模型的峰值差异相对较大,可能的原因是模型 Ⅰ 中断层与自由地表的直接接触使两者之间的相互作用更为强烈,PGV数值也更大。
3. 讨论
2.2节提到,当高应力降引起的超剪切破裂未传播至地表时,本文认为模型 Ⅰ 中自由地表附近出现的相对较弱的超剪切破裂前锋是自由地表超剪切,而模型Ⅱ中实际地形阻碍了自由地表超剪切的产生,这一结论是否合理需要进一步的验证。15.3 s后的破裂过程中高应力降引起的超剪切破裂占主导地位,无法直接确认是否存在自由地表超剪切,即使该现象存在,其演化过程无法直接获取,本节也将对此展开讨论。此外,在本文设定的断层模型中,发震断层中存在分段和弯折的区域以不能破裂的障碍体区域6表示,本节将通过改变区域6的屈服应力来探讨障碍体区域在玉树地震破裂过程中所起的作用。
3.1 均匀初始应力条件下的震源破裂演化过程
为直观考察自由地表超剪切是否存在,本节设定一个相对均匀的断层初始应力模型,即在模型Ⅰ和Ⅱ的断层初始应力模型中去掉高初始应力区域2—4,使初始应力场相对均匀,此时,背景应力场的初始应力不会产生由高应力降引起的超剪切破裂。基于该初始应力模型,本节对水平自由地表(以下称模型Ⅲ)及实际地形(以下称模型Ⅳ)条件下的震源破裂过程进行模拟。
模型Ⅲ和Ⅳ中断层面滑动速率随时间的演化过程如图9所示。模型Ⅲ的结果(图9a)显示,自15 s起,以亚剪切波速传播的破裂前锋与自由地表的相互作用使自由地表附近出现了自由地表超剪切,且随着时间的推移,自由地表超剪切逐步扩展到整个断层面。由此可知,模型 Ⅰ 中自由地表附近出现的相对较弱的超剪切破裂前锋确实是自由地表超剪切,模型 Ⅰ 中的震源破裂过程自15.3 s起即为两种超剪切破裂共同作用的结果,但高应力降引起的超剪切破裂占主导地位,模型Ⅲ与模型 Ⅰ 中断层面滑动速率及破裂传播速度在数值上的差异也表明了这一点。对于模型Ⅳ而言(图9b),其破裂传播速度始终为亚剪切波速,可能是实际地形条件改变了波的反射路径,从而改变了SV波到衍射P波的相位转化,影响了自由地表超剪切的产生。与模型Ⅲ的破裂过程对比可知,实际地形对自由地表超剪切的产生有阻碍作用,模型Ⅱ破裂过程中出现的超剪切破裂仅由断层面上的高应力降引起,高应力降也是造成模型Ⅱ中断层面滑动速率远大于模型Ⅳ的主要原因。
3.2 障碍体区域6对震源破裂过程的影响
本文模拟中以障碍体区域6表示玉树地震发震断层中分段和弯折的区域,该区域在破裂过程中所起作用有待进一步探讨。
首先,本文测试不存在障碍体区域6时的情况,结果发现最终滑移量分布中滑动量较大的区域主要集中在地表附近,并未像模型Ⅰ和模型Ⅱ出现两个滑动量相对较大的区域。这表明障碍体区域6的存在对滑移量分布特征有较大影响,实际地震过程中,断层的分段、弯折可能是实际震源破裂过程可以分为两个子事件的主要原因。然后,本文通过改变障碍体区域6的屈服应力来考察该区域对破裂过程的影响。本节使用的模型仅障碍体区域6的屈服应力及该区域内的临界滑动弱化距离发生变化,其它参数与模型Ⅰ和模型Ⅱ一致。图10给出了障碍体区域6的屈服应力降至5σu时(临界滑动弱化距离与断层面其它位置一致)水平自由地表及实际地形条件下的最终滑移量分布。可见:当障碍体区域6的屈服应力降至5σu时,该区域可发生破裂,由于区域6内的应力增强(屈服应力与初始应力之差)较大,该区域内出现了较大的滑移量。两个模型的滑移量分布分别与模型Ⅰ及模型Ⅱ结果(图4a,b)相比表明,区域6的破裂对地表附近极值区域的滑移量基本无影响,但由于区域6距破裂成核区较近,区域6的破裂增加了破裂起始点附近极值区域的滑移量。
相应的破裂起始点深度上,破裂前锋沿走向方向的传播图像如图11所示。与模型Ⅰ及模型Ⅱ的结果(图6a,b)相比,区域6虽然发生了破裂,但其对整个断层的破裂传播过程影响较小,破裂传播速度及破裂前锋花样均未变化。这是因为区域6内屈服应力较高,破裂传播初期区域6内的应力积累并未超过其屈服应力,直到破裂传播后期才触发区域6的破裂。值得一提的是,本文在测试障碍体区域6的屈服应力变化模型的过程中发现,当屈服应力降至6σu时,水平自由地表模型中区域6发生了部分破裂,而实际地形模型中区域6并未发生破裂。这一现象表明实际地形可通过地震波的反射与断层发生相互作用,从而改变震源破裂过程。综合滑移量分布特征及破裂前锋的传播特征可知障碍体区域6对震源破裂特征的影响,因此,在后续更深入的研究中,有必要考虑玉树地震发震断层的分段、弯折等复杂几何特征的影响。
4. 结论
本文基于震源动力学模型,采用曲线网格有限差分方法计算了玉树地震在水平自由地表和实际地形两种情形下的破裂过程及地震动,对比分析了实际地形对破裂过程及地震动的影响。基于本文设定的模型,其结果表明,断层面上的高应力降是玉树地震出现超剪切破裂的主要原因,实际起伏地形阻碍了自由地表引起的超剪切破裂的出现,并对断层面滑移量的分布特征及滑动速率产生影响,进而影响到地震动的分布特征,同时在一定程度上降低了地震动的峰值,实际地形对地震动平行断层面的水平分量的影响相对更大。对震源动力学破裂过程的研究,可以更深入理解震源过程及产生相应地震动特征的物理机制,进而为合理评估可能的破坏性地震的近场地震动提供依据。
需要说明的是,为相对直观地考察实际地形对玉树地震破裂过程的影响,保证两个模型中断层几何的一致性,本文在实际地形模型中设置的断层上界并未到达起伏地形的表面。而实际地震中断层几何与起伏地形的耦合作用会使断层破裂过程更为复杂,亚剪切破裂向超剪切破裂的转化方式也更复杂,因此,有必要针对破裂到起伏地形表面及断层存在弯折的断层模型展开更深入的研究,考察断层几何与起伏地形耦合时的断层破裂过程及相应地震动特征的复杂性。此外,模拟研究中有必要通过运动学反演及地表形变等多种结果共同约束初始应力场参数的选取,使初始应力参数更贴近实际。
-
图 8 水平自由地表模型(模型Ⅰ,左侧)和实际地形模型(模型Ⅱ,右侧)中峰值地面速度三分量分布
(a) 垂直于断层面的水平分量;(b) 平行于断层面的水平分量;(c) 垂向分量
Figure 8. Three components of peak ground velocity distribution for horizontal free surface model (model Ⅰ ,left) and actual topography model (model Ⅱ ,right)
(a) Fault-normal component;(b) Fault-parallel component;(c) Vertical component
表 1 断层面上各区域应力参数
Table 1 Stress parameters for the areas on fault plane
区域 初始剪切
应力$ {\sigma }_{0} $ 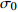
剪切破裂
强度${\sigma }_{{\rm{u}}}$ 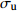
临界滑动弱化
距离Dc/m1 1.01 1.0 0 2 0.60 1.0 0.15 3 0.96 1.5 0.15 4 0.72 1.2 0.15 5 0.20 16.0 40.0 6 0.20 16.0 40.0 7 0.20 16.0 40.0 断层其它区域 0.49 1.0 0.15 断层外 0.20 200.0 40.0 -
胡峰. 2014. 非平面断层与等效平面断层的破裂动力学及辐射特征研究[D]. 合肥: 中国科学技术大学: 9–20. Hu F. 2014. Research on Nonplanar Fault and ESPFM of Dynamic Rupture and Radiation Pattern[D]. Hefei: University of Science and Technology of China: 9–20 (in Chinese).
刘超,许力生,陈运泰. 2010. 2010年4月14日青海玉树地震快速矩张量解[J]. 地震学报,32(3):366–368. Liu C,Xu L S,Chen Y T. 2010. Quick moment tensor solution for 14 April 2010 Yushu,Qinghai,earthquake[J]. Acta Seismologica Sinica,32(3):366–368 (in Chinese).
王海云. 2010. 2010年4月14日玉树MS7.1地震加速度场预测[J]. 地球物理学报,53(10):2345–2354. Wang H Y. 2010. Prediction of acceleration field of the 14 April 2010 Yushu earthquake[J]. Chinese Journal of Geophysics,53(10):2345–2354 (in Chinese).
王铭锋. 2018. 震源动力学破裂过程影响因素及强地震动场特征的研究[D]. 北京: 中国科学院大学: 24–25. Wang M F. 2018. Study on the Influence of Different Factors on Earthquake Dynamic Rupture Process and Its Strong Ground Motions[D]. Beijing: University of Chinese Academy of Sciences: 24–25 (in Chinese).
王铭锋,郑傲,于湘伟,章文波. 2018. 局部山体地形对断层动力学破裂过程的影响研究[J]. 地震学报,40(6):737–752. Wang M F,Zheng A,Yu X W,Zhang W B. 2018. Study on the influence of local mountainous topography to fault dynamic rupture[J]. Acta Seismologica Sinica,40(6):737–752 (in Chinese).
王洵,周云,孙蒙,王卫民. 2014. 青海玉树MW6.9级地震震源破裂过程[J]. 地质通报,33(4):517–523. Wang X,Zhou Y,Sun M,Wang W M. 2014. Rupture process of the 2010 MW6.9 Yushu earthquake in Qinghai Province[J]. Geological Bulletin of China,33(4):517–523 (in Chinese).
张丽芬. 2016. 不同因素对于断层动力学破裂过程复杂性的影响研究[D]. 北京: 中国地震局地球物理研究所: 104–114. Zhang L F. 2016. Influences of Different Factors on the Complexities of Fault Dynamic Rupture Propagation[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 104–114 (in Chinese).
张伟. 2006. 含起伏地形的三维非均匀介质中地震波传播的有限差分算法及其在强地面震动模拟中的应用[D]. 北京: 北京大学: 7–109. Zhang W. 2006. Finite Difference Seismic Wave Modelling in 3D Heterogeneous Media With Surface Topography and Its Implementation in Strong Ground Motion Study[D]. Beijing: Peking University: 7–109 (in Chinese).
张勇,许力生,陈运泰. 2010. 2010年青海玉树地震震源过程[J]. 中国科学:地球科学,40(7):819–821. Zhang Y,Xu L S,Chen Y T. 2010. Source process of the 2010 Yushu,Qinghai,earthquake[J]. Science China Earth Sciences,53(9):1249–1251. doi: 10.1007/s11430-010-4045-5
周慧芳,张景发,胡乐银,罗毅. 2011. 青海玉树地震的InSAR数据同震形变场模拟与参数反演分析[J]. 地球信息科学学报,13(3):418–423. Zhou H F,Zhang J F,Hu L Y,Luo Y. 2011. Co-seismic deformation field and parameters inversion of the Yushu earthquake from InSAR[J]. Journal Geo-Information Science,13(3):418–423 (in Chinese). doi: 10.3724/SP.J.1047.2011.00418
朱守彪,袁杰,缪淼. 2017. 青海玉树地震(MS=7.1)产生超剪切破裂过程的动力学机制研究[J]. 地球物理学报,60(10):3832–3843. Zhu S B,Yuan J,Miao M. 2017. Dynamic mechanisms for supershear rupture processes of the Yushu earthquake (MS=7.1)[J]. Chinese Journal of Geophysics,60(10):3832–3843 (in Chinese).
Andrews D J. 1976. Rupture velocity of plane strain shear cracks[J]. J Geophys Res,81(32):5679–5687. doi: 10.1029/JB081i032p05679
Andrews D J. 2010. Ground motion hazard from supershear rupture[J]. Tectonophysics,493(3/4):216–221.
Ben-Menahem A,Shingh S J. 1987. Supershear accelerations and Mach-waves from a rupturing front. Part I. Theoretical model and implications[J]. J Phys Earth,35(5):347–365. doi: 10.4294/jpe1952.35.347
Burridge R. 1973. Admissible speeds for plane-strain self-similar shear cracks with friction but lacking cohesion[J]. J Geophys Res,35(4):439–455.
Dalguer L A,Day S M. 2007. Staggered-grid split-node method for spontaneous rupture simulation[J]. J Geophys Res,112(B2):B02302.
Day S M. 1982. Three-dimensional finite difference simulation of fault dynamics:Rectangular faults with fixed rupture velocity[J]. Bull Seismol Soc Am,72(3):705–727.
Ely G P,Day S M,Minster J B. 2010. Dynamic rupture models for the southern San Andreas fault[J]. Bull Seismol Soc Am,100(1):131–150. doi: 10.1785/0120090187
Harris R A,Barall M,Aagaard B,Ma S,Roten D,Olsen K,Duan B C,Liu D Y,Luo B,Bai K C,Ampuero J P,Kaneko Y,Gabriel A A,Duru K,Ulrich T,Wollherr S,Shi Z Q,Dunham E,Bydlon S,Zhang Z G,Chen X F,Somala S N,Pelties C,Tago J,Cruz-Atienza V M,Kozdon J,Daub E,Aslam K,Kase Y,Withers K,Dalguer L. 2018. A suite of exercises for verifying dynamic earthquake rupture codes[J]. Seismol Res Lett,89(3):1146–1162. doi: 10.1785/0220170222
Huang H Q,Zhang Z G,Chen X F. 2018. Investigation of topographical effects on rupture dynamics and resultant ground motions[J]. Geophys J Int,212(1):311–323. doi: 10.1093/gji/ggx425
Ida Y. 1972. Cohesive force across the tip of a longitudinal-shear crack and Griffith’s specific surface energy[J]. J Geophys Res,77(20):3796–3805. doi: 10.1029/JB077i020p03796
Kaneko Y,Lapusta N. 2010. Supershear transition due to a free surface in 3-D simulations of spontaneous dynamic rupture on vertical strike-slip faults[J]. Tectonophysics,493(3/4):272–284.
Kyriakopoulos C,Oglesby D D,Funning G J,Ryan K J. 2017. Dynamic rupture modeling of the M7.2 2010 EI Mayor-Cucapah earthquake:Comparison with a geodetic model[J]. J Geophys Res:Solid Earth,122(12):10263–10279. doi: 10.1002/2017JB014294
Li Z H,Elliott J R,Feng W P,Jackson J A,Parsons B E,Walters R J. 2011. The 2010 MW6.8 Yushu (Qinghai,China) earthquake:Constraints provided by InSAR and body wave seismology[J]. J Geophys Res,116(B10):B10302. doi: 10.1029/2011JB008358
Madariaga R. 1976. Dynamics of an expanding circular fault[J]. Bull Seismol Soc Am,66(3):639–666.
Oglesby D D,Day S M. 2001. Fault geometry and the dynamics of the 1999 Chi-Chi (Taiwan) earthquake[J]. Bull Seismol Soc Am,91(5):1099–1111.
Somerville P,Irikura K,Graves R,Sawda S,Wald D,Abrahamson N,Iwasaki Y,Kagawa T,Smith N,Kowada A. 1999. Characterizing crustal earthquake slip models for the prediction of strong ground motion[J]. Seismol Res Lett,70(1):59–80. doi: 10.1785/gssrl.70.1.59
USGS. 2014. M6.9: Southern Qinghai, China[EB/OL]. [2020-03-10]. https://earthquake.usgs.gov/earthquakes/eventpage/usp000hbbt/focal-mechanism.
Wang D,Mori J. 2012. The 2010 Qinghai,China,earthquake:A moderate earthquake with supershear rupture[J]. Bull Seismol Soc Am,102(1):301–308. doi: 10.1785/0120110034
Zhang W,Zhang Z G,Chen X F. 2012. Three-dimensional elastic wave numerical modelling in the presence of surface topography by a collocated-grid finite-difference method on curvilinear grids[J]. Geophys J Int,190(1):358–378. doi: 10.1111/j.1365-246X.2012.05472.x
Zhang W B,Iwata T,Irikura K. 2006. Dynamic simulation of a dipping fault using a three-dimensional finite difference method with nonuniform grid spacing[J]. J Geophys Res,111(B5):B05301.
Zhang W B,Iwata T,Irikura K. 2010. Dynamic simulation of the 1999 Chi-Chi,Taiwan,earthquake[J]. J Geophys Res,115(B4):B04305.
Zhang Z G,Zhang W,Chen X F. 2014. Three-dimensional curved grid finite-difference modelling for non-planar rupture dynamics[J]. Geophys J Int,199(2):860–879. doi: 10.1093/gji/ggu308
-
期刊类型引用(6)
1. 郭昱琴,龚丽文,郭瑛霞,胡久常,李盛. 定点形变资料变化的动力学机制——以五指山台定点形变为例. 大地测量与地球动力学. 2023(08): 869-874 .  百度学术
百度学术
2. 李萌,卢和雄,赵爱平,严丽. 有限元建模与实测应变分析——以九江地震台为例. 大地测量与地球动力学. 2023(10): 1063-1067 .  百度学术
百度学术
3. 刘珠妹,张景发,李盛乐. 2000—2018年全国形变台站周边环境时空变化特征及对垂直摆观测影响分析. 地震工程学报. 2021(03): 583-593 .  百度学术
百度学术
4. 龚丽文,陈丽娟,郭卫英,陈涛,唐小勇. 奉节钻孔应变前兆异常机理分析——区域应力场应力传递的结果. 地震工程学报. 2021(05): 1087-1094+1102 .  百度学术
百度学术
5. 龚丽文,陈丽娟,吕品姬,张燕,郭卫英,肖家强. 黔江台水管仪与垂直摆预报效能对比分析. 地震. 2021(04): 168-179 .  百度学术
百度学术
6. 袁曲,许裕之,吕品姬,张辉,王慧,宋潇潇. 宜昌台三类地倾斜仪观测数据的对比研究. 地震工程学报. 2019(06): 1536-1544 .  百度学术
百度学术
其他类型引用(0)





 下载:
下载:











