Earthquake detection using convolutional neural network and its optimization
-
摘要: 本文以西昌台阵观测的8 321次近震数据为例，详细介绍了利用深度卷积神经网络检测地震的数据处理流程，包括数据预处理、模型训练、波形长度、网络层数、学习率和概率阈值等关键参数对检测结果的影响，并将训练得到的最优模型，应用于事件波形和连续波形的检测。研究表明，数据预处理和数据增强可以提升模型的检测精度和抗干扰能力。用于模型训练的波形窗口长度可近似于S-P到时差的最大值。不同网络层数（5—8层）的检测结果差别不大。对于地震检测，学习率设为10−4—10−3较为合适。卷积神经网络检测出的地震数量与选择的概率阈值有关，通过绘制精确率-召回率变化曲线，可以为选择合适的概率阈值提供参考。本文为进一步利用深度学习算法提高地震检测效果提供了参考。Abstract: Earthquake detection is the key step of automatic processing such as earthquake quick report and earthquake early warning. In recent years, the use of deep learning algorithm to detect earthquakes has developed rapidly. However, there are few detailed researches on data processing flow and neural network parameter optimization. Taking 8 321 near earthquake data observed by Xichang array as an example, this paper introduces in detail the data processing flow of detecting earthquakes by using the deep convolution neural network, such as data preprocessing, model training, waveform length, network layers, learning rate and probability threshold on the detection results. Then we detect the continuous waveform with the optimal model. Our research shows that data preprocessing, data augmentation can improve the detection accuracy and anti-interference ability of the model. The length of waveform window used for model training can be approximated to the maximum value from arrival time difference between S- and P- wave. The detection results of different network layers （5—8 layers） are similar. For seismic detection, it is more appropriate to set the learning rate as 10−4—10−3. The earthquakes detected by convolution neural network are related to the probability threshold. By drawing the tradeoff curve of precision with recall rate, it can provide a reference for selecting the appropriate probability threshold. This paper provides an important reference for further study of earthquake detection with deep learning algorithm.
-
Keywords:
- deep learning /
- convolutional neural network /
- earthquake detection /
- model training /
- Xichang array
-
引言
据中国地震台网测定，北京时间2023年12月18日23点59分在甘肃省积石山县发生MS 6.2地震，震中位于（35.70°N，102.79°E ），震源深度为10 km。此次地震震中距离积石山县城仅8 km，距离兰州市102 km，人口相对密集。青海省循化县、民和县（青海省地震局，2023）、甘肃省兰州市、定西市、武威市、金昌市、庆阳市、平凉市、天水市、陇南市等地震感明显（甘肃省地震局，2023）。地震发生后，甘肃省抗震救灾指挥部于12月20日召开新闻发布会通报，截至当日9时，积石山地震共造成131人死亡，980人受伤，16人失联，此次地震是2023年我国人员伤亡最为严重的地震。
此次积石山MS6.2地震发生在柴达木—祁连地块东北缘，拉脊山断裂系南段附近（图1），是继2001年昆仑山口西MS8.1地震（Li et al，2005；Xu et al，2006），2016年门源MS6.4地震（胡朝忠等，2016），2021年玛多MS7.4地震（Pan et al，2022；Ren et al，2022）和2022年门源MS6.9地震（Li et al，2023a）之后，在柴达木—祁连地块内部发生的一次最大地震。距今约
3700 —3136 年，此次地震震中区域曾发生过至少两次强烈的古地震事件，造成的地震灾害直接导致了齐家文化的毁灭（李智敏等，2014），表明区域内具备发生强震的可能。郭祥云等（2024）的震源机制解结果显示，此次地震以逆冲机制为主，两个断层节面分别为：节面Ⅰ走向301°—307°、倾角50°—58°，滑动角57°—70°，节面Ⅱ走向156°—164°、倾角42°—47°、滑动角112°—127°。然而，由于震源区地质构造复杂，对余震的精细分布和断层的空间展布认识尚不清晰，无法准确判断发震断裂，从而限制了对此次地震发震构造及动力学机制的认识。![]()
图 1 积石山MS6.2地震区域主要断裂和历史地震分布图（a） 柴达木—祁连地块主要活动断裂及历史地震分布图；（b） 震中区主要活动断裂及历史地震分布图（块体主要活动断裂及历史地震分布引自文献Tapponnier 等 （2001），Yuan 等 （2013），徐锡伟等 （2014），Li 等（2023a）GPS矢量引自Wang和Shen （2020）；烈度圈（等震线）引自甘肃省地震局（2023）Figure 1. Maps showing the major active faults and epicenters of historical earthquakes in the regional area of Jishishan MS6.2 earthquake（a） Map showing major active faults in epicenters of historical earthuqakes in Qaidam-Qilian block；（b） Map showing the active faults and epicenters of historic earthquakes in the region of Jishishan MS6.2 earthquakeFault trace is based on the map （Tapponnier et al，2001；Yuan et al，2013； Xu et al，2014；Li et al，2023a）；GPS vectors are from Wang and Shen （2020）；Isoseismal map from Gansu Earthquake Agency （2023）对地震序列进行重定位和反演震源机制解是理解区域地震活动特征、确定发震断裂以及认识断层空间展布特征的重要手段（Waldhauser，Ellsworth，2000；房立华等，2014；鲁人齐等，2022；蔡妍等，2023）。因此，本文基于甘肃和青海地震台网的观测数据，利用双差定位方法（Waldhauser，Ellsworth，2000；房立华等，2018）对积石山MS6.2地震震后10天的地震序列进行重定位，应用FocMech-Flow流程（Li et al，2023b）对主震以及M＞2.0的余震序列进行自动化震源机制解反演。最后，本文结合区域重力异常、历史地震和地质资料等，对此次积石山地震的发震断层和空间展布特征进行分析，以期探讨出此次发震构造的动力学背景，为区域内未来强震活动性的评估提供科学依据。
1. 区域活动构造背景
柴达木—祁连地块位于青藏高原东北缘，表现为挤压环境下的盆−山构造特征，是高原北部构造变形和强震频发的地区（李海兵等，2021），地块边界的活动断裂主要由ENE−EW走向的左旋走滑的东昆仑断裂带、阿尔金断裂带和海原断裂带以及WNW走向的逆冲的祁连山断裂带组成（图1a，郑文俊等，2016），地块内部主要活动断裂为NW走向的日月山断裂和向NE凸出、呈弧形展布的拉脊山断裂带（图1，袁道阳等，2005）。该区域的地震活动十分强烈，自有历史记载以来，发生在柴达木—祁连活动地块边界带内的M≥7强震达20次，其中M≥8的大地震已达4次，包括1654年天水M8地震、1920年海原M8½地震、1927年古浪M8.0地震和2001年昆仑山口西MS8.1地震（图1a）。
拉脊山断裂带是柴达木—祁连地块东部一条重要的逆冲型活动断裂，是介于NNW向的日月山右旋走滑断裂带和WNW向的西秦岭北缘左旋走滑断裂带之间的一个大型挤压构造带（袁道阳等，2005）。在几何展布上，拉脊山断裂带可分为南、北两段，北段约形成于22 Ma （Yuan et al，2013）由近EW向展布的、左旋兼逆冲性质的拉脊山北缘断裂和拉脊山南缘断裂组成。南段约形成于13 Ma （Lease et al，2011）由近NW走向的、以逆冲为主的积石山东缘断裂和积石山西缘断裂组成。积石山西缘断裂走向NW，倾向NE，全长约45 km，为一条逆冲断裂，线性地貌明显，在积石山西侧表现为将加里东期花岗岩向西逆冲到新近系之上（图2）；积石山东缘断裂总体走向NNW，倾向SW，长约40 km，向北延伸与拉脊山北缘断裂斜交，向南则与倒淌河—临夏断裂相连（图1b），断裂运动以逆冲为主，构成了积石山隆起与盆地的分界线，在积石山县西侧可见加里东期花岗闪长岩逆冲到新近系之上（图2）（张波，2012）。此次积石山MS6.2地震震中位于积石山东缘断裂附近（图1b）。
![]()
图 2 积石山MS6.2地震震中区域活动断层分布图地层分布根据青海省地质矿产局（1991）绘制，区域断层数据由桂林理工大学陈立春提供，图中红色断层为本文推测的发震断层，基于遥感解译和野外调查确定Figure 2. Maps showing the detailed active faults in the regional area of Jishishan MS6.2 earthquakeStratigraphic distribution based on the map Qinghai Bureau of Geology and Mineral Resources （1991），fault traces provided by the Professor Chen Lichun from Guilin University of Technology，the red fault in the figure is the conjectural seismogenic faults determined by interpretation of remote sensing images and geological surveying在积石山东缘断裂西侧，分布有几条较小规模的分支断裂，自西向东依次为：锁同断裂、牙儿咱断裂、扎几楞断裂、协拉断裂及位于大河家盆地内部东倾的逆冲断裂，这些分支断裂自NW向SE逐渐收敛至积石山东缘断裂的主断裂带上（图2）。由于第四系覆盖严重，积石山东缘断裂在震中区域的展布特征并不清晰。据地震历史资料显示，拉脊山周缘地区共发生过20余次M5左右的破坏性地震（袁道阳等，2005），但积石山东缘断裂带附近未见历史强震记录。已有的古地震研究显示，大河家盆地的北侧区域在距今
3700 年至3136 年之间，曾发生过两次强震事件，晚第四纪以来发震断裂的垂直活动速率约为0.5 mm/a （李智敏等，2014），大地测量结果则揭示出积石山东缘断裂带现今的垂向活动速率为（1.1±0.2） mm/a （Zhuang et al，2023）。2. 余震精定位结果
截至2023年12月27日6时，甘肃地震台网给出的地震目录中包含了823次余震，震级范围分布在ML−0.7—4.1。使用震中距30 km以内的32个地震台站的数据，其中震中距10 km以内有6个地震台，最近台站的震中距约3.2 km。采用Hypo2000测定主震位置，主震位于（35.748°N，102.812°E ），震源深度16.4 km，水平误差0.73 km，垂直误差0.95 km。采用双差定位方法（Waldhauser，Ellsworth，2000）对震后10天内余震序列进行重新定位，首先根据初始震源位置组成地震对，然后选择相邻较近、到达同一台站的一组震相的走时差来反演震源位置，可较好地消除震源至台站间共同传播路径效应的影响，在国内地震序列特征分析研究中得到了广泛应用（Fang et al，2015；房立华等，2018；易桂喜等，2019；Yang et al，2023； Zhang et al，2023）。本研究采用的一维速度模型分为4层，顶界面深度分别为0，23.1，46.0，56.0 km。P波速度值分别为6.1，6.3，7.0，8.3 km/s。图3a为使用双差定位方法获得的重定位结果，共获得605次地震的位置参数，东西、南北和垂直方向的平均定位误差分别为0.071，0.083，0.138 km。从平面图上看，重新定位后的余震在震中附近主要沿NW向分布，向北逐渐变为近NS向分布（图3a），总长约15 km，且主要集中在南段，北段的余震数量较少。重定位后的震源深度显示，余震主要位于6—15 km深度（图3b），而主震位于整个地震序列的底部。沿BB′方向，余震序列表现为向NE方向倾斜的分布特征（图3c）。
![]()
图 3 余震序列重定位结果分布图（a） 余震震中位置及断层分布图；（b−c） 震源沿AA’和BB’剖面的深度分布图，黄色阴影区为余震集中分布深度，红色条带为拟合的发震断层面Figure 3. Relocation results of the aftershock sequence（a） Distribution of the aftershock epicenters and regional faults；（b−c） Distribution of focal depth along profile AA’ and BB’，yellow shaded area represent the depth of most aftershocks，while the red shaded area shows the fit line of the fault plane3. 震源机制解与应力反演
为进一步确定发震断层及区域应力场的状态，本文使用甘肃省地震局提供的2023年12月18日—12月21日共41个地震事件波形数据和观测报告，应用FocMech-Flow流程（Li et al，2023b）自动化反演震源机制，获得了M2.0—6.2共31个地震事件的震源机制解（图4a）。该流程主要包含三个环节：数据预处理、DiTingMotion判别P波初动极性以及利用格点尝试法（俞春泉等，2009）反演震源机制解。首先根据观测报告筛选出可用于反演震源机制解的地震事件；其次，根据到时信息截取地震波形，并输入DiTingMotion判别P波初动极性；最后，组合P波初动极性和地震事件信息，反演获得震源机制解。其中，主震MS6.2节面Ⅰ走向302°、倾角58°、滑动角45°，节面Ⅱ走向 184°、倾角53°、滑动角138° （图4a）。
![]()
图 4 2023年积石山MS6.2主震和12月18—21日M≥2.0余震的震源机制解（a） 震源机制解空间分布，断层性质与图3a一致；（b） 震源机制分类三角图；（c） 应力场反演结果震源机制类型：蓝色代表逆冲型，紫红色为走滑型，黑色为正断型Figure 4. Focal mechanism solutions of the Jishishan MS6.2 main shock and M≥2.0 after shocks during 18−21 December 2023（a） Distribution of focal mechanism solutions，the fault type is consistent with fig.3a；（b） Triangular diagram of focal mechanism types；（c） Stress field inversion results. Focal mechanisms：Blue represents thrust type， purple represents strike-slip type，black represents normal type参照俞春泉等（2009）评价标准，所获得的31个地震事件震源机制A类12个，B类13个，C类6个。根据震源机制解三个应力轴倾角的大小，使用FMC程序（Álvarez-Gómez，2019）对震源机制进行分类。结果显示，积石山地震序列地震事件的震源机制以逆冲型为主，占总体震源机制的90%以上（图4b）。
采用Vavryčuk （2014）提出的线性迭代联合反演法，分析积石山MS6.2地震应力场，结果显示，此次地震周边整体区域应力场呈WSW−ENE向挤压。σ1方位角约244°，倾角约4°，倾角较低；σ2方位角约153°，倾角约23°，中低角度倾斜；σ3方位角约343°，倾角约67° （图4c，表1）。研究结果说明应力场类型为逆冲型应力场，发震区域整体应力场处于挤压状态（图4a）。
表 1 震区应力场反演结果表Table 1. Stress field inversion results in Jishishan area应力 方位角/° 倾角/° σ1 244.30±6.86 3.67 σ2 152.77±12.26 22.63 σ3 343.01±11.95 67.04 4. 重力异常分析
由于震源区断裂结构复杂，且缺少精细的活动断裂基础调查工作。本文收集并分析了中国地质调查局平均测点间距为5—10 km的布格重力异常数据，以刻画断裂带结构和几何形态（Liu，2021；石磊等，2022；Wang et al，2022b），为发震构造和区域地震危险性研究提供相关参考。此次地震主震和余震深度都分布在30 km以浅区域（图3b），因此首先对布格重力异常进行优化滤波（Guo et al，2013）去除深部（＞30 km）异常，获得震源区剩余异常（图5a）。然后对剩余异常进行频率域换算（Mickus，Hinojosa，2001），得到全张量梯度。重力张量的最小和最大特征向量（Beiki，2013）可分别表示断裂带的走向和倾角（图5）。
![]()
图 5 研究区布格重力异常∆G （a）和断裂倾角β图（b）Figure 5. Bouguer gravity anomalies ∆G （a） and dip angle β distribution map （b） of the study area重力全张量梯度矩阵${\boldsymbol{ \varGamma}} $可分解为三个矩阵：
$$ {\boldsymbol{ \varGamma}} {＝}\left[ {\begin{array}{*{20}{c}} {{g_{xx}}}&{{g_{xy}}}&{{g_{x{\textit{z}}}}} \\ {{g_{yx}}}&{{g_{yy}}}&{{g_{y{\textit{z}}}}} \\ {{g_{zx}}}&{{g_{zy}}}&{{g_{{\textit{z}}{\textit{z}}}}} \end{array}} \right] ＝ {{{\boldsymbol{US}}}}{{{{\boldsymbol{V}}}}^{\rm T}} \text{，} $$ (1) 式中，$ {g_{\textit{z}}} $是在$ （ x\text{，} y ） $水平面上测量的，U是一个正交矩阵，$ {\boldsymbol{S }＝}\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&0&0 \\ 0&{{\lambda _2}}&0 \\ 0&0&{{\lambda _3}} \end{array}} \right] $包含三个正的特征值（$ {\lambda _1} {\text{≥}} {\lambda _2} {\text{≥}} {\lambda _3} $），$ {\boldsymbol{V }＝} ［ {{{\boldsymbol{V}}_1}\,\,{{\boldsymbol{V}}_2}\,\,{{\boldsymbol{V}}_3}} ］ $包含三个特征向量。张量的最小和最大特征向量可分别表示断裂带的走向和倾角。其中，倾角$ \beta $由最大特征向量$ {{\boldsymbol{V}}_1} $的三个分量$ {\nu _{1{{x}}}}\text{，} {\nu _{1{{y}}}}\text{，} {\nu _{1{\textit{z}}}} $定义为（Beiki，2013）：
$$ \beta {＝}{\tan ^{ - 1}}\left( {\frac{{{\nu _{1{\textit{z}}}}}}{{\sqrt {\nu _{1x}^2 ＋ \nu _{1y}^2} }}} \right) \text{，} $$ (2) 由此可对断裂带的倾角进行定量估计，且分析$ \beta $沿断裂带的分布常用来评估断层类型（Beiki，2013； Matsumoto et al，2016）。
剩余重力异常图较好地呈现了西秦岭北缘断裂带，但其位置与地表分布存在差异，重力异常划分出的断裂位置位于地表调查位置的北侧。断裂带以南主要表现为负异常，断裂带以北产生明显变化，相对异常转变为正值，且达到正的最大值（0.15 mm/s2，图5a），与断裂带所在的地块边界上断裂属性相对应。积石山东缘断裂带同样位于异常变化梯级带附近，但与西秦岭北缘断裂带相比，断裂两侧异常值变化较为平缓，表明此次地震震中南北两侧断裂是连续展布的。
重力全张量梯度估计得到的断层倾角为壳内平均值（石磊等，2022）。前人数值模拟研究显示，正断层两侧倾角随深度变化而减小，逆断层两侧倾角随深度变化而增加，走滑断层两侧倾角一般没有明显的变化（Beiki，Pedersen，2010；Beiki，2013；Kusumoto，2015）。由图5b可以看出，西秦岭北缘断裂带两侧倾角没有明显的变化，主要表现为走滑性质。积石山东缘断裂带倾角由西侧的50°—60°增加为70°—80°，表现为明显的逆冲性质。
5. 讨论
5.1 发震构造及三维模型
地震在空间上的分布可直观地反映出发震断层的形态及破裂范围（房立华等，2013；蔡妍等，2023）。由震后十天的余震分布可以看出，在水平方向上，余震由近震中的NW向展布向北逐渐转变为近NS向展布（图3a）；在深度剖面上，余震主要分布深度为6—15 km，且主要发生在主震上方（图3b），总体上余震揭示的断层面倾向NE，倾角近62° （图3c）。本文通过震源机制解，得到主震的节面Ⅰ走向302°、倾角58°、滑动角45°，节面Ⅱ走向 184°、倾角53°、滑动角138° （图4a），其中节面Ⅱ倾向W，这与余震深度剖面揭示的断层倾向明显相反（图3c），由此可以认为，余震的空间展布与断层面解的节面Ⅰ基本一致。已有地质资料表明，震中位于积石山东缘断裂带东侧（图2），该断裂倾向W，倾角60° （Lease et al，2012），这与本文确定的余震分布和震源机制解显示的断层面特征并不一致。本文通过震后野外调查，结合李智敏等（2014）对震区的遥感解译结果，认为大河家盆地东部至南部出露一条逆冲活动断层，该断层南段产状为：走向330°、倾向NE、倾角70°，北段产状为：走向350°、倾向ENE、倾角80°，擦痕指示为逆冲兼左旋走滑特征（图6），该断层的走向、倾向和余震所揭示的断层面产状较为一致（图3a，4a），且余震沿该断层连续、密集分布，因此，可判定为此次地震的发震断裂。该断裂自大河家镇起，呈近NS向展布，在大河家盆地南缘转变为走向NW，总长约15 km，本文将其命名为“大河家断裂”（图2，3a，4a）。
![]()
图 6 大河家断裂野外特征照片（照片位置见图2）大河家断裂南（a）、北（c）段断层野外照片和大河家断裂断层面擦痕（b，d）指示了逆冲兼左旋滑的运动特征。图（a−b）位置由中国地震局地质研究所郭鹏提供，图（c−d）由青海省地震局李智敏提供Figure 6. Field photos of Dahejia fault （location in fig.2）Figs.（a，c） are field photos of Dahejia fault in the southern and northern section；Figs.（b，d） are lineation on the fault plane show-ing the thrust with left-lateral slip component of Dahejia fault. Location of Figs.（a−b） are provided by Guo Peng from the Institute of Geology，China Earthquake Administration； Figs.（c−d） are provided by Li Zhimin from Qinghai Earthquake Agency另一方面，本文的重力异常结果显示积石山主断裂带在震中区域连续展布（图5a），并未出现明显阶区，而积石山主断裂带应位于震中东侧（图2a，3a，4a）。此次地震震中位于右旋走滑的日月山断裂和左旋走滑的西秦岭北缘断裂形成的挤压构造带（图2b，袁道阳等，2005），该类区域应力较易聚集，是典型的孕震构造区域（Lozos et al，2011），在WSW−ENE向挤压应力下（图4a，4c，袁道阳等，2005），可能因局部地壳介质的力学强度存在差异（蔡妍等，2023），大河家断裂带作为积石山东缘断裂系的一条反冲断裂（图6）产生了破裂滑动。在大地构造尺度上，西秦岭北缘断裂带宝鸡—锅麻滩地区晚第四纪以来的左旋走滑速率约为2.1—2.9 mm/a （图7，李传友等，2007；Chen，Lin，2019），向西延伸至尾端，近1 mm/a的速率被小规模的走滑断裂所吸收（Hao et al，2021），近1.6 mm/a的速率则被积石山垂向活动所吸收（Zhuang et al，2023）。大地测量结果显示，现今积石山西缘断裂带垂向活动速率约为（0.5±0.2） mm/a，东缘断裂带则为（1.1±0.2） mm/a，其中约0.5 mm/a的垂向速率又被大河家断裂所吸收（图6，Zhuang et al，2023）。可以看出，在WSW−ENE向挤压应力场下，大河家断裂吸收了积石山地区将近三分之一的应变量，这种应变量的集中分布也是此次地震的一个重要孕震背景。
![]()
5.2 区域危险性分析
在印度板块的持续向北挤压下，青藏高原内部板块沿大型走滑断裂带向东挤出（Tapponnier，Molnar，1976），在此背景下，柴达木—祁连地块沿阿尔金左旋走滑断裂、东昆仑左旋走滑断裂和海源左旋走滑断裂不断向东运移（图7）（徐锡伟等，2014）。自2001年昆仑山口西MS8.1地震之后，近年来柴达木—祁连地块地震活动性逐渐增强，相继发生了2021年玛多MS7.4地震、2022年门源MS6.9地震和此次2023年积石山MS6.2地震。虽然在地理位置上2021年玛多MS7.4地震位于巴颜喀拉地块内部，但Pan等（2022）通过详细的地表破裂调查，认为该地震的发生是昆仑断裂带“截弯取直”的结果，因此也可以认为2021年玛多MS7.4地震发生在柴达木—祁连地块的边界断裂带上。虽然这些数据量还十分有限，但由这些地震的空间分布特征大致可以观察到柴达木—祁连地块应力自西向东传递的趋势，由此可能会导致地块东部的应力增加，进而造成积石山东部区域的强震危险性增加（图8a）。该区域北部的海原断裂1920年发生过M81/2地震，产生了长约220 km的地表破裂（Lasserre et al，1999），相比之下，南部未有地表破裂记录的西秦岭北缘断裂带可能更具强震风险，其中的宝鸡—天水段、武山—锅麻滩段的离逝时间均大于1 000年（邵延秀等，2011），按照约2.1—2.9 mm/a （李传友等，2007；Chen，Lin，2019 ）的滑动速率计算，这两段目前的位移量亏损至少约为2.1—2.9 m。依据最大位错量D和发震震级MW的经验关系式（MW＝6.69＋0.74lgD，Wells，Coppersmith，1994），可以得出该段已具备发生MW6.9—7.0地震的能力，应为重点关注的强震危险性区域。
![]()
图 8 柴达木—祁连块体构造运动与变形模式图（a） 柴达木—祁连地块活动断裂与历史地震分布图，修改自Li 等（2023a）；（b） 印度板块与欧亚板块碰撞下的青藏高原向东逃逸运动学模型，修改自Tapponnier和Molnar （1976）及Wang等（2022a）. 橘色条带为近年来柴达木—祁连地块的强震向东迁移趋势，蓝色箭头代表GPS滑动矢量，棕色、红色箭头分别代表北向和东向的运动分量，GPS矢量据引自Wang和Shen （2020）Figure 8. Model showing Qidam-Qilian block motion and the structural deformation pattern（a） Active faults and historical earthquaks in Qaidam-Qilian block，modified from Li et al （2023a）；（b） Extrusion model of Qinghai-Xizang Plateau under the collision of Indian and Eurasian plates，modified from Tapponnier ，Molnar （1976） and Wang et al （2022a）. The orange bands show the eastward moving trend of strong earthquakes in the Qidam-Qilian block. The blue arrow represents the GPS vector，and the brown and red arrows represent the northern and eastern components of movement，respectively. The GPS vector is based on Wang and Shen （2020）6. 结论
本文利用双差定位和FocMech-Flow震源机制自动反演流程，分别对甘肃积石山MS6.2地震序列进行了重定位和震源机制解分析，通过余震序列的分布特征和震源机制的应力反演，结合重力异常、历史地震和区域地质资料，得到以下主要结论：
1） 积石山地震余震序列在水平分布上表现为近震源区域长轴沿NW−SE向展布，向北转变为近NS向展布的特征，震源深度剖面显示发震断层倾向NE；
2） 震源机制反演结果揭示此次余震序列主要以逆冲型为主，地震周边整体区域应力场呈WSW−ENE向挤压；
3） 积石山东缘断裂带两侧重力异常值变化较为平缓，表明断裂带在震中附近是连续展布的，倾角由其西侧的50°—60° 增加为70°—80°，表现为明显的逆冲性质；
4） 积石山地震的发震断裂为积石山东缘断裂系的一条反冲断裂，该断裂位于大河家盆地东部，在震中附近沿NW向展布，向北逐渐转变为近NS向，与余震序列优势方位一致，本文将其命名为大河家断裂。
中国地震局地球物理研究所蒋长胜研究员、桂林理工大学陈立春教授提供了行文指导；中国地震局地质研究所郭鹏副研究员、青海省地震局李智敏高级工程师提供了野外帮助；审稿专家为本文提出了建设性的意见。作者在此一并表示感谢。
本文第一作者谨以此文表达对Paul Tapponnier先生的沉痛悼念和深切缅怀：Paul Tapponnier先生是国际知名的地球科学学家、青藏高原研究的奠基者之一。他于1976提出了青藏高原滑移线场理论、青藏高原向东逃逸运动学模型，开创了将卫星遥感成功应用于青藏高原活动构造研究之先河。2020年9月1日我有幸成为先生的博士后，得到他的悉心指导，获益良多。先生学术思想气象恢弘，远见卓识，思想敏锐，治学严谨，是我们学习的榜样。2023年12月24日先生突然辞世，学生深表追忆与敬意！
-
![]()
图 4 卷积、池化、全连接层局部示意图
Figure 4. Schematic diagram of convolution，pooling and fully connected layers
![]()
图 5 训练和验证曲线
Figure 5. The training accuracy，validation accuracy for events and noise and loss function curves
![]()
图 6 预处理前后的训练和验证曲线
Figure 6. Training and validation accuracy curves before and after data preprocess
![]()
图 8 不同窗长的训练步数与训练时间的关系
Figure 8. Relationship between training step and training time for different window lengths
![]()
图 9 P波到时前不同窗长的检测结果
（a） P波到时前窗长为4 s；（b） P波到时前窗长为0—7.5 s的随机值
Figure 9. Detection results of different window lengths before the P-wave arrival
（a） The window length before P-wave arrival is 4 s；（b） The window length beforeP-wave arrival is a random varying between 0 and 7.5 s
![]()
图 11 不同概率阈值的精确率-召回率权衡曲线
Figure 11. Precision-recall tradeoff curves fordifferent probability thresholds
![]()
图 12 筛选前后的地震数量统计
Figure 12. Histogram of earthquakesdetected before and after screening
![]()
图 13 CNN检测出的一个近震波形
地震发震时刻为2018年4月28日23时2分43.8秒；震中位置为 （101.846°E，29.251°N）；震级为ML1.5. 图中仅显示了垂直分量；红线是人工拾取的P波到时；虚线框是检测到的地震窗口
Figure 13. Waveforms of a local earthquake detected with CNN
Occurrence time：23:02:43.8 on April 28，2018；epicenter location：101.846°E，29.251°N；ML1.5. Only vertical component is shown in the figure. The red line is the manually picked P wave arrivals. The dotted box is the detected earthquake window
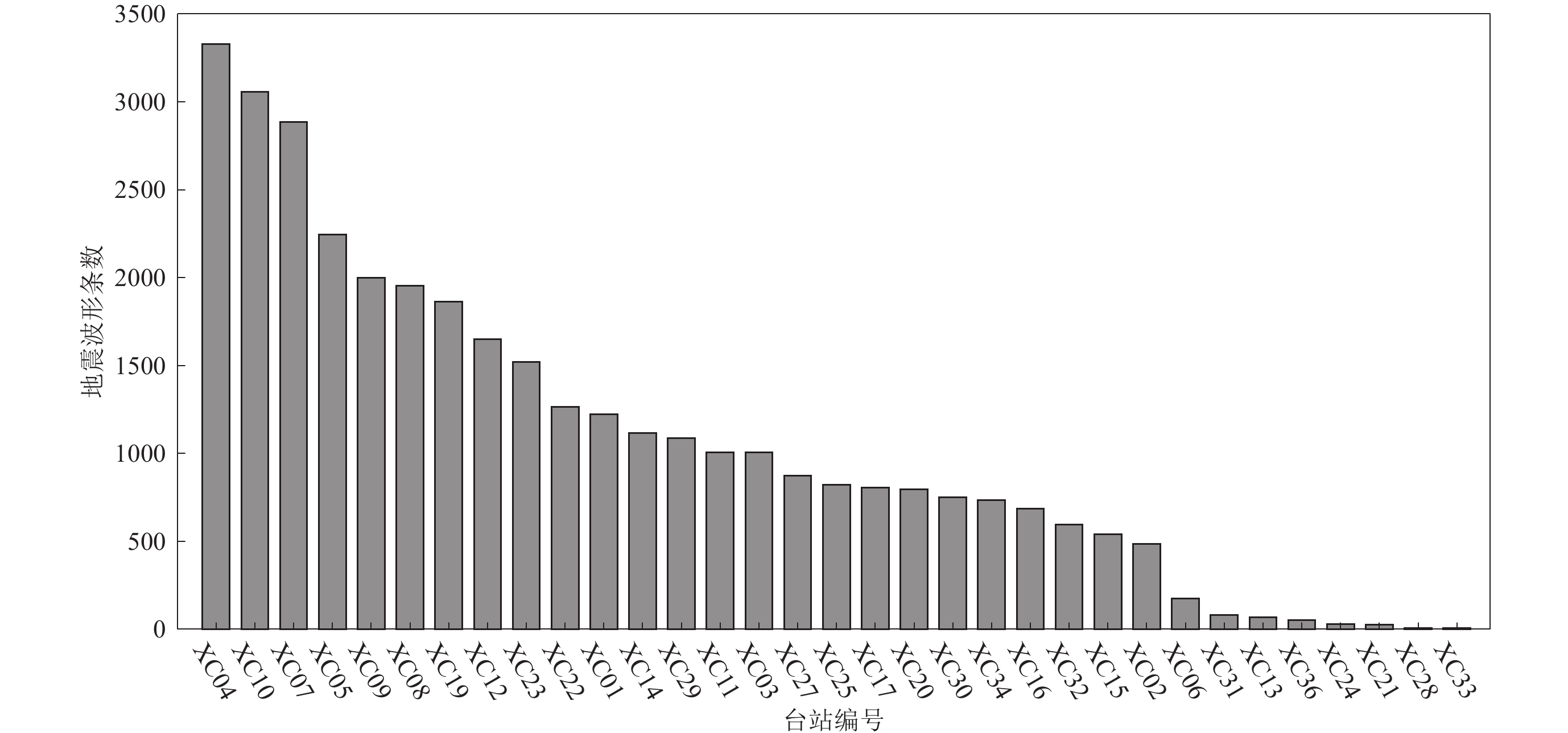
表 1 利用不同规模训练集训练得到的CNN模型检测结果对比
Table 1 Comparison of CNN model detection results from different training sets
编号 训练集
地震次数训练集地震
波形条数检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 1 1 334 6 595 2 882 2 937 97.02% 96.10% 97.89% 96.99% 2 1 334×3 19 785 2 924 2 936 97.70% 97.50% 97.89% 97.69% 3 1334×6 39 570 2 925 2 938 97.75% 97.53% 97.96% 97.75% 4 3 422 17 465 2 910 2 957 97.82% 97.03% 98.58% 97.79% 5 6 790 34 671 2 929 2 957 98.13% 97.67% 98.59% 98.13% 6 6 790×5 173 355 2 938 2 972 98.53% 97.97% 99.09% 98.53% 注：×号表示数据增强的倍数。测试集中的地震波形条数和噪声波形条数均为2 999条。 
下载: 导出CSV
表 2 采用不同窗长的训练集训练得到的CNN模型检测结果对比
Table 2 Comparison of CNN model detection results by training sets with different window lengths
窗口长度/s 检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 10 2 904 2 950 97.60% 96.83% 98.34% 97.58% 15 2 929 2 957 98.13% 97.67% 98.57% 98.12% 20 2 920 2 944 97.77% 97.37% 98.15% 97.76% 25 2 904 2 948 97.57% 96.83% 98.27% 97.54% 30 2 900 2 944 97.43% 96.70% 98.14% 97.41% 35 2 895 2 959 97.60% 96.53% 98.64% 97.57% 40 2 904 2 954 97.67% 96.83% 98.47% 97.64%
下载: 导出CSV
表 3 不同网络层数的检测结果对比
Table 3 Comparison of detection results with different network layers
层数 检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 5 2 916 2 963 98.02% 97.23% 98.80% 98.01% 6 2 946 2 933 98.02% 98.23% 97.81% 98.02% 7 2 941 2 952 98.25% 98.07% 98.43% 98.25% 8 2 941 2 939 98.03% 98.07% 98.00% 98.03% 9 2 912 2 982 98.27% 97.10% 99.42% 98.25%
下载: 导出CSV
-
蒋策,吴建平,房立华. 2018. 地震检测与震相自动拾取研究[J]. 地震学报,40(1):45–57. doi: 10.11939/jass.20170093 Jiang C,Wu J P,Fang L H. 2018. Earthquake detection and automatic phase picking[J]. Acta Seismologica Sinica,40(1):45–57 (in Chinese).
刘芳,蒋一然,宁杰远,张建中,赵艳红. 2020. 结合台阵策略的震相拾取深度学习方法[J]. 科学通报,65(11):1016–1026. Liu F,Jiang Y R,Ning J Y,Sun J Z,Zhao Y H. 2020. An array-assisted deep learning approach to seismic phase-picking[J]. Chinese Science Bulletin,65(11):1016–1026 (in Chinese).
李安. 2019. 基于深度学习的地震事件与震相自动识别[D]. 北京: 中国地震局地球物理研究所: 40–41. Li A. 2019. Automatic Recognition of Seismic Events and Phase Picking Based on Deep Learning[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 40–41 （in Chinese）.
杨旭,李永华,苏伟,孙莲. 2019. 基于优化参数的地震P、S波震相到时自动拾取及质量评估[J]. 地球物理学报,62(11):4290–4299. doi: 10.6038/cjg2019M0059 Yang X,Li Y H,Su W,Sun L. 2019. Optimized automatic pickers and quality assessment:Application to identification of local and regional P and S wave phases[J]. Chinese Journal of Geophysics,62(11):4290–4299 (in Chinese).
于子叶,储日升,盛敏汉. 2018. 深度神经网络拾取地震P和S波到时[J]. 地球物理学报,61(12):151–164. Yu Z Y,Chu R S,Sheng M H. 2018. Pick onset time of P and S phase by deep neural network[J]. Chinese Journal of Geophysics,61(12):4873–4886 (in Chinese).
赵明,陈石,房立华,David A Y. 2019. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报,62(8):3034–3042. Zhao M,Chen S,Fang L H,David A Y. 2019b. Earthquake phase arrival auto-picking based on U-shaped convolutional neural network[J]. Chinese Journal of Geophysics,62(8):3034–3042 (in Chinese).
Allen R V. 1978. Automatic earthquake recognition and timing from single traces[J]. Bull Seismol Soc Am,68(5):1521–1532.
Baer M,Kradolfer U. 1987. An Automatic phase picker for local and teleseismic events[J]. Bull Seismol Soc Am,77(4):1437–1445.
Baillard C,Crawford W C,Ballu V,Hibert C,Mangeney A. 2014. An automatic kurtosis- based P- and S- phase picker designed for local seismic networks[J]. Bull Seismol Soc Am,104(1):394–409.
Dokht R M H,Kao H,Visser R,Smith B. 2019. Seismic event and phase detection using time–frequency representation and convolutional neural networks[J]. Seismol Res Lett,90(2A):481–490.
Earle P S,Shearer P M. 1994. Characterization of global seismograms using an automatic-picking algorithm[J]. Bull Seismol Soc Am,84(2):366–376.
Gibbons S J,Ringdal F. 2006. The detection of low magnitude seismic events using array-based waveform correlation[J]. Geophys J Int,165(1):149–166.
Haykin, Simon S. 2010. Neural Networks and Learning Machines[M]. Third Edition. Prentice Hall: Pearson Education India: 146–147.
Hensman P, Masko D. 2015. The Impact of Imbalanced Training Data for Convolutional Neural Networks[M]. Sweden: KTH Royal Institute of Technology: 1–28.
Kingma, Diederik P, Jimmy Ba. 2015. Adam: A method for stochastic optimization[EB/OL] [2020–12–17]. https://arxiv.org/abs/1412.6980.
Kriegerowski M,Petersen G M,Vasyura-Bathke H,Ohrnberger M. 2018. A deep convolutional neural network for localization of clustered earthquakes based on multistation full waveforms[J]. Seismol Res Lett,90(2A):510–516.
Krizhevsky A, Sutskever I, Hinton G E. 2012. Imagenet classification with deep convolutional neural networks[C]//Advances in Neural Information Processing Systems. Tahoe: NV: 1097–1105.
Mousavi S M,Zhu W Q,Sheng Y X,Beroza G C. 2019. CRED:A deep residual network of convolutional and recurrent units for earthquake signal detection[J]. Scientific Reports,9(1):1–14.
Nair V, Hinton G E. 2010. Rectified linear units improve restricted boltzmann machines[C]//Proceedings of the 27th International Conf. on Machine Learning ICML-10. Haifa: Israel: 807–814.
Ng A Y. 2004. Feature selection, L1 vs L2 regularization, and rotational invariance[C]//Proceedings of the Twenty-First International Conference on Machine Learning. Banff: 78.
Peng Z G,Zhao P. 2009. Migration of early aftershocks following the 2004 Parkfield earthquake[J]. Nat Geosci,2(12):877–881.
Powers,David M W. 2011. Evaluation:From precision,recall and F-measure to roc,informedness,markedness and correlation[J]. J Mach Learning Techn,2(1):37–63.
Perol T,Gharbi M,Denolle M. 2018. Convolutional neural network for earthquake detection and location[J]. Sci Adv,4(2):e1700578.
Ross Z E,Meier M A,Hauksson E,Heaton T H. 2018a. Generalized seismic phase detection with deep learning[J]. Bull Seismol Soc Am,108(5A):2894–2901.
Ross Z E,Meier M A,Hauksson E. 2018b. P wave arrival picking and first-motion polarity determination with deep learning[J]. J Geophys Res,123(6):5120–5129.
Saragiotis C D,Hadjileontiadis L J,Panas S M. 2002. PAI-S/K:A robust automatic seismic P phase arrival identification scheme[J]. IEEE T Geosci Remote,40(6):1395–1404.
Sleeman R,van Eck T V. 1999. Robust automatic P-phase picking:An on-line implementation in the analysis of broadband seismogram recordings[J]. Phys Earth Planet In,113(1-4):0–275.
Wang J,Xiao Z W,Liu C,Zhao D P,Yao Z X. 2019. Deep learning for picking seismic arrival times[J]. J Geophys Res,124(7):6612–6624.
Wilson D R,Martinez T R. 2003. The general inefficiency of batch training for gradient descent learning[J]. Neural Netw,16:1429–1451.
Yoon C E,O’Reilly O,Bergen K J. 2015. Earthquake detection through computationally efficient similarity search[J]. Sci Adv,1(11):e1501057.
Zhou Y J,Yue H,Kong Q K,Zhou S Y. 2019. Hybrid event detection and phase-picking algorithm using convolutional andrecurrent neural networks[J]. Seismol Res Lett,90(3):1079–1087.
Zhu W Q,Beroza G C. 2018. PhaseNet:A deep-neural-network-based seismic arrival-time picking method[J]. Geophys J Int,216(1):261–273.
-
期刊类型引用(1)
1. 夏文鹤，谢万洋，唐印东，李皋，韩玉娇. 砂样岩屑图像特征的岩性智能高效识别. 石油地球物理勘探. 2023(03): 495-506 . 
百度学术
其他类型引用(1)
计量
- 文章访问数: 1529
- HTML全文浏览量: 793
- PDF下载量: 185
- 被引次数: 2
