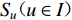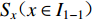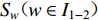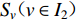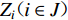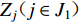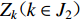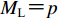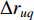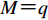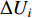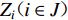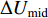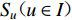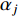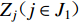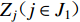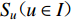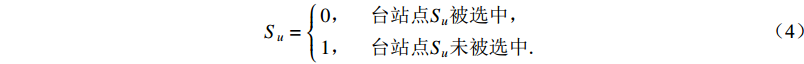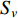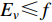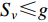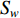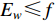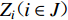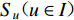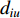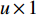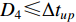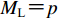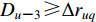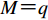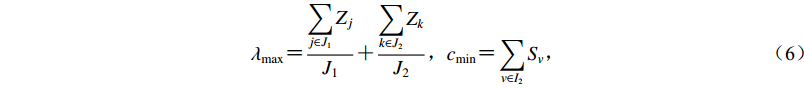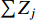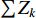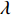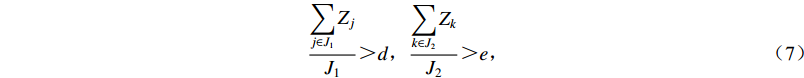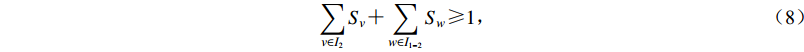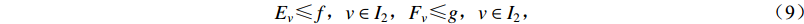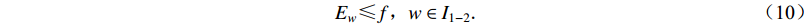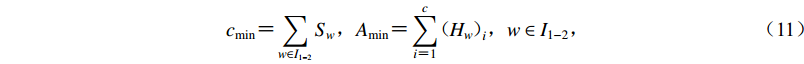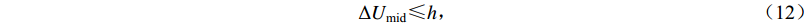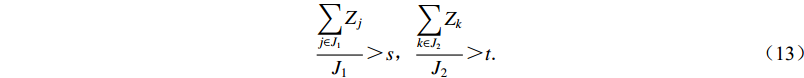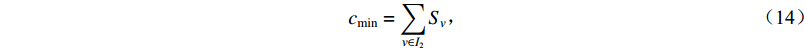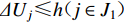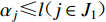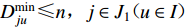Optimization of local seismic network layout based on seismic monitoring capability
-
摘要: 为解决带约束条件的台站选址问题,本文借鉴公共服务设施选址最优化理论,深入分析测震台网监测能力的构成要素,并考虑地形坡度、环境噪声水平、台站布局等约束条件,建立了基于地震检测能力、记录能力和定位精度的台网布局最优化模型。之后以成都市测震台网为例,经模拟退火算法求解,获得了分别满足重点监测区和非重点监测区地震监测能力需求的台网布局优化方案,明确给出了新增或新建监测台站的地理位置。Abstract: In order to solve the problem of station location with constraints, the optimization theory of public service facility location is used for reference, and the constituent elements of seismic network monitoring capacity are deeply analyzed, the constraints such as terrain slope, environmental noise level and station layout are also added. Finally, the optimization model of station network layout based on the seismic detection capacity, the recording capacity and the positioning accuracy is established in this paper. Taking the seismic network in Chengdu as an example, the network layout optimization scheme that meets the seismic monitoring capacity requirements of focus and non-focus monitoring areas respectively are obtained by the use of simulated annealing algorithm. And the geographical location of new or newly-built monitoring stations is clearly given.
-
Keywords:
- seismic network /
- station layout /
- optimization model /
- monitoring capability
-
引言
测震台网以实时检测地震事件和测定地震要素为主要任务,其成果被广泛应用于震源运动学和动力学、地震波传播机制、地球圈层结构成像、地震灾害损失评估以及各类地面振动发生机理等的研究(邱宇等,2020)。一次地震事件通常需被至少4个分布合理的台站记录并检测到,才能被测震台网有效地监测和定位(中国地震局监测预报司,2017),测震台站的几何布局是决定台网监测能力的重要因素,合理的台网布局是保证较高监测能力的基础。
经过数十年努力,我国已经建成由国家、省和地方三级组成、技术水平较高、规模庞大的数字测震台网,地震监测能力得到显著提升(庄灿涛,杨晓源,2007;刘瑞丰,2016)。但随着防震减灾工作的发展和科学研究的不断深入,对测震台网的地震监测能力和台站布局提出了更高的要求:① 对于微震活动频繁的区域,需要提高台网密度,进一步降低可监测地震的震级下限,增强微震检测能力;② 对于强震发生可能性较大的区域,地方台网需要保证一定的远台数量,提高能被监测到地震的震级上限,增强大震记录能力;③ 对于水库和采矿区周边等诱发地震多发的区域,需要增加近台数量、降低台站分布方位均匀度,进一步提高地震定位精度,尤其是震源深度的定位精度。
但在长期实践中,较高的地震监测能力需求与有限的资金投入之间存在必然矛盾,如何投入尽可能少的资金来最大限度地提高监测能力是测震台网规划、设计和建设过程中自始至终必须考虑的问题(葛焕称,1998;Bormann,2002)。最优化方法即在一定限制条件下,选取某种方案使目标达到最优(宋巨龙等,2012),可较好地平衡地震监测能力需求和经济投入之间的矛盾。经过多年发展,D-优化准则(Kijko,1977;Ghalib et al,1984;García-Fernandez et al,1988;Bartal,2000;巩思园等,2010,2012)、C值最优理论(Mendecki,1997)、DETMAX算法(Rabinowitz,Steinberg,1990;Steinberg et al,1995)等多种最优化分析方法被应用于地方或专用测震台网布局,在提高台网布局的经济性、合理性和科学性方面发挥了重要作用。但现有的研究较少考虑台网的综合监测能力,大多仅将震源定位精度作为台网布局优化的唯一目标,未能同时兼顾检测能力、记录能力等其它监测能力要素,研究成果难以广泛应用。
本研究拟将检测能力、记录能力和定位精度共同作为测震台网监测能力的重要组成部分,使用地形坡度、环境噪声水平、台站布局等作为约束条件,分别构建台站布局最优化模型,并以成都市测震台网为例,经模拟退火算法求解,以期获得科学、有效的台网布局优化方案。
1. 测震台网地震监测能力
1.1 地震的检测能力
检测能力指测震台网对微小地震的识别能力。通常情况下,检测能力依赖于地震观测台站的环境噪声水平。环境噪声越大,从波形记录中识别出地震波越困难,监测台站检测小地震事件的能力就越弱。当小地震的振幅低于台站环境噪声振幅时,地震波形将淹没在环境噪声记录中,地震事件将无法被有效检测。
根据地方性震级ML的计算公式,结合初动震相信噪比、优势频率、峰值因数等参数,可推导出基于台基环境噪声有效值En 的台站地震检测能力定量评估公式(中国地震局监测预报司,2017):
$$ {M_{\text{L}}} = \lg {E_{\text{n}}} + R(\varDelta ) + {{C}} {,} $$ (1) 式中:Δ为震中距,单位为km;R(Δ)为与震中距相关的近震震级量规函数,单位为m/s;C为常数,可通过已运行台站可记录到的地方微震统计数据来确定。当已知台基环境噪声有效值和指定震中距时,即可由上式估算出台站所能检测出的地震最小震级。
对于测震台网及其邻近区域,存在能够被检测到的微小地震的震级下限,震级大于该下限的地震,就可被台网中至少四个台站检测到,该震级下限就是测震台网在该区域的检测能力。
1.2 地震的记录能力
记录能力指测震台网完整记录地震事件波形的能力。通常情况下,记录能力强弱取决于台站观测仪器的动态范围,而观测仪器的动态范围又取决于采样字长L,也就是数据采集器模拟信号/数字信号(A/D)转换的位数,位数越高,其动态范围越大,所能记录地震的震级越大(傅再扬,1999)。当大震来临时,如果地震记录的振幅超过了数据采集器的动态范围,就会出现限幅现象,无法完整记录地震波形。
目前,测震台站普遍使用速度型地震计,而数据采集器所能记录的最大地震波速度为
$$ V_{\max} = \frac{2^L}G {,} $$ (2) 式中,G为台站观测系统的灵敏度,它与地震计灵敏度、数据采集器转换因子等参数相关(刘栋,2018)。基于面波震级计算方法,得到台站所能记录的最大震级为
$$ M{{ = {\rm{lg}}}}\left( {\frac{{{V_{\max }}}}{{{{2\pi }}}}} \right)+1.66{{{\rm{lg}}}}\varDelta + 3.5{,} $$ (3) 式中,Δ为震中距,单位为°。当已知台站数据采集器A/D转换位数和指定震中距时,即可估算出台站所能记录的地震最大震级。
同理,对于测震台网及其邻近区域,存在能够被记录的地震的震级上限,低于该上限的地震,就能被台网中至少四个台站有效记录到,该震级上限就是测震台网在该区域的记录能力。
1.3 地震定位精度
地震定位精度是测震台网对地震震源位置定位能力的重要评价指标,其与台站分布、速度模型、定位方法、仪器工作状态、震相到时拾取精度、震相的类型和数量等多个因素相关,其中台站分布是最重要、也是现实中最容易改进的因素。
《DB/T 66—2016地震编目规范》(中国地震局,2016)规定,依据台站分布方位均匀度、最大次空隙角、近台震中距、定位反演水平误差估计等参数,将地震定位精度划分为四类。其中,最大次空隙角、台站分布均匀度和近台震中距等取决于台站布局,较为合理的台站布局可保证较高的地震定位精度。
2. 地方测震台网布局最优化模型构建
地震监测台站属于公共服务设施,地方测震台网布局优化问题可归为公共服务设施选址问题,其基本形式是在明确地震监测能力需求的前提下,从可建台站区域或备选台站点中选择拟建台站位置,以达到经济投入最小或台站数量最少的目的。
2.1 模型假设和参数定义
2.1.1 需求点与监测点
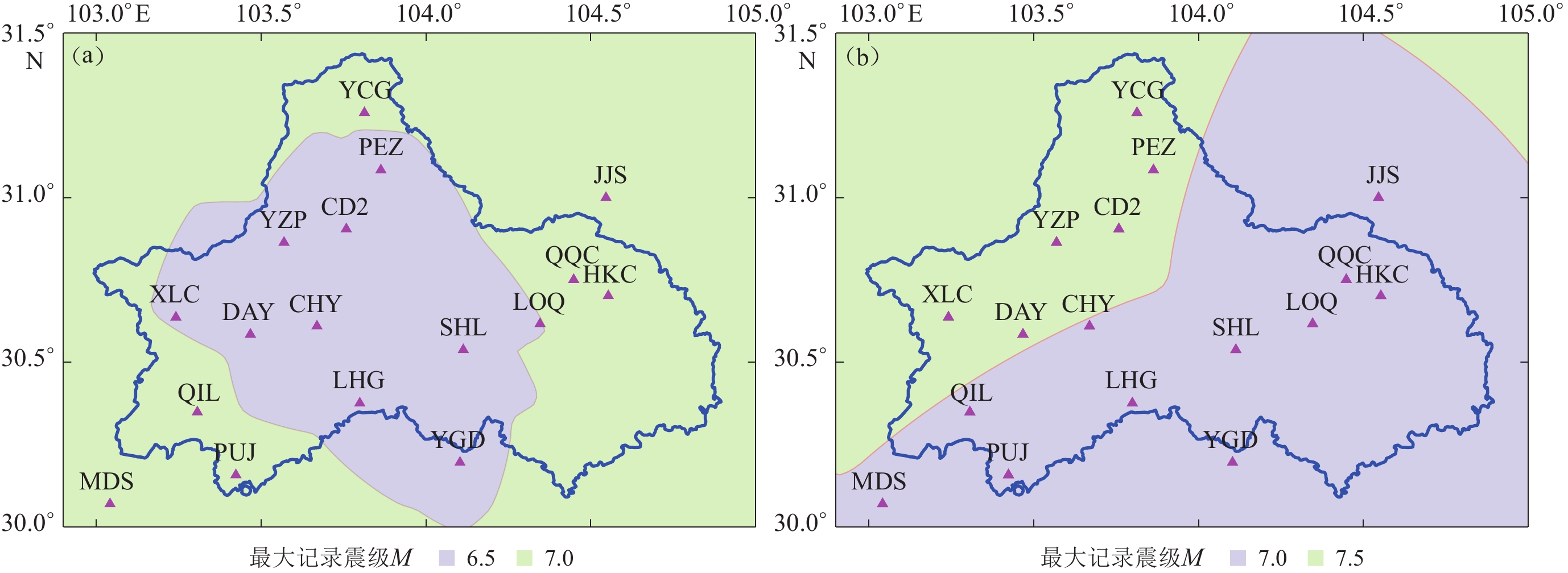
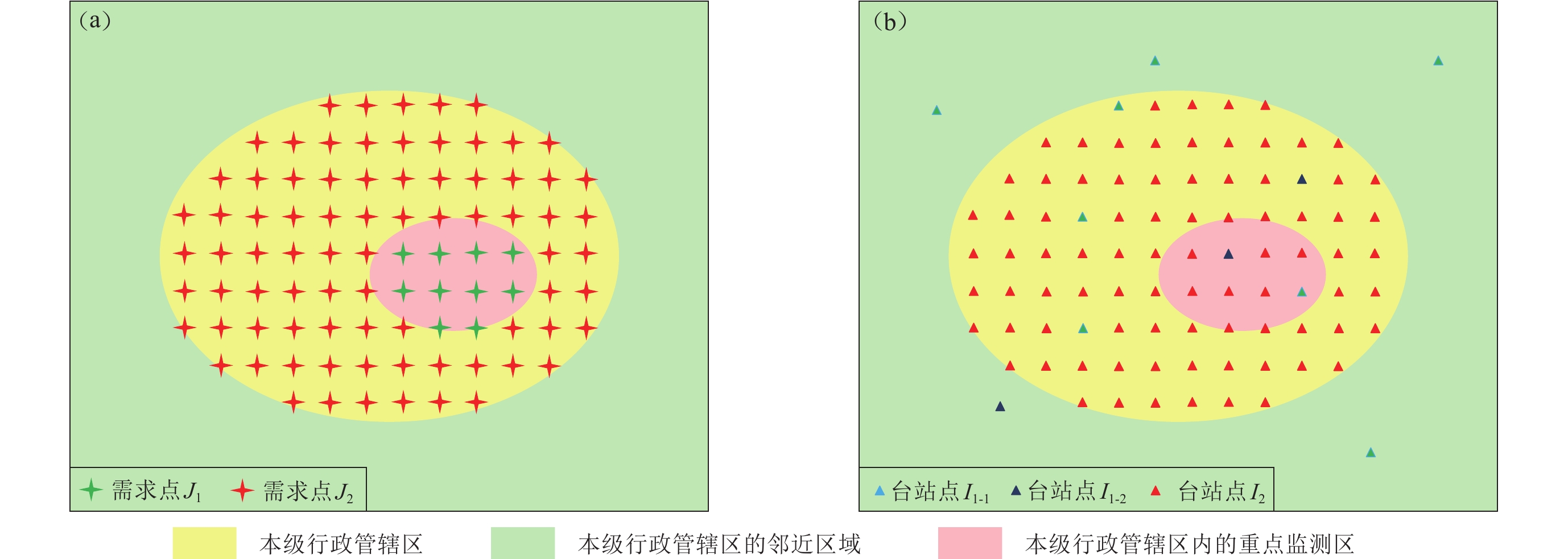
测震台网布局优化问题中的需求点为地震监测需求区内的需求点J,监测点为地震监测台站分布区内的台站点I,两者不完全重合。地方测震台网一般由市、县地方政府或企业投资建设,地震监测需求区域通常为其行政管辖区。根据地震危险性和活动特点,可将需求点划分为两类:第一类是活动断层发育、地震频发的重点监测区内的需求点J1;第二类是除重点监测区以外区域的需求点J2 (图1a)。地震监测台站分布区则包含了地震监测需求区及其邻近地区,依据台站点的当前建成状态,也可将其划分为两类:一类为已经建成的台站点I1,它可能在本级行政管辖区内,也可能在其邻近地区;另一类为需要新建的台站点I2,通常只能位于本级行政管辖区内(图1b)。
对于拟新建的测震台网,地震监测台站分布区内的所有台站点均可作为备选台站点;但对于拟扩建的测震台网,因其有已经正在运行的监测台站,地震监测台站分布区内其它剩余的台站点才可作为备选台站点。为此,可将已经建成的台站点I1进一步细分为已经入网运行的台站点I1-1和尚未入网的备选台站点I1-2 (图1b)。
2.1.2 基本假设
① 台站点与需求点均离散,且两者位置可能重叠;② 台站点与需求点之间的距离为两者间的最短直线距离;③ 台站点集合中每个台站点的环境条件和观测仪器所能记录的最大地震动速度均已知,其中环境条件超过规定限值的台站点不作为备选台站点;④ 根据台站点的环境条件,可以确定每个台站点针对某一震级水平的有效检测半径;每个台站点可以检测到有效检测半径内所有需求点处发生的大于该震级水平的地震;⑤ 根据台站点观测仪器所能记录的最大地震动速度,确定每个台站点针对某一震级水平的有效记录半径,每个台站点可以完整记录有效记录半径外所有需求点处发生的小于该震级水平的地震;⑥ 当计算台网地震检测能力时,需求点应处于4个及以上台站点的有效检测半径内;当计算台网地震记录能力时,需求点应处于4个及以上台站点的有效记录半径外。
2.1.3 参数定义
本文构建的多个数学模型参数可共用,按照数据集合、变量和常量参数进行统一定义。
${S_{ u}} ( u \in I ) $ 为台站点,其中${S_{ x}} ( x \in {I_{1 - 1}} ) $ 为I1−1类台站点,${S_{ w}} ( w \in {I_{1 - 2}} ) $ 为I1−2类台站点,${S_{ v}} ( v \in {I_2} ) $ 为I2类台站点;${Z_i} ( i \in J ) $ 为需求点,其中${Z_j} ( j \in {J_1} ) $ 为J1类需求点,${Z_k} ( k \in {J_2} ) $ 为J2类需求点。mi1为台网针对J1需求点所能检测到的最小震级;mi2为台网针对J2需求点所能检测到的最小震级;
$\Delta {t_{up}}$ 为台站点Su可检测$ {M_{\text{L}}} = p $ 地震的有效检测半径,单位:km;Eu为台站点Su的环境噪声水平,单位:m/s;Fu为台站点Su所处位置的地形坡度,单位:°;ma1为台网针对J1需求点所能记录的最大震级;ma2为台网针对J2需求点所能记录的最大震级;$\Delta {r_{uq}}$ 为台站点Su可完整记录$ M = q $ 地震的有效记录半径,单位:km;$\Delta{U_i}$ 为参与需求点${Z_i} ( i \in J ) $ 定位的台站点的分布方位均匀度,其中$\Delta{U_{{\text{mid}}}}$ 为参与需求区中心点定位的台站点的分布方位均匀度;H u为台站点${S_{ u}} ( u \in I ) $ 与地震监测需求区域边界的距离,单位:km;${\alpha _j}$ 为参与需求点$ {Z_j} ( j \in {J_1} ) $ 定位的台站点的最大次空隙角,单位:°; D ju为需求点$ {Z_j} ( j \in {J_1} ) $ 与台站点$ {S_{ u}} ( u \in I ) $ 之间的距离,单位:km。a为已接入测震台网的已建台站点数;d为台网对J1类需求点mi1以上地震检测率指标;e为台网对J2类需求点mi2以上地震检测率指标;s为台网对J1类需求点ma1以下地震完整记录率指标;t为台网对J2类需求点ma2以下地震完整记录率指标;f为台站点的环境噪声水平指标,单位:m/s;g为台站点所处位置的地形坡度指标,单位:°;h为参与地震定位的台站点的方位均匀度指标;l为参与地震定位的台站点的最大次空隙角指标,单位:°;n为距离需求点最近的台站点的震中距指标,单位:km。
2.1.4 决策变量
对于台站点Su有
$$ {S_u} = \left\{ \begin{array}{l} 0,\quad 台站点{S_{ u}}被选中,\\ 1,\quad 台站点{S_{ u}}未被选中{\text{.}} \end{array} \right. $$ (4) 对于I2类台站点
${S_{ v}}$ ,当其噪声水平$ {E_v}{\text{≤}} f $ 且地形坡度${S_{ v}} {\text{≤}} g$ 时,表示其所处位置人类活动较少、干扰较小且地形条件有利于监测设施建设,如果此时其对提高台网地震检测能力、记录能力或定位精度有贡献时,则该台站点被选中;反之,表示其所处位置人类活动频繁、干扰较多且地形条件不利于监测设施建设,无论其是否对提高台网地震检测能力、记录能力或定位精度有贡献,该台站点均不能被选中。对于I1−2类台站点$ {S_{ w}} $ ,当其噪声水平$ {E_w}{\text{≤}} f $ 且对提高台网地震检测能力、记录能力或定位精度有贡献时,该台站点被选中;反之,不能被选中。对于需求点
$ {Z_i} ( i \in J ) $ ,分别求取其与每个台站点$ {S_u} ( u \in I ) $ 的距离$ {d_{iu}} $ ,并按从小到大的顺序存入$u \times 1$ 阶矩阵D。当计算台网地震检测能力时,若D中第四个元素$D_4 {\text{≤}}\Delta {t_{up}}$ ,则此需求点发生$ {M_{\text{L}}} = p $ 以上地震时可以被有效检测,反之,则不能被有效检测;当计算台网地震记录能力时,若D中倒数第四个元素$D_{u - 3} {\text{≥}} \Delta {r_{uq}}$ ,则此需求点发生$ M = q $ 以下地震时可以被完整记录,反之,则不能被完整记录。其表达式为$$ {Z_i} = \left\{ \begin{array}{l} 0,\quad 需求点{Z_i}被有效检测或完整记录,\\ 1,\quad 需求点{Z_i}未被有效检测或完整记录{\text{.}} \end{array} \right. $$ (5) 2.2 模型构建
2.2.1 基于地震检测能力的台网布局优化模型
根据测震台网地震检测能力定义和工作实践,模型可描述为:在测震台网已经包含a个已建成台站点的情况下,再从I1-2类和I2类台站点集合中,分别选择若干个已建成台站点和新建台站点,使得测震台网对J1类需求点mi1以上地震和J2类需求点mi2以上地震的检测能力最强,且投资最小。其模型可以表示为
$$ \lambda _{\max} = \frac{{\displaystyle\sum\limits_{j \in {J_1}} {{Z_j}} }}{{{J_1}}} + \frac{{\displaystyle\sum\limits_{k \in {J_2}} {{Z_k}} }}{{{J_2}}} , c_{\min} = \sum\limits_{v \in {I_2}} {{S_{ v}}}, $$ (6) 式中:J1和J2分别为J1类和J2类需求点总个数;
$ \sum {{Z_j}} $ 为发生mi1地震时J1类需求点被有效检测的个数;$\sum {{Z_k}}$ 为发生mi2地震时J2类需求点被有效检测的个数;该式表示针对两类地震监测需求区域,被有效检测的需求点占比$ \lambda $ 越高越好,即要求有效监测范围尽可能大;考虑到已建成台站点接入台网的成本可以忽略不计,只要求新建台站点数量c越少越好。模型的约束条件:对重点监测区及其以外其它区域发生的地震的检测率要达到一定指标 [ 式(7) ] ;至少新增一个台站点 [ 式(8) ] ;新建台站点所在位置具备较低的环境噪声水平和较好的地形条件 [ 式(9) ] ;新增已建成的台站点所在位置具备较低的环境噪声水平 [ 式(10) ] 。
$$ \frac{{\displaystyle\sum\limits_{j \in {J_1}} {{Z_j}} }}{{{J_1}}} > d , \frac{{\displaystyle\sum\limits_{k \in {J_2}} {{Z_k}} }}{{{J_2}}} > e , $$ (7) $$ \sum\limits_{v \in {I_2}} {{S_{ v}}} + \sum\limits_{w \in {I_{1 - 2}}} {{S_{ w}}} {\text{≥}} 1 , $$ (8) $$ {E_v} {\text{≤}} f,v \in {I_2} , {F_v} {\text{≤}} g,v \in {I_2} , $$ (9) $$ {E_w} {\text{≤}} f,w \in {I_{1 - 2}}{\text{.}} $$ (10) 2.2.2 基于地震记录能力的台网布局优化模型
由于绝大部分市、县和企业的行政管辖区面积较小,仅依靠本级行政区内的台站难以实现对本区内所有可能发生的大地震进行完整记录,必须借助域外已建成的台站。但同时,随着震中距的增大,地震波形记录信息增多,震相越来越复杂,识别难度也会显著增加,因此,在完整记录大地震波形的前提下,应选择其中震中距最小、数量最少的域外台站参与地震监测。故模型可以描述为:在测震台网已经包含a个台站点的情况下,再在I1−2类台站点集合中,选择尽可能少的台站点,使得测震台网对J1需求点记录的最大震级为ma1,对J2需求点记录的最大震级为ma2,且选择的台站点到行政区边界的总距离最小。其目标函数为
$$ c_{\min} = \sum\limits_{w \in {I_{1 - 2}}} {{S_{ w}}} , A_{\min} = \sum\limits_{i = 1}^c {{{ ( {{H_w}} ) }_i}} ,w \in {I_{1 - 2}} , $$ (11) 式中,Hw为台站点与地震监测需求区域边界的距离;从I1−2类台站点集合中选择加入台网的台站数量c要尽可能少。同时,选择的台站点到行政区边界的总距离A要尽可能小。
模型的约束条件为:避免选择的台站点过度集中于监测目标区域的某一个方位上 [ 式(12) ] ;对重点和非重点监测区发生地震的完整记录率要达到一定指标 [ 式(13) ] 。此外,基于地震检测能力的台网布局优化模型中关于环境噪声水平和地形的约束条件也适用于本模型。
$$ \Delta{U_{{\text{mid}}}} {\text{≤}} h \text{,} $$ (12) $$ \frac{{\displaystyle\sum\limits_{j \in {J_1}} {{Z_j}} }}{{{J_1}}} > s {,} \frac{{\displaystyle\sum\limits_{k \in {J_2}} {{Z_k}} }}{{{J_2}}} > t {\text{.}} $$ (13) 2.2.3 基于地震定位精度的台网布局优化模型
对于地震监测需求区域内活动断层密集、工业活动频繁、小震多发的重点地区,需要通过新增台站、优化台网布局提高地震定位精度。其模型可描述为:在测震台网已经包含a个已建成台站点的情况下,再在I1-2类和I2类台站点集合中,分别选择若干个已建成台站点和新建台站点,使得测震台网对J1类需求点mi1以上地震的定位精度达到一定要求。其目标函数为
$$ c_{\rm{min}} = \sum\limits_{v \in {I_2}} {{S_{ v}}} ,$$ (14) 表示新建台站数量c越少越好。
模型的约束条件要求:参与定位的台站在分布方位均匀度
$\varDelta{U_j} {\text{≤}} h ( j \in {J_1} ) $ 、最大次空隙角${\alpha _j} {\text{≤}} l ( j \in {J_1} ) $ ;距离震中最近的台站的震中距$D_{ju}^{\min} {\text{≤}} n, j \in {J_1} ( u \in I ) $ 等方面要满足相应指标。此外,基于地震检测能力的台网布局优化模型中关于环境噪声水平和地形的约束条件也适用于本模型。3. 成都市测震台网布局优化实例
3.1 基本概况
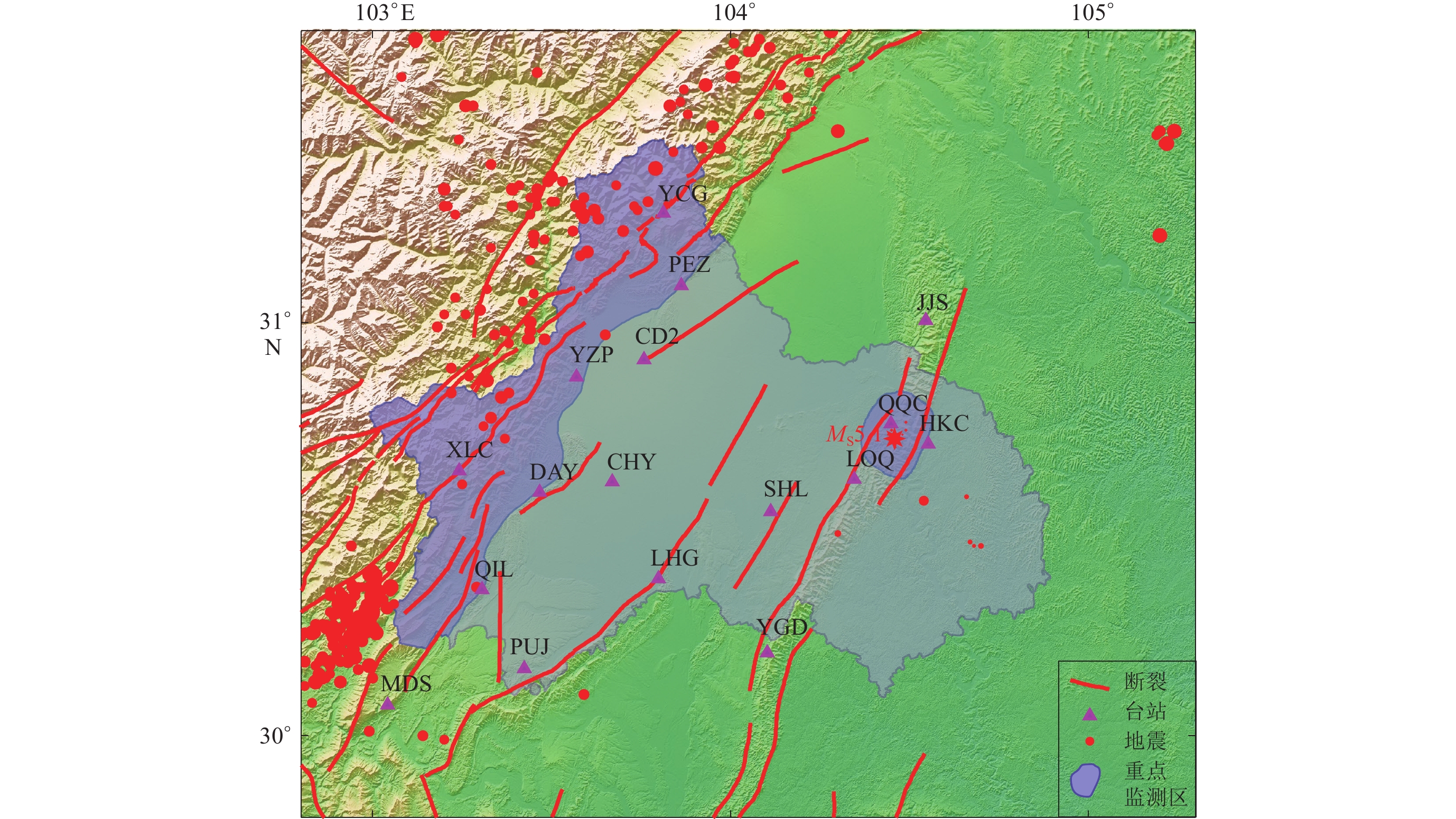
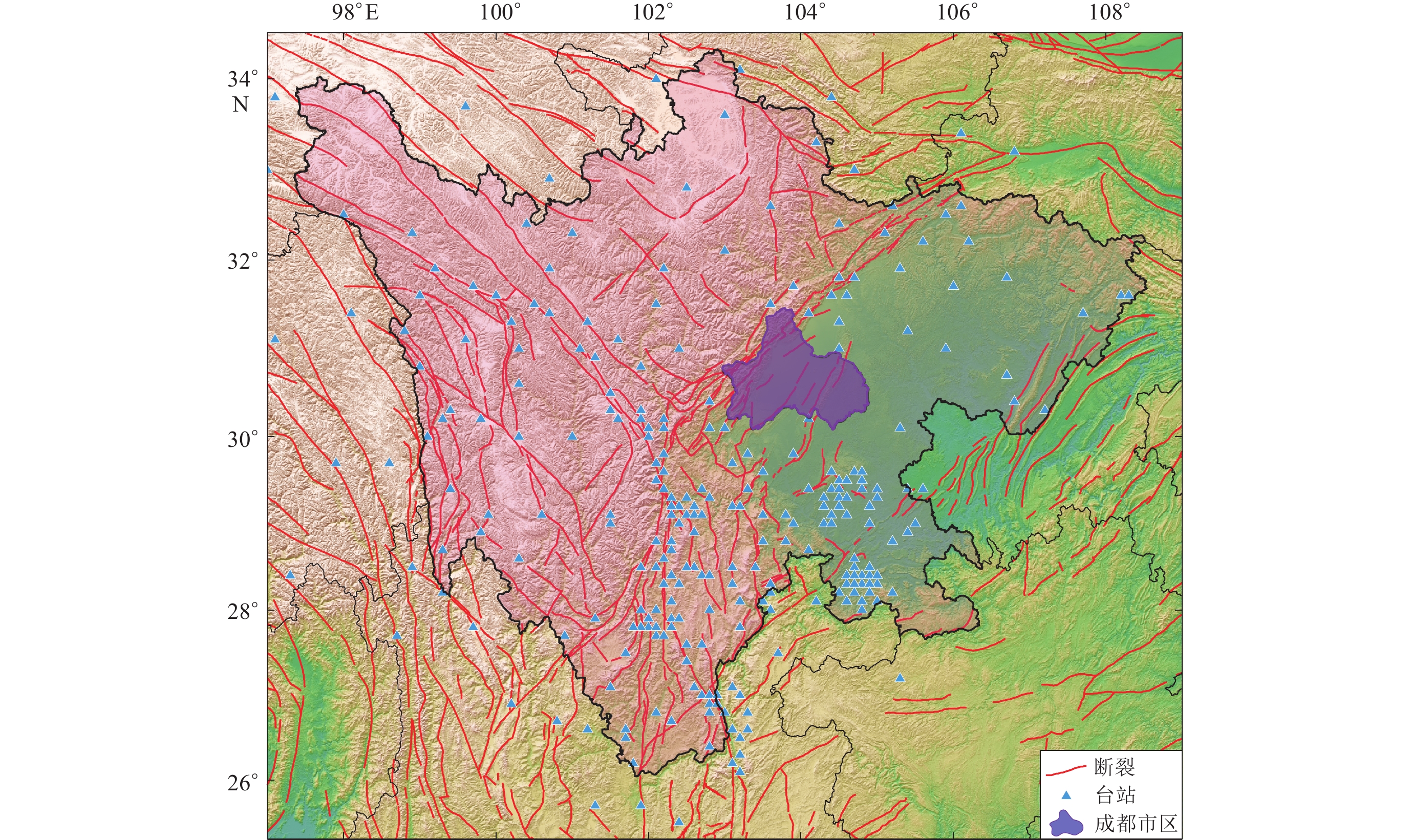
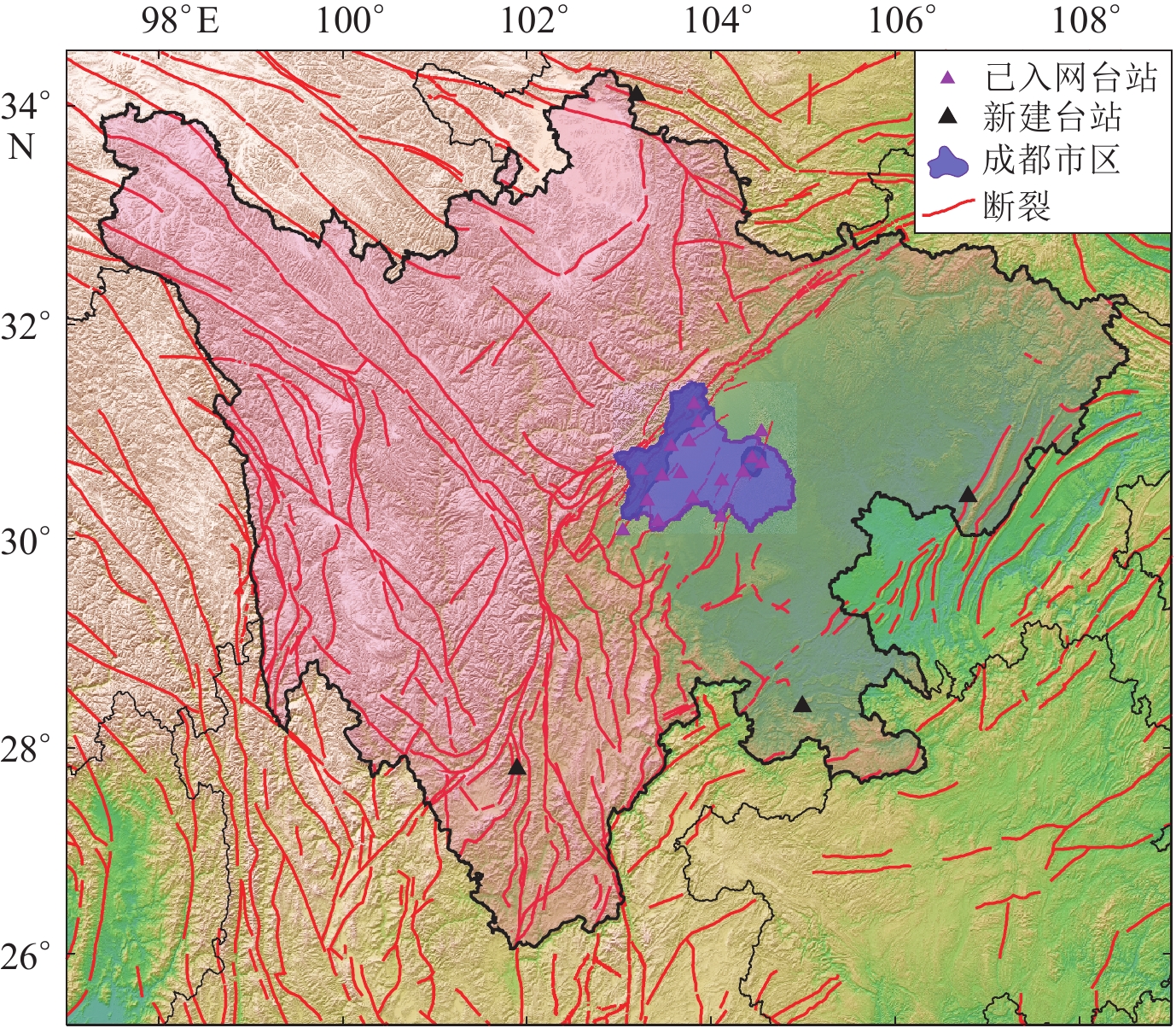
成都市位于青藏高原东缘与四川盆地接壤地带,地处南北地震带中段,区内有龙门山断裂、龙泉山断裂等多条活动断裂带,具有发生重大地震灾害的风险。历史上,成都市及邻近地区地震活动较为活跃,2008年汶川M8.0特大地震和2013年芦山M7.0强震均波及成都,造成严重破坏。近年来,成都市及邻区的地震活动主要沿龙门山断裂分布,同时在龙泉山断裂中北段有中小地震活动(图2)。成都市测震台网建成于1999年,后经两次扩建和改造,目前共由17个数字测震台站组成,包括10个成都市本级自建台、2个所属县(市)自建台和5个四川省地震局共享台。台网最大孔径约100 km,平均台站密度12台/104 km2 (图2)。
3.2 约束条件
3.2.1 台站点备选点位和区域
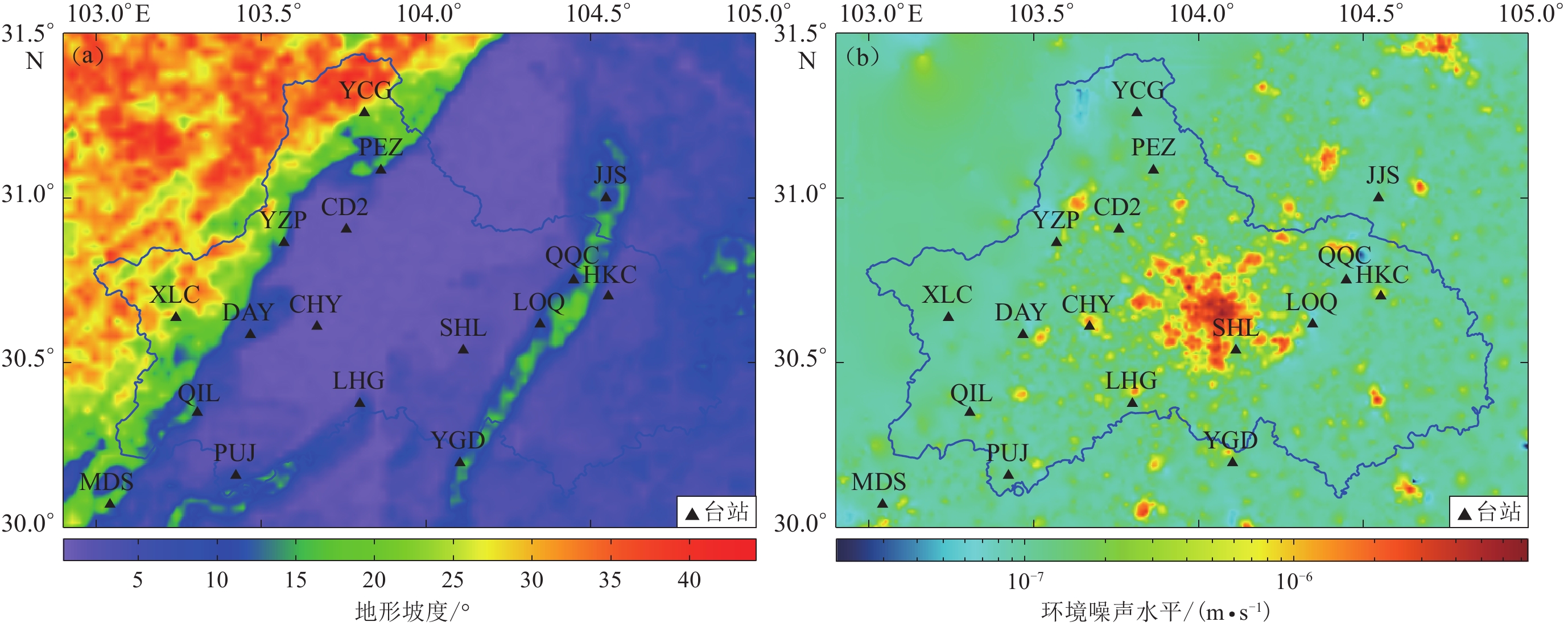
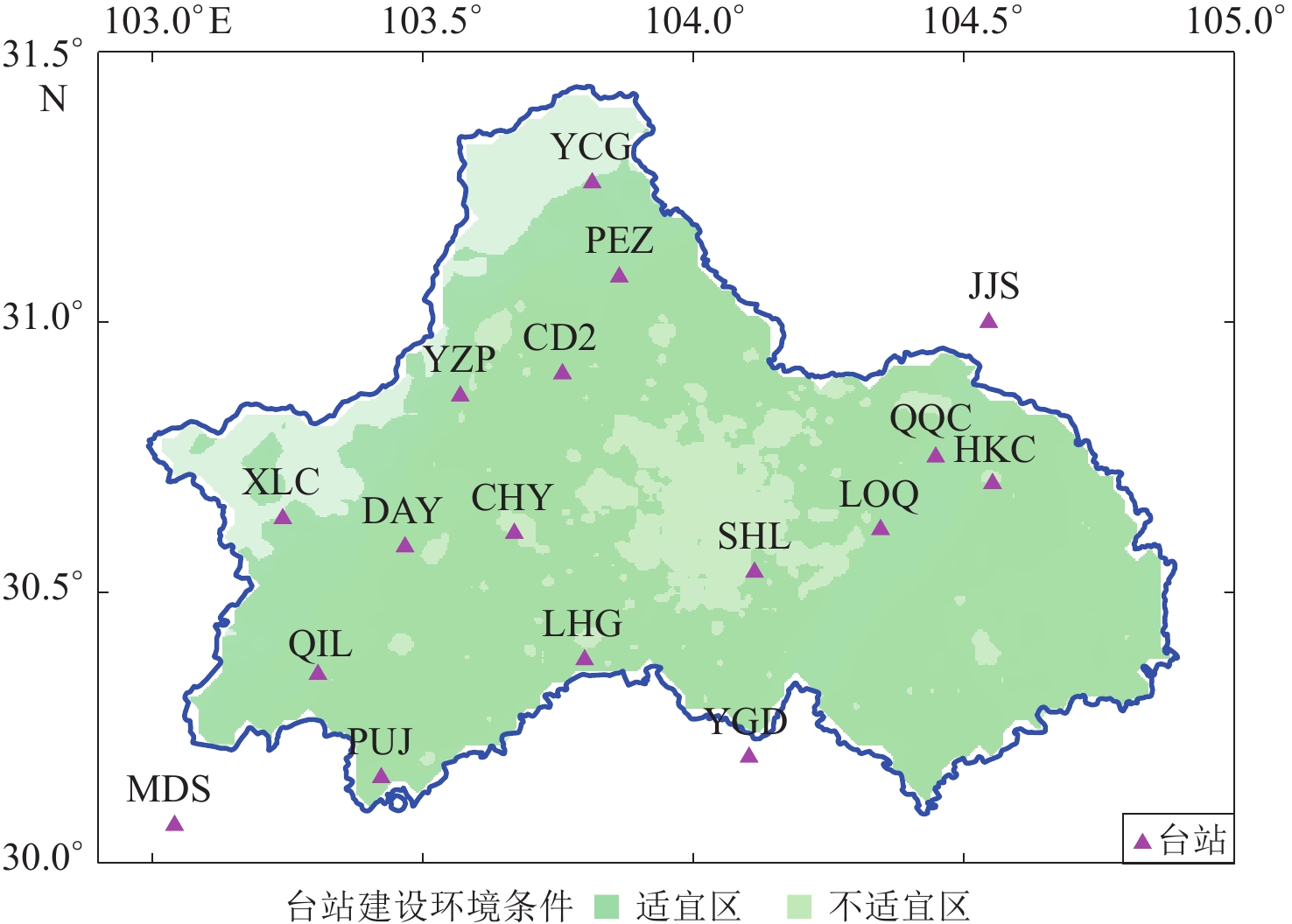
收集了成都市周边共计267个已建成台站,获得其坐标、环境噪声水平、观测仪器类型等信息,将之作为已建成台站的备选点位(图3);对成都市数字高程和热力值数据进行处理,将之转换为地形坡度和环境噪声水平(图4),排除其中地形坡度较大的西部龙门山区和环境噪声水平较高的中心城区等不适宜建设测震台站的区域,将其它同时具备较好地形条件和较低环境噪声水平的区域,作为新建台站点的备选区域(图5)。
3.2.2 地震重点监测区
成都市西部龙门山地区因位于大型活动断裂带之上,且紧靠汶川和芦山两大地震的余震区,近年来区内地震呈多发、易发态势,地震数量占全市的90%以上,对强震和微小地震监测均有较强的需求,将该区域作为地震检测能力模型和地震记录能力模型中的重点监测区(图2)。此外,位于中东部的龙泉山断裂中北段在2020年2月3日发生M5.1地震,因该区域台站数量较少,主震的震源深度定位精度不高,加之后期余震频次偏低且震级较小,使得震源机制和发震构造研究难以深入。为此,将该次地震的余震区确定为地震定位精度模型中的重点监测区(图2)。
3.3 模型计算
在上述模型中,当备选台站点数量较多时,传统的优化算法难以对其快速求解。而采用模拟退火算法通过赋予搜索过程一种时变且最终趋于零的概率突跳性,可有效避免陷入局部极小并最终趋于全局最优(Kirkpatrick,1984;Aarts,Kors,1988;王强,1993),为本文模型求解的基本算法。
3.3.1 地震检测能力优化
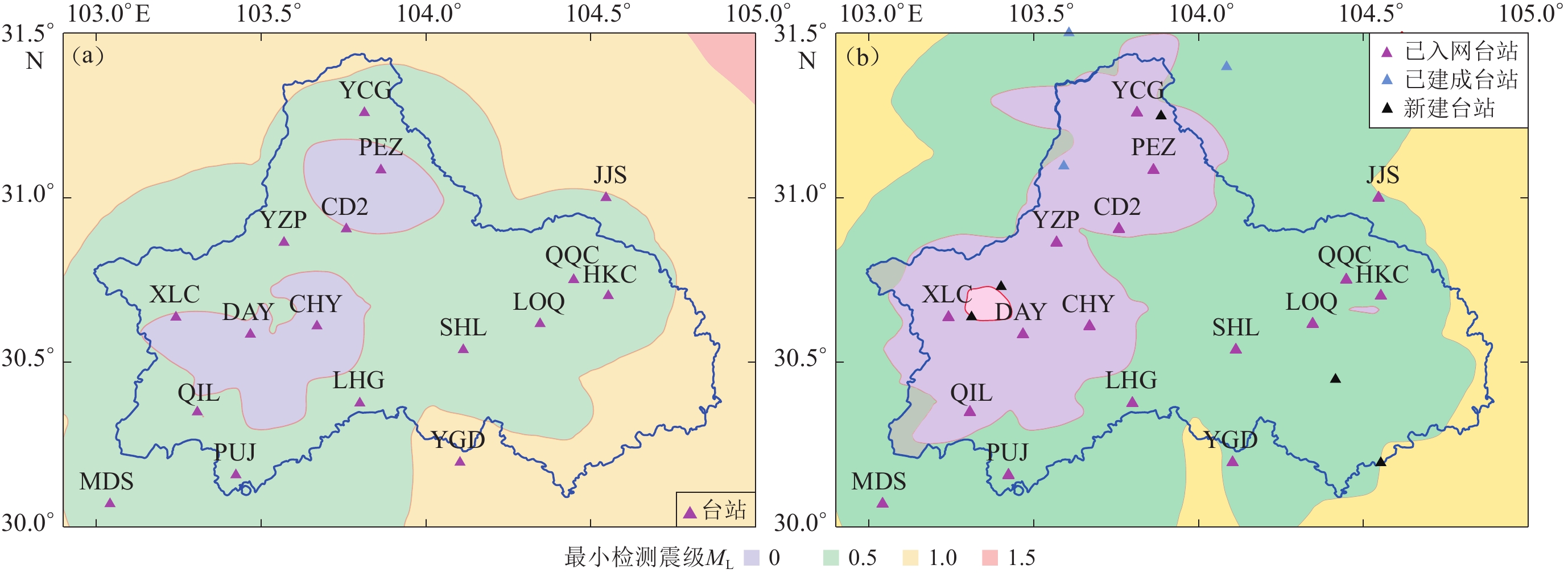
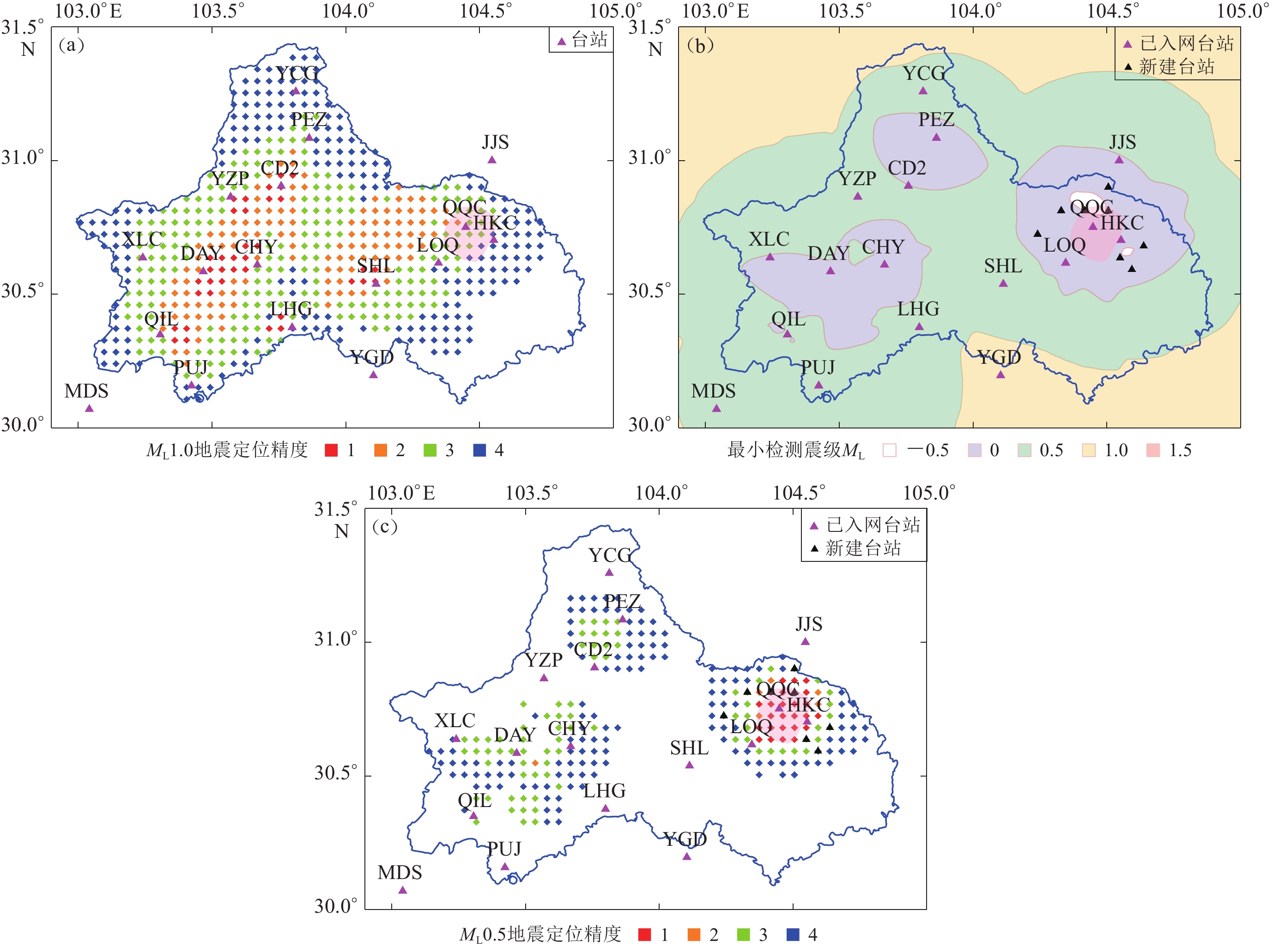
当前台网能对全市86.69%的区域实现ML≥1.0地震的有效检测,局部地区可以实现ML≥0.5地震的有效检测。与非重点监测区相比,西部龙门山断裂带重点监测区的地震检测能力相对较强,高达96.67%的区域的检测能力达到ML1.0 (图6a)。设定台网地震检测能力优化指标为:重点监测区90%以上的区域为ML0.5,其它非重点监测区95%以上的区域为ML1.0。求解得出,当迭代次数为43 000时模型收敛,需要在成都市周边已建成台站点中优选3个台站,同时在市域内新建6个台站,可以实现91.11%的重点监测区的检测能力达到ML0.5,96.72%的非重点监测区的检测能力达到ML1.0 (图6b)。
3.3.2 地震记录能力优化
当前台网能对成都市全域范围M6.5地震实现完整记录,近一半地区可以实现M7.0地震的完整记录。与非重点监测区相比,西部龙门山断裂带重点监测区的地震记录能力并无明显优势(图7a)。设定台网地震记录能力指标为:重点监测区90%以上区域为M7.5,其它非重点监测区90%以上区域为M7.0,同时要求新加入的台站点相对于市中心的方位分布均匀度小于0.3。通过求解可得,迭代次数为38 000时模型收敛,需在市域外已建台站点中优选4个台站,可以实现91.67%的重点监测区的记录能力达到M7.5,100%的非重点监测区的记录能力达到M7.0,此时4个台站点距离成都市域边界总距离为972 km,相对于成都市中心的方位均匀度为0.21 (图7a、图8)。
3.3.3 地震记定位精度优化
当前台网对龙泉山断裂带中北段重点监测区ML≥1.0地震的定位精度多为Ⅲ类或Ⅳ类精度,极个别区域能达到Ⅱ类精度,无达到Ⅰ类精度的区域(图6a、图9a)。考虑到2月3日M5.1地震后的余震震级普遍在ML1.0以下,故设定台网定位精度指标为:对重点监测区90%以上区域ML0.5以上地震的定位精度达到Ⅰ类精度。通过求解,当迭代次数为6 000时模型收敛,需要在重点监测区附近新建8个流动台站,可以实现重点监测区100%的区域地震检测能力达到ML0.5,其中94.44%的区域ML0.5以上地震的定位精度达到了Ⅰ类精度(图9b,c)。
![]() 图 9 成都市测震台网地震定位精度优化(a) 当前台网ML1.0地震定位精度;(b) 优化后台网地震检测能力;(c) 优化后台网ML0.5地震定位精度Figure 9. Optimization of seismic positioning accuracy of Chengdu seismic network(a) The positioning accuracy of the current network for ML1.0 earthquake;(b) Seismic detection capability of optimized network;(c) The positioning accuracy of optimized network for ML0.5 earthquake
图 9 成都市测震台网地震定位精度优化(a) 当前台网ML1.0地震定位精度;(b) 优化后台网地震检测能力;(c) 优化后台网ML0.5地震定位精度Figure 9. Optimization of seismic positioning accuracy of Chengdu seismic network(a) The positioning accuracy of the current network for ML1.0 earthquake;(b) Seismic detection capability of optimized network;(c) The positioning accuracy of optimized network for ML0.5 earthquake4. 讨论与结论
本文针对地方测震台网布局优化问题,借鉴设施选址最优化理论在生产、生活、应急、军事上的应用成果,构建了基于地震检测能力、记录能力和定位精度的有约束、多场景最优化数学模型,并以成都市测震台网为例,经模拟退火算法求解,获得台网布局优化方案。
最优化数学模型考虑了地形条件、环境噪声水平对台网(站)地震监测能力的影响,将新建台站数量最少、满足地震检测能力指标区域的覆盖率最高、地震定位精度最好、域外台站距离行政区边界总距离最小等作为优化目标,以地形坡度、台基环境噪声有效值、台站分布方位均匀度、最大次空隙角等作为约束条件,较为符合工作实际。成都市测震台网布局优化方案表明,在设定的约束条件下,将位于成都市西北方向的3个已建成台站纳入,并在成都市西部和东南部分别新建部分台站,可有效提高台网针对西部重点监测区ML0.5和其它地区ML1.0地震的检测能力;将位于四川省西南部和西北部的4个已建成台站纳入,可有效提高台网针对西部重点监测区M7.5和其它区域M7.0地震的记录能力;在东部重点监测区附近合理布设8个流动台站,可实现对该区域ML0.5以上地震的较高定位精度。
为降低计算难度,文中构建的数学模型均为单目标模型,分别用于解决地方测震台网地震监测能力需求中某一方面的优化问题。当研究对象同时出现地震检测能力、记录能力和定位精度方面的优化需求时,就需要依次求解三个模型,花费较长的时间,且获得的解可能不是最优解。因此,整合约束条件、优化目标函数、建立多目标数学模型、进一步提高模型适用性是今后研究工作的一个重点。另外,因资料收集困难,本文仅以地形坡度和热力值转换的环境噪声水平作为确定备选区域的依据,未能考虑风力、河流、城市规划等更多因素,可能与实际情况存在一定差异,故选择台站位置时,应以模型计算结果为基础,结合现场条件综合确定。
-
图 9 成都市测震台网地震定位精度优化
(a) 当前台网ML1.0地震定位精度;(b) 优化后台网地震检测能力;(c) 优化后台网ML0.5地震定位精度
Figure 9. Optimization of seismic positioning accuracy of Chengdu seismic network
(a) The positioning accuracy of the current network for ML1.0 earthquake;(b) Seismic detection capability of optimized network;(c) The positioning accuracy of optimized network for ML0.5 earthquake
-
傅再扬. 1999. 数字地震仪记录近震震级范围估算[J]. 福建地震,15(2):42–43. Fu Z Y. 1999. Evaluation on the range of local magnitude recorded by digital seismograph[J]. Fujian Seismology,15(2):42–43 (in Chinese).
葛焕称. 1998. 区域地震台网的动态监测能力[J]. 地震地磁观测与研究,19(4):26–30. Ge H C. 1998. Dynamic detectability of the regional seismic network[J]. Seismological and Geomagnetic Observation and Research,19(4):26–30 (in Chinese).
巩思园,窦林名,曹安业,贺虎,杜涛涛,江衡. 2010. 煤矿微震监测台网优化布设研究[J]. 地球物理学报,53(2):457–465. doi: 10.3969/j.issn.0001-5733.2010.02.025 Gong S Y,Dou L M,Cao A Y,He H,Du T T,Jiang H. 2010. Study on optimal configuration of seismological observation network for coal mine[J]. Chinese Journal of Geophysics,53(2):457–465 (in Chinese).
巩思园,窦林名,马小平,牟宗龙,陆菜平. 2012. 提高煤矿微震定位精度的台网优化布置算法[J]. 岩石力学与工程学报,31(1):8–17. doi: 10.3969/j.issn.1000-6915.2012.01.002 Gong S Y,Dou L M,Ma X P,Mu Z L,Lu C P. 2012. Optimization algorithm of network configuration for improving location accuracy of microseism in coal mine[J]. Chinese Journal of Rock Mechanics and Engineering,31(1):8–17 (in Chinese).
刘栋. 2018. 福建省测震台网监测能力研究[D]. 哈尔滨: 中国地震局工程力学研究所: 35–36. Liu D. 2018. Research on Monitoring Capacity of Seismological Network in Fujian Province[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 35–36 (in Chinese).
刘瑞丰. 2016. 中国地震台网的建设与发展[J]. 地震地磁观测与研究,37(4):201. Liu R F. 2016. Construction and development of China Seismic Network[J]. Seismological and Geomagnetic Observation and Research,37(4):201 (in Chinese).
邱宇,蒋长胜,司政亚. 2020. 地震监测台网优化布局技术方法综述[J]. 地球物理学进展,35(3):866–873. doi: 10.6038/pg2020DD0069 Qiu Y,Jiang C S,Si Z Y. 2020. Summary of technical methods for optimizing layout of seismic monitoring network[J]. Progress in Geophysics,35(3):866–873 (in Chinese).
宋巨龙, 王香柯, 冯晓慧. 2012. 最优化方法[M]. 西安: 西安电子科技大学出版社: 1–2. Song J L, Wang X K, Feng X H. 2012. Optimization Methods[M]. Xi’an: Xidian University Press: 1–2 (in Chinese).
王强. 1993. 模拟退火算法的改进及其应用[J]. 应用数学,6(4):392–397. Wang Q. 1993. The improved simulated annealing algorithm and its application[J]. Mathematica Applicata,6(4):392–397 (in Chinese).
中国地震局. 2016. DB/T 66—2016 地震编目规范[S]. 北京: 地震出版社: 1–2. China Earthquake Administration. 2016. DB/T 66-2016 Specification for Earthquake Cataloguing[S]. Beijing: Seismological Press: 1–2 (in Chinese).
中国地震局监测预报司. 2017. 测震学原理与方法[M]. 北京: 地震出版社: 223–225. Monitoring and Forecasting Department of China Earthquake Administration. 2017. Surveying Principles and Methods[M]. Beijing: Seismological Press: 223–225 (in Chinese).
庄灿涛, 杨晓源. 2007. 我国地震台网发展回顾[C]//辉煌的历程: 回顾中国地球物理学会60周年专刊. 北京: 中国地球物理学会: 17. Zhuang C T, Yang X Y. 2007. Review of the development of seismic network in China[C]//Brilliant History: Review of the Special Issue of the 60th anniversary of the Chinese Geophysical Society. Beijing: Chinese Geophysical Society: 17 (in Chinese).
Aarts, Korst. 1988. Simulated Annealing and Boltzmann Machines[M]. Massachusetts: MIT Press: 17–21.
Bartal Y. 2000. Optimal seismic networks in Israel in the context of the comprehensive test ban treaty[J]. Bull Seismol Soc Am,90(1):151–165. doi: 10.1785/0119980164
Bormann P. 2002. New Manual of Seismological Observatory Practice[M]. Potsdam: GeoForschungs Zentrum.
García-Fernandez M,Kijko A,Carracedo J C,Soler V. 1988. Optimum station distribution to monitor seismic activity of Teide volcano,Tenerife,Canary Islands[J]. J Volcanol Geoth Res,35(3):195–204. doi: 10.1016/0377-0273(88)90016-9
Ghalib H A A,Russell D R,Kijko A. 1984. Optimal design of a regional seismological network for the Arab countries[J]. Pure Appl Geophys,122(5):694–712. doi: 10.1007/BF01101875
Kijko A. 1977. An algorithm for the optimum distribution of a regional seismic network:I[J]. Pure Appl Geophys,115(4):999–1009. doi: 10.1007/BF00881222
Kirkpatrick S. 1984. Optimization by simulated annealing:Quantitative studies[J]. J Stat Phys,34(5):975–986.
Mendecki A J. 1997. Seismic Monitoring in Mines[M]. London: Chapman & Hall: 87–106.
Rabinowitz N,Steinberg D M. 1990. Optimal configuration of a seismographic network:A statistical approach[J]. Bull Seismol Soc Am,80(1):187–196. doi: 10.1785/BSSA0800010187
Steinberg D M,Rabinowitz N,Shimshoni Y,Mizrachi D. 1995. Configuring a seismographic network for optimal monitoring of fault lines and multiple sources[J]. Bull Seismol Soc Am,85(6):1847–1857. doi: 10.1785/BSSA0850061847
-
期刊类型引用(3)
1. 郭攀,李子昊,王晓睿,田雨佳. 基于SN-CAST方法的辽宁预警站网监测能力评估. 防灾减灾学报. 2024(03): 53-58 .  百度学术
百度学术
2. 孙青峰,吴兵. 地震海啸及海洋气象观测场设计解析. 城市建筑. 2024(22): 216-219 .  百度学术
百度学术
3. 唐淋,祁国亮. 地方测震台网布局优化软件的设计与实现. 华南地震. 2023(03): 31-38 .  百度学术
百度学术
其他类型引用(2)




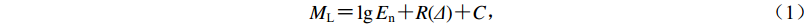
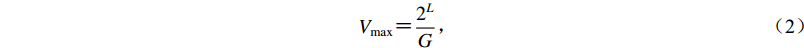
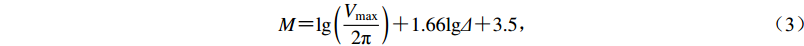
 下载:
下载: