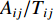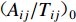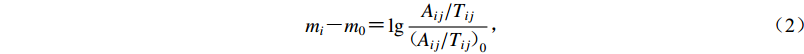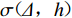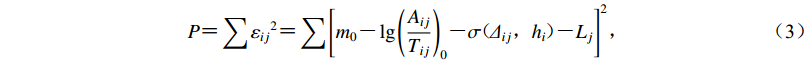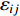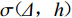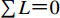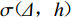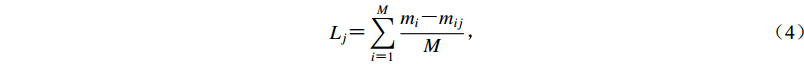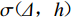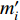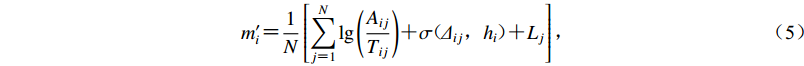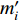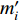Modeling and applications on amplitude-magnitude-distance-depth of some teleseism and ultra-teleseism phases
-
摘要: 不同震相具有不同的振动特性和传播规律,对应各自不同的幅值-震中距-深度衰减规律,本文基于禁核试核查国际数据中心公报,统计P,PcP,PKP,PKPbc及PKPab远震和极远震震相样本随震中距的分布,运用基于残差统计的迭代方法回归上述震相的幅值-震级-震中距-深度模型,通过震级残差标准差与均值的统计进行模型评估,结果显示:P,PcP,PKP,PKPbc及PKPab震相的震级残差标准差范围为0.30—0.36,满足一般震相相容性判断的需求;除PKPbc的残差均值大于0.03外,其余震相残差均值均为0.01左右,模型的系统偏差极小,甚至可以忽略不计。最后针对模型进行了幅值预测比对、震级相容性检测、极远震体波震级计算等三个不同场景的应用研究,验证模型可用于日常地震监测。
-
关键词:
- 事件检测 /
- 震相相容性 /
- 残差统计 /
- 幅值-震级-震中距-深度模型
Abstract: The consistency analysis of the signal feature is an important method to estimate the relationship between the event and the signal in the detection of seismic event. The consistency of amplitude can be used for determination of association through the comparison of amplitude residuals with numerous signal features on time and frequency domain. Different phases comply with the different propagation and attenuation law of amplitude-distance-depth. In this paper, the distribution of sample size varying with the distance of teleseism and ultra-teleseism phases such as P, PcP, PKP, PKPab and PKPbc based on the IDC is made. The model of amplitude-magnitude- distance-depth is constructed by iterative regression based on the residual statistics. The model is estimated through the standard deviation and mean of residual of magnitude. The range of standard deviation of residual of magnitude is 0.30−0.36. It could satisfy the requirements of phase consistency. Besides the mean of residual of magnitude of PKPbc phase is greater than 0.03, the rest phases is about 0.01. It demonstrates that the system deviation of the model is so tiny that it could be neglected. The application research of model is carried out by three different cases such as comparison of predicted amplitude, detection of magnitude consistency and magnitude calculation of ultra-teleseism events. The application research demonstrates that these models could be applied to routine seismic monitoring. -
引言
禁核试核查国际监测系统(International Monitoring System,缩写为IMS)地震监测台网计划建设一个由50个主要台站和120个辅助台站构成的全球地震监测系统,预期具备对全球1 kt以上当量地下核试验的监测能力,为全球核试验及中小地震监测提供了丰富的数据资料。然而台网形成监测能力需要数据处理技术作为支撑,针对IMS全球大尺度台网地震数据处理,可靠关联来自同一地震事件的不同震相是一件十分困难的事情。在禁核试核查国际数据中心(International Data Center,缩写为IDC)自动处理中,实际存在大量的虚假事件,其比例占到所有自动检测事件的20%—30%左右,这些虚假事件主要由震相错误关联所造成。同时还存在相当一部分震相被错误命名,需要在后续人工对事件的审核中进行修正。因此,确保震相的可靠关联或正确命名是提高地震数据自动处理质量的重要途径。震相相容性检测是地震信号震相正确关联的有效途径,在信号诸多的时频域整体与局部特征中,通过震相幅值计算震级并与平均震级比对,可以比较直观地判断震相是否来自该事件,便于地震信号震相相容性检测(Greg et al,1999)。IDC在实际处理中,定义了P波、Pn波与LR面波震相对应的震级,因此可以利用其震级进行震相相容性检测,但其它远震及极远震震相如PcP,PKP,PKPbc,PKPab等震相还没有相对精确的幅值-震级-震中距-深度模型,故无法对其进行震相相容性检测。因此有必要建立远震和极远震震相的幅值-震级-震中距-深度模型,实现通过相容性检测的方法对远震和极远震震相进行关联性判断。
早期的幅值-震级-震中距模型并未考虑深度的影响,例如Carpenter等(1967)仅仅通过6个区域的地下爆炸事件在65个台站的记录波形数据,运用最小二乘法拟合得到幅值-震中距模型与各个台站的场地响应项;IDC计算体波mb震级所用的幅值-震级-震中距-深度模型是由Veith和Clawson (1972)基于43个地下爆炸和259个不同深度天然地震事件的2 400余个观测数据在震级-幅值归一化的基础上运用震级残差统计的方法拟合得到的;Murphy和Barker (2003)运用禁核试核查国际数据中心原型系统(prototype International Data Center,缩写为pIDC)公报中1996—1998年共计22万余个P波震相数据,统计不同震中距台站震级与台网震级的残差,得到对Veith模型的震中距修正参数,进而建立体波震相0°—180°区域远震至极远震范围通用的模型,该模型也被IDC所采纳;国内地震研究者严尊国和薛军蓉(1987)及严尊国等(1992)采用震级残差统计与近震最大震相平均衰减特征研究相结合的方法,给出了适用于我国不同地区的量规函数并比较了不同地区对应量规函数的差别,认为中国东西部差异较大,在地方震范围内,西部比东部震级大0.2级;陈培善和秦嘉政(1983)比较了台站场地响应项、震相测量方法及辐射花样等对量规函数的影响,在加入场地响应项的条件下,可将震级方差从0.23降为0.20;还有很多国内科研人员运用与Murphy相近似的方法,统计区域震震级偏差随震中距的变化曲线,得到针对内蒙(刘芳等,2016)、陕西(张媛媛等,2017)、江苏(康清清等,2019)等不同区域的修正震级-幅值-震中距模型。
上述文献资料的研究目的及方向是为准确计算震级,给出的是针对P和Pn震相的模型,对于全球地震监测,特别是以地下核试验监测为主要目的的全球地震监测,更多时候需要利用远震信号以及其它一些极远震震相进行事件关联或震级计算,因此还需要得到其余远震以及极远震相关震相的模型。本文统计得到了IDC数据库中P,PcP,PKP,PKPab及PKPbc震相的检测数目随震中距的分布,运用基于震级残差统计的迭代方法,得到上述震相幅值-震级-震中距-深度模型,并通过结果残差均值与标准差统计,评估了模型的准确性和适用性,并给出了模型在震相关联检测中的应用实例。
1. 方法原理
在分析震相幅值相容性问题时,幅值-震级-震中距-深度模型中的震级应采用同一震级标准,本文采用IDC的mb震级。震级-幅值-震中距-深度建模即确定震相的震中距、幅值、周期相对于事件震级与深度的关系,一般震级关系式表示为
$$ m= \lg \Bigg(\frac{A}{T}\Bigg) +\sigma ( \varDelta ,h ) + L , $$ (1) 式中,m表示震级,A表示幅值,T表示测量周期,σ(Δ,h)表示与震中距、深度相关的量规函数,L表示台站的场地响应项。上式包含5个独立参数,一般可将问题简化为计算不同深度对应的幅值-震级-震中距模型,本文通过基于残差统计的迭代法计算模型参数,计算流程如图1所示。
第一步公报读取,建立回归所需的数据样本。为提高回归模型准确性和适用性,需要对事件的震级、时间、深度、定义台站数、定义台站最大张角等进行限定,在此基础上读取IDC公报,统计各震相的幅值、周期、震中距及对应事件的震级,形成震级-幅值-震中距-深度数据样本。
第二步幅值归一化,进一步减少模型未知量。地震信号的幅值周期比A/T表征波振面能量密度,同时震级与能量之间满足对数关系,那么可通过幅值归一化的方法直接建立幅值-震级关系进一步简化回归计算。以各事件样本的台网震级mi作为初始震级,将所有事件样本的幅值归一为同一震级m0对应的幅值,本文事件样本震级分布为mb3.0—6.0,将震级统一划归为mb4.5,然后计算各样本数据实测幅值周期比
$ {A_{ij}}/{T_{ij}} $ 相应的归一化幅值周期比$ { ( {A_{ij}}/{T_{ij}} ) _0} $ ,那么所有样本幅值均对应于mb4.5,其大小仅与震中距和深度相关。根据体波震级的定义,幅值周期比与震级满足对数关系,即$$ {m_i} - {m_0} = \lg \frac{{{A_{ij}}/{T_{ij}}}}{{{{ ( {A_{ij}}/{T_{ij}} ) }_0}}} , $$ (2) 式中,Aij和Tij分别表示事件i在台站j上记录到的幅值与周期。
第三步对样本进行筛选并分组。将归一化后的幅值样本按震中距进行分组,为减小设备故障、干扰噪声等带来的影响,去除归一化后幅值大于3倍标准差的样本值。
第四步运用最小二乘法回归各样本组对应的量归函数
$\sigma ( \varDelta ,h ) $ 的最优估计值。目标函数P表达式为$$ P = \sum {{{{\varepsilon _{ij}}}^2}} = \sum {\Bigg[{m_0} - \lg {{\Bigg(\frac{{A{}_{ij}}}{{{T_{ij}}}}\Bigg)}_0} - \sigma ( {\varDelta _{ij}},{h_i} ) } - {L_j}{\Bigg]^2} , $$ (3) 式中,
$ {\varepsilon _{ij}} $ 表示运用台站j震相幅值计算事件i的震级残差,Δij表示台站j至事件i的震中距,Lj表示台站j的场地响应项。在实际回归过程中,虽然量规函数项$\sigma ( \varDelta ,h ) $ 是随震中距变化的量,而场地响应项L是随台站变化的量,但因为$ \sum {L = 0} $ 这一内在约束,不需要同时回归量规函数项与台站场地响应项,可将两项合并回归,得到包含台站场地响应项的量规函数$\sigma ( \varDelta ,h ) $ 。通过计算单台震级与台网平均震级的系统偏差即可分离各台站j的场地响应项Lj,计算表达式为$$ {L_j} = \sum\limits_{i = 1}^M {\frac{{{m_i} - {m_{ij}}}}{M}} , $$ (4) 式中,
$ {m_{ij}} $ 表示台站j根据量规函数$ \sigma ( \varDelta ,h ) $ 计算得到的事件i的单台震级,场地响应项为对M个样本事件残差求均值得到的,在计算过程中同样去除标准差过大的震级样本。第五步重新计算震级。运用上文回归得到的量规函数及台站场地响应项重新计算事件样本的台网震级
$ {m'_i} $ ,计算表达式为$$ {m'_i} = \frac{1}{N}\left[{{\displaystyle\sum\limits_{j = 1}^N {\lg \Bigg(\dfrac{{{A_{ij}}}}{{{T_{ij}}}}\Bigg) + \sigma ( {\varDelta _{ij}},{h_i} ) + {L_j}} }}\right] , $$ (5) 式中N表示事件i的定义台站数。统计mi与
$ {m'_i} $ 的残差,通过残差均值与阈值比对判断是否需要迭代计算,若需要,则初始震级mi替换为$ {m'_i} $ ,重复步骤2,直到计算结果趋于稳定,输出回归结果。2. 数据处理
不同震相服从不同的路径传播规律,对应各自不同的幅值-震中距衰减特性。对于远震事件,地震波穿透下地幔到达核幔边界。该范围最常见的震相是完全在地幔中传播,未经地壳或外核反射的P波与S波。当震中距大于40°时,地震波上行至自由表面经过一次或多次反射,形成PP,SS或PPP,SSS等反射震相,以及反射面处发生转换的PS或SP震相。除被自由表面反射的上行波,反射波还包括被外核外表面反射的下行波,形成PcP,ScS以及发生偏振的PcS和ScP。
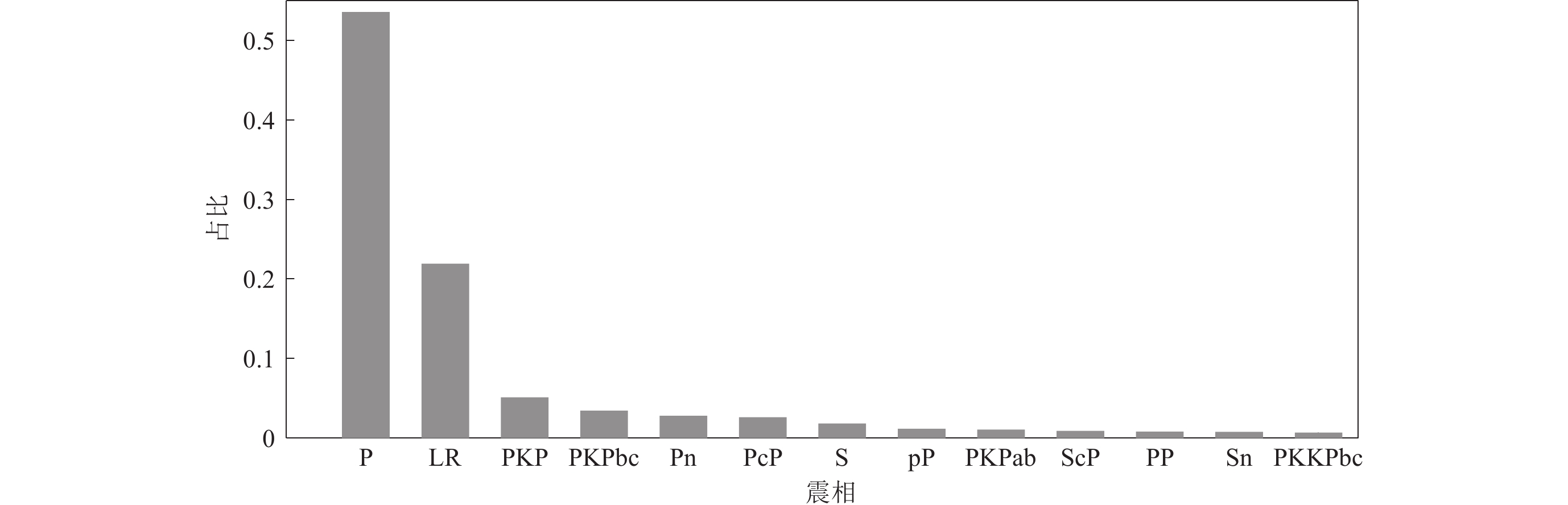
对于极远震事件,地震波穿透至地核。在该范围内,除了自由表面多次反射的PPP等震相,在核幔边界,较长周期的P波发生衍射,在100°—150°震中距范围内形成Pdif震相。若地震波离源角比发生衍射时更加陡峭,将穿透核幔边界,形成PKP,SKS,PKS及SKP震相。在大于140°左右,PKP出现两个走时分支,分别为PKPab和PKPbc,而PKP,PKPab和PKPbc均在外核传播。若离源角进一步陡峭,射线进入内核,经过内核外侧和内侧分别形成PKiKP与PKIKP震相(库尔哈奈克,1992)。通过统计IDC公报中事件的定义震相数量,在一定程度上可以反映该震相出现的频次与稳定性,限定事件时间为2010—2020年,考虑震级饱和及远震信号信噪比,限定震级为mb3.0—6.0,震中距大于10°,共筛选出记录事件20余万个,震相560余万个,其中占比较高的震相结果如图2所示。
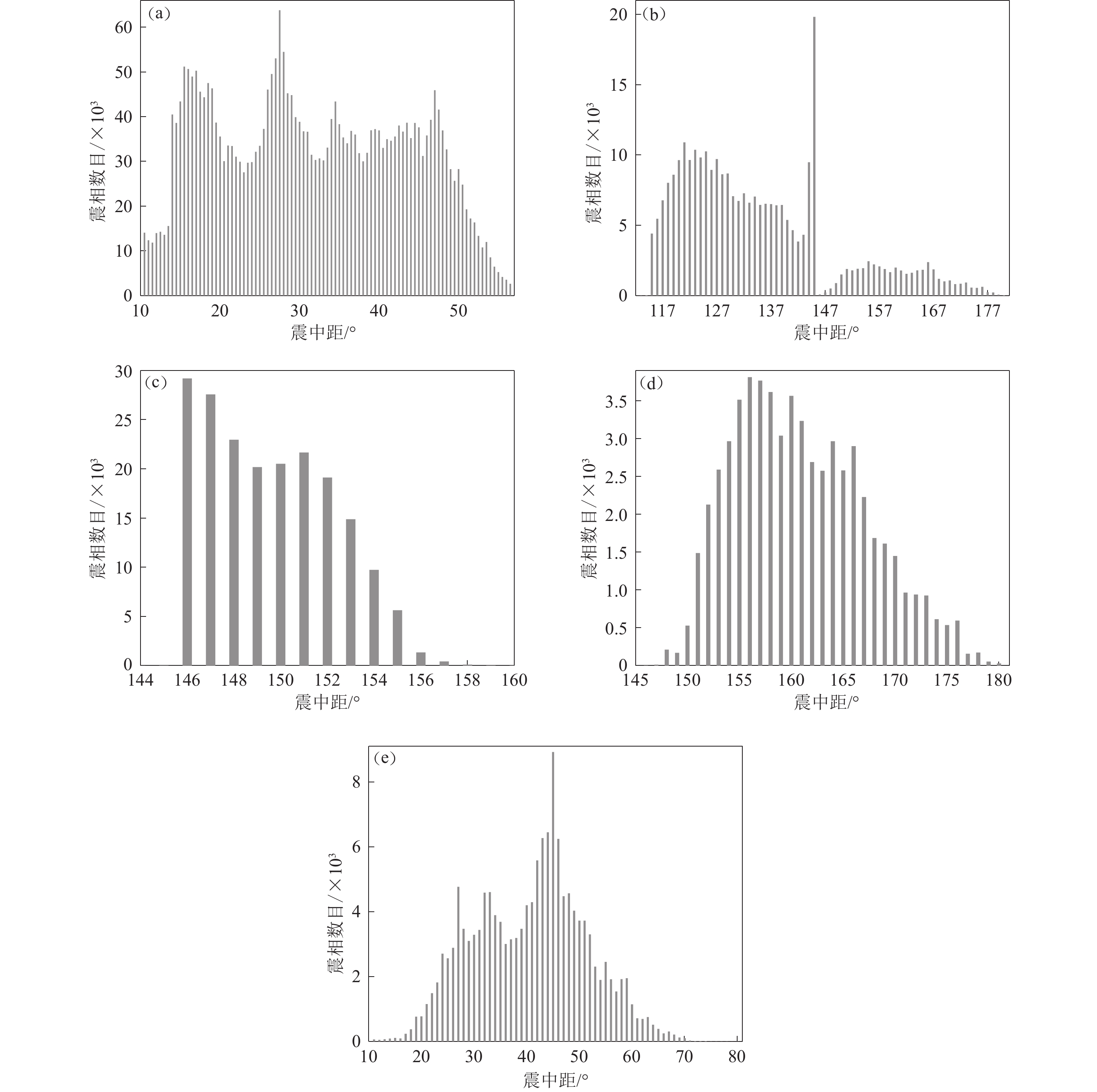
图2中列举了占比较高的前13种震相,其中P震相占比最高,超过0.5,除此之外,占比较高的震相包括面波震相LR,区域震震相Pn和深震震相pP,其中远震与极远震体波震相包括PKP,PKPbc,PcP及PKPab等,其占比分别为0.051,0.035,0.026及0.011。图3给出了上述P,PKP,PKPbc,PcP及PKPab震相数目随震中距分布的统计结果。
从图3可以看出,远震P波震相分布最广,在10°—103°均有分布,大于103°时IDC不再检测并测算P波幅值。小于20°与接近100°时,数目显著降低(图3a),这是由于上地幔150 km深度左右存在一个低速层,在低速层内地震波发生下弯,导致射线出露地面的部分向后移动,在震中距10°—15°地表形成一个无射线出露的影区,导致观测震相数量显著降低。同时,射线出露后移的部分射线会导致震中距20°附近射线密度增大,P波幅值增大。而且由于深度410—660 km即上地幔与下地幔的过渡层,P波速度出现不连续,P波走时曲线发生重叠,导致震中距20°左右P波幅值剧烈增加。以上原因可能导致震中距20°左右的观测震相数目显著增大。震中距大于100°时,P波开始进入地核,在核幔边界处P波速度发生不连续突变,地震波受到明显的折射进入地核,在该震中距范围内形成“核影区”,同时核幔边界出现高非弹性衰减区,进一步导致P波幅值减小,从而使观测数目减小。
PKP震相的分布如图3b所示,图中表明该分布以震中距145°为界明显分为两段,前半段震相观测数目明显高于后半段,并且在震中距140°—145°之间,观测数目显著增大。这是由于震中距自145°左右处开始,PKP出现两个走时分支即PKPbc和PKPab,如图3b和3c所示,PKPbc和PKPab的走时曲线在145°附近重合,导致幅值增强,形成焦散点,PKP震相幅值显著增大,导致该震相观测数目增大。震中距大于焦散点时,IDC定义并测算PKPbc和PKPab的震相幅值,导致PKP震相观测数目减小。图3e中PcP震相观测数目在45°附近显著增大,可能是由于在该震中距范围内核幔反射的PcP震相与地表反射震相PP震相的走时曲线相交,导致幅值有所加强,观测数目相应增大。
3. 震级-幅值-震中距-深度模型建模
不同介质对地震波的衰减效果不同,为减小区域介质差异的影响,在选择事件时,应避免定义台站趋向于某一个方位所导致的事件震级系统偏差,限制事件最小震级为mb4.0,最大震级与上文一致为mb6.0,并进一步限制定义台站数目大于10,张角小于70°,同时为保证足够样本数目,事件时间区间限制扩大为2000—2018年。IDC公报中给出的震相幅值为峰值,计算时以峰-峰值作为幅值,即计算峰值的两倍公报中的周期即为最大峰谷对应时间的两倍,计算时作为周期直接使用。
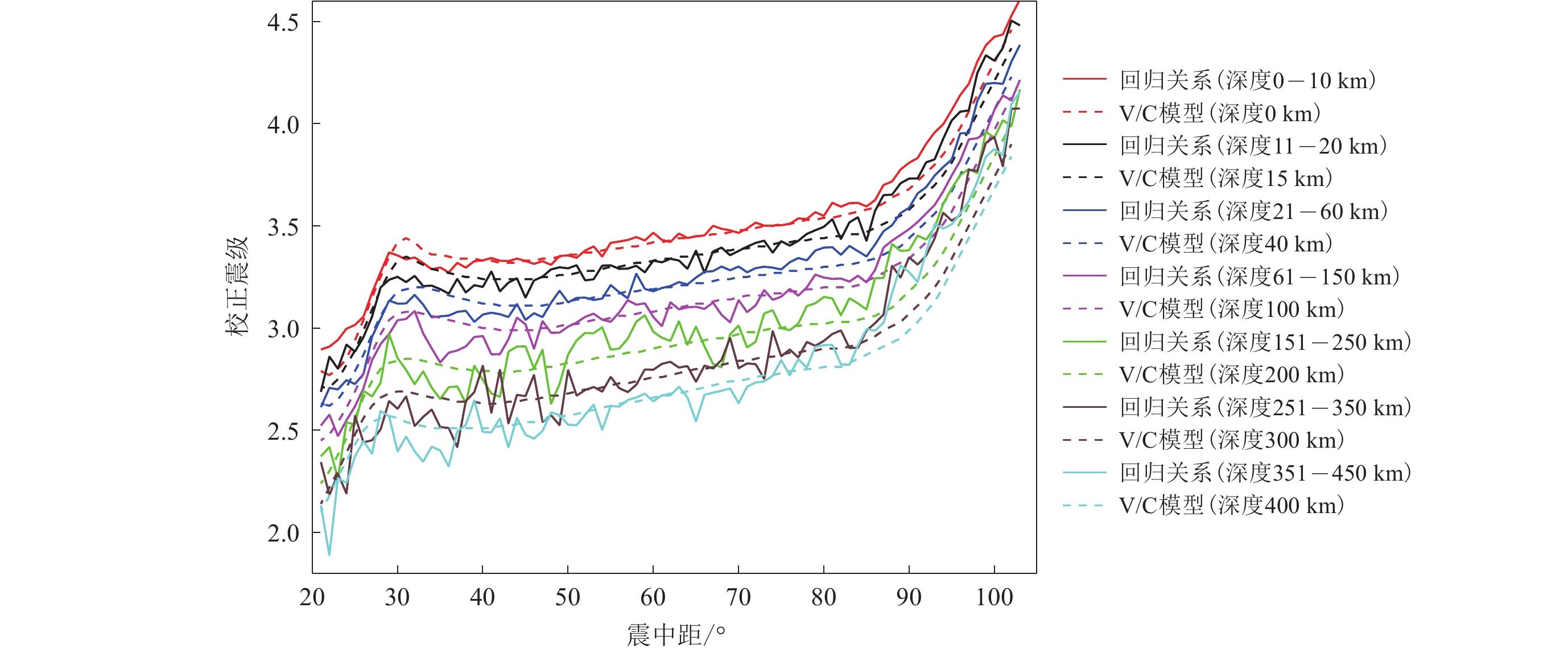
首先回归远震P震相模型,按事件深度划分为0—10 km,11—20 km,21—60 km,61—150 km,151—250 km,251—350 km及351—450 km共计7个深度区间,计算结果如图4所示。将结果与IDC计算体波震级所运用的量规函数模型进行对比,在图中简称V/C模型。
图中实线为不同深度P震相对应的回归模型,虚线为V/C模型,二者在各深度上走势相同,总体相差小于0.2,在深度超过200 km,震中距大于80°时相差最大达到0.4。造成此结果的原因,一方面由于随着深度的增大,震相样本数量急剧减小,导致回归曲线的标准差增大;另一方面本项目回归基于IDC给出的事件深度,由于该机构主要关注核爆炸监测,即浅源地震事件,所以对深源事件的深度估算并不是十分准确,而且V/C模型给出的深度是一固定深度,而本项目给出的则是一个包括该深度在内的一个深度区间,导致二者存在一定差异。
从图4可以看出,不同深度的量规函数曲线明显分为三段,震中距20°左右的量规函数较小,并迅速增大,这与图3a中P震相在该震中距范围观测震相数目显著增大一致,这是由于射线在该震中距上重叠导致幅值增大。震中距大于90°时量规函数迅速增大,与图3a中P震相在该震中距范围观测震相数目显著减小相一致,这是由于该震中距范围内“核影区”导致幅值减小。
选取未参与建模的样本数据对回归结果进行验证,统计IDC公报台网震级与运用模型计算得到的震相震级的残差,通过残差样本均值和标准差评判模型的适用性,若均值过大表明该模型存在系统偏差,若标准差过大,则表明该模型不能适用于所有台站。利用2018—2020年的数据,运用回归得到的模型计算台网震级并与IDC的结果进行比对,震级残差分布如图5所示,分布标准差为0.06,均值为−0.006。经统计98.97%的事件的残差小于3倍标准差,即震级相差在±0.18以内,计算震级系统偏差为−0.006,基本不存在系统偏差。
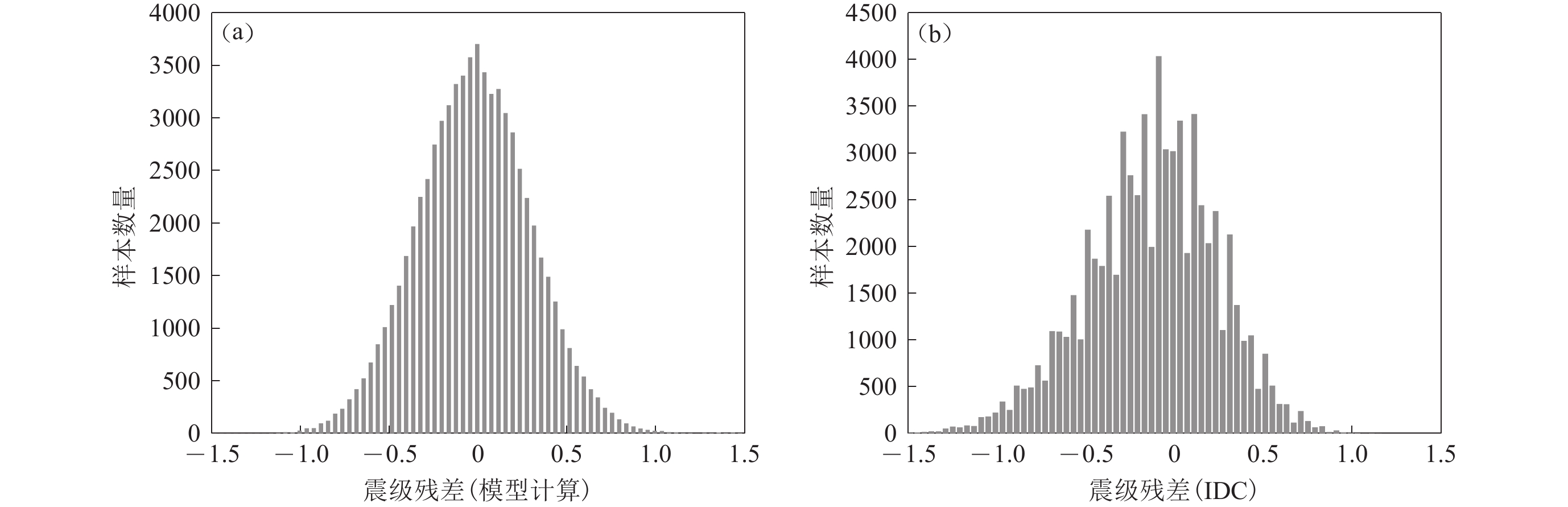
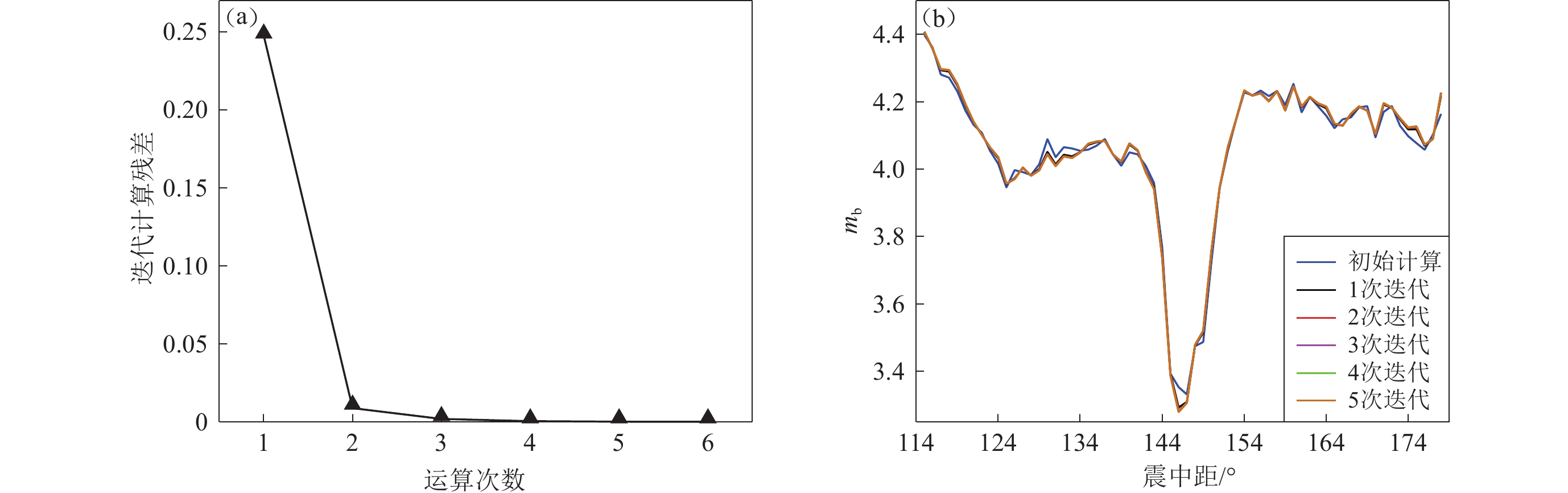
运用同样的事件样本,统计单台震级与台网震级残差分布,结果如图6所示。图6a为运用模型计算得到的震级残差分布,样本标准差为0.32;图6b为运用IDC给出的单台震级与台网震级统计得到的残差分布,样本标准差为0.37。IDC单台残差较大的原因可能是未参与建模的数据来自2018—2020年公报,该时间段公报中给出的台站震级为“mbtmp”,为未最后确定的震级。运用相同的方法计算PKP震相不同深度对应的量规函数,0—10 km深度PKP震相的量规函数通过五次迭代完成运算,结果及各次迭代残差如图7所示。
图7a表示初始计算及历次迭代计算的残差均值,残差逐步减小,五次迭代后残差均值满足阈值要求停止运算。图7b表示初始计算及五次迭代回归得到的PKP震相的量规函数,从图中可以看出,除初始运算与第一次迭代回归结果存在相对较大偏差,2次迭代后结果偏差均较小。由于PKP等震相的样本数目远小于P震相,所以为保证回归精度,将深度分为0—10 km,11—70 km,71—150 km,151—250 km及大于250 km共计五个区间,量规函数回归结果及台站震级相对台网震级残差分布如图8a所示。
图8a表明PKP震相的量规函数在145°焦散点附近呈现明显下凹,与图3b中观测数目在该震中距显著增大相对应。从图中可以看出,除了焦散点附近,量规函数并没有随震中距的增大发生明显改变,说明PKP震相地震波主要在下地幔及外核传播,能量随震中距衰减很小。对计算结果进行验证,同样取未参与建模的2018—2020年的公报数据进行计算。运用P震相回归结果验证所使用的事件样本,统计台站震级与IDC给出的对应事件的震级的残差分布(图8a),结果显示,残差样本均值为−0.019,标准差为0.355,相较P震相残差略大,说明PKP震级稳定性低于P震相震级。
PKPbc震相的不同深度量规函数回归结果及台站震级相对台网震级残差分布如图8b所示。图中显示,震级残差分布的均值为−0.031,标准差为0.361,与PKP震相的计算结果相当。
PKPab震相的不同深度量规函数回归结果及台站震级相对台网震级残差分布如图8c所示。量规函数随着震中距的增大而增大,但由于样本数目相较于P及PKP震相明显减少,所以量规函数平滑性较差,在计算残差时须对量规函数进行平滑处理。震级残差分布的均值为−0.016,标准差为0.352,与PKP震相的计算结果相当。
PcP震相的不同深度量规函数回归结果及台站震级相对台网震级残差分布如图8d所示。PcP震相量规函数基本不随震中距发生变化,计算残差时对量规函数进行平滑处理,震级残差分布的均值为−0.010,标准差为0.301。上文针对P,PKP,PKPab,PKPbc及PcP震相回归得到对应的量规函数,通过残差样本统计,除PKPbc的残差均值大于0.03外,其余震相均为0.01左右,模型的系统偏差极小,甚至可以忽略不计。残差标准差均为0.3左右,满足一般幅值相容性判断的要求。
4. 模型应用研究
基于幅值-震级-震中距-深度模型,通常采用震级反算幅值或幅值计算震级的方式判断震相相容。以一次mb5.3天然地震事件为例,发震时刻为2012年4月17日08:51:24,发震地点(31.63°S,177.22°W),该事件在多个台站同时记录到P,PcP,PKP,PKPab及PKPbc震相,部分台站震相波形如图9所示。
图9a,b的STKA台站 (震中距为39.8°)和PMG台站(震中距为34.8°)同时记录到了P震相和PcP震相。图9c,d的BRTR台站 (震中距为153.8°)和AKASG台站(震中距为153.8°)同时记录到了PKP,PKPbc和PKPab震相。运用各震相对应的震级-幅值-震中距-深度模型预测幅值,并与实测幅值相比较,残差结果如图10所示。
图10中不同颜色图形表示不同震相的预测幅值与实测幅值的残差对数值,图中同时记录到多个震相的7个台站的残差最大不超过0.4,结合信号到时,可认为上述震相均来自同一事件。
若通过震相幅值计算得到的震级明显高于或低于台网震级,则说明震相不属于该次事件。位于澳大利亚的ASAR台阵的中心台站AS31同时记录到震中距分别为128.3°和43.3°的两次事件的PKP和P震相,事件、台站及记录到的波形如图11所示。
图中波形显示共检测到两个信号,震相到时相差约5 s左右。对于极远震事件,考虑走时模型误差与到时拾取误差,在事件自动检测时可能出现震相误关联。运用PKP震相模型计算前后两个信号的震级分别为mb4.99和mb5.85,显然第一个震相与mb4.7事件相容。运用P震相模型计算前后两个信号的震级分别为mb4.31和mb5.18,那么第二个震相与mb5.1事件相容。
此外,PKP,PKPab及PKPbc震相的量规函数模型还可应用于极远震体波震级的计算,例如位于中国地区的台站对南美洲地震事件的监测,震中距大于103°,无法通过P波计算体波震级,此时只能依靠台站记录到的PKP,PKPab及PKPbc进行计算。以南美洲某区域为例:IDC目录给出了2018—2019年发生在南美地区(60°W—80°W,0°S—30°S)体波震级大于5级的浅源地震事件共计13次。由于新疆台网地处欧亚腹地,远离海洋,不受海潮等低频噪声干扰,同时该地区人口密度较低,各种人文噪声源相对较少,该地区台站本底噪声显著低于中国内地台站。运用新疆部分信号检测能力较强的台站记录的上述13次事件的PKP震相信号幅值及相应的量规函数计算震级,台站记录的某次mb5.3事件(12.1°S,74.1°E,2019-02-14 14:33:14)的PKP震相及计算震级如图12所示。
![]() 图 12 新疆地区部分台站记录的南美地区某次mb5.3地震事件的PKP震相(右上角为台站名,括号内为计算的体波震级,波形滤波频带为0.8—4.5 Hz)Figure 12. PKP phases of some mb5.3 event located in South America observed by stations in Xinjiang (Station code is labeled on right top of the waveform,and the number in bracket is the computed mb. The filter band is 0.8 to 4.5 Hz)
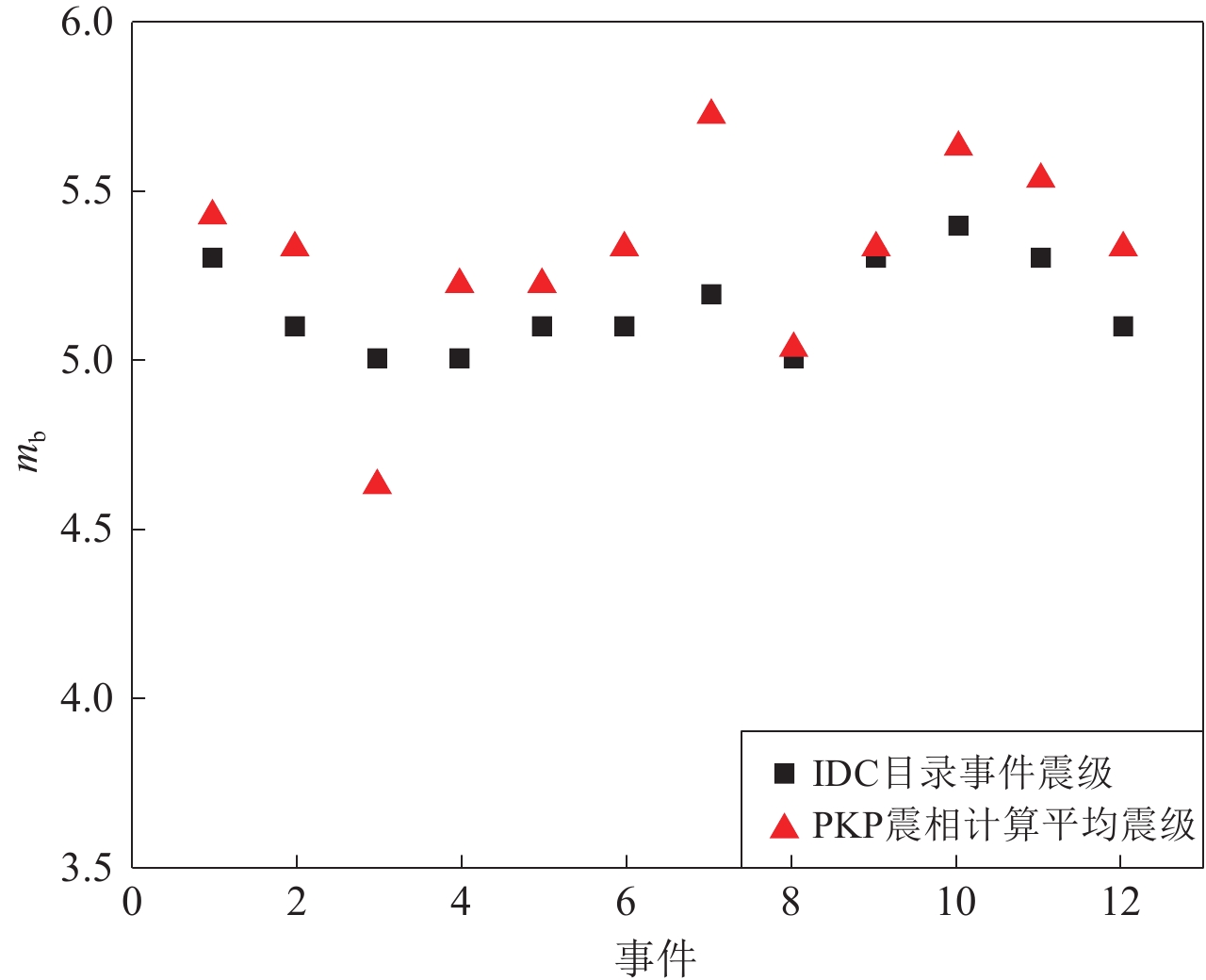
图 12 新疆地区部分台站记录的南美地区某次mb5.3地震事件的PKP震相(右上角为台站名,括号内为计算的体波震级,波形滤波频带为0.8—4.5 Hz)Figure 12. PKP phases of some mb5.3 event located in South America observed by stations in Xinjiang (Station code is labeled on right top of the waveform,and the number in bracket is the computed mb. The filter band is 0.8 to 4.5 Hz)新疆地区台站实际记录到13次事件中的12次,将各台站记录到的震级求平均,并与IDC目录中的震级作比对,结果如图13所示。针对图中的12个事件,通过PKP震相得到的平均震级与IDC目录震级相比较,最大相差0.5级,大部分相差0.1—0.2级,说明将PKP震相的量规函数模型用于极远震体波震级计算是合理的,同时从图中可以看出,计算得到的平均震级普遍高于IDC目录震级0.1—0.2级,说明该地区台站需要进行台站场地响应校正以消除偏差。
5. 讨论与结论
在信号时频域整体与局部特征中,震相的幅值相容性通过幅值残差比对可以方便直观地进行信号关联性判断。本文基于IDC数据库,统计P,PcP,PKP,PKPbc及PKPab远震与极远震震相样本分布,运用基于残差统计的迭代方法计算上述震相的幅值-震级-震中距-深度模型,为震相幅值相容性判断提供了支撑,主要结论如下:
1) 通过地震波传播特征及震相数目随震中距分布的统计,分析了不同震相的分布特点:P震相在震中距10°—20°及100°左右出现影区;PKP震相在震中距144°附近呈现局部聚焦效应;PKPab和PKPbc随震中距分布区间较窄,并随震中距增大,样本数目逐渐减小。以上特征与各震相幅值-震级-震中距-深度模型的部分特征相对应,相互印证了结果的合理性。
2) 通过公报读取、幅值归一化、样本筛选分组、回归模型等步骤建立初始模型,根据模型重新计算震级,通过残差均值和阈值比对判断是否需要迭代计算,设置迭代残差阈值为0.000 1,经过3—5步迭代完成运算。通过震级残差样本统计,除PKPbc的残差均值大于0.03外,其余震相均为0.01左右,模型系统震级偏差极小;残差标准差均为0.3级左右,满足一般幅值相容性判断的要求。
3) 针对模型开展不同场景的应用研究:预测某次事件在多个台站同时记录到P,PcP,PKP,PKPab及PKPbc震相的幅值,通过震相的幅值相容性判断震相是否来自该事件;根据不同事件在某台站同时记录到到时相近的P与PKP震相的幅值计算震级,通过震级比对确定震相与事件的所属关系;对于无法计算P震相对应的体波震级的极远震事件,将PKP,PKPab及PKPbc震相的量规函数模型应用于体波震级的计算。
本文在回归幅值-震级-震中距-深度模型时使用全球范围事件样本,针对具体台站实际并未区分样本事件所处区域,也就没有考虑不同传播路径衰减导致的差异,这样在使用模型计算震级时,会由于实际传播路径的差异导致存在一定的偏差。同时,通过大量数据回归得到的模型理论上可以反映全球传播介质一维的平均衰减情况,但实际上,全球地震多发于板块之间的特定区域,导致不同传播路径对应的样本密度存在较大差异,这样回归得到的模型主要反映样本密度大的区域对应的路径衰减情况,若事件远离以上区域,必然会导致结果的偏差。若需要更精确的模型,可面向具体台站针对不同区域建立幅值-震级关系。
本文在计算量规函数时,同时得到了台站的场地响应项,该值是通过统计的方法得到的。统计结果表明,处在造山带等构造活动频繁区域的台站,其台站震级普遍小于台网震级;处在克拉通等稳定构造区域的台站,其台站震级普遍大于台网震级。但是,存在一小部分台站的场地响应与预期存在较大差异,在以后的工作中需要通过台站区域地壳及上地幔衰减对这部分台站的场地响应异常进行深入分析。
本文给出的幅值-震级-震中距-深度模型为曲线的形式,并未将其拟合为以震中距为变量的表达式,在实际使用中显然不够便捷。在以后的工作中可将其拟合为多项式或包含震中距对数项在内的表达式,这样就需要对多项式阶数等参数进行具体分析。
面向实际应用,还需要将本文所得到的模型以合适的方式在地震实时监测实系统中真正实施,在线检测其可靠性与准确性,在实践中进一步完善。
-
图 12 新疆地区部分台站记录的南美地区某次mb5.3地震事件的PKP震相(右上角为台站名,括号内为计算的体波震级,波形滤波频带为0.8—4.5 Hz)
Figure 12. PKP phases of some mb5.3 event located in South America observed by stations in Xinjiang (Station code is labeled on right top of the waveform,and the number in bracket is the computed mb. The filter band is 0.8 to 4.5 Hz)
-
陈培善,秦嘉政. 1983. 量规函数、台站方位、台基及不同测量方法对近震震级ML的影响[J]. 地震学报,5(1):87–98. Chen P S,Qin J Z. 1983. The effects of the calibration function,azimuths and sites of the stations and different methods of approach on the magnitude determination of near earthquakes,ML[J]. Acta Seismologica Sinica,5(1):87–98 (in Chinese).
康清清,顾勤平,于悦颖,钱婷,黄群,霍祝青. 2019. 江苏及邻区地方性震级量规函数的研究[J]. 中国地震,35(3):521–530. doi: 10.3969/j.issn.1001-4683.2019.03.010 Kang Q Q,Gu Q P,Yu Y Y,Qian T,Huang Q,Huo Z Q. 2019. Study on calibration function of local earthquakes in Jiangsu and its adjacent areas[J]. Earthquake Research in China,35(3):521–530 (in Chinese).
库尔哈奈克. 1992. 地震图解析[M]. 刘启元, 吴宁远, 修济刚译. 北京: 地震出版社: 10–33. Ota K. 1992. Anatomy of Seismograms[M]. Liu Q Y, Wu N Y, Xiu J G trans. Beijing: Seismological Press: 10–33 (in Chinese).
刘芳,张帆,张晖,赵铁锁,娜热,魏建民. 2016. 内蒙古地区地方性震级的量规函数研究[J]. 中国地震,32(3):485–493. doi: 10.3969/j.issn.1001-4683.2016.03.005 Liu F,Zhang F,Zhang H,Zhao T S,Na R,Wei J M. 2016. Study on calibration function of near earthquakes in the Inner Mongolia region[J]. Earthquake Research in China,32(3):485–493 (in Chinese).
严尊国,薛军蓉. 1987. 中国近震震级ML综述[J]. 中国地震,3(4):44–51. Yan Z G,Xue J R. 1987. On local magnitude ML for earthquakes in China[J]. Earthquake Research in China,3(4):44–51 (in Chinese).
严尊国,李普丽,薛军蓉. 1992. 中国近震震级量规函数研究[J]. 中国地震,8(4):76–91. Yan Z G,Li P L,Xue J R. 1992. Study on calibration function of local magnitude ML in China[J]. Earthquake Research in China,8(4):76–91 (in Chinese).
张媛媛,王平,惠少兴,古云鹤. 2017. 陕西地区近震震级的量规函数研究[J]. 内陆地震,31(4):368–375. Zhang Y Y,Wang P,Hui S X,Gu Y H. 2017. Study on calibration function of local earthquakes in Shaanxi region[J]. Inland Earthquake,31(4):368–375 (in Chinese).
Carpenter E W,Marshall P D,Douglas A. 1967. The amplitude-distance curve for short period teleseismic P-waves[J]. Geophys J Int,13(1/2/3):61–70.
Le Bras R, Wuster J. IDC Processing of Seismic, Hydroacoustic and Infrasonic Data. Revision 1. IDC Documentation User Guides.[M]. Vienna: Science Applications International Corporation: 74–96.
Murphy J R,Barker B W. 2003. Revised distance and depth corrections for use in the estimation of short-period P-wave magnitudes[J]. Bull Seismol Soc Am,93(4):1746–1764. doi: 10.1785/0120020084
Veith K F,Clawson G E. 1972. Magnitude from short-period P-wave data[J]. Bull Seismol Soc Am,62(2):435–452. doi: 10.1785/BSSA0620020435
-
期刊类型引用(0)
其他类型引用(1)




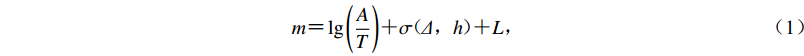

 下载:
下载: