Application of generalized extreme value distribution based on profile likelihood estimation in long term earthquake prediction
-
摘要: 为描述强震预测的不确定性,在地震预报极值分析模型的参数估计中,引入轮廓似然估计法。对广义极值分布中形状参数和地震重现水平的轮廓似然估计原理及数值算法进行了详细地阐述,并利用构建的广义极值分布模型对东昆仑地震带进行了地震危险性分析。关于形状参数和重现水平的点估计,以及10年以内的重现水平置信区间的估计,轮廓似然估计法与极大似然估计法效果基本相同,但在中长期地震重现水平置信区间的预测中,轮廓似然估计法得到的关于置信水平不对称的置信区间,在强震水平下对预测震级的不确定性表达更准确,预测结果更加有效。Abstract: To describe the uncertainty of strong earthquake prediction, we introduced the profile likelihood estimation into parameter estimation of extreme value model for earthquake prediction. It is elaborated that the profile likelihood estimation principle and numerical algorithm of shape parameters and earthquake return level in generalized extreme value distribution. Meanwhile, a model of generalized extreme value distribution was created and was used to analyze the seismic risk of the East Kunlun seismic belt. The results showed that profile likelihood estimation and maximum likelihood estimation generated basically the same effect in point estimation of shape parameters and return level as well as the estimation of confidence interval of earthquake return level within 10 years. However, in the confidence interval estimation of moderate and long interval earthquake return level, the asymmetric confidence interval of return level obtained through the profile likelihood estimation can more accurately express the uncertainty of predicted magnitude of a strong earthquake and more effectively predict the outcome.
-
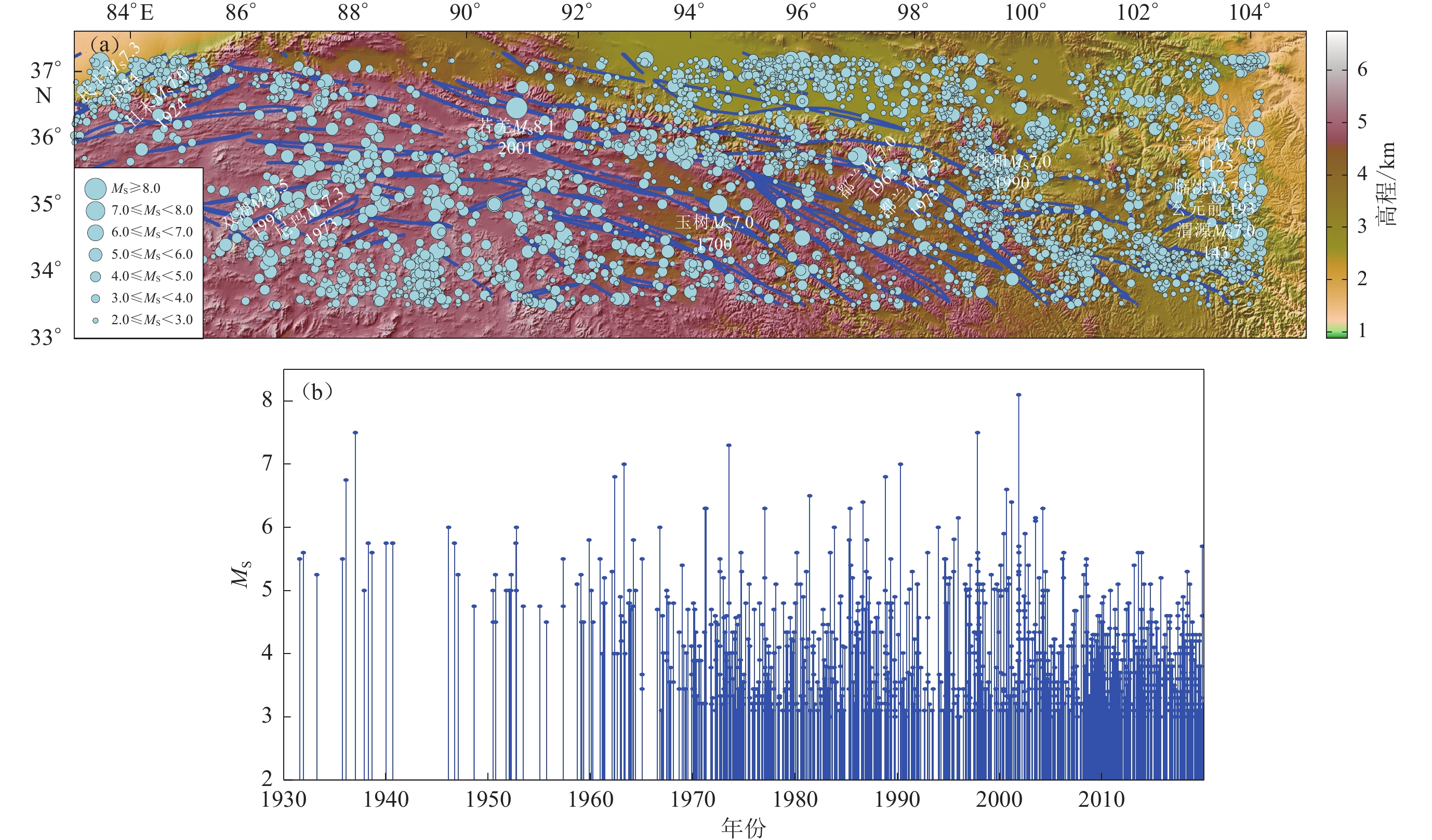
据中国地震台网正式测定,2022年1月8日1时45分,青海省海北州门源县发生MS6.9地震,震中位置(37.77°N,101.26°E),震源深度为10 km。此次地震造成地表破裂长约22 km,地震震中位于门源县皇城蒙古族乡附近,距门源县城54 km,西宁、兰州等地有明显震感。研究区处于青藏高原东北缘,位于柴达木—祁连地块、阿拉善地块和鄂尔多斯地块的交会处,属祁连地震构造带,距此次地震震中最近(约5 km)的断层为冷龙岭断裂带西北端与托莱山断裂的阶区。此次地震的发震断层以左旋为主,震源机制解为走滑型(图1)。
门源MS6.9地震前,青海地区地下流体先后出现八项中短期异常,异常形态多以上升、下降、破年变为主(表1,图2)。震前,笔者依据流体异常出现的时间顺序多次开展现场核实,排除了人为、环境和仪器等干扰,确定了门源静水位、佐署动水位、佐署浅层水温等多项信度较高的异常,经综合分析,于2021年12月6日填卡较好地预测了门源MS6.9地震。震后,进一步对部分显著流体异常进行现场采样和分析,并对可能的前兆孕震机理进行分析,为门源MS6.9地震跟踪过程提供科学的参考依据。
表 1 2022年青海门源MS6.9地震前定点流体观测异常Table 1. Observation of fluid anomalies at the fixed points before MS6.9 Menyuan,Qinghai earthquake in 2022台站 异常项 异常形态 起止时间 震后变化 异常幅值 震中距/km 门源台 静水位 上升—下降 2021-09-17—11-30 异常恢复 0.089—0.16 m 37 佐署台 动水位 下降 2021-07-10—08-25 异常未恢复 0.27 m 132 佐署台 水温 上升 2021-07-10—至今 异常未恢复 0.12 m 132 平安台 静水位 破年变 2021-08-13—10-11 异常恢复 160 乐都台 气氡 上升—下降 2021-09-15—10-06 异常恢复 360—298 Bq/L 169 西宁台 气氡 下降—上升 2021-09-22—11-08 异常恢复 14.2 Bq/L 133 德令哈台 水温 上升—下降 2021-12-02—12-16 异常恢复 0.02—0.007 ℃ 344 共和台 水温 下降 2021-01-06—12-15 异常未恢复 0.1—0.4 ℃ 180 依据 《地下流体分析预报手册》 (中国地震局监测预报司,2020)中异常识别方法的原始曲线法,2021年7—9月出现的流体群体异常对门源MS6.9地震的发生具有较好的指示意义。以水位、逸出气氡异常为主,从异常出现时间及空间演化来看,最早于震前6个月出现的异常为佐署动水位、水温异常,距震中132 km;随后于震前4.5个月出现平安静水位破年变异常,距震中160 km;2021年9月15—22日(震前3.5个月)先后集中出现乐都逸出气氡、门源静水位和西宁逸出气氡异常,距震中分别为169 ,37和133 km。从异常出现及持续时间推测优势发震时间在2022年1月31日前;依据异常空间分布及演化特征推测优势发震地区有两个,其一为青海中南部地区,其二为祁连地震带,以青海中南部地区为主;所发生历史地震的震级均介于M5.6—7.4之间,综合分析后认为目标地震震级约为M6,最终给出预测震级为M6.0—6.4。
图2所示的异常时空演化显示:在时间尺度上,异常均在地震前半年出现,具有中期趋势向短期演化的特征,并且一半以上的异常具有短临预报指示意义;在空间分布上,异常总体呈现由外围异常区向震中区域发散—聚拢—发散的特点。
异常出现后通过现场水化学取样分析,并与较早的取样结果(背景值)进行对比(刘磊等,2017,2021;苏维刚等,2021)。样品分别委托中国地震局地壳应力地壳动力学重点实验室、中国地震局地震预测重点实验室、中国科学院青海盐湖研究所分析测试中心依据 《DZ/T0064—1993 地下水质检验方法》 ,数据结果见表2和图3。
表 2 各异常台站水样的离子浓度Table 2. The analysis results of water chemical composition台站 Na+/(mg·L−1) K+/(mg·L−1) Mg2+/(mg·L−1) Ca2+/(mg·L−1) Cl−/(mg·L−1) SO4 2−/(mg·L−1) HCO3 −/(mg·L−1) B A B A B A B A B A B A B A 西宁台 3200.54 3386 14.52 14.49 16.37 19.03 34.27 38.00 92.64 1154 3857.94 3531 2753.64 2667 门源台 368.2 386.6 3.61 8.56 5.18 4.22 8.01 9.02 155.3 168.8 31.7 55.05 695.6 671.2 佐署台 165.3 593.9 2.29 1.456 12.54 1.571 26.64 3.976 251.7 203.5 119.1 430.2 545.2 522.5 平安台 610 1136 9.03 11.72 84.74 82.9 441.6 445.5 224.1 306.1 2207 2763 183.1 203.8 注:B为各离子背景值,A为各离子浓度异常值。 门源台静水位异常前后Cl−和Na+的浓度变化显著,其它离子的浓度变化程度相当,具体表现为:Cl−和Na+的浓度在水位异常出现后均有升高迹象,两者可形成水体中的氯化物,说明沉积岩中岩盐及其它氯化物溶解反应相较未出现异常前有所增强;SO4 2−浓度呈反向变化,西宁地区样本出现气氡异常后,SO4 2−浓度低于背景值,佐署台动水位、水温及平安台静水位出现异常后SO4 2−浓度高于背景值,分析认为这是由于SO4 2−离子是中等矿化水中含量最多的阴离子,西宁台逸出气氡水体是温泉水,循环深度较深,SO4 2−浓度降低指示有部分低矿化水混入,反之,佐署台动水位、水温及平安台静水位水体均为地表水,循环深度浅,SO4 2−浓度升高指示有部分中等矿化水混入;Ca2+和Mg2+浓度只在佐署台动水位、水温出现异常后显著变化,表现为异常出现后Ca2+和Mg2+浓度明显低于背景值,说明Ca2+的地下水径流途径比较长(刘耀炜,施锦,2000;官致君,2001)。
结合所得实验数据,依据舒卡分类法,西宁台逸出气氡、平安台静水位采样点水样的水化学类型为Na-SO4,门源台静水位采样点水样的水化学类型为Na-HCO3,佐署台静水位、水温采样点水样水化学类型由背景值的Na-HCO3型转变为异常出现后的Na-SO4型。从Na-K-Mg三角形图解可以看出:大部分采样点测值结果集中分布于部分平衡水与未成熟水的交界区域,并且位于Mg2+端元,表明水样与周围环境的水岩作用加剧,显示有深、浅两部分水的混合(高小其等,2002;刘耀炜等,2004);西宁台逸出气氡的背景值与异常值均位于部分平衡水区域,说明水岩反应程度较强,循环深度较深。另外,佐署台动水位、水温采样点由背景值位于未成熟水区域转变至异常出现后的部分平衡水区域,显示有其它深部水体的混入,水岩反应程度增强,此现象与离子浓度分析结果一致。
综上所述,震前青海地区出现罕见群体性流体异常,且大部分出现在震中200 km范围内,较为集中,并且呈现出由外围异常区向震中区域发散—聚拢—发散的特点。2021年玛多MS7.4地震后部分流体异常并未完全恢复至正常观测状态,表明区域应力调整还在继续,随后新增多项流体同步异常,致使异常数量整体不减反增,为后续震情判定提供了科学的参考依据。此次门源MS6.9地震的发生表明震前对预测时间的判断正确,但优势发震地区与门源MS6.9地震震中相差240 km;最终预测震级为M6.0—6.4,与实际发生地震存在0.5的偏差。这表明地下流体异常对于优势发震时间具有较好指示意义,但对震级及发震地区判断不够准确,需要结合测震学及其它地球物理异常进一步梳理预测指标。
震前的区域应力加载导致周围岩石产生裂隙孔隙,使承压井水位、井水温发生持续变化,同一时段的水岩反应加剧,使得水化学离子组分的浓度亦发生相应变化,需特别关注的是最早出现的佐署台动水位、水温异常,其水化学类型及水化学组分也发生很大改变,由此推断该观测点是构造灵敏点,对后续该区震情判定具有地点指示意义。综合所有异常形态、时空演化特征分析认为,基于现场异常核实和异常信度分类认识,排除干扰,对提高震情跟踪工作效能具有重要作用。尽管本次群体性异常特征与观测点密度存在一定关系,但对于震例总结仍具有重要参考意义,同时也有助于提升该区的震情研判能力。
-
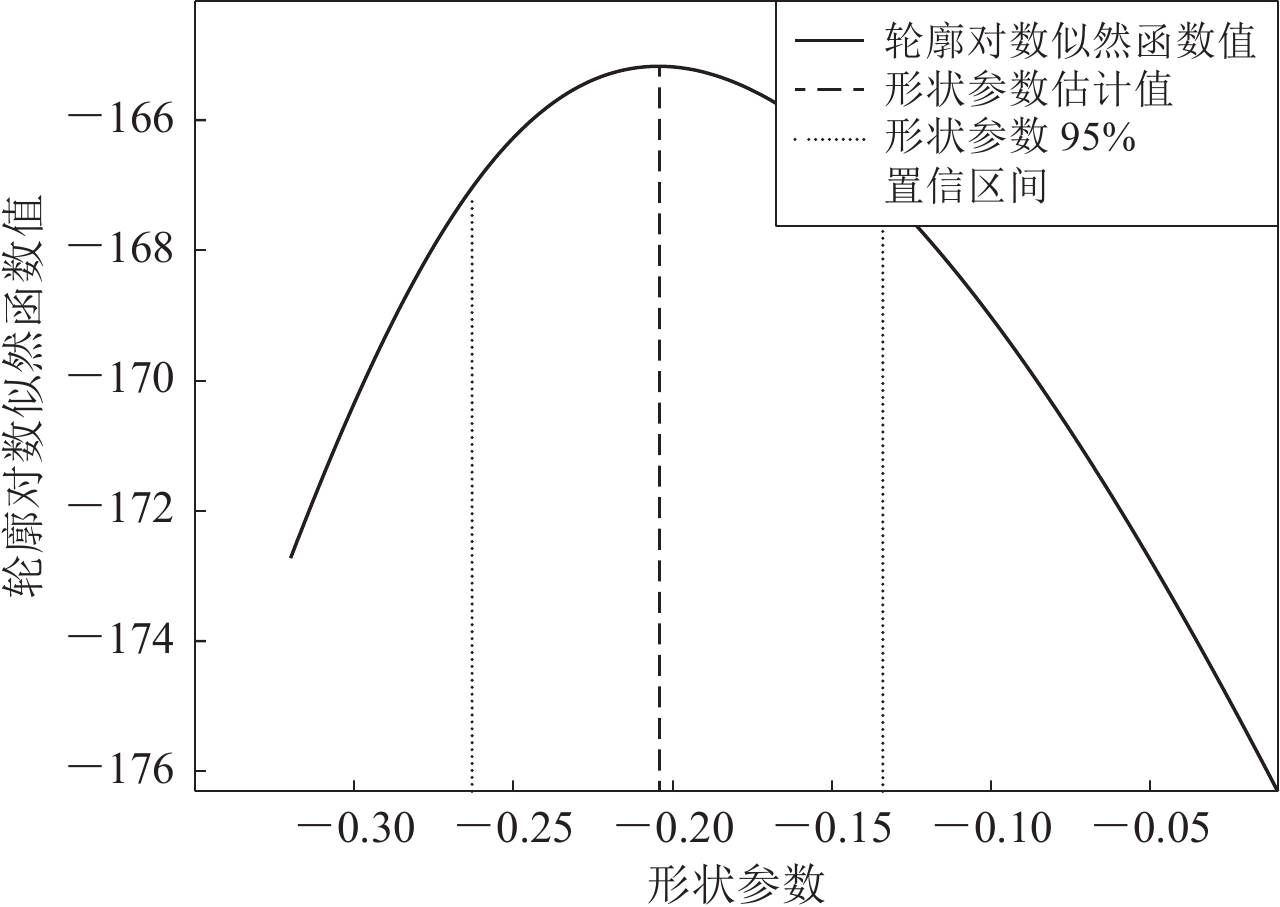
表 1 轮廓似然估计与极大似然估计GEV的分布结果对比
Table 1 Comparation of the profile likelihood estimation and maximum likelihood estimationof GEV distribution
模型分析项目 轮廓似然估计 极大似然估计 参数估计 (−0.204 0,0.847 5,4.834 5) (−0.204 4,0.847 8,4.834 8) 形状参数置信区间 [ −0.259 0,−0.134 0 ] [ −0.268 8,−0.140 1 ] 震级理论上限 MS8.989 1 MS8.981 9 地震带最大震级均值 MS5.178 9 MS5.179 0 表 2 极大似然估计与轮廓似然估计的重现水平对比
Table 2 Comparation of the recurrence level between profile likelihood estimation and maximum likelihood estimation
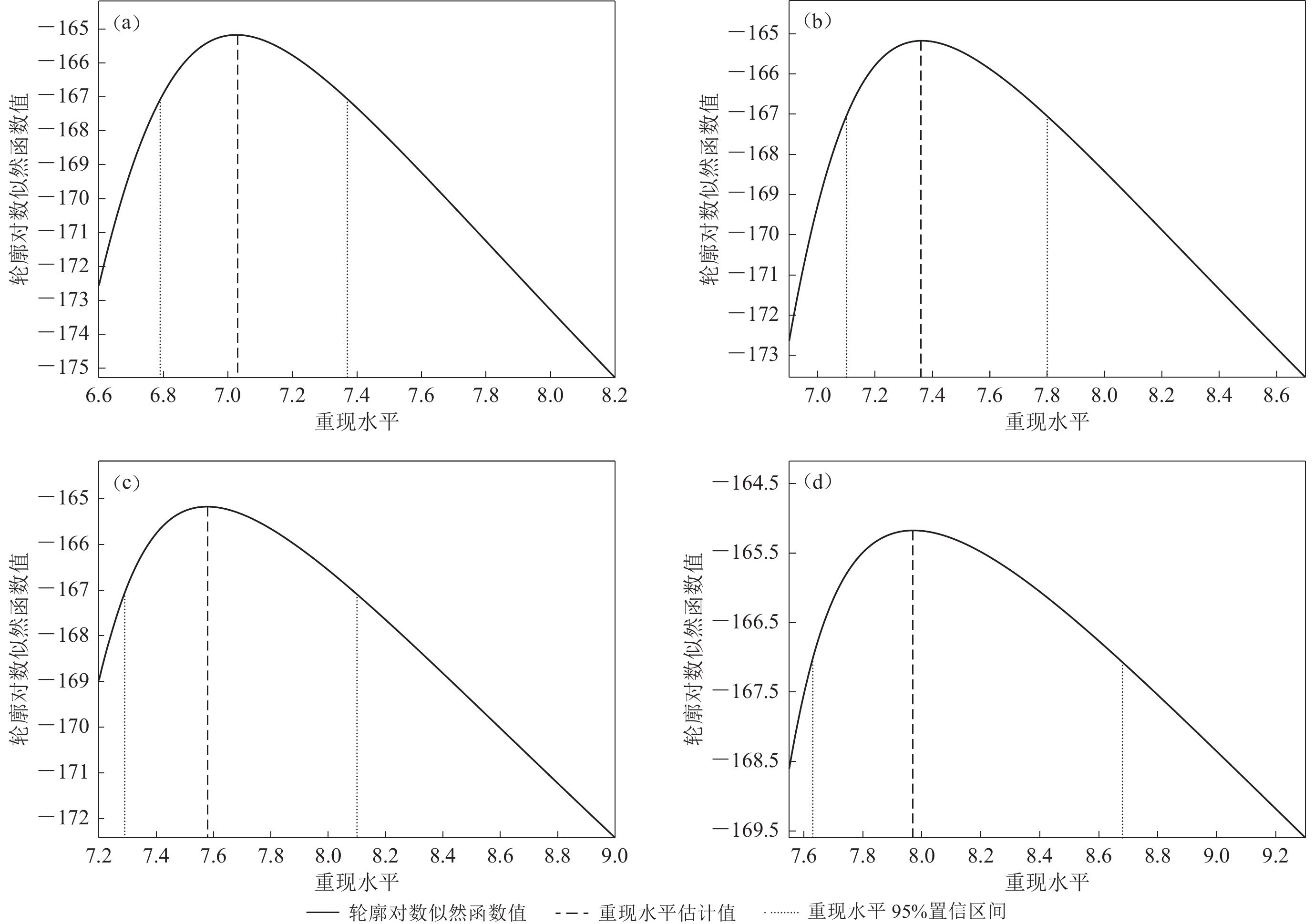
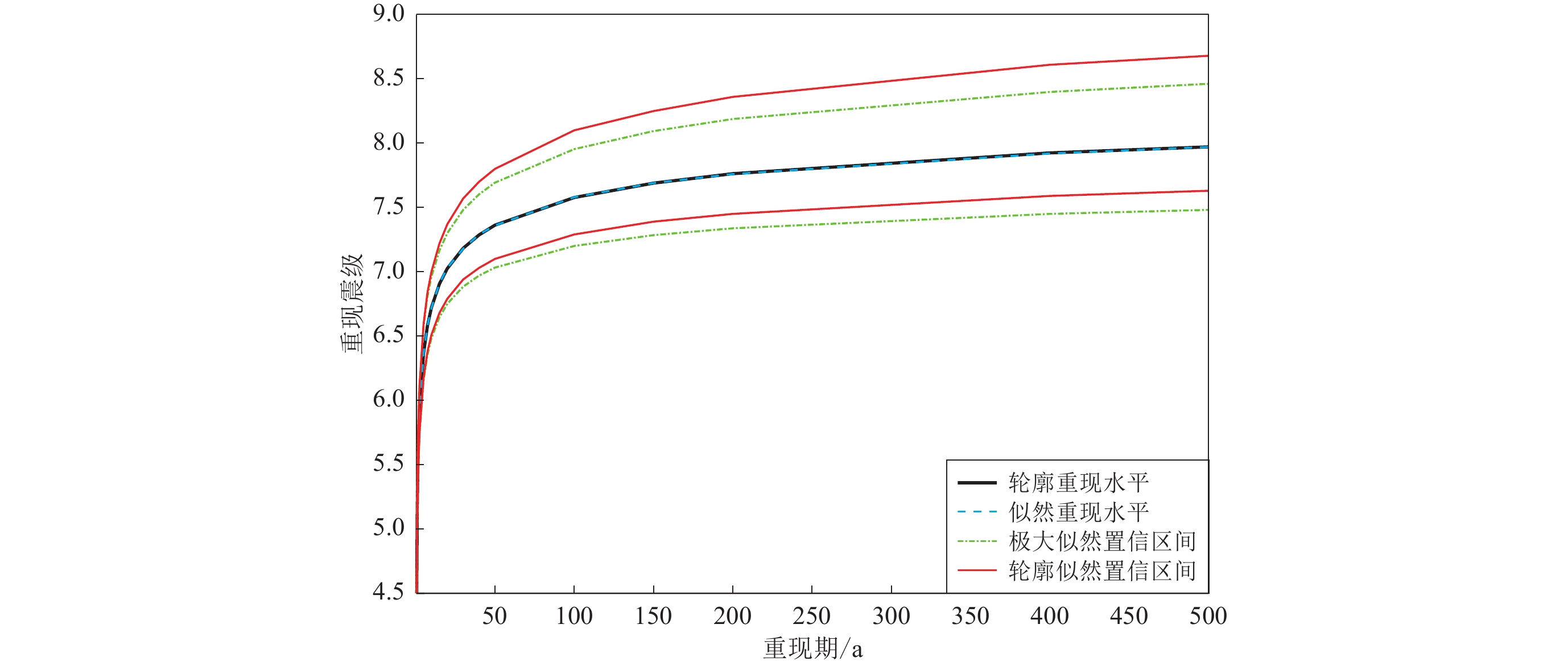
重现期
/年极大似然估计
重现水平极大似然估计95%
置信区间轮廓似然估计
重现水平轮廓似然估计95%
置信区间轮廓估计重现水平
两侧区间长度比1 MS5.13 [ 4.97,5.29 ] MS5.13 [ 4.98,5.29 ] 1.07 5 MS6.36 [ 6.15,6.57 ] MS6.36 [ 6.17,6.59 ] 1.21 10 MS6.72 [ 6.48,6.96 ] MS6.72 [ 6.51,7.00 ] 1.33 20 MS7.03 [ 6.75,7.30 ] MS7.03 [ 6.79,7.37 ] 1.42 50 MS7.36 [ 7.03,7.69 ] MS7.36 [ 7.10,7.80 ] 1.69 100 MS7.58 [ 7.20,7.95 ] MS7.58 [ 7.29,8.10 ] 1.79 500 MS7.97 [ 7.48,8.46 ] MS7.97 [ 7.63,8.68 ] 2.09 -
陈虹,黄忠贤. 1995. 应用混合极值理论及最大似然法估计中国大陆地震危险性[J]. 地震学报,17(2):264–269. Chen H,Huang Z X. 1995. Estimation of seismic risk in China mainland using mixed extreme value theory and maximum likelihood method[J]. Acta Seismologica Sinica,17(2):264–269 (in Chinese).
陈凌,刘杰,陈颙,陈龙生. 1998. 地震活动性分析中余震的删除[J]. 地球物理学报,41(增刊):244–252. Chen L,Liu J,Chen Y,Chen L S. 1998. Aftershock deletion in seismicity analysis[J]. Acta Geophysica Sinica,41(S1):244–252 (in Chinese).
陈培善,林邦慧. 1973. 极值理论在中长期地震预报中的应用[J]. 地球物理学报,16(1):6–24. Chen P S,Lin B H. 1973. An application of statistical theory of extreme values to moderate and long interval earthquake prediction[J]. Acta Geophysica Sinica,16(1):6–24 (in Chinese).
高孟潭,贾素娟. 1988. 极值理论在工程地震中的应用[J]. 地震学报,10(3):317–326. Gao M T,Jia S J. 1988. The application of extremum analysis to earthquake engineering problems[J]. Acta Seismologica Sinica,10(3):317–326 (in Chinese).
黄玮琼,李文香,曹学锋. 1994. 中国大陆地震资料完整性研究之二:分区地震资料基本完整的起始年分布图象[J]. 地震学报,16(4):423–432. Huang W Q,Li W X,Cao X F. 1994. Seismic data integrity in mainland China II:The initial year distribution image of basically completion for subdistrict seismic data[J]. Acta Seismologica Sinica,16(4):423–432 (in Chinese).
鲁帆,王浩,严登华,张冬冬,肖伟华. 2013. 轮廓似然函数在水文气象极值推断不确定性分析中的应用[J]. 中国科学:技术科学,43(12):1299–1308. Lu F,Wang H,Yan D H,Zhang D D,Xiao W H. 2013. Application of profile likelihood function to the uncertainty analysis of hydrometeorological extreme inference[J]. Science China Technological Sciences,56(12):3151–3160. doi: 10.1007/s11431-013-5421-0
钱小仕,王福昌,曹桂荣,任晴晴. 2012. 广义极值分布在地震危险性分析中的应用[J]. 地震研究,35(1):73–78. doi: 10.3969/j.issn.1000-0666.2012.01.013 Qian X S,Wang F C,Cao G R,Ren Q Q. 2012. Application of the generalized extreme value distribution in seismic hazard analysis[J]. Journal of Seismological Research,35(1):73–78 (in Chinese).
钱小仕,王福昌,盛书中. 2013. 基于广义帕累托分布的地震震级分布尾部特征分析[J]. 地震学报,35(3):341–350. doi: 10.3969/j.issn.0253-3782.2013.03.006 Qian X S,Wang F C,Sheng S Z. 2013. Characterization of tail distribution of earthquake magnitudes via generalized Pareto distribution[J]. Acta Seismologica Sinica,35(3):341–350 (in Chinese).
史道济. 2006. 实用极值统计方法[M]. 天津: 天津科学技术出版社: 11–13. Shi D J. 2006. Practical Extremum Statistical Method[M]. Tianjin: Tianjin Science and Technology Press: 11–13 (in Chinese).
史宁中. 2008. 统计检验的理论与方法[M]. 北京: 科学技术出版社: 59–68. Shi N Z. 2008. The Theory and Method of Statistical Test[M]. Beijing: Science and Technology Press: 59–68 (in Chinese).
汪素云,高阿甲,冯义钧,和锐. 2010. 中国地震目录间的对比及标准化[J]. 地震,30(2):38–45. doi: 10.3969/j.issn.1000-3274.2010.02.005 Wang S Y,Gao A J,Feng Y J,He R. 2010. Comparison and standardization of the Chinese earthquake catalogs[J]. Earthquake,30(2):38–45 (in Chinese).
张国民,马宏生,王辉,王新岭. 2005. 中国大陆活动地块边界带与强震活动[J]. 地球物理学报,48(3):602–610. doi: 10.3321/j.issn:0001-5733.2005.03.018 Zhang G M,Ma H S,Wang H,Wang X L. 2005. Boundaries between active-tectonic blocks and strong earthquakes in the China mainland[J]. Chinese Journal of Geophysics,48(3):602–610 (in Chinese). doi: 10.1002/cjg2.693
Bhunya P K,Singh R D,Berndtsson R,Panda S N. 2012. Flood analysis using generalized logistic models in partial duration series[J]. J Hydrol,420-421:59–71. doi: 10.1016/j.jhydrol.2011.11.037
De Haan L. 1970. On regular Variation and its Application to the Weak Convergence of Sample Extremes[M]. Amsterdam: Mathe-matisch Centrum: 124.
De Haan L. 1971. A form of regular variation and its application to the domain of attraction of the double exponential distribution[J]. Z Wahrsch Geb,17(3):241–258. doi: 10.1007/BF00536760
Epstein B,Lomnitz C. 1966. A model for the occurrence of large earthquakes[J]. Nature,211(5052):954–956.
Fisher R A,Tippett L H C. 1928. Limiting forms of the frequency distribution of the largest or smallest member of a sample[J]. Math Proc Camb Phil Soc,24(2):180–190. doi: 10.1017/S0305004100015681
Fréchet M. 1927. Sur la loi de probabilité de l’écart maximum[J]. Ann Soc Polon Math Cracovie,6:93–116.
Gilli M,Këllezi E. 2006. An application of extreme value theory for measuring financial risk[J]. Comput Econ,27(2):207–228.
Gnedenko B. 1943. Sur la distribution limite du terme maximum d'une serie aleatoire[J]. Ann Math,44(3):423–453. doi: 10.2307/1968974
Jenkinson A F. 1955. The frequency distribution of the annual maximum (or minimum) values of meteorological elements[J]. Quart J Roy Meteor Soc,81(348):158–171. doi: 10.1002/qj.49708134804
Murphy S A,Van der Vaart A W. 2000. On profile likelihood[J]. J Am Stat Assoc,95(450):449–465. doi: 10.1080/01621459.2000.10474219
Nordquist J M. 1945. Theory of largest values applied to earthquake magnitudes[J]. Trans AGU,26(1):29–31. doi: 10.1029/TR026i001p00029
Rao C R. 1965. Linear Statistical Inference and its Applications[M]. New York: John Wiley and Sons: 155–209.
Tajvidi N. 2003. Confidence intervals and accuracy estimation for heavy-tailed generalized Pareto distributions[J]. Extremes,6(2):111–123. doi: 10.1023/B:EXTR.0000025662.09067.3b
von Bortkiewicz L. 1922. Variationsbreite und mittlerer Fehler[J]. Sitzungsber Berlin Math Ges,21:3–11.
von Mises R. 1923. Uber die Variationsbreite einer Beobachtungsreihe[J]. Sitzungsber Berlin Math Ges,22:3–8.
Yegulalp T M,Kuo J T. 1974. Statistical prediction of the occurrence of maximum magnitude earthquakes[J]. Bull Seismol Soc Am,64(2):393–414. doi: 10.1785/BSSA0640020393
-
期刊类型引用(3)
1. 贾永斌,刘萍,王斌,汪成国,邓明文. 2022年昌吉M_S4.8地震地下流体异常特征. 内陆地震. 2024(04): 376-386 .  百度学术
百度学术
2. 欧晓斌,鲍志诚,吕坚,肖健,赵影,陈浩. 全南—寻乌断裂带温泉水文地球化学特征. 地震研究. 2023(04): 529-541 .  百度学术
百度学术
3. Xiao Tian,Guoying Su. Correlation analysis between fault frequency and service time of underground fluid instruments. Geodesy and Geodynamics. 2023(04): 411-418 .  必应学术
必应学术
其他类型引用(0)





 下载:
下载: