高级搜索

面向地震烈度仪的现地地震动预测模型的构建与验证

彭朝勇, 郑钰, 徐志强, 姜旭东, 杨建思

彭朝勇，郑钰，徐志强，姜旭东，杨建思. 2021. 面向地震烈度仪的现地地震动预测模型的构建与验证. 地震学报，43（5）：643−655. DOI: 10.11939/jass.20210075
引用本文: 彭朝勇，郑钰，徐志强，姜旭东，杨建思. 2021. 面向地震烈度仪的现地地震动预测模型的构建与验证. 地震学报，43（5）：643−655. DOI: 10.11939/jass.20210075
shu
Peng C Y，Zheng Y，Xu Z Q，Jiang X D，Yang J S. 2021. Construction and verification of onsite ground motion prediction models for seismic intensity instrument. Acta Seismologica Sinica，43（5）：643−655. DOI: 10.11939/jass.20210075
Citation: Peng C Y，Zheng Y，Xu Z Q，Jiang X D，Yang J S. 2021. Construction and verification of onsite ground motion prediction models for seismic intensity instrument. Acta Seismologica Sinica，43（5）：643−655. DOI: 10.11939/jass.20210075
shu

面向地震烈度仪的现地地震动预测模型的构建与验证

  • 中国北京 100081 中国地震局地球物理研究所

基金项目: 国家重点研发计划（2018YFC1503904）、中国地震局地球物理研究所基本科研业务专项（DQJB20B17，DQJB20R14）和北京市自然科学基金（8202051）联合资助
详细信息
    通讯作者:

    彭朝勇: e-mail：pengchaoyong@cea-igp.ac.cn

  • 中图分类号: P315.9

Construction and verification of onsite ground motion prediction models for seismic intensity instrument

  • Institute of Geophysics，China Earthquake Administration，Beijing 100081，China

摘要

    摘要
  • 摘要: 利用初期P波预警参数构建现地地震动预测模型，使其在达到设定阈值时快速发出报警信息，是现地地震预警系统面临的一个关键问题，直接关系到发布信息的准确性和及时性。针对地震烈度仪基于微机电系统传感器记录到的数据质量较差，通过两次积分获取的位移存在较大偏差，会引起更多的误报和漏报，本文采用不同阶数（1—4阶）的巴特沃斯滤波器，分别构建了基于P波3 s和全P波段数据的位移幅值PD、速度幅值PV和加速度幅值PA与地震动峰值速度PGV和峰值加速度PGA的现地地震动预测模型，然后利用收集到的川滇示范预警网地震事件记录进行验证。结果表明，对于地震烈度仪微机电系统传感器的记录，采用1阶巴特沃斯滤波器处理、基于全P波段波形拟合获取到的PV与PGV的相关性和PA与PGA的相关性为两种最优现地地震动预测模型。具体应用时，应同时利用两种或两种以上的统计关系进行现地地震动预测，并将实际地震动观测值作为额外的判定条件，以降低误报率和漏报率。
    Abstract: Using the initial P-wave early warning parameters to construct onsite ground motion prediction models, so as to quickly release an alarm message when it reaches the predefined threshold, is a key issue of the onsite earthquake early warning system, which is directly related to the accuracy and timeliness of the early warning information. For micro-electro-mechanical-systems-based seismic intensity instrument with poor data quality, the obtained displacement record after two integrations has a large deviation, which will lead to more false and missed alarms. Therefore, for waveforms recorded by seismic intensity instrument, in this paper, we adopted Butterworth filters of different orders （1−4） to build up several onsite ground motion prediction models based on the P-wave 3 seconds data and the whole P-wave window. These models are the relationships between displacement amplitude PD and peak ground velocity PGV, PD and peak ground acceleration PGA, velocity amplitude PV and PGV, PV and PGA, acceleration amplitude PA and PGV, PA and PGA, respectively. The models are then verified using the collected micro-electro-mechanical-systems-based seismic event records from the Sichuan-Yunnan Demonstration Early Warning Network. The results show that for the seismic intensity instrument records, the two optimal onsite ground motion prediction models are the relationship between PV and PGV and the one between PA and PGA obtained by the first-order Butterworth filter processing and derived from the whole P-wave window. In specific applications, two or more statistical relationships should be simultaneously adopted to predict onsite ground motion, and observed ground motion values should be used as additional judgment conditions to reduce the probability of false and missed alarms.
    • HTML全文

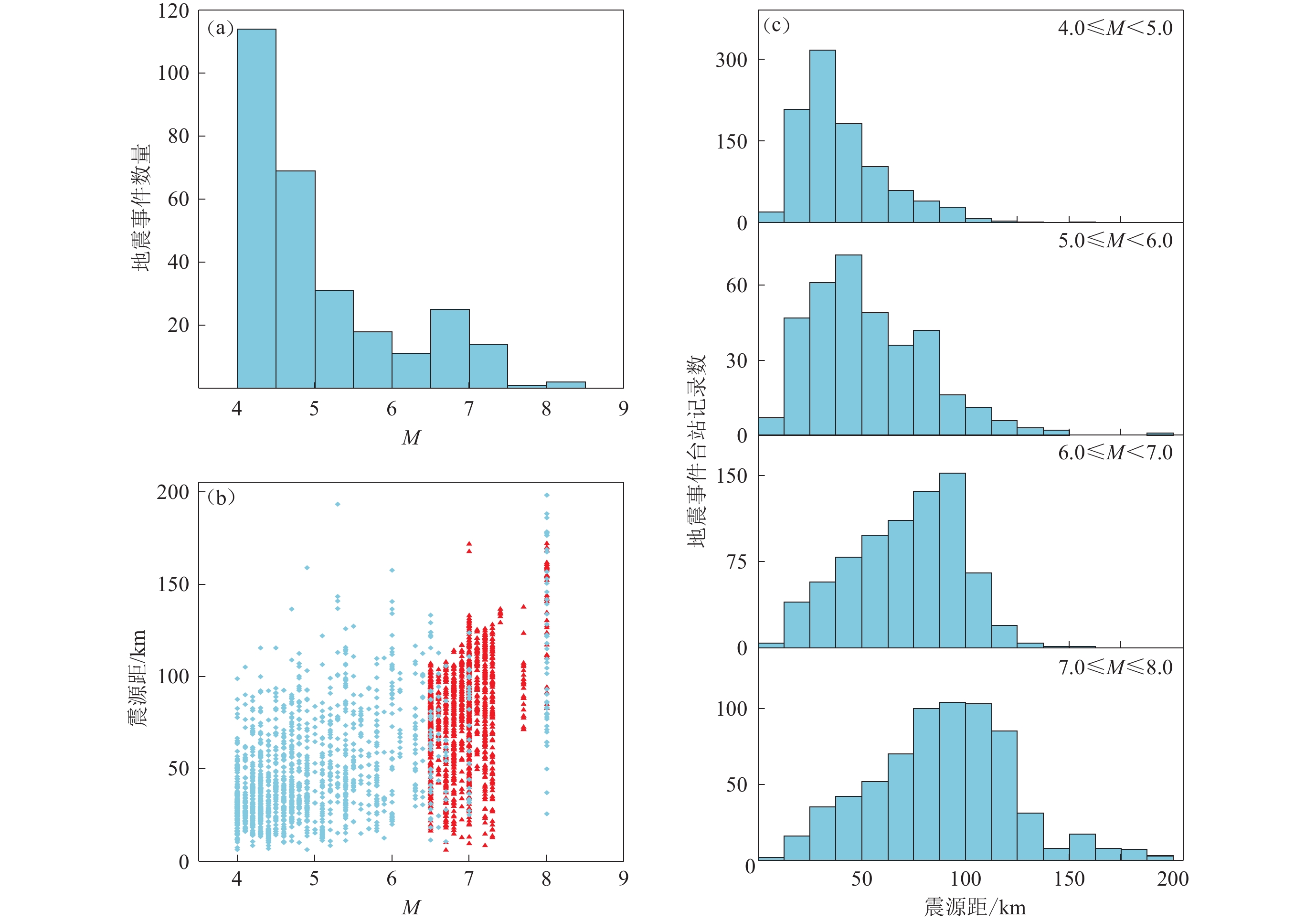
  • 图  1   本研究所用震例分布

    （a） 各震级地震分布；（b） 所用地震记录的震源距−震级分布，青色菱形为我国4.0≤MS≤8.0地震事件记录，红色三角形为日本6.5≤MJ≤8.0地震事件记录；（c） 不同震级范围台站记录数−震源距分布

    Figure  1.   Distribution of earthquakes used in this study

    （a） Distribution of the number of events with magnitude；（b） Distribution of hypocentral distance versus magnitude for the selected earthquake records，the cyan diamonds represent earthquake the records （4.0≤MS≤8.0） from China database，while the red triangles indicate the selected waveform data （6.5≤MJ≤8.0） from Japan database；（c） Histogram of the hypocentral distance of the records with different magnitude ranges

    下载: 全尺寸图片 幻灯片

    图  2   最优相关性前四名对应的拟合曲线

    （a） PVall与PGV；（b） PAall与PGA；（c） PAall与PGV；（d） PDall与PGV

    Figure  2.   Fitting curves for the top four best correlations

    （a） PVall and PGV；（b） PAall and PGA；（c） PDall and PGV；（d） PAall and PGV

    下载: 全尺寸图片 幻灯片

    表  1   位移幅值PD与地震动峰值参数PGV和PGA的相关性

    Table  1   Correlation between displacement amplitude PD and peak ground motion parameters PGV and PGA

    参数滤波器阶数系数A系数B标准差相关系数R
    PD3与PGV10.673 21.392 00.373 40.794 6
    20.677 61.448 10.367 80.801 5
    30.679 51.491 40.368 50.802 6
    40.678 21.545 40.363 50.806 7
    PDall与PGV10.610 61.063 50.362 50.807 9
    20.624 81.162 50.339 90.833 5
    30.614 61.212 10.328 30.845 7
    40.603 81.235 50.325 90.848 1
    PD3与PGA10.501 32.472 10.343 60.727 1
    20.503 22.511 80.341 30.731 5
    30.503 42.550 20.340 00.733 8
    40.501 72.580 80.340 30.733 4
    PDall与PGA10.424 42.194 60.362 30.690 0
    20.438 02.268 00.348 40.718 0
    30.431 82.304 10.342 00.730 2
    40.423 12.319 00.341 90.730 4
    下载: 导出CSV

    表  2   速度幅值PV与地震动峰值参数PGV和PGA相关性

    Table  2   Correlation between velocity amplitude PV and peak ground motion parameter PGV and PGA

    参数滤波器阶数系数A系数B标准差相关系数R
    PV3与PGV10.805 40.983 90.415 20.737 8
    20.788 60.977 60.421 60.725 0
    30.760 10.961 90.432 60.711 0
    40.766 80.973 60.430 60.714 1
    PVall与PGV10.947 70.885 60.277 90.892 1
    20.943 30.889 30.279 70.890 6
    30.924 80.886 60.292 90.879 4
    40.942 60.905 30.281 90.888 8
    PV3与PGA10.652 92.206 80.339 40.735 0
    20.638 22.201 00.345 10.724 2
    30.615 62.188 60.353 60.707 7
    40.621 02.198 00.352 10.710 7
    PVall与PGA10.714 92.099 80.281 40.827 0
    20.709 42.101 50.284 20.823 1
    30.694 42.098 90.292 40.811 6
    40.707 22.112 60.286 80.819 5
    下载: 导出CSV

    表  3   加速度幅值PA与地震动峰值参数PGV和PGA相关性

    Table  3   Correlation between acceleration amplitude PA and peak ground motion parameter PGV and PGA

    相关性滤波器阶数系数A系数B标准差相关系数R
    PA3与PGV10.642 1−0.109 80.512 80.552 3
    20.664 0−0.096 20.503 90.573 6
    30.657 5−0.074 00.503 00.575 7
    40.676 0−0.074 80.497 00.589 1
    PAall与PGV10.995 3−0.582 20.359 50.811 5
    21.008 2−0.548 70.334 30.828 6
    30.988 3−0.504 90.348 30.824 3
    41.007 4−0.504 60.335 70.837 9
    PA3与PGA10.620 91.240 50.377 60.656 3
    20.624 81.266 50.374 50.663 4
    30.609 31.294 30.377 90.655 7
    40.619 71.298 30.374 40.663 7
    PAall与PGA10.848 60.896 00.263 40.850 3
    20.842 70.940 60.262 70.851 2
    30.816 90.985 50.273 60.837 4
    40.826 40.991 50.267 90.844 7
    下载: 导出CSV

    表  4   各参数的最优相关性

    Table  4   Optimal correlations between parameters

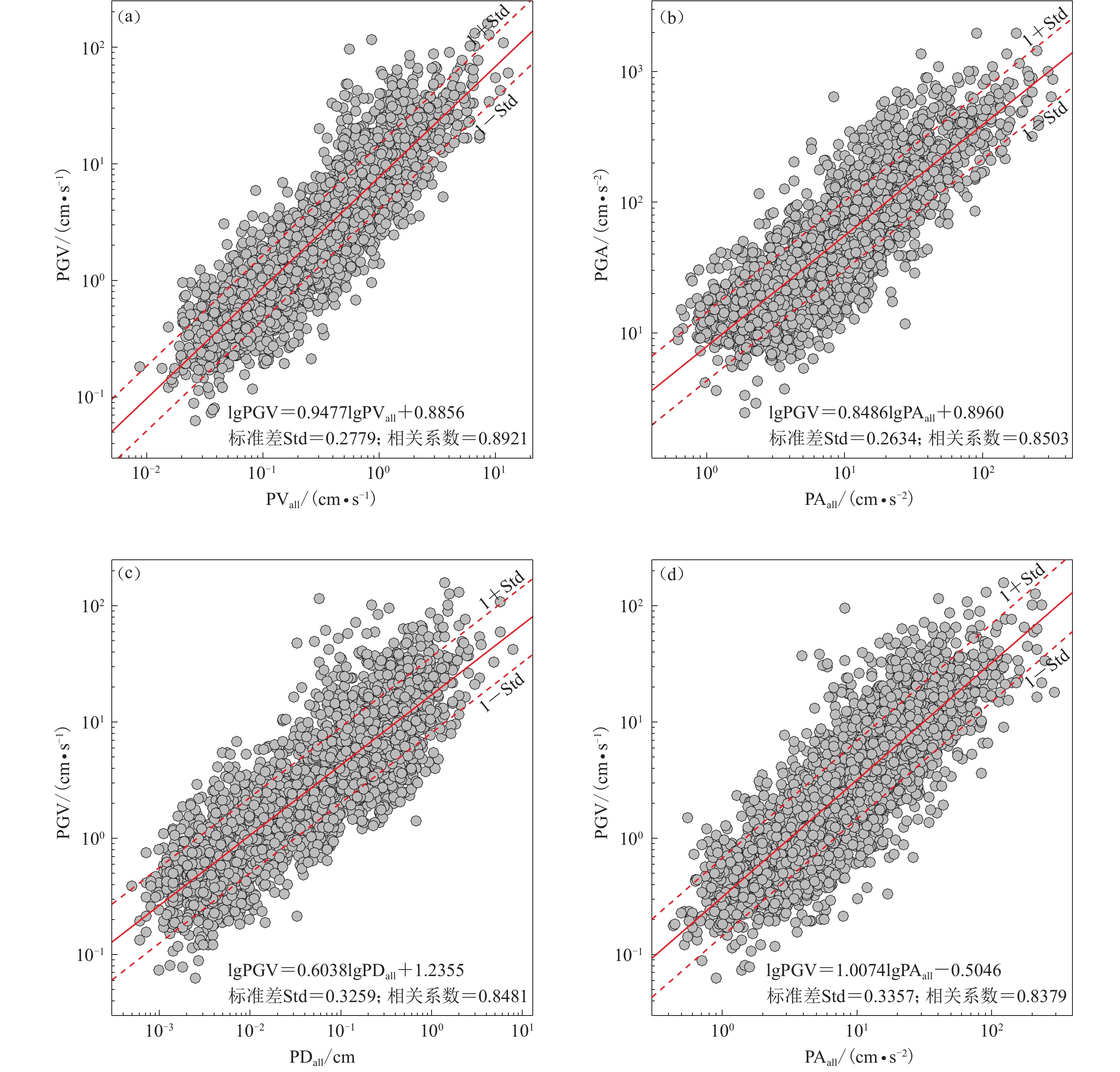
    参数滤波器阶数系数A系数B标准差相关系数R
    PVall与PGV10.947 70.885 60.277 90.892 1
    PAall与PGA10.848 60.896 00.263 40.850 3
    PDall与PGV40.603 81.235 50.325 90.848 1
    PAall与PGV41.007 4−0.504 60.335 70.837 9
    PVall与PGA10.714 92.099 80.281 40.827 0
    PD3与PGA30.503 42.550 20.340 00.733 8
    下载: 导出CSV

    表  5   本研究选取的MEMS传感器记录的地震事件测试用例

    Table  5   MEMS seismic event test cases selected in this study

    发震时刻
    　年-月-日　时:分:秒    		东经/º北纬/º震源深度/kmMGL-P2B记录数
    2017-01-04　23:14:2929.536102.154234.48
    2017-01-18　22:35:1428.134104.710104.71
    2017-03-12　20:21:1827.072103.421125.141
    2017-03-30　07:48:1827.120103.35674.17
    2017-04-04　04:57:4027.093103.41183.86
    2017-05-04　13:40:2128.234104.922215.12
    2017-07-02　03:40:5827.081103.24473.715
    2017-10-18　02:54:2128.326102.815153.833
    2018-02-27　03:00:5329.403102.131183.812
    2018-05-02　04:28:4528.502102.704143.830
    2018-05-08　23:11:3328.140103.478104.537
    2018-05-16　16:44:0329.201102.265113.933
    2018-05-16　16:46:1129.190102.262124.654
    2018-05-16　16:46:4029.180102.27094.951
    2018-05-18　02:40:2927.413103.95843.63
    2018-08-11　14:11:3128.623103.31794.132
    2018-08-18　01:36:3827.400103.984104.25
    2018-10-28　08:25:1628.074103.53863.611
    2018-10-30　05:00:0528.105103.529114.321
    2018-10-31　16:29:5627.700102.080195.128
    2018-11-19　22:29:5129.484104.499113.316
    2018-11-20　06:01:1127.697102.092183.925
    2018-12-23　22:22:4028.116103.588103.715
    2019-05-16　04:33:3128.070103.530104.765
    下载: 导出CSV

    表  6   1阶巴特沃斯滤波器带通滤波后数据的测试结果

    Table  6   Test results with data filtered by the first-order Butterworth bandpass filter

    类别GL-P2B记录数占总记录数的百分比
    成功不预警 478 86.75%
    成功预警 40 7.26%
    漏报 14 2.54%
    误报 19 3.45%
    下载: 导出CSV

    表  7   成功预警测试震例（1阶巴特沃斯带通滤波处理）理论预警发布时间

    Table  7   Theoretical warning release time list for successful early warning test earthquake cases with data filtered by the first-order Butterworth bandpass filter

    理论预警发布时间/sGL-P2B记录数占总记录数的百分比
    0.52870.0%
    1.0512.5%
    1.5512.5%
    2.512.5%
    4.012.5%
    下载: 导出CSV

    表  8   成功预警测试震例（1阶巴特沃斯带通滤波处理）理论预警时间

    Table  8   Theoretical lead-time list for successful early warning test earthquake cases with data filtered by the first-order Butterworth bandpass filter

    理论预警时间/sGL-P2B记录数占总记录数的百分比
    ＜0.037.5%
    （0.0，1.0]1127.5%
    （1.0，2.0]922.5%
    （2.0，5.0]1332.5%
    ＞5.0410.0%
    下载: 导出CSV

    表  9   经1—4阶巴特沃斯滤波器带通滤波后数据测试结果

    Table  9   Test results of the data filtered by 1st-to-4th-order Butterworth bandpass filter

    滤波器阶数成功不预警占比成功预警占比漏报占比误报占比成功处理占比成功处理（含漏报）占比
    186.75%7.26%2.54%3.45%94.01%96.55%
    286.75%7.08%2.72%3.45%93.83%96.55%
    386.75%6.72%3.09%3.45%93.47%96.56%
    486.57%6.53%3.27%3.63%93.10%96.37%
    下载: 导出CSV
    • 参考文献(37)
  • 国家市场监督管理总局, 国家标准化管理委员会. 2020. GB/T1774—2020中国地震烈度表[S/OL].[2021-01-05].http://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=6FD8F9071FAC980D5B2A636A9EA79DE9.

    State Administration for Market Regulation, Standardization Administration. 2020. GB/T 1774−2020: The Chinese Seismic Intensity Scale[S/OL].[2021-01-05].http://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=6FD8F9071FAC980D5B2A636A9EA79DE9 (in Chinese).
    马强. 2008. 地震预警技术研究及应用[D]. 哈尔滨: 中国地震局工程力学研究所: 1–9.

    Ma Q. 2008. Study and Application on Earthquake Early Warning[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 1–9 （in Chinese）.
    彭朝勇,杨建思. 2019. 利用P波参数阈值实时估算地震预警潜在破坏区范围[J]. 地震学报,41(3):354–365.

    Peng C Y,Yang J S. 2019. Real-time estimation of potentially damaged zone for earthquake early warning based on thresholds of P-wave parameters[J]. Acta Seismologica Sinica,41(3):354–365 (in Chinese).
    彭朝勇,杨建思,薛兵,陈阳,朱小毅. 2013. 基于汶川主震及余震的预警参数与震级相关性研究[J]. 地球物理学报,56(10):3404–3415. doi: 10.6038/cjg20131016

    Peng C Y,Yang J S,Xue B,Chen Y,Zhu X Y. 2013. Research on correlation between early-warning parameters and magnitude for the Wenchuan earthquake and its aftershocks[J]. Chinese Journal of Geophysics,56(10):3404–3415 (in Chinese).
    宋晋东,教聪聪,李山有,侯宝瑞. 2018a. 基于地震P波双参数阈值的高速铁路Ⅰ级地震警报预测方法[J]. 中国铁道科学,39(1):138–144.

    Song J D,Jiao C C,Li S Y,Hou B R. 2018a. Prediction method of first-level earthquake warning for high speed railway based on two-parameter threshold of seismic P-wave[J]. China Railway Science,39(1):138–144 (in Chinese).
    宋晋东,教聪聪,李山有,侯宝瑞,汪源. 2018b. 一种基于地震早期辐射P波能量的高速铁路Ⅰ级地震警报预测方法[J]. 振动与冲击,37(19):14–22.

    Song J D,Jiao C C,Li S Y,Hou B R,Wang Y. 2018b. A predicting method for magnitude 1 earthquake alarm of high-speed railways based on seismic early radiated P-wave energy[J]. Journal of Vibration and Shock,37(19):14–22 (in Chinese).
    张红才,金星,王士成,李军. 2017. 烈度仪记录与强震及测震记录的对比分析:以2015年河北昌黎ML4.5地震为例[J]. 地震学报,39(2):273–285. doi: 10.11939/jass.2017.02.010

    Zhang H C,Jin X,Wang S C,Li J. 2017. Comparative analyses of records by seismic intensity instrument with strong ground motion records and seismograph stations records:Taking the ML4.5 Changli earthquake of Hebei Province for an example[J]. Acta Seismologica Sinica,39(2):273–285 (in Chinese).

    Allen R M,Melgar D. 2019. Earthquake early warning:Advances,scientific challenges,and societal needs[J]. Annu Rev Earth Planet Sci,47:361–388. doi: 10.1146/annurev-earth-053018-060457

    Bormann P,Liu R F,Ren X,Gutdeutsch R,Kaiser D,Castellaro S. 2007. Chinese National Network Magnitudes,their relation to NEIC magnitudes,and recommendations for new IASPEI magnitude standards[J]. Bull Seismol Soc Am,97(1B):114–127. doi: 10.1785/0120060078

    Colombelli S,Amoroso O,Zollo A,Kanamori H. 2012a. Test of a threshold-based earthquake early-warning method using Japanese data[J]. Bull Seismol Soc Am,102(3):1266–1275. doi: 10.1785/0120110149

    Colombelli S,Zollo A,Festa G,Kanamori H. 2012b. Early magnitude and potential damage zone estimates for the great MW9 Tohoku-Oki earthquake[J]. Geophys Res Lett,39(22):L22306.

    Cuéllar A, Espinosa-Aranda J M, Suárez R, Ibarrola G, Uribe A, Rodríguez F H, Islas R, Rodríguez G M, García A, Frontana B. 2014. The Mexican seismic alert system （SASMEX）: Its alert signals, broadcast results and performance during the M7.4 Punta Maldonado earthquake of March 20th, 2012[G]// Early Warning for Geological Disasters. Berlin, Germany: Springer: 71-87.

    Evans J R,Allen R M,Chung A I,Cochran E S,Guy R,Hellweg M,Lawrence J F. 2014. Performance of several low-cost accelerometers[J]. Seismol Res Lett,85(1):147–158. doi: 10.1785/0220130091

    Fujinawa Y,Noda Y. 2013. Japan’s earthquake early warning system on 11 March 2011:Performance,shortcomings,and changes[J]. Earthq Spectra,29(1S):341–368.

    Hsu T Y,Wang H H,Lin P Y,Lin C M,Kuo C H,Wen K L. 2016. Performance of the NCREE’s on-site warning system during the 5 February 2016 MW6.53 Meinong earthquake[J]. Geophys Res Lett,43(17):8954–8959. doi: 10.1002/2016GL069372

    National Research Institute of Earth Science and Disaster Resilience. 2019. Strong-motion seismograph networks: NIED K-NET, KiK-net[DB/OL]. [2020−02−20]. http://www.kyoshin.bosai.go.jp/. doi: 10.17598/NIED.0004.

    Peng C Y,Yang J S,Xue B,Zhu X Y,Chen Y. 2014. Exploring the feasibility of earthquake early warning using records of the 2008 Wenchuan earthquake and its aftershocks[J]. Soil Dyn Earthq Eng,57:86–93. doi: 10.1016/j.soildyn.2013.11.005

    Peng C Y,Yang J S,Zheng Y,Zhu X Y,Xu Z Q,Chen Y. 2017a. New τc regression relationship derived from all P wave time windows for rapid magnitude estimation[J]. Geophys Res Lett,44(4):1724–1731.

    Peng C Y,Chen Y,Chen Q S,Yang J S,Wang H T,Zhu X Y,Xu Z Q,Zheng Y. 2017b. A new type of tri-axial accelerometers with high dynamic range MEMS for earthquake early warning[J]. Comput Geosci,100:179–187. doi: 10.1016/j.cageo.2017.01.001

    Peng C Y,Jiang P,Chen Q S,Ma Q,Yang J S. 2019. Performance evaluation of a dense MEMS-based seismic sensor array deployed in the Sichuan-Yunnan border region for earthquake early warning[J]. Micromachines,10(11):735. doi: 10.3390/mi10110735

    Peng C Y,Ma Q,Jiang P,Huang W H,Yang D K,Peng H S,Chen L,Yang J S. 2020. Performance of a hybrid demonstration earthquake early warning system in the Sichuan-Yunnan border region[J]. Seismol Res Lett,91:835–846. doi: 10.1785/0220190101

    Peng C Y,Jiang P,Ma Q,Wu P,Su J R,Zheng Y,Yang J S. 2021. Performance evaluation of an earthquake early warning system in the 2019−2020 M6.0 Changning,Sichuan,China,seismic sequence[J]. Front Earth Sci,9:699941. doi: 10.3389/feart.2021.699941

    Shieh J T,Wu Y M,Allen R M. 2008. A comparison of τc and $ \tau _{\rm{P}}^{\max } $ for magnitude estimation in earthquake early warning[J]. Geophys Res Lett,35(20):L20301. doi: 10.1029/2008GL035611

    Tsuboi C. 1954. Determination of the Gutenberg-Richter’s magnitude of earthquakes occurring in and near Japan[J]. J Seismol Soc Jpn,7(3):185–193.

    Wang W T,Ni S D,Chen Y,Kanamori H. 2009. Magnitude estimation for early warning applications using the initial part of P waves:A case study on the 2008 Wenchuan sequence[J]. Geophys Res Lett,36(16):L16305. doi: 10.1029/2009GL038678

    Wang Y,Colombelli S,Zollo A,Song J D,Li S Y. 2021. Source parameters of moderate-to-large Chinese earthquakes from the time evolution of P-wave peak displacement on strong motion recordings[J]. Front Earth Sci,9:616229. doi: 10.3389/feart.2021.616229

    Wu Y M,Kanamori H. 2005. Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of P waves[J]. Bull Seismol Soc Am,95(3):1181–1185. doi: 10.1785/0120040193

    Wu Y M,Kanamori H. 2008. Development of an earthquake early warning system using real-time strong motion signals[J]. Sensors,8(1):1–9. doi: 10.3390/s8010001

    Zhu J B,Li S Y,Song J D,Wang Y. 2021. Magnitude estimation for earthquake early warning using a deep convolutional neural network[J]. Front Earth Sci,9:653226. doi: 10.3389/feart.2021.653226

    Zollo A,Amoroso O,Lancieri M,Wu Y M,Kanamori H. 2010. A threshold-based earthquake early warning using dense accelerometer networks[J]. Geophys J Int,183(2):963–974. doi: 10.1111/j.1365-246X.2010.04765.x
    • 相关文章
    • 施引文献
    • 资源附件(0)
图(2)  /  表(9)
计量
  • 文章访问数:  607
  • HTML全文浏览量:  334
  • PDF下载量:  199
  • 被引次数: 0
出版历程
  • 收稿日期:  2021-05-18
  • 修回日期:  2021-07-14
  • 网络出版日期:  2021-09-08
  • 发布日期:  2021-09-29

目录

摘要
HTML全文
    参考文献(37)
    相关文章
    施引文献
    资源附件(0)

    /

    返回文章
    返回

    本系统由 北京仁和汇智信息技术有限公司 开发  技术支持：info@rhhz.net 百度统计