Construction and verification of onsite ground motion prediction models for seismic intensity instrument
-
摘要: 利用初期P波预警参数构建现地地震动预测模型，使其在达到设定阈值时快速发出报警信息，是现地地震预警系统面临的一个关键问题，直接关系到发布信息的准确性和及时性。针对地震烈度仪基于微机电系统传感器记录到的数据质量较差，通过两次积分获取的位移存在较大偏差，会引起更多的误报和漏报，本文采用不同阶数（1—4阶）的巴特沃斯滤波器，分别构建了基于P波3 s和全P波段数据的位移幅值PD、速度幅值PV和加速度幅值PA与地震动峰值速度PGV和峰值加速度PGA的现地地震动预测模型，然后利用收集到的川滇示范预警网地震事件记录进行验证。结果表明，对于地震烈度仪微机电系统传感器的记录，采用1阶巴特沃斯滤波器处理、基于全P波段波形拟合获取到的PV与PGV的相关性和PA与PGA的相关性为两种最优现地地震动预测模型。具体应用时，应同时利用两种或两种以上的统计关系进行现地地震动预测，并将实际地震动观测值作为额外的判定条件，以降低误报率和漏报率。Abstract: Using the initial P-wave early warning parameters to construct onsite ground motion prediction models, so as to quickly release an alarm message when it reaches the predefined threshold, is a key issue of the onsite earthquake early warning system, which is directly related to the accuracy and timeliness of the early warning information. For micro-electro-mechanical-systems-based seismic intensity instrument with poor data quality, the obtained displacement record after two integrations has a large deviation, which will lead to more false and missed alarms. Therefore, for waveforms recorded by seismic intensity instrument, in this paper, we adopted Butterworth filters of different orders （1−4） to build up several onsite ground motion prediction models based on the P-wave 3 seconds data and the whole P-wave window. These models are the relationships between displacement amplitude PD and peak ground velocity PGV, PD and peak ground acceleration PGA, velocity amplitude PV and PGV, PV and PGA, acceleration amplitude PA and PGV, PA and PGA, respectively. The models are then verified using the collected micro-electro-mechanical-systems-based seismic event records from the Sichuan-Yunnan Demonstration Early Warning Network. The results show that for the seismic intensity instrument records, the two optimal onsite ground motion prediction models are the relationship between PV and PGV and the one between PA and PGA obtained by the first-order Butterworth filter processing and derived from the whole P-wave window. In specific applications, two or more statistical relationships should be simultaneously adopted to predict onsite ground motion, and observed ground motion values should be used as additional judgment conditions to reduce the probability of false and missed alarms.
-
引言
滇西北地区（25.5°N—28°N，98.5°E—101°E）位于青藏高原的东南隅，属于喜马拉雅—缅甸弧向东北楔入的前缘地带，地质构造和动力学环境十分复杂。第四纪以来，区内构造活动以断裂活动为主，发育有NW，NE和近NS向的三组主要活动断裂（谢富仁等，1994），曾发生1996年丽江MS7.0地震、1998年宁蒗MS6.2地震，近年来陆续发生了多次中强地震，如2013年洱源MS5.5和MS5.0双震、2016年云龙MS5.0地震、2017年漾濞MS4.7和MS5.1双震。
构造应力场是地球动力学研究中的重要课题，对于认识地震孕育的力学背景、发展机理及规律均具有重要意义。构造应力场细结构及其连续动态变化图像是目前应力场研究的发展趋势（Audemard et al，2005；Bohnhoff et al，2006；Hardebeck，Michael，2006），而通过震源机制解和P波极性等数据均可以求解构造应力场。由于震源机制解携带有地球深部信息，同时能够反映断层的力学性质，使用充足的地震震源机制解资料可以更好地表征区域应力场情况。针对此，不同研究人员给出了不同的应力张量反演算法（Ellsworth，1981；许忠淮，戈澍谟，1984；Gephart，Forsyth，1984；Michael，1984，1987；Hardebeck，Michael，2006；Wan et al，2016），其中：Ellsworth （1981）和许忠淮（1985）提出了将震源机制解的两个节面都作为地震断层面进行尝试的计算方法；Gephart和Forsyth （1984）提出了以网格搜索方式对应力张量进行全空间搜索的计算方法；Wan等（2016）在前人基础上，对网格搜索法作了进一步改进，在给出最优解的同时，采用F检验给出了求解结果的置信区间；Michael （1984，1987，1991）根据断层面上剪应力方向与滑动方向相一致的原则，提出了将非线性问题转化为线性叠加反演应力张量的算法，大大提高了反演的效率。
获取研究区域的现代构造应力场基本状态是分析应力场动态调整变化的前提（付虹等，2004）。自二十世纪八十年代以来，随着我国地震观测能力的不断提高和构造应力研究的逐步深入，研究人员利用云南地区丰富的地震观测资料，对滇西北地区的构造应力场进行了深入研究，其结果显示滇西北及邻区的现代构造应力场以水平作用为主，最大主压应力方向为NNW向和近NS向（阚荣举等，1983；向宏发等，1986；谢富仁等，1994；郭祥云等，2014；罗钧等，2014）。谢富仁等（1994）利用由断层滑动方向反演构造应力张量的计算方法，获得了滇西北地区及邻区的现代构造应力场特征；崔效锋等（2006）利用逐次收敛法并结合原地应力测量结果和断层滑动反演资料分析认为，川滇地区的构造应力场格局并非完全受已有构造的控制，而是很有可能形成了新的应力转换带；孙业君等（2017）的研究显示，云南地区的应力场空间上呈现非均匀性，滇西和滇西北地区的最大水平主应力方向发生较大偏转，表明其区域构造应力场的复杂性。
在以往研究中，针对滇西北地区小尺度构造应力状态的研究较少，且年代久远，近些年的研究多以云南乃至川滇地区这样的大区域构造应力场为主。同时，关于该地区应力场的时空变化及其与地震活动相关性方面的探讨研究尚且不足。为此，我们拟收集滇西北地区MS≥3.0中小地震的震源机制解数据，划分震源机制解类型，分析其P轴和T轴的分布特征，再利用Michael （1987，1991）的线性叠加反演法进行最优应力张量反演和区域分网格反演计算，详细分析滇西北地区的构造应力状态，以及应力张量方差时空分布与中强地震活动的关系，深入研究滇西北地区现今构造应力状态的时空演变特征，以期为探索构造应力场与地震孕育的关系、解释研究区的地球动力学过程提供参考依据。
1. 震源机制解数据
1.1 震源机制解类型
本研究收集了滇西北地区（25.5°N—28°N，98.5°E—101°E）2000年1月1日至2018年12月31日期间发生的MS≥3.0地震的震源机制解，共计205个，其分布如图1所示。数据主要来自中国地震科学实验场大理中心利用小孔径台网计算得到的震源机制以及徐彦和李丹宁（2016）的研究成果。Zoback等（1992）将震源机制解分为六类，即正断型、正走滑型、走滑型、逆走滑型、逆断型和不确定型．参照划分标准对搜集到的震源机制解进行类型划分，结果显示：走滑型震源机制解最多，共有94个，占46%；正断型（包括正断型和正走滑型）震源机制解次之，共有55个，占27%；逆断型（包括逆断型和逆走滑型）震源机制解共有33个，占16%；不确定型震源机制解有23个，占11%。这与前人的研究结果（钱晓东等，2011；罗钧等，2014）基本一致。
![]()
图 1 本研究所用滇西北地震震源机制解的空间分布图震源机制解按照Zoback等（1992）分类，震源机制解沙滩球大小随震级增大而增大Figure 1. The spatial distribution of focal mechanism solutions of the earthquakes in northwestern Yunnan used in this studyThe mechanism solutions are classified according to Zoback et al （1992），the size of the beach balls increases with the magnitude of the earthquakes1.2 震源机制解分布特征
滇西北地区位于川滇菱形地块西边界，区内活动断裂以NW向右旋走滑断裂为主，主要有维西—乔后断裂和洱源—弥渡断裂；NE向断裂在区内普遍发育，但其规模较小，主要为一些密集排列或平行、叠错，并与近NS向张性断裂（如程海—宾川断裂）相伴的左旋走滑活动断裂（谢富仁等，1994）。另外在研究区西侧还发育怒江断裂和澜沧江断裂这两条深大断裂。
从图1可以看出，滇西北地区的地震主要沿研究区内的大小断裂展布，在研究区北部分布较少，并以正断型和逆断型地震为主，其中：走滑型地震主要分布在NW向的维西—乔后断裂及NNE向的程海—宾川断裂和鹤庆—洱源断裂上，以NW向展布最为密集，这与研究区内以走滑型断层为主的特点相符合；正断型地震除在维西—乔后断裂中南段和程海—宾川断裂上集中分布外，其它地区分布均较为分散；逆断型地震大多分布在维西—乔后断裂南段和鹤庆—洱源断裂以及研究区北部，大致呈NNE向展布；不确定型地震在研究区北部和南部零散分布，且大多未发生在区内主要断裂上。另外，在怒江断裂和澜沧江断裂上鲜有地震分布。
1.3 P轴和T轴的分布特征
对震源机制解的P轴、T轴方位角和倾伏角进行统计分析，结果见图2和图3。统计结果显示：震源机制解的P轴优势方位为NNW−近NS向，T轴优势方位以ENE向为主；P轴和T轴方位在空间上存在较为明显的区域特征。在研究区南部如维西—乔后断裂中南段、鹤庆—洱源断裂南段以及程海断裂中南段，P轴和T轴的方位一致性较好，P轴基本上呈NW向的低倾伏角分布，T轴呈ENE向低倾伏分布，少数为陡倾伏分布，P轴和T轴的倾伏角大都在30°以内。而研究区北部地区，地震分布较为离散，并未沿主要断裂分布，仅在永宁断裂附近较为集中，该地区震源机制解的P轴和T轴的方位展布也十分复杂且紊乱，一致性较差，倾伏角也有较大差异，表明研究区北部的应力场存在明显的非均匀性。
![]()
图 2 P轴（a）和T轴（b）的方位分布及方位角统计玫瑰图图中N为地震频次；线段的长短代表倾伏角大小，线段越长，倾伏角越小Figure 2. The distribution of azimuth and azimuth roses of P axes and T axesN is the number of earthquakes. The length of the line represents the size of the plunge. The longer the lines，the lower the plunges![]()
图 3 P轴（a）和T轴（b）的倾伏角统计玫瑰图（图中N为地震频次）Figure 3. The plunge roses of P axes （a） and T axes （b） where N is the number of earthquakes2. 应力张量反演
2.1 应力张量反演方法
Michael （1984，1987，1991）根据断层面上剪应力方向与滑动方向相一致的原则，提出了将非线性问题转化为线性反演应力张量的算法。Wiemer和Malone （2001）将Michael算法进行集成后研发了ZMAP软件包，ZMAP为Michael算法的应力张量反演提供了两种计算方式，即最优应力张量反演和区域分网格反演。前者可以提供三个主应力的方位及其置信区间，反映三个主应力相对大小的应力形因子φ。三个主应力方向的置信区间越大，表明参与计算的震源机制解对反演结果的约束越差，反演结果的可靠性越低。后者在反演前先将研究区域进行网格划分，利用每个网格节点周边的震源机制解数据进行反演，给出最大水平主应力方位的分布图和应力张量方差的空间分布，网格节点上的应力张量方差较大，表明该网格节点周围的震源机制解比较紊乱，一致性程度较低，对反演结果的约束较差。应力张量方差为每个节面的滑动矢量与最优应力张量预测的理论滑动角之间的夹角与其均值之差的平方和的平均数，其单位为度的平方，用来表征震源区应力场与区域构造应力场的一致性程度（Michael，1987，1991；张致伟等，2015）。
Lu等（1997）使用应力张量方差来表征反演所得的构造应力场的均匀程度，其结果表明：当应力张量方差大于0.2时，区域构造应力场是非均匀的，表明该区域的震源机制解类型比较紊乱；当方差小于0.1时，该区域的应力场是均匀的，表明震源机制解的一致性较好，可以用一个统一的应力张量来解释所观测到的震源机制解。
2.2 最优应力张量反演
本文利用Michael （1984，1987，1991）的线性叠加反演算法对搜集到的205次地震的震源机制解进行反演，结果列于表1，包括三个主应力方向和应力形因子ϕ＝（S2－S3）/（S1－S3），其中S1，S2和S3分别代表最大、中间、最小主应力。图4给出了三个主应力轴及其95%的置信区间。
表 1 线性叠加反演得到的滇西北地区最优应力张量Table 1. The best-fitting stress tensor of northwestern Yunnan by using linear superposition stress inversion最大主应力S1 中间主应力S2 最小主应力S3 应力形因子ϕ 应力类型 方位/º 倾伏角/º 方位/º 倾伏角/º 方位/º 倾伏角/º 167.8 7.9 5.8 81.6 258.3 2.5 0.8 走滑型 ![]()
图 4 主应力轴及其95%置信区间（彩色区域）的下半球等面积投影Figure 4. Lower-hemisphere equal-area projection of principle stress axes and their 95% confidence regions （colorful part）从表1和图4可以看出：最大主应力S1的方位为167.8°，倾伏角为7.9°，最小主应力S3为ENE向，倾伏角为2.5°，应力类型为走滑型，应力形因子为0.8，其中三个主应力轴的置信区间范围均较小，且基本上是成簇分布，说明反演结果对三个主应力的约束较好。从最优应力张量反演结果来看，压应力和张应力的倾伏角很小，均接近水平，说明该区域主要受走滑断层控制，多为走滑型震源机制解（约占总量的46%），滇西北地区受到NNW向的水平挤压和ENE向的拉张作用，与前人研究结果（谢富仁等，1994；罗钧等，2014）一致。
2.3 区域分网格应力张量反演
为了进一步验证反演结果的可靠性，我们将研究区划分成0.05°×0.05°的网格，采用区域分网格反演方法进行反演，选取网格节点附近至少5个震源机制解数据参与计算，得到了最大主应力方位分布，如图5所示，可以看出，总体上整个滇西北地区尤其是研究区南部的最大主应力方向的一致性较好，以NNW至近NS向为优势方位，与最优应力张量反演给出的计算结果（图4）基本一致。研究区内尤其是北部地区的震源机制解类型复杂多样，以走滑型为主，兼有其它类型或应力结构，但最大主应力方位基本以NNW向和近NS向为主，与前人结果（Zhao et al，2013；李君等，2019）一致。反演结果显示，研究区北部区域的最大主应力方位较为紊乱，一致性相对较差，甚至转向，这种现象可能是由于本文网格点分区较细，这些区域地震的震源机制解分布不均匀且类型多样，以及区域动力学机制和地质结构较为复杂所致（田优平等，2020），同时也反映了研究区局部应力场的非均匀性和相对复杂性。
![]()
图 5 区域分网格反演得到的研究区最大主应力方位分布图Figure 5. Distribution of maximum principal stress orientation in the studied area by regional grid inversion3. 应力张量方差与地震的关系
3.1 应力张量方差空间分布和地震的关系
在获得滇西北地区最大主应力方位的基础上，计算了研究区各节点的震源机制一致性参数，并采用应力张量方差来表征应力场的非均匀程度，结果如图6所示。为了分析研究区应力场非均匀性与中强地震的关系，将2000—2018年期间该地区发生的MS≥5.0地震投影到应力张量方差的空间分布图（图6）上，地震信息列于表2。结果显示：在研究区南部地区，应力张量方差整体上相对较低，基本小于0.1，说明南部地区的应力场是均匀的；而北部地区的应力张量方差相对较高，普遍大于0.2，说明其应力场在空间上具有非均匀性。从图6还可以看出，2000—2018年期间MS≥5.0地震的发震地点基本上都处于应力张量方差相对较低（＜0.2）的区域。李金等（2015）基于2003—2014年期间天山地震带震源机制解数据的研究结果同样显示，2003年以来天山中东段地区的MS≥5.5中强地震大多发生在应力张量方差低值分布区或其边缘附近，本文研究结果与其一致。
![]()
图 6 区域分网格反演得到的研究区应力张量方差分布图Figure 6. Distribution of stress tensor variance in the studied area obtained by regional grid inversion表 2 2000—2018年研究区MS≥5.0地震的基本信息Table 2. The general information of MS≥5.0 earthquakes from 2000 to 2018 in the studied area序号 发震时间
年-月-日东经/° 北纬/° MS 地点 1 2001-05-24 100.90 27.63 5.8 宁蒗 2 2001-10-27 100.57 26.23 6.0 永胜 3 2009-07-10 101.05 25.55 5.2 姚安 4 2009-11-02 100.70 25.95 5.0 宾川 5 2012-06-24 100.70 27.70 5.7 宁蒗 6 2013-03-03 99.78 25.93 5.5 洱源 7 2013-04-17 99.80 25.90 5.0 洱源 8 2016-05-18 99.53 26.09 5.0 云龙 9 2017-03-27 99.80 25.89 5.1 漾濞 3.2 应力张量方差变化与地震的关系
为了进一步分析滇西北地区中强地震与应力张量方差随时间演化的关系，我们选取10个地震事件为窗长，5个地震事件为步长进行滑动计算，得到了应力张量方差随时间的变化情况，如图7所示，可见，研究区的应力张量方差在2000—2018年期间大致经历了三次下降过程，下降期间发生了多次MS≥5.0地震。第一次为2001年，此时段内应力张量方差快速下降，期间发生宁蒗MS5.8地震和永胜MS6.0地震；第二次为2006年初至2014年上半年，此下降过程持续时间较长，且下降过程中存在多次起伏变化，整体趋势下降反映了研究区震源机制趋于一致的过程，而这一过程中发生的五次MS≥5.0地震也验证了这一现象；第三次为2015年下半年至2017年初，此次下降速度较快，期间发生云龙MS5.0地震，后期又发生漾濞MS5.1地震。张致伟等（2015）的研究显示汶川MS8.0地震的MS6.0以上强余震也发生在应力张量方差逐渐减小、震源机制趋于一致的过程中。从图7还可以看出，这些MS5.0以上地震主要发生在应力张量方差低于0.2时，这表明当应力张量方差低于阈值0.2时，可能意味着研究区震源机制解已趋于一致，存在发生中强地震的危险。
![]()
图 7 2000—2018年研究区应力张量方差随时间变化曲线以及MS≥5.0地震分布Figure 7. Variation of stress tensor variance and MS≥5.0 earthquakes in the studied area in the period of 2000−20184. 讨论与结论
本文基于2000—2018年滇西北地区MS≥3.0地震的震源机制解，使用Michael的线性叠加反演法对滇西北地区进行了构造应力场反演，结果显示滇西北地区现今构造应力状态在空间上呈现整体的一致性和局部的不均匀性。
研究区的构造应力场整体上以NNW向的低倾伏挤压和ENE向的低倾伏拉张为主，应力类型为走滑型，说明研究区受到来自NNW向的水平挤压作用，这与震源机制解的P轴方位统计结果也相一致，表明NNW向挤压的区域构造应力场一直控制着该区地壳上部的现代地壳运动和地震破裂特征。滇西北地区位于印度板块与欧亚板块碰撞的边界带，由于印度板块NNE向的推挤力，青藏高原内部物质沿青藏高原边缘发生东流逃逸现象（吴中海等，2015），继而受到四川盆地的阻挡而向南沿NW−SE向挤压云南北部（李泽潇等，2020）。张智奇等（2020）通过反演得到青藏高原东南缘三维S波速度结构，并结合GPS速度场观测结果（Zhang et al，2004）的研究显示青藏高原东南缘在上地壳的运动变形过程主要受到大规模走滑断层的控制，本文反演所获的该区构造应力场结果与其相吻合。
尽管滇西北地区的应力状态整体上相对稳定，但局部地区仍呈现非均匀特征，这种现象在研究区北部最为显著。区域分网格反演结果显示，这些地区的最大主应力方位分布较为紊乱，一致性差，可能与该地区复杂的震源机制解类型有关。万永革（2020）关于不同应力体系所呈现的震源机制类型的模拟结果显示，走滑应力体系下可以产生正断型、正走滑型、逆断型、逆走滑型和走滑型震源机制。滇西北地区正是在整体NNW向水平挤压的走滑应力体系作用下，产生了各种类型兼有的复杂震源机制，进而造成研究区北部的构造应力场具有非均匀性。同时，北部地区的地质构造也印证了该结果，区内分布着许多断陷盆地，如鹤庆盆地、丽江盆地等，它们是第三纪以来形成的拉分盆地，控制这些盆地发育的边界断裂多具剪切拉张或正断性质，如鹤庆盆地东西缘断裂、梨园—鸣音断裂等（吴大宁，邓起东，1985）。拉分盆地通常是走滑断层系中局部拉伸形成的断陷盆地，这种局部拉伸促成了垂直断错运动的产生，使得研究区北部地区的正断型和逆断型地震较多。地质结构和震源机制解类型的复杂多样，使得研究区北部应力状态表现出一定的非均匀特征。
震源机制一致性可用来表征震源区应力释放与区域应力场的一致性程度（刘方斌等，2018）。区域分网格应力张量反演结果显示，滇西北地区的应力张量方差大多在0.2以下，个别地区大于0.2，应力场基本处于均匀状态。应力张量方差处于低值，说明震源机制趋于一致。中强地震前震源区小震震源机制趋于一致实质上是，在区域构造应力场的作用下震源区一定范围的应力集中过程（韩晓明，荣代潞，2015）。根据应力张量方差随时间的变化情况来看，研究区M5.0以上地震多数发生在应力张量方差低于阈值0.2时，且地震大都发生在应力张量方差下降即震源机制解趋于一致的过程中。刘自凤等（2020）研究了2014年云南三次MS6.0以上强震前应力张量方差的变化情况，其结果显示这三次强震均发生在应力张量方差低值区域及其边缘，地震前一两年应力张量方差开始下降，本文研究结果与其一致。发震地点多分布在应力方差低值区及其边缘附近这一共性特征，对于了解震源区应力集中增强过程、判断地震危险性有一定参考价值。
虽然本文研究表明中强地震的发生与应力张量方差的变化存在一定关系，但是由于研究区范围较小，样本数量有限，这一现象的普适性尚需更多的、不同地区的震例回溯来验证。此外，本文对构造应力状态的动力学机理尚未进行深入研究，有待进一步研究。
感谢审稿专家对本文提出的建设性意见和建议。本研究的相关图件采用GMT （Wessel，Smith，1995）和ZMAP （Wiemer，Malone，2001）绘制。
-
![]()
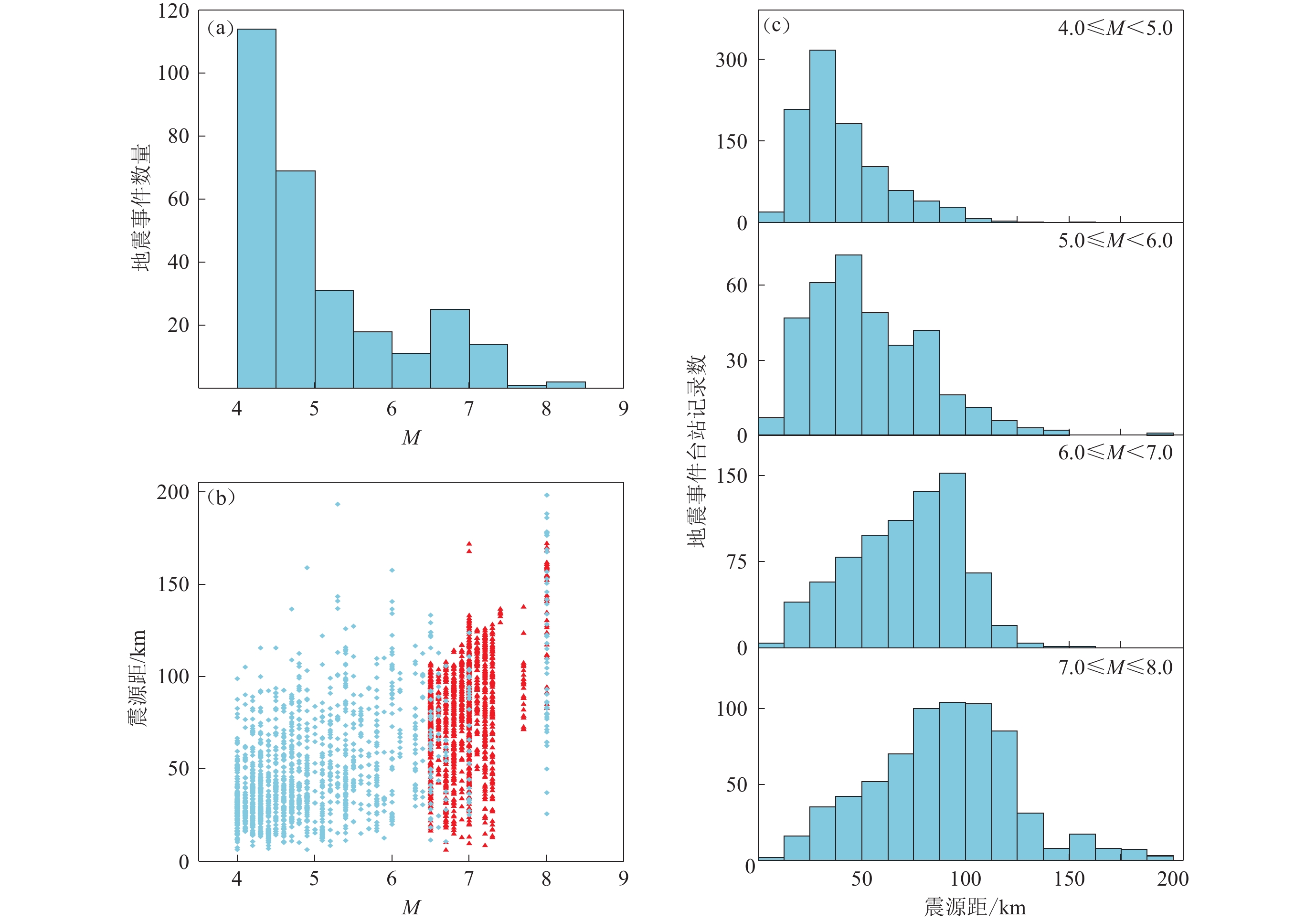
图 1 本研究所用震例分布
（a） 各震级地震分布；（b） 所用地震记录的震源距−震级分布，青色菱形为我国4.0≤MS≤8.0地震事件记录，红色三角形为日本6.5≤MJ≤8.0地震事件记录；（c） 不同震级范围台站记录数−震源距分布
Figure 1. Distribution of earthquakes used in this study
（a） Distribution of the number of events with magnitude；（b） Distribution of hypocentral distance versus magnitude for the selected earthquake records，the cyan diamonds represent earthquake the records （4.0≤MS≤8.0） from China database，while the red triangles indicate the selected waveform data （6.5≤MJ≤8.0） from Japan database；（c） Histogram of the hypocentral distance of the records with different magnitude ranges
![]()
图 2 最优相关性前四名对应的拟合曲线
（a） PVall与PGV；（b） PAall与PGA；（c） PAall与PGV；（d） PDall与PGV
Figure 2. Fitting curves for the top four best correlations
（a） PVall and PGV；（b） PAall and PGA；（c） PDall and PGV；（d） PAall and PGV
表 1 位移幅值PD与地震动峰值参数PGV和PGA的相关性
Table 1 Correlation between displacement amplitude PD and peak ground motion parameters PGV and PGA
参数 滤波器阶数 系数A 系数B 标准差 相关系数R PD3与PGV 1 0.673 2 1.392 0 0.373 4 0.794 6 2 0.677 6 1.448 1 0.367 8 0.801 5 3 0.679 5 1.491 4 0.368 5 0.802 6 4 0.678 2 1.545 4 0.363 5 0.806 7 PDall与PGV 1 0.610 6 1.063 5 0.362 5 0.807 9 2 0.624 8 1.162 5 0.339 9 0.833 5 3 0.614 6 1.212 1 0.328 3 0.845 7 4 0.603 8 1.235 5 0.325 9 0.848 1 PD3与PGA 1 0.501 3 2.472 1 0.343 6 0.727 1 2 0.503 2 2.511 8 0.341 3 0.731 5 3 0.503 4 2.550 2 0.340 0 0.733 8 4 0.501 7 2.580 8 0.340 3 0.733 4 PDall与PGA 1 0.424 4 2.194 6 0.362 3 0.690 0 2 0.438 0 2.268 0 0.348 4 0.718 0 3 0.431 8 2.304 1 0.342 0 0.730 2 4 0.423 1 2.319 0 0.341 9 0.730 4 
下载: 导出CSV
表 2 速度幅值PV与地震动峰值参数PGV和PGA相关性
Table 2 Correlation between velocity amplitude PV and peak ground motion parameter PGV and PGA
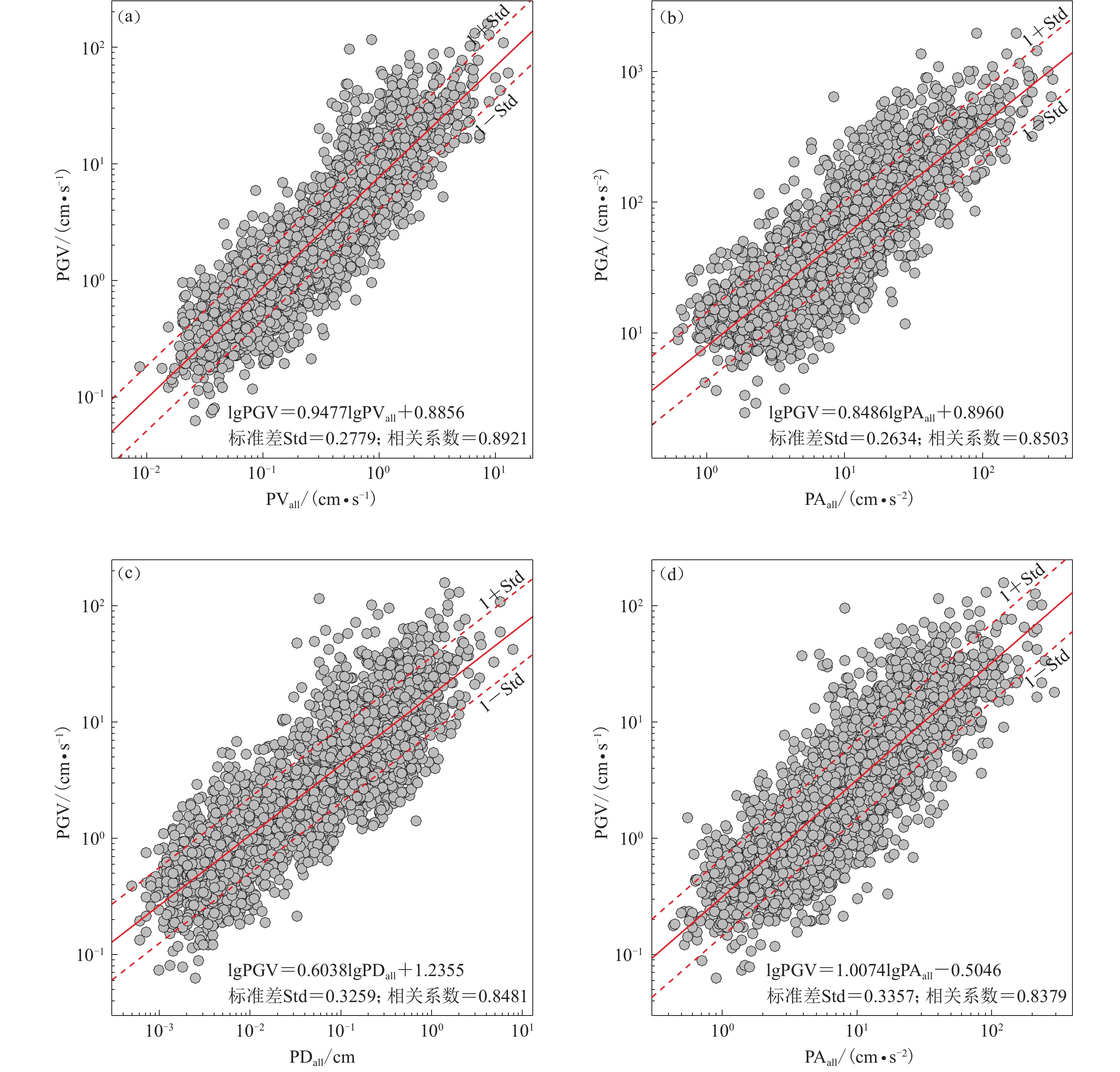
参数 滤波器阶数 系数A 系数B 标准差 相关系数R PV3与PGV 1 0.805 4 0.983 9 0.415 2 0.737 8 2 0.788 6 0.977 6 0.421 6 0.725 0 3 0.760 1 0.961 9 0.432 6 0.711 0 4 0.766 8 0.973 6 0.430 6 0.714 1 PVall与PGV 1 0.947 7 0.885 6 0.277 9 0.892 1 2 0.943 3 0.889 3 0.279 7 0.890 6 3 0.924 8 0.886 6 0.292 9 0.879 4 4 0.942 6 0.905 3 0.281 9 0.888 8 PV3与PGA 1 0.652 9 2.206 8 0.339 4 0.735 0 2 0.638 2 2.201 0 0.345 1 0.724 2 3 0.615 6 2.188 6 0.353 6 0.707 7 4 0.621 0 2.198 0 0.352 1 0.710 7 PVall与PGA 1 0.714 9 2.099 8 0.281 4 0.827 0 2 0.709 4 2.101 5 0.284 2 0.823 1 3 0.694 4 2.098 9 0.292 4 0.811 6 4 0.707 2 2.112 6 0.286 8 0.819 5
下载: 导出CSV
表 3 加速度幅值PA与地震动峰值参数PGV和PGA相关性
Table 3 Correlation between acceleration amplitude PA and peak ground motion parameter PGV and PGA
相关性 滤波器阶数 系数A 系数B 标准差 相关系数R PA3与PGV 1 0.642 1 −0.109 8 0.512 8 0.552 3 2 0.664 0 −0.096 2 0.503 9 0.573 6 3 0.657 5 −0.074 0 0.503 0 0.575 7 4 0.676 0 −0.074 8 0.497 0 0.589 1 PAall与PGV 1 0.995 3 −0.582 2 0.359 5 0.811 5 2 1.008 2 −0.548 7 0.334 3 0.828 6 3 0.988 3 −0.504 9 0.348 3 0.824 3 4 1.007 4 −0.504 6 0.335 7 0.837 9 PA3与PGA 1 0.620 9 1.240 5 0.377 6 0.656 3 2 0.624 8 1.266 5 0.374 5 0.663 4 3 0.609 3 1.294 3 0.377 9 0.655 7 4 0.619 7 1.298 3 0.374 4 0.663 7 PAall与PGA 1 0.848 6 0.896 0 0.263 4 0.850 3 2 0.842 7 0.940 6 0.262 7 0.851 2 3 0.816 9 0.985 5 0.273 6 0.837 4 4 0.826 4 0.991 5 0.267 9 0.844 7
下载: 导出CSV
表 4 各参数的最优相关性
Table 4 Optimal correlations between parameters
参数 滤波器阶数 系数A 系数B 标准差 相关系数R PVall与PGV 1 0.947 7 0.885 6 0.277 9 0.892 1 PAall与PGA 1 0.848 6 0.896 0 0.263 4 0.850 3 PDall与PGV 4 0.603 8 1.235 5 0.325 9 0.848 1 PAall与PGV 4 1.007 4 −0.504 6 0.335 7 0.837 9 PVall与PGA 1 0.714 9 2.099 8 0.281 4 0.827 0 PD3与PGA 3 0.503 4 2.550 2 0.340 0 0.733 8
下载: 导出CSV
表 5 本研究选取的MEMS传感器记录的地震事件测试用例
Table 5 MEMS seismic event test cases selected in this study
发震时刻
年-月-日 时:分:秒东经/º 北纬/º 震源深度/km M GL-P2B记录数 2017-01-04 23:14:29 29.536 102.154 23 4.4 8 2017-01-18 22:35:14 28.134 104.710 10 4.7 1 2017-03-12 20:21:18 27.072 103.421 12 5.1 41 2017-03-30 07:48:18 27.120 103.356 7 4.1 7 2017-04-04 04:57:40 27.093 103.411 8 3.8 6 2017-05-04 13:40:21 28.234 104.922 21 5.1 2 2017-07-02 03:40:58 27.081 103.244 7 3.7 15 2017-10-18 02:54:21 28.326 102.815 15 3.8 33 2018-02-27 03:00:53 29.403 102.131 18 3.8 12 2018-05-02 04:28:45 28.502 102.704 14 3.8 30 2018-05-08 23:11:33 28.140 103.478 10 4.5 37 2018-05-16 16:44:03 29.201 102.265 11 3.9 33 2018-05-16 16:46:11 29.190 102.262 12 4.6 54 2018-05-16 16:46:40 29.180 102.270 9 4.9 51 2018-05-18 02:40:29 27.413 103.958 4 3.6 3 2018-08-11 14:11:31 28.623 103.317 9 4.1 32 2018-08-18 01:36:38 27.400 103.984 10 4.2 5 2018-10-28 08:25:16 28.074 103.538 6 3.6 11 2018-10-30 05:00:05 28.105 103.529 11 4.3 21 2018-10-31 16:29:56 27.700 102.080 19 5.1 28 2018-11-19 22:29:51 29.484 104.499 11 3.3 16 2018-11-20 06:01:11 27.697 102.092 18 3.9 25 2018-12-23 22:22:40 28.116 103.588 10 3.7 15 2019-05-16 04:33:31 28.070 103.530 10 4.7 65
下载: 导出CSV
表 6 1阶巴特沃斯滤波器带通滤波后数据的测试结果
Table 6 Test results with data filtered by the first-order Butterworth bandpass filter
类别 GL-P2B记录数 占总记录数的百分比 成功不预警 478 86.75% 成功预警 40 7.26% 漏报 14 2.54% 误报 19 3.45%
下载: 导出CSV
表 7 成功预警测试震例（1阶巴特沃斯带通滤波处理）理论预警发布时间
Table 7 Theoretical warning release time list for successful early warning test earthquake cases with data filtered by the first-order Butterworth bandpass filter
理论预警发布时间/s GL-P2B记录数 占总记录数的百分比 0.5 28 70.0% 1.0 5 12.5% 1.5 5 12.5% 2.5 1 2.5% 4.0 1 2.5%
下载: 导出CSV
表 8 成功预警测试震例（1阶巴特沃斯带通滤波处理）理论预警时间
Table 8 Theoretical lead-time list for successful early warning test earthquake cases with data filtered by the first-order Butterworth bandpass filter
理论预警时间/s GL-P2B记录数 占总记录数的百分比 ＜0.0 3 7.5% （0.0，1.0] 11 27.5% （1.0，2.0] 9 22.5% （2.0，5.0] 13 32.5% ＞5.0 4 10.0%
下载: 导出CSV
表 9 经1—4阶巴特沃斯滤波器带通滤波后数据测试结果
Table 9 Test results of the data filtered by 1st-to-4th-order Butterworth bandpass filter
滤波器阶数 成功不预警占比 成功预警占比 漏报占比 误报占比 成功处理占比 成功处理（含漏报）占比 1 86.75% 7.26% 2.54% 3.45% 94.01% 96.55% 2 86.75% 7.08% 2.72% 3.45% 93.83% 96.55% 3 86.75% 6.72% 3.09% 3.45% 93.47% 96.56% 4 86.57% 6.53% 3.27% 3.63% 93.10% 96.37%
下载: 导出CSV
-
国家市场监督管理总局, 国家标准化管理委员会. 2020. GB/T1774—2020中国地震烈度表[S/OL].[2021-01-05].http://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=6FD8F9071FAC980D5B2A636A9EA79DE9. State Administration for Market Regulation, Standardization Administration. 2020. GB/T 1774−2020: The Chinese Seismic Intensity Scale[S/OL].[2021-01-05].http://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=6FD8F9071FAC980D5B2A636A9EA79DE9 (in Chinese).
马强. 2008. 地震预警技术研究及应用[D]. 哈尔滨: 中国地震局工程力学研究所: 1–9. Ma Q. 2008. Study and Application on Earthquake Early Warning[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 1–9 （in Chinese）.
彭朝勇,杨建思. 2019. 利用P波参数阈值实时估算地震预警潜在破坏区范围[J]. 地震学报,41(3):354–365. Peng C Y,Yang J S. 2019. Real-time estimation of potentially damaged zone for earthquake early warning based on thresholds of P-wave parameters[J]. Acta Seismologica Sinica,41(3):354–365 (in Chinese).
彭朝勇,杨建思,薛兵,陈阳,朱小毅. 2013. 基于汶川主震及余震的预警参数与震级相关性研究[J]. 地球物理学报,56(10):3404–3415. doi: 10.6038/cjg20131016 Peng C Y,Yang J S,Xue B,Chen Y,Zhu X Y. 2013. Research on correlation between early-warning parameters and magnitude for the Wenchuan earthquake and its aftershocks[J]. Chinese Journal of Geophysics,56(10):3404–3415 (in Chinese).
宋晋东,教聪聪,李山有,侯宝瑞. 2018a. 基于地震P波双参数阈值的高速铁路Ⅰ级地震警报预测方法[J]. 中国铁道科学,39(1):138–144. Song J D,Jiao C C,Li S Y,Hou B R. 2018a. Prediction method of first-level earthquake warning for high speed railway based on two-parameter threshold of seismic P-wave[J]. China Railway Science,39(1):138–144 (in Chinese).
宋晋东,教聪聪,李山有,侯宝瑞,汪源. 2018b. 一种基于地震早期辐射P波能量的高速铁路Ⅰ级地震警报预测方法[J]. 振动与冲击,37(19):14–22. Song J D,Jiao C C,Li S Y,Hou B R,Wang Y. 2018b. A predicting method for magnitude 1 earthquake alarm of high-speed railways based on seismic early radiated P-wave energy[J]. Journal of Vibration and Shock,37(19):14–22 (in Chinese).
张红才,金星,王士成,李军. 2017. 烈度仪记录与强震及测震记录的对比分析:以2015年河北昌黎ML4.5地震为例[J]. 地震学报,39(2):273–285. doi: 10.11939/jass.2017.02.010 Zhang H C,Jin X,Wang S C,Li J. 2017. Comparative analyses of records by seismic intensity instrument with strong ground motion records and seismograph stations records:Taking the ML4.5 Changli earthquake of Hebei Province for an example[J]. Acta Seismologica Sinica,39(2):273–285 (in Chinese).
Allen R M,Melgar D. 2019. Earthquake early warning:Advances,scientific challenges,and societal needs[J]. Annu Rev Earth Planet Sci,47:361–388. doi: 10.1146/annurev-earth-053018-060457
Bormann P,Liu R F,Ren X,Gutdeutsch R,Kaiser D,Castellaro S. 2007. Chinese National Network Magnitudes,their relation to NEIC magnitudes,and recommendations for new IASPEI magnitude standards[J]. Bull Seismol Soc Am,97(1B):114–127. doi: 10.1785/0120060078
Colombelli S,Amoroso O,Zollo A,Kanamori H. 2012a. Test of a threshold-based earthquake early-warning method using Japanese data[J]. Bull Seismol Soc Am,102(3):1266–1275. doi: 10.1785/0120110149
Colombelli S,Zollo A,Festa G,Kanamori H. 2012b. Early magnitude and potential damage zone estimates for the great MW9 Tohoku-Oki earthquake[J]. Geophys Res Lett,39(22):L22306.
Cuéllar A, Espinosa-Aranda J M, Suárez R, Ibarrola G, Uribe A, Rodríguez F H, Islas R, Rodríguez G M, García A, Frontana B. 2014. The Mexican seismic alert system （SASMEX）: Its alert signals, broadcast results and performance during the M7.4 Punta Maldonado earthquake of March 20th, 2012[G]// Early Warning for Geological Disasters. Berlin, Germany: Springer: 71-87.
Evans J R,Allen R M,Chung A I,Cochran E S,Guy R,Hellweg M,Lawrence J F. 2014. Performance of several low-cost accelerometers[J]. Seismol Res Lett,85(1):147–158. doi: 10.1785/0220130091
Fujinawa Y,Noda Y. 2013. Japan’s earthquake early warning system on 11 March 2011:Performance,shortcomings,and changes[J]. Earthq Spectra,29(1S):341–368.
Hsu T Y,Wang H H,Lin P Y,Lin C M,Kuo C H,Wen K L. 2016. Performance of the NCREE’s on-site warning system during the 5 February 2016 MW6.53 Meinong earthquake[J]. Geophys Res Lett,43(17):8954–8959. doi: 10.1002/2016GL069372
National Research Institute of Earth Science and Disaster Resilience. 2019. Strong-motion seismograph networks: NIED K-NET, KiK-net[DB/OL]. [2020−02−20]. http://www.kyoshin.bosai.go.jp/. doi: 10.17598/NIED.0004.
Peng C Y,Yang J S,Xue B,Zhu X Y,Chen Y. 2014. Exploring the feasibility of earthquake early warning using records of the 2008 Wenchuan earthquake and its aftershocks[J]. Soil Dyn Earthq Eng,57:86–93. doi: 10.1016/j.soildyn.2013.11.005
Peng C Y,Yang J S,Zheng Y,Zhu X Y,Xu Z Q,Chen Y. 2017a. New τc regression relationship derived from all P wave time windows for rapid magnitude estimation[J]. Geophys Res Lett,44(4):1724–1731.
Peng C Y,Chen Y,Chen Q S,Yang J S,Wang H T,Zhu X Y,Xu Z Q,Zheng Y. 2017b. A new type of tri-axial accelerometers with high dynamic range MEMS for earthquake early warning[J]. Comput Geosci,100:179–187. doi: 10.1016/j.cageo.2017.01.001
Peng C Y,Jiang P,Chen Q S,Ma Q,Yang J S. 2019. Performance evaluation of a dense MEMS-based seismic sensor array deployed in the Sichuan-Yunnan border region for earthquake early warning[J]. Micromachines,10(11):735. doi: 10.3390/mi10110735
Peng C Y,Ma Q,Jiang P,Huang W H,Yang D K,Peng H S,Chen L,Yang J S. 2020. Performance of a hybrid demonstration earthquake early warning system in the Sichuan-Yunnan border region[J]. Seismol Res Lett,91:835–846. doi: 10.1785/0220190101
Peng C Y,Jiang P,Ma Q,Wu P,Su J R,Zheng Y,Yang J S. 2021. Performance evaluation of an earthquake early warning system in the 2019−2020 M6.0 Changning,Sichuan,China,seismic sequence[J]. Front Earth Sci,9:699941. doi: 10.3389/feart.2021.699941
Shieh J T,Wu Y M,Allen R M. 2008. A comparison of τc and
$ \tau _{\rm{P}}^{\max } $ for magnitude estimation in earthquake early warning[J]. Geophys Res Lett,35(20):L20301. doi: 10.1029/2008GL035611Tsuboi C. 1954. Determination of the Gutenberg-Richter’s magnitude of earthquakes occurring in and near Japan[J]. J Seismol Soc Jpn,7(3):185–193.
Wang W T,Ni S D,Chen Y,Kanamori H. 2009. Magnitude estimation for early warning applications using the initial part of P waves:A case study on the 2008 Wenchuan sequence[J]. Geophys Res Lett,36(16):L16305. doi: 10.1029/2009GL038678
Wang Y,Colombelli S,Zollo A,Song J D,Li S Y. 2021. Source parameters of moderate-to-large Chinese earthquakes from the time evolution of P-wave peak displacement on strong motion recordings[J]. Front Earth Sci,9:616229. doi: 10.3389/feart.2021.616229
Wu Y M,Kanamori H. 2005. Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of P waves[J]. Bull Seismol Soc Am,95(3):1181–1185. doi: 10.1785/0120040193
Wu Y M,Kanamori H. 2008. Development of an earthquake early warning system using real-time strong motion signals[J]. Sensors,8(1):1–9. doi: 10.3390/s8010001
Zhu J B,Li S Y,Song J D,Wang Y. 2021. Magnitude estimation for earthquake early warning using a deep convolutional neural network[J]. Front Earth Sci,9:653226. doi: 10.3389/feart.2021.653226
Zollo A,Amoroso O,Lancieri M,Wu Y M,Kanamori H. 2010. A threshold-based earthquake early warning using dense accelerometer networks[J]. Geophys J Int,183(2):963–974. doi: 10.1111/j.1365-246X.2010.04765.x
计量
- 文章访问数: 607
- HTML全文浏览量: 334
- PDF下载量: 199
