Preliminary discussion and identification of pulse-like strong motion for the 1979 Imperial Valley earthquake
-
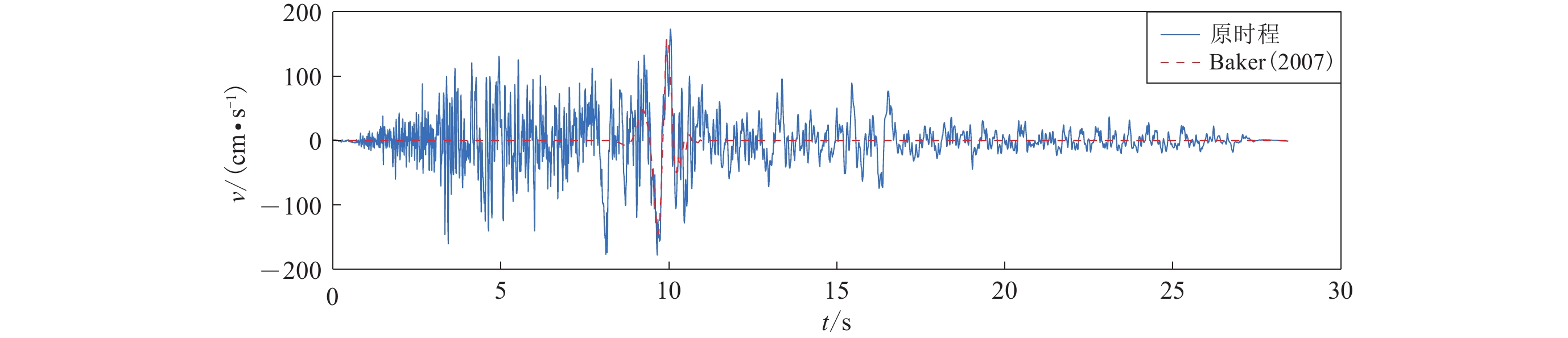
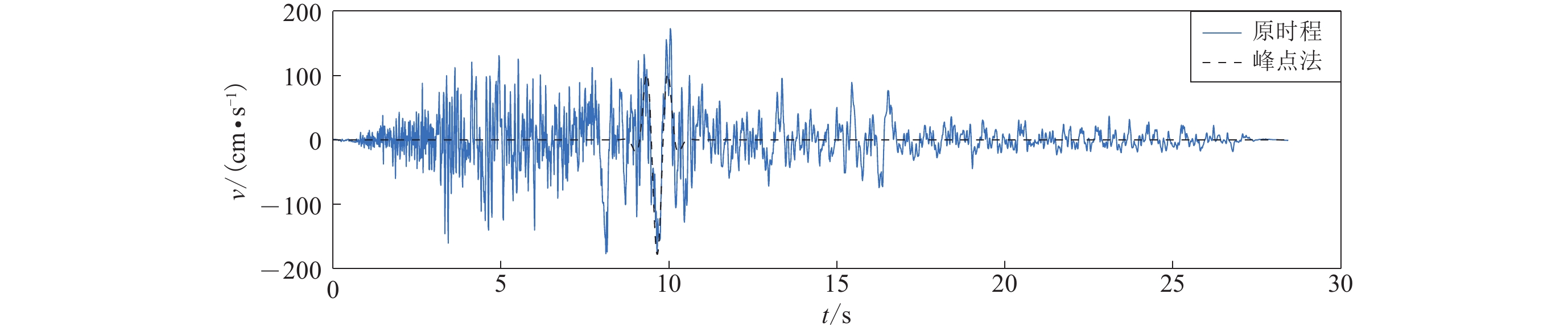
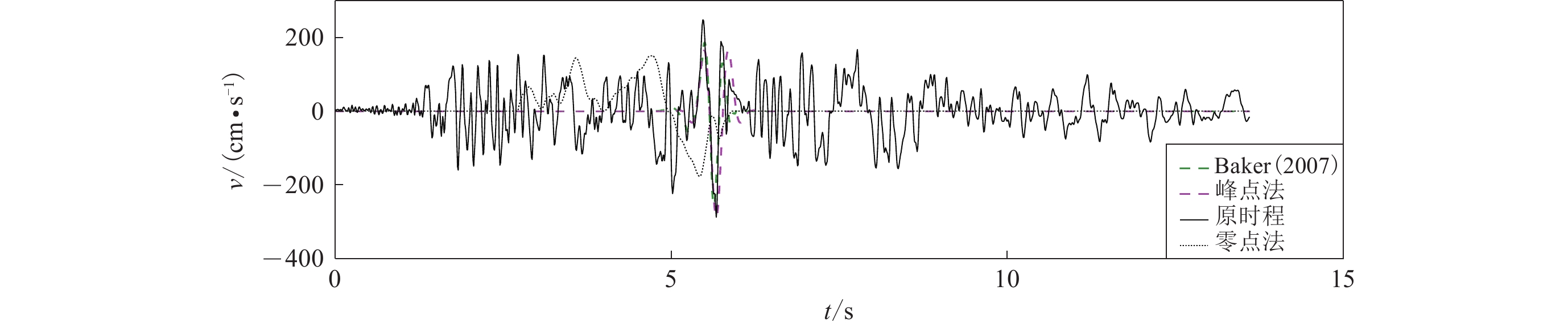
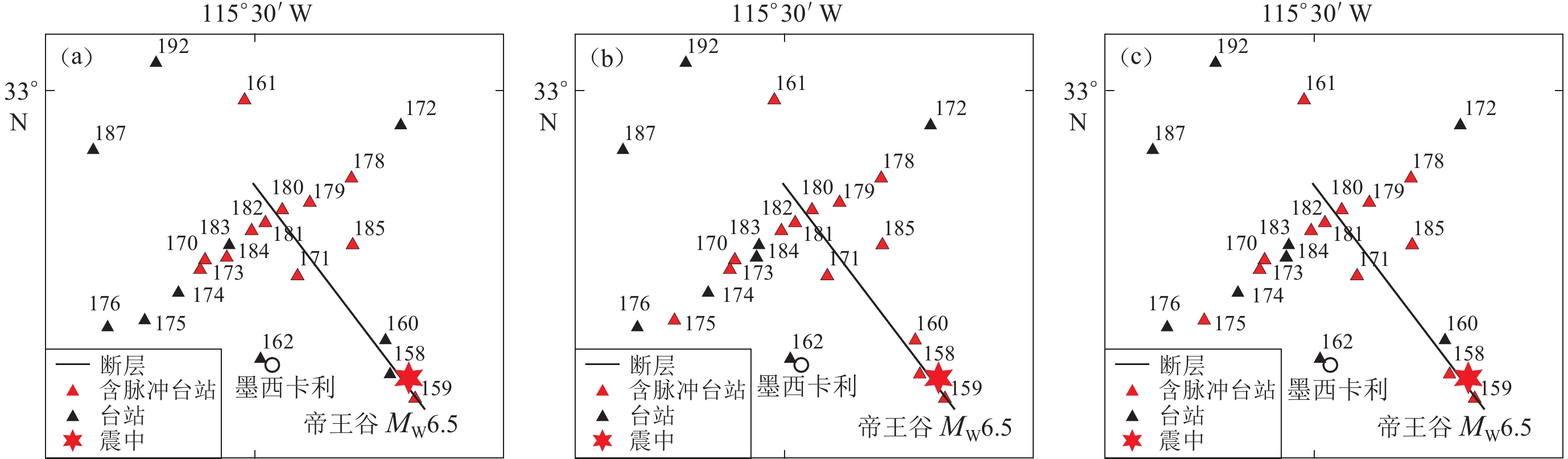
摘要: 以1979年MW6.5帝王谷地震为例，比较了小波变换法、峰点法（PPM）和零点法（ZVPM）识别近断层速度脉冲型强震记录的能力，三种方法识别出的脉冲峰值基本一致，脉冲周期略有差别。为分析速度脉冲的产生机制，包括产生时间、位置以及凹凸体的影响，借助频率-波数域格林函数法（FK法）合成近断层宽频带地震动，采用峰点法逐步识别各子源地震动叠加过程中产生的速度脉冲。通过时频方法分析叠加过程中子源地震动频率成分的变化，分析凹凸体和台站的空间关系对脉冲产生的影响，初步探讨近断层速度脉冲的产生机制。Abstract: Taking the 1979 MW6.5 Imperial Valley earthquake as an example, we compared the three methods of pulse-like strong motion identification, that is, wavelet analysis, peak-point method （PPM） and zero velocity point method （ZVPM）. The identified peak values are similar, however, the identified pulse periods are slightly different. To analyze the mechanism of the velocity pulse, including the generation time, location, and the impact of asperity, we use the frequency-wavenumber Green’s function （FK method） to synthesize broadband ground motion. PPM is used to gradually identify the velocity pulses during the superposition of the sub-source ground motions. Analyzing the changes of the frequency components in sub-fault ground motion during the superposition process by using time-frequency analysis method and the impact of the spatial relationship between the asperity and the station on the pulse generation, preliminarily discuss the generation mechanism of the velocity pulse.
-
Keywords:
- velocity pulse /
- pulse identification /
- FK method /
- asperity /
- pulse indicator
-
-
![]()
图 1 帝王谷地震震中、断层投影和台站位置 （a）及31个台站的加速度时程 （b）
Figure 1. The location of epicenter, fault projection and stations （a） and acceleration records at 31 stations （b） of the Imperial Valley earthquake
![]()
图 2 小波变换法识别出的速度脉冲型地震动
Figure 2. Identification of pulse-like ground motion by wavelet transform
![]()
图 4 三种方法提取RSN158台站记录的脉冲
Figure 4. Identification of pulse-like ground motion by three methods
![]()
图 5 小波变换（a）、峰点法（b）和零点法（c）识别出的速度脉冲的台站
Figure 5. Stations with velocity pulse identified by wavelet transform （a），PPM （b），and ZVPM （c）
![]()
图 6 帝王谷地震断层面上的错动分布
Figure 6. Slip distribution on the fault plane of the Imperial Valley earthquake
![]()
图 7 台站RSN158 （a）和台站RSN179 （b）在破裂过程中出现脉冲的子源
Figure 7. The velocity pulse appears during rupture process at station RSN158 （a） and station RSN179 （b）
![]()
图 8 最初产生脉冲的子源位置与凹凸体和错动量的关系
Figure 8. The relationship between the sub-source position that the pulsefirst generated， the asperity and the slip distribution
表 1 三种方法识别出的帝王谷地震中脉冲型地震动的脉冲参数
Table 1 The pulse indicators of pulse-like ground motions in the Imperial Valley earthquake identified by three methods
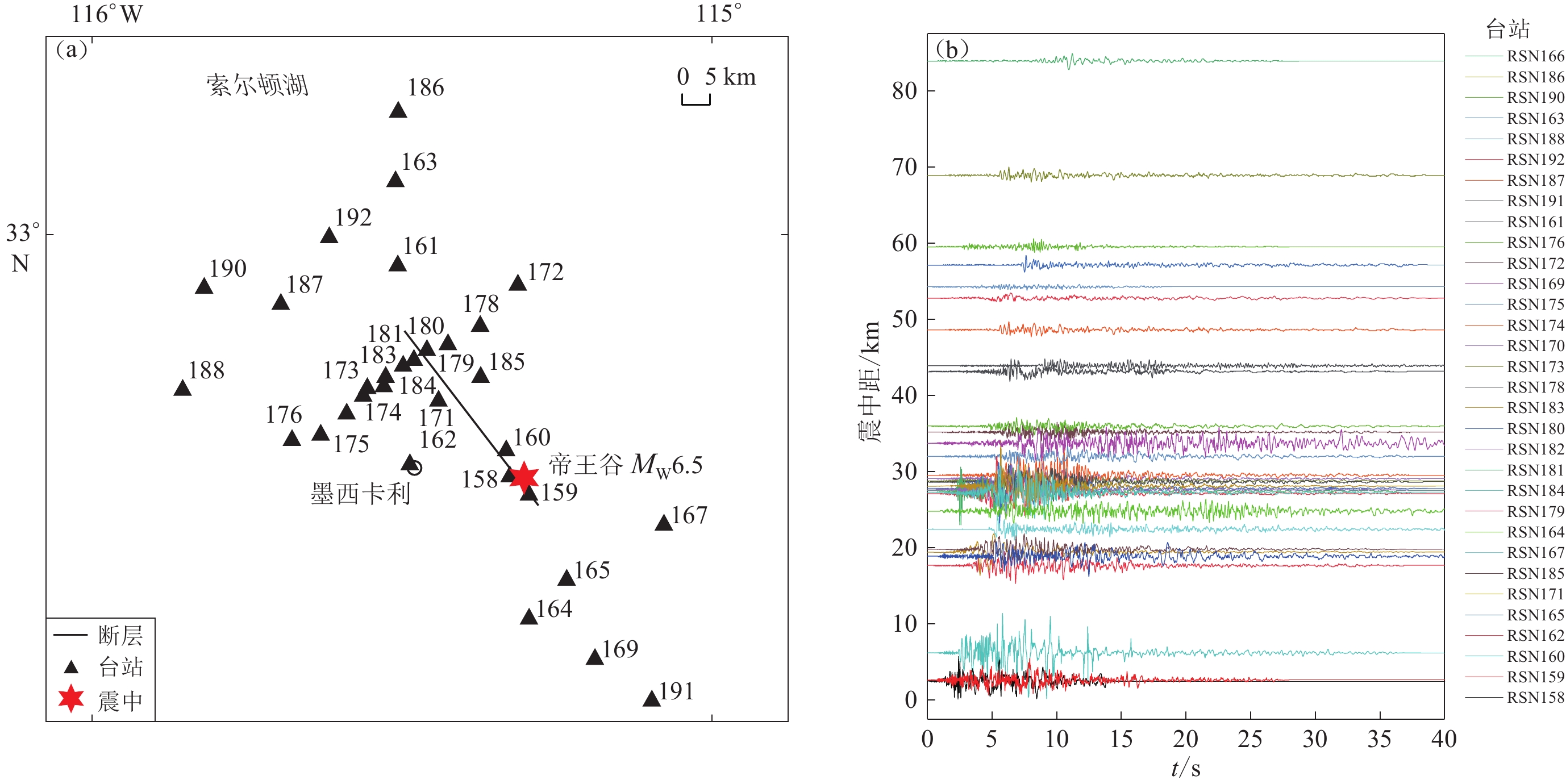
RSN台站编号 脉冲周期Tp/s 脉冲峰值Vp/（cm·s−1） 小波变换法 峰点法 零点法 小波变换法 峰点法 零点法 158 − 1.9 1.9 − 59 60 159 2.3 1.9 1.9 53 50 53 161 4.3 4.2 3.3 51 55 52 170 4.4 3.9 3.5 79 63 71 171 3.4 3.2 3.1 121 111 115 173 4.5 3.3 4.9 69 71 70 178 4.5 4.4 4.4 69 61 60 179 4.8 4.4 3.8 81 89 82 180 4.1 3.9 2.1 130 133 136 181 3.8 3.5 4.8 155 156 160 182 4.4 3.1 4.4 98 100 109 185 2.8 3.5 3.0 68 71 72 
下载: 导出CSV
表 2 帝王谷地震的震源参数
Table 2 Source parameters of Imperial Valley earthquake
震源
机制走向/° 倾角/° 断层参数 子源个数 凹凸体 埋深
/km长度
/km宽度
/km面积
/km2沿走向 沿倾向 个数 面积
/km2长度
/km宽度
/km中心沿走向、
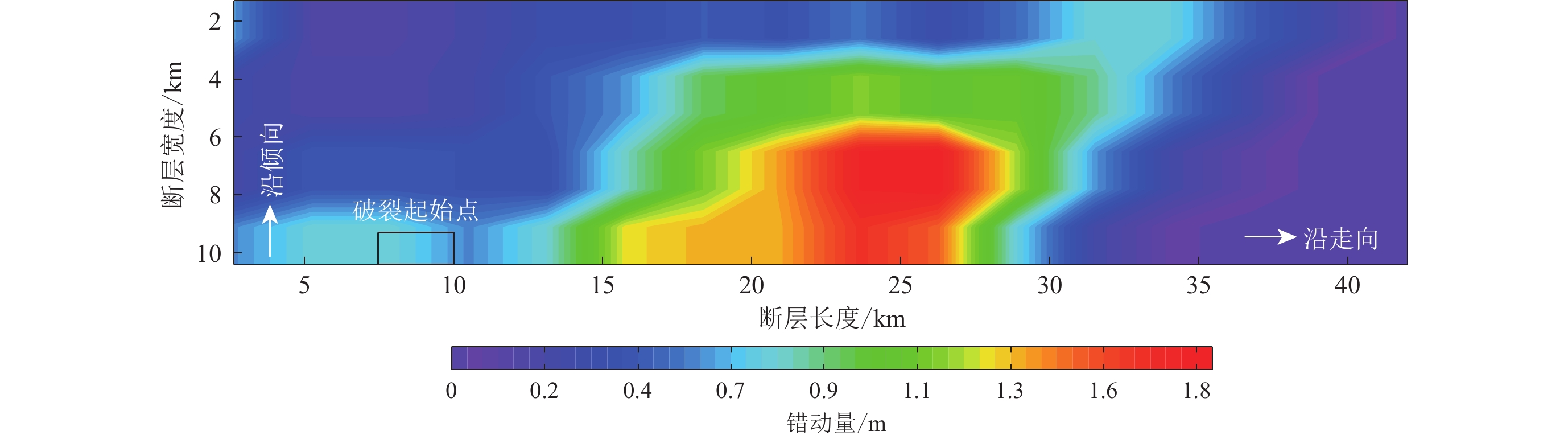
倾向位置/km走滑型 323 90 8 42 10.4 436.8 16 8 1 102 13 7.8 22，6.4
下载: 导出CSV
-
曹泽林. 2020. 基于FK法的三分量宽频带强地震动场合成[D]. 哈尔滨: 哈尔滨工业大学: 141−142. Cao Z L. 2020. Synthesis of Three-Component Broadband Strong Ground Motion Field Based on FK Approach[D]. Harbin: Harbin Institute of Technology: 141−142 （in Chinese）.
刘启方. 2005. 基于运动学和动力学震源模型的近断层地震动研究[D]. 哈尔滨: 中国地震局工程力学研究所: 19−98. Liu Q F. 2005. Studies on Near-Fault Ground Motions Based on Kinematic and Dynamic Source Models[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 19−98 （in Chinese）.
罗全波. 2019. 基于运动学震源模型的近断层速度大脉冲数值模拟研究[D]. 北京: 中国地震局地球物理研究所: 47−49. Luo Q B. 2019. Studies on Numerical Simulation of Near-Fault Large Velocity Pulse Based on Kinematic Source Model[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 47−49 （in Chinese）.
蒋连接,白国良. 2016. 不同类型的近断层脉冲型地震动能量特性研究[J]. 结构工程师,32(6):92–96. Jiang L J,Bai G L. 2016. Study on energy characteristics of different types of near fault pulse ground motions[J]. Structural Engineers,32(6):92–96.
Aki K. 1967. Scaling law of seismic spectrum[J]. J Geophys Res,72(4):1217–1231. doi: 10.1029/JZ072i004p01217
Aki K. 1968. Seismic displacements near a fault[J]. J Geophys Res,73(16):5359–5376. doi: 10.1029/JB073i016p05359
Anderson J C,Bertero V V. 1987. Uncertainties in establishing design earthquakes[J]. J Struct Eng,113(8):1709–1724. doi: 10.1061/(ASCE)0733-9445(1987)113:8(1709)
Archuleta R J. 1984. A faulting model for the 1979 Imperial Valley earthquake[J]. J Geophys Res,89(B6):4559–4585. doi: 10.1029/JB089iB06p04559
Baker J W. 2007. Quantitative classification of near-fault ground motions using wavelet analysis[J]. Bull Seismol Soc Am,97(5):1486–1501. doi: 10.1785/0120060255
Benioff H. 1955. Mechanism and strain characteristics of the White Wolf fault as indicated by the aftershock sequence; earthquakes in Kern County,California during 1955[J]. Calif Div Mines Bull,171:199–202.
Dickinson B W, Gavin H P. 2011. Parametric statistical generalization of uniform-hazard earthquake ground motions[J]. J Struct Eng 137（3）: 410–422.
Fayjaloun R,Causse M,Voisin C,Cornou C,Cotton F. 2017. Spatial variability of the directivity pulse periods observed during an earthquake[J]. Bull Seismol Soc Am,107(1):308–318. doi: 10.1785/0120160199
Hartzell S H,Heaton T H. 1983. Inversion of strong ground motion and teleseismic waveform data for the fault rupture history of the 1979 Imperial Valley,California,earthquake[J]. Bull Seismol Soc Am,73(6A):1553–1583. doi: 10.1785/BSSA07306A1553
Housner G W,Hudson D E. 1958. The port Hueneme earthquake of March 18,1957[J]. Bull Seismol Soc Am,48(2):163–168. doi: 10.1785/BSSA0480020163
Housner G W,Trifunac M D. 1967. Analysis of accelerograms:Parkfield earthquake[J]. Bull Seismol Soc Am,57(6):1193–1220. doi: 10.1785/BSSA0570061193
Iervolino I,Cornell C A. 2008. Probability of occurrence of velocity pulses in near-source ground motions[J]. Bull Seismol Soc Am,98(5):2262–2277. doi: 10.1785/0120080033
Kagawa T. 2009. Conditions of fault rupture and site location that generate damaging pulse waves[C]//Proceedings of the 6th International Conference on Urban Earthquake Engineering. Japan: CUEE2009: 53–58.
Lin Y Y,Kanamori H,Zhan Z W,Ma K F,Yeh T Y. 2020. Modelling of pulse-like velocity ground motion during the 2018 MW6.3 Hualien earthquake,Taiwan[J]. Geophys J Int,223(1):348–365. doi: 10.1093/gji/ggaa306
Mena B,Mai P M. 2011. Selection and quantification of near-fault velocity pulses owing to source directivity[J]. Georisk,5(1):25–43.
Mukhopadhyay S,Gupta V K. 2013. Directivity pulses in near-fault ground motions-I:Identification,extraction and modeling[J]. Soil Dyn Earthq Eng,50:1–15. doi: 10.1016/j.soildyn.2013.02.017
Osaki Y. 1994. A Primer on the Spectral Analysis of Ground Motions[M]. Tokoy: Kajirna Institute Publishing Co: 14−15 （in Japanese）.
Poiata N, Miyake H, Koketsu K. 2018. Mechanisms for generation of near-fault ground motion pulses for dip-slip faulting[M]//Dalguer L, Fukushima Y, Irikura K, Wu C, eds. Best Practices in Physics-based Fault Rupture Models for Seismic Hazard Assessment of Nuclear Installations. Cham: Birkhäuser: 197–212.
Scala A,Festa G,Del Gaudio S. 2018. Relation between near-fault ground motion impulsive signals and source parameters[J]. J Geophys Res:Solid Earth,123(9):7707–7721. doi: 10.1029/2018JB015635
Shahi S K,Baker J W. 2014. An efficient algorithm to identify strong-velocity pulses in multicomponent ground motions[J]. Bull Seismol Soc Am,104(5):2456–2466. doi: 10.1785/0120130191
Somerville P G,Smith N F,Graves R W,Abrahamson N A. 1997. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J]. Seism Res Lett,68(1):199–222. doi: 10.1785/gssrl.68.1.199
Somerville P G. 2003. Magnitude scaling of the near fault rupture directivity pulse[J]. Phys Earth Planet Inter,137(1/4):201–212.
Zhai C H,Chang Z W,Li S,Chen Z Q,Xie L L. 2013. Quantitative identification of near-fault pulse-like ground motions based on energy[J]. Bull Seismol Soc Am,103(5):2591–2603. doi: 10.1785/0120120320
Zhao G C,Xu L J,Xie L L. 2016. A simple and quantitative algorithm for identifying pulse-like ground motions based on zero velocity point method[J]. Bull Seismol Soc Am,106(3):1011–1023. doi: 10.1785/0120150226
计量
- 文章访问数: 471
- HTML全文浏览量: 144
- PDF下载量: 75
