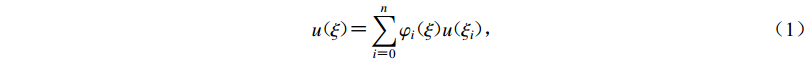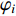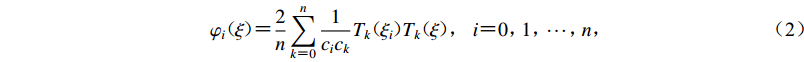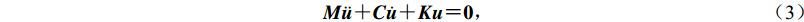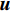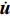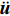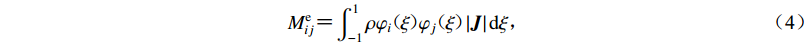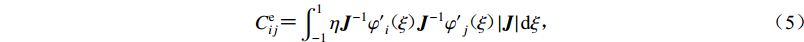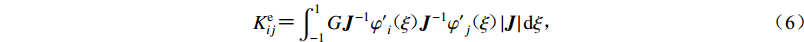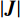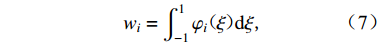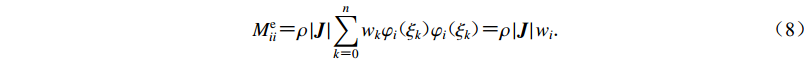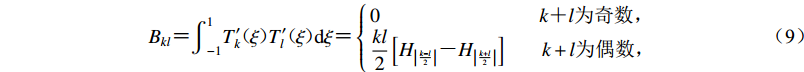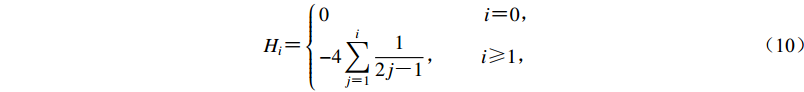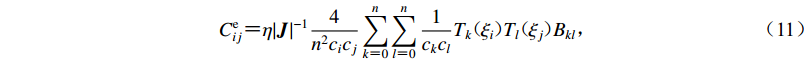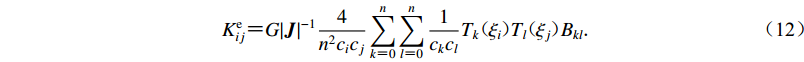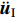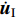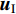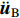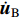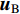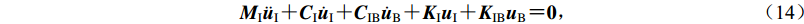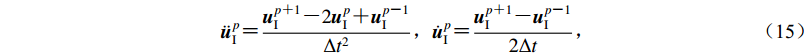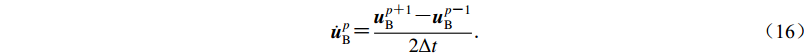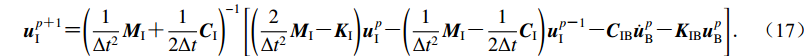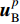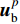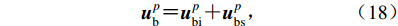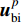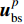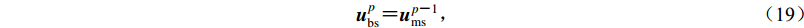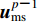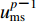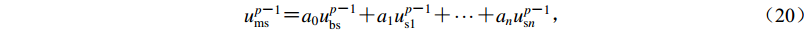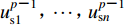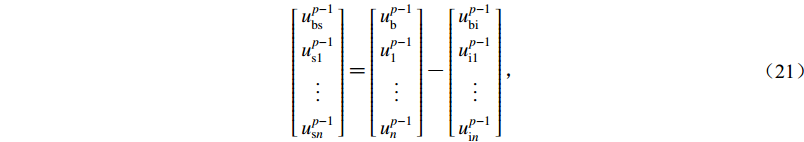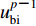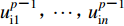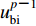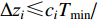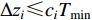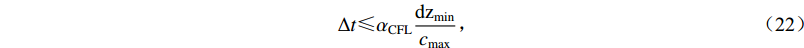The Lumped mass Chebyshev spectral element method for seismic response analysis of horizontally layered soil sites
-
摘要: 提出了一种用于水平成层场地地震反应分析的时域高阶显式算法. 首先，将覆盖土层和基岩划分为若干个切比雪夫谱单元，在模型底部设置多次透射人工边界；其次，以切比雪夫正交多项式构建高阶单元位移模式，通过高斯−洛巴托积分严格导出对角形式的切比雪夫谱单元集中质量矩阵，结合中心差分时域逐步积分格式，建立了高效的集中质量切比雪夫谱元波动模拟方法；最后，利用日本Kik-net强震台网提供的不同类型场地上获得的实际地震观测记录检验了本文方法的有效性. 该方法避免了传统切比雪夫谱元法由于具有一致质量矩阵形式而造成的计算效率不高的问题。数值结果表明，本文方法能够较好地预测Ⅰ1，Ⅱ和Ⅳ类场地在较弱地震和中等强度地震作用下的地面运动特征，每个波长内仅需布置少量单元即可取得较高精度的计算结果。Abstract: A time-domain high-order explicit method for the seismic response analysis of horizontally layered soil sites is proposed. The upper soil and bedrock are discretized by several Chebyshev spectral elements. The multi-transmitting artificial boundary is set at the bottom of the model. The Chebyshev orthogonal polynomials are employed for establishing high-order element displacement field. By means of the Gauss-Lobatto quadrature, the lumped mass matrix, which has diagonal form, for the Chebyshev spectral element is rigorously derived. Combined with the central difference time-stepping scheme, an efficient lumped mass Chebyshev spectral element method for simulating wave motion is constructed. Earthquake records obtained from different kinds of sites provided by the Kik-net strong earthquake network are used to examine the validity of the proposed method. This method overcomes the shortage in efficiency of conventional Chebyshev spectral element method resulted from having consistent form ofmass matrix. Numerical results show that the proposed method can give reasonable prediction on the ground motions of Ⅰ 1, Ⅱ and Ⅳ type sites under weak or moderate earthquakes, and good accuracy can be achieved only by deploying a small number of elements per wavelength.
-
引言
覆盖土层对地震波传播特性具有重要影响（高武平等，2012；李平等，2012），通过土层地震反应分析获得工程场地的地面运动特征，为工程结构抗震评估、设计和加固提供依据。许多实际工程场地都可以被简化为水平成层场地模型，即假定覆盖土层的力学性质沿竖向呈水平成层变化，沿横向均匀无限延伸，将地震激励考虑为垂直向上入射的剪切波。按照此模型分析，土层地震反应分析实际即为一维波动问题。由于该模型形式简洁，物理意义明确，至今依然是场地地震反应分析的一种重要途径（Zalachoris，Rathje，2015）。
常用的一维土层地震反应分析方法主要包括频域和时域两类方法。频域法以等效线性化方法为代表，最早由Idriss和Seed （1968）提出。该方法将不同应变水平下的剪切模量和阻尼比以一个等效剪切模量和阻尼比代替，从而把非线性问题转化为线性问题并在频域内求解。廖振鹏（1989）根据等效线性化方法开发出了土层地震反应分析计算程序LSSRLI-1，在实践中得到了广泛认可。近年来，袁晓铭等（2016）采用直频法动剪模量阻尼比求解技术，提出了新一代土层地震反应分析方法，克服了传统方法低估软弱场地和深厚场地放大效应的缺陷。孙锐和袁晓铭（2021）提出了全局等效剪应变的概念和算法，建立了一种新的等效线性化分析方法。然而，等效线性化方法尚存在一些缺点，比如无法反映土层真实的受力状态（王志良，韩清宇，1981；栾茂田，林皋，1992），且忽略了较多的高频成分（齐文浩，薄景山，2007）。为了解决上述问题，发展出了土层地震反应分析的时域方法，可以真实地反映土层在地震作用下的表现。丁海平和周正华（1998）提出了一维土层地震反应分析的时域有限元解法，并指出时域算法能够达到与频域算法相同的计算精度，但其计算耗时远少于频域算法。然而传统有限单元法由于形函数阶次较低，通常需将每个波长内布置6—10个单元（廖振鹏，2002）才能准确刻画出波场特征，在土层复杂或地震动高频成分较丰富的情况下可能会需要较大的计算工作量。对此，邢浩洁等（2017）提出了分析成层场地地震反应的切比雪夫（Chebyshev）谱元法，仅需划分少量单元即可获得较高的计算精度。但其在计算切比雪夫谱单元质量矩阵时沿用了传统谱元法的做法，即利用切比雪夫多项式的性质获得单元质量矩阵的解析解，由此导出的质量矩阵为非对角形式，无法充分发挥显式时间积分算法的高效率优势。
本文在邢浩洁等（2017）的工作基础上，拟通过节点积分法（Fried，Malkus，1975）建立集中质量切比雪夫谱单元，解决传统切比雪夫谱元法由于需要对质量矩阵求逆而造成计算效率不高的问题，同时避免传统的质量集中方法的随意性，如行和集中法（Zienkiewicz et al，2013）或对角元素放大法（Hinton et al，1976）。在该集中质量切比雪夫谱单元模型中嵌入多次透射人工边界（multi-transmitting formula，缩写为MTF）（Liao，Wong，1984），结合中心差分形成一种求解一维土层波动问题的高阶显式算法.并利用日本Kik-net强震观测台网提供的井下和地面实测记录，以检验本文方法的适用性。
1. 水平成层场地的集中质量切比雪夫谱元模型
1.1 水平成层场地简化模型
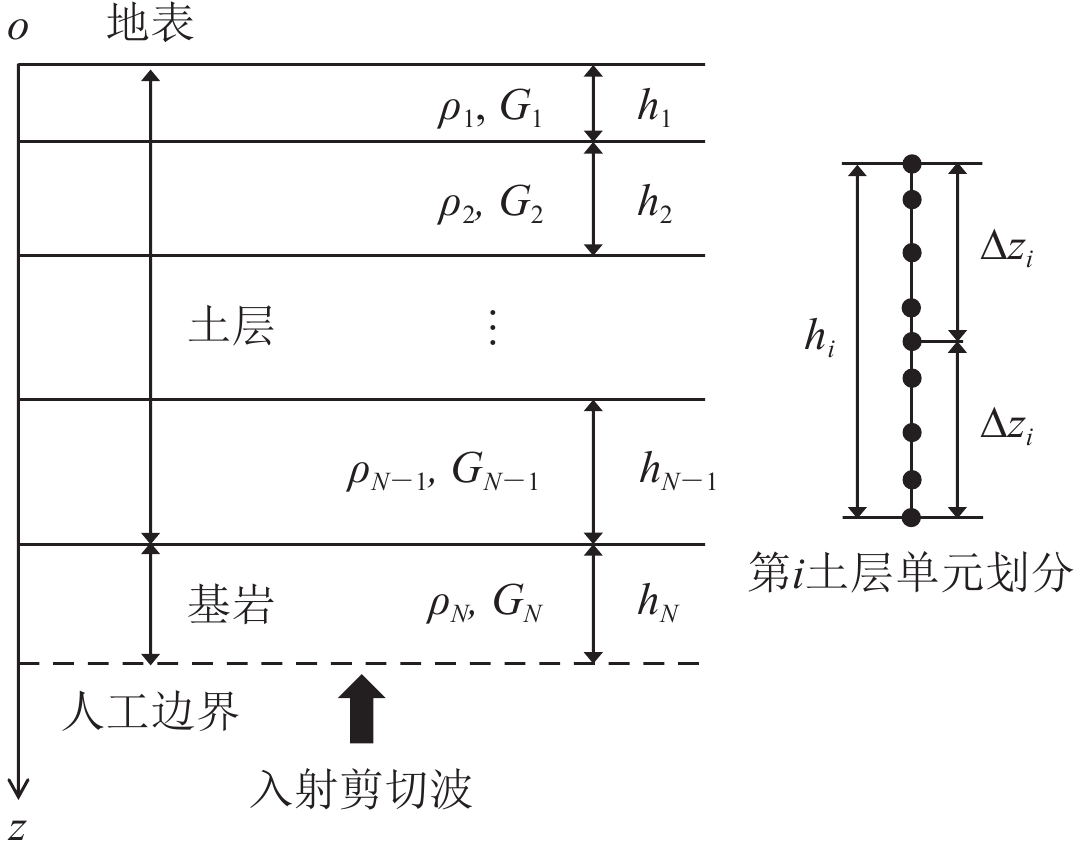
将水平成层场地简化为如图1所示的计算模型。设坐标原点位于自由地表，建立正方向竖直向下的一维坐标系z。假设有N−1个土层覆盖于基岩半空间上，各覆盖土层的厚度、质量密度和剪切模量分别为hi，ρi和Gi，i = 1，2，…，N－1。在基岩半空间中，从基岩面向下截取一定深度hN，并在底部设置多次透射人工边界模拟无限域对内域波动的影响，以消除外行波场在边界处的反射。从而，N－1个土层和1个基岩层组成的计算模型总厚度为
$H {\text{＝}} \sum\nolimits_{i {\text{＝}} 1}^N {{h_i}}$ 。入射地震波为从模型底部竖直向上传播的剪切波。采用切比雪夫谱元法对土层模型进行空间离散，每个土层划分为若干个大小相等的一维切比雪夫谱单元，以图1中第i土层为例，将hi厚度的土层划分为两个大小为∆zi的谱单元，而基岩层则被单独划分为一个谱单元。![]()
图 1 水平成层场地切比雪夫谱元模型Figure 1. Chebyshev spectral element model of horizontal layered soil site1.2 切比雪夫谱单元位移模式
一维土层分析的切比雪夫谱单元以 ［ −1，1 ］ 区间内不等间距分布的高斯-洛巴托-切比雪夫（Gauss-Lobatto-Chebyshev，缩写为GLC）节点为参考单元节点，它们是第一类切比雪夫多项式的极值点。对于n阶切比雪夫谱单元，GLC节点的位置为ξi＝−cos（iπ/n），i＝0，1，···，n。
设单元位移模式为
$$ u（ \xi ） {\text{＝}} \sum\limits_{i {\text{＝}} 0}^n {{\varphi _i}（ \xi ）u（ {{\xi _i}} ）} {\text{，}} $$ (1) 式中：u（ξi）为节点水平位移；
$\varphi _i $ （ξ）为建立在单元节点上的拉格朗日形函数；考虑到GLC节点与切比雪夫多项式之间的关系，该形函数亦可表示为一组截断的切比雪夫多项式组合$$ {\varphi _i}（ \xi ） {\text{＝}} \frac{2}{n}\sum\limits_{k {\text{＝}} 0}^n {\frac{1}{{{c_i}{c_k}}}{T_k}（ {{\xi _i}} ）{T_k}（ \xi ）} {\text{，}}\;\;\;\;i {\text{＝}} 0{\text{，}}1{\text{，}}\cdots {\text{，}}n {\text{，}} $$ (2) 式中，Tk（ξ）为k阶第一类切比雪夫多项式，其表达式为Tk（ξ）＝cos（kcos−1ξ），ci和ck为多项式系数，当i＝0或n时，取值为2，当i＝1，···，n－1时，取值为1。
1.3 切比雪夫谱单元特性矩阵
利用切比雪夫谱单元对水平成层场地模型进行空间离散后，得到离散方程
$$ {\boldsymbol{M}}\ddot {\boldsymbol{u}} {\text{＋}} {\boldsymbol{C}}\dot {\boldsymbol{u}} {\text{＋}} {\boldsymbol{Ku}} {\text{＝}}{\boldsymbol{0}} {\text{，}} $$ (3) 式中：
$ {\boldsymbol{u}} $ ，$ \dot {\boldsymbol{u}}$ 和$\ddot {\boldsymbol{u}} $ 分别为位移、速度和加速度；总体质量矩阵M；总体阻尼矩阵C和总体刚度矩阵K分别由单元刚度矩阵Me、单元阻尼矩阵Ce和单元刚度矩阵Ke按照单元编号组装而成。Me，Ce和Ke计算如下：$$ {M}_{ij}^{\rm e} {\text{＝}} \int_{ - 1}^1 {\rho {\varphi _i}（ \xi ）{\varphi _j}（ \xi ）\left| {{\boldsymbol{J}}} \right|{\rm d}\xi } {\text{，}} $$ (4) $$ {C}_{ij}^{\rm e} {\text{＝}} \int_{ - 1}^1 {\eta {{\boldsymbol{J}}^{ - 1}}{{\varphi '}_i}（ \xi ）{{\boldsymbol{J}}^{ - 1}}{{\varphi '}_j}（ \xi ）\left| {{\boldsymbol{J}}} \right|{\rm d}\xi } {\text{，}} $$ (5) $$ {K}_{ij}^{\rm e} {\text{＝}} \int_{ - 1}^1 {G{{\boldsymbol{J}}^{ - 1}}{{\varphi '}_i}（ \xi ）{{\boldsymbol{J}}^{ - 1}}{{\varphi '}_j}（ \xi ）\left| {\boldsymbol{J}} \right|{\rm d}\xi } {\text{，}} $$ (6) 式中ρ，η和G分别表示土体的质量密度、阻尼系数和剪切模量，
$ \left| {\boldsymbol{J}} \right| $ 为雅可比矩阵的行列式。对于一维谱单元，雅可比矩阵仅包含一个元素，即J＝∆z/2，∆z为物理单元的长度。为了建立集中质量矩阵，本文采用节点积分法求解单元质量矩阵，即以单元节点作为数值积分点，利用高斯-洛巴托（Gauss-Lobatto）数值积分计算单元质量矩阵的积分（式（4））。由于拉格朗日形函数具有克罗内克（Kronecker-δ）性质，由此导出的质量矩阵仅有主对角元素非零，其余非对角元素全部为零。单元GLC节点对应的高斯-洛巴托积分权系数为
$$ {w_i} = \int_{ - 1}^1 {{\varphi _i}（ \xi ）{\rm{d}}\xi }{\text{,}} $$ (7) 式中：wi为与节点ξi相对应的积分权系数；φi（ξ）为式（2）中的单元形函数。1—5阶切比雪夫谱单元的GLC节点位置及对应的积分权系数，列于表1。
表 1 GLC节点上的高斯−洛巴托积分权系数Table 1. Gauss-Lobatto quadrature weights based on GLC points谱单元阶次 GLC节点坐标 积分权系数 1 ±1 1 2 ±1, 0 0.333 3, 1.333 3 3 ±1, ±0.5 0.111 1, 0.888 9 4 ±1, ±0.707 1, 0 0.066 7, 0.533 3, 0.8 5 ±1, ±0.809 0, ±0.309 0 0.04, 0.360 7, 0.599 3 利用式（7）的数值积分格式计算式（4）单元质量矩阵，则质量矩阵的非对角元素全部为零，主对角元素可进一步计算为
$$ M_{ii}^{\rm e} {\text{＝}} \rho \left| {\boldsymbol{J}} \right|\sum\limits_{k {\text{＝}} 0}^n {{w_k}{\varphi _i}（ {{\xi _k}} ）{\varphi _i}（ {{\xi _k}} ）} {\text{＝}} \rho \left| {\boldsymbol{J}} \right|{w_i} {\text{.}} $$ (8) 由于切比雪夫正交多项式积分性质表现为
$$ {B}_{kl}{\text{＝}}{\displaystyle {\int }_{-1}^{1}{{T}}_{k}^{\prime }（\xi ）{{T}}_{l}^{\prime }（\xi ）{\rm d}\xi }{\text{＝}}\left\{\begin{array}{l}0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k{\text{＋}}l{\text{为奇数}}{\text{，}} \\ \dfrac{kl}{2}\left[{H}_{\left|{}\frac{{k - l}}{2}\right|}{\text{－}}{H}_{\left|\frac{{k + l}}{2}\right|}\right]\;\;\;\;\;\;\;\;k+l{\text{为偶数}}{\text{，}} \end{array} \right. $$ (9) 其中：
$$ {H_i} {\text{＝}} \left\{ {\begin{array}{*{20}{l}} {0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i {\text{＝}} 0}{\text{，}} \\ { - 4\displaystyle\sum\limits_{j {\text{＝}} 1}^i {\frac{1}{{2j {\text{－}} 1}}} {\text{，}}\;\;\;\;\;\;\;\;i {\text{≥}} 1} {\text{，}} \end{array}} \right. $$ (10) 利用以上性质，Ce和Ke可精确计算为
$$ C_{ij}^{\rm e} {\text{＝}} \eta {\left|{\boldsymbol{ J}} \right|^{ - 1}}\frac{4}{{{n^2}{c_i}{c_j}}}\sum\limits_{k {\text{＝}} 0}^n {\sum\limits_{l {\text{＝}} 0}^n {\frac{1}{{{c_k}{c_l}}}{T_k}（ {{\xi _i}} ）} } {T_l}（ {{\xi _j}} ）{B_{kl}} {\text{，}}$$ (11) $$ K_{ij}^{\rm e} {\text{＝}} G{\left| {\boldsymbol{J}} \right|^{ - 1}}\frac{4}{{{n^2}{c_i}{c_j}}}\sum\limits_{k {\text{＝}} 0}^n {\sum\limits_{l {\text{＝}} 0}^n {\frac{1}{{{c_k}{c_l}}}{T_k}（ {{\xi _i}} ）} } {T_l}（ {{\xi _j}} ）{B_{kl}} {\text{.}} $$ (12) 2. 时域逐步积分
对于土层地震反应分析问题，一般将入射波作为边界处的运动形式施加，因此需要将模型内域节点和边界节点分开处理。在本文建立的水平成层场地谱元模型中，边界节点仅有一个，即模型底部人工边界上的单元节点，其余节点均属于内域节点。将式（3）中的矩阵和向量按照内域和边界进行分块，得
$$ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}_{\rm{I}}}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{{{\boldsymbol{M}}_{\rm{B}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\ddot {\boldsymbol{u}}}_{\rm{I}}}} \\ {{{\ddot {\boldsymbol{u}}}_{\rm{B}}}} \end{array}} \right] {\text{＋}} \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{C}}_{\rm{I}}}}&{{{\boldsymbol{C}}_{{\rm{IB}}}}} \\ {{{\boldsymbol{C}}_{{\rm{BI}}}}}&{{{\boldsymbol{C}}_{\rm{B}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot {\boldsymbol{u}}}_{\rm{I}}}} \\ {{{\dot {\boldsymbol{u}}}_{\rm{B}}}} \end{array}} \right] {\text{＋}} \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{K}}_{\rm{I}}}}&{{{\boldsymbol{K}}_{{\rm{IB}}}}} \\ {{{\boldsymbol{K}}_{{\rm{BI}}}}}&{{{\boldsymbol{K}}_{\rm{B}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{u}}_{\rm{I}}}} \\ {{{\boldsymbol{u}}_{\rm{B}}}} \end{array}} \right] {\text{＝}} {\boldsymbol{0}} {\text{，}} $$ (13) 式中：
${\ddot {\boldsymbol{u}}_{\rm{I}}}$ ，${\dot {\boldsymbol{u}}_{\rm{I}}}$ 和${{\boldsymbol{u}}_{\rm{I}}}$ 分别为内域节点的加速度、速度和位移向量；${\ddot {\boldsymbol{u}}_{\rm{B}}}$ ，${\dot {\boldsymbol{u}}_{\rm{B}}}$ 和${{\boldsymbol{u}}_{\rm{B}}}$ 分别为边界节点的加速度、速度和位移；MI和MB为总体质量矩阵M按照内域节点和边界节点的节点编号进行分块后的子矩阵；CI，CIB，CBI和CB以及KI，KIB，KBI和KB分别为总体阻尼矩阵C和总体刚度矩阵K按照相同的方式分块后的子矩阵。将上式中的第一行方程单独写为$$ {{\boldsymbol{M}}_{\rm{I}}}{\ddot {\boldsymbol{u}}_{\rm{I}}} {\text{＋}} {{\boldsymbol{C}}_{\rm{I}}}{\dot {\boldsymbol{u}}_{\rm{I}}} {\text{＋}} {{\boldsymbol{C}}_{{\rm{IB}}}}{\dot {\boldsymbol{u}}_{\rm{B}}} {\text{＋}} {{\boldsymbol{K}}_{\rm{I}}}{{\boldsymbol{u}}_{\rm{I}}} {\text{＋}} {{\boldsymbol{K}}_{{\rm{IB}}}}{{\boldsymbol{u}}_{\rm{B}}} {\text{＝}} {\bf 0} {\text{，}} $$ (14) 对式（14）进行时间域离散，设时间间隔为∆t，并采用中心差分法进行时步积分。在t＝p∆t时刻，内域节点的加速度和速度可插值表示为
$$ \ddot {\boldsymbol{u}}_{\rm{I}}^p {\text{＝}} \frac{{{\boldsymbol{u}}_{\rm{I}}^{p {\text{＋}} 1} {\text{－}} 2{\boldsymbol{u}}_{\rm{I}}^p {\text{＋}} {\boldsymbol{u}}_{\rm{I}}^{p {\text{－}} 1}}}{{\Delta {t^2}}}{\text{，}}\dot {\boldsymbol{u}}_{\rm{I}}^p {\text{＝}} \frac{{{\boldsymbol{u}}_{\rm{I}}^{p {\text{＋}} 1} {\text{－}} {\boldsymbol{u}}_{\rm{I}}^{p {\text{－}} 1}}}{{2\Delta t}} {\text{，}} $$ (15) 式中，上标p表示p∆t时刻；边界节点的速度插值表示为
$$ \dot {\boldsymbol{u}}_{\rm B}^p {\text{＝}} \frac{{{\boldsymbol{u}}_{\rm B}^{p {\text{＋}} 1} {\text{－}} {\boldsymbol{u}}_{\rm B}^{p {\text{－}} 1}}}{{2\Delta t}} {\text{.}} $$ (16) 将式（15）和（16）代入式（14），得到内域节点位移的递推格式
$$ {\boldsymbol{u}}_{ {\rm{I}}}^{p {\text{＋}} 1} {\text{＝}} {\left( {\frac{1}{{\Delta {t^2}}}{{\boldsymbol{M}}_{\rm{I}}} {\text{＋}} \frac{1}{{2\Delta t}}{{\boldsymbol{C}}_{\rm I}}} \right)^{ - 1}}\left[ {\left( {\frac{2}{{\Delta {t^2}}}{{\boldsymbol{M}}_{\rm{I}}} {\text{－}} {{\boldsymbol{K}}_{\rm I}}} \right){\boldsymbol{u}}_{\rm{I}}^p {\text{－}} } {\left( {\frac{1}{{\Delta {t^2}}}{{\boldsymbol{M}}_{\rm I}} {\text{－}} \frac{1}{{2\Delta t}}{{\boldsymbol{C}}_{\rm I}}} \right){\boldsymbol{u}}_{\rm I}^{p {\text{－}} 1} {\text{－}} {{\boldsymbol{C}}_{{\rm{IB}}}}\dot {\boldsymbol{u}}_{\rm{B}}^p {\text{－}} {{\boldsymbol{K}}_{{\rm{IB}}}}{\boldsymbol{u}}_{\rm{B}}^p} \right] {\text{.}} $$ (17) 一般情况下质量矩阵MI为对角阵，而阻尼矩阵CI通常不会呈对角矩阵形式，故由MI与CI组合的矩阵亦会是非对角阵。此情形下可考虑构建仅同质量矩阵呈比例的瑞雷阻尼矩阵，或者将阻尼矩阵对角化（Thomson et al，1974）等措施。
3. 基于透射边界的地震动输入
由针对节点的总波场给出的方程式（17）可知，求p＋1时刻的内域节点位移时，除已知的p时刻和p－1时刻内域节点位移外，还需要知道p时刻边界点的位移
${ { {\boldsymbol{u}}}_{\rm{B}}^p} $ 。而当采用MTF人工边界时，还需要先将总波场分离为内行波和外行波，再针对外行波应用MTF条件。如图2所示，人工边界取基岩面以下一定深度，将这一深度范围内的基岩划分为一个谱单元。底部边界节点的总位移场
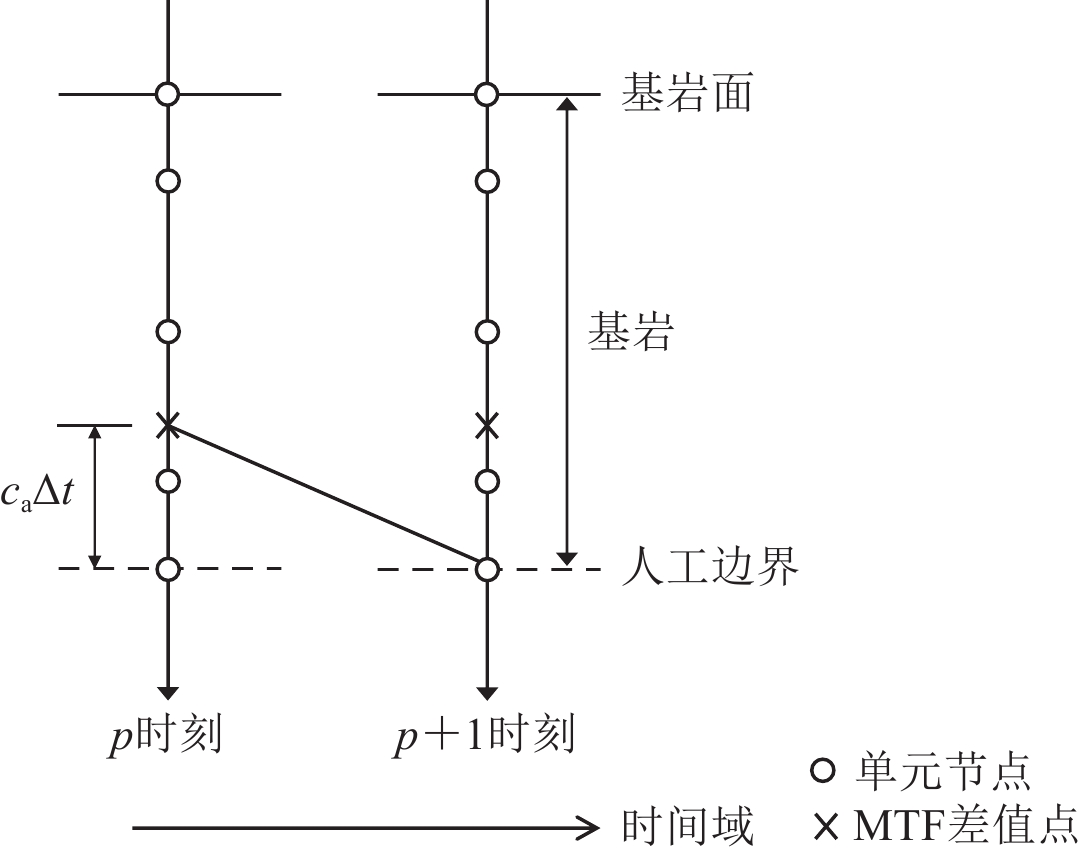
${\boldsymbol u}_{\rm b}^p$ 可分解为![]()
图 2 切比雪夫谱单元的一阶MTF插值方案Figure 2. Interpolation scheme for first-order MTF in Chebyshev spectral element$$ {\boldsymbol u}_{\rm b}^p {\text{＝}} {\boldsymbol u}_{{\rm bi}}^p {\text{＋}} {\boldsymbol u}_{{\rm bs}}^p {\text{，}} $$ (18) 式中，
${\boldsymbol{u}}_{{\rm bi}}^p$ 为已知的p时刻边界上的入射波，${\boldsymbol{u}}_{{\rm bs}}^p$ 为p时刻边界上的外行波。根据一阶MTF条件，边界点的外行波由距离边界caΔt处的外行波递推得到，即$$ {\boldsymbol u}_{{\rm {bs}}}^p {\text{＝}} {\boldsymbol u}_{{\rm {ms}}}^{p {\text{－}} 1} {\text{，}} $$ (19) 式中，
${\boldsymbol{u}}_{{\rm {ms}}}^{p{{\text{－}}}1}$ 表示p－1时刻距离边界caΔt处的MTF插值点的外行波场，ca为人工波速，在本文中ca取基岩的剪切波速。由于MTF插值点与单元节点一般不重合，故${{u}}_{{\rm {ms}}}^{p{\text{－}}1}$ 需要根据p－1时刻整个基岩单元的外行波场插值求出，即$$ u_{{\rm {ms}}}^{p {\text{－}} 1}{\text{＝}}{a_0}u_{{\rm {bs}}}^{p {\text{－}} 1} {\text{＋}} {a_1}u_{{\rm {s1}}}^{p {\text{－}} 1} {\text{＋}} \cdots {\text{＋}} {a_n}u_{{ {{\rm{s}}n}}}^{p {\text{－}} 1}{\text{，}} $$ (20) 式中
$u_{\rm{s}1}^{p{\text{－}}1}{\text{，}} \cdots {\text{，}}u_{{\rm{s}}n}^{p{\text{－}}1}$ 为基岩单元中非边界节点在p－1时刻的外行波。根据式（1）所定义的单元位移模式，插值系数a0，a1，···，an即为定义在各单元节点上的形函数在MTF插值点处的取值。基岩单元中所有节点在p－1时刻的外行波场则可从已求出的p－1时刻总波场中扣除内行波场得到$$ \left[ {\begin{array}{*{20}{c}} {u_{\rm {bs}}^{p-1}} \\ {u_{\rm {s1}}^{p-1}} \\ \vdots \\ {u_{{\rm {s}}n}^{p-1}} \end{array}} \right] {\text{＝}} \left[ {\begin{array}{*{20}{c}} {u_{\rm b}^{p-1}} \\ {u_1^{p-1}} \\ \vdots \\ {u_{ n}^{p-1}} \end{array}} \right] {\text{－}} \left[ {\begin{array}{*{20}{c}} {u_{\rm {bi}}^{p-1}} \\ {u_{\rm {i1}}^{p-1}} \\ \vdots \\ {u_{{\rm {i}}n}^{p-1}} \end{array}} \right] {\text{，}} $$ (21) 式中，
$u_{{\rm {bi}}}^{p{\text{－}}1}$ 为p－1时刻边界上的入射波，$u_{\rm {i1}}^{p{{\text{－}}}1}{\text{，}}\cdots {\text{，}}u_{{\rm {i}}{n}}^{p{{\text{－}}}1}$ 比$u_{{\rm {bi}}}^{p{{\text{－}}}1}$ 滞后一定时间间隔，该时间间隔的长度等于各点到边界点的距离与基岩剪切波速之比。至此，求解土层模型所有节点的位移反应得以显式地完成。对于土层地震波动的有限元模拟，廖振鹏（2002）建议第i层土层中的有限单元尺寸取为
$\Delta {{\textit{z}}_i} {\text{≤}} {{{c_i}{T_{\min }}} \mathord{\left/ {\vphantom {{{c_i}{T_{\min }}} }} \right. } }$ α（α取6—10），其中ci为第i层土层的剪切波速，Tmin为具有工程意义的输入波的最短周期。而采用本文提出的集中质量切比雪夫谱元法时，经过试算发现一般情况下谱单元阶次n取4即可取得良好的精度，此时谱单元尺寸取$\Delta {{\textit{z}}_i} {\text{≤}} {c_i}{T_{\min }}$ 即可，单元尺寸明显大于传统有限单元法。本文采用的中心差分法为有条件稳定算法，时间步距∆t需要满足稳定性要求
$$ \Delta t {\text{≤}} {\alpha _{{\rm{CFL}}}}\frac{{{{\rm{d}}{\rm{z}}_{\min }}}}{{{c_{\max }}}}{\text{，}} $$ (22) 式中：dzmin为模型网格中任意两个节点之间的最小距离，cmax为最大剪切波速；αCFL为无量纲的库朗-弗雷德里奇-李维（Courant-Friedrichs-Lewy，缩写为CFL）条件数，本文将其取为0.75可保证数值结果始终稳定。
4. 算例分析
4.1 均匀半空间土体地震反应分析
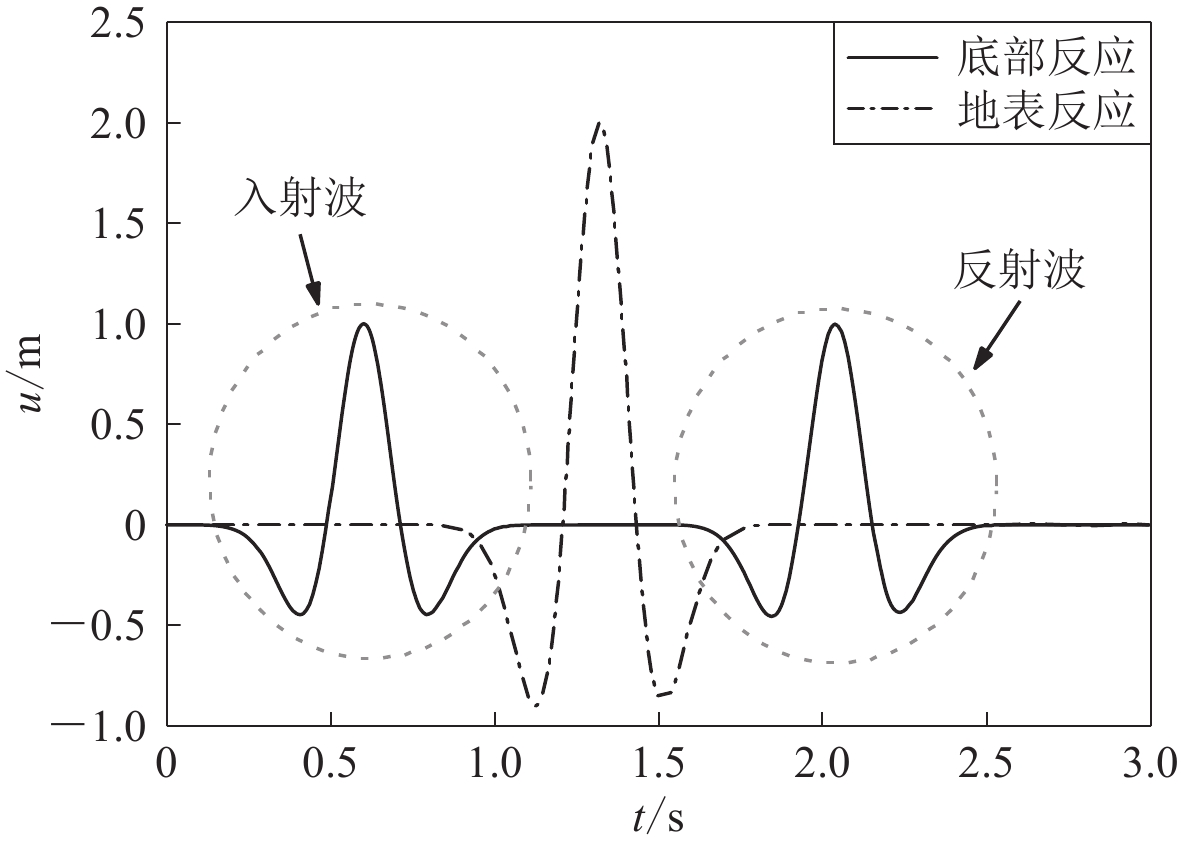
为了检验本文方法的正确性，首先对一个均匀半空间场地模型进行分析，根据行波理论得到其解析解。该模型土体厚度为180 m，土体质量密度为2000 kg/m3，剪切波速为250 m/s。底部设置一阶MTF人工边界，垂直向上输入幅值为1 m、主频为2 Hz的雷克（Ricker）波位移脉冲。将整个模型划分为8个4阶谱单元，则单元尺寸约为输入波最短波长的一半。图3显示了土层底部和地表的位移反应时程，其中底部反应时程的第一个波峰为入射波，第二个波峰为地表反射波。由图可知，入射波从底部传至地表时间约为0.7 s，与解析解吻合，同时，地表位移反应峰值等于入射波峰值的2倍，符合自由地表条件。此外，地表未出现模型底部反射而来的地震波，说明MTF人工边界条件成功实现。本例表明集中质量切比雪夫谱元法能够处理土层地震反应分析问题，而且在网格较为稀疏的情况下依然能够获得较高的计算精度。
![]()
图 3 均匀半空间模型在雷克波入射下的地表和底部位移反应Figure 3. Displacement responses of ground surface and bottom of a homogeneous half-space model under Ricker wave incidence4.2 Kik-net台站记录模拟
利用日本Kik-net强震观测台网（NIED，2021）提供的实测地震动记录和钻孔数据检验本文方法处理实际场地地震反应分析的能力。从Kik-net台网中随机选取4个具有代表性的台站，分别对应中国《GB 50011—2010 建筑抗震设计规范》（中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局，2010）所定义的Ⅰ1，Ⅱ ，Ⅲ和Ⅳ等四类场地。在每个台站中选择实测地面峰值加速度（peak ground acceleration，缩写为PGA）等于0.05—0.1g，0.1—0.2g和0.2—0.4g的EW向或NS向地震记录各一条，分别对应较弱地震动、中等强度地震动和较强地震动。以井下实测记录作为一维水平成层场地模型底部的基岩输入波，计算地表加速度反应并与地表实测加速度记录进行对比。由于Kik-net数据库中未提供土体质量密度数据，本文利用Boore （2016）提出的公式根据P波波速和剪切波速估算土体密度。各台站的土层剖面剪切波速如图4所示，按照《GB 50011—2010建筑抗震设计规范》计算得到的基本信息列于表2。
![]()
图 4 四个Kik-net台站的土层剪切波速图Figure 4. Shear wave velocity profiles at the four Kik-net stations表 2 选用Kik-net台站的基本信息Table 2. Basic information of selected Kik-net stations台站名称 覆盖层厚度/m 等效剪切波速/（m·s−1） 场地类别 TCGH08 2 170 Ⅰ1 MYGH10 34 330 Ⅱ KMMH14 88 200 Ⅲ IKRH02 ＞108 112 Ⅳ 4个台站在不同强度地震作用下地表的加速度时程反应，如图5所示。可见，在多数情况下，本文方法计算得到的地表加速度时程与实测的地表加速度记录均能较好吻合。与输入的基岩实测加速度时程相比，所有台站的地表计算反应均显示出了土层的放大效应。即便对于IKRH02台站这样覆盖层厚度超过100 m的深厚场地，也依然体现出了土层的放大效应，未出现类似土层时域非线性软件DEEPSOIL严重低估地表反应的问题（袁晓铭等，2016）。
![]()
图 5 不同强度地震动作用下四个台站地表加速度反应时程（a） 较弱地震动；（b） 中等强度地震动；（c） 较强地震动Figure 5. Ground acceleration response histories of four stations under ground motions with different intensities（a） Weak ground motions；（b） Moderate ground motions； （c） Strong ground motions表3给出了按本文方法计算得到的PGA与地震中实际记录PGA的对比。由表中数据可知，对于Ⅱ类场地（MYGH10），本文预测PGA最接近实际值，误差小于2.1%。但对于Ⅲ类场地（KMMH14），本文方法计算得到的PGA大于实测值。总体而言，本文方法计算得到的PGA总是稍小于或偏大于实际值，而未出现严重偏小的情况。表4列出了本文计算得到的PGA放大倍数及实际测得的PGA放大倍数。所选台站的实测放大倍数介于3.28—7.40之间不等，而计算放大倍数在3.67—10.48之间不等。对于Ⅰ 1类场地（TCGH08）、 Ⅱ 类场地（MYGH10）和Ⅳ类场地（IKRH02）在小震和中震情况下本文方法得到的PGA放大倍数均与实测值相差不大，但在大震情况下本文结果偏大。
表 3 不同强度地震动作用下各台站计算PGA与实测PGA对比Table 3. Comparison of computed PGA and recorded PGA for the stations under ground motions different intensities台站名称 较弱地震动 中等强度地震动 较强地震动 计算PGA/g 实测PGA/g 计算PGA/g 实测PGA/g 计算PGA/g 实测PGA/g TCGH08 0.090 0.065 0.142 0.145 0.226 0.204 MYGH10 0.066 0.067 0.154 0.156 0.240 0.235 KMMH14 0.121 0.083 0.227 0.144 0.369 0.228 IKRH02 0.082 0.084 0.102 0.104 0.329 0.227 表 4 不同强度地震动作用下各台站PGA放大倍数Table 4. Amplification factors of PGA for the stations under ground motions different intensities台站名称 较弱地震动 中等强度地震动 较强地震动 井下实测
峰值/g计算放大
倍数实测放大
倍数井下实测
峰值/g计算放大
倍数实测放大
倍数井下实测
峰值/g计算放大
倍数实测放大
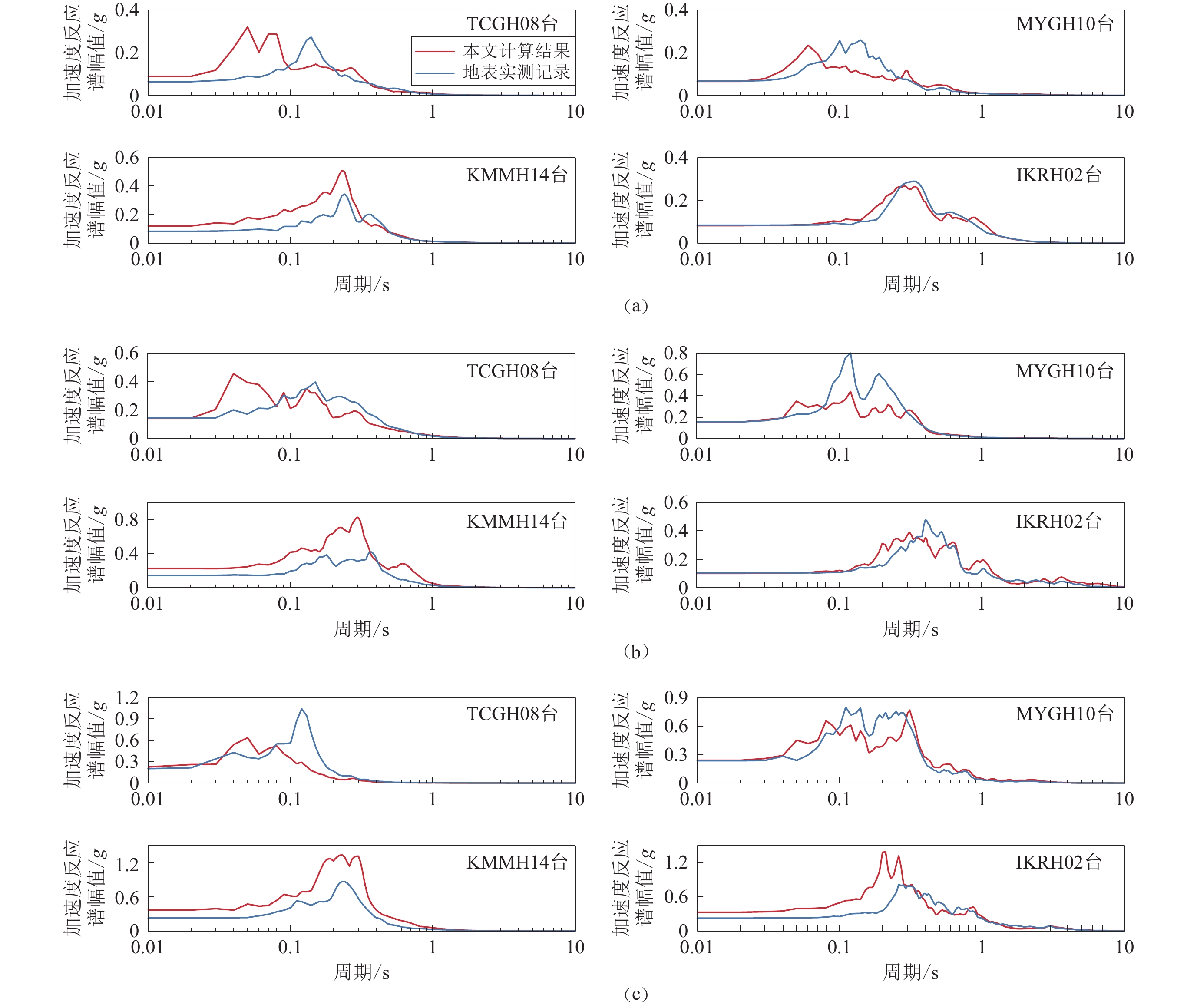
倍数TCGH08 0.015 5.96 4.31 0.037 3.80 3.89 0.028 8.21 7.40 MYGH10 0.016 4.14 4.22 0.042 3.67 3.71 0.065 3.69 3.62 KMMH14 0.016 7.36 5.07 0.031 7.36 4.69 0.035 10.48 6.48 IKRH02 0.018 4.54 4.63 0.023 4.45 4.55 0.069 4.75 3.28 图6为4个台站在不同强度的地震作用下的地表加速度反应谱，阻尼比按5%计算.总体而言，本文计算反应谱在低频段（周期＞0.5 s）与实测记录的反应谱较为接近。观察图6可知，在较弱的地震作用下，Ⅰ1和 Ⅱ 类场地的反应谱峰值与实测记录相近，而Ⅲ和Ⅳ类场地的反应谱形状与实测值吻合，其中Ⅳ类场地的计算反应谱曲线与实测反应谱十分接近。在中等强度地震作用下，Ⅰ1和Ⅳ类场地的反应谱峰值与实测记录较为吻合。在较强地震作用下，本文计算反应谱曲线的形状大致与实测记录得到的反应谱一致，但对于Ⅲ和Ⅳ类场地计算得到的反应谱峰值比观测结果偏大.
![]()
图 6 不同强度地震动作用下四个台站的地表加速度反应谱（a） 较弱地震动；（b） 中强地震动；（c） 较强地震动Figure 6. Ground acceleration response spectra of four stations under ground motions with different intensities（a） Weak ground motions；（b） Moderate ground motion； （c） Strong ground motions造成本文计算结果与实际台阵记录存在一定差异的原因可能有：① 本文采用的一维水平成层场地模型是一种高度简化的计算模型，无法反映出实际三维场地的地形特征，因此一维波动的数值计算结果一般无法体现出对实际场地地震动有重要影响的地形放大效应；② 实际场地并不一定仅受剪切波作用，还有可能受到纵波、面波等多种地震波的作用，并且地震波的传播方向也不一定恰好垂直向上的；③ 本文方法未考虑土体的非线性特性。
5. 结论
本文提出了一种求解水平成层场地地震反应的时域集中质量切比雪夫谱元法。通过节点积分法严格地导出集中质量矩阵，克服了传统切比雪夫谱元法由于质量矩阵为非对角矩阵形式所带来的计算效率不高的问题。采用中心差分法进行时间积分，并嵌入多次透射人工边界，形成了高效的时域显式算法。与传统有限单元法相比，该方法在每个波长内仅需布置一个谱单元即可获得令人满意的计算精度，显著降低了对空间网格尺寸的要求.
选择日本Kik-net强震台网中分属四种不同场地类型的台站记录检验了本文方法处理实际场地的能力。计算结果表明，本文方法对于Ⅰ 1，Ⅱ和Ⅳ类场地在较弱地震和中等强度地震作用下能够较好地预测地面运动特征，但对于Ⅲ类场地及强震作用下的地表反应计算结果与观测结果相比仍存在一定误差，后续工作中可考虑添加土体的时域非线性本构关系.
-
![]()
图 1 水平成层场地切比雪夫谱元模型
Figure 1. Chebyshev spectral element model of horizontal layered soil site
![]()
图 2 切比雪夫谱单元的一阶MTF插值方案
Figure 2. Interpolation scheme for first-order MTF in Chebyshev spectral element
![]()
图 3 均匀半空间模型在雷克波入射下的地表和底部位移反应
Figure 3. Displacement responses of ground surface and bottom of a homogeneous half-space model under Ricker wave incidence
![]()
图 4 四个Kik-net台站的土层剪切波速图
Figure 4. Shear wave velocity profiles at the four Kik-net stations
![]()
图 5 不同强度地震动作用下四个台站地表加速度反应时程
（a） 较弱地震动；（b） 中等强度地震动；（c） 较强地震动
Figure 5. Ground acceleration response histories of four stations under ground motions with different intensities
（a） Weak ground motions；（b） Moderate ground motions； （c） Strong ground motions
![]()
图 6 不同强度地震动作用下四个台站的地表加速度反应谱
（a） 较弱地震动；（b） 中强地震动；（c） 较强地震动
Figure 6. Ground acceleration response spectra of four stations under ground motions with different intensities
（a） Weak ground motions；（b） Moderate ground motion； （c） Strong ground motions
表 1 GLC节点上的高斯−洛巴托积分权系数
Table 1 Gauss-Lobatto quadrature weights based on GLC points
谱单元阶次 GLC节点坐标 积分权系数 1 ±1 1 2 ±1, 0 0.333 3, 1.333 3 3 ±1, ±0.5 0.111 1, 0.888 9 4 ±1, ±0.707 1, 0 0.066 7, 0.533 3, 0.8 5 ±1, ±0.809 0, ±0.309 0 0.04, 0.360 7, 0.599 3 
下载: 导出CSV
表 2 选用Kik-net台站的基本信息
Table 2 Basic information of selected Kik-net stations
台站名称 覆盖层厚度/m 等效剪切波速/（m·s−1） 场地类别 TCGH08 2 170 Ⅰ1 MYGH10 34 330 Ⅱ KMMH14 88 200 Ⅲ IKRH02 ＞108 112 Ⅳ
下载: 导出CSV
表 3 不同强度地震动作用下各台站计算PGA与实测PGA对比
Table 3 Comparison of computed PGA and recorded PGA for the stations under ground motions different intensities
台站名称 较弱地震动 中等强度地震动 较强地震动 计算PGA/g 实测PGA/g 计算PGA/g 实测PGA/g 计算PGA/g 实测PGA/g TCGH08 0.090 0.065 0.142 0.145 0.226 0.204 MYGH10 0.066 0.067 0.154 0.156 0.240 0.235 KMMH14 0.121 0.083 0.227 0.144 0.369 0.228 IKRH02 0.082 0.084 0.102 0.104 0.329 0.227
下载: 导出CSV
表 4 不同强度地震动作用下各台站PGA放大倍数
Table 4 Amplification factors of PGA for the stations under ground motions different intensities
台站名称 较弱地震动 中等强度地震动 较强地震动 井下实测
峰值/g计算放大
倍数实测放大
倍数井下实测
峰值/g计算放大
倍数实测放大
倍数井下实测
峰值/g计算放大
倍数实测放大
倍数TCGH08 0.015 5.96 4.31 0.037 3.80 3.89 0.028 8.21 7.40 MYGH10 0.016 4.14 4.22 0.042 3.67 3.71 0.065 3.69 3.62 KMMH14 0.016 7.36 5.07 0.031 7.36 4.69 0.035 10.48 6.48 IKRH02 0.018 4.54 4.63 0.023 4.45 4.55 0.069 4.75 3.28
下载: 导出CSV
-
丁海平,周正华. 1998. 土层地震反应的数值模拟[J]. 世界地震工程,14(3):26–31. Ding H P,Zhou Z H. 1998. Numerical simulation of seismic response of soil layers[J]. World Information on Earthquake Engineering,14(3):26–31 (in Chinese).
高武平,高孟潭,陈学良. 2012. 天津滨海软土场地的大震远场作用[J]. 地震学报,34(2):235–243. Gao W P,Gao M T,Chen X L. 2012. Far-field strong earthquake effect in Tianjin coastal soft site[J]. Acta Seismologica Sinica,34(2):235–243 (in Chinese).
李平,薄景山,齐文浩,刘德东,肖瑞杰. 2012. 土层结构对汉源烈度异常的影响[J]. 地震学报,34(6):851–857. Li P,Bo J S,Qi W H,Liu D D,Xiao R J. 2012. Effects of soil structure on abnormal intensity in Hanyuan old town[J]. Acta Seismologica Sinica,34(6):851–857 (in Chinese).
廖振鹏. 1989. 地震小区划: 理论与实践[M]. 北京: 地震出版社: 250−265. Liao Z P. 1989. Seismic Microzonation: Theory and Application[M]. Beijing: Seismological Press: 250−265 （in Chinese）.
廖振鹏. 2002. 工程波动理论导论[M]. 2版. 北京: 科学出版社: 59−63. Liao Z P. 2002. Introduction to Wave Motion Theories in Engineering[M]. 2nd ed. Beijing: Science Press: 59−63 （in Chinese）.
栾茂田,林皋. 1992. 场地地震反应一维非线性计算模型[J]. 工程力学,9(1):94–103. Luan M T,Lin G. 1992. Computational model for nonlinear analysis of soil site seimic response[J]. Engineering Mechanics,9(1):94–103 (in Chinese).
齐文浩,薄景山. 2007. 土层地震反应等效线性化方法综述[J]. 世界地震工程,23(4):221–226. Qi W H,Bo J S. 2007. Summarization on equivalent linear method of seismic responses for soil layers[J]. World Earthquake Engineering,23(4):221–226 (in Chinese).
孙锐,袁晓铭. 2021. 全局等效线性化土层地震反应分析方法[J]. 岩土工程学报,43(4):603–612. Sun R,Yuan X M. 2021. Holistic equivalent linearization approach for seismic response analysis of soil layers[J]. Chinese Journal of Geotechnical Engineering,43(4):603–612 (in Chinese).
王志良,韩清宇. 1981. 粘弹塑性土层地震反应的波动分析法[J]. 地震工程与工程振动,1(1):117–137. Wang Z L,Han Q Y. 1981. Analysis of wave propagation for the site seismic response,using the viscoelastoplastic model[J]. Earthquake Engineering and Engineering Vibration,1(1):117–137 (in Chinese).
邢浩洁,李鸿晶,杨笑梅. 2017. 基于切比雪夫谱元模型的成层场地地震反应分析[J]. 岩土力学,38(2):593–600. Xing H J,Li H J,Yang X M. 2017. Seismic response analysis of horizontal layered soil sites based on chebyshev spectral element model[J]. Rock and Soil Mechanics,38(2):593–600.
袁晓铭,李瑞山,孙锐. 2016. 新一代土层地震反应分析方法[J]. 土木工程学报,49(10):95–102. Yuan X M,Li R S,Sun R. 2016. A new generation method for earthquake response analysis of soil layers[J]. China Civil Engineering Journal,49(10):95–102 (in Chinese).
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 2010. GB 50011—2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社: 18–20. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. 2010. GB 50011−2010 Code for Seismic Design of Buildings[S]. Beijing: China Architecture & Building Press: 18–20 （in Chinese）.
Boore D M. 2016. Determining generic velocity and density models for crustal amplification calculations,with an update of the Boore and Joyner (1997) generic site amplification for`VS(Z)=760 m/s[J]. Bull Seismol Soc Am,106(1):313–317. doi: 10.1785/0120150229
Fried I,Malkus D S. 1975. Finite element mass matrix lumping by numerical integration with no convergence rate loss[J]. Int J Solids Struct,11(4):461–466. doi: 10.1016/0020-7683(75)90081-5
Hinton E,Rock T,Zienkiewicz O C. 1976. A note on mass lumping and related processes in the finite element method[J]. Earthq Eng Struct Dyn,4(3):245–249. doi: 10.1002/eqe.4290040305
Idriss I M,Seed H B. 1968. Seismic response of horizontal soil layers[J]. J Soil Mech Found Div,94(4):1003–1031. doi: 10.1061/JSFEAQ.0001163
Liao Z P,Wong H L. 1984. A transmitting boundary for the numerical simulation of elastic wave propagation[J]. Int J Soil Dyn Earthq Eng,3(4):174–183.
National Research Institute for Earth Science and Disaster Resilience （NIED）. 2021. Strong-motion seismograph networks（K-NET, Kik-net）[EB/OL]. [2021-05-10]. http://www.kyoshin.bosai.go.jp/.
Thomson W T,Calkins T,Caravani P. 1974. A numerical study of damping[J]. Earthq Eng Struct Dyn,3(1):97–103. doi: 10.1002/eqe.4290030108
Zalachoris G,Rathje E M. 2015. Evaluation of one-dimensional site response techniques using borehole arrays[J]. J Geotech Geoenviron Eng,141(12):04015053. doi: 10.1061/(ASCE)GT.1943-5606.0001366
Zienkiewicz O C, Taylor R L, Zhu J Z. 2013. The Finite Element Method: Its Basis and Fundamentals[M]. 7th ed. London: Elsevier: 383–386.
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 283
- HTML全文浏览量: 87
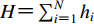
- PDF下载量: 42
- 被引次数: 1
