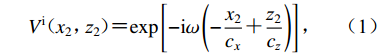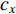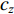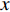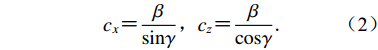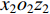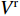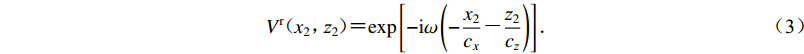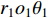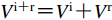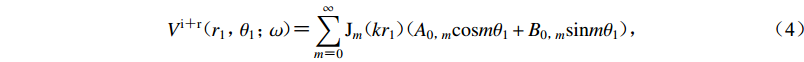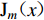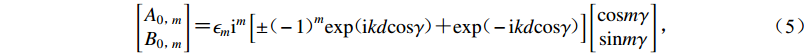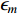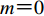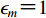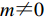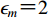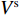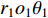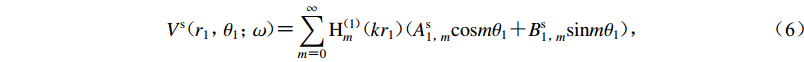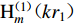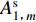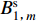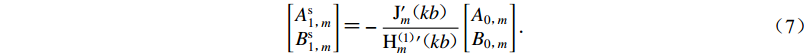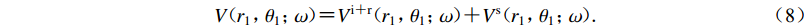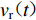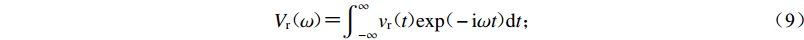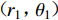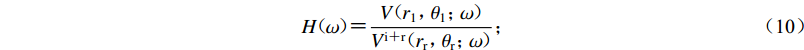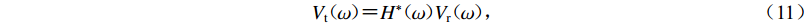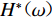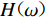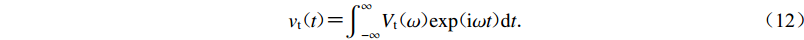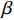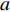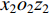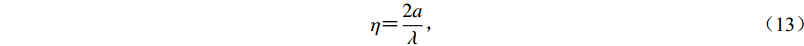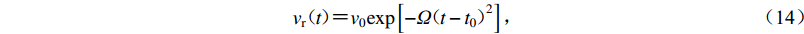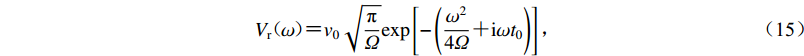Analytical solution to the transient response of arc-shaped canyon incident by plane SH wave
-
摘要: 针对现有地震波散射问题的解析解均在频域内给出,其适用的频带较窄,不能获取到可靠的瞬态反应解析解的问题,本文利用宽频带频域解析解进一步获取了不同空间点地震反应的宽频带频响函数,并基于傅里叶变换得出SH波入射下圆弧形凹陷地形瞬态动力响应的解析解。以上述为基础,研究了输入脉冲与实际地震动时凹陷的瞬态反应的基本特征,并重点分析了凹陷对地震动的放大效应,该效应定义为凹陷周围不同空间点的地震反应参数,如其峰值和反应谱等与自由场(即弹性半空间)地震反应参数之间的比值。结果表明:输入脉冲时,凹陷角点位移幅值显著放大,该放大效应与入射角度和脉冲持时有关;输入实际地震动时,凹陷迎波面角点反应谱放大显著,地震动反应谱比最大值可高达2.0,且放大效应与凹陷几何参数和入射角度等因素有关。Abstract: The existing analytical solutions to scattering of seismic waves are presented in the frequency domain and valid only in narrow frequency band, from which the reliable transient solution cannot be obtained. Addressing this problem, this paper used the broad-band frequency-rdomain analytical solution to obtain the broad-band frequency-esponse function for different spatial locations, and by Fourier transform, presented the analytical solution to the transient response of canyon topography SH wave incidence. Based on this, this paper studied the fundamental characteristics of transient response of canyon under the inputs of impulses and real ground motions, with the emphasis on the amplifying effect of the canyon on ground motion. This effect was defined by the ratio between the parameters, such as the peak and the spectral acceleration, etc., of seismic responses around the canyon, to those of seismic responses of free field, i.e. the elastic half-space. It was demonstrated that, under the impulse input, the displacement of the canyon corner was amplified distinctly, which was related to the impulse duration and the incident angle. As to the input of real ground motion, the spectral acceleration on the corner at the incident side of canyon is significantly amplified, with the maximum spectral ratio being as high as 2.0, which is related to the canyon geometries and the incident angle.
-
Keywords:
- plane SH wave /
- canyon topography /
- scattering /
- analytical solution /
- response spectrum
-
引言
研究规则凹陷地形对地震波散射问题解析解可以为局部地形对地震动的影响效应提供量化的估计,也可以用于标定数值方法的计算精度(廖振鹏,2002)。Trifunac (1972)与Wong和Trifunac (1974)分别利用波函数的傅里叶-贝塞尔级数展开法和马修级数展开法得出了半圆形凹陷和半椭圆形凹陷对SH波散射问题的解析解。相比半圆形和半椭圆形,具有不同深宽比的浅圆形在模拟实际凹陷几何状态时具有更大的灵活性。Cao和Lee (1989)与Yuan和Liao (1994)利用傅里叶-贝塞尔级数展开法,分别基于内域型和外域型格拉夫加法公式得出了具有不同深宽比的浅圆形凹陷在SH波入射下稳态反应的解析解。其中,Cao和Lee (1989)采用的近似方法,是利用一个半径非常大的圆弧近似模拟水平地表,被用于求解单一凹陷(Cao,Lee,1990)、层状凹陷(梁建文等,2001;2002;2003;Zhang,2010)以及饱和介质中凹陷地形对地震波的散射问题(Li,Zhao,2005;巴振宁等,2010)。通过利用大圆弧面近似模拟水平地表,梁建文等求解了三维空间中沉积谷地对P波(梁建文等,2010)、SV波(梁建文等,2009a)和瑞雷波(梁建文等,2009b)的散射问题。
上述求解方法均是将散射波展开成无穷级数的形式,引入问题边界条件,形成关于级数中待定系数的线性方程组,求解方程组最终得到散射问题的级数形式解析解。此外,现有工作均是在频域内给出散射问题的稳态解析解,可以很好地研究凹陷地形对地震动傅里叶谱分量的放大效应。而地震工程中更受关注的是地震动的反应谱,研究凹陷地形对地震动反应谱的放大效应更具工程意义。尽管地震动反应谱与傅里叶谱之间存在定性的对应关系,并且在特殊条件下还存在一定的定量关系,但相较于傅里叶谱,由于地震动反应谱考虑了相邻频率分量的影响,反应谱具有“平滑”效应(胡聿贤,2006),因而不能将凹陷地形对傅里叶谱放大效应的结果直接用于评估其对地震动反应谱的放大效应。而研究凹陷地形对地震动反应谱的放大必须借助散射问题瞬态反应的解析解,即时域解析解。
事实上,利用傅里叶变换可以容易地获取瞬态反应的解析解。但是,随着入射地震波频率的增加,稳态级数解收敛所需的截断项数随之增大,数值计算问题将导致上述线性方程组无法成功求解。因此,现有大部分稳态解析解研究的无量纲频率η (凹陷宽度与入射地震波波长之比)最大值不超过3。对于较大规模的凹陷地形,此频带范围在大部分情况下无法获得合理的时域瞬态解,从而无法应用在对工程有影响的高频范围内合理地评估凹陷地形对地震动反应谱的放大效应。
通过对求解技术的改进,梁建文等(2004)获得了含隧洞凸起地形对高频入射波(η=10)的解答,并将该方法用于求解凹陷对瑞雷波的散射问题,给出了η=10的高频稳态解析解(梁建文等,2005)。杨彩红(2009)则通过选择求解极坐标系,避免了线性方程组的求解,得到了圆弧状凹陷对SH波散射问题的宽频带稳态解析解,其研究的无量纲频率η高达30。本文延续了该项研究工作,拟利用该宽频带稳态解析解,通过傅里叶变换得到圆弧凹陷地形在SH波入射下瞬态反应的解析解,并以此为基础,研究凹陷地形对地震动反应谱的放大效应。以期为深入认识局部地形对地震动放大效应提供相关参考,并将研究结果应用于对数值方法计算结果进行验证和标定。
1. 瞬态响应解析解
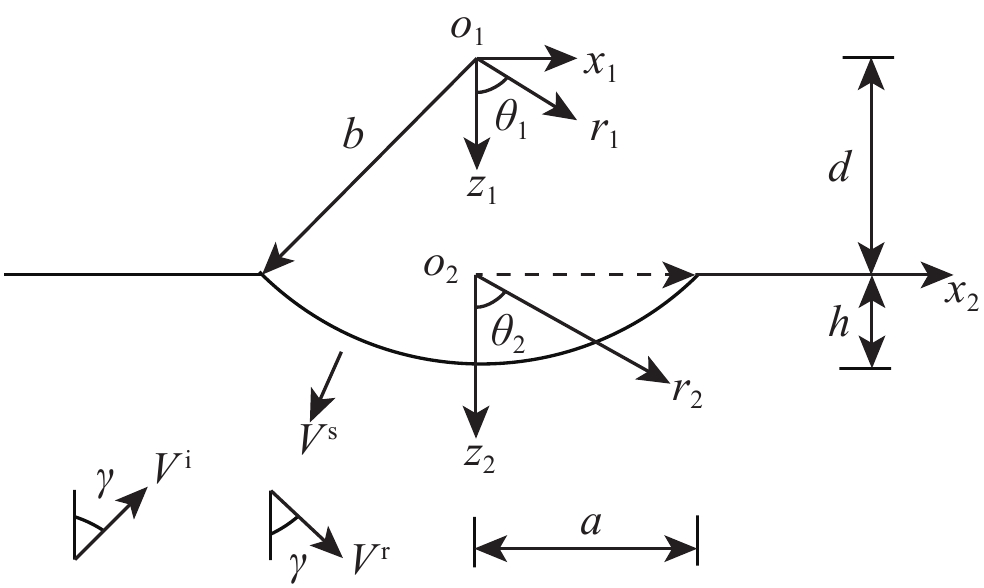
凹陷地形的模型如图1所示。将半空间介质性质假定为均匀、线弹性、各向同性,剪切波速为
$\; \beta $ ,密度为$ \;\rho $ 。凹陷表面为一圆弧,其圆心为点$ {{o}}_{1} $ ,半径为$ b $ ,凹陷的半宽为$ a $ ,深度为$ h $ ,圆心$ {{o}}_{1} $ 与地表之间的垂直距离为$ d $ 。入射SH波的幅值为1、圆频率为$ \omega $ 、入射角为$ \gamma $ ,其稳态位移在坐标系${x}_{2}{{o}}_{2}{{\textit{z}}}_{2}$ 下的表达式为$$ {V}^{\mathrm{i}}({x}_{2}{\text{,}}{{\textit{z}}}_{2}){\text{=}}\mathrm{exp}\left[-\text{i}\omega \left(-\frac{{x}_{2}}{{c}_{x}}{\text{+}}\frac{{{\textit{z}}}_{2}}{{c}_{{\textit{z}}}}\right)\right]{\text{,}} $$ (1) 式中,
$ {c}_{x} $ 和${c}_{{\textit{z}}}$ 分别为$ x $ 和z方向上的相速度,即$$ {c}_{x}{\text{=}}\frac{\beta }{\mathrm{s}\mathrm{i}\mathrm{n}\gamma }{\text{,}}{c}_{{\textit{z}}}{\text{=}}\frac{\beta }{\mathrm{c}\mathrm{o}\mathrm{s}\gamma } {\text{.}} $$ (2) 在坐标系
${x}_{2}{o_2}{{\textit{z}}}_{2}$ 下,反射波$ {V}^{\mathrm{r}} $ (图1)的稳态位移表达式$$ {V}^{\mathrm{r}}({x}_{2}{\text{,}}{{\textit{z}}}_{2}){\text{=}}\mathrm{exp}\left[-{\rm{i}}\omega \left(-\frac{{x}_{2}}{{c}_{x}}{\text{-}}\frac{{{\textit{z}}}_{2}}{{c}_{{\textit{z}}}}\right)\right]{\text{.}} $$ (3) 在极坐标系
${r}_{1}{o_1}{\theta }_{1}$ 下,整个自由场位移${V}^{\mathrm{i}{\text{+}}\mathrm{r}}{\text{=}}{V}^{\mathrm{i}}{\text{+}}{V}^{\mathrm{r}}$ 可表示为傅里叶-贝塞尔级数形式(杨彩红,2009),具体表达式如下:$$ {V}^{\mathrm{i}{\text{+}}\mathrm{r}}({r}_{1}{\text{,}}{\theta }_{1}{\text{;}}\omega ){\text{=}}\sum _{m{\text{=}}0}^{\infty }{\mathrm{J}}_{m}(k{r}_{1})({A}_{0{\text{,}}m}\mathrm{cos}m{\theta }_{1}+{B}_{0{\text{,}}m}\mathrm{sin}m{\theta }_{1}) {\text{,}}$$ (4) 其中,
${\mathrm{J}}_{m}(x)$ 为第一类贝塞尔函数,且有$$ \left[\begin{array}{c}{A}_{0{\text{,}}m}\\ {B}_{0{\text{,}}m}\end{array}\right]{\text{=}}{\mathrm{\epsilon }}_{m}{\mathrm{i}}^{m}\left[\pm {(-1)}^{m}\mathrm{exp}(\mathrm{i}kd\mathrm{cos}\gamma ){\text{+}}\mathrm{exp}(-\mathrm{i}kd\mathrm{cos}\gamma )\right]\left[\begin{array}{c}\mathrm{cos}m\gamma \\ \mathrm{sin}m\gamma \end{array}\right]{\text{,}} $$ (5) 式中,
$ {\mathrm{\epsilon }}_{m} $ 为标识符号,当$m{\text{=}}0$ 时,${\mathrm{\epsilon }}_{m}{\text{=}}1$ ,当$m{\text{≠}} 0$ 时,${\mathrm{\epsilon }}_{m}{\text{=}}2$ ;圆波数k=ω/β。由于凹陷地形的存在,半空间介质中存在散射波
$ {V}^{\mathrm{s}} $ (图1),在极坐标系${r}_{1}{o_1}{\theta }_{1}$ 下可展开成级数形式$$ {V}^{\mathrm{s}}({r}_{1}{\text{,}}{\theta }_{1}{\text{;}}\omega ){\text{=}}\sum _{m{\text{=}}0}^{\infty }{\mathrm{H}}_{m}^{(1)}(k{r}_{1})({A}_{1{\text{,}}m}^{\mathrm{s}}\mathrm{cos}m{\theta }_{1}{\text{+}}{B}_{1{\text{,}}m}^{\mathrm{s}}\mathrm{sin}m{\theta }_{1}){\text{,}} $$ (6) 式中,
${\mathrm{H}}_{m}^{(1)}(k{r}_{1})$ 为第一类汉克尔函数。根据杨彩红(2009)的推导,系数${A}_{1{\text{,}}m}^{\mathrm{s}}$ 和${B}_{1{\text{,}}m}^{\mathrm{s}}$ 计算为$$ \left[\begin{array}{c}{A}_{1{\text{,}}m}^{\mathrm{s}}\\ {B}_{1{\text{,}}m}^{\mathrm{s}}\end{array}\right]{\text{=}}-\frac{{\mathrm{J}}_{m}'(kb)}{{\mathrm{H}}_{m}^{(1)}{'}(kb)}\left[\begin{array}{c}{A}_{0{\text{,}}m}\\ {B}_{0{\text{,}}m}\end{array}\right]{\text{.}} $$ (7) 利用式(4)和(6),可以计算在圆频率为
$ \omega $ 的谐波入射下,任意空间点(r1,θ1)的稳态位移反应$$ V({r}_{1}{\text{,}}{\theta }_{1}{\text{;}}\omega ){\text{=}}{V}^{\mathrm{i}{\text{+}}\mathrm{r}}({r}_{1}{\text{,}}{\theta }_{1}{\text{;}}\omega ){\text{+}}{V}^{\mathrm{s}}({r}_{1}{\text{,}}{\theta }_{1}{\text{;}}\omega ){\text{.}} $$ (8) 在计算瞬态反应时,首先给定一参考空间点
$({r}_{\mathrm{r}}{\text{,}}{\theta }_{\mathrm{r}})$ 处自由场的位移时间过程${v}_{\mathrm{r}}(t)$ ,其傅里叶变换为$$ {V}_{\mathrm{r}}(\omega ){\text{=}}{\int }_{-\infty }^{\infty }{v}_{\mathrm{r}}(t)\mathrm{exp}(-\mathrm{i}\omega t)\mathrm{d}t{\text{;}}$$ (9) 其次,确定凹陷存在条件下任意空间点
$({r}_{1}{\text{,}}{\theta }_{1})$ 的运动与上述参考点自由场运动之间的传递函数$$ H(\omega ){\text{=}}\frac{V({r}_{1}{\text{,}}{\theta }_{1}{\text{;}}\omega )}{{V}^{\mathrm{i}{\text{+}}\mathrm{r}}({r}_{\mathrm{r}}{\text{,}}{\theta }_{\mathrm{r}}{\text{;}}\omega )}{\text{;}}$$ (10) 进而,任意空间点瞬态动力响应的傅里叶变换可表示为
$$ {V}_{\mathrm{t}}(\omega ){\text{=}}{H}^{*}(\omega ){V}_{\mathrm{r}}(\omega ){\text{,}} $$ (11) 式中,
${H}^{*}(\omega )$ 表示$H(\omega )$ 的共轭复数;最后,任意空间点瞬态动力响应的时间过程可利用傅里叶逆变换确定,即$$ {v}_{\mathrm{t}}(t){\text{=}}{\int }_{-\infty }^{\infty }{V}_{\mathrm{t}}(\omega )\mathrm{exp}(\mathrm{i}\omega t)\mathrm{d}t{\text{.}}$$ (12) 2. 结果分析
以下所有算例中,半空间介质的剪切波速
$ \;\beta $ 均取为1 000 m/s,凹陷的半宽$ a $ 取为500 m;坐标系$ {x}_{2}{o_2}{{\textit{z}}}_{2} $ 下参考点坐标为(−3a,0)。需要指出的是,本文仅研究凹陷地形对工程有影响的地表地震动的影响,未涉及对地下地震动的影响。如果将参考点选择在地下,讨论凹陷对地下地震动的影响,将会与地表的谱比结果存在一定的差别。限于篇幅,本文将重点集中在对工程有影响的地表地震动谱比,对于地下地震动的谱比,按照本文提供的思路,可以很容易地开展相关研究工作获取相关的规律。现有稳态解析解的研究工作均采用无量纲频率
$$ \eta {\text{=}}\frac{2a}{\lambda }{\text{,}} $$ (13) 式中,入射地震波波长λ=β/f,因此,η=(2a/β)f。将β=1 000 m/s,a=500 m代入,可知本文算例中,η在数值上与频率f相等。
实际计算时所采用的地震动数据均是离散的时间序列,因此,式(9)和式(12)所示傅里叶积分也采用离散形式,即采用快速傅里叶变换算法进行计算。设离散地震动时间序列的时间步长为Δt,总数据点数为Nd (通常取为2的整数次幂),则计算所考虑的最大频率fmax=1/(2Δt),离散频率间隔Δ f=1/(NdΔt)。在离散的圆频率点ωk=2πkΔ f (k为小于Nd的整数)上,可先后利用快速傅里叶变换处理式(8)得到参考运动的傅里叶谱,利用式(10)和式(11)得到传递函数的值和待求解运动的傅里叶谱。所有频率点上待求解运动的傅里叶谱确定后,即可利用快速傅里叶变换处理式(12),最终获得待求解运动的时域解。
2.1 脉冲输入下凹陷地形瞬态反应
首先,分析脉冲输入下凹陷地表瞬态位移反应的特征。取如下钟形脉冲作为参考点自由场的位移时程
$$ {v}_{\mathrm{r}}(t){\text{=}}{v}_{0}\mathrm{exp}\left[-\varOmega {(t-{t}_{0})}^{2}\right]{\text{,}} $$ (14) 其傅里叶变换具有解析表达式
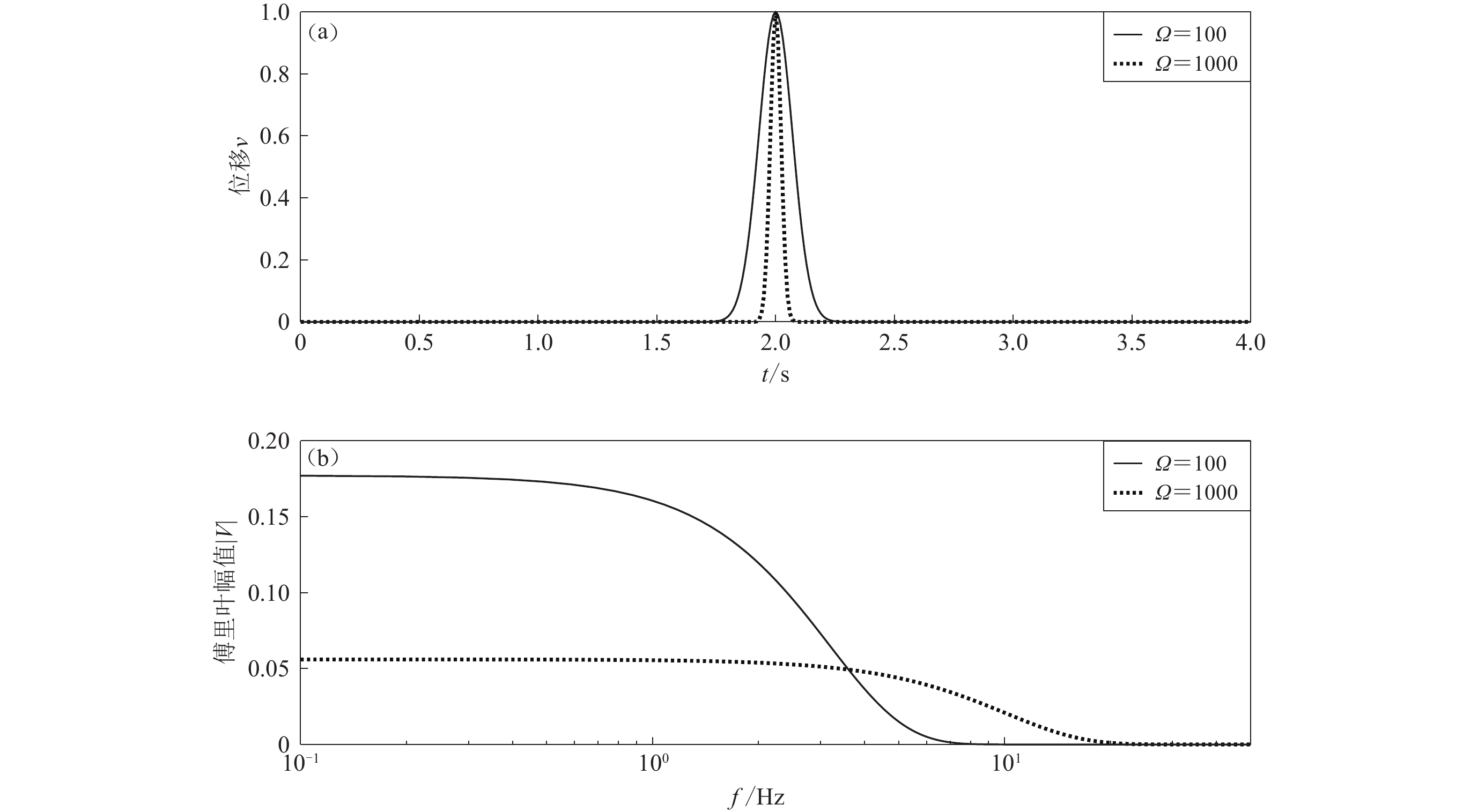
$$ {V}_{\mathrm{r}}(\omega ){\text{=}}{v}_{0}\sqrt{\frac{\mathrm{\pi }}{\varOmega }}\mathrm{exp}\left[-\left(\frac{{\omega }^{2}}{4\varOmega }{\text{+}}\mathrm{i}\omega {t}_{0}\right)\right]{\text{,}} $$ (15) 式中,v0为脉冲幅值,t0为脉冲中心时刻,参数Ω控制脉冲的宽窄,其值越大,脉冲越窄,其傅里叶谱的频带越宽,高频成分越丰富。当Ω分别取为100和1 000时,位移脉冲的波形和傅里叶幅值谱(v0=1.0,t0=2.0 s,离散时间间隔Δt=0.01 s),如图2所示。可以看出,当Ω=100时,脉冲能量主要集中在f<5 Hz (η>5)的频带范围内,而当Ω=1 000时,其脉冲能量则分布在f<20 Hz (η<20)的宽频带范围。
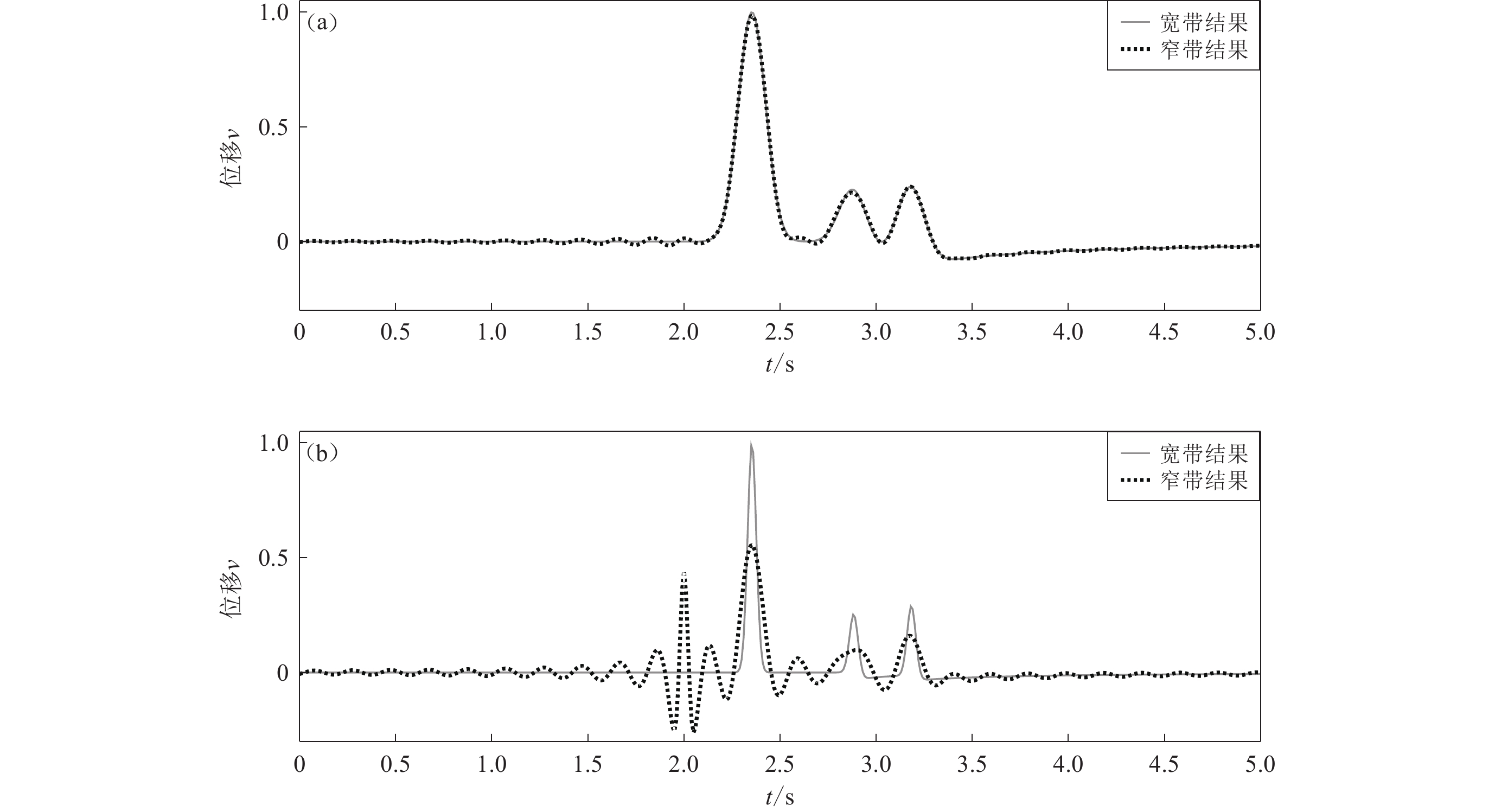
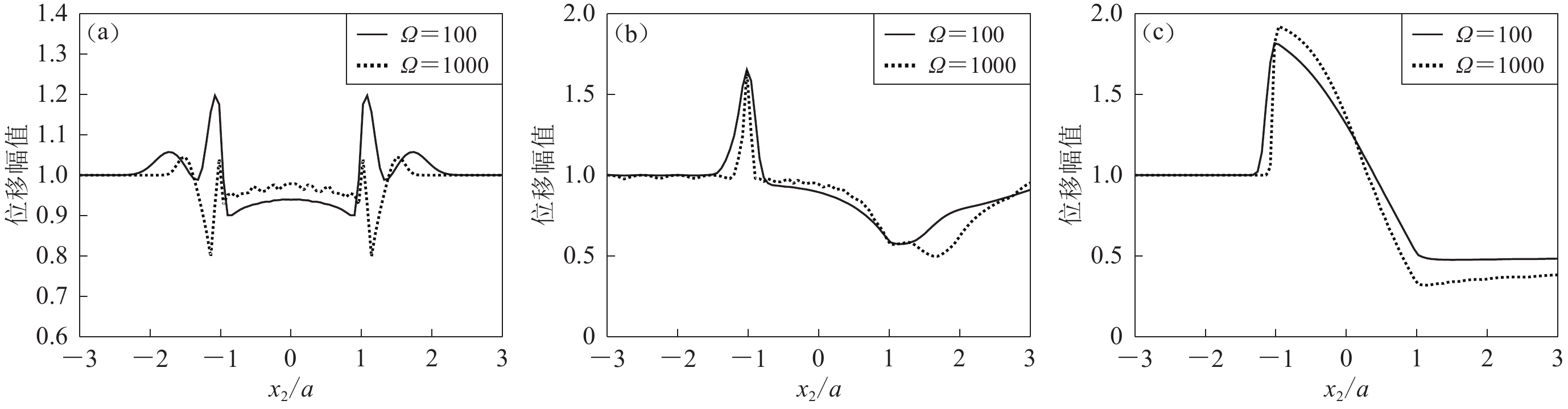
取地震波的入射角γ=45°,凹陷深度h=250 m,参考点自由场的位移时间函数分别取图2所示低频和高频脉冲,计算所得地表点(x2=−2a,z2=0)的位移响应时程(图3灰色实线)。仅考虑η<5的窄带传递函数的计算结果(图3点线),对于η≥5的传递函数取为1.0。可以看出,对于能量集中在窄带范围(Ω=100)内的输入地震波,采用窄带稳态解析解能够满足计算精度要求(图3a);如果输入地震波的能量分布在宽频带范围内(Ω=1 000),依然采用窄带稳态解析解计算瞬态响应就会出现较大偏差(图3b)。而图2b所示的频带5 Hz<f<20 Hz也是对工程有影响的频带范围。因此,要获取可靠的瞬态响应,必需采用宽频带稳态解析解。
![]() 图 3 钟形脉冲输入下给定地表点(x2=−2a,z2=0)的位移响应(a) 低频脉冲响应($\varOmega $=100);(b) 高频脉冲响应($\varOmega $=1 000)Figure 3. Displacement responses of specified surface location (x2=−2a,z2=0) under the inputs of bell-like impulses(a) Low-frequency impulse response ($\varOmega $=100);(b) High-frequency impulse response ($\varOmega $=1 000)
图 3 钟形脉冲输入下给定地表点(x2=−2a,z2=0)的位移响应(a) 低频脉冲响应($\varOmega $=100);(b) 高频脉冲响应($\varOmega $=1 000)Figure 3. Displacement responses of specified surface location (x2=−2a,z2=0) under the inputs of bell-like impulses(a) Low-frequency impulse response ($\varOmega $=100);(b) High-frequency impulse response ($\varOmega $=1 000)入射角γ=0°,45°,90°,凹陷深度h=250 m情况下,Ω取为100和1 000时,不同地表观测点的位移反应时程,如图4所示,可以较为清晰地识别出地震波的传播和散射过程:垂直入射条件下(γ=0°),当入射波传播至凹陷表面时,产生两组显著的反射脉冲,它们传播至参考点(x2=−3a,z2=0)处的时刻分别为2.49 s和2.99 s。而不同入射角条件下,地表瞬态位移反应最大值的分布情况,如图5所示。可以看出:① 凹陷表面的瞬态位移反应幅值低于自由场位移幅值(1.0);② 凹陷角点处,其瞬态位移反应最大值达到较高水平;③ 距离凹陷越远的地表点,其瞬态反应的最大值与自由场相等,但由于反射波(图4)的存在,以致其持时相对较长;④ 入射波频带越窄,凹陷地形对位移幅值的影响范围越大。
在地震波斜入射条件下(γ=45°),当入射波传播至凹陷表面时,将会产生两组显著的反射脉冲,脉冲传播至参考点(x2=−3a,z2=0)处的时刻分别为3.29 s和3.68 s (图4);在地震波掠入射条件下(γ=90°),当入射波传播至凹陷表面时,仅产生一组显著的反射脉冲,其传播至参考点的时刻为3.81 s (图4)。在掠入射条件,凹陷左角点(x2=−a,z2=0)的位移幅值达到最大值,该值在高频波入射条件下接近自由场的2.0倍;随着观测点的右移,凹陷表面瞬态位移响应的幅值越来越小(图4和图5)。而在斜入射条件下,在凹陷左角点处达到最大值之后,地表位移幅值迅速降低到略低于自由场的水平,并且在凹陷右角点附近达到最小值,而且凹陷左角点处的最大值与入射波频率相关性(图5b)不如掠入射条件下的相关性大(图5c);但入射波频带越宽,凹陷左角点附近位移幅值大于自由场的范围越窄(图5b)。
2.2 强震动记录输入下凹陷地形瞬态反应
分析实际地震动输入凹陷地形的地震反应特征,研究其对地震动反应谱的放大效应。取凹陷的深度h=250 m,入射角γ=45°,分析凹陷左角点的地震动反应谱谱比特征。其中,反应谱谱比定义为凹陷给定空间点地震动反应谱与参考点自由场地面运动反应谱之间的比值,以此描述凹陷地形对地震动反应谱的放大效应。选择15组天然地震动的水平分量作为参考点自由场的地面运动,基本信息如表1所示。前5组输入地震动加速度及凹陷左角点地震反应加速度,如图6所示。根据前面对脉冲输入的结果分析可知,在地震波斜入射条件下,凹陷左角点具有显著的能量汇聚效应,因此,其地震反应加速度的幅值显著高于自由场地震动加速度的幅值。
表 1 本文所用天然地震动基础信息Table 1. Basic information of natural ground motions in this paper编号 发震年 发震地点 MW 台站名称 震中距/km 1 1999 美国赫克托矿 7.1 卡巴宗 89.40 2 1999 中国台湾集集 7.6 TCU122 21.80 3 2002 美国阿拉斯加德纳里 7.9 鹰河- AK Geologic Mat 266.35 4 1999 中国台湾集集 7.6 TCU051 38.53 5 1999 中国台湾集集 7.6 TCU050 41.46 6 1999 中国台湾集集-03 6.2 TCU120 30.67 7 1999 美国赫克托矿 7.1 圣贝纳迪诺 - Fire Sta. #4 107.43 8 1979 美国帝王谷-06 6.5 埃尔森特罗台阵#12 31.99 9 1999 中国台湾集集 7.6 TCU122 21.80 10 1987 美国迷信山-02 6.5 威斯特摩兰消防站 19.51 11 1999 中国台湾集集 7.6 CHY057 88.48 12 1999 中国台湾集集 7.6 CHY102 70.48 13 1989 美国洛玛普列塔 6.9 海沃德市政厅-北 73.18 14 1999 土耳其科喀艾里 7.5 伊斯坦布尔 89.12 15 1940 美国帝王谷 7.0 埃尔森特罗 13.00 将表1中所有天然地震波输入下,凹陷左角点的反应谱比曲线如图7中细点线所示。可以看出,输入天然地震波的差异造成了谱比计算结果的较大差异,因此,在研究局部地形对地震动反应谱的放大倍数时,应考虑输入地震动随机性对计算结果的影响。这与局部地形对傅里叶谱放大效应(或地形的传递函数)的研究是不同。针对傅里叶谱放大效应的研究,采用简单脉冲输入或噪声输入即可获得可靠的结果;但是,针对反应谱放大效应的研究,必须使用实际地震记录作为输入,且必须充分考虑输入地震动随机性对分析结果的影响。
所有地震动反应谱谱比的平均值如图7中红色实线所示。周期小于6.0 s时,凹陷左角点反应谱比值均大于1.3;当周期小于0.7 s,地震动反应谱谱比值大于1.7,而大部分工程结构基本自振周期介于0.7—6.0 s范围之间。周期T约为0.1 s时,其反应谱比值接近1.8。将T=0.1 s代入式(14)可得η=10。因此,现有大部分窄频带稳态解析解很难满足评估凹陷地形对高频(短周期)地震动反应谱放大效应的要求。图7中黑色实线为利用汉宁窗对对埃尔森特罗(El Centro)波(表1中编号为15的天然地震动)计算所得地震动反应谱比曲线进行平滑后所得结果。可以看出,针对该输入地震波进行平滑后所得反应谱比曲线与所有地震波的反应谱比均值曲线相近。因此,本文后续的讨论均基于对埃尔森特罗波计算所得谱比曲线进行平滑后所得的结果。
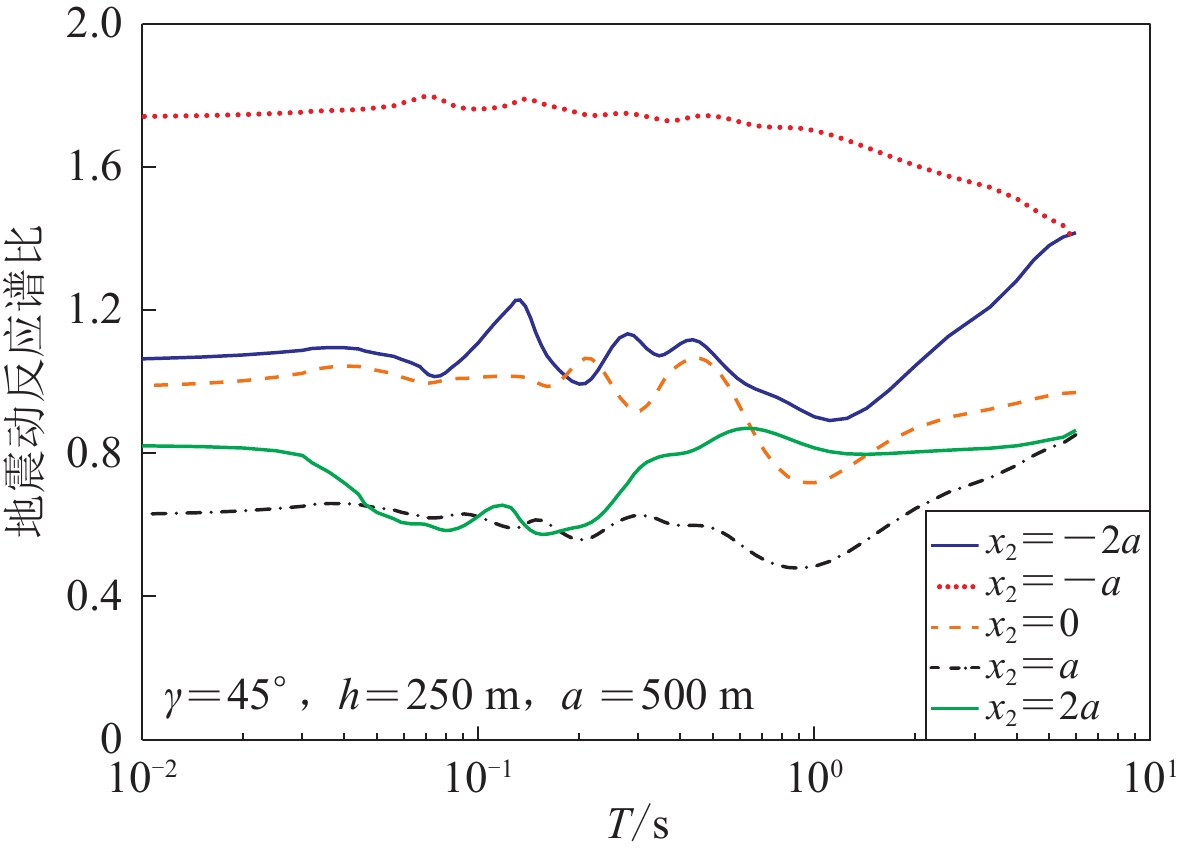
不同地表点的反应谱谱比曲线(凹陷深度h=250 m,地震波入射角γ=45°),如图8所示。其中,x2=±a分别表示凹陷的右和左角点,x2=0表示凹陷最底部的点。可以看出,在斜入射条件下,凹陷左角点对应的谱比最大,大部分周期对应的反应谱比值均大于1.4。对于凹陷左侧远离散射源点(x2=−2a)在周期小于0.6 s的范围内,凹陷底部点反应的谱比值略高于1.0,最大值超过了1.2;当周期大于1.0 s后,该点的反应谱比值开始增大,在6.0 s处,反应谱比值超过了1.4。对于凹陷最底部点,在周期小于0.6 s的范围内,其反应谱比值在1.0附近上下波动;当周期大于0.6 s时,其反应谱比值小于1.0。斜入射条件下,凹陷右侧地表点(x2=a,2a)的谱比均小于1.0。从中可以看出,在凹陷附近,不同地表点地震动反应谱谱比曲线具有不同的性质:① 通常迎波面的凹陷角点对应的反应谱比值最大,并且可以达到非常高的水平(如图8所示的最大值高达1.8);② 凹陷表面点的谱比值略大于1.0;③ 背波面地表点的谱比通常小于1.0;④ 距离凹陷越远的地表点,其反应谱比值越接近1.0。
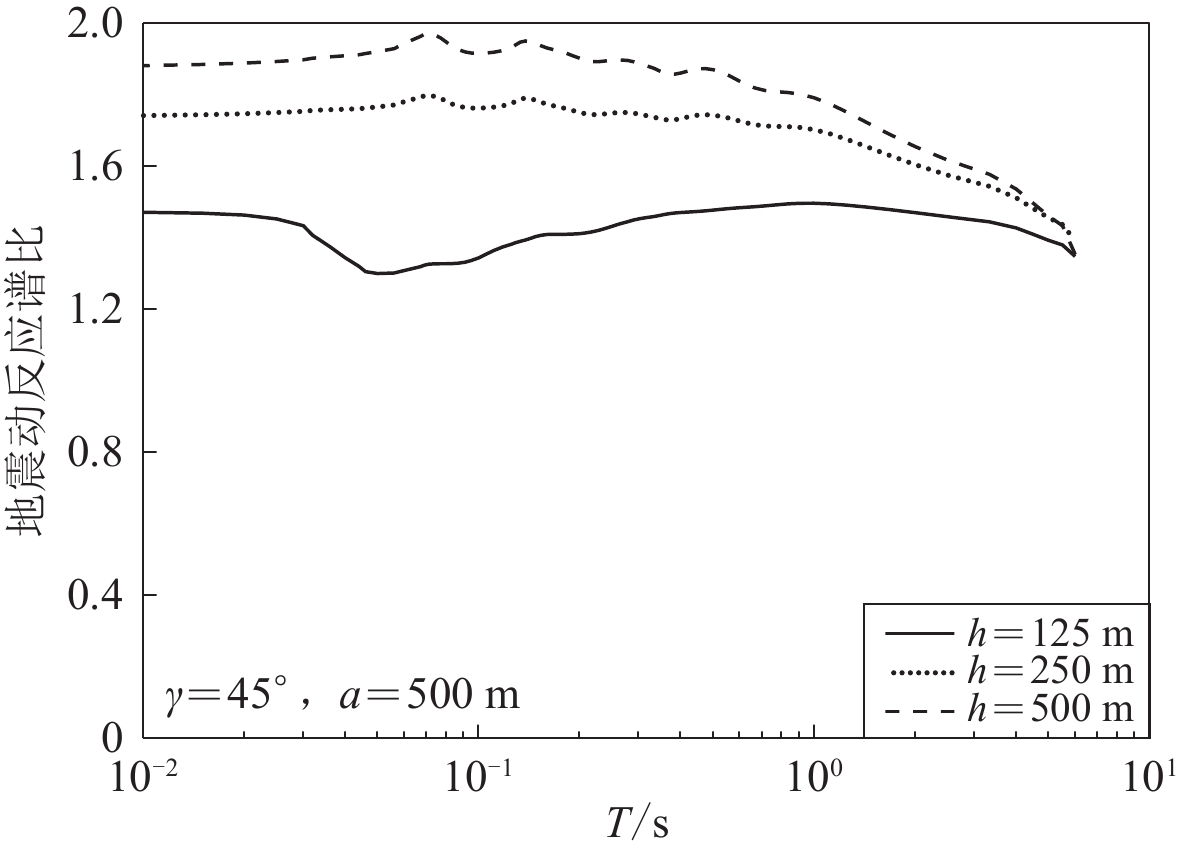
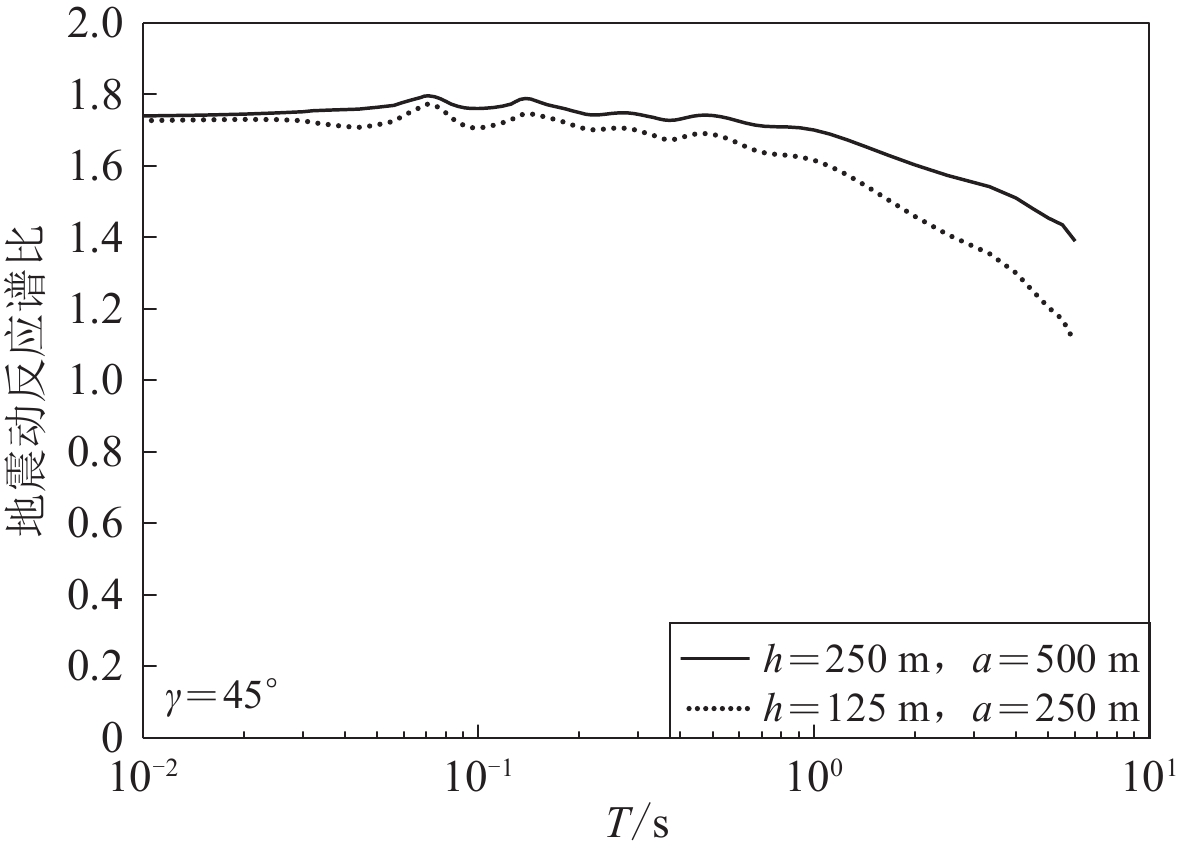
为分析凹陷地形深度对谱比的影响,取h为125,250和500 m三个不同深度的凹陷左角点的反应谱比(γ=45°)(图9),其中h=500 m即为Trifunac (1972)所研究的半圆形凹陷。凹陷越深,凹陷表面与水平地表之间的交角越小(最小为半圆形凹陷的90°),以致凹陷角点处地震波的干涉效应越强,相应的谱比值越大。半圆凹陷的谱比值在0.07 s处几乎达到了2.0。
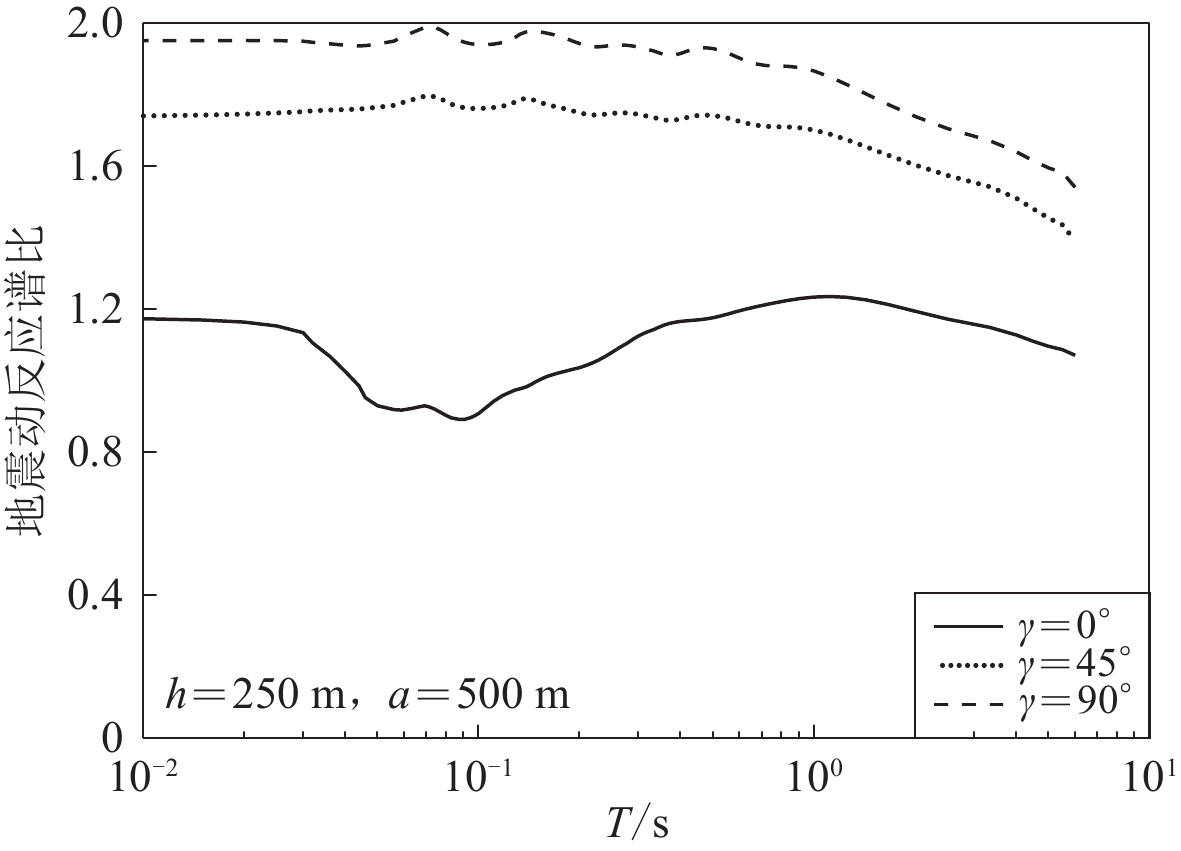
地震波入射角γ=0°,45°,90°条件下,凹陷左角点的反应谱比曲线(h=250 m)如图10所示。可以看出:在地震波掠入射(γ=90°)条件下,反应谱比值达到了非常高的水平,在T=0.07 s处反应谱比达到了2.0;在垂直入射(γ=0°)条件下,周期大范围内,反应谱比值略高于1.0,远低于斜入射(γ=45°)和掠入射情况。因此,在评估局部地形对地震动反应谱的放大效应时,应考虑地震波入射方向对评估结果的影响。
利用式(13)研究凹陷地形自身动力特性,即分析其对自由场傅里叶谱的放大效应时,控制凹陷自身动力特性的参数为深宽比h/a。当无量纲频率η固定时,凹陷对谐波的放大系数仅取决其深宽比,与凹陷绝对大小无关。这一结论无法用于评估凹陷对地震动反应谱的放大倍数。为此,考虑两个深宽比相同但大小相差1倍的凹陷,较大凹陷的深度h=250 m、宽度a=500 m,较小凹陷的深度h=125 m、宽度a=250 m。这两个凹陷左角点的谱比曲线如图11所示。在T<1.0 s高频范围内,二者相差不大,较小凹陷的谱比略低于较大凹陷。当T>1.0 s时,随着周期的增大,二者相差越来越大。这是因为,随着入射地震波周期的增大,其波长相应增大,空间范围较小的凹陷对地震波的影响越来越小,相应凹陷附近的地震反应越来越接近自由场地震动,其反应谱谱比值越来越接近1.0。需要指出的是,本文结果是针对半空间介质剪切波速为1 000 m/s的条件下得到的,半空间剪切波速变化后,尽管上述规律和变化趋势一致,但对应结果的差别程度将会有所不同,例如,图11所示的周期分界点会不同于1.0 s。
3. 结论
本文在推导宽频带瞬态解析解的基础上,研究了圆弧形凹陷对地震动的放大效应,结果表明:
1) 在对工程有影响的频带范围内,传统的窄带解析解无法用于研究凹陷对时域地震动参数的放大效应;
2) 脉冲输入下,凹陷角点处位移幅值放大显著,而且该放大效应受地震波入射角度和输入脉冲持时的影响;
3) 天然强震动记录输入下,凹陷不同地表点的地震动反应谱比曲线差异较大,迎波面角点地震动反应谱放大显著,谱比值最高达2.0,而且该放大效应受凹陷深度、地震波入射角度以及凹陷空间范围等因素的影响。
本文的研究对于利用解析解实现对局部地形对地震动放大效应的量化评估具有一定的理论意义和工程参考价值。基于宽频带瞬态解析解,可进一步构建评估地形效应的预测模型,从而为实际工程中合理地评估凹陷对地震动参数的放大效应提供科学依据。
-
图 3 钟形脉冲输入下给定地表点(x2=−2a,z2=0)的位移响应
(a) 低频脉冲响应($\varOmega $=100);(b) 高频脉冲响应($\varOmega $=1 000)
Figure 3. Displacement responses of specified surface location (x2=−2a,z2=0) under the inputs of bell-like impulses
(a) Low-frequency impulse response ($\varOmega $=100);(b) High-frequency impulse response ($\varOmega $=1 000)
表 1 本文所用天然地震动基础信息
Table 1 Basic information of natural ground motions in this paper
编号 发震年 发震地点 MW 台站名称 震中距/km 1 1999 美国赫克托矿 7.1 卡巴宗 89.40 2 1999 中国台湾集集 7.6 TCU122 21.80 3 2002 美国阿拉斯加德纳里 7.9 鹰河- AK Geologic Mat 266.35 4 1999 中国台湾集集 7.6 TCU051 38.53 5 1999 中国台湾集集 7.6 TCU050 41.46 6 1999 中国台湾集集-03 6.2 TCU120 30.67 7 1999 美国赫克托矿 7.1 圣贝纳迪诺 - Fire Sta. #4 107.43 8 1979 美国帝王谷-06 6.5 埃尔森特罗台阵#12 31.99 9 1999 中国台湾集集 7.6 TCU122 21.80 10 1987 美国迷信山-02 6.5 威斯特摩兰消防站 19.51 11 1999 中国台湾集集 7.6 CHY057 88.48 12 1999 中国台湾集集 7.6 CHY102 70.48 13 1989 美国洛玛普列塔 6.9 海沃德市政厅-北 73.18 14 1999 土耳其科喀艾里 7.5 伊斯坦布尔 89.12 15 1940 美国帝王谷 7.0 埃尔森特罗 13.00 -
巴振宁,梁建文,Lee V W. 2010. 平面P波在饱和半空间中凹陷地形周围的散射规律[J]. 天津大学学报,43(6):523–529. Ba Z N,Liang J W,Lee V W. 2010. Diffraction of plane P waves by a shallow circular-arc canyon in a saturated poroelastic half-space[J]. Journal of Tianjin University,43(6):523–529 (in Chinese).
胡聿贤. 2006. 地震工程学[M]. 北京: 地震出版社: 96–97. Hu Y X. 2006. Earthquake Engineering[M]. Beijing: Seismological Press: 96–97 (in Chinese).
梁建文,严林隽,Lee V W. 2001. 圆弧形凹陷地形表面覆盖层对入射平面SV波的影响[J]. 地震学报,23(6):622–636. doi: 10.3321/j.issn:0253-3782.2001.06.008 Liang J W,Yan L J,Lee V W. 2001. Effects of a covering layer in a circular-arc canyon on incident plane SV waves[J]. Acta Seismologica Sinica,23(6):622–636 (in Chinese).
梁建文,严林隽,Lee V W. 2002. 圆弧形凹陷地形表面覆盖层对入射平面P波的影响[J]. 固体力学学报,23(4):397–411. doi: 10.3969/j.issn.0254-7805.2002.04.004 Liang J W,Yan L J,Lee V W. 2002. Scattering of incident plane P waves by a circular-arc canyon with a covering layer[J]. Acta Mechanica Solida Sinica,23(4):397–411 (in Chinese).
梁建文,罗昊,Lee V W. 2004. 任意圆弧形凸起地形中隧洞对入射平面SH波的影响[J]. 地震学报,26(5):495–508. doi: 10.3321/j.issn:0253-3782.2004.05.006 Liang J W,Luo H,Lee V W. 2004. Scattering of plane SH waves by a circular-arc hill with a circular tunnel[J]. Acta Seismologica Sinica,26(5):495–508 (in Chinese).
梁建文,李方杰,顾晓鲁. 2005. Rayleigh波在浅圆凹陷地形附近的散射:高频解答[J]. 地震工程与工程振动,25(5):24–29. Liang J W,Li F J,Gu X L. 2005. Scattering of Rayleigh waves by a shallow circular canyon:High-frequency solution[J]. Earthquake Engineering and Engineering Vibration,25(5):24–29 (in Chinese).
梁建文,魏新磊,Lee V W. 2009a. 圆弧形沉积谷地对平面SV波三维散射解析解[J]. 岩土工程学报,31(9):1345–1353. Liang J W,Wei X L,Lee V W. 2009a. 3D scattering of plane SV waves by a circular-arc alluvial valley[J]. Chinese Journal of Geotechnical Engineering,31(9):1345–1353 (in Chinese).
梁建文,魏新磊,Lee V W. 2009b. 圆弧形沉积谷地对Rayleigh波三维散射解析解[J]. 天津大学学报,42(1):24–34. Liang J W,Wei X L,Lee V W. 2009b. Analytical solution for 3D scattering of Rayleigh waves by a circular-arc alluvial valley[J]. Journal of Tianjin University,42(1):24–34 (in Chinese).
梁建文,魏新磊,Lee V W. 2010. 圆弧形沉积谷地对平面P波的三维散射解析解[J]. 岩土力学,31(2):461–470. doi: 10.3969/j.issn.1000-7598.2010.02.022 Liang J W,Wei X L,Lee V W. 2010. 3-D scattering of plane P waves by a circular-arc alluvial valley[J]. Rock and Soil Mechanics,31(2):461–470 (in Chinese).
梁建文,张郁山,顾晓鲁,Lee V W. 2003. 圆弧形层状凹陷地形对平面SH波的散射[J]. 振动工程学报,16(2):158–165. doi: 10.3969/j.issn.1004-4523.2003.02.006 Liang J W,Zhang Y S,Gu X L,Lee V W. 2003. Scattering of plane SH waves by a circular-arc layered canyon[J]. Journal of Vibration Engineering,16(2):158–165 (in Chinese).
廖振鹏. 2002. 工程波动理论导论[M]. 第2版. 北京: 科学出版社: 207–211. Liao Z P. 2002. Introduction to Wave Motion Theories in Engineering[M]. 2nd ed. Beijing: Science Press: 207–211 (in Chinese).
杨彩红. 2009. 圆弧状凹陷地形在平面SH波入射下的动力响应:高频解答[J]. 震灾防御技术,4(2):158–166. doi: 10.3969/j.issn.1673-5722.2009.02.004 Yang C H. 2009. Dynamic response of circular-arc-shaped canyon under the incidence of plane SH wave:High-frequency solution[J]. Technology for Earthquake Disaster Prevention,4(2):158–166 (in Chinese).
Cao H,Lee V W. 1989. Scattering of plane SH waves by circular cylindrical canyons with variable depth-to-width ratio[J]. European J Earthq Eng,2:29–37.
Cao H,Lee V W. 1990. Scattering and differaction of plane P waves by circular cylindrical canyons with variable depth-to-width ratio[J]. Soil Dyn Earthq Eng,9(3):141–150. doi: 10.1016/S0267-7261(09)90013-6
Li W H,Zhao C G. 2005. Scattering of plane SV waves by cylindrical canyons in saturated porous medium[J]. Soil Dyn Earthq Eng,25(12):981–995. doi: 10.1016/j.soildyn.2004.10.004
Trifunac M D. 1972. Scattering of plane SH waves by a semi-cylindrical canyon[J]. Earthq Eng Struct Dyn,1(3):267–281. doi: 10.1002/eqe.4290010307
Wong H L,Trifunac M D. 1974. Scattering of plane SH waves by a semi-elliptical canyon[J]. Earthq Eng Struct Dyn,3(2):157–169. doi: 10.1002/eqe.4290030205
Yuan X M,Liao Z P. 1994. Scattering of plane SH waves by a cylindrical canyon of circular-arc cross-section[J]. Soil Dyn Earthq Eng,13(6):407–412. doi: 10.1016/0267-7261(94)90011-6
Zhang Y S. 2010. Scattering of plane P waves by canyons containing multiple circular-arc-shaped layers[J]. Earthquake Science,23(2):157–165. doi: 10.1007/s11589-009-0086-2
-
期刊类型引用(1)
1. 柳国环,陈欣宇,李鑫洋. 半覆水相变V形峡谷场地P波入射下的空间地震动散射频域理论解、验证及特征. 计算力学学报. 2023(05): 764-772 .  百度学术
百度学术
其他类型引用(3)




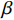
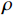
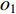
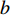
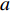
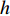
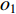
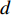
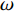
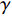
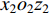
 下载:
下载: