Research on bandwidth of ground motion simulated using FK approach
-
摘要: 地震动合成方法的应用前景与其所能表达的有效频带范围紧密相关。本文研究基于频率波数域格林函数的地震动合成方法（FK法），分析频带范围的关键影响要素及处理措施。在介绍计算原理的基础上，概括FK法合成地震动的主要影响要素，分析地壳速度模型对子源地震矩、破裂时间和传播时间的影响。随后，分析格林函数传播宽频带地震波的能力，提出格林函数计算中的频带影响参数的建议值。为分析FK法的震源模型辐射宽频带地震波的能力，重点考察控制子源错动过程的震源时间函数和上升时间。研究认为，FK法具有合成宽频带地震动的能力，这需要采用合理的参数和模型。Abstract: The application prospect of ground motion simulation approach is closely related to the effective bandwidth of synthetics. Hence we studied the simulation approach based on the frequency-wavenumber Green’s function （FK approach）, and analyzed the key factors affecting the bandwidth and the treatment measures. On the basis of the calculation principle introduction, we summarized the main factors influencing the ground motion simulated by FK approach, and analyzed the influences of the crustal velocity model on sub-source seismic moment, rupture time and propagation time. Then, we analyzed the ability of the Green’s function to propagate broadband seismic waves, and put forward the recommended values of parameters affecting bandwidth in the calculation of Green’s function. The source time function and the rise time controlling the sub-source slip process are investigated to analyze the ability of source model in FK approach to radiate broadband seismic waves. The results show that the FK approach has the ability to simulate broadband ground motion, and this requires reasonable parameters and models.
-
引言
地震发生前后电离层的异常是近年来的研究热点。诸多研究均显示强震（ML＞5.0）会导致电离层异常（Liu et al，2004；Dabas et al，2007；Zhao et al，2008），且地震发生前后均可观测到许多异常的地球物理现象，例如一些化学气体的异常增加（Virk，Singh，1994；Heinicke et al，1995）、电离层电子密度的变化（Oyama et al，2008）等。这些异常现象的出现与一定的物理或化学机制存在联系，自从Leonard和Barnes （1965）使用电离层观测数据首次分析阿拉斯加地震前的电离层异常迹象起，关于震前电离层异常（pre-earthquake ionospheric abnormal，缩写为PEIA）的研究就在不断深入（Pulinets，2004）。而岩石圈-大气层-电离层耦合机制（lithosphere-atmosphere-ionosphere coupling，缩写为LAIC）作为地震电离层效应研究的理论基础（Liperovsky et al，2008；Freund et al，2009；Pulinets，Ouzounov，2011；Pulinets，Davidenko，2014；Zhou et al，2017），其理论解释目前主要集中在两个方面：一方面为LAIC声重力波扰动产生异常，即声重波机制；另一方面为异常直流电场效应，即LAIC直流电场机制（Hayakawa et al，2004）。LAIC声重波机制主要以同震效应和震后效应为主，而LAIC直流电场机制还包括震前效应，本文主要关注LAIC直流电场机制。Virk和Singh （1994）和Heinicke等（1995）报道，在地震发生前几天到几周观测到了包括氡在内的惰性气体和带电气溶胶的密集出现；Sorokin等（2005，2007）提出，带电气溶胶会随着岩石碎裂逸出的土壤气体从岩石层（地表的大气底层）渗透进低层大气，该对流输送会形成附加电流，并因此导致低层大气和电离层中的电场异常；滕荣荣等（2010）对强震地壳溢出氡与电离层异常耦合关系的基本理论、观测依据和物理解释进行了研究总结；Pulinets等（2000）基于大气层-热层-电离层耦合模型的研究结果表明，地球表面强烈的垂直电场可以渗透至电离层中，从而在地震发生之前引起电离层异常，并且估计地表1 kV / m的垂直电场可以在电离层高度产生1 mV / m左右的水平电场。
在地震电离层异常的观测研究方面，通过基于地面的电离层测高仪数据获得了大量的地震电离层扰动异常的观测证据（Liu et al，2000；Chuo et al，2002；Popov et al，2004；Dabas et al，2007；Zhao et al，2008；丁宗华等，2010；Sharma et al，2010；Carter et al，2013），所分析的电离层参数包括F2层临界频率（foF2）、F2层峰值电子密度（NmF2）、F2层电子密度的峰值高度（hmF2）、E层临界频率（foE）、偶发E层临界频率（foEs）等。此外，随着卫星观测的发展，基于星载的电离层观测数据的地震电离层异常现象的报道也逐渐增多，例如电子浓度、电离层电子温度（Te）、总电子含量（total electron content，缩写为TEC）等（Pulinets，Legen’ka，2003；Liu et al，2004；Oyama et al，2008；Zhao et al，2008；Sharma et al，2010；刘静等，2011；马新欣等，2014；Kong et al，2018；Tariq et al，2019）。研究结果表明，强震发生之前，上述观测参数均会出现不同程度的异常扰动。近年来，全球导航卫星系统（Global Navigation Satellite System，缩写为GNSS）技术的发展促使许多研究人员使用TEC数据探测震前电离层异常。Liu等（2004）基于台湾地区20次MW≥6.0强震的GPS-TEC数据提出这种异常一般发生在地震前1—5天内。
以LAIC直流电场机制为理论基础，本文将对地震实例进行多参量的观测研究和理论分析。基于已有的电离层参量foF2和TEC数据，本文拟选择近几年发生在我国附近的、震级在M6.0以上的强震，对其进行震前电离层异常扰动探测。2018年8月5日（年积日217） UTC 11:46:34 （LT 18:46:34），印度尼西亚西努沙登加拉省龙目岛东北部发生了一次MS6.8地震，震源深度为10 km，震中位于（116.45°E，8.33°S）。本文主要关注此次地震在主震发生前所产生的电离层扰动，并通过数据分析和模型模拟结果研究其潜在的物理过程。由于北半球、南半球地震区域上的电离层异常现象可以通过磁力线映射到对应半球的磁共轭区域（Zhao et al，2008；余涛等，2009；丁宗华等，2010），而此次地震发生在南半球，因此可以在北半球找到其磁共轭区域，本文分别以地震震中、磁共轭点为圆心、以2 000 km为半径绘制圆得到地震区域和磁共轭区域。此次地震的地理震中的地理位置为（116.45°E，8.33°S），地磁位置为（170.23°W，17.67°S），则其对应磁共轭点的地理位置为（117.50°E，27.20°N），地磁位置为（170.23°W，17.67°N），具体分布如图1所示。本文拟通过Dst指数，Kp指数，F10.7，南半球地震震中附近和北半球磁共轭点附近两个区域的foF2以及主震前电离层TEC序列对该地震发生前是否存在电离层异常扰动进行深入分析，同时使用从美国国家大气研究中心获取的TIEGCM模拟异常电场出现情况下全球TEC和NmF2的变化特征，以期为震前电离层异常效应和地震预测提供参考。
![]()
图 1 印度尼西亚地震震中、磁共轭点、电离层测高仪站、IGS站的地理位置分布Figure 1. Geographic locations of Indonesia earthquake epicenter，magnetically conjugated point，ionosondes and IGS stations1. 观测数据
1.1 太阳和地磁数据
由于电离层受到地磁活动和太阳活动的影响，这种影响可以通过地磁和太阳活动指数来表征，目前主要的地磁和太阳活动指数有赤道环电流地磁活动指数Dst、全球地磁活动指数Kp和太阳射电通量F10.7，其中Dst指数和Kp指数用于反映地磁活动，F10.7用于反映太阳活动。Dst指数和Kp指数由日本京都地磁数据中心（http://wdc.kugi.kyoto-u.ac.jp/dstae/index.html）提供，其中：Dst指数的分辨率为1 h，主要用于衡量地磁水平方向的变化强度，地磁平静状态下该指数处于−30—30 nT之间；Kp指数的分辨率为3 h，主要用于描述全球地磁扰动过程，共分为10个等级（从0到9），地磁平静状态下小于4。F10.7数据由中国科学院空间中心（http://www.sepc.ac.cn）提供，其分辨率为1 d，主要用于反映太阳对地球高层气体的加热和电离效应，太阳平静状态下小于100 SFU （张明敏等，2018）。2018年8月5日印度尼西亚地震前后43天内Dst指数、Kp指数和F10.7的变化如图2所示，可以看出，在地震当天（年积日217），Dst指数处于±15 nT范围内，且Kp指数均小于2，F10.7较为稳定且小于100 SFU，所以地震当天（年积日217）的地磁活动和太阳活动对电离层的影响均不明显。
![]()
图 2 2018年7月1日到8月12日Dst指数（a），Kp指数（b）和F10.7 （c）的变化Figure 2. Variation of the indices Dst （a），Kp （b） and F10.7 （c） from July 1 to August 12，2018从图2中还可以看出，在地震发生前后43天中：Dst指数基本在±30 nT以内；而Kp指数经历了四个超过3的峰值，分别位于2018年的第187，202，206和224天附近，除此之外，Kp指数基本在3以内，根据磁暴的确定标准值，这43天中大部分时间未发生磁暴；F10.7较为稳定且小于100 SFU，太阳辐射对电离层的影响不大。下面将围绕2018年7月1日（年积日182）至2018年8月12日（年积日224）期间一系列参数的变化进行分析。
1.2 foF2
武汉站的foF2数据由子午工程数据中心（https://data.meridianproject.ac.cn/）提供，澳大利亚达尔文站的foF2数据由澳大利亚气象局空间天气服务中心（https://www.sws.bom.gov.au/World_Data_Centre/2/2）提供，在本文的数据分析过程中统一其分辨率为15 min。武汉站和达尔文站（图1）分别位于磁共轭区域和地震区域，两台站的电离层测高仪2018年8月3日（年积日215）至9日（年积日221）的foF2原始数据如图3a所示。许多研究人员对foF2数据的扰动采用95%置信区间以寻找可能的异常扰动（Chuo et al，2002；Carter et al，2013），本文使用同样的方法对武汉站和达尔文站的数据进行分析。图3a给出了2018年7月1日（年积日182）至7月31日（年积日212）共31天的月中值和月均值。为了探查8月的foF2数据相较7月异常的时间点，计算7月foF2的标准差，并使用两倍的标准差±2σ进行比较，结果如图3b所示。可以看出地震前、后都有明显的异常点，但这些异常不一定均由地震引起，也可能是由太阳活动、地磁活动或者 “其它” 因素的影响（Carter et al，2013）所致。由上文已知，印度尼西亚地震发生时太阳活动和地磁活动对电离层的影响较小，因此可排除太阳活动和地磁活动的影响。而区分地震扰动与磁暴等活动的一个很重要的评判标准是，由磁暴引起的扰动具有行星特征，而由地震引起的扰动是局部的，且幅度更小（Pulinets，Legen’ka，2003）。考虑到武汉站和达尔文站是共轭的，达尔文站位于地震区域，武汉站位于磁共轭区域，电离层异常现象会通过磁力线实现映射，所以如果出现地震前兆，两地的foF2应该在同一时间点呈现异常，但其它地区不存在类似异常。为便于观察，将图3b中原始foF2数据与月中值的差值（红色曲线）和原始foF2数据与月均值的差值（绿色曲线）超出两倍标准差±2σ的正、负异常结果绘制于图4中。图中使用蓝色方框标示出了武汉台和达尔文台foF2同时呈现异常的时间点：2018年8月4日（年积日216） UTC 03:45。参看图2，这一时刻的Dst指数在±5 nT范围内，Kp指数在2以内，说明此时地磁活动对电离层的影响不明显。同时可知这一时刻F10.7较为稳定且小于100 SFU，说明太阳辐射对电离层影响不明显。因此此时刻的电离层异常可能与地震有关。
![]()
图 3 2018年8月3日至9日武汉站和达尔文站的foF2观测变化（a） foF2原始数据；（b） foF2标准差Figure 3. The variations of foF2 observed by Wuhan station and Darwin station from August 3 to 9，2018（a） Original data of foF2；（b） Standrad deviation of foF2![]()
图 4 2018年8月3日至9日武汉站和达尔文站的foF2异常扰动观测红色、绿色曲线分别表示原始foF2数据减去月中值、月均值后再减去两倍标准差的结果，蓝色方框为武汉站和达尔文站的foF2同时呈现异常的时间点Figure 4. The abnormal disturbances of foF2 observed by the stations Wuhan and Darwin from August 3 to 9，2018The red curve indicates the result that the original foF2 data minuses the 31-day median and then subtracts twice the standard deviation. The green curve indicates the result that the original foF2 data minuses the 31-day mean and then subtracts twice the standard deviation. The blue box indicates the time point at which the foF2 in Wuhan and Darwin stations are simultaneously anomalous1.3 TEC
近年来，GNSS技术的发展使得许多研究人员便于使用TEC数据探测震前电离层异常。本文通过观测主震前电离层TEC序列是否有明显扰动来判断电离层是否存在异常。这里使用IGS （Internet GNSS Service）提供的30 s时间分辨率的总电子含量（TEC）数据，对此次地震前几天的电离层TEC异常扰动进行观测和分析。本文用到的IGS站的地理位置见图1。分别以地震震中和磁共轭点为圆心，以2 000 km为半径绘制圆，即地震区域和磁共轭区域，而后筛选地震区域和磁共轭区域附近的IGS站进行分析。本文参照Kong等（2018）的方法从GNSS双频观测数据中提取TEC数据。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {{\text{δ}}\rm{TE}}{{\rm{C}}_i} {\text{＝}} {\rm{TE}}{{\rm{C}}_{i {\text{＋}} 1}}{\text{－}} \frac{{{\rm{TE}}{{\rm{C}}_i}{\text{＋}} {\rm{TE}}{{\rm{C}}_{i{\text{＋}} 2}}}}{2}{\text{，}} $
(1) 式中，TECi为第i个TEC数据点，δTECi为TEC的一阶中心差分。
图5显示了2018年8月4日（年积日216）由30号卫星观测到的不同站点的δTEC序列，可以看出，2018年8月4日（年积日216） UTC 03:45附近，有11个站点观测到的TEC序列存在异常扰动，如图中红色曲线所示。这11个站点的TEC序列的异常时间点为UTC 03:41:00，与观测到foF2异常的时间点非常接近。考虑到foF2的分辨率为15 min，IGS的分辨率为30 s，因此推断foF2序列和TEC序列有可能在同一时间点发生扰动。其它站点的TEC序列有较大的波动，可能是缘于多径效应。图6给出了对应于图5中站点的电离层穿刺点（ionosphere pierce point，缩写为IPP）轨迹。
![]()
图 5 30号卫星观测到各站点的δTEC序列Figure 5. The δTEC sequences from different stations observed by the satellite No.30![]()
图 6 30号卫星观测到的13个站点的IPP分布Figure 6. IPP distribution of 13 sites observed by the satellite No.302. TIEGCM模拟
TIEGCM是美国国家大气研究中心研发的一种高层大气物理模型，该模型使用有限差分方法，自洽地求解关于三维热层和电离层的动力学方程、能量方程及连续性方程，且考虑了极区粒子沉降、低层大气的潮汐以及高纬电场等作用。TIEGCM模型研究的范围为（87.5°S—87.5°N，180°W—175°E），高度从96 km到600 km （Richmond et al，1992；Richmond，1995）。目前，TIEGCM模型可分别采用单精度模式和双精度模式，前者的经纬度网格为5°×5°，垂直方向的分辨率为0.5个大气标高，后者的经纬度分辨率为2.5°×2.5°，垂直方向分辨率为0.25个大气标高。
本文利用TIEGCM模型的双精度模式计算2018年8月4—5日期间印度尼西亚地震前期的异常电场对地震区域和对应共轭区域电离层TEC和NmF2的影响。首先基于Zhou等（2017）提出的LAIC电场渗透模型，模拟地震前期产生的地表异常电场对电离层底部水平电场的影响。图7给出了地震区域2018年8月4日（年积日216） UTC 03:40电离层底部z＝90 km处的异常水平电场分布图。可以看出，地震产生的异常电场渗透进电离层后会在电离层底部产生异常电场，其方向由震中向外，形状基本为圆形，而且随着水平距离的增加，异常电场值先增大而后减小，最大电场值为4 mV/m。将电离层底部扰动电场值加入到TIEGCM模型中，由此模拟得到地震区域和磁共轭区域电离层高度上的TEC和NmF2扰动的分布，并与观测结果进行对比。图8为在2018年8月4日（年积日216） UTC 03:40处插入异常电场四个小时后全球的TEC情况，可以看出，插入异常电场后，地震区域和磁共轭区域TEC均出现了明显的扰动现象，即地震区域和磁共轭区域的赤道方向均出现了TEC的增加，而在远离赤道方向均出现了TEC的降低。此外，TEC的扰动量在UTC 05:00时达到最大值，与背景TEC值相比较，最大偏离量为背景TEC值的15%。图9为插入异常电场四个小时后全球的NmF2情况，可以看出，插入异常电场后NmF2在地震区域和磁共轭区域也都出现了相似的扰动现象，而且NmF2扰动量随着时间的变化与TEC扰动的变化相一致。
![]()
图 7 地震区域2018年8月4日（年积日216） UTC 03:40电离层底部z＝90 km处的异常水平电场分布（a） 总电场强度E；（b） 磁南北向电场强度ESN；（c） 磁东西向电场强度EEWFigure 7. Distribution of the abnormal horizontal electric field at UTC 03:40 on August 4，2018（216 day of the year） at the bottom of the ionosphere （z＝90 km）（a） Total electric field intensity E；（b） The electric field intensity ESN in magnetic north-south direction；（c） The electric field intensity EEW in magnetic east-west direction![]()
图 8 基于TIEGCM模型对插入异常电场四小时后地震及磁共轭区域TEC情况的模拟结果Figure 8. Simulation results of TEC evolution in the seismically active area and magnetically conjugated area four hours after insertion of an abnormal electric field based on the model TIEGCM![]()
图 9 基于TIEGCM模型对插入异常电场四小时后地震及磁共轭区域NmF2情况的模拟结果Figure 9. Simulation results of NmF2 evolution in the seismically active area and magnetically conjugated area four hours after insertion of an abnormal electric field based on the model TIEGCM3. 讨论与结论
地震引起电离层异常最常见的解释是岩石圈-大气层-电离层耦合机制（LAIC），其中的异常电场机制由于引起的电离层异常扰动程度更大、范围更广而更易被接受。以往的数据观测研究结果表明，强震发生数天前地震震中区域和磁共轭区域附近的电离层会出现异常，包括电离层参量foF2和TEC的异常扰动。Liu等（2000）对foF2扰动采用15天中位值来寻找1994—1999年期间MW≥6.0地震的前兆，其结果显示所有地震前兆均在地震发生前六天内出现，本文使用的观测foF2的方法与其一致。Chuo等（2002）研究了我国台湾地区1999年集集地震和嘉义地震期间中坜电离层测高仪站得到的foF2数据，发现分别于地震发生前3—4天和1—3天数据出现扰动，并认为其是地震的前兆。Dabas等（2007）通过研究2003—2005年之间发生的11次M＞6.0大地震主震前后低纬度地区观测到的foF2扰动，发现在每次地震的主震发生前1—25天和发生后2—3天内可以观测到foF2呈现一些与地震相关的不寻常的明显扰动。Zhao等（2008）的研究显示在汶川地震发生前3天，地震震中附近观测到了F2层峰值电子密度NmF2不寻常的大幅增强，同时TEC在90°E—130°E之内的区域持续增强很长一段时间。Sharma等（2010）研究了2008年三次地震中心在中国的大地震（MS＞6.0）主震前几天与地震相关的电离层总电子含量TEC和F2层临界频率foF2的异常变化，结果显示在地磁平静的情况下，主震前1—4天特别是在当地时间11:00—17:00之间，foF2和TEC发生的异常（有很大的增强）很可能与地震相关。Tariq等（2019）基于GPS的总电子含量TEC数据研究了2015—2017年尼泊尔和伊朗—伊拉克边境的三次MW＞7.0地震，观测到在地震发生前10天内出现显著的TEC异常。本文观测到的foF2数据和TEC数据异常出现在印度尼西亚地震发生32小时之前 ［2018年8月4日（年积日216） UTC 03:45 （LT 10:45） ］ ，与之前的研究结果一致，即在主震前一天可以观测到电离层异常扰动，因此，本文观测到的异常可以被认为可能是地震前兆，然而目前仍然缺乏直接的证据。虽然通过Dst指数、Kp指数和F10.7变化曲线的分析排除了太阳和地磁活动的影响，但尚需要进行更多的研究才有可能找到地震与电离层参量异常扰动之间的联系。
为了进一步探讨印度尼西亚地震发生前期地震区域及其共轭地区foF2和TEC的异常现象，本文采用TIEGCM模型模拟了2018年8月4—5日地震引起的异常电场对全球foF2和TEC的影响。基于模拟结果可知，在插入异常电场后地震区域及其共轭区域均出现了明显foF2和TEC的扰动现象，这与我们的观测结果相一致。通过结合数据观测和模型模拟，可以更加直观、有效地对震前电离层异常现象进行分析。
综上所述，本文基于观测分析和理论模拟研究了2018年8月5日印度尼西亚地震发生之前电离层的变化特征，得到以下结论：
1） 地震发生前一天，地震区域和磁共轭区域foF2序列和TEC序列观测到了同步异常，foF2序列和TEC序列出现异常的时间一致，其中南半球达尔文站测高仪的扰动强度强于北半球武汉站测高仪的扰动。
2） 使用直流电磁模式和TIEGCM模拟地震区域和对应共轭区域全球TEC和NmF2的变化情况，模拟结果显示地震区域和磁共轭区域发生异常，TEC和NmF2扰动在不同的共轭半球一致。但是模拟结果和观测在扰动的强度和空间尺度上还有不一致之处，在后续工作中需要进一步研究。
-
![]()
图 2 不同破裂速度计算的破裂时间。星号表示破裂起始点
（a） 同一破裂速度；（b） 深度相关破裂速度；（c） 深度相关破裂速度的分布；（d） 图（b）相对图（a）的差值
Figure 2. Rupture time calculated by different rupture velocity vr
（a） The same vr ；（b） Depth-related vr；（c） Distribution of depth-related vr； （d） Difference between Fig.（b） and Fig.（a）
![]()
图 3 不同剪切波速计算的S波的传播时间
（a） 同一剪切波速；（b） 深度相关剪切波速；（c） 图（b） 相对图 （a） 的差值
Figure 3. Propagation time of S wave calculated by different
$v_{\rm{S}} $ （a） The same $v_{\rm{S}} $；（b） Depth-related $v_{\rm{S}} $；（c） Difference between Fig.（b） and Fig.（a）
![]()
图 4 上升时间为0 s （a）和1.5 s （b） 时奈奎斯特频率对合成地震动加速度幅值谱FAS的影响
Figure 4. Influence of Nyquist frequency on FAS of synthetic ground motion with rise time of 0 s （a） and 1.5 s （b）
![]()
图 5 最大波数（a）和波数间隔（b）对合成地震动加速度幅值谱FAS和位移时程的影响
Figure 5. Influence of the maximum wavenumber （a） and the wavenumber interval （b） on FAS and displacement time history of synthetic ground motion
![]()
图 6 品质因子对合成地震动加速度幅值谱FAS的影响
Figure 6. Influence of quality factor on FAS of synthetic ground motion
![]()
图 7 五种震源时间函数的错动速率（a）及其加速度幅值谱FAS （b）
Figure 7. Slip rate （a） and its FAS （b） for five source time functions
![]()
图 8 震源时间函数对合成地震动加速度幅值谱FAS的影响
Figure 8. Influence of source time function on FAS of synthetic ground motion
![]()
图 9 上升时间（a）和破裂速度（b）对合成地震动加速度幅值谱FAS的影响
Figure 9. Influence of rise time （a） and rupture velocity （b） on FAS of synthetic ground motion
表 1 本文采用的地壳速度结构模型
Table 1 Crustal velocity structure model adopted in this study
厚度/km vP/（km·s−1） vS/（km·s−1） ρ/（g·cm−3） QP QS 3 4.88 2.86 2.55 300 150 5 5.80 3.40 2.70 400 200 14 6.04 3.55 2.75 400 200 21 6.82 3.98 2.90 600 300 25 7.61 4.45 3.10 800 400 - 8.08 4.47 3.38 1 000 500 
下载: 导出CSV
表 2 不同dt时FK法合成地震动的计算量
Table 2 Calculation cost of ground motion simulation using FK approach for different dt
算例 子源数 dt/s 地表某点地震动的
计算耗时/s地震动场（网格2×2 km2） 耗时/h 存储空间/GB 范围/km2 本文算例
MW6.516×8 0.02 1.4 0.7 0.23 100×70 16×8 0.01 2.8 1.4 0.46 100×70 汶川地震
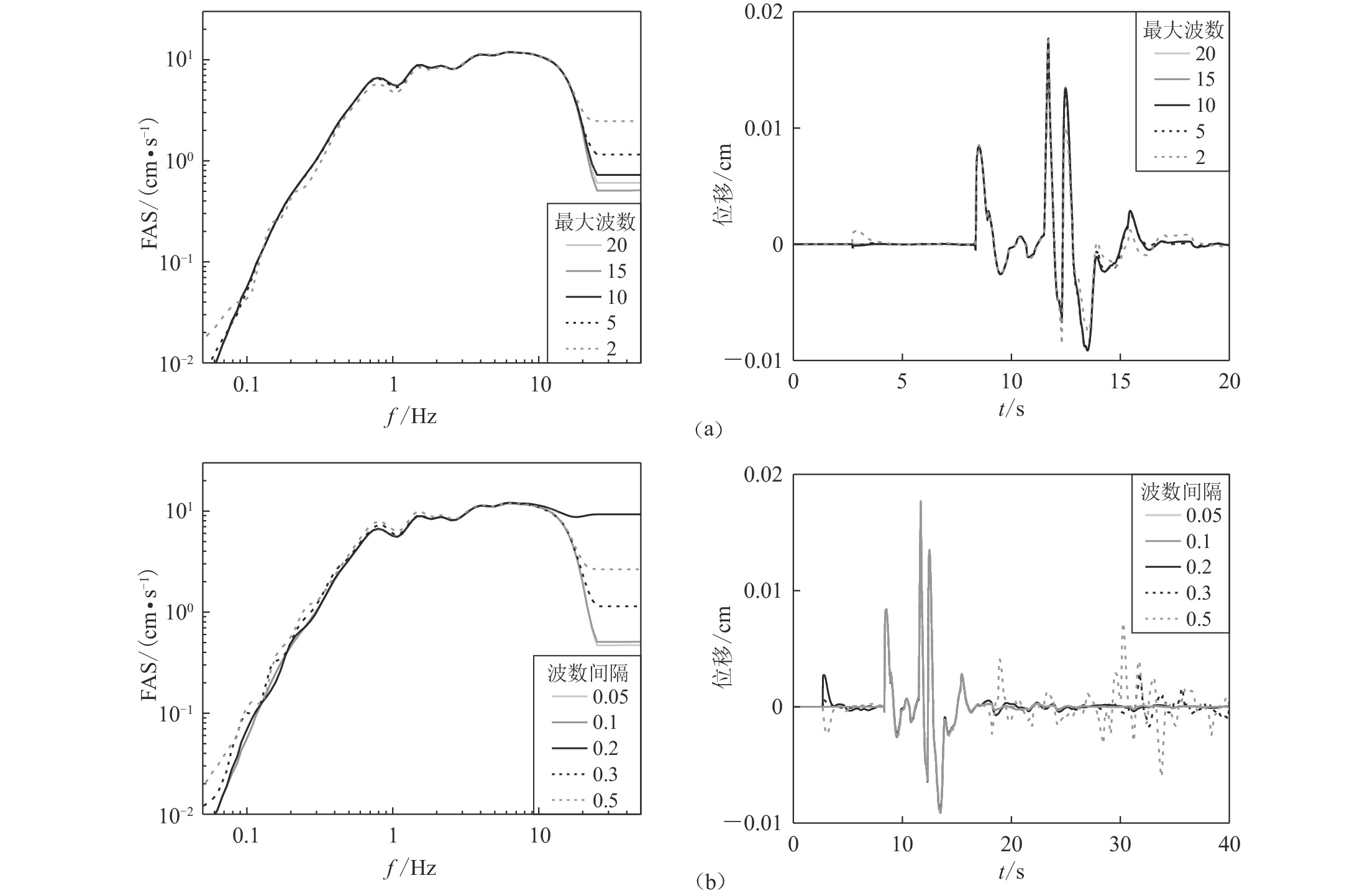
MW7.964×32 0.02 22.4 126.3 2.56 400×200 64×32 0.01 44.8 252.6 5.12 400×200
下载: 导出CSV
表 3 不同dt，dk和kmax时FK法格林函数的计算量
Table 3 Calculation cost of Green’s function in FK approach with different dt, dk and kmax
dt/s dk kmax 计算耗时（源深6 km）/s 150个地表点60组（源深差0.5 km） 30 km处一点 150个地表点 耗时/h 存储空间/GB 0.02 0.1 15 8 239 3.98 3.09 0.01 0.1 15 34 954 15.90 6.18 0.02 0.05 15 17 483 8.05 3.09 0.02 0.3 15 3 81 1.35 3.09 0.02 0.1 5 8 236 3.93 3.09 0.02 0.1 20 8 240 4.00 3.09 注：150个地表点的震中距设为1，2，···，150 km
下载: 导出CSV
-
曹泽林,陶夏新. 2018. 基于频率波数域格林函数的宽频带地震动合成方法综述[J]. 地震工程与工程振动,38(5):35–42. Cao Z L,Tao X X. 2018. Review on broadband ground motion simulation based on frequency-wavenumber Green’s function[J]. Earthquake Engineering and Engineering Dynamics,38(5):35–42 (in Chinese).
姜伟,陶夏新,赵凯. 2017. 基于NGA数据的震源模型全局参数定标律的统计[J]. 地震工程学报,39(2):221–226. doi: 10.3969/j.issn.1000-0844.2017.02.0221 Jiang W,Tao X X,Zhao K. 2017. Scaling laws of the global parameters of source models from NGA data[J]. China Earthquake Engineering Journal,39(2):221–226 (in Chinese).
孙晓丹,陶夏新. 2012. 宽频带地震动混合模拟方法综述[J]. 地震学报,34(4):571–577. doi: 10.3969/j.issn.0253-3782.2012.04.013 Sun X D,Tao X X. 2012. Hybrid simulation of broadband ground motion:Overview[J]. Acta Seismologica Sinica,34(4):571–577 (in Chinese).
Aki K, Richards P G. 2002. Quantitative Seismology[M]. 2nd ed. Sausalito, California: University Science Books: 37−62.
Beresnev I A. 2002. Source parameters observable from the corner frequency of earthquake spectra[J]. Bull Seismol Soc Am,92(5):2047–2048. doi: 10.1785/0120010266
Brune J N. 1970. Tectonic stress and the spectra of seismic shear waves from earthquakes[J]. J Geophys Res,75(26):4997–5009. doi: 10.1029/JB075i026p04997
Cao Z L,Tao X X,Tao Z R,Tang A P. 2019. Kinematic source modeling for the synthesis of broadband ground motion using the f-k approach[J]. Bull Seismol Soc Am,109(5):1738–1757. doi: 10.1785/0120180294
Day S M. 1982. Three-dimensional simulation of spontaneous rupture:The effect of nonuniform prestress[J]. Bull Seismol Soc Am,72(6A):1881–1902.
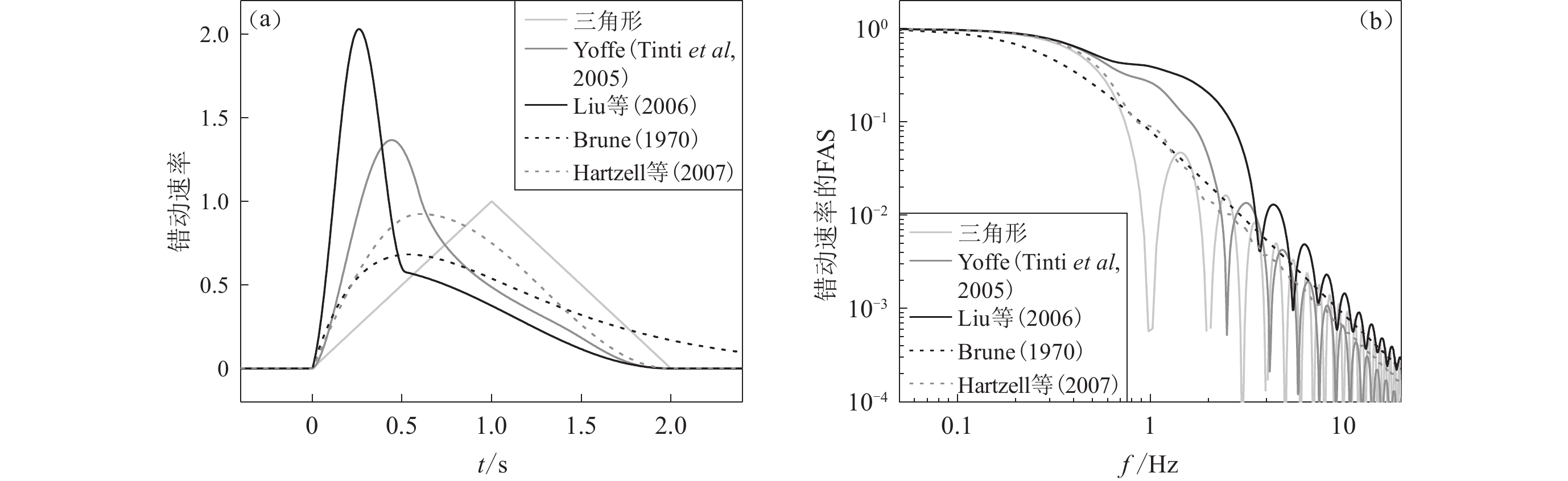
Dreger D,Tinti E,Cirella A. 2007. Slip velocity function parameterization for broadband ground motion simulation[J]. Seismol Res Lett,78(2):308.
Douglas J,Aochi H. 2008. A survey of techniques for predicting earthquake ground motions for engineering purposes[J]. Surv Geophys,29(3):187–220. doi: 10.1007/s10712-008-9046-y
Fortuño C,de la Llera J C,Wicks C W,Abell J A. 2014. Synthetic hybrid broadband seismograms based on InSAR coseismic displacements[J]. Bull Seismol Soc Am,104(6):2735–2754. doi: 10.1785/0120130293
Frankel A. 2009. A constant stress-drop model for producing broadband synthetic seismograms:Comparison with the Next Generation Attenuation relations[J]. Bull Seismol Soc Am,99(2A):664–680. doi: 10.1785/0120080079
Graves R,Pitarka A. 2010. Broadband ground-motion simulation using a hybrid approach[J]. Bull Seismol Soc Am,100(5A):2095–2123. doi: 10.1785/0120100057
Hao J L,Ji C,Wang W M,Yao Z X. 2013. Rupture history of the 2013 MW6.6 Lushan earthquake constrained with local strong motion and teleseismic body and surface waves[J]. Geophys Res Lett,40(20):5371–5376. doi: 10.1002/2013GL056876
Hartzell S. 1978. Earthquake aftershocks as Green’s functions[J]. Geophys Res Lett,5(1):1–4. doi: 10.1029/GL005i001p00001
Hartzell S,Guatteri M,Mai P M,Liu P C,Fisk M. 2005. Calculation of broadband time histories of ground motion,Part Ⅱ:Kinematic and dynamic modeling using theoretical Green’s functions and comparison with the 1994 Northridge earthquake[J]. Bull Seismol Soc Am,95(2):614–645. doi: 10.1785/0120040136
Hartzell S,Liu P,Mendoza C,Ji C,Larson K M. 2007. Stability and uncertainty of finite-fault slip inversions:Application to the 2004 Parkfield,California,earthquake[J]. Bull Seismol Soc Am,97(6):1911–1934. doi: 10.1785/0120070080
Hartzell S,Frankel A,Liu P,Zeng Y,Rahman S. 2011. Model and parametric uncertainty in source-based kinematic models of earthquake ground motion[J]. Bull Seismol Soc Am,101(5):2431–2452. doi: 10.1785/0120110028
Irikura K,Miyake H. 2011. Recipe for predicting strong ground motion from crustal earthquake scenarios[J]. Pure Appl Geophys,168(1/2):85–104.
Kennett B L N. 2009. Seismic Wave Propagation in Stratified Media[M]. 2nd ed. Canberra: ANU Press: 59–100.
Kieling K,Wang R,Hainzl S. 2014. Broadband ground-motion simulation using energy-constrained rise-time scaling[J]. Bull Seismol Soc Am,104(6):2683–2697. doi: 10.1785/0120140063
Konno K,Ohmachi T. 1998. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor[J]. Bull Seismol Soc Am,88(1):228–241. doi: 10.1785/BSSA0880010228
Liu P,Archuleta R J,Hartzell S H. 2006. Prediction of broadband ground-motion time histories:Hybrid low/high-frequency method with correlated random source parameters[J]. Bull Seismol Soc Am,96(6):2118–2130. doi: 10.1785/0120060036
Motazedian D,Atkinson G M. 2005. Stochastic finite-fault modeling based on a dynamic corner frequency[J]. Bull Seismol Soc Am,95(3):995–1010.
Sun X,Hartzell S,Rezaeian S. 2015. Ground-motion simulation for the 23 August 2011,Mineral,Virginia,earthquake using physics-based and stochastic broadband methods[J]. Bull Seismol Soc Am,105(5):2641–2661. doi: 10.1785/0120140311
Tinti E,Fukuyama E,Piatanesi A,Cocco M. 2005. A kinematic source-time function compatible with earthquake dynamics[J]. Bull Seismol Soc Am,95(4):1211–1223. doi: 10.1785/0120040177
Wang R. 1999. A simple orthonormalization method for stable and efficient computation of Green’s functions[J]. Bull Seismol Soc Am,89(3):733–741.
Zhu L,Rivera L A. 2002. A note on the dynamic and static displacements from a point source in multilayered media[J]. Geophys J Int,148(3):619–627. doi: 10.1046/j.1365-246X.2002.01610.x
-
期刊类型引用(6)
1. 段沛然，谷丙洛，李振春，李青阳. 起伏地表QR径向基函数有限差分及其在弹性波逆时偏移中的应用. 地球物理学报. 2024(03): 1181-1207 . 
百度学术
2. Mu-Ming Xia，Hui Zhou，Chun-Tao Jiang，Han-Ming Chen，Jin-Ming Cui，Can-Yun Wang，Chang-Chun Yang. Wave propagation across fluid-solid interfaces with LBM-LSM coupling schemes. Petroleum Science. 2024(05): 3125-3141 . 必应学术
3. 陈苏，丁毅，孙浩，赵密，王进廷，李小军. 物理驱动深度学习波动数值模拟方法及应用. 力学学报. 2023(01): 272-282 . 百度学术
4. 李广才，王兴宇，李培，张鹏辉，何梅兴. 地震正演模拟技术在膏盐岩识别中的应用. 中国煤炭地质. 2023(02): 67-72 . 百度学术
5. 刘家豪，雍凡，刘振东，张辉，严加永，阮小敏，高凤霞，陈昌昕. 江南造山带中段地壳结构特征——来自武宁—吉安深反射地震随机介质相关长度分析的认识. 地球学报. 2022(06): 803-816 . 百度学术
6. 刘立彬，段沛然，张云银，田坤，谭明友，李振春，窦婧瑛，李青阳. 基于无网格的地震波场数值模拟方法综述. 地球物理学进展. 2020(05): 1815-1825 . 百度学术
其他类型引用(7)
计量
- 文章访问数: 388
- HTML全文浏览量: 222
- PDF下载量: 91
- 被引次数: 13
