Global sensitivity analysis of the generalized Pareto distribution model for seismicity in the northeast Tibetan
-
摘要: 基于广义帕累托分布构建地震活动性模型，因其输入参数取值难以避免不确定性，导致依据该模型所得的地震危险性估计结果具有不确定性。鉴于此，本文选取青藏高原东北缘为研究区，提出了基于全域敏感性分析的地震危险性估计的不确定性分析流程和方法。首先，利用地震活动性广义帕累托模型，进行研究区地震危险性估计；然后，选取地震记录的起始时间和震级阈值作为地震活动性模型的输入参数，采用具有全域敏感性分析功能的E-FAST方法，对上述两个参数的不确定性以及两参数之间的相互作用对地震危险性估计不确定性的影响进行定量分析。结果表明：地震危险性估计结果（不同重现期的震级重现水平、震级上限及相应的置信区间）对两个输入参数中的震级阈值更为敏感；不同重现期的地震危险性估计结果对震级阈值的敏感程度不同；对不同的重现期而言，在影响地震危险性估计结果的不确定性上，两个输入参数之间存在非线性效应，且非线性效应程度不同。本文提出的不确定性分析流程和方法，可以推广应用于基于其它类型地震活动性模型的地震危险性估计不确定性分析。Abstract: Because the selected values of input parameters of generalized Pareto distribution （GPD） model are difficult to avoid uncertainty, the input parameters uncertainty of this model may lead to uncertainty in the seismic hazard estimation. In this paper, we selected northeastern Tibetan Plateau as the case studied area, and proposed an uncertainty analysis process and method of seismic hazard estimation based on the global sensitivity analysis. First, we used the GPD seismicity model to obtain the results of seismic hazard estimation. And then, we selected starting time of earthquake catalog and magnitude threshold to be the input parameters of seismicity model. The E-FAST method with global sensitivity analysis function was used to quantitatively analyze the influence of the uncertainties of the two parameters and the interaction between the two parameters on the uncertainty of seismic hazard estimation. The results show that the seismic hazard estimation of the GPD model is more sensitive to the magnitude threshold. With different return periods, the sensitivity degree of seismic hazard estimation to magnitude threshold is different. For different return periods, there are nonlinear effects between the two input parameters on the uncertainty of seismic hazard estimation, and the degree of nonlinear effects is different. The uncertainty analysis process and method proposed in this paper can be applied to the uncertainty analysis of seismic hazard estimation based on other seismicity models.
-
引言
山东地区位于中国大陆东部，自中生代以来经历了复杂的地质构造运动，如中生代早期华北地块与扬子地块的碰撞、中生代中晚期的华北克拉通破坏以及新生代以来的拉张变形等。陆地区域内发育沂沭断裂带（郯庐断裂带山东段）和聊考断裂带两大断裂系统，北部海域发育张家口—蓬莱断裂带，导致地震活动频繁，并伴有大地震的发生，如1668年郯城M8.5地震，造成了重大的人员伤亡和经济损失。
2003年6月5日和2020年2月18日，山东省最大的两个城市青岛和济南分别发生了一次M4.1地震（图1），虽然未导致较大的人员伤亡和经济损失，但由于其发生于人口均近千万的两大城市，且有感范围较大，余震次数较多，而上述两个地区通常被认为属于“弱震”区，因此，这两次地震仍然引发了非常大的关注。前人综合余震重定位结果、震源机制解等数据，推测这两次地震可能属于相对完整岩体条件下的一次新破裂活动（潘元生等，2004）或区域构造应力作用下附近断裂或次级派生断裂活动的结果（张斌等，2020）。另外，自2000年以来，山东半岛地区相继发生了崂山震群、乳山震群和长岛震群，但目前上述发震区尚未有高精度的层析成像数据，速度结构与发震机理仍不清楚。因此，有必要查明上述地区的浅部及深部速度结构形态，探讨速度结构与地震发震机理之间的关系，为后期的防震减灾提供理论支持。
![]()
图 1 山东及周边地区构造分区图（修改自苏道磊等，2016）Figure 1. Tectonic settings in and around Shandong area （modified from Su et al，2016）1. 数据与方法
本文所用数据来源于山东及邻区96个台站（图2a）记录的区域内地震事件的P波和S波到时数据，主要分为两部分：第一部分为1975年1月至2014年1月发生的天然地震事件（苏道磊等，2016）；第二部分为2016年1月至2019年12月发生的天然地震事件。原始数据共包含7 271个地震事件。
![]()
图 2 台站（a）及地震（b）分布图Figure 2. Distribution of seismic stations （a） and local earthquakes （b） used in this study为保证反演结果的准确性，需要对地震事件进行严格挑选，设定标准如下：① 每个地震事件至少被4个台站接收；② 震相走时残差绝对值小于3.0 s；③ 重定位前后，发震时刻偏差小于2.0 s，水平向偏差小于6 km，震源深度偏差小于8 km。最终筛选出4 652个地震事件，包括3万6 482个P波震相到时和3万2 600个S波震相到时用于成像反演（图2b）。
本文采用TOMOG3D三维层析成像反演方法（Zhao et al，1992）。该方法采用三维网格节点表示空间的速度分布，空间内每一点的速度值由周围八个节点的速度值进行线性插值获得，允许三维空间内存在间断面，通过伪弯曲算法快速准确地计算射线路径和走时，并能够同时处理近远震及后续震相到时数据。
合适的一维初始速度模型对最终反演结果的准确性至关重要。苏道磊等（2016）分别测试了三个初始速度模型：① 鲁西地区地壳速度模型，同时考虑莫霍面起伏（嘉世旭，张先康，2005）；② 山东地震台网定位用地壳速度模型；③ 华北地区地壳速度模型（陈立华，宋仲和，1990）。测试结果表明，鲁西地区地壳速度模型的走时残差均方根最小，也更符合真实地层情况，而华北地区地壳速度模型走时残差远大于其它两个速度模型。因此，本文仅对比前两个初始速度模型的走时残差，并同时考虑莫霍面起伏的影响。其中，莫霍面埋深数据来自于CRUST1.0模型（Laske et al，2013）和郑宏等（2021）利用接收函数反演得到的山东地区莫霍面埋深等（图3）。初始S波速度模型由P波速度除以1.732得到。
![]()
图 3 基于不同模型反演所得的莫霍面埋深（a，b）及本研究所用莫霍面埋深（c）Figure 3. Moho depths inverted from different models （a，b） and used in this study （c）经过计算，上述两个初始速度模型的残差均方根分别为0.841 s和0.860 s，走时残差分布如图4所示。对比发现，鲁西地区速度模型要优于山东地震台网定位用地壳速度模型，与苏道磊等（2016）的结论相似。因此，后续的层析成像反演采用鲁西地区速度模型，并考虑莫霍面起伏的影响。
![]()
图 4 使用鲁西地区地壳速度模型（a）和山东地震台网定位用地壳速度模型（b）在地震重定位前后所得的走时残差分布图Figure 4. Travel time residual distribution based on crustal velocity model in Luxi area （a） and Shandong seismic network （b） before and after relocation本研究中，初始模型三维网格节点横向间隔为0.2°×0.2°，纵向上分别在1，10，20和30 km深度处设置节点层。反演前，基于初始速度模型和原始到时数据对所有地震事件进行了重新定位。重定位前后的走时残差分布如图4所示，重定位后的总体走时残差均方根由0.841 s降低到0.649 s，其中P波走时残差均方根由0.792 s降低到0.620 s，S波走时残差均方根由0.893 s降低到0.680 s，说明地震定位精度有了较大幅度的提高。走时残差绝大多数位于±2 s以内，因此选择走时残差在±2 s以内的震相参与最终的成像反演。反演采用带阻尼和平滑因子的最小二乘（least squares QR-factorization，缩写为LSQR）方法（Paige，Saunders，1982）得到最终的三维速度结构。通过大量的测试，P波和S波速度反演采用的最优阻尼和平滑因子均为5.0和50.0 （图5）。
![]()
图 5 P波（a，b）和S波（c，d）成像中不同阻尼和平滑因子对应的三维速度模型标准差与走时残差均方根关系曲线Figure 5. Trade-off curves between the standard deviation of the 3-D velocity model and the root-mean-square of travel time residual according to the damping （a and c） and smoothing （b and d） parameters for P- （a，b） and S-wave （c，d） tomographies2. 分辨率测试
在分析成像结果之前，需要对成像结果的可靠性进行评估，一般采用检测板（checkerboard）方法（Zhao et al，1992）。在该方法中，首先将三维空间内相邻网格节点分别设置±3%的速度扰动，然后利用相同的地震和台站分布计算理论走时，并在计算理论走时过程中加入标准差为0.1 s的随机误差来检测计算稳定性。随后对得到的理论走时在初始一维速度模型的基础上进行反演，通过对比三维网格节点处扰动值的恢复情况对成像结果的可靠性进行评估。如果反演后扰动值与反演前扰动值的分布相似，则说明分辨率较好。
图6显示了横向间隔分别为0.33°×0.33°，0.4°×0.4°和0.5°×0.5°的分辨率测试结果。结果显示，对于P波和S波成像结果，研究区内大部分地区的分辨率能达到0.4°×0.4°，部分地区如鲁西南地区和山东半岛地区可达到0.33°×0.33°的分辨率。其中：网格间距为0.33°×0.33°时，P波和S波检测板扰动值恢复准确性分别达到74%和81%，振幅恢复达到70%的比例约为47%和59%，振幅恢复达到100%的比例约为32%和41%；网格间距为0.4°×0.4°时，P波和S波检测板扰动值恢复准确性分别达到76%和82%，振幅恢复达到70%的比例约为52%和62%，振幅恢复达到100%的比例约为36%和41%；网格间距为0.5°×0.5°时，P波和S波检测板扰动值恢复准确性分别达到77%和82%，振幅恢复达到70%的比例约为55%和64%，振幅恢复达到100%的比例约为37%和42%。
![]()
图 6 检测板分辨率测试结果Figure 6. Results of checkerboard resolution tests（a） 0.33°×0.33°；（b） 0.4°×0.4°；（c） 0.5°×0.5°3. 结果与讨论
经过反演，P波和S波走时残差均方根由反演前的0.620 s和0.680 s分别降低到0.378 s和0.417 s，减少近40%。利用P波、S波反演结果计算得到了泊松比成像结果，如图7所示。苏道磊等（2016）的P波层析成像结果揭示出：在1—10 km深度切片上，沂沭断裂带沿构造走向表现出强烈的横向不均一性，高低速异常交替出现，胶东半岛北部海域、胶莱盆地和济阳坳陷主要表现为低速异常；20—30 km深度，鲁西地区存在较大范围的低速异常（苏道磊等，2016）。上述结果与本文的P波成像结果非常一致（图7a）。另外，本文的S波成像结果与Li等（2018）基本一致，如在10 km深度上，沂沭断裂带北部以低速异常为主（图7b），20—30 km山东半岛表现为大范围的低速异常（图7a）。但由于本文应用了更多的P波和S波到时数据，因此本文的成像结果具有更高的分辨率，如在1 km和10 km深度，沂沭断裂带南部西侧的两个低速异常区相互分离，断裂带东侧表现为高速异常（图7a），这在苏道磊等（2016）的研究中揭示得并不明显。同时，本文的检测板测试结果也要优于苏道磊等（2016），鲁西南和山东半岛地区分辨率能够达到0.33°×0.33°。山东半岛地区中下地壳存在大范围低速异常，说明该地区可能存在较强烈的地幔上涌（李志伟等，2006）。本文同时利用Liu和Zhao （2018）提出的方法计算了1—30 km的P波、S波和泊松比的平均值。平均泊松比异常与郑宏等（2021）利用接收函数反演得到的山东地区的泊松比分布基本一致，进一步说明了本文成像结果的可靠性。
![]()
图 7 山东地区不同深度P波速度扰动（a）、S波速度扰动（b）及泊松比相对扰动（c）结果底部3幅图分别为1—30 km的P波、S波速度扰动及泊松比相对扰动的平均值Figure 7. Map views of P-wave （a），S-wave （b） and Poisson’s ratio （c） perturbations in Shandong areaThe averages of P-wave，S-wave and Poisson’s ratio anomalies from 1 to 30 km are shown at the bottom泰山作为山东地区的最高点，自新生代以来经历了多期快速抬升（李理，钟大赉，2006）。接收函数研究结果显示，泰山地区具有较薄的地壳厚度（32 km左右）和较大的泊松比（0.27），且没有明显的方位各向异性（郑宏等，2021）。本文的成像结果显示，泰山地区下方存在明显的低速异常（图8左下四幅图），这说明该地区仍存在较强的地幔上涌，导致泰山新生代以来出现显著抬升，并且现在仍处于抬升阶段（郑宏等，2021）。另外，在浅部1—10 km深度（图8左上四幅图），泰山北部为高速异常，南部为低速异常，这与泰山的岩性和地质构造是一致的：以泰山山前断裂为界，断裂北侧为泰山主体，主要出露前寒武纪泰山变质杂岩，以隆升为主；山前断裂南侧以沉降为主，主要为泰安—莱芜盆地巨厚的第三系碎屑岩及第四系沉积物（李理，钟大赉，2006）。
![]()
图 8 长清地震及泰山周边不同深度处P波速度扰动（a）、S波速度扰动（b）及泊松比相对扰动（c）结果Figure 8. Map views of P-wave （a），S-wave （b） and Poisson’s ratio （c） perturbations around Changqing earthquake and Mount Tai2020年2月18日，济南长清发生了一次MS4.1地震，震源深度约为2.7 km，并引发近40次的余震活动（张斌等，2020）。本文的成像结果显示，该地震震中位于P波、S波高低速异常和高低泊松比异常过渡带，可能与该地震有关的长清断裂也位于P波、S波和泊松比高低异常过渡带（图8上半部和图9）。震中东部的高速异常与该地区的背景噪声成像结果一致，可能与济南侵入岩体有关（雷霆，2020）。震源机制解显示，该地震具有正断兼走滑性质，其余震多为走滑性质（张斌等，2020）。另外，余震重定位结果显示，主震两侧的破裂呈明显不对称分布，以西北侧破裂为主（张斌等，2020）。因此，济南长清MS4.1地震可能是区域构造应力下长清断裂发生左旋走滑运动的结果（张斌等，2020），这与本文的层析成像结果相一致。另外，主震的西北向不对称破裂的形成可能是由于震中东侧高速异常体的存在阻碍了地震的东向破裂。
![]()
图 9 过长清地震的剖面AA′（a）的P波速度扰动（b）、S波速度扰动（c）和泊松比扰动（d）Figure 9. Vertical cross section of P-wave （b），S-wave （c） and Poisson’s ratio （d） perturbations along a profile AA′ （a） across the Changqing earthquake shown in the inset map2003年6月5日青岛崂山地区发生了ML4.1地震（图10a左侧），2004年11月1日附近地区又发生一次ML3.6地震，这两次地震都形成了震群序列。根据定位结果，这两次震群序列大致呈北西走向，与附近的主要断裂近似垂直、与次级断裂展布方向基本一致但并不重合，可能属于相对完整岩体条件下的一次新的破裂（潘元生等，2003，2005）。根据本文的成像结果，这两次地震及震群序列发生在P波高低速异常过渡带、S波低速异常区和高低泊松比过渡区且偏向于高泊松比区域（图10a—c 1km），同时深部存在明显的P波和S波低速异常（图10a，b 10—30 km），这与1995年日本神户地震（ML7.2）震源区的速度和泊松比结构非常相似（Zhao et al，1996）。另外，震中附近水资源丰富，同时为花岗岩侵入形成地区，且构造裂隙发育（赵广涛等，1996）。因此本文认为，可能是深部的流体填充相对完整岩体内的裂隙并引发破裂，从而导致地震的发生。需要注意的是，虽然这两次地震及震群序列与本地区北东走向的主断层没有直接关系，但本文的成像结果显示，该地区北东走向的主断层基本位于低速区内以及高低泊松比异常的过渡带（图10），因此仍需警惕该地区发生震级更大的中强地震的可能性。
![]()
图 10 山东半岛地区不同深度P波速度扰动（a）、S波速度扰动（b）及泊松比相对扰动（c）结果Figure 10. Map views of P-wave （a），S-wave （b） and Poisson’s ratio （c） perturbations in and around Shandong Peninsula乳山地区位于大别—苏鲁超高压变质带的东部，可能存在大量的中生代岩浆侵入体（郭敬辉等，2005）。自2013年10月开始，记录到的乳山震群地震数已超过1万余次，最大震级为M5.0，目前震群活动可能已结束。震群周边的断裂大多以NE-NNE向为主，而近期的重定位结果和震源机制解显示，乳山地震序列主要呈NW向展布，绝大多数地震发生于中上地壳，发震断层可能为倾角近直立的左旋走滑断层，与区域内的主要断裂并不一致（张斌等，2017）。本文的成像结果显示，乳山震群周边1 km深度以高速异常和高泊松比异常为主，10 km深度主要为高低速异常过渡区，20—30 km深度以低速异常和低泊松比异常为主（图10）。另外，震群附近地热资源较为丰富（田粟，2012）。因此，本文认为，乳山地区深部存在热地幔物质上涌，内部含有的流体注入浅部相对较完整的侵入体内或侵入体之间，在区域应力场的作用下导致侵入体的破裂或侵入体之间隐伏断裂的活动，从而引发乳山震群。这与前人对乳山震群进行的震源谱参数反演、震中空间分布、震中随时间的演化规律以及震源区应力状态的研究结果是一致的（郑建常等，2016；王鹏，2019）。
长岛震群的发生可能主要受控于NWW向的张家口—蓬莱断裂，这是一条深大断裂，可能已切穿莫霍面甚至岩石圈，成为地幔热物质或基性物质上涌的通道（张岭等，2007），断裂主要以正断兼走滑运动为主（索艳慧等，2013）。历史上，附近海域曾发生过M6.0和M7.0左右的大地震（王志才等，2006）。本文的成像结果显示（图10），张家口—蓬莱断裂带的地壳速度结构特征与沂沭断裂带具有非常大的相似性（苏道磊等，2016），地壳速度和泊松比结构在1—10 km深度处具有非常强烈的横向不均一性，断裂一侧高低速异常交替分布，断裂带整体位于高低速异常与高低泊松比异常的过渡带，20 km以下以低速和低泊松比异常为主，但部分地区仍有显著的高泊松比异常，可能反映了地幔热物质的上涌。速度和泊松比异常在10 km左右发生明显变化，这与前人得到的b值在8.5 km左右发生转折是一致的（申金超等，2019）。本文认为，深部地幔热物质沿断裂带上涌所产生的构造应力，和/或地幔热物质内部含有的流体沿断裂上涌或侵入裂隙导致了长岛震群、甚至周边地区的强震活动。
4. 结论
利用山东及邻区的地震台站记录的P波和S波到时数据反演获得了研究区内高精度的纵横波速度结构和泊松比异常分布形态。研究结果揭示了研究区内的地壳结构具有强烈的横向不均一性。2020年济南长清MS4.1地震可能是区域构造应力下长清断裂发生左旋走滑运动的结果，震中东侧的高速异常体可能阻碍了地震的东向破裂。2003年青岛崂山ML4.1地震可能是由深部的流体填充相对完整岩体内的裂隙并引发破裂所致。崂山震群、乳山震群和长岛震群可能与深部流体有非常强的相关性。
-
![]()
图 1 青藏高原东北缘主要活动断裂及M≥4.0地震分布图
Figure 1. Map of main active faults and M≥4.0 earthquakes distribution in northeastern Tibetan Plateau
![]()
图 2 青藏高原东北缘1880—2020年M≥5.0地震的M-t图
Figure 2. M-t map of the M≥5.0 earthquakes from 1880 to 2020 in northeastern Tibetan Plateau
![]()
图 4 修饰的尺度参数（a）和形状参数（b）估计值随震级阈值选取的变化
Figure 4. Variation diagram of estimators for modified scale parameter （a） and shape parameter （b） according to the magnitude threshold
![]()
图 5 广义帕累托分布拟合诊断图
（a） 概率图；（b） 分位数图；（c） 重现水平图；（d） 概率密度图
Figure 5. Diagnostic plots of the generalized Pareto distribution fitted to magnitude
（a） Probability plot；（b） Quantile plot；（c） Return level plot；（d） Probability density plot
![]()
图 6 地震危险性估计结果对地震目录起始时间ts和震级阈值u的主效应指标Si直方图
横轴数字代表的含义下同
Figure 6. Histogram of the first-order effect Si of seismic hazard estimation on earthquake catalogue start time ts and magnitude threshold u
The meanings of the number represent are the same below
![]()
图 8 地震危险性估计结果对地震目录起始时间ts和震级阈值u的主效应指标和交互效应指标直方图
Figure 8. Histogram of the first-order effect and interactions on earthquake catalogue start time ts and magnitude threshold u
![]()
图 7 地震危险性估计结果对地震目录起始时间ts和震级阈值u的全效应指标
$S^{\rm{T}}_i$ 直方图Figure 7. Histogram of the total effect
$S^{\rm{T}}_i$ of seismic hazard estimation on earthquake catalogue start time ts and magnitude threshold u表 1 不同震级地震的余震时间窗（Gardner，Knopoff，1974）
Table 1 Aftershock time windows of different magnitudes（Gardner，Knopoff，1974）
主震震级 持续天数/d 主震震级 持续天数/d M4.0 42 M6.5 790 M4.5 83 M7.0 915 M5.0 155 M7.5 960 M5.5 290 M8.0 985 M6.0 510 M8.5 985 
下载: 导出CSV
表 2 青藏高原东北缘地震危险性估计
Table 2 Seismic hazard estimation for northeastern Tibetan Plateau
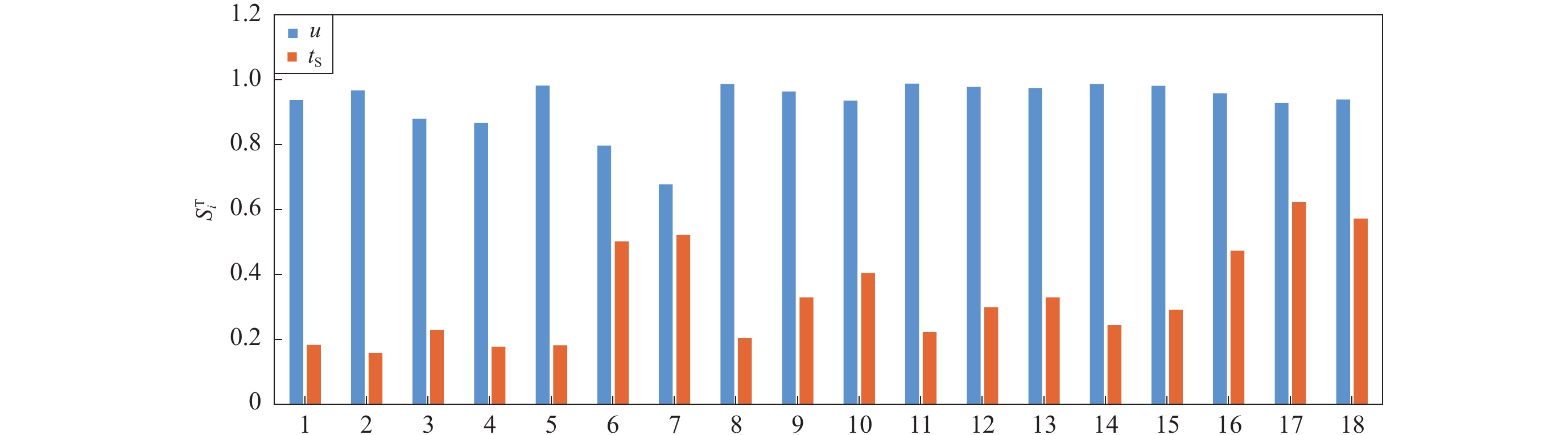
重现期/a M 置信度95%的置信区间 20 7.40 ［ 7.10，7.69 ］ 50 7.80 ［ 7.49，8.11 ］ 100 8.03 ［ 7.69，8.37 ］ 200 8.22 ［ 7.84，8.59 ］ 500 8.41 ［ 7.97，8.84 ］ ∞ 8.95 ［ 8.03，9.87 ］
下载: 导出CSV
表 3 地震危险性估计结果对地震目录起始时间ts和震级阈值u的主效应指标Si和全效应指标
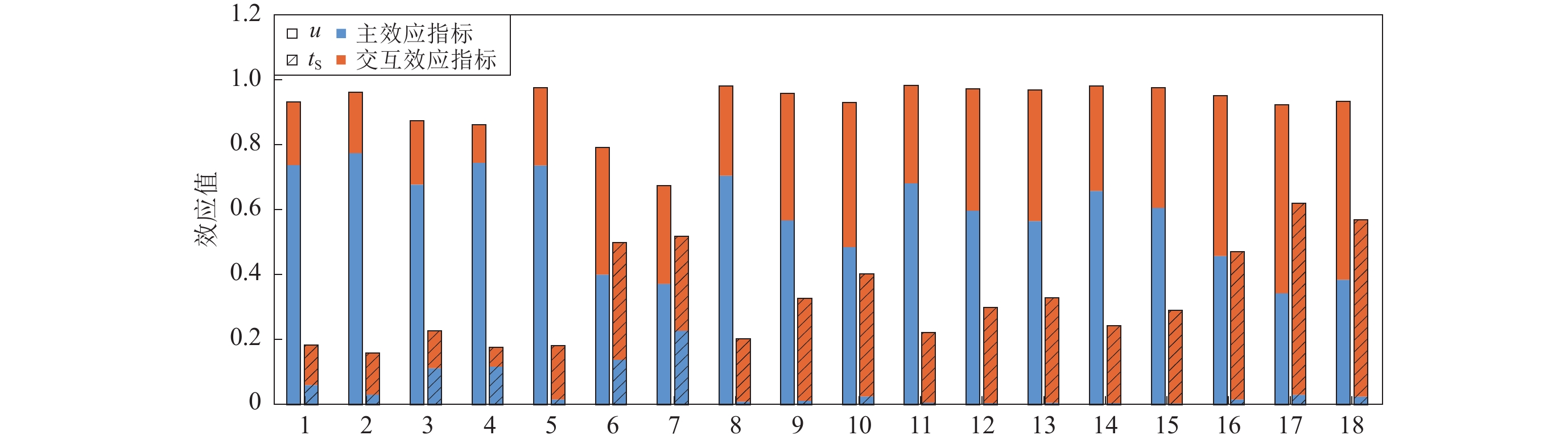
$S^{\rm{T}}_i$ Table 3 Total and the first-order effects of the seismic hazard estimation on earthquake catalogue initial time ts and magnitude threshold u
重现期/a 参数 M 置信度95%的置信区间下端点 置信度95%的置信区间上端点 Si $S^{\rm{T}}_i$ Si $S^{\rm{T}}_i$ Si $S^{\rm{T}}_i$ 20 u 0.742 4 0.937 8 0.779 1 0.968 4 0.681 3 0.880 5 ts 0.059 5 0.184 0 0.030 2 0.158 9 0.112 5 0.229 4 50 u 0.749 5 0.868 0 0.740 6 0.982 8 0.402 3 0.797 9 ts 0.117 8 0.178 2 0.015 3 0.182 4 0.138 9 0.502 4 100 u 0.374 1 0.678 8 0.709 5 0.987 7 0.570 5 0.964 7 ts 0.228 6 0.522 3 0.008 8 0.204 5 0.011 8 0.329 7 200 u 0.487 6 0.936 6 0.685 8 0.988 9 0.600 7 0.978 9 ts 0.024 9 0.405 1 0.005 6 0.223 1 0.004 3 0.300 2 500 u 0.568 6 0.975 0 0.661 6 0.987 6 0.609 4 0.982 2 ts 0.004 8 0.329 7 0.004 0 0.244 3 0.003 3 0.292 1 ∞ u 0.460 0 0.958 8 0.345 0 0.929 2 0.386 0 0.940 2 ts 0.015 2 0.473 8 0.029 5 0.623 5 0.024 2 0.573 0
下载: 导出CSV
-
顾功叙. 1983. 中国地震目录: 公元前1831—公元1969年[M]. 北京: 科学出版社: 773–791. Gu G X. 1983. Catalogue of Earthquakes in China: 1831BC-1969AD[M]. Beijing: Science Press: 773–791 （in Chinese）.
国家地震局震害防御司. 1995. 中国历史强震目录[M]. 北京: 地震出版社: 496–499. Department of Earthquake Damage Prevention, State Seismological Bureau. 1995. Catalogue of Historical Strong Earthquakes in China[M]. Beijing: Seismological Press: 496–499 （in Chinese）.
洪明理,任鲁川,霍振香. 2014. 基于E-FAST法分析海啸波高对潜在海啸源参数的敏感性[J]. 地震学报,36(2):252–260. Hong M L,Ren L C,Huo Z X. 2014. Sensitivity analysis on maximum tsunami wave heights to the potential tsunami source parameters based on extended FAST method[J]. Acta Seismologica Sinica,36(2):252–260 (in Chinese).
胡聿贤, 鹿林. 1990. 地震活动性估计的不确定性[G]//地震危险性分析中的综合概率法. 北京: 地震出版社: 176–177. Hu Y X, Lu L. 1990. Uncertainty in seismicity estimation[G]//Synthetic Probability Method in Seismic Hazard Analysis. Beijing: Seismological Press: 176–177 （in Chinese）.
胡聿贤. 1999. 地震安全性评价技术教程[M]. 北京: 地震出版社: 227–228. Hu Y X. 1999. Seismic Safety Evaluation Technology Tutorial[M]. Beijing: Seismological Press: 227–228 （in Chinese）.
黄玮琼,李文香,曹学锋. 1994. 中国大陆地震资料完整性研究之二:分区地震资料基本完整的起始年分布图象[J]. 地震学报,16(4):423–432. Huang W Q,Li W X,Cao X F. 1994. Study on the integrity of seismic data in Mainland China Ⅱ:The initial year distribution images of the complete data on each seismic zone[J]. Acta Seismologica Sinica,16(4):423–432 (in Chinese).
蒋溥, 戴丽思. 1993. 工程地震学概论[M]. 北京: 地震出版社: 110. Jiang P, Dai L S. 1993. Introduction to Engineering Seismology[M]. Beijing: Seismological Press: 110 （in Chinese）.
刘杰,陈棋福,陈顒. 1996. 华北地区地震目录完全性分析[J]. 地震,16(1):59–67. Liu J,Chen Q F,Chen Y. 1996. Completeness analysis of the seismic catalog in North China region[J]. Earthquake,16(1):59–67 (in Chinese).
潘华,李金臣. 2016. 新一代地震区划图的地震活动性模型[J]. 城市与减灾,(3):28–33. doi: 10.3969/j.issn.1671-0495.2016.03.008 Pan H,Li J C. 2016. A seismicity model for a new generation of seismic zoning maps[J]. City and Disaster Reduction,(3):28–33 (in Chinese).
钱小仕,王福昌,盛书中. 2013a. 基于广义帕累托分布的地震震级分布尾部特征分析[J]. 地震学报,35(3):341–350. Qian X S,Wang F C,Sheng S Z. 2013a. Characterization of tail distribution of earthquake magnitudes via generalized Pareto distribution[J]. Acta Seismologica Sinica,35(3):341–350 (in Chinese).
钱小仕,蔡晓光,任晴晴. 2013b. 中国大陆活动地块边界带强震震级分布特征研究[J]. 地震工程与工程振动,33(1):212–220. Qian X S,Cai X G,Ren Q Q. 2013b. Characteristics of the great earthquake magnitude distributions for active tectonic boundaries in Chinese mainland[J]. Earthquake Engineering and Engineering Vibration,33(1):212–220 (in Chinese).
任梦依. 2018. 龙门山地区的地震活动性广义帕累托模型构建[J]. 地震研究,41(2):226–232. doi: 10.3969/j.issn.1000-0666.2018.02.010 Ren M Y. 2018. The establishment of generalized Pareto distribution model of seismicity in Longmenshan region[J]. Journal of Seismological Research,41(2):226–232 (in Chinese).
任雪梅,高孟潭,俞言祥. 2012a. 基于MGR模型修正我国大陆中强以上地震的震级-频度关系和确定震级极限值[J]. 地震学报,34(3):331–338. Ren X M,Gao M T,Yu Y X. 2012a. Modification of magnitude-frequency relation and magnitude limit determination based on MGR model for moderate-strong earthquakes in Chinese mainland[J]. Acta Seismologica Sinica,34(3):331–338 (in Chinese).
任雪梅,高孟潭,张纳莉. 2012b. 基于MGR模型的我国大陆地区各地震带1970年以来震级·频度关系和震级上限[J]. 中国地震,28(3):320–327. Ren X M,Gao M T,Zhang N L. 2012b. Magnitude-frequency relation and magnitude limit of seismic zones based on the MGR model in Chinese mainland since 1970[J]. Earthquake Research in China,28(3):320–327 (in Chinese).
史道济. 2006. 实用极值统计方法[M]. 天津: 天津科学技术出版社: 28–32. Shi D J. 2006. Practical Extremum Statistical Methods[M]. Tianjin: Tianjin Science and Technology Press: 28–32 （in Chinese）.
宋明丹,冯浩,李正鹏,高建恩. 2014. 基于Morris和EFAST的CERES-Wheat模型敏感性分析[J]. 农业机械学报,45(10):124–131. doi: 10.6041/j.issn.1000-1298.2014.10.020 Song M D,Feng H,Li Z P,Gao J E. 2014. Global sensitivity analyses of DSSAT-CERES-Wheat model using Morris and EFAST methods[J]. Transactions of the Chinese Society for Agricultural Machinery,45(10):124–131 (in Chinese).
田建伟,刘哲,任鲁川. 2017. 基于广义帕累托分布的马尼拉海沟俯冲带地震危险性估计[J]. 地震,37(1):158–165. Tian J W,Liu Z,Ren L C. 2017. Seismic hazard estimation of the Manila trench subduction zone based on generalized Pareto distribution[J]. Earthquake,37(1):158–165 (in Chinese).
王健,高孟潭. 1996. 地震危险性分析中的参数敏感性研究[J]. 地震学报,18(4):489–493. Wang J,Gao M T. 1996. Study on parameter sensitivity in seismic hazard analysis[J]. Acta Seismologica Sinica,18(4):489–493 (in Chinese).
徐化超. 2018. 青藏高原东北缘地区主要活动断裂带的运动学研究[D]. 北京: 中国地震局地震预测研究所: 15–41. Xu H C. 2008. Kinematics Study of Main Active Fault Zones in the Northeastern Qinghai-Tibet Plateau[D]. Beijing: Institute of Earthquake Forecasting, China Earthquake Administration: 15–41 （in Chinese）.
徐伟进. 2012. 地震危险性分析中地震时空统计分布模型研究[D]. 北京: 中国地震局地球物理研究所: 4–5. Xu W J. 2012. Study on Space-Time Statistical Distribution Models of Earthquakes in Seismic Hazard Analysis[D]. Beijing: Institute of Earthquake Forecasting, China Earthquake Administration: 4–5 （in Chinese）.
Coles S. 2001. An Introduction to Statistical Modeling of Extreme Values[M]. London: Springer-Verlag: 74–91.
Cramer C H,Petersen M D,Reichle M S. 1996. A Monte Carlo approach in estimating uncertainty for a seismic hazard assessment of Los Angeles,Ventura,and Orange counties,California[J]. Bull Seismol Soc Am,86(6):1681–1691. doi: 10.1785/BSSA0860061681
Cukier R I,Fortuin C M,Shuler K E. 1973. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients I:Theory[J]. J Chem Phys,59(8):3873–3878. doi: 10.1063/1.1680571
Cukier R I,Levine H B,Shuler K E. 1978. Nonlinear sensitivity analysis of multiparameter model systems[J]. J Comput Phys,26(1):1–42. doi: 10.1016/0021-9991(78)90097-9
Dutfoy A. 2019. Estimation of tail distribution of the annual maximum earthquake magnitude using extreme value theory[J]. Pure Appl Geophys,176(2):527–540. doi: 10.1007/s00024-018-2029-0
Fisher R A,Tippett L H C. 1928. Limiting forms of the frequency distribution of the largest or smallest member of a sample[J]. Math Proc Camb Philos Soc,24(2):180–190. doi: 10.1017/S0305004100015681
Gan W J,Zhang P Z,Shen Z K,Niu Z J,Wang M,Wan Y G,Zhou D M,Cheng J. 2007. Present-day crustal motion within the Tibetan Plateau inferred from GPS measurements[J]. J Geophys Res:Solid Earth,112(B8):B08416.
Gardner J K, Knopoff L. 1974. Is the sequence of earthquakes in southern California, with aftershocks removed, Poissonian?[J] Bull Seismol Soc Am, 64（5）: 1363-1367.
Knopoff L,Gardner J K. 1972. Higher seismic activity during local night on the raw worldwide earthquake catalogue[J]. Geophys J Int,28(3):311–313. doi: 10.1111/j.1365-246X.1972.tb06133.x
Lawrence Livermore National Laboratory （LLNL）. 1989. Seismic hazard characterization of 69 nuclear plant sites East of the Rocky Mountains: Methodology, input data and comparisons to previous results for ten test site[J]. NUREG/CR-5250-V1.
Li Y H,Wang X C,Zhang R Q,Wu Q J,Ding Z F. 2017. Crustal structure across the NE Tibetan Plateau and Ordos block from the joint inversion of receiver functions and Rayleigh-wave dispersions[J]. Tectonophysics,705:33–41. doi: 10.1016/j.tecto.2017.03.020
McGuire R K,Shedlock K M. 1981. Statistical uncertainties in seismic hazard evaluations in the United States[J]. Bull Seismol Soc Am,71(4):1287–1308.
McGuire R K. 1987. Seismic hazard uncertainty and its effects on design earthquake ground motions[C]//Proceeding of International Seminar on Seismic Zonation. Guangzhou: State Seismological Bureau: 351–359.
Petersen M D, Frankel A D, Harmsen S C, Mueller C S, Haller K M, Wheeler R L, Wesson R L, Zeng Y H, Boyd O S, Perkins D M, Luco N, Field E H, Wills C J, Rukstales K S. 2008. Documentation for the 2008 Update of the United States National Seismic Hazard Maps[R]. Reston, Virginia: U.S. Geological Survey: 1–60.
Pisarenko V F,Sornette D. 2003. Characterization of the frequency of extreme earthquake events by the generalized Pareto distribution[J]. Pure Appl Geophys,160(12):2343–2364. doi: 10.1007/s00024-003-2397-x
Pisarenko V F,Sornette A,Sornette D,Rodkin M V. 2014. Characterization of the tail of the distribution of earthquake magnitudes by combining the GEV and GPD descriptions of extreme value theory[J]. Pure Appl Geophys,171(8):1599–1624. doi: 10.1007/s00024-014-0882-z
Saltelli A,Tarantola S,Chan K P S. 1999. A quantitative model-independent method for global sensitivity analysis of model output[J]. Technometrics,41(1):39–56. doi: 10.1080/00401706.1999.10485594
Sobol I M. 1993. Sensitivity estimates for nonlinear mathematical models[J]. Math Model Comput Exp,1(4):407–414.
Taylor M,Yin A. 2009. Active structures of the Himalayan-Tibetan orogen and their relationships to earthquake distribution,contemporary strain field,and Cenozoic volcanism[J]. Geosphere,5(3):199–214. doi: 10.1130/GES00217.1
Yin A,Harrison T M. 2000. Geologic evolution of the Himalayan-Tibetan orogen[J]. Annu Rev Earth Planet Sci,28:211–280. doi: 10.1146/annurev.earth.28.1.211
-
期刊类型引用(4)
1. 冀国强，雷建设，赵大鹏. 利用多震相走时成像研究胶东地区三维地壳速度结构与震群孕震环境. 地球物理学报. 2025(01): 123-138 . 
百度学术
2. 汪煜昆，赵丹，刘婷芝，淦文杰，王永强，张清秀，郭静姝. 致密砂岩压裂后的储层敏感性特征实验——以四川盆地JQ地区沙溪庙组8号砂体为例. 天然气勘探与开发. 2024(03): 85-93 . 百度学术
3. 孟秋，王子韬，张怀. 2023年8月6日山东德州平原M 5.5地震同震变形及地震活动性变化数值模拟. 地质学报. 2024(07): 2101-2109 . 百度学术
4. 韩光洁，刘奕君，席楠. 2023年山东平原M_S 5.5地震宽频带面波震级和近场地震动反应谱空间分布特征分析. 地震地磁观测与研究. 2023(06): 13-19 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 252
- HTML全文浏览量: 123
- PDF下载量: 72
- 被引次数: 4
