Magnetotelluric static correction of two-dimensional model based on the highest frequency phase method and spatial filtering method
-
摘要: 静态效应一直是影响大地电磁测深法精确性的主要原因之一。在相位校正法的基础上提出了一种更适用于电性变化较为平缓的地质情况的静态校正方法—最高频相位法，其核心是用需要校正测点两侧受静态效应影响较小测点的最高频视电阻率的算术平均值代替相位法递推公式中每个频点前一个频点的视电阻率值，以消除相位法中的误差积累。以二维模型的正反演为例，通过对比空间滤波法、相位法和最高频相位法对不同模型静态校正前后的正反演结果，证明了最高频相位法的有效性和优越性，同时表明，对于电阻率变化大并且静态位移严重的水平层状地层模型，采用与空间滤波法相结合的联合校正效果更佳。Abstract: Static effect is one of the main reasons for affecting the accuracy of magnetotelluric sounding. In this paper, a static correction method, the highest frequency phase method, is proposed on the basis of the phase correction method, which is more suitable for geological conditions with smooth electrical changes. Its principle is to eliminate the error accumulation in the phase correction method by replacing the apparent resistivity value of the previous frequency point in the recurrence formula with the arithmetic mean of the highest frequency apparent resistivity of the measuring points on both sides of the measuring points that need to be corrected and are less affected by the static effect. Taking the forward and inversion of two-dimensional model as an example, the effectiveness and superiority of the highest frequency phase method are proved by comparing the forward and inversion results from spatial filtering method, phase correction method and highest frequency phase method before and after static correction for different models. It also shows that for the horizontal layered formation model with sharp resistivity difference and severe static shift, the static correction effect of joint correction which combines highest frequency phase method with spatial filtering method is much better.
-
根据美国地质调查局（United States Geological Survey，缩写为USGS）国家地震信息中心（National Earthquake Information Centre，缩写为NEIC）的测定，2020年6月23日15时29分04秒（UTC），墨西哥南部瓦哈卡州发生了一次矩震级MW7.4的地震，NEIC初步确定的震中（preliminary determination epicenter， 缩写为PDE）位于（15.916 3°N，95.953 3°W），震源深度为20 km。美国地质调查局（USGS，2020）和全球矩心矩张量组（GCMT，2020）随后发布了这次地震的矩心矩张量解（表1）。根据USGS （2020）发布的地震目录，在该主震发生后的48小时内发生了9次较大余震，其中最大余震震级达到MW5.4，5次事件深达35 km。
表 1 不同机构所得墨西哥MW7.4地震矩心矩张量解的比较Table 1. Comparison of the centroid moment tensor solutions for the MW7.4 Mexico earthquake obtained by different institutions机构 矩张量/（1020 N·m） 矩心参数 Mrr Mtt Mpp Mrt Mrp Mtp τc/s 北纬/° 西经/° 矩心深度/km GCMT （2020） 0.729 −0.737 0.008 1.220 −0.712 0.200 7.0 16.04 96.06 20 USGS （2020）（W震相） 0.731 −0.752 0.020 1.104 −0.479 0.168 13.2 15.93 95.90 21.5 USGS （2020）（体波反演） 0.527 −0.544 0.017 0.504 −0.289 0.101 − 16.04 95.90 32 本文 0.700 −0.789 0.089 0.825 −0.491 0.218 8.0 15.96 95.89 22 类似于上述两个组织的工作（Dziewonski et al，1981；Kanamori，Rivera，2008；Duputel et al，2012；Ekström et al，2012），我们收集了震中距处于32.5°—88.9°范围内全球地震台网（Global Seismograph Network，缩写为GSN）和数字地震台网联盟（International Federation of Digital Seismograph Networks，缩写为FDSN）的42个台站的长周期垂直分量数据，基于AK135模型计算格林函数（Wang，1999），利用我们自主研发的反演软件（张喆，许力生，2020），通过反演0.01—0.05 Hz频带内的P波波形得到了这次地震的矩心矩张量解。根据反演结果（图1），矩心时间为8 s，矩心震中位于（15.96°N，95.89°W），矩心深度为22 km，标量地震矩为1.24×1024 N·m，相当于MW7.4。基于矩心矩张量解（表1，图2），我们也求得了相应的最佳双力偶解（图2，表2），最佳双力偶成分占97%。最后，我们利用反演结果计算了合成波形，并与观测波形进行了比较，结果如图3所示，可见二者之间的相关系数平均值达到0.93，大多数台站的相关系数在0.90以上，均方根误差达1.33×10−5 m。
![]()
图 1 矩心矩张量反演过程（a） 矩心时间搜索；（b） 矩心搜索；（c） 矩心深度搜索；（d） PDE位置（灰色）和矩心位置（红色）反演得到的矩张量解Figure 1. Inversion process of the centroid moment tensor（a） Search for the centroid time；（b） Search for the centroid；（c） Search for the centroid depth； （d） The moment tensor solutions at the PDE （gray） and centroid （red） locations![]()
图 2 矩心矩张量反演参数以及台站分布与反演结果Figure 2. The parameters of the centroid moment tensor inversion，the station distribution and the inversion results表 2 不同机构所得墨西哥MW7.4地震的最佳双偶解Table 2. The best double-couple solutions for the MW7.4 Mexico earthquake obtained by different institutes机构 标量地震矩
/（1020 N·m）双力偶成分
占比节面Ⅰ 节面Ⅱ 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° GCMT （2020） 1.600 100% 270 16 62 118 76 97 USGS （2020）（W震相） 1.423 96% 271 17 70 112 74 96 USGS （2020）（体波） 0.797 99% 266 24 63 114 69 101 本文 1.236 97% 266 22 60 118 71 101 ![]()
图 3 观测波形与合成波形的比较Figure 3. Comparison between the observed （blue） and synthetic （red） waveforms与USGS和GCMT的结果相比（图4），我们反演所得矩心位置（15.96°N，95.89°W，深度22 km）、矩心时间、最佳双力偶解均与其非常相近。根据最佳双力解的节面参数、矩心位置、余震分布以及地震所处的构造环境，我们判断走向266°、倾角22°、滑动角60°的节面为真实的发震断层面（图4）。这是一次以逆冲为主、具有相当走滑分量的断层错动，或者说这是一次发生在俯冲带的斜滑事件。
![]()
图 4 主震震源机制解与余震分布不同颜色的沙滩球和正方形代表不同机构确定的震源机制解及其矩心位置，小圆圈表示余震（来自USGS地震目录），大圆圈表示主震的PDE位置，圆圈和正方形的填充色显示了震源深度Figure 4. The focal mechanism solutions of the mainshock and the aftershock distributionColored beach-balls and squares represent the focal mechanism solutions and centroid locations determined by the various institutions，the small circles refer to the aftershocks （from the USGS catalog），and the large circle indicates the PED locations of the mainshock. The colors filled in the circles and squares indicate the focal depths本研究使用的数字波形数据均通过地震学联合研究会（Incorporated Research Institutions for Seismology，缩写为IRIS）数据中心获取，震源机制数据分别来自全球矩心矩张量（GCMT）和美国地质调查局（USGS），余震数据来自于美国地质调查局（USGS），作者在此表示感谢！
-
![]()
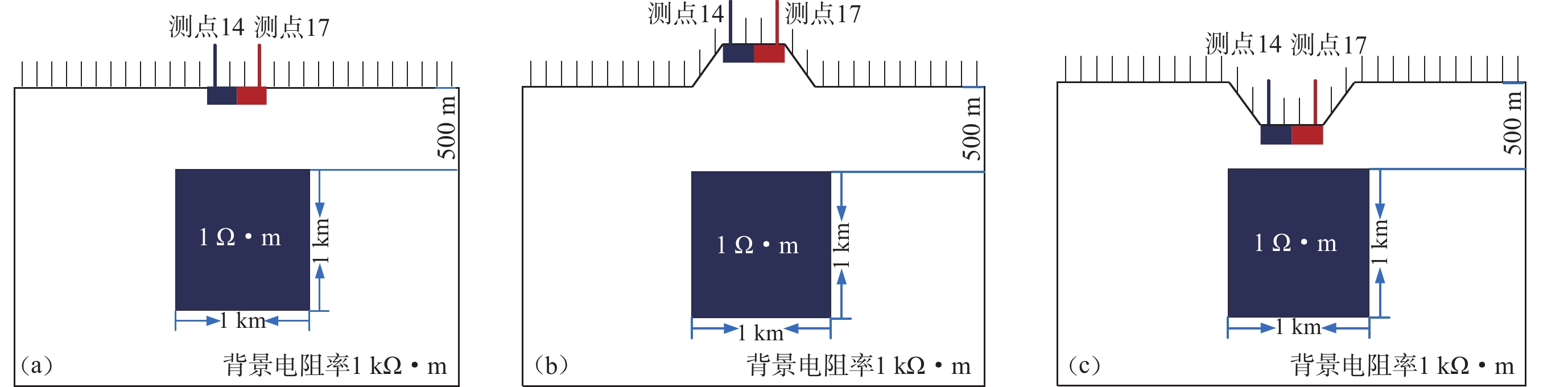
图 1 无地形（a）、含地垒（b）、含地堑（c）的均匀半空间介质近地表存在低阻和高阻电性异常体的模型
测线长3 km，测点数为30，点距为100 m；左侧低阻异常体长200 m，高40 m，电阻率为1 Ω·m；右侧高阻异常体长200 m，高40 m，电阻率为105 Ω·m
Figure 1. Schematic of the half space model with low and high resistivity anomaly near surface for the model of flat surface （a），horst terrain （b） and graben terrain （c），respectively
The measuring line is 3 km long，and there are 30 measuring points，and the point spacing is 100 m；the left low resistivity anomaly body and the right high resistivity body are both 200 m in length and 40 m in height，while the electrical resistivity are 1 Ω·m and 105 Ω·m，respectively；the horst is 300 m high and the graben is 300 m deep. The same below
![]()
图 2 利用三种静态校正方法对无地形（a）、含地垒（b）、含地堑（c）的均匀半空间介质近地表低阻异常体正上方测点的静态校正效果对比
Figure 2. Comparison of static correction effects of the measuring point above the near surface low resistivity anomaly body of homogeneous half-space with flat surface （a），horst terrain （b） and graben terrain （c），respectively
![]()
图 3 无地形（a）、含地垒（b）、含地堑（c）的均匀半空间介质近地表高阻异常体正上方测点静态校正效果对比
Figure 3. Comparison of static correction effects of the measuring point above near surface high resistivity anomaly of homogeneous half-space with flat surface （a），horst terrain （b） and graben terrain （c），respectively
![]()
图 4 三层地层加近地表低阻和高阻异常体的模型
（a） 无地形；（b） 含地垒地形；（c） 含地堑地形
Figure 4. Schematic model of three-layer strata with low and high resistivity anomaly near surface
（a） The flat surface；（b） With the horst terrain；（c） With the graben terrain
![]()
图 5 使用四种方法对无地形（a）、含地垒（b）、含地堑（c）的水平层状介质近地表低阻异常体正上方测点进行静态校正效果对比
Figure 5. Comparison of static correction effects of measuring points above near surface low resistivity anomaly of the horizontal layered medium with flat surface （a），horst terrain （b） and graben terrain （c） using four methods，respectively
![]()
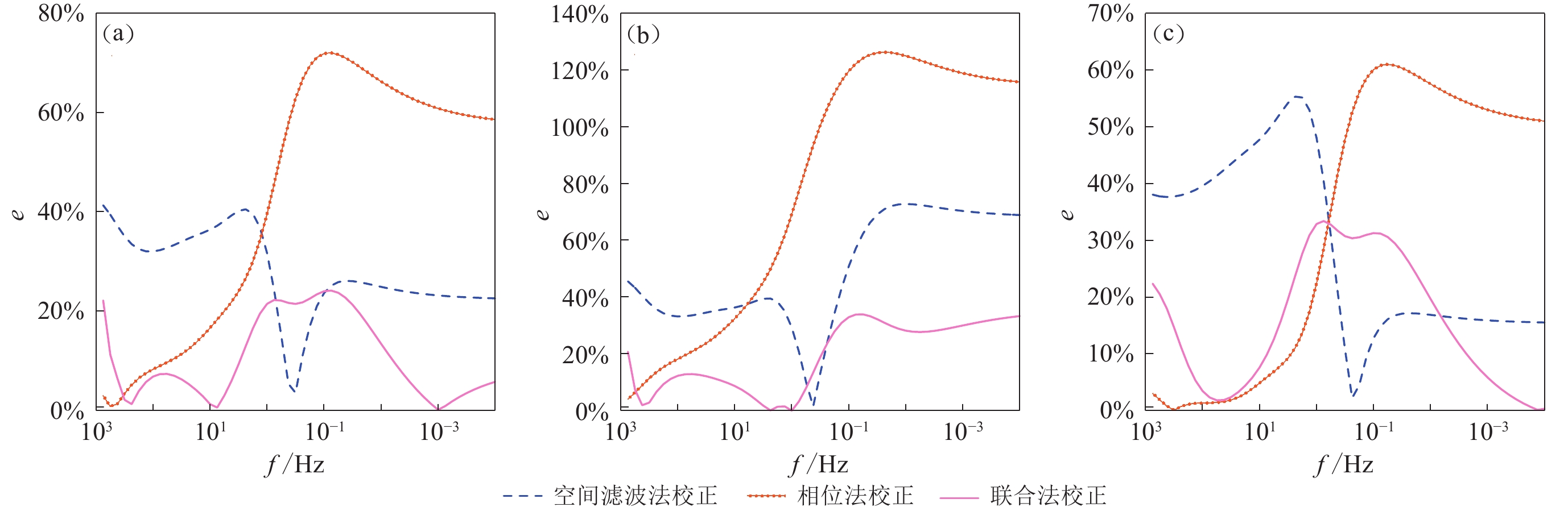
图 6 使用三种不同方法对无地形（a）、含地垒（b）、含地堑（c） 的水平层状介质近地表低阻异常体正上方测点的静态校正误差e对比
Figure 6. Comparison of static correction errors of measuring points above near surface low resistivity anomaly of the horizontal layered medium with flat surface （a），horst terrain （b）， and graben terrain （c） using three methods，respectively
![]()
图 7 使用四种方法对无地形（a）、含地垒（b）、含地堑（c）的水平层状介质近地表高阻异常体正上方测点静态校正效果对比
Figure 7. Comparison of static correction effects of the measuring points above near surface high resistivity anomaly of the horizontal layered medium with flat surface （a），horst terrain （b）， and graben terrain （c） using four methods，respectively
![]()
图 8 无地形（a）、含地垒（b）、含地堑（c）的均匀半空间介质近地表存在低阻和高阻且深部存在低阻电性异常体的模型
Figure 8. Schematic of the homogeneous half space model with near surface electrical anomaly bodies and deep embedding anomaly bodies with flat surface （a），horst terrain （b） and graben terrain （c），respectively
![]()
图 9 无地形（a）、含地垒（b）、含地堑（c）的三层地层近地表和深部存在电性异常体的模型
Figure 9. Schematic of three-layer strata model with near surface electrical anomalies and deep embedding anomaly with flat surface （a），horst terrain （b） and graben terrain （c），respectively
![]()
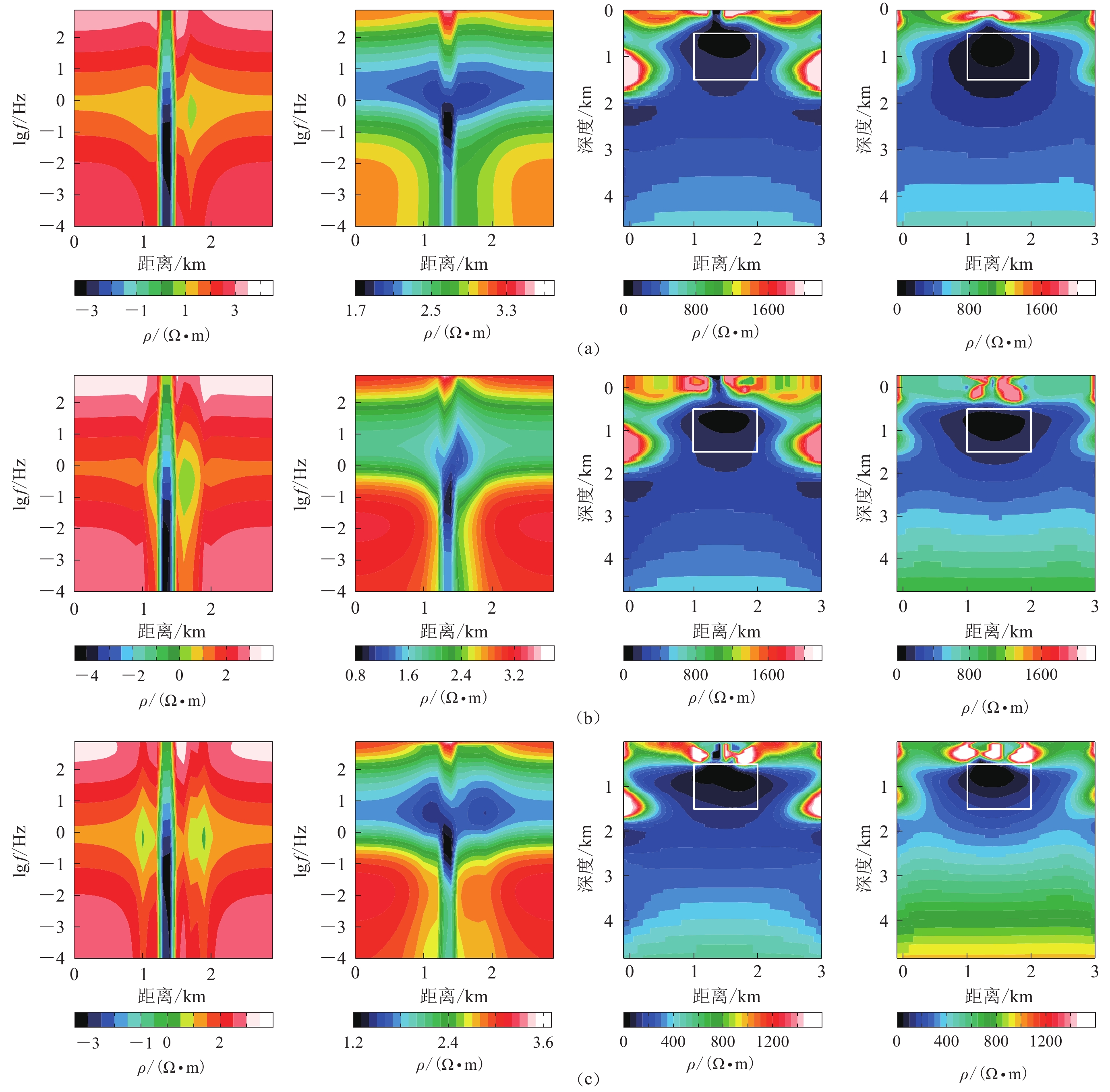
图 10 无地形（a）、含地垒（b）、含地堑（c）的均匀半空间介质中利用最高频相位法静态校正前后的正演（左侧两列）与反演（右侧两列）效果对比（白色矩形区域为模型中异常体的位置，下同）
Figure 10. Comparison of correction effects of the forward （left two columns） and inversion （right two columns） results before and after correction by the highest frequency phase method for homogeneous half-space with flat surface （a），horst terrain （b） and graben terrain （c），respectively （The white rectangle represents the anomalous body，the same below）
![]()
图 11 无地形（a）、含地垒（b）、含地堑（c）时水平均匀层状介质的联合校正法校正前后的正演（左侧两列）与反演（右侧两列）效果对比
Figure 11. Comparison of correction effects of the forward （left two columns） and inversion （right two columns） results before and after correction by the joint correction method for three-layer stratum model with flat surface （a），horst terrain （b） and graben terrain （c），respectively
-
陈清礼,张翔,胡文宝. 1999a. 南方碳酸盐岩区大地电磁测深曲线静态偏移校正[J]. 江汉石油学院学报,21(3):30–32. Chen Q L,Zhang X,Hu W B. 1999a. A correction method for static shift in magnetotellurics in carbonate area of southern China[J]. Journal of Jianghan Petroleum Institute,21(3):30–32 (in Chinese).
陈清礼,胡文宝,李金铭,杨华. 1999b. 利用地表电阻率校正大地电磁静态偏移[J]. 物探与化探,23(4):289–295. Chen Q L,Hu W B,Li J M,Yang H. 1999b. The application of surface resistivity to the correction of magnetotelluric static migration[J]. Geophysical and Geochemical Exploration,23(4):289–295 (in Chinese).
程少华. 2012. 大地电磁静态效应校正方法对比研究[D]. 西安: 长安大学: 9–12. Cheng S H. 2012. Contrastive Analysis of Different Static Shift Correction Methods in Megnetotelluric （MT）[D]. Xi’an: Chang’an University: 9–12 （in Chinese）.
高红伟,张胜业. 1998. 阻抗张量分解进行大地电磁静校正的研究[J]. 地质科技情报,17(1):91–96. Gao H W,Zhang S Y. 1998. Study of correction for static shift:The decomposition of magnetotelluric impedance tensors[J]. Geological Science and Technology Information,17(1):91–96 (in Chinese).
谷海亮,李云鹏. 2013. 大地电磁测深静校正方法在新疆彩华沟铜矿区的应用[J]. 西部探矿工程,25(5):91–93. doi: 10.3969/j.issn.1004-5716.2013.05.029 Gu H L,Li Y P. 2013. The application of magnetotelluric sounding static correction method in Caihuagou copper deposits of Xinjiang[J]. West-China Exploration Engineering,25(5):91–93 (in Chinese).
黄潜生,王友胜,汪卫毛. 2004. 大地电磁曲线校正技术在六盘山盆地研究中的应用[J]. 江汉石油学院学报,26(3):76–78. Huang Q S,Wang Y S,Wang W M. 2004. Application of magnetotelluric curve correction technology in the study of Liupanshan basin[J]. Journal of Jianghan Petroleum Institute,26(3):76–78 (in Chinese).
梁生贤,张胜业,祁晓雨,石研斌. 2010. 基于空间滤波和相位换算的MT静校正方法比较[J]. 工程地球物理学报,7(3):300–306. Liang S X,Zhang S Y,Qi X Y,Shi Y B. 2010. Comparison of static correction methods in magnetotellurics based on spatial filtering and phase conversion technology[J]. Chinese Journal of Engineering Geophysics,7(3):300–306 (in Chinese).
刘宏,王家映. 1997. 三维电磁阵列剖面法的基本原理及应用[J]. 地球物理学进展,12(1):61–73. Liu H,Wang J Y. 1997. The basic principle and applications the electromagnetic array profiling[J]. Progress in Geophysics,12(1):61–73 (in Chinese).
刘建利. 2011. 大地电磁测深法阻抗相位的特性与应用[J]. 陕西地质,30(2):56–61. doi: 10.3969/j.issn.1001-6996.2011.02.008 Liu J L. 2011. Characteristics and application of impedance phase by magnetotelluric sounding[J]. Geology of Shaanxi,30(2):56–61 (in Chinese).
刘鸣,李文尧,马国强,李攀峰,王福国. 2015. EH4静态校正相位法在云南某矿区圈定含煤层位的应用[J]. 河南科学,32(2):248–252. Liu M,Li W Y,Ma G Q,Li P F,Wang F G. 2015. The application of EH4 static corrective phase method in delineating the coal strata of an orefield in Yunnan[J]. Henan Science,32(2):248–252 (in Chinese).
刘铁. 2015. 基于高频大地电磁法相位信息压制静态效应方法研究[J]. 铁道建筑技术,(10):34–37. doi: 10.3969/j.issn.1009-4539.2015.10.010 Liu T. 2015. Study on the method of suppressing static effect based on the phase information of high-frequency magnetotelluric sounding[J]. Railway Construction Technology,(10):34–37 (in Chinese).
罗延钟,何展翔,马瑞伍,郭建华. 1991. 可控源音频大地电磁法的静态效应校正[J]. 物探与化探,15(3):196–202. Luo Y Z,He Z X,Ma R W,Guo J H. 1991. The correction of static effects in sonic frequency telluric electromagnetic method of controllable source[J]. Geophysical and Geochemical Exploration,15(3):196–202 (in Chinese).
罗志琼. 1990. 用电磁阵列剖面法压制MT静态效应影响的研究[J]. 地球科学:中国地质大学学报,15(增刊):13–22. Luo Z Q. 1990. The study of attenuating static effects with electromagnetic array profiling[J]. Earth Science:Journal of China University of Geosciences,15(S1):13–22 (in Chinese).
仇根根,钟清,刘君平,白大为,袁永真. 2012. 大地电磁测深视电阻率和相位曲线之间近似互算方法及程序实现[J]. 物探化探计算技术,34(4):402–405. doi: 10.3969/j.issn.1001-1749.2012.04.06 Qiu G G,Zhong Q,Liu J P,Bai D W,Yuan Y Z. 2012. Approximately calculating method of bounding between magnetotelluric apparent resistivity curve and phase curve and its programing realization[J]. Computing Techniques for Geophysical and Geochemical Exploration,34(4):402–405 (in Chinese).
宋守根,汤井田,何继善. 1995. 小波分析与电磁测深中静态效应的识别、分离及压制[J]. 地球物理学报,38(1):120–128. doi: 10.3321/j.issn:0001-5733.1995.01.014 Song S G,Tang J T,He J S. 1995. Wavelets analysis and the recognition,separation and removal of the static shift in electromagnetic soundings[J]. Chinese Journal of Geophysics,38(1):120–128 (in Chinese).
汤井田,何继善. 1993. 静效应校正的波数域滤波方法[J]. 物探与化探,17(3):209–216. Tang J T,He J S. 1993. The wavenumber domain filtering method for static effect correction[J]. Geophysical and Geochemical Exploration,17(3):209–216 (in Chinese).
王家映. 1990. 电磁阵列剖面法的基本原理[J]. 地球科学:中国地质大学学报,15(增刊):1–11. Wang J Y. 1990. The basic principle of the electromagnetic array profiling[J]. Earth Science:Journal of China University of Geosciences,15(S1):1–11 (in Chinese).
王家映. 1992. 关于大地电磁的静校正问题[J]. 地质科技情报,11(1):69–76. Wang J Y. 1992. Problem about static correction in magnetotellurics[J]. Geological Science and Technology Information,11(1):69–76 (in Chinese).
王书明. 1998. 表面局部三维大地电磁曲线畸变校正:MT畸变校正阻抗张量分解方法[J]. 西北地震学报,20(4):1–11. Wang S M. 1998. The correction of magnetotelluric curve distortion caused by surficial local three-dimension inhomogeneities:The impedance tensor decomposition technique for the correction of MT curves distortion[J]. Northwestern Seismological Journal,20(4):1–11 (in Chinese).
谢成良,魏文博,金胜,叶高峰,景建恩,张乐天,董浩,张帆,王辉,姚硕. 2013. 相位张量分析约束下的大地电磁测深阻抗张量分解方法研究[J]. 地球物理学进展,28(3):1208–1218. doi: 10.6038/pg20130312 Xie C L,Wei W B,Jin S,Ye G F,Jing J E,Zhang L T,Dong H,Zhang F,Wang H,Yao S. 2013. Study of magnetotelluric impedance tensor decomposition under the constraint of analysis of phase tensor[J]. Progress in Geophysics,28(3):1208–1218 (in Chinese).
杨淼鑫,李晓晨,刘小畔. 2012. MT数据处理中静校正方法对比[J]. 物探化探计算技术,34(3):310–313. doi: 10.3969/j.issn.1001-1749.2012.03.12 Yang M X,Li X C,Liu X P. 2012. Comparison of different static correction methods in MT data processing[J]. Computing Techniques for Geophysical and Geochemical Exploration,34(3):310–313 (in Chinese).
杨生,鲍光淑,张少云. 2001. MT法中利用阻抗相位资料对畸变视电阻率曲线的校正[J]. 地质与勘探,37(6):42–45. Yang S,Bao G S,Zhang S Y. 2001. The correction to aberrant appearance resistivity curve by using impedance phase data in magenetotelluric method[J]. Geology and Prospecting,37(6):42–45 (in Chinese).
杨生,鲍光淑,李爱勇. 2002. MT法中静态效应及阻抗张量静态校正法[J]. 中南工业大学学报,33(1):8–13. Yang S,Bao G S,Li A Y. 2002. The static migration to MT data and the impedance tensor static correction method[J]. Journal of Central South University of Technology,33(1):8–13 (in Chinese).
尹曜田,魏文博,叶高峰,金胜,董浩. 2012. 基于遗传算法的大地电磁阻抗张量分解方法研究[J]. 地球物理学报,55(2):671–682. Yin Y T,Wei W B,Ye G F,Jin S,Dong H. 2012. An improved GB decomposition method based on genetic algorithm[J]. Chinese Journal of Geophysics,55(2):671–682 (in Chinese).
张翔,胡文宝,严良俊,张世忠. 2002. 小波变换在大地电磁测深静校正中的应用[J]. 江汉石油学院学报,24(2):40–41. Zhang X,Hu W B,Yan L J,Zhang S Z. 2002. Application of wavelet transformation of static correction in magnetotelluric depth measurement[J]. Journal of Jianghan Petroleum Institute,24(2):40–41 (in Chinese).
朱仁学. 1999. 大地电磁测深中相位微分的研究[J]. 地球物理学报,42(增刊):209–218. Zhu R X. 1999. A study of the phase-derivative in magnetotelluric method[J]. Chinese Journal of Geophysics,42(S1):209–218 (in Chinese).
Andrieux P, Wightman W E. 1984. The so-called static corrections in magnetotelluric measurements[C]//Proceedings of the 54th Annual International Meeting. Atlanta: Society of Exploration Geophysicists: 270–270.
Bostick F X. 1986. Electromagnetic array profiling （EMAP）[C]//56th Annual SEG Meeting. Houston: Society of Exploration Geophysicists: 60–61.
Cagniard L. 1953. Basic theory of the magneto-telluric method of geophysical prospecting[J]. Geophysics,18(3):605–635. doi: 10.1190/1.1437915
Groom R W,Bailey R C. 1989. Decomposition of magnetotelluric impedance tensors in the presence of local three-dimensional galvanic distortion[J]. J Geophys Res,94(B2):1913–1925. doi: 10.1029/JB094iB02p01913
Sternberg B K,Washburne J C,Pellerin L. 1988. Correction for the static shift in magnetotellurics using transient electromagnetic soundings[J]. Geophysics,53(11):1459–1468. doi: 10.1190/1.1442426
Tikhonov A N. 1950. On determining electric characteristics of the deep layers of the earth’s crust[J]. Doklady,73(2):295–297.
-
期刊类型引用(1)
1. 杨天春，朱德兵，付国红，杨追，黄睿. 天然电场选频法在高压线干扰环境下的浅层地下水勘探. 中国科技论文. 2024(10): 1065-1072 . 
百度学术
其他类型引用(1)
下载:
计量
- 文章访问数: 346
- HTML全文浏览量: 115
- PDF下载量: 29
- 被引次数: 2
