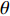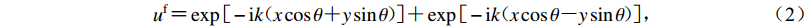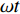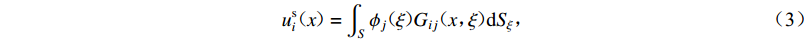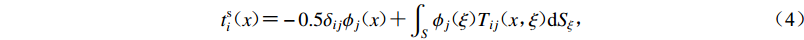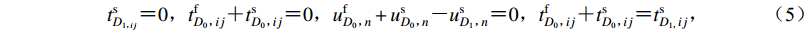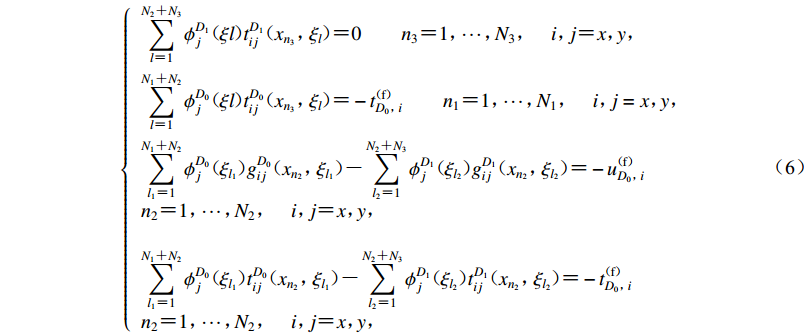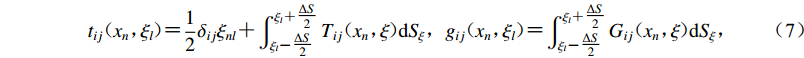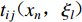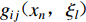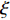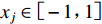Prediction model of seismic amplification effect in sedimentary valley based on differential evolution-artificial neural network
-
摘要: 探讨了基于差分进化-人工神经网络构建沉积河谷地震响应代理模型的可行性。首先建立沉积河谷对地震波散射的求解方法，以半圆形、V形沉积河谷为例，以入射波条件、沉积内外介质属性、场地形状为特征参数，以沉积河谷地震动放大系数为预测目标参数，构建数据集；其次，建立沉积河谷地震动放大效应人工神经网络、差分进化-人工神经网络算法预测模型，对比两种算法计算精度和稳定性，并进行了特征参数敏感性分析。结果表明：人工神经网络能较好地预测沉积河谷地震动放大效应，使差分进化-人工神经网络预测模型的精度和稳定性显著提高；入射波频率是影响沉积河谷地震动放大系数的主要原因，沉积内外介质密度比的影响较小。本研究结论可对地震作用下更为复杂的局部场地效应预测和评估提供参考。Abstract: Sedimentary valley has obvious amplification effect on ground motions, which has an increase on the engineering damage. However, the propagation mechanism of seismic wave in sedimentary valley is complex, resulting in high nonlinearity and high coupling of influences of incident wave and site parameters on seismic amplification effect. First, based on the boundary element method, the scattering of seismic waves by sedimentary valley is solved. Prediction models of seismic amplification effect of semicircular and V-shaped sedimentary valley are established, with incident wave conditions, material properties and valley shapes as characteristic parameters and the seismic amplification factor of sedimentary valley as target parameters, and the dataset is constructed; Second, the calculation accuracy and stability of artificial neural network （ANN） and its optimization algorithm, i.e., differential evolution, are compared, and the sensitivity of characteristic parameters is analyzed. The results show that the ANN can predict the amplification effect of sedimentary valley, and the accuracy and stability of differential evolution-ANN prediction model are significantly improved; The incident wave frequency is the main influence factor of the seismic amplification coefficient of sedimentary valley, and the density ratio of internal and external medium has little effect. The conclusions can provide references for more complex local site effect prediction and assessment.
-
引言
沉积河谷是一种典型的复杂场地，其对地震动的显著放大效应已被大量实际震害和理论分析所证实（肖文海，2009；李平等，2016；高玉峰等，2021）。研究沉积河谷地震动放大效应对地震危险性分析、地震区划和重大工程抗震设计具有重要的科学意义和应用价值。
为揭示地震波在沉积河谷中的传播机理、定量评估沉积河谷地震动放大效应，国内外科研人员采用解析法和数值法开展了诸多理论研究。解析法主要为波函数展开法（Trifunac，1971；Yuan，Liao，1995；张宁等，2017），数值法包括离散域法、边界元法等。有限元法（李伟华，赵成刚，2006；刘必灯等，2011；周国良等，2012；陈少林等，2014；陈国兴等，2015）和有限差分法（Boore，1973；Sun et al，2019）是常用的两种离散域方法。边界元法具有降维、节省计算内存、自动满足无限远辐射条件、无高频数值频散等优势，因而其广泛地应用于地震波动理论的研究中（梁建文，巴振宁，2007；Luzón et al，2009；Liu et al，2018；黄磊等，2020）。此外，综合利用上述方法的优势，Zhou和Chen （2008），Ducellier和Aochi （2012）及Shyu 等（2018）采用混合方法研究了河谷对地震波传播的影响规律。
值得指出的是，地震波在沉积河谷中的传播机理十分复杂，局部放大效应是沉积河谷对地震波的散射、波型转换、相干作用等波动现象共同作用的结果。入射波条件、介质属性、场地形状与沉积河谷地震动放大系数直接相关，且具有高非线性和高耦合性，因此，基于传统回归方法建立两者映射关系、实现沉积河谷地震动放大效应预测、量化各关键参数对放大系数的影响均存在困难。
近年来，机器学习算法广泛用于地震学领域。作为机器学习常用算法，人工神经网络及其优化方法可提供完全数据驱动的预测模型、进行独立特征参数对目标参数的敏感性分析，地震动预测是其主要应用（Kong et al，2019）。Derras等 （2012）构建了矩震级、震源深度、震中距、场地共振频率和近地表30 m等效剪切波速度五个特征参数与地震动加速度峰值的关系，此后将该方法推广至包括地震动加速度峰值、速度峰值和谱加速度等多个目标参数（Derras et al，2014）；Dhanya和Raghukanth （2018）建立了基于人工神经网络的浅层地壳地震地面运动预测方程，特征参数为矩量、离破裂面最近的距离、剪切波速和震源机制；Raghucharan等（2019）采用人工神经网络推导了喜马拉雅山和印度恒河平原地震动预测模型，此模型具有良好的精度。上述研究中数据集主要来源于实测地震记录，以震源机制、传播路径、近地表平均剪切波速为特征参数，未考虑局部场地效应对地震动的影响、未定量阐明各参数对场地效应的贡献。针对局部场地效应，Giacinto等（1997）采用一维波动理论对三角形峡谷场地放大效应进行了预测；Tavakoli和Kutanaei （2015）针对介质参数的不确定性，对伊朗某地区场地放大系数进行了评估。上述结合人工神经网络的场地效应研究均未考虑地震波的散射作用。而Paolucci等（2000）的研究表明，沉积谷地一维分析存在较大误差，需考虑二维或三维放大效应。
鉴于此，本文针对沉积河谷这一典型局部复杂场地，采用边界元法求解沉积河谷对地震波的散射；以半圆形、V形沉积河谷为计算模型，以入射波条件、介质属性、场地形状为特征参数、以五个典型地表位置的沉积河谷地震动放大系数为预测目标参数，构建数据集；建立基于人工神经网络、差分进化-人工神经网络算法的沉积河谷地震动放大系数预测模型，并对预测精度和稳定性进行对比与验证，最后分析了各特征参数对地震动放大效应的敏感性。本研究可进一步揭示沉积河谷对地震动的影响规律，为考虑地震波散射、含局部复杂地形的场地地震动预测提供参考。
1. 基于边界元法的沉积河谷地震动放大效应求解及数据集构建
本文基于边界元，准确求解SH波入射下一系列半空间沉积河谷场地动力反应。以入射波条件、介质属性、场地形状为特征参数、以沉积河谷地震动放大系数为预测目标参数，构建数据集。
1.1 计算模型
为构建沉积河谷地震动放大效应预测模型，首先建立地震作用下沉积河谷-基岩半空间计算模型（图1）。假设基岩半空间D0和沉积河谷D1均为各向同性的均匀弹性介质，半空间中存在一沉积河谷，SH波从半空间入射。由于沉积河谷沿纵向无限延长，假设横截面不变，将其简化为SH波入射下二维沉积河谷出平面散射问题。L2为D0与D1的交界线，L1和L3分别为基岩半空间地表和沉积河谷地表。
1.2 基于边界元法的沉积河谷地震动放大效应求解
根据弹性波动理论，总波场可表示为自由波场和散射波场叠加，即
$$ {u_i} {\text{＝}} u_i^{\rm{f}} {\text{＋}} u_i^{\rm{s}} {\text{，}} $$ (1) 式中，
$ {u}_{i} $ 为总位移场，${u}_{i}^{{\rm{f}}}$ ，${u}_{i}^{{\rm{s}}}$ 分别为自由波场和散射波场。假设平面SH波从半空间射入，入射角度为
$ \theta $ ，则自由波场位移表达式为$$ {u^{\rm{f}}}{\text{＝}}\exp ［ - {\rm{i}}k（x\cos \theta {\text{＋}} y\sin \theta ） ］{\text{＋}}\exp ［ - {\rm{i}}k（x\cos \theta {\text{－}} y\sin \theta ） ］{\text{，}}$$ (2) 式中，k为半空间横波波数，时间因子exp（i
$ \omega t $ ）已略去。散射场引起散射体内任一点的位移、应力积分表达式为（Luzón et al，2009）
$$ u_i^{ {\rm{s}} }（ x ） = \int_S {{\phi _j}（ \xi ）} {G_{ij}}（ {x，\xi } ）{\rm{d}}{S_{\xi} }{\text{，}} $$ (3) $$ t_i^{{\rm{s}}}（x） {\text{＝}} - 0.5{\delta _{ij}}{\phi _j}（x） {\text{＋}} \int_S {{\phi _j}（\xi ）} {T_{ij}}（x{\text{，}}\xi ）{\rm{d}}{S_{\xi} }{\text{，}} $$ (4) 式中：
${\phi _j}{\rm{d}}{S_{\xi} }$ 为离散边界单元的应力，S为虚拟源面；Gij（x，$\xi $ ）和Tij（x，$\xi $ ）（i，j＝x，y）分别代表位移格林函数和应力格林函数，表示单位力方向j作用在ξ引起x点i向的位移和应力。格林函数自动满足无限远辐射条件，同时满足波动方程。对边界L1，L2，L3进行离散，以构造散射波场。根据单层位势理论，D0中的散射场可通过在L1和L2上布置的虚拟荷载构建，D1中的散射场可通过在L2和L3上布置的虚拟荷载构建。沉积河谷边界元模型及虚拟荷载点布置见图2。
边界条件包括沉积地表L3和半空间地表L1应力为零、沉积域和半空间域交界线L2满足位移应力连续条件，即
$$ t_{{D_{1{\text{，}}ij}}}^{{\rm{s}}} {\text{＝}} 0 {\text{，}} t_{{{D_0}{\text{，}}ij}}^{{\rm{f}}} {\text{＋}} t_{{{D_0}{\text{，}}ij}}^{{\rm{s}}} {\text{＝}} 0 {\text{，}} u_{{D_0}{\text{，}}n}^{{\rm{f}}} + u_{{D_0}{\text{，}}n}^{{\rm{s}}} {\text{－}} u_{{D_1}{\text{，}}n}^{{\rm{s}}}{{ {\text{＝}} 0}} {\text{，}} t_{{{D_0}{\text{，}}ij}}^{{\rm{f}}} {\text{＋}} t_{{{D_0}{\text{，}}ij}}^{{\rm{s}}} {\text{＝}} t_{{{D_{1{\text{，}}}}ij}}^{{\rm{s}}} {\text{，}} $$ (5) 将地表、沉积表面离散为若干个单元，虚拟波源设置在离散边界单元上，将所有边界L1—L3对应离散成N1—N3，到此式（5）可转化为离散形式，表达式为
$$\begin{split}& \left\{ \begin{array}{l} \displaystyle\sum\limits_{l＝1}^{{N_2} ＋ {N_3}} {\phi _j^{{D_1}}（ {\xi l} ）t_{ij}^{{D_1}}} （ {{x_{{n_3}}}{{，}}} {{\xi _l}} ）＝0 \qquad {n_3}＝1，\cdots，{N_3}，\quad i，j ＝ x，y，\\ \displaystyle\sum\limits_{l ＝ 1}^{{N_1}＋{N_2}} {\phi _j^{{D_0}}（ {\xi l} ）t_{ij}^{{D_0}}（ {{x_{{n_3}}}{{，}}} {{\xi _l}} ） ＝ } - t_{{D_0}，i}^{（{\rm{ f }}）}\qquad {n_1}＝1，\cdots，{N_1}，\quad i，j = x，y，\\ \displaystyle\sum\limits_{{l_1} ＝ 1}^{{N_1}＋{N_2}} {\phi _j^{{D_0}}（ {{\xi _{{l_1}}}} ）g_{ij}^{{D_0}}（ {{x_{{n_2}}}，{\xi _{{l_1}}}} ）} － \displaystyle\sum\limits_{{l_2}＝1}^{{N_2}＋{N_3}} {\phi _j^{{D_1}}（ {{\xi _{{l_2}}}} ）g_{ij}^{{D_1}}（ {{x_{{n_2}}}，{\xi _{{l_2}}}} ） ＝ } - u_{{D_0}，i}^{（ {\rm{f}} ）}\qquad \\{n_2}＝1，\cdots，{N_2}{{，\quad }}i{{，}}j ＝ x，y，\\ \displaystyle\sum\limits_{{l_1} ＝ 1}^{{N_1}＋{N_2}} {\phi _j^{{D_0}}（ {{\xi _{{l_1}}}} ）t_{ij}^{{D_0}}（ {{x_{{n_2}}}，{\xi _{{l_1}}}} ）} － \displaystyle\sum\limits_{{l_2}＝1}^{{N_2}＋{N_3}} {\phi _j^{{D_1}}（ {{\xi _{{l_2}}}} ）t_{ij}^{{D_1}}（ {{x_{{n_2}}}，{\xi _{{l_2}}}} ） ＝ } - t_{{D_0}，i}^{（ {\rm{f}} ）}\qquad \\ {n_2}＝1，\cdots，{N_2}{{，\quad }}i{{，}}j＝ x，y， \end{array}\right. \end{split}$$ (6) 其中，
$$ {t_{ij}}（ {{x_n}，{\xi _l}} ） ＝ \dfrac{1}{2}{\delta _{ij}}{\xi _{nl}}＋\int_{{\xi _l} － \tfrac{{\Delta S}}{2}}^{{\xi _l}＋\tfrac{{\Delta S}}{2}} {{T_{ij}}（ {{x_n}，\xi } ）} {\rm{d}}{S_{\xi} }，{g_{ij}}（ {{x_n}，{\xi _l}} ）＝\int_{{\xi _l}－\tfrac{{\Delta S}}{2}}^{{\xi _l}＋\tfrac{{\Delta S}}{2}} {{G_{ij}}（ {{x_n}，\xi } ）{\rm{d}}{S_{\xi} }} ， $$ (7) 式中：当x
$\ne \xi $ 时，利用高斯积分法来求解上式中${t}_{ij}（{x}_{n}{\text{，}}{\xi }_{l}）$ 和${g}_{ij}（{x}_{n}{\text{，}}{\xi }_{l}）$ ；当x＝$\xi $ 时，需利用格林函数展开式解析解求得；ΔS为边界离散单元长度。基于单层位势理论，求解各单元虚拟荷载密度，得到散射波场；沉积河谷中散射波场即为总波场，半空间中需将散射波与自由波场叠加得到总波场，继而可求解任意点的位移和应力。
1.3 基于边界元法的沉积河谷地震动放大效应精度验证
本节以半圆形沉积河谷为例，验证2.2节所述方法求解弹性半空间中沉积河谷对SH波散射问题的正确性。无量纲频率η取为1，入射角θ取为0°和90°，本文所求地表各点位移放大系数与文献结果（Yuan，Liao，1995）对比如图3所示，图中a为半圆形河谷半径。由图3可知，本文结果与文献结果吻合程度良好，验证了本文方法的准确性。
![]()
图 3 本文地表位移放大系数结果与文献结果对比Figure 3. Comparison of amplification coefficient of surface displacement between the results in this paper and those in literature1.4 特征参数与预测目标参数
本文以半圆形、V形河谷为例，构建沉积河谷地震动放大效应人工神经网络、差分进化-人工神经网络数据集。设基岩半空间和沉积河谷密度分别为ρ1和ρ2，剪切波速分别为c1和c2，入射角为θ，入射波无量纲频率为η；半圆形河谷半径为a，V形河谷对称，宽度为2a、深度为h （图4）。预测模型特征参数及取值范围见表1，半圆形河谷算例中考虑了入射条件和介质参数，V形河谷还考虑了场地形状，且假设各特征参数满足均匀分布。
![]()
图 4 半圆形河谷（a）和V形河谷（b）的预测模型点位分布Figure 4. Location distribution of prediction model for semicircular valley （a） and V-shaped valley （b）表 1 预测模型的特征参数及取值范围Table 1. Characteristic parameters and value ranges of the prediction model入射角θ/° 无量纲频率η 密度比ρ2/ρ1 剪切波速比c2/c1 半圆形河谷 ［60，90］ ［0.1，5］ ［0.5，1］ ［0.7，0.8］ V形河谷 ［60，90］ ［0.1，5］ ［0，1］ ［0.4，0.6］ 地表位移放大系数是衡量局部复杂场地地震动放大效应的重要指标，其快速评定对于待建结构抗震设计、既有结构震后灾害评估具有重要作用。因此，将入射波位移幅值标准化后的地表位移放大系数作为预测目标参数，此系数为无量纲物理量。
2. 沉积河谷地震动放大效应预测模型建立
基于人工神经网络模型，结合差分进化算法，建立沉积河谷地震动放大效应预测模型。人工神经网络包括输入层、隐藏层和输出层，可将样本中隐含的特征规律分布于神经元之间的连接权值上，解决多参数非线性映射问题（Derras et al，2012，2014；Raghucharan et al，2019），差分进化算法是一种随机启发式搜索算法，包括初始化、变异、交叉和选择四个步骤，具有自适应迭代寻优能力和较好的鲁棒性（潘兆东等，2018）。人工神经网络、差分进化算法基本原理在此不再赘述。
针对半圆形、V形河谷，采用1.2节所述方法各生成7 000个样本对人工神经网络、差分进化-人工神经网络进行训练，随机选取其中85%作为训练集，15%作为验证集和测试集。每个样本均可得出地表各位置的位移放大系数，理论上，可将任意数量地表位移放大系数作为预测目标参数。当以某个地表位置作为目标参数，即神经网络输出层节点数为1时，采用更少的样本数即可获得较高精度的预测模型，但需构建多个神经网络预测模型；当以所有地表位置作为目标参数，即神经网络输出层节点数为地表边界离散元个数n时，获得较高精度的预测模型需采用巨量样本。本文以5个典型地表位置（图4）为预测目标参数构建预测模型，分析人工神经网络、差分进化-人工神经网络预测沉积河谷地震动放大效应的适用性。
3. 沉积河谷地震动放大效应预测结果与分析
3.1 预测模型结果与分析
通过改变神经元数量和隐藏层数量，确定人工神经网络最佳结构（Moayedi et al，2020）。经多次试算，本模型采用双隐含层神经网络，神经网络结构为4×28×26×5 （图5）。差分进化-人工神经网络预测模型精度对于差分进化算法的参数设定有很强的依赖性。本文通过对差分进化-人工神经网络预测模型多次训练确定出种群数量N＝400，初始变异因子F0＝1，最大迭代次数Gmax＝400。参数变量的界限为
${x}_{j}\in ［-\mathrm{1{\text{，}}1}］$ 。图6给出了半圆形和V形沉积河谷地表位移放大系数预测结果的决定系数，图7，8给出了五个地表位置位移放大系数边界元结果、人工神经网络、差分进化-人工神经网络预测结果，受篇幅限制，图7，8以测试集中随机选取的50个测试样本为例，定义相对误差ε1和ε2分别为人工神经网络和差分进化-人工神经网络预测模型结果与边界元结果的差值与边界元结果之比的绝对值。
![]()
图 6 人工神经网络（左）和差分进化-人工神经网络（右）预测模型测试集决定系数（a） 半圆形河谷； （b） V形河谷Figure 6. Artificial neural network （ANN） （left） and differentical evolution-ANN （right） determination coefficient of test set of prediction model（a） Semicircular valley； （b） V-shaped valley![]()
图 7 采用边界元法和神经网络预测模型得到的半圆形河谷地表点A−E （a−e）的位移幅值对比Figure 7. Comparison of displacement amplitudes between boundary element method and neural network prediction model of surface points A−E （a−e） for semicircular valley![]()
图 8 采用边界元法和神经网络预测模型得到的V形河谷地表点A−E （a−e） 的位移幅值对比Figure 8. Comparison of displacement amplitudes between boundary element method and neural network prediction model of surface points A−E （a−e） for V-shaped valley结合图6—8可知，人工神经网络进行沉积河谷预测具有较高的精度，将差分进化算法与人工神经网络结合，可整体提高人工神经网络预测的精度和稳定性，半圆形、V形沉积河谷模型决定系数分别由0.899，0.854提高至0.961，0.930，半圆形沉积河谷预测精度优于V形沉积河谷，同一个神经网络中不同目标参数（本文为地表位置）的预测精度有所不同。
3.2 特征参数敏感性分析
本节采用Garson算法求解特征参数对预测目标参数的影响程度（Derras et al，2012）。针对本文所给的参数范围（表1），SH波入射频率对地表位移放大系数的影响最大，半圆形、V形河谷模型结果分别为65.12%和68.45%；对于半圆形沉积河谷，基岩半空间与沉积河谷波速比、SH波入射角度的影响分别为23.4 %和9.97 %，影响最小的参数是基岩半空间与沉积河谷密度比，只有1.51%；对于V形沉积河谷，河谷深宽比的影响为14.02%，略大于波速比（10.15%）和入射角（7.38%）的影响程度。
4. 沉积河谷地震动放大效应预测模型应用
地震波能量为宽频分布，在考虑单频入射波基础上，可求得地表位移幅值谱，本节采用所建沉积河谷地震动放大效应的差分进化-人工神经网络预测模型，以入射角为60°为例，给出半圆形、V形沉积河谷中心点的地表位移幅值谱预测结果，预测模型计算时间约为1 s，结果如图9所示。作为对比，图10给出了基于边界元法的半圆形和V形沉积河谷中心点的地表位移放大系数计算结果，无量纲入射频率间隔取为0.1。结合图9，10可知，基于预测模型、边界元法的地表位移幅值谱具有良好的吻合度。
![]()
图 9 基于差分进化-神经网络预测模型的半圆形河谷（a）和V型河谷（b） 地表位移放大系数频谱Figure 9. Surface displacement amplification factor spectrum based on differential evolution-ANN prediction model for semicircular valley （a） and V-shaped valley （b）![]()
图 10 基于边界元法的半圆形河谷 （a）和V型河谷（b）地表位移放大系数频谱Figure 10. Surface displacement amplification factor spectrum based on boundary element method for semicircular valley （a） and V-shaped valley （b）5. 结论
本文以入射波条件、沉积内外介质属性、河谷场地形状为特征参数，以沉积河谷地震动放大系数为预测目标参数，建立半圆形、V形沉积河谷地震动放大效应的人工神经网络、差分进化-人工神经网络预测模型，对比分析了不同方法的适用性。结果表明：
人工神经网络、差分进化-人工神经网络均可实现沉积河谷地震动放大效应预测，但差分进化-人工神经网络预测模型具有更高的预测精度和稳定性；沉积河谷对地震波的散射导致半空间、河谷地表位移均表现出很强的离散性，入射波频率对半圆形和V形沉积河谷地表位移放大系数影响最大，对半空间和河谷密度比的影响相对较小，V形沉积河谷场地形状和介质属性的影响基本相同。最后需说明的是，本文算例仅限于二维出平面分析，若结合三维动力格林函数和三维场地模型，本文方法和理论框架很容易拓展到三维场地放大效应预测。
-
![]()
图 3 本文地表位移放大系数结果与文献结果对比
Figure 3. Comparison of amplification coefficient of surface displacement between the results in this paper and those in literature
![]()
图 4 半圆形河谷（a）和V形河谷（b）的预测模型点位分布
Figure 4. Location distribution of prediction model for semicircular valley （a） and V-shaped valley （b）
![]()
图 6 人工神经网络（左）和差分进化-人工神经网络（右）预测模型测试集决定系数
（a） 半圆形河谷； （b） V形河谷
Figure 6. Artificial neural network （ANN） （left） and differentical evolution-ANN （right） determination coefficient of test set of prediction model
（a） Semicircular valley； （b） V-shaped valley
![]()
图 7 采用边界元法和神经网络预测模型得到的半圆形河谷地表点A−E （a−e）的位移幅值对比
Figure 7. Comparison of displacement amplitudes between boundary element method and neural network prediction model of surface points A−E （a−e） for semicircular valley
![]()
图 8 采用边界元法和神经网络预测模型得到的V形河谷地表点A−E （a−e） 的位移幅值对比
Figure 8. Comparison of displacement amplitudes between boundary element method and neural network prediction model of surface points A−E （a−e） for V-shaped valley
![]()
图 9 基于差分进化-神经网络预测模型的半圆形河谷（a）和V型河谷（b） 地表位移放大系数频谱
Figure 9. Surface displacement amplification factor spectrum based on differential evolution-ANN prediction model for semicircular valley （a） and V-shaped valley （b）
![]()
图 10 基于边界元法的半圆形河谷 （a）和V型河谷（b）地表位移放大系数频谱
Figure 10. Surface displacement amplification factor spectrum based on boundary element method for semicircular valley （a） and V-shaped valley （b）
表 1 预测模型的特征参数及取值范围
Table 1 Characteristic parameters and value ranges of the prediction model
入射角θ/° 无量纲频率η 密度比ρ2/ρ1 剪切波速比c2/c1 半圆形河谷 ［60，90］ ［0.1，5］ ［0.5，1］ ［0.7，0.8］ V形河谷 ［60，90］ ［0.1，5］ ［0，1］ ［0.4，0.6］ 
下载: 导出CSV
-
陈国兴,金丹丹,朱姣,李小军. 2015. 河口盆地非线性地震效应及设计地震动参数[J]. 岩土力学,36(6):1721–1736. Chen G X,Jin D D,Zhu J,Li X J. 2015. Nonlinear seismic response of estuarine basin and design parameters of ground motion[J]. Rock and Soil Mechanics,36(6):1721–1736 (in Chinese).
陈少林,张莉莉,李山有. 2014. 半圆柱型沉积盆地对SH波散射的数值分析[J]. 工程力学,31(4):218–224. Chen S L,Zhang L L,Li S Y. 2014. Numerical analysis of the plane SH waves scattering by semi-cylindrical alluvial valley[J]. Engineering Mechanics,31(4):218–224 (in Chinese).
高玉峰,代登辉,张宁. 2021. 河谷地形地震放大效应研究进展与展望[J]. 防灾减灾工程学报,41(4):734–752. Gao Y F,Dai D H,Zhang N. 2021. Progress and prospect of topographic amplification effects of seismic wave in canyon sites[J]. Journal of Disaster Prevention and Mitigation Engineering,41(4):734–752 (in Chinese).
黄磊,刘中宪,张雪,李程程. 2020. 含流体层的河谷场地对地震波散射的间接边界元法模拟[J]. 地震学报,42(6):657–668. Huang L,Liu Z X,Zhang X,Li C C. 2020. IBEM simulation of seismic wave scattering by valley topography with fluid layer[J]. Acta Seismologica Sinica,42(6):657–668 (in Chinese).
李平,薄景山,李孝波,肖瑞杰. 2016. 安宁河河谷及邛海地区土层场地对地震动的放大作用[J]. 岩土工程学报,38(2):362–369. doi: 10.11779/CJGE201602022 Li P,Bo J S,Li X B,Xiao R J. 2016. Amplification effect of soil sites on ground motion in Anning River valley and Qionghai Lake area[J]. Chinese Journal of Geotechnical Engineering,38(2):362–369 (in Chinese).
李伟华,赵成刚. 2006. 具有饱和土沉积层的充水河谷对平面波的散射[J]. 地球物理学报,49(1):212–224. doi: 10.3321/j.issn:0001-5733.2006.01.028 Li W H,Zhao C G. 2006. Scattering of plane waves by circular-arc alluvial valleys with saturated soil deposits and water[J]. Chinese Journal of Geophysics,49(1):212–224 (in Chinese).
梁建文,巴振宁. 2007. 弹性层状半空间中沉积谷地对入射平面SH波的放大作用[J]. 地震工程与工程振动,27(3):1–9. doi: 10.3969/j.issn.1000-1301.2007.03.001 Liang J W,Ba Z N. 2007. Surface motion of an alluvial valley in layered half-space for incident plane SH waves[J]. Journal of Earthquake Engineering and Engineering Vibration,27(3):1–9 (in Chinese).
刘必灯,周正华,刘培玄,李小军,王伟. 2011. SV波入射情况下V型河谷地形对地震动的影响分析[J]. 地震工程与工程振动,31(2):17–24. Liu B D,Zhou Z H,Liu P X,Li X J,Wang W. 2011. Influence of V-shaped canyon site on ground motions for incident SV waves[J]. Journal of Earthquake Engineering and Engineering Vibration,31(2):17–24 (in Chinese).
潘兆东,谭平,刘良坤,周福霖. 2018. 基于自适应RBF神经网络算法的建筑结构递阶分散控制研究[J]. 土木工程学报,51(1):51–57. Pan Z D,Tan P,Liu L K,Zhou F L. 2018. Hierarchical decentralized control of building structure based on adaptive RBF neural network algorithm[J]. China Civil Engineering Journal,51(1):51–57 (in Chinese).
肖文海. 2009. 大型河谷场地地震动特征研究[D]. 哈尔滨: 中国地震局工程力学研究所: 1–2. Xiao W H. 2009. Research on Ground Motion Characteristic at the Site of Large-Scale Valley[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 1–2 （in Chinese）.
张宁,高玉峰,何稼,徐婕,陈欣,代登辉. 2017. 平面SH波作用下部分充填圆弧形沉积谷的二维土层和地形放大效应[J]. 地震学报,39(5):778–797. doi: 10.11939/jass.2017.05.012 Zhang N,Gao Y F,He J,Xu J,Chen X,Dai D H. 2017. Two-dimensional soil and topographic amplification effects of a partially filled circular-arc alluvial valley under plane SH waves[J]. Acta Seismologica Sinica,39(5):778–797 (in Chinese).
周国良,李小军,侯春林,李铁萍. 2012. SV波入射下河谷地形地震动分布特征分析[J]. 岩土力学,33(4):1161–1166. doi: 10.3969/j.issn.1000-7598.2012.04.029 Zhou G L,Li X J,Hou C L,Li T P. 2012. Characteristic analysis of ground motions of canyon topography under incident SV seismic waves[J]. Rock and Soil Mechanics,33(4):1161–1166 (in Chinese).
Boore D M. 1973. The effect of simple topography on seismic waves:Implications for the accelerations recorded at Pacoima Dam,San Fernando Valley,California[J]. Bull Seismol Soc Am,63(5):1603–1609. doi: 10.1785/BSSA0630051603
Derras B,Bard P Y,Cotton F,Bekkouche A. 2012. Adapting the neural network approach to PGA prediction:An example based on the KiK-net data[J]. Bull Seismol Soc Am,102(4):1446–1461. doi: 10.1785/0120110088
Derras B,Bard P Y,Cotton F. 2014. Towards fully data driven ground-motion prediction models for Europe[J]. Bull Earthq Eng,12(1):495–516. doi: 10.1007/s10518-013-9481-0
Dhanya J,Raghukanth S T G. 2018. Ground motion prediction model using artificial neural network[J]. Pure Appl Geophys,175(3):1035–1064. doi: 10.1007/s00024-017-1751-3
Ducellier A,Aochi H. 2012. Interactions between topographic irregularities and seismic ground motion investigated using a hybrid FD-FE method[J]. Bull Earthq Eng,10(3):773–792. doi: 10.1007/s10518-011-9335-6
Giacinto G,Paolucci R,Roli F. 1997. Application of neural networks and statistical pattern recognition algorithms to earthquake risk evaluation[J]. Pattern Recogn Lett,18(11/12/13):1353–1362.
Kong Q K,Trugman D T,Ross Z E,Bianco M J,Meade B J,Gerstoft P. 2019. Machine learning in seismology:Turning data into insights[J]. Seismol Res Lett,90(1):3–14. doi: 10.1785/0220180259
Liu Z X,Wang D,Liang J W,Wu F J,Wu C Q. 2018. The fast multi-pole indirect BEM for solving high-frequency seismic wave scattering by three-dimensional superficial irregularities[J]. Eng Anal Bound Elem,90:86–99. doi: 10.1016/j.enganabound.2018.02.009
Luzón F,Sánchez-Sesma F J,Pérez-Ruiz J A,Ramírez-Guzmán L,Pech A. 2009. In-plane seismic response of inhomogeneous alluvial valleys with vertical gradients of velocities and constant Poisson ratio[J]. Soil Dyn Earthq Eng,29(6):994–1004. doi: 10.1016/j.soildyn.2008.11.007
Moayedi H,Raftari M,Sharifi A,Jusoh W A W,Rashid A S A. 2020. Optimization of ANFIS with GA and PSO estimating α ratio in driven piles[J]. Eng Comput,36(1):227–238. doi: 10.1007/s00366-018-00694-w
Paolucci R,Colli P,Giacinto G. 2000. Assessment of seismic site effects in 2-D alluvial valleys using neural networks[J]. Earthq Spectra,16(3):661–680. doi: 10.1193/1.1586133
Raghucharan M C,Somala S N,Rodina S. 2019. Seismic attenuation model using artificial neural networks[J]. Soil Dyn Earthq Eng,126:105828. doi: 10.1016/j.soildyn.2019.105828
Shyu W S,Teng T J,Chou C S. 2018. Effect of geometry on in-plane responses of a symmetric canyon subjected by P waves[J]. Soil Dyn Earthq Eng,113:215–229. doi: 10.1016/j.soildyn.2018.06.003
Sun Y C,Ren H X,Zheng X Z,Li N,Zhang W,Huang Q H,Chen X F. 2019. 2-D poroelastic wave modelling with a topographic free surface by the curvilinear grid finite-difference method[J]. Geophys J Int,218(3):1961–1982. doi: 10.1093/gji/ggz263
Tavakoli H,Kutanaei S S. 2015. Evaluation of effect of soil characteristics on the seismic amplification factor using the neural network and reliability concept[J]. Arab J Geosci,8(6):3881–3891. doi: 10.1007/s12517-014-1458-z
Trifunac M D. 1971. Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves[J]. Bull Seismol Soc Am,61(6):1755–1770. doi: 10.1785/BSSA0610061755
Yuan X M,Liao Z P. 1995. Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section[J]. Earthq Eng Struct Dyn,24(10):1303–1313. doi: 10.1002/eqe.4290241002
Zhou H,Chen X F. 2008. The localized boundary integral equation-discrete wavenumber method for simulating P-SV wave scattering by an irregular topography[J]. Bull Seismol Soc Am,98(1):265–279. doi: 10.1785/0120060249
-
期刊类型引用(1)
1. 刘中宪，孟思博，李文轩，赵嘉玮，黄振恩. 考虑岩土参数随机性的三维沉积盆地地震动高效模拟方法. 岩土工程学报. 2024(03): 529-538 . 
百度学术
其他类型引用(2)
计量
- 文章访问数: 362
- HTML全文浏览量: 165
- PDF下载量: 70
- 被引次数: 3
