Experiment and numerical simulation of co-seismic water level response in unconsolidated confined aquifer
-
摘要: 为深入理解井水位同震响应机理，本文开展了向完整井-松散含水层系统输入由不同频率和振幅（加速度）组成的正弦波荷载的振动台实验。以实验模型为物理模型，建立了振动作用下松散承压含水层中孔隙水压力响应的流固耦合模型和含水层水流与井流的相互作用模型，并运用多物理场耦合模拟软件COMSOL Multiphysics对实验过程进行了数值模拟。实验中观测到的四种典型水位变化形态与野外场地同震井水位变化形态相似。数值模拟结果显示，本研究建立的数学模型能较好地反映松散承压含水层中孔隙水压力和水位的响应情况。本文研究对解释地下水同震响应机制、岩体渗流稳定性和安全问题具有重要意义。Abstract: In order to promote understanding mechanisms of co-seismic response of water level in well shaking table experiments have been carried out with sinusoidal loading in different vibration frequencies and amplitudes （accelerations） for complete well unconsolidated confined aquifer system. The physical model has been built based on experimental model, and fluid-solid coupled model of pore pressure response in unconsolidated aquifer and mathematical model of flow interaction between aquifer well under vibrations have been established. The experimental processes have been simulated in COMSOL Multiphysics, a multi-field coupling simulation software. Four typical water level variation forms observed in experiment are similar to those of field studies, and the results of numerical simulation show that the mathematical model established in this study can well reflect the response of pore water pressure and water level in unconfined aquifer. This research is of great significance to explain the mechanism of co-seismic responses of groundwater, and stability and safety of seepage in rock and soil mass.
-
引言
井水位同震响应是指地震发生时所产生的应变能瞬间改变了地壳的介质状态，进而导致井水位出现持续变化、阶变或振荡变化现象的总称（Muir-Wood，King，1993；Manga，Wang，2007；Wang，Manga，2014；Shi et al，2015）。井水位同震响应蕴含着复杂的流固耦合过程：① 应力场对渗流场的作用，鉴于含水层的非均质性，地震作用使介质变形，进而导致含水层内部孔隙水压力（水头）分布不均，在水头差驱动下，含水层内部产生周期性的水流动，打破了含水层压力水头与井水位之间的平衡，致使井-含水层之间水呈周期性流动；② 渗流场对应力场、应变场的作用，含水层内部孔隙水压力的改变，以及井-含水层之间的水流运动又会影响含水层的形变（Ge，Stover，2000；刘春平，2017）。影响井水位同震响应过程的因素众多，有地震参数（震级、震中距以及震源深度）、地质条件（地层岩性、构造性质与含水层展布）、井-含水层系统特征（含水层介质类型、水文地质参数以及井结构）和流体性质（黏滞度和密度）等（Cooper et al，1965；贾化周，秦清娟，1996；车用太，鱼金子，2014）。
关于井水位同震响应现象的研究始于1928年美国加州的一口监测井所记录的水位变化（Stearns，1928）。此后，许多学者对同震响应现象和机理进行了相关研究。Cooper等（1965）认为地震波引起了含水层压缩和膨胀从而引起孔隙水压力的振荡，当含水层渗透性足够大时，孔隙水压力的振荡会引起地下水流入或流出井孔，从而引起井水位的振荡，也有学者认为S波和勒夫波同样能引起井水位的振荡现象（Wang et al，2009）。对于固结含水层，井水位同震响应的机理主要运用静态应变模型（Wakita，1975；Ge，Stover，2000） 来解释，即：地震发生时，发震断层错动产生的静态应变导致含水层的压缩与膨胀，从而致使水位发生了变化（Quilty，Roeloffs，1997）。对于松散介质的含水层，其响应机理主要运用含水层固结模型（Wang，Chia，2008）来解释，即：地震波的振动引起未固结的含水层发生固结压密，从而引起含水层孔隙水压力增大进而导致井水位的上升。除此之外，还出现了几种假说模型：地震引发的含水层渗透性变化模型（Elkhoury et al，2006）、深层水量交换模型（Gulley et al，2013）以及气泡成核机理（Crews，Cooper，2014）等。这些解释井水位同震响应的模型多以定性解释为主，已有的定量和半定量模型也难以在实际地震中得到验证。
实验室尺度涉及渗流场与应力应变场方面的研究大多数以动三轴实验为主，实验目的大多针对于循环荷载下孔隙水压力的响应情况，如阎澍旺（1991）、许才军和周红波（1998）、周健等（1996，2011）主要针对循环荷载下饱和软黏土的孔压变化进行了试验。Gu等（2021a）通过室内实验研究了在松散沉积物中动力振动对水位波动的影响，认为颗粒结构的非均质固结、机械共振、压实、膨胀和再充填等可能构成水位波动和水力参数调整的物理变化机制。而利用自行设计的以非固结饱水砂层为介质的井-承压含水层物理模型，分别在渗流和非渗流状态下对其施加正弦波荷载，通过改变频率和加速度等条件模拟了振动作用下承压含水层中井水位和孔隙水压力的变化规律和特征，结果表明，其变化特征与天然同震水位响应有一定的相似性，为研究同震水位变化提供了新视角（张璜等，2016；张艳等，2017；张艳，2020；张耀文等，2019；谷洪彪等，2017；Gu et al ，2021b）。
运用解析方程定量刻画饱和土渗透固结过程，Terzaghi （1943）提出的一维固结理论是解决应力场-渗流场耦合问题最早的理论之一，经典弹性理论（Jaeger et al，2009）是研究介质变形的基础，而著名的扩散理论（Carslaw，Jaeger，1959）是研究孔隙水压力扩散的基础。Biot （1941，1955，1956a，b，1962）在一维固结理论的基础上推导出含水层受力过程中应力-应变-孔隙水压力之间完整描述变形和孔隙水压力扩散的解析表达式，为流固耦合的深入研究奠定了基础。但是，描述应力场-渗流场耦合作用的方程为偏微分方程组，其中涉及到的多个变量不仅自身随时间和位置变化且相互耦合，绝大部分偏微分方程只能通过数值法求出其数值解。Bowen （1980）利用混合物热力学理论建立了不可压缩多孔介质经典模型。Cheung和Tham （1983）基于变分法和最小二乘法给出了层状土固结的数值解。Oka等（1994）利用两相混合理论研究了砂土液化现象，得到了固相位移与液相位移耦合的控制方程，采用FEM-FDM方法对方程进行空间离散，建立了一种简单实用的数值模拟方法。
综上，鉴于影响井水位同震响应因素的复杂性，野外现场资料获取难度大且精度不够，又考虑到该响应过程涉及应力场、应变场、温度场和渗流场同时变化，属于多场耦合问题。不易建立精确表达该过程的解析模型，即使能够建立，模型的解析表达式求解难度也极大，从此角度分析，定量揭示井水位同震响应过程是极其困难的。虽然实验室尺度的模拟和验证研究不能完全复制野外场地井水位同震响应的实际过程，但是基于地震模拟振动台构建同震井水位响应的实验模型，开展松散介质含水层对振动响应的模拟实验研究不失为一种值得尝试和探索的方法。
本研究拟针对井水位同震响应现象开展松散承压含水层振动台模拟实验，输入不同频率和加速度振幅组成的正弦波荷载，分析松散含水层井水位随不同振动频率和振幅的变化机制。运用应力场-渗流场耦合数值模拟手段，定量揭示振动作用下含水层中孔隙水压力和井水位的响应过程。以期为探索地壳应力与地下水动力过程的相关性和定量模型的建立提供技术思路，为揭示野外尺度井水位同震响应机理研究提供参考。
1. 实验模型
1.1 实验装置
本次实验建立了简化的各向同性孔隙承压含水层模型，通过施加不同加速度振幅、频率的正弦波荷载，监测含水层内部孔隙水压力和水位的变化情况，旨在模拟浅层非固结含水层同震水位响应的水动力过程。
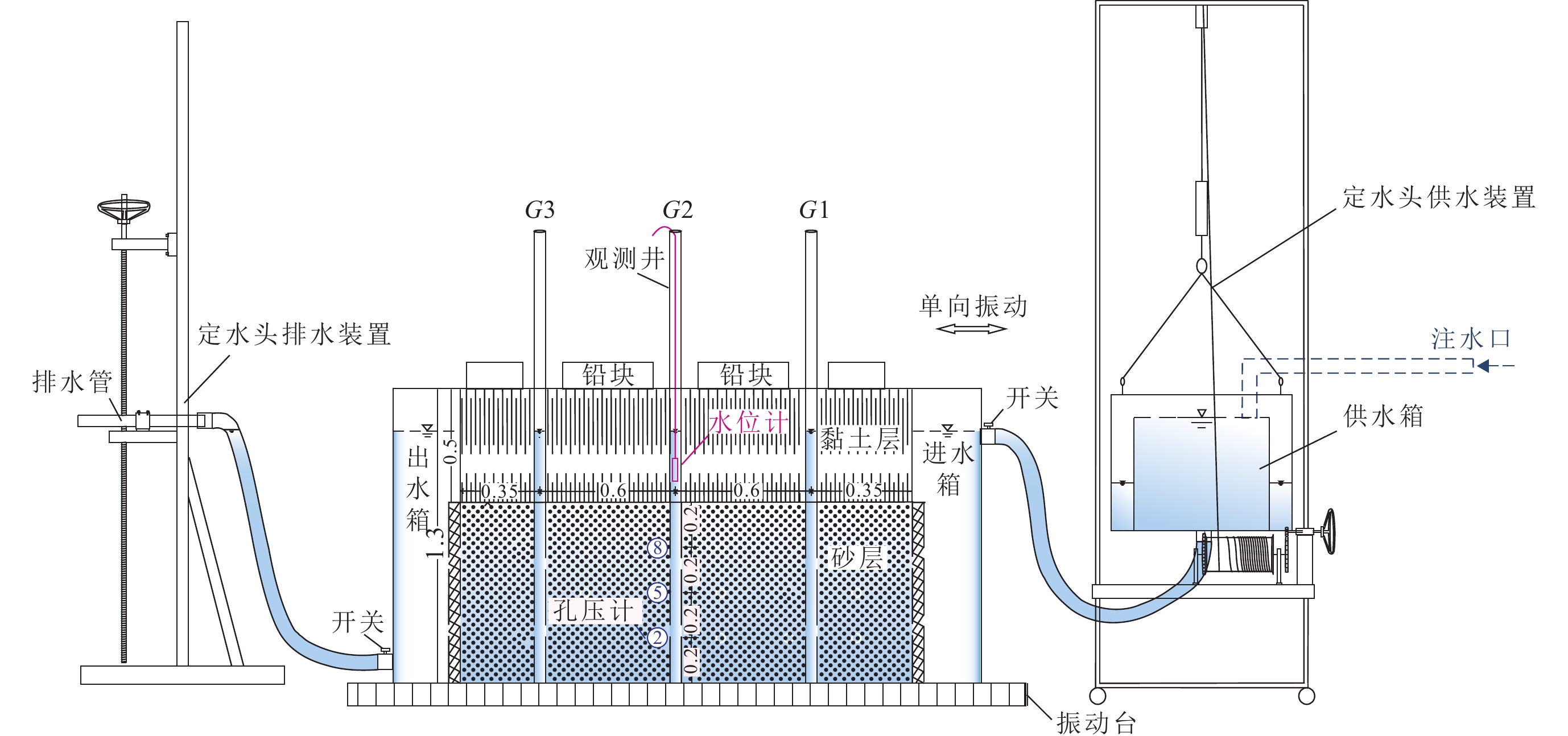
根据设计的孔隙承压含水层模型，建立由含水层、隔水层、观测井及上覆自由荷载四部分组成的完整井-承压含水层系统（图1）：含水层介质由松散的石英砂充填，粒径为0.15—0.30 mm，湿密度为2.3 g/cm3，总厚度为0.8 m；隔水层采用黏性土模拟，湿密度为2.857 g/cm3，厚度为0.5 m，同时在隔水层顶端加盖1 100 kg的铅块模拟上覆自由荷载；三口水位观测井（G1，G2，G3）等间距排布在含水层中，井高均为2 m，井口直径为0.05 m。装置设计的主要技术问题详见张艳（2020），本文此处不再赘述。实验开始前，测得含水层渗透系数为33 m/d，孔隙度为0.398，水动力条件为静水条件。
1.2 实验工况
本次主要输入水平方向的正弦波荷载（表1）来研究孔隙水压力和水位的响应形态、变幅与振动频率和加速度振幅的关系。
表 1 正弦波的振动参数Table 1. Shaking parameters of different sine waves工况编号 频率/Hz 加速度/g 加载时间/s 工况编号 频率/Hz 加速度/g 加载时间/s 1 0.5 0.1 35 4 5 0.25 35 2 2 0.25 35 5 10 0.25 35 3 5 0.15 35 6 15 0.15 35 注：1g＝9.81 m/s2。 1.3 实验结果
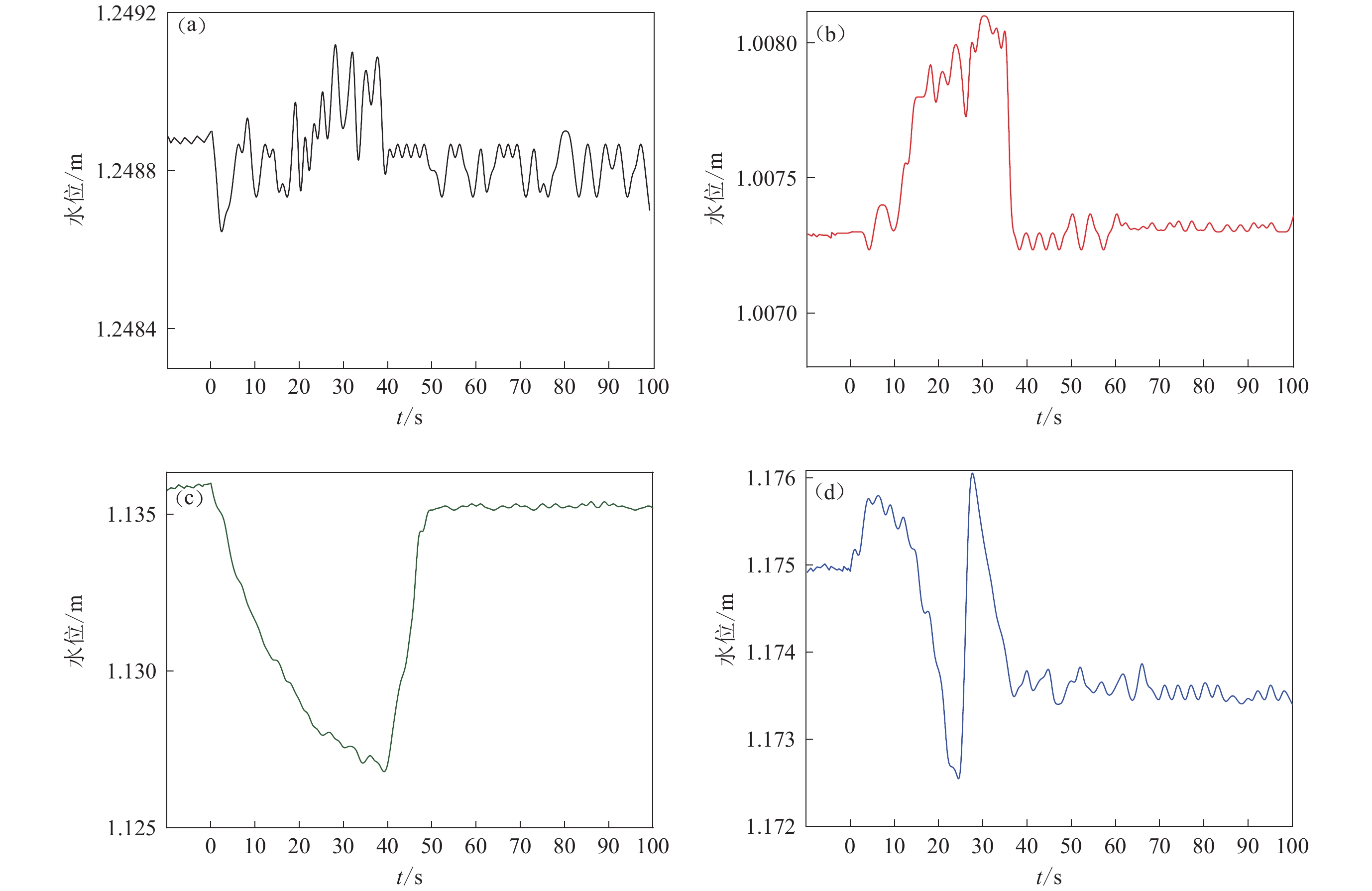
实验中所记录到的典型井水位变化主要呈现四种形态：振荡、上升、下降和阶变变化（图2）。这些现象与现场研究中认识到的同震水位变化形状相似（Quilty，Roeloffs，1997；Brodsky，2003；Matsumoto，Roeloffs，2003；Elkhoury et al，2006；Wang，Chia，2008；Wang，Manga，2009；Shi et al，2015）。
![]()
图 2 实验所记录的典型井水位变化形态（以G2井为例）（a） 振荡；（b） 上升；（c） 下降；（d） 阶变Figure 2. Typical change forms of well water level in experiments （taking well G2 as an example）（a） Oscillation；（b） Rise；（c） Drop；（d） Step-like change2. 孔隙水压力和井水位响应的数学模型
地震动态应力扰动作用下井水位响应的水动力过程由振动作用下孔隙水压力的响应和孔隙水压力扰动下井水位的响应两部分组成。
2.1 孔隙水压力响应的数学模型
含水层物理模型如图1所示，由于振动作用下含水层的弹性变形和孔隙水压力的扩散是相互耦合的过程，需要考虑弹性变形对孔隙水压力的影响和孔隙水压力扩散对变形的影响。因此，建立数学模型，采用理论推导的方法得出描述荷载作用与孔隙水压力之间的偏微分方程以定量解释二者关系。本研究对控制方程的建立和求解做如下假设：
1） 含水层是承压含水层，隔水顶、底板水平，为均质各向同性的线弹性体；
2） 孔隙水流动符合达西定律，即含水层中渗流速度
${v_x}$ 与水力坡降${{{\text{∂}} h}}/{{{\text{∂}} x}}$ 之间呈线性关系，表示为${v_{{x}}} ＝ K{{{\text{∂}} {\text{h}}}}/{{{\text{∂}} x}}$ ，其中K为渗透系数；3） 含水层变形为小变形，符合广义胡克定律，即含水层所受应力
$\sigma $ 与应变$\varepsilon $ 之间呈线性关系，表示为$\sigma ＝ E\varepsilon $ ，其中E为弹性模量；4） 孔隙水流动的加速度远远小于土颗粒的加速度。
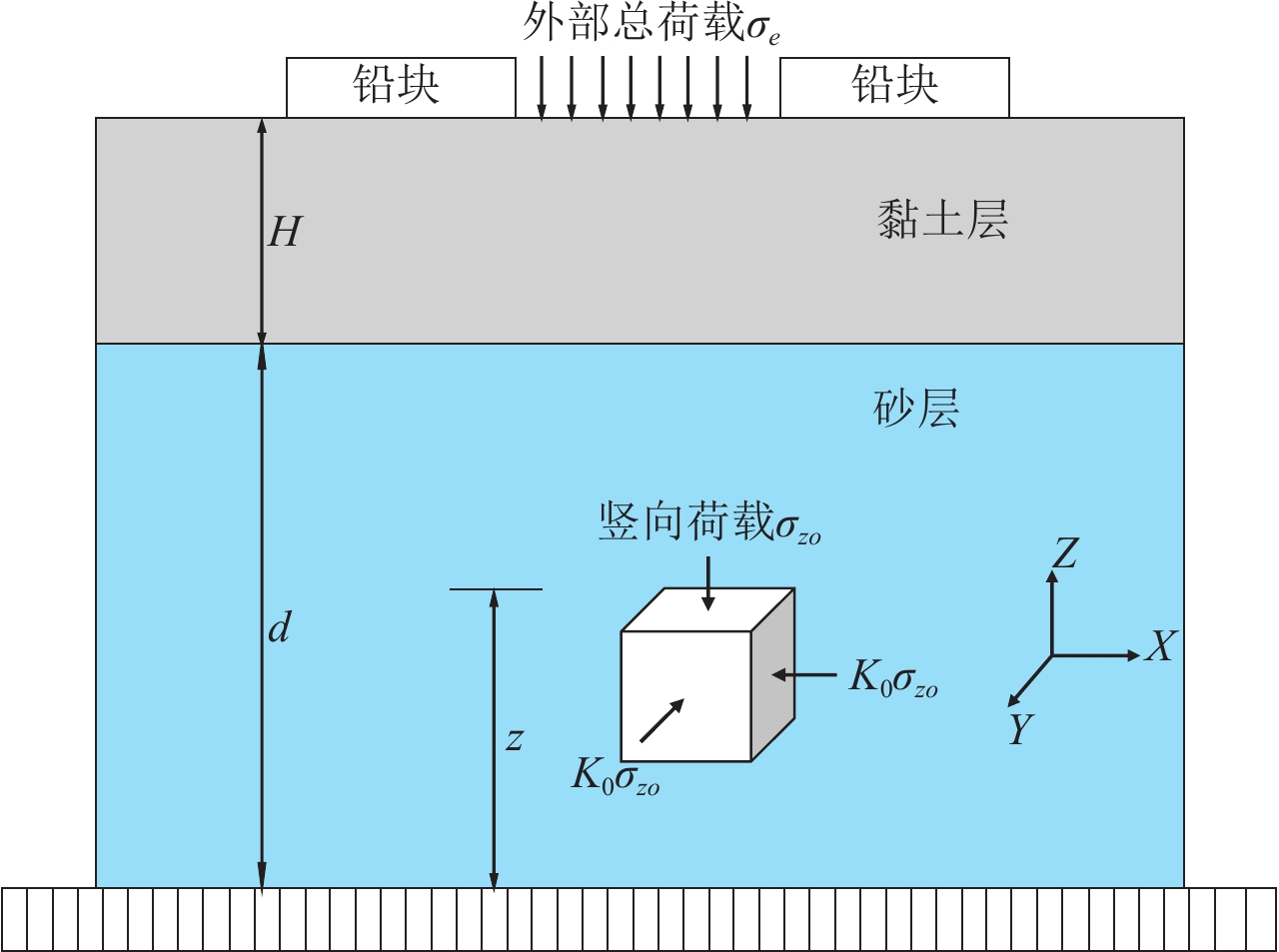
不考虑温度场的影响，建立如图3所示的承压含水层概念模型，黏土层厚度为
$H$ ，砂层厚度为$d$ 。为精细刻画应力场-渗流场的耦合过程，数学模型的建立基于初始平衡状态，运用动力平衡方程、达西定律、有效应力原理、胡克定律和质量守恒定律，给出了距离底板高度z处单元体受振动作用下孔隙水压力响应的控制方程 ［ 式（1） ］ ，具体推导过程见参考翟泽宇（2021）。![]()
图 3 初始平衡状态下承压含水层模型剖面图Figure 3. Profile of confined aquifer model at initial equilibrium state$$ \left\{\begin{split}& \mu {\nabla ^2}u ＋ （ \lambda ＋ \mu ） {\rm{grad}} （ {u_{i}} ） ＋ {\rm{grad}} （ p ） ＝ {\rho _{\rm{m}}}\frac{{{{\text{∂}} ^2}{u_i}}}{{{\text{∂}} {t^2}}} ，\\& \frac{k}{n}{\nabla ^2}p － \frac{{{K_x}}}{g}{\rm{grad}}\Bigg(\frac{{{{\text{∂}} ^2}{u_i}}}{{{\text{∂}} {t^2}}}\Bigg) ＋ {\rm{grad}} （ {\dot u _i} ） － \frac{1}{Q}\frac{{{\text{∂}} p}}{{{\text{∂}} t}} ＝ 0 ， \end{split} \right.$$ (1) 式中，
$\lambda $ ，$\mu $ 为拉梅参数；$u$ 为固相位移；$p$ 为孔隙水压力；平均密度$\;{\rho _{\rm{m}}} ＝ （ 1 － n ） {\rho _{\rm{s}}} ＋ n{\rho _{\rm{f}}}$ ，$\;{\rho _{\rm{s}}}$ 和$\;{\rho _{\rm{f}}}$ 分别为固相和液相的密度；$K$ 为渗透系数，渗透率$k ＝ K/{\rho _{\rm{f}}}g$ ；$n$ 为孔隙度，$1/Q ＝ n/{E_{\rm{f}}}$ ，${E_{\rm{f}}}$ 为液相体积模量；${\nabla ^2} ＝ {{{{\text{∂}} ^2}}}/{{{\text{∂}} {x^2}}} ＋ {{{{\text{∂}} ^2}}}/{{{\text{∂}} {{\textit{z}}^2}}}$ ，${\rm{grad}}f （ x，{\textit{z}} ） ＝ （ {{{{\text{∂}} f}}/{{{\text{∂}} x}}，{{{\text{∂}} f}}/{{{\text{∂}} {\textit{z}}}}} ） $ 。振动开始前，系统处于静力平衡状态，初始状态的含水层中z处单元体的孔隙水压力（距离砂层顶端高度为
$h$ ）等于静水压力，含水层内固相位移为0，即初始条件为：$p ＝ {\rho _{\rm{f}}}gh$ ；${u_x} ＝ {u_{\textit{z}}} ＝ 0$ 。向系统输入幅值为A、频率为F的水平向正弦荷载，即设置边界条件为：上边界$p ＝ 0$ ；两侧${u_{\textit{z}}} ＝ 0$ ，${u_x} ＝ A\sin （ 2\pi Ft ） $ ；下边界${u_x} = {u_{\textit{z}}} = 0$ 。2.2 井水位响应的数学模型
在井-含水层系统中，井可以视为压力计，它对孔隙水压力的扰动响应非常敏感，并且井-含水层系统的响应行为与机械弹簧非常相似（Rexin et al，1962；Bredehoeft et al，1966）。因此，这种孔隙水压力扰动从源头到井内水位波动的传播过程应包括含水层中的压力扩散和井中的水柱运动两部分。
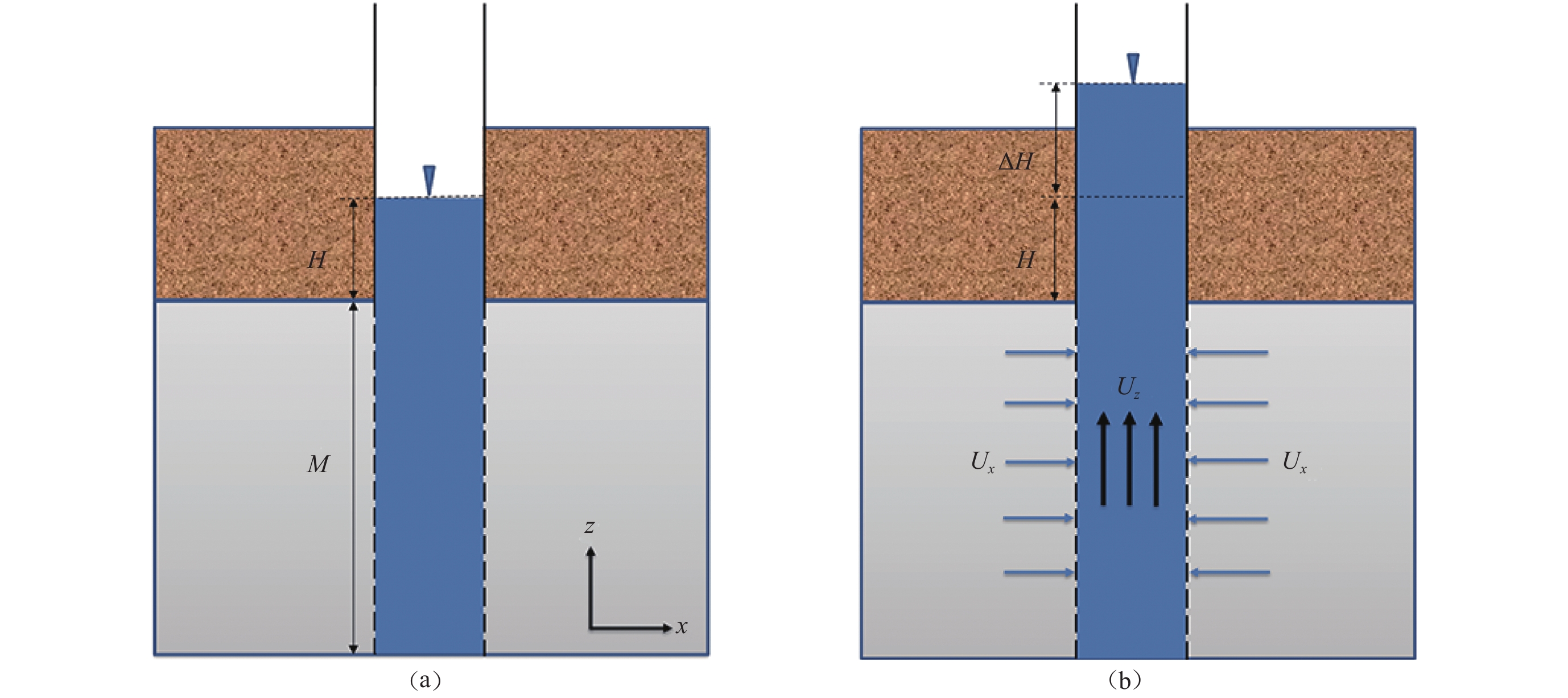
为了描述孔隙水压力变化时井水位的响应过程，将振动台实验装置简化为三维模型，如图4所示。它包括井和承压含水层两个部分，承压含水层中安装了半径为
${r_{\rm{w}}}$ 的完整井，由于正弦波振动作用下含水层内部孔隙水压力产生波动，在侧边界上突然产生一个振幅为${p_0}$ （即为第2.1节中计算所得的孔隙水压力振幅）、频率为F的孔隙水压力扰动，驱动水流入井中。当水流入井孔后，水流运动方向由水平径向变为垂向（图5）。由于地下水在纯流体域中流动，因此采用Novier-Stocks方程（Zlotnik，McGuire，1998a；Zlotnik，McGuire，1998b）来描述![]()
图 4 压力扰动井-含水层系统的概念模型Figure 4. Conceptual model of the well-aquifer system disturbing by a harmonic pressure![]()
图 5 井流运动示意图（a） 静止状态；（b） 运动状态Figure 5. Schematic diagram of well flow（a） Stationary state；（b） Motion state$$ \frac{{{\text{∂}} {U_{\textit{z}}}}}{{{\text{∂}} t}} ＝ - \frac{1}{\rho }\nabla {p_0} ＋ \mu {\nabla ^2}{U_{\textit{z}}} ＋ F \text{，} $$ (2) 式中，
${U_{\textit{z}}}$ 为井中水流速度，$\;\rho $ 和$\;\mu $ 为水的密度和动力黏度系数，${p_0}$ 为孔隙水压力。井口为自由边界，故井口处F＝0。在含水层中，假设含水层为均质各向同性，地下水向井流动遵循达西定律：
$$ \rho {S}_{ {\rm{s}}}M\frac{{\text{∂}} {p}_{0}}{{\text{∂}} t}＋\nabla \cdot （ \rho {U}_{ x} ） ＝{Q}_{{\rm{m}}} \text{，} $$ (3) 式中，
${S_{ {\rm{s}}}}$ 为储水率，M为含水层厚度，${U_x}$ 为地下水流向井时的速度，${Q_{\rm{m}}}$ 为源汇项，实验中，水动力条件为静水条件，与外界无水量交换，即${Q_{\rm{m}}} ＝ 0$ 。振动开始前，系统处于静力平衡状态，含水层中z处单元体的孔隙水压力（距离砂层顶端高度为
$h$ ）等于静水压力，即初始条件为$$ p ＝ {\rho _f}gh ； $$ (4) 而边界条件为
$$ p ＝ \rho gh ＋ {p_0}\sin （ 2\pi Ft ） {\text{.}} $$ (5) 3. 数值模拟与结果分析
3.1 数值模拟过程
COMSOL Multiphysics是一款大型的高级数值仿真软件，以有限元法为基础，通过求解偏微分方程（单场）或偏微分方程组（多场）来实现对真实物理现象和过程的模拟仿真。本研究中，基于井-含水层概念模型（如图4所示）构建二维轴对称几何模型用于数值模拟。采用自由三角形网格剖分计算网格，运用格林-高斯（Green-Gauss）公式将应力-渗流作用下孔隙水压力响应的耦合控制方程（式1）表示为弱形式（式6），以输入COMSOL Multiphysics的偏微分方程模块，设置模型参数、初始条件和边界条件进行数值模拟，模型参数设置见表2。
表 2 数值模拟中的参数取值Table 2. Parameters used in numerical experiments.参数 单位 数值 弹性模量$E$ Pa 2.63×1010 泊松比$\upsilon $ 1 0.25 渗透系数$K$ m/d 33 孔隙度$n$ 1 0.398 ${{{\rm{Biot}}'{\rm{s}}} }$系数 1 1 固相密度$\;{\rho _{\rm{s}}}$ kg/m3 2 650 液相密度$\;{\rho _{\rm{f}}}$ kg/m3 1 000 固相体积模量${E_{\rm{s}}}$ Pa 1.56×1010 液相体积模量${E_{\rm{f}}}$ Pa 1×108 储水率${S_{ {\rm{s} }} }$ 1 1×10−3 动力黏度系数$\;\mu$ Pa·s 1×10−4 $$\left\{ \begin{split}& - \int\nolimits_\varOmega ［ \mu \nabla u ＋ （ \lambda ＋ \mu ） {u_{i} ］ } \Bigg(\frac{{{\text{∂}} \delta {u_x}}}{{{\text{∂}} x}} ＋ \frac{{{\text{∂}} \delta {u_{\textit{z}}}}}{{{\text{∂}} {\textit{z}}}}\Bigg){\rm{d}}\varOmega ＋ \int\nolimits_\varGamma [\mu \nabla u ＋ \Bigg(\lambda ＋ \mu \Bigg){u_{i}]\delta {u_i}{\rm{d}}\varGamma } - \\& {\int\nolimits _\varOmega p\Bigg(\frac{{{\text{∂}} \delta {u_x}}}{{{\text{∂}} x} }＋ \frac{{{\text{∂}} \delta {u_{\textit{z}}}}}{{{\text{∂}} {\textit{z}}}}\Bigg){\rm{d}}\varOmega ＋ {\int\nolimits _\varGamma p\delta {u_i}{\rm{d}}\varGamma － {\int\nolimits_\varOmega {\rho _m}\frac{{{{\text{∂}} ^2}{u_i}}}{{{\text{∂}} {t^2}}}{\rm{d}}\varOmega ＝ 0} } } ，\\& {\int\nolimits_\varOmega \frac{k}{n}} \Bigg(\frac{{{{\text{∂}} ^2}p}}{{{\text{∂}} {x^2}}} ＋ \frac{{{{\text{∂}} ^2}p}}{{{\text{∂}} {{\textit{z}}^2}}}\Bigg)\delta p{\rm{d}}\varOmega － {\int\nolimits_\varOmega \frac{K}{g}} {\rm{grad}}\Bigg(\frac{{{{\text{∂}} ^2}{u_i}}}{{{\text{∂}} {t^2}}}\Bigg)\delta p{\rm{d}}\varOmega ＋ {\int\nolimits_\varOmega \Bigg(\frac{{{\text{∂}} {{\dot u}_x}}}{{{\text{∂}} x}} ＋ \frac{{{\text{∂}} {{\dot u}_{\textit{z}}}}}{{{\text{∂}} {\textit{z}}}}\Bigg)\delta p{\rm{d}}\varOmega }- \\& \int {\frac{1}{Q}} \frac{{{\text{∂}} p}}{{{\text{∂}} t}}\delta p{\rm{d}}\varOmega = 0{\text{.}} \end{split}\right. $$ (6) 3.2 振动作用下含水层孔隙水压力的响应
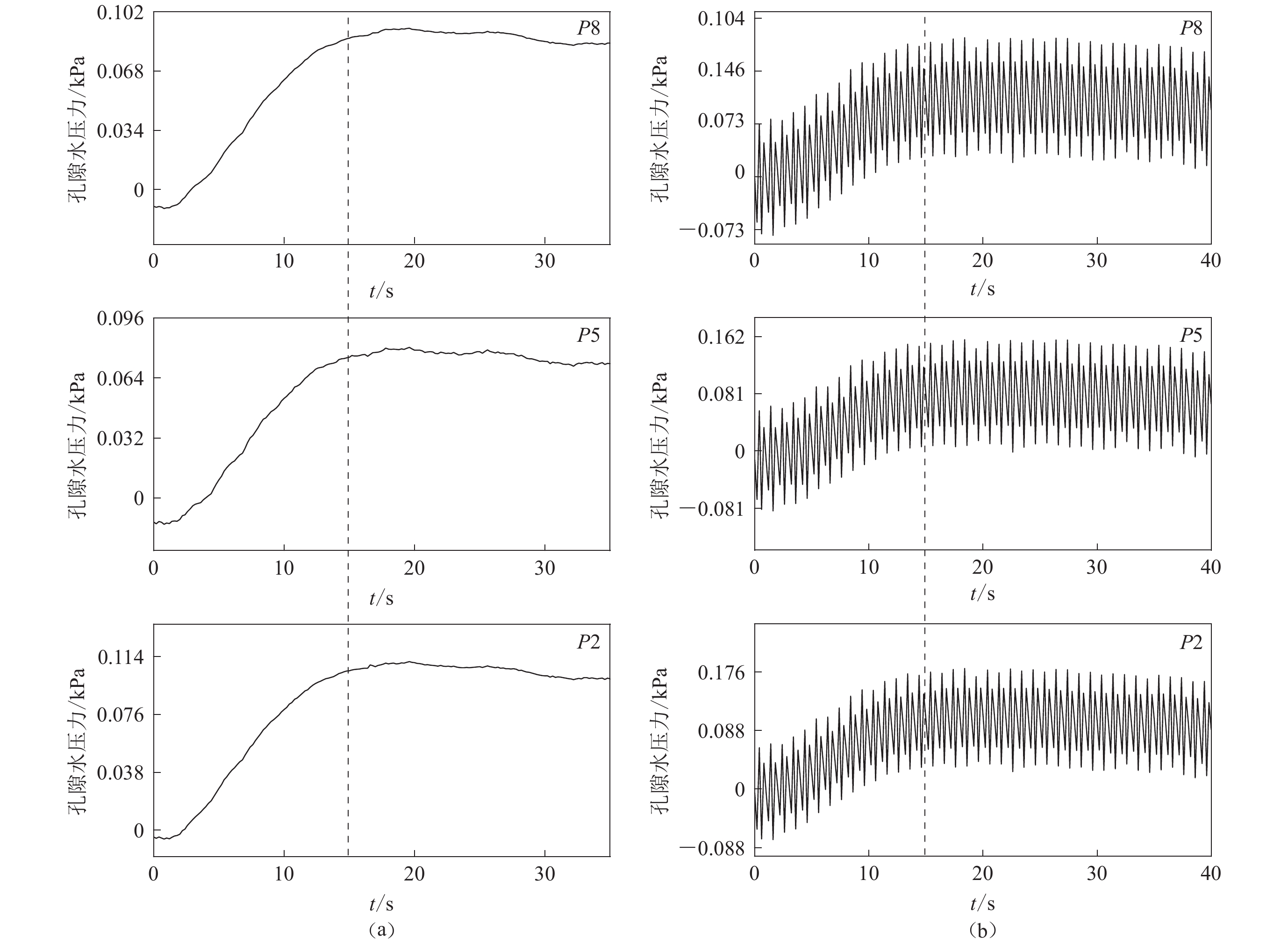
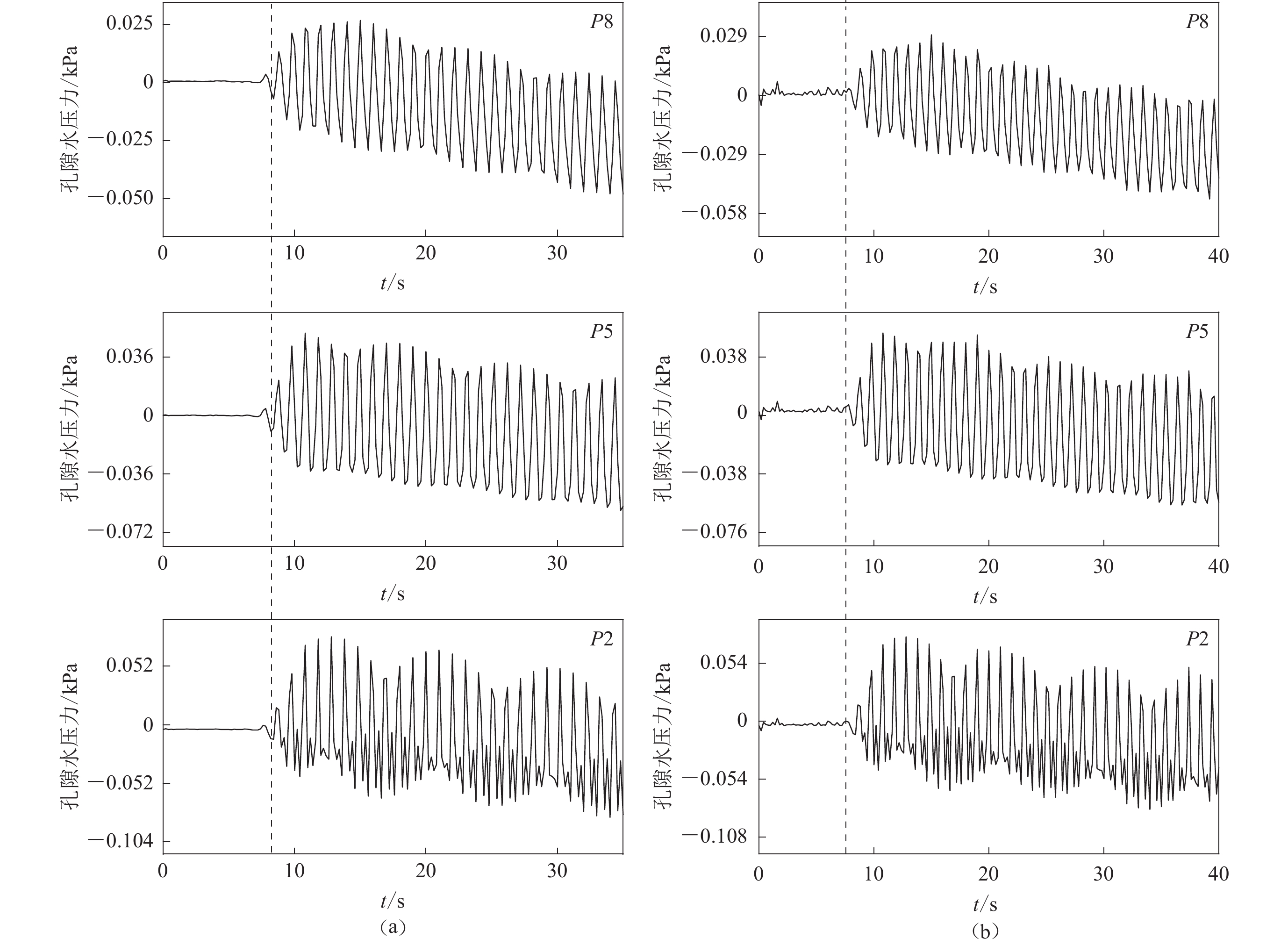
工况1：输入正弦波频率为0.5 Hz，振幅为0.1g、循环加载次数为17.5次情形下，孔隙水压力时程变化，如图6所示。可以看出实测值和模拟值的总体趋势上吻合程度较高，实验中孔压计P2，P5和P8分别记录到了含水层不同深度处于的孔压变化情况，其变幅分别为0.063 kPa，0.036 kPa和0.035 kPa，模拟值为0.093 kPa，0.059 kPa和0.056 kPa。振动开始后，孔隙水压力实测值和模拟值的时程变化均呈现出正弦波形态，振幅也大致吻合，说明振动作用使含水层周期性扩张和压缩从而引起孔隙水压力振荡。然而对比实测值和模拟值的相位发现前者较后者存在相位延迟的现象。具体表现为：实验过程中振动开始大约5 s之后孔隙水压力才开始波动，而数值模拟中，振动开始瞬间孔隙水压力即产生波动现象。造成二者相位差异的原因是在数值模型建立时假设含水介质是均匀、弹性、理想的饱和多孔介质，而实验中的含水砂层并非均匀介质，孔隙度会随着振动的进行发生变化，所以振动开始时孔隙水压力不能立即产生波动，需要一个压力传导的过程，并且这种非均质性也使得模拟值振幅较高于实测值。
![]()
图 6 工况1中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图Figure 6. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 1当输入正弦波频率达到2 Hz，振幅为0.25g，循环加载为70次情形下（工况2）的孔隙水压力的时程变化，如图7所示。实验中孔压计P2，P5和P8的变幅分别为0.113 kPa，0.098 kPa和0.100 kPa，模拟值为0.175 kPa，0.160 kPa和0.146 kPa。由图可以看出孔隙水压力在逐步累积，之后逐渐平稳，说明此时由于振动次数的增大，砂土逐步被压密，孔隙水压力也随之逐渐增大，而由于砂土的压密，孔隙度的变化就会减小，所以导致孔隙水压力在上升到一定程度后达到平稳。孔隙水压力曲线表明，实测值和模拟值相位相同而振幅不同，说明孔隙水压力响应的时间一致，但由于砂层的非均质性导致振动幅度不同，而且在数值模拟中孔隙度和渗透系数都为定值，所以导致了模拟值高于实测值。
![]()
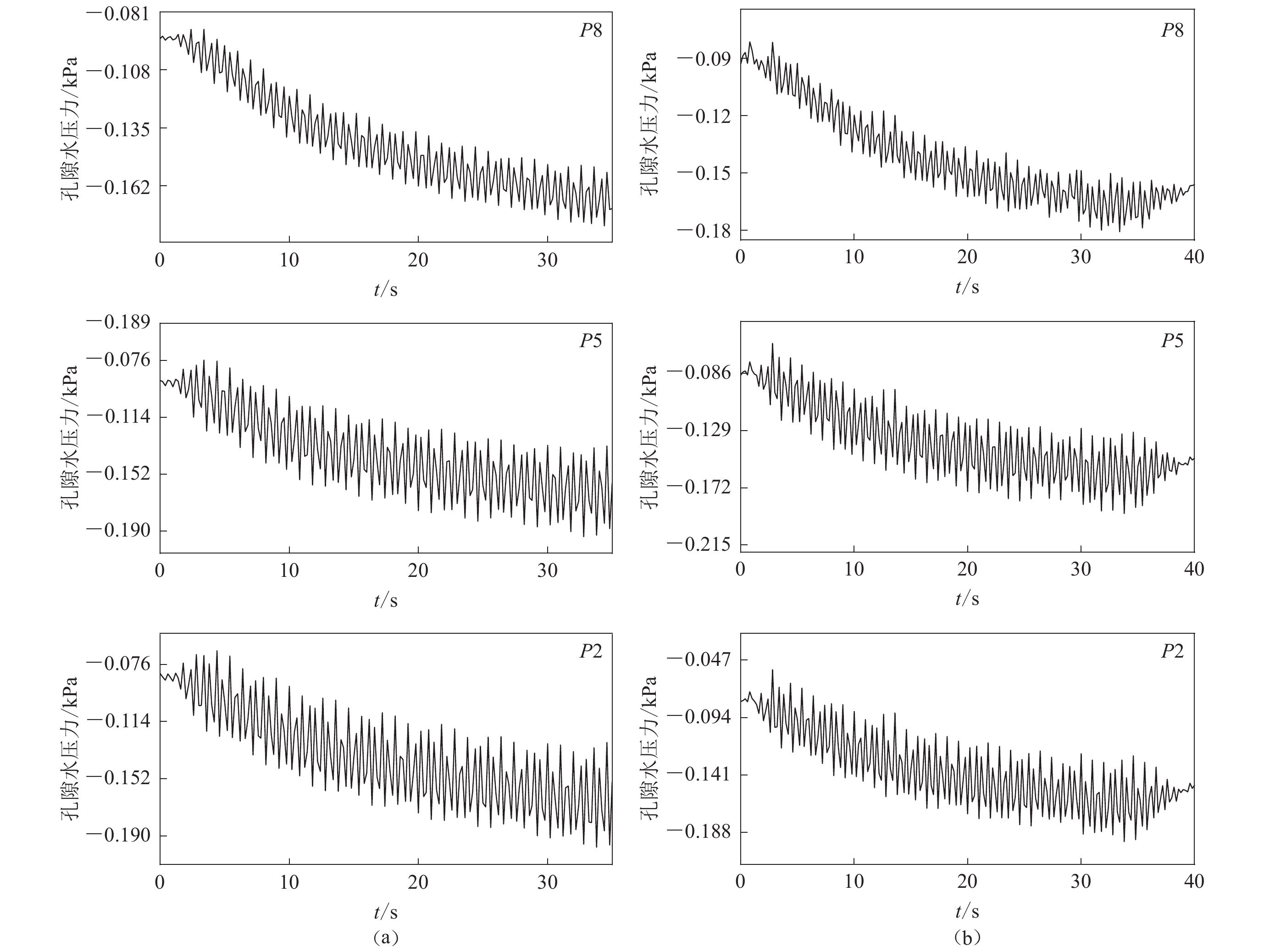
图 7 工况2的孔隙水压力实测值（a）与模拟值（b）时程变化对比Figure 7. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 2图8显示了输入正弦波频率增加到5 Hz，振幅减小到0.15g，振动次数达到175次情形下（工况3）的孔隙水压力时程变化。实验中孔压计P2，P5和P8的变幅分别为0.104 kPa，0.072 kPa和0.05 kPa，模拟值为0.108 kPa，0.076 kPa和0.058 kPa。本次工况中，孔隙水压力呈现出下降变化，并且会出现负值，说明振动幅度的减小导致饱和砂土中扩张作用占主导，砂土表现出剪胀性，导致孔隙水压力逐渐变小。孔隙水压力曲线表明相位相同，模拟值的振幅接近于实测值。
![]()
图 8 工况3中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图Figure 8. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 3保持频率不变，即振动次数不变，将振幅增大到0.25g时（工况4），孔隙水压力的时程变化情况如图9所示，实验中孔压计P2，P5和P8的变幅分别为0.080 kPa，0.076 kPa和0.054 kPa，模拟值为0.050 kPa，0.086 kPa和0.030 kPa。孔隙水压力表现仍然为下降变化，并且下降速率会随着振幅的增大而增大。孔隙水压力曲线表明相位相同，振幅不同，由于此工况下含水层处于膨胀状态，孔隙度和渗透系数将会增大，导致实测值高于模拟值。
![]()
图 9 工况4中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图Figure 9. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 4图10展示了输入正弦波频率达到10 Hz，振幅为0.25g，振动次数达到350次时（工况5）孔隙水压力的时程变化，实验中孔压计P2，P5和P8的变幅分别为0.025 kPa，0.023 kPa和0.022 kPa，模拟值为0.045 kPa，0.039 kPa和0.048 kPa。此工况下也会出现孔隙水压力的累积现象，但是在前期有一个孔隙水压力下降的阶段，这是由于振动初期含水层仍然会在短时间内处于上一次工况中的膨胀状态，之后孔隙水压力又会逐步累积而导致的。由于含水层在振动作用下逐渐压密，孔隙度和渗透系数会减小，导致模拟值仍然高于实测值。
![]()
图 10 工况5中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图Figure 10. Comparison diagram of time history changes between measured （a）and simulated （b） pore water pressure values in working condition 5继续增大频率达到15 Hz，振动次数达到525次，振幅减小到0.15g时（工况6），孔隙水压力的时程变化如图11所示。从图中可以看出此工况下孔隙水压力的变化更为剧烈，呈现出阶降-阶升现象，说明此工况下，砂土颗粒的剪切膨胀和压缩致密化更加剧烈，会表现出很强的不均匀性，颗粒经过前期膨胀、致密化、再次膨胀、继续致密化等一系列过程，砂土整体的结构也会有较大的变化，孔隙度和渗透性系数会发生随机变化，导致孔隙水压力呈现出阶降-阶升现象。孔隙水压力曲线表明发生阶降-阶升现象的相位保持一致，由于孔隙度和渗透系数的变化导致模拟值振幅仍然高于实测值。通过以上分析可知，含水层的压缩和膨胀会引发孔隙水压力的上升和下降，这可能与振动作用的频率和振幅有关，振动频率增大可能会使含水层处于压缩状态，振幅减小可能会导致含水层局部处于膨胀状态。
![]()
图 11 工况6中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图Figure 11. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 6此外，在振动过程中，各工况条件下孔压计P2，P5和P8的孔隙水压力虽然处于不同深度，但是其变化趋势基本相同，没有明显的深度依赖性变化，但变化幅度表现为P2＞P5＞P8，这是由于P2点位于含水层底部，与振动台装置相连，在振动过程中大量的孔隙水不断向上流动，并在流动过程中水头会有一定的损失，造成了底部的孔隙水压力较大，实测值和模拟值中均有这种现象，这说明在小尺度矩形箱体内孔隙水压力的累积和消散是比较均匀的。
3.3 孔隙水压力扰动下井水位的响应
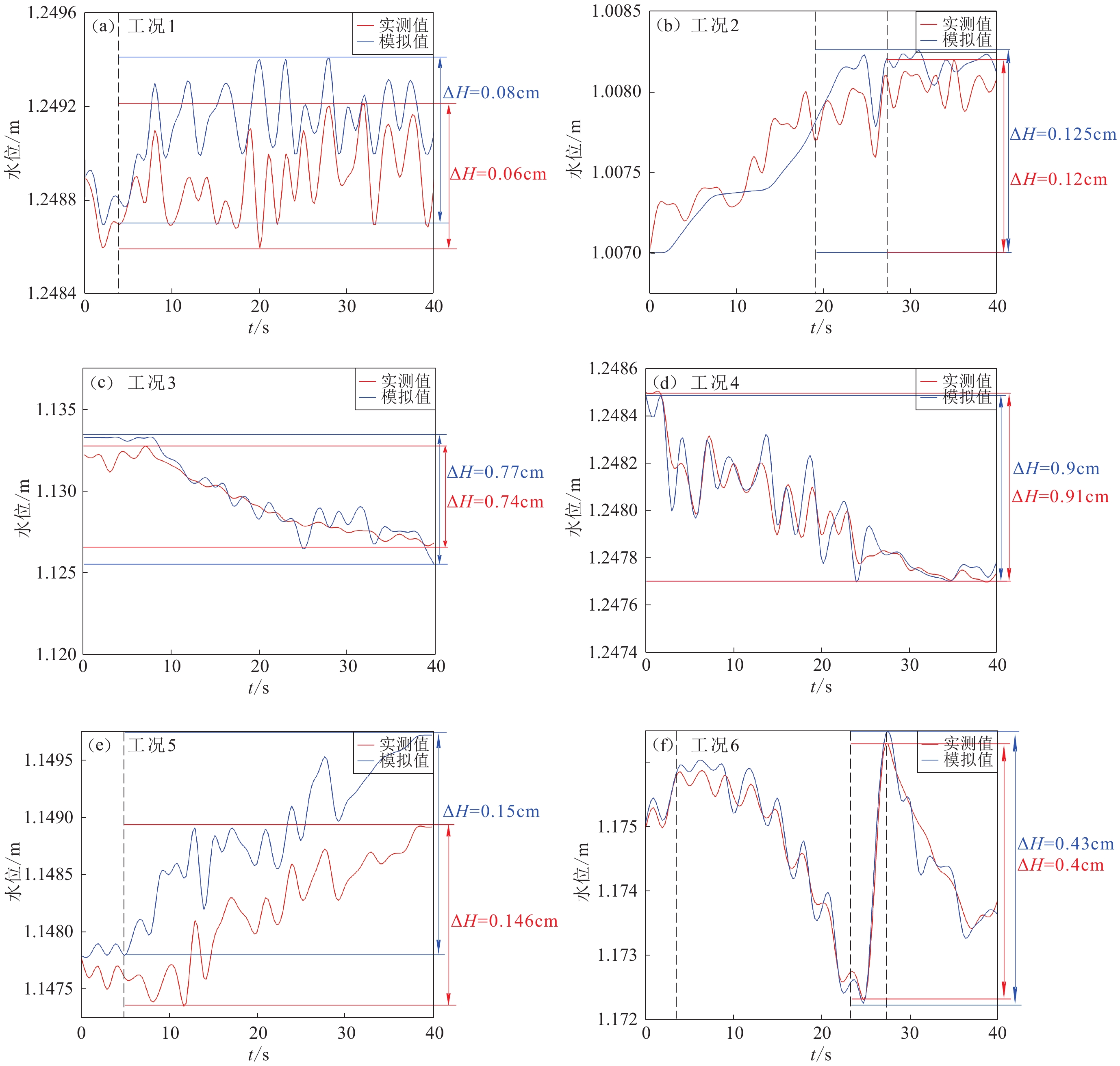
图12以G2井为例，给出了各工况中孔隙水压力扰动下井水位的时程变化情况，井水位曲线的变化形态与孔隙水压力保持一致，井水位的模拟值与实测值表现出同位相变化，总体上略高于实测值。采用SPSS进行相关性分析，水位与P2，P5和P8孔隙水压力相关系数为0.655，0.928和0.957，二者显著相关，说明符合水位对振动响应机理即由于振动引起了孔隙水压力的变化进而导致水位的变化。
![]()
图 12 G2井中各工况的水位的实测值与模拟值时程变化对比图Figure 12. Comparison diagram of time history changes between measured and simulated water levels in well G2输入的正弦波频率为0.5 Hz，振幅为0.1g时，实测值和模拟值中井水位的时程变化都呈现出正弦波形态，这与该工况下孔隙水压力的模拟结果一致，说明井水位的波动可能是由孔隙水压力的振荡引起的。
当输入的正弦波频率达到2 Hz，振幅为0.25g时，井水位呈现出上升变化，之后逐渐平稳，水位与孔隙水压力的响应一致，但在19—27 s之间，水位出现了短时间的阶降，这可能是表皮效应或水流与观测井井壁之间的摩擦效应使得井水位响应滞后，也可能是因为含水层局部位置膨胀所致。
将输入的正弦波频率增加到5 Hz，振幅减小到0.15g时，井水位呈现出下降变化，这与孔隙水压力出现负值有关。保持频率不变，将振幅增大到0.25g时，井水位仍然为下降变化，并且下降速率会随着振幅的增大而增大。
当输入的正弦波达到10 Hz，振幅为0.25g时，井水位呈现出上升变化，表明砂土中又表现为压缩作用，逐步致密化，孔隙水压力逐步累积，井水位也会呈现上升变化。
继续将正弦波频率增大到15 Hz，振幅减小到0.15g时，井水位的变化更为剧烈，呈现出阶降-阶升现象，说明此工况下，砂土颗粒的剪切膨胀和压缩致密化更加剧烈，表现出很强的不均匀性，颗粒经过前期膨胀、致密化、再次膨胀，继续致密化等一系列过程，砂土整体的结构也会有较大的变化，渗透性也会发生随机变化，所以导致井水位呈现出阶降-阶升现象。
通过对比孔隙水压力和井水位在同一种工况中实测值和模拟值的大小可以看出，两者始终保持一致，说明井水位和孔隙水压力显著相关。但水位振幅与孔隙水压力的变化幅度之间又有一定的区别，这是因为当孔隙水压力驱动水流向井中时，井储效应、表皮效应，以及水流与井壁之间的摩擦效应均会对井内的水位响应产生影响（Ramey，Agarwal，1972；Barrash et al，2006；Houben，2015）。
3.4 孔隙水压力和井水位的实测值与模拟值误差分析
图13给出了孔隙水压力和井水位模拟值与实测值之间的误差，正值表示模拟值高于实测值，负值表示模拟值低于实测值。各工况条件下孔隙水压力的误差范围在−2%—6%之间，井水位误差范围在−0.1%—0.4%之间，说明本次建立的数学模型能够较好地反映出振动过程中松散承压含水层中孔隙水压力和井水位的响应情况。
![]()
图 13 孔隙水压力（a）和井水位（b）的模拟值与实测值误差分析对比图Figure 13. Comparison diagram of error analysis between simulated and experimental measured values of pore water pressure （a）and groundwater level （b）本次数学模型的建立依据振动台实际受力情况，在一定的假设条件下解释了井水位同震响应的变化现象，孔隙水压力和井水位的变化趋势主要受振动频率和振幅的影响，换言之就是受到含水层在振动作用下的压缩和膨胀控制，压缩导致孔隙水压力和井水位的上升，膨胀导致孔隙水压力和井水位的下降，两种作用同时存在的话，可能导致孔隙水压力和井水位的振荡或者阶升-阶变变化，这取决于含水层的实际状态。综合来看，井水位变化趋势与野外观测到的同震水位变化相似，其变化机理在一定程度上可以解释地下水同震响应变化机理。
4. 讨论与结论
本文研究了力学周期性加载对封闭的、饱和松散多孔介质中的孔隙水压力变化影响机制和一般物理过程。周期性的正弦振动引起了砂层的形变，导致砂层压缩或膨胀，砂层变形引起孔隙水压力的变化，孔压变化又对砂层变形产生影响，这是典型的流-固耦合相互作用过程。孔隙水压力梯度变化诱导水流进出观测孔，导致水位变化。在本次实验中，水力响应包括不同类型的水位波动、孔隙水压力变化，这与野外观测到的同震水文响应部分现象类相类似，表明本次建立的振动台实验模型能在一定程度上验证地震荷载下松散沉积物的压缩膨胀以及井水位和孔隙水压力的同震响应情况，反映了封闭、饱和松散砂土中振动作用诱发的压实、固结和剪胀过程。
针对上述物理过程，本文建立了饱和多孔介质的动力学平衡方程，结合达西定律、胡克定律和质量守恒定律，建立了正弦荷载作用下承压饱水砂层中孔隙水压力响应的数学模型，利用COMSOL Multiphysics多物理场数值模拟软件进行求解，数值模拟结果与实验结果吻合程度较好，说明本次建立的数学模型能够较好地反映出振动作用下承压饱水砂层中孔隙水压力的响应过程。此外，通过实验和数值模拟还发现动态振动后观测到的水位变化与孔隙水压力变化趋势相同，说明实验中井水位的同震响应是由孔隙水压力的扰动产生的，地震荷载引起的含水层的压缩和膨胀是井水位变化的主要机制，同时伴随着机械振荡。
在此需要说明实验和数值模拟中的几个局限性：
1） 不能在相同的初始条件下重复每次试验，以准确地评估由于振动频率和振幅变化的作用而导致砂土层的变形；
2） 实验中的正弦形式振动和真实地震波对含水层的影响是存在差异的；
3） 实验中忽略了一些可能对实验结果有重要影响的因素，如边界效应和井间效应；
4） 在建立数学模型时，为了简化模型便于计算，始终假设砂层是各向同性介质，在未来的研究中，计划考虑砂层的各向异性。
中国地震局工程力学研究所郭迅研究员及其团队在实验开展方面给予了的指导和帮助，德国哥廷根大学刘泉博士在建模方面予以指导，防灾科技学院硕士研究生徐邑荣在论文修改上提供了帮助，作者在此一并表示感谢。
-
![]()
图 13 孔隙水压力（a）和井水位（b）的模拟值与实测值误差分析对比图
Figure 13. Comparison diagram of error analysis between simulated and experimental measured values of pore water pressure （a）and groundwater level （b）
![]()
图 2 实验所记录的典型井水位变化形态（以G2井为例）
（a） 振荡；（b） 上升；（c） 下降；（d） 阶变
Figure 2. Typical change forms of well water level in experiments （taking well G2 as an example）
（a） Oscillation；（b） Rise；（c） Drop；（d） Step-like change
![]()
图 3 初始平衡状态下承压含水层模型剖面图
Figure 3. Profile of confined aquifer model at initial equilibrium state
![]()
图 4 压力扰动井-含水层系统的概念模型
Figure 4. Conceptual model of the well-aquifer system disturbing by a harmonic pressure
![]()
图 5 井流运动示意图
（a） 静止状态；（b） 运动状态
Figure 5. Schematic diagram of well flow
（a） Stationary state；（b） Motion state
![]()
图 6 工况1中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图
Figure 6. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 1
![]()
图 7 工况2的孔隙水压力实测值（a）与模拟值（b）时程变化对比
Figure 7. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 2
![]()
图 8 工况3中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图
Figure 8. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 3
![]()
图 9 工况4中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图
Figure 9. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 4
![]()
图 10 工况5中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图
Figure 10. Comparison diagram of time history changes between measured （a）and simulated （b） pore water pressure values in working condition 5
![]()
图 11 工况6中孔隙水压力的实测值（a）与模拟值（b）时程变化对比图
Figure 11. Comparison diagram of time history changes between measured （a） and simulated （b） pore water pressure values in working condition 6
![]()
图 12 G2井中各工况的水位的实测值与模拟值时程变化对比图
Figure 12. Comparison diagram of time history changes between measured and simulated water levels in well G2
表 1 正弦波的振动参数
Table 1 Shaking parameters of different sine waves
工况编号 频率/Hz 加速度/g 加载时间/s 工况编号 频率/Hz 加速度/g 加载时间/s 1 0.5 0.1 35 4 5 0.25 35 2 2 0.25 35 5 10 0.25 35 3 5 0.15 35 6 15 0.15 35 注：1g＝9.81 m/s2。 
下载: 导出CSV
表 2 数值模拟中的参数取值
Table 2 Parameters used in numerical experiments.
参数 单位 数值 弹性模量$E$ Pa 2.63×1010 泊松比$\upsilon $ 1 0.25 渗透系数$K$ m/d 33 孔隙度$n$ 1 0.398 ${{{\rm{Biot}}'{\rm{s}}} }$系数 1 1 固相密度$\;{\rho _{\rm{s}}}$ kg/m3 2 650 液相密度$\;{\rho _{\rm{f}}}$ kg/m3 1 000 固相体积模量${E_{\rm{s}}}$ Pa 1.56×1010 液相体积模量${E_{\rm{f}}}$ Pa 1×108 储水率${S_{ {\rm{s} }} }$ 1 1×10−3 动力黏度系数$\;\mu$ Pa·s 1×10−4
下载: 导出CSV
-
车用太,鱼金子. 2014. 地壳流体对地震活动的影响与控制作用[J]. 国际地震动态,(8):1–9. doi: 10.3969/j.issn.0235-4975.2014.08.001 Che Y T,Yu J Z. 2014. Influence and controlling of fluid in the crust on earthquake activity[J]. Recent Developments in World Seismology,(8):1–9 (in Chinese).
谷洪彪,张璜,谷健芬,张艳,迟宝明. 2017. 静水条件下振动对测压水位影响实验[J]. 地震学报,39(3):407–419. Gu H B,Zhang H,Gu J F,Zhang Y,Chi B M. 2017. Experiments on response of piezometric level to vibrations under hydrostatic condition[J]. Acta Seismologica Sinica,39(3):407–419 (in Chinese).
贾化周,秦清娟. 1996. 利用地下水位预报地震的新思路与新方法[J]. 华北地震科学,14(3):28–37. Jia H Z,Qin Q J. 1996. A new idea and a new method for earthquake prediction by groundwater level[J]. North China Earthquake Sciences,14(3):28–37 (in Chinese).
刘春平. 2017. 地壳应力与地下水动力响应[M]. 北京: 地震出版社: 1−199. Liu C P. 2017. Crustal Stress and Groundwater Dynamic Response[M]. Beijing: Seismological Press: 1–199 （in Chinese）.
许才军,周红波. 1998. 不排水循环荷载作用下饱和软粘土的孔压增长模型[J]. 勘察科学技术,(1):3–7. Xu C J,Zhou H B. 1998. Pore pressure increase model of saturated soft clay under undrained cyclic load[J]. Site Investigation Science and Technology,(1):3–7 (in Chinese).
阎澍旺. 1991. 往复荷载作用下重塑软粘土的变形特性[J]. 岩土工程学报,(1):48–53. doi: 10.3321/j.issn:1000-4548.1991.01.005 Yan P W. 1991. Deformation characteristics of remolded soft clay under cyclic loading[J]. Chinese Journal of Geotechnical Engineering,13(1):48–53.
翟泽宇. 2021. 浅层非固结含水层对简谐振动响应的水动力模型研究[D]. 廊坊: 防灾科技学院: 1−115. Zhai Z Y. 2021. Study on Hydrodynamic Model of Response of Shallow Unconsolidated Aquifer to Harmonic Vibration[D]. Langfang: Institute of Disaster Prevention: 1−115 （in Chinese）.
张璜,谷洪彪,张艳,迟宝明. 2016. 渗流条件下振动对测压水位的影响实验[J]. 地球物理学进展,31(4):1857–1866. doi: 10.6038/pg20160459 Zhang H,Gu H B,Zhang Y,Chi B M. 2016. Effect experiment of the vibration on piezometric level under seepage condition[J]. Progress in Geophysics,31(4):1857–1866 (in Chinese).
张艳. 2020. 承压含水层井水位对循环荷载响应的水动力过程研究[D]. 哈尔滨: 中国地震局工程力学研究所: 1−163. Zhang Y. 2020. Research on Hydrodynamic Process of Response of Well Water Level of Confined Aquifer to Cyclic Loading[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 1−163 （in Chinese）.
张艳,谷洪彪,兰双双,迟宝明,姜海宁. 2017. 井-含水层系统水位响应规律振动台试验初探[J]. 科技通报,33(12):80–84. doi: 10.13774/j.cnki.kjtb.2017.12.016 Zhang Y,Gu H B,Lan S S,Chi B M,Jiang H N. 2017. Shaking table tests on water level response of well-aquifer system[J]. Bulletin of Science and Technology,33(12):80–84 (in Chinese).
张耀文,谷洪彪,那金,宋洋,张艳. 2019. 承压含水层中孔压变化规律的振动台实验研究[J]. 科学技术与工程,19(17):18–24. doi: 10.3969/j.issn.1671-1815.2019.17.003 Zhang Y W,Gu H B,Na J,Song Y,Zhang Y. 2019. Experimental study on the variation law of pore pressure in confined aquifer by vibration table[J]. Science Technology and Engineering,19(17):18–24 (in Chinese).
周健,屠洪权,安原一哉. 1996. 动力荷载作用下软粘土的残余变形计算模式[J]. 岩土力学,17(1):54–60. Zhou J,Tu H Q,Yaswhara K. 1996. A model for predicting the cyclic behaviour of soft clay[J]. Rock and Soil Mechanics,17(1):54–60 (in Chinese).
周健,陈小亮,杨永香,贾敏才. 2011. 饱和层状砂土液化特性的动三轴试验研究[J]. 岩土力学,32(4):967–972. doi: 10.3969/j.issn.1000-7598.2011.04.002 Zhou J,Chen X L,Yang Y X,Jia M C. 2011. Study of liquefaction characteristics of saturated stratified sands by dynamic triaxial test[J]. Rock and Soil Mechanics,32(4):967–972 (in Chinese).
Barrash W,Clemo T,Fox J J,Johnson T C. 2006. Field,laboratory,and modeling investigation of the skin effect at wells with slotted casing,Boise hydrogeophysical research site[J]. J Hydrol,326(1/2/3/4):181–198.
Biot M A. 1941. General theory of three-dimensional consolidation[J]. J Appl Phys,12(2):155–164. doi: 10.1063/1.1712886
Biot M A. 1955. Theory of elasticity and consolidation for a porous anisotropic solid[J]. J Appl Phys,26(2):182–185. doi: 10.1063/1.1721956
Biot M A. 1956a. General solutions of the equations of elasticity and consolidation for a porous material[J]. J Appl Mech,23(1):91–96. doi: 10.1115/1.4011213
Biot M A. 1956b. Theory of deformation of a porous viscoelastic anisotropic solid[J]. J Appl Phys,27(5):459–467. doi: 10.1063/1.1722402
Biot M A. 1962. Mechanics of deformation and acoustic propagation in porous media[J]. J Appl Phys,33(4):1482–1498. doi: 10.1063/1.1728759
Bowen R M. 1980. Incompressible porous media models by use of the theory of mixtures[J]. Int J Eng Sci,18(9):1129–1148. doi: 10.1016/0020-7225(80)90114-7
Bredehoeft J D,Cooper H H,Papadopulos I S. 1966. Inertial and storage effects in well-aquifer systems:An analog investigation[J]. Water Resour Res,2(4):697–707. doi: 10.1029/WR002i004p00697
Brodsky E E. 2003. A mechanism for sustained groundwater pressure changes induced by distant earthquakes[J]. J Geophys Res:Solid Earth,108(B8):2390. doi: 10.1029/2002JB002321
Carslaw H S, Jaeger J C. 1959. Conduction of Heat in Solids[M]. Oxford: Clarendon Press: 1–520.
Cheung Y K,Tham L G. 1983. Numerical solutions for Biot’s consolidation of layered soil[J]. J Eng Mech,109(3):669–679.
Cooper H H Jr,Bredehoeft J D,Papadopulos I S,Bennett R R. 1965. The response of well-aquifer systems to seismic waves[J]. J Geophys Res,70(16):3915–3926. doi: 10.1029/JZ070i016p03915
Crews J B, Cooper C A. 2014. Experimental investigation of remote seismic triggering by gas bubble growth in groundwater[C]//American Geophysical Union 2014 Fall Meeting. San Francisco, California: AGU.
Elkhoury J E,Brodsky E E,Agnew D C. 2006. Seismic waves increase permeability[J]. Nature,441(7097):1135–1138. doi: 10.1038/nature04798
Ge S M,Stover S C. 2000. Hydrodynamic response to strike- and dip-slip faulting in a half-space[J]. J Geophys Res. :Solid Earth,105(B11):25513–25524. doi: 10.1029/2000JB900233
Gu H B,Lan S S,Zhang H,Wang M Y,Chi B M,Sauter M. 2021a. Water level response in wells to dynamic shaking in confined unconsolidated sediments:A laboratory study[J]. J Hydrol,597:126150. doi: 10.1016/j.jhydrol.2021.126150
Gu H B,Lan S S,Zhang H,Wang M Y,Sauter M . 2021b. Water level response in wells to dynamic shaking in confined unconsolidated sediments:A laboratory study[J]. Journal of Hydrology,597(2):126150.
Gulley A K,Dudley Ward N F,Cox S C,Kaipio J P. 2013. Groundwater responses to the recent Canterbury earthquakes:A comparison[J]. J Hydrol,504:171–181. doi: 10.1016/j.jhydrol.2013.09.018
Houben G J. 2015. Review:Hydraulics of water wells—head losses of individual components[J]. Hydrogeol J,23(8):1659–1675. doi: 10.1007/s10040-015-1313-7
Jaeger J C, Cook N G W, Zimmerman R W. 2009. Fundamentals of Rock Mechanics[M]. John Wiley & Sons: 1–488.
Manga M, Wang C Y. 2007. Earthquake hydrology[G]// Treatise on Geophysics. London: Elsevier:4:293–320.
Matsumoto N,Roeloffs E A. 2003. Hydrological response to earthquakes in the Haibara well,central Japan:Ⅱ. Possible mechanism inferred from time-varying hydraulic properties[J]. Geophys J Int,155(3):899–913. doi: 10.1111/j.1365-246X.2003.02104.x
Muir-Wood R,King G C P. 1993. Hydrological signatures of earthquake strain[J]. J Geophys Res:Solid Earth,98(B12):22035–22068. doi: 10.1029/93JB02219
Oka F,Yashima A,Shibata T,Kato M,Uzuoka R. 1994. FEM-FDM coupled liquefaction analysis of a porous soil using an elasto-plastic model[J]. Appl Sci Res,52(3):209–245. doi: 10.1007/BF00853951
Quilty E G,Roeloffs E A. 1997. Water-level changes in response to the 20 December 1994 earthquake near Parkfield,California[J]. Bull Seismol Soc Am,87(2):310–317. doi: 10.1785/BSSA0870020310
Ramey H J Jr,Agarwal R G. 1972. Annulus unloading rates as influenced by wellbore storage and skin effect[J]. Soc Petrol Eng J,12(5):453–462. doi: 10.2118/3538-PA
Rexin E E,Oliver J,Prentiss D. 1962. Seismically-induced fluctuations of the water level in the Nunn-Bush well in Milwaukee[J]. Bull Seismol Soc Am,52(1):17–25. doi: 10.1785/BSSA0520010017
Shi Z,Wang G,Manga M,Wang C Y. 2015. Continental-scale water-level response to a large earthquake[J]. Geofluids,15(1/2):310–320.
Stearns H T. 1928. Record of earthquake made by automatic recorders on wells in California[J]. Bull Seismol Soc Am,18(1):9–15. doi: 10.1785/BSSA0180010009
Terzaghi K. 1943. Theoretical Soil Mechanics[M]. New York: Wiley:1−528.
Wakita H. 1975. Water wells as possible indicators of tectonic strain[J]. Science,189(4202):553–555. doi: 10.1126/science.189.4202.553
Wang C Y,Chia Y. 2008. Mechanism of water level changes during earthquakes:Near field versus intermediate field[J]. Geophys Res Lett,35(12):L12402.
Wang C Y, Manga M. 2009. Earthquakes and Water[M]. Berlin, Heidelberg: Springer: 1–225.
Wang C Y, Manga M. 2014. Encyclopedia of complexity and systems science[M]//Earthquakes and Water .Berlin, Heidelberg: Springer: 1–38.
Wang C Y,Chia Y,Wang P L,Dreger D. 2009. Role of S waves and Love waves in coseismic permeability enhancement[J]. Geophys Res Lett,36(9):L09404.
Zlotnik V A,McGuire V L. 1998a. Multi-level slug tests in highly permeable formations:1. Modification of the Springer-Gelhar (SG) model[J]. J Hydrol,204(1/2/3/4):271–282.
Zlotnik V A,McGuire V L. 1998b. Multi-level slug tests in highly permeable formations:2. Hydraulic conductivity identification,method verification,and field applications[J]. J Hydrol,204(1/2/3/4):283–296.
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 364
- HTML全文浏览量: 151
- PDF下载量: 117
- 被引次数: 1
