Comparative study on two kinds of electrode grounding resistance measurement methods in geo-resistivity observation
-
摘要: 利用传统三极接地电阻率测量方法对井下电极接地电阻进行测量会存在较大的测量误差,表明该方法已不适用于井下电极接地电阻测量。针对此问题,提出了利用台站现有地电阻率仪器进行电极接地电阻测量的新方法—直接测量法,并使用传统三极法和直接测量法对北京平谷地震台井下观测供电电极接地电阻进行了测量。测量结果表明:与传统三极法对比,直接测量法的测量结果更为准确、可靠,而且节省人力、物力和时间。Abstract: When using the traditional three-pole method to measure the underground electrode grounding resistance, there will be a large measurement error, which suggests that the method will not be suitable for the underground electrode grounding resistance measurement. In view of this problem, this paper proposes a new method for measuring the electrode grounding resistance by using the geo-electric resistivity observation system, which is so called direct measurement method. And then, the grounding resistances of the underground observation power supply electrodes of Pinggu seismic station in Beijing were measured by using the traditional three-pole method and the direct measurement method. The measurement results show that, compared with the traditional three-pole method, the direct measurement method can get more reliable measurement results with less error, and can save human and material resources and measuring time.
-
引言
地震地电阻率观测旨在研究某一特定区域地下介质电阻率随时间的变化与地震孕育的关系,在我国的地震监测、预测的科学实践中发挥了重要作用(杜学彬,2010;钱家栋等,2013;Lu et al,2016)。地电阻率观测系统包括测量仪器和观测装置两个部分,大部分地电阻率观测采用地表四极对称观测装置进行观测,一般供电极距为1 000 m,测量极距为300—400 m。为了确保观测数据长期稳定可靠,需要对测量仪器的性能和观测装置的稳定性进行定期检查,而电极接地电阻是影响观测装置稳定性的一个重要因素。郑兆苾和吴培稚(1986)的研究结果已表明,引起观测装置不稳定的原因主要是与电极连接的外线路漏电,且漏电所造成的影响与电极接地电阻成正比,接地电阻越大,漏电影响越大。若供电电极的接地电阻过大,地电阻率观测时会在供电线上产生较高的供电电压,电压越高,漏电产生的影响越大(钱家栋,2010)。为了满足地震监测长期定点观测的需求,同时保障观测系统的稳定可靠,我国地电阻率观测方法行业标准(中国地震局, 2009)明确要求,测量电极接地电阻不应大于100 Ω,供电电极接地电阻不应大于30 Ω,并且在台站实际观测中,须定期对电极的接地电阻进行测量,以判断该电极接地电阻是否满足该行业标准的要求。
对于接地电阻测量,美国电气与电子工程师协会编制的接地电阻测量指南(IEEE Power and Energy Society,2012)和我国的接地电阻测量规程(中华人民共和国国家质量监督检验检疫总局,2000)均推荐使用三电极法测量地表接地体的接地电阻,通过测量接地体与电流极之间的电位降曲线找到电位极电压为零的位置,进而由欧姆定律得到接地电阻值。但是由于三电极法测量的过程较为复杂,一般采用其中的直线法(也称为0.618法)进行接地电阻测量。
在我国以往的地电阻率电极接地电阻测量中,普遍采用的电极为1 m×1 m尺寸、3 mm厚的正方形铅板,一般埋设在地表以下1—1.5 m深度,测量均采用直线三极法,测量时将两个辅助电极和被测电极布设在一条直线上。近年来,随着地电阻率井下观测方法的推广和应用,我国目前已有30余个地电阻率台站改为井下观测(王兰炜等,2015;高曙德,2016;解滔等,2019)。井下地电阻率观测与地表观测的不同之处在于供电电极和测量电极改为埋设在地表以下几十米至几百米的井下,此种情形下,由于被测电极和两个辅助电极的相对水平位置不在一条直线上,且若井下电极与地表辅助电极所处位置的介质电阻率不同,就不能构成均匀半空间,如果仍采用直线三极法测量电极接地电阻,就会产生一定的误差。
鉴于我国地电阻率井下观测不断发展的实际情况,本文提出了一种电极接地电阻测量的新方法即直接测量法,并对传统三极法和直接测量法进行对比分析,以期为电极接地电阻的准确测量提供一种更优的测量方法。
1. 接地电阻计算
1.1 地表电极接地电阻计算
电流由接地体流向大地或流经大地时均会产生电阻,这些电阻统称为接地电阻(冯慈璋,1983;王洪泽等,2007;杨德荣,梁丹,2007)。接地电阻一般由三部分组成,即接地体自身的电阻、接地电极表面与大地土壤接触处的接触电阻和接地电极周围土壤所具有的电阻。
通常情况下,一般金属如纯铜的电阻率为1.7×10−6 Ω•m,而一般土壤(无岩石)的电阻率在几百到几千Ω•m,两者相差很大,因此计算接地电极的接地电阻时可以忽略金属接地极自身的电阻。此外,金属的接地电极与土壤固体颗粒通常为“点”接触,接触界面处存在接触电阻,但这个接触电阻非常小,在计算接地电阻时也可以忽略。因此在实际应用中,接地电阻的计算只考虑接地电极周围大地土壤的电阻。
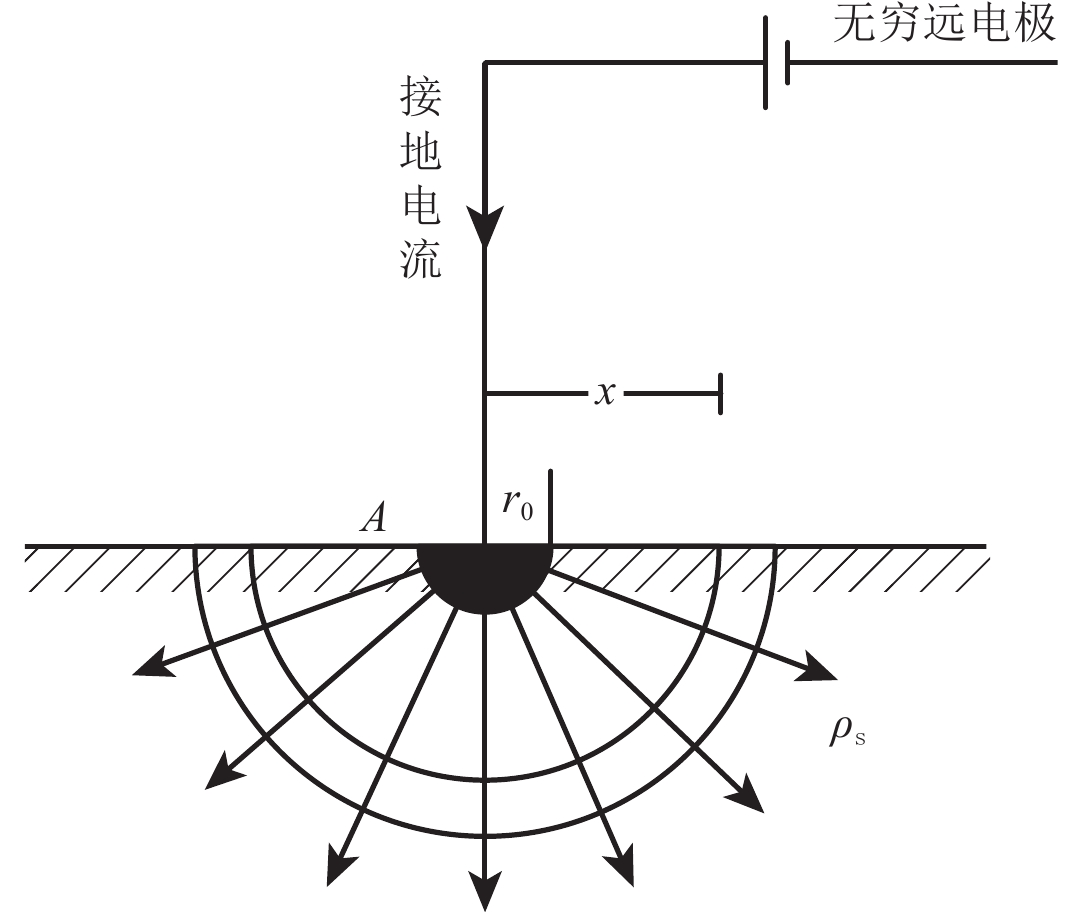
图1是半球形电极接地电阻示意图。半球状电极A埋设于地表,其半径为r0,大地土壤为均质,其电阻率为ρs,且大地为零电位,则电极的接地电阻是接地体表面至大地无限远处的电阻,实际上就是大地很多段电阻分布的总和。
电流I从电极流向无限远处,由于地下介质是均匀的,所以以电极为中心,距离球心x处的电流密度J为
$$ J=\frac{I}{2\pi {x}^{2}} , $$ (1) 该处的电场强度E可由欧姆定律的微分形式得到:
$$ E=J{\rho }_{\mathrm{s}}=\frac{I{\mathrm{\rho }}_{\mathrm{s}}}{2\pi {x}^{2}} , $$ (2) 则半球电极的电位U为
$$ U={\int }_{ {r}_{0}}^{\infty }{E}{{\rm{d}}}x=\frac{I{\mathrm{\rho }}_{\mathrm{s}}}{2\pi {r}_{0}} {\text{.}} $$ (3) 当r0趋于无穷远时,U=0,即距离电极无穷远处的电位为零。所以电极处与无穷远处的电位差V=U-0=U,由欧姆定律可以计算半球电极的接地电阻R1为
$$ {R}_{1}=\frac{V}{I}=\frac{{\mathrm{\rho }}_{{\rm{s}}}}{2\pi {r}_{0}} {\text{.}} $$ (4) 式(4)表明,半球电极的接地电阻与土壤电阻率ρs成正比,而与其半径r0成反比。
1.2 井下电极接地电阻计算
在地电阻率观测实践中,为了减小地表观测时地电阻率年变化和地表杂散电流及金属管线等的影响,很多地电台站开展了井下深埋电极的地电阻率观测,将供电电极和测量电极深埋在井下几十米或上百米(王兰炜等,2015;高曙德,2016;解滔等,2019)。此时,电极接地电阻的计算需按照全空间中的球形电极进行分析。
通过球形接地电极流入地下的电流所形成的电场是恒定电场,不随时间而变化,与静电场有相似之处,因此可用静电比拟法计算接地电极的接地电阻(冯慈璋,1983)。
$$ {R}_{2}=\frac{{{\varepsilon }\mathrm{\rho }}_{{\rm{s}}}}{C}, $$ (5) 式中,R2为球形接地电极的接地电阻,C为接地电极的电容,ρs为土壤电阻率,ε=ε0/(4π×9×104)为大地介电系数,ε0为大地相对介电系数。式(5)表明接地电极的接地电阻与其电容成反比,因此可以利用静电学中电极的电容公式来计算接地电极的接地电阻。充满电介质(介电系数为ε)的无穷大的全空间中,孤立导体球的电容为
$$ C=4\mathrm{\pi }\varepsilon {r}_{0} ,$$ (6) 将其代入式(5),可得到球形接地电极在全空间中的接地电阻为
$$ {R}_{2}=\frac{{{\varepsilon }{\rho }}_{{\rm{s}}}}{C}=\frac{{{\varepsilon }{\rho }}_{{\rm{s}}}}{4{\pi }\varepsilon {r}_{0}}=\frac{{{\rho }}_{{\rm{s}}}}{4{\pi }{r}_{0}}{\text{.}} $$ (7) 本文将基于以上球形电极和半球形电极的接地电阻理论计算结果,对现有地电阻率观测中电极接地电阻测量方法及误差进行分析。
2. 三极测量法
2.1 原理
三极测量法是最为常用的接地电阻测量方法,通常用来测量地表接地电极的接地电阻率,图2为直线三极法的测量原理示意图(杨德荣,梁丹,2007)。
当向被测电极A与电流极C之间注入电流I时,地面电位将发生变化,同时测量I和A与P之间的电位差VAP。电位极P从A的左侧开始沿布极方向向右侧移动,当P位于零电位点(区)时,VAP为被测电极A的电位,则被测电极A的接地电阻为
$$ {R}_{A}=\frac{{V}_{AP}}{I} {\text{.}} $$ (8) 由式(8)可知,影响接地电阻测量值
$ {R}_{A} $ 的因素是VAP和I,电流I为恒定电流。因此,关键是要测量出待测接地极A的准确电位值,即要求电位极P布设在零电位点(区)。若电位极P不在零电位区,就会使测量结果产生误差(应顺潮,1992;冯志伟,马金福,2009)。将图2中电极A和C视为半球形,且地下介质均匀,通过接地极A入地的电流I为正,而通过电流极C回流的电流为负,由GB/T 17949.1—2000 (中华人民共和国国家质量监督检验检疫总局,2000)中的电位降法测量原理计算各点电位:
$$ {U}_{P}={V^A_P} I+{V_P^C} ( -I ) ,$$ (9) $$ {U}_{A}={V_A^A} I+{V_A^C} ( -I ) , $$ (10) 式(9)和(10)中,UP和UA分别为电位极P和A的电位,
$V^A_P $ 和$V_A^A $ 分别为当1 A电流通过接地极A入地后电位极P和A的电位差,$V_P^C $ 和$V_A^C $ 分别为当1 A电流通过接地极C入地后电位极P与A的电位差。电极A与P之间的电压VAP为(中华人民共和国国家质量监督检验检疫总局,2000;徐程,庞亮,2010):
$$ {V}_{AP}={U}_{A}-{U}_{P}=I ( {V_A^A}-{V_A^C}-{V_P^A}+{V_P^C} ) = \frac{I{\rho }_{{\rm{s}}}}{2\pi }\left(\frac{1}{{r}_{0}}-\frac{1}{x}-\frac{1}{d}+\frac{1}{d-x}\right) ,$$ (11) 由此得到接地电阻RA为
$$ {R}_{A}=\frac{{V}_{AP}}{I}=\frac{{\rho }_{{\rm{s}}}}{2\pi }\left(\frac{1}{{r}_{0}}-\frac{1}{x}-\frac{1}{d}+\frac{1}{d-x}\right) {\text{.}}$$ (12) 由式(4)可知,地表半球形接地电极的接地电阻理论计算结果为
$ {R}_{1}={\rho }_{{\rm{s}}}/2\mathrm{\pi }{r}_{0} $ 。令Rl=RA,则$$ \frac{{\rho }_{{\rm{s}}}}{2\pi }\left(\frac{1}{{r}_{0}}-\frac{1}{x}-\frac{1}{d}+\frac{1}{d-x}\right)=\frac{{\rho }_{{\rm{s}}}}{2\pi {r}_{0}}{\text{.}} $$ (13) 若使式(13)成立,则须
$ -{1}/{x}+{1}/ ( {d-x} ) -{1}/{y} $ =0。设$c=-{1}/{x}+{1}/ ( {d-x} ) -{1}/{d}$ 为测量误差系数,测量误差为$e={\rho_{{\rm{s}}}c}/ ( 2\pi ) $ ,可见测量误差e与辅助电极P的位置有关。图3为测量误差系数c随着辅助电极P位置的变化曲线,可见:当P位于A与C之间(0与d之间)时,接地电阻测量误差曲线呈单调递增,x=0.618d时测量误差为0;当P位于C右侧(大于d)时,接地电阻测量误差曲线呈单调递减,x=1.618d时测量误差为0;当P位于A左侧(小于0)时,接地电阻测量误差曲线单调递减。
以上是在视电极为半球形且土壤均匀条件下进行讨论的。虽然实际中电极的形状大多不是半球形,但是当电位极与电流极之间的距离d足够大(至少为电极尺寸的10倍)时,接地体就可近似为半球体,计算接地电阻值时可以按半球形考虑(徐程,庞亮,2010)。
在我国地电阻率观测台站的日常工作中,通常都采用接地电阻测试仪进行电极接地电阻测量,接地电阻测试仪的测试原理正是基于直线布设的三极法。一般认为距离接地电极20 m以外区域的电位趋近于零,因此实际测量工作中,通常将电位极P布设于距离被测电极20 m的位置,电流极C布设于距离被测电极40 m的位置。
2.2 井下电极接地电阻测量及误差分析
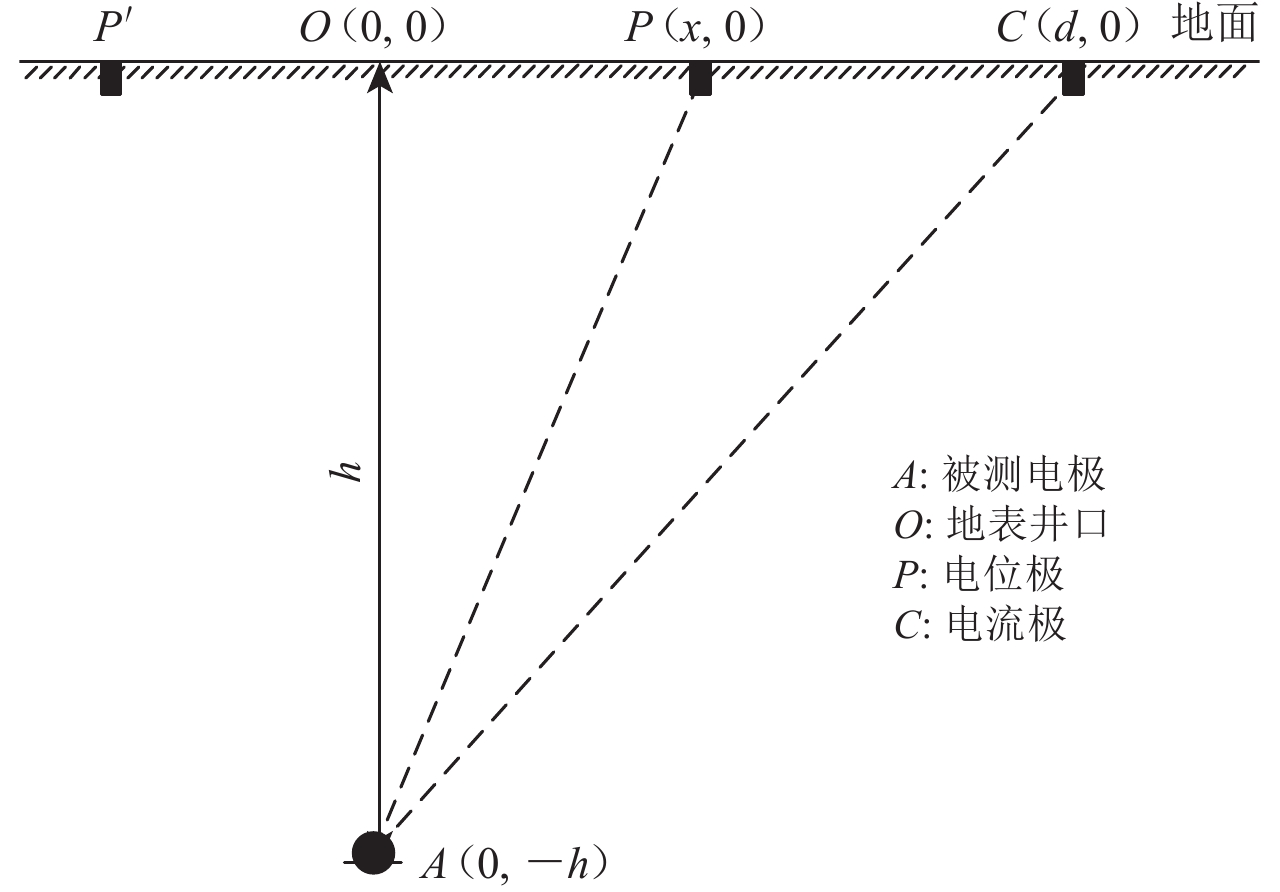
目前,对于开展井下地电阻率观测的台站,仍沿用2.1节的测量方法进行井下电极的接地电阻测量,将辅助电极布设在井口或者断线装置附近的地表。图4为井口布设辅助电极的示意图,由于被测电极埋设较深,被测电极和两辅助电极构成三角形,不满足直线型布设要求,若仍采用接地电阻测试仪在地表以直线型进行测量,将会产生一定的测量误差。在此仅讨论均匀介质条件下的测量误差。
使用接地电阻测量仪进行测量时,在A与C之间供电,A流出电流在各点产生的电位用球形全空间模型计算,C流入电流在各点产生的电位用半球半空间模型计算。设供电电流为I,A与P之间的电压为VAP,则
$$ {V}_{AP}=\frac{{\mathrm{\rho }}_{{\rm{s}}}I}{2\pi }\left(\frac{1}{2{r}_{0}}-\frac{1}{{D}_{AC}}-\frac{1}{{D}_{AP}}+\frac{1}{{D}_{PC}}\right) ,$$ (14) 式中,DAC为A与C之间的距离,DAP为A与P之间的距离,DPC为P与C之间的距离,则
$$ {D}_{AC}=\sqrt{{h}^{2}+{d}^{2}} ,$$ (15) $$ {D}_{AP}=\sqrt{{h}^{2}+{x}^{2}} ,$$ (16) $$ {D}_{PC}=d-x ,$$ (17) 将式(15)—(17)代入式(14),有
$$ {V}_{AP}=\frac{{\mathrm{\rho }}_{{\rm{s}}}I}{2\pi }\left(\frac{1}{2{r}_{0}}-\frac{1}{\sqrt{{h}^{2}+{d}^{2}}}-\frac{1}{\sqrt{{h}^{2}+{x}^{2}}}+\frac{1}{d-x}\right), $$ (18) 接地电阻测量值RA为
$$ {R}_{A}=\frac{{V}_{AP}}{I}=\frac{{\mathrm{\rho }}_{{\rm{s}}}}{2\pi }\left(\frac{1}{2{r}_{0}}-\frac{1}{\sqrt{{h}^{2}+{d}^{2}}}-\frac{1}{\sqrt{{h}^{2}+{x}^{2}}}+\frac{1}{d-x}\right){\text{.}} $$ (19) 由式(7)可知井下球形电极的接地电阻理论计算值
$ {R}_{2}={\mathrm{\rho }}_{{\rm{s}}}/4\pi {r}_{0} $ ,要使RA=R2,即$$ \frac{{\mathrm{\rho }}_{{\rm{s}}}}{2\pi }\left(\frac{1}{2{r}_{0}}-\frac{1}{\sqrt{{h}^{2}+{d}^{2}}}-\frac{1}{\sqrt{{h}^{2}+{x}^{2}}}+\frac{1}{d-x}\right)=\frac{{\mathrm{\rho }}_{{\rm{s}}}}{4\pi {r}_{0}} ,$$ (20) 则
$-\dfrac{1}{\sqrt{{h}^{2}+{d}^{2}}}-\dfrac{1}{\sqrt{{h}^{2}+{x}^{2}}}+\dfrac{1}{d-x}=0 $ 。若此项不为零,由其引起的接地电阻测量误差e为$$ e=\frac{{\mathrm{\rho }}_{{\rm{s}}}}{2\pi }\left(\frac{1}{d-x}-\frac{1}{\sqrt{{h}^{2}+{d}^{2}}}-\frac{1}{\sqrt{{h}^{2}+{x}^{2}}}\right) ,$$ (21) 测量相对误差δ为
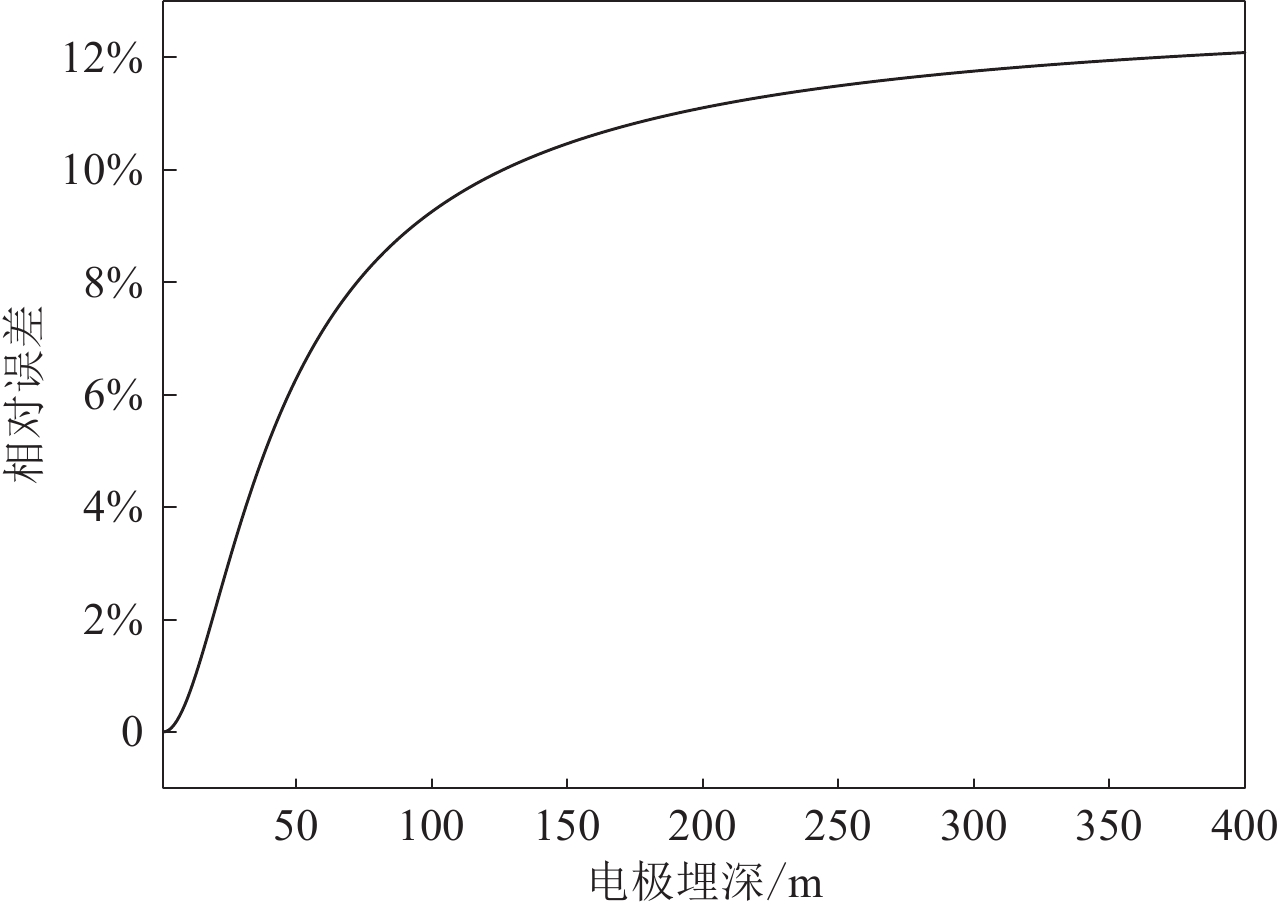
$$ \delta =\frac{e}{{R}_{2}}=2{r}_{0}\left(\frac{1}{d-x}-\frac{1}{\sqrt{{h}^{2}+{d}^{2}}}-\frac{1}{\sqrt{{h}^{2}+{x}^{2}}}\right)=\frac{2{r}_{0}}{d-x}-\frac{2{r}_{0}}{\sqrt{{h}^{2}+{d}^{2}}}-\frac{2{r}_{0}}{\sqrt{{h}^{2}+{x}^{2}}}{\text{.}}$$ (22) 当电极尺寸和地表辅助电极位置确定后,式(22)中的第一项为固定值,电极接地电阻相对误差的大小只与电极埋深有关。图5给出了电极半径为1 m时,接地电阻相对误差随电极埋深的变化情况,可见随着电极埋深的增加,相对误差逐渐增大,无限接近最大相对误差值,即式(22)第一项。
当井下电极埋深h=100 m时,电流极C距离O点40 m时,可计算出x=−12.048 m时相对误差δ=0,即电位极位于图4中O点左侧P′位置,此时测得的接地电阻值才是准确的。但是实际测量时,台站工作人员仍按照传统方法,将电位极P和电流极C布设在同一侧,与被测电极在地表投影点的距离分别为x=20 m和d=40 m,此时就会产生较大的测量误差。表1给出了不同土壤电阻率、不同电极埋深和不同电极尺寸条件下的测量误差和相对误差。
表 1 不同土壤电阻率ρs、不同电极埋深h和不同电极尺寸条件下的接地电阻测量误差e和相对误差δTable 1. Measurement error e and relative error δ of grounding resistance with different soil resistivity ρs,electrode buried depth h and electrode size电极半径r0
/mh=100 m h=200 m ρs=100 Ω•m ρs=200 Ω•m ρs=100 Ω•m ρs=200 Ω•m e/Ω δ e/Ω δ e/Ω δ e/Ω δ 0.2 0.492 1.24% 0.984 1.24% 0.638 1.60% 1.276 1.60% 0.5 0.491 3.08% 0.982 3.08% 0.638 4.01% 1.276 4.01% 1.0 0.492 6.17% 0.984 6.17% 0.638 8.02% 1.277 8.02% 从表1可以看出,若仍按照传统的测量方法来测量接地电阻,对于1 m半径的球形电极,深埋地下100 m时将产生6.17%的测量误差,埋深为200 m时将产生8.02%的测量误差。
实际测量中,从各个不同方向布设辅助电极来测量同一接地电极的接地电阻时,有时测量结果会不同,有时测量结果会相同,这是由于接地电极周围的土壤沿水平方向存在比较剧烈的各项异性,或者接地电极附近有金属管道等介质造成土壤介质不均匀而导致的(曾嵘等,2001)。此外,当地下介质存在分层结构时,井下被测电极与地表辅助电极所处位置土壤的电阻率不同时,也会导致测量误差较大(冯志伟,2011)。这都会对地电阻率接地电阻的准确测量造成一定的影响。
3. 直接法测量
为了更准确地测量井下电极的接地电阻,本文提出一种新的方法—直接测量法,该方法基于欧姆定律,利用台站观测所使用的地电阻率观测系统直接测量,具体方法为:向一对(两个)被测电极供电,同时测量这一对被测电极间的电流和电位差,依据欧姆定律计算出包括电极接地电阻和线电阻在内的电阻值,并利用多对电极供电测量结果和对应的线电阻值计算出每个电极的接地电阻,弥补了传统方法的不足。
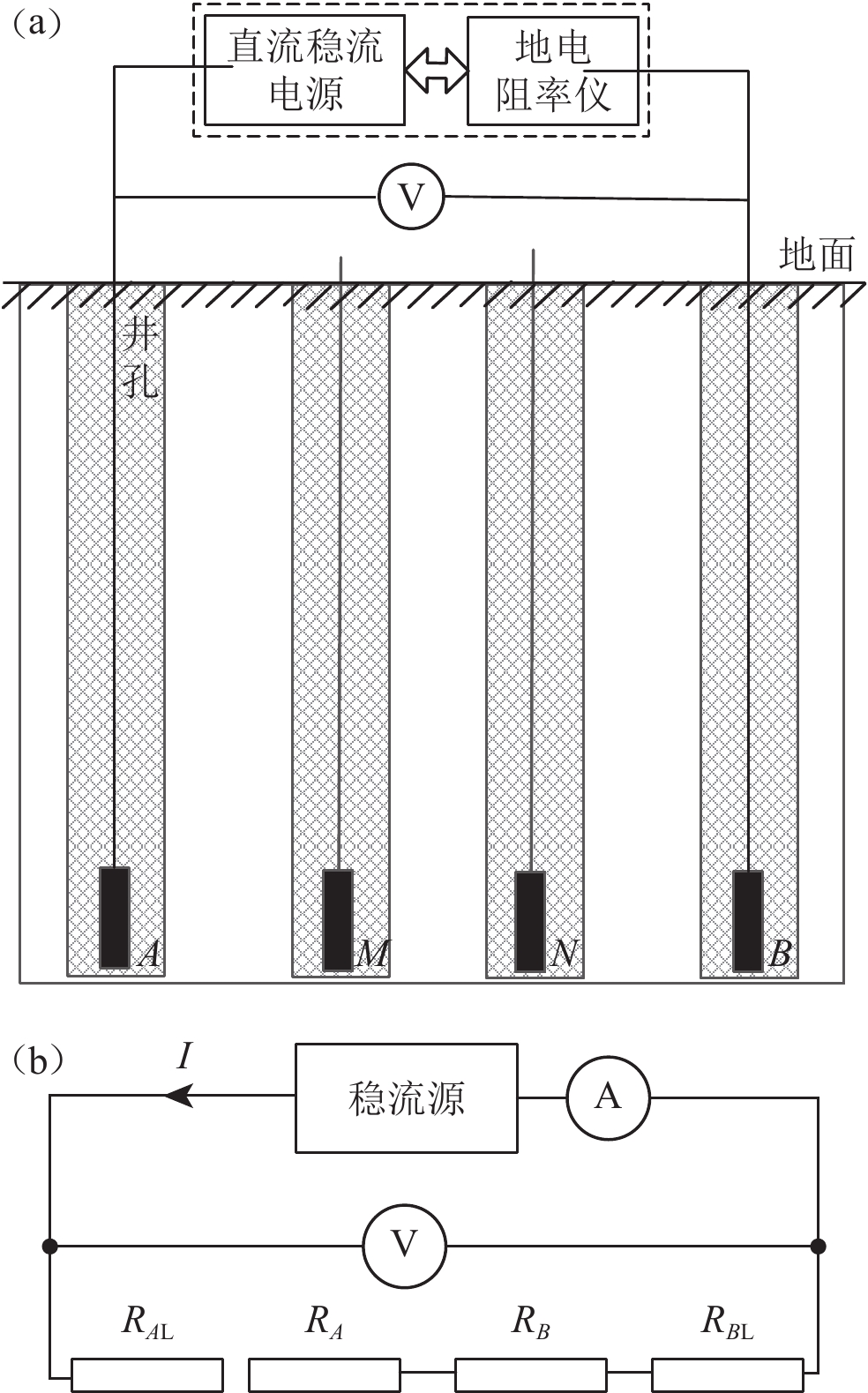
地震地电阻率测量中,每个测道的测量需要布设四个电极,假设四个井下电极的接地电阻分别为RA,RB,RM和RN,每个井下电极所连接的电缆线阻值分别为RAL,RBL,RML和RNL,接地电阻测量示意图及等效电路图如图6所示。
测量步骤如下:
1) 直流稳流电源向电极A和B供电;
2) 待电流稳定后,利用地电阻率仪测量供电电流IAB,同时用高精度数字电压表测量A与B之间的供电电位差VAB,由欧姆定律计算出测量回路上的电阻,测量回路电阻包含两电极接地电阻和两电极线电阻,即
$$ {R}_{A}+{R}_{A{\rm{L}}}+{R}_{B}+{R}_{B{\rm{L}}}=\frac{{V}_{AB}}{{I}_{AB}}; $$ (23) 3) 依次选择B和N,B和M,M和N组成电极对,重复上述测量过程,得到各对电极间的电位差和电流值,计算回路电阻,组成以下方程组:
$$ \left\{ \begin{array}{l}{R}_{A}+{R}_{A{\rm{L}}}+{R}_{B}+{R}_{B{\rm{L}}}=\dfrac{{V}_{AB}}{{I}_{AB}},\\ {R}_{B}+{R}_{B{\rm{L}}}+{R}_{N}+{R}_{N{\rm{L}}}=\dfrac{{V}_{BN}}{{I}_{BN}},\\ {R}_{B}+{R}_{B{\rm{L}}}+{R}_{M}+{R}_{M{\rm{L}}}=\dfrac{{V}_{BM}}{{I}_{BM}},\\ {R}_{M}+{R}_{M{\rm{L}}}+{R}_{N}+{R}_{N{\rm{L}}}=\dfrac{{V}_{MN}}{{I}_{MN}};\end{array}\right. $$ (24) 4) 由于线电阻仅与线路材料、长度和线径有关,不随时间变化,因此在架设线路时,可以通过实际测量得到各电极引线的电阻,式(24)中的RAL,RBL,RML和RNL为已知量,则各个电极的接地电阻RA,RB,RM和RN可由
$$\left\{ \begin{array}{l}{R}_{A}=\dfrac{{V}_{AB}}{{I}_{AB}}-{\dfrac{{V}_{BN}}{{2I}_{BN}}-\dfrac{{V}_{BM}}{2{I}_{BM}}+\dfrac{{V}_{MN}}{{2I}_{MN}}-{R}_{A{\rm{L}}}}\\ {R}_{B}={\dfrac{{V}_{BN}}{{2I}_{BN}}+\dfrac{{V}_{BM}}{2{I}_{BM}}-\dfrac{{V}_{MN}}{{2I}_{MN}}-}{R_{B{\rm{L}}}}\\ {R}_{M}=\dfrac{{V}_{MN}}{{2I}_{MN}}-\dfrac{{V}_{BN}}{{2I}_{BN}}+\dfrac{{V}_{BM}}{2{I}_{BM}}-{R}_{M{\rm{L}}}\\ {R}_{N}=\dfrac{{V}_{BN}}{{2I}_{BN}}-\dfrac{{V}_{BM}}{2{I}_{BM}}+\dfrac{{V}_{MN}}{{2I}_{MN}}-{R}_{N{\rm{L}}}\end{array}\right. $$ (25) 计算得到。
4. 不同测量方法结果分析
为了研究不同测量方法所得井下电极测量结果的准确度和一致性,分别采用直线三极法和直接测量法对北京市地震局平谷地震台地电阻率井下观测供电电极的接地电阻进行测量和对比分析。直线三极法使用Fluke1623接地电阻测试仪测量(接地电阻测量精度为2%);直接测量法采用WL6B直流稳流电源供电,电流稳定度优于0.5%,最大输出电流为2.5 A,ZD8M地电阻率仪测量供电电流,其直流电流测量精度为0.02%,Fluke17B数字万用表测量两电极的电压,其直流电压测量精度为0.5%。
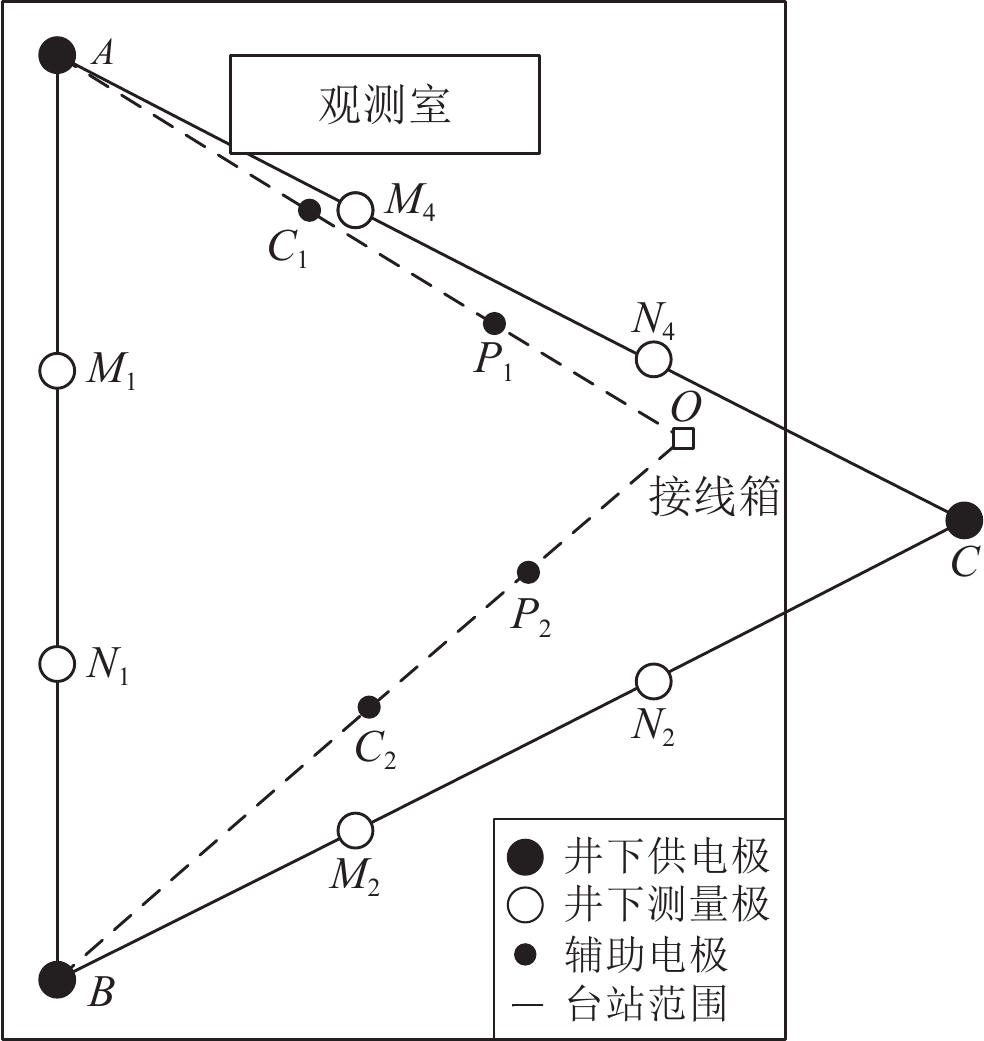
平谷地震台的井下地电阻率观测采用对称四极观测装置,水平方向布设NS,NE,NW等三个测道(图7)。井下水平方向的供电极距为90 m,测量极距为30 m,所有电极埋深为110 m,电极近似为0.5 m半径球形铅电极。所有井下电极线路汇集到图7中的接线箱O点位置,再从接线箱统一回到观测室。接线箱距离供电电极A,B和C的距离分别为65 m,76.6 m和26.8 m,供电电极A,B和C到观测室线路的电阻分别为1.5 Ω,1.6 Ω和1.1 Ω。
采用传统三极法测量,在测量前需要将电极与室内仪器断开,但是无法直接在电极井口连接被测电极,只能从接线箱位置断开与室内的连线并接入被测井下电极。以接线箱O点为起点,按照直线三极法布设辅助电极,电流极C1和C2距离O点40 m,电位极P1和P2距离O点20 m,这也是开展井下地电阻率观测台站经常采用的方法。测量A电极的接地电阻时,辅助电极位置见图7中的C1和P1;测量B电极的接地电阻时,辅助电极位置见图7中的C2和P2。一共进行五组测量,每组十次,将其算术平均值作为测量结果(表2)。利用该方法,在台站院内测量A和B电极的接地电阻,每组耗时20 min。
表 2 利用不同方法测量得到的井下供电极A和B的接地电阻Table 2. Grounding resistance of the underground power supply electrodes A and B by different methods测量次数 被测电极A的接地电阻/Ω 被测电极B的接地电阻/Ω 直接测量法 直线三极法 直接测量法 直线三极法 第一次 59.36 54.7 54.46 51.0 第二次 59.40 54.8 54.39 50.8 第三次 59.43 54.8 54.35 50.9 第四次 59.37 55.4 54.38 51.0 第五次 59.44 54.7 54.41 50.9 均值 59.40 54.9 54.40 50.9 均方差 0.03 0.28 0.04 0.08 实测差值 −4.52 −3.48 实测相对误差 −7.62% −6.39% 采用直接测量法测量,利用台站地电阻率常规观测的WL6B直流稳流电源对A,B,C电极两两供电,供电过程中测量电流值和两电极间供电电位差,计算出A,B,C电极的接地电阻值,一共进行五组测量,每组十次,将其算术平均值作为测量结果(表2)。利用该方法在观测室内完成A,B,C三个电极的接地电阻测量,每组仅需5 min即可完成。
表2中,均值和均方差分别为五组测量结果的算术平均值和均方根误差,差值为直线三极法与直接测量法对于同一电极的测量结果差值,根据差值计算出相对误差。从表2可以看出:直接测量法五组测量值的均方差较小,多次重复测量结果的一致性较好;直线三极法由于每次测量需要重新布设辅助电极,且很难保证被测电极与两个辅助电极严格在一条直线上,因此会引入布极误差和人工操作误差,五组测量值的均方差均大于直接测量法。
图8给出了井下A电极接地电阻测量时被测电极与辅助电极的位置关系,被测电极A投影至地表的位置为A′,这是一种更为复杂的情况,辅助电极布设起点不是被测电极投影到地表井口的位置。此时,辅助电极C1和P1与A′在一条直线上,与被测井下电极A在同一个平面。根据2.2节井下电极的接地电阻测量误差分析方法进行理论计算,若采用地表直线三极法测量平谷台的井下电极的接地电阻,A电极和B电极的测量误差分别为−6.73%和−6.67%,这与实测相对误差−7.62%和−6.39%基本吻合,理论计算与实测结果的差别主要在于辅助电极布设距离和方向误差。因此,采用地表常规三极法测量井下电极的接地电阻,不能准确地测量该电极的实际接地电阻值,存在较大的误差。
从表2还可以分析出:基于直接测量法的五次测量结果更为稳定,均方差较小;而三极测量法由于每次测量布极位置和方向均不能保证完全一致,存在布极误差,造成五次观测结果的均方差较大,数据一致性不高。
5. 结论
目前我国地电阻率观测台站广泛使用基于直线三极法原理的接地电阻测试仪来测量电极的接地电阻,然而该方法由于实际测量中多种因素的影响,测量结果可能会存在一定的误差,特别是该方法并不适合井下地电阻率电极接地电阻的准确测量。
本文基于地电阻率台站现有的地电阻率观测系统,提出了利用现有设备的直接测量法,该方法与传统三极测量法相比,具有以下优点:
1) 直接测量法基于欧姆定律,利用现有地电阻率观测系统进行测量,无需布设线路,无需增加辅助电极,不存在布极误差和电极接触不良的问题,重复测量结果一致性高;
2) 利用台站已有观测设备,无需配备接地电阻测试仪,且观测设备精度较高,测量误差小;
3) 克服了传统方法需要人工到室外每个电极处断开电极与电极引线才能测量接地电阻的缺点,只需在室内通过不同电极组合,即可测量各个电极的接地电阻值。由原来八个电极需要一两个小时才能完成的室外工作,提高到10—15 min即可完成的室内测量,极大地降低了台站工作人员的工作量。
本文提出的地电阻率电极接地电阻直接测量法原理清晰,操作简便,测量精度高,可用于地表电极和井下电极的接地电阻测量,目前已推广到我国多个地电阻率井下观测台站和省局,已经在四川省冕宁地震台、甘肃省平凉地震台、江苏省江宁地震台等地电阻率观测台站应用,可作为台站日常观测中常规的接地电阻测量方法。
感谢审稿专家为本文提出的宝贵意见,感谢北京市地震局王同利正研级高工和平谷地震台邢海林工程师在台站试验中的帮助。
-
表 1 不同土壤电阻率ρs、不同电极埋深h和不同电极尺寸条件下的接地电阻测量误差e和相对误差δ
Table 1 Measurement error e and relative error δ of grounding resistance with different soil resistivity ρs,electrode buried depth h and electrode size
电极半径r0
/mh=100 m h=200 m ρs=100 Ω•m ρs=200 Ω•m ρs=100 Ω•m ρs=200 Ω•m e/Ω δ e/Ω δ e/Ω δ e/Ω δ 0.2 0.492 1.24% 0.984 1.24% 0.638 1.60% 1.276 1.60% 0.5 0.491 3.08% 0.982 3.08% 0.638 4.01% 1.276 4.01% 1.0 0.492 6.17% 0.984 6.17% 0.638 8.02% 1.277 8.02% 表 2 利用不同方法测量得到的井下供电极A和B的接地电阻
Table 2 Grounding resistance of the underground power supply electrodes A and B by different methods
测量次数 被测电极A的接地电阻/Ω 被测电极B的接地电阻/Ω 直接测量法 直线三极法 直接测量法 直线三极法 第一次 59.36 54.7 54.46 51.0 第二次 59.40 54.8 54.39 50.8 第三次 59.43 54.8 54.35 50.9 第四次 59.37 55.4 54.38 51.0 第五次 59.44 54.7 54.41 50.9 均值 59.40 54.9 54.40 50.9 均方差 0.03 0.28 0.04 0.08 实测差值 −4.52 −3.48 实测相对误差 −7.62% −6.39% -
杜学彬. 2010. 在地震预报中的两类视电阻率变化[J]. 中国科学:地球科学,40(10):1321–1330. Du X B. 2010. Two types of changes in apparent resistivity in earthquake prediction[J]. Science China Earth Science,54(1):145–156.
冯慈璋. 1983. 电磁场[M]. 第二版. 北京: 高等教育出版社: 108–110. Feng C Z. 1983. Electromagnetic Field[M]. Second edition. Beijing: Higher Education Press: 108–110 (in Chinese).
冯志伟,马金福. 2009. 电位降法测量接地电阻时电压极补偿点位置分析[J]. 电气应用,28(8):18–19. Feng Z W,Ma J F. 2009. Analysis of the position of the voltage pole compensation point when measuring grounding resistance by fall-of-potential method[J]. Electrotechnical Application,28(8):18–19 (in Chinese).
冯志伟. 2011. 影响接地电阻测量的因素分析[D]. 南京: 南京信息工程大学: 28–37. Feng Z W. 2011. Analysis of the Effect Factors of the Measurement of Grounding Resistance[D]. Nanjing: Nanjing University of Information Science and Technology: 28–37 (in Chinese).
高曙德. 2016. 深井地电观测技术在地震监测中的应用探讨[J]. 地球物理学进展,31(5):2078–2088. doi: 10.6038/pg20160526 Gao S D. 2016. Discussion on the deep well geoelectric observation technique applied in earthquake monitoring[J]. Progress in Geophysics,31(5):2078–2088 (in Chinese).
钱家栋. 2010. 地震电磁学理论基础与观测技术[M]. 北京: 地震出版社: 293. Qian J D. 2010. Underpinnings and Observation Technology of Seismic Electro-Magnetism[M]. Beijing: Seismological Press: 293 (in Chinese)
钱家栋,马钦忠,李劭秾. 2013. 汶川MS8.0地震前成都台NE测线地电阻率异常的进一步研究[J]. 地震学报,35(1):4–17. doi: 10.3969/j.issn.0253-3782.2013.01.002 Qian J D,Ma Q Z,Li S N. 2013. Further study on the anomalies in apparent resistivity in the NE configuration at Chengdu station associated with Wenchuan MS8.0 earthquake[J]. Acta Seismologica Sinica,35(1):4–17 (in Chinese).
王洪泽, 杨丹, 王梦云. 2007. 电力系统接地技术手册[M]. 北京: 中国电力出版社: 15–17. Wang H Z, Yang D, Wang M Y. 2007. Manual of Grounding Technology of Power System[M]. Beijing: China Electric Power Press: 15–17 (in Chinese).
王兰炜,张宇,张世中,颜蕊,王子影,张兴国,胡哲. 2015. 我国井下地电阻率观测技术现状分析[J]. 地震地磁观测与研究,36(2):95–102. doi: 10.3969/j.issn.1003-3246.2015.02.018 Wang L W,Zhang Y,Zhang S Z,Yan R,Wang Z Y,Zhang X G,Hu Z. 2015. The status of deep-well geo-electrical resistivity observation in China[J]. Seismological and Geomagnetic Observation and Research,36(2):95–102 (in Chinese).
解滔,于晨,卢军. 2019. 开展小极距井下地电阻率观测的可行性分析[J]. 中国地震,35(1):14–24. doi: 10.3969/j.issn.1001-4683.2019.01.002 Xie T,Yu C,Lu J. 2019. Feasibility analysis on short-electrode spacing well apparent resistivity observation[J]. Earthquake Research in China,35(1):14–24 (in Chinese).
徐程,庞亮. 2010. 直线三极法接地电阻测试原理与方法[J]. 科技创业月刊,(10):177–179. doi: 10.3969/j.issn.1672-2272.2010.10.080 Xu C,Pang L. 2010. Principle and method of grounding resistance measurement by three pole method[J]. Pioneering With Science &Technology Monthly,(10):177–179 (in Chinese).
杨德荣,梁丹. 2007. 接地电阻测量中应注意的几个问题[J]. 气象研究与应用,28(2):72–74. doi: 10.3969/j.issn.1673-8411.2007.02.019 Yang D R,Liang D. 2007. Several problems paying attention to in measuring grounding resistance[J]. Journal of Meteorological Research and Application,28(2):72–74 (in Chinese).
应顺潮. 1992. 接地电阻测量中测试极位置的确定[J]. 高电压技术,(1):80–83. Ying S C. 1992. Spacing of test electrodes for measurement of ground resistance[J]. High Voltage Engineering,(1):80–83 (in Chinese).
曾嵘,何金良,高延庆,孙为民,屠幼萍. 2001. 电极位置对垂直三层土壤结构中接地系统接地电阻测量结果的影响[J]. 清华大学学报(自然科学版),41(3):28–31. Zeng R,He J L,Gao Y Q,Sun W M,Tu Y P. 2001. Effects of electrode placement on grounding resistance of grounding system measured in vertical three-layer soil[J]. Journal of Tsinghua University (Science and Technology)
,41(3):28–31 (in Chinese). 郑兆苾,吴培稚. 1986. 地电阻率法的一个重要干扰因素:线间漏电[J]. 地震,(3):26–30. Zheng Z B,Wu P Z. 1986. An important interference factor of geo-electric resistivity method:Leakage between lines[J]. Earthquake,(3):26–30 (in Chinese).
中国地震局. 2009. DB/T 33.1—2009 地震地电观测方法地电阻率观测第1部分: 单极距观测[S]. 北京: 中国标准出版社: 3. China Earthquake Administration. 2009. DB/T 33.1−2009 The Method of Earthquake-Related Geoelectrical Monitoring: Geoelectrical Resistivity Observation: Part 1: Single Separation Configuration[S]. Beijing: Standards Press of China: 3 (in Chinese).
中华人民共和国国家质量监督检验检疫总局. 2000. GB/T 17949.1—2000 接地系统的土壤电阻率、接地阻抗和地面电位测量导则第1部分: 常规测量[S]. 北京: 中国标准出版社: 20–24. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. 2000. GB/T 17949.1−2000 Guide for Measuring Earth Resistivity, Ground Impedance and Earth Surface Potentials of a Ground System: Part 1: Normal Measurements[S]. Beijing: Standards Press of China: 20–24 (in Chinese).
IEEE Power and Energy Society. 2012. IEEE Std. 81−2012 Guide for Measuring Earth Resistivity, Ground Impedance, and Earth Surface Potentials of a Grounding System[S]. New York: Institute of Electrical and Electronics Engineers, Inc.: 22
Lu J,Xie T,Li M,Wang Y L,Ren Y X,Gao S D,Wang L W,Zhao J L. 2016. Monitoring shallow resistivity changes prior to the 12 May 2008 M8.0 Wenchuan earthquake on the Longmen Shan tectonic zone,China[J]. Tectonophysics,675:244–257. doi: 10.1016/j.tecto.2016.03.006
-
期刊类型引用(2)
1. 褚文超. 基于径向基函数拟合的多频杆塔接地电阻测量方法. 电气传动. 2024(11): 81-86 .  百度学术
百度学术
2. 孔祥美,刘程. 输电杆塔接地引下线专用螺栓研发及应用. 光源与照明. 2023(02): 172-174 .  百度学术
百度学术
其他类型引用(1)




 下载:
下载: