Seismic events classification based on Gram’s angle field and multi-scale residual neural network
-
摘要:
以江苏地震台网中心搜集并标注的天然地震、人工爆破和塌陷事件为试验数据样本，提出了一种基于格拉姆角场和多尺度残差神经网络的新的地震事件分类方法。首先对波形数据进行滤波、归一化等预处理，然后应用格拉姆角场对地震波形数据进行二维编码得到二维图像，再将此经过编码后的图像作为多尺度残差神经网络的输入进行分类模型的训练和测试，从而得出分类结果。采用上述方法对1 078个天然地震台站记录、981个爆破台站记录和830个塌陷台站记录进行试验，结果显示：最终以单条波形为单位的地震事件分类准确率为92.55%，以单个台站为单位的分类准确率为96.36%，这表明基于格拉姆角场和多尺度残差神经网络的地震分类方法具有良好的效果。
-
关键词:
- 地震分类 /
- 格拉姆角场（GAF） /
- 深度学习 /
- 多尺度残差网络
Abstract:The rapid advancement of seismic observation systems has ushered in an era of seismic big data, encompassing both artificial and natural events. This development presents new challenges that necessitates precise seismic event classification to enhance earthquake response strategies and seismological research. This paper presents a novel approach for classification seismic events, integrating Gram’s angle field （GAF） with a multi-scale residual neural network, designated as QxceptionNet. The GAF method converts seismic wave time series into a graphic representation, preserving the interdependencies among different sampling points. The application of multi-scale convolutional analysis in this context reveals a more detailed feature set within the GAF images. Additionally, the residual structure of networks is designed to prevent performance degradation, even as network depth increases. The synergy of these elements forms the foundation of our proposed methodology. The approach utilizes a dataset meticulously compiled and labeled by the Jiangsu Earthquake Agency, encompassing station records of natural earthquakes, artificial blasts, and collapses. Each record consists of three-channel waveforms. As an initial step, the raw seismic waveforms are normalized in amplitude, linearly detrended, and filtered to reduce effects from the recording instruments. To maintain consistency, all waveforms are truncated to a standardized length of 40 seconds. Subsequently, those waveforms are transformed into GAF images. These images, along with their respective category labels, serve as inputs for the QxceptionNet. The network’s training results in outputting probabilities, categorizing the waveform data into one of the three seismic event types. Our results indicate impressive classification accuracies across various seismic event categories, emphasizing the efficacy of this approach in seismic classification. The test results show that the accuracy for 1 078 natural seismic event records, 981 blast records, and 830 collapse records are 92.55% for classifications based on individual waveform records and 96.36% for those based on single station records. Notably, these accuracies surpass those achieved by other methods, such as support vector machine （SVM）, multi-layer perceptron （MLP） and short-time Fourier transform （STFT） combined with convolutional neural network （CNN）. These findings suggest that the combined use of the Gram’s angle field and multi-scale residual neural networks is highly effective in distinguishing different types of seismic events. In summary, this paper elucidates the process of transforming seismic waveform data into GAF images, the architectural design of the network model, and the comprehensive experimental setup and results. Looking ahead, broadening the scope of the classification system to encompass a more diverse array of seismic occurrences and integrating a wider variety of samples will be essential in creating an all-encompassing and intelligent seismic event detection system.
-
引言
随着我国地震观测系统数字化的快速推进，各地架设的地震台站不断增加，观测仪器的精度不断提升，海量的地震数据得以被记录，地震学研究领域也进入了大数据时代。海量的数据中包含各类地震事件，主要分为天然地震和非天然地震。及时、准确地排除非天然地震，提高天然地震事件数据集的可靠性，将有助于提升地震活动性研究的科学性和地震危险性评价的准确性。快速准确地识别可能引发灾害的地震事件，如天然地震、爆破和塌陷，可以为相关部门应对突发地震提供决策支持。
不同的地震事件由于其震源性质（如尺寸、时间函数、震源机制和深度等）不同，其所观测到的地震记录也存在差异。国内外学者针对地震事件分类进行了长期的、大量的研究，探索出诸多方法，其中包括时频分析方法和传统地震识别方法等。时频分析方法是基于不同类别地震事件的时频特征具有明显差异而提出的，可为非天然地震监测等提供参考依据，然而该方法受到时间-频率分辨率的限制，而且对噪声非常敏感，这使其在地震事件分类识别中的广泛应用上颇为受限（高家乙等，2020）；传统的地震事件识别方法则依据地震学先验知识从地震事件中提取水平分量振幅比、尾波持续时间、倒谱参数、频谱比等相关特征设计识别模型，但该方法的特征提取存在标准不一、过程复杂等问题。
近年来，随着深度学习的快速发展和地震数据的海量增加，地震事件的特征提取和分类过程变得更加高效和精确，这一变化极大地促进了深度学习在地震事件分类领域的应用和发展。例如：Ross等（2018）应用卷积神经网络（convolutional neural network，缩写为CNN）对俄克拉荷马地区连续的波形记录进行了识别与定位，模型拾取震相的精度达到95%，能够与人工拾取相匹敌；赵明等（2019）利用卷积神经网络对汶川地震后四川及邻区的1万3 839个余震事件所建立的数据集进行地震事件和噪声的自动分类，准确率高达95%；Yano等（2021）使用地震台阵波形数据利用卷积神经网络深度学习方法进行地震检测试验；黎炳君等（2021）采用短时傅立叶变换生成时频图像并将其作为CNN输入进行分类，其结果显示天然地震和爆破事件的平均分类准确率达到97.39%。
以上研究主要集中于解决天然地震与人工爆破识别或者地震事件与噪声识别的二分类问题，分类模型均采用传统卷积神经网络，存在空间分辨率低、梯度消失或爆炸等问题。部分方法直接将地震波形的时间序列作为神经网络的输入，不能充分利用其一维序列时间上的相关性。
为增加可识别地震事件的种类、提升各类事件的识别准确率，本文拟提出一种基于深度可分离网络的天然地震、爆破和塌陷的三分类地震事件识别方法。该方法将一维序列进行编码并转化为图像，以有效地提升分类效果（Wang，Oates，2015）。为了充分保留序列的相关性，本文使用格拉姆角场（Gram’s angle field，缩写为GAF）将预处理后的地震波形数据经二维化转化为图像，并构建深度多尺度残差神经网络模型进行特征提取和地震事件分类，以期探索和验证格拉姆角场在地震数据处理中的有效性，以及多尺度残差神经网络在提取地震波形特征方面的优势，为地震预测研究提供新的技术路径。
1. 格拉姆角场
格拉姆（Gram）矩阵，作为一种常用于数据分析的工具，主要用于评估一组向量的线性相关性（Horn，Johnson，2012）。但是格拉姆矩阵遵循平均值为0的高斯分布，不利于神经网络的特征提取和模型训练。因此，格拉姆角场采用极坐标向量替代笛卡尔坐标向量对一维数据进行二维编码（Wang，Oates，2015），其中每个元素对应于两个由幅值变换而来的极坐标角度之和的余弦值。地震事件波形数据是典型的时序信号，x轴方向表示采样时间，y轴方向表示振动振幅。通过将其转换为格拉姆角场，能够保留序列采样点之间的相关性。经格拉姆二维转换后的图像能够表征地震信号的特征，具体转化过程如下：
1） 对于给定长度为n的一维序列X＝{x1，x2，···，xn}，利用max-min方法将X缩放至$ ［ -1\text{，} 1 ］ $之间。归一化后时间序列的第i个观测值${{\tilde x}_i} $为
$$ {\tilde x_i} ＝ \dfrac{{ {{x_i} － \max （ X ）} ＋ {{x_i} － \min （ X ） }}}{{\max （ X ） － \min （ X）}} \text{，} \qquad i ＝ 1 \text{，} 2 \text{，} \cdots \text{，} n .$$ (1) 2） 对$ {\tilde x_i} $进行极坐标空间上的编码，公式为
$$ \left\{ \begin{gathered} {\phi _i} ＝ {\mathrm{arccos}} {{{\tilde x}_i}} \text{，} \quad- 1 {\text{≤}} {{\tilde x}_i} {\text{≤}} 1 \text{，} {{\tilde x}_i} \in X \text{，} \\ {r_i} ＝ \frac{i}{n} \text{，} \\ \end{gathered} \right. $$ (2) 式中：ϕi为${{\tilde x}_i} $对应的极坐标角度，处于$ ［0 \text{，}\text{π}］ $范围内；ri为${{\tilde x}_i} $对应的极坐标半径。随着时间的增加，极坐标图上对应点的半径逐渐增长，角度则与其幅值相关。对于一个给定的一维序列，有且仅有一个转换结果，而且这种转化是双射。
3） 将时间序列转换为格拉姆角场，其定义为：
$$ {\boldsymbol{G}} ＝\left( {\begin{array}{*{20}{c}} { \cos （ {{\phi _1} ＋ {\phi _1}} ） }&{ \cos （ {{\phi _1} ＋ {\phi _2}} ） }& \cdots &{ \cos （ {{\phi _1} ＋ {\phi _n}} ） } \\ { \cos （ {{\phi _2} ＋ {\phi _1}} ） }&{ \cos （ {{\phi _2} ＋ {\phi _2}} ） }& \cdots &{ \cos （ {{\phi _2} ＋ {\phi _n}} ） } \\ \vdots & \vdots & \vdots & \vdots \\ { \cos （ {{\phi _n} ＋ {\phi _1}} ） }&{ \cos （ {{\phi _n} ＋ {\phi _2}} ） }& \cdots &{ \cos （ {{\phi _n} ＋ {\phi _n}} ） } \end{array}} \right) \text{，} $$ (3) 式中每个元素可通过下式由笛卡尔坐标系坐标快速得到：
$$ \begin{aligned} \cos （ {{\phi _i} ＋ {\phi _j}} ） ＝ &\cos （ {\arccos x ＋ \arccos y } ） ＝ \cos （ \arccos x ） \cos （ \arccos y ） －\\& \sin （ \arccos x ） \sin （ \arccos y ） ＝ x y － \sqrt { （ {1 － {x^2}} ） （ {1 － {y^2}} ） } \text{，} \end{aligned} $$ (4) 式中x和y表示ϕi和ϕj在一维序列中所对应的幅值。在格拉姆角场中，时间从左上角向右下角递增，因此一维序列中的时间维度信息被编码在矩阵的几何结构中。G（i， j， |i－j|＝k）表示对应时间间隔为k的两点间的相关性，其中主对角线G（i， j）为k＝0的特殊情况，反映原始值信息。
对于长度为n的一维序列，可将其直接转换为n×n的格拉姆矩阵。此外，可采用分段聚合近似方法（Keogh，Pazzani，2000）在保留序列变化趋势的同时减小格拉姆矩阵的尺寸。
2. 网络模型
卷积神经网络是目前普遍使用且在多种任务中表现优秀的网络模型结构之一，其出色的特征提取能力和泛化能力使其在图像分类中应用广泛（Simonyan，Zisserman，2015），主要结构包含输入层、隐含层和输出层。隐含层通常包括卷积层、池化层和全连接层，其中：卷积层提取图像特征；池化层通过对卷积层输出特征图降采样，提取区域内最具代表性的特征，保留特征图中的主要信息；全连接层对卷积神经网络提取到的特征进行汇总，将多维特征映射为二维的输出（Szegedy et al，2016）。
2.1 多尺度卷积
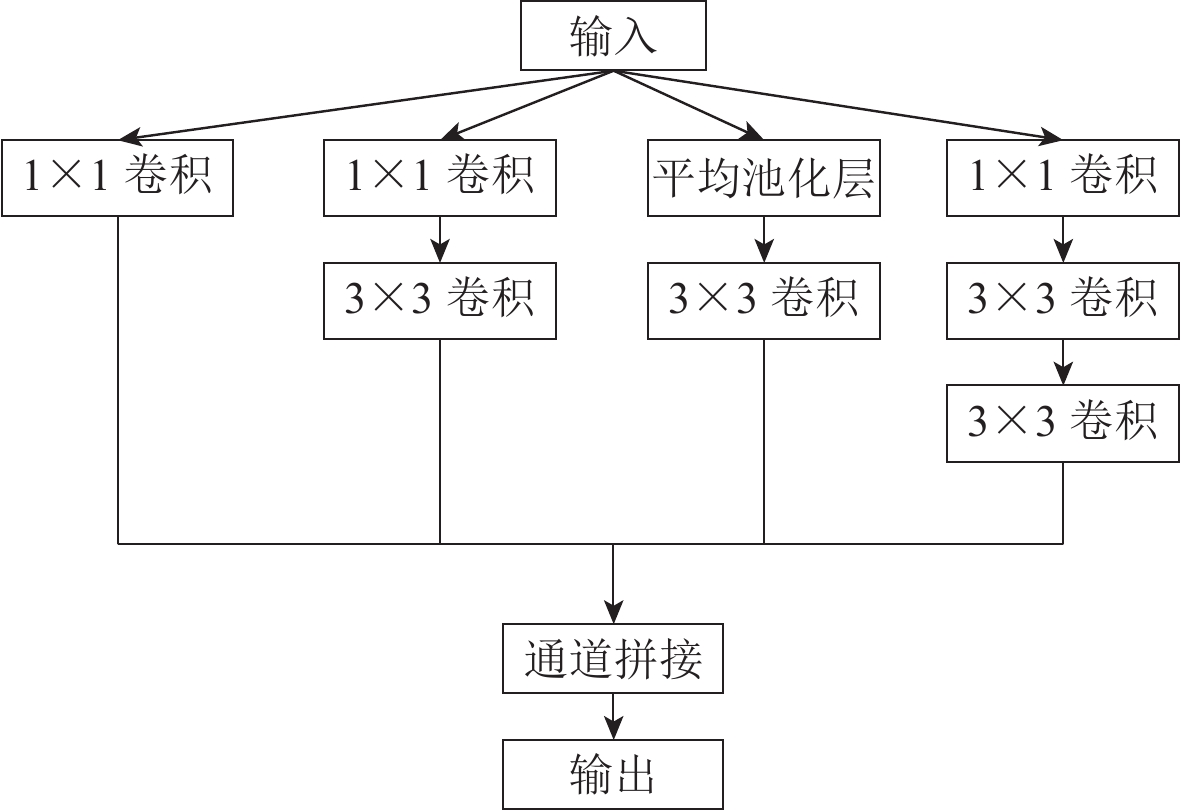
卷积神经网络随着网络层数的增加，更深层次的特征得以被提取，但是伴随而来的梯度消失问题使得网络难以训练，并且模型尺寸的增大、计算量的增加导致其在实时判断和嵌入式系统应用时受限（Szegedy et al，2016）。基于特征图中的通道相关性和空间相关性可以完全解耦的假设，Chollet （2017）提出一种完全基于深度可分离卷积层的Xception卷积神经网络结构，其中包含的深度可分离卷积模块是使用1×1卷积来映射跨通道相关性，这不仅优化了网络性能，还减小了模型大小和计算成本。因此本文在Xception网络模型的基础上选取多尺度卷积单元（图1）进行特征提取。区别于传统卷积神经网络堆叠同一卷积核进行卷积运算，多尺度卷积单元通过组合1×1和3×3两种尺寸的卷积核和平均池化层进行特征提取，之后将各部分结果进行通道拼接得到更高维度的信息（Li et al，2018），实现了使用较少的参数数量学习到更丰富的特征表示。因此，通过可分离卷积单元可以快速搭建出高效、准确和轻量型的地震事件分类网络模型。
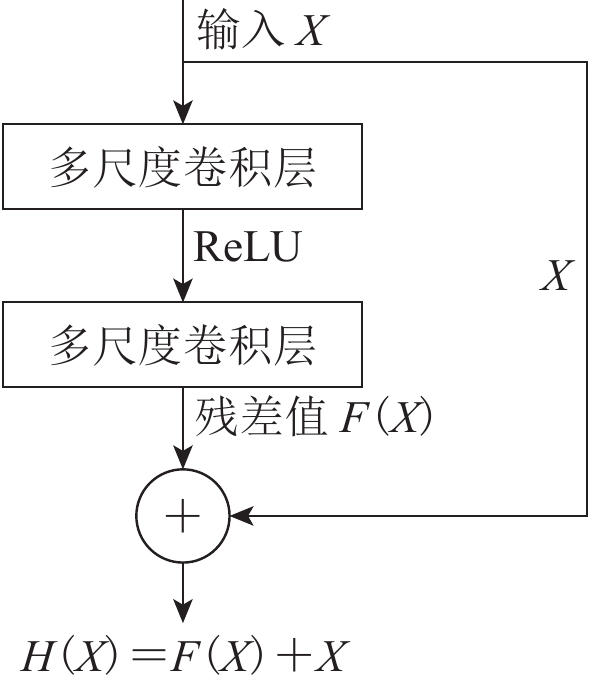
2.2 残差结构
为解决网络模型深度增加所引起的梯度消失和梯度爆炸问题，He等（2016）提出残差神经网络，即在网络结构中引入残差结构，让网络拥有恒等映射能力。本文结合多尺度卷积单元和残差结构得到多尺度残差结构，并将其作为网络的基本结构（图2），其中输入为X，需要拟合的输出函数为H（X）＝F（X）＋X，其中F（X）为残差部分，X为原始输入部分。卷积层使用多尺度卷积代替传统卷积，并增加跳层连接结构，脱离了传统的下一层输入只能是上一层输出的常规做法。随着网络层数的增加，F（X）逼近于0，这使得网络的精度在最优浅层网络的基础上不会下降，保证挖掘更深层次特征的同时不会产生梯度消失问题所致的模型性能退化现象。
2.3 QxceptionNet网络模型
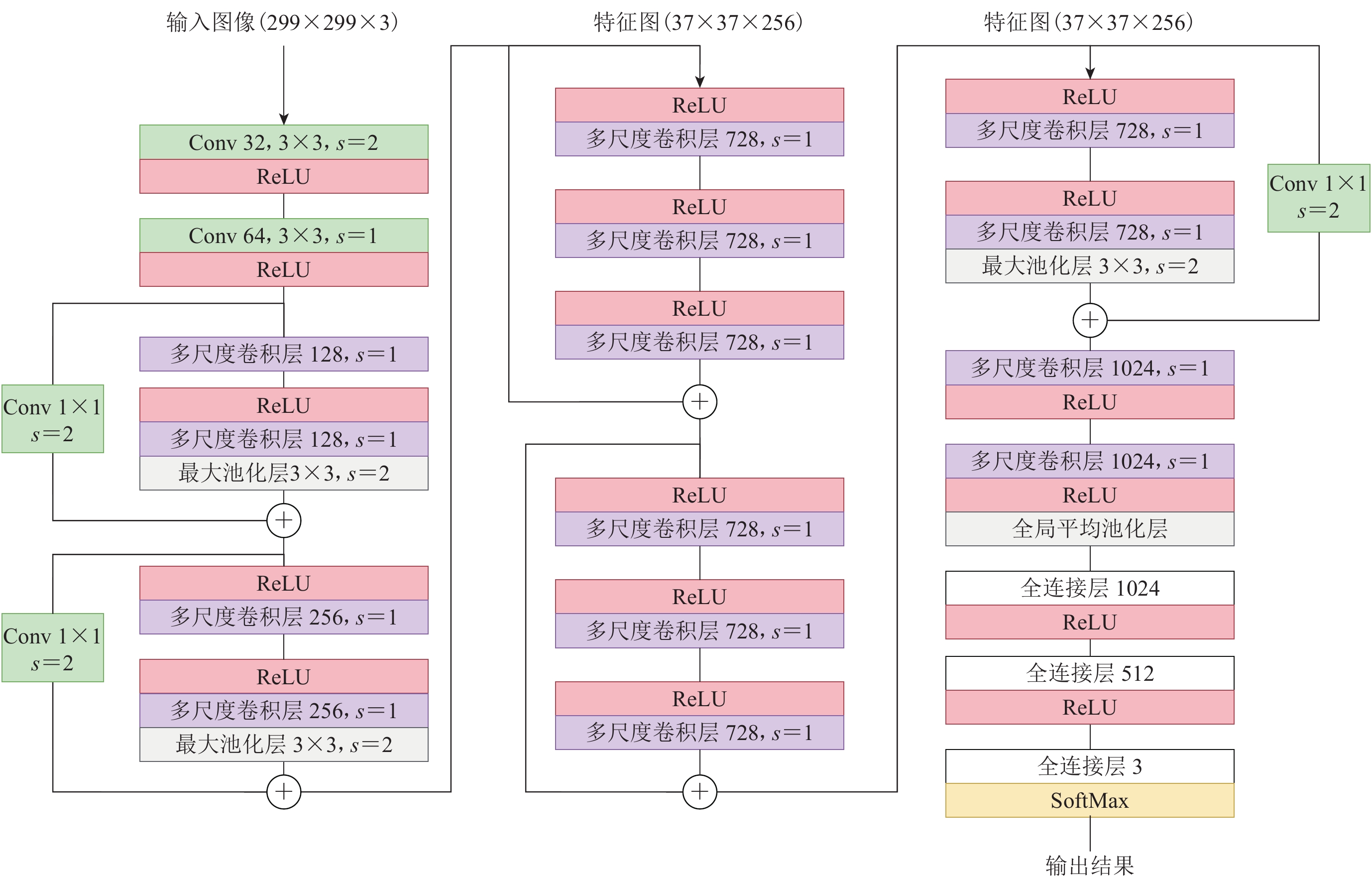
本文在Xception网络模型（Chollet，2017）的基础上结合多尺度卷积和残差结构构建适用于地震事件分类的神经网络模型QxceptionNet，其结构如图3所示，经本文试验证明，QxceptionNet能够较好地应用于地震事件分类问题。
![]()
图 3 本文应用于地震事件分类的多尺度残差网络模型QxceptionNet图中Conv表示常规卷积，紧跟其后的数字表示卷积核的个数，也是经过该层操作后的输出通道数。s表示卷积步长。未特殊标明大小的常规卷积核大小均为3×3，图中的多尺度卷积均采用图1所示的多尺度卷积单元，紧跟多尺度卷积层后数字表示经过该卷积层的输出通道数Figure 3. QxceptionNet as the multi-scale residual network model applied to classification of seismic events in this study“Conv” represents regular convolution，and the number immediately following it indicates the number of convolutional kernels，which is also the number of output channels after passing through that layer. “s” represents the stride of the convolution. Unless specifically noted，the size of the regular convolutional kernels is 3×3. The multi-scale convolutions in Fig. 1 all use the multi-scale convolutional units shown in Fig. 1，with the number immediately following the multi-scale convolutional layer indicating the number of output channels after passing through that convolutional layerQxceptionNet总共包含16层卷积层，开始两层常规卷积用于特征的初步提取和缩小图片尺寸，中间部分全部采用带残差结构的多尺度卷积，残差结构中加入1×1卷积使得分支通道数增加，从而与主干部分的通道数一致，确保它们能够进行相加操作。激活函数采用修正线性单元ReLU实现非线性操作，使用最大池化层实现下采样。为减少过拟合，所有卷积层和分离卷积层后面均带有批处理规范化层（图中未画出）。在输出阶段，通过添加全局平均池化层将多维数据变为一维，并连接至全连接层。全连接层的神经元数目分别为1 024，512，3。输出层节点数为分类类别数目，各输出值表示对应类别得分。本文将地震事件类型分为天然地震、爆破和塌陷等三种类别，并采用SoftMax公式将分类得分转化为概率值，转换公式为：
$$ {y_{ij}} ＝ \frac{{{{\mathrm{e}}^{{a_{ij}}}}}}{{\displaystyle\sum\limits_{k ＝ 0}^{M － 1} {{{\mathrm{e}}^{{a_{ik}}}}} }}\qquad \forall \,\, i \in 0 \text{，} 1 \text{，} 2 \text{，} \cdots \text{，} N － 1\text{；} \forall \,\,j \in 0 \text{，} 1 \text{，} \cdots \text{，} M － 1 \text{，} $$ (5) 式中，M表示分类类别数，N表示样本个数，aij表示第i个样本的第j类得分，yij表示第i个样本分类为第j类别的概率。
3. 试验与结果
3.1 试验设置
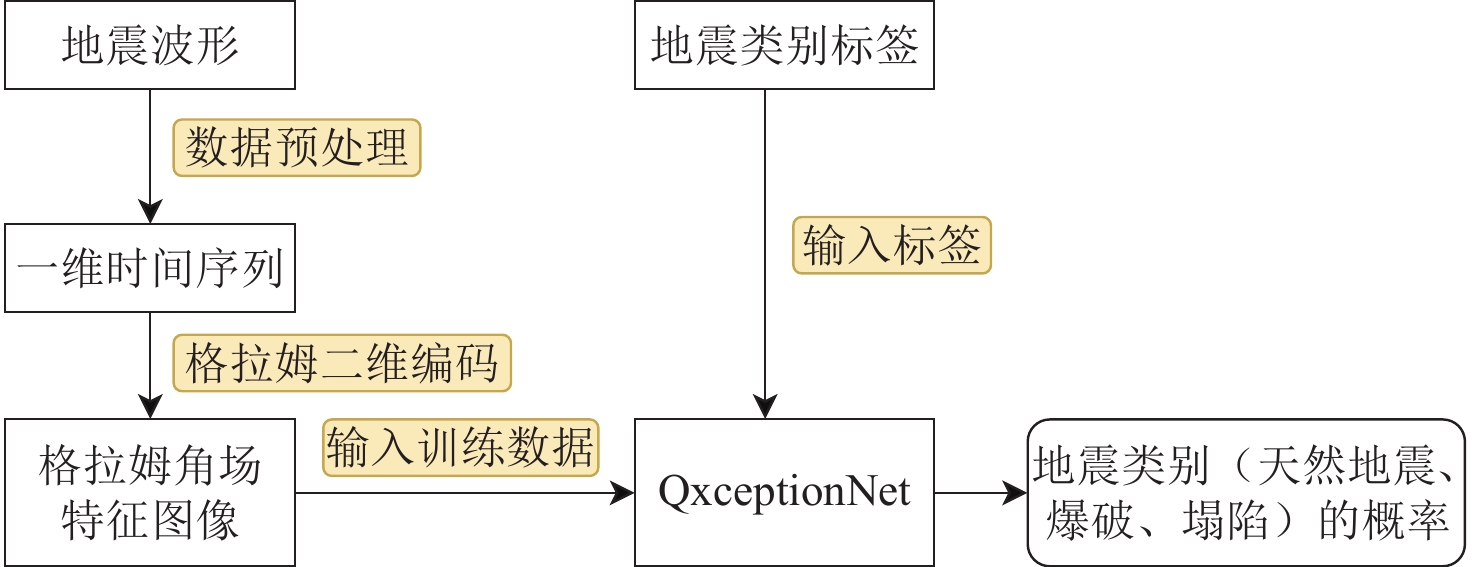
本文地震事件分类算法流程图如图4所示。将地震原始波形数据作为输入，为消除记录仪器、量纲等影响，首先对原始波形数据进行振幅归一化、去线性趋势、滤波等预处理操作，然后将一维波形数据进行格拉姆二维编码得到格拉姆角场特征图像。将格拉姆角场特征图和对应的地震类别标签作为QxceptionNet的输入进行训练，最终输出波形数据属于各类地震事件的概率。
本文地震事件数据由江苏省地震局搜集、整理并标注，其中爆破和塌陷两类非天然地震事件数据选自2008年以来国内首都圈地区（北京、河北、天津、辽宁、山西等）地震编目，外加2015年来江苏及邻区的非天然地震，其分布如图5a所示。最终所用的数据集仅为其中ML2.5以上的非天然地震数据。为避免不同区域地形、地貌等差异对数据的影响，选取2016年至2018年距上述非天然地震震中距离小于50 km且震级处于M2.0—4.0的天然地震，其分布如图5b所示。
![]()
图 5 本文所选取的非天然地震（a）和天然地震（b）事件分布Figure 5. Distribution of collapse and blast events （a） and natural earthquakes （b）一个地震事件指地表的一次震动，该地震事件可以被多个台站记录，而一个台站对于一个地震事件仅产生一个“台站记录”。为避免混淆，以下“台站记录”均指某个台站对于某一个地震事件的记录，包含该地震事件垂直、东西和南北三个方向的地震波形数据。为了确保用于训练的数据样本可靠，江苏省地震局对台站记录的地震事件波形进行人工检查和复核，剔除信噪比低、仪器设备记录异常、存在重大噪声干扰等记录后，最终挑选出天然地震事件的1 078个台站记录、爆破事件的981个台站记录和塌陷事件的830个台站记录。本文以地震事件的波形数据作为研究对象进行分类，每个台站记录数据包含东西、南北和垂直三个方向的波形。因此天然地震波形条数为3 234，爆破波形条数为2 943，塌陷波形条数为2 490。
网络模型QxceptionNet采用Adam优化算法最小化交叉熵损失函数，其定义如下：
$$ {J_0} ＝ - \frac{1}{N}\sum\limits_{i ＝ 0}^N {\sum\limits_{c ＝ 0}^{M－ 1} {{y_{ic}}{\mathrm{lg}} {{p_{ic}}} } } \text{，} $$ (6) 式中：N为样本数量；M为类别数量；yic为样本标签，如果样本i真实类别等于c取1，否则取0；pic表示样本$ i $为类别c的概率。
本文模型训练所用的计算显卡为NVIDIA GeForce GTX 2080Ti。设定训练批处理大小为32，即每批选取32个样本，输入网络进行网络的参数调整。训练结束条件设定为训练集准确率不再提高。
3.2 波形预处理和二维编码
QxceptionNet网络模型采用格拉姆角场（GAF）特征图作为输入，因此有必要对波形进行预处理和GAF二维编码，获得GAF特征图，其流程如图6所示。
![]()
图 6 波形预处理和格拉姆角场二维编码流程图Figure 6. Flow chart of waveform preprocessing and GAF encoding由于经过挑选的原始数据持续时间不一定相等，因此本文将所有地震事件波形截取为P波到时前5 s至S波到时后10 s，该时段包含地震波形主要的关键信息（赵明等，2019）。波形的采集率为100 Hz，所有波形统一长度为40 s，长度不足以零值填充，若长度超过则从尾部进行截断，每条试验波形将会生成一个包含4 000个采样点的一维波形数据。
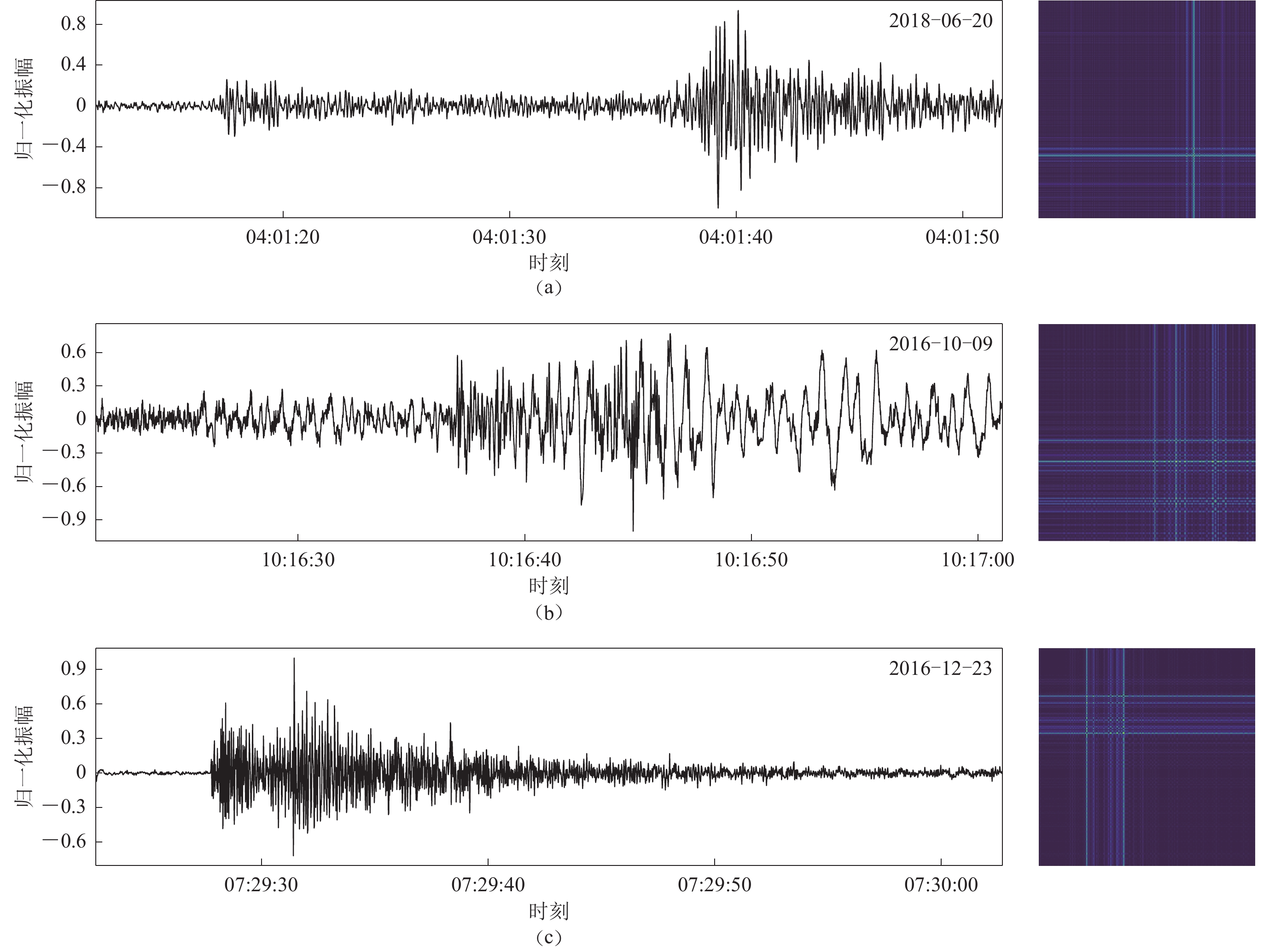
为生成高质量低噪声的GAF图像，首先对原始波形振幅归一化，使得振幅被限定在区间$ ［ -1\text{，} 1 ］ $内；采用最小二乘法去线性趋势以去除记录设备传感器的系统性偏移，并进行上限截止频率为20 Hz和下限截止频率为1.7 Hz的带通滤波，以去除非有效频带的干扰。由于直接转换为GAF图像所需的数据量庞大，不利于计算，故本文采用分段聚合近似方法（Keogh，Pazzani，2000）缩小波形序列长度，将原始数据分割为若干等长段，在每个段内计算其均值以代表该段数据。经过多次试验，窗口大小设定为10，最终形成的GAF图像尺寸为400×400。最后采用双线性插值将图像尺寸调整至299×299。天然地震、塌陷和爆破三种类型的典型原始波形和对应的GAF图像如图7所示。可见，通过格拉姆转换能够将一维的地震波形特征映射到二维平面上，且天然地震、塌陷和爆破在GAF图像上存在明显差异。单一的典型样本无法作为整体类型判别和分析的依据，因此我们将样本转换的GAF图像作为QxceptionNet的输入进行训练，将数据分为测试集和验证集进行试验。
![]()
图 7 不同类别地震事件的原始波形（左）和格拉姆角场图（右）（a） 天然地震；（b） 塌陷；（c） 爆破Figure 7. Original waveforms （left） and GAF images （right） of different types of seismic events（a） Earthquake；（b） Collapse；（c） Blast3.3 试验结果
为评估本文方法（GAF＋QxceptionNet），本文使用相同的地震数据，采用支持向量机（support vector machine，缩写为SVM）（Tang et al，2020）、多层感知机（multi-layer perceptron，缩写为MLP）（Laasri et al，2013）以及基于短时傅里叶变化（short-time Fourier transform，缩写为STFT）和CNN的地震信号分类识别方法（黎炳君等，2021）进行地震事件分类的对比试验。对于传统分类器SVM和MLP，输入4 000个采样点的一维波形数据，即经过预处理的波形数据，而后在此基础上生成STFT图片和GAF图片，分别在CNN和QxceptionNet网络结构上进行对比试验。
由于每个台站记录均包含东西、南北和垂直方向上的三条波形数据，为了说明GAF图像结合QxceptionNet对于地震类别分类的有效性，本文分别以单条波形和单个台站记录为分类对象进行试验。以单条波形为分类对象，本文从三类事件中无差别地各随机取出80%的波形作为训练集，余下20%用于验证模型对地震单条波形的分类能力，测试数据完全不参与网络训练。使用不同方法得到不同类别地震波形的分类准确率和平均值，如表1所示。从单项类别准确率和平均准确率来看，将原始信号作为分类器输入端的传统分类器SVM和MLP的分类效果不佳。就采用CNN作为分类器而言，使用STFT图片作为输入的准确率要高于使用GAF图作为输入，可能的原因是地震波形事先经过短时傅里叶变换，时频域特征得以初步提取，传统CNN已经能够较好地提取特征进行分类，而GAF图片只是进行简单的二维转化，能够保留更多的原始信息，然而这需要更深层次的网络模型进行特征提取。表1显示，采用GAF＋QxceptionNet方法的准确率最高，表明该种方法能更好地保留原始波形的特性，并充分提取其细节信息进行分类，鲁棒性和泛化性更好。
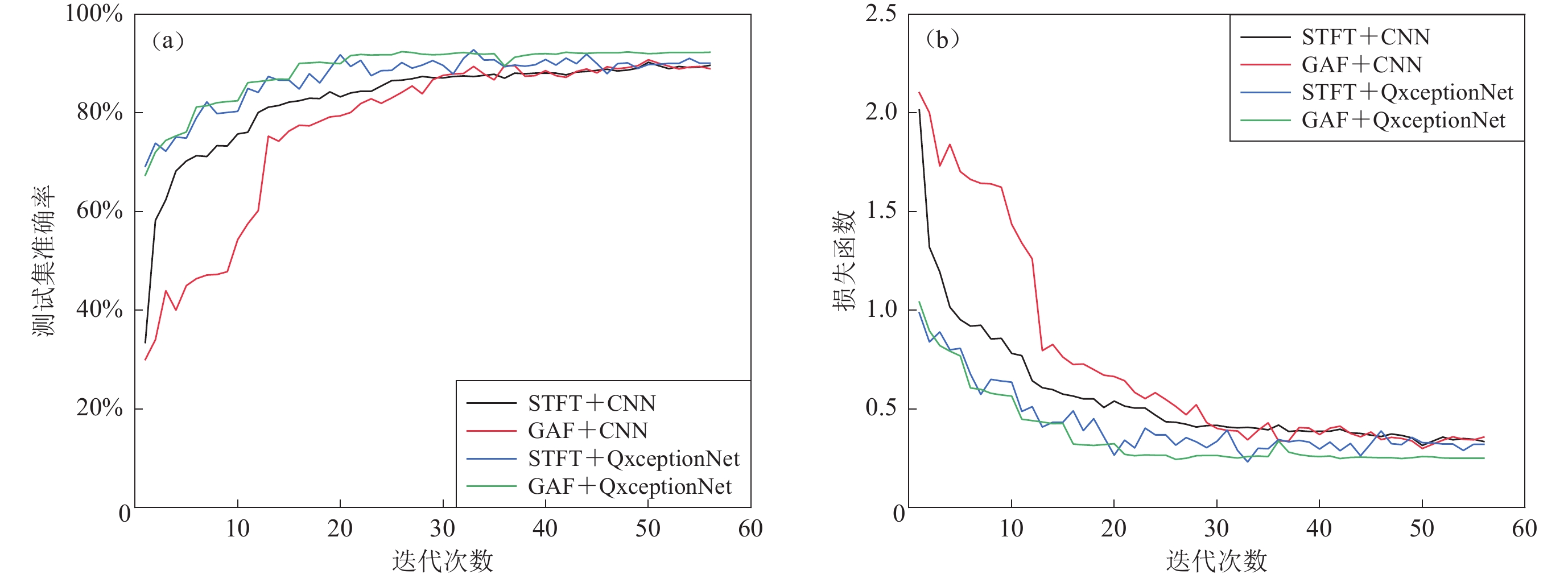
表 1 以单条波形为单位的地震事件分类准确率Table 1. Accuracy of earthquake events classification by single waveform方法 地震事件类别的准确率 平均准确率 天然地震 爆破 塌陷 原始信号＋SVM 73.75% 56.32% 67.45% 65.84% 原始信号＋MLP 76.42% 60.72% 68.49% 68.54% STFT＋CNN 89.17% 89.75% 90.23% 89.72% GAF＋CNN 88.14% 88.85% 90.04% 89.01% STFT＋QxceptionNet 91.97% 90.14% 89.96% 90.69% GAF＋QxceptionNet 93.56% 91.75% 92.34% 92.55% 为了对比采用神经网络的四种方法的性能和收敛速度，对四种神经网络方法的训练性能，包含训练过程中测试集的准确率和损失函数的变化曲线，进行分析，结果如图8所示。可见：采用QxceptionNet的初始准确率最高，在经历16次迭代后趋于稳定，能够较快地达到最优，且最终平均识别率要高于采用传统的CNN方法；采用CNN训练的初始准确率低，训练初期收敛速度快，需要26次迭代后趋于稳定；GAF＋QxceptionNet方法收敛最快且准确率最高。
![]()
图 8 四种神经网络方法训练性能对比（a） 准确率曲线；（b） 损失函数曲线Figure 8. Comparison of training performance of four neural network methods（a） Accuracy curves；（b） Loss function curves上述结果仅能体现模型对于单条波形的分类效果，然而判断地震事件的类别不能简单地依据其中某一个方向分量的分类结果，而应该根据其多个方向分量进行综合判断，因此有必要根据单个台站记录多个方向的波形进行分类。本文以单个台站记录为研究对象，若单个台站对于某地震事件不低于两个方向的波形被划分为同一事件类别，本文就将该事件归为该种类别。为此，本文以单个台站记录为单位，将80%作为训练集，剩余20%的台站记录作为测试集进行验证，得到不同类别地震事件的台站记录的分类准确率和平均值，详见表2。
表 2 以单个台站记录为单位的地震事件分类准确率Table 2. Accuracy of earthquake events classification by single station records方法 地震事件类别的准确率 平均准确率 天然地震 爆破 塌陷 原始信号＋SVM 76.17% 64.74% 72.57% 71.16% 原始信号＋MLP 78.67% 72.21% 71.12% 74.00% STFT＋CNN 94.64% 94.11% 93.67% 94.14% GAF＋CNN 92.14% 92.37% 93.88% 92.80% SFTT＋QxceptionNet 95.74% 94.32% 94.01% 94.69% GAF＋QxceptionNet 96.75% 95.75% 96.58% 96.36% 试验结果表明，较以单条波形为单位而言，以单个台站记录为单位的试验准确率都得到了有效提升，这表明综合所有方向的波形进行融合能够有效地提升地震事件分类识别的准确率，其中采用GAF＋QxceptionNet的分类准确率最高，平均准确率为96.36%。
4. 讨论与结论
本文通过格拉姆角场将地震波形数据转化为GAF图，并搭建深度可分离残差卷积神经网络模型QxceptionNet用于天然、爆破和塌陷三类地震事件的识别。结果表明：相比于直接输入波形数据和其它二维化方法，经格拉姆角场转化后的二维图片能够有效保留地震信号的细节信息，可以较好地表征地震信号的特征，计算简单，转换速度快，适用于快速检测。QxceptionNet通过引入可分离模块和残差单元，能够较好地提取输入图片的特征，提高分类识别的准确率。
在以单个台站记录为单位进行试验时，本文仅对各分量进行简单统计来判断该地震的类别。对于单个台站对某一地震事件的记录，其不同分量的波形存在差异，如何更加全面综合各分量并有效判断该地震类别是本研究的下一步工作。如何联系多个台站对同一地震的记录进行分析和判别也是未来的一部分工作。地震信号复杂多变，类型多样，仅用天然地震、爆破和塌陷三分类不能囊括所有的地震事件类别。下一步工作中，本文将增加来自更多不同地域、不同类别的地震事件样本和噪声样本进行进一步分类，实现地震数据检测的全面性和智能化。
江苏省地震局提供试验数据，审稿专家提出修改意见和建议，作者在此一并表示感谢。
-
![]()
图 8 四种神经网络方法训练性能对比
（a） 准确率曲线；（b） 损失函数曲线
Figure 8. Comparison of training performance of four neural network methods
（a） Accuracy curves；（b） Loss function curves
![]()
图 3 本文应用于地震事件分类的多尺度残差网络模型QxceptionNet
图中Conv表示常规卷积，紧跟其后的数字表示卷积核的个数，也是经过该层操作后的输出通道数。s表示卷积步长。未特殊标明大小的常规卷积核大小均为3×3，图中的多尺度卷积均采用图1所示的多尺度卷积单元，紧跟多尺度卷积层后数字表示经过该卷积层的输出通道数
Figure 3. QxceptionNet as the multi-scale residual network model applied to classification of seismic events in this study
“Conv” represents regular convolution，and the number immediately following it indicates the number of convolutional kernels，which is also the number of output channels after passing through that layer. “s” represents the stride of the convolution. Unless specifically noted，the size of the regular convolutional kernels is 3×3. The multi-scale convolutions in Fig. 1 all use the multi-scale convolutional units shown in Fig. 1，with the number immediately following the multi-scale convolutional layer indicating the number of output channels after passing through that convolutional layer
![]()
图 5 本文所选取的非天然地震（a）和天然地震（b）事件分布
Figure 5. Distribution of collapse and blast events （a） and natural earthquakes （b）
![]()
图 6 波形预处理和格拉姆角场二维编码流程图
Figure 6. Flow chart of waveform preprocessing and GAF encoding
![]()
图 7 不同类别地震事件的原始波形（左）和格拉姆角场图（右）
（a） 天然地震；（b） 塌陷；（c） 爆破
Figure 7. Original waveforms （left） and GAF images （right） of different types of seismic events
（a） Earthquake；（b） Collapse；（c） Blast
表 1 以单条波形为单位的地震事件分类准确率
Table 1 Accuracy of earthquake events classification by single waveform
方法 地震事件类别的准确率 平均准确率 天然地震 爆破 塌陷 原始信号＋SVM 73.75% 56.32% 67.45% 65.84% 原始信号＋MLP 76.42% 60.72% 68.49% 68.54% STFT＋CNN 89.17% 89.75% 90.23% 89.72% GAF＋CNN 88.14% 88.85% 90.04% 89.01% STFT＋QxceptionNet 91.97% 90.14% 89.96% 90.69% GAF＋QxceptionNet 93.56% 91.75% 92.34% 92.55% 
下载: 导出CSV
表 2 以单个台站记录为单位的地震事件分类准确率
Table 2 Accuracy of earthquake events classification by single station records
方法 地震事件类别的准确率 平均准确率 天然地震 爆破 塌陷 原始信号＋SVM 76.17% 64.74% 72.57% 71.16% 原始信号＋MLP 78.67% 72.21% 71.12% 74.00% STFT＋CNN 94.64% 94.11% 93.67% 94.14% GAF＋CNN 92.14% 92.37% 93.88% 92.80% SFTT＋QxceptionNet 95.74% 94.32% 94.01% 94.69% GAF＋QxceptionNet 96.75% 95.75% 96.58% 96.36%
下载: 导出CSV
-
高家乙,刘晓锋,闫睿. 2020. 河南平顶山平煤矿区天然地震、爆破、塌陷时频特征分析[J]. 地震地磁观测与研究,41(3):67–74. Gao J Y,Liu X F,Yan R. 2020. Time-frequency analysis of seismic records generated by natural earthquakes,blasts,and collapses near Pingmei mine based on STFT[J]. Seismological and Geomagnetic Observation and Research,41(3):67–74 (in Chinese).
黎炳君,黄汉明,王婷婷,王鹏飞,王梦琪,施佳朋,薛思敏. 2021. 基于STFT和CNN的地震信号分类识别研究[J]. 地球物理学进展,36(4):1404–1411. Li B J,Huang H M,Wang T T,Wang P F,Wang M Q,Shi J P,Xue S M. 2021. Research on seismic signal classification and recognition based on STFT and CNN[J]. Progress in Geophysics,36(4):1404–1411 (in Chinese).
赵明,陈石,Yuen D. 2019. 基于深度学习卷积神经网络的地震波形自动分类与识别[J]. 地球物理学报,62(1):374–382. Zhao M,Chen S,Yuen D. 2019. Waveform classification and seismic recognition by convolution neural network[J]. Chinese Journal of Geophysics,62(1):374–382 (in Chinese).
Chollet F. 2017. Xception:Deep learning with depthwise separable convolutions[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu,Hawaii:IEEE:1800−1807.
Horn R A,Johnson C R. 2012. Matrix Analysis[M]. 2nd ed. Cambridge:Cambridge University Press:441−442.
He K,Zhang X,Ren S,Sun J. 2016. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas:IEEE:770−778.
Keogh E J,Pazzani M J. 2000. Scaling up dynamic time warping for datamining applications[C]//Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York:Association for Computing Machinery:285–289.
Laasri E H A,Akhouayri E,Agliz D,Atmani A. 2013. Seismic signal classification using multi-layer perceptron neural network[J]. Int J Comput Appl,79(15):35−43.
Li J,Fang F M,Mein K F,Zhang G X. 2018. Multi-scale residual network for image super-resolution[C]//Proceedings of the 15th European Conference on Computer Vision. Munich:Springer:527−542.
Ross Z E,Meier M A,Hauksson E,Heaton T H. 2018. Generalized seismic phase detection with deep learning[J]. Bull Seismol Soc Am,108(5A):2894–2901. doi: 10.1785/0120180080
Simonyan K,Zisserman,A. 2015. Very deep convolutional networks for large-scale image recognition[C]//Proceedings of the 3rd International Conference on Learning Representations. San Diego:Institute for Catastrophic Loss Redu Ction:1−12.
Szegedy C,Vanhoucke V,Ioffe S,Shlens J,Wojna Z. 2016. Rethinking the inception architecture for computer vision[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas:IEEE:2818−2826.
Tang L,Zhang M,Wen L X. 2020. Support vector machine classification of seismic events in the Tianshan orogenic belt[J]. J Geophys Res: Solid Earth,125(1):e2019JB018132. doi: 10.1029/2019JB018132
Wang Z G,Oates T. 2015. Imaging time-series to improve classification and imputation[C]//Proceedings of the 24th International Conference on Artificial Intelligence. Buenos Aires,Argentina:AAAI:3939−3945.
Yano K,Shiina T,Kurata S,Kato A,Komaki F,Sakai S,Hirata N. 2021. Graph-partitioning based convolutional neural network for earthquake detection using a seismic array[J]. J Geophys Res: Solid Earth,126(5):e2020JB020269. doi: 10.1029/2020JB020269
计量
- 文章访问数: 227
- HTML全文浏览量: 64
- PDF下载量: 53
