A frequency domain elastic wave full waveform inversion method based on nearly analytic discrete operator
-
摘要:
全波形反演是一种利用地震波传播的动力学特征来获取地下介质物性参数的反演方法,可为揭示地下精细结构提供重要依据。本文以弹性波方程作为数学模型来模拟地震波传播规律并进行相应的反演方法研究。为提高计算效率与反演结果的准确性,可将近似解析离散化(NAD)算子用于频率域弹性波方程的正演模拟。本文在频率域NAD离散的基础上推导阻抗矩阵的稀疏分块结构与反演目标函数对模型参数的梯度计算公式,由此建立基于NAD算子的频率域弹性波全波形反演方法。为验证该方法的有效性,文中通过数值实验对多种典型介质模型进行反演计算,均得到了理想的反演结果。
Abstract:Since ancient times, earthquakes have been an unavoidable natural phenomenon. As one of the regions with frequent seismic activities, China urgently needs advanced underground detection technology to characterize the fine structure of the lithosphere. This will provide a better understanding of the generation and development laws of earthquakes and minimize their impact on human society. Full waveform inversion (FWI) is an inversion method that utilizes the dynamic characteristics of seismic wave propagation to obtain subsurface physical parameters, providing important insights into the fine structure of the subsurface. This method further enriches the theoretical framework of conventional velocity modeling methods and has gradually become a research hotspot due to its high accuracy, multi-parameter, and multi-dimensional modeling advantages. As a high-resolution seismic inversion method, FWI minimizes the objective function that measures the discrepancy between the synthetic waveform and seismic observation data through wavefield simulation and optimization iteration, obtaining optimal subsurface medium parameters and constructing imaging. In the early stages of research, FWI was primarily performed in the time domain. Subsequently, researchers extended the inversion theory to the frequency domain. In comparison, frequency-domain inversion methods are conducive to parallel computing, reducing computational burden, and easy characterization of attenuation effects. By selecting a small number of frequencies that sufficiently cover the wavenumber, the fine structural details of the inversion model can be characterized without compromising inversion accuracy, thereby further reducing the computational cost of frequency-domain FWI. Additionally, frequency-domain wavefield simulation exhibits higher efficiency, especially in the case of multiple sources and increased attenuation factors. Therefore, conducting FWI in the frequency domain holds significant importance. With the continuous development of seismic research and rapid improvement in computer hardware, traditional acoustic wave equations have difficulty meeting the requirements of fine subsurface detection. FWI has gradually evolved towards the direction of elastic parameter inversion based on isotropic, anisotropic, viscoelastic wave equations, among others. Compared to acoustic waves, elastic waves include the propagation laws of P-waves and S-waves, providing richer wavefield information. Furthermore, in the near-surface region where the propagation time is short, it is challenging to separate body waves and surface waves, and attenuating or filtering surface waves is not easy. Both types of waves need to be considered for imaging. The elastic wave equation accurately simulates seismic wave propagation in subsurface media. Therefore, this study adopts the elastic wave equation as a mathematical model to simulate the propagation laws of seismic waves and conducts corresponding research on inversion methods. In FWI, the main computational burden lies in the forward modeling process, and the computational efficiency and accuracy of the inversion heavily depend on the quality of the forward simulation method. Considering the complex structure of the elastic wave equation, traditional numerical solving methods require more computational costs. Therefore, employing efficient forward simulation methods is crucial for improving computational efficiency and the accuracy of inversion results. The nearly analytie discrete (NAD) operator has emerged as an important class of differencing operators in recent years. Its construction principle involves approximating high-order partial derivatives using the cross-combination of nodal displacements and their gradient values. The NAD operator offers high accuracy and significantly enhances computational efficiency. Therefore, in order to improve computational efficiency and the accuracy of inversion results, this study introduces the NAD operator for frequency-domain elastic wave equation forward simulation. This study establishes a frequency-domain elastic wave FWI framework based on the NAD operator. It derives the gradient calculation formula for the inversion objective function using the sparse block structure of the impedance matrix. The idea of separating compressional and shear waves is implemented throughout the entire solution process, greatly reducing the scale of gradient calculation and suppressing interference between them, further improving inversion computational efficiency. Finally, numerical experiments using three classic media models are conducted, obtaining ideal inversion results. The effectiveness and correctness of the proposed elastic wave inversion method are validated through the trend curves of inversion errors at different frequencies. In summary, the frequency-domain elastic wave FWI method based on the NAD operator derived in this study exhibits significant advantages in the inversion of subsurface physical parameters. Through numerical experiments, we have demonstrated the effectiveness and accuracy of this method in capturing fine subsurface structures. We believe that this method has broad application prospects in geological exploration and resource development and provides valuable references for researchers in related fields.
-
引言
自古以来,地震都是一种难以避免的自然现象(龙锋等,2006)。中国作为全球地震频发的地区之一,迫切需要先进的地下探测技术来刻画岩石圈的精细结构,从而更好地了解地震的孕育与发展规律,尽可能减少其对人类社会的危害(王椿镛等,2016)。自20世纪80年代以来,全波形反演逐渐兴起(Tarantola,1984;Jeong et al,2012),进一步丰富了常规速度建模方法的理论体系(Virieux,Operto,2009)。这种反演方法凭借高精度、多参数、多维度的建模优势,引起了许多研究者的关注(张文生等,2015;Virieux et al,2017)。
作为一种高分辨率地震反演方法,全波形反演通过波场模拟与最优化迭代来极小化衡量合成波形与地震观测数据偏差的目标函数,获得最优地下介质参数并进行构造成像(Bornstein et al,2013;Yang et al,2020)。在研究的早期阶段,全波形反演主要是在时间域上进行(Tarantola,1984;Tessmer et al,1992;Hestholm et al,1999)。随后,Pratt (1990)使用频率域波动方程进行逐个频率点的迭代计算,将反演理论推广到频率域。相比之下,频率域反演方法易于并行可减轻计算负担且容易刻画衰减效应(Pratt et al,1998;Shin et al,2001)。Sirgue和Pratt (2004)提出只需要选取少量频率在保证波数充分覆盖的前提下即可刻画反演模型的细节结构,从而在不损伤反演精度的条件下进一步降低频率域全波形反演的计算代价。殷文等(2006)研究得出若频率域各频率点之间相互独立计算,则各个频率点误差不会产生累积,可极大提高模拟精度。此外,还有研究发现,频率域波场模拟对于多震源和增加衰减因子更加有效(Ben-Hadj-Ali et al,2011)。由此可见,在频率域上进行全波形反演具有重要意义(Geng et al,2018)。
随着地震学研究的不断深入与计算机硬件水平的快速提升,传统声波方程较难满足地下精细探测的需求(张霖斌,姚振兴,2000;Jeong et al,2012)。全波形反演逐步在向基于各向同性、各向异性、黏弹性介质波动方程等的多弹性参数反演方向发展(宋海斌,张关泉,1998;Operto et al,2007)。从物理的角度来讲,在短时间震源激发下,离震源作用地点较远处的地下岩层可近似地看成弹性体,此时地震波在地球介质中的传播可以看成弹性波(孙成禹,李振春,2011)。相较于声波,弹性波包括了P波与S波的传播规律,包含的波场信息更加丰富。另外,在地表区域较短的传播时间导致体波和面波不容易分离,此时过滤或减弱表面波并不容易,两种类型的波都需要参与成像。因此,弹性波方程能够更加准确地模拟地震波在地下介质中的传播情况(Brossier et al,2009;Zhao et al,2020)。相较于声波情形,弹性波全波形反演能同时获取P波、S波速度等参数,但由于不同波形之间会相互干扰,因此会产生严重的非线性问题(Virieux,Operto,2009)。到目前为止,对于弹性波反演出现的串扰问题已有很多学者进行了研究,所使用较多的方法有辐射模式法(Prieux et al,2013)、Hessian矩阵法(Wang et al,2016)、纵横波分离法(黄少华等,2019)等,其中纵横波分离法早期被运用到弹性波逆时偏移来压制串扰噪声,近几年很多学者将其运用到弹性波全波形反演中。针对多参数反演的梯度有很强的串扰问题,Ren和Liu (2016)首先提出了在波数域进行P波与S波分离的方法以降低梯度串扰从而提高反演精度,而Qu等(2018)应用矢量纵横波分离方法直接对纵横波速度进行扰动来求取P波梯度和S波梯度也取得不错的效果。
由于全波形反演的主要计算量集中在正演过程,反演的计算效率和精度在很大程度上取决于正演模拟方法的优劣。同时考虑到弹性波方程本身结构较为复杂,数值求解需要更多的计算代价,因此采用高效的正演方法至关重要(刘璐等,2013;Li et al,2018)。目前频率域计算普遍采用的正演方法包括有限差分方法(Moczo et al,2007)、有限元方法(Liu et al,2017)、谱元法(Komatitsch et al,2005)等。其中有限差分法凭借原理直观、离散算子结构简单及易于实现并行等优点而被广泛应用。相比而言,传统差分格式精度较低且容易引起数值频散假象,为克服这一缺点通常需要加密网格,这势必导致计算效率的明显下降。
近似解析离散化(nearly analytic discrete,缩写为NAD)算子是近些年来兴起的一类重要差分算子(Yang et al,2003),构造思想是利用节点位移及其梯度值的交叉组合来逼近高阶偏导数(Yang et al,2009)。这同时具备较高精度,可显著提升计算效率。Yang等(2010)、Tong等(2011)及Li等(2013)将NAD算子用于时间域声波和弹性波方程的数值离散过程并进一步优化了算子结构。Lang和Yang (2017)采用NAD算子进行了频率域声波方程正演模拟,并通过与其它经典数值方法(例如九点有限差分法(OFD)和交错网格(SG)方法)的对比,显示了该算子在压制数值频散与提高计算效率方面的优势。随后,Lang等(2020)与郎超等(2022)将NAD算子用于频率域声波全波形反演和逆时偏移计算中,均得到了可靠的成像结果。然而该算子在频率域弹性波方程反演中的讨论还处于空白阶段,相应算法的适用性尚不明确。
为此,本文试图搭建基于NAD算子的频率域弹性波全波形反演框架;利用阻抗矩阵的稀疏分块结构来推导反演目标函数的梯度计算公式,并且将分离纵横波的思想贯彻整个求解过程,充分缩减梯度计算的规模并压制纵横波之间的串扰从而进一步提高反演计算效率;最后利用三种经典介质模型进行数值实验,结合不同频率的反演误差曲线趋势图验证所提出弹性波反演方法的有效性和正确性.
1. 基于NAD算子的频率域弹性波正演模拟
在各向同性介质中的二维频率域弹性波方程可表示为
$$ \left\{ \begin{gathered} - \rho {\omega ^2}u = ( \lambda + 2\mu ) \frac{{{ {\text{∂}} ^2}u}}{{ {\text{∂}} {x^2}}} + \mu \frac{{{ {\text{∂}} ^2}u}}{{ {\text{∂}} {{\textit{z}}^2}}} + ( \lambda + \mu ) \frac{{{ {\text{∂}} ^2}v}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}}+ {s_1}\text{,} \\ - \rho {\omega ^2}v = ( \lambda + 2\mu ) \frac{{{ {\text{∂}} ^2}v}}{{ {\text{∂}} {{\textit{z}}^2}}} + \mu \frac{{{ {\text{∂}} ^2}v}}{{ {\text{∂}} {x^2}}}+ ( \lambda + \mu ) \frac{{{ {\text{∂}} ^2}u}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}} + {s_2}\text{,} \\ \end{gathered} \right. $$ (1) 式中,$ x $表示地面横向坐标,$ {\textit{z}} $表示地下纵向坐标,$ u $,$ v $分别定义为弹性波场的水平和垂直分量,$ \mu $和$ \lambda $为拉梅系数,$ {s}_{1} $和$ {s}_{2} $为震源分量,$ \rho $和$ \omega $分别为介质密度和角频率。由于在影响地震成像相关参数的分析中,速度参数的作用更为关键(张文生,张丽娜,2020),所以在下文的正演模拟与反演迭代计算中,本文假定反演的密度值为某一常数且不再变动,只反演P波与S波速度。
为后续论述清晰明了,可将式(1)归结为矩阵与向量形式,即
$$ \begin{gathered} \rho {\omega ^2}{\boldsymbol{w}} + {{{\boldsymbol{P}}}_1}\frac{{{ {\text{∂}} ^2}{\boldsymbol{w}}}}{{ {\text{∂}} {x^2}}} + {{{\boldsymbol{P}}}_2}\frac{{{ {\text{∂}} ^2}{{\boldsymbol{w}}}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}}+ {{{\boldsymbol{P}}}_3}\frac{{{ {\text{∂}} ^2}{{\boldsymbol{w}}}}}{{ {\text{∂}} {{\textit{z}}^2}}} = - {{\boldsymbol{s}}}.{\text{ }} \\ {\text{ }} \\ \end{gathered} $$ (2) 其中
$$ \begin{array}{l}{\boldsymbol{P}}_{1}= \left(\begin{array}{cc}\text{ }\lambda + 2\mu & 0\\ 0& \mu \end{array}\right) \text{,} \text{ }{\boldsymbol{P}}_{2}=\left(\begin{array}{cc}0& \lambda \text + \mu \\ \lambda \text+\mu & 0\end{array}\right) \text{,} \text{ }{\boldsymbol{P}}_{3}=\left(\begin{array}{cc}\mu & 0\\ 0& \lambda +2\mu \end{array}\right) \text{,} \\ \\ {{\boldsymbol{w}}}=\left[\begin{array}{c}u\\ v\end{array}\right] \text{,} \text{ }{{\boldsymbol{s}}}=\left[\begin{array}{l}{s}_{1}\\ {s}_{2}\end{array}\right]\text{,} \text{ }\end{array} $$ (3) 式中${\boldsymbol{w}} $和${\boldsymbol{s}} $分别为波场向量和震源向量。
在使用NAD算子对式(2)进行离散时,需要对其两端分别沿着$ x $和$ {\textit{z}} $轴求偏导,可得到如下偏微分方程组:
$$ \left\{ \begin{gathered} {{\boldsymbol{P}}_1}\frac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} {x^2}}} + {{\boldsymbol{P}}_2}\frac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}} + {{\boldsymbol{P}}_3}\frac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} {{\textit{z}}^2}}} + \rho {\omega ^2}\boldsymbol{w} = - \boldsymbol{s} \text{,} {\text{ }} \\ {{\boldsymbol{P}}_{\text{1}}}\frac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {x^3}}} + {{\boldsymbol{P}}_2}\frac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {x^2} {\text{∂}} {\textit{z}}}} + {{\boldsymbol{P}}_3}\frac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {{\textit{z}}^2}}} + \rho {\omega ^2}\frac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} x}} = - \frac{{ {\text{∂}} \boldsymbol{s}}}{{ {\text{∂}} x}} \text{,} \\ {{\boldsymbol{P}}_1}\frac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {x^2} {\text{∂}} {\textit{z}}}} + {{\boldsymbol{P}}_2}\frac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {{\textit{z}}^2}}} + {{\boldsymbol{P}}_3}\frac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {{\textit{z}}^3}}} + \rho {\omega ^2}\frac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {\textit{z}}}} = - \frac{{ {\text{∂}} \boldsymbol{s}}}{{ {\text{∂}} {\textit{z}}}}. \\ \end{gathered} \right. $$ (4) 1.1 吸收边界条件
当使用计算机进行地震波正演模拟时,由于计算空间的局限性,研究者会引入人工截断边界,这导致波传播至人工边界时会引发非物理的反射而产生虚假反射波,因此必须对边界进行处理。本文采用完全匹配层(perfectly matched layer,缩写为PML)吸收边界条件,它的构造思想是在边界处加一个吸收层,数学上可采用衰减函数来表征这一衰减效应(Komatitsch,Tromp,2003)。
具体地,以$ x $方向为例,首先在PML区域内引入复坐标$ \tilde x $替换式(4)中的实坐标$ x $,即
$$ \tilde x = x - \frac{{\text{i}}}{\omega }\displaystyle\int_0^x {{{{d}}_x} ( r ) } {{\mathrm{d}}r}\text{,} $$ (5) 关于$ x $求偏导,可得
$$ \frac{{ {\text{∂}} \tilde x}}{{ {\text{∂}} x}} = 1 - \frac{{\text{i}}}{\omega }{{{d}}_x} ( x ) {\triangleq}\, {t_x}\text{,} $$ (6) 式中:$ \mathrm{i}=\sqrt{-1} $;衰减函数的具体表达式为${d_x} ( x ) = - \dfrac{{3{v_x}}}{{2\delta }}\ln \left(R\right){\left( {\dfrac{x}{\delta }} \right)^2}$,其中$ \delta $表示$ x $方向PML层厚度,$ {v}_{x} $为PML区域和计算区域交界处的波速,$ x $为PML区域内的网格点到计算区域的投影距离,$ R $为反射系数(一般取10−3)。
将式(4)中的实坐标替换为复坐标,再将式(5)、(6)代入后($ {\textit{z}} $方向同理可得),可得带有PML边界条件的方程组
$$ \left\{ \begin{array}{l} {\boldsymbol{P}_1}\left(\dfrac{1}{{t_x^2}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} {x^2}}} + \dfrac{{{\mathrm{i}}d_x { \text{′}}}}{{\omega t_x^3}}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} x}}\right) + {\boldsymbol{P}_2}\dfrac{1}{{{t_x}{t_{\textit{z}}}}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}} + {\boldsymbol{P}_3}\left(\dfrac{1}{{t_{\textit{z}}^2}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} {{\textit{z}}^2}}} + \dfrac{{{\mathrm{i}}d_{\textit{z}}{ \text{′}}}}{{\omega t_{\textit{z}}^3}}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {\textit{z}}}}\right) + \rho {\omega ^2}\boldsymbol{w} = - \boldsymbol{s}\text{,}{\rm{ }}\\ {\boldsymbol{P}_1}\left(\dfrac{1}{{t_x^2}}\dfrac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {x^3}}} + \dfrac{{3{\mathrm{i}}d_x{ \text{′}}}}{{\omega t_x^3}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} {x^2}}} - \dfrac{{3{{d_x{ \text{′}}}^2}}}{{{\omega ^2}t_x^4}}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} x}} + \dfrac{{{\mathrm{i}}d{ \text{′′}_ { x}}{}}}{{\omega t_x^3}}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} x}}\right) + {\boldsymbol{P}_2}\left(\dfrac{1}{{{t_x}{t_{\textit{z}}}}}\dfrac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {x^2} {\text{∂}} {\textit{z}}}} + \dfrac{{{\mathrm{i}}d_x{ \text{′}}}}{{\omega t_x^2{t_{\textit{z}}}}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}}\right)+\\ {\rm{ }} {\boldsymbol{P}_3}\left(\dfrac{1}{{t_{\textit{z}}^2}}\dfrac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {{\textit{z}}^2}}} + \dfrac{{{\mathrm{i}}d_{\textit{z}}{ \text{′}}}}{{\omega t_{\textit{z}}^3}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}}\right) + \rho {\omega ^2}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} x}} = - \dfrac{{ {\text{∂}} \boldsymbol{s}}}{{ {\text{∂}} x}}\text{,}\\ {\boldsymbol{P}_1}\left(\dfrac{1}{{t_x^2}}\dfrac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {x^2} {\text{∂}} {\textit{z}}}} + \dfrac{{{\mathrm{i}}d_x{ \text{′}}}}{{\omega t_x^3}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}}\right) + {\boldsymbol{P}_2}\left(\dfrac{1}{{{t_x}{t_{\textit{z}}}}}\dfrac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {{\textit{z}}^2}}} + \dfrac{{{\mathrm{i}}d_{\textit{z}}{ \text{′}}}}{{\omega t_{\textit{z}}^2{t_x}}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}}\right)+\\ {\rm{ }} {\boldsymbol{P}_3}\left(\dfrac{1}{{t_{\textit{z}}^2}}\dfrac{{{ {\text{∂}} ^3}\boldsymbol{w}}}{{ {\text{∂}} {{\textit{z}}^3}}} + \dfrac{{3{\mathrm{i}}d_{\textit{z}}{ \text{′}}}}{{\omega t_{\textit{z}}^3}}\dfrac{{{ {\text{∂}} ^2}\boldsymbol{w}}}{{ {\text{∂}} {{\textit{z}}^2}}} - \dfrac{{3{{d_{\textit{z}}{ \text{′}}}^2}}}{{{\omega ^2}t_{\textit{z}}^4}}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {\textit{z}}}} + \dfrac{{{\mathrm{i}}d{\text{′′}_{ \textit{z}}}{}}}{{\omega t_{\textit{z}}^3}}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {\textit{z}}}}\right) + \rho {\omega ^2}\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {\textit{z}}}} = - \dfrac{{ {\text{∂}} \boldsymbol{s}}}{{ {\text{∂}} {\textit{z}}}}. \end{array}\right. $$ (7) 1.2 四阶NAD算子
若式(7)中波场${\boldsymbol{w}} $在点(i,j)处的二阶、三阶偏导数离散,则所采用的$ x $方向上的单方向四阶NAD网格差分模板为(Yang et al,2003,2004)
$$ \left\{\begin{array}{l} \dfrac{{{ {\text{∂}} ^2}{\boldsymbol{w}_{i \text{,} j}}}}{{ {\text{∂}} {x^2}}} {\text{≈}} \dfrac{2}{{{h^2}}} ( {\boldsymbol{w}_{i - 1 \text{,} j}} - 2{\boldsymbol{w}_{i \text{,} j}} + {\boldsymbol{w}_{i + 1 \text{,} j}} ) + \dfrac{1}{{2h}}\left(\dfrac{{ {\text{∂}} {\boldsymbol{w}_{i - 1 \text{,} j}}}}{{ {\text{∂}} x}} - \dfrac{{ {\text{∂}} {\boldsymbol{w}_{i + 1 \text{,} j}}}}{{ {\text{∂}} x}}\right) \text{,} \\ \dfrac{{{ {\text{∂}} ^3}{\boldsymbol{w}_{i \text{,} j}}}}{{ {\text{∂}} {x^3}}} {\text{≈}} \dfrac{{15}}{{2{h^3}}} ( {\boldsymbol{w}_{i + 1 \text{,} j}}- {\boldsymbol{w}_{i - 1 \text{,} j}} ) -\dfrac{3}{{2{h^2}}}\left(\dfrac{{ {\text{∂}} {\boldsymbol{w}_{i - 1 \text{,} j}}}}{{ {\text{∂}} x}} + 8\dfrac{{ {\text{∂}} {\boldsymbol{w}_{i \text{,} j}}}}{{ {\text{∂}} x}} + \dfrac{{ {\text{∂}} {\boldsymbol{w}_{i + 1 \text{,} j}}}}{{ {\text{∂}} x}}\right). \\ \end{array} \right. $$ (8) $ {\textit{z}} $方向可相应推导.
通过单方向上的NAD模板再借助旋转坐标轴的思想(童平,2012)可推导出双方向四阶NAD差分格式为
$$ \begin{aligned} \frac{{{ {\text{∂}} ^2}{\boldsymbol{w}_{i \text{,} j}}}}{{ {\text{∂}} x {\text{∂}} {\textit{z}}}} {\text{≈}}& \frac{1}{{2{h^2}}} ( {\boldsymbol{w}_{i + 1 \text{,} j + 1}} + {\boldsymbol{w}_{i - 1 \text{,} j - 1}} - {\boldsymbol{w}_{i - 1 \text{,} j + 1}} - {\boldsymbol{w}_{i + 1 \text{,} j - 1}} ) - \\& {\text{ }} \frac{1}{{8h}}\left(\frac{{ {\text{∂}} {\boldsymbol{w}_{i + 1 \text{,} j + 1}}}}{{ {\text{∂}} {\textit{z}}}}- \frac{{ {\text{∂}} {\boldsymbol{w}_{i - 1 \text{,} j- 1}}}}{{ {\text{∂}} {\textit{z}}}} - \frac{{ {\text{∂}} {\boldsymbol{w}_{i - 1 \text{,} j + 1}}}}{{ {\text{∂}} {\textit{z}}}} + \frac{{ {\text{∂}} {\boldsymbol{w}_{i + 1 \text{,} j - 1}}}}{{ {\text{∂}} {\textit{z}}}}\right)- \\& {\text{ }} \frac{1}{{8h}}\left(\frac{{ {\text{∂}} {\boldsymbol{w}_{i + 1 \text{,} j + 1}}}}{{ {\text{∂}} x}} - \frac{{ {\text{∂}} {\boldsymbol{w}_{i- 1 \text{,} j - 1}}}}{{ {\text{∂}} x}} + \frac{{ {\text{∂}} {\boldsymbol{w}_{i - 1 \text{,} j + 1}}}}{{ {\text{∂}} x}} - \frac{{ {\text{∂}} {\boldsymbol{w}_{i + 1 \text{,} j - 1}}}}{{ {\text{∂}} x}}\right) \text{,} \\ \end{aligned} $$ (9) $$ \begin{aligned} \frac{{{ {\text{∂}} ^2}{{\boldsymbol{w}}_{i \text{,} j}}}}{{ {\text{∂}} {x^2} {\text{∂}} {\textit{z}}}} {\text{≈}}& \frac{5}{{4{h^3}}} ( {{\boldsymbol{w}}_{i + 1 \text{,} j + 1}} + {{\boldsymbol{w}}_{i - 1 \text{,} j + 1}} - {{\boldsymbol{w}}_{i + 1 \text{,} j - 1}} - {{\boldsymbol{w}}_{i - 1 \text{,} j - 1}} + 2{{\boldsymbol{w}}_{i \text{,} j - 1}} - 2{{\boldsymbol{w}}_{i \text{,} j + 1}} ) - \\& {\text{ }} \frac{1}{{4{h^2}}}\left(\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j + 1}}}}{{ {\text{∂}} x}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j - 1}}}}{{ {\text{∂}} x}} - \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j + 1}}}}{{ {\text{∂}} x}} - \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j - 1}}}}{{ {\text{∂}} x}}\right)- \\& {\text{ }} \frac{1}{{4{h^2}}}\left(\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j + 1}}}}{{ {\text{∂}} {\textit{z}}}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j - 1}}}}{{ {\text{∂}} {\textit{z}}}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j + 1}}}}{{ {\text{∂}} {\textit{z}}}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j - 1}}}}{{ {\text{∂}} {\textit{z}}}} - 2\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i \text{,} j + 1}}}}{{ {\text{∂}} {\textit{z}}}} - 2\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i \text{,} j - 1}}}}{{ {\text{∂}} {\textit{z}}}}\right) \text{,} \\ \end{aligned} $$ (10) $$ \begin{aligned} \frac{{{ {\text{∂}} ^2}{{\boldsymbol{w}}_{i \text{,} j}}}}{{ {\text{∂}} x {\text{∂}} {{\textit{z}}^2}}} {\text{≈}}& \frac{5}{{4{h^3}}} ( {{\boldsymbol{w}}_{i + 1 \text{,} j + 1}} + {{\boldsymbol{w}}_{i + 1 \text{,} j - 1}} - {{\boldsymbol{w}}_{i - 1 \text{,} j + 1}} - {{\boldsymbol{w}}_{i - 1 \text{,} j - 1}} + 2{{\boldsymbol{w}}_{i - 1 \text{,} j}} - 2{{\boldsymbol{w}}_{i + 1 \text{,} j}} ) - \\& {\text{ }} \frac{1}{{4{h^2}}}\left(\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j + 1}}}}{{ {\text{∂}} {\textit{z}}}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j - 1}}}}{{ {\text{∂}} {\textit{z}}}} - \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j - 1}}}}{{ {\text{∂}} {\textit{z}}}} - \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j + 1}}}}{{ {\text{∂}} {\textit{z}}}}\right)- \\& {\text{ }} \frac{1}{{4{h^2}}}\left(\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j + 1}}}}{{ {\text{∂}} x}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j - 1}}}}{{ {\text{∂}} x}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j + 1}}}}{{ {\text{∂}} x}} + \frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j - 1}}}}{{ {\text{∂}} x}} - 2\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i + 1 \text{,} j}}}}{{ {\text{∂}} x}} - 2\frac{{ {\text{∂}} {{\boldsymbol{w}}_{i - 1 \text{,} j}}}}{{ {\text{∂}} x}}\right). \\ \end{aligned} $$ (11) 式中$ h $表示空间离散步长($ x $和$ {\textit{z}} $方向上的相等)。将差分模板式(8)—(11)代入式(7)进行离散,可形成大型稀疏线性方程组(郎超等,2021)
$$ {{\boldsymbol{C}}} ( {{\boldsymbol{p}}} \text{,} \omega ) {{\boldsymbol{w}}} ( {{\boldsymbol{p}}} \text{,} \omega ) {{ = }}{{\boldsymbol{s}}} ( \omega ) \text{,} $$ (12) 式中C为阻抗矩阵。
1.3 阻抗矩阵的稀疏分块结构
线性方程组式(12)中的矩阵$ \boldsymbol{C} $称为阻抗矩阵(Pratt,1999),$ {{\boldsymbol{w}}} $表示弹性波场的水平与垂直分量交叉排列所组成的波场向量,$ \boldsymbol{s} $为右端震源向量,$ \boldsymbol{C} $,$ \boldsymbol{w} $,$ \boldsymbol{s} $随反演模型向量$ \boldsymbol{P} $的更新而改变,同时也依赖于角频率$ \omega $。为了选择合适的算法以快速而稳定地求解式(12)并在反演过程中推导出目标函数梯度计算的有效方法,阻抗矩阵$ \boldsymbol{C} $的稀疏分块结构必不可少,其示意图如下所列(郎超等,2021)
$$ \left(\begin{array}{ccccccccccccc} {\boldsymbol{C}}_{5}^{ ( 1 ) }& {\boldsymbol{C}}_{6}^{ ( 1 ) }& \stackrel{{n}_{x}-3}{\overbrace{\cdots }}& {\boldsymbol{C}}_{7}^{ ( 1 ) }& {\boldsymbol{C}}_{8}^{ ( 1 ) }& {\boldsymbol{C}}_{9}^{ ( 1 ) }& & & & & & & \\ {\boldsymbol{C}}_{4}^{ ( 2 ) }& {\boldsymbol{C}}_{5}^{ ( 2 ) }& {\boldsymbol{C}}_{6}^{ ( 2 ) }& \cdots & {\boldsymbol{C}}_{7}^{ ( 2 ) }& {\boldsymbol{C}}_{8}^{ ( 2 ) }& {\boldsymbol{C}}_{9}^{ ( 2 ) }& & & & & & \\ & \ddots & & \ddots & & \ddots & & & & & & & \\ & {\boldsymbol{C}}_{1}^{ ( j ) }& {\boldsymbol{C}}_{2}^{ ( j ) }& {\boldsymbol{C}}_{3}^{ ( j ) }& \cdots & {\boldsymbol{C}}_{4}^{ ( j ) }& {\boldsymbol{C}}_{5}^{ ( j ) }& {\boldsymbol{C}}_{6}^{ ( j ) }& \cdots & {\boldsymbol{C}}_{7}^{ ( j ) }& {\boldsymbol{C}}_{8}^{ ( j ) }& {\boldsymbol{C}}_{9}^{ ( j ) }& \\ & & & & & & \ddots & & \ddots & & \ddots & & \\ & & & & & & {\boldsymbol{C}}_{1}^{ ( N-1 ) }& {\boldsymbol{C}}_{2}^{ ( N-1 ) }& {\boldsymbol{C}}_{3}^{ ( N-1 ) }& \cdots & {\boldsymbol{C}}_{4}^{ ( N-1 ) }& {\boldsymbol{C}}_{5}^{ ( N-1 ) }& {\boldsymbol{C}}_{6}^{ ( N-1 ) }\\ & & & & & & & {\boldsymbol{C}}_{1}^{ ( N ) }& {\boldsymbol{C}}_{2}^{ ( N ) }& {\boldsymbol{C}}_{3}^{ ( N ) }& \underset{{n}_{x}-3}{\underbrace{\cdots }}& {\boldsymbol{C}}_{4}^{ ( N ) }& {\boldsymbol{C}}_{5}^{ ( N ) }\end{array}\right)\text{,} $$ (13) 式中,非零子块矩阵$ {\boldsymbol{C}}_{i}^{ ( j ) } ( i=1 \text{,} \cdots \text{,} 9 \text{,} j=1 \text{,} \cdots \text{,} N ) $的规模为$ 6{\text{×}} 6 $,其余空白位置未列出的均为零元素,$ N={n}_{x}{\text{×}}{n}_{{\textit{z}}} $表示正演离散网格点总数,$ {\boldsymbol{C}}_{i}^{ ( j ) } $的具体元素表达式参考郎超等(2021)。利用式(13)的稀疏结构特点,本文中相应的反演计算依然选择以往研究工作中(Lang et al,2020)所采用的三角分块预处理GMRES迭代方法对线性方程组(12)进行求解,该方法配合频率域NAD离散已展现其在提高计算效率方面的优势(郎超等,2021)。
2. 基于NAD算子的频率域弹性波反演原理
全波形反演的基本思路是通过合成波场与观测波场数据残差的欧式范数建立反演目标函数,并利用最优化方法(例如:梯度类方法)更新模型参数向量,实现观测波场与合成波场的最佳匹配,从而达到重构速度场的效果(祝贺君等,2023)。对于极小化反演目标函数的计算过程,本文采用梯度类迭代方法来实施(张文生,张丽娜,2020)。
常用梯度类算法主要包括最速下降法(Jeong et al,2012)、非线性共轭梯度法(Tong et al,2014)、高斯牛顿法(Pratt,Worthington,1988)、拟牛顿法(例如:BFGS)(Tromp et al,2005)等。在上述所有算法中,最速下降法的优点是迭代流程直观,计算操作简单,缺点是收敛速度较慢,计算效率偏低;而牛顿类方法作为二阶方法,所得反演结果的精度较高,但计算量较大,不适用于大规模计算(任志明,2016)。为了平衡精度和计算量,本文采用非线性共轭梯度方法(Saad,2003)。
根据非线性共轭梯度方法的原理,求解目标函数的梯度值是整个迭代算法不可缺少的环节(卞爱飞等,2010)。因此,本节着重推导基于NAD算子的目标函数梯度计算公式,由此实现相应的频率域全波形反演流程。相应的具体算法流程如图1所示,虚线轮廓斜体文字部分是本研究的重要环节。
在本文的讨论中,反演目标函数的建立采用不同频率与震源设置下所对应的观测波场与合成波场差值的欧氏范数来表示,记作
$$ E ( \boldsymbol{p} ) =\frac{1}{2}\sum\limits_\omega ^{} {\sum\limits_{{n_{\mathrm{s}}}}^{} {{{ [ {{{\boldsymbol{\delta}} }{\boldsymbol{d}^{ ( {n_{\mathrm{s}}} ) }} ( \boldsymbol{p} \text{,} \omega ) } ] }^{\text{T}}}} } { [ {{{\boldsymbol{\delta}} }{\boldsymbol{d}^{ ( {n_{\mathrm{s}}} ) }} ( \boldsymbol{p} \text{,} \omega ) } ] ^* } \text{,} $$ (14) 式中,$ { ( \cdot ) }^{\mathrm{T}}{\mathrm{和} ( \cdot ) }^{\mathrm{*}} $分别表示向量的转置与复共轭,$ \boldsymbol{p}\in {R}^{2m {\text{×}} 1} $为反演模型的参数向量,$ {{{\boldsymbol{\delta}} }\mathit{d}}^{ ( {n}_{{\mathrm{s}}} ) } ( \boldsymbol{p} \text{,}\omega ) $表示在角频率$ \omega $取值下第$ {n}_{{\mathrm{s}}} $个震源的合成波场与观测波场的残差向量。假设在地表有$ {N}_{r} $个接收器,则$ {{{\boldsymbol{\delta}} }\boldsymbol{d}}^{ ( {n}_{{\mathrm{s}}} ) } $的分量表达形式为
$$ \begin{aligned} {{\boldsymbol{\delta}} {\boldsymbol{d}}}_i^{ ( {n_{\mathrm{s}}} ) } ( {{\boldsymbol{p}}} \text{,} \omega ) =& {{\boldsymbol{w}}}_i^{ ( {n_{\mathrm{s}}} ) } ( {{\boldsymbol{p}}} \text{,} \omega ) - {{\boldsymbol{d}}}_i^{ ( {n_{\mathrm{s}}} ) } ( {{\boldsymbol{p}}} \text{,} \omega ) \text{,} {\text{ }}\\i =& 1 \text{,} 2 \text{,} \cdot \cdot \cdot \text{,} {N_r} \text{,} \end{aligned} $$ (15) 式中,${\boldsymbol{w}}_{i}^{ ( {n}_{{\mathrm{s}}} ) } ( \boldsymbol{p} \text{,} \omega ) \text{,} {\boldsymbol{d}}_{i}^{ ( {n}_{{\mathrm{s}}} ) } ( \boldsymbol{p} \text{,} \omega ) $表示由第$ {n}_{{\mathrm{s}}} $个震源激发并且在第$ i $个接收器上的合成波场和观测波场数据,$ {\boldsymbol{\delta }\boldsymbol{d}}_{i}^{ ( {n}_{{\mathrm{s}}} ) } ( \boldsymbol{p}\text{,}\omega ) $为相应的残差数据分量。
梯度类优化迭代格式的一般形式为
$$ {{\boldsymbol{p}}_{k + 1}}= {{\boldsymbol{p}}_k}{{+ }}{\alpha _k}{d_k} \text{,} \qquad k = 1 \text{,} 2 \text{,} \cdots \text{,} $$ (16) 式中,$ k $表示迭代步指标,$ {\mathrm{\alpha }}_{k} $为搜索步长,${d_k} = - {\nabla _{ {\boldsymbol{p}}}}E ( {{\boldsymbol{p}}_k} ) + {\beta _{k - 1}}{d_{k - 1}}$表示第$ k $步的共轭梯度搜索方向,参数${\beta _k} = {{{\nabla _{ \boldsymbol{p}}}E ( {{\boldsymbol{p}}_{k +1}} ) \cdot {\nabla _{ \boldsymbol{p}}}E ( {{\boldsymbol{p}}_{k + 1}} ) }}{ {/}} [ {{{\nabla _{ \boldsymbol{p}}}E ( {{\boldsymbol{p}}_k} ) \cdot {\nabla _{ \boldsymbol{p}}}E ( {{\boldsymbol{p}}_k} ) }} ] $。
梯度迭代算法的关键环节在于计算反演目标函数的梯度,接下来详细列出这一过程,将式(14)两端分别关于模型参数$ \boldsymbol{p} $进行求导可得(Pratt et al,1998)
$$ {\nabla _{ {\boldsymbol{p}}}}E = \frac{{ {\text{∂}} E ( {\boldsymbol{p}} ) }}{{ {\text{∂}} {\boldsymbol{p}}}} = {\mathrm{Re}} ( {{\boldsymbol{J}}^{\text{T}}}{\boldsymbol{\delta}} {{\boldsymbol{d}}^*} ) \text{,} $$ (17) 其中${\mathrm{Re}} ( \cdot ) $表示取实部,$ \boldsymbol{J} $ 表示雅克比矩阵,即
$$ {\boldsymbol{J}}= \left( {\begin{array}{*{20}{c}} {\dfrac{{ {\text{∂}} {\boldsymbol{w}_1}}}{{ {\text{∂}} {p_1}}}}&{\dfrac{{ {\text{∂}} {\boldsymbol{w}_1}}}{{ {\text{∂}} {p_2}}}}&{\dfrac{{ {\text{∂}} {\boldsymbol{w}_1}}}{{ {\text{∂}} {p_3}}}}& \cdots &{\dfrac{{ {\text{∂}} {\boldsymbol{w}_1}}}{{ {\text{∂}} {p_m}}}} \\ \vdots & \vdots & \vdots &{}& \vdots \\ {\dfrac{{ {\text{∂}} {\boldsymbol{w}_n}}}{{ {\text{∂}} {p_1}}}}&{\dfrac{{ {\text{∂}} {\boldsymbol{w}_n}}}{{ {\text{∂}} {p_2}}}}&{\dfrac{{ {\text{∂}} {\boldsymbol{w}_n}}}{{ {\text{∂}} {p_3}}}}& \cdots &{\dfrac{{ {\text{∂}} {\boldsymbol{w}_n}}}{{ {\text{∂}} {p_m}}}} \end{array}} \right)= \left[ {\begin{array}{*{20}{c}} {\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_1}}} \text{,} }&{\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_2}}} \text{,} }&{\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_3}}} \text{,} }& \cdots &{ \text{,} \dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_m}}}} \end{array}} \right] . $$ (18) 在实际计算中,显式地求解雅克比矩阵需要大量的正演过程,所消耗计算代价过大,应当尽可能避免。具体的化归思路可叙述为:对线性方程组式(12)两端同时关于模型参数$ \boldsymbol{p} $进行求导,则有
$$ \begin{gathered} \boldsymbol{C}\frac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_i}}} + \frac{{ {\text{∂}} \boldsymbol{C}}}{{ {\text{∂}} {p_i}}}\boldsymbol{w} = 0 \\ \Rightarrow \boldsymbol{C}\frac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_i}}} = - \frac{{ {\text{∂}} \boldsymbol{C}}}{{ {\text{∂}} {p_i}}}\boldsymbol{w} \\ \Rightarrow \frac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_i}}}=- {\boldsymbol{C}^{ - 1}}\frac{{ {\text{∂}} \boldsymbol{C}}}{{ {\text{∂}} {p_i}}}\boldsymbol{w} \text{,}\qquad i =1 \text{,} \cdots \text{,} m \text{,} \\ \end{gathered} $$ (19) 将式(19)代入式(18)得
$$ \boldsymbol{J} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_1}}} \text{,} }&{\dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_2}}} \text{,} }& \cdots &{ \text{,} \dfrac{{ {\text{∂}} \boldsymbol{w}}}{{ {\text{∂}} {p_m}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {{{\boldsymbol{C}}}^{ - 1}}\dfrac{{ {\text{∂}}\boldsymbol{C}}}{{ {\text{∂}} {p_1}}}\boldsymbol{w} \text{,} }&{ - {{{\boldsymbol{C}}}^{ - 1}}\dfrac{{ {\text{∂}}\boldsymbol{C}}}{{ {\text{∂}} {p_2}}}\boldsymbol{w} \text{,} }& \cdots\text{,} { - {{{\boldsymbol{C}}}^{ - 1}}\dfrac{{ {\text{∂}}\boldsymbol{C}}}{{ {\text{∂}} {p_m}}}\boldsymbol{w}} \end{array}} \right] \text{,} $$ (20) 记$\boldsymbol{y}={\boldsymbol{C}}^{-\mathrm{T}}{\boldsymbol{\delta }\boldsymbol{d}}^{*}$,同时将式(20)代入梯度表达式式(17)得
$$ {\nabla _{\boldsymbol{p}}}E = {\mathrm{Re}} ( {\boldsymbol{J}^{\rm{T}}}\boldsymbol{\delta }{\boldsymbol{d}^*} ) = - {\mathrm{Re}} \left[ \begin{array}{*{20}{c}} {{\boldsymbol{w}^{\rm{T}}}\dfrac{{\partial {\boldsymbol{C}^{\rm{T}}}}}{{\partial {p_1}}}{\boldsymbol{C}^{ - {\rm{T}}}}\boldsymbol{\delta }{\boldsymbol{d}^ * }}\\ {{\boldsymbol{w}^{\rm{T}}}\dfrac{{\partial {\boldsymbol{C}^{\rm{T}}}}}{{\partial {p_2}}}{\boldsymbol{C}^{ - {\rm{T}}}}\boldsymbol{\delta }{\boldsymbol{d}^ * }}\\ \vdots \\ {{\boldsymbol{w}^{\rm{T}}}\dfrac{{\partial {\boldsymbol{C}^{\rm{T}}}}}{{\partial {p_m}}}{\boldsymbol{C}^{ - {\mathop{\rm T}\nolimits} }}\boldsymbol{\delta }{\boldsymbol{d}^ * }} \end{array} \right] = - {\mathrm{Re}} \left[ \begin{array}{l} {\boldsymbol{w}^{\rm{T}}}\dfrac{{\partial {\boldsymbol{C}^{\rm{T}}}}}{{\partial {p_1}}}\boldsymbol{y}\\ {\boldsymbol{w}^{\rm{T}}}\dfrac{{\partial {\boldsymbol{C}^{\rm{T}}}}}{{\partial {p_2}}}\boldsymbol{y}\\ \qquad \vdots \\ {\boldsymbol{w}^{\rm{T}}}\dfrac{{\partial {\boldsymbol{C}^{\rm{T}}}}}{{\partial {p_m}}}\boldsymbol{y} \end{array} \right] \text{,} $$ (21) 观察式(21)可知,梯度值的计算可避免直接求解雅克比矩阵,而只需求解一次关于${\boldsymbol{C}}^{\mathrm{T}}$的线性方程组获取虚拟震源激发的反传波场(Lang et al,2020)。$ {v}_{{\mathrm{P}}} $和$ {v}_{{\mathrm{S}}} $与拉梅系数$ \lambda $和$ \mu $有着如下一一对应关系
$$ \left\{ \begin{gathered} {v_{\mathrm{P}}} = \sqrt {\frac{{\lambda + 2\mu }}{\rho } \text{,}} \\ {v_{\mathrm{S}}} = \sqrt {\frac{\mu }{\rho }}\text{;} \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \lambda = \rho v_{\mathrm{P}}^2 - 2\rho v_{\mathrm{S}}^2 \text{,} \\ \mu = \rho v_{\mathrm{S}}^2. \\ \end{gathered} \right. $$ (22) 接下来需求解阻抗矩阵的转置对模型参数的偏导数,首先将式(22)中P,S波速度和拉梅系数的关系代入式(3),可得
$$ {{{\boldsymbol{P}}}_1} = \left( {\begin{array}{*{20}{c}} {\rho v_{\rm{P}}^2{\text{ }}}&0 \\ 0&{\rho v_{\rm{S}}^2} \end{array}} \right) \text{,}{\text{ }}{{{\boldsymbol{P}}}_2} = \left( {\begin{array}{*{20}{c}} 0&{\rho v_{\rm{P}}^2 -\rho v_{\mathrm{S}}^2} \\ {\rho v_{\rm{P}}^2- \rho v_{\rm{S}}^2}&0 \end{array}} \right) \text{,}{\text{ }}{{{\boldsymbol{P}}}_3}= \left( {\begin{array}{*{20}{c}} {{\text{ }}\rho v_{\mathrm{S}}^2}&0 \\ 0&{\rho v_{\rm{P}}^2} \end{array}} \right). $$ (23) 然后分别对$ {\boldsymbol{P}}_{1} $,$ {\boldsymbol{P}}_{2} $,$ {\boldsymbol{P}}_{3} $关于$ {v}_{{\mathrm{P}}},{v}_{{\mathrm{S}}} $求偏导,结果如下
$$ \begin{gathered} {\boldsymbol{Q}_1} =\frac{{ {\text{∂}} {\boldsymbol{P}_1}}}{{ {\text{∂}} {v_{\mathrm{P}}}}} =\left( {\begin{array}{*{20}{c}} {2\rho {v_{\mathrm{P}}}}&0 \\ 0&0 \end{array}} \right) \text{,}{\text{ }}{\boldsymbol{Q}_2} =\frac{{ {\text{∂}} {\boldsymbol{P}_2}}}{{ {\text{∂}} {v_{\mathrm{P}}}}} =\left( {\begin{array}{*{20}{c}} 0&{2\rho {v_{\mathrm{P}}}} \\ {2\rho {v_{\mathrm{P}}}}&0 \end{array}} \right) \text{,}{\text{ }}{\boldsymbol{Q}_3} =\frac{{ {\text{∂}} {\boldsymbol{P}_3}}}{{ {\text{∂}} {v_{\mathrm{P}}}}} =\left( {\begin{array}{*{20}{c}} 0&0 \\ 0&{2\rho {v_{\mathrm{P}}}} \end{array}} \right) \text{,} \\ \\ {\boldsymbol{Z}_1} =\frac{{ {\text{∂}} {\boldsymbol{P}_1}}}{{ {\text{∂}} {v_{\mathrm{S}}}}} =\left( {\begin{array}{*{20}{c}} 0&0 \\ 0&{2\rho {v_{\mathrm{S}}}} \end{array}} \right) \text{,}{\text{ }}{\boldsymbol{Z}_2} =\frac{{ {\text{∂}} {\boldsymbol{P}_2}}}{{ {\text{∂}} {v_{\mathrm{S}}}}} =\left( {\begin{array}{*{20}{c}} 0&{ - 2\rho {v_{\mathrm{S}}}} \\ { - 2\rho {v_{\mathrm{S}}}}&0 \end{array}} \right) \text{,}{\text{ }}{\boldsymbol{Z}_3} =\frac{{ {\text{∂}} {\boldsymbol{P}_3}}}{{ {\text{∂}} {v_{\mathrm{S}}}}} =\left( {\begin{array}{*{20}{c}} {2\rho {v_{\mathrm{S}}}}&0 \\ 0&0 \end{array}} \right). \\ \end{gathered} $$ (24) 式中$ {\boldsymbol{Q}}_{1} $,$ {\boldsymbol{Q}}_{2} $,$ {\boldsymbol{Q}}_{3} $,$ {\boldsymbol{Z}}_{1} $,$ {\boldsymbol{Z}}_{2} $,$ {\boldsymbol{Z}}_{3} $均为对称矩阵,则阻抗矩阵式(13)对$ {v}_{{\mathrm{P}}} $求导得如下稀疏矩阵
$$ \left(\begin{array}{ccccccccccccc}{\boldsymbol{E}}_{5}^{ ( 1 ) } & {\boldsymbol{E}}_{6}^{ ( 1 ) } & \stackrel{{n}_{x}-3}{\overbrace{\cdots }} & {\boldsymbol{E}}_{7}^{ ( 1 ) } & {\boldsymbol{E}}_{8}^{ ( 1 ) } & {\boldsymbol{E}}_{9}^{ ( 1 ) } & & & & & & & \\ {\boldsymbol{E}}_{4}^{ ( 2 ) } & {\boldsymbol{E}}_{5}^{ ( 2 ) } & {\boldsymbol{E}}_{6}^{ ( 2 ) } & \cdots & {\boldsymbol{E}}_{7}^{ ( 2 ) } & {\boldsymbol{E}}_{8}^{ ( 2 ) } & {\boldsymbol{E}}_{9}^{ ( 2 ) } & & & & & & \\ & \ddots & & \ddots & & \ddots & & & & & & & \\ & {\boldsymbol{E}}_{1}^{ ( j ) } & {\boldsymbol{E}}_{2}^{ ( j ) } & {\boldsymbol{E}}_{3}^{ ( j ) } & \cdots & {\boldsymbol{E}}_{4}^{ ( j ) } & {\boldsymbol{E}}_{5}^{ ( j ) } & {\boldsymbol{E}}_{6}^{ ( j ) } & \cdots & {\boldsymbol{E}}_{7}^{ ( j ) } & {\boldsymbol{E}}_{8}^{ ( j ) } & {\boldsymbol{E}}_{9}^{ ( j ) } & \\ & & & & & & \ddots & & \ddots & & \ddots & & \\ & & & & & & {\boldsymbol{E}}_{1}^{ ( N-1 ) } & {\boldsymbol{E}}_{2}^{ ( N-1 ) } & {\boldsymbol{E}}_{3}^{ ( N-1 ) } & \cdots & {\boldsymbol{E}}_{4}^{ ( N-1 ) } & {\boldsymbol{E}}_{5}^{ ( N-1 ) } & {\boldsymbol{E}}_{6}^{ ( N-1 ) }\\ & & & & & & & {\boldsymbol{E}}_{1}^{ ( N ) } & {\boldsymbol{E}}_{2}^{ ( N ) } & {\boldsymbol{E}}_{3}^{ ( N ) } & \underset{{n}_{x}-3}{\underbrace{\cdots }} & {\boldsymbol{E}}_{4}^{ ( N ) } & {\boldsymbol{E}}_{5}^{ ( N ) }\end{array}\right)\text{,} $$ (25) 同理,阻抗矩阵$\boldsymbol{C}$对$ {v}_{{\mathrm{S}}} $求导得到与式(25)稀疏结构完全相同,非零子块不同的稀疏矩阵,其子块表示为${\boldsymbol{F}}_{i}^{ ( j ) } ( i=1 \text{,}\cdots 9\text{,}j=1\text{,}\cdots \text{,}N ) \mathrm{。}{\boldsymbol{F}}_{i}^{ ( j ) }$具体表达式见附件。
为叙述方便,本文将阻抗矩阵式(13)改写为如下形式:
$$ \boldsymbol{C} =\left( {\begin{array}{*{20}{c}} {{\boldsymbol{C}_{11}}}&{{\boldsymbol{C}_{12}}}& \cdots &{{\boldsymbol{C}_{1N}}} \\ {{\boldsymbol{C}_{21}}}&{{\boldsymbol{C}_{22}}}& \cdots &{{\boldsymbol{C}_{2N}}} \\ \vdots & \vdots &{}& \vdots \\ {{\boldsymbol{C}_{N1}}}&{{\boldsymbol{C}_{N2}}}& \cdots &{{\boldsymbol{C}_{NN}}} \end{array}} \right)\text{.} $$ (26) 根据模型参数向量排列规则,若将${\boldsymbol{p}} $写作分量形式则为${\boldsymbol{p}} = ( {{p_1}}\text{,} {{p_2}}\text{,} \cdots \text{,} {{p_{2m}}} ) _{2m {\text{×}}1}^{{\mathrm{T}}}$。为缓解P波与S波之间的串扰,缩减梯度计算规模,本文将P波与S波速度进行分离,令${\boldsymbol{p}} = ( {{q_1}}\text{,} {{q_2}} \text{,} \cdots \text{,} {{q_{2i}}} ) ^{{\mathrm{T}}}$,P波速度出现在模型参数分量$2i-1$位置处的取值,而S波速度为模型参数分量$ 2i $处的取值,其中$i=\mathrm{1\text{,} 2} \text{,} \cdots \text{,} m$。
将阻抗矩阵对模型参数分量的偏导数分解为两部分讨论,一部分为阻抗矩阵对$ {v}_{\mathrm{P}} $分量的偏导数,另一部分为对$ {v}_{\mathrm{S}} $分量的偏导数也可相应推导,则有
$$ \dfrac{{ {\text{∂}} \boldsymbol{C}}}{{ {\text{∂}} {q_{2i - 1}}}} = \left( {\begin{array}{*{20}{c}} 0&0& \cdots &0 \\ \vdots & \vdots &{}& \vdots \\ {\dfrac{{ {\text{∂}} {\boldsymbol{C}_{i1}}}}{{ {\text{∂}} {q_{2i - 1}}}}}&{\dfrac{{ {\text{∂}} {\boldsymbol{C}_{i2}}}}{{ {\text{∂}} {q_{2i - 1}}}}}& \cdots &{\dfrac{{ {\text{∂}} {\boldsymbol{C}_{iN}}}}{{ {\text{∂}} {q_{2i - 1}}}}} \\ \vdots & \vdots &{}& \vdots \\ 0&0& \cdots &0 \end{array}} \right)= \left( {\begin{array}{*{20}{c}} 0&0& \cdots &0 \\ \vdots & \vdots &{}& \vdots \\ {{\boldsymbol{E}_{i1}}}&{{\boldsymbol{E}_{i2}}}& \cdots &{{\boldsymbol{E}_{iN}}} \\ \vdots & \vdots &{}& \vdots \\ 0&0& \cdots &0 \end{array}} \right) \text{,} $$ (27) $$ \dfrac{{ {\text{∂}} \boldsymbol{C}}}{{ {\text{∂}} {q_{2i}}}} = \left( {\begin{array}{*{20}{c}} 0&0& \cdots &0 \\ \vdots & \vdots &{}& \vdots \\ {\dfrac{{ {\text{∂}} {\boldsymbol{C}_{i1}}}}{{ {\text{∂}} {q_{2i}}}}}&{\dfrac{{ {\text{∂}} {\boldsymbol{C}_{i2}}}}{{ {\text{∂}} {q_{2i}}}}}& \cdots &{\dfrac{{ {\text{∂}} {\boldsymbol{C}_{iN}}}}{{ {\text{∂}} {q_{2i}}}}} \\ \vdots & \vdots &{}& \vdots \\ 0&0& \cdots &0 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&0& \cdots &0 \\ \vdots & \vdots &{}& \vdots \\ {{\boldsymbol{F}_{i1}}}&{{\boldsymbol{F}_{i2}}}& \cdots &{{\boldsymbol{F}_{iN}}} \\ \vdots & \vdots &{}& \vdots \\ 0&0& \cdots &0 \end{array}} \right) \text{,}$$ (28) 记$\boldsymbol{w} = \left( {\begin{array}{*{20}{c}} {{\boldsymbol{w}_1}} \\ {{\boldsymbol{w}_2}} \\ \vdots \\ {{\boldsymbol{w}_N}} \end{array}} \right) \text{,} {\text{ }}{\boldsymbol{y}} =\left( {\begin{array}{*{20}{c}} {{{\boldsymbol{y}} _1}} \\ {{{\boldsymbol{y}} _2}} \\ \vdots \\ {{{\boldsymbol{y}} _N}} \end{array}} \right)$,$ {\boldsymbol{w}}_{i} $,$ {{\boldsymbol{y}}}_{i}\in {\boldsymbol{C}}^{6 {\text{×}} 1} $,$i=\mathrm{1 \text{,} 2} \text{,} \cdots N$,则
$$ \begin{aligned} {\boldsymbol{w}^{\text{T}}}\frac{{ {\text{∂}} {{{\boldsymbol{C}}}^{\text{T}}}}}{{ {\text{∂}} {p_{2i - 1}}}}{\boldsymbol{y}} = & [ {\begin{array}{*{20}{c}} {\boldsymbol{w}_1^{\text{T}}}&{\boldsymbol{w}_2^{\text{T}}}& \cdots &{\boldsymbol{w}_N^{\text{T}}} \end{array}} ] \left( {\begin{array}{*{20}{c}} 0& \cdots &{{\boldsymbol{E}_{i1}}}& \cdots &0 \\ 0& \cdots &{{\boldsymbol{E}_{i2}}}& \cdots &0 \\ \vdots &{}& \vdots &{}& \vdots \\ 0& \cdots &{{\boldsymbol{E}_{iN}}}& \cdots &0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\boldsymbol{y}}_1}} \\ {{{\boldsymbol{y}}_2}} \\ \vdots \\ {{{\boldsymbol{y}}_N}} \end{array}} \right) \\ {\text{ }} =& [ {\begin{array}{*{20}{c}} {\boldsymbol{w}_1^{\text{T}}}&{\boldsymbol{w}_2^{\text{T}}}& \cdots &{\boldsymbol{w}_N^{\text{T}}} \end{array}} ] \left( {\begin{array}{*{20}{c}} {{\boldsymbol{E}_{i1}}{{\boldsymbol{y}}_i}} \\ {{\boldsymbol{E}_{i2}}{{\boldsymbol{y}}_i}} \\ \vdots \\ {{\boldsymbol{E}_{iN}}{{\boldsymbol{y}}_i}} \end{array}} \right) = \sum\limits_{j = 1}^N {\boldsymbol{w}_j^{\text{T}}{\boldsymbol{E}_{ij}}{{\boldsymbol{y}}_i}} \text{,} \\ \end{aligned} $$ (29) $$ \begin{aligned} {\boldsymbol{w}^{\text{T}}}\frac{{ {\text{∂}} {{{\boldsymbol{C}}}^{\text{T}}}}}{{ {\text{∂}} {p_{2i}}}}{\boldsymbol{y}} =& [ {\begin{array}{*{20}{c}} {\boldsymbol{w}_1^{\text{T}}}&{\boldsymbol{w}_2^{\text{T}}}& \cdots &{\boldsymbol{w}_N^{\text{T}}} \end{array}} ] \left( {\begin{array}{*{20}{c}} 0& \cdots &{{\boldsymbol{F}_{i1}}}& \cdots &0 \\ 0& \cdots &{{\boldsymbol{F}_{i2}}}& \cdots &0 \\ \vdots &{}& \vdots &{}& \vdots \\ 0& \cdots &{{\boldsymbol{F}_{iN}}}& \cdots &0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\boldsymbol{y}}_1}} \\ {{{\boldsymbol{y}}_2}} \\ \vdots \\ {{{\boldsymbol{y}}_N}} \end{array}} \right) \\ {\text{ }} =& [ {\begin{array}{*{20}{c}} {\boldsymbol{w}_1^{\text{T}}}&{\boldsymbol{w}_2^{\text{T}}}& \cdots &{\boldsymbol{w}_N^{\text{T}}} \end{array}} ] \left( {\begin{array}{*{20}{c}} {{\boldsymbol{F}_{i1}}{{\boldsymbol{y}}_i}} \\ {{\boldsymbol{F}_{i2}}{{\boldsymbol{y}}_i}} \\ \vdots \\ {{\boldsymbol{F}_{iN}}{{\boldsymbol{y}}_i}} \end{array}} \right) = \sum\limits_{j = 1}^N {\boldsymbol{w}_j^{\text{T}}{\boldsymbol{F}_{ij}}{{\boldsymbol{y}}_i}} . \\ \end{aligned} $$ (30) 为了便于计算,根据式(27)—(30)可将阻抗矩阵对$ {v}_{\mathrm{P}} $的偏导数式(25)改写为如下形式
$$ \boldsymbol{E}{=}\left( {\begin{array}{*{20}{c}} {{\boldsymbol{E}_{11}}}&{{\boldsymbol{E}_{12}}}& \cdots &{{\boldsymbol{E}_{1N}}} \\ {{\boldsymbol{E}_{21}}}&{{\boldsymbol{E}_{22}}}& \cdots &{{\boldsymbol{E}_{{\text{2N}}}}} \\ \vdots & \vdots &{}& \vdots \\ {{\boldsymbol{E}_{N1}}}&{{\boldsymbol{E}_{N2}}}& \cdots &{{\boldsymbol{E}_{NN}}} \end{array}} \right) \text{,} $$ (31) 同理,阻抗矩阵对$ {v}_{\mathrm{S}} $的偏导数改写为
$$ \boldsymbol{F}=\left( {\begin{array}{*{20}{c}} {{\boldsymbol{F}_{11}}}&{{\boldsymbol{F}_{12}}}& \cdots &{{\boldsymbol{F}_{1N}}} \\ {{\boldsymbol{F}_{21}}}&{{\boldsymbol{F}_{22}}}& \cdots &{{\boldsymbol{F}_{{\text{2N}}}}} \\ \vdots & \vdots &{}& \vdots \\ {{\boldsymbol{F}_{N1}}}&{{\boldsymbol{F}_{N2}}}& \cdots &{{\boldsymbol{F}_{NN}}} \end{array}} \right) .$$ (32) 按照式(13)$ \boldsymbol{C} $的稀疏结构,子块矩阵${\boldsymbol{C}}_{ij}= {\text{∂}} {\boldsymbol{C}}_{ij}/{ {\text{∂}} {q}_{2i-1}}$和${\boldsymbol{C}}_{ij}={ {\text{∂}} {\boldsymbol{C}}_{ij}}/{ {\text{∂}} {q}_{2i}} ( i=\mathrm{1\text{,} 2} \text{,} \cdots \text{,} N ) $大部分为零矩阵,非零取值为式(13)中的子块${\boldsymbol{C}}_{i}^{ ( j ) }$分别对$ {v}_{\mathrm{P}} $和$ {v}_{\mathrm{S}} $的偏导数.事实上,这两个矩阵是通过阻抗矩阵$ \boldsymbol{C} $分别对$ {v}_{\mathrm{P}} $与$ {v}_{\mathrm{S}} $求偏导数获得,由于矩阵大量元素值为零,实际计算中所需的计算代价均非常小。通过观察式(21)的表达式,进一步计算过程为
$$ \begin{aligned} {\boldsymbol{w}^{\text{T}}}{\boldsymbol{E}^{\text{T}}} =& [ {\begin{array}{*{20}{c}} {\boldsymbol{w}_1^{\text{T}}}&{\boldsymbol{w}_2^{\text{T}}}& \cdots &{\boldsymbol{w}_N^{\text{T}}} \end{array}} ] \left( {\begin{array}{*{20}{c}} {{\boldsymbol{E}_{11}}}&{{\boldsymbol{E}_{21}}}& \cdots &{{\boldsymbol{E}_{N1}}} \\ {{\boldsymbol{E}_{12}}}&{{\boldsymbol{E}_{22}}}& \cdots &{{\boldsymbol{E}_{N2}}} \\ \vdots & \vdots &{}& \vdots \\ {{\boldsymbol{E}_{1N}}}&{{\boldsymbol{E}_{2N}}}& \cdots &{{\boldsymbol{E}_{NN}}} \end{array}} \right) \\ \\ {\text{ }} =& \left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{E}_{1i}}} }&{\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{E}_{2i}}} }& \cdots &{\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{E}_{Ni}}} } \end{array}} \right]\text{,} \\ \end{aligned} $$ (33) $$ \begin{aligned} {\boldsymbol{w}^{\text{T}}}{\boldsymbol{F}^{\text{T}}} =& \left[ {\begin{array}{*{20}{c}} {\boldsymbol{w}_1^{\text{T}}}&{\boldsymbol{w}_2^{\text{T}}}& \cdots &{\boldsymbol{w}_N^{\text{T}}} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{\boldsymbol{F}_{11}}}&{{\boldsymbol{F}_{21}}}& \cdots &{{\boldsymbol{F}_{N1}}} \\ {{\boldsymbol{F}_{12}}}&{{\boldsymbol{F}_{22}}}& \cdots &{{\boldsymbol{F}_{N2}}} \\ \vdots & \vdots &{}& \vdots \\ {{\boldsymbol{F}_{1N}}}&{{\boldsymbol{F}_{2N}}}& \cdots &{{\boldsymbol{F}_{NN}}} \end{array}} \right) \\ \\ {\text{ }} = & \left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{F}_{1i}}} }&{\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{F}_{2i}}} }& \cdots &{\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{F}_{Ni}}} } \end{array}} \right] \text{,} \\ \end{aligned} $$ (34) 所以
$$ { ( {{\boldsymbol{w}^{\text{T}}}{\boldsymbol{E}^{\text{T}}}} ) ^{\text{T}}} \cdot \boldsymbol{\boldsymbol{\boldsymbol{y}}}= \left( {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{E}_{1i}}{{\boldsymbol{y}}_1}} } \\ {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{E}_{2i}}} {{\boldsymbol{y}}_2}} \\ \vdots \\ {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{\boldsymbol{E}_{Ni}}} {{\boldsymbol{y}}_N}} \end{array}} \right){\text{,}}{ ( {{\boldsymbol{w}^{\text{T}}}{{\boldsymbol{F}}^{\text{T}}}} ) ^{\text{T}}} \cdot {{\boldsymbol{y}}}= \left( {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{{\boldsymbol{F}}_{i1}}{{\boldsymbol{y}}_1}} } \\ {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{{\boldsymbol{F}}_{i1}}} {{\boldsymbol{y}}_2}} \\ \vdots \\ {\displaystyle\sum\limits_{i = 1}^N {\boldsymbol{w}_i^{\text{T}}{{\boldsymbol{F}}_{Ni}}} {{\boldsymbol{y}}_N}} \end{array}} \right) \text{,} $$ (35) 代入到${\nabla _{ {\boldsymbol{p}}}}{\boldsymbol{E}} =\left(\cdots \text{,} {{\boldsymbol{w}^{\text{T}}}\dfrac{{ {\text{∂}} {\boldsymbol{C}^{\text{T}}}}}{{ {\text{∂}} {p_{2i - 1}}}}{{\boldsymbol{y}}} } \text{,} {{\boldsymbol{w}^{\text{T}}}\dfrac{{ {\text{∂}} {\boldsymbol{C}^{\text{T}}}}}{{ {\text{∂}} {p_{2i}}}}{{\boldsymbol{y}}} }\text{,} \cdots\right)^{{\mathrm{T}}}$中,把式(35)中的两式交叉组合即可求得梯度向量。
经过上述过程求出反演目标函数梯度值后,根据共轭梯度法原理,搜索方向也可随之确定。在反演迭代过程中,另一个需要确定的关键参数是先搜索步长$ {\alpha }_{k} $。为保证良好的迭代效果且不至于消耗过多的正演计算次数,可采用二次抛物线拟合策略(Tape et al,2007;Lang et al,2020)。
3. 数值实验
为验证所研究频率域弹性波全波形反演方法的可行性,本节分别选取异常块模型、双层介质模型和Marmousi模型进行数值实验。反演迭代过程采取逐频反演策略(Bunks et al,1995):上一个频率的迭代结果作为下一频率的初始模型,即先利用低频数据勾勒出模型的大致结构,再利用高频反演细化内部结构。震源项统一选取雷克子波施加在垂直方向,其频率域表达式为
$$ F ( f ) = \frac{{\sqrt 2 A}}{{\text{π} {f_0}}} {\left(\frac{f}{{{f_0}}}\right)^2}{{\mathrm{e}}^{ - {{\left(\tfrac{f}{{{f_0}}}\right)}^2}}} \text{,} $$ (36) 式中,$ A $为振幅,$ {f}_{0} $为主频,$ f $为频率。在本文的所有数值实验中,振幅和主频统一设置为1.0×105和10 Hz,PML层数均设置为10层。三次实验的部分参数设置如表1所示。
表 1 三种介质模型的反演参数设置Table 1. Inversion parameter settings of three media models正演网格点数(nx×nz) 空间步长h/km 计算区域/km2 介质密度ρ/(kg·m−3) 异常块模型 101×81 0.025 1.75×2.25 2.63 双层介质模型 101×81 0.025 1.75×2.25 2.63 Marmousi模型 233×78 0.015 5.775×1.9 2.63 3.1 异常块模型
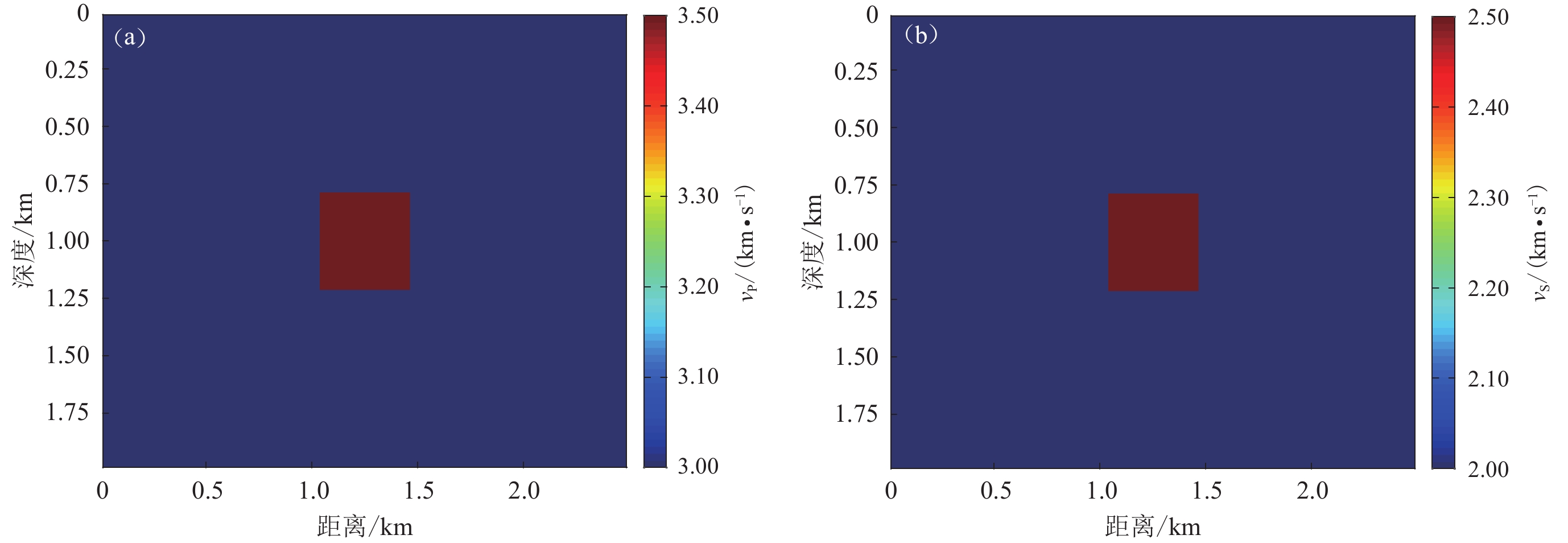
反演的真实模型如图2所示:图2a为P波速度模型,背景速度为3 km/s,中间是边长为0.4 km的矩形异常块,其$ {v}_{\mathrm{P}} $取值为3.5 km/s;图2b为S波速度模型,背景速度为2 km/s,异常块区域的速度为2.5 km/s。初始模型设置为真实模型的背景速度,即$ {v}_{\mathrm{P}}= $3 km/s,$ {v}_{\mathrm{S}}= $2 km/s.
接收器和震源的放置方式如图3所示。根据上文所介绍的频率域全波形反演原理可知,增加接收器数目不会引起计算代价的增加,而震源的数目过多会增大计算量(尽管这一因素可通过震源间并行计算得到缓解)。因此可选择适当的震源数量来保证反演成像的准确性和清晰度。在整个反演阶段,接收器(图中蓝点)在初始模型PML边界逐个排列,上下分别安置98个,共计196个;震源(红色稀疏点)在接收器靠内一层排列,共计2×27=54个。
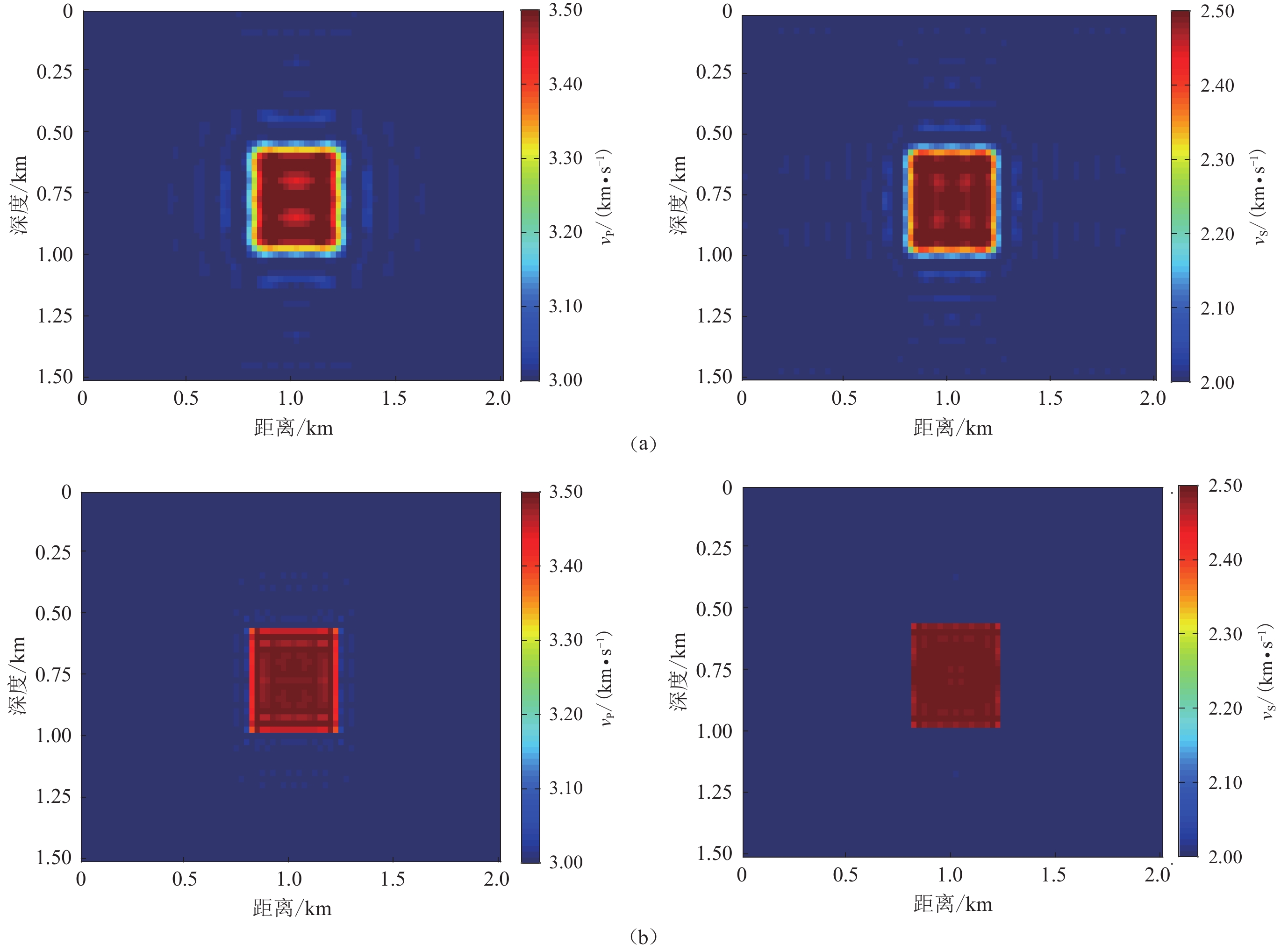
异常块反演共采用20个频率,频率取值区间为1—30 Hz,间隔为1.5 Hz。第1—10个频率最大迭代步数为120步,剩余频率的最大迭代步数为100步。低频时$ f $=10.5 Hz的反演成像如图4a所示,可以看出反演模型的大致轮廓开始显现并接近真实模型,但异常块和背景区域的界面还较模糊,此时反演误差较大。为进一步提高成像效果,迭代过程继续向高频阶段进行,当迭代至$ f $=30 Hz时,相应的反演成像如图4b所示,相比于图4a,异常块和背景的界限逐步趋于清晰,对应的反演结果基本接近真实模型,成像效果较好。
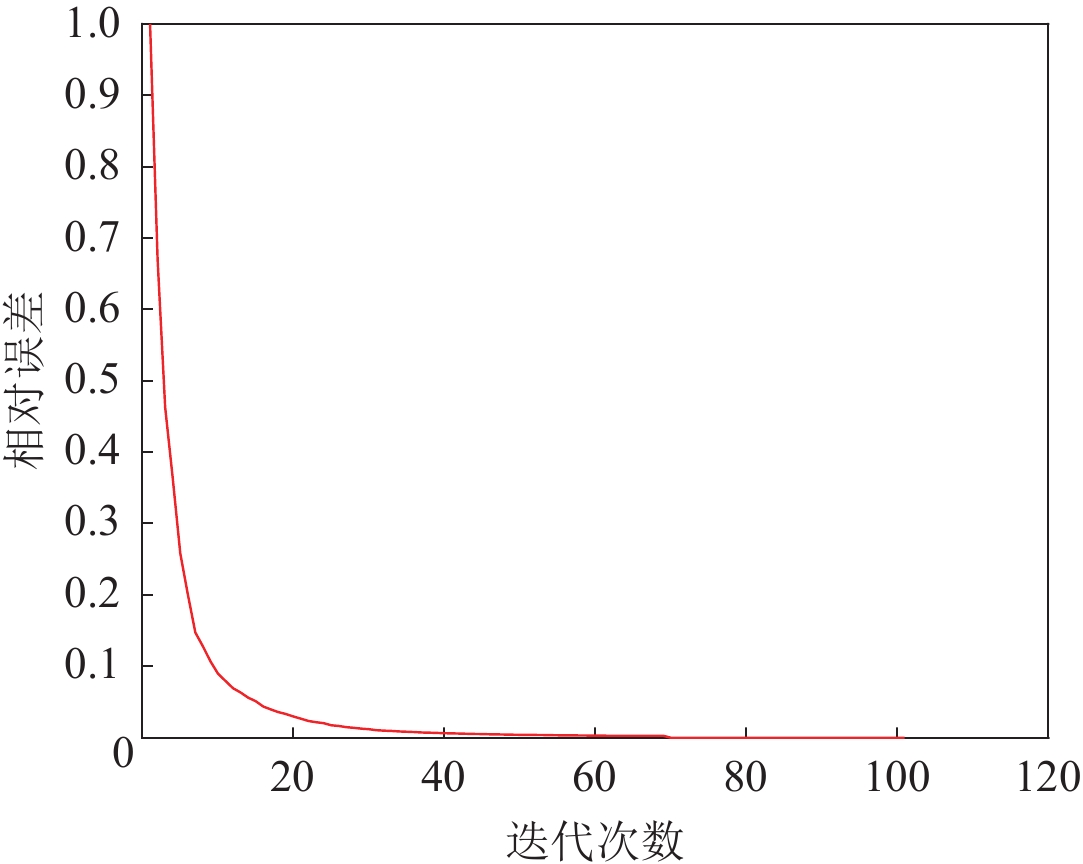
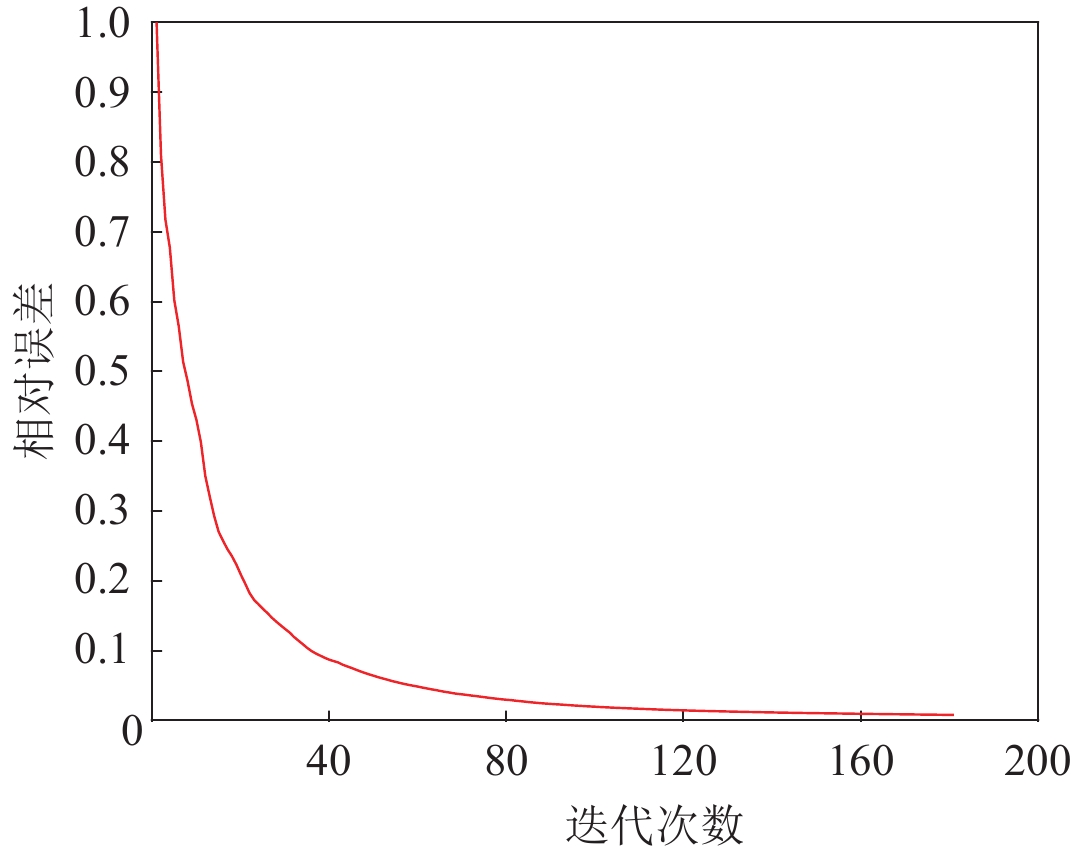
当挑选某一频率考察反演误差下降情况时,频率取值$ f $=9 Hz所对应的反演误差曲线如图5所示:相对误差随着迭代步数的增加总体呈下降趋势,并逐步接近于零;在迭代次数小于20次时,相对误差下降较快,然后逐步平稳并最终下降至0.1 (一个量级)以内,这与大多数成功反演情形所表现出的趋势类似(张文生等,2015)。
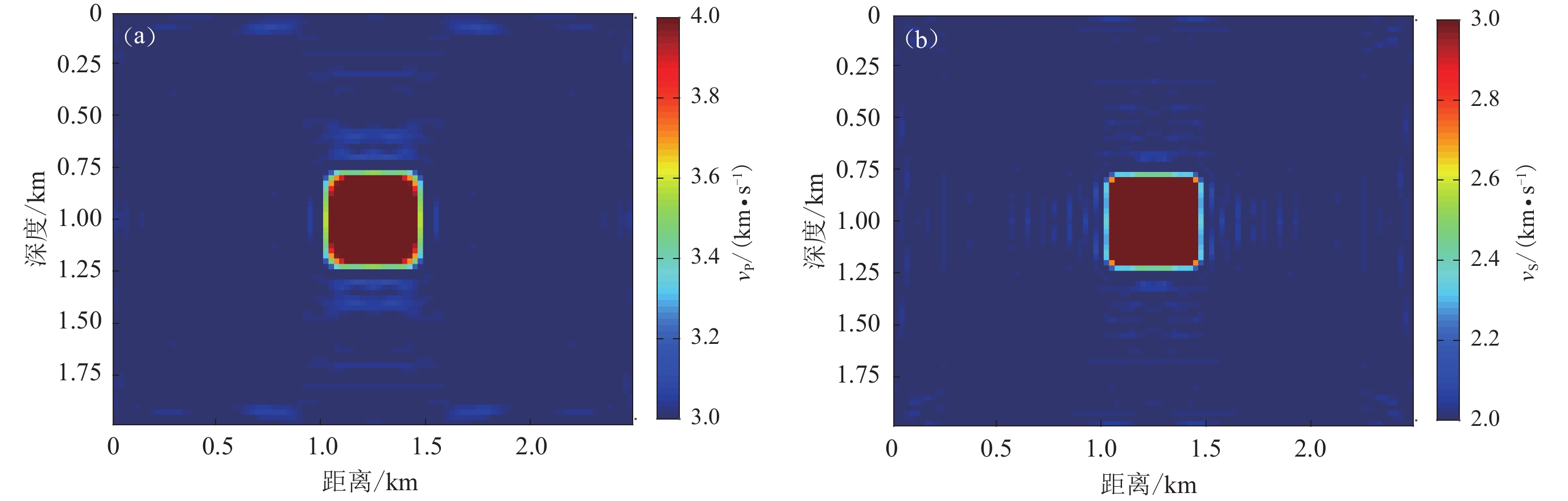
众所周知,当异常块与背景速度差异较大时,反演的难度也随之上升。为了进一步测试NAD方法弹性波场模拟的有效性,本文将P波速度调整至4 km/s,S波速度调整至3 km/s,背景速度和震源接收器的放置位置均不变。此时的成像结果如图6所示,可以观察到异常块清晰可见,整体反演效果明显。
3.2 双层介质模型
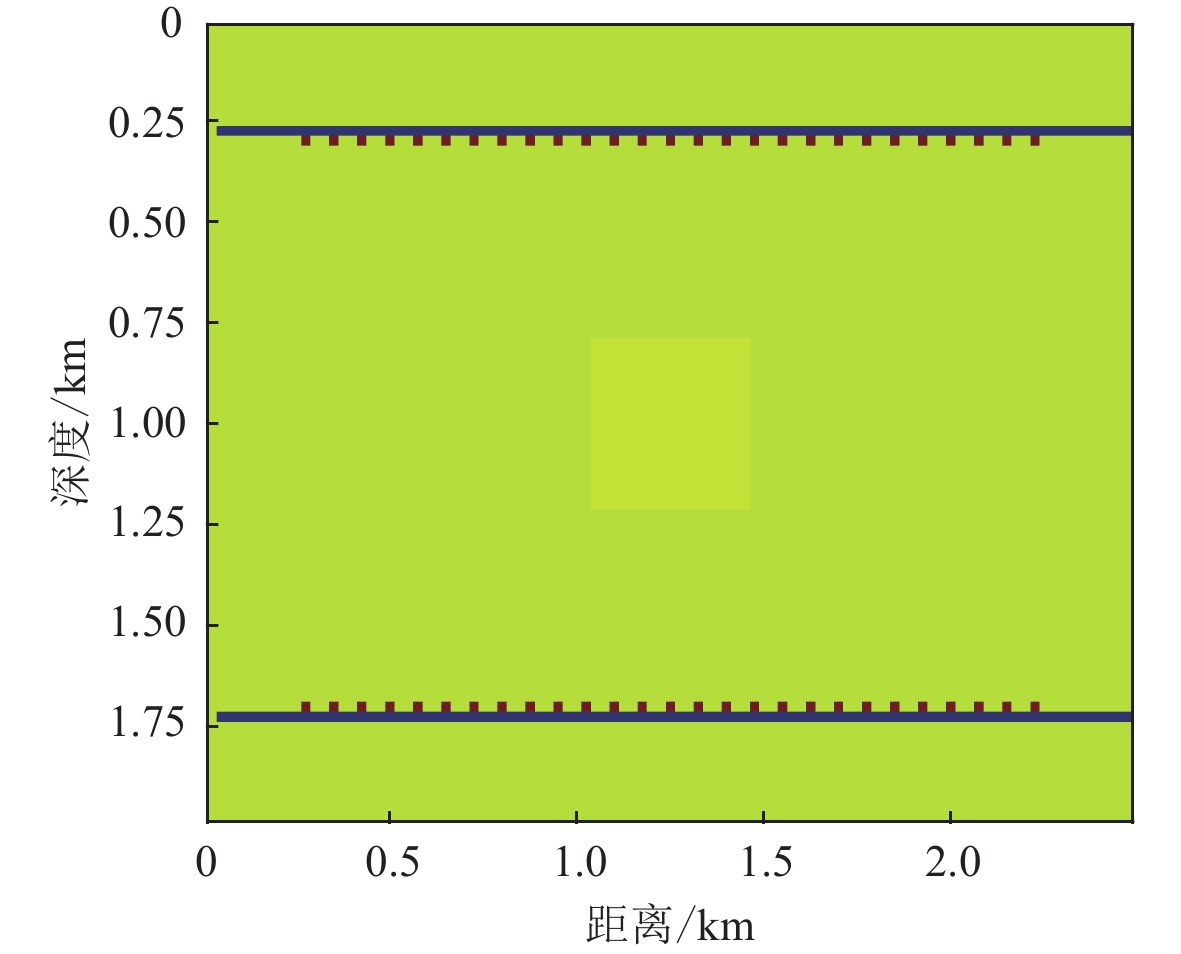
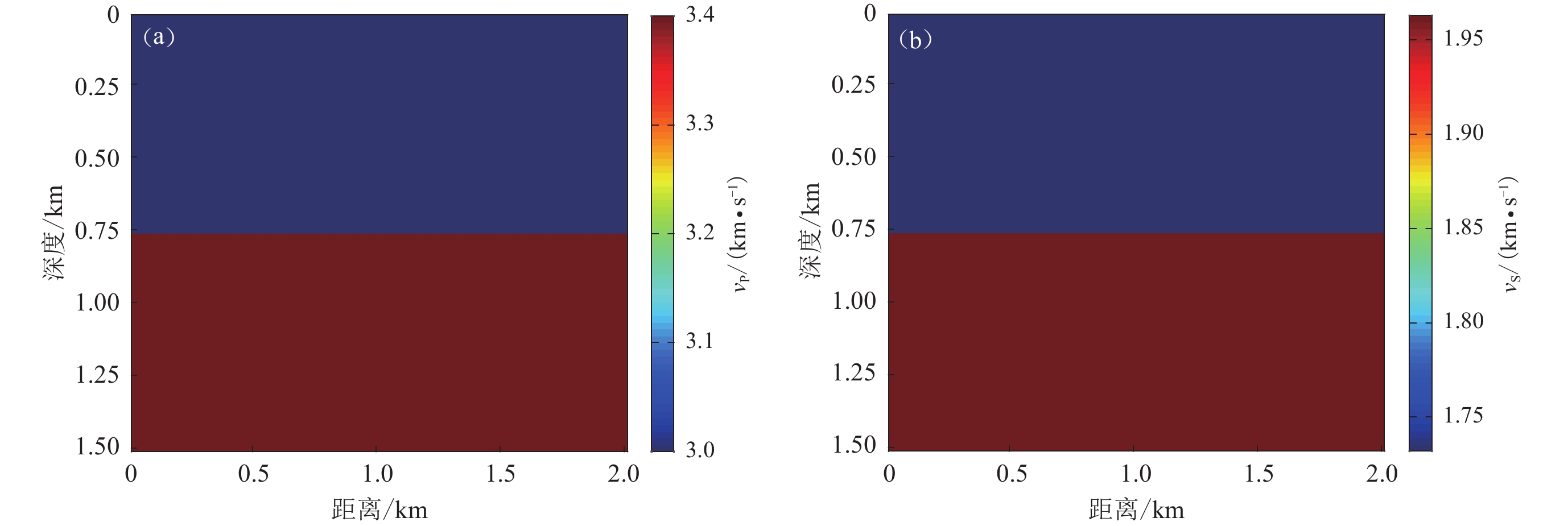
双层介质反演的真实模型如图7所示:图7a为P波速度的双层介质模型,其中上层$ {v}_{\mathrm{P}} $为3 km/s,下层$ {v}_{\mathrm{P}} $为3.4 km/s;图7b为S波速度模型,其中上层$ {v}_{\mathrm{S}} $为1.732 km/s,下层$ {v}_{\mathrm{S}} $为1.963 km/s,反演初始模型均选取真实模型的上层速度值。
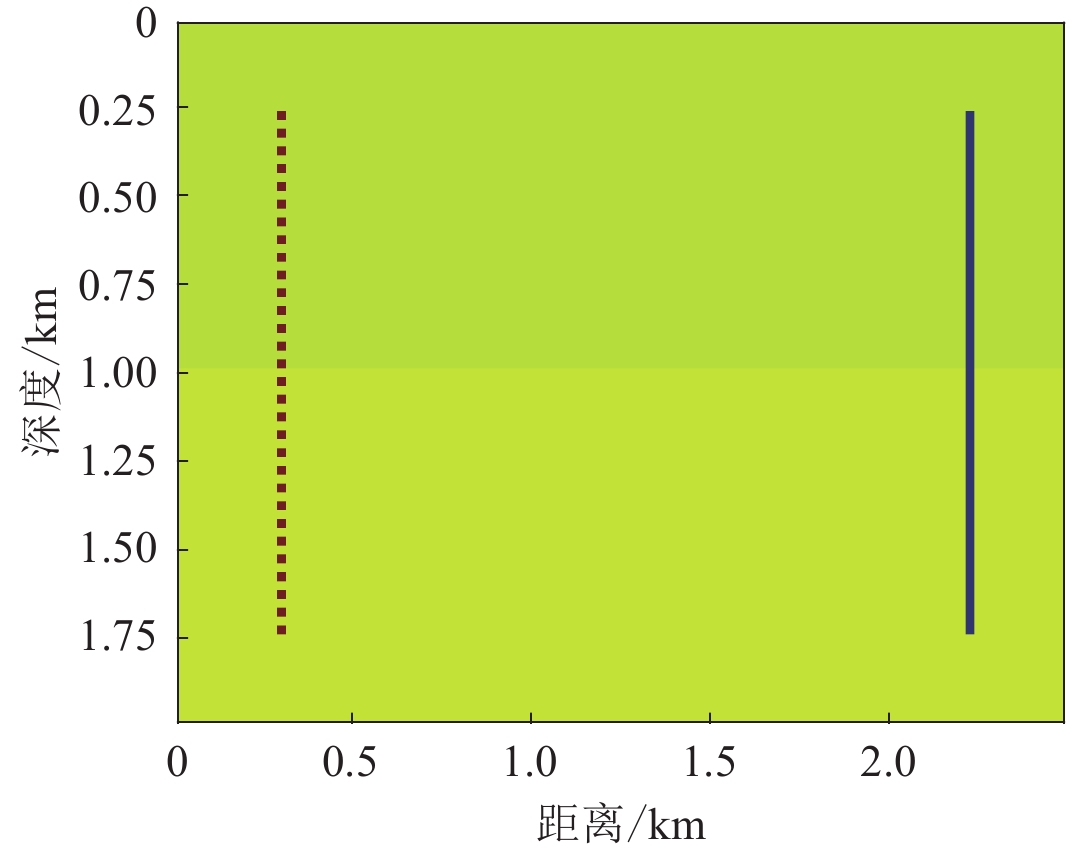
接收器和震源采用井间数据(cross-hole)方式放置(Wang,Rao,2006),如图8所示,震源(红色离散点)在反演区域的左右两侧间隔放置,共计40个,接收器(蓝色点)左右放置,不间隔,共计240个。
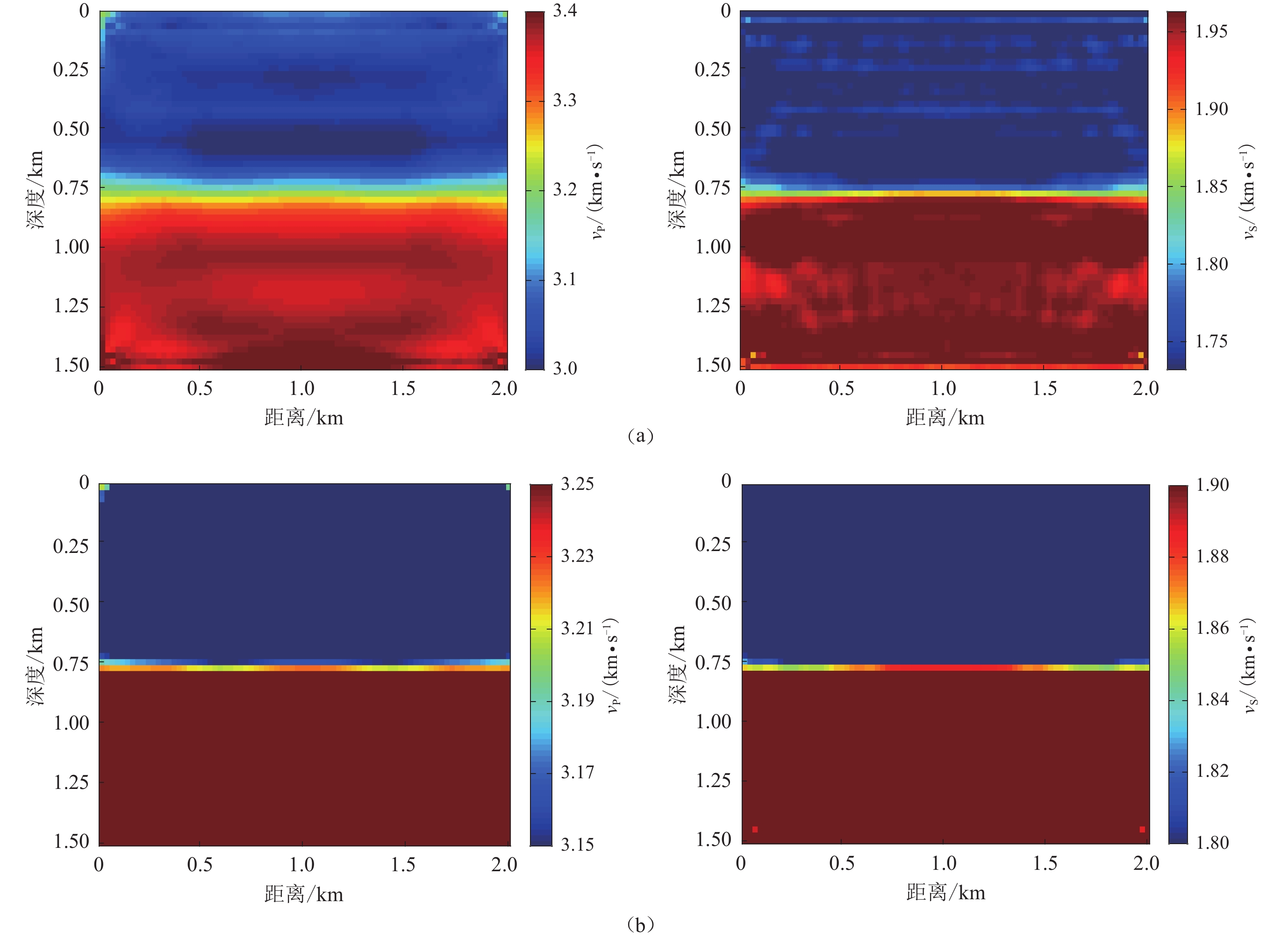
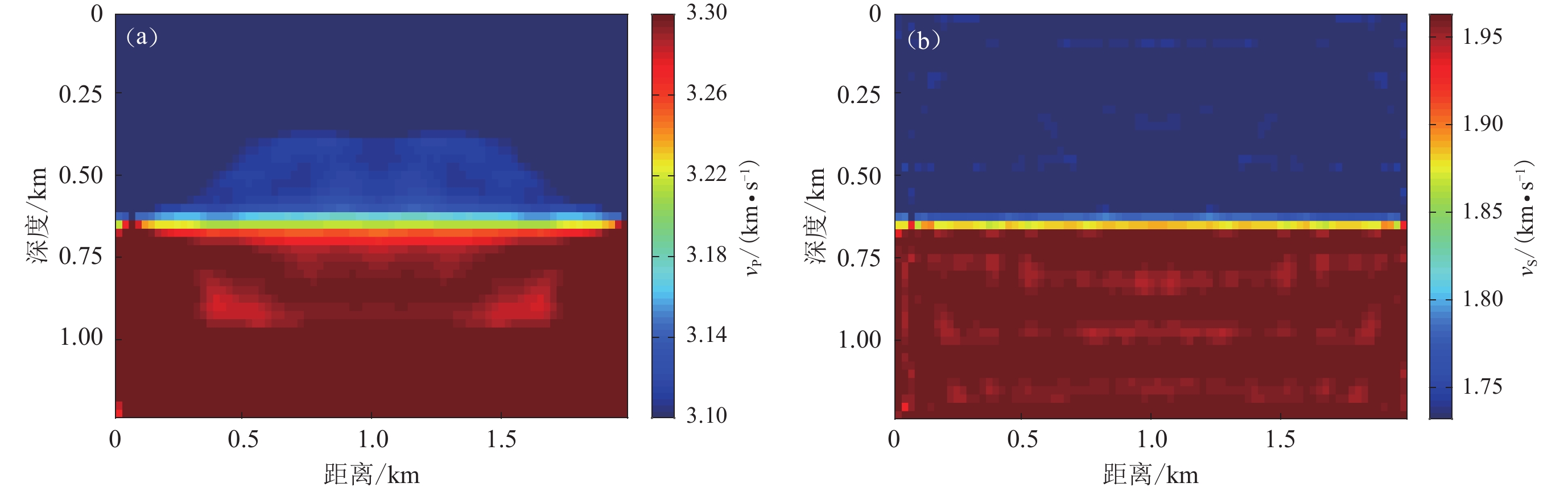
双层介质反演共采用30个频率,频率取值区间为1—30 Hz,间隔为1 Hz。每个频率最大迭代步数为130步。第一阶段迭代至$ f $=10 Hz的反演模型如图9a所示,可以看出整体的双层结构较为准确,但上下层的分界面比较模糊,分辨率较低。当迭代至30 Hz时所对应的反演结果如图9b所示,相较于图9a,上下层的分界面趋于清晰,图9b对模型的细节刻画更加准确,反演结果与真实模型基本相似,精度较高。
同样地,提取频率取值为2 Hz时双层介质模型反演的误差曲线如图10所示(实际上,其它频率迭代情况也基本类似),当迭代步数在40以内时,相对误差下降速度较快,随后相对误差下降速度变慢,逐步趋于平缓,并且接近于0。
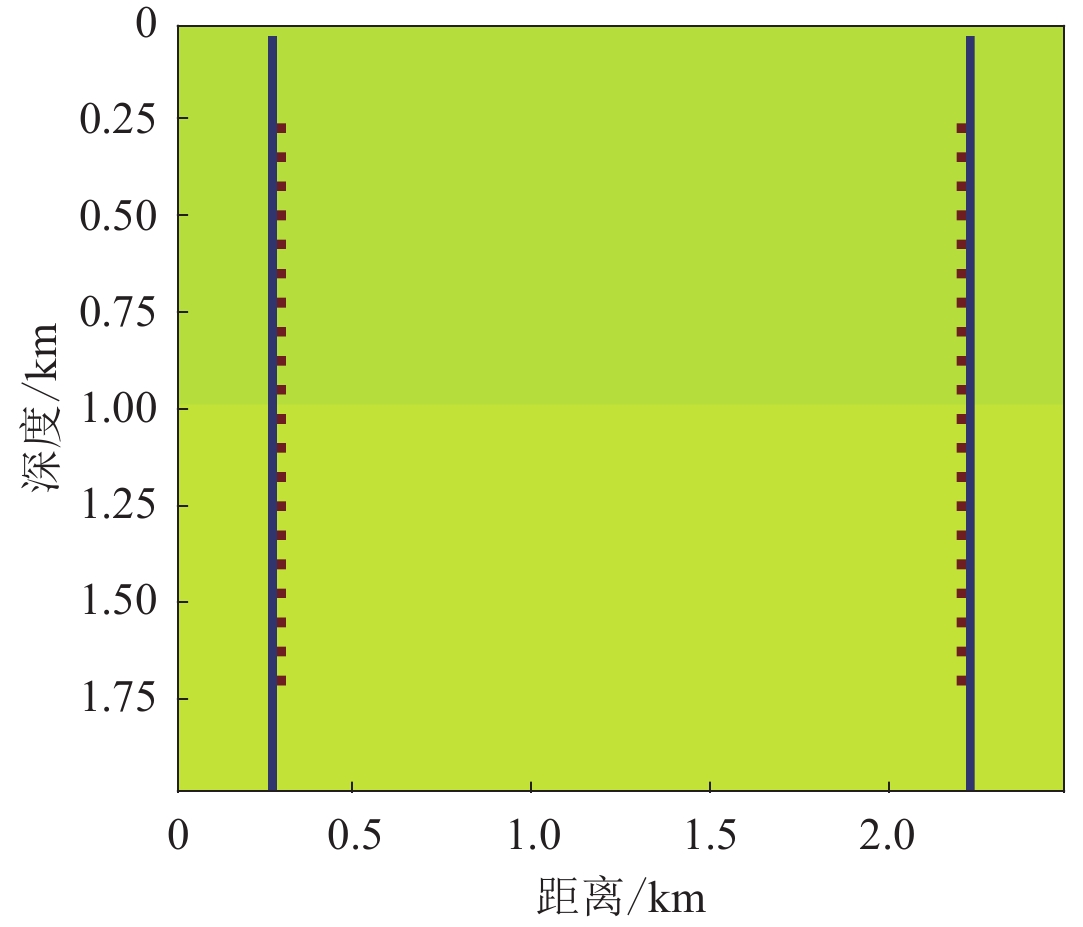
接下来探索只浅部接收的方式生成合成数据时的反演情况,震源接收器的放置如图11所示,接收器放置于右侧,共计59个,震源放置于左侧,共计30个,其它参数设置均不变。最终成像效果如图12所示,可以看到S波上下层界面依旧清晰,P波界面较为模糊。因为本文反演实验主要用到直达波震相,所以其整体反演效果略逊色于图9b深浅两侧接收数据时的成像。
3.3 Marmousi模型
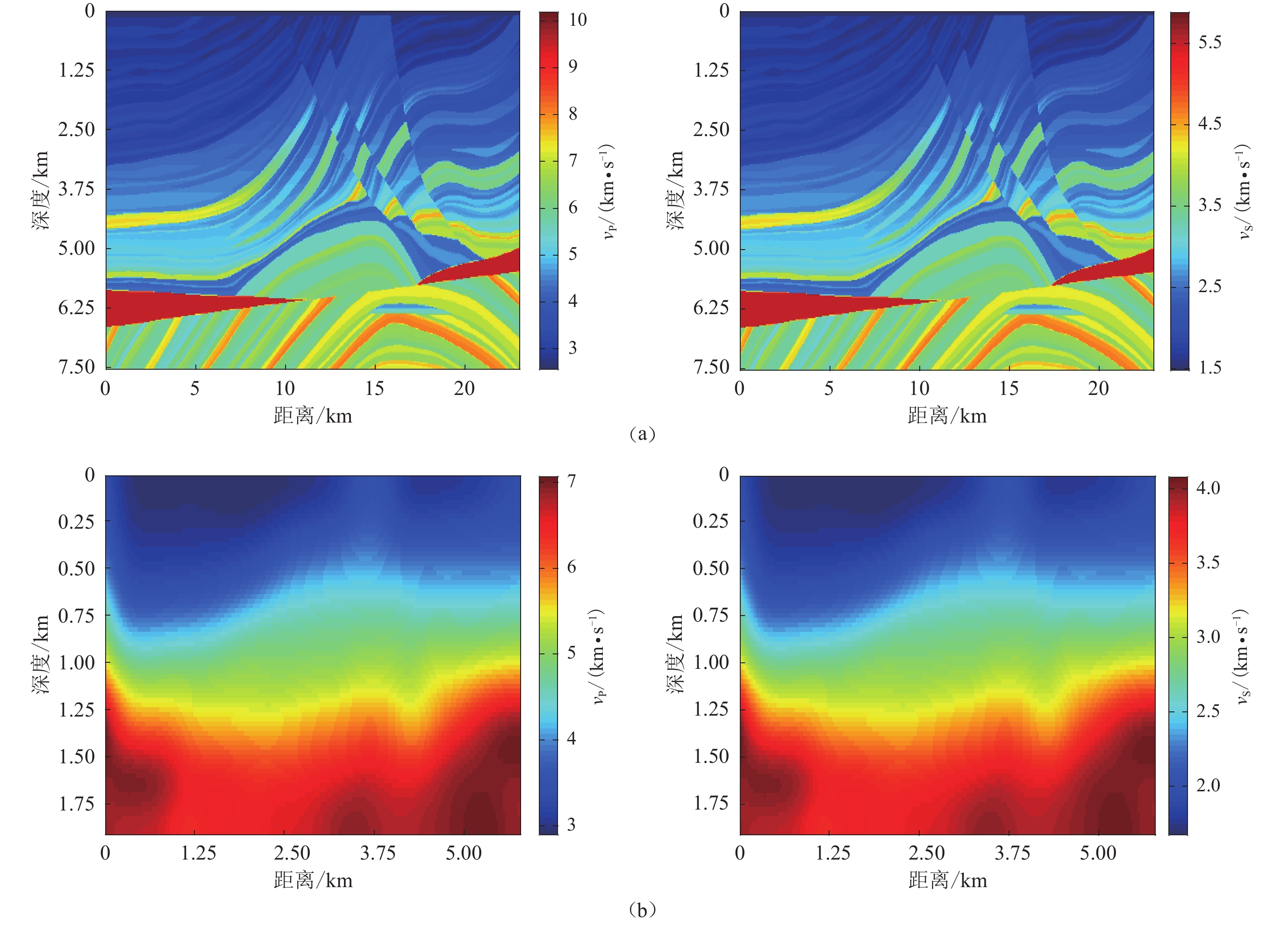
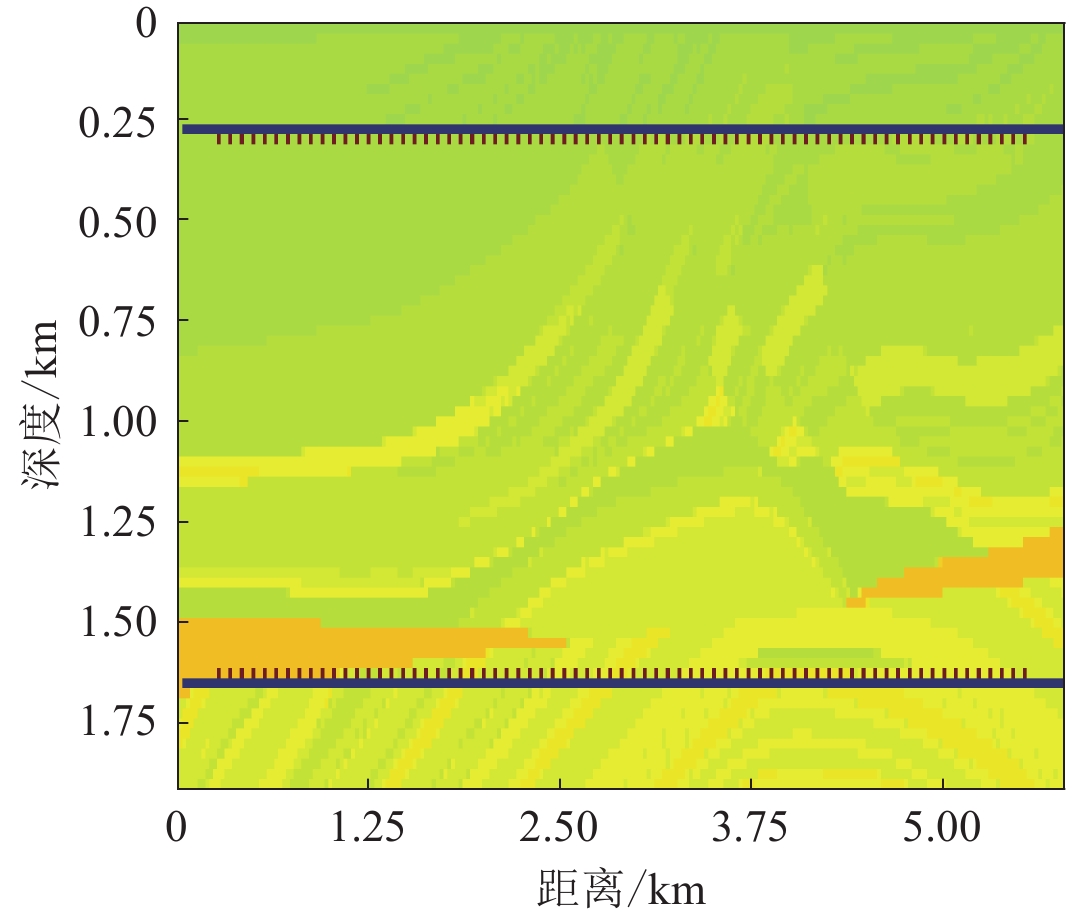
Marmousi真实模型如图13a所示,P波和S波满足一定的比例关系,即$ {v}_{\mathrm{P}}=\sqrt{3}{v}_{\mathrm{S}} $ (齐诚等,2006),S波速度变化范围为1.5—5.5 km/s (Youn,Zhou,2001)。图13b显示的初始模型形态是真实模型经过高斯平滑化得到的,可看到只具有大致的层状结构。
接收器和震源的放置方式如图14所示,为获得高分辨率成像结果,震源(红色离散点)分上下两行且只间隔一个节点放置,各安置71个,共计142个,接收器(蓝色点)逐个放置,共计2×230=460个。
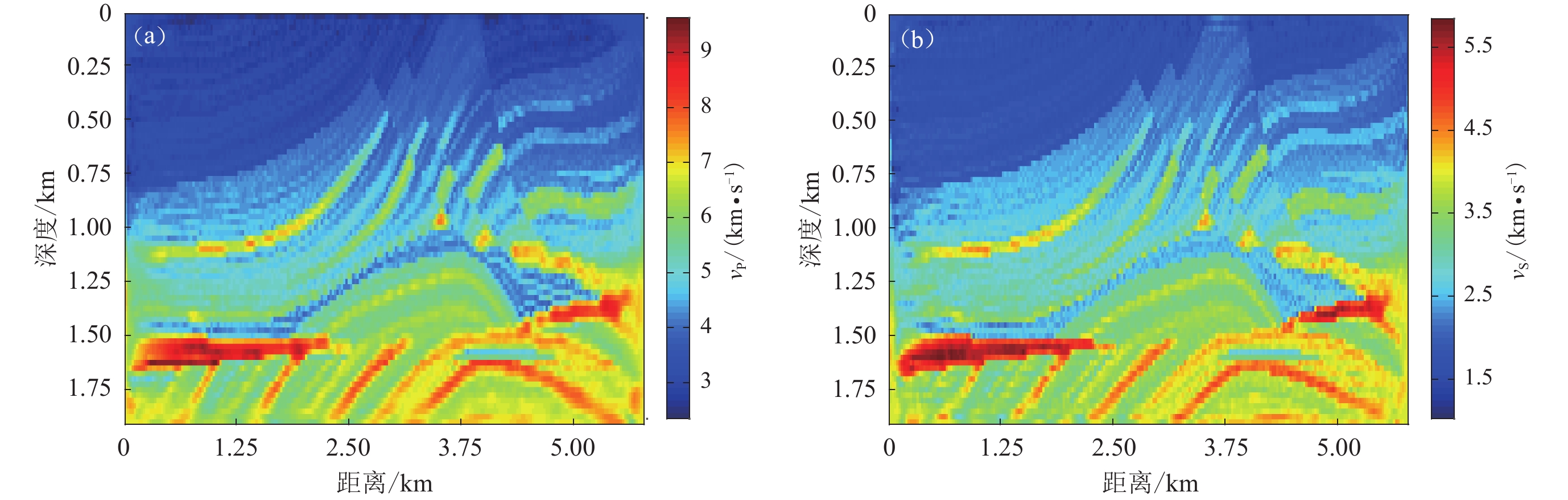
迭代过程选取1—30 Hz范围内的频率值,均分为20个频率,间隔为1.5 Hz。在频率取值1—20 Hz内的最大迭代步数为150步,20—30 Hz内的最大迭代步数为120步。第一阶段反演至$ f $=15 Hz的反演成像如图15a所示,可以看出整体的结构轮廓与真实模型大体一致,但是中间层的细节结构清晰度较差,不易区分,深层的高速体描绘刻画不够理想。迭代至第二阶段$ f $=30 Hz的反演成像如图15b所示:与图13b相比,细节刻画更加准确,滑脱背斜结构显现更加清晰,深层高速体呈现效果较好,反演结果与真实模型基本一致。整体迭代过程再一次诠释了这一规律:低频时勾勒出了大体轮廓,高频反演则反映更多细节结构。
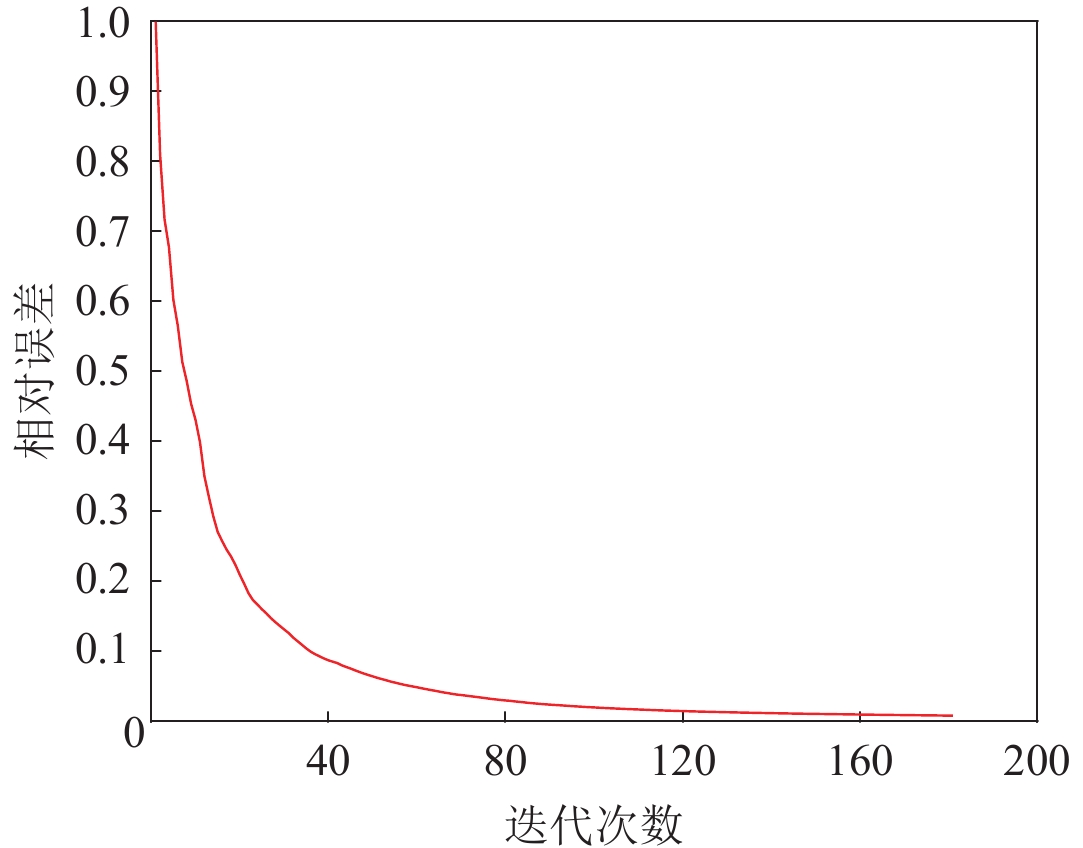
Marmousi模型反演实验中,在频率取值为4.5 Hz时的误差曲线如图16所示,整体的趋势与前两个模型很类似:先快速下降,后平缓接近于零。
为了进一步验证近似解析离散化方法的有效性,本文对Marmousi模型的观测数据加入40%的高斯白噪声(Pyun et al,2009)后进行反演。其它实验参数设置均不变,最终成像结果如图17所示,可以观察到滑脱背斜结构显现清晰,深层高速体呈现效果较好,反演结果比较接近真实模型,分辨率较高。
4. 讨论与结论
本文在频率域弹性波方程NAD正演模拟的基础上,进一步构造相应的全波形反演方法。首先通过NAD算子离散频率域弹性波方程形成大型稀疏线性方程组;然后充分利用相应阻抗矩阵的稀疏分块结构,研究如何花费较小计算代价得到阻抗矩阵对模型参数向量的导数信息与反演目标函数梯度的计算方法,进而建立基于NAD算子的频率域弹性波反演框架;最后,通过数值实验分别对异常块模型、双层介质模型和Marmousi模型进行反演计算。在这三种实验的绝大多数频率迭代过程中,通过反演误差趋势图可发现相对误差均下降一个量级(10%以内),最终也得到了准确可靠的反演结果,从而验证了所提出频率域弹性波反演方法的有效性。
数值频散是由波动方程数值离散引起的非物理现象。减少数值频散的一种有效方法是加密网格,但此方法会带来计算成本的显著增加。由于NAD方法相较于传统的有限差分方法和交错网格方法可以更加有效地压制数值频散并且具有较高的稳定性,所以NAD的总CPU时间较短,在大规模地震图计算中效率更高,此方法在弹性波反演中具有一定的优势。全波形反演作为一种高精度成像方法,目前还有两个难点需要进一步解决:第一,正演过程中离散弹性波方程会得到大型稀疏线性方程组,如何高效求解该方程组是全波形反演面临的难题;第二,全波形反演流程主要用到了直达波震相,对于反射波的利用相对较少。对于以上两个问题,作者今后将构造更加高效的求解线性方程组的方法,同时将进一步研究利用反射波震相的全波形反演算法。
-
表 1 三种介质模型的反演参数设置
Table 1 Inversion parameter settings of three media models
正演网格点数(nx×nz) 空间步长h/km 计算区域/km2 介质密度ρ/(kg·m−3) 异常块模型 101×81 0.025 1.75×2.25 2.63 双层介质模型 101×81 0.025 1.75×2.25 2.63 Marmousi模型 233×78 0.015 5.775×1.9 2.63 -
卞爱飞,於文辉,周华伟. 2010. 频率域全波形反演方法研究进展[J]. 地球物理学进展,25(3):982–993. doi: 10.3969/j.issn.1004-2903.2010.03.037 Bian A F,Yu W H,Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics,25(3):982–993 (in Chinese).
黄少华,任志明,李振春,谷丙洛,李红梅. 2019. 纵横波分离的多震源弹性波全波形反演[J]. 石油地球物理勘探,54(5):1084–1093. Huang S H,Ren Z M,Li Z C,Gu B L,Li H M. 2019. Multi-source elastic full waveform inversion based on P-wave and S-wave separation[J]. Oil Geophysical Prospecting,54(5):1084–1093 (in Chinese).
郎超,仇楚钧,刘少林,申文豪,李小凡,徐锡伟. 2021. 求解弹性波动方程的频率域近似解析离散化波场模拟方法[J]. 地球物理学报,64(8):2838–2857. doi: 10.6038/cjg2021O0332 Lang C,Qiu C J,Liu S L,Shen W H,Li X F,Xu X W. 2021. A nearly discrete analytic method of wave-field simulation for elastic wave equations in the frequency domain[J]. Chinese Journal of Geophysics,64(8):2838–2857 (in Chinese).
郎超,刘少林,杨晓婷,徐锡伟. 2022. 基于改进NAD方法的频率域声波逆时偏移[J]. 地球物理学报,65(3):1071–1085. doi: 10.6038/cjg2022P0501 Lang C,Liu S L,Yang X T,Xu X W. 2022. Frequency-domain acoustic reverse time migration based on improved NAD method[J]. Chinese Journal of Geophysics,65(3):1071–1085 (in Chinese).
刘璐,刘洪,刘红伟. 2013. 优化15点频率-空间域有限差分正演模拟[J]. 地球物理学报,56(2):644–652. Liu L,Liu H,Liu H W. 2013. Optimal 15-point finite difference forward modeling in frequency-space domain[J]. Chinese Journal of Geophysics,56(2):644–652 (in Chinese).
龙锋,闻学泽,徐锡伟. 2006. 华北地区地震活断层的震级-破裂长度、破裂面积的经验关系[J]. 地震地质,28(4):511–535. doi: 10.3969/j.issn.0253-4967.2006.04.001 Long F,Wen X Z,Xu X W. 2006. Empirical relationships between magnitude and rupture length,and rupture area,for seismogenic active faults in North China[J]. Seismology and Geology,28(4):511–535 (in Chinese).
齐诚,赵大鹏,陈颙,陈棋福,王宝善. 2006. 首都圈地区地壳P波和S波三维速度结构及其与大地震的关系[J]. 地球物理学报,49(3):805–815. doi: 10.3321/j.issn:0001-5733.2006.03.024 Qi C,Zhao D P,Chen Y,Chen Q F,Wang B S. 2006. 3-D P and S wave velocity structures and their relationship to strong earthquakes in the Chinese Capital region[J]. Chinese Journal of Geophysics,49(3):805–815 (in Chinese).
任志明. 2016. 声波和弹性波波动方程有限差分正反演方法研究[D]. 北京:中国石油大学(北京):2−3. Ren Z M. 2016. Research on Finite-Difference Modeling and Inversion Methods Based on Acoustic and Elastic Wave Equations[D]. Beijing:China University of Petroleum (Beijing):2−3 (in Chinese).
宋海斌,张关泉. 1998. 层状介质弹性参数反演问题研究综述[J]. 地球物理学进展,13(4):67–78. Song H B,Zhang G Q. 1998. A summary of inversion problem research on elastic parameters of stratified media[J]. Progress in Geophysics,13(4):67–78 (in Chinese).
孙成禹,李振春. 2011. 地震波动力学基础[M]. 北京:石油工业出版社:1−2. Sun C Y,Li Z C. 2011. Seismic Wave Dynamics Basis[M]. Beijing:Petroleum Industry Press:1−2 (in Chinese).
童平. 2012. 地震层析成像方法及其应用研究[D]. 北京:清华大学:187−189. Tong P. 2012. Seismic Tomography Methods and Their Applications[D]. Beijing:Tsinghua University:187−189 (in Chinese).
王椿镛,段永红,吴庆举,王志铄. 2016. 华北强烈地震深部构造环境的探测与研究[J]. 地震学报,38(4):511–549. Wang C Y,Duan Y H,Wu Q J,Wang Z S. 2016. Exploration on the deep tectonic environment of strong earthquakes in North China and relevant research findings[J]. Acta Seismologica Sinica,38(4):511–549 (in Chinese).
殷文,印兴耀,吴国忱,梁锴. 2006. 高精度频率域弹性波方程有限差分方法及波场模拟[J]. 地球物理学报,49(2):561–568. Yin W,Yin X Y,Wu G C,Liang K. 2006. The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation[J]. Chinese Journal of Geophysics,49(2):561–568 (in Chinese).
张霖斌,姚振兴. 2000. 层状介质的声波波动方程反演[J]. 地球物理学进展,15(2):22–29. Zhang L B,Yao Z X. 2000. Wavform inversion of acoustic data in layered media[J]. Progress in Geophysics,15(2):22–29 (in Chinese).
张文生,罗嘉,滕吉文. 2015. 频率多尺度全波形速度反演[J]. 地球物理学报,58(1):216–228. doi: 10.6038/cjg20150119 Zhang W S,Luo J,Teng J W. 2015. Frequency multiscale full-waveform velocity inversion[J]. Chinese Journal of Geophysics,58(1):216–228 (in Chinese).
张文生,张丽娜. 2020. 基于有限元方法的频率域弹性波全波形反演[J]. 数值计算与计算机应用,41(4):315–336. Zhang W S,Zhang L N. 2020. Elastic wave full-waveform inversion based on the finite-element method in the frequency domain[J]. Journal on Numerical Methods and Computer Applications,41(4):315–336 (in Chinese).
祝贺君,刘沁雅,杨继东. 2023. 地震学全波形反演进展[J]. 地球与行星物理论评(中英文),54(3):287–317. Zhu H J,Liu Q Y,Yang J D. 2023. Recent progress on full waveform inversion[J]. Reviews of Geophysics and Planetary Phy sics,54(3):287–317 (in Chinese).
Ben-Hadj-Ali H,Operto S,Virieux J. 2011. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J]. Geophysics,76(4):R109–R124. doi: 10.1190/1.3581357
Bornstein G,Biescas B,Sallarès V,Mojica J F. 2013. Direct temperature and salinity acoustic full waveform inversion[J]. Geophys Res Lett,40(16):4344–4348. doi: 10.1002/grl.50844
Brossier R,Operto S,Virieux J. 2009. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion[J]. Geophysics,74(6):WCC105–WCC118. doi: 10.1190/1.3215771
Bunks C,Saleck F M,Zaleski S,Chavent G. 1995. Multiscale seismic waveform inversion[J]. Geophysics,60(5):1457–1473. doi: 10.1190/1.1443880
Geng Y,Pan W Y,Innanen K A. 2018. Frequency-domain full-waveform inversion with non-linear descent directions[J]. Geophys J Int,213(2):739–756. doi: 10.1093/gji/ggy002
Hestholm S O,Ruud B O,Husebye E S. 1999. 3-D versus 2-D finite-difference seismic synthetics including real surface topography[J]. Phys Earth Planet Inter,113(1/2/3/4):339–354.
Jeong W,Lee H Y,Min D J. 2012. Full waveform inversion strategy for density in the frequency domain[J]. Geophys J Int,188(3):1221–1242. doi: 10.1111/j.1365-246X.2011.05314.x
Komatitsch D,Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation[J]. Geophys J Int,154(1):146–153. doi: 10.1046/j.1365-246X.2003.01950.x
Komatitsch D,Tsuboi S,Tromp J. 2005. The spectral-element method in seismology[G]//Seismic Earth:Array Analysis of Broadband Seismograms,Volume 157. Washington:American Geophysical Union:205.
Lang C,Yang D H. 2017. A nearly analytic discrete method for solving the acoustic-wave equations in the frequency domain[J]. Geophysics,82(1):T43–T57. doi: 10.1190/geo2016-0248.1
Lang C,Li Q S,Zhou Y J,He X J,Han R B. 2020. A high-precision low-dispersive nearly analytic difference method with its application in frequency-domain seismic waveform inversion[J]. Explor Geophys,51(3):355–377. doi: 10.1080/08123985.2019.1699786
Li A M,Liu H,Yuan Y X,Hu T,Guo X B. 2018. Modeling of frequency-domain elastic-wave equation with a general optimal scheme[J]. J Appl Geophys,159:1–15. doi: 10.1016/j.jappgeo.2018.07.014
Li J S,Yang D H,Liu F Q. 2013. An efficient reverse time migration method using local nearly analytic discrete operator[J]. Geophysics,78(1):S15–S23. doi: 10.1190/geo2012-0247.1
Liu S L,Yang D H,Ma J. 2017. A modified symplectic PRK scheme for seismic wave modeling[J]. Comput Geosci,99:28–36. doi: 10.1016/j.cageo.2016.11.001
Moczo P,Robertsson J O A,Eisner L. 2007. The finite-difference time-domain method for modeling of seismic wave propagation[J]. Adv Geophys,48:421–516.
Operto S,Virieux J,Amestoy P,L’Excellent J Y,Giraud L,Ali H B H. 2007. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver:A feasibility study[J]. Geophysics,72(5):SM195–SM211. doi: 10.1190/1.2759835
Pratt R G,Worthington M H. 1988. The application of diffraction tomography to cross-hole seismic data[J]. Geophysics,53(10):1284–1294. doi: 10.1190/1.1442406
Pratt R G. 1990. Frequency-domain elastic wave modeling by finite differences:A tool for crosshole seismic imaging[J]. Geophysics,55(5):626–632. doi: 10.1190/1.1442874
Pratt R G,Shin C,Hick G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophys J Int,133(2):341–362. doi: 10.1046/j.1365-246X.1998.00498.x
Pratt R G. 1999. Seismic waveform inversion in the frequency domain,part 1:Theory and verification in a physical scale model[J]. Geophysics,64(3):888–901. doi: 10.1190/1.1444597
Prieux V,Brossier R,Operto S,Virieux J. 2013. Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field,part 2:Imaging compressive-wave and shear-wave velocities[J]. Geophys J Int,194(3):1665–1681. doi: 10.1093/gji/ggt178
Pyun S,Son W,Shin C. 2009. Frequency-domain waveform inversion using an l1-norm objective function[J]. Explor Geophys,40(2):227–232. doi: 10.1071/EG08103
Qu Y M,Li J L,Li Z C,Huang J P. 2018. An elastic full-waveform inversion based on wave-mode separation[J]. Explor Geophys,49(4):530–552. doi: 10.1071/EG16158
Ren Z M,Liu Y. 2016. A hierarchical elastic full-waveform inversion scheme based on wavefield separation and the multistep-length approach[J]. Geophysics,81(3):R99–R123. doi: 10.1190/geo2015-0431.1
Saad Y. 2003. Iterative Methods for Sparse Linear Systems[M]. Philadelphia:Society for Industrial and Applied Mathematics:157−214.
Shin C,Yoon K,Marfurt K J,Park K,Yang D,Lim H Y,Chung S,Shin S. 2001. Efficient calculation of a partial-derivative wavefield using reciprocity for seismic imaging and inversion[J]. Geophysics,66(6):1856–1863. doi: 10.1190/1.1487129
Sirgue L,Pratt R G. 2004. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies[J]. Geophy sics,69(1):231–248. doi: 10.1190/1.1649391
Tape C,Liu Q Y,Tromp J. 2007. Finite‐frequency tomography using adjoint methods-methodology and examples using membrane surface waves[J]. Geophys J Int,168(3):1105–1129. doi: 10.1111/j.1365-246X.2006.03191.x
Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics,49(8):1259–1266. doi: 10.1190/1.1441754
Tessmer E,Kosloff D,Behle A. 1992. Elastic wave propagation simulation in the presence of surface topography[J]. Geophys J Int,108(2):621–632. doi: 10.1111/j.1365-246X.1992.tb04641.x
Tong P,Yang D H,Hua B L. 2011. High accuracy wave simulation-revised derivation,numerical analysis and testing of a nearly analytic integration discrete method for solving acoustic wave equation[J]. Int J Solids Struct,48(1):56–70. doi: 10.1016/j.ijsolstr.2010.09.003
Tong P,Chen C W,Komatitsch D,Basini P,Liu Q Y. 2014. High-resolution seismic array imaging based on an SEM-FK hybrid method[J]. Geophys J Int,197(1):369–395. doi: 10.1093/gji/ggt508
Tromp J,Tape C,Liu Q Y. 2005. Seismic tomography,adjoint methods,time reversal and banana-doughnut kernels[J]. Geophys J Int,160(1):195–216.
Virieux J,Operto S. 2009. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics,74(6):WCC1–WCC26. doi: 10.1190/1.3238367
Virieux J,Asnaashari A,Brossier R,Métivier L,Ribodetti A,Zhou W. 2017. An introduction to full waveform inversion[G]//Encyclopedia of Exploration Geophysics. Society of Exploration Geophysicists:R1-1−R1-40.
Wang Y H,Rao Y. 2006. Crosshole seismic waveform tomography,I:Strategy for real data application[J]. Geophys J Int,166(3):1224–1236. doi: 10.1111/j.1365-246X.2006.03030.x
Wang Y W,Dong L G,Liu Y Z,Yang J Z. 2016. 2D frequency-domain elastic full-waveform inversion using the block-diagonal pseudo-Hessian approximation[J]. Geophysics,81(5):R247–R259. doi: 10.1190/geo2015-0678.1
Yang D H,Teng J W,Zhang Z J,Liu E R. 2003. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media[J]. Bull Seismol Soc Am,93(2):882–890. doi: 10.1785/0120020125
Yang D H,Lu M,Wu R S,Peng J M. 2004. An optimal nearly analytic discrete method for 2D acoustic and elastic wave equations[J]. Bull Seismol Soc Am,94(5):1982–1992. doi: 10.1785/012003155
Yang D H,Liu E R,Song G J,Wang N. 2009. Elastic wave modelling method based on the displacement-velocity fields:An improving nearly analytic discrete approximation[J]. J Seismol,13(2):209–217. doi: 10.1007/s10950-008-9122-2
Yang D H,Song G J,Zhang J H. 2010. A modified NAD algorithm with minimum numerical dispersion for simulation of anisotropic wave propagation[J]. J Seism Explor,19(1):21–42.
Yang J D,Zhu H J,Li X Y,Ren L,Zhang S. 2020. Estimating P wave velocity and attenuation structures using full waveform inversion based on a time domain complex‐valued viscoacoustic wave equation:The method[J]. J Geophys Res: Solid Earth,125(6):e2019JB019129. doi: 10.1029/2019JB019129
Youn O K,Zhou H W. 2001. Depth imaging with multiples[J]. Geophysics,66(1):246–255. doi: 10.1190/1.1444901
Zhao Z C,Chen J Y,Liu X B. 2020. Frequency-domain finite-difference elastic wave modeling in the presence of surface topography[J]. Pure Appl Geophys,177(6):2821–2839. doi: 10.1007/s00024-019-02402-1
-
本文视频
其他相关附件
-
PDF格式
2023-0038Appendix 点击下载(310KB)
-





 下载:
下载: