Analysis of the overall response of mountain-isolation layer-tunnel under P-wave incidence
-
摘要:
采用高精度间接边界元方法（IBEM）开展了山体−隔震层−隧道的整体响应分析，研究了P波入射下柔性隔震层对高斯形山体内双线隧道地震动响应的减弱作用。在隔震层与围岩之间考虑了碎土的错动滑移，以模拟不完美交界面，并系统讨论了隔震层弹性模量、厚度、P波入射频率等因素对隧道地震动响应的影响。数值模拟结果表明：适当增加隔震层厚度可以显著降低隧道应力，有效提升隔震效果，应力降低幅度约达50%以上，且使得结构受力更为均匀；随着隔震层材料的弹性模量减小，隧道动应力数值明显减小，有效减少了其应力放大区的面积，从而有效避免因地震而导致的衬砌裂缝。
Abstract:As an important transportation facility, the safety and stability of mountain tunnels are of great concern when natural disasters such as earthquakes occur. Seismic wave reflection and coherence effect will occur in the mountain body, and the mountain body, seismic isolation layer, and tunnel as “scattering body” and “secondary source” can change the spatial distribution of ground shaking distribution and values of seismic ground motion. In order to study the influence of isolation measures on seismic wave scattering in double line tunnels within mountains, we uses high-precision indirect boundary element method （IBEM） to analyze the overall response of mountains, isolation layers, and tunnels under P-wave incidence. The isolation effect of flexible isolation layers on double line tunnels crossing Gaussian-shaped mountains.
Firstly, a comprehensive computational model was developed. A two-lane lined tunnel is traversed within the Gaussian-shaped mountain, and a seismic isolation layer is set between the tunnel and the mountain site. It is assumed that the mountain site, the tunnel and the seismic isolation layer are all linear isotropic media. In this article, there is not complete consolidation between the tunnel and the surrounding rock, but rather dislocation slip. Therefore, a series of virtual linear springs and dampers are used to connect the isolation layer and the surrounding rock, and a viscoelastic boundary is set to simulate this imperfect boundary.
Secondly, wave field analysis was conducted based on elastic wave theory. The formulas for the free field and scattering field are provided in the article, and an equilibrium equation is established based on the displacement and stress continuity conditions at the interface of each computational domain. Solving this equation can obtain the virtual wave source density. Multiplying the concentration of the virtual wave source by the corresponding Green’s function can obtain the scattering field of observation points in each domain. The superposition of scattering field and free field yields the full wave field.
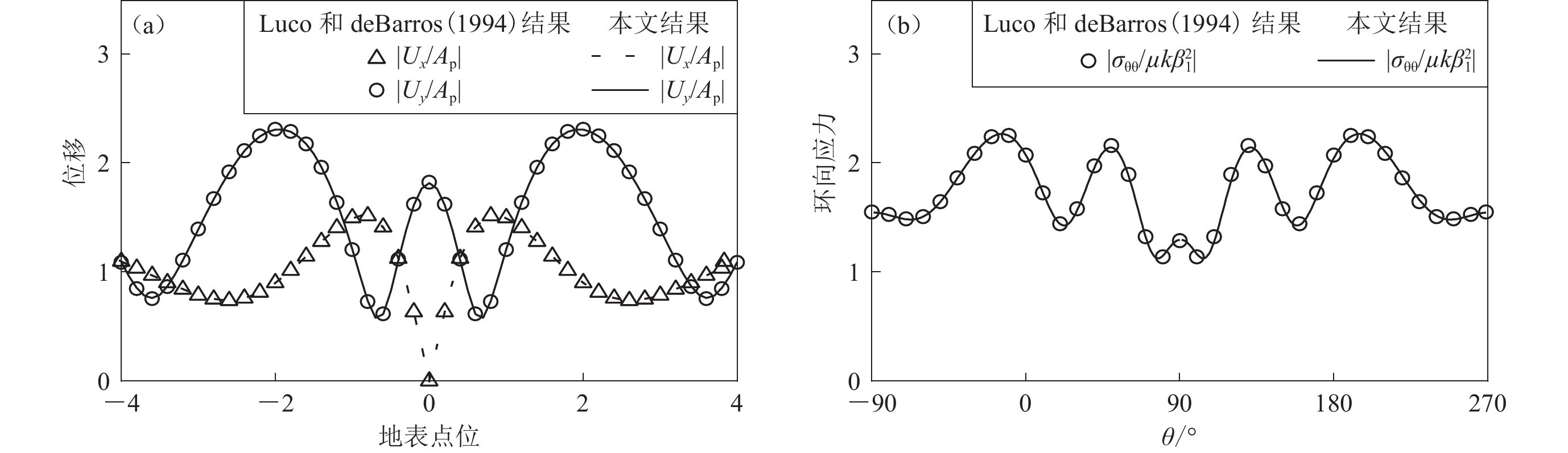
Thirdly, the correctness of the results is also verified. Due to the lack of an accurate analytical solution for mountainous tunnels under P-wave incidence in current research, we degenerates the model into a half space tunnel model and compares it with published results, with the same setting of the calculation parameters. It can be found that the results of this paper are in good agreement with those of published paper, thus verifying the accuracy of this method.
Finally, the effects of the modulus of elasticity, thickness, and incident frequency of the seismic isolation layer on the seismic ground motion response of the tunnels were discussed in detail, and the displacements and stresses of the tunnel inside the mountain and the displacements on the mountain surface are obtained. The research results can provide some reference for seismic isolation design and construction of double-line tunnel in mountain site. The following main conclusions are obtained:
1） IBEM can accurately solve the seismic dynamic response of lined tunnels in mountain, including the amplification effect of seismic ground motion in mountain ranges and the stress concentration effect of the lining, etc. Setting up seismic isolation and damping measures can effectively change the distribution of the stress and give full play to the load-bearing capacity of the surrounding rock, thus playing a role in protecting the tunnel lining.
2） As the modulus of elasticity of the isolation layer material decreases, there is a significant reduction in the values of dynamic tunnel stresses. The structural response of the flexible seismic isolation layer for suppressing high-frequency waves is more obvious. When high-frequency waves are incident, an isolation layer with elastic modulus of 12 MPa can reduce the tunnel peak stress to 25.4% of which without an isolation layer. At the same time, when the modulus of elasticity is small, it can effectively reduce the area of its stress amplification zone, thus effectively avoiding lining cracks caused by seismic action.
3） The seismic isolation layer can make the lining circumferential stress distribution tend to be uniform, and with the increase of the thickness of the vibration isolation layer, the tunnel lining dynamic stress gets smaller, and the reduction can be about 50% or more.
4） Considering the efficiency of seismic isolation as well as the cost of the project, among the several sets of parameters studied in this paper, the combined effect of a seismic isolation layer with a modulus of elasticity of 12 MPa and a thickness of 20 cm is superior.
5） Considering the existence of broken soil between the tunnel and the surrounding rock, a staggered slip boundary is introduced on the boundary. The staggered slip boundary model proposed in this paper is still simplified and does not take into account the nonlinear effects such as elastic-plasticity and large deformation.
-
引言
如何测定地震辐射能量ES是地震学的一个重要问题（Gutenberg，Richter，1956；Boatwright，Choy，1986）。传统地震学一般用震级来推算辐射能量，地方性震级ML、面波震级MS和体波震级mb都仅表示单一频率地震辐射能量的大小，由ML，MS和mb推算出的地震辐射能量，仅代表一个特定小频率范围内的能量，由震级推算出的地震辐射能量只是对地震辐射能量的粗略估计，实际上是一种“以偏概全”的结果（Bormann，Saul，2008；刘瑞丰等，2018）。当特大地震激发了更长周期的地震波，并且携带更多的能量时，传统震级会出现震级饱和现象（Bormann，2009）。Kanamori （1977）提出了只由地震矩决定的震级标度—矩震级MW，矩震级是由震源物理参数测定的震级，不存在震级饱和现象，因此越来越多的地震台网将矩震级MW作为日常测定的首选震级。矩震级MW反映的震源静态特征与地震产生的断层长度、断层宽度、震源破裂的平均位错量等静态的构造效应密切相关。而地震矩M0与震源谱的低频渐近线有关，描述震源构造效应，对断层破裂的过程不敏感，所以M0由地震波的低频成分决定。辐射能量代表了地震发生后从震源释放地震波的能量，因此辐射能量只占地震前后断层发生位移后能量变化的很小一部分，相比于利用地震矩与辐射能量的经验关系得到地震的辐射能量的方法，使用直接测定地震辐射能量的方法得到的结果会更加准确。地震以地震波形式辐射的能量主要集中在震源谱的拐角频率附近，因此辐射能量ES更适合描述地震的潜在破坏性。而在进行地震灾害与风险评估时，更关注的是辐射能量ES和能量震级Me大小，特别是辐射能量的高频部分。因此，联合测定矩震级MW和能量震级Me对于量化和评估地震灾害具有十分重要的意义。
全球宽频带数字地震台网提供的高质量地震数据使在较宽频带内测定地震辐射能量的想法变为可能，利用地震波能量正比于地面质点运动速度平方的物理性质，Boatwright和Choy （1986）提出了利用宽频带记录直接计算辐射能量的方法。1987年美国地质调查局（United States Geological Survey，缩写为USGS）国家地震信息中心（National Earthquake Information Center，缩写为NEIC）开始采用Boatwright和Choy （1986）的方法，并利用全球矩心矩张量计划（The Global Centroid-Moment-Tensor Project，缩写为GCMT）产出的震源机制对地震的震源进行校正，测定了全球范围内M＞5.5中强震的辐射能量和能量震级。2013年，美国地震学研究联合会（Incorporated Research Institutions for Seismology，缩写为IRIS）的地震能量查询网站公布了1990年以来全球MW≥6.0地震的辐射能量和能量震级，这些资料在全球地震学研究、地震灾害评估中发挥了重要作用。在测定辐射能量时，由于需要GCMT的结果，IRIS测定的辐射能量和能量震级一般需要一天以上的时间才能获得最后的结果，对于破裂过程复杂的地震，则需要更长时间。
本研究利用Giacomo等（2008）提出的利用宽频带远震P波快速测定浅源地震的辐射能量和能量震级的方法，开展了快速测定辐射能量和能量震级的测定方法研究。与IRIS的方法相比，本文方法可在获得地震数据后十五分钟至一小时内得到稳定结果，从而快速评估地震所造成的危害，提高防震减灾工作的反应效率。同时利用计算程序测定了2014—2019年发生的MW6.0—8.3共115次地震的辐射能量和能量震级，得出的地震目录可以为未来实时地震监测和快速评估地震灾害的发展提供可靠的帮助。
1. 研究方法
1.1 辐射能量和能量震级测定原理
通过远震P波测定辐射能量的基本方法，即地震波释放的能量与地面运动速度的平方成正比的性质，利用运动速度的记录对地震的震源机制和传播路径进行校正，积分后可以得到地震波的辐射能量（Boatwright，Choy，1986；Lomax，2005；Di Giacomo et al，2010；Picozzi et al，2017）。
本研究假设地震震源的模型为点源模型，周围看作均匀球形包络面，使用远震P波的垂直分量计算辐射能量
$${E_{\rm{S}}} {\text{≈}} \left( {\frac{2}{{15{\rm{\pi }}\rho {\alpha ^5}}} {\text{＋}} \frac{1}{{5{\rm{\pi }}\rho {\beta ^5}}}} \right){\int\nolimits_{{f_1}}^{{f_2}} {\left| {\hat {\ddot M}\!\!\!\!{\text{（}}\!f\!{\text{）}}\!\!\!\!} \right|} ^2}{\rm{d}}f{\text{，}}$$ (1) 其中，
$| {\hat {\ddot M}\!\!\!\!{\text{（}}\!f\!{\text{）}}\!\!\!\!} |$ ＝${{\dot u\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!}/ {\dot {{G}}\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!}}$ ，$\dot u\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!$ 为实际波形的速度谱，$\dot {{G}}\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!$ 为地震震源深度对应的格林函数的速度谱，α为P波速度，β为S波速度，ρ为介质密度。由于介质特性在18 km处会存在变化，因此本文以震源深度18 km 为分界，α，β和ρ分别使用不同的数值，深度大于18 km时，取$\alpha {\text{＝}}6.8\;{{{\rm{ km}}} / {\rm{s}}}$ ，$\;\beta {\text{＝}}4.0\;{{{\rm{ km}}} / {\rm{s}}}$ ，$\;\rho {\text{＝}}2.9\;{{{\rm{ cm}}} / {{{\rm{s}}^3}}}$ ；深度小于18 km时，取$\alpha{\text{＝}}8.0\;{{{\rm{ km}}} / {\rm{s}}}$ ，$\;\beta {\text{＝}}4.5\;{{{\rm{ km}}} / {\rm{s}}}$ ，$\;\rho {\text{＝}} 3.6\;{{{\rm{ cm}}} / {{{\rm{s}}^3}}}$ 。根据式（1）通过远震P波求得地震波的辐射能量ES。将ES代入关于Me和ES的转换公式（Choy，Boatwright，1995）：$$ {M_{\rm{e}}} {\text{＝}} {\frac{2} {3}}\!\!\!\!{\text{（}}\!{\lg {E_{\rm{S}}} {\text{－}} 4.4} \!{\text{）}}\!\!\!\! {\text{，}}$$ (2) 得到单台记录计算的Me值（Bormann，Di Giacomo，2010）。去掉不同震中距台站接收到的地震记录中信噪比较低的信号，计算所有台站结果的算数平均值，即可在较短时间内得到一个相对稳定的计算结果，即使是某些破裂过程复杂，持续时间较长的地震，也可在一小时内给出结果。而在实际应用中，为了提高计算效率，实现快速响应的目的，必须选择合适的方法处理数据和简化模型。
1.2 快速测定辐射能量和能量震级方法
为了实现快速测定地震的辐射能量和能量震级的目的，在计算流程中使用了以下方法来提高计算结果的效率。
1） 确定适当的积分频率。
处理地震数据前要确定积分截止频率的值。远震体波的辐射能量主要集中在0.01—5.00 Hz频段，地震释放的辐射能量主要集中在拐角频率附近，所以选用数据的带宽必须能够覆盖拐角频率，震源谱的积分至少包含辐射总能量的80%，才可忽略计算中Me的误差值（Di Giacomo et al，2008）。美国地震学研究联合会采用的频率范围为16 mHz—2 Hz （Convers，Newman，2011），实践中，当地震信号频率＞1 Hz时，信号的信噪比很低，校正对应频率的衰减结果不准确，从而影响结果；由于大部分地震的破裂时间都少于80 s，故将积分截止频率的下限定为12.4 mHz。破裂时间超过80 s的大地震，将时间窗定于80 s，对结果的影响也较小（Convers，Newman，2011）。本研究选用频率带宽为12.4 mHz—1 Hz，经验证符合上述要求。因此，在确定积分频率后，将地震波垂直向速度记录去除仪器响应后转化为速度记录，选择初至P波作为波头，使用Convers和Newman （2011）的方法计算地震估计破裂时间，并将得到的时间作为时间窗的长度，即可得到截取的垂直向速度记录
$\dot u\!\!\!\!{\text{（}}\!t \!{\text{）}}\!\!\!\!$ ，再对$\dot u\!\!\!\!{\text{（}}\!t \!{\text{）}}\!\!\!\!$ 进行快速傅里叶变换得到式（1）的$\dot u\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!$ 。2） 选取稳定可靠的初始模型。
恢复地震波在传播过程中损耗的能量时选择合适的地球结构模拟地球的衰减特性十分重要，地球模型和震源模型越复杂，考虑的因素越多越耗时。由于计算能量震级时必须考虑频率高于1 Hz的震源谱的高频部分，为了考虑计算结果的时效性，选择简单稳定的初始模型，重点考虑主要影响因素，尽量简化其它因素。因此本文使用了参考地球模型AK135模型作为理论地震图的震相走时模型，使用爆炸源作为初始震源机制，通过理论地震图软件QSSP提前计算球对称多层模型中不同深度的理论地震图（Wang，1999），在发生地震后，根据震源深度调取对应深度的理论地震图，提取出对应频率的理论波形，将时间域的格林函数
$\dot G\!\!\!\!{\text{（}}\!t \!{\text{）}}\!\!\!\!$ 进行快速傅里叶变化得到式（1）的$\dot {{G}}\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!$ 。经上述处理后，将
$\dot u\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!$ 和$\dot {{G}}\!\!\!\!{\text{（}}\!f \!{\text{）}}\!\!\!\!$ 代入式（1）即可得到单个地震台的辐射能量结果（Venkataraman，Kanamori，2004；Di Giacomo et al，2008）。再将辐射能量代入式（2），即可得到单台的Me值。由于使用了一维模型模拟垂直向地球结构，在实际计算中会受到真实地球三维模型内部介质的方向性和各向异性、震源辐射地震波的方向性的影响，不同方位、不同震中距的台站测定的结果也存在差异，为此本文采用了均匀覆盖震源的各个方向的台站数据，去掉信噪比较低的台站后计算各个台站结果的平均值和标准差。结果显示，超过80%的地震Me偏差在±0.3以内；而偏差大于0.3的地震中，偏差大于＋0.3的地震多于偏差小于−0.3的地震，但因其数量较少不影响最后计算结果。大多数地震均可在15—30 min内得到稳定结果，与利用震中距内的所有台站计算的最终结果的差小于0.15，对于破裂过程较复杂的地震，也能在1 h内得到结果，满足计算结果速度和稳定性的要求。2. 研究结果
2.1 数据集
使用全球地震台网（Global Seismographic Network，缩写为GSN）和国家测震台网数据备份中心的宽频带记录数据测定了2014—2019年的115次MW6.0—8.3浅源地震的Me，研究所用的地震分布如图1所示，按照震级大小进行分类，其中MW6.0—6.9地震72次，MW7.0—7.9地震40次，MW≥8.0地震3次。其中，有两次发生在中国大陆上；震级最大的事件为北京时间2015年9月17日发生在智利近海的MW8.3地震。
![]()
图 1 本文研究所用地震的震中分布图Figure 1. Distribution of the epicenter of the earthquakes used in this study2.2 结果分析
2.2.1 本文测定的Me和IRIS测定的MeIRIS对比
为了验证结果的可靠性，我们将本文测定的Me和IRIS测定的
$M_{\rm{e}}^{{\rm{IRIS}}} $ 进行了对比，结果如图2a所示（其中有3次地震GCMT上未记录其震源机制，故图中仅为112次地震结果）。统计分析得出，当美国全球矩张量项目数据中心产出的$M_{\rm{W}}^{{\rm{GCMT}}} $ ≤7.0时，Me平均值比$M_{\rm{e}}^{{\rm{IRIS}}} $ 的平均值大0.16，当$M_{\rm{W}}^{{\rm{GCMT}}} $ ＞7.0时，Me平均值比$M_{\rm{e}}^{{\rm{IRIS}}} $ 的平均值大0.1。按照震源机制将地震分类后，当地震的震源机制为正断型时，Me平均值比$M_{\rm{e}}^{{\rm{IRIS}}} $ 平均值大0.07，标准差为0.35；地震的震源机制为逆断型时，Me平均值比$M_{\rm{e}}^{{\rm{IRIS}}} $ 平均值大0.18，标准差为0.48；地震的震源机制为走滑型时，Me平均值比$M_{\rm{e}}^{{\rm{IRIS}}} $ 平均值大0.1，标准差为0.47。由此可以看出本文结果与IRIS测定的结果一致性较好，偏差均在0.2以内。![]()
图 2 本文测定的Me与$M_{\rm{e}}^{{\rm{IRIS}}} $ （a）和$M_{\rm{W}}^{{\rm{GCMT}}} $ （b）对比Figure 2. Comparison of the$M_{\rm{e}}^{{\rm{IRIS}}} $ （a） and$M_{\rm{W}}^{{\rm{GCMT}}} $ （b） with Me determined by this study本文测定的Me和
$M_{\rm{e}}^{{\rm{IRIS}}} $ 存在差异的原因如下：其一，在对地震波传播路径所损耗的能量补偿时使用的方法和计算公式与IRIS不同。不同的补偿方法会对传播过程中损耗能量的校正产生影响；为了实现快速反应的目的，本文使用了与IRIS不同的方法，为了在地震发生后能够快速调取此次地震对应深度的格林函数，先利用Wang （1999）开发的QSSP提前计算出不同深度的格林函数，再将其转换成格林函数谱来模拟地震波在地球内的传播效应。其二，是否应用了对地震震源机制的校正。破裂过程复杂的地震的震源机制解一般在发震后1小时以上才能得到，使用经过震源机制校正后的辐射能量会影响能量震级产出的快速性和时效性。因此我们选取了两次震源机制不同的代表性地震，比较了震源机制校正前后的能量震级，结果列于表1。表 1 根据震源机制修正后的$ M_{\rm{e}}^{{\rm{rev}}}$ 与未修正的Me的比较Table 1. Comparison of Me corrected for focal mechanisms with uncorrected Me发震日期 MW $M_{\rm{e}}^{{\rm{IRIS}}} $ Me $M_{\rm{e}}^{{\rm{rev}}} $ 震源机制解 地点 2018-12-20 7.4 7.7 7.5 7.6 正断型 科曼多尔群岛 2019-09-29 6.7 6.9 6.9 6.9 逆冲型 智利中部沿海 从表1可知，经过震源机制修正后的两次地震的平均Me与修正前相比，差距小于0.1，单个台站的影响可能会大于0.1，但对最后的平均结果影响较小。因此，虽然与IRIS相比，本文方法可能会造成小的震级偏差，但与计算出
$M_{\rm{e} }^{ {\rm{IRIS} } } $ 有时需要一天甚至几天时间相比，本文在保证计算结果可靠性的同时，又具有显著的时效性优势。2.2.2 Me和MW的对比
矩震级MW反映了地震发生前后断层的应力变化，与地震的静态性质有关；能量震级Me反映了地震发生过程中能量释放的大小，与地震的动态性质有关。因此，将两个震级标度进行比较能够很好地反映地震特性。对于MW≥6.0来说，一般使用美国全球矩张量项目数据中心产出的
$M_{\rm{W}}^{{\rm{GCMT}}} $ 作为参考，本文将测定的Me与$M_{\rm{W}}^{{\rm{GCMT}}} $ 进行比较（其中缺少3次地震的震源机制数据）。将地震根据矩震级分类后，可以看出，平均值Me大于$M_{\rm{W}}^{{\rm{GCMT}}} $ ；当$M_{\rm{W}}^{{\rm{GCMT}}} $ ≤7.0时，Me平均值比$M_{\rm{W}}^{{\rm{GCMT}}} $ 的平均值大0.17；$M_{\rm{W}}^{{\rm{GCMT}}} $ ＞7.0时，Me平均值比$M_{\rm{W}}^{{\rm{GCMT}}} $ 的平均值大0.11，在统计意义上，震级大小对Me与$ M_{\rm{W}}^{{\rm{GCMT}}} $ 之差的影响不显著。以单次地震进行分析，比较一次地震的Me和
$ M_{\rm{W}}^{{\rm{GCMT}}} $ 的差异更能反应此次地震的特征，即反映此次地震的应力变化和能量释放过程。如果此次地震的Me大于$M_{\rm{W}}^{{\rm{GCMT}}} $ ，表明此次地震释放的能量较多，造成的灾害较大；如果这次地震的Me小于$M_{\rm{W}}^{{\rm{GCMT}}} $ ，表明此次地震的能量释放较少，但这种地震发生在海洋中，有引发海啸的可能。例如根据GCMT和美国国家海洋和大气管理局（National Oceanic and Atmospheric Administration，缩写为NOAA）提供的信息，2017年9月8日发生在墨西哥附近沿海的震源深度为44 km的MW8.2地震，是继1985年9月19日发生在墨西哥城的MW8.0强震之后，墨西哥遭遇的最强烈地震，此次地震同时引发了大规模海啸，最高海平面变化超过3 m。本文和IRIS测定的此次地震Me分别为8.4和8.3，均高于MW，而且引发的海啸的过程会损耗地震波携带的能量中的高频部分，如果考虑地震发生时引起海水上下起伏的能量损耗，此次地震的辐射能量更大。存在的差距说明，如果仅仅考虑矩震级的大小，可能低估此次地震释放的能量和造成的破坏；相反，2015年9月16日发生在智利西海岸的MW8.3地震，本文和IRIS测定的Me结果均为8.1，即此次地震释放的能量没有使用MW的经验公式估计的辐射能量大，相较于墨西哥发生的地震造成的破坏可能更小。因此，将Me和MW作为日常产出震级并比较，能够更好的评估地震可能造成的破坏。2.2.3 震源机制对能量释放的影响
根据震源机制解类型，将所有地震事件分为正断型、逆断型和走滑型地震后发现，数据集中的地震的震源机制主要为逆断型和走滑型，正断型地震数量较少。在Me≥7.5的18次地震中，9次地震的震源机制都是逆断型，震源机制为走滑型和正断型的数量分别为7次和2次。Me＜7.5的94次地震中，47次地震的震源机制为逆断型，30次为走滑型，17次为正断型。
从图2a可以看出，走滑型地震Me平均值比
$M_{\rm{W}}^{{\rm{GCMT}}} $ 大0.18，标准差为0.45，正断型地震Me平均值比$M_{\rm{W}}^{{\rm{GCMT}}} $ 大0.13，标准差为0.34；逆断型地震Me平均值比$M_{\rm{W}}^{{\rm{GCMT}}} $ 大0.12，标准差为0.45。表明走滑型的地震的能量震级与矩震级差距更大。从其统计学意义上分析，走滑型地震其辐射地震能量的效率要高于其它两种震源机制的地震。例如2016年3月2日印尼MW7.8地震，是一次走滑型地震，本文与IRIS测定的Me分别为8.0和8.1，Me显著大于MW，说明此次地震释放能量的效率较高。同样的现象也在震源机制是走滑型的2016年8月12日洛亚蒂群岛MW7.8地震、2016年九州岛MW7.0地震等地震事件中出现。对比3个震例，矩震级MW相同，能量震级Me之间存在的差异，其原因不仅可以从两个震级的测定原理差异加以解释，同时由于能量震级Me的大小与一次地震的能量释放过程密切相关，还可以利用谱分析方法对地震的能量释放过程进行分析。本文选取了一对代表性震例，它们具有相近的震中位置和震级大小，通过对一个单台记录的分析，表明Me与地震的能量释放过程的关系，从而说明在地震后测定一个地震的能量震级Me的重要性。
根据中国地震台网中心（China Earthquake Networks Centers，缩写为CENC）测定，2019年4月18日台湾花莲MS6.7地震是近五年来台湾地区震级最大的地震，震源距离海岸线仅1 km。地震不仅造成台湾岛震感强烈，福建、浙江等地震感明显，江苏、安徽等地有感。而IRIS测定此次地震MW为6.1，与CENC测定的结果相差达到0.6，这在震级较低的情况下如此差距是十分罕见的。而2018年2月4日发生在台湾花莲的MW6.1地震（IRIS测定），CENC测定其MS为6.4。两次地震的震中仅相距5.6 km，GCMT测定，两次地震的震源机制均为逆断型。两次地震都有一个显著特征，即CENC测定的MS远大于MW。因此本文选取两次地震进行对比，参数列于表2。
表 2 台湾地区花莲县两次地震震源参数对比Table 2. Source parameters of two earthquakes occurred in Hualien County，Taiwan region发震日期 东经/° 北纬/° 震源深度/km 震源机制 MW Me MeIRIS 2018-02-04 121.72 24.20 7.8 逆断型 6.1 6.2±0.23 5.7 2019-04-18 121.69 23.99 20 逆断型 6.1 6.6±0.29 6.4 使用牡丹江台（IC.MDJ）提供的两次地震的波形数据为例，对两次地震的波形信息（图3）和时频分析谱（图4）进行比较。由于地震信号的非平稳性，且使用频率范围较宽，为了研究频率的局部特征，本文使用了Stockwell变换（简称为S变换）对时间窗内的波形进行时频分析，经过理论计算及地震信号仿真表明，S变换不仅能够得到地震波形的时频信息，属于多分辨率时频分析方法，并且避免了使用短时傅里叶变换中使用的窗函数的宽度固定，以及基本小波变换必须满足容许性条件等问题，弥补了短时傅里叶变换和小波变换的存在的缺点（Stockwell et al，1996）。
![]()
图 3 台湾花莲2018年2月4日（a）和2019年4月18日（b）两次地震的截取波形（红色）Figure 3. Time windows （marked in red） taken by two earthquakes on 4th February 2018 （a） and 18th April 2019 （b） in Hualien County，Taiwan region![]()
图 4 台湾花莲2018年2月4日（a）和2019年4月18日（b）两次地震的时频分析图（色标代表S变换的振幅的对数）Figure 4. Time-frequency analysis of two earthquakes on 4th February 2018 （a） and 18th April 2019 （b） in Hualien County，Taiwan region （The color scale represents the logarithm of the amplitude of the S-transform）尽管两次地震具有相似的震源机制和地震矩，但本文和IRIS测定的发生于2019年4月的地震能量震级都远大于2018年2月地震。从图4可以看出，在0.1 Hz以下的低频部分，两次地震的谱振幅相似，但是在高频部分（＞0.1 Hz），第二次地震的谱振幅明显更大。而MW的测定由频谱的低频部分决定，虽然两次地震具有相同的MW，但释放的能量具有显著差异。并且，相较于第二次地震事件，第一次地震释放能量的过程更加平缓，分布在整个时间窗内，而第二次事件的高频部分在20—40 s和50—70 s内有两次较集中的能量释放。可以表明两次具有相同震源机制和地震构造环境的地震在能量释放上可能存在巨大差异。使用牡丹江台单台的波形记录观察到的现象也在其它台的波形记录中出现。
从Me的结果可以看出，两次地震释放的能量差距超过4倍，在时频分析图中发生于2019年4月的地震的振幅谱中高频成分十分显著，这也是发生此次地震具有较大震感的原因。对于类似情况的地震，如果能快速测定出Me的结果，就能够较快评估出此次地震的灾害潜能，为后续的地震应急工作提供参考。
由以上分析可知，对于Me显著大于MW的地震，如果仅考虑MW的大小，有时会大大低估此次地震造成破坏的程度，从而降低应急救援反应速度，而在地震发生后快速测定Me能够正确评估出此次地震释放能量的大小。因此在短时间内得到有关Me的信息，对地震的危险性更早作出判断，具有重要的现实意义。
3. 讨论和结论
本文利用全球地震台网和中国测震数字台网记录到的高质量宽频带记录，测定了发生在2014—2019年115次全球浅源地震的能量震级Me，覆盖范围为MW6.0—8.3，并将结果与其它震级标度进行比较，得出以下结论：
1） 将本文计算的115次地震的能量震级Me与美国IRIS的结果进行比较，结果显示两者具有较好的一致性，偏差在0.2以内。在正断型地震中，本文结果比IRIS平均值偏大0.07，逆断型地震平均值偏大0.18；走滑型地震平均值偏大0.1。本文方法将Me的测定时间缩短到1个小时内，保证Me测定方法的稳定性的同时满足了对获得结果的时效性要求。
2） 通过对比本文得到的能量震级Me与矩震级MW，能量震级Me大于矩震级MW的地震，震源释放能量的能力较强，一般会造成较大破坏性；Me小于MW的地震，震源释放能量的能力较弱，但可能会具有较长的破裂持续时间，因而可能引发海啸等自然灾害。同时将地震按照震源机制分类表明，具有走滑断层的地震的辐射地震能量的效率高，Me要明显大于MW，这种现象是由地震断层释放能量的能力决定的。
3） 利用时频分析方法分析对比两次发生在台湾花莲两次位置相近、震源机制相同的地震且矩震级MW相同的地震，但能量震级Me的差异很大，释放能量的差距超过4倍，这是由于两次地震释放能量的过程不同，其它地震也存在类似情况。表明与矩震级MW相比，利用能量震级Me更能体现地震的能量释放过程，地震的能量释放过程与地震造成破坏的程度有很大关系。
由于本文的方法主要应用于快速测定MW≥6.0地震的能量震级Me，受到能量补偿中地球模型的限制和小震的远震信号信噪比影响，测定MW＜6.0地震的误差较大。在未来的工作中可以使用更精确的地球模型（如三维地球模型）进行传播过程中能量衰减的校正，从而将震级的测定范围降低到6.0以下，把国家地震台网和区域地震台网的数据应用于测定国内的中小地震的能量震级Me，台站数据的增加可以进一步提高获得稳定结果的速度。
总而言之，使用远震P波记录快速产出能量震级Me，借助能量震级Me提供的信息可以在震后快速评估地震所造成破坏的程度，为未来的地震应急和防震减灾工作提供参考，提高应急救援工作的时效性。
-
![]()
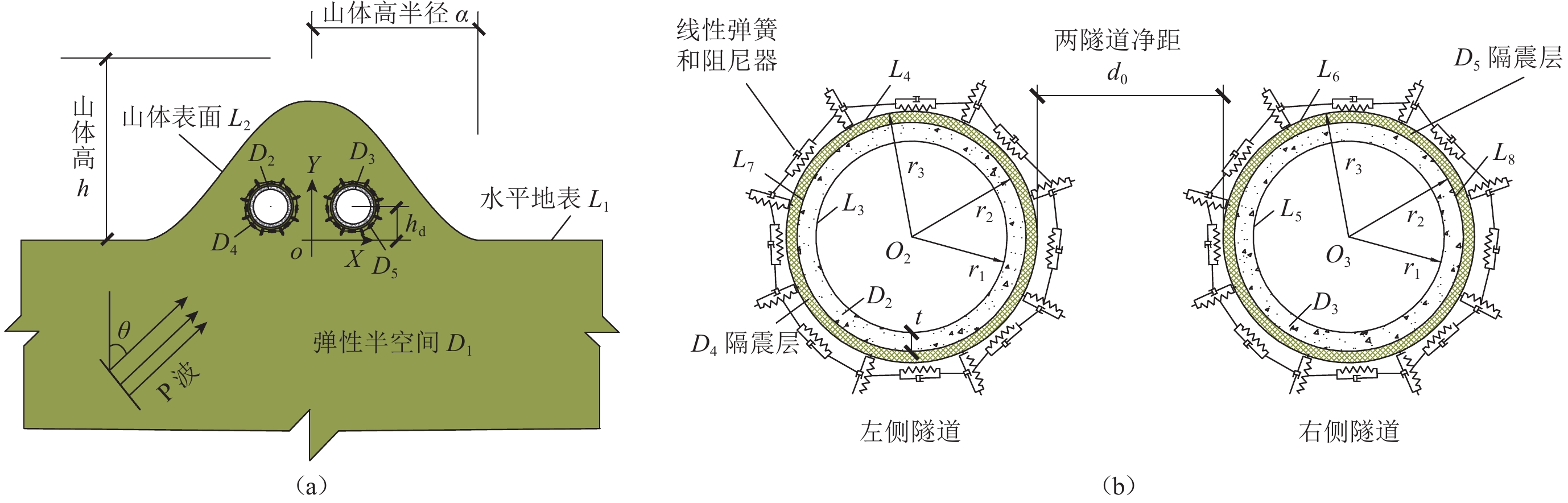
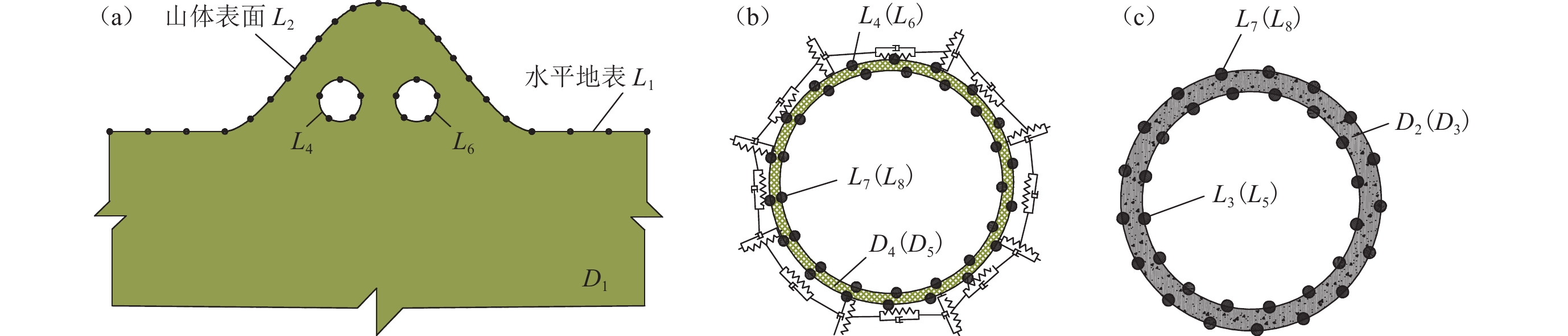
图 1 山体内双圆形衬砌隧道计算模型（a）和错动滑移边界构造（b）
L3和L5分别表示左右隧道衬砌内边界；L7和L8分别表示左右隧道衬砌外边界；D2和D3代表隧道域；r1和r2为隧道内外半径；r3为隔震层外半径；t为衬砌厚度，下同
Figure 1. Calculation model of double circular lining tunnel in the mountain （a） and staggered slip boundary structure （b）
L3 and L5 are the inner boundaries of the left and right tunnels，respectively；L7 and L8 are the outer boundaries of the left and right tunnels，respectively；D2 and D3 represent tunnel domains；r1 and r2 are the inner and outer radii of the tunnel，respectively；r3 is the outer radius of the isolation layer；t is the thickness of the lining，the same below
![]()
图 2 隧道—山体系统域划分及边界离散
（a） 弹性半空间域D1；（b） 隔震层域D4 和D5；（c） 隧道域D2 和D3
Figure 2. Domain-division of the tunnel-hill system and boundary discrete elements
（a） Elastic half-space domain D1；（b） Seismic isolation layer domain D4 （D5）；（c） Tunnel domain D2 （D3）
![]()
图 3 当前模型退化结果同Luco和de Barros （1994）对P波垂直入射所得结果对比
（a） 地表位移；（b） 衬砌环向应力
Figure 3. The comparison of the present results with the degenerated results of Luco and Barros （1994） for vertical incident P waves
（a） Surface displacement；（b） Lining circumferential stress
![]()
图 4 P波垂直入射下隔震层d和弹性模量$\eta $不同时左隧道的动应力集中因子DSCF
（a） 无隔震层；（b） 隔震层弹性模量100 MPa；（c） 隔震层弹性模量50 MPa；（d） 隔震层弹性模量12 MPa
Figure 4. DSCF of the left tunnel with different elastic modulus of isolation layer under vertical incident P wave
（a） No isolation layer；（b） Elastic modulus of isolation layer 100 MPa；（c） Elastic modulus of isolation layer 50 MPa；（d） Elastic modulus of isolation layer 12 MPa
![]()
图 5 P波垂直入射下不同隔震层厚度d和弹性模量$\eta $时DSCF
（a） 隔震层厚度10 cm；（b） 隔震层厚度20 cm；（c） 隔震层厚度40 cm
Figure 5. DSCF of the left tunnel with different shock absorption layer thickness under P wave incidence
（a） Isolation layer thickness 10 cm；（b） Isolation layer thickness 20 cm；（c） Isolation layer thickness 40 cm
![]()
图 6 P波垂直入射下不同隔震层厚度的左隧道加速度时程（不设隔震层时的加速度时程为参照，如灰色线条所示）
（a） 隔震层厚度为0 cm与10 cm对比图；（b） 隔震层厚度为0 cm与15 cm对比图；（c） 隔震层厚度为0 cm与20 cm对比图
Figure 6. Acceleration time history of the left tunnel with different seismic isolation layer thickness under P wave incidence （taking the acceleration time histories without isolation layer as reference，which are denoted by gray curves）
（a） Comparison of isolation layer thickness 0 cm and 10 cm；（b） Comparison of isolation layer thickness 0 cm and 15cm；（c） Comparison of isolation layer thickness 0 cm and 20 cm
表 1 材料参数
Table 1 Material parameters
介质 弹性模量
/MPa密度
/（kg·m−3）剪切波速
/（ m·s−1）泊松比 围岩 5000 2000 1000 0.25 隧道 32000 2500 2260 0.25 隔震层① 12 1000 70 0.38 隔震层② 50 1200 130 0.38 隔震层③ 100 1400 170 0.38 
下载: 导出CSV
-
李天斌. 2008. 汶川特大地震中山岭隧道变形破坏特征及影响因素分析[J]. 工程地质学报,16(6):742–750. doi: 10.3969/j.issn.1004-9665.2008.06.003 Li T B. 2008. Failure characteristics and influence factor analysis of mountain tunnels at epicenter zones of great Wenchuan earthquake[J]. Journal of Engineering Geology,16(6):742–750 (in Chinese).
梁清华,刘中宪,周晓洁,何颖. 2018. 基于粘性—滑移界面接触模型半空间隧道衬砌对平面P波的散射[J]. 世界地震工程,34(3):111–123. Liang Q H,Liu Z X,Zhou X J,He Y. 2018. Scattering of plane P waves by a lined tunnel in a half-space based on viscous-slip interface contact model[J]. World Earthquake Engineering,34(3):111–123 (in Chinese).
梅松华,盛谦,崔臻,梅贤丞. 2022. 黏弹性阻尼减震层的吸能特性试验研究[J]. 岩土工程学报,44(6):997–1005. Mei S H,Sheng Q,Cui Z,Mei X C. 2022. Experimental study on energy absorption property of viscoelasticity damping layer[J]. Chinese Journal of Geotechnical Engineering,44(6):997–1005 (in Chinese).
杨长卫,张良,张凯文,岳茂,童心豪,温浩. 2023. 山岭隧道跨断裂带段及洞口段地震响应大型振动台模型试验研究[J]. 岩石力学与工程学报,42(4):993–1002. Yang C W,Zhang L,Zhang K W,Yue M,Tong X H,Wen H. 2023. Large scale shaking table model test on seismic response of mountain tunnel portal section passing through fault zone[J]. Chinese Journal of Rock Mechanics and Engineering,42(4):993–1002 (in Chinese).
禹海涛,李晶,王祺. 2022. 软土隧道基于地震响应的输入地震动排序[J]. 地震学报,44(1):123–131. doi: 10.11939/jass.20210166 Yu H T,Li J,Wang Q. 2022. Ranking the seismic input motion based on seismic response of soft soil tunnels[J]. Acta Seismologica Sinica,44(1):123–131 (in Chinese).
Ba Z N,Yin X. 2016. Wave scattering of complex local site in a layered half-space by using a multidomain IBEM:Incident plane SH waves[J]. Geophys J Int,205(3):1382–1405. doi: 10.1093/gji/ggw090
Bobet A. 2009. Elastic solution for deep tunnels:Application to excavation damage zone and rockbolt support[J]. Rock Mech Rock Eng,42(2):147–174. doi: 10.1007/s00603-007-0140-0
Fang X Q,Jin H X,Liu J X,Huang M J. 2016. Imperfect bonding effect on dynamic response of a non-circular lined tunnel subjected to shear waves[J]. Tunnell Undergr Space Technol,56:226–231. doi: 10.1016/j.tust.2016.03.008
Huang L,Liu Z X,Wu C Q,Liang J W. 2019. The scattering of plane P,SV waves by twin lining tunnels with imperfect interfaces embedded in an elastic half-space[J]. Tunnell Undergr Space Technol,85:319–330. doi: 10.1016/j.tust.2018.12.024
Jiang X L,Wang F F,Yang H,Sun G C,Niu J Y. 2018. Dynamic response of shallow-buried small spacing tunnel with asymmetrical pressure:Shaking table testing and numerical simulation[J]. Geotech Geol Eng,36(4):2037–2055. doi: 10.1007/s10706-017-0444-0
Lin Z,Yan L,Xiang C,Yang H Y. 2020. Study on dynamic response laws and shock absorption measures of mountain tunnel under strong earthquake[J]. Adv Civil Eng:1671838.
Luco J E,de Barros F C P. 1994. Dynamic displacements and stresses in the vicinity of a cylindrical cavity embedded in a half-space[J]. Earthq Eng Struct Dyn,23(3):321–340. doi: 10.1002/eqe.4290230307
Ma X,Wang F M,Guo C C,Sun B. 2020. Seismic isolation effect of non-water reacted two-component polymeric material coating on tunnels[J]. Appl Sci,10(7):2606. doi: 10.3390/app10072606
Meng G W,Gao B,Zhou J M,Cao G D,Zhang Q. 2016. Experimental investigation of the mechanical behavior of the steel fiber reinforced concrete tunnel segment[J]. Constr Build Mater,126:98–107. doi: 10.1016/j.conbuildmat.2016.09.028
Su L J,Liu H Q,Yao G C,Zhang J L. 2019. Experimental study on the closed-cell aluminum foam shock absorption layer of a high-speed railway tunnel[J]. Soil Dyn Earthq Eng,119:331–345. doi: 10.1016/j.soildyn.2019.01.012
Wang W L,Wang T T,Su J J,Lin C H,Seng C R,Huang T H. 2001. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi earthquake[J]. Tunnell Undergr Space Technol,16(3):133–150. doi: 10.1016/S0886-7798(01)00047-5
Wang Z,Zhu W,Zhang Z. 2012. Seismic isolation effect of a tunnel covered with a buffer layer[J]. Dis Adv,5(4):1372–1376.
Xu X Y,Wu Z J,Sun H,Weng L,Chu Z F,Liu Q S. 2021. An extended numerical manifold method for simulation of grouting reinforcement in deep rock tunnels[J]. Tunnell Undergr Space Technol,115:104020. doi: 10.1016/j.tust.2021.104020
Yi C P,Zhang P,Johansson D,Nyberg U. 2014. Dynamic response of a circular lined tunnel with an imperfect interface subjected to cylindrical P-waves[J]. Comput Geotech,55:165–171. doi: 10.1016/j.compgeo.2013.08.009
Zhou X H,Cheng X S,Qi L,Wang P,Chai S F,Liu Y J. 2021. Shaking table model test of loess tunnel structure under rainfall[J]. KSCE J Civ Eng,25(6):2225–2238. doi: 10.1007/s12205-021-1064-z
计量
- 文章访问数: 127
- HTML全文浏览量: 37
- PDF下载量: 36
