The secular variation prediction method of geomagnetic field in Chinese mainland based on long short-term memory neural network
-
摘要:
选取中国大陆及邻近地区32个地磁台站地磁场要素即磁偏角D、地磁场水平分量H、垂直分量Z的时均值数据，利用磁静条件筛选并剔除异常值，通过月均值年差分得到主磁场各要素的长期变化序列，然后将深度学习方法应用到地球主磁场长期变化研究中，利用长短时记忆神经网络（LSTM）建立了未来一年台站各要素数据的预测模型。预测结果表明：LSTM模型预测的D要素均方根误差（RMSE）、归一化均方根误差（NRMSE）平均值为1.139′和0.040；H分量的RMSE、NRMSE平均值为11.85 nT和0.086；Z分量的RMSE、NRMSE平均值为15.10 nT和0.026，LSTM模型对Z分量的预测精度最高，其次是D要素，最差的是H分量。分别计算由LSTM模型、线性外推、二次外推得到的台站各要素年变率误差，结果显示：对于D要素，LSTM预测结果的RMSE平均值为0.361′/a，较线性外推法提高了54%，较二次外推法提高了59%；对于H分量，LSTM预测结果的RMSE平均值为3.921 nT/a，较线性外推法提高了58%，较二次外推法提高了76%；对于Z分量，LSTM预测结果的RMSE平均值为4.339 nT/a，较线性外推法提高了47%，较二次外推法提高了57%。
-
关键词:
- 地球磁场 /
- 长短时记忆（LSTM） /
- 长期变化 /
- 深度学习 /
- 中国大陆
Abstract:The geomagnetic field is the result of the superposition of different magnetic substances and their dynamic processes within the Earth, as well as the magnetic field generated by the current systems both inside and outside the Earth. Researching the geomagnetic field is not only crucial for revealing the Earth’s spatial electromagnetic environment, exploring the Earth’s internal structure, and understanding the magnetohydrodynamic dynamics of the Earth’s core, but also plays an extremely important role in monitoring earthquake and volcanic activity, exploring mineral and energy resources, as well as positioning and navigating carrier. The magnetic field of the Earth’s core, also known as the main magnetic field, is widely believed to be generated by the magnetohydrodynamic generator mechanism in the Earth’s core, accounting for over 95% of the total magnetic field. The wavelength of the main magnetic field is relatively long, and its spatial distribution is dominated by dipole fields. The temporal variation shows long-term changes on the scale of hundreds to thousands of years and polarity reversal on the scale of millions of years. The main magnetic field and its secular variation have always been important research topics in geomagnetism.
Machine learning can extract features from large amounts of data, and can also learn and iterate to discover the data patterns and features we need. As an important branch of machine learning, deep learning learns and mines data features through deep neural networks. Deep learning can handle non-linear data without relying on the spectral characteristics of temporal data, and has good performance. LSTM （long short-term memory） adds a gate mechanism to the traditional RNN （recurrent neural network） structure, which can effectively solve the problems of gradient explosion and vanishing during RNN training. Therefore, LSTM has more complex temporal information memory units and is widely used in temporal data analysis and modeling.
Thus, we apply deep neural network LSTM to the research of secular variation prediction of geomagnetic field. We select the time averaged data of the horizontal component H, magnetic declination D, and vertical component Z of the geomagnetic field from 32 geomagnetic stations in Chinese mainland and its neighboring regions; use local time conditions and geomagnetic index conditions to select and calculate the daily mean of the time averaged data; further filter the data based on the geomagnetic quiet days published by the World Geomagnetic Data Center, and perform linear fitting on the filtered data to remove outliers and calculate the monthly mean; further obtain the secular variation time-series of the main magnetic field through the annual difference of the monthly mean. Finally, the secular variation time-series of the main magnetic field is input into the LSTM model for training, and the predicted results of the model are compared and analyzed with those of general methods.
The prediction results shows that for the D element the average RMSE and NRMSE of LSTM are 1.139' and 0.040, for the H element the average RMSE and NRMSE of LSTM are 11.85 nT and 0.086, for the Z element the average RMSE and NRMSE of LSTM are 15.10 nT and 0.026, suggesting the LSTM model has the highest prediction accuracy for Z element, followed by D element, and the worst for H element. There are two main reasons why the model has poor accuracy in predicting H elements. Firstly, during the geomagnetic quiet period, the distribution of Sq current system and equatorial current directly affects the recording of H elements at ground stations, especially in low latitude areas where H elements undergo significant changes. Secondly, the training set has limited sample data and lacks comprehensive secular variation information, resulting in the model which is able to fit well on the training set but has poor prediction accuracy on the testing set. Expanding the sample size of the training set as much as possible can improve this situation.
We calculate the annual rate error for various elements of the station obtained from LSTM model, linear extrapolation, and quadratic extrapolation. For the D element, the average RMSE of the LSTM prediction results is 0.361'/a, which is 54% higher than linear extrapolation and 59% higher than quadratic extrapolation. For the H element, the average RMSE of the LSTM prediction results is 3.921 nT/a, which is 58% higher than linear extrapolation and 76% higher than quadratic extrapolation. For the Z element, the average RMSE of the LSTM prediction results is 4.339 nT/a, which is 47% higher than linear extrapolation and 57% higher than quadratic extrapolation.
-
Keywords:
- geomagnetic field /
- LSTM /
- secular variation /
- deep learning /
- Chinese mainland
-
引言
地磁场作为地球最基本的物理场之一，是由地球内部不同的磁性物质及其动力学过程以及存在于地球内部和外部的电流体系所产生的磁场共同叠加的结果（徐文耀，2009）。研究地磁场不仅对揭示地球的空间电磁环境、探究地球内部结构以及理解地核的磁流体动态过程至关重要，而且在地震和火山活动的监测、矿产能源资源的勘查以及载体定位和导航等领域也发挥着极其重要的作用（邱耀东，2018）。
地磁场是一个随时间和空间变化的矢量场，由不同来源的磁场相互叠加而成。根据磁场源的位置和变化规律特征，它分为内源场和外源场两大类。内源场源于地球内部的磁性物质和电流系统，进一步细分为地核磁场、地壳磁场和感应磁场。其中，地核磁场也被称为主磁场，现在普遍认为由地核中的磁流体发电机机制产生的，占据了总磁场的95%以上（徐文耀，2009）。主磁场的波长较长、空间分布以偶极子场为主，时间变化呈现百年至千年尺度的长期变化（secular variation，缩写为SV）和百万年尺度的极性倒转。主磁场及其长期变化一直是地磁学的重要研究内容。
为了描述全球地磁场及其长期变化，国际地磁学与高空物理学协会（International Association of Geomagnetism and Aeronomy，缩写为IAGA）于1968年发布了1965.0年代的国际地磁参考场（The International Geomagnetic Reference Field，缩写为IGRF），每五年更新一次（Finlay et al，2010）。最新的IGRF-13于2019年12月发布，提供了
2020.0 历元时刻的地球主磁场模型（球谐系数截断至13阶），以及2020.0 —2025.0 预测的长期变化模型（球谐系数截断至8阶）（Alken et al，2021）。IGRF的高斯系数$ {{g}}_{{n}}^{{m}} （ {t} ） {和}{{h}}_{{n}}^{{m}} （ {t} ） $是随时间变化的，并以5年为间隔分段线性拟合外推。这种方法可将较短的时间尺度内（1—2年） F要素的误差控制在13 nT以内，当地磁场的长期变化率突然发生较大变化时，模型对地球主磁场的估计误差便会显著增加，F要素误差可达到153 nT （毛宁等，2023）。因此研究地球主磁场长期变化的方法需要进一步改善。关于地球主磁场长期变化的研究，国内外研究人员进行了很多相关的研究。Hamed等（1994）利用POGO （polar orbiting geophysical observatories）卫星磁测数据，通过计算功率谱对地磁场长期变化特征进行了研究。Nevanlinna （1987）利用IGRF模型分析了1955—1985年全球地磁场长期变化的功率谱特征。Pushkov等（1976）利用自然正交分量法（natural orthogonal component，缩写为NOC）分析了地磁基本场的时空分布；Golovkov等（1978）应用NOC方法分析了各种地磁变化，并提出建立国际地磁参考场NOC模型的想法。王月华（2002）使用1985—1997年中国和日本的部分地磁台站年均值数据建立了地磁场长期变化的正交模型。顾左文等（2009）利用1995—2006年中国地区地磁台站的观测数据应用NOC方法对地磁场长期变化进行了研究，分离并描述了地磁场时空变化中的线性成分和非线性成分，为探讨地磁时空变化的规律并揭示其物理机制提供了良好的基础。康国发等（2009）利用地磁场模型POMME-4.2S对中国地区地磁场长期变化和长期加速度分布特征进行分析，其结果显示磁四极子对长期变化起主要贡献，磁八极子对长期加速度变化贡献最大。陈斌等（2010）建立了2000.0—2005.0年代中国地区地磁场长期变化泰勒多项式模型和曲面样条模型，并与国际地磁参考场长期变化模型（IGRF-SV）对比分析，其结果表明这三种模型得到的变化趋势是一致的，但中国地区的地磁长期变化具有区域特征。常宜峰（2015）通过在空中建立“虚拟测站”利用CHAMP卫星磁测资料提取地磁场长期变化，结果表明由地面台站数据和卫星磁测数据得到的主磁场长期变化率之间具有很高的相关性，“虚拟测站”能很好地捕捉到主磁场长期变化中的细节信息。Xu和Lin （2023）根据CHAOS-7模型得到主磁场的长期变化和长期加速度时空分布，将流体力学领域中的动力学模态分解（dynamic mode decomposition，缩写为DMD）引入地磁场研究，发现过去二十年的主磁场时空变化可以分解为三个主要的模态组合，分别是：周期为58年的全球模态、周期为16年的局部模态和周期为8.5年的赤道模态。上述研究多是基于地磁台站数据和地磁场模型研究地磁场长期变化的分布特征，很少关注地磁场长期变化的预测研究。
近年来随着人工智能及计算机的飞速发展，机器学习已经成为人工智能领域的核心技术之一。机器学习方法能够从大量数据中提取特征、学习并迭代，从而发现我们需要的数据模式和特征。作为机器学习的一个重要分支，深度学习通过深度神经网络（deep neural network，缩写为DNN）来对数据特征进行学习和挖掘。深度学习可以不依赖时序数据的频谱特征，在处理非线性数据上具有显著的优势。卢兆兴等（2021）以地磁台站的观测数据为基础，构建了基于反向传播神经网络的地磁变化场预测模型，结果表明对于任选的100组验证数据，均方根误差为4.8 nT。长短时记忆神经网络（LSTM）在传统的递归神经网络（recurrent neural network，缩写为RNN）的基础上增加了门控机制的网络结构，能有效地解决RNN训练过程中的梯度爆炸和梯度消失等问题（Hochreiter，Schmidhuber，1997）。因此LSTM具有更加复杂的时序信息记忆单元，被广泛应用于时序数据分析和建模。例如：在数据去噪方面，汪凯翔等（2020）利用LSTM对地电场数据进行去噪处理，处理后的数据噪声得到了很好的压制，并包含了明显的潮汐响应；在缺失数据重构方面，杜奕（2023）基于时空融合的卷积长短时记忆神经网络（ConvLSTM）对长三角地区PM2.5数据进行了重构，该模型减少了时空插值方法产生的不确定性误差；在时序数据预测方面，熊波等（2022）利用太阳活动和地磁活动参量基于LSTM建立了电离层总电子含量（total electron content，缩写为TEC）预测模型，该模型不仅能够准确反映电离层TEC时空变化特征，而且预测精度优于国际参考电离层模型IRI-2016和传统BP神经网络模型。
由于LSTM在时序数据处理方面有着较高的精度，因此本文拟将深度神经网络LSTM应用于地磁场长期变化预测研究，针对各台站各要素训练了预测模型，并将模型预测结果与一般方法预测结果对比分析。
1. 方法原理
1.1 长短时记忆网络
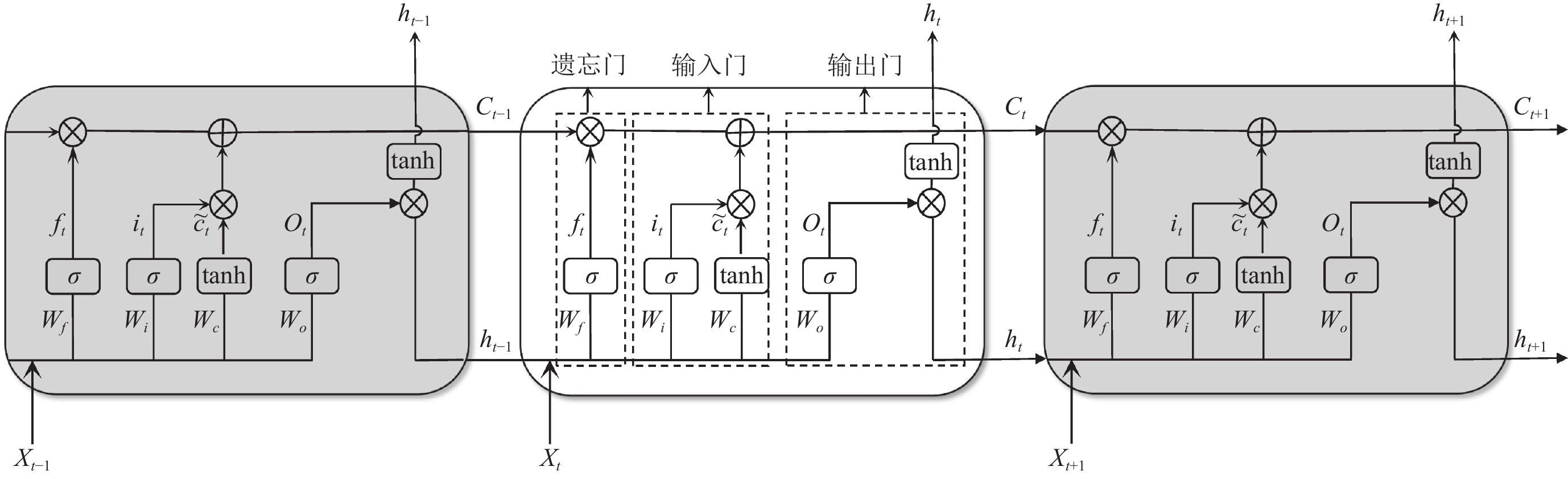
LSTM神经网络是在RNN递归神经网络的基础上改进实现的，在其隐藏层神经元中加入输入门、输出门、遗忘门对深度神经网络的权重进行选择性修正，从而实现在长时间序列网络中误差函数随梯度下降方向的传播。
LSTM的网络结构如图1所示，在某一时刻$ t $，输入LSTM神经元的数据由三部分组成分别是：当前时刻的输入值Xt、上一个时刻神经元的隐藏状态ht−1、以及上一个时刻记忆单元的状态Ct−1。输出的数据为当前神经元的隐藏状态ht和当前时刻记忆单元的状态Ct。
LSTM神经元的具体结构如图1所示，包括了遗忘门（f）、输入门（i）、输出门（O）以及记忆单元的状态（C），其中：符号$ \oplus $表示两个向量之间的加法运算；符号$ \otimes $表示两个向量之间的乘法运算；$ \sigma $表示sigmoid激活函数，其取值范围是$ ［ $0，1$ ］ $，能控制数据传输的比例，取值为0表示没有信息，传输取值为1表示全部信息都能传输；tanh表示双曲正切激活函数，其取值范围是$ ［ $−1，1$ ］ $；引入激活函数可以增加网络的非线性表达和逼近能力（Hochreiter，Schmidhuber，1997），其计算公式分别如下：
$$ \sigma （ x ） ＝ \frac{1}{{1 ＋ {{\mathrm{e}}^{ - x}}}} \text{，} $$ (1) $$ {{\mathrm{tan}}}{\mathrm{h}}x＝\frac{{{\mathrm{e}}}^{x}-{{\mathrm{e}}}^{-x}}{{{\mathrm{e}}}^{x} ＋ {{\mathrm{e}}}^{-x}} \text{，} $$ (2) LSTM网络在某一t时刻具体的计算过程如下：
$$ {f}_{t}＝\sigma \left({W}_{f} \bullet ［ {h}_{t-1} \text{，} {X}_{t} ］ ＋ {b}_{f}\right)\text{，} $$ (3) $$ {i}_{t}＝\sigma （ {W}_{f} \bullet ［ {h}_{t-1} \text{，} {X}_{t} ］ ＋ {b}_{i} ） \text{，} $$ (4) $$ {O}_{t}＝\sigma （ {W}_{f} \bullet ［ {h}_{t-1} \text{，} {X}_{t} ］ ＋ {b}_{o} ） \text{，} $$ (5) $$ {{\tilde {C}}_{t}}＝{\tan}{\mathrm{h}} （ {W}_{c} \bullet ［ {{{h}}}_{t-1} \text{，} {X}_{t} ］ ＋ {b}_{c} ） \text{，} $$ (6) $$ {C}_{t}＝{f}_{t} \bullet {C}_{t-1} ＋ {i}_{t} \bullet \stackrel{~}{{\tilde {C}}_{t}} \text{，} $$ (7) $$ {h}_{t}＝{O}_{t} \bullet {\tan}{\rm{h}} （ {C}_{t} ） \text{，} $$ (8) 式中：Wf，Wi，Wo，Wc分别是遗忘门、输入门、输出门、记忆单元的权重量；bf，bi，bo和bc分别是遗忘门、输入门、输出门、记忆单元的偏置量；$ ［ {h}_{t-1} \text{，} {X}_{t} ］ $表示上一个时刻单元的隐藏状态ht−1与当前时刻的输入数据$ {X}_{t} $构成的向量；ft是t时刻遗忘门决定从记忆单元中删除的信息；it是t时刻输入门决定增加到记忆单元中的信息；O是t时刻输出门决定从记忆单元中选择信息进行输出；${{\tilde {C}}_{t}} $是t时刻候选记忆单元的状态；Ct是t时刻最终的记忆单元状态；ht是t时刻细胞的隐藏状态。对于输入进LSTM神经网络的数据，首先通过遗忘门，这控制了在当前单元状态中要舍弃的历史信息；然后通过输入门，这控制了在当前单元状态中要保留多少信息；接着要对单元状态进行更新，遗忘门的结果与上一时刻的单元状态相乘，其结果再与输入门的结果相加，实现了单元状态由Ct−1更新为Ct；最后通过输出门得到当前单元的隐藏状态ht。
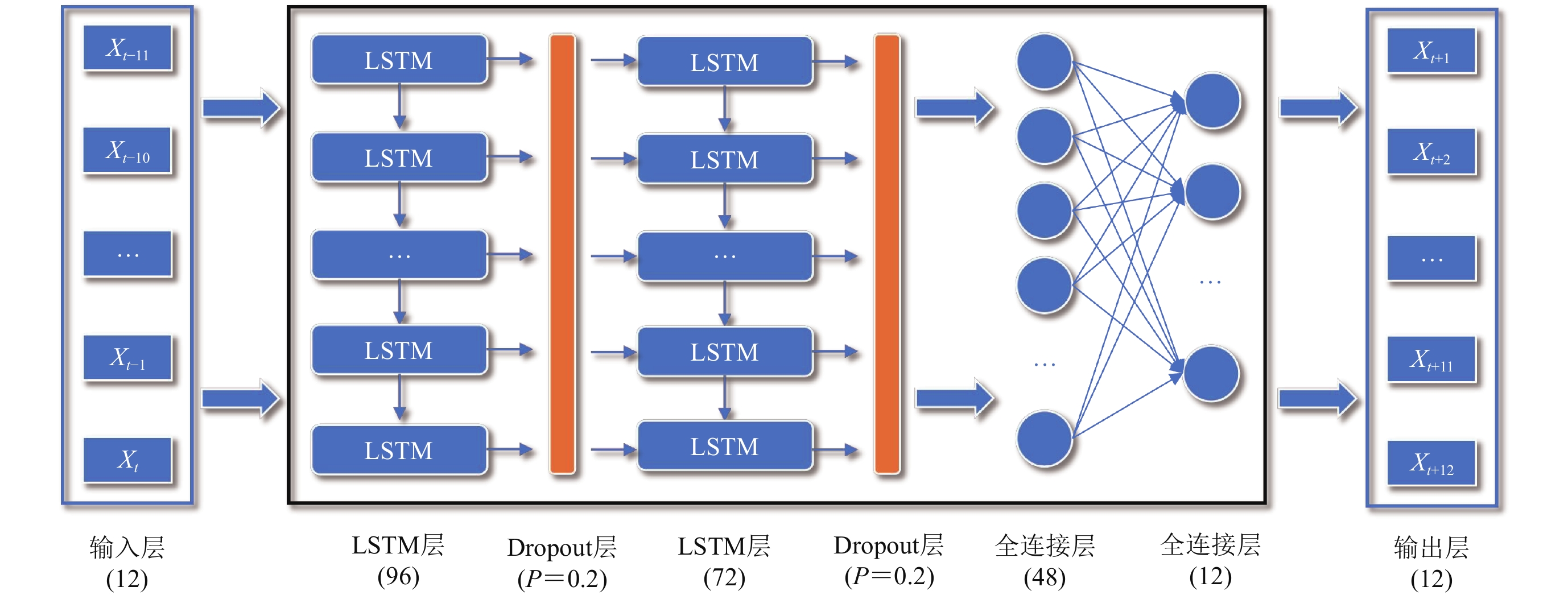
如图2所示，本文基于LSTM网络构建了5层的深度学习神经网络模型来预测主磁场长期变化。首先根据目标任务需求、数据规模和硬件资源设定神经网络初始结构为5层，然后在不同层设置不同神经元个数进行试验，每层的神经元个数从48，60，72，84，96，108中选取，得到不同的神经元组合。以训练集和测试集均方误差（MSE）接近并且测试集MSE尽可能小为原则，最终的网络结构和参数如下，输入数据为过去12个月的数据，第一、二个LSTM层分别有96个和72个神经元，为防止网络过拟合在每个LSTM层之后加入了Dropout层（神经元失活概率P＝0.2），这使得LSTM层的神经元在每次训练的过程中有20%的几率失活，增加了网络的泛化性。后面是两个全连接层分别有48个和12个神经元，最终输出层的结果即第二个全连接层的结果就是未来12个月的数据。本文构建的LSTM深度学习神经网络是基于TensorFlow2.1的Keras实现的，网络中激活函数选择ReLU函数，损失函数选择均方误差（MSE），更新权重量和偏置量的优化器选择适应性动量估计（adaptive moment estimation，缩写为Adam）算法，模型训练的硬件环境为NVIDIA Tesla T4 （16G）。
2. 数据处理
2.1 数据说明
本文选用中国大陆地区28个地磁台站1995年1月1日至2021年12月31日的地磁场水平分量H、磁偏角D、垂直分量Z的时均值。国家地磁台网中心对1985—1990年的历史资料系统收集整理，采用数码拍照和人工录入方式，并对数据质量进行审核，实现纸质资料数字化（张素琴等，2021）。利用该数据集结合国家地磁台网中心的历史数据，对长春、拉萨、广州、武汉、兰州、乌鲁木齐地磁台站数据进行扩充得到1985年1月1日至2021年12月31日水平分量H、磁偏角D、垂直分量Z的时均值。为提高模型的适用性，增加境外地磁台站数据以扩大模型预测的空间区域。考虑到境外地磁台站数据的连续性和稳定性，从INTERMAGNET获取IRT，KAK，KNY，GUA地磁台站1958年1月1日至2021年12月31日的地磁场水平分量H、磁偏角D、垂直分量Z的时均值。地磁台站分布如图3所示。
![]()
图 3 本文研究所用的地磁台站位置分布地形图来自于Natural Earth提供的公共地图数据集Figure 3. Location of geomagnetic observatories used in this paperRelief map is available from Natural Earth public domain map dataset2.2 提取长期变化
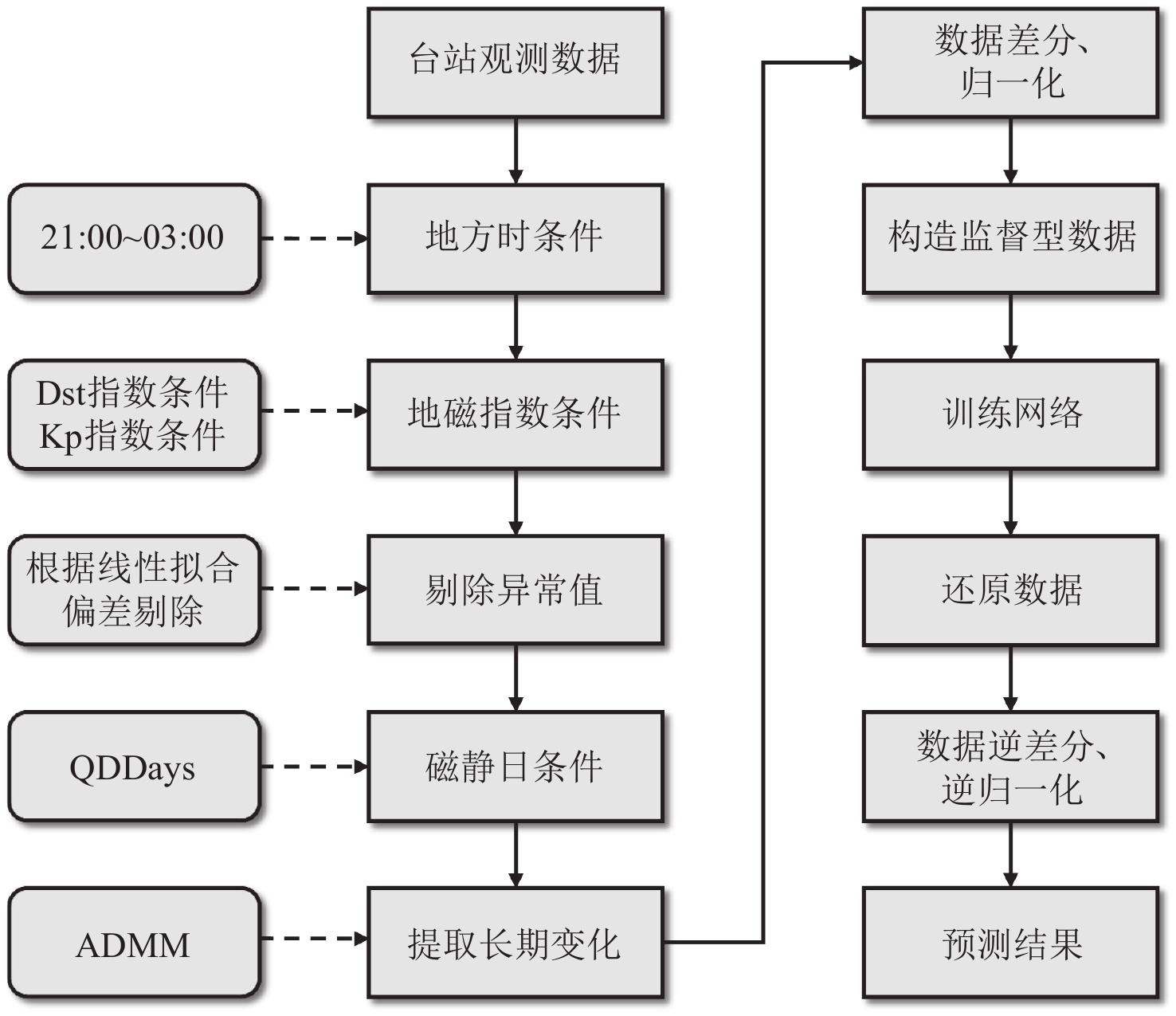
台站观测数据是内外多种场源叠加的结果，地球主磁场、地壳磁场和变化磁场各自有不同的时间变化特征。主磁场变化十分缓慢，每年一般是几十nT；地壳磁场几乎不随时间变化，但地震、火山等剧烈活动会造成局部地壳磁场的迅速变化；变化磁场主要是由高空电流体系与太阳风相互作用产生，虽然其强度比主磁场弱很多，但随时间的变化十分迅速。因此，在训练模型之前须通过各种数据筛选条件和算法来对数据进行预处理，尽可能地去除外源场的干扰，具体步骤如下：
1） 地方时条件。电离层潮汐风发电机电流会产生以太阳日为周期的太阳静日变化Sq。对于中低纬度地区，无磁暴等地磁扰动时，Sq是地磁场最主要的变化成分；而极区的Sq经常被淹没在亚暴的剧烈扰动中。Sq主要出现在白天，幅值变化白天大而迅速，夜间小而缓慢。因此为了最大程度地消除地磁静日变化Sq对主磁场观测数据的干扰，本文选取台站地方时为21:00—03:00的观测数据。
2） 地磁指数条件。为了抑制磁暴、亚暴、磁层大尺度对流等地磁扰动对台站观测数据的影响，本文根据国际地磁指数服务机构发布的Dst和Kp指数，参考岩石圈磁场建模过程中筛选卫星磁测数据的地磁指数条件（Maus et al，2008；Olsen et al，2014；Kother et al，2015），来对台站观测数据进行筛选，地磁指数条件如下：
$$ \left\{\begin{array}{l} \left|D_{{\mathrm{st}}}\right|\leqslant 10\,\,\, \,{\mathrm{nT}}\text{}\text{，} \text{}\dfrac{{\mathrm{d}}\left|D_{{\mathrm{st}}}\right|}{{\mathrm{d}}t}\leqslant 3\,\,{\mathrm{nT}}/{\mathrm{hour}}\\ K_{{\mathrm{p}}}\leqslant2\text{}\text{，} \text{}\dfrac{{\mathrm{d}}\left|K_{{\mathrm{p}}}\right|}{{\mathrm{d}}t}\leqslant2/3\,\,\,\,{\mathrm{hour}}\end{array}\right. $$ (9) 3） 剔除异常值。台站观测的时均值数据经过地方时和地磁指数条件筛选后计算得到不连续的日均值数据。本文认为主磁场长期变化在短时间内呈线性变化，所以将邻近的10个日均值数据分为一组，对每组数据进行线性拟合并计算每个点的偏差，然后得到每组数据偏差的上、下四分位点并将其设为阈值，最后剔除偏差超过阈值范围的日均值数据。
4） 磁静日条件。根据世界地磁数据中心（WDC for Geomagnetism）发布的磁静扰日数据，选择每月地磁场最为安静的5日，在上述剔除异常值的基础上进一步筛选数据，最终计算得到月均值数据。有些月份的日均值经过这四种预处理方法已无符合条件的日均值来计算月均值，对于缺失数据的月份用邻近两月的月均值数据线性插值得到。
5） 主磁场长期变化。本文通过地磁台站月均值年差分方法（annual differences of monthly means，缩写为ADMM）来计算得到长期变化年变率，这种方法可以在不引入平滑的情况下提取出长期变化趋势（Brown et al，2013）。ADMM具体计算公式如下：
$$ \frac{{\text{∂}}\boldsymbol{B}}{{\text{∂}} t} （ {t}_{n-6} ） ＝\boldsymbol{B} （ {t}_{n} ） -\boldsymbol{B} （ {t}_{n-12} ） \text{，} $$ (10) 式中，B是地磁场分量，t是时间，单位为mo。最后根据计算得到的长期变化年变率，进行积分计算得到主磁场D，H和Z各要素的长期变化序列。
2.3 训练模型前数据处理
1） 数据差分。由于地磁场各要素的长期变化序列本身就具有趋势性，若直接使用有着明显趋势性的数据进行网络训练，这种数据内在的趋势性会对网络的预测结果产生影响（Zhang，Qi，2005）。因此，我们通过差分法对长期变化序列进行处理，得到相邻两个月数据之间的变化量并输入网络中进行训练，最后将模型预测结果进行逆差分即可。这样我们就需关注连续数据之间的变化情况，忽视由数据本身的累计增加造成的趋势性，提高模型预测的准确性。
2） 数据归一化。数据归一化可以加快梯度下降求最优解的速度，同时提高模型预测的精度（Singh，Singh，2020）。将差分后的数据进行归一化处理，将数据映射转换到$ ［ $0，1$ ］ $，计算公式如下：
$$ {X_{{\mathrm{scaled}}}} ＝ \frac{{X - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}} $$ (11) 其中，X为原始数据，Xscaled为归一化后的数据，Xmax和Xmin别为原始数据的最大值和最小值。
2.4 数据增强
深度神经网络的优越性能依赖于大量的训练数据得以避免过度拟合和无法收敛，虽然本文已收集了宝贵的近30年时间长度的地磁台站数据，但所能收集到的地磁台站观测数据量距神经网络收敛的需求仍有差距，因此需对时序数据进行数据增强处理。时序数据增强方法主要分为直接增强法和间接增强法，直接增强法是在时频域内对原始数据进行诸如增加噪声、下采样、数据翻转、动态窗口扭曲等操作；间接增强法是基于统计分析模型和生成模型来产生新的时序数据，所采用得模型如自回归滑动平均模型（auto-regressive moving average model，缩写为ARMA）、深度生成模型（deep generative model，缩写为DGM）等（葛轶洲等，2021；Wen et al，2021）。本文采用增加噪声和数据翻转来对时序数据进行数据增强处理。
1） 增加噪声。向原始数据中增加均值为0、标准差为数据范围的5‰高斯噪声，得到增强后的数据集。
2） 数据翻转。数据翻转就是通过翻转原始时序数据X1，X2，···，XN生成新的时序数据$X'_1 $，$X'_2 $，···，$X'_{{N}} $的方法，其中XN＝$-X'_{{N}} $。
2.5 构造数据集
本文选用的是地磁台站的时均值，每个台站的D，H和Z要素经过上述数据筛选和数据增强处理过程得到月变化量；然后将数据构造为监督型数据集，前12个月数据变化量作为输入数据$ X $，后12个月数据变化量作为输出数据$ Y $。其中，前80%的数据作为训练集来训练网络，后20%的数据作为测试集来验证网络的泛化性。
2.6 模型训练
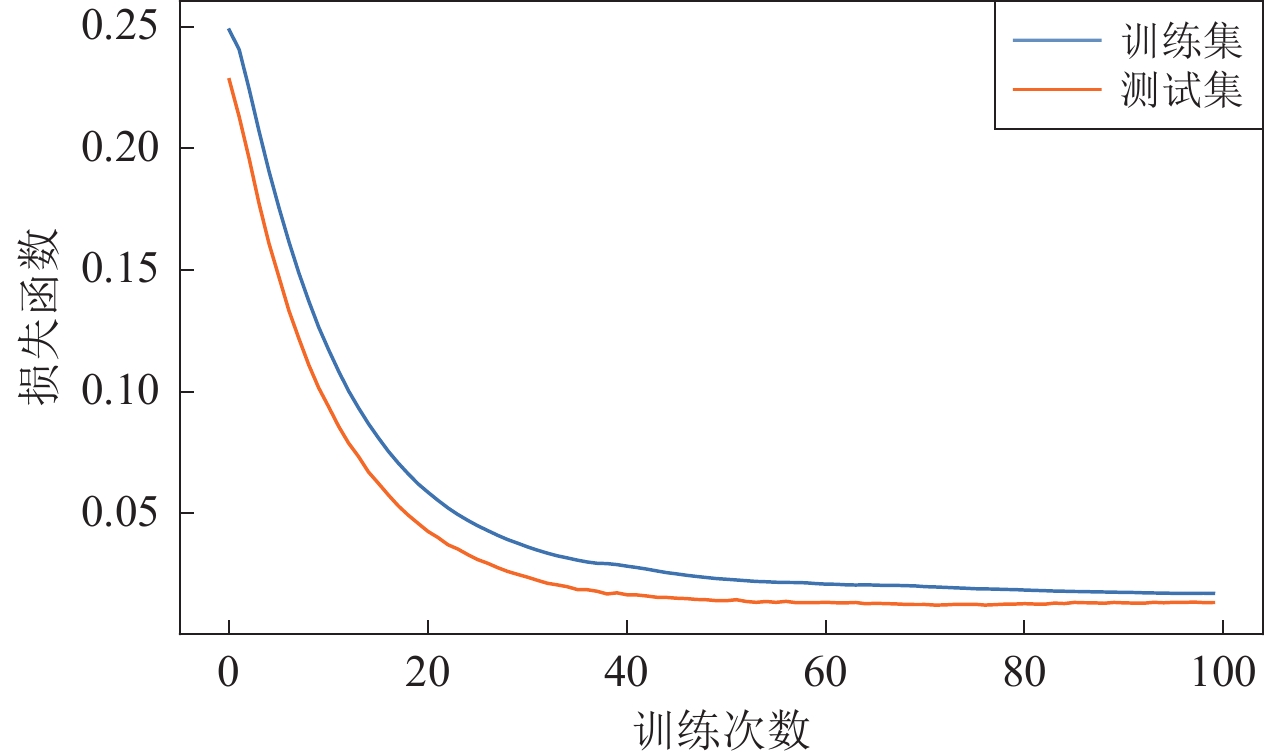
使用训练集训练已设定的网络模型，模型每进行一次参数更新，分别计算模型在训练集和测试集上的损失函数，当二者的损失函数相近且不再降低时，终止训练模型，认为此时的模型已学会处理此类数据的能力。将测试集数据输入训练所得的模型得到预测数据和测试集原有输出数据进行对比，以此判断所得网络的有效性。图5为模型训练过程中，每一次参数更新时损失函数的变化。
3. 结果与分析
3.1 精度评估
为了评估模型预报精度，本文使用均方根误差（root mean square error，缩写为RMSE）、平均绝对误差（mean absolute deviation，缩写为MAE）、归一化均方根误差（normalized root mean square error，缩写为NRMSE）以及决定系数R2作为评估预测模型精度的指标，公式如下：
$$ {\mathrm{RMSE}}＝\sqrt{\frac{\sum\limits _{i＝1}^{N} （ {y}_{i}-{\hat{y}}_{i}{ ） }^{2}}{N}} $$ (12) $$ {\mathrm{NEMSE}}＝\sqrt{\frac{\sum\limits _{i＝1}^{N} （ {y}_{i}^{{\mathrm{nor}}}-{\hat{y}}_{i}^{{\mathrm{nor}}}{ ） }^{2}}{N}} $$ (13) $$ {\mathrm{MAE}} ＝ \frac{1}{N}\sum\limits_{i ＝ 1}^N {\left| {{y_i} - {{\hat y}_i}} \right|} $$ (14) $$ _{^{}} {R}^{2}＝1-\frac{\sum\limits _{i＝1}^{N} （ {y}_{i}-{\hat y}_{i}{ ） }^{2}}{\sum\limits _{i＝1}^{N} （ {y}_{i}-{\bar y}_{i}{ ） }^{2}} $$ (15) $$ \bar y ＝ \frac{1}{N}\sum\limits_{i ＝ 1}^N {{y_i}} $$ (16) 式中，yi和${\hat y}_i $分别是i时刻地磁场各要素的观测值和模型预测值，${{y}}^{{{\mathrm{nor}}}}_{{i}} $和${\hat{y}}^{{{\mathrm{nor}}}}_{{i}} $分别是归一化后的观测值和模型预测值。RMSE中对平方项的引入，对较大的误差能够更加敏感，而且RMSE的单位与原始数据相同，其结果更容易被理解和解释。NRMSE是将数据进行归一化后再计算RMSE，这消除了由于数据量纲而对误差值的影响，更加关注于预测值与真实值之间的相对差异，确保不同量纲数据集之间的模型结果比较是有意义的，是一个综合考虑预测精度的指标。MAE使用了差异的绝对值，受异常值和正负值的影响较小，对大误差和小误差有着平等的关注，这使得MAE指标较为稳健。R2是评估模型对观测值拟合精度的统计指标，它表示模型对观测值变异性的解释比例。R2的取值范围一般在0到1之间，0表示模型的预测值与实际观测值没有关联，1表示模型的预测值与实际观测值完全一致，R2越大意味模型的拟合性能越好。R2一般不为负值，当R2为负值时，表示模型预测结果很差，比直接使用平均值预测的效果还要差。
3.2 长期变化
不同台站的不同要素其长期变化趋势是不完全一样的，因此本文针对各台站各要素都训练了特定的LSTM模型。本文计算了LSTM模型在各台站D，H和Z要素验证集上的精度评估指标，定量分析LSTM深度学习模型的预测精度，结果如表1和2所示。可见：LSTM模型预测的D要素MAE的变化范围0.229′—2.674′，RMSE变化范围为0.277′—3.062′； H要素MAE变化范围为0.96—24.03 nT，RMSE变化范围为1.94—24.03 nT；Z要素MAE变化范围为3.90—39.15 nT、RMSE变化范围为4.85—43.80 nT；D，H和Z要素的决定系数平均值分别为0.982，0.883和0.991，这表明LMTM模型能对数据进行很好的解释，对数据的拟合程度非常高；D，H和Z要素上的NRMSE平均值分别为0.040，0.086和0.026，与决定系数结合分析得出LSTM模型对Z要素预测精度最高，其次是D要素，预测精度最差的是H要素。
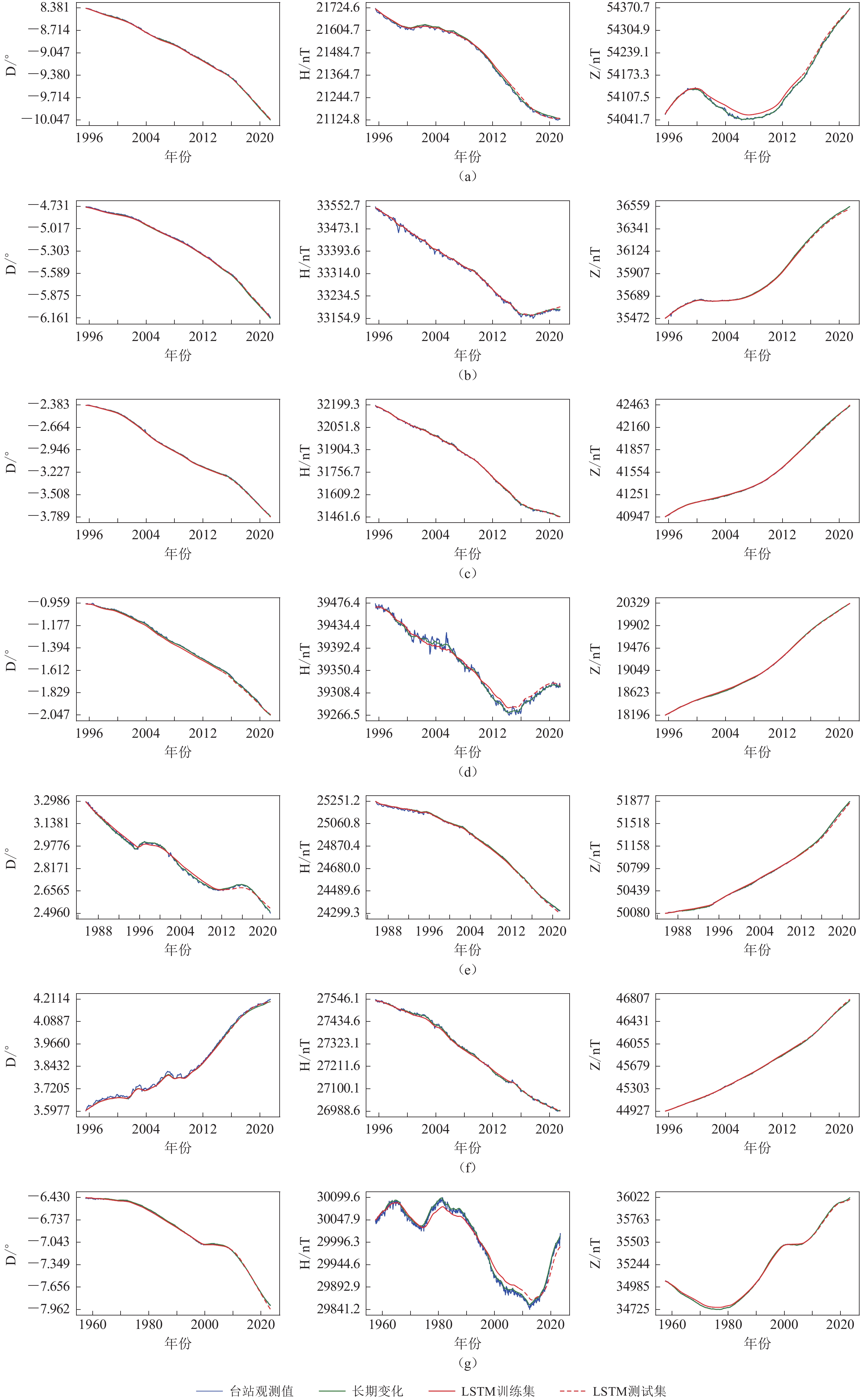
表 1 LSTM模型在各台站的预测精度Table 1. Prediction accuracy of LSTM model at each stationsD/´ H/nT Z/nT MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 CDP 0.615 0.837 0.037 0.991 15.265 17.04 0.039 0.927 9.66 10.28 0.012 0.999 CHL 0.983 1.072 0.030 0.994 11.45 13.14 0.074 0.959 5.82 6.51 0.038 0.998 CNH 1.254 1.362 0.037 0.988 15.58 16.83 0.072 0.873 7.91 9.10 0.026 0.992 COM 0.578 0.649 0.009 0.998 0.96 1.94 0.016 0.994 13.523 13.80 0.008 0.995 DED 0.386 0.452 0.014 0.999 6.34 7.17 0.024 0.989 3.90 4.85 0.052 0.996 DLG 0.516 0.551 0.018 0.998 10.587 11.41 0.073 0.959 11.293 12.56 0.024 0.993 GLM 1.438 1.683 0.121 0.929 8.31 10.05 0.040 0.985 12.933 14.27 0.014 0.998 GZH 2.640 2.776 0.022 0.930 10.03 10.81 0.084 0.569 8.51 10.92 0.022 0.998 JIH 0.823 0.901 0.026 0.996 11.086 12.83 0.043 0.968 4.56 7.03 0.019 0.998 JYG 0.670 0.772 0.036 0.993 10.112 11.17 0.042 0.989 6.91 8.49 0.014 0.999 KSH 0.229 0.277 0.023 0.998 3.01 4.01 0.024 0.995 9.53 11.27 0.013 0.998 LSA 0.857 0.920 0.158 0.897 4.27 5.56 0.022 0.886 39.15 43.80 0.019 0.979 LYH 0.591 0.681 0.032 0.998 11.912 13.32 0.065 0.966 12.787 13.26 0.029 0.996 LZH 1.347 1.513 0.057 0.975 7.88 9.33 0.047 0.985 14.20 21.60 0.025 0.991 MCH 1.004 1.248 0.030 0.991 12.940 13.89 0.041 0.906 16.467 17.87 0.033 0.993 MZL 0.430 0.504 0.028 0.995 9.12 9.82 0.052 0.987 7.39 8.12 0.023 0.991 QGZ 0.669 0.701 0.019 0.995 6.89 7.17 0.028 0.836 7.75 8.55 0.008 0.999 QIX 0.282 0.307 0.006 0.999 2.94 3.27 0.012 0.998 9.12 10.51 0.016 0.998 QZH 0.793 1.211 0.037 0.992 12.682 15.64 0.130 0.030 17.004 19.28 0.028 0.992 SYG 1.058 1.270 0.024 0.983 14.713 17.09 0.108 0.362 15.319 16.90 0.033 0.996 TAA 0.919 1.189 0.024 0.992 16.291 19.53 0.069 0.892 14.583 16.23 0.039 0.992 TAY 1.552 1.729 0.040 0.981 12.059 14.67 0.066 0.965 4.53 5.69 0.024 0.999 THJ 0.572 0.635 0.038 0.990 8.05 9.03 0.070 0.902 19.547 21.42 0.020 0.995 TSY 1.078 1.216 0.030 0.988 10.249 12.19 0.034 0.965 4.79 6.01 0.014 0.999 WHN 1.337 1.437 0.045 0.985 13.02 15.39 0.057 0.801 13.64 14.02 0.021 0.996 WMQ 0.899 0.982 0.086 0.926 10.67 12.09 0.018 0.987 28.81 30.12 0.015 0.985 XIC 0.577 0.674 0.048 0.990 4.11 5.11 0.023 0.988 9.72 16.31 0.020 0.997 YON 0.892 1.256 0.047 0.980 6.01 6.66 0.911 0.880 16.822 20.06 0.015 0.995 IRT 2.674 3.062 0.076 0.979 24.03 27.84 0.038 0.977 17.46 19.39 0.059 0.974 KAK 0.795 1.090 0.043 0.994 13.38 15.66 0.191 0.906 11.17 12.07 0.013 0.994 KNY 2.590 2.713 0.014 0.981 11.39 12.47 0.113 0.864 19.31 20.18 0.015 0.989 GUA 0.588 0.784 0.025 0.997 14.88 17.15 0.123 0.962 27.01 32.68 0.118 0.885 注：RMSE为均方根误差，MAE为平均绝对误差，NRMSE为归一化均方根误差，R2为决定系数，下同。 表 2 LSTM模型预测精度汇总Table 2. Summary for prediction accuracy of LSTM modelD/（´） H/（nT） Z/（nT） MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 Min 0.229 0.277 0.006 0.897 0.96 1.94 0.012 0.030 3.90 4.85 0.008 0.885 Max 2.674 3.062 0.158 0.999 24.03 27.84 0.911 0.998 39.15 43.80 0.118 0.999 Mean 0.989 1.139 0.040 0.982 10.32 11.85 0.086 0.883 13.16 15.10 0.026 0.991 本文选取地处不同经纬度且分布较为均匀的六个境内台站和一个境外台站来展示LSTM模型的预测效果。从图6中可以看出，整体上我国地磁台站D和H要素呈现下降趋势，Z要素呈现上升趋势，而KSH站的D要素呈现上升趋势；各要素长期变化呈现非线性变化趋势，其中D要素和Z要素长期变化趋势较为缓慢，而H要素易受到Sq电流体系和赤道电集流的干扰，其长期变化趋势中含有一部分外部短周期噪声。
![]()
图 6 LSTM模型在D （左） ，H （中），Z （右）要素的模型值与相应的台站观测值对比图中蓝实线是台站的观测值，绿实线是基于地磁台站观测值提取的长期变化，红实线是LSTM模型在训练集上的拟合值，红虚线是LSTM模型在测试集上的预测值（a） MZL台；（b） COM台；（c） QIX台；（d） QGZ台；（e） WMQ台；（f） KSH台；（g） KAK台Figure 6. Comparison of LSTM model values for elements D （left），H （middle） and Z （right） with corresponding station observationsThe blue solid line represents the station observation，the green solid line represents the secular variation extracted from the observations of the geomagnetic station，the red solid line represents the fitted value of the LSTM model on the training set，and the red dashed line represents the predicted value of the LSTM model on the validation set （a） MZL station；（b） COM station；（c） QIX station；（d） QGZ station；（e） WMQ station；（f） KSH station；（g） KAK station从表1看出：LSTM模型对于D和Z要素的预测效果很好，NRMSE较低且除LSA外其余台站的R2都在0.9以上，这表明该模型不仅能预测出D和Z要素的变化趋势，而且对于数值预测也有较好的性能；相较而言H要素的平均NRMSE较大，约是D和Z要素的2—4倍且R2较低；境内台站CHL，CNH，DLG，LYH，YON，TAA，WHN，TAY和境外台站KAK，KNY，GUA表现出R2较高但是NRMSE也较大，这表明模型能较好地预测长期变化趋势，但是对于数值预测精度低。在QZH，SYG和GZH台站R2显著偏低、NRMSE也较大，这表明模型对于长期变化趋势和数值的预测效果都较差。
模型在H要素预测精度较差主要有两个原因。其一，在磁静时期由于Sq电流体系和赤道电集流的分布，会直接影响地面台站H要素记录，尤其在地磁低纬地区H要素会显著变化（赵旭东等，2022）。这就导致H要素的长期变化信号中包含了较多不易消除的外部扰动，从而使变化特征更为复杂，进而使LSTM模型的预测精度降低、H要素的R2偏低和NRMSE偏大。其二，训练集样本数据较少，包含的长期变化信息不够全面，导致模型在训练集上能很好拟合，但在测试集上的预测精度较差。尽可能地扩充训练集样本量能改善这种情况，如GUA台站相较于QZH，SYG和GZH台站的地磁纬度更低，H要素长期变化信号中包含的外部噪声信号更多，但GUA台站的训练集数据量近乎是它们的两倍，训练集中包含了更多的长期变化信号，训练后的模型在测试集上的精度也更高。
3.3 年变率
在主磁场长期变化的研究中，通常计算地磁场各要素的年变率，以此来得到长期变化的强度变化与空间分布特征。目前地磁台站对于主磁场长期变化的预测主要依赖于IGRF，而IGRF仅采用线性外推的方式对球谐系数进行更新（阶次至8阶，空间分辨率约5 000 km），从而预测主磁场长期变化，这种方法预测的时效性较差，且不能准确地描述中国局部地区的地磁场长期变化特征（王振东等，2019；毛宁等，2023）。顾左文等（2009）利用NOC方法分析了地磁场的时空结构，其结果显示：时间域第一本征向量具有很好的线性特征，描述了主磁场长期变化的线性特征；时间域第二本征向量表现为二次曲线，描述了主磁场长期变化的非线性特征。线性外推和二次外推是构建中国地区长期变化预测模型的常用方法，因此本文分别计算由原始数据、线性外推法、二次外推法、LSTM模型得到的年变率，来分析一般方法与深度学习的优劣。
本文计算由线性外推法、二次外推法、LSTM模型这三种方法得到的年变率序列和原始年变率序列的精度评估指标，结果如表3所示。综合对比LSTM模型和线性外推、二次外推的精度指标可以得出，LSTM模型误差最小、精度最高，在D，H，Z要素RMSE的平均值分别为0.361′⋅a−1，3.921 nT⋅a−1，4.339 nT⋅a−1。线性外推、二次外推的误差都比LSTM模型误差要大，甚至可以达到3倍以上，而线性外推的结果要优于二次外推。值得注意的是，线性外推、二次外推在H要素$ {R}^{2} $平均值为0.075和−1.745，这表明两种外推法的预测结果与原始序列相关性很差，二次外推$ {R}^{2} $平均值甚至为负数，其预测结果比直接使用平均值预测的效果还差。
表 3 LSTM模型、线性外推、二次外推预测的D，H，Z要素年变率精度Table 3. The accuracy of annual rate for D，H，and Z elements predicted by LSTM model，liner extrapolation and quadratic extrapolation台站 D年变/（′⋅a−1） H年变/（nT⋅a−1） Z年变/（nT⋅a−1） 方法 MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $ CDP LSTM 0.222 0.288 0.195 0.942 4.545 5.545 0.424 0.785 2.674 3.368 0.140 0.981 线性外推 0.398 0.512 0.327 0.817 6.598 9.445 0.632 0.375 5.109 6.306 0.242 0.933 二次外推 0.354 0.475 0.354 0.843 14.88 18.814 0.885 −1.481 4.662 5.924 0.231 0.941 CHL LSTM 0.352 0.453 0.300 0.909 3.830 4.680 0.369 0.812 3.082 3.854 0.170 0.972 线性外推 0.660 0.895 0.506 0.645 5.492 6.839 0.508 0.600 4.543 5.908 0.232 0.934 二次外推 0.567 0.694 0.407 0.786 13.87 16.380 0.907 −1.297 8.046 10.042 0.402 0.809 CNH LSTM 0.337 0.502 0.318 0.884 3.576 4.534 0.358 0.859 3.128 4.152 0.206 0.957 线性外推 0.484 0.571 0.351 0.850 6.844 8.162 0.567 0.543 5.367 7.277 0.321 0.869 二次外推 0.672 1.156 0.619 0.384 12.81 15.556 0.821 −0.661 8.741 11.486 0.501 0.674 COM LSTM 0.151 0.197 0.124 0.984 0.894 1.837 0.181 0.959 1.615 2.782 0.102 0.988 线性外推 0.533 0.724 0.427 0.784 6.185 8.400 0.747 0.137 5.580 8.318 0.289 0.895 二次外推 0.516 0.638 0.388 0.832 11.92 14.526 0.936 −1.580 8.189 10.196 0.381 0.842 DED LSTM 0.219 0.305 0.210 0.954 2.066 2.549 0.172 0.966 2.749 3.516 0.217 0.954 线性外推 0.496 0.673 0.453 0.776 7.208 9.438 0.571 0.532 6.354 7.890 0.433 0.767 二次外推 0.890 1.148 0.685 0.349 12.10 14.817 0.761 −0.152 7.203 9.696 0.532 0.648 DLG LSTM 0.271 0.360 0.263 0.927 3.359 4.222 0.406 0.822 2.519 2.977 0.120 0.984 线性外推 0.496 0.676 0.448 0.743 5.587 6.965 0.555 0.516 5.463 7.079 0.272 0.909 二次外推 0.557 0.708 0.485 0.718 11.94 14.201 0.933 −1.011 6.792 8.964 0.356 0.853 GLM LSTM 0.501 0.656 0.422 0.807 3.091 3.631 0.318 0.837 3.110 3.993 0.176 0.969 线性外推 0.937 1.251 0.656 0.298 6.170 7.929 0.706 0.225 7.064 9.033 0.371 0.840 二次外推 0.944 1.201 0.679 0.353 14.41 17.390 1.028 −2.730 9.053 11.905 0.464 0.721 GZH LSTM 0.157 0.214 0.095 0.989 3.384 4.040 0.418 0.788 4.419 5.723 0.225 0.948 线性外推 0.266 0.416 0.187 0.958 5.803 7.141 0.626 0.337 8.291 12.332 0.447 0.760 二次外推 0.564 0.791 0.351 0.848 10.41 12.718 0.900 −1.102 10.125 14.212 0.501 0.681 JIH LSTM 0.216 0.303 0.224 0.947 2.725 3.395 0.305 0.900 2.274 3.333 0.141 0.981 线性外推 0.333 0.453 0.297 0.882 4.721 6.028 0.467 0.686 3.808 5.087 0.190 0.955 二次外推 0.544 0.671 0.471 0.741 12.91 15.893 0.879 −1.183 5.848 6.873 0.273 0.917 JYG LSTM 0.165 0.241 0.134 0.972 2.925 3.674 0.345 0.866 3.915 5.155 0.204 0.959 线性外推 0.768 0.984 0.533 0.537 7.782 10.522 0.767 −0.100 9.179 12.754 0.456 0.748 二次外推 0.618 0.780 0.442 0.709 11.04 13.002 0.731 −0.679 10.725 12.683 0.460 0.751 KSH LSTM 0.141 0.167 0.168 0.973 2.200 2.831 0.287 0.884 3.743 4.412 0.193 0.958 线性外推 0.972 1.657 1.110 −1.65 10.56 15.045 1.184 −2.276 8.898 11.765 0.486 0.701 二次外推 1.144 1.556 0.869 −1.34 13.10 15.314 0.878 −2.394 6.125 7.716 0.323 0.871 LSA LSTM 0.255 0.350 0.315 0.876 2.390 3.942 0.322 0.897 5.106 6.289 0.189 0.959 线性外推 0.578 0.768 0.598 0.405 8.991 11.874 0.759 0.063 8.145 10.640 0.319 0.883 二次外推 0.482 0.624 0.527 0.607 16.05 23.492 0.935 −2.667 6.962 8.610 0.264 0.923 LYH LSTM 0.490 0.659 0.490 0.718 3.755 4.766 0.406 0.811 2.603 3.202 0.132 0.983 线性外推 0.683 0.936 0.619 0.430 5.225 6.410 0.470 0.657 4.994 6.933 0.259 0.921 二次外推 1.019 1.635 0.841 −0.74 17.16 21.387 1.041 −2.816 5.337 6.504 0.248 0.930 LZH LSTM 0.411 0.536 0.336 0.837 3.988 4.797 0.420 0.774 2.785 4.536 0.176 0.951 线性外推 0.815 1.198 0.698 0.186 8.578 12.882 0.945 −0.627 5.358 7.398 0.328 0.871 二次外推 0.862 1.165 0.700 0.230 15.27 22.319 0.871 −3.883 10.247 13.422 0.562 0.575 MCH LSTM 0.261 0.340 0.246 0.920 2.495 3.633 0.291 0.892 4.396 5.115 0.199 0.962 线性外推 0.734 1.075 0.737 0.200 7.035 9.009 0.623 0.336 7.389 9.072 0.323 0.879 二次外推 0.692 0.853 0.579 0.496 18.39 21.430 0.989 −2.755 9.028 11.092 0.398 0.819 MZL LSTM 0.194 0.253 0.161 0.973 3.025 4.173 0.284 0.921 1.915 2.219 0.119 0.982 线性外推 0.563 0.710 0.398 0.791 5.268 6.800 0.400 0.791 5.328 6.679 0.365 0.832 二次外推 0.624 0.786 0.435 0.744 12.41 16.565 0.797 −0.242 6.961 8.457 0.449 0.731 QGZ LSTM 0.114 0.165 0.126 0.969 2.116 2.858 0.316 0.896 2.863 4.121 0.159 0.974 线性外推 0.582 0.766 0.656 0.326 8.834 11.160 0.949 −0.586 6.213 7.912 0.284 0.905 二次外推 0.734 0.893 0.603 0.085 14.86 18.402 1.081 −3.311 8.916 11.902 0.428 0.785 QIX LSTM 0.077 0.145 0.110 0.985 0.816 0.975 0.071 0.991 2.753 3.986 0.161 0.975 线性外推 0.459 0.563 0.368 0.779 7.115 8.569 0.673 0.306 4.923 6.140 0.229 0.940 二次外推 0.513 0.735 0.484 0.623 13.97 17.477 0.980 −1.885 8.186 10.228 0.380 0.833 QZH LSTM 0.228 0.368 0.214 0.916 3.793 5.074 0.506 0.734 4.675 5.604 0.222 0.950 线性外推 0.657 0.910 0.608 0.485 7.955 9.824 0.764 0.002 4.997 6.433 0.233 0.935 二次外推 0.620 0.792 0.503 0.610 15.60 19.366 1.025 −2.877 6.195 8.256 0.309 0.892 SYG LSTM 0.246 0.351 0.324 0.885 3.743 5.301 0.374 0.801 4.216 5.357 0.189 0.964 线性外推 0.438 0.602 0.449 0.660 11.89 17.502 1.079 −1.164 5.255 6.877 0.223 0.941 二次外推 0.624 0.772 0.576 0.442 16.81 19.542 1.052 −1.697 6.784 9.348 0.312 0.891 TAA LSTM 0.276 0.357 0.279 0.913 4.464 5.181 0.494 0.766 4.029 4.650 0.192 0.963 线性外推 0.487 0.703 0.489 0.663 7.638 9.009 0.671 0.293 6.313 8.079 0.306 0.889 二次外推 0.467 0.591 0.435 0.762 12.19 14.390 0.814 −0.803 6.354 9.361 0.360 0.851 TAY LSTM 0.575 0.774 0.494 0.646 4.511 5.512 0.436 0.775 3.337 4.486 0.198 0.962 线性外推 0.954 1.328 0.740 −0.04 9.085 11.003 0.750 0.103 6.555 8.597 0.345 0.860 二次外推 1.517 1.980 0.945 −1.31 18.75 28.224 1.098 −4.902 6.905 8.272 0.336 0.871 THJ LSTM 0.174 0.207 0.164 0.958 3.185 4.323 0.419 0.830 3.677 4.883 0.214 0.954 线性外推 0.342 0.449 0.341 0.805 6.149 7.727 0.577 0.457 4.817 6.475 0.262 0.920 二次外推 0.307 0.368 0.329 0.868 12.07 14.113 0.824 −0.811 5.103 6.332 0.263 0.923 TSY LSTM 0.283 0.353 0.254 0.923 5.178 6.948 0.691 0.498 3.513 4.464 0.188 0.965 线性外推 0.634 0.815 0.519 0.591 10.36 14.890 1.057 −1.308 5.861 8.257 0.325 0.880 二次外推 0.544 0.740 0.500 0.662 13.63 16.474 1.058 −1.825 6.355 7.402 0.297 0.904 WHN LSTM 0.192 0.326 0.199 0.929 3.269 4.208 0.393 0.801 4.148 5.250 0.215 0.947 线性外涂 0.556 0.767 0.540 0.605 5.735 7.552 0.607 0.360 8.213 14.070 0.532 0.621 二次外推 0.641 0.827 0.528 0.541 9.705 12.099 0.842 −0.642 9.227 13.362 0.481 0.658 WMQ LSTM 0.347 0.466 0.390 0.817 1.504 2.034 0.154 0.974 3.802 4.501 0.169 0.970 线性外推 0.659 1.002 0.711 0.153 6.708 8.291 0.577 0.576 7.164 8.661 0.303 0.890 二次外推 0.738 1.091 0.790 −0.004 8.861 11.928 0.664 0.123 9.198 12.274 0.418 0.779 XIC LSTM 0.268 0.316 0.248 0.909 1.979 2.509 0.172 0.969 4.144 5.646 0.190 0.958 线性外推 0.572 0.799 0.591 0.420 8.932 12.246 0.647 0.272 8.479 11.392 0.369 0.830 二次外推 0.663 0.885 0.560 0.290 19.14 24.864 0.887 −2.003 12.220 16.116 0.470 0.660 YON LSTM 0.245 0.331 0.322 0.851 1.917 2.467 0.180 0.952 2.767 3.911 0.158 0.975 线性外推 0.420 0.527 0.489 0.622 6.527 8.712 0.603 0.407 4.585 6.065 0.222 0.940 二次外推 0.502 0.745 0.636 0.246 11.47 13.378 0.775 −0.398 6.459 7.450 0.286 0.909 IRT LSTM 0.532 0.796 0.260 0.914 3.619 4.408 0.214 0.950 3.774 5.111 0.218 0.949 线性外推 0.750 1.001 0.341 0.865 5.788 7.471 0.351 0.856 7.499 10.957 0.449 0.764 二次外推 0.971 1.209 0.408 0.803 8.129 11.606 0.526 0.652 11.499 15.821 0.595 0.508 KAK LSTM 0.178 0.254 0.216 0.944 2.500 3.221 0.314 0.888 0.345 2.891 0.117 0.984 线性外推 0.266 0.335 0.293 0.902 4.618 6.035 0.541 0.608 4.186 0.889 0.198 0.955 二次外推 0.342 0.471 0.419 0.806 8.103 11.395 0.864 −0.399 5.543 7.227 0.301 0.902 KNY LSTM 0.178 0.264 0.208 0.957 2.842 3.604 0.347 0.873 2.350 2.893 0.116 0.986 线性外推 0.233 0.291 0.215 0.948 4.799 6.127 0.514 0.634 3.687 4.623 0.178 0.963 二次外推 0.340 0.465 0.333 0.867 8.297 11.233 0.763 −0.232 5.078 6.300 0.251 0.932 GUA LSTM 0.155 0.195 0.142 0.979 3.154 4.112 0.319 0.889 3.871 5.472 0.172 0.970 线性外推 0.352 0.453 0.321 0.887 6.679 8.376 0.591 0.541 6.561 8.524 0.252 0.927 二次外推 0.391 0.458 0.324 0.885 11.55 14.381 0.815 −0.354 5.756 8.547 0.251 0.927 表 4 LSTM模型、线性外推和二次外推预测的各要素年变率精度汇总Table 4. Summary of annual rate accuracy for elements predicted by LSTM model，linear extrapolation and quadratic extrapolation方法 D年变/（′⋅a−1） H年变/（nT⋅a−1） Z年变/（nT⋅a−1） MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $
LSTMMin 0.077 0.145 0.095 0.646 0.816 0.975 0.071 0.498 0.345 2.219 0.102 0.947 Max 0.575 0.796 0.494 0.989 5.178 6.948 0.691 0.991 5.106 6.289 0.225 0.988 Mean 0.264 0.361 0.251 0.909 3.021 3.921 0.335 0.854 3.283 4.339 0.177 0.966
线性外推Min 0.233 0.291 0.187 −1.653 4.618 6.028 0.351 −2.276 3.687 0.889 0.178 0.621 Max 0.972 1.657 1.110 0.958 11.89 17.502 1.184 0.856 9.179 14.070 0.532 0.963 Mean 0.568 0.777 0.502 0.541 7.160 9.374 0.676 0.150 6.185 8.173 0.320 0.866
二次外推Min 0.307 0.368 0.324 −1.340 8.103 11.233 0.526 −4.902 5.078 6.300 0.248 0.489 Max 1.517 1.980 0.945 0.885 19.14 28.224 1.098 0.652 12.220 16.116 0.595 0.932 Mean 0.663 0.889 0.546 0.416 13.15 16.652 0.885 −1.499 7.800 10.133 0.389 0.796 从图6可以看出，由LSTM模型得到的年变率序列与原始数据的年变率序列之间的一致性较好，而线性外推、二次外推由于本身算法的缺陷导致得到的年变率序列在原始年变率序列附近振荡。结合图5可以发现：当主磁场要素长期变化较为平缓时，线性外推、二次外推有不错的结果；但当出现拐点或变化趋势出现轻微改变时，线性外推、二次外推法得到的年变率便会有较大的误差，特别是在易受到外部电流体系干扰的H要素，二次外推得到的年变率序列会产生更大的波动，最大可达原始数据年变率的3倍以上。
![]()
图 7 由LSTM、线性外推、二次外推法得到的D （左），H （中）和Z（右）要素年变率图中蓝线表示由原始数据计算的年变率，红线表示由LSTM模型计算的年变率，绿线表示由线性外推计算的年变率，黄线表示由二次外推计算的年变率（a） MZL台；（b） COM台；（c） QIX台；（d） QGZ台；（e） WMQ台；（f） KSH台；（g） KAK台Figure 7. Annual variation rates of the elements D （left），H （middle） and Z （right） obtained from LSTM，Liner extrapolation and Quadratic extrapolationThe blue line represents the annual variation rates calculated from the original data，the red line represents the annual variation rates calculated from the LSTM model，the green line represents the annual variation rates calculated from the linear extrapolation，and the yellow line represents the annual variation rates calculated from the Quadratic extrapolation （a） MZL station；（b） COM station；（c） QIX station；（d） QGZ station；（e） WMQ station；（f） KSH station；（g） KAK station4. 讨论与结论
本文选取中国大陆地区28个地磁台站和4个境外地磁台站的地磁场D，H和Z要素的时均值数据，通过各种磁静条件筛选并剔除异常值计算得到月均值，再通过月均值年差分提取出主磁场各要素的长期变化信号。利用深度学习方法，构造了LSTM深度学习模型用上一年的地磁场数据来预测未来一年的地磁场数据，评估了LSTM模型的精度，并与一般线性外推、二次外推的精度进行对比分析，得到以下结论：
1） LSTM深度学习模型在地磁场D、H、Z要素验证集上的精度如下：D要素MAE，RMSE，NRMSE，R2的平均值分别为0.989'，1.139'，0.040，0.982；H要素MAE，RMSE，NRMSE，R2的平均值分别为10.32 nT，11.85 nT，0.086，0.883；Z要素MAE，RMSE，NRMSE，R2的平均值分别为13.16 nT，15.10 nT，0.026，0.991。通过分析三个要素的NRMSE得到LSTM模型对Z要素的预测精度最高，其次是D要素，精度最差的是H要素。
2） 将LSTM模型预测的各要素地磁场数据计算的年变率与一般线性外推、二次外推得到的年变率进行比较分析。LSTM模型在D，H，Z要素RMSE的平均值分别为0.361′⋅a−1，3.921 nT⋅a−1，4.339 nT⋅a−1，由LSTM模型预测数据计算得到的年变率更接近于实际数据的年变率。LSTM模型相较于线性外推法在D，H和Z要素年变率的预测精度提升了54%，58%，47%；相较于二次外推法在D，H和Z要素年变率的预测精度提升了59%，76%，57%。
3） 对于中国大陆地区地磁台站而言，LSTM模型能较好地根据过去一年数据来对未来一年的数据进行预测，且在年变率的预测上较一般方法有很大的提升，预测精度最高的是Z要素，其次是D要素，最差是H要素。
4） 造成LSTM模型在H要素预测精度低主要有两个原因：其一是由于Sq电流体系和赤道电集流的分布，H要素的长期变化信号中包含了外部噪声，变化特征较为复杂；其二是训练集样本数据较少，包含的长期变化信息不够全面，在个别台站训练集很好拟合，在测试集预测精度差。
本文建立了LSTM模型用前一年数据对未来一年数据进行预测，基于LSTM网络的特点，输入进网络中数据包含的长期变化信息越多，对于未来一年数据的预测效果越好。因此未来打算利用三年或五年数据来对未来一年数据进行预测。
本文针对各台站各要素分别训练了预测模型，但由于各台站各要素长期变化之间有一定的关联性，因此未来打算基于最新的Transformer网络架构并考虑台站之间的空间位置关系，综合建立起中国地区地磁场各要素长期变化预测模型。
感谢中国地震局地球物理研究所地磁台网中心和INTERMAGNET提供高质量的地磁台站观测数据，感谢世界地磁数据中心（WDC for Geomagnetism）提供的地磁指数和磁静扰日数据。感谢两位匿名审稿人对本文提出的建设性意见和建议。
-
![]()
图 3 本文研究所用的地磁台站位置分布
地形图来自于Natural Earth提供的公共地图数据集
Figure 3. Location of geomagnetic observatories used in this paper
Relief map is available from Natural Earth public domain map dataset
![]()
图 6 LSTM模型在D （左） ，H （中），Z （右）要素的模型值与相应的台站观测值对比
图中蓝实线是台站的观测值，绿实线是基于地磁台站观测值提取的长期变化，红实线是LSTM模型在训练集上的拟合值，红虚线是LSTM模型在测试集上的预测值（a） MZL台；（b） COM台；（c） QIX台；（d） QGZ台；（e） WMQ台；（f） KSH台；（g） KAK台
Figure 6. Comparison of LSTM model values for elements D （left），H （middle） and Z （right） with corresponding station observations
The blue solid line represents the station observation，the green solid line represents the secular variation extracted from the observations of the geomagnetic station，the red solid line represents the fitted value of the LSTM model on the training set，and the red dashed line represents the predicted value of the LSTM model on the validation set （a） MZL station；（b） COM station；（c） QIX station；（d） QGZ station；（e） WMQ station；（f） KSH station；（g） KAK station
![]()
图 7 由LSTM、线性外推、二次外推法得到的D （左），H （中）和Z（右）要素年变率
图中蓝线表示由原始数据计算的年变率，红线表示由LSTM模型计算的年变率，绿线表示由线性外推计算的年变率，黄线表示由二次外推计算的年变率（a） MZL台；（b） COM台；（c） QIX台；（d） QGZ台；（e） WMQ台；（f） KSH台；（g） KAK台
Figure 7. Annual variation rates of the elements D （left），H （middle） and Z （right） obtained from LSTM，Liner extrapolation and Quadratic extrapolation
The blue line represents the annual variation rates calculated from the original data，the red line represents the annual variation rates calculated from the LSTM model，the green line represents the annual variation rates calculated from the linear extrapolation，and the yellow line represents the annual variation rates calculated from the Quadratic extrapolation （a） MZL station；（b） COM station；（c） QIX station；（d） QGZ station；（e） WMQ station；（f） KSH station；（g） KAK station
表 1 LSTM模型在各台站的预测精度
Table 1 Prediction accuracy of LSTM model at each stations
D/´ H/nT Z/nT MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 CDP 0.615 0.837 0.037 0.991 15.265 17.04 0.039 0.927 9.66 10.28 0.012 0.999 CHL 0.983 1.072 0.030 0.994 11.45 13.14 0.074 0.959 5.82 6.51 0.038 0.998 CNH 1.254 1.362 0.037 0.988 15.58 16.83 0.072 0.873 7.91 9.10 0.026 0.992 COM 0.578 0.649 0.009 0.998 0.96 1.94 0.016 0.994 13.523 13.80 0.008 0.995 DED 0.386 0.452 0.014 0.999 6.34 7.17 0.024 0.989 3.90 4.85 0.052 0.996 DLG 0.516 0.551 0.018 0.998 10.587 11.41 0.073 0.959 11.293 12.56 0.024 0.993 GLM 1.438 1.683 0.121 0.929 8.31 10.05 0.040 0.985 12.933 14.27 0.014 0.998 GZH 2.640 2.776 0.022 0.930 10.03 10.81 0.084 0.569 8.51 10.92 0.022 0.998 JIH 0.823 0.901 0.026 0.996 11.086 12.83 0.043 0.968 4.56 7.03 0.019 0.998 JYG 0.670 0.772 0.036 0.993 10.112 11.17 0.042 0.989 6.91 8.49 0.014 0.999 KSH 0.229 0.277 0.023 0.998 3.01 4.01 0.024 0.995 9.53 11.27 0.013 0.998 LSA 0.857 0.920 0.158 0.897 4.27 5.56 0.022 0.886 39.15 43.80 0.019 0.979 LYH 0.591 0.681 0.032 0.998 11.912 13.32 0.065 0.966 12.787 13.26 0.029 0.996 LZH 1.347 1.513 0.057 0.975 7.88 9.33 0.047 0.985 14.20 21.60 0.025 0.991 MCH 1.004 1.248 0.030 0.991 12.940 13.89 0.041 0.906 16.467 17.87 0.033 0.993 MZL 0.430 0.504 0.028 0.995 9.12 9.82 0.052 0.987 7.39 8.12 0.023 0.991 QGZ 0.669 0.701 0.019 0.995 6.89 7.17 0.028 0.836 7.75 8.55 0.008 0.999 QIX 0.282 0.307 0.006 0.999 2.94 3.27 0.012 0.998 9.12 10.51 0.016 0.998 QZH 0.793 1.211 0.037 0.992 12.682 15.64 0.130 0.030 17.004 19.28 0.028 0.992 SYG 1.058 1.270 0.024 0.983 14.713 17.09 0.108 0.362 15.319 16.90 0.033 0.996 TAA 0.919 1.189 0.024 0.992 16.291 19.53 0.069 0.892 14.583 16.23 0.039 0.992 TAY 1.552 1.729 0.040 0.981 12.059 14.67 0.066 0.965 4.53 5.69 0.024 0.999 THJ 0.572 0.635 0.038 0.990 8.05 9.03 0.070 0.902 19.547 21.42 0.020 0.995 TSY 1.078 1.216 0.030 0.988 10.249 12.19 0.034 0.965 4.79 6.01 0.014 0.999 WHN 1.337 1.437 0.045 0.985 13.02 15.39 0.057 0.801 13.64 14.02 0.021 0.996 WMQ 0.899 0.982 0.086 0.926 10.67 12.09 0.018 0.987 28.81 30.12 0.015 0.985 XIC 0.577 0.674 0.048 0.990 4.11 5.11 0.023 0.988 9.72 16.31 0.020 0.997 YON 0.892 1.256 0.047 0.980 6.01 6.66 0.911 0.880 16.822 20.06 0.015 0.995 IRT 2.674 3.062 0.076 0.979 24.03 27.84 0.038 0.977 17.46 19.39 0.059 0.974 KAK 0.795 1.090 0.043 0.994 13.38 15.66 0.191 0.906 11.17 12.07 0.013 0.994 KNY 2.590 2.713 0.014 0.981 11.39 12.47 0.113 0.864 19.31 20.18 0.015 0.989 GUA 0.588 0.784 0.025 0.997 14.88 17.15 0.123 0.962 27.01 32.68 0.118 0.885 注：RMSE为均方根误差，MAE为平均绝对误差，NRMSE为归一化均方根误差，R2为决定系数，下同。 
下载: 导出CSV
表 2 LSTM模型预测精度汇总
Table 2 Summary for prediction accuracy of LSTM model
D/（´） H/（nT） Z/（nT） MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 MAE RMSE NRMSE R2 Min 0.229 0.277 0.006 0.897 0.96 1.94 0.012 0.030 3.90 4.85 0.008 0.885 Max 2.674 3.062 0.158 0.999 24.03 27.84 0.911 0.998 39.15 43.80 0.118 0.999 Mean 0.989 1.139 0.040 0.982 10.32 11.85 0.086 0.883 13.16 15.10 0.026 0.991
下载: 导出CSV
表 3 LSTM模型、线性外推、二次外推预测的D，H，Z要素年变率精度
Table 3 The accuracy of annual rate for D，H，and Z elements predicted by LSTM model，liner extrapolation and quadratic extrapolation
台站 D年变/（′⋅a−1） H年变/（nT⋅a−1） Z年变/（nT⋅a−1） 方法 MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $ CDP LSTM 0.222 0.288 0.195 0.942 4.545 5.545 0.424 0.785 2.674 3.368 0.140 0.981 线性外推 0.398 0.512 0.327 0.817 6.598 9.445 0.632 0.375 5.109 6.306 0.242 0.933 二次外推 0.354 0.475 0.354 0.843 14.88 18.814 0.885 −1.481 4.662 5.924 0.231 0.941 CHL LSTM 0.352 0.453 0.300 0.909 3.830 4.680 0.369 0.812 3.082 3.854 0.170 0.972 线性外推 0.660 0.895 0.506 0.645 5.492 6.839 0.508 0.600 4.543 5.908 0.232 0.934 二次外推 0.567 0.694 0.407 0.786 13.87 16.380 0.907 −1.297 8.046 10.042 0.402 0.809 CNH LSTM 0.337 0.502 0.318 0.884 3.576 4.534 0.358 0.859 3.128 4.152 0.206 0.957 线性外推 0.484 0.571 0.351 0.850 6.844 8.162 0.567 0.543 5.367 7.277 0.321 0.869 二次外推 0.672 1.156 0.619 0.384 12.81 15.556 0.821 −0.661 8.741 11.486 0.501 0.674 COM LSTM 0.151 0.197 0.124 0.984 0.894 1.837 0.181 0.959 1.615 2.782 0.102 0.988 线性外推 0.533 0.724 0.427 0.784 6.185 8.400 0.747 0.137 5.580 8.318 0.289 0.895 二次外推 0.516 0.638 0.388 0.832 11.92 14.526 0.936 −1.580 8.189 10.196 0.381 0.842 DED LSTM 0.219 0.305 0.210 0.954 2.066 2.549 0.172 0.966 2.749 3.516 0.217 0.954 线性外推 0.496 0.673 0.453 0.776 7.208 9.438 0.571 0.532 6.354 7.890 0.433 0.767 二次外推 0.890 1.148 0.685 0.349 12.10 14.817 0.761 −0.152 7.203 9.696 0.532 0.648 DLG LSTM 0.271 0.360 0.263 0.927 3.359 4.222 0.406 0.822 2.519 2.977 0.120 0.984 线性外推 0.496 0.676 0.448 0.743 5.587 6.965 0.555 0.516 5.463 7.079 0.272 0.909 二次外推 0.557 0.708 0.485 0.718 11.94 14.201 0.933 −1.011 6.792 8.964 0.356 0.853 GLM LSTM 0.501 0.656 0.422 0.807 3.091 3.631 0.318 0.837 3.110 3.993 0.176 0.969 线性外推 0.937 1.251 0.656 0.298 6.170 7.929 0.706 0.225 7.064 9.033 0.371 0.840 二次外推 0.944 1.201 0.679 0.353 14.41 17.390 1.028 −2.730 9.053 11.905 0.464 0.721 GZH LSTM 0.157 0.214 0.095 0.989 3.384 4.040 0.418 0.788 4.419 5.723 0.225 0.948 线性外推 0.266 0.416 0.187 0.958 5.803 7.141 0.626 0.337 8.291 12.332 0.447 0.760 二次外推 0.564 0.791 0.351 0.848 10.41 12.718 0.900 −1.102 10.125 14.212 0.501 0.681 JIH LSTM 0.216 0.303 0.224 0.947 2.725 3.395 0.305 0.900 2.274 3.333 0.141 0.981 线性外推 0.333 0.453 0.297 0.882 4.721 6.028 0.467 0.686 3.808 5.087 0.190 0.955 二次外推 0.544 0.671 0.471 0.741 12.91 15.893 0.879 −1.183 5.848 6.873 0.273 0.917 JYG LSTM 0.165 0.241 0.134 0.972 2.925 3.674 0.345 0.866 3.915 5.155 0.204 0.959 线性外推 0.768 0.984 0.533 0.537 7.782 10.522 0.767 −0.100 9.179 12.754 0.456 0.748 二次外推 0.618 0.780 0.442 0.709 11.04 13.002 0.731 −0.679 10.725 12.683 0.460 0.751 KSH LSTM 0.141 0.167 0.168 0.973 2.200 2.831 0.287 0.884 3.743 4.412 0.193 0.958 线性外推 0.972 1.657 1.110 −1.65 10.56 15.045 1.184 −2.276 8.898 11.765 0.486 0.701 二次外推 1.144 1.556 0.869 −1.34 13.10 15.314 0.878 −2.394 6.125 7.716 0.323 0.871 LSA LSTM 0.255 0.350 0.315 0.876 2.390 3.942 0.322 0.897 5.106 6.289 0.189 0.959 线性外推 0.578 0.768 0.598 0.405 8.991 11.874 0.759 0.063 8.145 10.640 0.319 0.883 二次外推 0.482 0.624 0.527 0.607 16.05 23.492 0.935 −2.667 6.962 8.610 0.264 0.923 LYH LSTM 0.490 0.659 0.490 0.718 3.755 4.766 0.406 0.811 2.603 3.202 0.132 0.983 线性外推 0.683 0.936 0.619 0.430 5.225 6.410 0.470 0.657 4.994 6.933 0.259 0.921 二次外推 1.019 1.635 0.841 −0.74 17.16 21.387 1.041 −2.816 5.337 6.504 0.248 0.930 LZH LSTM 0.411 0.536 0.336 0.837 3.988 4.797 0.420 0.774 2.785 4.536 0.176 0.951 线性外推 0.815 1.198 0.698 0.186 8.578 12.882 0.945 −0.627 5.358 7.398 0.328 0.871 二次外推 0.862 1.165 0.700 0.230 15.27 22.319 0.871 −3.883 10.247 13.422 0.562 0.575 MCH LSTM 0.261 0.340 0.246 0.920 2.495 3.633 0.291 0.892 4.396 5.115 0.199 0.962 线性外推 0.734 1.075 0.737 0.200 7.035 9.009 0.623 0.336 7.389 9.072 0.323 0.879 二次外推 0.692 0.853 0.579 0.496 18.39 21.430 0.989 −2.755 9.028 11.092 0.398 0.819 MZL LSTM 0.194 0.253 0.161 0.973 3.025 4.173 0.284 0.921 1.915 2.219 0.119 0.982 线性外推 0.563 0.710 0.398 0.791 5.268 6.800 0.400 0.791 5.328 6.679 0.365 0.832 二次外推 0.624 0.786 0.435 0.744 12.41 16.565 0.797 −0.242 6.961 8.457 0.449 0.731 QGZ LSTM 0.114 0.165 0.126 0.969 2.116 2.858 0.316 0.896 2.863 4.121 0.159 0.974 线性外推 0.582 0.766 0.656 0.326 8.834 11.160 0.949 −0.586 6.213 7.912 0.284 0.905 二次外推 0.734 0.893 0.603 0.085 14.86 18.402 1.081 −3.311 8.916 11.902 0.428 0.785 QIX LSTM 0.077 0.145 0.110 0.985 0.816 0.975 0.071 0.991 2.753 3.986 0.161 0.975 线性外推 0.459 0.563 0.368 0.779 7.115 8.569 0.673 0.306 4.923 6.140 0.229 0.940 二次外推 0.513 0.735 0.484 0.623 13.97 17.477 0.980 −1.885 8.186 10.228 0.380 0.833 QZH LSTM 0.228 0.368 0.214 0.916 3.793 5.074 0.506 0.734 4.675 5.604 0.222 0.950 线性外推 0.657 0.910 0.608 0.485 7.955 9.824 0.764 0.002 4.997 6.433 0.233 0.935 二次外推 0.620 0.792 0.503 0.610 15.60 19.366 1.025 −2.877 6.195 8.256 0.309 0.892 SYG LSTM 0.246 0.351 0.324 0.885 3.743 5.301 0.374 0.801 4.216 5.357 0.189 0.964 线性外推 0.438 0.602 0.449 0.660 11.89 17.502 1.079 −1.164 5.255 6.877 0.223 0.941 二次外推 0.624 0.772 0.576 0.442 16.81 19.542 1.052 −1.697 6.784 9.348 0.312 0.891 TAA LSTM 0.276 0.357 0.279 0.913 4.464 5.181 0.494 0.766 4.029 4.650 0.192 0.963 线性外推 0.487 0.703 0.489 0.663 7.638 9.009 0.671 0.293 6.313 8.079 0.306 0.889 二次外推 0.467 0.591 0.435 0.762 12.19 14.390 0.814 −0.803 6.354 9.361 0.360 0.851 TAY LSTM 0.575 0.774 0.494 0.646 4.511 5.512 0.436 0.775 3.337 4.486 0.198 0.962 线性外推 0.954 1.328 0.740 −0.04 9.085 11.003 0.750 0.103 6.555 8.597 0.345 0.860 二次外推 1.517 1.980 0.945 −1.31 18.75 28.224 1.098 −4.902 6.905 8.272 0.336 0.871 THJ LSTM 0.174 0.207 0.164 0.958 3.185 4.323 0.419 0.830 3.677 4.883 0.214 0.954 线性外推 0.342 0.449 0.341 0.805 6.149 7.727 0.577 0.457 4.817 6.475 0.262 0.920 二次外推 0.307 0.368 0.329 0.868 12.07 14.113 0.824 −0.811 5.103 6.332 0.263 0.923 TSY LSTM 0.283 0.353 0.254 0.923 5.178 6.948 0.691 0.498 3.513 4.464 0.188 0.965 线性外推 0.634 0.815 0.519 0.591 10.36 14.890 1.057 −1.308 5.861 8.257 0.325 0.880 二次外推 0.544 0.740 0.500 0.662 13.63 16.474 1.058 −1.825 6.355 7.402 0.297 0.904 WHN LSTM 0.192 0.326 0.199 0.929 3.269 4.208 0.393 0.801 4.148 5.250 0.215 0.947 线性外涂 0.556 0.767 0.540 0.605 5.735 7.552 0.607 0.360 8.213 14.070 0.532 0.621 二次外推 0.641 0.827 0.528 0.541 9.705 12.099 0.842 −0.642 9.227 13.362 0.481 0.658 WMQ LSTM 0.347 0.466 0.390 0.817 1.504 2.034 0.154 0.974 3.802 4.501 0.169 0.970 线性外推 0.659 1.002 0.711 0.153 6.708 8.291 0.577 0.576 7.164 8.661 0.303 0.890 二次外推 0.738 1.091 0.790 −0.004 8.861 11.928 0.664 0.123 9.198 12.274 0.418 0.779 XIC LSTM 0.268 0.316 0.248 0.909 1.979 2.509 0.172 0.969 4.144 5.646 0.190 0.958 线性外推 0.572 0.799 0.591 0.420 8.932 12.246 0.647 0.272 8.479 11.392 0.369 0.830 二次外推 0.663 0.885 0.560 0.290 19.14 24.864 0.887 −2.003 12.220 16.116 0.470 0.660 YON LSTM 0.245 0.331 0.322 0.851 1.917 2.467 0.180 0.952 2.767 3.911 0.158 0.975 线性外推 0.420 0.527 0.489 0.622 6.527 8.712 0.603 0.407 4.585 6.065 0.222 0.940 二次外推 0.502 0.745 0.636 0.246 11.47 13.378 0.775 −0.398 6.459 7.450 0.286 0.909 IRT LSTM 0.532 0.796 0.260 0.914 3.619 4.408 0.214 0.950 3.774 5.111 0.218 0.949 线性外推 0.750 1.001 0.341 0.865 5.788 7.471 0.351 0.856 7.499 10.957 0.449 0.764 二次外推 0.971 1.209 0.408 0.803 8.129 11.606 0.526 0.652 11.499 15.821 0.595 0.508 KAK LSTM 0.178 0.254 0.216 0.944 2.500 3.221 0.314 0.888 0.345 2.891 0.117 0.984 线性外推 0.266 0.335 0.293 0.902 4.618 6.035 0.541 0.608 4.186 0.889 0.198 0.955 二次外推 0.342 0.471 0.419 0.806 8.103 11.395 0.864 −0.399 5.543 7.227 0.301 0.902 KNY LSTM 0.178 0.264 0.208 0.957 2.842 3.604 0.347 0.873 2.350 2.893 0.116 0.986 线性外推 0.233 0.291 0.215 0.948 4.799 6.127 0.514 0.634 3.687 4.623 0.178 0.963 二次外推 0.340 0.465 0.333 0.867 8.297 11.233 0.763 −0.232 5.078 6.300 0.251 0.932 GUA LSTM 0.155 0.195 0.142 0.979 3.154 4.112 0.319 0.889 3.871 5.472 0.172 0.970 线性外推 0.352 0.453 0.321 0.887 6.679 8.376 0.591 0.541 6.561 8.524 0.252 0.927 二次外推 0.391 0.458 0.324 0.885 11.55 14.381 0.815 −0.354 5.756 8.547 0.251 0.927
下载: 导出CSV
表 4 LSTM模型、线性外推和二次外推预测的各要素年变率精度汇总
Table 4 Summary of annual rate accuracy for elements predicted by LSTM model，linear extrapolation and quadratic extrapolation
方法 D年变/（′⋅a−1） H年变/（nT⋅a−1） Z年变/（nT⋅a−1） MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $ MAE RMSE NRMSE $ {R}^{2} $
LSTMMin 0.077 0.145 0.095 0.646 0.816 0.975 0.071 0.498 0.345 2.219 0.102 0.947 Max 0.575 0.796 0.494 0.989 5.178 6.948 0.691 0.991 5.106 6.289 0.225 0.988 Mean 0.264 0.361 0.251 0.909 3.021 3.921 0.335 0.854 3.283 4.339 0.177 0.966
线性外推Min 0.233 0.291 0.187 −1.653 4.618 6.028 0.351 −2.276 3.687 0.889 0.178 0.621 Max 0.972 1.657 1.110 0.958 11.89 17.502 1.184 0.856 9.179 14.070 0.532 0.963 Mean 0.568 0.777 0.502 0.541 7.160 9.374 0.676 0.150 6.185 8.173 0.320 0.866
二次外推Min 0.307 0.368 0.324 −1.340 8.103 11.233 0.526 −4.902 5.078 6.300 0.248 0.489 Max 1.517 1.980 0.945 0.885 19.14 28.224 1.098 0.652 12.220 16.116 0.595 0.932 Mean 0.663 0.889 0.546 0.416 13.15 16.652 0.885 −1.499 7.800 10.133 0.389 0.796
下载: 导出CSV
-
常宜峰. 2015. 卫星磁测数据处理与地磁场模型反演理论与方法研究[D]. 郑州:中国人民解放军战略支援部队信息工程大学,106−110. Chang Y F. 2015. Research On Satellite Geomagnetic Data Process And Geomagnetic Model Recovery Theory And Method[D]. Zhengzhou:Information Engineering University,106−110 (in Chinese).
陈斌,顾左文,高金田,袁洁浩,狄传芝. 2010. 中国地区地磁长期变化研究[J]. 地球物理学报,53(9):2114–2154. Chen B,Gu Z W,Gao J T,Yuan J H,Di C Z. 2010. Study of geomagnetic secular variation in China[J]. Chinese Journal of Geophysics,53(9):2114–2154 (in Chinese).
杜奕. 2023. 基于多源遥感数据的大气PM2.5产品缺失数据重构方法研究[D]. 上海:上海师范大学,12−23. Du Y. 2023. Research On the Reconstruction Method of Missing Data For Atmospheric PM2.5 Products Based on Multi-source Remote Sensing Data[D]. Shanghai:Shanghai Normal University,12−23 (in Chinese).
葛轶洲,许翔,杨锁荣,周青,申富饶. 2021. 序列数据的数据增强方法综述[J]. 计算机科学与探索,15(7):1207–1219. doi: 10.3778/j.issn.1673-9418.2012062 Ge Y Z,Xu X,Yang S R,Zhou Q,Shen F R. 2021. Survey on Sequence Data Augmentation[J]. Journal of Frontiers of Computer Science and Technology,15(7):1207–1219 (in Chinese).
顾左文,陈斌,高金田,辛长江,袁洁浩,狄传芝. 2009. 应用NOC方法研究中国地区地磁时空变化[J]. 地球物理学报,52(10):2602–2612. doi: 10.3969/j.issn.0001-5733.2009.10.020 Gu Z W,Chen B,Gao J T,Xin C J,Yuan J H,Di C Z. 2009. Research of geomagnetic spatial-temporal variations in China by the NOC method[J]. Chinese Journal of Geophysics,52(10):2602–2612 (in Chinese).
康国发,高国明,白春华,狄传芝. 2009. CHAMP卫星主磁场长期变化和长期加速度的分布特征[J]. 地球物理学报,52(8):1976–1984. doi: 10.3969/j.issn.0001-5733.2009.08.004 Kang G F,Gao G M,Bai C H,Di C Z. 2009. Characteristics of the secular variation and secular acceleration distributions of the main geomagnetic field for the CHAMP satellite[J]. Chinese Journal of Geophysics,52(8):1976–1984 (in Chinese).
卢兆兴,吕志峰,李婷,张金生,姚垚. 2021. 基于BP神经网络的地磁变化场预测研究[J]. 大地测量与地球动力学,41(3):229–233. Lu Z Y,Lü Z F,Li T,Zhang J S,Yao Y. 2021. Forecasting of the Variable Geomagnetic Field Based on BP Neural Network[J]. Journal of Geodesy and Geodynamics,41(3):229–233 (in Chinese).
毛宁,陈石,杨永友,吴旭,李永波. 2023. 地磁长期变化信号提取和模型预测精度评估[J]. 地球物理学报,66(8):3302–3315. doi: 10.6038/cjg2022Q0499 Mao N,Chen S,Yang Y Y,Wu X,Li Y B. 2023. Extraction of secular variation signals of geomagnetic field and evaluation of prediction accuracy of geomagnetic field models[J]. Chinese Journal of Geophysics,66(8):3302–3315 (in Chinese).
邱耀东. 2018. 联合CHAMP和Swarm卫星磁测数据反演中国大陆区域岩石圈磁场[D]. 武汉:武汉大学,1−2. Qiu Y D. 2018. Invert the Lithospheric Magnetic Field in China Mainland by Combining CHAMP And Swarm Satellite Data[D]. Wuhan:Wuhan University:1−2 (in Chinese).
汪凯翔,黄清华,吴思弘. 2020. 长短时记忆神经网络在地电场数据处理中的应用[J]. 地球物理学报,63(8):3015–3024. doi: 10.6038/cjg2020O0119 Wang K X,Huang Q H. Wu S H. 2020. Application of long short-term memory network in geoelectric field data processing[J]. Chinese Journal of Geophysics,63(8):3015–3024 (in Chinese).
王月华. 2002. 1985-1997年中国地磁场长期变化的正交模型[J]. 地球物理学报,45(5):624–630. doi: 10.3321/j.issn:0001-5733.2002.05.004 Wang Y H. 2002. Regional orthogonal model of secular variation of the geomagnetic field in China during 1985-1997[J]. Chinese Journal of Geophysics,45(5):624–630 (in Chinese).
王振东,王粲,袁洁浩,毛丰龙. 2019. 中国及邻近地区地磁长期变化分析[J]. 地震研究,42(1):102–111. doi: 10.3969/j.issn.1000-0666.2019.01.014 Wang Z D,Wang C,Yuan J J,Mao F L. 2019. Analysis of Geomagnetic Secular Variation in China and Its Neighboring Regions[J]. Journal of Seismological Research,42(1):102–111 (in Chinese).
熊波,李肖霖,王宇晴,张瀚铭,刘子君,丁锋,赵必强. 2022. 基于长短时记忆神经网络的中国地区电离层TEC预测[J]. 地球物理学报,65(7):2365–2377. doi: 10.6038/cjg2022P0557 Xiong B,Li X L,Wang Y Q,Zhang H M,Liu Z J,Ding F,Zhao B Q. 2022. Prediction of ionospheric TEC over China based on long and short-term memory neural network[J]. Chinese Journal of Geophysics,65(7):2365–2377 (in Chinese).
徐文耀. 2009. 地球电磁现象物理学[M]. 合肥:中国科学技术大学出版社:19−29. Xu W Y. 2009. Physics of Electromagnetic Phenomena of the Earth[M]. Hefei:Science and technology of China press:19−29 (in Chinese).
张素琴,陈传华,王建军,赵旭东,何宇飞,李琪,杨冬梅,胡秀娟. 2021. 1985-1990年地磁基准台时均值数据集[J]. 地震地磁观测与研究,42(4):173–182. Zhang S Q,Chen C H,Wang J J,Zhao X D,He Y F,Li Q,Yang D M,Hu X J. 2021. Hourly mean values datasets of geomagnetic stations from 1985-1990[J]. Seismological and Geomagnetic Observation and Research,42(4):173–182 (in Chinese).
赵旭东,何宇飞,李琪,刘晓灿. 2022. 基于中国地磁台网数据的太阳静日期间地磁场Z分量日变化幅度分析[J]. 地球物理学报,65(10):3728–3742. doi: 10.6038/cjg2022P0628 Zhao X D,He Y F,Li Q,Liu X C. 2022. Analysis of the geomagnetic component Z daily variation amplitude based on the Geomagnetic Network of China during solar quiet days[J]. Chinese Journal of Geophysics, 65 (10):3728−3742 Regional orthorgonal model of secular variation of the geomagnetic f.
Alken P,Thébault E,Beggan C D,Amit H,Aubert J,Baerenzung J,Bondar T N,Brown W J,Califf S,Chambodut A,Chulliat A,Cox G A,Finlay C C,Fournier A,Gillet N,Grayver A,Hammer M D,Holschneider M,Huder L,Hulot G,Jager T,Kloss C,Korte M,Kuang W,Kuvshinov A,Langlais B,Léger J M,Lesur V,Livermore P W,Lowes F J,Macmillan S,Magnes W,Mandea M,Marsal S,Matzka J,Metmab M C,Minami T,Morschhauser A,Mound J E,Nair M,Nakano S,Olsen N,Pavón-Carrasco F J,Petrov V G,Ropp G,Rother M,Sabaka T J,Saturnino D,Schnepf N R,Shen X,Stolle C,Tangborn A,TØffner-Clausen L,Toh H,Torta J M,Varner J,Vervelidou F,Vigneron P,Wardinski I,Wicht J,Woods A,Yang Y,Zeren Z,Zhou B. 2021. International Geomagnetic Reference Field:the thirteenth generation[J]. Earth Planets and Space,73(1):1–25. doi: 10.1186/s40623-020-01323-x
Brown W J,Mound J E,Livermore P W. 2013. Jerks abound:An analysis of geomagnetic observatory data from 1957 to 2008[J]. Physics Earth Planet Inter,223:62–76. doi: 10.1016/j.pepi.2013.06.001
Finlay C C,Maus S,Beggan C D,Bondar T N,Chambodut A,Chernova T A,Chulliat A,Golovkov V P,Hamilton B,Hamoudi M,Holme R,Hulot G,Kuang W,Langlais B,Lesur V,Lowes F J,Lühr H,Macmillan S,Mandea M,McLean S,Manoj C,Menvielle M,Michaelis I,Olsen N,Rauberg J,Rother M,Sabaka T J,Tangborn A,TØffner-Clausen L,Thébault E,Thomson A W P,Wardinski I,Wei Z,Zvereva T I. 2010. International Geomagnetic Reference Field:the eleventh generation[J]. Geophys J Inter,183(3):1216–1230. doi: 10.1111/j.1365-246X.2010.04804.x
Golovkov V P,Papitashvili N E,Tiupkin I S,Kharin E P. 1978. Separation of geomagnetic field variations on the quiet and disturbed components by the MNOC[J]. Geomagnetic and Aeronomy,18(18):511–515.
Hamed A,Langel A,Purucker M. 1994. Secular magnetic anomaly maps of earth derived from POGO and MAGSAT data[J]. Journal of Geophysical Research Solid Earth,99(B12):24075–24090.
Hochreiter S,Schmidhuber J. 1997. Long Short-Term Memory[J]. Neural Computation, 9 (8):1735–1780.
Kother L,Hammer M D,Finlay C C,Olsen N. 2015. An equivalent source method for modelling the global lithospheric magnetic field[J]. Geophysical Journal International,203(1):553–566.
Maus S,Yin F,Lühr H,Manoj C,Rother M,Rauberg J,Michaelis I,Stolle C,Müller R D. 2008. Resolution of direction of oceanic magnetic lineations by the sixth-generation lithospheric magnetic field model from CHAMP satellite magnetic measurements[J]. Geochemistry,Geophysics,Geosystems,9(7):1335–1346.
Nevanlinna H. 1987. On the drifting parts in the spatial power spectrum of geomagnetic secular variation[J]. Journal of Geomagnetism and Geoelectricity,39(6):367–376.
Olsen N,Lühr H,Finlay C C,Sabaka T J,Rauberg J,TØffner-Clausen Lr. 2014. The CHAOS-4 geomagnetic field model[J]. Geophysical Journal International,197(2):815–827.
Pushkov A N,Frynberg E B,Chernova T A,Fiskina M V. 1976. Analysis of the space-time structure of the main geomagnetic field by expansion into natural orthogonal component[J]. Geomagnetic and Aeronomy,16:337–343.
Singh D,Singh B. 2020. Investigating the impact of data normalization on classification performance[J]. Applied Soft Computing,97.
Wen Q,Sun L,Yang F,Song X M,Gao J K,Wang X,Xu H. 2021. Time Series Data Augmentation for Deep Learning:A Survey. International Joint Conferences on Artifical Intelligence Organization.
Xu J Y,Lin Y F. 2023. Dynamic mode decomposition of the geomagnetic field over the last two decades[J]. Earth Planet. Phys,7(1):32–38
Zhang G P,Qi M. 2005. Neural network forecasting for seasonal and trend time series[J]. Operations Research,160(2):501–514.
计量
- 文章访问数: 118
- HTML全文浏览量: 31
- PDF下载量: 26
