Spatial-temporal variation characteristics of geomagnetic field in China and model accuracy evaluation
-
摘要:
首先，基于第十三代国际地磁参考场（IGRF-13），以五年为时间间隔，对中国地区2000—2020年地磁场七个要素（X，Y，Z，H，D，I和F）的长期变化进行了系统的分析与探讨；其次，利用中国地磁台站的实际观测数据，研究了此期间地磁场逐年变化的特点，并以五年为间隔，探讨了1960—2020年中国地区内地磁场的变化模式；最后，通过分析IGRF-13和世界地磁模型WMM2020的计算结果与实际观测值之间的差值和均方根误差，深入探究了这些模型在中国地区的适用性差异。研究结果表明：2000—2020年间，中国地磁场的总磁场强度呈现出整体逐渐增强的趋势，等值线总体呈西北—东南走向；在2000—2005年、2005—2010年以及2010—2015年这三个时段内，地磁场七个要素的等值线移动方向一致，而在2015—2020年间，等值线的移动方向与前三个阶段相反；垂直分量与总磁场强度的变化模式基本相同，但总磁场强度的变化时间相比垂直分量滞后了1—3年。中国地磁场的长期变化周期约为30年，预计未来十年地磁场将呈现下降趋势。此外，IGRF-13和WMM2020模型的计算结果与实际观测值的差值和均方根误差相当一致，表明这两个模型都能较好地反映中国地区地磁场的长期变化特征。
Abstract:Since 1968, the International Association of Geomagnetism and Aeronomy （IAGA） has continuously published the International Geomagnetic Reference Field （IGRF） models. In 2019, the 13th generation IGRF model （IGRF-13） was released; at the same year, the U.S. National Centers for Environmental Information （NCEI） and the British Geological Survey （BGS） jointly issued the World Magnetic Model 2020 （WMM2020）. This study aims to use the IGRF-13 model, along with data from Chinese geomagnetic observatories, to conduct an in-depth analysis of the spatio-temporal variation characteristics of the seven elements of the geomagnetic field: magnetic declination D, magnetic inclination I, horizontal intensity H, northward component X, eastward component Y, vertical component Z, and total intensity F from 2000 to 2020.
Furthermore, this study evaluates the applicability and accuracy of the IGRF-13 and WMM2020 models in China using data from 28 Chinese geomagnetic observatories. By studying the morphological changes and trends of these elements over the aforementioned period, we aim to gain a deeper understanding of the evolution process of the geomagnetic field and provide a detailed description of geomagnetic activities in China.
We selected geomagnetic observatories within China that have continuous observation records. Subsequently, the IGRF-13 model was utilized to calculate the geomagnetic field model values spanning the period from 2000 to 2020. By analyzing these model values, we studied the change characteristics of the seven elements of the geomagnetic field （D, I, H, X, Y, Z, F） in different time intervals, each interval being five years long, throughout the period from 2000 to 2020.
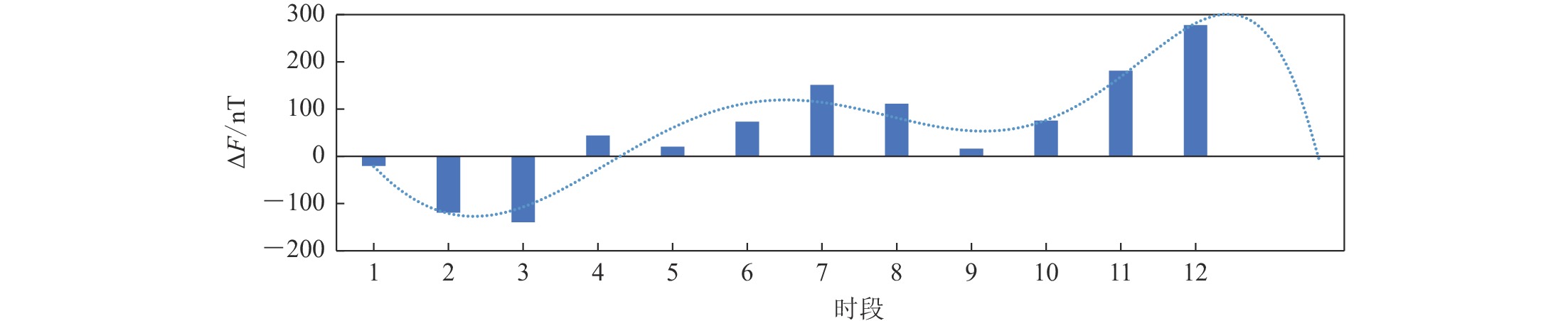
Twelve geomagnetic observatories were chosen from different regions across eastern, southern, western, northern, and central China, all with long-term and continuous observation records and located at similar latitudes and longitudes. For the data from 2000 to 2020, we performed a first-difference analysis on the time series of H, Z, F, so as to explore the trends and short-term fluctuations of these three components over time, thereby achieving a better understanding of the dynamic changes in the geomagnetic field.
Meanwhile by using the IGRF-13 model, we computed the model values of the total intensity of the geomagnetic field in China at five-year intervals spanning from 1960 to 2020. The analysis of these data enabled us to identify the long-term trends in the changes of the geomagnetic field and detect any potential periodic patterns. Comprehending these historical changes and predicting future trends is crucial for understanding the evolution of the geomagnetic field.
To evaluate the applicability and accuracy of the IGRF-13 and WMM2020 within the China, we adopted the difference and root mean square error （RMSE） to compare the differences between the model predicted-values and the actual measurements obtained from Chinese geomagnetic observatories. By this way, we could distinctly identify the advantages and disadvantages of the two models for China.
After a detailed analysis of the geomagnetic field in China from 2000−2020, this study has drawn the following main conclusions:
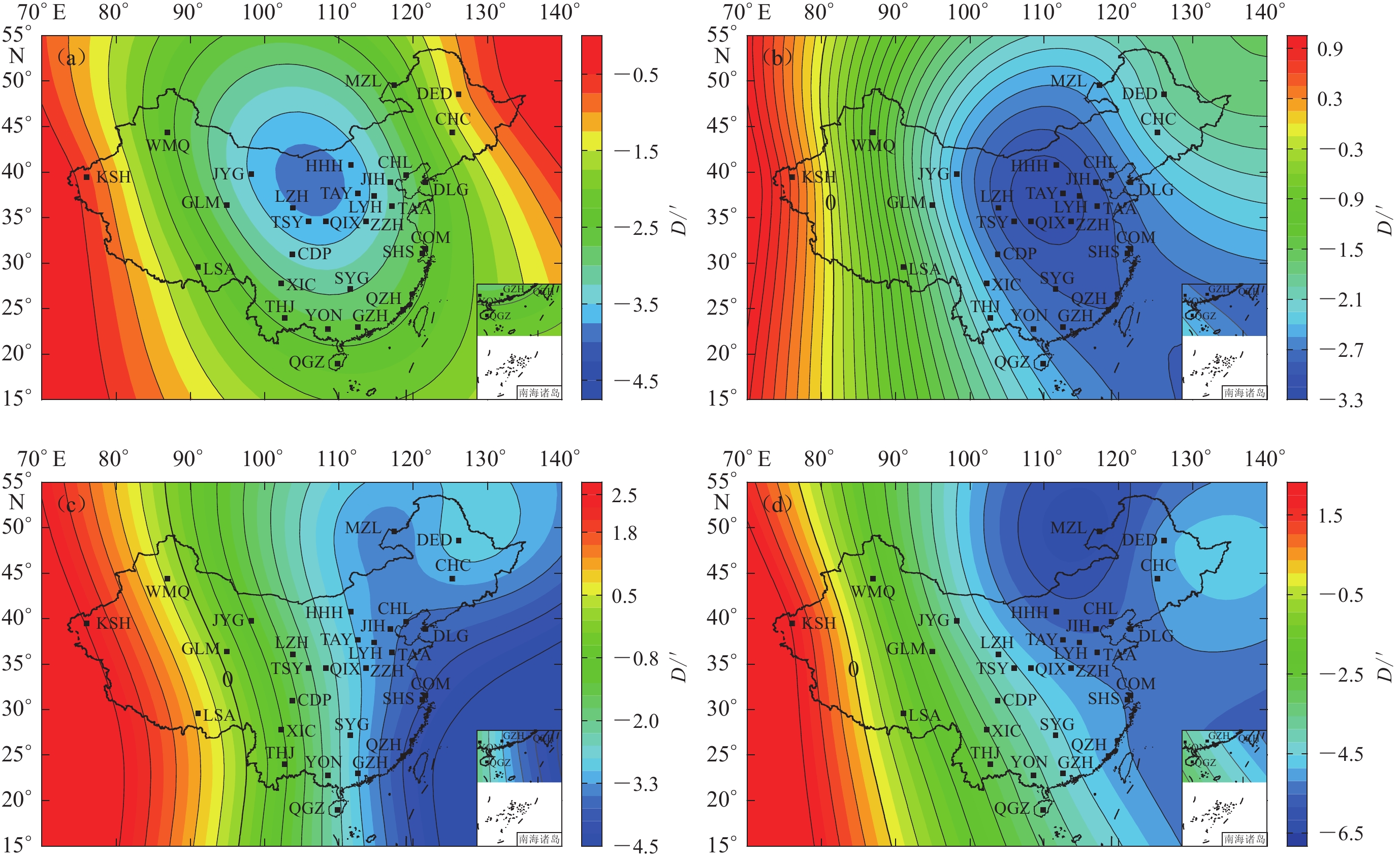
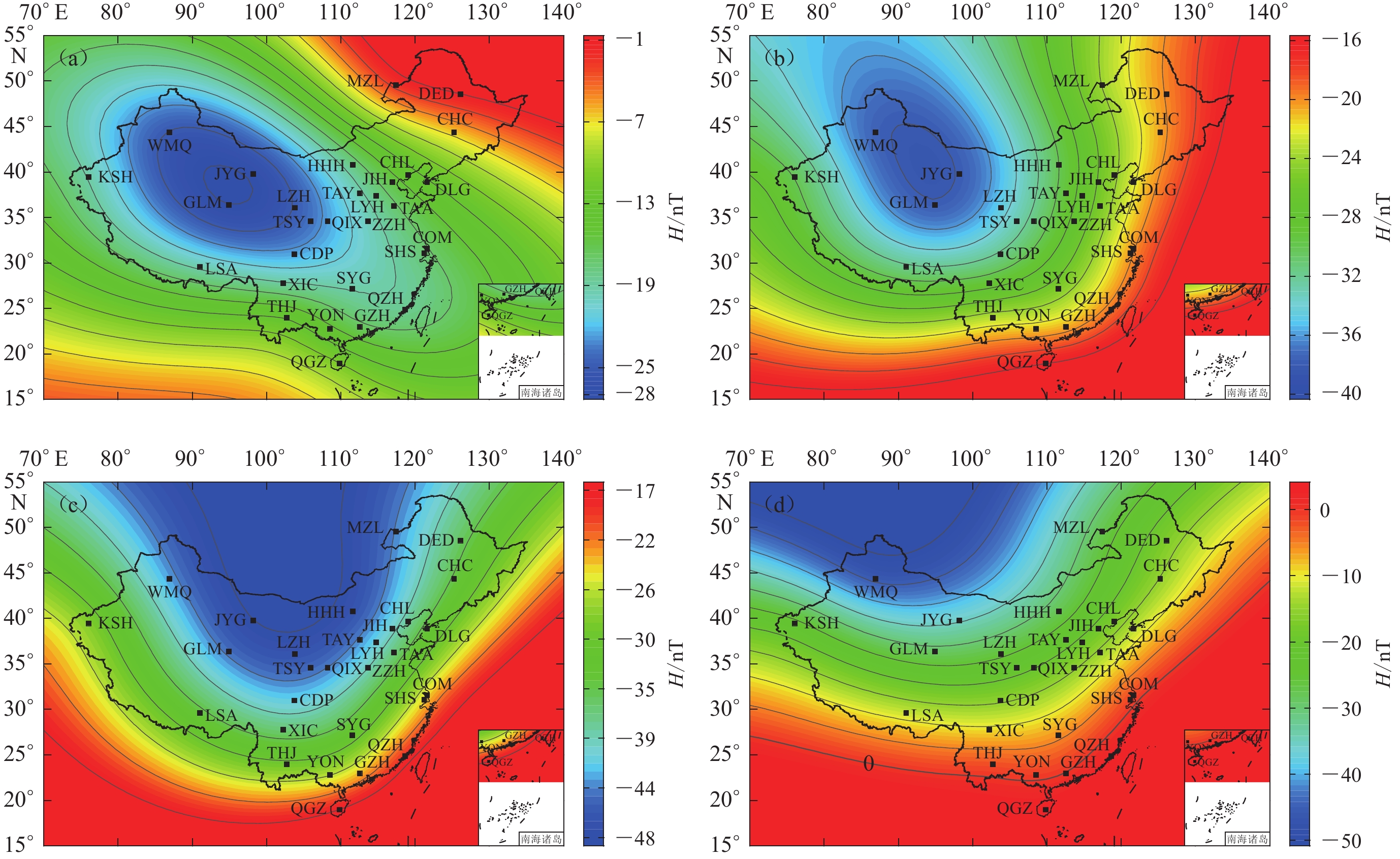
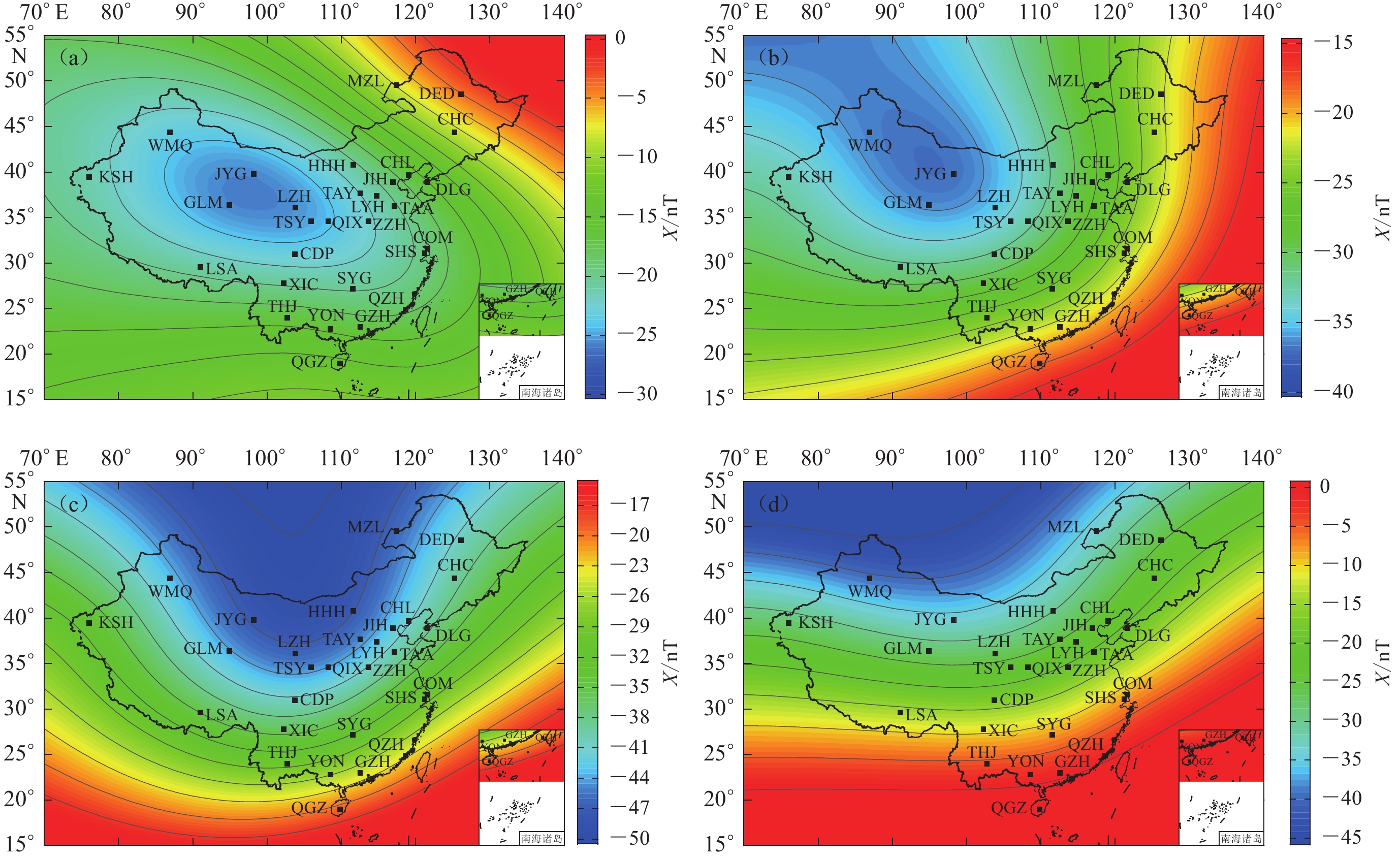
1） The seven elements of the geomagnetic field displayed alterations in varying degrees over different time periods. The moving directions of the isolines of the seven elements are also defferent. During the three periods from 2000 to 2005, from 2005 to 2010, and from 2010 to 2015, the isolines for all seven geomagnetic elements demonstrated a consistent movement direction. Conversely, during the period from 2015 to 2020, the moving direction reversed. This indicates that the geomagnetic field is characterized not only by gradual long-term trends but also by relatively abrupt short-term fluctuations, which can be affected by a multitude of internal and external factors.
During the period from 2000 and 2020, the geomagnetic field in China generally exhibited a trend of gradual strengthening. The region with the maximum change amplitude was located in the northwestern area, where the maximum increase about
1000 nT. In contrast, the northeastern region experienced the smallest increase. The isolines generally ran from northwest to southeast, indicating that the changes in the geomagnetic field during this period had distinct spatial distribution characteristics.2） By analyzing the overall changes in the geomagnetic field at five-year interval from 1960 to 2020, we found that the variations of the geomagnetic field exhibit a “trough-peak-trough” pattern, with a cycle of approximately 30 years. Based on this cyclical characteristic, it is predicted that the geomagnetic field in China will show a downward trend in the next decade.
3） The accuracy of the IGRF-13 and WMM2020 models was evaluated by comparing their values with actual observations. The resulting average absolute errors for the D, I, H, X, Y, Z, and F components were as follows: 0, −0.1′, 2 nT, 1 nT, 1 nT, −1 nT, and −1 nT. The RMS errors are D＝0.2′, I＝0.0′, H＝0 nT, X＝1 nT, Y＝1 nT, and Z＝1 nT, and F＝1 nT. These RMS errors are consistent and fall within the accuracy range of the global model estimation, indicating that both models can accurately reflect the long-term variation characteristics of the geomagnetic field in the China.
-
Keywords:
- IGRF-13 /
- WMM2020 /
- geomagnetic variation /
- isoline /
- period
-
引言
隧道线路设计经常会遇到隧道穿越断层及其破碎带的情形。跨断层隧道震灾调查表明，隧道震害较为突出，其中受到断层位错影响区段的震害尤为严重。例如2008年汶川MS8.0地震中，龙溪、龙洞子等穿越断层破碎带的隧道损害较严重，其震害类型主要表现为衬砌开裂、隧道垮塌和混凝土剥落等。断层错动将导致围岩产生永久变形，从而对隧道结构造成破坏，而如何减小断层对隧道衬砌的影响是设计和建设跨断层或破裂带隧道过程中的难点。
国内外对断层错动作用下隧道的力学响应分析及对应措施已有大量研究，主要集中在对断层类型、断层倾角、位错量、隧道结构类型及材料属性、隧道与断层走向交角及分析方法等的研究。Kontogianni和Stiros （2003）结合过去100年内受强震影响的地区区内隧道受损情况，研究了在地震作用下断层隧道衬砌管片的应力应变反应。熊炜等（2010）通过有限元方法分析断层错动下隧道结构的受力变形，认为断层位错量、倾角、隧道埋深和隧道与断层走向交角对衬砌结构影响程度不同，衬砌受力与变形对断层位错量变化最敏感。陈熹（2017）通过三维有限差分程序分别对走滑断层、正断层和逆断层进行建模，研究隧道衬砌在断层错动作用下的损伤机制，数值模拟结果表明衬砌内力变化主要集中在断层及附近位置。孙飞等（2019）通过有限元方法与实验相结合，研究衬砌开裂破坏形式，得出在正断层错动作用下衬砌在断层面处承受压−剪−扭的组合作用。
邵润萌（2011）以成兰铁路为研究对象建立数值模型，对断层错动下隧道衬砌损伤模式进行了分析，但其分析模型采用单一断层面，未考虑断层破碎带产生的影响。焦鹏飞和来弘鹏（2019）利用FLAC3D 有限差分软件分析了不同倾角逆断层错动对隧道结构应力分布影响，但其研究对象为倾角为45°，64°，75°的逆断层，未涉及倾角较小的逆冲断层。胡辉（2013）采用有限元数值模拟分析方法，模拟了上盘下错衬砌破坏情况，但其尚未对上盘逆冲过程进行研究。赵宝平（2018）运用FLAC3D三维有限差分软件根据相关地质资料建立数值模型，研究不同断层错距下逆断层错动引起的衬砌破坏形式，但研究对象仅为倾角为75°逆断层，该结果是否适用于小角度逆冲断层尚待研究。鉴于特定的工程具有其特殊性，关于穿越逆断层隧道变形和受力特征的相关研究成果，能否刻画特定隧道工程在逆断层错动下的变形与受力特征有待进一步研究。为此本文在已有相关隧道穿越断层的研究成果基础上，以Abaqus通用有限元软件为分析平台，以成兰铁路穿越北川—映秀断裂的跃龙门隧道工程为分析对象，分别模拟了倾角为30°，45°和60°逆断层错动作用下隧道衬砌结构的响应，以期得到逆断层错动对隧道工程受力和变形的影响特征。
1. 模型建立及参数选取
断层错动作用下的隧道衬砌力学响应复杂，可利用数值方法求解，其中有限元方法网格划分灵活，可以处理任意几何形态断层问题（张丽芬，姚运生，2013）。本文计算采用有限元软件Abaqus建立三维模型，选择围岩和衬砌材料参数并设置边界条件，模拟分析逆断层错动对衬砌结构的影响。
1.1 模型尺寸
有限元分析模型的隧道采用圆拱模型，其外轮廓宽为12 m，高为9.43 m。为简化计算并结合实际的受力状态，将初期支护和二次衬砌简化为一体（熊炜等，2010），视为一均质衬砌，不考虑两者相互作用影响，衬砌等效厚度为0.5 m。模型的长×宽×高为700 m×100 m×100 m，破碎带宽度为20 m。断层倾角为60°时分析模型如图1a所示；衬砌与破碎带相交方式为正交（图1b）。模型有限元离散单元对于隧道、破碎带和围岩均采用实体单元。
![]()
图 1 衬砌结构模型示意图（a） 模型整体；（b） 衬砌-破碎带相交方式Figure 1. Schematic diagram of lining structure model（a） Whole model；（b） Lining fracture zone intersection mode1.2 模型参数选择
1） 本构模型选择。在有限元分析中，隧道衬砌为C30混凝土，为了更好地体现衬砌对断层位错量和倾角变化的敏感性，衬砌采用线弹性本构；围岩及破碎带采用德鲁克-普拉格（Drucker-Prager，缩写为DP）弹塑性模型，不同介质物理力学参数的取值列于表1。在数值分析中，选择面面接触模拟围岩与隧道相互作用，接触面行为设定为滑动不分离，摩擦类型采用库仑摩擦。
表 1 介质物理力学参数Table 1. Physical mechanics parameters of medium材料 密度
/（kg·m−3）弹性模量
/MPa泊松比 黏聚力
/MPa内摩擦角
/°围岩 2300 10000 0.250 0.25 30 破碎带 2000 5000 0.300 0.30 25 衬砌 2500 30000 0.167 2） 边界条件设置。衬砌破坏主要归因于断层错动产生的围岩永久变形，本文在计算活动断层错动作用下隧道衬砌的响应时，采用静力方法。设置边界条件时，基于逆冲断层错动特征，在上下盘底边界对位移进行约束，下盘（被动盘）底边界约束位移为0，上盘（主动盘）底边界同时加以竖向与水平向位移模拟逆断层错动，错动方式如图2所示；模型顶部为自由边界；四周侧边界上沿断层走向方向设置为固定边界。
2. 相同倾角不同竖向位错量的模拟结果
断层沿断层面发生位错可以分解为竖向和水平两个方向。由于衬砌和围岩采用摩擦接触，其可以和围岩发生水平相对位移，从而在很大程度上抵消断层水平位错产生的影响。因此，选择断层竖向位错分量为变量，研究不同竖向位错对隧道衬砌的变形与受力影响。基于前述分析模型，通过数值模拟得到了逆断层位错竖向分量分别为10，20，30，40和50 cm时衬砌的数值计算结果，并据此就竖向位移及衬砌结构纵向应力进行分析。
2.1 竖向位移分析
倾角为30°的逆断层，其竖向位错分量为50 cm时，断层和衬砌放大15倍的竖向位移云图如图3所示。由图3可知，隧道在逆断层错动作用下，衬砌结构沿纵向产生“S”状弯曲变形。为分析衬砌竖向位移在不同纵向距离下的变化规律，选取衬砌顶部为分析对象。倾角为30°的逆断层在不同位错下衬砌顶部的竖向位移量曲线，如图4所示。可以看出，上盘衬砌的竖向位移量随着位错量的增加逐渐增大，衬砌在上盘内发生相对竖向位移较大，当位错竖向分量为50 cm时，衬砌最大竖向位移为53.1 cm；而衬砌在下盘内发生竖向位移较小，距断层一定范围以外竖向位移降为0。
![]()
图 3 断层（a）和衬砌（b）竖向位移云图Figure 3. Vertical displacement nephogram of fault （a） and lining （b）![]()
图 4 逆断层倾角为30°时不同竖向位错分量的衬砌竖向位移Figure 4. Vertical displacement curves of lining with different vertical dislocation components at 30° dip angle of reverse fault为对比不同倾角逆断层错动作用下衬砌竖向变形特点，分别选取倾角为45°和60°的逆断层衬砌顶部作为分析对象。图5a，b分别为45°和60°倾角逆断层在不同位错下衬砌顶部的竖向位移量曲线。从图中可以看出，衬砌变形特征与30°倾角的逆断层相同：衬砌在上盘内发生相对竖向位移的范围较大，在下盘内发生竖向位移的范围较小，衬砌总体沿纵向发生“S”状弯曲变形。
![]()
图 5 逆断层倾角为45° （a）和60° （b）时不同竖向位错分量的衬砌竖向位移Figure 5. Vertical displacement curves of lining with different vertical dislocation components at 45° （a） and 60° （b） dip angle of reverse fault2.2 衬砌结构纵向应力分析
倾角为30°的逆断层位错其竖向分量为50 cm时衬砌结构的纵向应力，如图6所示。从图中可以看出，纵向应力集中分布在破碎带附近拱顶和拱底位置，因此选取拱顶和拱底作为分析对象。
![]()
图 6 倾角为30°的逆断层竖向位错为50cm时的衬砌纵向应力云图Figure 6. Longitudinal stress nephogram of lining with vertical dislocation of 50 cm in 30° dip reverse fault衬砌顶部与底部所受拉压应力分布相反（图7），且顶部所受拉应力和压应力都大于底部，说明逆断层位错下拱顶更易受损。由衬砌所受拉压应力分布区间及最大值（表2）可以看出，衬砌顶部和底部的共同特点为：拉压应力主要分布在断层两侧各50 m区间内，压应力大于拉应力，且拉压应力最大值均随位错竖向分量的增加而增加。
![]()
图 7 不同竖向位错作用下衬砌纵向应力曲线纵坐标为正值表示拉应力，为负值表示压应力（a） 逆断层倾角为30°；（b） 逆断层倾角为45°； （c） 逆断层倾角为60°；Figure 7. Longitudinal stress curves of lining under different vertical dislocationsTensile stress is indicated when longitudinal stress is positive，and negative denotes compressive stress （a） The dip angle of reverse fault is 30°；（b） The dip angle of reverse fault is 45°；（c） The dip angle of reverse fault is 60°表 2 拉压应力分布区间和最大值Table 2. Range and maximum value of tensile and compressive stress distribution断层倾角/° 衬砌位置 受拉区间/m 拉应力最大值/MPa 受压区间/m 压应力最大值/MPa 30 顶部 400—440 41 440—500 123 底部 460—500 23 400—460 101 45 顶部 400—440 47 440—500 167 底部 460—500 29 400—460 118 60 顶部 400—440 46 440—500 143 底部 460—500 34 400—460 108 3. 相同竖向位错量不同倾角下模拟结果
为了进一步分析相同竖向位错量不同倾角下衬砌结构变形与受力特征，本节以断层位错竖向分量为50 cm，断层倾角分别为30°，45°，60°为例，分析了衬砌结构的变形与受力随倾角而变化的特征。
1） 竖向位移分析。当断层位错竖向分量相同时，衬砌最大竖向位移随倾角的减小而增加（图8a），倾角为60°，45°和30°时断层对应的最大竖向位移值分别为50.5，52.2和53.1 cm，其主要原因为断层位错竖向分量一定时，倾角越小断层沿滑动面方向的总位错越大，从而导致衬砌变形增大。
![]()
图 8 竖向位错为50 cm时不同倾角逆断层作用下衬砌的竖向位移曲线（a）和纵向应力曲线（b）Figure 8. Vertical displacement curves （a） and longitudinal stress curves （b） of lining under the action of reverse faults with different dip angles when the vertical dislocation is 50 cm2） 隧道衬砌结构纵向应力分析。断层位错竖向分量为50 cm，不同断层倾角下衬砌顶部及底部纵向应力如图8b所示，从图中可以看到衬砌受力范围基本不受倾角影响，拉压应力值变化范围主要分布在断层两侧各50 m的区间内。倾角为45°的逆断层拱顶拱底压应力值均为最大，拱顶拉应力最大值不随倾角变化而变化，拱底拉应力最大值随倾角增大而增大。
4. 讨论与结论
本文通过数值模拟得到了不同位错量条件、不同倾角的逆断层对隧道工程结构的受力情况，并分析得到如下主要结论：
1） 逆断层错动会引起隧道衬砌结构沿纵向“S”状弯曲变形，倾角为30°，45°和60°，竖向位错分别为10，20，30，40和50 cm时，衬砌竖向位移随着位错量的增加逐渐增大。衬砌在上盘内发生相对竖向位移的范围较大，而衬砌在下盘内发生竖向位移的范围较小。
2） 衬砌顶部与底部受到的拉应力和压应力分布相反，即在上盘衬砌顶部受拉应力作用，底部受压应力作用，而在下盘衬砌顶部受压应力作用，底部受拉应力作用。衬砌顶部和底部所受压应力均大于拉应力，且拉压应力均随位错竖向分量的增加而增大；衬砌顶部所受拉应力和压应力都大于衬砌底部。
3） 竖向位错相同条件下，倾角越小，衬砌最大竖向位移越大；倾角改变不影响纵向应力分布范围，纵向应力变化范围主要分布在断层两侧各50 m区间内。
基于本文得出的结论，针对衬砌弯曲变形以及断层附近纵向应力变化急剧现象，可在穿越断层地区隧道施工时可在断层破碎区段设置柔性接头。柔性接头作用在于将衬砌分段，限制变形和内力的传递，同时衬砌纵向变形可由柔性接头的转动和拉伸吸收，减小隧道结构变形。
-
![]()
图 1 2000—2020年中国地区磁偏角D等值线分布图
Figure 1. Distribution of isolines of magnetic declination D in China during 2000−2020
（a） 2000—2005；（b） 2005—2010；（c） 2010—2015；（d） 2015—2020
![]()
图 7 2000—2020年中国地区地磁场总强度F等值线分布图
Figure 7. Distribution of isolines of total intensity F of the geomagnetic field in China during 2000−2020
（a） 2000—2005；（b） 2005—2010；（c） 2010—2015；（d） 2015—2020
![]()
图 2 2000—2020年中国地区磁倾角I等值线分布图
Figure 2. Distribution of isolines of magnetic dips I in China during 2000−2020
（a） 2000—2005；（b） 2005—2010；（c） 2010—2015；（d） 2015—2020
![]()
图 3 2000—2020年中国地区地磁场水平分量H等值线分布图
Figure 3. Distribution of isolines of horizontal component H of the geomagnetic fieldin China during 2000−2020
（a） 2000—2005；（b） 2005—2010；（c） 2010—2015；（d） 2015—2020
![]()
图 4 2000—2020年中国地区地磁场北向分量X等值线分布图
Figure 4. Distribution of isolines of northward component X of the geomagnetic field in China during 2000−2020
（a） 2000—2005；（b） 2005—2010；（c） 2010—2015；（d） 2015—2020
![]()
图 5 2000—2020年中国地区地磁场东向分量Y等值线分布图
Figure 5. Distritution of isolines of eastward component Y of the geomagnetic field in China during 2000−2020
（a） 2000—2005；（b） 2005—2010；（c） 2010—2015；（d） 2015—2020
![]()
图 6 2000—2020年中国地区地磁场垂直分量Z等值线分布图
Figure 6. Distribution of isolines of vertical component Z of the geomagnetic field in China during 2000−2020
（a） 2000—2005；（b） 2005—2010；（c） 2010—2015；（d） 2015—2020
![]()
8 2000—2020年地磁台地磁场水平分量H （a）、垂直分量Z （b）和总强度F （c）的年变率分布
8. Distribution of annual variation rate of horizontal component H （a），vertical component Z （b） and total intensity F （c） of the geomagnetic field for the observatories during 2000−2020
![]()
8 2000—2020年地磁台地磁场水平分量H （a）、垂直分量Z （b）和总强度F （c）的年变率分布
8. Distribution of annual variation rate of horizontal component H （a），vertical component Z （b） and total intensity F （c） of the geomagnetic field for the observatories during 2000−2020
![]()
图 9 1960—2020年间以5年为间隔的地磁场总强度F变化量ΔF及趋势图
Figure 9. Variation quantity ΔF and trend of total intensity F of the geomagnetic field at five-year interval from 1960 to 2020
![]()
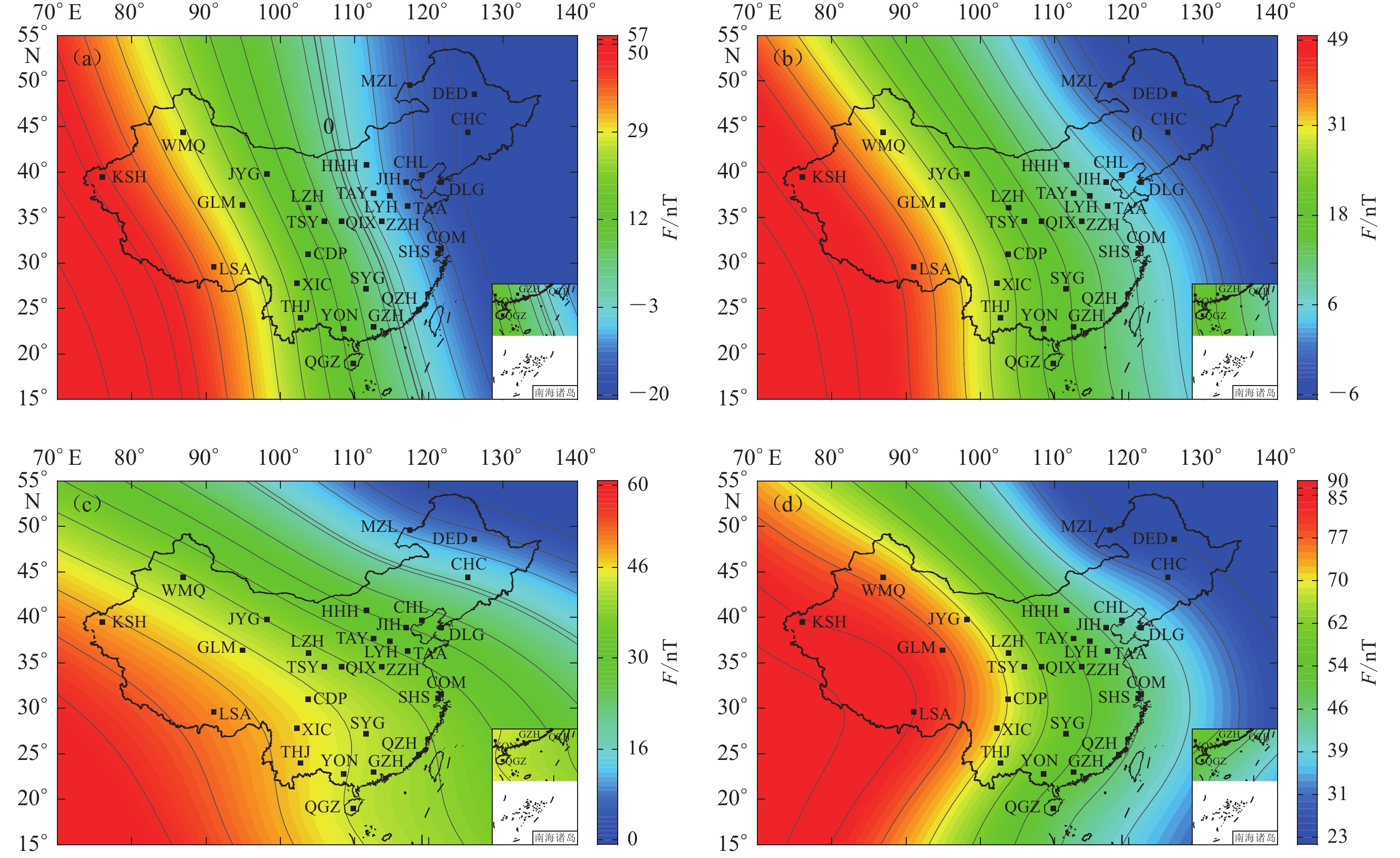
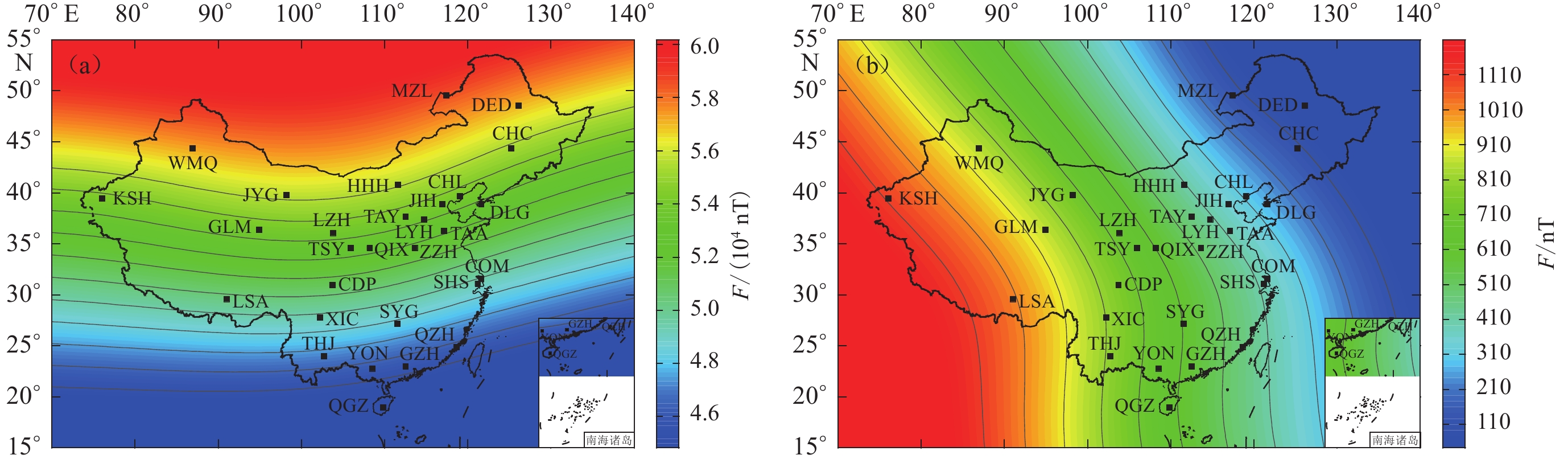
图 10 基于IGRF-13模型的中国地区地磁场总强度F等值线图
（a） 2020年地磁场总强度等值线图；（b） 2000—2020年地磁场总强度等值线图
Figure 10. Isoline map of the total intensity F of the geomagnetic field in China based on IGRF-13
（a） Isoline map of total intensity F of the geomagnetic field in 2020；（b） Isoline map of total intensity F of the geomagnetic field during 2000−2020
表 1 2000—2020年不同时段地磁场七要素变化量及0等值线位置
Table 1 Variation of the seven elements of the geomagnetic field in different time periods and position of the 0 isoline during 2000—2020
时段 D/′ I/′ H/nT X/nT Y/nT Z/nT F/nT 变化量 0等值
线位置变化量 0等值
线位置变化量 0等值
线位置变化量 0等值
线位置变化量 0等值
线位置变化量 0等值
线位置变化量 0等值
线位置2 000—2 005 −14 无 9.8 30°N—55°N −86 无 −97 无 −120 无 103 100°E—
130°E13 105°E—
120°E2 005—2 010 −12.4 75°E—85°E 16.9 无 −134 无 −141 无 −108 70°E—
85°E217 110°E—
140°E75 115°E—
140°E2 010—2 015 −11.2 85°E—95°E 27.1 无 −179 无 −188 无 −92 85°E—
100°E392 无 181 无 2 015—2 020 −20.8 75°E—90°E 22.1 无 −75 19°N—30°N −91 20°N—
30°N−185 75°E—
85°E420 无 278 无 
下载: 导出CSV
表 2 我国地磁台IGRF-13和WMM2020的模型值与观测值的差值统计
Table 2 Statistics on the differences between the model values of IGRF-13 and WMM2020 and the annual mean observed values at Chinese geomagnetic observatories
序号 台站 代码 模型 D差值/′ I差值/′ H差值/nT F差值/nT X差值/nT Y差值/nT Z差值/nT 1 满洲里 MZL IGRF13 2.3 −0.7 147 372 147 −11 343 WMM2 020 1.6 −0.7 145 369 144 −15 339 2 德都 DED IGRF13 16.8 10.5 −104 135 −79 131 193 WMM2 020 15.9 10.5 −108 125 −84 126 184 3 长春 CHC IGRF13 −3.3 17.9 −212 91 −213 14 214 WMM2 020 −4.0 18.5 −222 85 −224 11 213 4 乌鲁木齐 WLM IGRF13 4.0 −1.1 −14.8 −76 −17 36 −77 WMM2 020 4.0 −0.9 −17.8 −75 −20 38 −74 5 呼和浩特 HHH IGRF13 −2.4 −5.2 −27 −205 −29 −16 −220 WMM2 020 −1.9 −5.1 −27 −204 −29 −12 −218 6 嘉峪关 JYG IGRF13 0.6 −0.9 −38 −102 −37 6 −97 WMM2 020 0.3 −1.1 −34 −101 −34 3 −97 7 昌黎 CHL IGRF13 11.5 2.1 57 164 70 86 157 WMM2 020 11.9 2.7 52 169 65 89 166 8 喀什 KSH IGRF13 −11.3 −11.2 75 −152 81 −83 −220 WMM2 020 −11.3 −10.8 68 −155 74 −77 −219 9 大连 DAL IGRF13 12.7 −47.0 413 −377 424 46 −710 WMM2 020 13.0 −46.3 408 −371 419 48 −699 10 静海 JIH IGRF13 −1.6 −5.1 56 −23 54 −20 −62 WMM2 020 −1.0 −4.7 54 −18 52 −14 −55 11 太原 TAY IGRF13 3.6 4.0 −59 −12 −56 37 24 WMM2 020 4.4 4.0 −58 −10 −55 43 26 12 红山 LYH IGRF13 14.9 2.3 55 153 69 122 147 WMM2 020 15.7 2.4 55 156 69 129 151 13 格尔木 GLM IGRF13 5.7 −3.7 −19 −121 −19 50 −133 WMM2 020 5.2 −3.9 −16 −121 −16 45 −135 14 泰安 TAA IGRF13 −23.3 52.2 −625 42 −644 −139 501 WMM2 020 −22.6 52.5 −625 48 −643 −132 508 15 兰州 LZH IGRF13 1.9 6.5 −23 109 −22 18 147 WMM2 020 2.1 6.1 −20 105 −19 19 141 16 郑州 ZZH IGRF13 −14.8 −2.1 −4 −48 −16 −135 −58 WMM2 020 −14.0 −2.1 −2 −46 −14 −128 −56 17 天水 TSY IGRF13 −8.5 11.2 −63 128 −67 −75 205 WMM2 020 −8.2 10.9 −61 124 −65 −72 199 18 乾陵 QIX IGRF13 0.4 5.4 7 123 7 4 148 WMM2 020 0.9 5.1 9 120 9 8 143 19 崇明 COM IGRF13 −15.5 −4.0 −62 −155 −77 −142 −154 WMM2 020 −15.0 −3.9 −56 −144 −71 −138 −144 20 成都 CDP IGRF13 −6.6 2.0 −18 7 −21 −64 25 WMM2 020 −6.5 1.8 −21 0 −23 −63 18 21 拉萨 LSA IGRF13 33.4 10.6 −272 −232 −270 337 −62 WMM2 020 33.1 10.3 −269 −232 −267 334 −65 22 西昌 XIC IGRF13 19.4 16.6 −215 −71 −208 210 123 WMM2 020 19.5 16.7 −222 −79 −215 211 119 23 邵阳 SYG IGRF13 −0.1 −0.2 18 22 18 −2 12 WMM2 020 −0.1 −0.3 16 18 16 −2 9 24 泉州 QZH IGRF13 3.1 −11.1 65 −32 67 28 −137 WMM2 020 3.1 −11.6 70 −31 73 27 −141 25 通海 THJ IGRF13 1.2 −11.0 7 −106 7 13 −185 WMM2 020 1.3 −10.4 −3 −112 −3 14 −181 26 广州 GZH IGRF13 −13.3 7.7 −118 −72 −125 −140 43 WMM2 020 −13.9 7.7 −120 −75 −127 −145 41 27 邕宁 YON IGRF13 2.0 4.9 −45 −9 −44 24 50 WMM2 020 1.6 5.5 −53 −13 −52 20 54 28 琼中 QGZ IGRF13 5.0 1.7 −34 −27 −32 58 7 WMM2 020 4.2 2.5 −40 −28 −38 49 16
下载: 导出CSV
表 3 IGRF13和WMM2020模型值与观测值差值的最值、均值与均方根误差统计
Table 3 Statistics on the maximum，minimum，mean values and root mean square errors of the differences between the IGRF-13 and WMM2020 model values and the observed values
模型 D/′ I/′ H/nT F/nT X/nT Y/nT Z/nT 最大值 IGRF13 33.4 52.2 413 372 424 337 501 WMM2 020 33.1 52.5 408 369 419 334 508 最小值 IGRF13 −23.3 −47.0 −625 −377 −644 −142 −710 WMM2 020 −22.6 −46.3 −625 −371 −643 −145 −699 平均值 IGRF13 1.4 1.9 −37 −17 −37 14 8 WMM2 020 1.4 2.0 −39 −18 −38 15 9 均方根误差 IGRF13 11.9 15.4 169 148 173 105 221 WMM2 020 11.7 15.4 169 147 172 104 220
下载: 导出CSV
-
安振昌,徐元芳,王月华. 1991. 1950—1980年中国地区主磁场模型的建立及分析[J]. 地球物理学报,34(5):585–593. doi: 10.3321/j.issn:0001-5733.1991.05.007 An Z C,Xu Y F,Wang Y H. 1991. Derivation and analysis of the main geomagnetic field models in China for 1950−1980[J]. Acta Geophysica Sinica,34(5):585–593 (in Chinese).
安振昌. 1999. 1900—2000年亚洲地磁场长期变化[J]. 地球物理学进展,14(2):58–64. An Z C. 1999. Geomagnetic secular variation over Asia for 1900−2000[J]. Progress in Geophysics,14(2):58–64 (in Chinese).
安振昌,王月华. 1999. 1900—2000年非偶极子磁场的全球变化[J]. 地球物理学报,42(2):169–177. doi: 10.3321/j.issn:0001-5733.1999.02.004 An Z C,Wang Y H. 1999. Global changes of the non-dipole magnetic fields for 1900−2000[J]. Chinese Journal of Geophysics,42(2):169–177 (in Chinese).
安振昌. 2003. 2000年中国地磁场及其长期变化冠谐分析[J]. 地球物理学报,46(1):68–72. doi: 10.3321/j.issn:0001-5733.2003.01.011 An Z C. 2003. Spherical cap harmonic analysis of the geomagnetic field and its secular variation in China for 2000[J]. Chinese Journal of Geophysics,46(1):68–72 (in Chinese).
陈斌,顾左文,高金田,袁洁浩,狄传芝. 2011. 2005.0年代中国地区地磁场及其长期变化球冠谐和分析[J]. 地球物理学报,54(3):771–779. doi: 10.3969/j.issn.0001-5733.2011.03.017 Chen B,Gu Z W,Gao J T,Yuan J H,Di C Z. 2011. Analyses of geomagnetic field and its secular variation over China for 2005.0 epoch using Spherical Cap Harmonic method[J]. Chinese Journal of Geophysics,54(3):771–779 (in Chinese).
陈斌,顾左文,高金田,袁洁浩,狄传芝. 2012. IGRF-11描述的2005—2010年中国地区地磁长期变化及其误差分析[J]. 地球物理学进展,27(2):512–521. doi: 10.6038/j.issn.1004-2903.2012.02.014 Chen B,Gu Z W,Gao J T,Yuan J H,Di C Z. 2012. Geomagnetic secular variation in China during 2005−2010 described by IGRF-11 and its error analysis[J]. Progress in Geophysics,27(2):512–521 (in Chinese).
高国明,康国发. 2010. 卫星地磁场模型和IGRF模型与中国地磁台观测值的比较分析[J]. 云南大学学报(自然科学版),32(5):547–552. Gao G M,Kang G F. 2010. The compare analysis of satellite geomagnetic model values and IGRF model values with observed values of geomagnetic observatories in China[J]. Journal of Yunnan University (Natural Sciences Edition),32(5):547–552 (in Chinese).
毛宁,陈石,杨永友,吴旭,李永波. 2023. 地磁长期变化信号提取和模型预测精度评估[J]. 地球物理学报,66(8):3302–3315. doi: 10.6038/cjg2022Q0499 Mao N,Chen S,Yang Y Y,Wu X,Li Y B. 2023. Extraction of secular variation signals of geomagnetic field and evaluation of prediction accuracy of geomagnetic field models[J]. Chinese Journal of Geophysics,66(8):3302–3315 (in Chinese).
聂琳娟,邱耀东,申文斌,张素琴,张兵兵. 2017. IGRF12和WMM2015模型在中国区域的精度评估及其适用性分析[J]. 武汉大学学报(信息科学版),42(9):1229–1235. Nie L J,Qiu Y D,Shen W B,Zhang S Q,Zhang B B. 2017. Accuracy evaluation and applicability of IGRF12 and WMM2015 model in Chinese mainland[J]. Geomatics and Information Science of Wuhan University,42(9):1229–1235 (in Chinese).
王亶文. 2003. 国际地磁参考场在中国大陆地区的误差分析[J]. 地球物理学报,46(2):171–174. doi: 10.3321/j.issn:0001-5733.2003.02.006 Wang D W. 2003. Analysis of the international geomagnetic reference field error in the China continent[J]. Chinese Journal of Geophysics,46(2):171–174 (in Chinese).
王亶文. 2004. 20世纪地磁长期变化场分析[J]. 地球物理学报,47(3):423–427. doi: 10.3321/j.issn:0001-5733.2004.03.009 Wang D W. 2004. The analysis of the geomagnetic secular variation in the 20th century[J]. Chinese Journal of Geophysics,47(3):423–427 (in Chinese).
王振东,顾左文,陈斌,王粲,袁洁浩. 2017. CHAOS-6模型描述的中国地区地磁长期变化及误差分析[J]. 地震研究,40(3):404–410. doi: 10.3969/j.issn.1000-0666.2017.03.015 Wang Z D,Gu Z W,Chen B,Wang C,Yuan J H. 2017. Geomagnetic secular variation in China described by CHAOS-6 model and its error analysis[J]. Journal of Seismological Research,40(3):404–410 (in Chinese).
徐文耀. 2003. 地磁学[M]. 北京:地震出版社:94. Xu W Y. 2003. Geomagnetism[M]. Beijing:Seismological Press:94 (in Chinese).
徐文耀,Nataf H C,魏自刚,杜爱民. 2006. 地磁场长期变化速率的30年周期[J]. 地球物理学报,49(5):1329–1338. doi: 10.3321/j.issn:0001-5733.2006.05.012 Xu W Y,Nataf H C,Wei Z G,Du A M. 2006. Thirty-year period in secular variation rate of the main geomagnetic field[J]. Chinese Journal of Geophysics,49(5):1329–1338 (in Chinese).
徐文耀. 2009. 地球电磁现象物理学[M]. 合肥:中国科学技术大学出版社:94. Xu W Y. 2009. Physics of Electromagnetic Phenomena of the Earth[M]. Hefei:Science and Technology University Press of China:94 (in Chinese).
曾凌云,曹晋滨,魏新华. 2014. 1980—2010地磁场的变化[J]. 地球物理学进展,29(1):116–121. doi: 10.6038/pg20140115 Zeng L Y,Cao J B,Wei X H. 2014. Global changes of the geomagnetic field during 1980−2010[J]. Progress in Geophysics,29(1):116–121 (in Chinese).
张秀玲,赵旭东. 2024. 基于第十三代国际地磁参考场模型在中国区域特征分析与研究[J]. 地震学报,46(1):120–128. doi: 10.11939/jass.20220137 Zhang X L,Zhao X D. 2024. Regional characteristics analysis in China based on the 13th International Geomagnetic Reference Model[J]. Acta Seismologica Sinica,46(1):120–128 (in Chinese).
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 112
- HTML全文浏览量: 41
- PDF下载量: 37
- 被引次数: 1
