A state-of-the-art review of the numerical simulation of seismic wave motion based on spectral element method
-
摘要:
基于谱元法(spectral element method,SEM)的地震波动数值模拟已被广泛用于地震震源破裂、大规模地震波传播、区域复杂场地及工程结构(群)地震反应、地震层析成像等重要问题的研究及应用当中,是目前地震工程学、地震学和地球物理学等地震科技领域共同关注的前沿热点技术。早期发展的Chebyshev谱元法(CSEM)和Legendre谱元法(LSEM)更接近谱方法的域分解思路,形式相对复杂且计算效率较低。目前广泛使用的是一种简洁形式的LSEM,其实施步骤和主要公式已经与有限元法完全一致,仅通过内置的Gauss-Lobatto-Legendre(GLL)高精度数值积分保留着与谱方法之间的联系。谱元法的巨大成功不仅源于算法本身的高精度、规整性和灵活性,更是得益于以SPECFEM2D/3D,SPECFEM_GLOBE,SPEED等为代表的开源软件集成了实现复杂模拟所需的三维复杂模型、不同地震震源模型或平面波输入、大规模并行计算、全球模拟、伴随方法(adjoint method)以及多尺度或不连续建模等关键技术。本文全面介绍CSEM、LSEM、间断伽辽金谱元法(discontinuous Galerkin,DG-SEM或DGM)、三角形单元谱元法、谱元法精度和稳定性方面的研究及应用进展,并详细阐述谱元法在我国的发展历程以及我国学者关于谱元法研究与工程应用的学术贡献。
Abstract:The spectral element method (SEM)-based numerical simulation of seismic wave motion has been widely applied in the study of earthquake source rupture process, large-scale seismic wave propagation, seismic response of regional complex sites without/with engineering structures (systems), seismic tomography, and so forth. This technique is currently a frontier hotspot of common concern in the fields of earthquake science and technology including earthquake engineering, seismology, geophysics, et al. Spectral element method, which is sometimes also termed as spectral finite element method (SPECFEM) or spectral/hp element method, is a combination of spectral method and finite element method (FEM). Hence, it shares the advantages of both the two methods, i.e., the high accuracy and fast convergence of spectral method, and the regularity and flexibility of FEM.
In early times, the Chebyshev spectral element method (CSEM) and Legendre spectral element method (LSEM) are originated from the domain decomposition of spectral methods, and therefore they inherit the complicated formulations of the latter, in which each of the interpolation basis functions is a linear combination of Chebyshev or Legendre orthogonal polynomials. Consequently, both the methods are as accurate as the spectral methods, but their applications are severely limited by the cumbersome and inefficient multi-layer nested computational structure that is resulted from those basis functions. Nowadays, the most frequently-used SEM is a concise form of LSEM developed by Komatitsch et al. In this method, the early-used complicated basis functions are simplified to the Lagrange shape functions that are commonly adopted in FEM, and those orthogonal polynomial-based analytical Gauss-Lobatto-Legendre (GLL) quadrature formulae are replaced by a simple numerical list of the GLL point coordinates and integration weights. Specifically, the non-equally distributed GLL points serve as the element nodes and the GLL high-precision numerical integration formula is applied to calculate the element mass, stiffness matrices and etc. This configuration makes the LSEM enjoy the same solution procedure and computational formulations as that of FEM, but avoid the significant defects of the classical high-order finite element method, including the intrinsic numerical error of the high-order polynomial interpolation based on equally-spaced grid and the lower computational efficiency due to the high-order consistent mass matrix. In a word, this LSEM has actually become a high-performance lumped-mass high-order finite element method. In addition to the above methods, the family of non-conforming spectral element methods has also been broadly studied and successfully applied in many problems, making themselves an important branch of the SEM. By introducing the so-called Lagrange multiplier or interior penalty term as a glue to effectively connect spectral elements with quite diffetent sizes, orders, shapes and so on, the non-conforming SEMs are more flexible and highly efficient in dealing with multi-scale or discontinuous problems, which apear frequently in large-scale or complicated seismic wave simulations.
The great success of SEM is not only due to the high accuracy, regularity and flexibility of the algorithm itself, but also attributed to those well-designed open-source SEM programs represented by SPECFEM2D/3D, SPECFEM_GLOBE, SPEED, etc. have incorporated a variety of key technologies that are required in complex simulations, such as three-dimensional complex models, different seismic source models or plane wave input method, large-scale parallel computing, global simulation, adjoint method, multi-scale or discontinuous modeling and so on. In the field of earthquake engineering, the SEM has been applied to perform physics-based deterministic numerical simulation of strong ground motion and to realize the “end-to-end” seismic response analysis that is from the source rupture to engineering structures or even engineering systems. The massive simulation data is a good supplement to the insufficient strong ground motion records, and the modeling of seismic wave propagation in actual geolocial structures can compensate for the weak physical background of traditional ground motion prediction equations (GMPEs) or stochastic methods. These simulations, which have reached a certain level of reliability, bring new vitality to earthquake engineering research and application. In the fields of seismology or geophysics, the highly-efficient forward simulation of SEM has been combined with the adjoint method, enabling a simultaneous modeling of the seismic wave fields generated from a number of observation stations, thus the number of forward simulations required for an inversion process can be reduced to an acceptable level. In this way, the advanced full wave inversion (FWI) or seismic tomography technique has been practically used to investigate seismic source mechanisms and to reveal regional or even global velocity structures. Finally, the development of SEM in China is elaborated. The SEM was introduced into China around the year of 2000, and the related studies mainly focused on the basic performance of the method and some preliminary applications until early 2010 s. In the past decade, the Chinese researchers have been conducting more and more innovative work on the SEM algorithms and various engineering applications, and some of the work has reached the research forefront of the world.
-
引言
基于谱元法(spectral element method,SEM)的地震波动数值模拟是一种能够高效地模拟复杂介质中地震波激发和传播过程的前沿技术(Komatitsch et al,2002,2004;Liu Q Y et al,2004;Tromp et al,2005;Tape et al,2009,2010;刘启方等,2013;Mazzieri et al,2013;贺春晖等,2017;刘少林等,2021,2022;于彦彦等,2023;巴振宁等,2023,2024)。该技术自上世纪九十年代问世以来发展迅速(Seriani,Priolo,1991,1994;Seriani et al,1992;Faccioli et al,1997;Komatitsch,Vilotte,1998;Komatitsch,Tromp,1999),近年来在地震工程学(Lu et al,2018;Wang XC et al,2023;Wang XC,Wang JT,2023;Ba et al,2024a,2024b)、地震学和地球物理学(Fichtner,Simutė,2018;Sawade et al,2022;Carmona et al,2024)等地震科技领域受到越来越多关注。这不仅源于算法本身的优势,更主要得益于相关开源软件完成了对复杂问题各个计算环节的集成化,以及超算中心的涌现为大规模并行计算提供了便利。在地震工程领域,现阶段应用谱元法已可以实现震源—路径—场地—结构的全链条地震动模拟与工程抗震分析(Mazzieri et al,2013;Wu et al,2022)。这种从地震发生到致灾整个物理过程的模拟已具备一定的可靠性,其产生的海量计算数据(Paolucci et al,2021;Wang XC et al,2023)能够有效地弥补观测记录不足和随机模拟方法物理背景偏弱等不足,为地震工程研究和应用注入了新的活力。地震学和地球物理领域将谱元法的高效正演模拟与能够实现大量台站记录快速分析的伴随方法(adjoint method)相结合(Tromp et al,2008;Liu,Gu,2012),使反演过程所需的正演模拟次数降至可承受的水平,实现了对震源参数(Stich et al,2010;Sawade et al,2022)、区域/全球速度结构(Tape et al,2009;Karaoğlu,Romanowicz,2018)的地震层析成像(seismic tomography)或全波形反演(full wave inversion,FWI)。
谱元法也被称为谱有限单元法(spectral finite element method,SPECFEM)或谱/hp型单元方法(Patera,1984;Karniadakis,Sherwin,2005),它是谱方法(Gottlieb,Orszag,1977;Canuto et al,1988,2006)和有限元法(finite element method,FEM;朱伯芳,1998;Zienkiewicz et al,2013)的结合,兼具谱方法的高精度、快速收敛性和有限元法的规整性与灵活性。从数值方法角度来看,谱元法既可以视为谱方法的域分解技术,又可以看作是采用谱插值构建的一种性能优良的特殊高阶有限元法。谱方法是一大类方法的统称,其共同特点是全域性和谱精度,谱精度使得它能够快速逼近任意光滑函数,但是全域表达式常常难以适应复杂问题。经典有限元法的高阶单元基于等距节点的多项式插值构建,多项式的解析延拓性所伴随的数值不稳定性以及无法导出集中质量矩阵等问题,都严重制约了其实际应用。谱元法成功地实现了二者的优势互补,逐步发展成为一种备受关注的高效数值方法。就地震波动应用而言,基于谱元法的地震波动数值模拟涉及地震工程学、地震学和地球物理学等多个学科领域,相关研究工作既存在着显著差别,又需要在发展地震科技和服务防震减灾的共同目标下进行交叉融合。例如,地震学和地球物理领域研究得出的震源参数和区域速度结构是地震工程领域利用谱元法开展基于物理的地震动模拟的必要资料。地震工程领域对谱元法的兴趣体现在其能够模拟宽频带地震动和具有较高计算效率,相应的理论依据则可以大量参考地震学和地球物理领域研究者的工作(De Basabe,Sen,2007,2010,2015;Antonietti et al,2012;Liu YS et al,2017)。谱元法性能优良且应用丰富,但是目前关于谱元法的综述及专著相对较少,大多散见于流体力学(Vosse,Minev,1996;Karniadakis,Sherwin,2005;Pozrikidis,2014)、结构动力学(Gopalakrishnan et al,2008;Lee U,2009;Ostachowicz et al,2012)、地震学(Schuberth,2003;Chaljub et al,2007;De Basabe,2009)等领域。谱元法的概念和方法还远未达到像有限元法和有限差分法那样为人熟知,这与它强大的应用能力不相匹配,不利于该方法的研究推广以及更多领域对于高效数值技术的需求。
基于上述现状,本文对地震波动谱元法数值模拟技术的研究进展进行概括性介绍。简要探讨谱元法与谱方法以及经典有限元法之间的关系,全面介绍Chebyshev谱元法(CSEM)、Legendre谱元法(LSEM)、间断伽辽金谱元法(discontinuous Galerkin,DG-SEM或DGM)、三角形谱元法、谱元法的精度和稳定性几个方面的研究和应用进展,并专门阐述我国学者在谱元法研究和应用方面的创新与贡献。本工作期望为发展基于谱元法的高效数值方法及其应用相关技术解决地震工程学、地震学和地球物理学等领域的重要问题提供一些有益的参考。
1. 谱元法概述
谱元法由Patera (1984)在计算流体动力学(computational fluid dynamics,CFD)领域提出,其雏形可以追溯至更早的谱方法域分解技术。同时,谱元法具有与有限元法相同的基本架构,区别仅在于它采用谱方法的插值函数来构建性能优良的高阶单元,所以它也可以被看作是一种特殊的高阶有限元法。
1.1 谱元法与谱方法的关系
谱元法与谱方法(Gottlieb,Orszag,1977;Canuto et al,1988,2006;向新民,2000;Trefethen,2000)的关系可以通过分析Chebyshev正交多项式的级数展开式与它的Lagrange型插值公式之间的区别迅速得出基本认识。
以一维标准区间$\xi\ $∈$ [ -1\text{,} 1 ] $ (实际区间由标准区间进行坐标拉伸得到)上的未知场函数u(ξ)为例,利用Chebyshev正交多项式,可以分别写出两种展开式,即
$$ \text{Chebyshev级数展开式:} u ( \xi ) =\sum\limits_{k= 0}^N {{a_k}{T_k} ( \xi ) } $$ (1) $$\text{Lagrange型插值公式:} u ( \xi ) =\sum\limits_{i = 0}^N {u ( {\xi _i} ) \varphi _i^N ( \xi ) } $$ (2) $$\text{插值基函数:}\varphi _i^N ( \xi ) =\dfrac{2}{N}\sum\limits_{k = 0}^N {\frac{1}{{{{\bar c}_i}{{\bar c}_k}}}{T_k} ( {\xi _i} ) {T_k} ( \xi ) \text{,} i = 0\text{,} 1\text{,} \cdots N \text{,} } {\bar c_i} = \left\{ \begin{gathered} 1\text{,} i {\text{≠}} 0\text{,} N \\ 2\text{,} i = 0\text{,} N \\ \end{gathered} \right. $$ (3) $$\text{插值节点:}{\xi _i} = - \cos \left({\frac{{i\pi }}{N}} \right) \text{,} i = 0\text{,} 1\text{,} \cdots\text{,} N $$ (4) 式中,$T_k ( {\mathrm{cos}} \theta ) ={\mathrm{cos}}k\theta $为Chebyshev正交多项式,$a_k $为待定系数。$\varphi _i^N ( \xi ) $为基于Chebyshev多项式的Lagrange型插值基函数,$u ( \xi_i ) $为待定系数。式(4)给出的插值节点是Gauss-Lobatto-Chebyshev求积公式的节点,简称GLC节点,具体为Chebyshev多项式一阶导数的零点。
式(1)和式(2)— (4)代表了谱方法中场函数的两类表达形式,除了这里的Chebyshev多项式之外,还可以基于Legendre正交多项式构建类似的插值函数,或者使用经典的Fourier级数。插值节点可以是Fourier级数的等距节点,也可以是根据不同求积公式导出的各种不等距节点。所以,谱方法有着多种不同的表达形式,在实际应用时可以根据具体问题的特点择优选用。这些不同形式的插值在结果上是等价的,它们都具有谱精度和快速收敛性,即通过提高插值阶次能够迅速逼近任意光滑函数。不过,式(1)和式(2)— (4)存在一个重要区别:后者待求系数是未知场函数的节点值,而前者则不是。这种区别使得二者在求解具体问题时的便利性大为不同。若对谱方法进行域分解,采用式(2)— (4)的形式更为便利,而式(1)则可能导致单元之间的衔接以及边界条件和初始条件的施加面临难以克服的困难。此外,将区间端点包含于配置点中更有利于进行单元之间的衔接。综上,谱方法的插值函数有多种不同形式,谱元法采用了其中以包含区间端点在内的配置点为插值节点的Lagrange型谱插值形式。
1.2 Chebyshev谱元法和Legendre谱元法
基于上述式(2)—(4)的单元场函数构建的数值求解方法被称为Chebyshev谱元法,简记为CSEM (Patera,1984;Seriani,Priolo,1991,1994)。在用于求解地震波动问题时,CSEM的实施步骤与有限元法相同,区别只在于此时单元节点为不等距分布的GLC节点,计算单元质量和刚度矩阵时采用GLC高精度数值积分。上述插值节点(即CSEM单元节点,见式4)同时也是GLC积分节点,而GLC积分权系数则为
$$\text{GLC积分权系数:}{\omega _n} = \left\{ \begin{gathered} {\pi \mathord{\left/ {\vphantom {\pi { ( 2N ) }}} \right. } { ( 2N ) }}\text{,} n = 0\text{,} N \\ {\pi \mathord{\left/ {\vphantom {\pi N}} \right. } N}\text{,} n = 1\text{,} 2\text{,} \cdots \text{,} N - 1 \\ \end{gathered} \right. $$ (5) 这里构建的是一维Chebyshev谱单元,对于二维四边形单元和三维六面体单元,可以简单地将不同坐标方向的一维插值函数进行乘积得到。在实际应用中,CSEM更多采用解析积分来计算单元特性矩阵。解析积分的核心公式为Chebyshev多项式乘积的积分,以及它的一阶导数乘积的积分,具有如下显式表达式:
$$ {A}_{kl}={\displaystyle {\int }_{-1}^{1}{T}_{k} ( \xi ) {T}_{l} ( \xi ) d\xi }=\left\{\begin{array}{ll}0\text{,} &k+l为奇数\\ \dfrac{1}{1-{ ( k+l ) }^{2}}+\dfrac{1}{1-{ ( k-l ) }^{2}},&k+l为偶数\end{array}\right. $$ (6) $$ B_{k l}=\displaystyle\int_{-1}^1 T_k^{\prime} ( \xi ) T_l^{\prime} ( \xi ) d \xi=\left\{\begin{array}{l} 0\text{,} \qquad \qquad \qquad \qquad \quad k+l \text { 为奇数 } \\ \dfrac{k l}{2} [ H_{| ( k-l ) / 2|}-H_{\mid ( k+l ) / 2|} ] \text{,} k+l \text { 为偶数 } \end{array}\text{,} H_n= \begin{cases}0\text{,} \qquad \qquad \,\,\,\,\,\,n=0 \\ -4 \displaystyle\sum_{j=1}^n \frac{1}{2 j-1}\text{,} n {\text{≥}} 1\end{cases}\right. $$ (7) 式(2)—(7)构成了CSEM的基本公式。除了Chebyshev正交多项式之外,还可以利用Legendre正交多项式构建如下的Legendre谱元法,简记为LSEM (Rønquist,Patera,1987;Ho,Patera,1990;Ma,1993)。
$$\text{Legendre谱单元:}u ( \xi ) = \sum\limits_{i = 0}^N {u ( {\xi _i} ) \phi _i^N ( \xi ) } $$ (8) $$\text{单元形函数:}\phi _i^N ( \xi ) = \dfrac{{ - 1}}{{N ( {N + 1} ) {L_N} ( {{\xi _i}} ) }}\dfrac{{ ( {1 - {\xi ^2}} ) {L { \text{′}}_N} ( \xi ) }}{{\xi - {\xi _i}}}\text{,} i = 0\text{,} 1\text{,} \cdots\text{,} N $$ (9) $$\text{单元节点 ( GLL ) :} {\xi }_{j}=\left\{ \begin{array}{l}-1\text{,} j=0 \\ L{ \text{′}}_{N} ( \xi ) 的零点\text{,} j=1\text{,} 2\text{,} \cdots \text{,} N-1 \\ 1\text{,} j=N \end{array} \right. $$ (10) $$\text{GLL积分权系数:} {\omega _j} = \frac{2}{{N ( {N + 1} ) }}\dfrac{1}{{{{ [ {{L_N} ( {{\xi _j}} ) } ] }^2}}} \text{,} j = 0\text{,} \cdots \text{,} N $$ (11) 式中,$L_N ( \xi ) $为N阶Legendre正交多项式,$L{ \text{′}}_{N} $$ ( \xi ) $为它的一阶导数。式(10)为Gauss-Lobatto-Legendre (GLL)高精度数值积分的节点,式(11)为GLL积分权系数。Legendre多项式由如下递推关系式定义。
$$ {L_0} ( x ) =1 \text{,} {L_1} ( x ) =x \text{,} {L_{n + 1}} ( x ) =\frac{{2n + 1}}{{n + 1}}x{L_n} ( x ) - \frac{n}{{n + 1}}{L_{n -1}} ( x ) $$ (12) Asmar (2005)给出了Legendre多项式的直接表达式:
$$ {L_n} ( x ) = \frac{1}{{{2^n}}}\sum\limits_{m = 0}^M {{{ ( { - 1} ) }^m}\frac{{ ( {2n - 2m} ) !}}{{m! ( {n - m} ) ! ( {n - 2m} ) !}}{x^{n - 2m}}} \text{,} M=\left\{ \begin{array}{ll}n/2\text{,} & n为偶数\\ ( n-1 ) /2\text{,} & n为奇数\end{array} \right.$$ (13) 式(8)—(12)为LSEM的基本公式。同样,二维四边形单元和三维六面体单元的场函数可以由一维插值函数乘积得到。LSEM与CSEM有很多相似之处,例如Chebyshev多项式也具有类似于式(12)的递推定义式以及类似于式(13)的直接表达式(Asmar,2005),LSEM的单元特性矩阵也具有类似于式(6)—(7)的解析形式计算公式(Karniadakis,Sherwin,2005)。不过,LSEM与CSEM亦存在显著差别:Legendre多项式无法写成Chebyshev多项式那样简单的三角函数形式,导致GLL节点和权系数不便于写成像GLC节点式(4)和权系数式(5)那样的显式表达式。为了顺利使用LSEM,人们参考有限元法中关于Gauss积分的使用方式,将GLL积分的数学分析结果以列表形式给出,供编程时使用。考虑到GLL积分节点和权系数的具体数值很少有文献给出,本文将其列于附录表A.1中。
1 Gauss-Lobatto-Legendre高精度数值积分的节点和权系数1. The nodes and weights of Gauss-Lobatto-Legendre high-precision numerical integrationGLL节点数 积分节点 积分权系数 2 ±1 1 3 0 1.333 333 333 333 333 3 ±1 0.333 333 333 333 333 3 4 ±0.447 213 595 499 957 9 0.833 333 333 333 333 4 ±1 0.166 666 666 666 666 7 5 0 0.711 111 111 111 111 1 ±0.654 653 670 707 977 2 0.544 444 444 444 444 5 ±1 0.100 000 000 000 000 0 6 ±0.285 231 516 480 645 1 0.554 858 377 035 486 2 ±0.765 055 323 929 464 7 0.378 474 956 297 847 0 ±1 0.066 666 666 666 666 7 7 0 0.487 619 047 619 047 6 ±0.468 848 793 470 714 2 0.431 745 381 209 862 7 ±0.830 223 896 278 567 0 0.276 826 047 361 565 9 ±1 0.047 619 047 619 047 6 8 ±0.209 299 217 902 478 9 0.412 458 794 658 703 8 ±0.591 700 181 433 142 3 0.341 122 692 483 504 4 ±0.871 740 148 509 606 6 0.210 704 227 143 506 1 ±1 0.035 714 285 714 285 7 9 0 0.371 519 274 376 417 2 ±0.363 117 463 826 178 2 0.346 428 510 973 046 3 ±0.677 186 279 510 737 7 0.274 538 712 500 161 7 ±0.899 757 995 411 460 2 0.165 495 361 560 805 5 ±1 0.027 777 777 777 777 8 10 ±0.165 278 957 666 387 0 0.327 539 761 183 897 6 ±0.477 924 949 810 444 5 0.292 042 683 679 683 8 ±0.738 773 865 105 505 0 0.224 889 342 063 126 4 ±0.919 533 908 166 458 9 0.133 305 990 851 070 1 ±1 0.022 222 222 222 222 2 注:积分节点和权系数的数目与GLL节点数相对应,数值相同、正负号不同的积分节点对应相同的积分权系数,为简化起见,表中只列出一个。 由式(2)—(7)表示的CSEM和由式(8)—(12)表示的LSEM都是在有限元法的计算框架下引入截断的谱插值来构建高阶单元,该类单元随着插值阶次的提高能够逼近任意场函数,即具有谱精度。但是,插值基函数式(3)和式(9)的形式比较复杂,这使得高精度谱单元在求解具体问题时所产生的公式数量会非常多而且彼此之间存在复杂的嵌套关系,计算过程相当繁琐。正是由于谱方法和谱元法的算法复杂度远大于有限差分法和有限元法,它们早期主要被用于对场函数插值精度需求较高的计算流体动力学领域,而在其它领域的研究和应用则相对较少。
1.3 Legendre谱元法的简洁形式
上述较为复杂的CSEM和LSEM与谱方法的联系比较紧密,基于Chebyshev正交多项式的Lagrange型基函数式(3)和基于Legendre正交多项式的Lagrange型基函数式(9)都来自谱方法的研究成果。可是若从有限元法的角度来看,构造插值基函数似乎不必如此复杂。有限元法直接采用单元节点上的Lagrange基函数作为形函数,形式简单且计算方便。那么,是否可以直接使用GLC节点或GLL节点上的Lagrange基函数作为单元形函数?它们与式(3)或式(9)又是什么关系?人们经过研究发现基于GLC节点的Lagrange基函数与式(3)有一定差别,但是基于GLL节点的Lagrange基函数与式(9)则是完全等价的!基于这个重要发现,由式(3)和式(9)所表示的早期复杂形式谱元法很快被由GLL节点Lagrange基函数所表示的简洁形式谱元法所取代(Komatitsch,Vilotte,1998;Komatitsch,Tromp,1999,2002a,2002b;Komatitsch et al,1999,2002,2004)。这是目前应用最广泛的谱元法形式,它极大地推动了该方法在多个领域的发展。这种Legendre谱元法的简洁形式表达式如下:
$$\text{LSEM谱单元:}u ( \xi \text{,} \eta \text{,} \chi ) = \sum\limits_{m= 1}^M {u ( {\xi _i}\text{,} {\eta _j}\text{,} {\chi _k} ) {N_m} ( {\xi \text{,} \eta \text{,} \chi } ) } $$ (14) 一维、二维和三维形函数分别为
$$ {N_m} ( \xi ) = l_i^{ngllx} ( \xi ) $$ (15a) $$ {N_m} ( {\xi \text{,} \eta } ) =l_i^{ngllx} ( \xi ) {\text{×}}l_j^{nglly} ( \eta ) $$ (15b) $$ {N_m} ( {\xi \text{,} \eta \text{,} \chi } ) = l_i^{ngllx} ( \xi ) {\text{×}}l_j^{nglly} ( \eta ) {\text{×}}l_k^{ngll{\textit{z}} } ( \chi ) $$ (15c) GLL节点的Lagrange基函数为
$$ l_i^{ngll} ( \xi ) = \prod\limits_ {j = 0\text{,} j \ne i }^{ngll} {\dfrac{{ ( {\xi - {\xi _j}} ) }}{{ ( {{\xi _i} - {\xi _j}} ) }}} \text{,} i= 0\text{,} 1\text{,} \cdots\text{,} ngll $$ (16) 式中,M表示谱单元的节点总数,ngllx,nglly,ngllz分别表示三个坐标方向的GLL节点数。GLL节点和积分权系数由式(10)和式(11)定义,具体数值见本文附录表A.1。
由式(14)—(16)所表示的简洁形式LSEM采用不等距分布GLL节点的Lagrange插值和GLL高精度数值积分来构建单元,这与经典有限元法所采用的等距节点Lagrange插值和Gauss高精度数值积分构建单元的方式类似,二者在计算模式上是完全一致的。此时,与谱方法有关的复杂理论内容,如谱展开、基于Legendre正交多项式的Lagrange型谱插值、高精度求积公式的构建、指数收敛率以及谱精度等,都被内置在GLL积分节点和积分权系数的简单数值列表当中。经典有限元法的高阶单元基于等距节点的多项式插值构建,多项式的解析延拓性所伴随的数值不稳定性以及无法导出集中质量矩阵等问题,都严重制约了其实际应用。与之相比,简洁形式LSEM因其单元节点与GLL积分节点一致,能够严格地导出集中质量矩阵,极大地提升了计算效率,同时,单元内部节点分布呈中部稀疏、两端密集的不等距分布,这能够规避多项式解析延拓性所带来的数值不稳定性,确保高阶精度的稳步实现。综上,式(14)—(16)的LSEM得以充分发挥其作为一种性能优良的集中质量高阶有限元法的优势,逐渐发展成为计算流体动力学(Karniadakis,Sherwin,2005)、地震波动模拟(Schuberth,2003;De Basabe,2009)、结构中波传播分析(Gopalakrishnan et al,2008;Lee U,2009;Ostachowicz et al,2012)等不同领域广泛关注的重要数值方法。
2. 谱元法研究
本节将从Chebyshev谱元法,Legendre谱元法,非协调/间断伽辽金谱元法,三角形单元谱元法,以及谱元法的精度和稳定性五个方面,全面介绍地震波动数值模拟领域关于谱元法的主要研究工作。
2.1 Chebyshev谱元法(CSEM)
意大利学者Seriani和Priolo等首先将谱元法引入地震波动领域,围绕Chebyshev谱元法开展了大量研究。Seriani和Priolo (1991)、Priolo和Seriani (1991)最早提出求解声波方程的CSEM方法,设计了一个宽频带波动的一维算例对高阶CSEM单元和经典1—4阶有限单元的模拟精度进行详细探讨。研究得出结论:为实现精确波动模拟需要在一个波长尺度内设置的网格点数目,1阶、2阶FEM单元分别约为22个、11个,而4—5阶CSEM单元只需约6个,7—8阶CSEM单元只需约5个。20阶以上CSEM单元甚至能够接近每个波长2个节点的采样频率上限,定量地揭示出CSEM的谱精度。Seriani等(1992)随后提出求解弹性波方程的CSEM方法,通过具有解析解的全空间点源问题算例验证了方法的高精度,给出含有台阶型地表和不规则界面的算例,展示了CSEM具有求解复杂地震波动问题的能力。Seriani (1997,1998)针对三维声波问题探讨了CSEM的并行计算技术,空间上采用逐单元(element-by-element,EBE)求解策略,时间上采用预条件共轭梯度法,在当时最先进的Cray T3E超级计算机上采用其内置优化通信的库函数SHMEM实现高效并行计算。Seriani (2004)针对大尺度谱单元难以处理介质复杂变化的问题,提出一种双网格CSEM,在波场建模和几何建模之外引入介质力学性质建模,三个维度的建模有机结合。文中以具有解析解的介质性质平滑变化的两个一维波动算例证实方法的可靠性。
Dauksher和Emery (1997)对CSEM的三种质量矩阵进行研究,发现原始的一致质量矩阵和通过行和集中得到的集中质量矩阵精度较高,而通过对角元素放大得到的集中质量矩阵精度较差。Mulder (1999)对FEM、CSEM和LSEM的高阶单元进行模态分析,证明主模态能够确保高精度,次级模态(伪模态)影响很小,LSEM单元较其它两类单元更优。Seriani和Oliveira (2007,2008a,2008b)对CSEM和LSEM用于波动模拟的网格频散和数值各向异性进行理论研究,发展出实用的分析方法,得出4阶谱单元的空间采样率为每个波长4个节点、大尺度和长持时模拟可适当提高采样率的结论,这后来成为谱元法波动模拟中最常用的网格尺寸标准。Oliveira和Seriani (2011)研究了单元畸变对谱元法波动模拟精度的影响,对允许的畸变程度进行界定并提出改进措施。
Zhu等(2011)探讨了CSEM与隐式Newmark时间积分相结合的声波问题求解方法,得出时间步长和Newmark参数取值越小,计算精度越高,探讨了吸收边界条件以及单极子、偶极子和四极子震源的模拟效果。Geng等(2016)研究了求解声波问题的时空耦合CSEM,空间采用较高阶次、时间采用较低阶次CSEM单元,计算精度优于传统方法。邢浩洁和李鸿晶(2017c)分析认为CSEM并非一定要与隐式时间积分方法结合,经典的二阶中心差分显式时间积分法同样可用,且更为便捷高效。Wang JX等(2022a,2022b)详细比较分析了有限元法和谱元法中不同的集中质量技术,研究提出一种具有C1连续性的CSEM谱单元,通过梁、板中的波动模拟算例证实了方法的高精度和快速收敛性。李鸿晶和王竞雄(2022)探讨了使用Gauss积分得出一致质量模型、Gauss-Lobatto积分得出集中质量模型的原理,指出后者的不完全积分并不影响其高精度特性,而集中质量模型则更能反映波传播的物理特征。
2.2 Legendre谱元法(LSEM)
法国学者Komatitsch和Vilotte以及美国学者Tromp等基于式(14)—(16)所示的简洁形式LSEM发展出适用于二维、三维复杂区域甚至是整个地球的地震波动模拟方法,并且在基于LSEM和伴随方法的全波形反演技术方面做了大量工作。他们开发和维护的谱元法开源软件SPECFEM2D,SPECFEM3D以及SPECFEM3D_GLOBE被全世界研究者广泛关注和使用,引领和推动了谱元法大规模地震波动模拟的发展。不同于流体力学领域大量使用早期复杂形式的CSEM和LSEM谱元法,Komatitsch等的工作是以式(14)—(16)这种非常接近有限元法表达形式的简单规整的谱元法为基础,这是该形式谱元法首次被系统地讨论和使用。
Komatitsch和Vilotte (1998,1999)、Komatitsch和Tromp (1999)以及Komatitsch等(1999)以式(14)—(16)作为单元插值函数,推导了含有点震源或矩张量震源以及吸收边界条件的弹性波方程离散表达式,编制出适用于二维、三维复杂区域地震波动模拟的规整化计算程序,给出大量算例,充分展示了谱元法的高精度和强适应性。他们指出LSEM相比于CSEM以及经典有限元法的最大优势是能够严格地导出集中质量矩阵,通过与显式时间积分方法组成全显式的求解格式,可以极大地节省内存占用、减少计算量和提高并行效率。文中给出以下模拟算例:弹性半空间表面力源的Lamb问题和内部矩张量源的Garvin问题,二维半圆形峡谷地形、起伏地表结合不规则地层的复杂模型、实际山区二维剖面、二维悬崖地形问题,三维半空间、成层半空间模型,半球谷地形、高斯山体地形问题,地表起伏结合内部不规则界面的三维区域模型,以及介质具有强衰减特性(品质因子较低)的三维地震波动问题。实现了点源、矩张量震源、平面波等不同波动输入,并基于消息传递接口(message passing interface,MPI)并行技术开发出并行计算程序,进行大规模三维波动模拟。通过与解析法、离散波数法、间接边界元法、频率—波数法(frequency-wavenumber,FK方法)、有限差分法等进行比较,证实LSEM模拟精度高且适应性强,发展前景巨大。文中详细交代了每个算例采用的谱单元阶次,模型的单元数目和节点数目,时间步长稳定界限以及使用的时间步长,对部分模型的内存占用和计算耗时也进行了具体分析。文中谱元法的并行计算效率令人印象深刻,如:10万个节点的二维问题,单核计算15分钟,64核并行计算时间缩减至4分钟。某N=8阶谱单元的500万节点三维模型,采用128核并行计算,仅需1.5小时就能完成。分别采用单核和8核进行测试,得出并行加速为7.3倍,并行效率达到91%。这样规模的计算可以不依赖于昂贵的超级计算机,能够在PC机组成的并行计算平台(被称为Beowulf机)上实现。为拓展谱元法能够求解的地震波动问题类型,Komatitsch等(2000a,2000b)研究了流固耦合地震波动问题以及各向异性介质地震波动问题的谱元模拟方法,Komatitsch等(2001)发展了能够适应复杂地质构造的四边形谱单元与三角形谱单元相结合的谱元法。在前述工作基础上,Komatitsch和Tromp (2002a,2002b)以及Komatitsch等(2002)成功实现基于谱元法的全球地震波动模拟,其中地壳、地幔、内地核采用固体介质弹性波方程,外地核采用流体介质声波方程,计算过程在由PC机组成的Beowulf集群上完成。研究表明,与有限差分法或伪谱法相比,谱元法能够建立包含纵横向不均匀性、椭圆度、海洋、自转、自重、以及各向异性和衰减等多种复杂性的三维地球模型,模拟精度更高,计算成本与之相当或更低。他们指出这项工作的重要意义在于谱元法为如此复杂、超大规模的地震波动模拟提供了可用的方法,算力的迅速提升使得将来有可能在几十分钟或更短时间内完成这类计算,这将会打开通向复杂地球结构层析反演或全波形反演技术(注:一次这样的反演往往包含对大量地震事件进行成千上万次正演模拟)的大门,可用于建立新一代高质量地幔模型或更准确地确定震源参数。可以看出,Komatitsch等的工作不同于大多数研究往往只注重提出理论或方法而仅对应用前景做出展望的做法,他们关于LSEM的研究一开始就很有系统性,详细给出性能优良的LSEM高阶单元用于求解不同地震波动问题的具体过程,让展望变成了现实。
Faccioli等(1997)提出一种二维、三维弹性波传播的伪谱域分解法,其中较为详细地探讨了点源、矩张量震源以及平面波的施加,给出二维全空间和半空间问题、三维全空间和圆柱形山谷地形问题以及含有品质因子的衰减波动模拟等算例。Faccioli和Quarteroni (1999)指出其工作与上述Komatitsch等的工作非常相似且提出时间更早,不过他们并没有给出单元插值函数的具体表达式,并且采用解析的Legendre导数矩阵而不是GLL数值积分来进行单元计算,其方法可能更接近于本文式(8)—(12)所表示的早期复杂形式LSEM。
Komatitsch等还对高精度的完美匹配层(perfectly matched layer,PML)人工边界开展了一系列研究。考虑到经典PML大多基于一阶微分方程(对于波动而言为速度—应力型方程),Komatitsch和Tromp (2003)推导出基于二阶弹性波方程的分裂形式PML,并在二维波动谱元模拟中展示了其高效吸收面波和体波的效果。由于该PML对于大角度外行波效果不佳,Komatitsch和Martin (2007)提出一种非分裂的卷积形式完美匹配层(convolutional PML,CPML),实现对于任意角度外行波的高效吸收,随后Martin等(2008)给出在谱元法中实现CPML的计算公式和验证算例。Martin等(2010)进一步提出PML的一种辅助微分方程表达形式,称之为ADE-PML。但是上述PML在长持时波动模拟中会暴露出数值失稳问题,Xie等(2014)在新的复频移— 非分裂— 卷积PML中去除奇异项,实现了长持时稳定的谱元法正演波动模拟和伴随方法敏感度核计算。
2.3 非协调/间断伽辽金谱元法(DG-SEM)
类似于非协调有限元法(Zienkiewicz et al,2013)被大量用于处理不连续或多尺度问题,非协调(non-conforming)谱元法(Käser,Dumbser,2006;De Basabe et al,2008;Antonietti et al,2012)也被学者们相继研究发展,其中基于间断伽辽金(discontinuous Galerkin)模式的非协调谱元法(DG-SEM或DGM)已成为大规模地震波动模拟尤其是区域复杂场地— 城市建筑群模拟的一种重要方法(Mazzieri et al,2013;Tian et al,2023;Smerzini et al,2024)。非协调有限元/谱元法打破了经典方法中相邻单元之间共用节点和插值函数的自然(严丝合缝)衔接方式,用专门定义的约束条件实现更为灵活的不同尺寸甚至是不同类型单元之间的衔接,形成从整体上满足收敛性的离散化方程。非协调单元需要的存储空间和计算耗时更多,前后处理也相对复杂,主要在协调型单元难以处理或处理效率低下的不连续或多尺度问题中具有显著优势,如地震波动领域的震源动力学破裂、高阻抗比的沉积盆地、流固耦合、复杂场地— 工程结构(群)等问题的数值模拟研究。
汪文帅等(2013)指出间断Galerkin方法在地震波场数值模拟中大量应用是一种称为任意阶精度微分(arbitrary high-order derivative,ADER)的时间积分格式推出后才开始的。Käser和Dumbser (2006)、Dumbser和Käser (2006)首次研究了ADER方法与DGM相结合求解二维和三维非均匀介质中的弹性波方程问题,时间域和空间域离散都能达到同样高的精度。Käser等(2007)、Puente等(2007)以及Dumbser等(2007)分别将ADER-DGM拓展到粘弹性介质、各向异性介质以及局部化的单元阶次和时间步长的地震波动模拟。Käser和Dumbser (2008)利用ADER-DGM研究了含有复杂界面和流体运动的流固耦合波动问题。Käser等(2008)通过基准算例对四面体网格ADER-DGM方法的精度进行了定量分析。
De Basabe等(2008)在研究间断伽辽金谱元法精度时考虑了Legendre多项式插值(称之为模态插值)、基于GLL节点或Gauss节点的Lagrange插值(称之为节点插值)三种不同单元形式,这表明非协调谱单元具有灵活多样的构建方式。De Basabe和Sen(2009)指出有限元法向高阶单元、对角质量阵以及高阶时间积分的发展促成了其在地震波动领域越来越多的应用。De Basabe等(2010)在研究谱元法与Lax-Wendroff高阶时间积分(其二阶形式为经典的中心差分格式)相结合的稳定性时,考虑了采用不完全(incomplete)、对称(symmetric)和非对称(non-symmetric)三种内部罚函数(interior penalty)的间断伽辽金谱元法,分别记为IIPG、SIPG、NIPG,表明单元衔接方式亦可以导出不同的非协调谱元法。Antonietti等(2012)指出弹性动力学方程的非协调高阶近似主要分为两大类,一类利用Lagrange乘子作为“砂浆”(mortar)来连接各个高阶单元,称之为Mortar SEM方法,另一类引入内部罚函数来衔接各个单元,称之为间断伽辽金谱元法,记为DG-SEM或DGM。文中详细比较了Mortar SEM和DG-SEM的精度、收敛性、网格频散以及数值稳定性。
意大利米兰理工大学在该国大量学者关于谱方法、谱元法以及非协调谱元法的工作基础上,开发出另一种被广泛使用的谱元法开源软件SPEED,全称为SPectral Elements in Elastodynamics with Discontinuous Galerkin (Faccioli et al,1997;Stupazzini et al,2009;Antonietti et al,2012;Mazzieri et al,2013)。Mazzieri等(2013)通过一个半空间上覆低速层的三维算例比较了SEM和DG-SEM的精度及计算效率,结果显示:二者与参考解的最大相对误差分别1%和2%,而DG-SEM使用的单元数量更少;采用512核并行求解时,SEM和DG-SEM的并行效率分别达到90%和70%。这表明DG-SEM的精度及计算效率与SEM相当,在高度不均匀介质或不规则模型中将能够充分发挥其优势。文中利用SPEED软件分别实现了意大利东北部一座铁路大桥和新西兰基督城在地震作用下的震源— 路径— 场地— 结构(群)全过程模拟。其中对铁路大桥— 表层土体— 下部基岩分别采用DG-SEM和SEM进行建模和计算,得出二者模拟结果较为一致,而前者的多尺度模型网格质量更好,且单元数量仅为后者的一半。对基督城CBD地区1 km×1 km范围内150栋建筑及50 m深度土体进行精细化建模,划分出50万个六面体单元,将其嵌入到尺度为60 km× 60 km×20 km的三维地质体中,后者也被划分为约50万个单元。SPEED软件成功模拟了这个多尺度的地震波动问题,得出建筑群的地震反应,并揭示出城市大型建筑对附近地面运动具有显著影响,即存在所谓的场地— 城市(site-city interaction,SCI)效应(Lu et al,2018;Kato,Wang,2021;Tian et al,2023)。Paolucci等(2015)将基于SPEED谱元软件开展的强地面运动模拟称为基于物理(physics-based)的三维数值模拟,继Graves等(2011)、Cui等(2013)以及Baker等(2014)之后进一步强化了基于物理的地震动模拟这个概念,使得有限差分、有限元或谱元等确定性数值模拟方法与基于地震数据统计的经验方法之间的区分更加明晰,该表述被后续研究大量使用(Smerzini,Pitilakis,2018;Bradley,2019;Paolucci et al,2021;Ba et al,2023;Wang XC,Wang JT,2023)。
2.4 三角形单元谱元法
由于四边形网格不能灵活地刻画复杂几何形状,学者们开展了关于三角形单元谱元法的研究(刘有山等,2014)。有限元法的三角形单元相对简单,利用面积坐标即可以方便地表示出3节点、6节点(含各边中点)以及10节点(含各边三等分点和一个内点)三角形单元的插值函数(朱伯芳,1998)。谱元法的三角形单元则比较复杂,它无法由面积坐标或者一维形函数张量积简单地表示出来,而是需要解决高阶插值模式下三角形内部最优节点配置、插值多项式表达和运算以及质量矩阵是否对角化等问题。Dubiner (1991)、Sherwin和Karniadakis (1995)较早开展了关于三角形谱单元的研究,他们使用扭曲的张量积网格来精确逼近单元积分,其精度与四边形单元相当,且能够与后者组成混合网格。然而,由于扭曲张量积网格是过采样的,它使用的节点数是多项式展开中自由度数的两倍,导致单元质量矩阵为非对角阵。Chen和Babuška (1995)以及Taylor等(2000)研究了在三角形中与精确多项式逼近相关而非与精确求积公式相关的临界采样点,其中最著名的是后来常用的Fekete节点。这些节点是四边形谱单元上节点向包括三角形单元在内的更一般情形的推广,它们不仅能够实现三角形单元与四边形单元之间的协调匹配,还保留了经典四边形单元的重要特性如对角质量矩阵。
Komatitsch等(2001)在二维地震波动模拟中探讨了Fekete节点三角形谱单元的性能及其与四边形谱单元的适配性。文中指出由于GLL节点无法延展到三角形单元上,人们根据三角形上的最优插值或逼近性质(而不是像GLL节点那样满足求积性质)建立极值问题,数值求解出Fekete点、最小二乘点以及最小能量静电点,这些点可以推广到三维情形。其中,Fekete节点是唯一与GLL节点存在密切联系的节点,一维单元、四边形单元以及三角形单元边界上的Fekete节点实际上就是GLL节点,所以Fekete节点三角形谱单元能够与四边形谱单元无缝衔接。计算量方面,三角形单元需要对每个二维基函数进行计算,四边形单元只需对两个坐标方向的一维基函数分别进行计算,前者计算量显著大于后者。若N为多项式阶次,三角形单元计算量为(N+1)(N+2)-1,四边形单元为2N+1。对于N=3—8阶单元,前者计算量分别为后者的2.7,3.2,3.7,4.2,4.7,5.2倍。模拟波场的精度方面,三角形单元只能达到插值多项式阶次N的代数精度,而四边形单元能够达到GLL数值积分的2N-1阶代数精度。二维波动算例表明,三角形谱单元精度低于四边形谱单元,需要更多的采样点来模拟波场,除了这少量精度差异之外,三角形谱单元(Fekete节点)与四边形谱单元的衔接则是完全协调的,波可以平滑地穿过两种网格的交界面。刘有山等(2014)和Liu YS等(2014)详细介绍了Fekete节点三角形谱单元的插值多项式、插值节点和数值积分,给出与PML人工边界相结合的均匀半空间和不规则介质地震波动模拟算例。Fekete节点三角形谱单元的表达式如下:
$$\text{Fekete节点三角形谱单元:} u ( \xi \text{,} \eta ) = \sum\limits_{p = 1}^{Nt} {u ( {\xi _p}\text{,} {\eta _p} ) {\varphi _p} ( {\xi \text{,} \eta } ) } $$ (17) $$\text{形函数:}{\varphi _p} ( {\xi \text{,} \eta } ) = \sum\limits_{k= 1}^{Nt} {c_k^p{D_k} ( {\xi \text{,} \eta } ) } $$ (18) $$\text{KD多项式:} D_k^{i\text{,} j} ( {\xi \text{,} \eta } ) = \sqrt {\frac{{ ( {2i + 1} ) ( {i + j + 1} ) }}{2}} J_i^{0\text{,} 0}\left( {\frac{{2\xi + \eta - 1}}{{1 - \eta }}} \right) J_j^{2i + 1\text{,} 0} ( {2\eta - 1} ) { ( {1 - \eta } ) ^i} $$ (19) 式中,$ D_k^{i\text{,} j} ( {\xi \text{,} \eta } ) $为Koornwinder-Dubiner (KD)正交多项式(Dubiner,1991),0≤i,j≤N,且0≤i+j≤N,每个三角形单元内有Nt = (N+1)(N+2)/2个KD多项式,N为所有多项式的最高阶数。$ J_i^{\alpha \text{,} \beta } ( \xi ) $为雅可比多项式,其中$ J_i^{0\text{,} 0} ( \xi ) $即为Legendre多项式。需要引入坍塌坐标变换(collapsed coordinate transform),将参考三角形变换成参考四边形,在参考四边形中完成单元质量和刚度矩阵的积分运算(Pasquetti,Rapetti,2004;Karniadakis,Sherwin,2005)。Fekete节点的具体数值由Briani等(2012)给出。单元特性矩阵计算中涉及形函数的导数,其中KD多项式的导数存在奇异点(ξ, η) = (0, 1),需要分为4类进行计算;计算单元特性矩阵的数值积分所需要的积分权系数由计算Fekete节点涉及的广义Vandermonde矩阵的逆矩阵来得到,详见刘有山等(2014)。文中算例得出比Komatitsch等(2001)更为详细的结论,包括:三角形单元每个波长需要11个采样点,远大于四边形单元的4个采样点;三角形单元内存占用巨大,约为四边形单元的5.5倍,且计算耗时更长;不建议单独使用Fekete节点三角形谱单元,可以在以四边形为主的网格中用于对局部不规则区域进行优化。
Liu YS等(2017)对具有更高精度的Cohen点三角形谱单元进行了研究,该类单元同样能够导出集中质量矩阵,但与四边形谱单元不适配。文中对三角形谱单元研究工作进行了较为详细的综述,指出Cohen等(2001)通过增加新的内部节点对三角形单元的多项式空间进行扩充,提出一种能够提高求积精度并生成集中质量矩阵的新型三角形高阶单元构建方法,不过他只给出了2阶和3阶单元。随后,Mulder (2001,2013)推导出4—6阶情形下的插值点,Giraldo和Taylor (2006)得出了6阶和7阶插值点。这些节点被称为Cohen点或容积点(cubature points)。Liu T等(2012)研究Fekete节点和Cohen节点三角形谱单元的数值频散,从理论上证明Cohen点三角形单元的精度显著高于Fekete点三角形单元。李琳等(2014)研究得出在地震波动模拟中2阶Cohen点三角形谱单元比3阶三角形有限单元的精度更高且稳定条件更宽松。Liu YS等(2017)推导出7—9阶Cubature点,列表给出其具体数值,通过数值频散分析定量比较了Cubature点、Fekete点以及精确积分方法的理论精度和时域积分稳定条件,数值算例结果显示7阶Cubature点三角形谱单元与7阶四边形谱单元以及14阶Fekete点三角形谱单元的模拟结果相当,优于10阶Fekete点三角形谱单元。
2.5 谱元法的精度和稳定性
波动数值模拟的离散网格相当于低通滤波器,为防止模拟波形失真(刘少林等,2014),需要在一个最短波长内设置足够数量的离散网格点(points per minimum wavelength,ppw),以确保足够精度。参数ppw也称为空间网格的节点采样率,其定义式如下:
$$ppw = \frac{{{\lambda _{\min }}}}{{\Delta {h_d}}} \text{,} 其中{\lambda _{\min }} = c {\text{×}}{T_{\min }} = {c \mathord{\left/ {\vphantom {c {{f_{\max }}}}} \right. } {{f_{\max }}}}\text{,} \Delta {h_d} = {{\Delta {h_E}} \mathord{\left/ {\vphantom {{\Delta {h_E}} N}} \right. } N} $$ (20) 式中,λmin为模拟波动的最短波长,它由波速c和最短周期Tmin或最高频率fmax决定。Δhd为离散网格点的平均间距,它等于单元尺寸ΔhE除以单元阶次N。
离散化方程的时域逐步积分求解需要确保数值稳定性,以防止模拟结果出现不合理的持续攀升甚至爆炸性增长。除了无条件稳定的隐式算法之外,显式算法的稳定条件可表示为
$$ {q_E} = \frac{{c\Delta t}}{{\Delta {h_E}}} {\text{≤}} {q_{E\max }} \text{,} {q_d} = \frac{{c\Delta t}}{{\Delta {h_{d\min }}}} {\text{≤}} {q_{d\max }} $$ (21) 式中,qE、qd分别为与单元尺寸ΔhE对应以及与最小节点间距Δhdmin对应的无量纲时间步长,也称为Courant数(Cohen,2002)。qEmax、qdmax为稳定临界值,它是小于等于1的常数,不同数值算法对应不同的值。对于一阶单元方法,qEmax和qdmax相同。式(20)和式(21)给出了波动数值模拟的网格尺寸和时间步长选取准则。
精度和稳定性常数ppw,qEmax或qdmax由数值频散(numerical dispersion)或网格频散(grid dispersion)分析确定(Cohen,2002)。通常做法是在离散网格$ u_{m\text{,} n}^p =u ( {m\Delta x\text{,} n\Delta {\textit{z}} \text{,} p\Delta t} ) $中将形如式(22)的平面波表达式代入形如式(23)的节点运动方程,经过较为复杂的推导,将式(24)的相速度或群速度表示成与波速、频率等物理参数以及单元阶次、节点间距、时间步长等网格参数有关的表达式(Mullen,Belytschko,1982),最后以式(25)表示的离散网格中相速度或群速度与介质物理波速之间的差异作为衡量波动模拟精度的指标。
$$\text{平面波表达式:} u_{m\text{,} n}^p = A\exp \left\{ {i\left[ {\omega {\text{×}}p\Delta t - k ( {\cos \theta {\text{×}}m\Delta x + \sin \theta {\text{×}}n\Delta {\textit{z}} } ) } \right]} \right\} $$ (22) $$\text{节点运动方程:} u_{m\text{,} n}^{p + 1}=2u_{m\text{,} n}^p- u_{m\text{,} n}^{p - 1} - \frac{{\Delta {t^2}}}{{{M_{m\text{,} n}}}}\sum\limits_j {{K_{ ( m\text{,} n ) \text{,} \;j}}{u_j}} $$ (23) $$\text{相速度:}{c_p} =\frac{\omega }{k} \text{,} \text{群速度:}{c_g} = \frac{{d\omega }}{{dk}} $$ (24) $$\text{相速度误差:} {e_p} = \left({\frac{{{c_p}}}{c} - 1} \right) {\text{×}}100{\text{%}}\text{,} \text{群速度误差:}{e_g} =\left( {\frac{{{c_g}}}{c}- 1} \right) {\text{×}}100{\text{%}} $$ (25) 值得指出,式(22)—式(25)表示的数值/网格频散分析可以分别在一维、二维或三维离散模型中进行,其中二维模型由于推导过程不难实现且结论的通用性较好,为多数研究所采用。虽然不同维度模型分析得到的指标数值存在一定差异,但是其精度和稳定性的变化规律是高度相似的。具体而言,式(20)表示的节点采样率ppw和式(21)表示的时间积分稳定常数qEmax或qdmax是一维化的控制条件,其表达形式适用于一维模型或者二维、三维模型的各个维度。二维、三维模型与一维模型之间的差异主要在于:精度由最大网格尺寸决定,二维、三维模型比一维模型增加了网格斜向的尺寸因素,精度分析时需要予以考虑。稳定性由网格最小尺寸和介质波速控制,二维、三维模型中网格尺寸和介质波速比一维模型复杂得多,需要筛选出最不利组合作为控制条件。稳定性还会由于所采用的空间、时间离散格式以及网格/单元形状的不同而存在显著差异,其总体规律是数值格式越复杂或网格形状越不规则,稳定条件越严格,反之则稳定条件越宽松。
Alford等(1974)研究了有限差分法的精度,得出二阶差分格式约需ppw ≥ 10,四阶差分格式约需ppw ≥ 5。Mullen和Belytschko (1982)研究揭示有限元法中一致质量单元精度好于集中质量和减缩积分单元,等边三角形单元好于其它形状或排列方式的三角形单元。Marfurt (1984)研究发现在低泊松比弹性波问题中,经典有限差分格式和有限元格式的精度相当;对于泊松比高于0.25的问题,有限元法精度高于有限差分法;对于泊松比大于0.45的问题,经典有限差分法和有限元法的精度都不理想,此时由一致质量和集中质量按一定比例组成的混合质量有限元数值频散最低。Virieux (1986)提出速度— 应力波动方程交错网格(staggered grid)有限差分格式,通过数值频散分析证明该格式对各种弹性波情形尤其是高泊松比(如0.499)介质都具有较高模拟精度,比经典的位移形式有限差分法更适用于大范围、长持时以及流固耦合地震波动模拟。Moczo等(2000)研究三维情形下交错网格有限差分格式的网格频散,给出二阶格式ppw ≥ 12,四阶格式ppw ≥ 6的建议。刘晶波和廖振鹏(1989)研究得出相速度误差ep ≤ 2%—5%对应的网格采样率为ppw ≥ 6—9的结果。
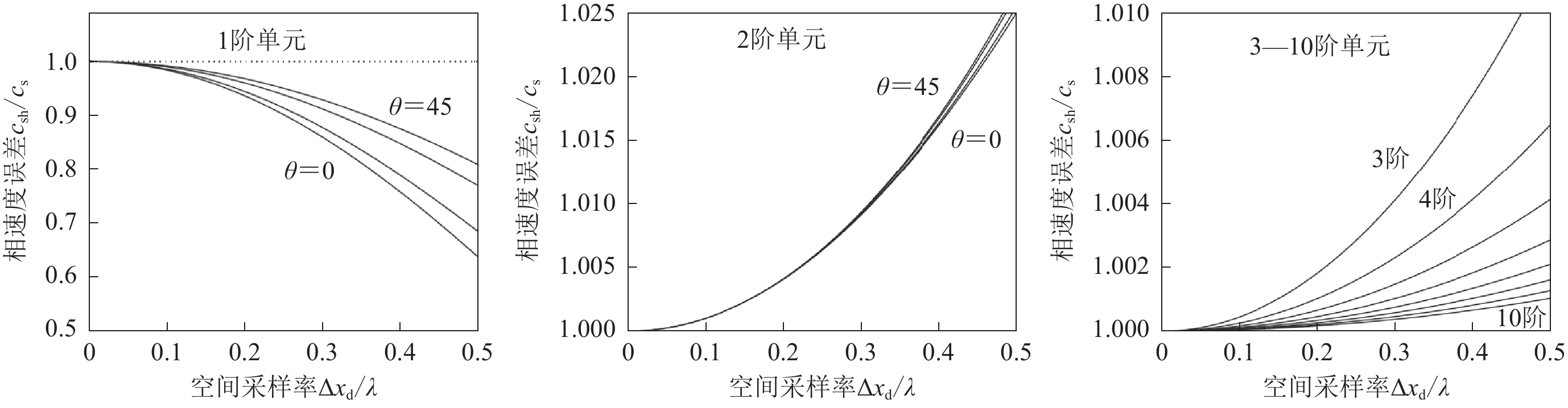
谱元法较高的单元阶次使其具有显著优于有限元法以及有限差分法的精度。除本文2.1节介绍的Seriani和Priolo (1991)、Priolo和Seriani (1991)、Dauksher和Emery (1997)、Mulder (1999)以及Seriani和Oliveira (2007,2008a,2008b)等对谱元法波动模拟精度的研究之外,Cohen (2002)推导出二阶和三阶LSEM单元数值频散的显式表达式,研究得出当节点采样率ppw ≥ 5时,二阶单元的相速度误差ep ≤ 2%,三阶单元则降低至ep ≤ 0.5%。De Basabe和Sen (2007)针对Mulder方法和Cohen方法不适用于较高单元阶次以及Seriani和Oliveira方法无法导出稳定条件等不足,将基于式(23)节点运动方程的平面波分析改进为基于单元运动方程的特征值分析,发展出一套能够便捷地导出波动有限元或谱元离散格式数值频散的通用方法。文中全面详细地比较了标量波和弹性波情形下1—10阶谱元(如图1所示)、经典的有限元、位移形式有限差分、以及交错网格有限差分的频散曲线。图1中空间采样率Δhd/λ对应于式(20)中ppw的倒数1/ppw,相速度误差csh/cs中的csh对应于式(24)中离散网格的相速度,cs表示S波的物理波速。
![]() 图 1 标量波情形下1—10阶谱元法的网格频散曲线(De Basabe,Sen,2007)Figure 1. Grid dispersion curves of 1st- to 10th-order spectral elements in acoustic case (De Basabe,Sen,2007)
图 1 标量波情形下1—10阶谱元法的网格频散曲线(De Basabe,Sen,2007)Figure 1. Grid dispersion curves of 1st- to 10th-order spectral elements in acoustic case (De Basabe,Sen,2007)De Basabe和Sen (2007)通过大量频散曲线不仅分析得出与前人各项研究高度一致的一系列结论,还明晰了关于不同方法模拟精度的几个重要基本认识,包括:(1)一阶有限元/谱元和经典二阶中心差分在极端情形下(如纵横波速比等于10)的数值频散远大于一般情形。(2)只需将单元阶次提升至二阶,就能够迅速降低网格频散和数值各项异性,高阶单元性能更优。(3)谱元法常用的4阶单元ppw=5的网格采样率能够达到ep ≤ 0.1%的超高精度。(4)谱元法和交错网格有限差分法在不同情形下的网格频散都很低,是模拟复杂波动如大纵横波速比弹性波、流固耦合波动(De Basabe,Sen,2015)等问题的较优选择。De Basabe等(2008)进一步研究不同插值函数的间断伽辽金谱元法的网格频散,结果表明其继承了谱元法的高精度。
式(21)中波动数值算法的稳定临界值qEmax和qdmax也可以通过数值频散分析导出。Cohen (2002)研究给出经典位移形式空间—时间二阶中心差分法的稳定临界值为$q_{{\mathrm{dmax}}}=1 ( \text{ 一维波动 } ) $,$ {q}_{d\mathrm{m}\mathrm{a}\mathrm{x}}=1/\sqrt{2} {\text{≈}} 0.707 ( \text{二维} ) $,以及$ {q}_{d\mathrm{m}\mathrm{a}\mathrm{x}}=1/\sqrt{3} {\text{≈}} 0.577 ( \text{三维} ) $。刘晶波和廖振鹏(1990)研究得到集中质量有限元结合二阶中心差分的稳定临界值为qdmax=1。De Basabe和Sen (2010)研究了标量波和弹性波情形下经典谱元法和对称、非对称、不完全三种内部罚函数的间断伽辽金谱元法的稳定条件,分别考虑二阶中心差分和四阶Lax-Wendroff两种时间积分格式,其中比较具有代表性的稳定临界值qEmax和qdmax如表1所示。这里,弹性波情形的纵横波速比为1.41,qEmax和qdmax计算公式(21)中的波速c取为P波波速。
表 1 谱元法结合二阶中心差分求解格式的稳定条件(De Basabe,Sen,2010)Table 1. Stability criteria for spectral element method solved by classical second-order centered-difference time integration algorithm (De Basabe,Sen,2010)谱单元阶次 1 2 3 4 5 6 7 8 标量波情形
(SH波动)qEmax 0.709 0.288 0.164 0.104 0.0714 0.0516 0.039 0 0.030 4 qdmax 0.709 0.577 0.593 0.604 0.608 0.608 0.608 0.607 弹性波情形
(P-SV波动)qEmax 0.816 0.333 0.189 0.120 0.082 3 0.059 5 0.044 9 0.035 0 qdmax 0.816 0.666 0.684 0.697 0.700 0.700 0.700 0.699 表1中与最小节点间距Δhdmin对应的稳定临界值qdmax随单元阶次的变化不大,其值略小于集中质量有限元的qdmax=1,与经典有限差分的qdmax ≈ 0.707相当。与单元尺寸ΔhE对应的稳定临界值qEmax则随着单元阶次的上升迅速降低。这表明在谱元法波动模拟中应当控制最小节点间距以确保计算效率,即随着单元阶次上升,单元尺寸需要相应增大。文中还研究得出:四阶Lax-Wendroff格式的稳定临界值比二阶中心差分大73%,不失为一种适用于谱元法的高阶精度时间积分格式。几种间断伽辽金谱元法的时间步长都显著小于经典谱元法,其中标量波情形约减小20%,弹性波情形则减小60%之多。再考虑到前者更多的公式数量,所以就单一均匀介质波动模拟而言,前者的计算量大大超过后者。Antonietti等(2012)研究得出弹性波情形下2—8阶谱元法的稳定临界值qdmax依次为0.675,0.711,0.698,0.704,0.702,0.701,0.701,与表1结果比较接近。
除了上述工作之外,Mulder等(2014)研究了间断伽辽金谱元法中罚因子(penalty)不同取值对稳定条件的影响。曹丹平等(2015)研究了不同形状和不同高宽比三角形单元的稳定临界值,如高宽比分别为0.8,0.7,0.6,0.5,0.4,0.3,0.2的直角三角形单元,对应的稳定临界值依次为0.61,0.56,0.51,0.43,0.35,0.27,0.18,揭示出单元形状不规则变化对稳定条件的影响规律。我国学者研究了完美匹配层人工边界与谱元法结合的稳定性问题(Xie et al,2014;谢志南,章旭斌,2017),以及廖氏透射人工边界与谱元法结合的稳定性问题(戴志军等,2015;于彦彦等,2017;邢浩洁和李鸿晶,2017a,2017b;章旭斌,谢志南,2022;Yu et al,2021,2024)。
3. 谱元法应用
3.1 基于CSEM的应用
Seriani和Priolo (1994)、Priolo等(1994)以及Padovani等(1994)将CSEM应用于大量二维复杂介质模型的地震波动模拟,探讨建模和计算的相关细节,并与全域的伪谱法进行比较。Seriani和Priolo (1994)在CSEM等效积分方程中添加吸收边界条件,给出含有折线形界面、折线形薄层、斜线界面的贴合网格和锯齿网格、含有台阶型地表及地层界面的断层场地模型算例,展示了CSEM模拟复杂波场的能力。Priolo等(1994)对比了伪谱法和CSEM的计算公式,给出两种方法模拟均匀半空间、成层半空间、以及存在竖向界面的半空间模型中波动的算例,结果表明谱元法在公式简洁程度、边界条件施加以及复杂模型适应性等方面都更有优势。Padovani等(1994)论述CSEM复杂介质波动模拟的空间离散、时间积分和吸收边界,探讨与稀疏存储、直接解法、迭代解法等相关的编程策略,定量分析了低阶有限元和高阶CSEM谱元的内存占用和计算时间等基本性能。
Priolo (1999,2001)成功地将二维CSEM应用于意大利卡塔尼亚地区多个地质剖面的地震波动模拟,其结果作为该地区地震危险性分析的参考。根据地震危险性工作其他环节提供的地质结构资料选取几个代表性二维地质剖面进行分析,划分CSEM离散网格,模型尺度最大达到16 km深和22 km宽。考虑点源和断层面源两种设定震源情形,前者设置于8 km深度某处,后者简单地由4.6 km,8 km和12.5 km深度三个点源叠加而成。模拟产出不同震源模式和区域地质条件下的地震动分布、幅值衰减、波场快照、地震剖面图、地震动反应谱等定量化结果。Priolo使用的CSEM后来被发展成为SPEM二维谱元程序,Laurenzano和Priolo (2005)利用SPEM程序模拟1990年意大利东西西里M5.8地震在Catania ENEA–ENEL台站产生的大幅值地震动,与基于均匀层状区域模型的波数积分法(wavenumber integration method,WIM)进行比较,并对比了实际记录、CSEM模拟结果和场地噪声记录的水平—竖向谱比(horizontal-to-vertical spectral ratio,HVSR)。基于实际复杂地质结构的CSEM模拟结果与实际记录吻合度较高,WIM结果差异较大,三种数据的HVSR较为一致。这表明考虑实际复杂地质结构的地震波动模拟对于准确解释地震资料和生成合理的强地面运动具有重要价值。Laurenzano等(2008)将SPEM程序应用于意大利Marche区域两个含有复杂地层和地质不整合面的地震地面运动模拟。Grasso和Maugeri (2014)对意大利 Ragusa市开展地震小区划新方法研究,利用SPEM程序计算多个历史地震震源产生的区域地震动,再对沉积层地区使用GEODIN或EERA程序计算一维非线性场地反应。Castelli等(2016)将SPEM程序的确定性地震动模拟结果和随机有限断层法的高频地震动模拟结果相结合,并在沉积层地区考虑一维场地反应,对Catania市开展地震小区划研究。
林伟军等(2005)、林伟军(2007)以及王秀明等(2007)首先在我国介绍了弹性波传播模拟的CSEM。车承轩(2007)和Che等(2010)开展了起伏自由表面地层中的弹性波传播的谱元法模拟,空间上采用逐单元(element by element,EBE)技术,时间上采用交错网格的预测—校正法。Seriani和Su (2012)、林伟军等(2018)以及Su和Seriani (2023)将Seriani (2004)提出的用于模拟小尺度复杂介质变化的双网格CSEM由一维声波拓展到二维声波和弹性波,给出多个模拟算例。邢浩洁等(2017)将CSEM方法用于水平成层场地一维地震反应计算,通过与有限元法和传递矩阵法比较得出谱元法的网格适应性更强。王竞雄等(2022)提出一种新型集中质量CSEM单元,用于层状场地一维地震反应计算并与日本Kik-net台站记录结果进行了比较。
3.2 基于LSEM的应用
如2.2节所述,Komatitsch和Vilotte (1998,1999)、Komatitsch和Tromp (1999)以及Komatitsch等(1999)提出简洁形式LSEM并成功地将其应用于二维和三维复杂地质结构甚至是全球地震波动模拟(Komatitsch,Tromp,2002a,2002b;Komatitsch et al,2002)。在上述工作基础上,Komatitsch等(2004)将LSEM应用于洛杉矶盆地在实际地震作用下产生的地面运动模拟,使用石油工业的数百个测井数据和20 000多公里地震反射剖面资料对已有的洛杉矶盆地速度结构模型进行细化,对516 km×507 km×60 km区域范围(盆地最大深度8.5 km)建立1.36亿自由度的谱元离散模型,模拟得到与实际记录吻合度较好的结果。Liu QY等(2004)将LSEM与加州地区实际速度结构模型相结合,通过最小化波形失配函数反演出加州地区三个地震的矩张量和震源位置,得到与传统体波或面波反演一致的结果,并指出利用该方法可以为南加州地区约40次ML≥3.5地震事件建立震源机制数据库,有助于增进对该区域断层和构造的认识。Capdeville等(2005)利用一种数据缩减技术和谱元法对多次地震事件同时模拟,发展出一种适用于地球尺度的地震层析成像方法。Tromp等(2005)证明地震层析成像(seismic tomography),气象和海洋动力学中广泛应用的伴随方法(adjoint methods),时间反转成像(time reversal imaging),以及有限频“香蕉—甜甜圈”核函数密切相关。他们用二维谱元程序演示了与地震层析成像和震源反演相关的Fréchet导数可以通过对地震事件的一次正演模拟和同时将各个台站作为虚拟源进行一次时间反转(即伴随)模拟得到。这些工作拉开了基于谱元法的高效正演模拟预测强震地面运动以及反演震源参数或地球介质速度结构的序幕。
Krishnan等(2006)利用谱元法和结构动力反应算法模拟了南加州一栋18层钢框架结构在圣安德烈斯断层两个7.9级设定地震作用下的动力反应,实现从震源破裂到结构响应的“端到端(end-to-end)”模拟。Komatitsch等(2010)、Michéa和Komatitsch (2010)将谱元法地震波动模拟程序应用到GPU并行计算当中,大幅提高计算效率。Lee SJ等(2008,2009)利用谱元法模拟台北盆地的三维地震波传播,分别建立无地形+无盆地,有地形+无盆地,有地形+有盆地三种分析模型,结果表明纯地形引起的PGA放大能够达到50%左右,而台北盆地几百米的低速沉积层导致的PGA放大最大能够达到5倍。Morency和Tromp (2008)详细探讨谱元法应用于孔隙介质弹性波传播模拟的相关问题,给出多个二维算例。Chaljub等(2010)以法国Grenoble山谷为例,全面比较交错网格有限差分法、间断伽辽金谱元法以及两种经典谱元法几种不同数值方法的算法特点和模拟效果,得出总体上模拟结果差别不大,不同方法各有优劣,对于复杂问题可以采用两种方法进行模拟等主要结论。Chaljub等(2015)以希腊Mygdonian盆地为例设计出不同一维和二维速度结构模型,建议在实际模拟中可以根据基准模型下的测试效果针对性地选用模拟方法。Stupazzini等(2009)、Pilz等(2011)以及Smerzini等(2011)利用谱元程序GeoELSE,通过三维波动模拟开展法国Grenoble山谷的近断层地震地面运动、智利圣地亚哥盆地效应对地震地面运动影响、以及意大利中部Gubbio平原长周期地震动的三维、二维和一维模拟结果对比的研究。Liu QF等(2015,2018)、Yu等(2017)使用SPECFEM3D程序分别对我国云南地区狭长的施甸盆地在中等设定地震作用下以及渭河盆地和四川盆地在2008年汶川大地震作用下的强地面运动进行模拟研究。He等(2015,2016)、贺春晖等(2017)以及Wang XC等(2021a)利用SPECFEM3D进行三维地震波动模拟,研究高坝场址地震动参数,将确定性数值模拟结果与实际地震记录以及传统的地震危险性分析方法进行比较,表明该方法可以作为传统方法之外的一种重要补充。Wang G等(2018)通过谱元法三维模拟探讨地形尺度和地表土体对地震动的影响机制,得出长波、短波分别对于大尺度、小尺度地形特征具有控制性影响,基岩地形主要表现出大尺度放大特征,土体场地则主要表现为小尺度放大特征,最大放大系数可达到4倍左右等结论。Huang等(2020)、Feng等(2022)将谱元法地震波动模拟与滑坡判定方法相结合,发展出一套基于物理的同震滑坡评估方法。Wu等(2022)将频率—波数方法(FK方法)与谱元法相结合,发展出一种能够高效实现震源—路径—场地多尺度模拟的方法。Ba等(2023)开发出一种高—低频混合震源模型并在SPECFEM3D软件中实现,对2022年中国四川泸定地震开展基于物理的三维地震动模拟分析。
Liu和Tromp (2006,2008)、Tape等(2007)详细探讨将基于伴随方法的谱元法地震波动模拟技术应用于地震反演的核心问题——有限频敏感度核(finite-frequency sensitivity kernels)的方法,夯实地震层析成像(seismic tomography)和全波形反演(full waveform inversion,FWI)等重要工作的理论和方法基础。Tromp等(2008)针对三维地震波动模拟用于反演地球内部结构或震源参数时大量地震事件模拟所导致的计算量难以承受的问题,建立了谱元法高效正演模拟和一种被称为伴随方法(将以场点作为虚拟源产生的波场称为伴随波场,同时对各个台站进行模拟)的新技术,让实现这类反演成为可能。Stich等(2010)用谱元法反演了2005—2008年西班牙Iberia–Maghreb地区77个地震的矩张量。Fichtner和Simutė (2018)将谱元法与哈密顿—蒙特卡洛方法相结合,对复杂介质中的震源参数进行反演。Sawade等(2022)将谱元法的全球地震波动模拟技术用于反演全球地震事件的矩心矩张量,建立包含
9382 次地震事件的CMT3D(3-D centroid-moment tensors)目录。Tape等(2009,2010)采用谱元法地震波动模拟与伴随方法相结合的地震层析成像技术,反演出精度更高的美国南加州地区地壳速度结构。Liu和Gu (2012)对地震成像的传统方法和新型伴随层析成像方法进行了全面详细的综述。French和Romanowicz (2014)基于谱元法的波形层析成像技术分析得到整个地幔的径向各向异性剪切波速度结构。Zhu等(2015,2017)利用伴随层析成像方法反演出欧洲上地幔和美国北部上地幔的速度结构。Chen等(2015,2017)利用伴随层析成像分析了东亚地区的地壳和上地幔结构。Karaoğlu和Romanowicz (2018)基于谱元法的波形层析成像推断了全球的上地幔剪切波衰减结构。Lloyd等(2020)利用伴随层析成像方法分析了南极上地幔的地震构造特征。Magnoni等(2022)分析了意大利岩石圈的伴随层析成像。Carmona等(2024)探讨了阿拉伯板块的滞弹性层析成像。3.3 基于DG-SEM的应用
如2.3节所述,间断伽辽金谱元法(DG-SEM或DGM)首先是Käser和Dumbser(2006)以及Dumbser和Käser(2006)发展的基于任意阶精度微分格式的ADER-DGM方法,他们将该方法与非结构化网格相结合,用于求解粘弹性介质(Käser et al,2007)、各向异性介质(Puente et al,2007)以及局部化的单元阶次和时间步长(Dumbser et al,2007)的地震波动模拟。继上述工作之后,Puente等(2008)将ADER-DGM方法应用于孔隙弹性介质波动模拟,使用非结构化的四面体网格,以零流入通量作为吸收边界条件,分析了方法的收敛性并通过一系列算例证实了方法的高精度和适应性。Puente等(2009)将基于非结构化网格的ADER-DGM方法用于模拟地震断层的动力学破裂,其优势在于非结构化网格能够刻画复杂几何形状,DGM则便于根据问题特点对不同区域网格进行细化或粗化。Pelties等(2012)将ADER-DGM方法与四面体网格相结合,用于模拟地震断层的三维动力学破裂过程。Pelties等(2010)、Hermann等(2011)探讨了DGM中非协调(non-conforming)网格的不同划分方式及其组成的混合网格,展示复杂模型的建模效果并分析其对地震动模拟结果的影响。
继Mazzieri等(2013)开发出基于DG-SEM的谱元法开源软件SPEED并成功地实现区域复杂场地—工程结构/城市建筑群的整体地震波动模拟之后,Paolucci等(2015)将SPEED软件的区域地震波动模拟称为基于物理的三维地震动模拟,深入剖析了断层破裂过程、区域速度结构、离散网格参数等因素对近断层地震动的影响。Abraham等(2016)模拟分析了意大利中部Gubbio峡谷沉积层的盆地边缘效应。Smerzini等(2017)对希腊塞萨洛尼基城区在三维有限断层震源作用下的地震地面运动及其场地效应进行研究。Evangelista等(2017)以意大利中部Aterno河谷为例,探讨将基于物理模拟得到的地震动作为工程抗震设计地震动的相关问题。Smerzini和Pitilakis (2018)探讨将三维物理模拟结果用于城市尺度地震危险性评估的一个示例。Paolucci等(2016)对意大利中部1915年Marsica地震的近源地震动进行模拟。Gatti等(2018)对某核电厂实现了震源—结构三维宽频带地震动模拟。Lu等(2018)提出了一种考虑场地—城市相互作用效应的建筑群非线性时程分析的耦合方法,通过与振动台试验结果对比、基准算例模型分析以及清华校园建筑示例展示了方法的可行性。Paolucci等(2018)利用人工神经网络方法将物理模拟得到的长周期地震动向短周期段进行延展,提出一种构建宽频带地震动的方法。Infantino等(2020)对土耳其北安纳托利亚断层Marmara段可能发生的地震对伊斯坦布尔市造成的地震地面运动开展研究,采用SPEED软件对66组MW7—7.4级设定地震情景进行三维物理模拟。Soto等(2020)对智利比尼亚德尔马市在Ricker子波平面波输入下的地震反应进行了模拟。Stupazzini等(2020)对土耳其伊斯坦布尔市开展了基于物理的概率地震危险性及地震损失评估研究。Infantino等(2021)探讨了基于物理模拟得到的宽频带地震动的空间相关性。Kato和Wang (2021)对香港屯门—元朗盆地的浅沉积层上的高层建筑群开展了区域地震反应的三维物理模拟,探讨了场地城市效应对地震地面运动的影响。Paolucci等(2021)针对近断层地震记录稀缺的问题,将SPEED软件问世以来的大量模拟结果整理成一套基于物理模拟的近断层宽频带地震动数据集,命名为BB-SPEEDset。Feng等(2022)将基于物理的三维地震波动模拟与滑坡领域的物质点法相结合,建立一套基于物理的同震滑坡大变形分析框架,并对2014年中国云南鲁甸地震中红石岩滑坡进行了分析。Tian等(2023)对上海陆家嘴区域134栋建筑及其附近2.5 km×2.3 km ×350 m范围岩土体在垂直入射地震波作用下的地震反应进行了模拟,分析了超高层建筑对城市尺度地震反应的影响。Aguirre等(2023)用SPEED模拟了墨西哥城在2019年一次MW3.2地震下的地面运动,对众所周知的墨西哥城的场地放大效应给出了一些定量化结果,揭示出其大盆地套小盆地的多层沉积结构发育了以面波成分为主的长持时、准单频的低频地面运动。
4. 谱元法在我国的发展
4.1 早期发展
进入21世纪以来,谱元法开始被我国学者关注,早期以方法介绍和一些初步应用为主。许传炬和林玉闽(2000)利用早期的谱元法计算流体软件SECF模拟二维矩形管道中不可压缩Poiseuille-Bénard流问题,探讨了不同出口边界条件处理对模拟效果的影响。秦国良和徐忠(2000,2001)给出采用CSEM求解不可压缩Navier-Stokes方程的算例,指出该方法求解精度很高,后来在流场中的声传播问题(Zhu et al,2011)、时空耦合谱元法(Geng et al,2016)等方面开展研究。林伟军和王秀明等与Seriani合作,在我国介绍了CSEM用于声波和弹性波模拟的基本公式(林伟军等,2005;林伟军,2007;王秀明等,2007;Che et al,2010),模拟展示了谱元法的高精度特性,并对多网格谱元法进行了发展(Seriani,Su,2012;林伟军等,2018;Su,Seriani,2023)。王童奎等(2007)在我国较早开展了基于LSEM的地震波场数值模拟研究,并介绍了地震波反演的谱元法叠后逆时偏移方法(王童奎等,2009)。严珍珍等(2009)基于SPECFEM3D_GLOBE谱元程序模拟了汶川大地震的地震波在全球范围内的传播。周红等(2010)利用谱元法模拟分析了不同震源机制下SH波的地形效应特征。胡元鑫等(2011)基于SPECFEM3D软件对汶川地区地震动的三维地形效应开展数值模拟研究。唐杰(2011)对水中气枪激发信号在双相多孔介质中的传播开展了谱元法数值模拟研究。汪文帅等(2013)对间断Galerkin方法在地震波场数值模拟中的应用进行了综述。
4.2 算法研究
近十余年来,我国地震学和地球物理领域开始不断产出与谱元法地震波动模拟有关的算法创新成果。Zhou和Chen(2010)研究出交叠网格谱元法,使得复杂地形和地质界面能够用规则的四边形/六面体谱单元进行离散,建模方式更加灵活。Zhou和Jiang (2015)提出一种加权速度Newmark时间积分法,改善了谱元法模拟震源动力学破裂时存在的虚假震荡问题。汪文帅等(2012)以及汪文帅和李小凡(2013)将谱元法与三阶辛算法的时间积分方法相结合,更好地控制长持时地震波动模拟中的误差积累。李冰非等(2019)发展出一种基于辛—谱元—FK混合方法的保结构远震波场模拟方法。李冰非等(2021)开展基于辛—谱元方法的地球自由振荡保弥散衰减数值模拟研究。刘有山等(2012)在频率域引入一个中间变量来避免卷积运算,提出一种简化计算的完美匹配层吸收边界条件并用于谱元法弹性波模拟。刘有山等(2014)、Liu YS等(2017)分别研究基于Fekete节点和Cubature节点(容积点或Cohen点)的三角网格谱元法,丰富了谱单元类型和谱元法的复杂区域建模。Liu YS等(2014)对二维地震波动模拟中谱元法和有限元法的精度、计算耗时和内存占用进行全面详细的对比。董兴朋和杨顶辉(2017)推导出球坐标系下三维弹性波方程的谱元解法,用于华北克拉通区域地震波动模拟。Liu SL等(2017)发展出适用于三维远震波动模拟的逐单元并行谱元法,采用频率—波数法计算大尺度背景场中地震波的激发和传播,然后在完美匹配层边界围成的小范围目标区域中计算背景场输入波产生的复杂地震波动。刘少林等(2021)将并行计算由主从通信模式改成缓存通信模式,并将刚度矩阵存储改进为仅存储雅可比矩阵,提升了三维逐元并行谱元法的模拟效率。刘少林等(2022)、孟雪莉等(2022)针对LSEM谱单元的不完全积分问题,研究出一种优化质量矩阵的Legendre谱元法,这项工作涉及有限差分/有限元/谱元波动算法的本质,值得重视。李昊臻等(2024)在逐元并行谱元法的基础上引入轴对称谱元,提高远震波场模拟的计算效率。任骏声等(2024)在谱元法的保结构时间积分方法基础上,引入空间卷积滤波使得时间步长能够突破稳定临界值,为长持时问题的高效模拟提供一种极具新意的方法。
地震工程领域学者为发展工程波动理论与方法开展了关于谱元法的人工边界条件、场地反应计算以及谱单元类型开发等方面的研究。Xie等(2014)通过在复频移—非分裂—卷积完美匹配层中去除奇异项,改善了SPECFEM2D和SPECFEM3D软件中完美匹配层(PML)边界的长持时稳定性,随后将其用于海洋声学的流固耦合波动模拟(Xie et al,2016)。谢志南和章旭斌(2017)提出将等效积分形式波动方程进行复坐标延展来构建PML的方法,称之为弱形式PML,在高泊松比介质中实现PML的稳定计算。谢志南等(2018,2019)研究常Q (品质因子)滞弹性介质地震波动模拟中时域本构的优化逼近,列表给出不同Q值下广义标准线性体参数,并将其与弱形式PML相结合。Xie等(2023)提出一种适用于各向异性地震波动模拟的改进多轴—非分裂—频移PML。戴志军等(2015)提出将廖氏透射边界(MTF)用于谱元法波动模拟,分析了空间域插值系数、小量修正因子、短时降阶方法对高频和低频稳定性的控制作用。于彦彦等(2017)在SPECFEM2D和SPECFEM3D软件中成功施加MTF,通过二维和三维算例证明其精度高于程序自带的粘性边界。章旭斌和谢志南(2022)研究指出谱元法中MTF稳定的机理为边界格式对谱元离散网格中真实模态和所有虚假模态的反射系数均小于等于1。Yu等(2021,2024)实现了谱元法结合MTF模拟均匀半空间、半圆形山谷、成层半空间含有半圆形山谷、半圆形沉积谷地等二维SH波动和P-SV波动的散射问题算例,结果表明该方法计算效率较高且谱元法中MTF的高频和低频稳定性更好。于彦彦等(2023)在SPECFEM3D中开发出基于MTF的平面波输入技术并基于消息传递接口(MPI)完成跨节点的并行计算,研究出一种适用于三维局部场地地震波散射问题的谱元并行模拟方法。
邢浩洁和李鸿晶等(2021a)以一维波动有限元模拟为例探讨高阶MTF的齐次内插(算子乘方形式)、简单内插(各个参考点统一插值)和单元内插(临近节点插值)三种不同实现方式的性能差异,发现前者精度和稳定性最好,但只适用于等距节点网格。邢浩洁和李鸿晶(2017a,2017b)、Xing等(2021a)指出在LSEM中实现MTF一般通过简单内插模式来实现,插值阶次可以在一阶至谱单元阶次之间选取,在一维和二维波动模拟中详细分析不同边界参数取值的影响并与PML、粘弹性边界以及有限元法中的MTF进行比较。Xing等(2021b)和邢浩洁等(2021b)将MTF与国际上经典的旁轴近似、Higdon边界等统称为外推型人工边界条件,然后将新提出的含有多个计算波速的优化外推公式应用于谱元法波动模拟(邢浩洁等,2022),算例表明新边界比传统单一计算波速的MTF更为高效。孔曦骏和李鸿晶等(2022)将谱元法结合MTF的方法用于模拟基于统一计算框架的流固耦合地震波动问题(陈少林等,2019a,2019b),结果表明高阶谱元法能够有效模拟的波动频率范围比低阶有限元法宽得多。Han等(2020)研究出一种在单元边界上满足场函数及其一阶导数连续的C1型LSEM谱单元并用于结构动力分析。邢浩洁和李鸿晶等(2017)将CSEM用于水平成层场地一维地震反应计算,通过与有限元法和传递矩阵法比较得出谱元法的网格适应性更强的结论。王竞雄和李鸿晶等(2022)提出一种新型集中质量CSEM谱单元,用于层状场地一维地震反应分析并与日本Kik-net台站记录进行比较。Wang JX和Li HJ等(2022a,2022b)详细探讨有限元法和谱元法中不同的集中质量技术,研究提出一种具有C1连续性的CSEM谱单元,通过梁、板中的波动传播模拟算例证实方法的高精度和快速收敛性。李鸿晶和王竞雄(2022)探讨了使用Gauss积分得出一致质量模型以及使用Gauss-Lobatto积分得出集中质量模型的原理,指出后者的不完全积分并未改变谱元法的高精度特性,集中质量模型更能反映波传播的物理特征。
4.3 工程应用
Lee SJ等(2008,2009)基于SPECFEM3D程序模拟台北盆地的三维地震波传播,分别建立无地形+无盆地,有地形+无盆地,有地形+有盆地三种分析模型,结果表明纯地形引起PGA放大能够达到50%左右,而台北盆地几百米的低速沉积层导致的PGA放大最大能够达到5倍。蒋涵等(2015)采用谱元法计算芦山地区三维地形在不同主频Ricker子波输入下的地震反应,得出放大系数均值和坡度的相关曲线。周红(2018)采用谱元法模拟2017年四川九寨沟7.0级地震产生的近断层地表地震动速度时程,积分得到地表位移时程,给出地表峰值位移和静态位移的空间分布。Zhou等(2020)利用谱元法地震波动模拟结果建立2013年我国芦山MS7.0地震的地震动地形效应预测模型。李孝波(2014)基于SPECFEM2D软件模拟唐山玉田县几个典型二维地质剖面在点源作用下的地震地面运动,揭示出较薄的土层厚度和基岩面凸起形状对地震波的发散作用是历次地震中该地区表现出低烈度异常的重要原因。刘启方等(2013)、Liu QF等(2015)利用SPECFEM3D软件模拟云南施甸盆地(尺度为18 km×4 km狭长的小型盆地)在设定地震下的三维地震动,得出由于陷波效应导致了持时增加和幅值放大,揭示出盆地中较深的小型凹陷和厚度剧烈变化区域更容易汇聚面波从而进一步放大地震动的重要现象。Yu等(2017)利用谱元法对四川盆地340 km×152 km×33 km区域在2008年汶川大地震震源(315 km×40 km破裂尺度、最大位错9 m)作用下的地震效应开展研究,模型总自由度5.8亿,模拟时间160 s,时间步长0.8 ms。在30节点240线程PC机并行系统上40小时完成计算。模拟结果与地震记录、烈度图以及其他结果具有较好的可比性,揭示出盆地边缘条带状区域破坏、地震动幅值放大和持时增加、基岩面起伏变化对地震动影响等典型特征。Liu QF等(2018)对汶川大地震距离震中500—800 km之外渭河盆地地震反应进行谱元法数值模拟研究,计算区域尺度达到740 km×552 km×60 km,模型自由度4.8亿,模拟时间450 s,时间步长3.5 ms。采用76处理单元并行系统80小时完成计算。模拟结果表明进入盆地的地震波主要为面波,基岩面上两个大型碗状凹陷的反射聚焦效应对地震动产生强烈放大,持时在直达波过去之后延续50—100 s之多,频谱分析显示0.125—0.175 Hz频率范围的地震动被显著放大,这解释了汶川地震中西安市高塔出现的震害现象。
Lu等(2018)将城市建筑群抗震弹塑性分析(陆新征等,2021)与SPEED间断伽辽金谱元法的区域地震动模拟(Mazzieri et al,2013)相结合,开展考虑场地—城市效应(site-city interaction,SCI)的区域建筑震害模拟,结果表明考虑SCI效应会降低大多数建筑的响应,但会导致部分建筑破坏更严重。Tian等(2020,2022,2023)对规则排列建筑、北京通州区建筑群、清华校园、新北川县城、上海CBD地区等开展SCI效应模拟分析,结果表明SCI效应会显著改变建筑的地震反应且不同建筑物差别很大,建议在抗震韧性或地震风险分析中根据具体分析指标对建筑破坏程度的敏感性高低来确定是否有必要考虑SCI效应。Kato和Wang (2021,2022)使用SPEED软件对香港地区城市建筑群在含有浅层沉积盆地的区域复杂场地上、以及在含有地铁车站综合体的岩土介质上的SCI地震效应进行模拟,揭示出三维模拟得到的地震动比一维结果大4—5倍,SCI效应最显著特征是多个散射体之间的陷波现象,主要改变2 Hz以上加速度反应谱,对低层建筑以及高楼附近的服务设施影响较大。Wang G等(2018)、Huang等(2021)分别使用SPECFEM3D软件模拟含有浅层土体的三维复杂地形以及使用SPECFEM2D软件模拟剪切波速随机变化的不均匀土体在平面波输入下的地震反应,定量地揭示出地形尺度和介质变化的大、小尺度特征对不同频段(更准确地说是不同波长)地震动的控制性影响。Chen等(2023a)基于SPECFEM3D软件对2016年日本熊本MW7.0地震的复杂地形和非线性土体反应进行模拟,根据模拟结果建立以地形尺度(相对高度)表征的PGA和PGV放大系数预测模型,揭示出对PGA、PGV放大效应最为显著的地形尺度分别为240 m和360 m。Huang等(2020)、Feng等(2022)、Chen等(2023b)以及Sun和Huang (2023)将SPECFEM3D谱元软件的区域地震动模拟分别与滑坡分析中的Newmark位移法、物质点法(material point method,MPM)、柔性滑动分析(flexible sliding analysis)等方法相结合,发展出一系列基于物理的同震滑坡评估方法。
He等(2015,2016)、贺春晖等(2017)以及Wang XC等(2021a)利用SPECFEM3D软件的确定性数值模拟研究高坝场址地震动参数,模拟结果与实际地震记录以及传统地震危险性分析结果具有较好可比性,该方法优势在于能够更好地考虑极端大震事件影响和给出坝址高山峡谷地形的空间地震动。Zhang等(2020)发展出谱元与有限元相结合的从断层到结构的三维地震模拟方法,将谱元法的区域地震波动模拟结果以等效节点力的方式输入到有限元的土—结计算模型当中,给出非发震断层和重力坝模拟算例。Wang XC等(2021b,2022)针对地震学反演给出的震源模型频率过低而难以激发出工程抗震分析所需的宽频带地震动的问题,研究提出一种多层叠加、各层子源尺度逐步递减、上升时间按子源尺度缩放、总地震矩按子源尺度分配的多维震源模型,基于SPECFEM3D软件对1994年MW6.7美国北岭地震正演模拟和1992年MW7.3兰德斯地震的震源参数反演模拟进行详细分析,证明震源的高频特性对宽频带地震动非常重要,各层子源的自相似性使之成为一种简洁高效的宽频带震源模型。在震源模型创新基础上,Wang XC等(2023)进一步在设定地震方面做出重要创新,发展出一种能够充分考虑工程场址附近发震断层不同破裂过程的确定性全情景地震危险性分析方法。利用SPECFEM3D软件的伴随方法(Tromp et al,2008)计算工程场址处设置虚拟震源在发震断层各个子源位置产生的反应(格林函数),根据空间互易性将其反转为各个子源在工程场址处的格林函数。考虑各个子源不同滑移量、破裂时间、上升时间以及滑动角等组成的大量地震情景,采用格林函数卷积的方法快速获得每种情景下工程场址的三分量地震动时程。以我国西南地区溪洛渡大坝为例,针对附近两个潜在发震断层计算出2 200万种震源破裂情景下的三分量地震动时程,基于如此充分的地震动数据可以方便地开展地震危险性分析、筛选设计地震动、计算区域ShakeMap震动图、构建地震动预测方程等一系列工作。Wang XC和Wang JT (2023)在上述方法基础上提出基于物理的谱匹配方法,用于生成完全场地相关的地震动。基于物理模拟产生的海量地震数据能够有效支撑考虑复杂地震动特性的多目标匹配需求。Zhang等(2023)基于上述方法建立一种新的震源—结构地震反应分析框架。
Ba等(2021)通过消除传统频率—波数方法(frequency-wavenumber,FK方法)中发散的指数项,建立一种能够对地壳厚层和岩土薄层相结合的多尺度层状模型以及多点源作用进行快速求解的改进FK方法。Liang等(2021)、Ba等(2022)、Wu等(2022)利用改进FK方法能够快速计算层状模型中设定震源产生的波场或直接生成平面波的优势,将其与复杂场地的谱元法(spectral element method,SEM)模拟相结合,组成能够高效地模拟震源—路径—场地的多尺度地震波动过程或计算平面波输入下场地地震反应的FK-SE方法,给出多个理论模型算例,并对平面波输入下自贡西山公园场地、位错点源作用下梯形盆地、1679年北京三河—平谷8级地震以及2021年云南漾濞MS6.4地震开展数值模拟研究。Ba等(2023)、巴振宁等(2023)、赵靖轩等(2023)将低波数的凹凸体震源模型与Graves和Pitarka (2015)的随机震源模型相结合,构建出一种宽频带震源模型并在SPECFEM3D软件中实现,在上述漾濞地震和2022四川泸定MS6.8地震模拟中获得与实测记录、烈度图以及地震动预测方程具有较好吻合度的结果。Fu等(2024)在场地—城市效应的地震反应计算(Lu et al,2018;Kato,Wang,2021)中引入FK方法实现地震波斜入射,建立场地城市效应的FK-SEM-MDOF模拟方法,以梯形盆地上正方形排列建筑群为例详细探讨SCI效应影响机制。Ba等(2024a)将谱元法的区域地震波动模拟与有限元法的结构或土—结系统地震反应计算相结合,对北京颐和园万寿山的佛香阁木结构开展全过程地震反应分析,针对附近区域发生的1665年通县6.5级地震和1730年颐和园6.5级地震设定震源,结果表明地震物理机制对结构反应具有显著影响。Ba等(2024b)、巴振宁等(2024)将岩土工程中广泛使用的Martin-Seed-Davidenkov非线性土体本构模型开发到SPECFEM3D程序当中,实现对于云南施甸盆地在2001年5.9级地震作用下的非线性地震反应计算,结果表明PGA和PGV较线性结果均有所降低,PGV受到影响更大,最大约降低30%,反应谱幅值降低且特征频率向长周期方向移动。Ba等(2024c)针对天津地区地震危险性分析,将谱元法和随机有限断层法相结合模拟得到大量设定震源情景下空间均布场点的地震动时程,然后基于遗传算法的反向传播神经网络方法(back propagation neural network developed by genetic algorithm,GA-BPNN)构建出天津地区的地震动预测模型。对模型性能开展详细的参数分析并与NGA-West2模型进行比较,证实了该方法的可行性并指出它非常适合于缺乏地震数据地区的地震危险性分析。
5. 讨论和结论
本文较为全面地介绍了基于谱元法的地震波动数值模拟技术的研究进展。谱元法是谱方法和有限元法的结合,兼具谱方法的高精度、快速收敛性和有限元法的规整性与灵活性。谱元法既可以看作是谱方法的域分解方法,又可以看作是采用谱插值构建有限单元的特殊高阶有限元法。早期的Chebyshev谱元法(CSEM)和Legendre谱元法(LSEM)使用由正交多项式线性组合构成的拉格朗日型插值基,形式比较复杂,计算过程相对繁琐。目前广泛使用的是Komatitsch等发展的简洁形式LSEM (Komatitsch,Vilotte,1998;Komatitsch,Tromp,1999;Komatitsch et al,1999),其实施步骤和主要公式与有限元法完全一致,仅通过内置的Gauss-Lobatto-Legendre (GLL)高精度数值积分保留着与谱方法之间的联系。此外,非协调谱元法便于处理多尺度或不连续问题,是谱元法的一个重要分支,其中间断伽辽金谱元法(discontinuous Galerkin,DG-SEM或DGM)的研究和应用较多(Antonietti et al,2012;Mazzieri et al,2013)。
基于谱元法的地震波动数值模拟技术已被广泛用于地震震源破裂、大规模地震波传播、区域复杂场地及工程结构(群)地震反应、地震层析成像等重要问题的研究当中,是目前地震工程学、地震学和地球物理学等地震科技领域共同关注的前沿热点。谱元法的巨大成功不仅源于算法本身的高精度、规整性和灵活性,更是得益于以SPECFEM2D/3D、SPECFEM_GLOBE、SPEED等为代表的开源软件集成了实现复杂模拟所需的三维复杂模型、不同地震震源模型或平面波输入、大规模并行计算、全球模拟、伴随方法(adjoint method)、以及多尺度或不连续建模等关键技术。谱元法在我国的发展早期以方法介绍和一些初步应用为主,近十余年来在算法研究和复杂工程应用方面不断涌现出一系列创新成果,已逐步跻身世界前沿水平并形成一些自己的特色。
-
图 1 标量波情形下1—10阶谱元法的网格频散曲线(De Basabe,Sen,2007)
Figure 1. Grid dispersion curves of 1st- to 10th-order spectral elements in acoustic case (De Basabe,Sen,2007)
1 Gauss-Lobatto-Legendre高精度数值积分的节点和权系数
1 The nodes and weights of Gauss-Lobatto-Legendre high-precision numerical integration
GLL节点数 积分节点 积分权系数 2 ±1 1 3 0 1.333 333 333 333 333 3 ±1 0.333 333 333 333 333 3 4 ±0.447 213 595 499 957 9 0.833 333 333 333 333 4 ±1 0.166 666 666 666 666 7 5 0 0.711 111 111 111 111 1 ±0.654 653 670 707 977 2 0.544 444 444 444 444 5 ±1 0.100 000 000 000 000 0 6 ±0.285 231 516 480 645 1 0.554 858 377 035 486 2 ±0.765 055 323 929 464 7 0.378 474 956 297 847 0 ±1 0.066 666 666 666 666 7 7 0 0.487 619 047 619 047 6 ±0.468 848 793 470 714 2 0.431 745 381 209 862 7 ±0.830 223 896 278 567 0 0.276 826 047 361 565 9 ±1 0.047 619 047 619 047 6 8 ±0.209 299 217 902 478 9 0.412 458 794 658 703 8 ±0.591 700 181 433 142 3 0.341 122 692 483 504 4 ±0.871 740 148 509 606 6 0.210 704 227 143 506 1 ±1 0.035 714 285 714 285 7 9 0 0.371 519 274 376 417 2 ±0.363 117 463 826 178 2 0.346 428 510 973 046 3 ±0.677 186 279 510 737 7 0.274 538 712 500 161 7 ±0.899 757 995 411 460 2 0.165 495 361 560 805 5 ±1 0.027 777 777 777 777 8 10 ±0.165 278 957 666 387 0 0.327 539 761 183 897 6 ±0.477 924 949 810 444 5 0.292 042 683 679 683 8 ±0.738 773 865 105 505 0 0.224 889 342 063 126 4 ±0.919 533 908 166 458 9 0.133 305 990 851 070 1 ±1 0.022 222 222 222 222 2 注:积分节点和权系数的数目与GLL节点数相对应,数值相同、正负号不同的积分节点对应相同的积分权系数,为简化起见,表中只列出一个。 表 1 谱元法结合二阶中心差分求解格式的稳定条件(De Basabe,Sen,2010)
Table 1 Stability criteria for spectral element method solved by classical second-order centered-difference time integration algorithm (De Basabe,Sen,2010)
谱单元阶次 1 2 3 4 5 6 7 8 标量波情形
(SH波动)qEmax 0.709 0.288 0.164 0.104 0.0714 0.0516 0.039 0 0.030 4 qdmax 0.709 0.577 0.593 0.604 0.608 0.608 0.608 0.607 弹性波情形
(P-SV波动)qEmax 0.816 0.333 0.189 0.120 0.082 3 0.059 5 0.044 9 0.035 0 qdmax 0.816 0.666 0.684 0.697 0.700 0.700 0.700 0.699 -
巴振宁,赵靖轩,桑巧稚,梁建文. 2024. 基于Davidenkov本构模型的三维沉积盆地非线性地震动谱元法模拟[J]. 岩土工程学报,46(7):1387–1397. doi: 10.11779/CJGE20230582 Ba Z N,Zhao J X,Sang Q Z,Liang J W. 2024. Nonlinear ground motion simulation of three-dimensional sedimentary basin based on Davidenkov constitutive model and spectral element method[J]. Chinese Journal of Geotechnical Engineering,46(7):1387–1397 (in Chinese).
巴振宁,赵靖轩,张郁山,梁建文,张玉洁. 2023. 基于GP14.3运动学混合震源模型和SPECFEM3D谱元法的宽频地震动模拟[J]. 地球物理学报,66(3):1125–1138. doi: 10.6038/cjg2022Q0181 Ba Z N,Zhao J X,Zhang Y S,Liang J W,Zhang Y J. 2023. Broadband ground motion spectral element simulation based on GP14.3 kinematic hybrid source model and SPECFEM3D[J]. Chinese Journal of Geophysics,66(3):1125–1138 (in Chinese).
曹丹平,周建科,印兴耀. 2015. 三角网格有限元法波动模拟的数值频散及稳定性研究[J]. 地球物理学报,58(5):1717–1730. doi: 10.6038/cjg20150522 Cao D P,Zhou J K,Yin X Y. 2015. The study for numerical dispersion and stability of wave motion with triangle-based finite element algorithm[J]. Chinese Journal of Geophysics,58(5):1717–1730 (in Chinese).
车承轩. 2007. 谱元法模拟起伏自由表面地层中的弹性波传播[D]. 大庆:大庆石油学院:1−49. Che C X. 2007. The Spectral Element Method for Elastic Wave Simulation in a Formation with a Topographic Traction Free Surface[D]. Daqing:Daqing Petroleum Institute:1−49 (in Chinese).
陈少林,程书林,柯小飞. 2019b. 海洋地震工程流固耦合问题统一计算框架——不规则界面情形[J]. 力学学报,51(5):1517–1529. Chen S L,Cheng S L,Ke X F. 2019b. A unified computational framework for fluid-solid coupling in marine earthquake engineering:Irregular interface case[J]. Chinese Journal of Theoretical and Applied Mechanics,51(5):1517–1529.
陈少林,柯小飞,张洪翔. 2019a. 海洋地震工程流固耦合问题统一计算框架[J]. 力学学报,51(2):594–606. Chen S L,Ke X F,Zhang H X. 2019a. A unified computational framework for fluid-solid coupling in marine earthquake engineering[J]. Chinese Journal of Theoretical and Applied Mechanics,51(2):594–606.
戴志军,李小军,侯春林. 2015. 谱元法与透射边界的配合使用及其稳定性研究[J]. 工程力学,32(11):40–50. doi: 10.6052/j.issn.1000-4750.2014.03.0196 Dai Z J,Li X J,Hou C L. 2015. A combination usage of transmitting formula and spectral element method and the study of its stability[J]. Engineering Mechanics,32(11):40–50 (in Chinese).
董兴朋,杨顶辉. 2017. 球坐标系下谱元法三维地震波场模拟[J]. 地球物理学报,60(12):4671–4680. doi: 10.6038/cjg20171211 Dong X P,Yang D H. 2017. Numerical modeling of the 3-D seismic wave field with the spectral element method in spherical coordinates[J]. Chinese Journal of Geophysics,60(12):4671–4680 (in Chinese).
贺春晖,王进廷,张楚汉. 2017. 基于震源-河谷波场数值模拟的坝址地震动参数确定方法[J]. 地球物理学报,60(2):585–592. doi: 10.6038/cjg20170213 He C H,Wang J T,Zhang C H. 2017. Determination of seismic parameters for dam sites by numerical simulation of the rupture-canyon wave field[J]. Chinese Journal of Geophysics,60(2):585–592 (in Chinese).
胡元鑫,刘新荣,罗建华,张梁,葛华. 2011. 汶川震区地震动三维地形效应的谱元法模拟[J]. 兰州大学学报(自然科学版),47(4):24–32. Hu Y X,Liu X R,Luo J H,Zhang L,Ge H. 2011. Simulation of three-dimensional topographic effects on seismic ground motion in Wenchuan earthquake region based upon the spectral-element method[J]. Journal of Lanzhou University (Natural Sciences),47(4):24–32 (in Chinese).
蒋涵,周红,高孟潭. 2015. 山脊线与坡度和峰值速度放大系数的相关性研究[J]. 地球物理学报,58(1):229–237. doi: 10.6038/cjg20150120 Jiang H,Zhou H,Gao M T. 2015. A study on the correlation of the ridge line and slope with peak ground velocity amplification factor[J]. Chinese Journal of Geophysics,58(1):229–237 (in Chinese).
孔曦骏,邢浩洁,李鸿晶. 2022. 流固耦合地震波动问题的显式谱元模拟方法[J]. 力学学报,54(9):2513–2528. doi: 10.6052/0459-1879-22-068 Kong X J,Xing H J,Li H J. 2022. An explicit spectral-element approach to fluid-solid coupling problems in seismic wave propagation[J]. Chinese Journal of Theoretical and Applied Mechanics,54(9):2513–2528 (in Chinese).
李冰非,董兴朋,李小凡,司洁戈. 2019. 基于辛-谱元-FK 混合方法的保结构远震波场模拟[J]. 地球物理学报,62(11):4339–4352. doi: 10.6038/cjg2019M0688 Li B F,Dong X P,Li X F,Si J G. 2019. Structure-preserving modeling of teleseismic wavefield using symplectic SEM-FK hybrid method[J]. Chinese Journal of Geophysics,62(11):4339–4352 (in Chiese).
李冰非,李小凡,李峰,龚飞. 2021. 基于辛-谱元方法的地球自由振荡保弥散衰减数值模拟[J]. 地球物理学报,64(11):4022–4030. doi: 10.6038/cjg2021P0019 Li B F,Li X F,Li F,Gong F. 2021. Dissipation preserving simulation for Earth’s free oscillations based on symplectic spectral element method[J]. Chinese Journal of Geophysics,64(11):4022–4030 (in Chinese).
李昊臻,刘少林,董兴朋,蒙伟娟,杨顶辉. 2024. 基于逐元和轴对称谱元的混合方法及远震波场模拟[J]. 地球物理学报,67(5):1819–1831. doi: 10.6038/cjg2023R0180 Li H Z,Liu S L,Dong X P,Meng W J,Yang D H. 2024. Hybrid method based on element-by-element and axisymmetric spectral element method for teleseismic wavefield simulation[J]. Chinese Journal of Geophysics,67(5):1819–1831 (in Chinese).
李鸿晶,王竞雄. 2022. 时域谱元法的质量特性模型及其构建方法[J]. 地震学报,44(1):60–75. doi: 10.11939/jass.20210117 Li H J,Wang J X. 2022. The mass property model and its implementation in the time-domain spectral element method[J]. Acta Seismologica Sinica,44(1):60–75 (in Chinese).
李琳,刘韬,胡天跃. 2014. 三角谱元法及其在地震正演模拟中的应用[J]. 地球物理学报,57(4):1224–1234. doi: 10.6038/cjg20140419 Li L,Liu T,Hu T Y. 2014. Spectra element method with triangular mesh and its application in seismic modeling[J]. Chinese Journal of Geophysics,57(4):1224–1234 (in Chinese).
李孝波. 2014. 基于谱元法的玉田震害异常研究[D]. 哈尔滨:中国地震局工程力学研究所:1−136. Li X B. 2014. The Investigation of Seismic Damage Anomaly in Yutian based on Spectral Element Method[D]. Harbin:Institute of Engineering Mechanics,China Earthquake Administration:1−136 (in Chinese).
林伟军,苏畅,Seriani G. 2018. 多网格谱元法及其在高性能计算中的应用[J]. 应用声学,37(1):42–52. doi: 10.11684/j.issn.1000-310X.2018.01.007 Lin W J,Su C,Seriani G. 2018. The poly-grid spectral element method and its application in high performance computing[J]. Journal of Applied Acoustics,37(1):42–52 (in Chinese).
林伟军,王秀明,张海澜. 2005. 用于弹性波方程模拟的基于逐元技术的谱元法[J]. 自然科学进展,15(9):1048–1057. doi: 10.3321/j.issn:1002-008X.2005.09.004 Lin W J,Wang X M,Zhang H L. 2005. An element-by-element spectral element method for the modeling of elastic wave equation[J]. Progress in Natural Science,15(9):1048–1057 (in Chinese).
林伟军. 2007. 弹性波传播模拟的Chebyshev谱元法[J]. 声学学报,32(6):525–533. doi: 10.3321/j.issn:0371-0025.2007.06.007 Lin W J. 2007. A Chebyshev spectral element method for elastic wave modeling[J]. Acta Acustica,32(6):525–533 (in Chinese).
刘晶波,廖振鹏. 1989. 离散网格中的弹性波动(Ⅱ)--几种有限元离散模型的对比分析[J]. 地震工程与工程振动, 9 (2):1−11. Liu J B,Liao Z P. 1989. Elastic wave motion in discrete grids (II) – Comparison of common finite element models[J]. Earthquake Engineering and Engineering Vibration,9(2):1–11 (in Chinese).
刘晶波,廖振鹏. 1990. 离散网格中的弹性波动(Ⅲ)--时域离散化对波传播规律的影响[J]. 地震工程与工程振动, 10 (2):1−10. Liu J B,Liao Z P. 1990. Elastic wave motion in discrete grids (III) – The effect of discretization in time domain on wave motion[J]. Earthquake Engineering and Engineering Vibration,10(2):1–10 (in Chinese).
刘启方,于彦彦,章旭斌. 2013. 施甸盆地三维地震动研究[J]. 地震工程与工程振动,33(4):54–60. Liu Q F,Yu Y Y,Zhang X B. 2013. Three-dimensional ground motion simulation of Shidian basin[J]. Journal of Earthquake Engineering and Engineering Vibration,33(4):54–60 (in Chinese).
刘少林,李小凡,刘有山,朱童,张美根. 2014. 三角网格有限元法声波与弹性波模拟频散分析[J]. 地球物理学报,57(8):2620–2630. doi: 10.6038/cjg20140821 Liu S L,Li X F,Liu Y S,Zhu T,Zhang M G. 2014. Dispersion analysis of triangle-based finite element method for acoustic and elastic wave simulations[J]. Chinese Journal of Geophysics,57(8):2620–2630 (in Chinese).
刘少林,杨顶辉,孟雪莉,汪文帅,徐锡伟,李小凡. 2022. 模拟地震波传播的优化质量矩阵Legendre谱元法[J]. 地球物理学报,65(12):4802–4815. doi: 10.6038/cjg2022Q0145 Liu S L,Yang D H,Meng X L,Wang W S,Xu X W,Li X F. 2022. A Legendre spectral element method with optimal mass matrix for seismic wave modeling[J]. Chinese Journal of Geophysics,65(12):4802–4815 (in Chinese).
刘少林,杨顶辉,徐锡伟,李小凡,申文豪,刘有山. 2021. 模拟地震波传播的三维逐元并行谱元法[J]. 地球物理学报,64(3):993–1005. doi: 10.6038/cjg2021O0405 Liu S L,Yang D H,Xu X W,Li X F,Shen W H,Liu Y S. 2021. Three-dimensional element-by-element parallel spectral-element method for seismic wave modeling[J]. Chinese Journal of Geophysics,64(3):993–1005 (in Chinese).
刘有山,刘少林,张美根,马德堂. 2012. 一种改进的二阶弹性波动方程的最佳匹配层吸收边界条件[J]. 地球物理学进展,27(5):2113. doi: 10.6038/j.issn.1004-2903.2012.05.036 Liu Y S,Liu S L,Zhang M G,Ma D T. 2012. An improved perfectly matched layer absorbing boundary condition for second order elastic wave equation[J]. Progress in Geophysics,27(5):2113 (in Chinese).
刘有山,滕吉文,徐涛,刘少林,司芗,马学英. 2014. 三角网格谱元法地震波场数值模拟[J]. 地球物理学进展,29(4):1715–1726. doi: 10.6038/pg20140430 Liu Y S,Teng J W,Xu T,Liu S L,Si X,Ma X Y. 2014. Numerical modeling of seismic wavefield with the SEM based on triangles[J]. Progress in Geophysics,29(4):1715–1726 (in Chinese).
陆新征,田源,许镇,熊琛. 2021. 城市抗震弹塑性分析[M]. 北京:清华大学出版社:237−317. Lu X Z,Tian Y,Xu Z,Xiong C. 2021. Elastoplastic Analysis of Urban Seismic Resistance[M]. Beijing:Tsinghua University Press:237−317 (in Chinese).
孟雪莉,刘少林,杨顶辉,汪文帅,徐锡伟,李小凡. 2022. 基于优化数值积分的谱元法模拟地震波传播[J]. 石油地球物理勘探,57(3):602–612. Meng X L,Liu S L,Yang D H,Wang W S,Xu X W,Li X F. 2022. Simulating seismic wave propagation using spectral element method based on optimized numerical integration[J]. Geophysical Exploration of Petroleum,57(3):602–612 (in Chinese).
秦国良,徐忠. 2000. 谱元方法求解二维不可压缩Navier-Stokes方程[J]. 应用力学学报,17(4):20–25. doi: 10.3969/j.issn.1000-4939.2000.04.004 Qin G L,Xu Z. 2000. A spectral element method for incompressible Navier-Stokes equations[J]. Chinese Journal of Applied Mechanics,17(4):20–25 (in Chinese).
秦国良,徐忠. 2001. 谱元方法求解正方形封闭空腔内的自然对流换热[J]. 计算物理,18(2):119–124. doi: 10.3969/j.issn.1001-246X.2001.02.005 Qin G L,Xu Z. 2001. Computation of natural convection in two-dimensional cavity using spectral element method[J]. Chinese Journal of Computational Physics,18(2):119–124 (in Chinese).
任骏声,张怀,周元泽,张振,石耀霖. 2024. 基于卷积滤波的谱元法在长时程波场模拟中的应用[J]. 地球物理学报,67(5):1832–1838. doi: 10.6038/cjg2022Q0160 Ren J S,Zhang H,Zhou Y Z,Zhang Z,Shi Y L. 2024. Application of spectral element method based on convolving filtering in long-term wavefield modeling[J]. Chinese Journal of Geophysics,67(5):1832–1838 (in Chinese).
唐杰. 2011. 气枪激发信号传播的谱元法数值模拟研究[J]. 地球物理学报,54(9):2348–2356. doi: 10.3969/j.issn.0001-5733.2011.09.018 Tang J. 2011. Study on SEM numerical simulation of airgun signal transition[J]. Chinese Journal of Geophysics,54(9):2348–2356 (in Chinese).
汪文帅,李小凡,鲁明文,张美根. 2012. 基于多辛结构谱元法的保结构地震波场模拟[J]. 地球物理学报,55(10):3427–3439. doi: 10.6038/j.issn.0001-5733.2012.10.026 Wang W S,Li X F,Lu M W,Zhang M G. 2012. Structure-preserving modeling for seismic wave fields based on a multisymplectic spectral element method[J]. Chinese Journal of Geophysics,55(10):3427–3439 (in Chinese).
汪文帅,李小凡. 2013. 基于辛格式的谱元法及其在横向各向同性介质波场模拟中的应用[J]. 数值计算与计算机应用,34(1):20–30. doi: 10.3969/j.issn.1000-3266.2013.01.003 Wang W S,Li X F. 2013. The SEM based on symplectical schemes and its application in modeling the wave propagation in transversely isotropic media[J]. Journal on Numerical Methods and Computer Applications,34(1):20–30 (in Chinese).
汪文帅,张怀,李小凡. 2013. 间断的 Galerkin 方法在地震波场数值模拟中的应用概述[J]. 地球物理学进展,28(1):171–179. doi: 10.6038/pg20130118 Wang W S,Zhang H,Li X F. 2013. Review on application of the discontinuous Galerkin method for modeling of the seismic wavefield[J]. Progress in Geophysics,28(1):171–179 (in Chinese).
王竞雄,李鸿晶,邢浩洁. 2022. 水平成层场地地震反应的集中质量切比雪夫谱元分析方法[J]. 地震学报,44(1):76–86. doi: 10.11939/jass.20210091 Wang J X,Li H J,Xing H J. 2022. The Lumped mass Chebyshev spectral element method for seismic response analysis of horizontally layered soil sites[J]. Acta Seismologica Sinica,44(1):76–86 (in Chinese).
王童奎,李瑞华,李小凡,张美根,龙桂华. 2007. 横向各向同性介质中地震波场谱元法数值模拟[J]. 地球物理学进展,22(3):778–784. doi: 10.3969/j.issn.1004-2903.2007.03.018 Wang T K,Li R H,Li X F,Zhang M G,Long G H. 2007. Numerical spectral element modeling for seismic wave propagation in transversely isotropic medium[J]. Progress in Geophysics,22(3):778–784 (in Chinese).
王童奎,谢占安,付兴深,高文中,刘萱. 2009. 弹性介质中谱元法叠后逆时偏移方法研究[J]. 石油物探,48(4):354–358. doi: 10.3969/j.issn.1000-1441.2009.04.006 Wang T K,Xie Z A,Fu X S,Gao W Z,Liu X. 2009. Research on post-stack reverse-time migration in elastic media based on spectral element method[J]. Geophysical Prospecting for Petroleum,48(4):354–358 (in Chinese).
王秀明,Seriani G,林伟军. 2007. 利用谱元法计算弹性波场的若干理论问题[J]. 中国科学:G辑,37(1):41–59. Wang X M,Seriani G,Lin W J. 2007. Several theoretical issues on the spectral-element calculation of elastic wave field[J]. Science China Series G,37(1):41–59 (in Chinese).
向新民. 2000. 谱方法的数值分析[M]. 北京:科学出版社:1−327. Xiang X M. 2000. Numerical Analysis of Spectral Methods[M]. Beijing:Science Press:1−327 (in Chinese).
谢志南,章旭斌. 2017,弱形式时域完美匹配层[J]. 地球物理学报, 60 (10):3823−3831. Xie Z N,Zhang X B. 2017. Weak-form time-domain perfectly matched layer[J]. Chinese Journal of Geophysics,60(10):3823–3831 (in Chinese).
谢志南,郑永路,章旭斌,唐丽华. 2019. 弱形式时域完美匹配层——滞弹性近场波动数值模拟[J]. 地球物理学报,62(8):3140–3154. doi: 10.6038/cjg2019M0425 Xie Z N,Zheng Y L,Zhang X B,Tang L H. 2019. Weak-form time-domain perfectly matched layer for numerical simulation of viscoelastic wave propagation in infinite domain[J]. Chinese Journal of Geophysics,62(8):3140–3154 (in Chinese).
谢志南,郑永路,章旭斌. 2018. 常Q滞弹性介质地震波动数值模拟——时域本构优化逼近[J]. 地球物理学报,61(10):4007–4020. doi: 10.6038/cjg2018L0704 Xie Z N,Zheng Y L,Zhang X B. 2018. Optimized approximation for constitution of constant Q viscoelastic media in time domain seismic wave simulation[J]. Chinese Journal of Geophysics,61(10):4007–4020 (in Chinese).
邢浩洁,李鸿晶,李小军. 2021a. 一维波动有限元模拟中透射边界的时域稳定条件[J]. 应用基础与工程科学学报,29(3):617–632. Xing H J,Li H J,Li X J. 2021a. Time-domain stability conditions of multi-transmitting formula in one-dimensional finite element simulation of wave motion[J]. Journal of Basic Science and Engineering,29(3):617–632 (in Chinese).
邢浩洁,李鸿晶,杨笑梅. 2017. 基于切比雪夫谱元模型的成层场地地震反应分析[J]. 岩土力学,38(2):593–600. Xing H J,Li H J,Yang X M. 2017. Seismic response analysis of horizontal layered soil sites based on Chebyshev spectral element model[J]. Rock and Soil Mechanics,2017, 38 (2):593−600 (in Chinese).
邢浩洁,李鸿晶. 2017a. 透射边界条件在波动谱元模拟中的实现:一维波动[J]. 力学学报,49(2):367–379. Xing H J,Li H J. 2017b. Implementation of multi-transmitting boundary condition for wave motion simulation by spectral element method:One dimension case[J]. Chinese Journal of Theoretical and Applied Mechanics,49(2):367–379 (in Chinese).
邢浩洁,李鸿晶. 2017b. 透射边界条件在波动谱元模拟中的实现:二维波动[J]. 力学学报,49(4):894–906. Xing H J,Li H J. 2017b. Implementation of multi-transmitting boundary condition for wave motion simulation by spectral element method:Two dimension case[J]. Chinese Journal of Theoretical and Applied Mechanics,49(4):894–906 (in Chinese).
邢浩洁,李鸿晶. 2017c. 波动切比雪夫谱元模拟的时间积分方法研究[J]. 南京工业大学学报(自然科学版),39(2):70–76. Xing H J,Li H J. 2017c. Investigation of time integration method for Chebyshev spectral element simulation of wave motion[J]. Journal of Nanjing Tech University (Natural Science Edition),39(2):70–76 (in Chinese).
邢浩洁,李小军,刘爱文,李鸿晶,周正华,陈苏. 2021b. 波动数值模拟中的外推型人工边界条件[J]. 力学学报,53(5):1480–1495. Xing H J,Li X J,Liu A W,Li H J,Zhou Z H,Chen S. 2021. Extrapolation-type artificial boundary conditions in the numerical simulation of wave motion[J]. Chinese Journal of Theoretical and Applied Mechanics,53(5):1480–1495 (in Chinese).
邢浩洁,刘爱文,李小军,陈苏,傅磊. 2022. 多人工波速优化透射边界在谱元法地震波动模拟中的应用[J]. 地震学报,44(1):26–39. doi: 10.11939/jass.20210090 Xing H J,Liu A W,Li X J,Chen S,Fu L. 2022. Application of an optimized transmitting boundary with multiple artificial wave velocities in spectral-element simulation of seismic wave propagation[J]. Acta Seismologica Sinica,44(1):26–39 (in Chinese).
许传炬,林玉闽. 2000. Poiseuille-Bénard流的出口边界条件及其谱元法计算[J]. 力学学报,32(1):1–10. doi: 10.3321/j.issn:0459-1879.2000.01.001 Xu C J,Lin Y M. 2000. Open boundary conditions in simulation by spectral element methods of Poiseuille-Bénard channel flow[J]. Chinese Journal of Theoretical and Applied Mechanics,32(1):1–10 (in Chinese).
严珍珍,张怀,杨长春,石耀霖. 2009. 汶川大地震地震波传播的谱元法数值模拟研究[J]. 中国科学:D辑,39(4):393–402. Yan Z Z,Zhang H,Yang C C,Shi Y L. 2009. Study on the seismic wave propagation of the great Wenchuan earthquake by using the numerical simulation of spectral element method[J]. Science China Series D,39(4):393–402 (in Chinese).
于彦彦,丁海平,刘启方. 2017. 透射边界与谱元法的结合及对波动模拟精度的改进[J]. 振动与冲击, 36 (2):13−22. Yu Y Y,Ding H P,Liu Q F. 2017. Integration of transmitting boundary and spectral element method and improvement on the accuracy of wave motion simulation[J]. Journal of Vibration and Shock, 36 (2):13−22 (in Chinese).
于彦彦,芮志良,丁海平. 2023. 三维局部场地地震波散射问题谱元并行模拟方法[J]. 力学学报,55(6):1342–1354. doi: 10.6052/0459-1879-23-052 Yu Y Y,Rui Z L,Ding H P. 2023. Parallel spectral element method for 3d local-site ground motion simulations of wave scattering problem[J]. Chinese Journal of Theoretical and Applied Mechanics,55(6):1342–1354 (in Chinese).
章旭斌,谢志南. 2022. 波动谱元模拟中透射边界稳定性分析[J]. 工程力学,39(10):26–35. doi: 10.6052/j.issn.1000-4750.2021.06.0428 Zhang X B,Xie Z N. 2022. Stability analysis of transmitting boundary in wave spectral element simulation[J]. Engineering Mechanics,39(10):26–35 (in Chinese).
赵靖轩,巴振宁,阔晨阳,刘博佳. 2023. 2022年9月5日泸定MS6.8地震宽频带地震动谱元法模拟[J]. 地震学报,45(2):179–195. doi: 10.11939/jass.20220190 Zhao J X,Ba Z N,Kuo C Y,Liu B J. 2023. Broadband ground motion simulations applied to the Luding MS6.8 earthquake on September 5,2022 based on spectral element method[J]. Acta Seismologica Sinica,45(2):179–195 (in Chinese).
周红,高孟潭,俞言祥. 2010. SH 波地形效应特征的研究[J]. 地球物理学进展,25(3):775–782. doi: 10.3969/j.issn.1004-2903.2010.03.005 Zhou H,Gao M T,Yu Y X. 2010. A study of topographical effect on SH waves[J]. Progress in Geophysics,25(3):775–782 (in Chinese).
周红. 2018. 九寨沟7.0级地震地表地震动位移及静态位移的模拟研究[J]. 地球物理学报,61(12):4851–4861. doi: 10.6038/cjg2018M0010 Zhou H. 2018. Research on ground motion displacement and static displacement near the fault of Jiuzhaigou MS7.0 earthquake[J]. Chinese Journal of Geophysics,61(12):4851–4861 (in Chinese).
朱伯芳. 1998. 有限单元法原理与应用[M]. 第二版. 北京:水利水电出版社:1−176. Zhu B F. 1998. The Finite Element Method Theory and Applications[M]. 2nd ed. Beijing:China Water&Power Press:1−176 (in Chinese).
Abraham J R,Smerzini C,Paolucci R,Lai C G. 2016. Numerical study on basin-edge effects in the seismic response of the Gubbio valley,Central Italy[J]. B Earthq Eng,14:1437–1459. doi: 10.1007/s10518-016-9890-y
Aguirre V M H,Paolucci R,Sánchez-Sesma F J,Mazzieri I. 2023. Three-dimensional numerical modeling of ground motion in the Valley of Mexico:A case study from the MW3. 2 earthquake of July 17,2019[J]. Earthq Spectra, 39 (4):2323−2351.
Alford R M,Kelly K R,Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation[J]. Geophysics,39(6):834–842. doi: 10.1190/1.1440470
Antonietti P F,Mazzieri I,Quarteroni A,Rapetti F. 2012. Non-conforming high order approximations of the elastodynamics equation[J]. Comput Method Appl M,209:212–238.
Asmar A H. 2005. Partial Differential Equations with Fourier Series and Boundary Value Problems[M]. 2nd ed. USA:Courier Dover Publications:227−321.
Ba Z N,Fu J S,Wang F B,Liang J W,Zhang B,Zhang L. 2024a. Physics-based seismic analysis of ancient wood structure:fault-to-structure simulation[J]. Earthq Eng Eng Vib,23(3):727–740. doi: 10.1007/s11803-024-2268-2
Ba Z N,Sang Q Z,Wu M T,Liang J W. 2021. The revised direct stiffness matrix method for seismogram synthesis due to dislocations:from crustal to geotechnical scale[J]. Geophys J Int,227(1):717–734. doi: 10.1093/gji/ggab248
Ba Z N,Wu M T,Liang J W,Zhao J X,Lee V W. 2022. A two-step approach combining FK with SE for simulating ground motion due to point dislocation sources[J]. Soil Dyn Earthq Eng,57:107224.
Ba Z N,Zhao J X,Sang Q Z,Liang J W. 2024b. Nonlinear seismic response of an alluvial basin modelled by spectral element method:Implementation of a Davidenkov constitutive model[J]. J Earthq Eng,1−30.
Ba Z N,Zhao J X,Wang Y. 2024c. GA-BPNN prediction model of broadband ground motion parameters in Tianjin area driven by synthetic database based on hybrid simulated method[J]. Pure Appl Geophys,181:1195–1220. doi: 10.1007/s00024-024-03431-1
Ba Z N,Zhao J X,Zhu Z H,Zhou G Y. 2023. 3D physics-based ground motion simulation and topography effects of the 05 September 2022 MW6. 6 Luding earthquake,China[J]. Soil Dyn Earthq Eng, 172 :108048.
Baker J W,Luco N,Abrahamson N A,Graves R W,Maechling P J,Olsen K B. 2014. Engineering uses of physics-based ground motion simulations[C]//Proceedings of the Tenth US Conference on Earthquake Engineering,Anchorage,Alaska:1−11.
Bradley B A. 2019. On-going challenges in physics-based ground motion prediction and insights from the 2010–2011 Canterbury and 2016 Kaikoura,New Zealand earthquakes[J]. Soil Dyn Earthq Eng,124:354–364. doi: 10.1016/j.soildyn.2018.04.042
Briani M,Sommariva A,Vianello M. 2012. Computing Fekete and Lebesgue points:simplex,square,disk[J]. J Comput Appl Math,236(9):2477–2486. doi: 10.1016/j.cam.2011.12.006
Canuto C,Hussaini M Y,Quarteroni A,Zang T A. 1988. Spectral Methods in Fluid Dynamics[M]. Berlin:Springer-Verlag:1−550.
Canuto C,Hussaini M Y,Quarteroni A,Zang T A. 2006. Spectral Methods – Fundamentals in Single Domains[M]. Berlin:Springer-Verlag:1−552.
Capdeville Y,Gung Y,Romanowicz B. 2005. Towards global earth tomography using the spectral element method:a technique based on source stacking[J]. Geophys J Int,162(2):541–554. doi: 10.1111/j.1365-246X.2005.02689.x
Carmona A E,Peter D B,Parisi L,Mai P M. 2024. Anelastic tomography of the Arabian plate[J]. B Seismol Soc Am,114(3):1347–1364.
Castelli F,Cavallaro A,Grasso S,Lentini V. 2016. Seismic microzoning from synthetic ground motion earthquake scenarios parameters:the case study of the City of Catania (Italy)[J]. Soil Dyn Earthq Eng,88:307–327. doi: 10.1016/j.soildyn.2016.07.010
Chaljub E,Komatitsch D,Vilotte J P,Capdeville Y,Valette B,Festa G. 2007. Spectral-element analysis in seismology[J]. Adv Geophys,48:365–419.
Chaljub E,Maufroy E,Moczo P,Kristek J,Hollender F,Bard P Y,Priolo E,Klin P,Martin F,Zhang Z G,Zhang W,Chen X F. 2015. 3-D numerical simulations of earthquake ground motion in sedimentary basins:testing accuracy through stringent models[J]. Geophys J Int,201(1):90–111. doi: 10.1093/gji/ggu472
Chaljub E,Moczo P,Tsuno S,Bard P Y,Kristek J,Käser M,Stupazzini M,Kristekova M. 2010. Quantitative comparison of four numerical predictions of 3D ground motion in the Grenoble Valley,France[J]. B Seismol Soc Am,100(4):1427–1455. doi: 10.1785/0120090052
Che C X,Wang X M,Lin W J. 2010. The Chebyshev spectral element method using staggered predictor and corrector for elastic wave simulations[J]. Appl Geophys,7(2):174–184. doi: 10.1007/s11770-010-0242-9
Chen M,Niu F L,Liu Q Y,Tromp J,Zheng X F. 2015. Multiparameter adjoint tomography of the crust and upper mantle beneath East Asia:1. Model construction and comparisons[J]. J Geophys Res-Sol Ea,120(3):1762–1786. doi: 10.1002/2014JB011638
Chen M,Niu F L,Tromp J,Lenardic A,Lee C T A,Cao W R,Ribeiro J. 2017. Lithospheric foundering and underthrusting imaged beneath Tibet[J]. Nat Commun,8(1):15659. doi: 10.1038/ncomms15659
Chen Q,Babuška I. 1995. Approximate optimal points for polynomial interpolation of real functions in an interval and in a triangle[J]. Comput Method Appl M, 128 (3−4):405−417.
Chen Z W,Huang D R,Wang G. 2023a. Large‐scale ground motion simulation of the 2016 Kumamoto earthquake incorporating soil nonlinearity and topographic effects[J]. Earthq Eng Struct D,52(4):956–978. doi: 10.1002/eqe.3795
Chen Z W,Huang D R,Wang G. 2023b. A regional scale coseismic landslide analysis framework:Integrating physics-based simulation with flexible sliding analysis[J]. Eng Geol,315:107040. doi: 10.1016/j.enggeo.2023.107040
Cohen G C. 2002. Higher-Order Numerical Methods for Transient Wave Equations[M]. Berlin:Springer:1−346.
Cohen G,Joly P,Roberts J E,Tordjman N. 2001. Higher order triangular finite elements with mass lumping for the wave equation[J]. SIAM J Numer Anal,38(6):2047–2078. doi: 10.1137/S0036142997329554
Cui Y,Poyraz E,Olsen K B,Zhu J,Withers K,Callaghan S,Larkin J,Guest C,Choi D,Chourasia A,Shi Z,Day S M,Maechling P J,Jordan T H. 2013. Physics-based seismic hazard analysis on petascale heterogeneous supercomputers[C]//Proceedings of the International Conference on High Performance Computing,Networking,Storage and Analysis:1−12.
Dauksher W,Emery A F. 1997. Accuracy in modeling the acoustic wave equation with Chebyshev spectral finite elements[J]. Finite Elem Anal Des,26(2):115–128. doi: 10.1016/S0168-874X(96)00075-3
De Basabe J D,Sen M K,Wheeler M F. 2008. The interior penalty discontinuous Galerkin method for elastic wave propagation:Grid dispersion[J]. Geophys J Int,175(1):83–93. doi: 10.1111/j.1365-246X.2008.03915.x
De Basabe J D,Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations[J]. Geophysics,72(6):T81–T95. doi: 10.1190/1.2785046
De Basabe J D,Sen M K. 2009. New developments in the finite-element method for seismic modeling[J]. The Leading Edge,28(5):562–567. doi: 10.1190/1.3124931
De Basabe J D,Sen M K. 2010. Stability of the high-order finite elements for acoustic or elastic wave propagation with high-order time stepping[J]. Geophys J Int,181(1):577–590. doi: 10.1111/j.1365-246X.2010.04536.x
De Basabe J D,Sen M K. 2015. A comparison of finite-difference and spectral-element methods for elastic wave propagation in media with a fluid-solid interface[J]. Geophys J Int,200(1):278–298. doi: 10.1093/gji/ggu389
De Basabe J D. 2009. High-Order Finite Element Methods for Seismic Wave Propagation[D]. Austin:The University of Texas at Austin:1−128.
Dubiner M. 1991. Spectral methods on triangles and other domains[J]. J Sci Comput,6:345–390. doi: 10.1007/BF01060030
Dumbser M,Käser M,Toro E F. 2007. An arbitrary high-order Discontinuous Galerkin method for elastic waves on unstructured meshes-V. Local time stepping and p-adaptivity[J]. Geophys J Int,171(2):695–717. doi: 10.1111/j.1365-246X.2007.03427.x
Dumbser M,Käser M. 2006. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes—II. The three-dimensional isotropic case[J]. Geophys J Int,167(1):319–336. doi: 10.1111/j.1365-246X.2006.03120.x
Evangelista L,Del Gaudio S,Smerzini C,d’Onofrio A,Festa G,Iervolino I,Landolfi L,Paolucci R,Santo A,Silvestri F. 2017. Physics-based seismic input for engineering applications:a case study in the Aterno river valley,Central Italy[J]. B Earthq Eng,15:2645–2671. doi: 10.1007/s10518-017-0089-7
Faccioli E,Maggio F,Paolucci R,Quarteroni A. 1997. 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method[J]. J Seismol,1:237–251. doi: 10.1023/A:1009758820546
Faccioli E,Quarteroni A. 1999. Comment on “The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures,” by D. Komatitsch and J. -P. Vilotte[J]. B Seismol Soc Am, 89 (1):331−331.
Feng K W,Huang D R,Wang G,Jin F,Chen Z W. 2022. Physics-based large-deformation analysis of coseismic landslides:A multiscale 3D SEM-MPM framework with application to the Hongshiyan landslide[J]. Eng Geol,297:106487. doi: 10.1016/j.enggeo.2021.106487
Fichtner A,Simutė S. 2018. Hamiltonian Monte Carlo inversion of seismic sources in complex media[J]. J Geophys Res-Sol Ea,123(4):2984–2999. doi: 10.1002/2017JB015249
French S W,Romanowicz B A. 2014. Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography[J]. Geophys J Int,199(3):1303–1327. doi: 10.1093/gji/ggu334
Fu J S,Ba Z N,Wang F B. 2024. A simulation approach for site-city interaction in basin under oblique incident waves and its applications[J]. Soil Dyn Earthq Eng,177:108407. doi: 10.1016/j.soildyn.2023.108407
Gatti F,Touhami S,Lopez-Caballero F,Paolucci R,Clouteau D,Fernandes V A,Kham M,Voldoire F. 2018. Broad-band 3-D earthquake simulation at nuclear site by an all-embracing source-to-structure approach[J]. Soil Dyn Earthq Eng,115:263–280. doi: 10.1016/j.soildyn.2018.08.028
Geng Y H,Qin G L,Wang Y,He W. 2016. The research of space-time coupled spectral element method for acoustic wave equations[J]. Chinese Journal of Acoustics,35(1):29–47.
Giraldo F X,Taylor M A. 2006. A diagonal-mass-matrix triangular-spectral-element method based on cubature points[J]. J Eng Math,56:307–322.
Gopalakrishnan S,Chakraborty A,Mahapatra D R. 2008. Spectral Finite Element Method:Wave Propagation,Diagnostics and Control in Anisotropic and Inhomogeneous Structures[M]. London:Springer-Verlag:1−22.
Gottlieb D,Orszag S A. 1977. Numerical Analysis of Spectral Methods:Theory and Applications[M]. Philadelphia:Society for Industrial and Applied Mathematics:1−167.
Grasso S,Maugeri M. 2014. Seismic microzonation studies for the city of Ragusa (Italy)[J]. Soil Dyn Earthq Eng,56:86–97. doi: 10.1016/j.soildyn.2013.10.004
Graves R,Jordan T H,Callaghan S,Deelman E,Field E,Juve G,Kesselman C,Maechling P,Mehta G,Milner K,Okaya D,Small P,Vahi K. 2011. CyberShake:A physics-based seismic hazard model for southern California[J]. Pure Appl Geophys,168:367–381. doi: 10.1007/s00024-010-0161-6
Graves R,Pitarka A. 2015. Refinements to the Graves and Pitarka (2010) broadband ground‐motion simulation method[J]. Seismol Res Lett,86(1):75–80. doi: 10.1785/0220140101
Han L,Wang J X,Li H J,Sun G J. 2020. A time-domain spectral element method with C1 continuity for static and dynamic analysis of frame structures[J]. Structures,28:604–613. doi: 10.1016/j.istruc.2020.08.074
He C H,Wang J T,Zhang C H,Jin F. 2015. Simulation of broadband seismic ground motions at dam canyons by using a deterministic numerical approach[J]. Soil Dyn Earthq Eng,76:136–144. doi: 10.1016/j.soildyn.2014.12.004
He C H,Wang J T,Zhang C H. 2016. Nonlinear spectral‐element method for 3D seismic‐wave propagation[J]. B Seismol Soc Am,106(3):1074–1087. doi: 10.1785/0120150341
Hermann V,Käser M,Castro C E. 2011. Non-conforming hybrid meshes for efficient 2-D wave propagation using the discontinuous Galerkin method[J]. Geophys J Int,184(2):746–758. doi: 10.1111/j.1365-246X.2010.04858.x
Ho L W,Patera A T. 1990. A Legendre spectral element method for simulation of unsteady incompressible viscous free-surface flows[J]. Comput Method Appl M,80:355–366. doi: 10.1016/0045-7825(90)90040-S
Huang D R,Wang G,Du C Y,Jin F,Feng K W,Chen Z W. 2020. An integrated SEM-Newmark model for physics-based regional coseismic landslide assessment[J]. Soil Dyn Earthq Eng,132:106066. doi: 10.1016/j.soildyn.2020.106066
Huang D R,Wang G,Du C Y,Jin F. 2021. Seismic amplification of soil ground with spatially varying shear wave velocity using 2D spectral element method[J]. J Earthq Eng,25(14):2834–2849. doi: 10.1080/13632469.2019.1654946
Infantino M,Mazzieri I,Özcebe A G,Paolucci R,Stupazzini M. 2020. 3D physics‐based numerical simulations of ground motion in Istanbul from earthquakes along the Marmara segment of the north Anatolian fault[J]. B Seismol Soc Am,110(5):2559–2576. doi: 10.1785/0120190235
Infantino M,Smerzini C,Lin J. 2021. Spatial correlation of broadband ground motions from physics‐based numerical simulations[J]. Earthq Eng Struct D,50(10):2575–2594. doi: 10.1002/eqe.3461
Karaoğlu H,Romanowicz B. 2018. Inferring global upper-mantle shear attenuation structure by waveform tomography using the spectral element method[J]. Geophys J Int,213(3):1536–1558. doi: 10.1093/gji/ggy030
Karniadakis G,Sherwin S J. 2005. Spectral/hp Element Methods for Computational Fluid Dynamics[M]. New York:Oxford University Press:1−652.
Käser M,Dumbser M,Puente J,Igel H. 2007. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes—III. Viscoelastic attenuation[J]. Geophys J Int,168(1):224–242. doi: 10.1111/j.1365-246X.2006.03193.x
Käser M,Dumbser M. 2006. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes—I. The two-dimensional isotropic case with external source terms[J]. Geophys J Int,166(2):855–877. doi: 10.1111/j.1365-246X.2006.03051.x
Käser M,Dumbser M. 2008. A highly accurate discontinuous Galerkin method for complex interfaces between solids and moving fluids[J]. Geophysics,73(3):T23–T35. doi: 10.1190/1.2870081
Käser M,Hermann V,Puente J. 2008. Quantitative accuracy analysis of the discontinuous Galerkin method for seismic wave propagation[J]. Geophys J Int,173(3):990–999. doi: 10.1111/j.1365-246X.2008.03781.x
Kato B,Wang G. 2021. Regional seismic responses of shallow basins incorporating site‐city interaction analyses on high‐rise building clusters[J]. Earthq Eng Struct D,50(1):214–236. doi: 10.1002/eqe.3363
Kato B,Wang G. 2022. Seismic site–city interaction analysis of super-tall buildings surrounding an underground station:A case study in Hong Kong[J]. B Earthq Eng,20(3):1431–1454. doi: 10.1007/s10518-021-01295-7
Komatitsch D,Barnes C,Tromp J. 2000a. Wave propagation near a fluid-solid interface:A spectral-element approach[J]. Geophysics,65(2):623–631. doi: 10.1190/1.1444758
Komatitsch D,Barnes C,Tromp J. 2000b. Simulation of anisotropic wave propagation based upon a spectral element method[J]. Geophysics,65(4):1251–1260. doi: 10.1190/1.1444816
Komatitsch D,Erlebacher G,Göddeke D,Michéa D. 2010. High-order finite-element seismic wave propagation modeling with MPI on a large GPU cluster[J]. J Comput Phys,229(20):7692–7714.
Komatitsch D,Liu Q,Tromp J,Süss P,Stidham C,Shaw J H. 2004. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method[J]. B Seismol Soc Am,94(1):187–206.
Komatitsch D,Martin R,Tromp J,Taylor M A,Wingate B A. 2001. Wave propagation in 2-D elastic media using a spectral element method with triangles and quadrangles[J]. J Comput Acoust,9(2):703–718.
Komatitsch D,Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics,72(5):SM155–SM167. doi: 10.1190/1.2757586
Komatitsch D,Ritsema J,Tromp J. 2002. The spectral-element method,Beowulf computing,and global seismology[J]. Science,298(5599):1737–1742. doi: 10.1126/science.1076024
Komatitsch D,Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation[J]. Geophys J Int,139(3):806–822. doi: 10.1046/j.1365-246x.1999.00967.x
Komatitsch D,Tromp J. 2002a. Spectral-element simulations of global seismic wave propagation—I. Validation[J]. Geophys J Int,149(2):390–412. doi: 10.1046/j.1365-246X.2002.01653.x
Komatitsch D,Tromp J. 2002b. Spectral-element simulations of global seismic wave propagation—II. Three-dimensional models,oceans,rotation and self-gravitation[J]. Geophys J Int,150(1):303–318. doi: 10.1046/j.1365-246X.2002.01716.x
Komatitsch D,Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation[J]. Geophys J Int,154(1):146–153. doi: 10.1046/j.1365-246X.2003.01950.x
Komatitsch D,Vilotte J P,Vai R,Castillo-Covarrubias J M,Sánchez-Sesma F J. 1999. The spectral element method for elastic wave equations — Application to 2‐D and 3‐D seismic problems[J]. Int J Numer Meth Eng,45(9):1139–1164. doi: 10.1002/(SICI)1097-0207(19990730)45:9<1139::AID-NME617>3.0.CO;2-T
Komatitsch D,Vilotte J P. 1998. The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures[J]. B Seismol Soc Am,88(2):368–392. doi: 10.1785/BSSA0880020368
Komatitsch D,Vilotte J P. 1999. Reply to comment by E. Faccioli and A. Quarteroni on “The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures,” by D. Komatitsch and J. -P. Vilotte[J]. B Seismol Soc Am, 89 (1):332−334.
Krishnan S,Ji C,Komatitsch D,Tromp J. 2006. Performance of two 18-story steel moment-frame buildings in southern California during two large simulated San Andreas earthquakes[J]. Earthq Spectra,22(4):1035–1061. doi: 10.1193/1.2360698
Laurenzano G,Priolo E,Tondi E. 2008. 2D numerical simulations of earthquake ground motion:examples from the Marche Region,Italy[J]. J Seismol,12:395–412. doi: 10.1007/s10950-008-9095-1
Laurenzano G,Priolo E. 2005. Numerical modeling of the 13 December 1990 M 5.8 east Sicily earthquake at the Catania accelerometric station[J]. B Seismol Soc Am,95(1):241–251. doi: 10.1785/0120030126
Lee S J,Chen H W,Liu Q,Komatitsch D,Huang B S,Tromp J. 2008. Three-dimensional simulations of seismic-wave propagation in the Taipei basin with realistic topography based upon the spectral-element method[J]. B Seismol Soc Am,98(1):253–264. doi: 10.1785/0120070033
Lee S J,Komatitsch D,Huang B S,Tromp J. 2009. Effects of topography on seismic-wave propagation:An example from northern Taiwan[J]. B Seismol Soc Am,99(1):314–325. doi: 10.1785/0120080020
Lee U. 2009. Spectral Element Method in Structural Dynamics[M]. Singapore:John Wiley & Sons (Asia) Pte Ltd:1−448.
Liang J W,Wu M T,Ba Z N,Liu Y. 2021. A hybrid method for modeling broadband seismic wave propagation in 3D localized regions to incident P,SV,and SH waves[J]. Int J Appl Mech,13(10):2150119. doi: 10.1142/S1758825121501192
Liu Q F,Yu Y Y,Yin D Y,Zhang X B. 2018. Simulations of strong motion in the Weihe basin during the Wenchuan earthquake by spectral element method[J]. Geophys J Int,215(2):978–995. doi: 10.1093/gji/ggy320
Liu Q F,Yu Y Y,Zhang X B. 2015. Three-dimensional simulations of strong ground motion in the Shidian basin based upon the spectral-element method[J]. Earthq Eng Eng Vib,14(3):385–398. doi: 10.1007/s11803-015-0031-4
Liu Q Y,Gu Y J. 2012. Seismic imaging:From classical to adjoint tomography[J]. Tectonophysics,566:31–66.
Liu Q Y,Polet J,Komatitsch D,Tromp J. 2004. Spectral-element moment tensor inversions for earthquakes in southern California[J]. B Seismol Soc Am,94(5):1748–1761. doi: 10.1785/012004038
Liu Q Y,Tromp J. 2006. Finite-frequency kernels based on adjoint methods[J]. B Seismol Soc Am,96(6):2383–2397. doi: 10.1785/0120060041
Liu Q Y,Tromp J. 2008. Finite-frequency sensitivity kernels for global seismic wave propagation based upon adjoint methods[J]. Geophys J Int,174(1):265–286. doi: 10.1111/j.1365-246X.2008.03798.x
Liu S L,Yang D H,Dong X P,Liu Q C,Zheng Y C. 2017. Element-by-element parallel spectral-element methods for 3-D teleseismic wave modeling[J]. Solid Earth,8(5):969–986. doi: 10.5194/se-8-969-2017
Liu T,Sen M K,Hu T Y,De Basabe J D,Li L. 2012. Dispersion analysis of the spectral element method using a triangular mesh[J]. Wave Motion,49:474–483. doi: 10.1016/j.wavemoti.2012.01.003
Liu Y S,Teng J W,Lan H Q,Si X,Ma X Y. 2014. A comparative study of finite element and spectral element methods in seismic wavefield modeling[J]. Geophysics,79(2):T91–T104. doi: 10.1190/geo2013-0018.1
Liu Y S,Teng J W,Xu T,Badal J. 2017. Higher-order triangular spectral element method with optimized cubature points for seismic wavefield modeling[J]. J Comput Phys,336:458–480. doi: 10.1016/j.jcp.2017.01.069
Lloyd A J,Wiens D A,Zhu H,Tromop J,Nyblade A A,Aster R C,Hansen S E,Dalziel I W D,Wilson T J,Ivins E R,O’Donnell J P. 2020. Seismic structure of the Antarctic upper mantle imaged with adjoint tomography[J]. J Geophys Res-Sol Ea, 125 (3).
Lu X Z,Tian Y,Wang G,Huang D R. 2018. A numerical coupling scheme for nonlinear time history analysis of buildings on a regional scale considering site‐city interaction effects[J]. Earthq Eng Struct D,47(13):2708–2725. doi: 10.1002/eqe.3108
Ma H. 1993. A spectral element basin model for the shallow water equations[J]. J Comput Phys,109:133–149. doi: 10.1006/jcph.1993.1205
Magnoni F,Casarotti E,Komatitsch D,Stefano R D,Ciaccio M G,Tape C,Melini D,Michelini A,Piersanti A,Tromp J. 2022. Adjoint tomography of the Italian lithosphere[J]. Commun Earth Environ,3(1):69. doi: 10.1038/s43247-022-00397-7
Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics,49(5):533–549. doi: 10.1190/1.1441689
Martin R,Komatitsch D,Gedney S D,Bruthiaux E. 2010. A high-order time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using Auxiliary Differential Equations (ADE-PML)[J]. CMES-Comp Model Eng,56(1):17–40.
Martin R,Komatitsch D,Gedney S D. 2008. A variational formulation of a stabilized unsplit convolutional perfectly matched layer for the isotropic or anisotropic seismic wave equation[J]. CMES-Comp Model Eng,37(3):274–304.
Mazzieri I,Stupazzini M,Guidotti R,Smerzini C. 2013. SPEED:SPectral Elements in Elastodynamics with Discontinuous Galerkin:A non‐conforming approach for 3D multi‐scale problems[J]. Int J Numer Meth Eng,95(12):991–1010. doi: 10.1002/nme.4532
Michéa D,Komatitsch D. 2010. Accelerating a three-dimensional finite-difference wave propagation code using GPU graphics cards[J]. Geophys J Int,182(1):389–402.
Moczo P,Kristek J,Halada L. 2000. 3D fourth-order staggered-grid finite-difference schemes:Stability and grid dispersion[J]. B Seismol Soc Am,90(3):587–603. doi: 10.1785/0119990119
Morency C,Tromp J. 2008. Spectral-element simulations of wave propagation in porous media[J]. Geophys J Int,175(1):301–345. doi: 10.1111/j.1365-246X.2008.03907.x
Mulder W A,Zhebel E,Minisini S. 2014. Time-stepping stability of continuous and discontinuous finite-element methods for 3-D wave propagation[J]. Geophys J Int,196(2):1123–1133. doi: 10.1093/gji/ggt446
Mulder W A. 1999. Spurious modes in finite-element discretizations of the wave equation may not be all that bad[J]. Appl Numer Math,30(4):425–445. doi: 10.1016/S0168-9274(98)00078-6
Mulder W A. 2001. Higher-order mass-lumped finite elements for the wave equation[J]. J Comput Acoust,9(2):671–680. doi: 10.1142/S0218396X0100067X
Mulder W A. 2013. New triangular mass-lumped finite elements of degree six for wave propagation[J]. Prog Electromagn Res,141:671–692. doi: 10.2528/PIER13051308
Mullen R,Belytschko T. 1982. Dispersion analysis of finite element semidiscretizations of the two‐dimensional wave equation[J]. Int J Numer Meth Eng,18(1):11–29. doi: 10.1002/nme.1620180103
Oliveira S P,Seriani G. 2011. Effect of element distortion on the numerical dispersion of spectral element methods[J]. Commun Comput Phys,9(4):937–958. doi: 10.4208/cicp.071109.080710a
Ostachowicz W,Kudela P,Krawczuk M,Zak A. 2012. Guided Waves in Structures for SHM:The Time-Domain Spectral Element Method[M]. London:John Wiley & Sons:1−334.
Padovani E,Priolo E,Seriani G. 1994. Low and high order finite element method:experience in seismic modeling[J]. J Comput Acoust,2(4):371–422. doi: 10.1142/S0218396X94000233
Paolucci R,Evangelista L,Mazzieri I,Schiappapietra E. 2016. The 3D numerical simulation of near-source ground motion during the Marsica earthquake,central Italy,100 years later[J]. Soil Dyn Earthq Eng,91:39–52. doi: 10.1016/j.soildyn.2016.09.023
Paolucci R,Gatti F,Infantino M,Smerzini C,Özcebe A G,Stupazzini M. 2018. Broadband ground motions from 3D physics‐based numerical simulations using artificial neural networks[J]. B Seismol Soc Am,108(3A):1272–1286. doi: 10.1785/0120170293
Paolucci R,Mazzieri I,Smerzini C. 2015. Anatomy of strong ground motion:near-source records and three-dimensional physics-based numerical simulations of the MW6.0 2012 May 29 Po Plain earthquake,Italy[J]. Geophys J Int,203(3):2001–2020. doi: 10.1093/gji/ggv405
Paolucci R,Smerzini C,Vanini M. 2021. BB‐SPEEDset:A validated dataset of broadband near‐source earthquake ground motions from 3D physics‐based numerical simulations[J]. B Seismol Soc Am,111(5):2527–2545. doi: 10.1785/0120210089
Pasquetti R,Rapetti F. 2004. Spectral element methods on triangles and quadrilaterals:comparisons and applications[J]. J Comput Phys,198(1):349–362. doi: 10.1016/j.jcp.2004.01.010
Patera A T. 1984. A spectral element method for fluid dynamics:Laminar flow in a channel expansion[J]. J Comput Phys,54:468–488. doi: 10.1016/0021-9991(84)90128-1
Pelties C,Käser M,Hermann V,Castro C E. 2010. Regular versus irregular meshing for complicated models and their effect on synthetic seismograms[J]. Geophys J Int,183(2):1031–1051. doi: 10.1111/j.1365-246X.2010.04777.x
Pelties C,Puente J,Ampuero J P,Brietzke G B,Käser M. 2012. Three‐dimensional dynamic rupture simulation with a high‐order discontinuous Galerkin method on unstructured tetrahedral meshes[J]. J Geophys Res-Sol Ea,117:B02309.
Pilz M,Parolai S,Stupazzini M,Paolucci R,Zschau J. 2011. Modelling basin effects on earthquake ground motion in the Santiago de Chile basin by a spectral element code[J]. Geophys J Int,187(2):929–945. doi: 10.1111/j.1365-246X.2011.05183.x
Pozrikidis C. 2014. Introduction to Finite and Spectral Element Methods Using MATLAB[M]. 2nd ed. USA:University of Massachusetts,CRC Press:1−793.
Priolo E,Carcione J M,Seriani G. 1994. Numerical simulation of interface waves by high‐order spectral modeling techniques[J]. J Acoust Soc Am,95(2):681–693. doi: 10.1121/1.408428
Priolo E,Seriani G. 1991. A numerical investigation of Chebyshev SEM for acoustic wave propagation[C]//Proceedings of 13th World Congress on Computation and Applied Mathematics,Ireland:Trinity College Dublin:551−556.
Priolo E. 1999. 2-D spectral element simulations of destructive ground shaking in Catania (Italy)[J]. J Seismol,3:289–309. doi: 10.1023/A:1009838325266
Priolo E. 2001. Earthquake ground motion simulation through the 2-D spectral element method[J]. J Comput Acoust,9(4):1561–1581. doi: 10.1142/S0218396X01001522
Puente J,Ampuero J P,Käser M. 2009. Dynamic rupture modeling on unstructured meshes using a discontinuous Galerkin method[J]. J Geophys Res-Sol Ea,114:B10302.
Puente J,Dumbser M,Käser M,Igel H. 2008. Discontinuous Galerkin methods for wave propagation in poroelastic media[J]. Geophysics,73(5):T77–T97. doi: 10.1190/1.2965027
Puente J,Käser M,Dumbser M,Igel H. 2007. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes-IV. Anisotropy[J]. Geophys J Int,169(3):1210–1228. doi: 10.1111/j.1365-246X.2007.03381.x
Rønquist E M,Patera A T. 1987. A Legendre spectral element method for the Stefan problem[J]. Int J Numer Meth Eng,24(12):2273–2299.
Sawade L,Beller S,Lei W,Tromp J. 2022. Global centroid moment tensor solutions in a heterogeneous earth:the CMT3D catalogue[J]. Geophys J Int,231(3):1727–1738. doi: 10.1093/gji/ggac280
Schuberth B. 2003. The Spectral Element Method for Seismic Wave Propagation:Theory,Implementation and Comparison to Finite Difference Methods [D]. München:Ludwig Maximilians Universität:1−163.
Seriani G,Oliveira S P. 2007. Optimal blended spectral-element operators for acoustic wave modeling[J]. Geophysics,72(5):SM95–SM106. doi: 10.1190/1.2750715
Seriani G,Oliveira S P. 2008a. Dispersion analysis of spectral element methods for elastic wave propagation[J]. Wave Motion,45(6):729–744. doi: 10.1016/j.wavemoti.2007.11.007
Seriani G,Oliveira S P. 2008b. DFT modal analysis of spectral element methods for acoustic wave propagation[J]. J Comput Acoust,16(4):531–561. doi: 10.1142/S0218396X08003774
Seriani G,Priolo E,Carcione J,Padovani E,Geofisica O. 1992. High-order spectral element method for elastic wave modeling[C]// Seg Technical Program Expanded Abstracts 1992. Society of Exploration Geophysicists:1285−1288.
Seriani G,Priolo E. 1991. High-order spectral element method for acoustic wave modeling[C]//Expanded Abstracts of the Society of Exploration Geophysicists,61st International Meeting of the SEG,Houston,Texas:1561−1564.
Seriani G,Priolo E. 1994. Spectral element method for acoustic wave simulation in heterogeneous media[J]. Finite Elem Anal Des,16:337–348. doi: 10.1016/0168-874X(94)90076-0
Seriani G,Su C. 2012. Wave propagation modeling in highly heterogeneous media by a poly-grid Chebyshev spectral element method[J]. J Comput Acoust,20(2):1240004. doi: 10.1142/S0218396X12400048
Seriani G. 1997. A parallel spectral element method for acoustic wave modeling[J]. J Comput Acoust,5(1):53–69. doi: 10.1142/S0218396X97000058
Seriani G. 1998. 3-D large-scale wave propagation modeling by spectral element method on Cray T3E multiprocessor[J]. Comput Method Appl M,164:235–247. doi: 10.1016/S0045-7825(98)00057-7
Seriani G. 2004. Double-grid Chebyshev spectral elements for acoustic wave modeling[J]. Wave Motion,39(4):351–360. doi: 10.1016/j.wavemoti.2003.12.008
Sherwin S J,Karniadakis G E. 1995. A triangular spectral element method; applications to the incompressible Navier-Stokes equations[J]. Comput Method Appl M, 123 (1−4):189−229.
Smerzini C,Amendola C,Paolucci R,Bazrafshan A. 2024. Engineering validation of BB-SPEEDset,a data set of near-source physics-based simulated accelerograms[J]. Earthq Spectra,40(1):420–445. doi: 10.1177/87552930231206766
Smerzini C,Paolucci R,Stupazzini M. 2011. Comparison of 3D,2D and 1D numerical approaches to predict long period earthquake ground motion in the Gubbio plain,Central Italy[J]. B Earthq Eng,9:2007–2029. doi: 10.1007/s10518-011-9289-8
Smerzini C,Pitilakis K,Hashemi K. 2017. Evaluation of earthquake ground motion and site effects in the Thessaloniki urban area by 3D finite-fault numerical simulations[J]. B Earthq Eng,15:787–812. doi: 10.1007/s10518-016-9977-5
Smerzini C,Pitilakis K. 2018. Seismic risk assessment at urban scale from 3D physics-based numerical modeling:the case of Thessaloniki[J]. B Earthq Eng,16:2609–2631. doi: 10.1007/s10518-017-0287-3
Soto V,Sáez E,Magna-Verdugo C. 2020. Numerical modeling of 3D site-city effects including partially embedded buildings using spectral element methods. Application to the case of Viña del Mar city,Chile[J]. Eng Struct,223:111188. doi: 10.1016/j.engstruct.2020.111188
Stich D,Martín R,Morales J. 2010. Moment tensor inversion for Iberia–Maghreb earthquakes 2005–2008[J]. Tectonophysics,483:390–398. doi: 10.1016/j.tecto.2009.11.006
Stupazzini M,Infantino M,Allmann A,Paolucci R. 2020. Physics‐based probabilistic seismic hazard and loss assessment in large urban areas:A simplified application to Istanbul[J]. Earthq Eng Struct D,50(1):99–115.
Stupazzini M,Paolucci R,Igel H. 2009. Near-fault earthquake ground-motion simulation in the Grenoble valley by a high-performance spectral element code[J]. B Seismol Soc Am,99(1):286–301. doi: 10.1785/0120080274
Su C,Seriani G. 2023. Poly-grid spectral element modeling for wave propagation in complex elastic media[J]. J Theor Comput Acous,31(1):2350003. doi: 10.1142/S2591728523500032
Sun P G,Huang D R. 2023. Regional-scale assessment of earthquake-induced slope displacement considering uncertainties in subsurface soils and hydrogeological condition[J]. Soil Dyn Earthq Eng,164:107593. doi: 10.1016/j.soildyn.2022.107593
Tape C,Liu Q,Maggi A,Tromp J. 2009. Adjoint tomography of the southern California crust[J]. Science,325(5943):988–992. doi: 10.1126/science.1175298
Tape C,Liu Q,Maggi A,Tromp J. 2010. Seismic tomography of the southern California crust based on spectral-element and adjoint methods[J]. Geophys J Int,180(1):433–462. doi: 10.1111/j.1365-246X.2009.04429.x
Tape C,Liu Q,Tromp J. 2007. Finite‐frequency tomography using adjoint methods — Methodology and examples using membrane surface waves[J]. Geophys J Int,168(3):1105–1129. doi: 10.1111/j.1365-246X.2006.03191.x
Taylor M A,Wingate B A,Vincent R E. 2000. An algorithm for computing Fekete points in the triangle[J]. SIAM J Numer Anal,38(5):1707–1720. doi: 10.1137/S0036142998337247
Tian Y,Chen S Y,Liu S M,Lu X Z. 2023. Influence of tall buildings on city-scale seismic response analysis:A case study of Shanghai CBD[J]. Soil Dyn Earthq Eng,173:108063. doi: 10.1016/j.soildyn.2023.108063
Tian Y,Lu X Z,Huang D R,Wang T. 2022. SCI effects under complex terrains:Shaking table tests and numerical simulation[J]. J Earthq Eng,27(5):1237–1260.
Tian Y,Sun C J,Lu X Z,Huang Y L. 2020. Quantitative analysis of site-city interaction effects on regional seismic damage of buildings[J]. J Earthq Eng,26(8):4365–4385.
Trefethen L N. 2000. Spectral Methods in MATLAB[M]. Philadelphia:Society for Industrial and Applied Mathematics:1−160.
Tromp J,Komatitsch D,Liu Q. 2008. Spectral-element and adjoint methods in seismology[J]. Commun Comput Phys,3(1):1–32.
Tromp J,Tape C,Liu Q. 2005. Seismic tomography,adjoint methods,time reversal and banana-doughnut kernels[J]. Geophys J Int,160(1):195–216.
Virieux J. 1986. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method[J]. Geophysics,51(4):889–901. doi: 10.1190/1.1442147
Vosse van de F N,Minev P D. 1996. Spectral Element Methods :Theory and Applications[R]. EUT report. Netherlands:Eindhoven University of Technology:1−117.
Wang G,Du C Y,Huang D R,Jin F,Koo R C H,Kwan J S H. 2018. Parametric models for 3D topographic amplification of ground motions considering subsurface soils[J]. Soil Dyn Earthq Eng,115:41–54. doi: 10.1016/j.soildyn.2018.07.018
Wang J X,Li H J,Sun G J,Han L. 2022a. Free vibration analysis of rectangular thin plates with corner and inner cutouts using C1 Chebyshev spectral element method[J]. Thin Wall Struct,181:110031. doi: 10.1016/j.tws.2022.110031
Wang J X,Li H J,Xing H J. 2022b. A lumped mass Chebyshev spectral element method and its application to structural dynamic problems[J]. Earthq Eng Eng Vib,21(3):843–859. doi: 10.1007/s11803-022-2117-0
Wang X C,Wang J T,Zhang C H. 2022. A broadband kinematic source inversion method considering realistic Earth models and its application to the 1992 Landers earthquake[J]. J Geophys Res-Sol Ea,127(3):e2021JB023216. doi: 10.1029/2021JB023216
Wang X C,Wang J T,Zhang C H. 2023. Deterministic full-scenario analysis for maximum credible earthquake hazards[J]. Nat Commun,14(1):6600. doi: 10.1038/s41467-023-42410-3
Wang X C,Wang J T,Zhang L,He C H. 2021a. Broadband ground-motion simulations by coupling regional velocity structures with the geophysical information of specific sites[J]. Soil Dyn Earthq Eng,145:106695. doi: 10.1016/j.soildyn.2021.106695
Wang X C,Wang J T,Zhang L,Li S,Zhang C H. 2021b. A multidimension source model for generating broadband ground motions with deterministic 3D numerical simulations[J]. B Seismol Soc Am,111(2):989–1013. doi: 10.1785/0120200221
Wang X C,Wang J T. 2023. A physics‐based spectral matching (PBSM) method for generating fully site‐related ground motions[J]. Earthq Eng Struct D,52(9):2812–2829. doi: 10.1002/eqe.3897
Wu M T,Ba Z N,Liang J W. 2022. A procedure for 3D simulation of seismic wave propagation considering source‐path‐site effects:Theory,verification and application[J]. Earthq Eng Struct D,51(12):2925–2955. doi: 10.1002/eqe.3708
Xie Z N,Komatitsch D,Martin R,Matzen R. 2014. Improved forward wave propagation and adjoint-based sensitivity kernel calculations using a numerically stable finite-element PML[J]. Geophys J Int,198(3):1714–1747. doi: 10.1093/gji/ggu219
Xie Z N,Matzen R,Cristini P,Komatitsch D,Marin R. 2016. A perfectly matched layer for fluid-solid problems:Application to ocean-acoustics simulations with solid ocean bottoms[J]. J Acoust Soc Am,140(1):165–175. doi: 10.1121/1.4954736
Xie Z N,Zheng Y L,Cristini P,Zhang X B. 2023. Multi-axial unsplit frequency-shifted perfectly matched layer for displacement-based anisotropic wave simulation in infinite domain[J]. Earthq Eng Eng Vib,22(2):407–421. doi: 10.1007/s11803-023-2170-3
Xing H J,Li X J,Li H J,Liu A W. 2021a. Spectral-element formulation of multi-transmitting formula and its accuracy and stability in 1D and 2D seismic wave modeling[J]. Soil Dyn Earthq Eng,140:1–15.
Xing H J,Li X J,Li H J,Xie Z N,Chen S L,Zhou Z H. 2021b. The theory and new unified formulas of displacement-type local absorbing boundary conditions[J]. Bull Seismol Soc Am,111(2):801–824. doi: 10.1785/0120200155
Yu Y Y,Ding H P,Liu Q F. 2017. Three-dimensional simulations of strong ground motion in the Sichuan basin during the Wenchuan earthquake[J]. B Earthq Eng,15:4661–4679. doi: 10.1007/s10518-017-0154-2
Yu Y Y,Ding H P,Zhang X B. 2021. Simulations of ground motions under plane wave incidence in 2D complex site based on the spectral element method (SEM) and multi-transmitting formula (MTF):SH problem[J]. J Seismol,25:967–985. doi: 10.1007/s10950-021-09995-y
Yu Y Y,Ding H P,Zhang X B. 2024. Formulation and performance of multi-transmitting formula with spectral element method in 2D ground motion simulations under plane-wave incidence:SV wave problem[J]. J Earthq Eng,28(7):1837–1860. doi: 10.1080/13632469.2023.2268748
Zhang L,Wang J T,Xu Y J,He C H,Zhang C H. 2020. A procedure for 3D seismic simulation from rupture to structures by coupling SEM and FEM[J]. B Seismol Soc Am,110(3):1134–1148. doi: 10.1785/0120190289
Zhang M Z,Zhang L,Wang X C,Su W,Qiu Y X,Wang J T,Zhang C H. 2023. A framework for seismic response analysis of dams using numerical source‐to‐structure simulation[J]. Earthq Eng Struct D,52(3):593–608. doi: 10.1002/eqe.3774
Zhou H,Chen X F. 2010. A new technique to synthesize seismography with more flexibility:the Legendre spectral element method with overlapped elements[J]. Pure Appl Geophys,167:1365–1376. doi: 10.1007/s00024-010-0106-0
Zhou H,Jiang H. 2015. A new time-marching scheme that suppresses spurious oscillations in the dynamic rupture problem of the spectral element method:the weighted velocity Newmark scheme[J]. Geophys J Int,203(2):927–942. doi: 10.1093/gji/ggv341
Zhou H,Li J T,Chen X F. 2020. Establishment of a seismic topographic effect prediction model in the Lushan MS7.0 earthquake area[J]. Geophys J Int,221(1):273–288. doi: 10.1093/gji/ggaa003
Zhu C Y,Qin G L,Zhang J Z. 2011. Implicit Chebyshev spectral element method for acoustics wave equations[J]. Finite Elem Anal Des,47(2):184–194. doi: 10.1016/j.finel.2010.09.004
Zhu H J,Bozdağ E,Tromp J. 2015. Seismic structure of the European upper mantle based on adjoint tomography[J]. Geophys J Int,201(1):18–52. doi: 10.1093/gji/ggu492
Zhu H J,Komatitsch D,Tromp J. 2017. Radial anisotropy of the North American upper mantle based on adjoint tomography with USArray[J]. Geophys J Int,211(1):349–377. doi: 10.1093/gji/ggx305
Zienkiewicz O C,Taylor R L,Zhu J Z. 2013. The Finite Element Method:Its Basis and Fundamentals[M]. 7th ed. UK:Butterworth-Heinemann,Elsevier:257−460.




 下载:
下载: