Multiscale simulation analysis of seismic response of mountain tunnels considering near-fault pulses and topographic effects
-
摘要:
针对近断层山岭隧道地震响应，基于一种间接边界元-有限元耦合（IBEM-FEM）方法，实现了千米尺度复杂场地放大效应到厘米尺度隧道截面动态损伤的跨尺度高效分析和规律揭示。采用基于等效脉冲模型的合成方法获取具有不同脉冲特性的近断层地震动，验证了地震动合成方法和结构响应耦合模拟方法的有效性和准确性；开展精细化数值模拟研究，重点分析了近断层脉冲型地震动的速度脉冲特性和脉冲参数对地形效应下山岭隧道地震响应的影响规律。结果表明：隧道衬砌结构的损伤程度随着脉冲幅值的增加而增大，相比于方向性效应，滑冲效应对脉冲幅值的变化更为敏感，在斜入射和高幅值脉冲下会引发更严重的结构破坏；隧道结构的损伤程度随着脉冲周期的增加而减小，方向性效应对脉冲周期变化更为敏感；在脉冲斜入射条件下，隧道结构损伤程度随着脉冲个数增加而增大。
Abstract:Mountain tunnels in western China are mostly located in regions with high seismic intensity and complex geological and topographic conditions, where active faults are densely distributed. Many tunnels are constructed in near-fault strong earthquake zones. For example, in the ongoing construction of the Sichuan-Tibet Railway, tunnels account for as much as 70% of the total route, and 54 active faults are distributed along and near the alignment. Numerous seismic investigations have shown that near-fault ground motions have a significant destructive impact on tunnel structures. Notable cases include the 1999 Chi-Chi earthquake in Taiwan, the 2008 Wenchuan earthquake in Sichuan, the 2016 Kumamoto earthquake in Japan, and the 2022 Menyuan earthquake in Qinghai, all of which resulted in severe tunnel damage.
The long-period velocity pulses commonly present in near-fault ground motions are considered key factors contributing to structural damage. However, due to the limited availability of strong earthquake observation records, especially near engineered structures, near-fault pulse-type ground motion records remain scarce. As a result, many existing studies have relied on synthetic ground motion methods to generate seismic time histories for analysis. Currently, research on the seismic response of mountain tunnels under near-fault pulse-type ground motions remains limited, particularly concerning the mechanisms through which pulse characteristics influence tunnel seismic responses, which are still not well understood.
On the other hand, topographic amplification effects induced by mountain terrain also significantly affect tunnel seismic responses. Studies have shown that mountain topography can amplify peak ground velocity （PGV） due to multiple reflections of seismic waves on the surface, leading to localized wave focusing effects and significant spatial variability within the mountain. However, most existing studies on mountain tunnel seismic responses commonly adopt full-space or half-space site models, neglecting topographic effects. Additionally, variations in the incident wave angle can alter the propagation path and energy distribution of seismic waves, further increasing the spatial variability of seismic damage.
This study comprehensively considers the coupled effects of near-fault ground motion characteristics and topographic amplification and proposes a systematic research framework. First, artificial synthesis techniques are employed to generate near-fault pulse-type ground motions. The high-frequency components of two representative recorded ground motions serve as the basis, while the low-frequency components are fitted using an equivalent pulse model. By adjusting pulse parameters, ground motions with different spectral characteristics are synthesized. Second, based on an indirect boundary element method-finite element method（IBEM-FEM）coupled method, a cross-scale efficient analysis was achieved, bridging the amplification effects in kilometer-scale complex sites to the dynamic damage of tunnel cross-sections at the centimeter scale, thereby revealing underlying seismic response patterns. Finally, taking pulse amplitude, pulse period, and pulse number as key parameters, the influence of near-fault pulse-type ground motions with different incident angles on tunnel seismic responses is examined, revealing the damage and failure patterns of tunnel linings.
The results indicate that tunnel lining damage severity increases with pulse amplitude. Compared with directivity effects, fling-step effects are more sensitive to changes in pulse amplitude, and oblique incidence combined with high-amplitude pulses can cause more severe structural damage. Tunnel damage severity decreases as pulse period increases, with directivity effects being more sensitive to pulse period variations. Under oblique incidence conditions, tunnel structural damage severity increases with the number of pulses.
For seismic design of mountain tunnels in near-fault regions, the combined impact of near-fault pulse effects and topographic amplification should be carefully considered, and tunnel seismic strategies should be optimized. Firstly, the locations of seismic wave focusing and amplification within the mountain should be identified and avoided to reduce the adverse effects of localized seismic motion amplification on tunnel structures. Secondly, for high-amplitude pulse effects, it is recommended to strengthen the seismic design of tunnel linings, particularly in areas where fling-step effects are prominent, to mitigate the damage caused by extreme ground motions. Additionally, during the design process, the influence of seismic wave incidence angle should be fully considered, and reinforcement measures for tunnel linings should be implemented accordingly to enhance tunnel seismic performance under complex wave propagation conditions.
-
引言
随着我国交通强国战略的持续推进，隧道总里程已超4.5万千米（巩江峰等，2024），其中大量山岭隧道建于地震烈度高、地质和地形条件均较为复杂的地区。特别是我国西部地区的活动断层发育密集，隧道建设常位于近断层强震区，例如：在建的川藏铁路，隧道占比高达70%，沿线及邻区发育有54条活动断层（薛翊国等，2020）。传统观念认为，由于围岩的约束作用，地下隧道结构通常具有较好的抗震性能（Sharma，Judd，1991）。然而大量震害调查显示，近断层地震动对隧道结构具有显著破坏作用，例如：1999年台湾集集地震（Wang et al，2001）、2008年四川汶川地震（李天斌，2008）、2016年日本熊本地震（Zhang et al，2018）和2022年青海门源地震（张威等，2022）。
近断层地震动的长周期速度脉冲（Housner，Hudson，1957；陈笑宇等，2021；禹海涛等，2024）是导致结构震损的关键因素（刘英等，2024）。由于强震观测记录有限，特别是工程结构附近的近断层脉冲型地震记录较为匮乏，已有研究多采用合成方法获取分析所需地震动时程（Li et al，2017）；针对近断层脉冲型地震动作用下山岭隧道地震响应的研究成果则较少（Mei et al，2021），特别是脉冲特性对山岭隧道地震响应特征的影响机制尚不明晰。
此外，山体地形引起的地震动放大效应对隧道地震响应的影响同样显著（Liu et al，2019）。研究表明山体地形可导致地震动峰值速度放大，其物理本质是地震波传播过程中在山体表面发生多次反射，从而在山体内部出现局部聚焦效应和显著的空间变异性（Yuan，Men，1992；Dai et al，2019；Liu et al，2019）。然而，目前针对山岭隧道地震响应研究通常采用全空间或半空间场地模型，忽略了山体地形效应。此外，入射波角度的改变也会导致地震波传播路径和能量分布的变化，进而增加工程震害的空间差异性（杜修力等，2014）。
鉴于此，本文综合考虑近断层效应与山体地形放大效应的耦合作用，首先利用人工合成技术生成近断层脉冲型地震动，以两条代表性地震动的高频部分为基础，采用等效脉冲模型拟合低频分量，并通过调整脉冲参数来合成具有不同频谱特征的地震动。然后，基于所建立的间接边界元-有限元耦合方法（indirect boundary element method-finite element method coupled method，IBEM-FEM），考虑地形效应求解山岭隧道地震响应。最后，以脉冲幅值、脉冲周期和脉冲数量为典型参数，研究不同角度入射的近断层脉冲型地震动对山岭隧道地震响应的影响，揭示隧道衬砌结构的损伤破坏规律。以期为近断层山岭隧道抗震分析与设计提供有益参考和有效方法。
1. 计算模型
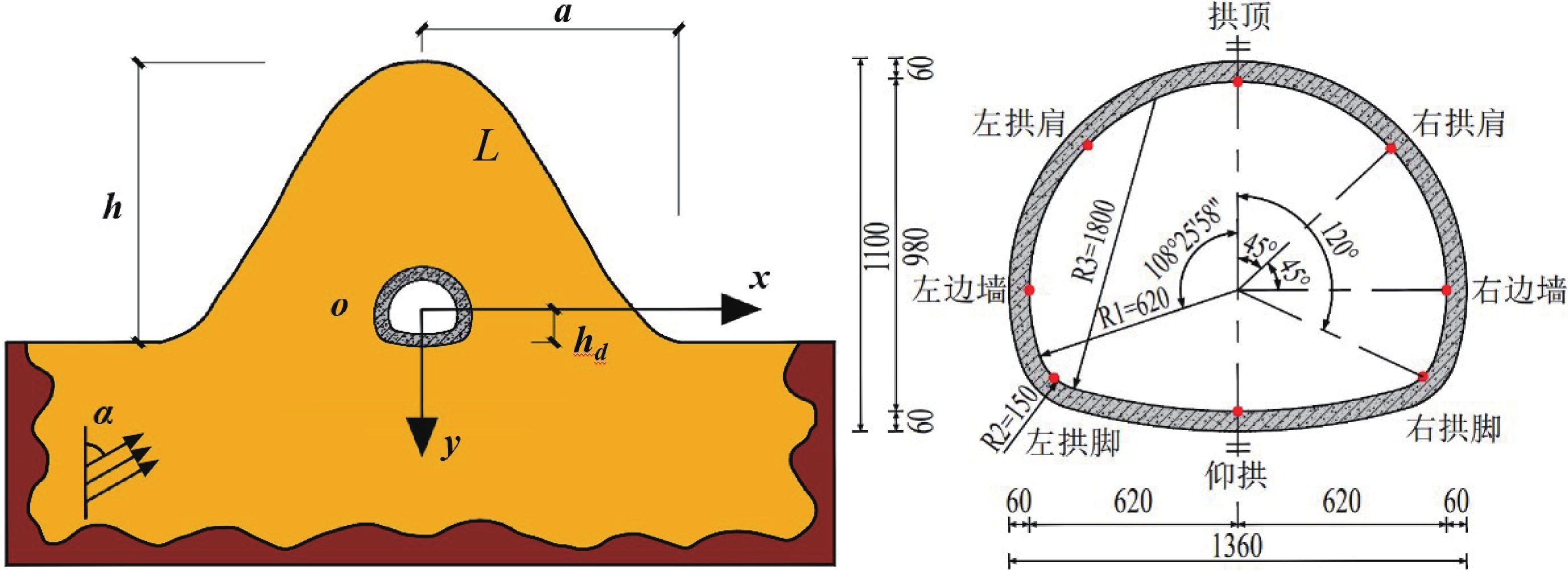
山岭隧道计算模型如图1所示。图1a中，山体半径为a＝200 m，高度h＝200 m。隧道中心与地面的距离为hd＝35 m。隧道横断面为马蹄形，几何形状和尺寸详见图1b。入射角α为平面波传播方向与数值模型y轴之间的夹角。
![]()
图 1 计算模型示意图（a） 数值模型；（b） 隧道模型详图 （单位：cm）Figure 1. Schematic diagram of calculation model（a） Numerical model；（b） Tunnel model detail （unit：cm）模型中围岩等级为Ⅳ级，采用摩尔-库伦（Mohr Coulomb，M-C）模型进行模拟。隧道衬砌结构采用C30混凝土，基于混凝土塑性损伤（concrete damaged plasticity model，CDP）模型考虑其本构关系。钢筋为双层环向布置，横截面积为490.6 mm2，采用双折线本构模型模拟。各材料物理力学特性列于表1。本文中，隧道衬砌结构与围岩之间不考虑土结构相对滑移，采用绑定约束（Corigliano et al，2011）。在进行山岭隧道结构地震反应分析前，首先对围岩施加重力并进行地应力平衡；然后采用收敛约束法模拟隧道开挖；为消除截断边界的反射效应，在截断边界处设置黏弹性人工边界。
表 1 各材料的本构模型和参数Table 1. The constitutive models and parameters of each material材料 本构模型 输入参数 围岩 M-C 密度ρ 弹性模量 E 泊松比 ζ 内摩擦角 φ 粘聚力c 2200 kg/m33 GPa 0.3 35° 1 MPa 混凝土衬砌 CDP 密度ρ 弹性模量 E 泊松比 ζ 抗压强度fc 抗拉强度ft 2500 kg/m330 GPa 0.2 21.20 MPa 2.43 MPa 钢筋 双折线本构 密度ρ 弹性模量 E 泊松比 ζ 抗压强度fc 抗拉强度ft 7850 kg/m3200 GPa 0.28 400 MPa 400 MPa 2. 计算方法及验证
2.1 IBEM-FEM耦合方法
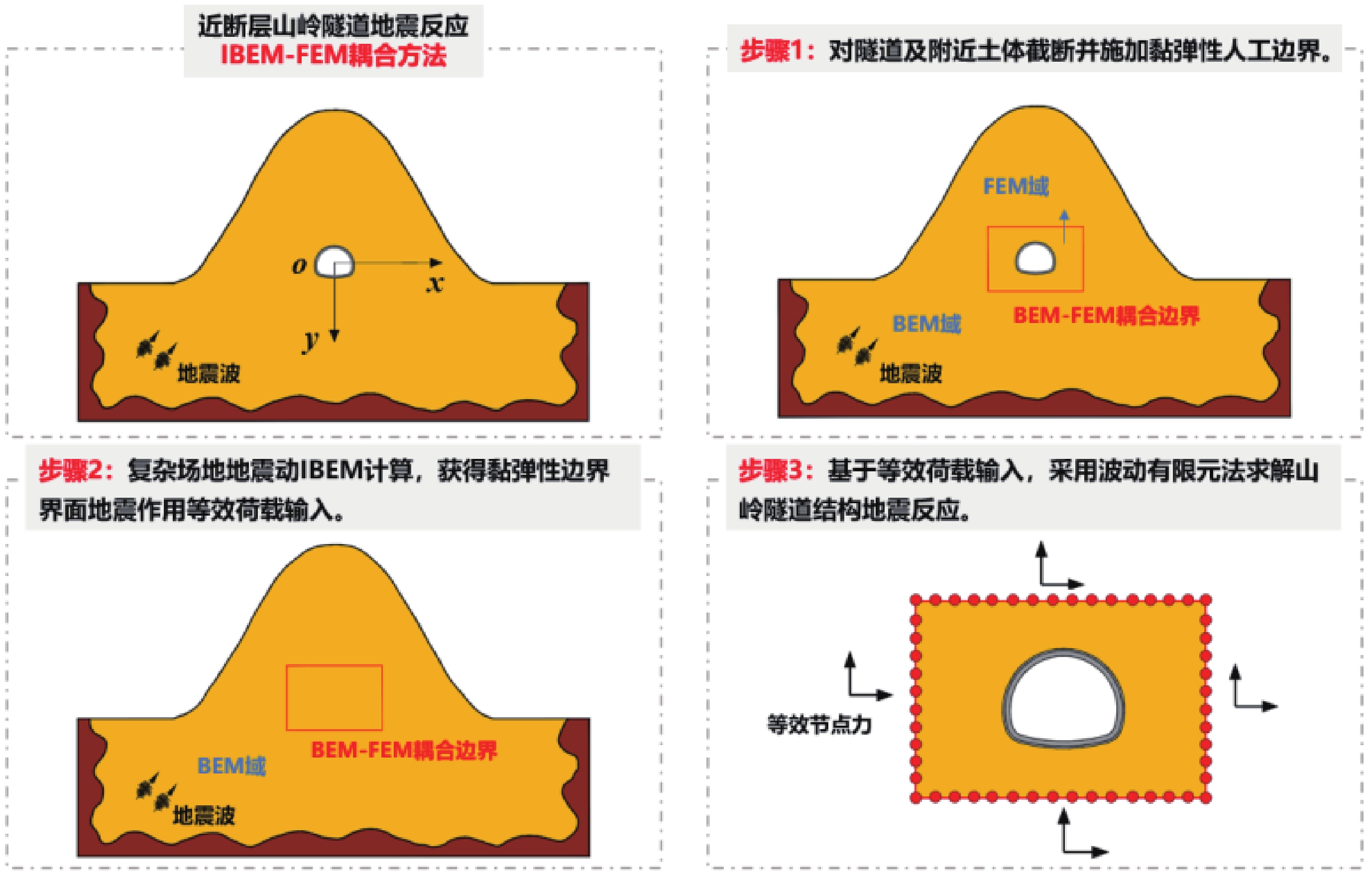
将IBEM-FEM耦合方法拓展到近断层山岭隧道地震响应模拟分析（图2）。IBEM作为一种半解析方法，其优势在于减少计算域维度，自动满足无限远边界条件，从而在保证高精度的同时显著减少计算资源，特别适合大规模地震波场的求解。相比之下，FEM需要对整个域进行网格划分并引入人工边界，处理大范围或无限域时计算成本较高，且可能因网格划分不足或人工边界问题导致精度下降。然而，FEM在复杂几何建模和局部非线性行为模拟中表现优异，因此广泛应用于工程领域。IBEM-FEM耦合方法结合了两者的优势，能高效解决大尺度复杂工程问题，避免FEM在处理大范围问题时的边界误差和计算资源浪费。对于本研究中考虑地形效应的近断层山岭隧道地震反应分析，IBEM用于精确模拟地震波在区域尺度山体内的传播（步骤1），FEM用于求解地震作用下隧道结构及临近围岩的非线性力学行为（步骤3），实现了千米级山体地形放大效应到厘米级隧道衬砌截面非线性损伤演化的跨尺度分析，显著降低了计算成本。在下一步的研究中，我们会把IBEM-FEM耦合方法扩展到三维，在处理大规模场地中复杂结构的三维问题时，其优势将更加突出，具有更广泛的应用前景。
IBEM利用满足波动方程的基本解间接构造地震波场并建立相关方程，实现近断层山体地震响应模拟。总位移矢量u应满足稳态弹性波动方程：
$$ （ \lambda ＋ \mu ） \nabla \nabla {\bf{u}} ＋ \mu {\nabla ^2}{\bf{u}}＝- \rho {\omega ^2}{\bf{u}} \text{，} $$ (1) 其中，λ和μ为Lame常数，ρ为质量密度，ω为圆频率，$ \nabla^{2} $为拉普拉斯算子。为简单起见，忽略时间因子exp （iωt）（i是虚数单位，i2＝−1）。总波场可表示为自由场和散射场的叠加，如下所示：
$$ {u_{\text{i}}}＝u_{\text{i}}^{\text{f}} ＋ u_{\text{i}}^{\text{s}} \text{，} $$ (2) 其中，i ＝1和2分别对应x方向和y方向。
散射波场通过在每个离散单元上施加虚拟均布载荷构建，直接体现了惠更斯原理。基于单层位势理论，离散单元的位移表达式可由Somigliana积分公式导出，如下所示：
$$ u_{\text{i}}^{\text{s}} （ X ） ＝\int_V {{G_{{\text{ij}}}}{ （ }X{{ \text{，} }}Y{ ） }{f_{\text{j}}}{ （ }Y ） {\text{d}}{V_Y}} ＋ \int_S {{G_{{\text{ij}}}} （ X \text{，} Y ） {\varphi _{\text{j}}}{ （ }Y ） {\text{d}}{S _Y}} \text{，} $$ (3) 类似地，牵引力可以通过胡克定律得出：
$$ \sigma _{\text{i}}^{\text{s}} （ X ） ＝\frac{1}{2}{\varphi _{\text{i}}} （ X ） ＋ \int_V {{T_{{\text{ij}}}} （ X \text{，} Y ） {f_{\text{j}}}{ （ }Y{\text{ ） d}}{V_Y}} ＋ \int_S {{T_{{\text{ij}}}} （ X \text{，} Y ） {\varphi _{\text{j}}}{ （ }Y{\text{ ） d}}{S _Y}} \text{，} $$ (4) 其中，i，j＝1，2分别对应x方向和y方向；V和S分别表示散射场域的体积和边界；fj（Y）是体力分量；φj（Y）是边界单元的虚拟均布载荷密度；Gij（X， Y）和Tij（X， Y）分别表示由点Y处j方向单位力引起的点X处i方向的位移和牵引力格林函数，具体表示为：
$$ {G_{{\text{ij}}}}＝\frac{1}{{{{\bf{i}}} 8\rho }} ［ {{\delta _{{\text{ij}}}}A - （ 2{\gamma _{\text{i}}}{\gamma _{\text{j}}} - {\delta _{{\text{ij}}}} ） B} ］ \text{，} $$ (5) $$ {T_{{\text{ij}}}}＝\frac{{{\text{i}}\mu }}{{2\rho r}}\left\{ {\left[ {B ＋ \frac{{\lambda D （ hr ） }}{{2\mu {c_{\text{s}}}^2}}} \right]{\gamma _{\text{j}}}{n_{\text{i}}} ＋ \left[ {B ＋ \frac{{D （ kr ） }}{{2{c_{\text{p}}}^2}}} \right] {\text{×}} \left[ {{\gamma _{\text{i}}}{n_{\text{j}}}{\text{ ＋ }}{\gamma _{\text{k}}}{n_{\text{k}}}{\delta _{{\text{ij}}}}} \right] ＋ （ C - 4B ） {\gamma _{\text{i}}}{\gamma _{\text{j}}}{\gamma _{\text{k}}}{n_{\text{k}}}} \right\} \text{，} $$ (6) 其中
$$ A＝\frac{{H_0^{ （ 2 ） } （ hr ） }}{{{c_{\text{s}}}^2}} ＋ \frac{{H_0^{ （ 2 ） } （ kr ） }}{{{c_{\text{p}}}^2}} \text{，} B＝\frac{{H_2^{ （ 2 ） } （ hr ） }}{{{c_{\text{s}}}^2}} - \frac{{H_2^{ （ 2 ） } （ kr ） }}{{{c_{\text{p}}}^2}} \text{，} C＝\frac{{D （ hr ） }}{{{c_{\text{s}}}^2}} - \frac{{D （ kr ） }}{{{c_{\text{p}}}^2}} \text{，} D （ p ） ＝pH_1^{ （ 2 ） } （ p ） \text{，} $$ (7) 其中，cs和cp分别为SV波速和P波速，由${c_{\text{s}}}＝\sqrt {\mu /\rho } $和${c_{\text{p}}}＝\sqrt { （ \lambda ＋ 2\mu ） /\rho } $定义；k和h分别为SV波数和P波数，由 k＝ω/cs 和h＝ω/cp定义；δij 是Delta函数；${\gamma _{\text{j}}}＝ （ {X_{\text{j}}} - {Y_{\text{j}}} ） /r$，$r＝\sqrt {{{ （ {X_{\text{i}}} - {Y_{\text{i}}} ） }^2} ＋ {{ （ {X_{\text{j}}} - {Y_{\text{j}}} ） }^2}} $；n是单位法向量；$ {H}_{\text{n}}^{ （ 2 ） } （ · ） $是n阶第二类Hankel函数。
根据方程（3）—（4），在无外力情况下，散射场引起的位移和牵引力的积分表达式如下：
$$ u_{\text{i}}^{\text{s}} （ X ） ＝\int_S {{G_{{\text{ij}}}} （ X \text{，} Y ） } {\varphi _{\text{j}}} （ Y ） {\text{d}}{S _Y}\text{，} $$ (8) $$ \sigma _{\text{i}}^{\text{s}} （ X ） ＝- 0.5{\varphi _{\text{i}}} （ X ） ＋ \int_S {{T_{{\text{ij}}}} （ X \text{，} Y ） } {\varphi _{\text{j}}} （ Y ） {\text{d}}{S _Y}\text{，} $$ (9) 计算模型的边界条件为自由表面L的牵引力为零：
$$ \sigma _{\text{i}}^{\text{f}} （ X ） ＋ \sigma _{\text{i}}^{\text{s}} （ X ） ＝0 \text{，} X \in L\text{，} $$ (10) 将方程（8）—（9）代入方程（10），将上述边界条件改写为以下积分形式：
$$ \sigma _{\text{i}}^{\text{f}} （ X ） - 0.5\varphi _{\text{i}}^{} （ X ） ＋ \int_S^{} {{T_{{\text{ij}}}} （ X \text{，} Y ） \varphi _{\text{j}}^{} （ Y ） {\text{d}}{S _Y}＝0 \text{，} X \in {L_{}}} \text{，} $$ (11) 此外，等式（11）可以转换成以下离散形式：
$$ - 0.5{\varphi _{\text{i}}} （ {X_m} ） ＋ \sum\limits_{n＝1}^N {{t_{{\text{ij}}}} （ {X_m} \text{，} {Y_n} ） {\varphi _{\text{j}}} （ {Y_n} ） ＝- \sigma _{\text{i}}^{\text{f}} （ {X_m} ） \text{，} \begin{array}{*{20}{c}} {}&{} \end{array}m \text{，} n＝1 \text{，} \cdots \text{，} N} \text{，} $$ (12) 其中，N表示边界L的离散单元数量；${t_{{\text{ij}}}} （ {X_m} \text{，} {Y_n} ） $表示如下：
$$ {t_{{\text{ij}}}} （ {X_m} \text{，} {Y_n} ） ＝\int_{\Delta S} {{T_{{\text{ij}}}} （ {X_m} \text{，} {Y_n} ） } {\text{d}}{S _Y} \text{，} $$ (13) 其中，ΔS表示离散单元的长度。
对于Xm≠Yn，可以通过等式（13）中的高斯积分直接计算tij（Xm，Yn）：
$$ {t_{{\text{ij}}}} （ {X_m} \text{，} {Y_n} ） ＝\int_{{Y_n} - \tfrac{{\Delta s}}{2}}^{{Y_n} ＋ \tfrac{{\Delta s}}{2}} {{T_{{\text{ij}}}} （ {X_m} \text{，} {Y_n} ） } {\text{d}}{S _Y} \text{，} $$ (14) 然而，当Xm＝Yn时，二者通过解析求解，以避免奇异性，具体描述如下：
$$ \;{t_{{\text{ij}}}} （ {X_m} \text{，} {Y_n} ） ＝\frac{1}{2}{\delta _{{\text{ij}}}} \text{，} $$ (15) 通过快速傅立叶逆变换，可以将上述频域响应结果转换为时域响应结果。对于隧道及其临近围岩的地震响应求解，需考虑截断边界处的位移、速度和牵引力。入射波运动可转换为模型边界节点的法向和切向的等效节点力。此外，通过黏弹性人工边界吸收向外传播的辐射波能量。具体实施步骤可参考文献（Liu et al，2024）。
2.2 方法验证
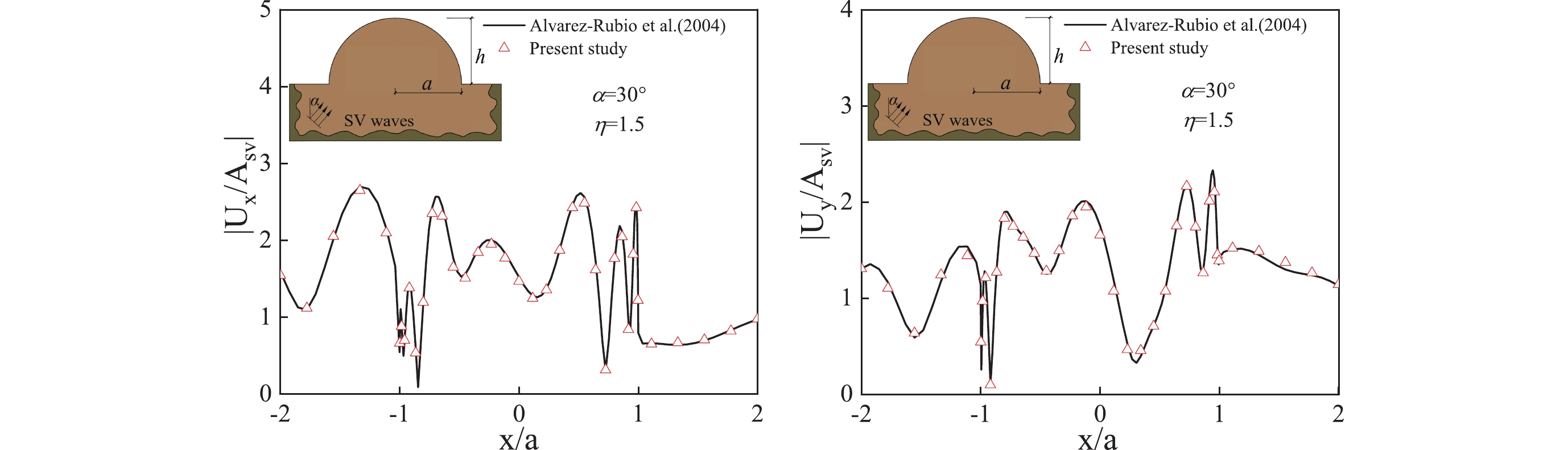
首先，采用IBEM求解SV波（α＝30°）入射下半椭圆山体地表的位移幅值，进而与Álvarez Rubio等人（Álvarez-Rubio et al，2004）基于DBEM（直接边界元法）的频域响应结果对比。参数设置为：阻尼比ξ＝0.01，泊松比ν＝0.25，山体高宽比h/a＝2.0 （h＝200 m），相应的无量纲频率为η＝1.5。如图3所示，两种方法所得山体地震响应具有良好的一致性。
![]()
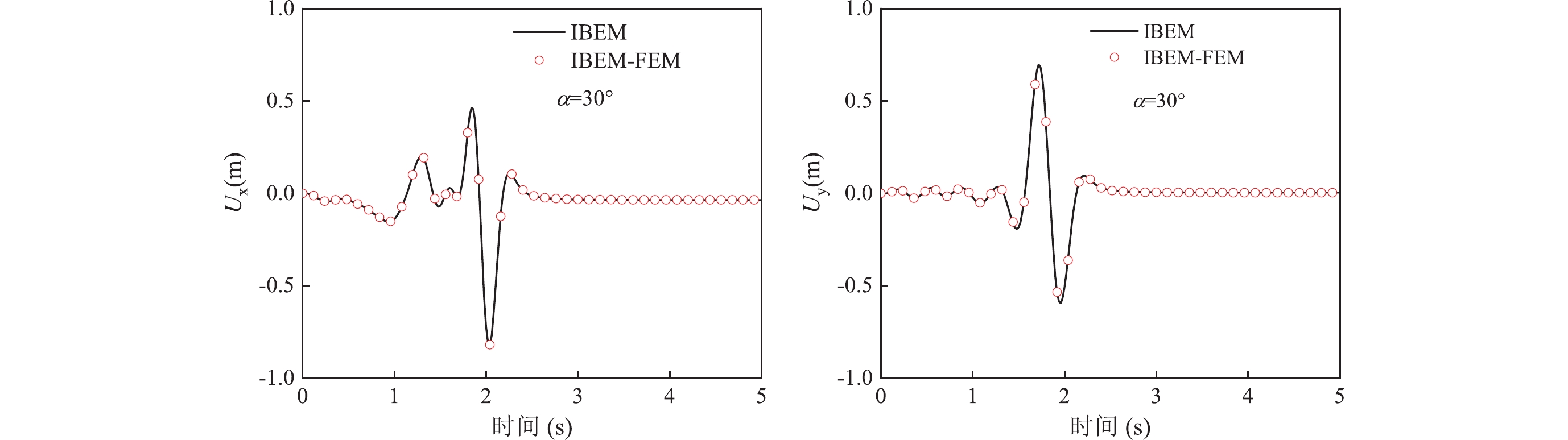
图 3 图3 IBEM与DBEM计算的斜入射SV波作用下（α=30°）山体地表位移响应对比（a） 水平位移；（b） 竖向位移Figure 3. Comparison of mountain displacement response under obliquely incident SV waves（α=30°）calculated by IBEM and DBEM（a） Horizontal displacement；（b） Vertical displacement进一步，通过对比IBEM-FEM耦合方法和IBEM计算的半圆形山体中隧道的动力响应结果，验证了IBEM-FEM耦合方法的有效性和准确性。半圆山的半径和高度均为200 m。有限元模型取50 m×50 m。隧道尺寸以及各材料的相关参数信息见第1节。设定入射波为振幅A＝1，主频f0＝5 Hz的Ricker小波，表达式为$ u （ t ） ＝{\text{ }}A （ 2{ （ \pi {f_0} （ t - {t_1} ） ） ^2} - 1 ） \exp { （ - \pi {f_0} （ t - {t_1} ） ） ^2} $。从图4可以看出，使用IBEM-FEM耦合方法计算的隧道拱顶位移时程与IBEM计算结果具有良好的一致性，表明了IBEM-FEM耦合方法的准确性。
![]()
图 4 IBEM与IBEM-FEM耦合法计算的斜入射SV波激励下（α＝30°）山岭隧道拱顶位移时程对比（a） 水平位移 ；（b） 竖向位移Figure 4. Comparison of arch displacement of mountain tunnel under oblique incident SV wave excitation （α＝30 °） calculated by IBEM and IBEM-FEM coupling method（a） Horizontal displacement；（b） Vertical displacement3. 近断层脉冲型地震动合成方法及有效性验证
3.1 近断层脉冲型地震动合成方法
目前，近断层地震记录，尤其是脉冲型地震动记录较为有限，可通过人工合成波来弥补这一不足。本文采用文献（Li et al，2017）提出的近断层脉冲型地震动合成方法。首先分解近断层地震记录以提取高频分量，再基于等效脉冲模型拟合低频分量，并将两者叠加以合成完整的地震动（以下简称合成波）。其优势在于，既保留了实测波的高频成分，又通过参数化的低频脉冲实现了更高的控制灵活性。通过调整脉冲参数，可生成符合不同抗震设计需求的地震动。
低频脉冲成分采用Mavroeidis和Papageorgiou （2003）提出的等效速度脉冲模型，该模型通过一组具有明确物理意义的参数来描述脉冲特性，包括脉冲振荡特性、脉冲幅值、脉冲周期和脉冲数量。其表达式如下：
$$ v （ t ） ＝\left\{ \begin{array}{*{20}{l}}A\dfrac{1}{2}\left[1 ＋ \mathrm{cos} \left( \dfrac{2\pi {f}_{\text{p}}}{\gamma } （ t-{t}_{0} ） \right) \right]\mathrm{cos} ［ 2\pi {f}_{\text{p}} （ t-{t}_{0} ） ＋ \varphi ］ \text{，} & {t}_{0}-\dfrac{\gamma }{2{f}_{\text{p}}} {\text{≤}} t {\text{≤}} {t}_{0} ＋ \dfrac{\gamma }{2{f}_{\text{p}}} \text{，} \gamma ＞ 1 \\ 0\text{，} & \text{otherwise} \end{array} \text{，}\right. $$ (16) 其中，A为速度脉冲峰值；fp为速度脉冲的卓越频率；t0为速度脉冲峰值对应时刻；γ为脉冲形状参数；φ为相位角。
3.2 基于时频特性分析的验证
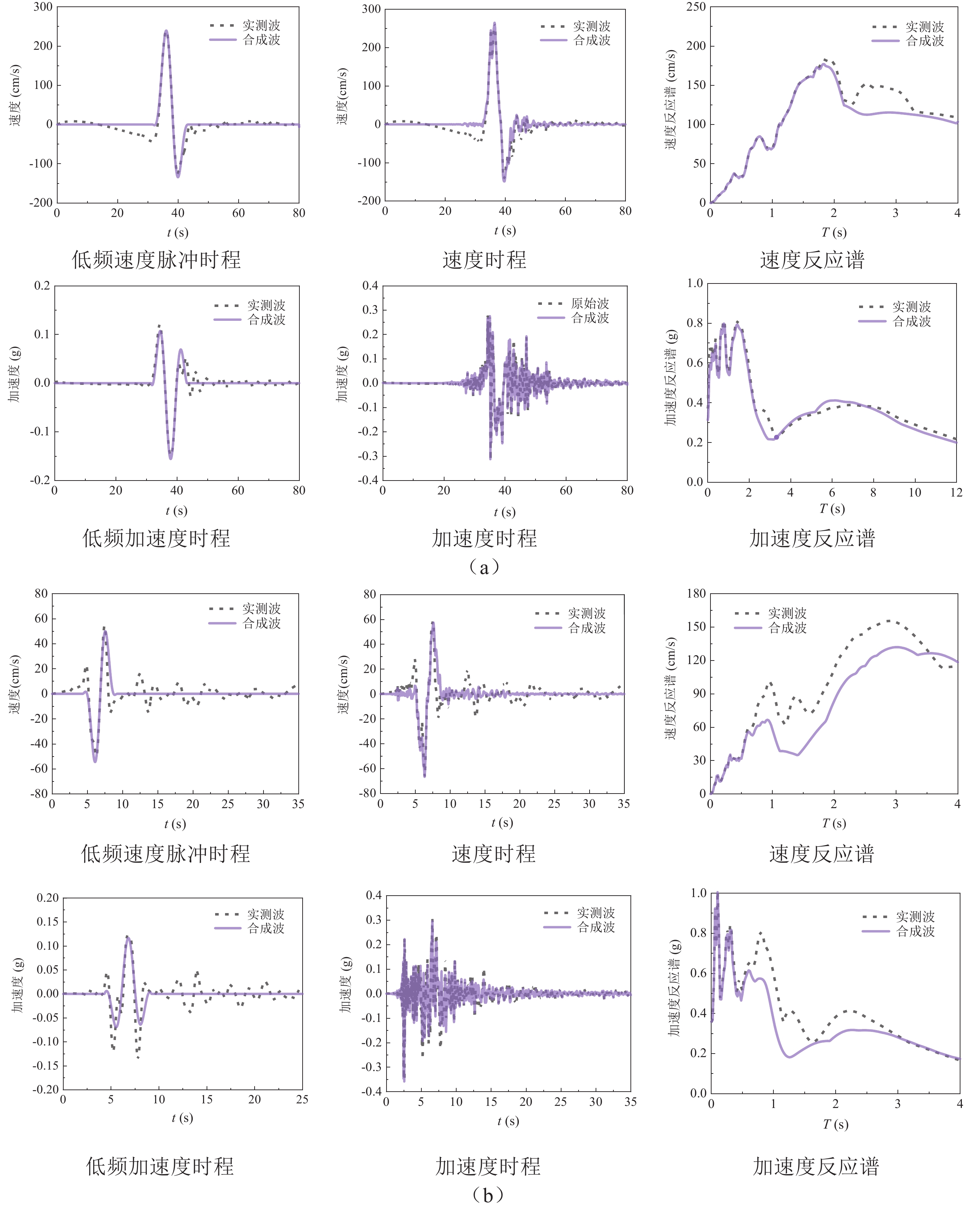
为了验证近断层脉冲型地震动合成的有效性，从太平洋地震工程研究中心数据库中选取了2条具有不同脉冲特性的近断层地震动记录，分别体现破裂向前方向性效应和滑冲效应，各地震动基本信息如表2所示，根据前文提到的参数确定方法获取了各信号脉冲参数（表3）。
表 2 近断层地震动基本信息Table 2. Basic information of near fault seismic ground motion近断层地震动类型 地震名称 台站 断层距/km 峰值速度/ （cm·s−1） Tp/s 向前方向性效应脉冲 帝王谷地震 El Centro Array #6 1.35 67.02 3.77 滑冲效应脉冲 集集地震 TCU-068 0.32 249.59 12.28 表 3 近断层地震动脉冲参数Table 3. Arterial parameters of near fault earthquakes近断层地震动类型 台站 A/（cm·s−1） Tp/s φ/（°） γ t0/s 向前方向性效应脉冲 El Centro Array #6 70 3.77 80 1.3 6.8 滑冲效应脉冲 TCU-068 289 11.50 -200 1.02 37.4 图5给出了台站TCU-068和台站El Centro Array #6的实测波和合成波时程与反应谱的结果比较。可以看出合成波与实测波的速度和加速度时程匹配良好，且速度和加速度反应谱的形状和大小高度相似。
![]()
图 5 合成波和实测波时程和反应谱的结果对比（a） TCU-068；（b） EI-Centro Array#6Figure 5. Comparison of synthetic wave and measured wave time history and response spectrum results3.3 基于山岭隧道地震响应的验证
为了进一步验证人工合成近断层脉冲型地震动在山岭隧道动力响应分析中的准确性，本小节开展了实测波与合成波作用下衬砌隧道结构的时程响应结果对比分析。表4—6分别列出了隧道各特征点的加速度、位移和应力峰值对比。结果显示，近断层合成波引起的隧道位移、加速度和应力响应与实测波结果较为接近。然而，由于在拟合低频脉冲波时，除主脉冲外剔除了其余较小的脉冲波，导致某些特征点存在一定的误差。总体而言，隧道在合成波和实测波下的动力响应具有较高的匹配度，可作为研究近场地震动脉冲特性的依据。
表 4 特征点加速度峰值Table 4. Peak acceleration of characteristic points特征点位置 实测地震动峰值加速度（m/s2） 合成地震动峰值加速度（m/s2） 误差（%） EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 拱顶 5.71 8.95 5.12 8.96 10.33 0.11 左拱肩 5.57 9.30 5.24 9.39 5.92 0.97 左边墙 5.08 8.83 4.64 8.95 8.66 1.36 左拱脚 5.33 8.21 4.97 8.86 6.75 7.91 仰拱 5.38 8.39 5.01 8.65 6.87 3.09 表 6 特征点Mises应力峰值Table 6. Mises stress peak values at characteristic points特征点位置 实测地震动Mises应力峰值（Mpa） 合成地震动Mises应力峰值（Mpa） 误差（%） EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 拱顶 7.91 10.64 7.42 10.42 6.19 2.07 左拱肩 21.47 22.17 19.42 22.3 9.55 0.58 左边墙 10.06 12.61 9.84 12.89 2.18 2.22 左拱脚 28.88 29.57 27.91 29.62 3.35 0.17 仰拱 3.61 5.09 3.54 4.63 1.94 9.03 表 5 特征点位移峰值Table 5. Peak displacement of characteristic points特征点位置 实测地震动峰值位移（m） 合成地震动峰值位移（m） 误差（%） EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 拱顶 0.862 13.4 0.831 13.15 3.59 3.59 左拱肩 0.86 13.41 0.829 13.14 3.6 3.6 左边墙 0.852 13.38 0.823 13.13 3.4 3.4 左拱脚 0.847 13.36 0.819 13.12 3.31 3.31 仰拱 0.844 13.34 0.818 13.12 3.08 3.08 4. 速度脉冲参数影响规律分析
为研究近断层脉冲参数对山岭隧道地震响应的影响，本节将脉冲幅值A、脉冲周期T、脉冲数量N （仅针对方向性效应脉冲）作为变量，分析这些参数对山岭隧道地震响应的影响规律。以各实测地震波的高频部分为基准，调整脉冲变量以合成具有不同频谱特征的脉冲型地震动。据统计，近断层脉冲周期多小于8 s，脉冲幅值基本不超过152 cm/s （徐略勤等，2024）。详细的工况设置如表7所示。
表 7 脉冲参数分析工况Table 7. Pulse parameter analysis working conditions地震波 脉冲幅值A/（cm/s） 脉冲周期T/s 脉冲数量N TCU-068 100 1、2、3、4、5 原地震动 EI-Centro Array#6 100 1、2、3、4、5 原地震动 TCU-068 50、100、150 3 原地震动 EI-Centro Array#6 50、100、150 3 原地震动 EI-Centro Array#6 100 3 2、3、4、5 本文除关注衬砌结构损伤分布外，进一步选择衬砌结构受拉损伤体积比来评估隧道地震响应，衬砌结构受拉损伤体积比R可作为整体损伤指标（Wu et al，2015），其具体表达式为：
$$ R＝\frac{{\int_V {{d_t}dv} }}{{\int_V {dv} }}\text{，} $$ (17) 其中，dt 为隧道衬砌结构受拉损伤因子；v为隧道衬砌损伤分布范围。
4.1 速度脉冲幅值的影响
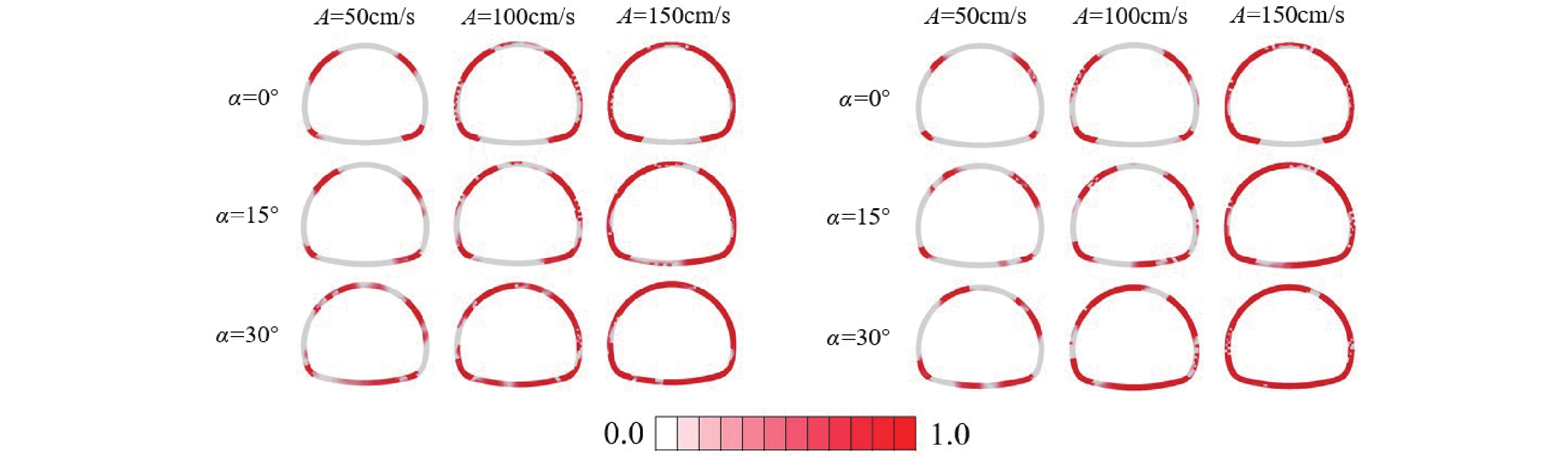
图6展示了相同脉冲周期、不同脉冲幅值和入射角度的近断层脉冲型地震动作用下山岭隧道衬砌结构的受拉损伤。由图6可知，入射角为0°时，山岭隧道衬砌结构损伤呈对称分布，主要集中在拱肩和拱脚。随着入射角增大，损伤面积增加，损伤区向拱腰、拱顶、仰拱不断扩展。一方面原因在于入射角度的增加改变了隧道衬砌结构内部应力分布，使得更多区域受到较大的拉应力作用，进而扩大了损伤范围；另一方面，较大的入射角可能使地震波传播路径更长，导致能量积累和放大效应更明显，进一步增加结构损伤。此外，对于相同的入射角度，隧道衬砌结构损伤区随着脉冲幅值的增加而增大。
![]()
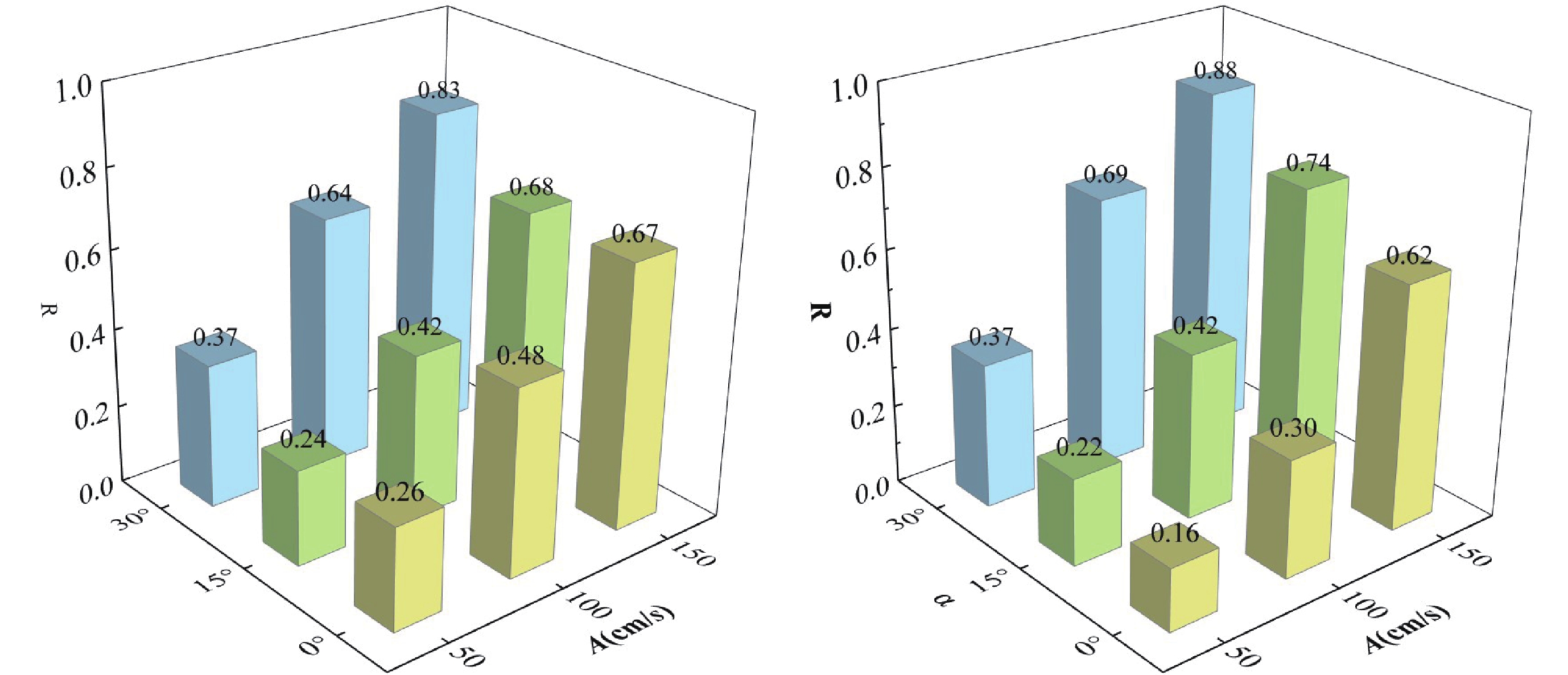
图 6 不同脉冲幅值下山岭隧道衬砌结构受拉损伤云图（a） 方向性效应脉冲；（b） 滑冲效应脉冲Figure 6. Cloud map of tensile damage to the lining structure of mountain tunnel with different pulse amplitudes（a） Directional effect pulse；（b） Sliding impulse effect pulse图7给出了不同脉冲幅值和入射角度的近断层脉冲型地震动作用下山岭隧道衬砌结构的受拉损伤体积比。从图7可以看出，对于不同脉冲特性的地震动，隧道衬砌结构在不同角度入射下的受拉损伤体积比均随入射波脉冲幅值的增加而增大。对于方向性效应脉冲型地震动，当脉冲幅值为50 cm/s时，损伤体积比从0°入射的0.26升至30°入射的0.37；脉冲幅值增至150 cm/s时，损伤体积比显著增加，在0°和30°入射时分别增加了157.69%和124.32%，显示出高幅值脉冲在大入射角下会显著加剧隧道结构的损伤。相比之下，滑冲效应脉冲型地震动在斜入射时会引发更严重的结构破坏，且该效应在高幅值下尤为突出，对脉冲幅值的变化更加敏感。例如，当脉冲幅值为50 cm/s时，损伤体积比从0°的0.16升至30°的0.37；当脉冲幅值增加为150 cm/s时，0°和30°入射的损伤体积比分别增加了287.50%和137.84%。
![]()
图 7 不同脉冲幅值下山岭隧道衬砌结构受拉损伤体积比（a） 方向性效应脉冲；（b） 滑冲效应脉冲Figure 7. Volume ratio of tensile damage to the lining structure of mountain tunnel under different pulse amplitudes（a） Directional effect pulse；（b） Sliding impulse effect pulse表8给出了不同幅值的两种脉冲型地震动垂直入射下隧道衬砌结构各特征点的最大位移。可以看出，各特征点的最大位移随脉冲幅值的增大而增大，其中仰拱的位移响应最大。此外，滑冲效应地震动引起的位移响应大于方向性效应。当A＝50 cm/s时，方向性效应脉冲引起的拱顶位移为0.539 m，而滑冲效应脉冲引起的位移为0.837 m，增加了55.29%。当A＝100 cm/s和150 cm/s时，后者分别比前者增加了55.21%和55.28%。
表 8 不同脉冲幅值下山岭隧道衬砌结构特征点水平位移（单位：m）Table 8. Horizontal displacement of characteristic points in the lining structure of mountain tunnel with different pulse amplitudes （unit：m）工况 方向性效应脉冲幅值 滑冲效应脉冲幅值 50 cm/s 100 cm/s 150 cm/s 50 cm/s 100 cm/s 150 cm/s 仰拱 0.527 1.049 1.567 0.822 1.639 2.450 左边墙 0.531 1.056 1.574 0.831 1.653 2.480 拱顶 0.539 1.074 1.611 0.837 1.667 2.500 右边墙 0.532 1.061 1.592 0.824 1.646 2.458 注：数据为监测点时程曲线最大绝对值。 4.2 速度脉冲周期的影响
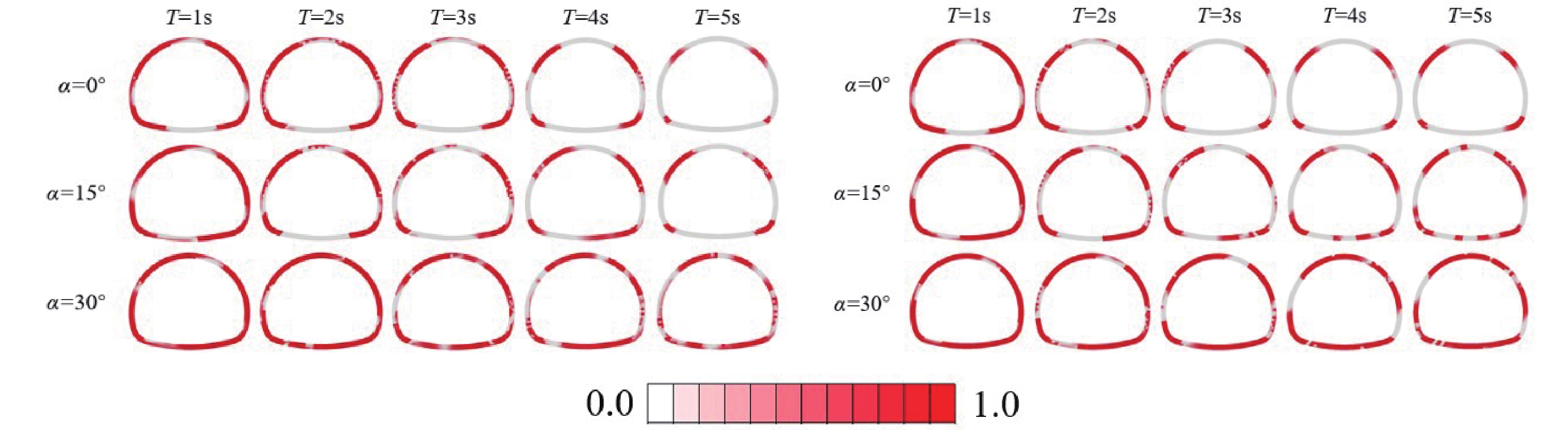
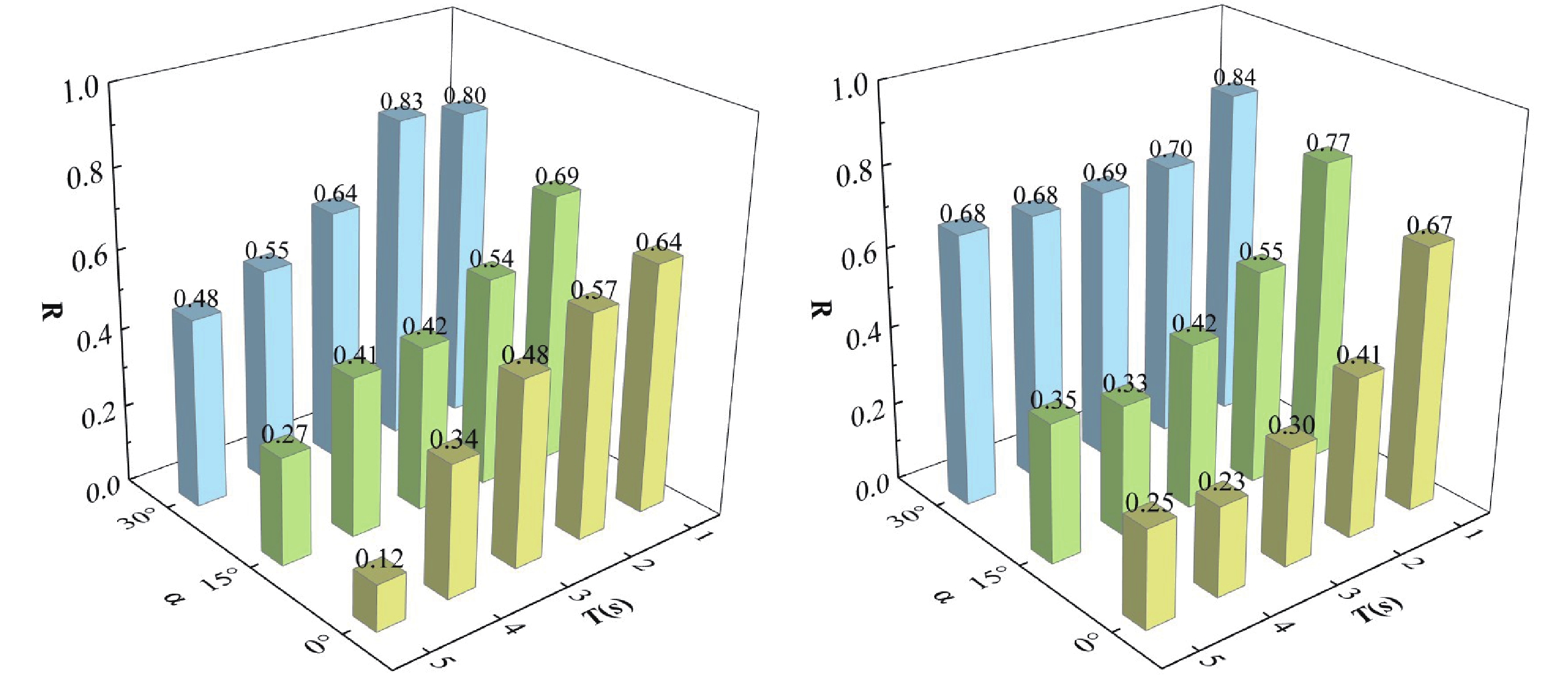
图8和图9分别展示了在相同脉冲幅值下，不同脉冲周期和入射角度的近断层脉冲型地震动对山岭隧道衬砌结构受拉损伤分布及损伤体积比的影响。总体来看，对于不同脉冲特性的地震动，隧道衬砌结构在不同角度入射下的受拉损伤体积比均随入射波脉冲周期的增加而减小。对于方向性效应脉冲型地震动，当脉冲周期为1 s时，随着入射角度从0°增至30°，损伤体积比从0.64升至0.80，损伤区显著扩展。当脉冲周期延长至5 s时，损伤体积比显著降低，0°和30°入射角下分别减少了81.25%和40%。这表明，较短脉冲周期和较大入射角度会加剧山岭隧道的损伤。通过模态分析，计算得到本算例场地的特征周期约为0.2 s，脉冲周期越短，越接近场地周期，对隧道的影响越显著。此外，在恒定PGV条件下，较短周期脉冲会导致更大的PGA，引发围岩更高的应变，增加衬砌结构损伤。同时，高频脉冲在短时间内对结构产生更强冲击效应，而较大入射角使隧道直接受波面积增大，能量分布更广，应力状态更复杂，从而进一步扩大损伤区域。相比之下，滑冲效应脉冲型地震动作用下的损伤体积比普遍高于方向性效应。当周期为1 s时，损伤体积比从0°的0.67增至30°的0.84；周期为5 s时，损伤体积比从0°的0.25升至30°的0.68，分别降低了62.69%和19.05%。可以看出，在较大的入射角度和较短的脉冲周期下，滑冲效应引发的损伤更为严重。同时，方向性效应对脉冲周期的变化更为敏感。
![]()
图 8 不同脉冲周期下山岭隧道衬砌结构受拉损伤云图（a） 方向性效应脉冲；（b） 滑冲效应脉冲Figure 8. Cloud map of tensile damage to the lining structure of mountain tunnel with different pulse periods（a） Directional effect pulse；（b） Sliding impulse effect pulse![]()
图 9 不同脉冲周期下山岭隧道衬砌结构损伤体积比（a） 方向性效应脉冲；（b） 滑冲效应脉冲Figure 9. Volume ratio of damage to the lining structure of mountain tunnel with different pulse periods（a） Directional effect pulse；（b） Sliding impulse effect pulse表9给出了不同脉冲周期的两种脉冲型地震动垂直入射下隧道衬砌结构各特征点的最大位移。可以看出，各特征点的最大位移随脉冲周期的增大而增大，这与损伤分布规律不同。长周期脉冲对整体结构产生持续的变形作用，导致水平位移增大。其中，仰拱的位移响应最大。同样，滑冲效应地震动引起的位移响应大于方向性效应。T＝1 s时，二者作用下位移差别最大。当T＝1 s时，方向性效应脉冲引起的拱顶位移为0.261米，而滑冲效应脉冲引起的位移为0.544 m，增加了1.08倍。当T＝2 s、3 s、4 s和5 s时，滑冲效应分别比方向性效应增加了0.48倍、0.55倍、0.68倍和0.66倍。
表 9 不同脉冲周期下山岭隧道衬砌结构特征点水平位移 （单位：m）Table 9. Horizontal Displacement of Characteristic Points in the Lining Structure of mountain tunnel with Different Pulse Cycles （unit：m）工况 方向性效应脉冲周期 滑冲效应脉冲周期 1 s 2 s 3 s 4 s 5 s 1 s 2 s 3 s 4 s 5 s 仰拱 0.246 0.737 1.049 1.206 1.419 0.519 1.111 1.639 2.028 2.359 左边墙 0.250 0.746 1.056 1.210 1.425 0.536 1.128 1.653 2.036 2.363 拱顶 0.261 0.774 1.074 1.220 1.426 0.544 1.145 1.667 2.045 2.367 右边墙 0.254 0.755 1.061 1.212 1.418 0.524 1.118 1.646 2.033 2.361 注：数据为监测点时程曲线最大绝对值。 4.3 速度脉冲数量的影响
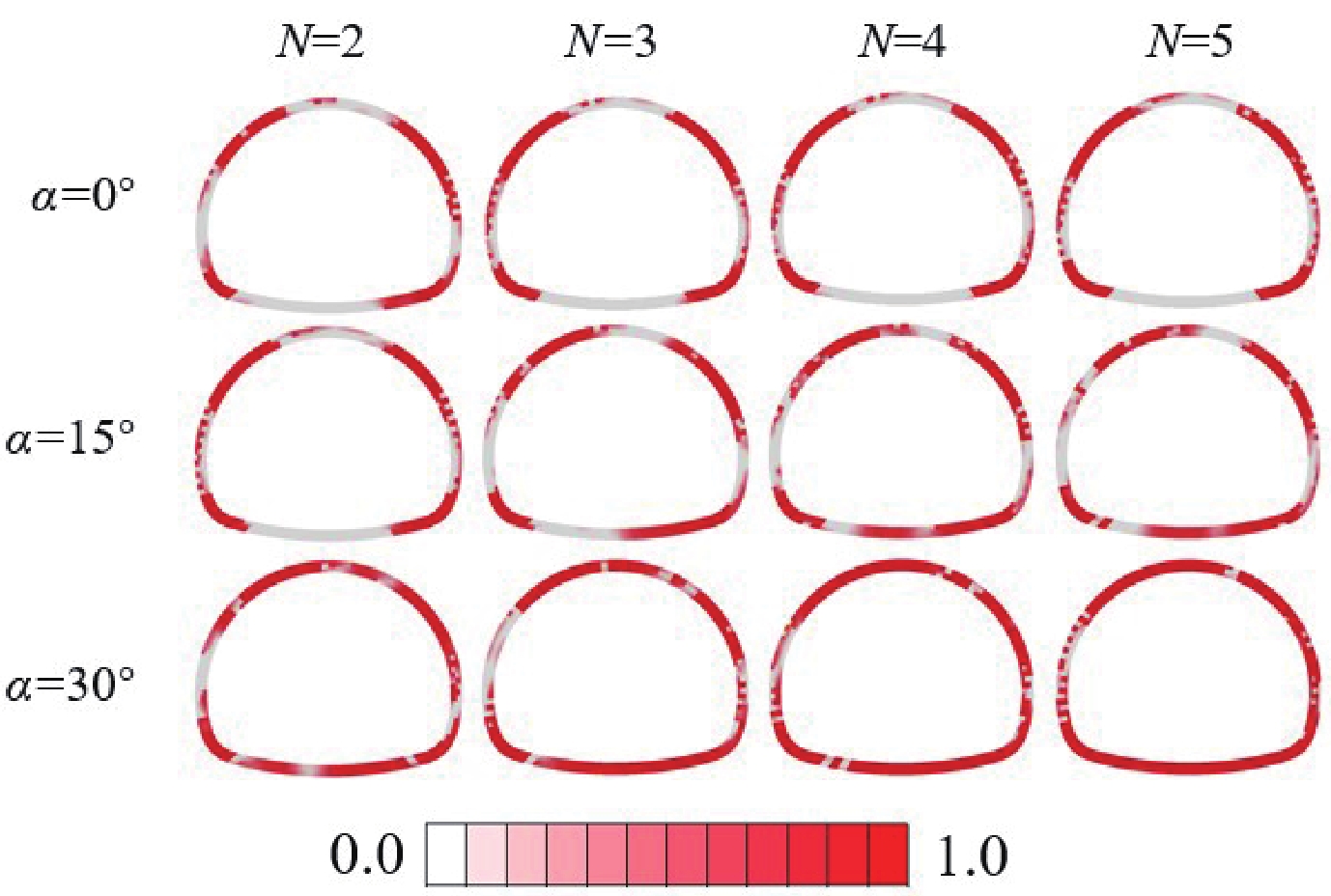
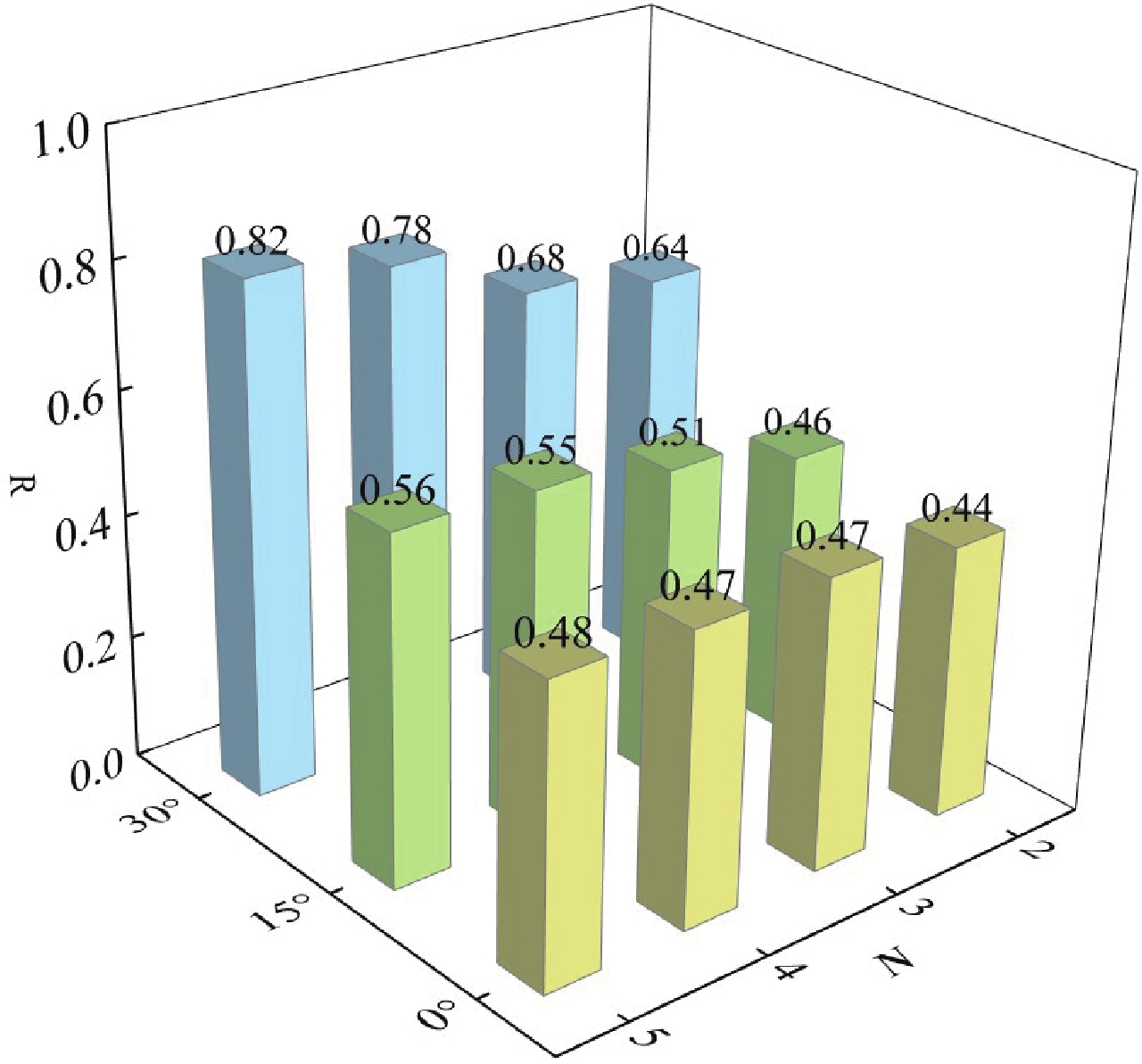
图10和图11分别展示了不同脉冲个数对山岭隧道衬砌结构损伤分布和损伤体积比的影响。可以看出，0°入射下，脉冲个数对隧道衬砌结构损伤影响较小；斜入射下，随着脉冲个数增加，隧道结构损伤区域扩展，损伤体积比逐渐增大。例如，当脉冲个数N＝2时，15°和30°入射下的损伤体积比分别为0.46和0.64；当N增加到5时，损伤体积比分别增加21.74%和28.12%。这是因为脉冲个数增加使地震波总能量积累，对隧道结构的激励作用更强，特别是在30°斜入射下。
![]()
图 10 不同脉冲个数下隧道衬砌受拉损伤云图Figure 10. Cloud map of tensile damage to the lining structure of the mountain tunnel with different numbers of pulses![]()
图 11 不同脉冲个数下山岭隧道衬砌损伤体积比Figure 11. Volume ratio of damage to the lining structure of the mountain tunnel with different numbers of pulses表10给出了不同脉冲个数的方向性效应脉冲波垂直入射对山岭隧道衬砌结构各特征点最大水平位移的影响。各特征点的最大位移随脉冲个数的增加而增大。对于仰拱，当脉冲个数N＝2时，拱顶位移为0.261 m；当N＝3、4和5时，位移分别增加了1.97倍、3.12倍和3.60倍。可以看出，脉冲个数的增加导致地震波累积更多能量，使隧道衬砌结构在多次冲击作用下产生更大的位移和应力集中效应。
表 10 不同脉冲个数下山岭隧道衬砌结构特征点水平位移Table 10. Horizontal displacement of characteristic points in the lining structure of mountain tunnel with different numbers of pulses （unit：m）特征点位置 不同脉冲个数下特征点的水平位移/m 2 3 4 5 仰拱 0.246 0.737 1.049 1.206 左边墙 0.250 0.746 1.056 1.210 拱顶 0.261 0.774 1.074 1.220 右边墙 0.254 0.755 1.061 1.212 注：数据为监测点时程曲线最大绝对值。 5. 结论
本文基于间接边界元-有限元耦合法（IBEM-FEM），实现了近断层地震动输入-山体地形放大效应-山岭隧道损伤破坏精细化高效模拟，着重研究了近断层脉冲效应和地形放大效应综合影响下山岭隧道损伤破坏机制。选取了具有代表性的近断层脉冲型地震动记录，分别体现了破裂向前方向性效应和滑冲效应。以脉冲幅值A、脉冲周期T和脉冲数量N为变量，通过基于等效脉冲模型的合成方法获取具有不同脉冲特性的近断层脉冲型地震动，并分析了这些重要参数对山岭隧道地震响应的影响规律。基于本文算例，获得主要结论如下：
1） 山岭隧道衬砌损伤程度随着脉冲幅值的增加而增大。相比于方向性效应脉冲型地震动，滑冲效应脉冲型地震动对脉冲幅值的变化更为敏感，在斜入射和高幅值脉冲下会引发更严重的结构破坏。30°入射角下，当脉冲幅值从50 cm/s增加到150 cm/s时，方向性效应和滑冲效应导致的损伤体积比分别增加了124.32%和137.84%。
2） 总体上看，山岭隧道衬砌结构损伤程度随着脉冲周期的增加而减小。在较大的入射角度和较短的脉冲周期下，滑冲效应引发的损伤更为严重。30°入射角下，当脉冲周期从1 s增加到5 s时，方向性效应和滑冲效应导致的损伤体积比分别减小40%和19.05%。此外，方向性效应对脉冲周期的变化更为敏感。
3） 地震波垂直入射下，速度脉冲数量对隧道衬砌结构的损伤影响相对较小；15°和30°斜入射下，隧道衬砌结构损伤程度随着脉冲个数的增加不断增大。脉冲个数从2增加到5时，15°和30°入射角下的损伤体积比分别增加了21.74%和28.12%。
4） 在近断层山岭隧道抗震设计中，应确定山体中地震波聚焦放大位置并尽量避开，同时重点考虑近断层脉冲效应与地形放大效应的综合影响。首先，在高幅值脉冲作用下，建议特别加强衬砌结构的抗震设计，尤其是在滑冲效应显著的区域。其次，设计时需考虑地震波入射角度的影响，适当强化衬砌结构的抗震措施，以提升隧道在复杂地震波作用下的抗震能力。
-
![]()
图 1 计算模型示意图
（a） 数值模型；（b） 隧道模型详图 （单位：cm）
Figure 1. Schematic diagram of calculation model
（a） Numerical model；（b） Tunnel model detail （unit：cm）
![]()
图 3 图3 IBEM与DBEM计算的斜入射SV波作用下（α=30°）山体地表位移响应对比
（a） 水平位移；（b） 竖向位移
Figure 3. Comparison of mountain displacement response under obliquely incident SV waves（α=30°）calculated by IBEM and DBEM
（a） Horizontal displacement；（b） Vertical displacement
![]()
图 4 IBEM与IBEM-FEM耦合法计算的斜入射SV波激励下（α＝30°）山岭隧道拱顶位移时程对比
（a） 水平位移 ；（b） 竖向位移
Figure 4. Comparison of arch displacement of mountain tunnel under oblique incident SV wave excitation （α＝30 °） calculated by IBEM and IBEM-FEM coupling method
（a） Horizontal displacement；（b） Vertical displacement
![]()
图 5 合成波和实测波时程和反应谱的结果对比
（a） TCU-068；（b） EI-Centro Array#6
Figure 5. Comparison of synthetic wave and measured wave time history and response spectrum results
![]()
图 6 不同脉冲幅值下山岭隧道衬砌结构受拉损伤云图
（a） 方向性效应脉冲；（b） 滑冲效应脉冲
Figure 6. Cloud map of tensile damage to the lining structure of mountain tunnel with different pulse amplitudes
（a） Directional effect pulse；（b） Sliding impulse effect pulse
![]()
图 7 不同脉冲幅值下山岭隧道衬砌结构受拉损伤体积比
（a） 方向性效应脉冲；（b） 滑冲效应脉冲
Figure 7. Volume ratio of tensile damage to the lining structure of mountain tunnel under different pulse amplitudes
（a） Directional effect pulse；（b） Sliding impulse effect pulse
![]()
图 8 不同脉冲周期下山岭隧道衬砌结构受拉损伤云图
（a） 方向性效应脉冲；（b） 滑冲效应脉冲
Figure 8. Cloud map of tensile damage to the lining structure of mountain tunnel with different pulse periods
（a） Directional effect pulse；（b） Sliding impulse effect pulse
![]()
图 9 不同脉冲周期下山岭隧道衬砌结构损伤体积比
（a） 方向性效应脉冲；（b） 滑冲效应脉冲
Figure 9. Volume ratio of damage to the lining structure of mountain tunnel with different pulse periods
（a） Directional effect pulse；（b） Sliding impulse effect pulse
![]()
图 10 不同脉冲个数下隧道衬砌受拉损伤云图
Figure 10. Cloud map of tensile damage to the lining structure of the mountain tunnel with different numbers of pulses
![]()
图 11 不同脉冲个数下山岭隧道衬砌损伤体积比
Figure 11. Volume ratio of damage to the lining structure of the mountain tunnel with different numbers of pulses
表 1 各材料的本构模型和参数
Table 1 The constitutive models and parameters of each material
材料 本构模型 输入参数 围岩 M-C 密度ρ 弹性模量 E 泊松比 ζ 内摩擦角 φ 粘聚力c 2200 kg/m33 GPa 0.3 35° 1 MPa 混凝土衬砌 CDP 密度ρ 弹性模量 E 泊松比 ζ 抗压强度fc 抗拉强度ft 2500 kg/m330 GPa 0.2 21.20 MPa 2.43 MPa 钢筋 双折线本构 密度ρ 弹性模量 E 泊松比 ζ 抗压强度fc 抗拉强度ft 7850 kg/m3200 GPa 0.28 400 MPa 400 MPa 
下载: 导出CSV
表 2 近断层地震动基本信息
Table 2 Basic information of near fault seismic ground motion
近断层地震动类型 地震名称 台站 断层距/km 峰值速度/ （cm·s−1） Tp/s 向前方向性效应脉冲 帝王谷地震 El Centro Array #6 1.35 67.02 3.77 滑冲效应脉冲 集集地震 TCU-068 0.32 249.59 12.28
下载: 导出CSV
表 3 近断层地震动脉冲参数
Table 3 Arterial parameters of near fault earthquakes
近断层地震动类型 台站 A/（cm·s−1） Tp/s φ/（°） γ t0/s 向前方向性效应脉冲 El Centro Array #6 70 3.77 80 1.3 6.8 滑冲效应脉冲 TCU-068 289 11.50 -200 1.02 37.4
下载: 导出CSV
表 4 特征点加速度峰值
Table 4 Peak acceleration of characteristic points
特征点位置 实测地震动峰值加速度（m/s2） 合成地震动峰值加速度（m/s2） 误差（%） EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 拱顶 5.71 8.95 5.12 8.96 10.33 0.11 左拱肩 5.57 9.30 5.24 9.39 5.92 0.97 左边墙 5.08 8.83 4.64 8.95 8.66 1.36 左拱脚 5.33 8.21 4.97 8.86 6.75 7.91 仰拱 5.38 8.39 5.01 8.65 6.87 3.09
下载: 导出CSV
表 6 特征点Mises应力峰值
Table 6 Mises stress peak values at characteristic points
特征点位置 实测地震动Mises应力峰值（Mpa） 合成地震动Mises应力峰值（Mpa） 误差（%） EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 拱顶 7.91 10.64 7.42 10.42 6.19 2.07 左拱肩 21.47 22.17 19.42 22.3 9.55 0.58 左边墙 10.06 12.61 9.84 12.89 2.18 2.22 左拱脚 28.88 29.57 27.91 29.62 3.35 0.17 仰拱 3.61 5.09 3.54 4.63 1.94 9.03
下载: 导出CSV
表 5 特征点位移峰值
Table 5 Peak displacement of characteristic points
特征点位置 实测地震动峰值位移（m） 合成地震动峰值位移（m） 误差（%） EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 EI-Centro Array#6 TCU-068 拱顶 0.862 13.4 0.831 13.15 3.59 3.59 左拱肩 0.86 13.41 0.829 13.14 3.6 3.6 左边墙 0.852 13.38 0.823 13.13 3.4 3.4 左拱脚 0.847 13.36 0.819 13.12 3.31 3.31 仰拱 0.844 13.34 0.818 13.12 3.08 3.08
下载: 导出CSV
表 7 脉冲参数分析工况
Table 7 Pulse parameter analysis working conditions
地震波 脉冲幅值A/（cm/s） 脉冲周期T/s 脉冲数量N TCU-068 100 1、2、3、4、5 原地震动 EI-Centro Array#6 100 1、2、3、4、5 原地震动 TCU-068 50、100、150 3 原地震动 EI-Centro Array#6 50、100、150 3 原地震动 EI-Centro Array#6 100 3 2、3、4、5
下载: 导出CSV
表 8 不同脉冲幅值下山岭隧道衬砌结构特征点水平位移（单位：m）
Table 8 Horizontal displacement of characteristic points in the lining structure of mountain tunnel with different pulse amplitudes （unit：m）
工况 方向性效应脉冲幅值 滑冲效应脉冲幅值 50 cm/s 100 cm/s 150 cm/s 50 cm/s 100 cm/s 150 cm/s 仰拱 0.527 1.049 1.567 0.822 1.639 2.450 左边墙 0.531 1.056 1.574 0.831 1.653 2.480 拱顶 0.539 1.074 1.611 0.837 1.667 2.500 右边墙 0.532 1.061 1.592 0.824 1.646 2.458 注：数据为监测点时程曲线最大绝对值。
下载: 导出CSV
表 9 不同脉冲周期下山岭隧道衬砌结构特征点水平位移 （单位：m）
Table 9 Horizontal Displacement of Characteristic Points in the Lining Structure of mountain tunnel with Different Pulse Cycles （unit：m）
工况 方向性效应脉冲周期 滑冲效应脉冲周期 1 s 2 s 3 s 4 s 5 s 1 s 2 s 3 s 4 s 5 s 仰拱 0.246 0.737 1.049 1.206 1.419 0.519 1.111 1.639 2.028 2.359 左边墙 0.250 0.746 1.056 1.210 1.425 0.536 1.128 1.653 2.036 2.363 拱顶 0.261 0.774 1.074 1.220 1.426 0.544 1.145 1.667 2.045 2.367 右边墙 0.254 0.755 1.061 1.212 1.418 0.524 1.118 1.646 2.033 2.361 注：数据为监测点时程曲线最大绝对值。
下载: 导出CSV
表 10 不同脉冲个数下山岭隧道衬砌结构特征点水平位移
Table 10 Horizontal displacement of characteristic points in the lining structure of mountain tunnel with different numbers of pulses （unit：m）
特征点位置 不同脉冲个数下特征点的水平位移/m 2 3 4 5 仰拱 0.246 0.737 1.049 1.206 左边墙 0.250 0.746 1.056 1.210 拱顶 0.261 0.774 1.074 1.220 右边墙 0.254 0.755 1.061 1.212 注：数据为监测点时程曲线最大绝对值。
下载: 导出CSV
-
陈笑宇,王东升,付建宇,国巍. 2021. 近断层地震动脉冲特性研究综述[J]. 工程力学,38(8):1–14+54. Chen X Y,Wang D S,Fu J Y,Guo W. 2021. A review of research on the characteristics of near fault seismic pulse[J]. Engineering Mechanics,38(8):1–14+54 (in Chinese).
杜修力,黄景琦,赵密,金浏. 2014. SV波斜入射对岩体隧道洞身段地震响应影响研究[J]. 岩土工程学报,36(8):1400–1406. Du X L,Huang J Q,Zhao M,Jin L. 2014. Effect of oblique incidence of SV waves on seismic response of portal sections of rock tunnels[J]. Chinese Journal of Geotechnical Engineering,2014, 36 (8):1400-1406 (in Chinese).
巩江峰,王伟,王芳,杨昌贤,袁溢. 2024. 截至2023年底中国铁路隧道情况统计及2023年新开通重点项目隧道情况介绍[J]. 隧道建设(中英文),44(2):377–392. Gong J F,Wang W,Wang F,Yang C X,Yuan Y. 2024. Statistics of railway tunnels in china as of the end of 2023 and introduction to key newly opened projects in 2023[J]. Tunnel Construction (Chinese and English),44(2):377–392 (in Chinese).
李天斌. 2008. 汶川特大地震中山岭隧道变形破坏特征及影响因素分析[J]. 工程地质学报,16(6):742–750. Li T B. 2008. Analysis of deformation and damage characteristics and influencing factors of mountain tunnels in the Wenchuan earthquake[J]. Journal of Engineering Geology,16(6):742–750 (in Chinese).
刘英,庄海洋,张季,周珍伟. 2024. 近直下型断层的地铁车站结构地震响应[J]. 岩土工程学报,46(4):843–852. Liu Y,Zhuang H Y,Zhang J,Zhou Z W. 2024. Seismic response of subway station structures under straight-down near-fault[J]. Chinese Journal of Geotechnical Engineering,46(4):843–852 (in Chinese).
薛翊国,孔凡猛,杨为民,邱道宏,苏茂鑫,傅康,马新民. 2020. 川藏铁路沿线主要不良地质条件与工程地质问题[J]. 岩石力学与工程学报,39(3):445–468. Xue Y G,Kong F M,Yang W M,Qiu D H,Su M X,Fu K,Ma X M. 2020. Main adverse geological conditions and engineering geological problems along the Sichuan Tibet Railway[J]. Journal of Rock Mechanics and Engineering,39(3):445–468 (in Chinese).
徐略勤,袁茂均,左英,沈正璇,徐粒寒. 2024. 近断层脉冲型地震作用下大跨拱桥动力响应分析[J]. 振动与冲击,43(9):94–104+148. Xu L Q,Yuan M J,Zuo Y,Shen Z X,Xu L H. 2024. Dynamic response analysis of long-span arch bridge under near-fault pulse seismic motion[J]. Journal of Vibration and Shock,43(9):94–104 (in Chinese).
禹海涛,朱晨阳,傅大宝,许乃星,卢哲超,蔡辉腾. 2024. 基于ST-CNN的脉冲型地震动与脉冲周期融合识别方法[J]. 岩土工程学报,46(12):2675–2683. Yu H T,Zhu C Y,Fu D B,Xu N X,Lu Z C,Cai H T. 2024. A hybrid method to identify pulse-like ground motions and pulse periods based on ST-CNN[J]. Chinese Journal of Geotechnical Engineering,46(12):2675–2683 (in Chinese).
张威,李明,姬云平,李国良,赵录学,李守刚. 2022. 青海门源M6.9地震典型隧道破坏特征分析与启示[J]. 地震工程学报,44(3):661–669. Zhang W,Li M,Ji Y P,Li G L,Zhao L X,Li S G. 2022. Analysis and Inspiration of Typical Tunnel Damage Characteristics in the M6.9 Earthquake in Menyuan,Qinghai Province[J]. China Earthquake Engineering Journal,44(3):661–669 (in Chinese).
Álvarez-Rubio S,Sánchez-Sesma F J,Benito J J,Alarcón E. 2004. The direct boundary element method:2D site effects assessment on laterally varying layered media (methodology)[J]. Soil Dyn. Earthq. Eng,24(2):167–180. doi: 10.1016/j.soildyn.2003.09.003
Corigliano M,Scandella L,Lai C G,Paolucci R. 2011. Seismic analysis of deep tunnels in near fault conditions:a case study in Southern Italy[J]. Bull. Earthq. Eng,9:975–995.
Dai D H,Zhang N,Lee V W,Gao Y F,Chen X. 2019. Scattering and amplification of SV waves by a semi-cylindrical hill in a half-space by a wavefunction-based meshless method using mapping and point-matching strategies[J]. Eng. Anal. Bound. Elem,106:252–263.
Li S,Zhang F,Wang J Q,Alam M S,Zhang J. 2017. Effects of near-fault motions and artificial pulse-type ground motions on super-span cable-stayed bridge systems[J]. J. Bridge Eng,22(3):04016128.
Liu Z X,Zhang H,Cheng A,Wu C Q,Yang G G. 2019. Seismic interaction between a lined tunnel and a hill under plane SV waves by IBEM[J]. Int. J. Struct. Stab. Dyn,19(2):1950004.
Liu Z X,Liu J Q,He W G,Meng S B,Chen H. 2024. Nonlinear seismic response and damage evolution of a mountain tunnel:Multi-scale simulation by IBEM-FEM coupled method[J]. Eng. Anal. Bound. Elem,159:364–377.
Mavroeidis G P,Papageorgiou A S. 2003. A mathematical representation of near-fault ground motions[J]. Bull. Seismol. Soc. Amer,93(3):1099–1131.
Mei X,Sheng Q,Cui Z. 2021. Effect of Near-Fault Pulsed Ground Motions on Seismic Response and Seismic Performance to Tunnel Structures[J]. Shock Vib,2021(1):9999007.
Sharma S,Judd W R. 1991. Underground opening damage from earthquakes[J]. Eng. Geol,30(3-4):263–276.
Wang W L,Wang T T,Su J J,Lin C H,Seng C R,Huang T H. 2001. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake[J]. Tunn. Undergr. Space Technol,16(3):133–150.
Wu D,Gao B,Shen Y,Zhou J,Chen G. 2015. Damage evolution of tunnel portal during the longitudinal propagation of Rayleigh waves[J]. Nat. Hazards,75:2519–2543.
Yuan X,Men F L. 1992. cattering of plane SH waves by a semi-cylindrical hill[J]. Earthq. Eng. Struct. Dyn,21(12):1091–1098.
Zhang X,Jiang Y,Sugimoto S. 2018. Seismic damage assessment of mountain tunnel:A case study on the Tawarayama tunnel due to the 2016 Kumamoto Earthquake[J]. Tunn. Undergr. Space Technol,71:138–148.
计量
- 文章访问数: 16
- HTML全文浏览量: 0
- PDF下载量: 4
