A method for calculating occurrence probability of large earthquakes based on Monte Carlo simulation
-
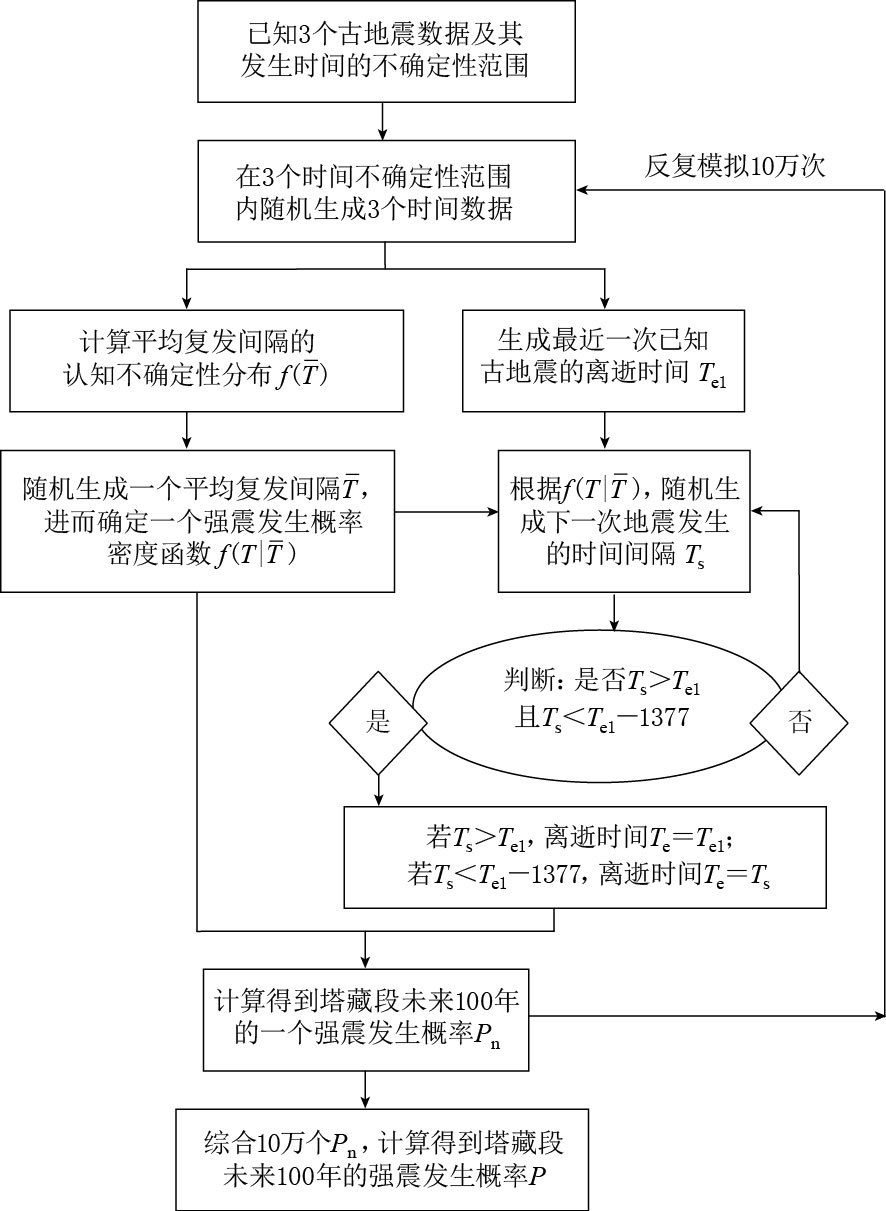
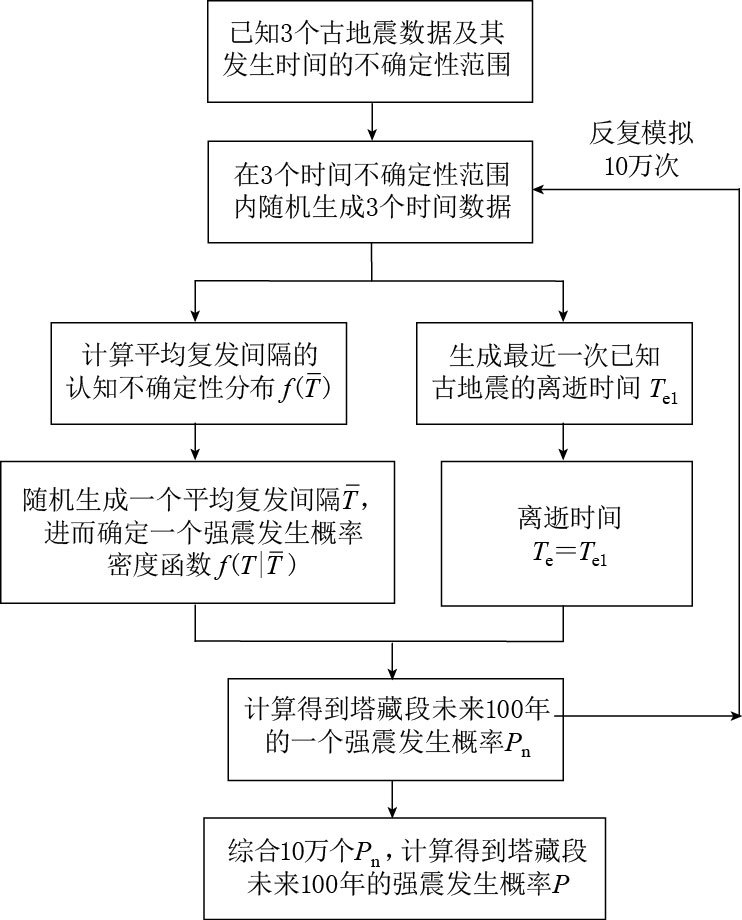
摘要: 针对大震发生概率计算过程中的不确定性， 本文分别对不确定性及其处理方法进行了探讨． 考虑到不确定构成的复杂性， 提出了一种基于蒙特卡罗模拟的大震发生概率计算方法, 并以东昆仑断裂带塔藏段为计算实例， 利用蒙特卡罗法处理发震概率计算过程中的各种不确定性. 结果表明, 古地震数据的不完整性对计算结果的影响很大. 本文采用逻辑树法考虑古地震数据的不完整性， 得到塔藏段未来100年的大震发生概率为0.12．Abstract: According to the uncertainty in the process of calculating the occurrence probability of large earthquakes， a study is made on uncertainty and its dealing methods. Considering the complexity of uncertainty， this paper presents a method for calculating the occurrence probability of large earthquakes based on Monte Carlo simulation. With the Tazang segment of eastern Kunlun fault zone as an example， we deal with different kinds of uncertainties in calculating the occurrence probability of large earthquakes using Monte Carlo method. The result shows that the incompleteness of paleo-earthquakes data has great effect on the calculation result. With the logical tree to deal with the incompleteness of paleo-earthquakes data， the occurrence probability of large earthquakes is 0.12 in the next 100 years on the Tazang segment.
-
Keywords:
- large earthquake /
- occurrence probability /
- Monte Carlo /
- uncertainty
-
-
![]()
图 2 塔藏段大震发生概率计算的分支A流程图
Figure 2. The process chart of branch A for calculating the occurrence probability of large earthquakes on the Tazang fault
-
陈春梅， 任雪梅. 2014. 我国大陆5个地区历史地震资料记载的完整性分析与比较[J]. 防灾减灾学报， 30(2): 66-70. http://www.cnki.com.cn/Article/CJFDTOTAL-DDYJ201402014.htm Chen C M， Ren X M. 2014. Integrity analysis and comparison of five regional historical earthquake records in mainland China[J]. Journal of Disaster Prevention and Reduction， 30(2): 66-70 (in Chinese).
郭星， 潘华. 2015. 强震复发间隔变异系数的一种计算方法[J]. 地震学报， 37(3): 411-419. http://www.dzxb.org/Magazine/Show?id=29086 Guo X， Pan H. 2015. A method for computing the aperiodicity parameter of the strong earthquake recurrence interval[J]. Acta Seismologica Sinica， 37(3): 411-419 (in Chinese).
郭星， 潘华. 2016. 强震复发概率模型中的参数不确定性研究[J]. 地震学报， 38(2): 298-306. http://www.dzxb.org/Magazine/Show?id=29183 Guo X， Pan H. 2016. Parameter uncertainty analysis on probability model of strong earthquake recurrence[J]. Acta Seismologica Sinica， 38(2): 298-306 (in Chinese).
李正芳， 周本刚， 冉洪流. 2012. 运用古地震数据评价东昆仑断裂带东段未来百年的强震危险性[J]. 地球物理学报， 55(9): 3051-3065. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201209024.htm Li Z F， Zhou B G， Ran H L. 2012. Strong earthquake risk assessment of eastern segment on the East Kunlun fault in the next 100 years based on paleo-earthquake data[J]. Chinese Journal of Geophysics， 55(9): 3051-3065 (in Chinese).
毛凤英， 张培震. 1995. 古地震研究中的逐次限定法与新疆北部主要断裂带的古地震研究[G]//活动断裂研究(4). 北京: 地震出版社: 153-164. Mao F Y， Zhang P Z. 1995. Progressive constraining method in paleo-earthquake study and the research on paleo-earthquakes along the major active faults in northern Xinjiang[G]//Research on Active Fault (4). Beijing: Seismological Press: 153-164 (in Chinese).
青海省地震局， 中国地震局地壳应力研究所. 1999. 东昆仑活动断裂带[M]. 北京: 地震出版社: 1-186. Earthquake Administration of Qinghai Province， Institute of Crustal Dynamics， China Earthquake Administration. 1999. East Kunlun Active Fault Zone[M]. Beijing: Seismological Press: 1-186 (in Chinese).
冉勇康， 邓起东. 1999. 古地震学研究的历史、 现状和发展趋势[J]. 科学通报， 44(1): 12-20. Ran Y K， Deng Q D. 1999. History， status and trend about the research of paleoseismlogy[J]. Chinese Science Bulletin， 44(10): 880-889. doi: 10.1007/BF02885057
Bommer J J. 2003. Uncertainty about the uncertainty in seismic hazard analysis[J]. Eng Geol， 70(1/2): 165-168. http://en.cnki.com.cn/article_en/cjfdtotal-dqwx201209024.htm
Cornell C A. 1968. Engineering seismic risk analysis[J]. Bull Seismol Soc Am， 58(5): 1583-1606.
Ellsworth W L， Matthews M V， Nadeau R M， Nishenko S P， Reasenberg P A， Simpson R W. 1999. A Physically-Based Earthquake Recurrence Model for Estimation of Long-Term Earthquake Probabilities[R]. Reston， Virginia: US Geological Survey Open-File Report: 99-522.
Hagiwara Y. 1974. Probability of earthquake occurrence as obtained from a Weibull distribution analysis of crustal strain[J]. Tectonophysics， 23(3): 313-318. doi: 10.1016/0040-1951(74)90030-4
Matthews M V， Ellsworth W L， Reasenberg P A. 2002. A Brownian model for recurrent earthquakes[J]. Bull Seismol Soc Am， 92(6): 2233-2250. doi: 10.1785/0120010267
Nishenko S P， Buland R A. 1987. A generic recurrence interval distribution for earthquake forecasting[J]. Bull Seismol Soc Am， 77(4): 1382-1399. http://cn.bing.com/academic/profile?id=2280357669&encoded=0&v=paper_preview&mkt=zh-cn
Reid H F. 1910. The Mechanics of the Earthquake， The California Earthquake of April 18， 1906[R]. Washington， DC: State Earthquake Investigation Commission: 43-47.
Rikitake T. 1974. Probability of earthquake occurrence as estimated from crustal strain[J]. Tectonophysics， 23(3): 299-312. doi: 10.1016/0040-1951(74)90029-8
Senior Seismic Hazard Analysis Committee. 1997. Recommendations for Probabilistic Seismic Hazard Analysis: Guidance on Uncertainty and Use of Experts[R]. Washington， DC: US Nuclear Regulartory Commission: 1-256.
Seshadri V. 1983. The inverse Gaussian distribution: Some properties and characterizations[J]. Canadian J Statist， 11(2): 131-136. doi: 10.2307/3314980
Utsu T. 1972. Large Earthquakes Near Hokkaido and the Expectancy of the Occurrence of A Large Earthquake Off Nemuro[R]. Hokkaido: Coordinating Committee for Earthquake Prediction: 7-13.
Wesnousky S G. 1986. Earthquakes， Quaternary faults， and seismic hazard in California[J]. J Geophys Res， 91(B12): 12587-12631. doi: 10.1029/JB091iB12p12587
下载:
计量
- 文章访问数: 439
- HTML全文浏览量: 304
- PDF下载量: 38
