引言

承压井(孔)水位往往对固体潮具有较好的响应，该响应称为井水位固体潮效应，简称为井潮． 关于井潮的研究一直受到研究者的关注(Bredehoeft，1967； Bowen，1983； Narasimhan et al，1984； Hsieh et al，1987； 张昭栋等，1991； Doan et al，2006； 廖欣等，2011)，目前已形成一个基本认识： 井潮是含水层孔(裂)隙弹性响应和潮汐排水(渗流)响应综合过程的产物(Bowen，1983； Doan et al，2006； Elkhoury et al，2006； 廖欣等，2011)． 井潮的孔隙弹性响应研究，往往以含水层均质各向同性的假设为前提，井潮与体应变固体潮、 重力固体潮及引潮位之间成正比关系(张昭栋等，1991； Doan et al，2006； 廖欣等，2009)． 然而含水层中裂隙的存在也会影响井潮． 在充分考虑裂隙含水层的力学各向异性后，Bowen(1983)建立了受单条裂隙控制的井孔水位潮汐响应模型，得出不排水条件下井潮的振幅和相位移与含水层裂隙方位角和岩石弹性参数之间的关系． 对于排水响应研究，广受相关学者认同的是Hsieh模型(Ritzi Jr et al，1991； Roeloffs，1996； Doan et al，2006； Elkhoury et al，2006)． Hsieh等(1987)建立了储水效应作用下井水位的相对振幅(或称振幅响应)和相位移与井孔半径、 潮汐频率、 导水系数和储水系数等参数之间的定量关系． 根据这种理论关系，可以利用井孔水位数据推求导水(渗透)系数和储水系数(Hsieh et al，1987； Doan et al，2006； Elkhoury et al，2006)．

我国绝大部分地震地下流体监测井揭露的是基岩裂隙含水层，这些井的井潮同时受到裂隙(方位)效应和井孔储水效应的影响． 这两种效应对井潮的影响是相互叠加的，目前并没有有效方法区分两种效应对井潮的影响，这使得井潮在理论探索及实际应用中出现很大的限制． 本文基于Hsieh模型，结合井潮的振幅和相位移随含水层导水(渗透)系数和储水系数变化的规律特征，有效提取排水效应对井潮的影响，通过定量分析井潮与其排水响应过程中的影响因素之间的关系，研究井孔储水效应对井潮的影响． 提取出渗流效应的影响后，进而分析潮汐排水响应过程中，含水层导水(渗透)系数和储水系数对井潮的影响．

1.   川06井概况及研究资料

大量的地震地下流体观测井孔资料，为井潮变化的研究提供了充足、 可靠的数据． 本文选取位于四川省会理县中厂镇的川06井进行实例分析． 该井位于磨盘山—西格达断裂与宁会断裂交汇部位，属国家级井网. 其它基本情况见表 1^①. ①四川省地震局台网中心. 1982. 地下水动态观测井卡片.

表  1  川06井基本情况

Table  1.  Basic information of the well Chuan06

下载: 导出CSV 

| 显示表格

川06井于1982年3月开始使用SW40型水位仪监测静水位，于1991年改用SW40-1型水位仪监测静水位，两种仪器观测均得到模拟值，由于采矿干扰于2007年6月停止观测． 该监测井的水位观测资料较好，能够清晰记录固体潮和水震波． 本文采用收集到的1990年以后的整点观测数据进行分析，偶尔有个别时间段的数据由于仪器问题出现削峰现象，未被本文采用．

根据成井剖面可知，观测层主要为大理岩断层破裂带，裂隙较发育，钻进至该层出现涌水现象，具有承压性． 井孔所处位置的表层2—3 m为第四系黄色松散浮土层和亚黏土，向下为裂隙比较发育的砂化白云石大理岩层，厚约50 m，它与表层浮土一起构成潜水含水层． 观测层上覆灰色和暗灰色辉绿岩、 蛇纹石化石英白云石大理岩，厚度大、 裂隙少且联通性差，钻进时无地下水，是良好的隔水顶板．

2.   理论基础

Hsieh等(1987)从排水响应机理出发，推导出了在周期性孔压扰动作用下，均质各向同性承压含水层排水响应引起井水位波动的相对振幅A和相位移η的解析表达式：

上式中，A为某一特定频率的井水位波动振幅M与离井孔无穷远处的含水层孔压(用水头表示)扰动振幅M_u(数值上等于不排水条件下井水位波动振幅)之间的比值，无量纲； η为井潮与含水层潮汐孔压之间的相位移，负值表示相位滞后； Ker和Kei分别为开尔文函数的实部和虚部； ω为潮汐分波频率； S为储水系数，无量纲； T为导水系数，数值等于渗透系数K与含水层厚度b的乘积； r_w为揭露含水层处井孔半径，或滤水管半径； r_c为井孔水位波动范围处的井孔套管半径．

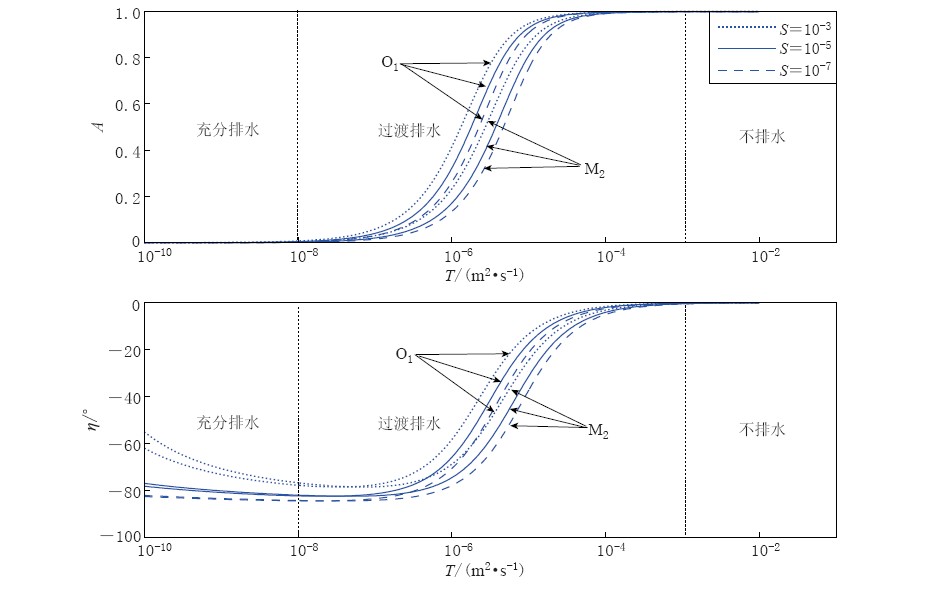
由Hsieh模型可知，对于某一特定井孔而言，其水位潮汐响应的渗流阶段受到S和T的影响， A和η对S不敏感，主要受T的影响(图 1). 具体分析可参见Hsieh等(1987)文章． 井水位在渗流响应阶段受到这种影响出现振幅变小、 相位滞后的响应称为井孔储水效应． 根据A和η随T变化的规律，可将响应区间划分为： 不排水、 过渡和充分排水区间(廖欣等，2011)． 井孔储水效应对井潮的影响可以表述为： A和η越小，影响越大．

图  1  井潮M₂和O₁波的相对振幅A和相位移η与储水系数S和 导水系数T的关系(其中r_w=r_c=10 cm)

Figure  1.  Plot of predicted amplitude response A and phase shift η for tidal constituents M₂ and O₁ of water level versus aquifer storativity (S) and transmissivity (T) for well radius r_w=r_c=10 cm

下载: 全尺寸图片 幻灯片

3.   结果与分析

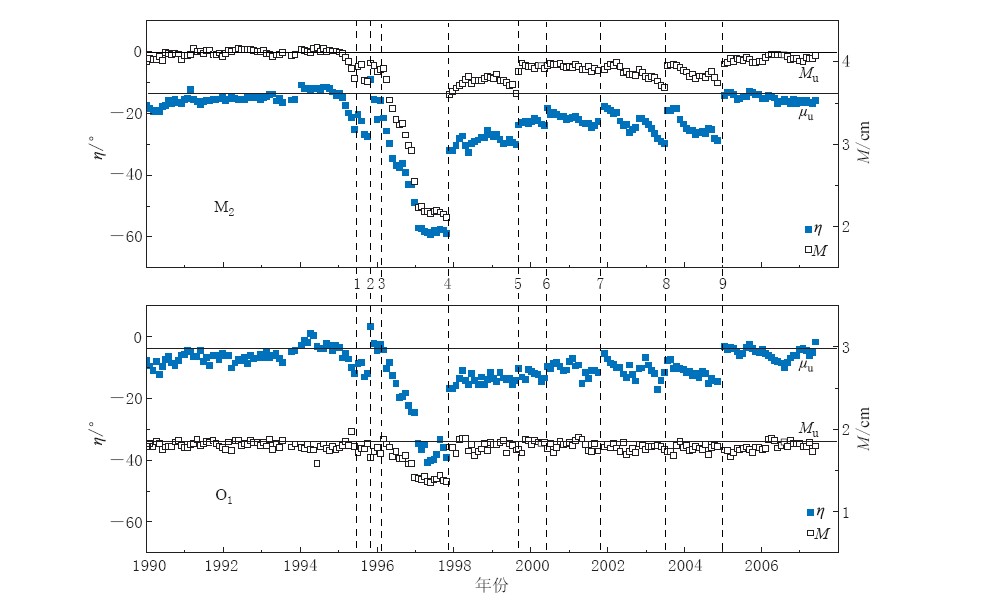
利用Baytap-G潮汐数据分析方法(Ishiguro，Tamura，1985； Tamura，1987； Tamura et al，1991)，对收集到的川06井1990—2007年6月的静水位整点观测数据进行潮汐分析，分析时间间隔为30天. 本文选择受气压影响较小，且具有代表性的半日波M₂和全日波O₁进行分析． 通过潮汐分析，推求M₂波和O₁波的振幅M和相位μ随时间变化的规律．

潮汐分析结果如图 2所示. 对于M₂波，M与μ表现为同步变化． 这种同步变化的规律性主要体现在： 周边几次较大地震出现后，M和μ出现同步阶梯变化，表现为M增大，μ减小； 地震发生之后，M和μ出现同步趋势减小． O₁波也出现类似的规律，但不如M₂波明显，这主要取决于潮汐分析结果的精度． 由于M₂波是振幅最大的潮波，同时在长度相同的时间内，观测数据所包含的M₂波波动次数大约是O₁波的两倍，因而O₁波的潮汐分析精度相对没有M₂波高，尤其是M．

图  2  川06井水位潮汐分析结果. 图中数字1—9表示地震编号， 具体见表2

Figure  2.  Tidal analysis result of well water level monitored in the well Chuan06. Digits 1—9 in the figure represent the earthquakes， for details see Table 2

下载: 全尺寸图片 幻灯片

表  2  影响川06井水位固体潮效应变化的地震基本参数

Table  2.  Earthquakes affecting changes in the well tide in the well Chuan06

下载: 导出CSV 

| 显示表格

川06井所揭露的含水层主要为大理岩断层破碎带，不排水条件下井潮将受到裂隙效应的影响． 假设裂隙效应和井孔储水效应对井潮的影响是相互独立且能够相互叠加，同时假设裂隙效应随时间不发生变化，即假设M_u和μ_u不随时间发生变化，则可以利用井孔储水效应作用下井潮的振幅和相位移随导水(渗透)系数增大而趋于稳定的特征，来判断井潮是否满足不排水响应，并以此推求不排水条件下井潮M₂和O₁波的振幅M_u和相位移μ_u，进而推求出不同时段的A和η值(廖欣等，2011)．

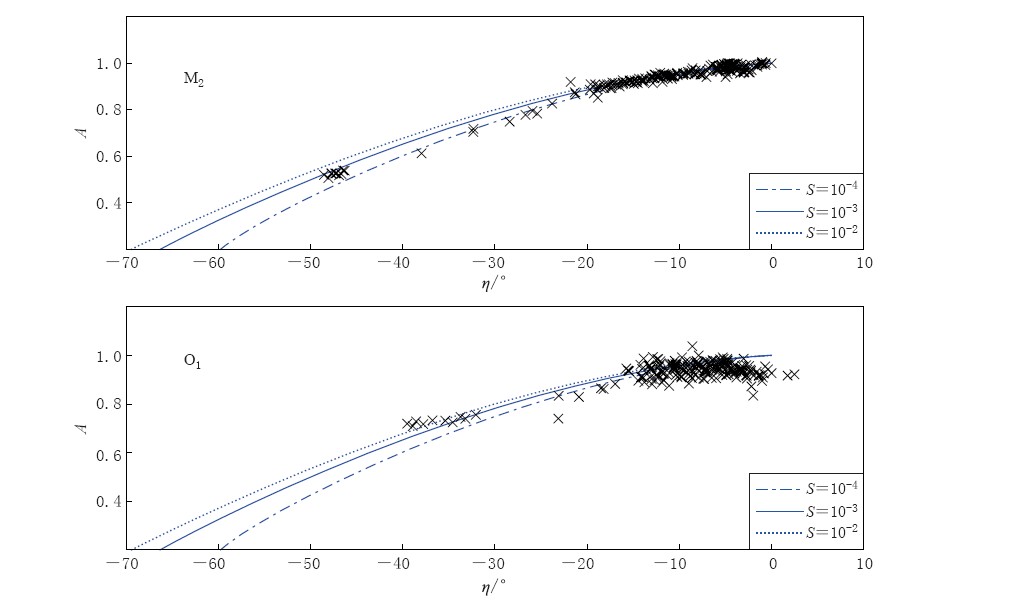
对于实际数据，A与η整体表现为正相关，随着η增大(相位差减小)，A也相应增大(图 3)． 对于M₂波，A的变化范围是0.5—1，η的变化范围是-50°—0°； 对于O₁波，A的变化范围是0.7—1，η的变化范围是-40°—0°． 对于理论曲线，S变化一个量级，A-η关系曲线相差不是很大，但这种差距有随A和η值(或T)变小而变大的趋势. 这意味着随着T变小，S对A和η影响程度变大． 通过Hsieh模型得出的理论关系曲线能够较好地拟合由实际值构成的A-η散点图： 当η＞-20°或A＞0.8时，不论S值取多大，理论曲线都能很好地拟合散点图； 当 η＜-20°或A＜0.8时，实际散点值不能通过某一特定S值的理论曲线进行拟合，理论曲线与散点图之间存在较小差距．

图  3  排水响应引起的相对振幅A和相位移η的实际散点图与Hsieh模型的理论关系曲线

Figure  3.  Plots of the amplitude response A and phase shift η induced by draining effects based on the actual measured well water level data and theoretical Hsieh model for waves M₂ and O₁

下载: 全尺寸图片 幻灯片

整体而言，特定S值的理论曲线能够较好地拟合实际A-η变化趋势. 这意味着潮汐排水响应能够通过Hsieh模型来描述. 进一步可以说明A和η的较大变化是T变化引起的; 而A和η(或T)较小时，理论曲线与实际散点之间的较小差距可能是S变化引起的： 在整个研究时段内，S变化对A和η值变化的影响较小，且这种影响只有当T较小时才得以体现当井潮处于不排水响应时，S变化不会造成A和η变化，只有当井潮处于过渡响应状态时，S变化才能引起A和η变化．

4.   讨论与结论

结合Hsieh模型对川06井水位观测数据的潮汐分析结果进行分析，得出结论如下：

1)该井潮汐振幅和相位的变化主要是含水层排水响应变化引起的． 孔(裂)隙弹性响应对井潮的影响主要体现在： 岩石弹性参数变化引起的振幅变化； 方位角发生变化引起的M₂和O₁波振幅和相位移出现的相反变化(Bowen，1983)． 在孔(裂)隙弹性响应不变的假设前提下，相对振幅和相位移构成的散点图能够通过Hsieh模型拟合，充分说明了Hsieh模型能够描述(相对)振幅和相位(移)的变化规律，这意味着井潮振幅和相位的变化不是由裂隙方位角变化引起的巧合，而是受到排水响应变化的影响. 同时也证实了该裂隙含水层满足Hsieh模型的基本条件，可以看成是均质各向同性的渗流介质，即含水层裂隙效应可以忽略. 当然这也否定了井潮变化是由孔(裂)隙弹性响应变化引起的．

如果相对振幅和相位移的相互关系满足Hsieh模型，则井潮变化主要受含水层排水响应变化控制. 反之则井潮变化可能受到其它原因，诸如新裂隙形成，原有裂隙闭合(裂隙开度变化造成的影响最终体现在渗透系数对井潮的振幅和相位的影响，可不将其看作裂隙系统变化的一部分)，或者含水层弹性参数变化等的影响．

2)影响排水响应的两个主要水文地质学参数中，导水(渗透)系数是主要影响因素，储水系数的影响可以忽略． 渗透系数变化对排水响应(或井潮)的影响，不仅体现在相位移(或相位)的变化上，也体现在相对振幅(或振幅)的变化上． 井潮的变化主要受排水响应影响的结论最终反过来能够验证裂隙效应不变假设的合理性．

结合裂隙效应不随时间发生变化的假设，可以得出振幅和相位变化主要取决于渗透系数变化的结论，这与Elkhoury等(2006)将相位变化(移)归因于渗透(导水)系数变化，而将(相对)振幅变化归因于储水系数变化的结论不同． 事实上，Elkhoury等(2006)将(相对)振幅变化归因于储水系数变化的观点与Hsieh模型关于相对振幅和相位移对储水系数不敏感的结论相矛盾，而Hsieh模型是他们的理论基础． 他们之所以得出这样的结论，是因为没有综合考虑(相对)振幅和相位(移)两者之间的变化规律所致．

Hsieh模型只考虑水平向渗流(可推广为径向渗流)，其假设垂向不存在水流交换． 川06井所揭露含水层的承压性较好，可以忽略垂向渗流作用，因而实际数据能够较好满足Hsieh模型． 当含水层承压性较差，在潮汐应力作用下，存在越流补给或排泄. 这时候含水层的垂向渗流不能忽略，这就需要更加符合实际的理论模型． 关于半承压性含水层的井潮的问题是本文无法探讨的． 同时，关于裂隙效应和井孔储水效应对井潮的影响相互独立的假设，其实质是在研究中对两种效应的解耦合，这种假设是目前研究裂隙含水层渗流对井潮影响乃至裂隙介质的渗流力学所必不可少的． 真正意义上的孔(裂)隙弹性响应和排水响应的耦合研究，需要依靠可靠的理论模型和详细的水文地质资料．

本文为深入研究井孔水位潮汐响应，检验理论响应模型，以及探讨地震孕育和发生过程中井孔水位潮汐异常机理提供了基础． 关于含水层渗透系数变化的形成机理，以及渗透系数与应力之间关系的场地研究，将是我们以后重点研究方向之一．

四川省地震局杨贤和为本研究提供了相应的资料，Ishiguro和Tamura为本研究提供了Baytap-G程序包，审稿人对本文提出宝贵的修改意见. 作者在此一并表示感谢.