Simultaneous traveltime inversion using the multi-phase Fresnel volume rays
-
摘要: 高频假设下的地震射线理论以及相应的地震成像理论表明,在射线稀疏条件下,不可能得到较高分辨率的构造成像;而有限频射线理论更符合实际地震的传播规律,即地震波的走时不仅与中心射线(传统的几何射线)上的速度分布有关,而且与中心射线附近一定范围(称其为第一菲涅耳体)内的速度异常分布有关.鉴于此,本文提出了计算多震相地震波菲涅耳体有限频射线的方法,并定义了走时敏感核函数,同时给出了利用多震相菲涅耳体有限频射线进行速度模型和反射界面同时反演成像的公式.利用多震相走时资料,使用传统射线层析成像方法与有限频射线层析成像方法进行了速度和界面的同时反演成像.结果表明,当射线密度较小时,无论是对速度模型的重建还是对反射界面几何形状的更新,有限频射线层析成像方法均优于传统射线层析成像方法, 而变频有限频射线层析成像则是实际地震层析成像的首选反演算法.Abstract: Traditional ray tomography method based on high frequency assumption is unable to obtain a high resolution tomographic picture with sparse rays. In contrast, the finite-frequency ray theory is more suitable for real seismic propagation law, that is to say that the travel time is dependent not only on the velocity distribution along a central ray (or traditional geometric ray), but also on the velocity anomaly within a region (referred as the first Fresnel volume), which embraces the central ray. In this paper we first put forward an algorithm to calculate the multi-phase Fresnel volume finite-frequency ray, and then give a inversion method to simultaneously invert both velocity and reflector geometry by using these multi-phase arrival time information. In synthetic example, both the traditional ray tomographic and finite-frequency ray tomographic methods are used to simultaneously update both velocity field and reflector geometry with multi-phase arrival times, the results show that the finite-frequency ray tomographic method is advantageous over the traditional ray tomographic method in terms of velocity reconstruction and reflector geometry updating when the ray density is relatively low. The finite-frequency ray tomographic method with varying frequency is a good choice in real seismic tomographic application.
-
引言
层析成像始于医学CT诊断技术,20世纪70年代首次应用于地震学研究(Aki,Lee,1976).经过多年的不断发展和完善,已成为目前研究地球内部结构行之有效的主要技术途径之一,出现了多种成像方法技术(成谷等,2002),主要有体波成像、面波成像、全波形反演成像、自由振荡成像、有限频成像及噪声成像等.波动方程层析成像方法在理论上比体波走时层析成像方法分辨率更高,但其计算效率较低,反演的目标函数与速度扰动之间表现为强烈的非线性关系,加之地震信号的信噪比较低、实际地震波传播难以准确描述等诸多现实问题,使得其在实际地震成像方法技术中的应用并不普遍,目前应用较广的依然是体波走时层析成像方法.除了高频假设的制约外,体波走时层析成像分辨率主要还受射线密度或射线交错概率的影响.为了在现有地震台网和地震分布的情况下提高走时层析成像的分辨率,多震相(如反射波、转换波)走时的引入至关重要(黄国娇,白超英,2010; 白超英等,2011).
实际地震波的频率是有限的,仅用无限高频的观点来看待地震波则具有一定的局限性.普林斯顿大学研究团队发展了可有效运用于层析成像研究的有限频理论.在有限频理论下,地震波对速度敏感的范围将不再仅仅局限于射线路径上,射线附近一定范围内速度异常的影响也将反映在走时数据上,这种影响程度可用走时敏感核函数来表示.Woodward(1992)利用波恩(Born)近似和利托夫(Rytov)近似给出了单频地震波的走时与空间速度分布的关系.结果发现,中心射线上的速度结构敏感度为零,中心射线附近一定范围(即第一菲涅耳体)内的速度异常对走时均有影响.有限频理论与传统射线理论的优劣之争,已经有了大量的研究成果(Montelli et al,2004;Tromp et al,2005; Zhao et al,2005; 刘玉柱等,2011),有限频层析成像的综述可参见文献(徐小明等,2009; 江燕,陈晓非,2011).
敏感核的计算是一个复杂而庞大的过程,为降低计算成本,可通过求取第一菲涅耳体来近似代替计算敏感核分布.Husen和Kissling(2001)讨论了初至波有限频射线成像.首先对多震相菲涅耳体有限频射线的追踪计算问题进行讨论,然后给出利用共轭梯度法求解带约束的阻尼最小二乘问题的反演算法,以及偏导(雅克比)矩阵的计算公式和双参数同时反演的迭代公式,最后利用数值模拟实例验证该反演算法的有效性和正确性.另外,文中还讨论了变频有限频射线成像的可能性.
1. 多震相菲涅耳体有限频地震射线追踪
本文在分区多步不规则最短路径算法(唐小平,白超英,2009; 赵瑞,白超英,2010)的基础上,引入第一菲涅耳体的概念,给出了计算多震相有限频射线的方法技术.
1.1 第一菲涅耳体的定义
求取第一菲涅耳体范围及其分布(类似于走时敏感核函数)是本文进行反演成像的关键.第一菲涅耳体定义(Červený,Soares,1992)为

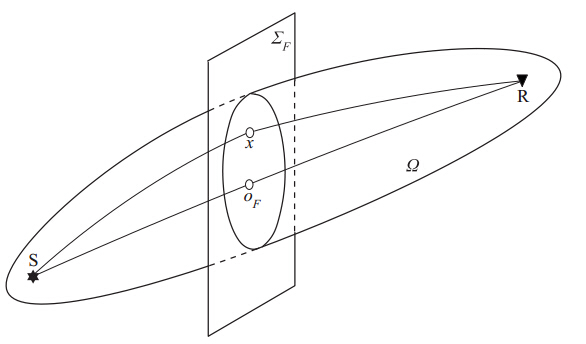
式中,x为空间任意一点,S为震源,R为检波器,T为地震波周期.tSR,tSx和tRx分别表示震源与检波器之间、震源与点x之间、检波器与点x之间的最小走时.满足式(1)所有点x的集合构成了第一菲涅耳体(图1).为简便起见,第一菲涅耳体在下文中均称为菲涅耳体.
菲涅耳体的边界由以下关系式确定(Červený,Soares,1992):

![]() 图 1 震源S到检波器R的菲涅耳体示意图(根据Červený, Soares,1992修改)Ω表示震源S与检波器R对应的第一菲涅耳体;oF表示空间点x在中心射线的投影点; ∑F 为过点oF的菲涅耳带所在的平面Figure 1. Diagram showing the first Fresnel volume between source S and receiver R(revised after Červený, Soares,1992) Ω is the first Fresnel volume for source S and receiver R,oF denotes the project point of x on central ray,and ∑F is a plane which contains the Fresnel zone crossing the point oF
图 1 震源S到检波器R的菲涅耳体示意图(根据Červený, Soares,1992修改)Ω表示震源S与检波器R对应的第一菲涅耳体;oF表示空间点x在中心射线的投影点; ∑F 为过点oF的菲涅耳带所在的平面Figure 1. Diagram showing the first Fresnel volume between source S and receiver R(revised after Červený, Soares,1992) Ω is the first Fresnel volume for source S and receiver R,oF denotes the project point of x on central ray,and ∑F is a plane which contains the Fresnel zone crossing the point oF1.2 菲涅耳体有限频射线追踪算法
1.2.1 直达波菲涅耳体有限频射线追踪算法
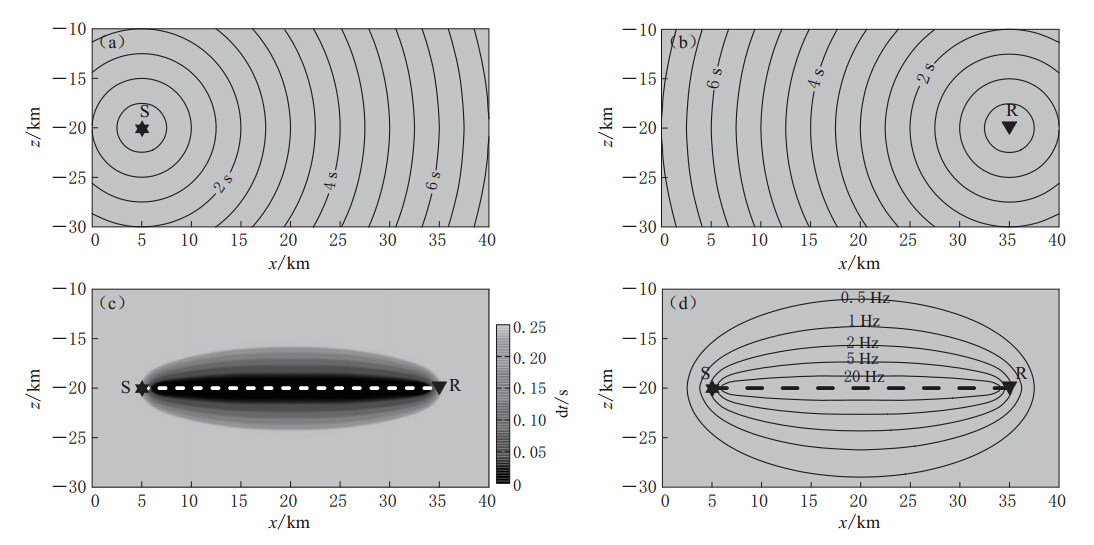
从菲涅耳体的定义(式(1)、(2))出发,求得的菲涅耳体即为直达波有限频射线.对于特定的炮检对(S-R)排列,直达波菲涅耳体可通过以下方法求得:① 以震源S为源点,计算全区所有节点的初至波走时tS,包括检波器点的到时tSR(图2a);② 以检波器点R为源点,反向计算全区所有节点的初至波走时tR(图2b);③ 计算各节点上的走时差dt=tS+tR-tSR;④ 满足dt≤T/2的点均属于该炮检对(S-R)排列所对应的菲涅耳体(图2c),类似于有限频敏感核函数的分布. 其中满足dt=T/2的节点所构成的集合即为菲涅耳体有限频射线的边界(图2d).图2d中给出了5种不同频率(0.5,1,2,5和20 Hz)下的直达波菲涅耳体有限频射线的边界:随着频率的增大,射线逐渐变窄;高频近似下,收缩成传统射线.
![]() 图 2 均匀速度场(v=5.0km/s)中直达波有限频射线追踪原理(a)由震源点计算所得的走时场;(b)由检波器点计算所得的走时场;(c)地震波频率为2Hz时的菲涅耳体射线分布,白色虚线为中心射线;(d)5种不同频率地震波的菲涅耳体边界,虚线代表传统射线路径Figure 2. Principle of finite frequency ray tracing for direct wave,velocity model is v=5.0 km/s (a)Travel time field calculated from the source point S;(b)Travel time field calculated from the receiver point R; (c)The first Fresnel volume ray with seismic frequence of 2 Hz,and the white dashed line denotes the central ray;(d)Boundaries of the first Fresnel volume with varying frequencies,from inside to outside the frequency is 20,5,2,1 and 0.5 Hz,respectively. Dashed line is the traditional ray path
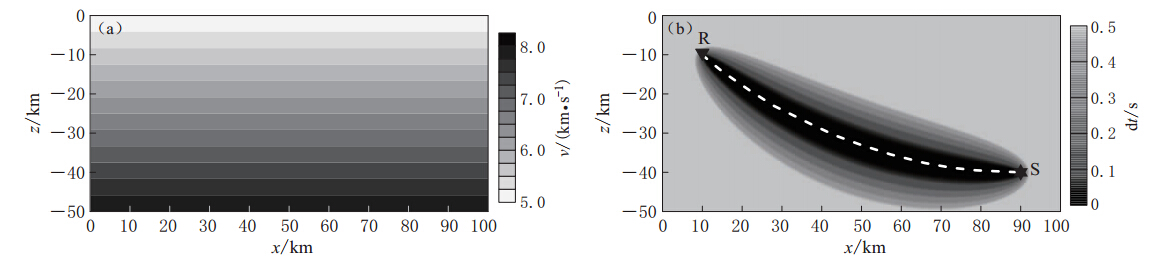
图 2 均匀速度场(v=5.0km/s)中直达波有限频射线追踪原理(a)由震源点计算所得的走时场;(b)由检波器点计算所得的走时场;(c)地震波频率为2Hz时的菲涅耳体射线分布,白色虚线为中心射线;(d)5种不同频率地震波的菲涅耳体边界,虚线代表传统射线路径Figure 2. Principle of finite frequency ray tracing for direct wave,velocity model is v=5.0 km/s (a)Travel time field calculated from the source point S;(b)Travel time field calculated from the receiver point R; (c)The first Fresnel volume ray with seismic frequence of 2 Hz,and the white dashed line denotes the central ray;(d)Boundaries of the first Fresnel volume with varying frequencies,from inside to outside the frequency is 20,5,2,1 and 0.5 Hz,respectively. Dashed line is the traditional ray path图3b给出了线性速度模型(图3a)中计算得到的直达波菲涅耳体有限频射线.从图中可以看出,在特定频率下,菲涅耳体射线的宽度与速度有关,速度越大,菲涅耳体射线就越宽.
1.2.2 反射波菲涅耳体有限频射线追踪算法
由震源S出发,经反射界面一点Pref反射,并到达检波器R的地震射线,可分为反射前和反射后两部分,分别记为射线段S-Pref和射线段Pref-R. 这两部分射线段对应的菲涅耳体有限频射线需要分别计算,然后连接成为该炮检对(S-R)经由反射点(Pref)的反射波菲涅耳体有限频射线.
根据多震相地震射线的分区多步最短路径法计算原理(唐小平,白超英,2009),反射波走时场由反射前和反射后两部分构成.具体计算步骤如下:① 以震源S为源点,分别计算反射前的走时场tS1(图4a)和反射后的走时场tS2(图4c),并获得检波器点的到时tSR;② 以检波器点R为源点,同样计算反射前的走时场tR1(图4b)和反射后的走时场tR2(图4d);③ 计算射线段S-Pref对应的菲涅耳体有限频射线(图4e):dt=tS1 +tR2 -tSR,满足dt≤T/2的点均属于射线段S-Pref对应的菲涅耳体有限频射线;④ 计算射线段Pref-R对应的菲涅耳体有限频射线(图4f): dt=tS2+tR1 -tSR,满足dt≤T/2的点均属于射线段Pref-R对应的菲涅耳体有限频射线; ⑤ 将步骤③和④所得的两段有限频射线连接,即可得到特定炮检对(S-R)经由反射点(Pref)的反射波菲涅耳体有限频射线(图4g).
![]() 图 4 反射波有限频射线追踪原理(a)自炮点S下行的走时场;(b)自检波器R下行的走时场;(c)自炮点S下行后经反射界面反射上行的走时场;(d)自检波器R下行后经反射界面反射上行的走时场;(e)自炮点S下行的菲涅耳体有限频射线;(f)自检波器R下行的菲涅耳体有限频射线;(g)最终得到的反射波菲涅耳体有限频射线. 模型上层速度v=5.0 km/s,下层速度v=5.5 km/s,地震波频率为1 Hz. 图中白色虚线为中心射线Figure 4. Diagram showing the principle of computing reflected Fresnel volume ray in two layered media(v=5.0 km/s for upper layer and v=5.5 km/s forlower layer) The downward traveltime fields from the source(a) and from the receiver(b),the reflected upward travel- fields from the reflector emitted from the source(c) andfromthereceiver(d),and the correspondingdownward Fresnel volume ray from the source to the reflector(e),from the receiver to the reflector(f)and the final reflected Fresnel volume ray for the source-receiver pair via the reflector(g)
图 4 反射波有限频射线追踪原理(a)自炮点S下行的走时场;(b)自检波器R下行的走时场;(c)自炮点S下行后经反射界面反射上行的走时场;(d)自检波器R下行后经反射界面反射上行的走时场;(e)自炮点S下行的菲涅耳体有限频射线;(f)自检波器R下行的菲涅耳体有限频射线;(g)最终得到的反射波菲涅耳体有限频射线. 模型上层速度v=5.0 km/s,下层速度v=5.5 km/s,地震波频率为1 Hz. 图中白色虚线为中心射线Figure 4. Diagram showing the principle of computing reflected Fresnel volume ray in two layered media(v=5.0 km/s for upper layer and v=5.5 km/s forlower layer) The downward traveltime fields from the source(a) and from the receiver(b),the reflected upward travel- fields from the reflector emitted from the source(c) andfromthereceiver(d),and the correspondingdownward Fresnel volume ray from the source to the reflector(e),from the receiver to the reflector(f)and the final reflected Fresnel volume ray for the source-receiver pair via the reflector(g)1.2.3 多震相菲涅耳体有限频射线追踪实例
基于上节所述方法,我们同样可以计算更为复杂震相的地震波菲涅耳体有限频射线.例如计算反射转换波的菲涅耳体有限频射线,仅需在正演计算走时场时根据所要计算的震相调用相应的速度模型(P波或S波)即可,其它步骤不变.计算多次反射波的菲涅耳体有限频射线时,需要根据实际情况将射线分为有限的射线段,分别计算每条射线段对应的菲涅耳体有限频射线,然后将各射线段对应的有限频射线连接即可.图5给出了在具有倾斜反射界面的3层速度模型中3种不同频率的多次反射和反射转换波的有限频射线,模型的速度从上至下依次为5.0,5.5,6.0 km/s.
![]() 图 5 具有倾斜界面的3层速度模型中3种不同频率的多次反射波(a,b,c)和反射转换波(d,e,f)有限频射线模型的速度从上至下依次为5.0,5.5,6.0 km/s. 多次反射波为P1P2P2P2P2P1,多次反射转换波为P1P2S2P2S2S1,震相符号上下标分别代表上行波和下行波,数字表示分区号. 中心虚线代表传统射线Figure 5. The multiple reflections P1P2P2P2P2P1(a,b,c)or reflections and conversions P1P2S2P2S2S1(d,e,f)of finite-frequency ray for three frequencies in three-layered velocity model with tilted interfaces The velocities of the model are 5.0,5.5,6.0 km/s from top to bottom. In seismic phase,the superscript and subscript indicate upward traveling wave and down traveling wave respectively,and the 1 or 2 is the subregion number,the dashed line indicates traditional ray
图 5 具有倾斜界面的3层速度模型中3种不同频率的多次反射波(a,b,c)和反射转换波(d,e,f)有限频射线模型的速度从上至下依次为5.0,5.5,6.0 km/s. 多次反射波为P1P2P2P2P2P1,多次反射转换波为P1P2S2P2S2S1,震相符号上下标分别代表上行波和下行波,数字表示分区号. 中心虚线代表传统射线Figure 5. The multiple reflections P1P2P2P2P2P1(a,b,c)or reflections and conversions P1P2S2P2S2S1(d,e,f)of finite-frequency ray for three frequencies in three-layered velocity model with tilted interfaces The velocities of the model are 5.0,5.5,6.0 km/s from top to bottom. In seismic phase,the superscript and subscript indicate upward traveling wave and down traveling wave respectively,and the 1 or 2 is the subregion number,the dashed line indicates traditional ray2. 多震相走时联合同时反演成像方法
2.1 方法原理
地下介质的速度分布和界面形态、 位置均是未知的,先验信息只能给出粗略的估计值,因此有必要进行速度和界面的同时反演.非线性多震相走时同时反演问题,可归结为带约束的阻尼最小二乘最优化问题,其反演的目标函数为

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

其中,Zm为模型约束算子. 上述方程可采用共轭梯度算法求解,关键问题是如何求取雅克比矩阵中的元素.
2.2 雅克比矩阵
依据射线理论,在射线坐标系下计算长度为L的第i条射线的走时ti,采用对沿射线路径上波慢度的线积分,即

式中,v(l)是沿射线路径上的速度分布.
由式(1)可知,在垂直于菲涅耳体的截面上,自中心射线到两边界,|tSx+tRx-tSR|值由0变化至T/2,这与有限频中的走时敏感核函数的分布类似.有限频成像中使用的是波形数据中的相关走时,而菲涅耳体有限频射线成像所用的依然是传统射线成像中的走时数据.因此,菲涅耳体有限频射线成像中走时敏感核函数在中心射线上的值应为最大,然后向边界(零值)逐渐衰减.
依据有限频理论,菲涅耳体内的所有空间速度结构均影响走时,相应的有限频走时方程为(Vasco et al,1995)

其中,R为垂直于射线路径L的菲涅耳带半径,Ar(l)为菲涅耳体射线的横截面面积.(6)中可以看出,其菲涅耳体射线内任一点对走时贡献的权重相同,它只是一种近似结果,而考虑走时敏感核函数Sr(l,r)下的有限频走时公式为

当地震波频率趋于无穷大时,菲涅耳体射线退化成传统射线,式(6)、(7)则退化成式(5).
同时反演速度和界面时,雅克比矩阵包含两部分内容:一是走时对速度的偏导数,二是走时对反射点的深度的偏导数,即

式中,ti为第i条射线的走时,vk为模型空间中该菲涅耳体射线所含第k个节点(主节点)的速度,N为该菲涅耳体射线包含的所有速度节点的个数,zj为该菲涅耳体射线所含第j个离散反射点的深度,M则是该菲涅耳体射线包含的所有离散反射点的个数.
由于菲涅耳体内空间各点对走时的贡献不同,故可定义一种走时敏感核函数Sik,表示菲涅耳体内第k个速度节点对第i条射线走时贡献的大小.一般而言,离中心射线越近,其权值越大;反之,其权值越小.令

由菲涅耳体的定义可知,在其轴线上dtk=0,而在边界上dtk=T/2,菲涅耳体内其它点上0<dtk<T/2.可以看出,dt值的差异可反映菲涅耳体内不同速度节点对走时的影响程度.据此,将第k个速度节点对第i条射线的走时贡献的权系数wik表示如下:

由上式可以看出,菲涅耳体轴线上走时贡献的权系数取最大值为1,而在边界上取最小值为0.考虑到各条射线在成像中的权重应相同,因此,对上述走时权系数还需作归一化处理,则定义归一化后的权系数为离散的走时敏感核函数:

式中,N为该菲涅耳体射线所含的速度节点总个数.对第i条菲涅耳体射线,速度变化对走时的影响则可表示为

当速度变化较小,即Δ\vk vk时,式(12)可简化为

最终得到走时对速度变化的偏导数

计算走时关于反射点深度变化的偏导数,可参照黄国娇和白超英(2010)文章,在深度方向,距反射界面Δz处引入一辅助界面,第i条射线经由这两个界面反射后的走时分别为ti和t′i,则由界面深度变化引起的走时变化量为

菲涅耳体射线入射到反射界面时具有一定的宽度(图4和图5),具有中心射线上敏感核函数值最大为1、 边界上最小为0的性质,即具有式(10)中wik的形式. 同样的考虑,其归一化后的形式为

所不同的是上述求和是对该菲涅耳体射线入射到反射界面时的射线宽度内所含离散反射点的个数总和M求和,则第i条菲涅耳体射线走时对第j个反射节点深度的偏导数为

由于有限频射线具有一定宽度,反射界面上将可能有多个界面节点包含其中,相比传统射线方法,有限频方法对界面采样则更加充分.
由于雅克比矩阵既包含了走时对速度的偏导数,又包含了走时对离散反射点深度的偏导数,二者量纲不同,数值大小差异较大,且未知个数后者较前者少. 这种情况下,反演时主要是更新速度模型,对界面的更新非常有限. 为使速度和界面都具有相当程度的更新,本文采用对两种参数各自归一的方法进行归一化处理. 具体做法可参见黄国娇和白超英(2010)文章.
3. 数值模拟实例
3.1 有限频射线层析成像与传统射线层析成像对比
本例中选用了一个较为复杂的层状起伏速度模型(图6a),模型大小为100 km×40 km,速度为一余弦函数且随深度线性递增. 其中含有两个反射界面,上界面类似余弦函数与速度起伏重合,中心位于20 km深度处,下界面则位于36—38km深度之间的倾斜台阶状界面.该模型网格单元为2km×2km,次级节点间距为0.2km.为了验证有限频射线成像的有效性和优越性,这里采用较为稀疏的炮检排列:11个炮点和21个检波器均匀地置于地表,即从模型顶部最左端开始,按照炮间距10 km、 道间距5 km布设炮点和检波器. 反演选用水平层状背景速度模型作为初始模型,即模型速度随深度线性递增(v=4.0+0.1z km/s),初始上界面置于水平(图8a),下界面为倾斜(图9a).所用震相资料为初至P波以及分别来自上、下界面的一次反射PP波走时.为了进行对比研究,反演中同时采用了两种不同的算法:一种是传统的射线方法,另一种则是本文提出的菲涅耳体有限频射线方法.反演中两种算法使用了相同的阻尼因子(0.2),各迭代30次. 有限频算法中采用了多种不同频率,这里给出了3种频率(0.5,3和50 Hz)的反演结果.
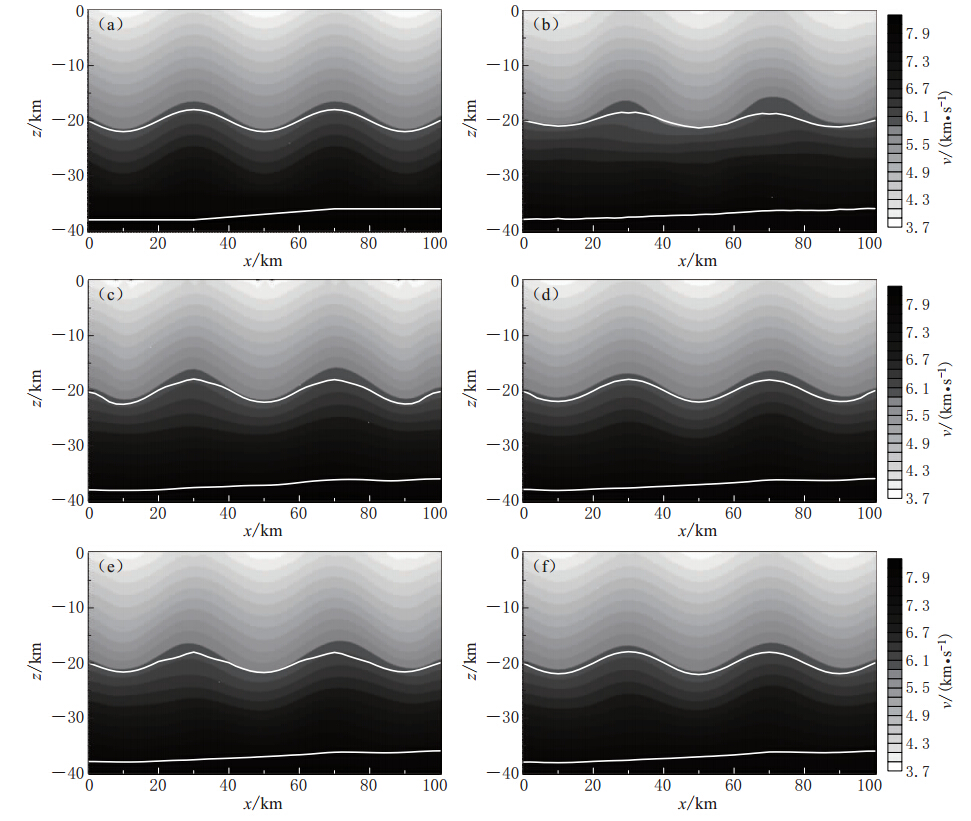
![]() 图 6 不同反演方法所得的速度场(a)真实速度模型和反射界面;(b)传统射线法所得的速度场;(c)-(e)分别为0.5,3和50 Hz有限频射线法所得的速度场;(f)变频有限频射线法所得的速度场.图中白色线为反射界面Figure 6. The velocity fields obtained by different methods(a)Real velocity model and reflected interfaces;(b)The velocity field obtained by traditional ray method; (c)-(e)The velocity fields obtained by finite-frequency method with frequency 0.5,3 and 50 Hz,respectively;(f)The velocity field obtained by finite-frequency method with varying frequency. In figure the white lines are the reflected interfaces
图 6 不同反演方法所得的速度场(a)真实速度模型和反射界面;(b)传统射线法所得的速度场;(c)-(e)分别为0.5,3和50 Hz有限频射线法所得的速度场;(f)变频有限频射线法所得的速度场.图中白色线为反射界面Figure 6. The velocity fields obtained by different methods(a)Real velocity model and reflected interfaces;(b)The velocity field obtained by traditional ray method; (c)-(e)The velocity fields obtained by finite-frequency method with frequency 0.5,3 and 50 Hz,respectively;(f)The velocity field obtained by finite-frequency method with varying frequency. In figure the white lines are the reflected interfaces图6给出了相应的速度模型反演结果,尽管炮检排列较为稀疏,但由于使用了3种震相的地震走时数据,我们依然得到了较好的成像效果.3种不同频率的有限频射线成像结果(图6c-e)均好于传统射线的成像结果(图6b),特别是对于上界面附近和上、下界面之间的速度分布.就3种不同频率有限频射线反演结果来看,3 Hz频率的结果(图6d)要好于其它两种频率的成像结果.另一方面,上界面以上区域有直达波射线和分别来自上、下界面的反射波射线穿过,射线密度较大,所以有限频射线法层析成像与传统射线层析成像法对这一区域内的速度重建大体相同;而在上、下界面之间的区域,由于主要是来自下界面的反射波射线,因此射线密度相对较小,则有限频射线层析成像法明显优于传统射线层析成像法.
上述结果表明,在进行有限频射线层析成像时,由于使用的地震波的频率不同,获取的结果将具有一定的差异.频率可根据所用地震波的主频率进行选取,但由于多震相数据中不同震相的频率不同,故可仿照传统射线层析成像的自适应反演方法(Thurber,Eberhart-Phillips,1999),进行变频有限频射线层析成像,即先采用低频地震资料反演大尺度结构,然后再用高频地震资料进行小尺度(细微结构)的细化反演.这样在变频有限频射线层析成像中,根据所用多震相地震资料的频率范围,反演迭代中从低频向高频过渡.本实例中依次使用的频率为1,3,6,10,15和20 Hz,每个频率迭代5次(共计30次),其结果见图6f. 总的来说,这种变频反演结果最好,这一点从图6d与图6f的对比中即可看出. 图6d是3种固定频率中反演结果最好的,而变频反演的结果(图6f)略好于固定频率为3 Hz的反演结果(图6d).从以上结果来看,采用变频反演是可行的.
为了直观地评价反演效果,即速度模型的更新程度,图7给出了反演速度与真实速度的百分比误差,百分比误差越小,速度场重建恢复率越高. 从图中可以得出这样的结论: ① 有限频射线层析成像法优于传统射线层析成像法; ② 就单一频率来讲,3 Hz有限频限射线反演的结果(图7d)是3种频率中最好的; ③ 变频有限频射线层析成像法的结果略好于3 Hz单一频率的反演结果.
![]() 图 7 不同反演方法所得的速度与真实速度的百分比误差(a)初始速度与真实速度的百分比误差;(b)传统射线法所得速度与真实速度的百分比误差;(c)-(e)分别为0.5,3和50Hz有限频射线法所得速度与真实速度的百分比误差;(f)变频有限频射线法所得速度与真实速度的百分比误差Figure 7. Percentage residual between the velocity fields obtained by different methods and the real velocity model(a)Percentage residual between the initial and the real velocity models;(b)Percentage residual between the velocity obtained by traditional ray method and the real model;(c)-(e)Percentage residual between the velocity obtained by finite-frequency method and the real model,and the frequency is 0.5,3 and 50 Hz,respectively;(f)Percentage residual between the velocity obtained by finite-frequency method with varying frequency and the real model
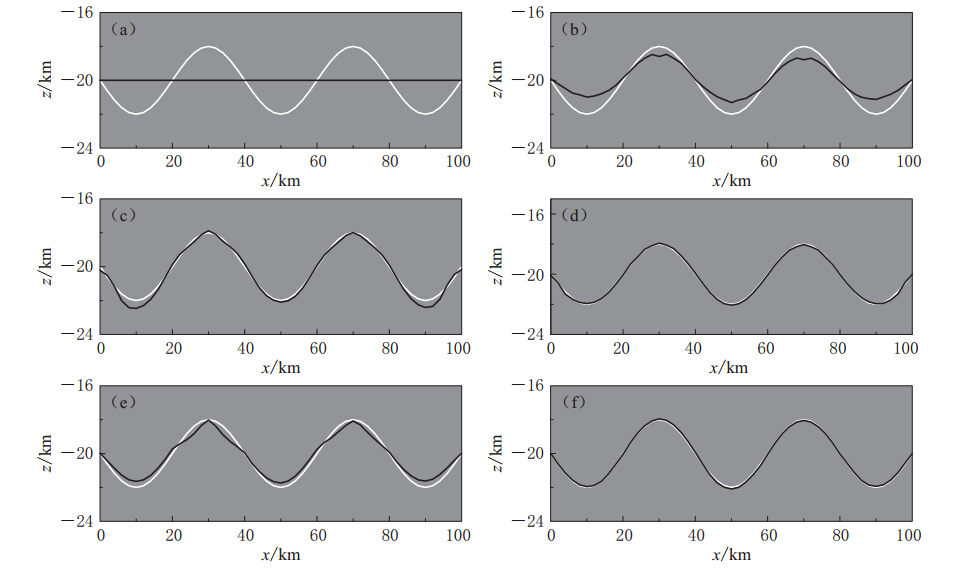
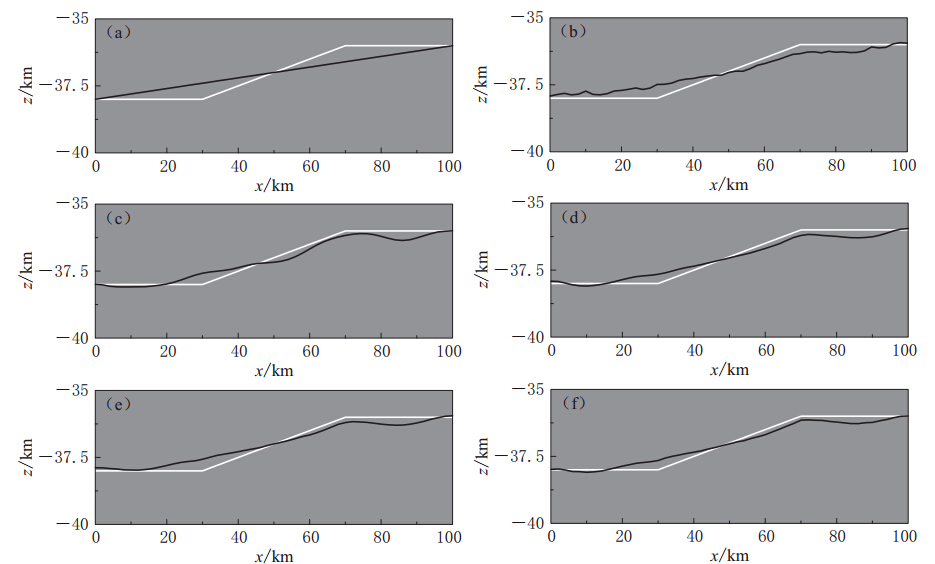
图 7 不同反演方法所得的速度与真实速度的百分比误差(a)初始速度与真实速度的百分比误差;(b)传统射线法所得速度与真实速度的百分比误差;(c)-(e)分别为0.5,3和50Hz有限频射线法所得速度与真实速度的百分比误差;(f)变频有限频射线法所得速度与真实速度的百分比误差Figure 7. Percentage residual between the velocity fields obtained by different methods and the real velocity model(a)Percentage residual between the initial and the real velocity models;(b)Percentage residual between the velocity obtained by traditional ray method and the real model;(c)-(e)Percentage residual between the velocity obtained by finite-frequency method and the real model,and the frequency is 0.5,3 and 50 Hz,respectively;(f)Percentage residual between the velocity obtained by finite-frequency method with varying frequency and the real model图8和图9分别给出了3种不同方法对上(图8)、 下(图9)反射界面更新的结果. 可以看出,无论是哪种单一频率有限频射线层析成像法,其对界面的更新情况均优于传统射线层析成像法. 相比之下,使用3 Hz地震波的结果是 3种频率结果中最好的(图8d和图9d),而变频有限频射线层析成像法界面的更新结果(图8f和图9f)均优于3 Hz单频有限频射线层析成像法的结果,尤其是对类似余弦函数的上界面的更新几乎与真实界面一样.
![]() 图 8 上界面的反演结果(a)初始界面;(b)传统射线反演结果;(c)-(e)分别为使用0.5,3和50 Hz有限频射线反演结果; (f)变频有限频射线反演结果. 图中白色线为真实界面,黑色线为更新后的界面Figure 8. The inverted result for upper reflected interface(a)Initial interface;(b)Result by traditional ray method;(c)-(e)Results by 0.5,3 and 50 Hzfinite-frequency ray method,respectively;(f)Result by finite-frequency ray method with varying frequency. The white lines are the real interfaces and dark lines are the updated interfaces
图 8 上界面的反演结果(a)初始界面;(b)传统射线反演结果;(c)-(e)分别为使用0.5,3和50 Hz有限频射线反演结果; (f)变频有限频射线反演结果. 图中白色线为真实界面,黑色线为更新后的界面Figure 8. The inverted result for upper reflected interface(a)Initial interface;(b)Result by traditional ray method;(c)-(e)Results by 0.5,3 and 50 Hzfinite-frequency ray method,respectively;(f)Result by finite-frequency ray method with varying frequency. The white lines are the real interfaces and dark lines are the updated interfaces![]() 图 9 下界面的反演结果(a)初始界面;(b)传统射线反演结果;(c)-(e)分别为使用0.5,3和50 Hz有限频射线反演结果; (f)变频有限频射线反演结果. 图中白色线为真实界面,黑色线为更新后的界面Figure 9. The inverted result for lower reflected interface(a)Initial interface;(b)Result by traditional ray method;(c)-(e)Results by 0.5,3 and 50 Hz finite-frequency ray method,respectively;(f)Result by finite-frequency ray method with varying frequency. The white lines are the real interfaces and dark lines are the updated interfaces
图 9 下界面的反演结果(a)初始界面;(b)传统射线反演结果;(c)-(e)分别为使用0.5,3和50 Hz有限频射线反演结果; (f)变频有限频射线反演结果. 图中白色线为真实界面,黑色线为更新后的界面Figure 9. The inverted result for lower reflected interface(a)Initial interface;(b)Result by traditional ray method;(c)-(e)Results by 0.5,3 and 50 Hz finite-frequency ray method,respectively;(f)Result by finite-frequency ray method with varying frequency. The white lines are the real interfaces and dark lines are the updated interfaces为了进一步了解反演解的收敛情况,表1给出了反演结果的误差值.从表中也可以明显地看出,无论是变频还是单一频率,有限频射线层析成像法的收敛均优于传统射线层析成像法,且3Hz有限频射线层析成像法的收敛在3种频率中是最好的,而变频有限频射线层析成像法的收敛又优于3Hz单频有限频射线层析成像法.这一结果与上述的讨论是一致的.因此可以得出这样的结论:不管是对速度结构还是对反射界面的更新,选择合适频率的有限频射线的成像效果均优于传统射线的成像效果,而变频有限频射线的成像效果又优于单频有限频射线的成像效果.
表 1 速度和界面同时反演结果误差Table 1. The residuals for simultaneous inversion
3.2 有限频射线层析成像算法有效性试验
为验证有限频射线层析成像算法的有效性,我们在上节中所使用的初始模型的基础上,将初始模型速度整体提升一定量(0.5km/s,相当于初始模型估计存在的系统误差),同时也将两个初始反射界面整体分别抬升0.5,1.0,1.5和2.0km,然后进行3 Hz单一频率的同时反演成像. 表2给出了采用4种不同偏移量作为初始模型(速度和界面)时,反演迭代30次结果(速度和界面)的误差情况.可以明显看出,4种情况下反演算法均收敛,但初始界面偏离真实界面越远,反演结果误差越大.
表 2 有效性试验误差Table 2. Residual errors in the efficiency tests
3.3 CPU时间对比分析
从以上反演结果来看,无论是单一频率还是变频有限频菲涅耳体射线层析成像的效果均优于传统射线层析成像的效果. 这里我们分析讨论两种不同反演算法的CPU运行时间(表3).所用笔记本电脑为:Intel(R)Core(TM)Duo CPU-2.0 GHz. 表3统计了上述同时反演中两种不同算法单次正演和反演的计算用时,其中无论是单一频率还是变频有限频菲涅耳体射线层析成像单次正、反演所用时间大体相当,属同一个数量级范围,但均比传统射线层析成像方法耗时.其主要原因是,正演算法中传统射线层析成像方法的用时主要与炮点个数(NS)有关,而有限频菲涅耳体射线层析成像方法的用时则与炮检总数(NS+NR)有关.本例中炮点为11个,而检波器为21个,则有限频菲涅耳体射线与传统射线单次正演所用CPU时间的比值为(11+21)/11≈2.9,这与表3中的比值大体相当;由于有限频菲涅耳体射线宽度的影响,雅克比矩阵中非零元素明显增加,从而导致有 限频菲涅耳体射线比传统射线单次反演所需的CPU时间要多. 至于非零元素明显增加现象,我们将在另文中讨论.从表3中可以大体估计本例中有限频菲涅耳体射线与传统射线成像单次正反演所需的CPU时间的比值约为3. 这一比值与炮检数有关. 不失一般性,两者的CPU用时应在同一数量级内.
表 3 CPU时间Table 3. CPU time
4. 讨论与结论
本文给出了多震相菲涅耳体射线的计算方法,将之用于层析成像研究,讨论同时反演速度模型和反射界面形状的问题.与传统射线层析成像方法相比,菲涅耳体射线层析成像方法具有更高的分辨率.数值模拟结果表明,选用合适频率的菲涅耳体射线法的成像效果优于传统射线法,而选用合适频率范围的变频菲涅耳体射线法的成像效果又优于单频菲涅耳体射线法.
影响层析成像分辨率的主要因素是地震射线密度和射线相互交叉概率,当射线密度较高、 相互交叉概率较高时,容易获得较高精度的成像结果. 实际情况下,地震台站和地震事件的分布及数量均受到限制,使得地震射线密度较小且分布不均,基于高频假设条件下的传统射线层析成像方法难以获得较高分辨率的成像结果. 实际地震波的传播不仅受传统射线上空间速度结构的影响,传统射线附近一定区域(第一菲涅耳体)内的空间速度结构也将影响地震波的传播,因此将菲涅耳体射线应用于层析成像研究. 当射线密度较小时,传统射线对速度模型和反射界面的采样受到制约,反演矩阵十分稀疏,而菲涅耳体射线具有一定空间范围,对模型采样更加充分,因此无论是对速度场的重建还是对反射界面几何形状的更新,菲涅耳体射线层析成像法的结果均优于传统射线层析成像法; 当射线密度很大时,菲涅耳体射线层析成像法与传统射线层析成像法对模型的采样和约束均较好,利用这两种方法同时进行反演,成像的结果大体相当. 鉴于实际地震波的频率具有一定的分布范围,我们使用了从低频逐渐过渡到高频的变频菲涅耳体射线层析成像,即首先进行大尺度(粗网格单元)的结构重建,然后有机地过渡到小尺度(精细结构)的重建,其物理意义是明显的,同时也降低了人为因素的影响,获得了更好的反演结果.下一步研究的重点是将其推广至三维情形,在利用多震相走时数据的同时,考虑引入多个频率(变频)成分的地震波,从而在利用天然地震资料对地球内部精细结构进行成像时,达到有效提高成像分辨率的目的.
-
图 1 震源S到检波器R的菲涅耳体示意图(根据Červený, Soares,1992修改)Ω表示震源S与检波器R对应的第一菲涅耳体;oF表示空间点x在中心射线的投影点; ∑F 为过点oF的菲涅耳带所在的平面
Figure 1. Diagram showing the first Fresnel volume between source S and receiver R(revised after Červený, Soares,1992) Ω is the first Fresnel volume for source S and receiver R,oF denotes the project point of x on central ray,and ∑F is a plane which contains the Fresnel zone crossing the point oF
图 2 均匀速度场(v=5.0km/s)中直达波有限频射线追踪原理(a)由震源点计算所得的走时场;(b)由检波器点计算所得的走时场;(c)地震波频率为2Hz时的菲涅耳体射线分布,白色虚线为中心射线;(d)5种不同频率地震波的菲涅耳体边界,虚线代表传统射线路径
Figure 2. Principle of finite frequency ray tracing for direct wave,velocity model is v=5.0 km/s (a)Travel time field calculated from the source point S;(b)Travel time field calculated from the receiver point R; (c)The first Fresnel volume ray with seismic frequence of 2 Hz,and the white dashed line denotes the central ray;(d)Boundaries of the first Fresnel volume with varying frequencies,from inside to outside the frequency is 20,5,2,1 and 0.5 Hz,respectively. Dashed line is the traditional ray path
图 4 反射波有限频射线追踪原理(a)自炮点S下行的走时场;(b)自检波器R下行的走时场;(c)自炮点S下行后经反射界面反射上行的走时场;(d)自检波器R下行后经反射界面反射上行的走时场;(e)自炮点S下行的菲涅耳体有限频射线;(f)自检波器R下行的菲涅耳体有限频射线;(g)最终得到的反射波菲涅耳体有限频射线. 模型上层速度v=5.0 km/s,下层速度v=5.5 km/s,地震波频率为1 Hz. 图中白色虚线为中心射线
Figure 4. Diagram showing the principle of computing reflected Fresnel volume ray in two layered media(v=5.0 km/s for upper layer and v=5.5 km/s forlower layer) The downward traveltime fields from the source(a) and from the receiver(b),the reflected upward travel- fields from the reflector emitted from the source(c) andfromthereceiver(d),and the correspondingdownward Fresnel volume ray from the source to the reflector(e),from the receiver to the reflector(f)and the final reflected Fresnel volume ray for the source-receiver pair via the reflector(g)
图 5 具有倾斜界面的3层速度模型中3种不同频率的多次反射波(a,b,c)和反射转换波(d,e,f)有限频射线模型的速度从上至下依次为5.0,5.5,6.0 km/s. 多次反射波为P1P2P2P2P2P1,多次反射转换波为P1P2S2P2S2S1,震相符号上下标分别代表上行波和下行波,数字表示分区号. 中心虚线代表传统射线
Figure 5. The multiple reflections P1P2P2P2P2P1(a,b,c)or reflections and conversions P1P2S2P2S2S1(d,e,f)of finite-frequency ray for three frequencies in three-layered velocity model with tilted interfaces The velocities of the model are 5.0,5.5,6.0 km/s from top to bottom. In seismic phase,the superscript and subscript indicate upward traveling wave and down traveling wave respectively,and the 1 or 2 is the subregion number,the dashed line indicates traditional ray
图 6 不同反演方法所得的速度场(a)真实速度模型和反射界面;(b)传统射线法所得的速度场;(c)-(e)分别为0.5,3和50 Hz有限频射线法所得的速度场;(f)变频有限频射线法所得的速度场.图中白色线为反射界面
Figure 6. The velocity fields obtained by different methods(a)Real velocity model and reflected interfaces;(b)The velocity field obtained by traditional ray method; (c)-(e)The velocity fields obtained by finite-frequency method with frequency 0.5,3 and 50 Hz,respectively;(f)The velocity field obtained by finite-frequency method with varying frequency. In figure the white lines are the reflected interfaces
图 7 不同反演方法所得的速度与真实速度的百分比误差(a)初始速度与真实速度的百分比误差;(b)传统射线法所得速度与真实速度的百分比误差;(c)-(e)分别为0.5,3和50Hz有限频射线法所得速度与真实速度的百分比误差;(f)变频有限频射线法所得速度与真实速度的百分比误差
Figure 7. Percentage residual between the velocity fields obtained by different methods and the real velocity model(a)Percentage residual between the initial and the real velocity models;(b)Percentage residual between the velocity obtained by traditional ray method and the real model;(c)-(e)Percentage residual between the velocity obtained by finite-frequency method and the real model,and the frequency is 0.5,3 and 50 Hz,respectively;(f)Percentage residual between the velocity obtained by finite-frequency method with varying frequency and the real model
图 8 上界面的反演结果(a)初始界面;(b)传统射线反演结果;(c)-(e)分别为使用0.5,3和50 Hz有限频射线反演结果; (f)变频有限频射线反演结果. 图中白色线为真实界面,黑色线为更新后的界面
Figure 8. The inverted result for upper reflected interface(a)Initial interface;(b)Result by traditional ray method;(c)-(e)Results by 0.5,3 and 50 Hzfinite-frequency ray method,respectively;(f)Result by finite-frequency ray method with varying frequency. The white lines are the real interfaces and dark lines are the updated interfaces
图 9 下界面的反演结果(a)初始界面;(b)传统射线反演结果;(c)-(e)分别为使用0.5,3和50 Hz有限频射线反演结果; (f)变频有限频射线反演结果. 图中白色线为真实界面,黑色线为更新后的界面
Figure 9. The inverted result for lower reflected interface(a)Initial interface;(b)Result by traditional ray method;(c)-(e)Results by 0.5,3 and 50 Hz finite-frequency ray method,respectively;(f)Result by finite-frequency ray method with varying frequency. The white lines are the real interfaces and dark lines are the updated interfaces
表 1 速度和界面同时反演结果误差
Table 1 The residuals for simultaneous inversion

表 2 有效性试验误差
Table 2 Residual errors in the efficiency tests

表 3 CPU时间
Table 3 CPU time

-
-
期刊类型引用(0)
其他类型引用(2)




 下载:
下载: