The seismic forward modeling using Born approximation equation based on rheological body
-
摘要: 常规τ值法假设应力松弛时间与应变延迟时间近似相等, 造成了常Q模型拟合精度低. 本文利用精确的广义流变体模型Q值计算公式, 研究改进的τ值法求解常Q模型参数. 根据地震波散射理论, 推导了基于广义流变体模型的黏滞性介质一阶波恩近似方程, 结合位移-速度关系得到了含卷积完全匹配层边界条件的黏滞性介质应力-速度方程的一阶波恩近似表达式. 通过数值实验验证并对比了黏滞性介质中全波波动方程、 一阶波恩近似方程以及单程波波动方程的波场特征, 讨论了基于流变体模型的黏滞性介质一阶波恩近似方程对速度扰动和Q扰动的适应性, 以及对旅行时和振幅精度的影响.Abstract: The conventional τ method assumes that the stress relaxation time is approximately equal to the strain delay time, leading to the constant Q model with low precision. In this study, an improved τ method is proposed by an accurate equation of Q value based on generalized rheological body so as to solve the parameters of constant Q model. According to the seismic wave scattering theory, the first-order Born approximation equation in viscoacoustic media is derived based on generalized rheological body and then the first-order Born approximation of stress-velocity equation is obtained for the viscoacoustic media with convolutional perfect matched layer (CPML) boundary. The wave fields and records are compared through numerical simulation by full wave equation, first-order Born approximation equation and one-way wave equation. And it is also discussed that the precision of travel time and amplitude of the seismic wave obtained by the viscoacoustic first-order Born approximation equation with velocity perturbation and Q perturbation.
-
Keywords:
- rheological body /
- Born approximation /
- improved τ method /
- velocity perturbation /
- Q perturbation
-
引言
油气储层与地下介质中的孔隙裂缝、地层的非均质性和孔隙流体有关.基于完全弹性假设的弹性波理论不能满足对油气储层中地震波能量损失、速度频散以及波形扭曲等波场特征的表达.为了更精确地描述实际油气储层中地震波的传播规律,需要建立与油气特征相应的介质模型.介质模型与地震波的传播特征密切相关(牛滨华,孙春岩,2004).基于黏弹性介质理论的地震波响应中包含了弹性响应和黏滞性响应,能够合理地表达油气储层所表现出的固相弹性介质和流相黏性介质特征,从而成为研究油气储层中地震波传播特征的主要介质模型.黏弹性介质中的黏滞性特征通常用地层品质因子Q进行衡量.实验测试表明,地层品质因子Q在地震频带内几乎与频率无关,但其衰减与频率密切相关,故频率域更有利于引入黏弹性特征的描述.时间域可利用弹簧与阻尼组合建立基于流变学的黏弹性模型,将黏滞性特征引入波动方程.基本流变体模型包含麦克斯韦模型和开尔文-佛格特模型,其中麦克斯韦模型中Q值随频率的增加呈线性关系;而开尔文-佛格特模型中Q值则与频率成反比关系,并且在地震频带内Q值随频率变化较为剧烈.这些基本流变体模型无法满足对黏弹性介质中常Q模型特征的精确模拟,其根本原因在于只包含单个松弛时间特征;而广义流变体模型将多个基本流变体模型进行组合,使其更能适合对常Q黏弹性模型的描述(Carcione et al,1988).流变体模型中采用应力松弛时间与应变延迟时间表示介质的黏滞性强度,需要建立地层品质因子Q与应力松弛时间和应变延迟时间之间的转化关系.常规的τ值法由于在应力松弛时间与应变延迟时间相等的假设条件下确定常Q模型参数,故得到的常Q模型误差较大,特别是对于低Q值的情况,地震波衰减程度存在很大的误差.
时间域黏弹性介质数值模拟方面,国内外研究均已成熟. Day和Minster(1984)通过Padé有理近似将时间域的褶积关系转化为微分关系,进而推动了时间域线性黏弹性体的数值模拟. Emmerich和Korn(1987)基于广义麦克斯韦模型确定了具有明确物理含义的有理近似式系数,解决了Padé有理近似只能适用于弱衰减短波长的问题. Carcione等(1988)和Carcione(1993)在广义标准线性黏弹体中引入记忆变量的概念,并利用伪谱法计算空间导数,实现了二维和三维黏弹性介质的数值模拟.伪谱法能够减弱频散特征的影响,但是离散傅里叶变换的计算降低了计算效率. Robertsson等(1994)利用时间-空间域有限差分算法,实现了基于广义标准线性固体模型的黏弹性介质的数值模拟. Štekl和Pratt(1998)在频率域利用旋转有限差分算法开展了黏弹性数值模拟. Kristek和Moczo(2003)基于广义麦克斯韦模型重新定义了与黏滞性系数无关的黏弹体方程,实现了三维黏弹性介质交错网格有限差分的正演模拟.杨文采(1986)基于谐Q模型,采用一维频率域递推实现了黏弹性介质中反射地震道的合成.毕玉英和杨宝俊(1995)推导了频率域波场递推关系,并形成了含有AVO特征的复反射系数,利用线源代替点源从一维计算推广到二维计算.崔建军和何继善(2001)从二维黏弹性波动方程出发,在f-k域内实现了基于开尔文介质的黏弹性波动方程的正演和偏移.杜启振等(2006)研究了线性黏弹性各向异性介质中速度频散和衰减特征.郭少华(2004)研究了基于开尔文-佛格特模型的黏弹性波动力学特征.苑春方等(2005)利用叠加原理推导了在任意震源条件下,开尔文-佛格特模型均匀黏弹性介质中三阶波动方程地震波传播的平面波解析解.单启铜(2007)基于开尔文模型实现了黏弹性波动方程正演模拟及参数反演.孙成禹等(2010)分析了矩形网格下不同黏弹模型波动方程有限差分解的稳定性,导出了开尔文-佛格特黏弹模型和麦克斯韦黏弹模型在任意空间差分精度下稳定性条件的表达式.
基于全波波动方程的黏弹性介质地震波不仅包含反射波,还包含折射波、潜水波以及多次波,能够有效地模拟复杂构造中地震波的传播特征.但在目前地震勘探中,地震资料的解释仍主要利用一次反射波的信息.特别是目前应用最为广泛的地震反射波反演方法对波场特征的敏感性强,而多种波场同时存在则容易引起反演结果的不准确性.单程波地震波数值模拟提供了一种适用于简单介质的一次反射波的构建方法(何兵红等, 2009,2014;何兵红,2011).但对于盐丘等复杂介质,单程波法对于其地下地质构造的模拟精度较低.基于地震波散射理论的一阶波恩近似波动方程在弱扰动假设下忽略多级散射,可以得到连续界面的一次反射波.与单程波波动方程相比,一阶波恩近似波动方程对于高角度波场信息模拟精度更高.郑江峰(2006)基于开尔文-佛格特模型推导了频率域黏弹性介质的波恩近似.本文基于广义流变体模型推导了时间域黏滞性声波介质的速度-应力方程,根据散射波理论得到了其一阶波恩近似方程;提出了改进的τ值法拟合常Q模型,由于该模型不再受应力松弛时间与应变延迟时间相等条件的约束,从而提高了低Q情况下常Q模型的拟合精度.卷积完全匹配层(convolutional perfect matched layer,简写为CPML)对大角度入射边界反射吸收效果要优于完全匹配层(perfect matched layer,简写为PML)(张鲁新等,2010),为消除边界反射进一步得到了含有CPML边界的时间域黏滞性介质的一阶波恩近似方程;数值试验对比了黏弹性介质中一阶波恩近似方程与全波波动方程以及单程波波动方程的模拟精度,并分析了一阶波恩近似方程对速度扰动和地层Q扰动的适应性.
1. 基于流变体模型改进的τ值法拟合常Q特征
实验证明地震波在介质中传播时的衰减与频率相关,在地震频带内地层品质因子Q与频率无关.为了在地震频带内构建与频率无关的黏弹性模型,以麦克斯韦模型和开尔文-佛格特模型为基础的广义流变体模型得以发展. Moczo和Kristek(2005)、曹丹平(2008)以及Cao和Yin(2014)等证明了广义麦克斯韦模型与广义标准线性体模型(基于麦克斯韦模型的标准线性体固体模型(generalized Maxwell st and ard linear solid model,简写为GMSLS)、基于开尔文-佛格特的标准线性体固体模型(generalized Kelvin-Voigt st and ard linear solid model,简写为GKSLS))是等价的.
基于GMSLS模型的Q值可以表示为(Blanch et al,1995)

式中,ω为角频率,L为标准线性黏弹体的个数,τε l和τσ l分别为应变松弛时间和应力松弛时间.
为了获得Q值的参数,定义松弛时间为

则式(1)重新整理为

强衰减低Q介质中不满足假设条件τl+1≈1,对于常Q模型拟合存在很大误差;常规τ值法稳定性虽得到提高,但其精度不高.本文为了提高Q值拟合精度,定义函数

则式(3)可表示为

假设真实品质因子为Qtrue,根据最小二乘法建立目标函数:

式中,ωs和ωe分别为积分范围的开始角频率和截止角频率.假设每个标准线性黏弹体τl相等,即τl=τ.对τ求导并令其为零,即

得到τ的计算表达式为

即为改进的τ值法. Blanch等(1995)提出的常规τ值表达式为

对比式(9)与式(10)可知,当∫ωsωeH(ω)/F2(ω)dω<<∫ωsωeQtrue/F(ω)dω时,改进的τ值法式(9)可简化为

此改进的τ值计算式与常规τ值计算式等价.
改进的τ值计算式中,H(ω)/F(ω)随频率变化的特征能够对Q(ω)进行与频率有关的修正.当L=5时,常规τ值法与改进的τ值法在地震频带内均能够对常Q模型进行较高精度的拟合.本文采用L=4对改进的τ值法进行测试.由测试结果(图 1)可知,改进的τ值法所确立的Q模型更能接近常Q模型,特别是在中高频部分对常规的τ值法进行了很大的修正.
2. 基于广义流变体模型的位移方程的建立
根据玻尔兹曼叠加原理,在线性黏弹性介质中应力-应变方程为

式中,σ为应力,ε为应变,*为卷积算子,ψ为松弛函数.黏滞性声波介质中松弛函数可以分别用松弛模量和未松弛模量来表示:

本文采用未松弛模量表达式.
根据定义,时间域模量是松弛函数对时间的导数,可得

将式(15)带入式(12)得到用模量表示的应力方程为

为了解决时间域卷积形式求解问题,Day和Minster(1984)基于Padé近似引入记忆变量的概念,该思想被逐步接纳并广泛应用.
定义记忆变量为

并对时间t求导可得

则式(16)可表示为

将应力、应变与位移之间的关系分别代入式(18)和式(19)中,可得黏滞性位移方程为

式中,体积模量K=c2ρ,c为地震波传播速度.
3. 基于地震波散射理论的波恩近似方程的建立
摄动理论假设下,地下介质可以划分为背景介质和扰动介质,其对应的地震波场分解为背景波场和扰动波场.在黏滞性声波介质中,介质参数包含弹性参数和黏滞性参数.本文中弹性参数包含体积模量K和密度ρ. GMSLS模型中黏滞性参数用τεl和τσl表示. τσl和τεl与Q值的对应关系通过式(2)和式(9)获得,因此在τσl固定的情况下,所对应的有3个背景介质参数和3个扰动介质参数.本文定义

黏弹性介质中地震波场除了总压力波场,还需要计算黏滞性波场.其对应的波场分为2个背景波场和2个扰动波场.根据地震波散射理论,总波场可以分解为入射波场和散射波场,即

对于变密度介质,位移方程式(20)重新表示为

其中可分离出背景波场

以及包含多级散射的散射波场

在弱散射条件下忽略多级散射,用背景场代替总波场,背景介质参数代替总介质参数,可得到基于一阶波恩近似的散射波场为

波场对于时间一阶导数的存在,导致常规网格数值求解可执行性差,通常利用速度、应力与位移三者之间的关系,即

将位移方程式(20)降阶为应力-速度方程:

该方程将所有关于时间和空间的二阶导数降低为一阶导数,从而可采用二维交错网格进行数值求解.但同时在该方程中也需引入变量vx和vz来分别表示x方向和z方向的速度分量,因此黏滞性声波介质中实际存在4个波场.
根据地震波散射理论,总波场可以分解为入射波场和散射波场,即

本文定义如下变量:

将式(30)中的各个变量带入应力-速度方程式(28)中,可将总波场分解为背景波场和散射波场.同时在散射波场计算中用背景波场代替总波场,背景介质参数代替总介质参数,可得到基于一阶波恩近似的散射波场满足的应力-速度方程:

4. 非分裂式CPML边界条件
地震波数值模拟对实际地球介质进行了有限区域假设,在区域边界通常会产生人为的边界反射. Berenger(1994)提出的PML吸收边界条件从电磁场模拟引入到地震波模拟中,因其能够有效地消除边界反射的影响而成为广泛应用的一种边界条件.研究表明,PML边界条件对于地震波的吸收具有方向性,垂直入射的波能够在较短的时间内衰减一个数量级,而对于大角度入射的波则吸收效果欠佳.目前,地震波的研究多数是基于地面地震反射波法.当震源位于地层表面时,远偏移距波场以大入射角到达PML吸收边界区域,边界反射部分被吸收. Kuzuoglu和Mittra(1996)提出了复频移PML边界条件,其在时间域表现为卷积的形式,因此又称为CPML边界条件.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

在CPML边界条件中,引入实数项κx和αx:

式中,α≥0,κ≥1.该式中对复坐标求导可得

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

通过傅里叶反变换得到时间域形式为

通过递归得到迭代解为

将式(35)和(38)带入式(31),得到基于CPML边界条件的黏滞性介质一阶波恩近似方程:


采用CPML边界条件避免了将原始方程进行分解的问题,只需要增加辅助变量φ即可大大提高计算效率.
5. 数值测试
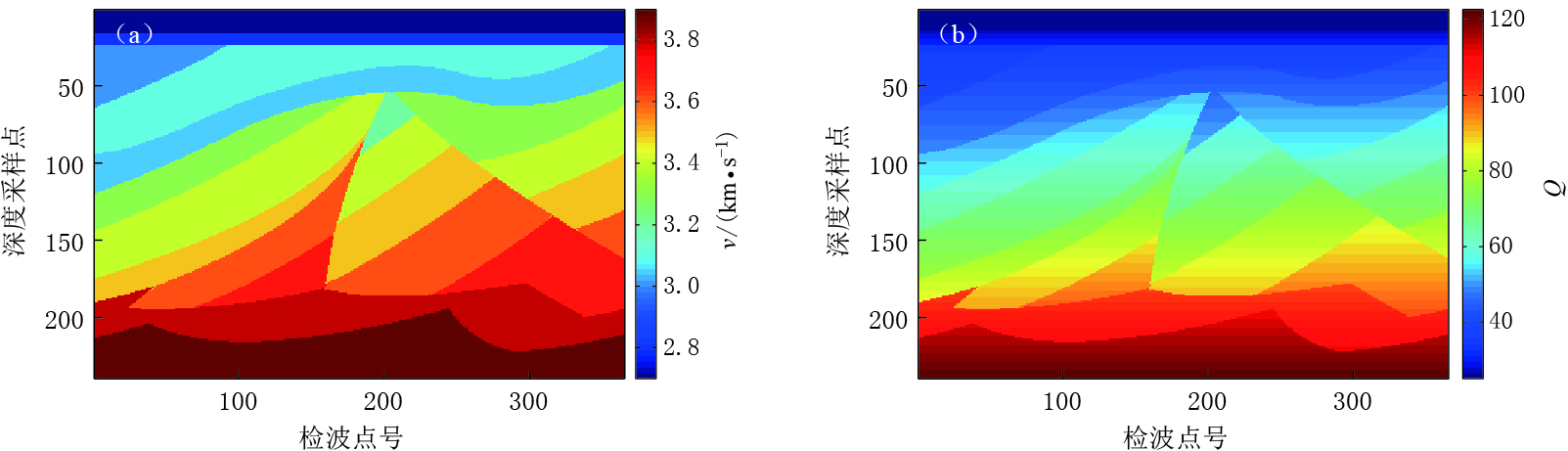
为研究黏滞性声波波动方程吸收衰减特征和基于一阶波恩近似的黏滞性声波介质散射波波场特征,本文建立了含有不整合界面的理论断层速度场.该模型纵测线长度为3 640 m,深度为2 380 m,采样间隔为10 m.炮点位于地表测线方向2 000 m处,检波器以10 m间隔均匀分布于地表.弱速度扰动模型中最低速度为2 600 m/s,最高速度为3 900 m/s(图 2a).弱Q扰动模型中Q值在李氏经验公式(李庆忠,1993)计算所得结果的基础上加入深度加权系数以增强浅层地层吸收特征(图 2b),浅层低Q值特征表示地表疏松介质的强衰减特征.在检波点号范围为180—220、深度约为750 m的断层构造中,其所对应的地层低Q特征表示了含气特征.
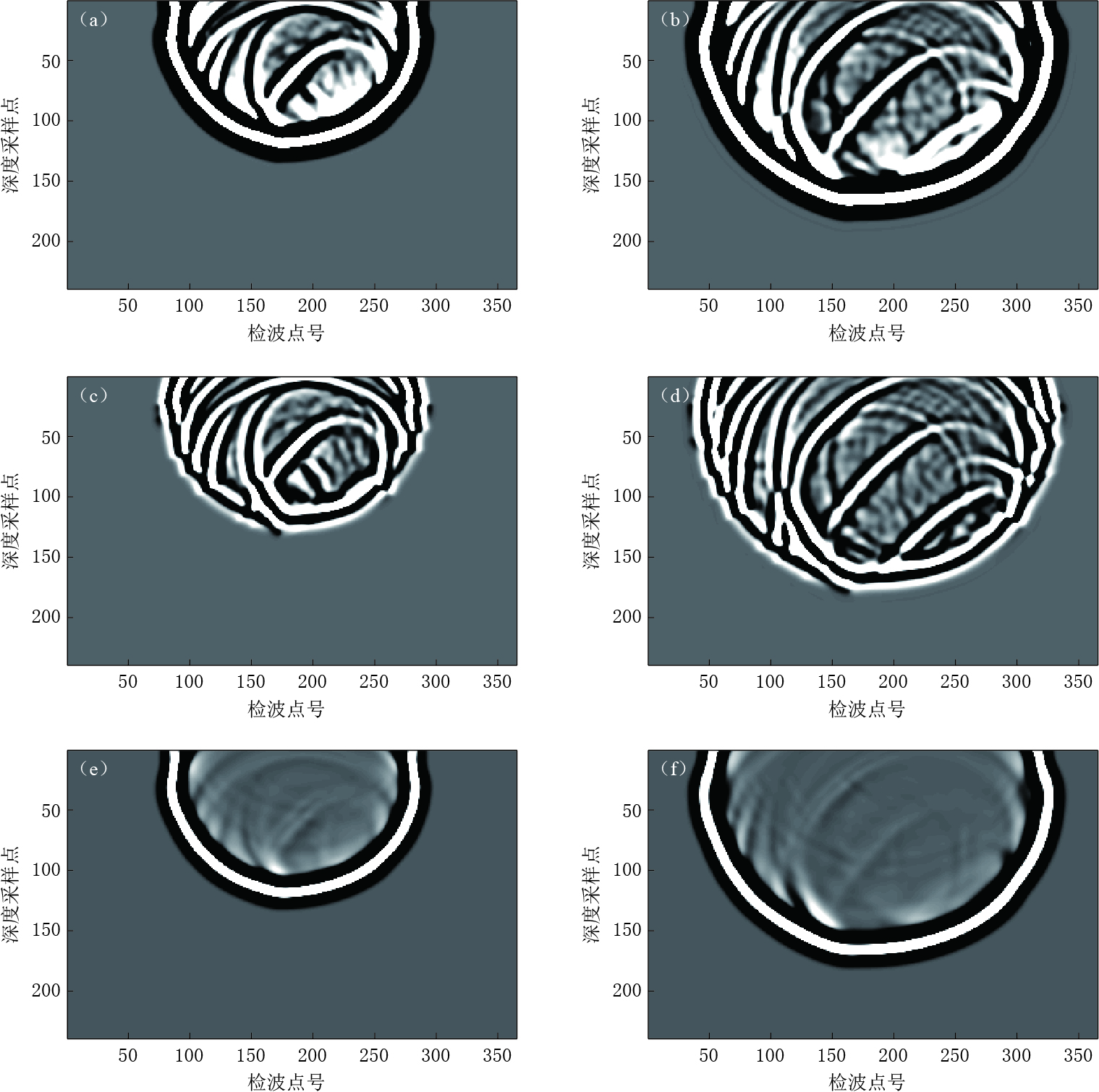
根据散射理论和量子力学理论,在弱散射条件下采用波恩近似用背景波场代替总波场得到散射波场.一阶波恩近似方程是对一级散射波场的描述,某个散射点处的散射波场可当做二次信号的激发源(吴如山,1993).由于地球介质中的散射问题满足辐射边界条件,即当地震波传播到无限远处时波场能量为零,因此可以利用格林函数求解方法得到其精确解的解析表达式.基于格林函数的散射波场求解既可以采用双程波思路,也可以采用波场分解理论将散射波场分为前向散射和背向散射,再利用单程波思路计算散射波场.本文采用时间域有限差分法利用双程波思路求解波恩近似方程,其计算简单且无须进行傅里叶变换.数值实验中全波波动方程包含了背景波场和散射波场(包含多级散射)(图 3a,b),在连续界面上基于波恩近似的一级散射波场表现为一次反射波(图 3c,d).由全波波动方程与一阶波恩近似方程所得到的波场差值中包含了透射波场和多级散射波场(图 3e,f).在反射波偏移成像中广泛使用的单程波法波场延拓能够实现主要反射波的数值模拟,是目前工业生产中主要使用的偏移成像方法之一.本文基于分步傅里叶算法得到了基于单程波波动方程的黏滞性介质波场(图 4a,b).数值结果表明,单程波法在低角度入射条件下能够获得较高的精度.但是对于高角度入射的情况,单程波波动方程与全波波动方程和一阶波恩近似方程相比,其精度较低.
![]() 图 3 弱速度扰动及弱Q扰动模型中由全波波动方程(a,b)和一阶波恩近似方程(c,d)得到的黏滞性介质波场以及由全波波动方程与一阶波恩近似方程得到的波场差值(e, f)(a), (c), (e)中t=420 ms; (b), (d), (f)中t=558 msFigure 3. The viscoacoustic wave fields obtained by different wave equations in the model with weak velocity perturbation and weak Q perturbation Figs.(a) and (b) are the wave fields obtained by full wave equation; Figs.(c) and (d) are the wave fields obtained by first-order Born approximation equation; Figs.(e) and (f) are the differencesbetween the wave fields in (a), (b) and those in (c), (d). In Figs.(a), (c),(e) t=420 ms and in Figs.(b), (d), (f) t=558 ms
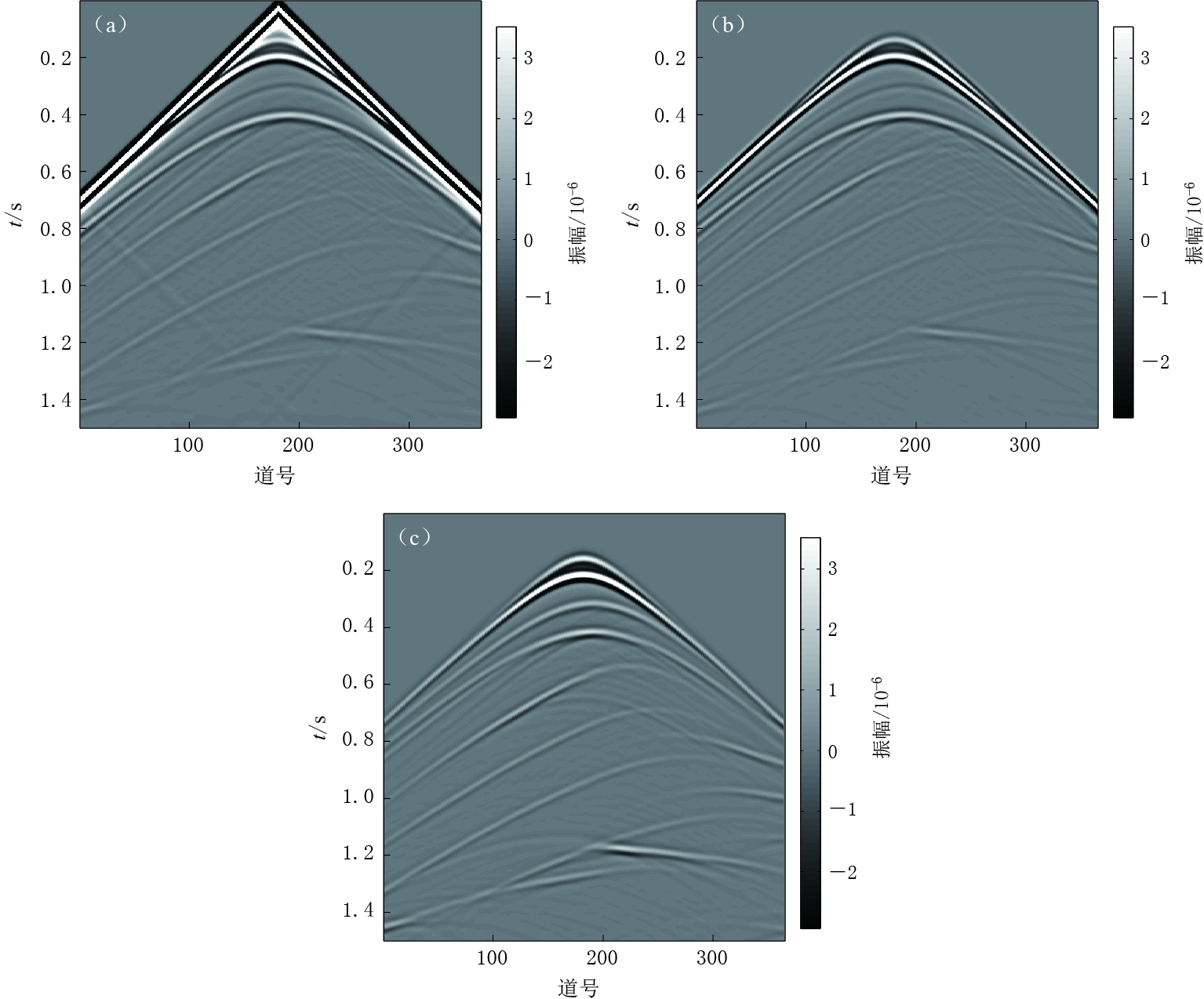
图 3 弱速度扰动及弱Q扰动模型中由全波波动方程(a,b)和一阶波恩近似方程(c,d)得到的黏滞性介质波场以及由全波波动方程与一阶波恩近似方程得到的波场差值(e, f)(a), (c), (e)中t=420 ms; (b), (d), (f)中t=558 msFigure 3. The viscoacoustic wave fields obtained by different wave equations in the model with weak velocity perturbation and weak Q perturbation Figs.(a) and (b) are the wave fields obtained by full wave equation; Figs.(c) and (d) are the wave fields obtained by first-order Born approximation equation; Figs.(e) and (f) are the differencesbetween the wave fields in (a), (b) and those in (c), (d). In Figs.(a), (c),(e) t=420 ms and in Figs.(b), (d), (f) t=558 ms图 5为弱速度扰动及弱Q扰动模型中得到的单炮地震记录,其中全波波动方程与一阶波恩近似方程所得地震记录在相同幅值范围内.由于单程波波动方程所得地震记录振幅能量范围与前两者相差较大,我们对其进行整体加权,使炮点位置处的检波器接收到的第一个反射界面的反射波振幅与对应的全波波动方程所得该反射界面的反射波振幅一致.由于利用一阶波恩近似方程得到的波场不包含透射波,因此地面地震接收记录中不包含直达波信息.由于直达波能量较强,当其传播到边界处时的反射能量较强.特别是对于弱散射介质,直达波在边界处的反射能量甚至能与一次散射波场能量相当(图 5a),从而增加了反射波地震勘探的复杂性.
由于本文单程波数值模拟中未考虑反射系数与偏移距及入射角的关系,故单程波波场在近炮点位置能够取得比较理想的效果.但在远偏移距处,采用单程波波动方程得到的反射波能量强度与全波波动方程及一阶波恩近似方程的明显不一致.因此如何准确地计算不同入射角下复杂介质界面的反射系数是单程波法准确描述反射波场要解决的关键问题.
图 6为近炮点处的检波点所接收到的一道地震记录.全波波动方程中包含直达波信息,当第一个反射界面较浅时,直达波与反射波发生干涉.在常规处理中通常用切除直达波的方法得到反射波信息,但这种切除方法也损失了重要的反射波信息.特别是在浅层疏松介质中直达波与反射波干涉尤为严重时.当切除直达波,有效的反射波信息也基本被切除.而利用基于一阶波恩近似的波动方程则能够得到只含有一次反射波的波场,从而避免了直达波与反射波分离的问题.从能量分布上看,基于一阶波恩近似方程得到的反射波场与全波波动方程得到的波场吻合较好.单程波法能够直接得到反射波信息,但在能量匹配上与全波波动方程不一致,特别是对于深层陡倾角的界面,其反射波能量误差较大.
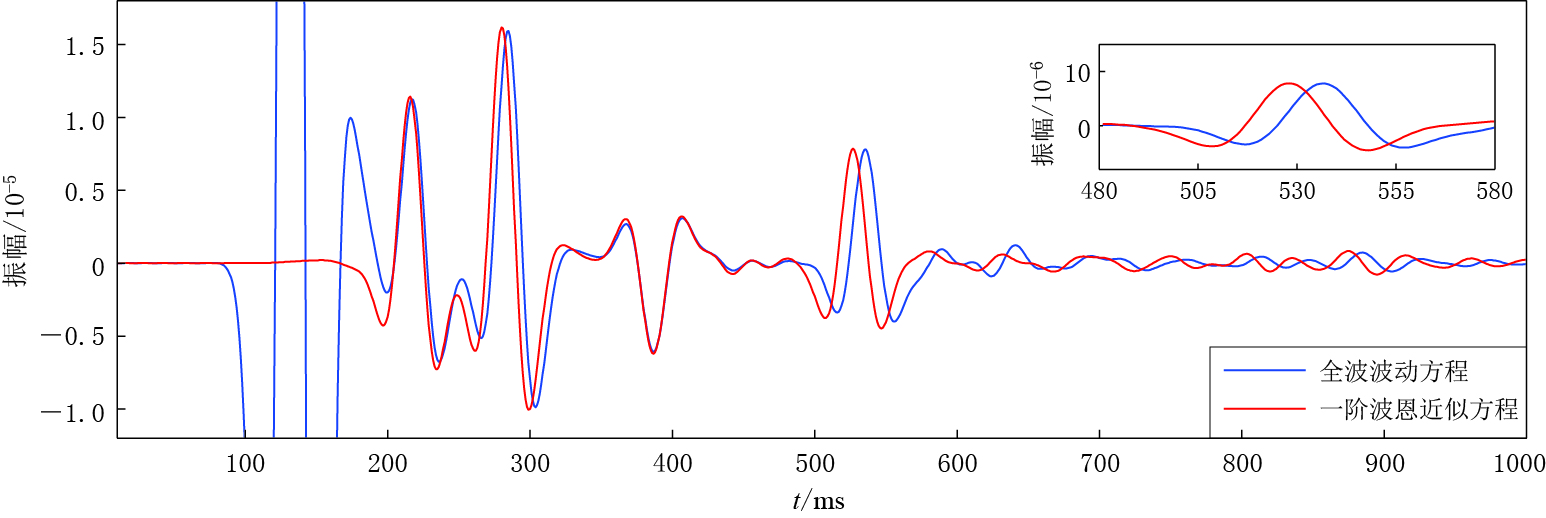
![]() 图 6 弱速度扰动及弱Q扰动模型中由全波波动方程、 一阶波恩近似方程与单程波波动方程得到的地震波形对比Figure 6. Comparison of the seismic waveforms obtained by full wave equation (blue lines) with that by first-order Born approximation wave equation (red lines) and one-way wave equation (black lines) in the model with weak velocity perturbation and weak Q perturbation
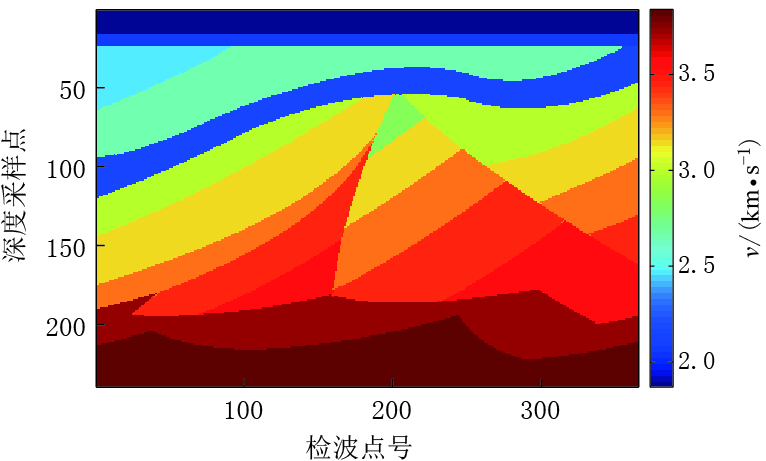
图 6 弱速度扰动及弱Q扰动模型中由全波波动方程、 一阶波恩近似方程与单程波波动方程得到的地震波形对比Figure 6. Comparison of the seismic waveforms obtained by full wave equation (blue lines) with that by first-order Born approximation wave equation (red lines) and one-way wave equation (black lines) in the model with weak velocity perturbation and weak Q perturbation黏滞性介质一阶波恩近似方程得到的波场与全波波动方程得到的波场匹配的前提条件是弱散射近似,即波恩近似成立的条件为kRδ σ/σ0≤1.其中,δ σ为散射波场,σ0为背景波场,k为波场波数,R为非均匀体的尺度(如球半径)(吴如山,1993).在以上讨论中我们所使用的速度模型在层速度及厚度上均满足波恩近似成立的条件.为了进一步探索在不满足波恩近似成立条件下的地震波场误差问题,本文将速度进行修改得到强速度扰动模型.修改后的速度模型最高速度为3 900 m/s,最低速度降低为1 800 m/s,相邻两层速度差增大,特别是对于不整合覆盖层,其速度明显降低(图 7).在地震记录剖面上,黏滞性介质全波波动方程与一阶波恩近似方程所得到的波场匹配较好,其波形形态与振幅能量保持一致(图 8).分别从图 8a,b中抽取检波点号为200的一道地震记录,得到如图 9所示的波形对比图.通过对比可知,一阶波恩近似方程与全波波动方程所得到的波场在振幅方面能够达到一致.但在旅行时方面,一阶波恩近似方程所得到的反射波场发生漂移,特别是在t=538 ms处的反射波旅行时向上移动约10 ms,这种误差将导致地震层位解释不准确,严重影响储层预测精度.
黏滞性介质一阶波恩近似方程得到的波场与全波波动方程得到的波场匹配的前提条件是弱散射近似,即波恩近似成立的条件为kRδ σ/σ0≤1.其中,δ σ为散射波场,σ0为背景波场,k为波场波数,R为非均匀体的尺度(如球半径)(吴如山,1993).在以上讨论中我们所使用的速度模型在层速度及厚度上均满足波恩近似成立的条件.为了进一步探索在不满足波恩近似成立条件下的地震波场误差问题,本文将速度进行修改得到强速度扰动模型.修改后的速度模型最高速度为3 900 m/s,最低速度降低为1 800 m/s,相邻两层速度差增大,特别是对于不整合覆盖层,其速度明显降低(图 7).在地震记录剖面上,黏滞性介质全波波动方程与一阶波恩近似方程所得到的波场匹配较好,其波形形态与振幅能量保持一致(图 8).分别从图 8a,b中抽取检波点号为200的一道地震记录,得到如图 9所示的波形对比图.通过对比可知,一阶波恩近似方程与全波波动方程所得到的波场在振幅方面能够达到一致.但在旅行时方面,一阶波恩近似方程所得到的反射波场发生漂移,特别是在t=538 ms处的反射波旅行时向上移动约10 ms,这种误差将导致地震层位解释不准确,严重影响储层预测精度.
为了消除全波波动方程中直达波对反射波的影响,以便与一阶波恩近似方程所得的反射波进行对比,我们将弱速度扰动模型(图 2a)第一个反射界面下移相同的深度得到修改后的弱速度扰动场(图 10b).通过对比可知,弱速度扰动和强Q扰动的情况下,全波波动方程与一阶波恩近似方程所得波场在旅行时方面能够匹配较好(图 12),但在振幅能量上略有差异.因此在黏滞性介质中,一阶波恩近似方程的波场精度主要取决于速度,Q值扰动所引起的振幅误差几乎可以忽略不计.
6. 讨论与结论
针对常规τ值法计算常Q模型参数精度低的问题,本文推导了改进的τ值法.该τ值法能够对常规τ值法不同频率成分的Q值拟合精度进行修正,得到更加精确的常Q模型.在此基础上,推导了包含CMPL边界条件的基于广义流变体模型的波恩近似位移方程.由于黏滞性项引入了时间一阶导数项,常规网格方法将波场参数和介质参数定义在同一网格点上而不利于黏滞性介质位移方程求解.本文根据应力、应变及位移之间的关系,进一步推导了基于交错网格的包含CPML边界条件的变密度一阶波恩近似应力-速度方程.在弱散射条件下,基于波恩近似的黏滞性声波介质方程对于散射波场的模拟能够与全波波动方程得到的波场匹配.对于全波波动方程,在弱散射条件下,直达波边界反射能量的强度甚至能与散射波波场相匹配;对于浅层反射界面,由于直达波与反射波发生干涉,常规的直达波切除方法不仅损失了反射波信息,而且严重影响了地震解释精度.黏滞性介质波恩近似方程由于不含透射波,不存在直达波的影响,从而有利于反射波勘探理论研究.相对于单程波法,黏滞性介质一阶波恩近似方程得到的波场无须计算反射系数与角度的关系,能够自动进行能量分配.当速度场存在强扰动时,黏滞性介质一阶波恩近似方程与全波波动方程得到的波场在旅行时上存在较大误差,需要采用高阶多级散射波波动方程;当速度场为弱扰动、模型Q值为强扰动时,尽管黏滞性所引起的速度频散会带来相速度变化,但黏滞性介质一阶波恩近似方程与全波波动方程所得波场基本吻合,说明其在弱速度扰动下能够适应地层Q值强扰动.
-
图 3 弱速度扰动及弱Q扰动模型中由全波波动方程(a,b)和一阶波恩近似方程(c,d)得到的黏滞性介质波场以及由全波波动方程与一阶波恩近似方程得到的波场差值(e, f)
(a), (c), (e)中t=420 ms; (b), (d), (f)中t=558 ms
Figure 3. The viscoacoustic wave fields obtained by different wave equations in the model with weak velocity perturbation and weak Q perturbation Figs.(a) and (b) are the wave fields obtained by full wave equation; Figs.(c) and (d) are the wave fields obtained by first-order Born approximation equation; Figs.(e) and (f) are the differences
between the wave fields in (a), (b) and those in (c), (d). In Figs.(a), (c),(e) t=420 ms and in Figs.(b), (d), (f) t=558 ms
图 6 弱速度扰动及弱Q扰动模型中由全波波动方程、 一阶波恩近似方程与单程波波动方程得到的地震波形对比
Figure 6. Comparison of the seismic waveforms obtained by full wave equation (blue lines) with that by first-order Born approximation wave equation (red lines) and one-way wave equation (black lines) in the model with weak velocity perturbation and weak Q perturbation
-
曹丹平. 2008. 多尺度地震资料正反演方法研究[D]. 青岛: 中国石油大学(华东)地球科学与技术学院: 16-86. Cao D P. 2008. Method Research of Multiscale Seismic Data Modeling and Inversion[D]. Qingdao: School of Geosciences, China University of Petroleum (East China): 16-86 (in Chinese).
何兵红. 2011. 基于衰减介质的地震波数值模拟及吸收属性提取方法研究[D]. 青岛: 中国石油大学(华东)地球科学与技术学院: 36-50. He B H. 2011. The Study of Numerical Simulation of Seismic Wave in Attenuation Medium and Extraction of Absorption Properties[D]. Qingdao: School of Geosciences, China University of Petroleum (East China): 36-50 (in Chinese).
单启铜. 2007. 粘弹性波动方程正演模拟与参数反演[D]. 青岛: 中国石油大学(华东)地球科学与技术学院: 13-83. Shan Q T. 2007. Simulation and Inversion of Wave Equation in Viscoelastic Media[D]. Qingdao: School of Geosciences, China University of Petroleum: 13-83 (in Chinese).
吴如山. 1993. 地震波的散射与衰减[M]. 北京: 地震出版社: 49-80. Wu R S. 1993. Scatter and Attenuation of Seismic Wave[M]. Beijing: Seismological Press: 49-80 (in Chinese).
郑江峰. 2006. 粘弹性介质中提高地震资料分辨率方法研究[D]. 大庆: 大庆石油学院地球科学学院: 30-32. Zheng J F. 2006. Methodology and Research on Improving Seismic Resolution in Viscoelastic Media[D]. Daqing: Geoscience College, Daqing Petroleum Institute: 30-32 (in Chinese).
-
期刊类型引用(0)
其他类型引用(1)





 下载:
下载: