Love wave modeling in viscoelastic media with unsplit CFS-CPML conditions
-
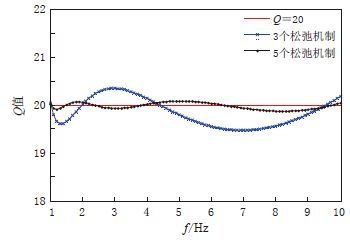
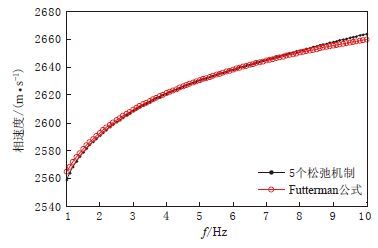
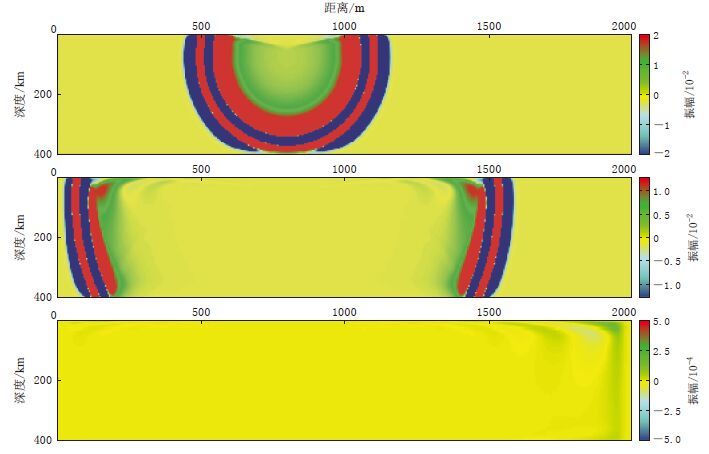
摘要: 本文建立了无分裂复频移卷积完全匹配层(CFS-CPML)吸收边界条件,利用交错网格下的高精度有限差分格式对黏弹性介质中的勒夫波场进行了数值模拟;分析了松弛机制个数对品质因子拟合精度的影响,验证了CFS-CPML边界条件对大角度掠射波的吸收效果.数值结果表明:本文方法所使用的5个松弛机制和空间4阶差分精度,即可在保证计算效率的前提下满足目前理论研究的需要;随着品质因子的减小,频散特征曲线的相速度逐渐向增高的方向偏离理论频散特征曲线的相速度,且各模式的高频能量也随之减弱.本文结果可为发展高精度的面波反演方法提供必要的理论依据.
-
关键词:
- 勒夫波 /
- 正演模拟 /
- 复频移卷积完全匹配层(CFS-CPML) /
- 吸收边界条件 /
- 频散特征
Abstract: Numerical simulation is an important way to study the characteristics of seismic wavefield. In this paper, we established the unsplit complex frequency shifted convolutional perfectly matched layer (CFS-CPML) absorbing boundary condition, and staggered grid and high precision finite difference were used to simulate Love wavefield in viscoelastic medium. And then we analyzed the influence of the number of relaxation mechanisms on the Q value fitting and verified the absorbing effect of CFS-CPML boundary conditions on the waves with large incident angles. The numerical results show that the requirements of the present theoretical wavefield study can be met with higher calculation efficiency if five relaxation mechanisms and finite difference with spatial four-order accuracy are selected for this method. At the same time, the phase velocity of dispersion curve gradually deviates from that of the theoretical curve with the decrease of quality factor, and the high frequency energy of each pattern also weakens. The study provided certain theoretical basis for high precision surface wave inversion method. -
-
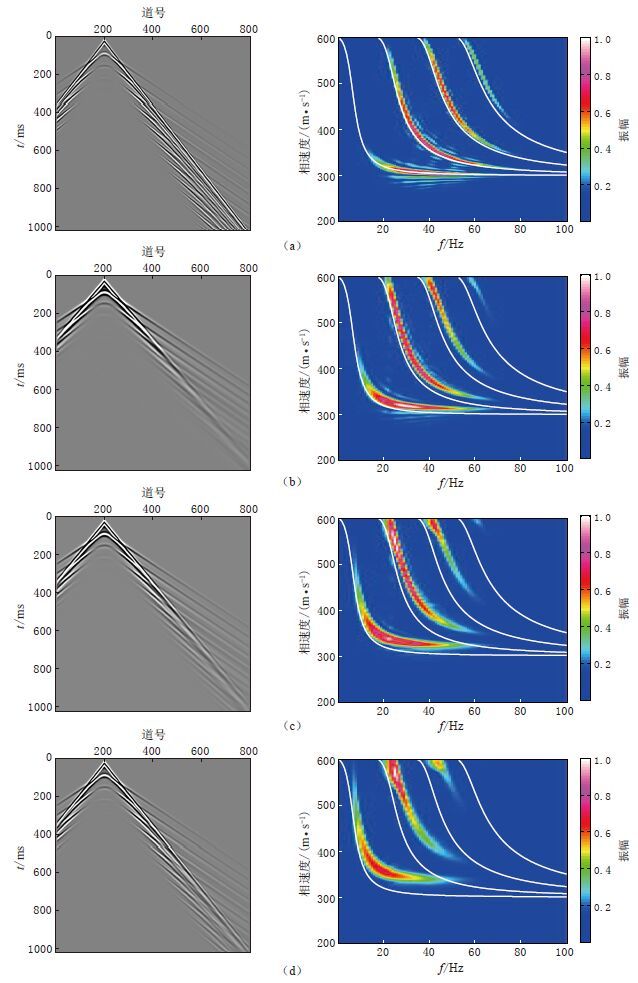
图 9 双层介质模型中的勒夫波记录(左)及其频散特征图(右)
频散图中的白色曲线为根据矩阵传递算法(Haskell,1953)正演所得的理论勒夫波频散曲线(a)上层QS=200;(b)上层QS=40;(c)上层QS=20;(d)上层QS=10
Figure 9. Love wave records(left panels)and their frequency-phase velocity field dispersion characteristic diagram(right panels)simulated in two-layer medium model
White curves in right panels are the theory Love wave dispersion curves based on the matrix transfer algorithm(Haskell,1953).(a)QS=200 for the first layer;(b)QS=40 for the first layer;(c)QS=20 for the first layer;(d)QS=10 for the first layer
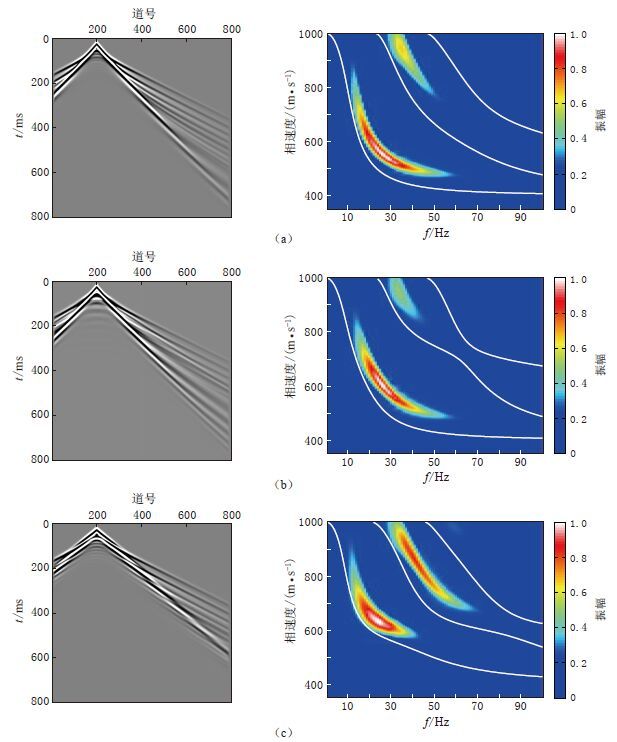
图 10 4层介质中勒夫波记录(左)及其频散特征图(右)
频散图中的白色曲线为根据矩阵传递算法(Haskell,1953)正演所得的理论勒夫波频散曲线(a)速度递增模型;(b)夹高速层模型;(c)夹低速层模型
Figure 10. Love wave records(left panels)and their frequency-phase velocity field dispersion characteristic diagram(right panels)simulated in four-layer medium. White curves are the theory Love wave dispersion curves based on the matrix transfer algorithm(Haskell,1953).
(a)Velocity increase model;(b)High velocity interlayer model;(c)Low velocity interlayer model
表 1 两层介质模型参数
Table 1 Parameters of a two-layer model
层号 层厚/m 密度/(kg·m-3) vS/(m·s-1) QS 1 10 2000 300 200,40,20,10 2 ∞ 2000 600 200 表 2 4层介质模型参数
Table 2 The parameters of the four-layer medium model
层号 层厚/m vS/(m·s-1) ρ/(kg·m-3) 递增模型 夹高速层模型 夹低速层模型 1 5 400 400 600 2000 2 5 600 800 400 2000 3 5 800 600 800 2000 4 ∞ 1000 1000 1000 2000 -
田坤.2014.黏性介质正演及逆时偏移成像方法研究[D].青岛: 中国石油大学(华东):35-39. Tian K.2014.Study on Method of Forward Modeling and Reverse Time Migration in Viscous Media[D].Qingdao: China University of Petroleum:35-39




 下载:
下载: