Analysis and revision of magnitude ML deviation between Fujian and Taiwan based on BP neural network
-
摘要: 选取我国台湾地区2012—2018年期间的浅源地震资料，将台湾气象局与福建地震台网中心测定的ML震级进行对比分析，得出两机构测定的震级之间的差异主要是受地震震级大小、震源深度、震源地理位置等因素的影响，并采用线性回归方法对两机构测定的ML之间的模型关系进行拟合。与此同时，引入反向传播神经网络技术对两机构测定震级之间的偏差进行预测训练，构建4−9−9−9−4的五层网络模型，利用2012—2017年台湾震例作为训练集进行学习训练，2018年数据作为测试集进行预测效果分析。测试结果表明，经过反向传播神经网络修正后，震级偏差较大改善，基本都控制在[−0.4，0.3]之内，预测效果优于传统的线性回归方法，特别是对多震、少震区域震例的修正效果更为显著，进一步验证了反向传播神经网络技术具有较强的非线性拟合能力和泛化能力。Abstract: In this paper, the shallow earthquake events in Taiwan island from 2012 to 2018 were used for analyses on magnitude deviation measured by Taiwan Weather Bureau （TWB） and Fujian Seismic Network Center （FSNC）. The result shows the differences in magnitude between Taiwan region and Fujian region were affected by magnitude value, focal depth and geographic location. And then we made linear regressions for magnitude ML of the earthquakes measured by TWB and FSNC, respectively. In the meanwhile, a BP neural network with 4−9−9−9−4 five-layer model was introduced into the prediction training of these two regions. For the model, the Taiwan earthquakes in 2012−2017 were taken as training set, and the events in 2018 were used as the testing set. After the revision of BP neural network, the deviation values of magnitude were basically controlled within −0.4 to 0.3, which is better than those from the traditional linear regression method, especially for multiple earthquakes and minority earthquakes. Furthermore, the testing results also validate the abilities of non-linear data fitting and generalization.
-
Keywords:
- BP neural network /
- magnitude /
- deviation correction /
- non-linear fitting /
- generalization ability
-
引言
震级是地震本身大小的量度，传统上用两个水平分量的S波峰值或面波水平矢量峰值来测定。由于地震波峰值不但与不同震中距发育的优势波组有关，而且与测量地震仪的动态和频带有关，因此不同震级标度方法、不同台网测定的震级大小可能存在一定的差异（陈运泰，刘瑞丰，2004；刘瑞丰等，2007，2018）。
我国台湾岛与福建地区隔海相望，台湾岛地震频发，而台湾发生的强震会对福建地区产生较大影响。例如：2018年2月4日的台湾花莲海域地震，福建省多地震感强烈，据台湾气象局网站公布该地震的震级为ML5.8，而福建地震台网中心测定的震级为M6.4 （速报震级），两地机构测定震级存在较大偏差，媒体报道不统一，造成了一定的社会舆论。两地机构测定的震级存在较大差异的原因主要有以下几点：首先，台湾岛地形南北狭长，导致其台站分布范围有限，台站之间的距离最远不超过300 km，因此大地震发生后很难测定面波震级，主要采用地方性震级ML来测定地震大小，而大陆面积广阔，台站分布较为均匀，展布范围大，台站间距离长达1 000 km以上，当较大地震发生时，福建地震台网中心则是以测定面波震级MS为主；其次，测定震级的方法不同，这是导致测定结果有较大差别的主要原因；再次，两机构关于里氏震级ML的度量方法和量规函数计算的差异也是一部分原因。
为进一步研究台湾与福建两地测定的震级偏差，傅再扬等（2008）统计了1971年以来闽、台两测震机构均有测定数据的发生于台湾及其邻近海域地区的ML6.0以上地震，获得了闽台两地地震台网不同时期测定台湾及其邻近海域强震的震级偏差。李军等（2016）通过对2008年1月至2013年9月期间福建地震台网中心记录到的台湾地区发生的1 257次地震的近震震级偏差进行了统计分析，研究了台湾地区近震震级偏差的影响因素，其结果显示福建地震台网中心测定的震级较台湾气象局测定的震级小约0.5，其中个别地震的震级相差达到1.0以上。鉴于前人研究分析考虑的震级偏差因素较为单一且有限，本文选取我国台湾地区2012—2018年期间的浅源地震资料，重点比较分析台湾气象局和福建地震台网中心所测震级间的差异，并引入反向传播神经网络技术对两机构之间的震级偏差进行学习训练，得出台湾气象局测得震级ML-tw与福建地震台网中心测得震级ML-fj之间的非线性关系模型，进而对其进行校正，使得两机构的震级偏差减小，以期为改善闽台震级偏差提供新的技术途径。
1. 地方性震级ML测定方法
地震震级是通过地震仪器测定出地震大小的一种量度，考虑到地震波在传播过程中的衰减，震级的测定需要考虑地震深度和震中距的影响。
震级标度是由Richter （1935）首次提出，其目的是使用仪器来测定地震的大小。里氏震级ML定义为：当伍德−安德森（Wood-Anderson，缩写为WA）标准地震仪（摆的固有周期为0.8 s，放大率为2 800，阻尼常数为0.8）在震中距Δ为100 km处，记录的两水平方向最大振幅的算术平均值为1 μm，则该地震的震级为0。若不在Δ为100 km处测定，则需根据量规函数（也称作衰减函数）来计算。量规函数是根据实测数据整理出来的震中距Δ的函数。Richter （1953）提出了里氏震级ML，该震级也称为地方性震级（刘瑞丰等，2015）。若取A0为一标准地震即参考事件的最大振幅，则任一地震的里氏震级ML可以定义为
$ {M_{\rm{L}}} {\text{＝}} {\rm{lg}}A\left(\varDelta \right) {\text{－}} {\rm{lg}}{A_0}\left(\varDelta \right),\qquad 30{\rm{}} {\text{≤}} \varDelta {\text{≤}} 600\;{\rm{km}}{\text{，}} $
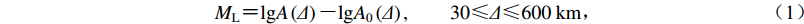
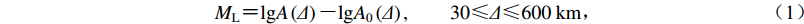
(1) 式中，A（Δ）为任一地震的最大振幅，且A（Δ）与A0（Δ）必须在同一距离用同样的地震仪测得。
1.1 福建地震台网中心的ML测定方法
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
${M_{\rm{L}}} {\text{＝}} {\rm{lg}}{A_{\mu}}\left( \varDelta \right) {\text{＋}} R\left( \varDelta \right) {\text{＋}} S\left( \varDelta \right){\text{，}}$
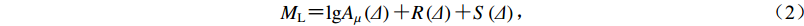
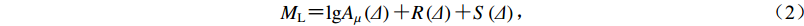
(2) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
目前福建地震台网中心测定震级ML的方法是将速度记录仿真成WA短周期地震仪位移记录，仿真后在位移记录上量取两水平向最大记录的振幅，使用近震震级公式计算震级ML （中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会，2017），即
${M_{\rm{L}}} {\text{＝}} {\rm{lg}}\frac{{{A_{\mu {\rm {EW}} }}{\text{＋}} {A_{\mu {\rm {NS}}}}}}{2} {\text{＋}} R\left(\varDelta \right){\text{，}}$
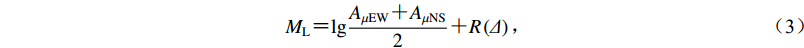
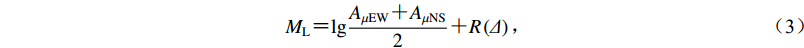
(3) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
1.2 台湾气象局的ML测定方法
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$A {\text{＝}} \sqrt {H_{{\rm{Nmax}}}^2 {\text{＋}} H_{{\rm{Emax}}}^2}\;\;{\text{.}} $
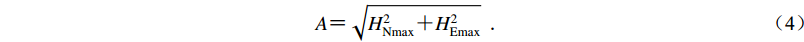
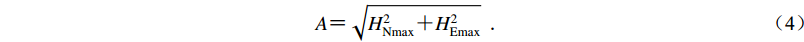
(4) Shin （1993）利用台湾实际震例获得了衰减函数：
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
${\rm{lg}}{A_0}\left(\varDelta \right) {\text{＝}} \left\{\!\!\! {\begin{array}{*{20}{c}} { \!\!- 0.007\;16R {\text{－}} \lg R {\text{－}} 0.39\qquad 0 {\text{＜}} \varDelta {\text{≤}} 80\;{\rm{km}}}{\text{，}}\\ { \!- 0.002\;61R {\text{－}} 0.83\lg R {\text{－}} 1.07\qquad \varDelta {\text{＞}} 80\;{\rm {km}}}{\text{；}} \end{array}} \right.$
(5) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
${\rm{lg}}{A_0}\left(\varDelta \right) {\text{＝}} - 0.003\;26R {\text{－}} 0.83{\rm{lg}}R {\text{－}} 1.01{\text{，}}$
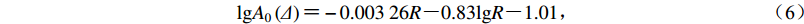
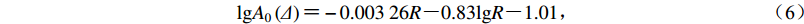
(6) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
从上面公式可以看出，台湾气象局测定的震级ML考虑了震源深度信息，这与福建地震台网中心测定的震级ML有很大的区别。
2. 闽台两机构测定ML的关系
2.1 数据资料
为了研究福建地震台网中心测定的震级ML-fj与台湾气象局测定的震级ML-tw之间的关系，本研究收集了福建地震台网中心测定的2012—2018年台湾发生的541次浅源地震的数据，包含福建台网中心和台湾气象局两机构测定的震级ML、各事件的震源信息（经度、纬度和深度），震级分布为：ML≤3.0的地震13次，3.0＜ML≤4.0的248次，4.0＜ML≤5.0的236次，5.0＜ML≤6.0的40次，ML＞6.0的地震4次，地震分布如图1所示。
![]()
图 1 福建地震台网中心记录的2012—2018年台湾地震分布图Figure 1. The distribution of earthquakes in Taiwan island and its vicinity recorded by Fujian Seismic Network Center from 2012 to 20182.2 闽台两机构测定震级ML的比较
为了直观地看出福建地震台网中心测定的震级ML-fj与台湾气象局测定的震级ML-tw之间的差异，本文绘出两机构测定的2012—2018年台湾发生地震闽台两机构的震级ML散点图（图2a）和直方图（图2b），可以看出台湾气象局测定的ML-tw比福建地震台网中心测定的ML-fj总体偏大0.51。
![]()
图 2 闽台两机构测定ML震级的比较（a） 震级散点图，绿线为ML-fj均值4.11，黄线为ML-tw均值4.62；（b） 震级频次直方图Figure 2. Comparison of magnitude ML measured by Fujian with that by Taiwan（a） Scatter diagram of magnitude，where the green line represents the mean magnitude 4.11 measured by Fujian Seismic Network Center，the yellow line represents the average magnitude 4.62 by Taiwan Weather Bureau；（b） Magnitude frequency histogram2.3 线性回归关系
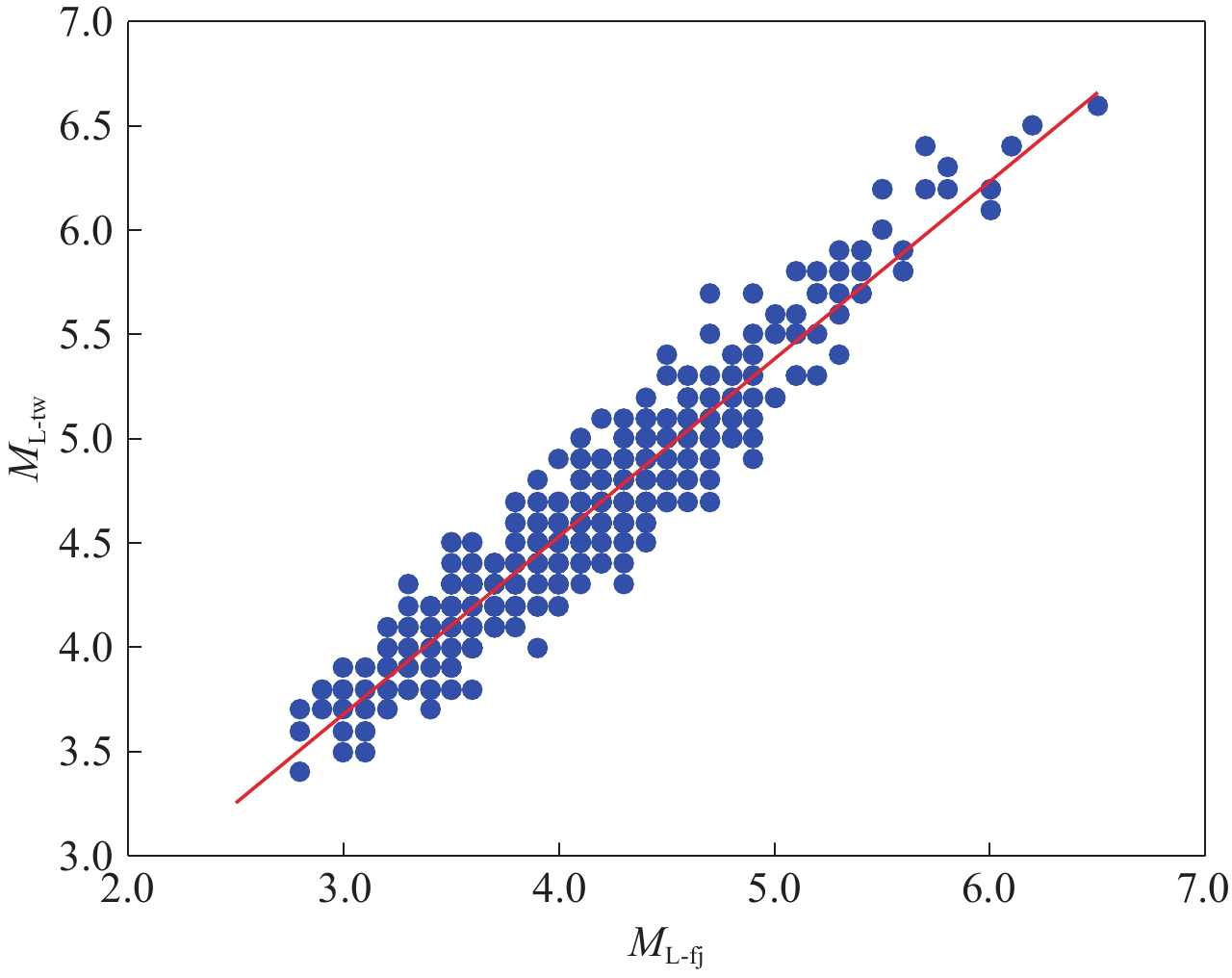
为了分析福建地震台网中心与台湾气象局测定ML震级之间的关系（唐淋等，2018），采用线性回归方法进行拟合分析，结果如图3所示。图中每个点表示一次地震事件对应的福建地震台网中心测定的震级ML-fj和台湾气象局测定的震级ML-tw，直线为一般线性回归所得结果。使用的地震事件为541次，采用线性回归方法得到的拟合相关系数为0.95，均方根为0.16。
![]()
图 3 闽台机构测定震级ML之间的线性回归关系Figure 3. The linear regression relationship between magnitude ML determined by Fujian and Taiwan由图3所示的线性回归拟合结果可以得到ML-fj与ML-tw之间的关系式：
$ {M_{{\rm{L}} {\text{-}} {\rm{tw}}}} {\text{＝}} 0.851\;7{M_{{\rm{L}} {\text{-}} {\rm{fj}}}} {\text{＋}} 1.124\;7{\text{.}} $
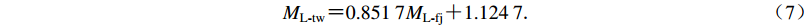
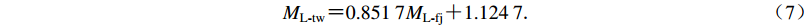
(7) 由式（8）可见ML-fj与ML-tw之间呈正相关，即随着ML-fj的增大，ML-tw也增大。从图3可以看出，绝大部分的点呈现出的线性关系较好，仅有小部分点的偏差较大，存在一定的离散度，这是由于不同震源深度与不同区域地震会导致闽台两机构测定震级偏差的差异，因此简单的线性关系不足以完全刻画出两者之间的关系。
3. 闽台两机构测定的ML震级偏差的影响因素分析
定义闽台两机构测定的震级偏差ΔML为ML-tw与ML-fj之差，即
${\rm{\Delta }}{M_{\rm L}} {\text{＝}} {M_{{\rm{L}} {\text{-}} {\rm{tw}}}} {\text{－}} {M_{{\rm{L}}{\text{-}}{\rm{fj}}}}{\text{.}}$
(8) 3.1 地震震级大小的影响
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
![]()
图 4 闽台震级偏差随地震震级（a）和震源深度（b）的变化Figure 4. Variation of magnitude deviation between Fujian and Taiwan with magnitude （a） and hypocenter depth （b）3.2 地震震源深度的影响
图4b给出了不同震源深度下闽台两机构震级偏差ΔML的变化。可以看出，随着震源深度的增加，闽台震级偏差ΔML逐渐增大，这是由于台湾气象局测定的震级ML是用震源距来求量规函数，综合考虑了震源深度的影响，而福建地震台网中心测定的ML是用震中距求量规函数，未考虑震源深度的影响。因此，对于震源深度较大的地震来说，台湾气象局测定的ML会明显大于福建地震台网中心测定的ML。
3.3 地震震源地理位置的影响
不同地理位置发生的地震，福建和台湾两机构测定的ML震级偏差也不同，例如花莲海域的地震震级偏差一般介于0.3—0.7之间，高雄的地震震级偏差一般介于0.1—0.3之间。这是因为不同区域的地震，其震源机制、场地效应和传播路径不同所致。
本文选取台湾宜兰海域、花莲、台东海域及台南等不同地理区域的震例进行两机构测定的震级偏差分析，所选地震震中分布如图5所示。为了突出震源地理位置的影响，本研究确保所选取震例的震级均为ML4.6左右，且震源深度均为10 km左右，以此来排除震级大小和震源深度的影响。从图5中可以看出宜兰海域震例的偏差为0.2，花莲震例的偏差为0.4，台东海域震例的偏差为0.6，台南震例的偏差为0.1，这说明震源的地理位置不同，闽台两机构所得震级偏差也不同。另外，花莲附近的两个震例，其偏差均为0.4，也验证了同一地理位置，相似地震的震级偏差相近。
![]()
图 5 震源的地理位置对闽台震级偏差的影响Figure 5. Effect of the location of the earthquake source on the magnitude deviation measured by Fujian and Taiwan3.4 综合评估分析
通过上述分析闽台震级偏差的影响因素，可以进一步提炼出闽台震级偏差的主要影响因素有地震震级大小、震源深度和震源地理位置。由式（8）利用线性回归方法拟合出本文所选几个震例的ML-tw的预测公式，给出福建地震台网中心测定的震级ML-fj分别为3.0，3.5，4.0，4.5，5.0，5.5，6.0，预测结果与实际结果的偏差见表1，可以得出通过线性回归预测结果校正后的震级偏差比校正前降低很多，但是还存在一定的偏差，最大偏差达0.49，这是因为该回归公式只考虑了震级大小的影响因素，而未考虑震源深度和震源地理位置的影响。
表 1 闽台震级偏差校正前后的对比Table 1. Comparison of the Fujian’s and Taiwan’s magnitude deviation before and after correctionML-fj ${M_{ {\rm{L} } {\simfont\text{-}} {\rm{tw} } }^{\rm{r} } }$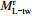 
${M_{ {\rm{L} } {\simfont\text{-} } {\rm{tw} } }^{\rm{f} } }$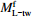 
${\Delta {M_{ {\rm{L} }{\simfont\text{校正前} } } } }$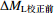 
${\Delta {M_{ {\rm{L} }{\simfont\text{校正后} } } } }$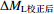 
3.0 3.6 3.68 0.60 −0.08 3.5 4.2 4.10 0.70 0.10 4.0 4.4 4.53 0.40 −0.13 4.5 4.8 4.95 0.30 −0.15 5.0 5.6 5.38 0.60 0.22 5.5 6.3 5.81 0.70 0.49 6.0 6.2 6.23 0.20 −0.03 注： ${M^{\rm r}_{\rm L{\text{-} } tw} }$ 为台湾气象局实测震级，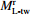
${M^{\rm f}_{\rm L{\text{-} } tw} }$ 为拟合得到的台湾地区震级值，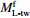
${\Delta {M_{ {\rm{L} }{\simfont\text{校正前} } } } {\simfont\text{＝} } M_{ {\rm{L} }{\text{-} } {\rm{tw} } }^{\rm{r} } {\simfont\text{－} } M_{ {\rm{L} } {\text{-} } {\rm{fj} } }^{} }， $ ，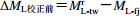
${\Delta {M_{ {\rm{L} }{\simfont\text{校正后} } } } {\simfont\text{＝} } M{_{ {\rm{L} } {\text{-} } {\rm{tw} } }^{\rm{r} } } {\simfont\text{－} } M_{ {\rm{L} } {\text{-} } {\rm{tw} } }^{\rm{f} } } $ .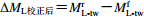
为了能充分考虑以上3个因素，传统方法可通过找寻合适公式进行非线性拟合，但是拟合公式并非特别明确有效。因此本文将引入目前较为成熟的反向传播（backward propagation，缩写为BP）神经网络方法，通过福建地震台网中心测定的ML-fj震级大小、震源深度、震源经度、纬度等信息，来预测台湾气象局测定的ML-tw震级。
4. BP神经网络的应用
BP神经网络从原始数据中自动找寻事物的内在特征，通过不断学习训练，得出最优检测模型，可以解决复杂问题的分类与判别。BP神经网络还具有非线性映射能力、自学习和自适应能力以及泛化能力，也就是说具有将学习成果应用于新知识的能力（Duda et al，2000）。
针对闽台震级偏差校正的问题，上一节已经得出台湾震级ML-tw的主要影响因素为福建台网测定的ML大小、震源深度、地理位置，本节将应用BP神经网络来预测台湾气象局测定的震级ML-tw，即将地震的经度、纬度、深度及福建地震台网中心测定的震级ML-fj作为输入，将台湾气象局测定的震级ML-tw作为输出，进行BP神经网络训练与识别（图6），其中2012—2017年地震数据作为训练集，2018年数据作为测试集。
![]()
图 6 本文BP神经网络模型的输入与输出Figure 6. The input and output of BP neural network model in this study4.1 BP神经网络的工作原理
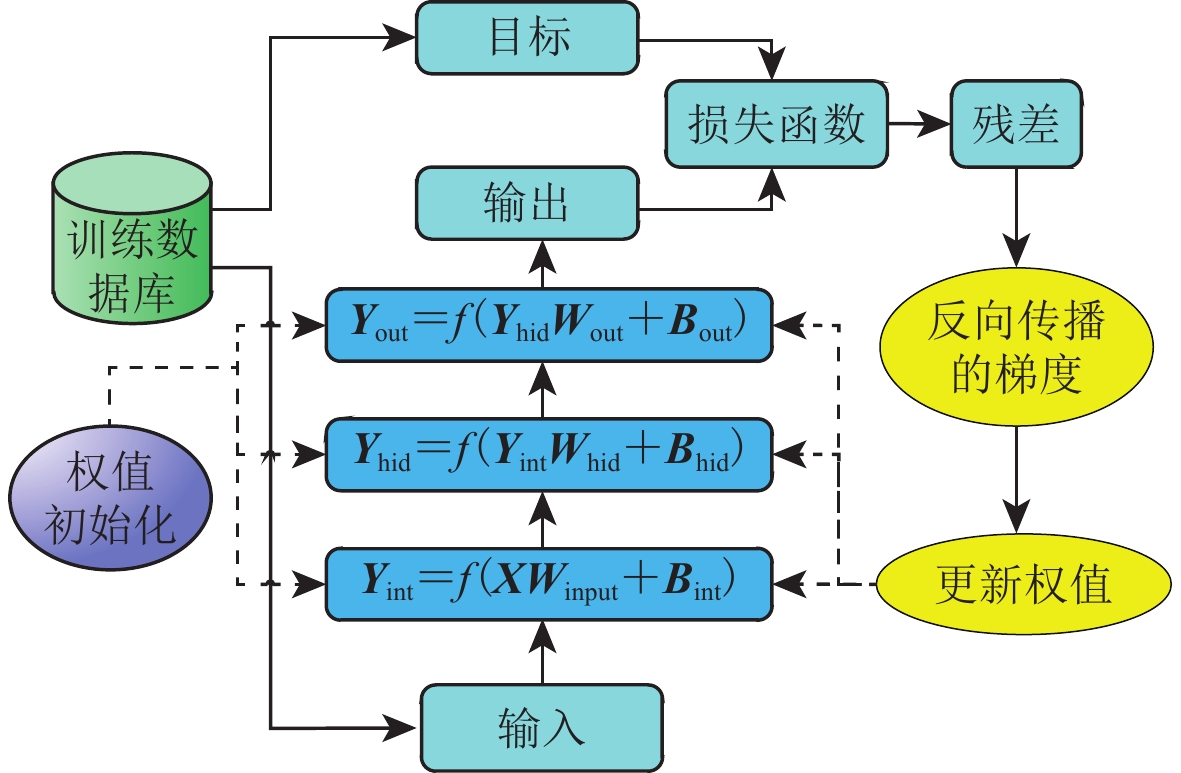
BP神经网络模型一般由输入层、隐藏层、输出层构成，通过初始化神经网络的权值和偏置，再利用训练数据不断学习来调整网络的权值和偏置参数，最终使得全局误差达到最小，得到调整后的权值和偏置就构成最优模型（杜百灵，2018），整个工作流程如图7所示。
4.2 前向传播
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$\left\{ {\begin{array}{*{20}{c}} \!\!\!{{y_{{\rm{in}}{{\rm{t}}_1}}} {\text{＝}} f\left({{\omega _{11}}{x_1} {\text{＋}} {\omega _{21}}{x_2} {\text{＋}} {b_1}} \right)}{\text{，}}\\ \!\!\!{{y_{{\rm{in}}{{\rm{t}}_2}}} {\text{＝}} f\left({{\omega _{12}}{x_1} {\text{＋}} {\omega _{22}}{x_2} {\text{＋}} {b_2}} \right)}{\text{，}}\\ \!\!\!{{y_{{\rm{in}}{{\rm{t}}_3}}} {\text{＝}} f\left({{\omega _{13}}{x_1} {\text{＋}} {\omega _{23}}{x_2} {\text{＋}} {b_3}} \right)}{\text{，}} \end{array}} \right.$
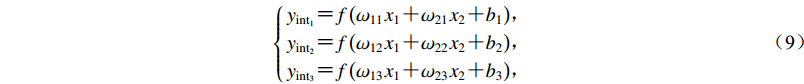
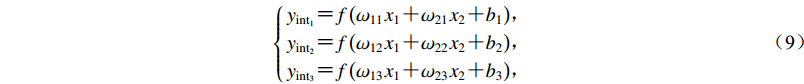
(9) 上式可以写成一般形式：
${{{Y}}_{{\rm{int}}}} {\text{＝}} f\left({{{X}}{{{W}}_{{\rm{int}}}} {\text{＋}} {{{B}}_{{\rm{int}}}}} \right){\text{；}}$
(10) 同理，隐藏层的输出结果为
${{{Y}}_{{\rm{hid}}}} {\text{＝}} f\left({{{{Y}}_{{\rm{int}}}}{{{W}}_{{\rm{hid}}}} {\text{＋}} {{{B}}_{{\rm{hid}}}}} \right){\text{；}}$
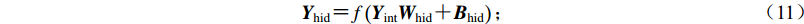
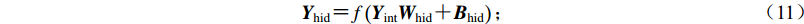
(11) 输出层的输出结果为
${{{Y}}_{{\rm{out}}}} {\text{＝}} f\left({{{{Y}}_{{\rm{hid}}}}{{{W}}_{{\rm{out}}}} {\text{＋}} {{{B}}_{{\rm{out}}}}} \right){\text{，}}$
(12) 前向传播得到整个网络的输出值Yout与目标值（标签）E＝（e1，e2）会存在误差。下面将讨论如何把这个误差反向传递回去，重新调整权值，使得误差达到最小。
4.3 权重和偏置的调整
将误差进行反向传播的思想是利用输出后的误差来估计输出层前一层的误差，再用这层误差来估计更前一层误差，如此获得所有层的误差估计（Mitchell，1997），进而可获得各层权重和偏置的改变量。为了使表达式更简洁，我们将其写成一般形式：
输出层的误差δout：
${{{\delta}} _{{\rm{out}}}} {\text{＝}} \left({{{{Y}}_{{\rm{out}}}} {\text{－}} {{E}}} \right){{Y}}{\rm{\,'}}_{{\rm{\!\!\!out}}}{\text{；}}$
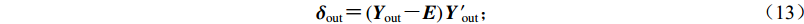
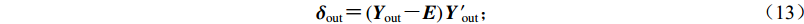
(13) 隐藏层的误差δhid：
${{{\delta}} _{{\rm{hid}}}} {\text{＝}} {{{\delta}} _{{\rm{out}}}}{{W}}_{{\rm{out}}}^{\rm{T}}{{Y}}{\rm{\,'}}_{{\rm{\!\!\!hid}}}{\text{；}}$
(14) 输入层的误差δint：
${{{\delta}} _{{\rm{int}}}} {\text{＝}} {{{\delta}} _{{\rm{hid}}}}{{W}}_{{\rm{hid}}}^{\rm{T}}{{Y}}{\rm{\,'}}_{{\rm{\!\!\!int}}}{\text{；}}$
(15) 输出层、隐藏层、输入层的权重调整如下：
$\left\{ \!\!{\begin{array}{*{20}{c}} \!\!{{{{W}}_{{\rm{out}}}} {\text{＝}} {{{W}}_{{\rm{out}}}} {\text{＋}} \Delta {{{W}}_{{\rm{out}}}} {\text{＝}} {{{W}}_{{\rm{out}}}} {\text{－}} \eta {{{\delta}} _{{\rm{out}}}}{{{Y}}_{{\rm{hid}}}}}{\text{，}}\\ \!\!{{{{W}}_{{\rm{hid}}}} {\text{＝}} {{{W}}_{{\rm{hid}}}} {\text{＋}} \Delta {{{W}}_{{\rm{hid}}}} {\text{＝}} {{{W}}_{{\rm{hid}}}} {\text{－}} \eta {{{\delta}} _{{\rm{hid}}}}{{{Y}}_{{\rm{int}}}}}{\text{，}}\\ \!\!\!\!{{{{W}}_{{\rm{int}}}} {\text{＝}} {{{W}}_{{\rm{int}}}} {\text{＋}} \Delta {{{W}}_{{\rm{int}}}} {\text{＝}} {{{W}}_{{\rm{int}}}} {\text{－}} \eta {{{\delta}} _{{\rm{int}}}}{{ X}_{{\rm{int}}}}}{\text{，}} \end{array}} \right.$
(16) 输出层、隐藏层、输入层的偏置调整如下：
$\left\{\!\!\!\! {\begin{array}{*{20}{c}} {{{{B}}_{{\rm{out}}}} {\text{＝}} {{{B}}_{{\rm{out}}}} {\text{＋}} \Delta {{{B}}_{{\rm{out}}}} {\text{＝}} {{{B}}_{{\rm{out}}}} {\text{－}} \eta {{{\delta}} _{{\rm{out}}}}}{\text{，}}\\ {{{{B}}_{{\rm{hid}}}} {\text{＝}} {{{B}}_{{\rm{hid}}}} {\text{＋}} \Delta {{{B}}_{{\rm{hid}}}} {\text{＝}} {{{B}}_{{\rm{hid}}}} {\text{－}} \eta {{{\delta}} _{{\rm{hid}}}}}{\text{，}}\\ \!\!{{{{B}}_{{\rm{int}}}} {\text{＝}} {{{B}}_{{\rm{int}}}} {\text{＋}} \Delta {{{B}}_{{\rm{int}}}} {\text{＝}} {{{B}}_{{\rm{int}}}} {\text{－}} \eta {{{\delta}} _{{\rm{int}}}}}{\text{，}} \end{array}} \right.$
(17) 重复以上步骤，迭代运算，误差不断减小，直到满足要求。
4.4 BP神经网络结构的确定
BP神经网络参数设计中最先遇到的问题是网络层数和节点数的选择，如果网络层数和节点数太小，网络则不具有必要的学习能力；若网络层数和节点数太大，虽然可使网络的系统误差减少，但一方面使网络训练时间延长，另一方训练容易陷入局部最小值，也可能出现 “过拟合” 的倾向。因此选取合适的网络层数和节点数至关重要。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
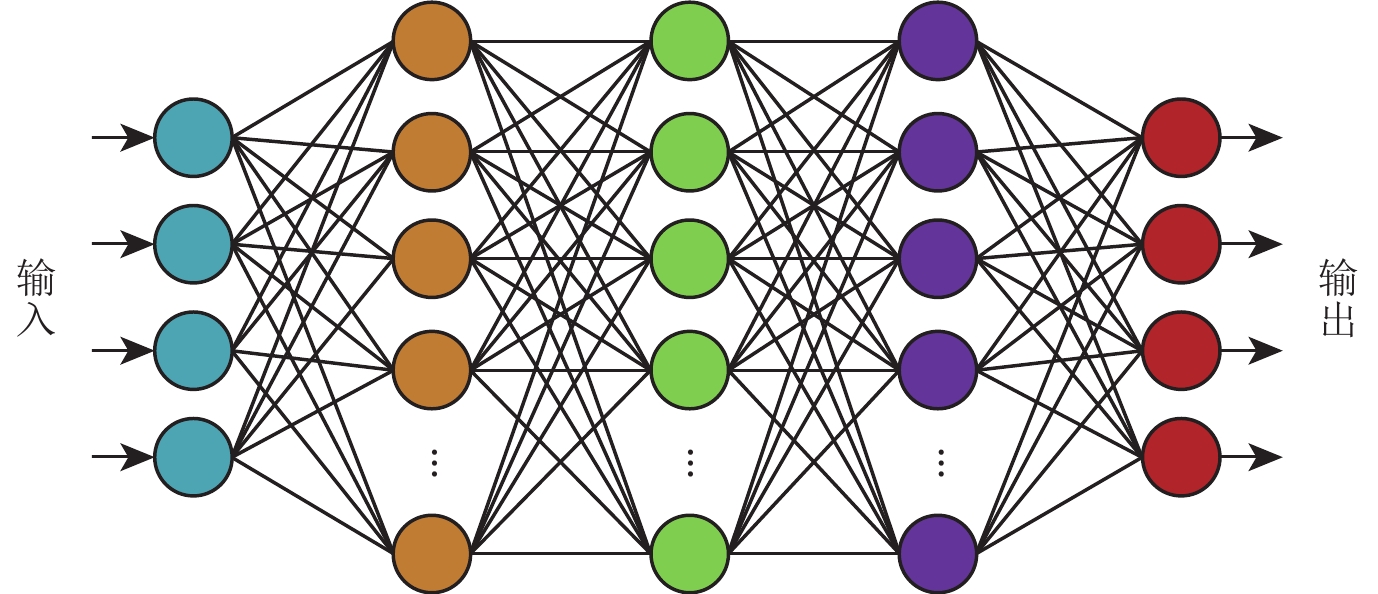
据蒋宗礼（2001）和Haykin （2008）的理论，3层的BP神经网络可以逼近任何函数，因此优先选择3层BP神经网络进行训练。本研究为了选取最优的层数，分别取3，5，7，9进行试验，结果列于表2，可以看出当输出层的节点数取4 （等于输入层的节点数）时，明显优于输出层节点数取1。在表2中也进一步说明当网络层数取5时，输出值与目标值的相关系数为0.984，最小误差为0.002 12。因此选取4−9−9−9−4的网络结构模型（图8）。取S形函数为激励函数，采用梯度下降法，学习率取0.001，训练的目标误差为0.001，迭代10 000次进行学习训练。
表 2 输出层节点数为1和4时的试验结果Table 2. The experimental results when the number of output layer nodes is taken as 1 and 4输出节点 网络层数 相关系数 最小误差 1 3 0.845 0.014 2 5 0.844 0.014 3 7 0.870 0.012 3 9 0.819 0.016 3 4 3 0.981 0.002 28 5 0.984 0.002 12 7 0.983 0.002 15 9 0.982 0.002 26 4.5 结果分析
利用matlab软件完成BP神经网络模型的构建，主要使用newff，train和sim等三个函数实现BP神经网络模型的学习训练与测试。通过训练集数据训练出最优神经网络模型net，将训练集数据通过模型net仿真预测，得到训练集的预测结果1，并与实际结果求偏差进行分析，结果如图9a所示；将测试集数据通过net仿真预测，得到测试集的预测结果2，并跟实际结果之间求偏差进行分析，结果如图9b所示。可以看出：训练集的偏差均控制在[−0.3，0.3]之间，最大偏差为0.29；而测试集的偏差绝大部分均控制在[−0.3，0.3]之间，最大偏差为−0.38。无论是训练集还是测试集，校正后的偏差绝大部分均未超出震级误差±0.3的范围，满足省级测震台网地震速报评比标准，预测结果与实际结果接近，预测效果较好。
![]()
图 9 台湾实际ML与基于BP神经网络模型的预测ML的偏差分析（a） 训练集；（b） 测试集Figure 9. Magnitude deviation analysis between the actual ML and the predicted ML based on the BP neural network model（a） Training set；（b） Testing set4.5.1 BP神经网络与传统方法预测结果比较
图10给出了传统线性回归方法的预测结果分布，可见实际ML值与预测ML值的偏差只控制在[−0.6，0.6]之间，最大偏差绝对值达0.53，与神经网络技术所得震级误差相比波动较大，预测效果较差。而BP神经网络模型考虑了震源深度和震源地理位置的影响因素，且该网络模型还具有较强的非线性拟合能力，因此拟合效果优于传统线性回归。
![]()
图 10 台湾气象局实际测定ML结果与传统线性回归的预测结果的偏差分析Figure 10. Magnitude deviation analysis between the actual results and the prediction results by conventional linear regression4.5.2 典型震例的预测效果分析
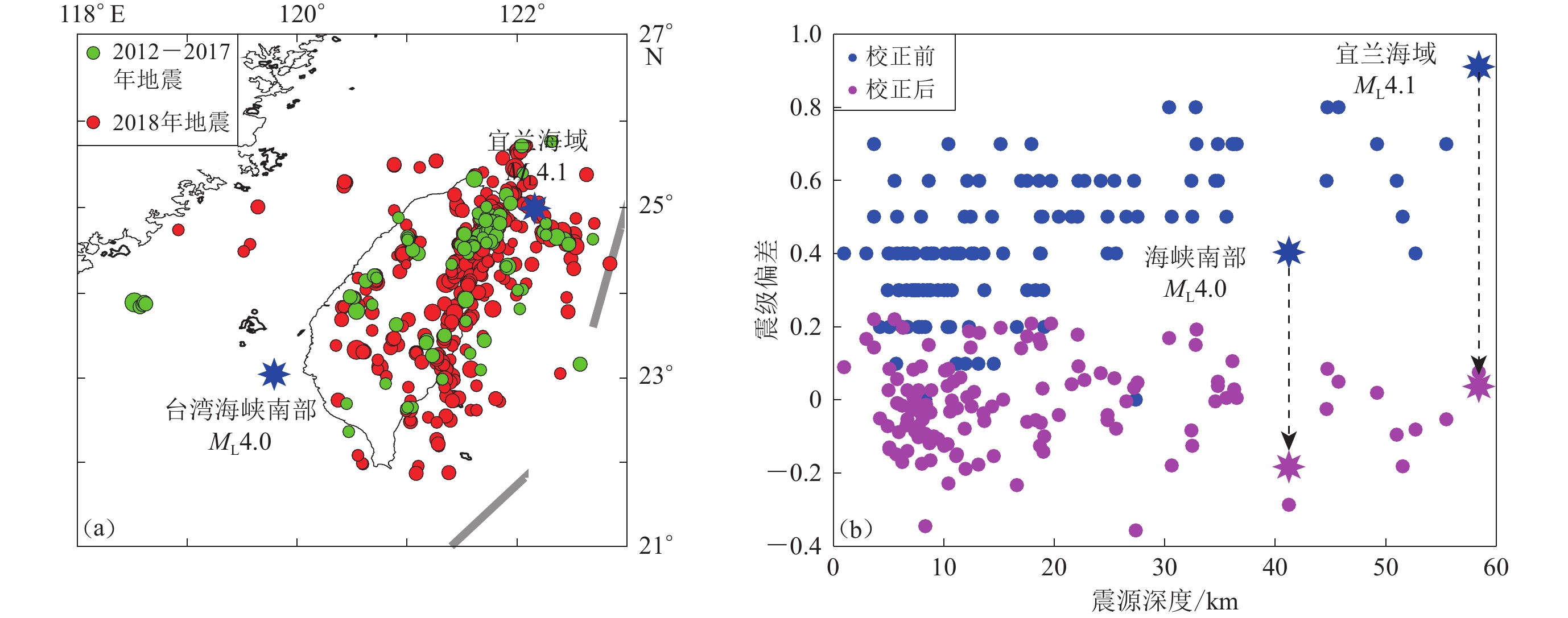
为了进一步验证神经网络的预测效果，本文选取地震高发的宜兰海域ML4.1地震和地震低发的台湾海峡南部ML4.0地震进行分析（图11a）。
![]()
图 11 典型震例预测效果分析（a） 地震分布图；（b） 2018年地震震例校正前后震级偏差对比图Figure 11. Analysis of prediction effect of typical earthquake cases（a） Distribution of earthquakes；（b） Comparison of magnitude deviation before and after correction of earthquake cases in 2018根据上述试验结果，利用训练好的BP神经网络模型对2018年台湾地震震例进行预测，并进行校正前后的震级偏差分析，结果如图11b所示。可以看出，随着震源深度的增加，台湾气象局实际测得的ML与福建地震台网中心测得的ML震级偏差逐渐增大，这与上述分析结果一致。而台湾实际测定的ML与台湾预测的ML的震级偏差则在零值附近浮动，基本都控制在[−0.4，0.3]之间，相比于台湾实际测得的ML与福建地震台网中心测得的ML的震级偏差，震级偏差大幅降低，特别是对于深度较大的震例，其偏差控制效果更加明显。从图11b可以看出：台湾宜兰海域ML4.1地震的偏差从0.9降低到0.01，这是由于该地震区域存在较多历史震例（如图11a），使得神经网络训练时对该区域震例的学习更加深入，预测效果更好；而台湾海峡南部ML4.0地震的震级偏差则从0.4降低至−0.19，偏差有所减小，虽然训练时神经网络未学习到该区域的历史震例，但神经网络同样能够给出较好的预测，这也验证了神经网络模型具有一定的泛化能力。
对于2017年11月4日台湾花莲地震，经过BP神经网络校正后，福建地震台网中心原先测定的震级可从ML4.8调整为ML5.1，更加接近台湾气象局实际测定的ML5.2。
综上所述，校正后的偏差比校正前的偏差降低较多，应用BP神经网络模型进行预测可以在很大程度上改善福建地震台网中心与台湾气象局两机构测定震级结果之间的差异。
5. 讨论与结论
针对闽台两机构震级对外发布时存在一定的差异问题，初步分析了导致闽台两机构震级偏差的主要原因有：
1） 闽台两机构测定震级方法不同，对于较大地震来说，福建地震台网中心以测定面波震级MS为主，而台湾中央气象局网站上以测定里氏震级ML为主。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
同时还开展了闽台ML震级偏差的分析与修正工作，研究分析了地震震级大小、震源深度、震源地理位置等对闽台两机构测定震级偏差的影响。若采用传统的线性拟合方法进行修正，震级偏差只控制在[−0.6，0.6]之间，最大偏差绝对值达0.53；而采用BP神经网络进行闽台两机构测定震级修正，可使得震级偏差基本控制在[−0.4，0.3]之间，最大偏差为−0.38，明显优于传统线性拟合方法，很好地发挥了BP神经网络具有较强的非线性拟合能力。另外，BP神经网络对少震区域，即未有历史地震记录的震例，其预测效果也很好，进一步验证了神经网络具有一定的泛化能力，不仅解决了闽台两机构测定的震级差异问题，也为后续神经网络在地震领域的应用提供了参考。
本研究采用BP神经网络技术对闽台两机构测定的震级校正，校正后的偏差得到极大的改善，也满足了地震速报及编目的要求，这种新方法在技术层面上是有效可行的。但是在对社会发布的问题上，还需要有关部门协商制定出明确的震级发布规则较为妥当，今后将继续跟踪闽台两机构测定震级偏差修正其实际应用效果。
-
![]()
图 1 福建地震台网中心记录的2012—2018年台湾地震分布图
Figure 1. The distribution of earthquakes in Taiwan island and its vicinity recorded by Fujian Seismic Network Center from 2012 to 2018
![]()
图 2 闽台两机构测定ML震级的比较
（a） 震级散点图，绿线为ML-fj均值4.11，黄线为ML-tw均值4.62；（b） 震级频次直方图
Figure 2. Comparison of magnitude ML measured by Fujian with that by Taiwan
（a） Scatter diagram of magnitude，where the green line represents the mean magnitude 4.11 measured by Fujian Seismic Network Center，the yellow line represents the average magnitude 4.62 by Taiwan Weather Bureau；（b） Magnitude frequency histogram
![]()
图 3 闽台机构测定震级ML之间的线性回归关系
Figure 3. The linear regression relationship between magnitude ML determined by Fujian and Taiwan
![]()
图 4 闽台震级偏差随地震震级（a）和震源深度（b）的变化
Figure 4. Variation of magnitude deviation between Fujian and Taiwan with magnitude （a） and hypocenter depth （b）
![]()
图 5 震源的地理位置对闽台震级偏差的影响
Figure 5. Effect of the location of the earthquake source on the magnitude deviation measured by Fujian and Taiwan
![]()
图 6 本文BP神经网络模型的输入与输出
Figure 6. The input and output of BP neural network model in this study
![]()
图 9 台湾实际ML与基于BP神经网络模型的预测ML的偏差分析
（a） 训练集；（b） 测试集
Figure 9. Magnitude deviation analysis between the actual ML and the predicted ML based on the BP neural network model
（a） Training set；（b） Testing set
![]()
图 10 台湾气象局实际测定ML结果与传统线性回归的预测结果的偏差分析
Figure 10. Magnitude deviation analysis between the actual results and the prediction results by conventional linear regression
![]()
图 11 典型震例预测效果分析
（a） 地震分布图；（b） 2018年地震震例校正前后震级偏差对比图
Figure 11. Analysis of prediction effect of typical earthquake cases
（a） Distribution of earthquakes；（b） Comparison of magnitude deviation before and after correction of earthquake cases in 2018
表 1 闽台震级偏差校正前后的对比
Table 1 Comparison of the Fujian’s and Taiwan’s magnitude deviation before and after correction
ML-fj ${M_{ {\rm{L} } {\simfont\text{-}} {\rm{tw} } }^{\rm{r} } }$ 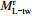${M_{ {\rm{L} } {\simfont\text{-} } {\rm{tw} } }^{\rm{f} } }$ 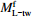${\Delta {M_{ {\rm{L} }{\simfont\text{校正前} } } } }$ 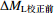${\Delta {M_{ {\rm{L} }{\simfont\text{校正后} } } } }$ 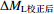3.0 3.6 3.68 0.60 −0.08 3.5 4.2 4.10 0.70 0.10 4.0 4.4 4.53 0.40 −0.13 4.5 4.8 4.95 0.30 −0.15 5.0 5.6 5.38 0.60 0.22 5.5 6.3 5.81 0.70 0.49 6.0 6.2 6.23 0.20 −0.03 注： ${M^{\rm r}_{\rm L{\text{-} } tw} }$ 为台湾气象局实测震级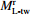，${M^{\rm f}_{\rm L{\text{-} } tw} }$ 为拟合得到的台湾地区震级值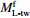，${\Delta {M_{ {\rm{L} }{\simfont\text{校正前} } } } {\simfont\text{＝} } M_{ {\rm{L} }{\text{-} } {\rm{tw} } }^{\rm{r} } {\simfont\text{－} } M_{ {\rm{L} } {\text{-} } {\rm{fj} } }^{} }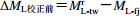， $ ，${\Delta {M_{ {\rm{L} }{\simfont\text{校正后} } } } {\simfont\text{＝} } M{_{ {\rm{L} } {\text{-} } {\rm{tw} } }^{\rm{r} } } {\simfont\text{－} } M_{ {\rm{L} } {\text{-} } {\rm{tw} } }^{\rm{f} } } $ .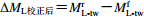
下载: 导出CSV
表 2 输出层节点数为1和4时的试验结果
Table 2 The experimental results when the number of output layer nodes is taken as 1 and 4
输出节点 网络层数 相关系数 最小误差 1 3 0.845 0.014 2 5 0.844 0.014 3 7 0.870 0.012 3 9 0.819 0.016 3 4 3 0.981 0.002 28 5 0.984 0.002 12 7 0.983 0.002 15 9 0.982 0.002 26
下载: 导出CSV
-
陈运泰,刘瑞丰. 2004. 地震的震级[J]. 地震地磁观测与研究,25(6):1–12. doi: 10.3969/j.issn.1003-3246.2004.06.001 Chen Y T,Liu R F. 2004. Earthquake magnitude[J]. Seismological and Geomagnetic Observation and Research,25(6):1–12 (in Chinese).
杜百灵. 2018. 地震多属性BP神经网络法在预测煤层厚度上的应用研究[J]. 工程地球物理学报,15(2):246–251. doi: 10.3969/j.issn.1672-7940.2018.02.020 Du B L. 2018. Application of seismic multi attribute BP neural network in prediction of coal seam thickness[J]. Chinese Journal of Engineering Geophysics,15(2):246–251 (in Chinese).
傅再扬,李祖宁,丁学仁,吴绍祖. 2008. 福建和台湾地震台网测定地震震级差异研究[J]. 地震研究,31(1):32–36. doi: 10.3969/j.issn.1000-0666.2008.01.006 Fu Z Y,Li Z N,Ding X R,Wu S Z. 2008. Difference research on magnitude determined by Fujian Seismic Networks and Taiwan’s[J]. Journal of Seismological Research,31(1):32–36 (in Chinese).
蒋宗礼. 2001. 人工神经网络导论[M]. 北京: 高等教育出版社: 1−114. Jiang Z L. 2001. Introduction to Artificial Neural Networks[M]. Beijing: Higher Education Press: 1−114 （in Chinese）.
李善邦. 1981. 中国地震[M]. 北京: 地震出版社: 120−156. Li S B. 1981. Earthquakes in China[M]. Beijing: Seismological Press: 120−156 （in Chinese）.
李军,金星,郭阳. 2016. 福建台网测定台湾地震震级偏差研究[J]. 自然灾害学报,25(3):143–152. Li J,Jin X,Guo Y. 2016. Study on the earthquake magnitude deviation in Taiwan region measured by Fujian Seismic Network[J]. Journal of Natural Disasters,25(3):143–152 (in Chinese).
刘瑞丰,陈运泰,任枭,徐志国,孙丽,杨辉,梁建宏,任克新. 2007. 中国地震台网震级的对比[J]. 地震学报,29(5):467–476. doi: 10.3321/j.issn:0253-3782.2007.05.003 Liu R F,Chen Y T,Ren X,Xu Z G,Sun L,Yang H,Liang J H,Ren K X. 2007. Comparison between different earthquake magnitudes determined by China Seismograph Network[J]. Acta Seismologica Sinica,29(5):467–476 (in Chinese).
刘瑞丰, 陈运泰, 任枭, 徐志国, 王晓欣, 邹立晔, 张立文. 2015. 震级的测定[M]. 北京: 地震出版社: 1−137. Liu R F, Chen Y T, Ren X, Xu Z G, Wang X X, Zou L Y, Zhang L W. 2015. Magnitude Measurement[M]. Beijing: Seismological Press: 1−137 （in Chinese）.
刘瑞丰,陈运泰,薛峰,李恩来. 2108. 如何正确使用新的震级国家标准[J]. 地震地磁观测与研究,39(4):1–10. Liu R F,Chen Y T,Xue F,Li E L. 2018. How to use the new national standard of magnitude correctly[J]. Seismological and Geomagnetic Observation and Research,39(4):1–10 (in Chinese).
唐淋,祁国亮,苏金蓉,黄春梅,傅莺,颜利君. 2018. 新国家标准震级标度与传统震级标度对比研究[J]. 地震学报,40(2):121–131. Tang L,Qi G L,Su J R,Huang C M,Fu Y,Yan L J. 2018. Comparison of the new national standard magnitude scales with the traditional magnitude scales[J]. Acta Seismologica Sinica,40(2):121–131 (in Chinese).
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 2017. GB 17740—2017地震震级的规定[S]. 北京: 中国标准出版社: 5−13. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of China. 2017. GB 17740−2017 General Ruler For Earthquake Magnitude[S]. Beijing: Standards Press of China: 5−13 （in Chinese）.
Duda R O, Haet P E, Stork D G. 2000. Pattern Classification[M]. Hoboken: Wiley-Interscience: 1−654.
Haykin S. 2008. Neural Networks and Learning Machines[M]. New Jersey: Prentice Hall Inc: 1−935.
Mitchell T M. 1997. Machine Learning[M]. New York: McGraw-Hill Education.
Richter C F. 1935. An instrumental earthquake magnitude scale[J]. Bull Seismol Soc Am,25(1):1–32.
Shin T C. 1993. The calculation of local magnitude from the simulated Wood-Anderson seismograms of the short-period seismograms in the Taiwan area[J]. Terrest Atmos Oceanic Sci,4(2):155–170. doi: 10.3319/TAO.1993.4.2.155(T)
-
期刊类型引用(4)
1. 郑周，林彬华，金星，韦永祥，丁炳火，陈辉. 基于卷积神经网络的地震波形智能识别研究. 世界地震工程. 2023(02): 148-157 . 
百度学术
2. 程先琼，蒋科植. 基于深度降噪自编码神经网络的中国大陆地壳厚度反演. 地震学报. 2021(01): 34-47+136 . 本站查看
3. 巫立华，张宝剑，林彬华，戴丽金，张丽娜. BP神经网络在地震噪声波形检测中的应用. 华南地震. 2021(03): 116-121 . 百度学术
4. 吴果，李建强，冉洪流，周庆，谢卓娟. 中国海域及邻区基于BP神经网络的矩震级转换模型. 中国地震. 2021(03): 659-670 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 1796
- HTML全文浏览量: 666
- PDF下载量: 45
- 被引次数: 4
