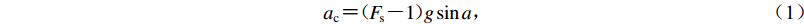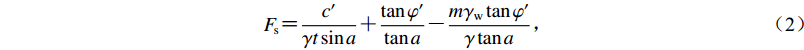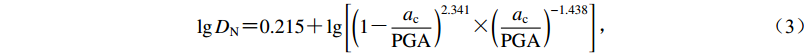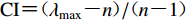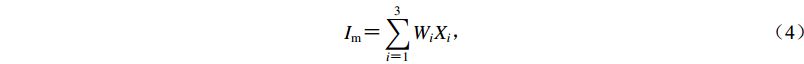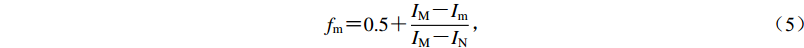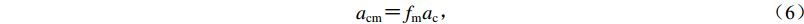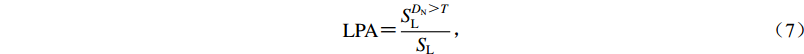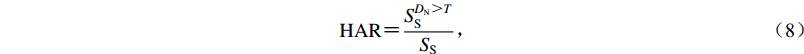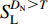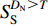A method for seismic landslide hazard assessment using simplified Newmark displacement model based on modified strength parameters of rock mass
-
摘要: 地震滑坡危险性评估可为震后应急响应等提供科学的决策依据。纽马克位移法可不依赖同震滑坡编目快速评估同震滑坡危险性。工程岩体物理力学参数是该方法的核心参数之一，但其赋值过于单一，难以反映复杂地质背景下岩体强度的空间差异性。针对上述问题，本文在分析地震滑坡影响因子的基础上，选择距断层距离、高程和距水系距离作为影响岩体强度的评价指标并建立岩体强度评价模型，获得区域岩体强度修正系数，进而修正传统方法的临界加速度。结合震后的即时地震动峰值加速度，采用简化纽马克位移法计算边坡累积位移，开展地震滑坡危险性快速评估，并以汶川MW7.9地震的地震滑坡危险性评估为例验证本文方法。结果表明，相对于传统方法，本文方法划分的地震滑坡危险区与同震滑坡分布更加一致。Abstract: Rapid assessment of seismic landslide hazard can provide a scientific basis fordecision-making aimed at post-earthquake emergency response. The Newmark displacement model can quickly assess the seismic landslide hazard after an earthquake without co-seismic landslide inventory. However, as one of the main parameters of the Newmark displacement model, physical and mechanical parameters of the rock mass assigned by traditional methods are too single to reflect the spatial differences of real rock mass strength under complex geological background. To tackle this issue, the distance to the fault, the elevation, and the distance to the river were selected as the evaluation indexes affecting the strength of rock mass, and the evaluation model of rock mass strength was established to obtain the regional rock mass strength modified coefficient, and then the critical acceleration obtained by the traditional method was modified. Combined with the instantaneous peak ground acceleration after an earthquake, the simplified Newmark empirical displacement model was used to calculate the slope cumulative displacement, and the rapid assessment of seismic landslide hazard was conducted. The Wenchuan MW7.9 earthquake was selected as the studied area to validate the performance of the presented method. Results show that the seismic landslide hazard area divided by the presented method is more consistent with the actual co-seismic landslide distribution compared to traditional method. The presented method in this paper can be used for rapid assessment of seismic landslide hazard, which has important reference value for guiding post-earthquake emergency rescue and land planning and also provides a new idea for the subsequent establishment of a basic geological spatial database.
-
引言
地震滑坡作为地震直接触发的一种地质灾害，具有突发性、群发性及广泛分布等特点，是一种常见的地震次生灾害（Zhou，Zhang，1994；黄润秋，李为乐，2008；Fan et al，2019）。快速可靠地开展地震滑坡危险性评估和分区，可为震后应急救援、土地利用规划等提供参考（Guzzetti et al，2006；王涛等，2013）。
地震滑坡危险性评估方法主要有基于滑坡编目的统计分析法和基于力学模型的纽马克（Newamrk）位移分析法。统计分析法是在统计大量地震滑坡的基础上，建立滑坡与地质环境因子间的统计关系模型，以评估区域地震滑坡危险性（王进等，2012）。此类方法基于地震滑坡编目，能够客观地评估地震滑坡危险性（Pourghasemi et al，2018；Reichenbach et al，2018）；但受限于现有技术条件，震后并不能快速获取完整的同震滑坡编目，降低了统计分析法的评估精度，限制了其在同震滑坡危险性快速评估中的应用（Xu et al，2013；Chen et al，2020）。相反，纽马克位移分析法，基于边坡的岩体物理力学参数、坡度和地震动参数，不依赖于滑坡编目，可用于地震滑坡危险性快速评估（Jibson，1993；刘甲美等，2015；李雪婧等，2019）。研究人员已将简化纽马克模型应用于1994年美国北岭地震（Jibson et al，2000）、1999年台湾集集地震（Tsai et al，2019）、2008年汶川地震（王涛，2010）和2017年九寨沟地震（陈晓利，2019）等地震滑坡危险性评估，验证了该模型的有效性。然而，纽马克位移法的可靠性依赖于准确的岩土体物理力学参数，然而获取准确的大区域岩土体物理力学参数成本高昂，限制了该方法在地震滑坡危险性快速评估中的应用。
滑坡是复杂地质环境下多因素综合作用的结果（Intrieri et al，2019）。对于地震滑坡而言，其主控因子多与地震相关，如地震类型和震源深度。事实上，地震滑坡是地震扰动超过了边坡所能承受的极限（即震前边坡的稳定性）所引发的边坡失稳。因此，震前边坡稳定性分析是评估地震滑坡危险性的前提。震前边坡稳定性与多种影响因子有关，如地形、水文和地质等因子。Pourghasemi等（2018）基于2005—2016年间发表的相关文献，分析了地震滑坡稳定性影响因子及其权重，结果表明：岩性、工程地质岩组、断层距离是典型的地质因子；高程、坡度、坡向是典型的地形因子；而水系距离、河网密度等常作为水文因子。因此，为可靠地分析震前边坡稳定性，须考虑地质环境因子的影响。
边坡临界加速度反映了震前边坡稳定性，是影响简化纽马克模型地震滑坡危险性评估可靠性的主要因素之一（Dreyfus et al，2013），其大小可利用边坡岩体力学参数及坡度信息并通过极限平衡方程计算获得。事实上，区域边坡岩体力学参数的获取极其困难，一般通过实验室测得，而标准的实验室样本太小，无法包含强度极限不连续面的规模和聚集效应，增大测试样本尺寸以捕捉岩体强度真实的空间异质性是不现实的。目前，区域边坡岩体力学参数的获取主要基于工程地质图，利用工程岩体分类和实践经验，赋予不同岩组统一的岩体力学参数（Godt et al，2008；Jibson，2011）。然而，即便对于同一类岩组，其岩体结构、风化程度、水理性质等也不尽相同。此外，岩体结构、风化程度、水理性质与所处地质环境紧密相关，如地形差异、水文条件等，使得岩体强度在区域尺度上存在明显的空间异质性（王涛等，2015）。因此，统一的岩体力学参数仅反映岩组的综合强度，忽略了岩体强度的空间差异性，并不能代表真实的岩体强度。针对这一问题，李鑫等（2018）基于地震滑坡调查数据探讨了区域岩土体强度的确定方法，研究结果指出了岩土体强度的空间差异性在区域地震滑坡危险性评估中的重要作用。然而上述方法仍然是以岩性为基本单元，对于同一种岩性内部在复杂地质条件影响下的空间差异性缺乏考虑。
针对在地震滑坡危险性快速评估中应用简化纽马克位移法存在的不足及对岩体强度的空间差异性欠缺考虑，本文拟在分析地震滑坡影响因子的基础上，筛选出影响岩体强度的地质环境因子并建立区域岩体强度修正模型，以期改进传统方法获得的临界加速度并计算边坡累积位移，最终评价区域地震滑坡危险性。以汶川MW7.9地震重灾区为研究区，利用同震滑坡编目验证本文方法的可靠性，为后续基于简化纽马克位移模型评估地震滑坡危险性提供参考。
1. 研究区及数据源
1.1 研究区概况
2008年5月12日汶川MW7.9大地震触发的滑坡覆盖了整个灾区，形成大量巨型、群发性滑坡，并造成了多处严重的堰塞湖。据统计，此次地震共诱发了196 007处地震滑坡（许冲等，2013），形成大量松散堆积体和潜在不稳定边坡，严重影响后续灾区重建工作（黄润秋，2011）。根据地震动分布，选择大致平行于发震断层的矩形区域作为研究区（图1），其覆盖了大部分高地震动区域，包括汶川县、茂县、北川县等重灾区。
![]()
图 1 研究区断层分布及地震动图Figure 1. Distribution of fault and ground motion map in the study area1.2 数据源
本文收集了与汶川地震相关的地震动图及研究区地质环境资料，主要包括：① 地震动图：汶川地震发生后，美国地质调查局在10分钟内即发布了汶川地震动峰值加速度（peak ground acceleration，缩写为PGA）、地震仪器烈度等一系列地震动图。本文选择PGA作为评估地震滑坡危险性的地震动参数。研究区的PGA分布如图2a所示，PGA值介于0.12g—1.74g，主要分布在发震断层两侧，低值区主要分布在远离发震断层区域，且在断层上盘，PGA衰减速度低于下盘，呈现典型的断层上盘效应。② 工程地质图：来源于中国地质调查局发布的1 ∶ 250 000工程地质图，包含地层年代及主要岩性信息，是确定岩体强度的重要参考。基于工程地质图中地层年代及岩性描述，参考《工程岩体分级标准》（中华人民共和国住房和城乡建设部，2015）和《岩土工程勘察规范》（中华人民共和国建设部，2004），将研究区的岩体强度划分为坚硬岩组、较坚硬岩组、较软岩组、软岩组（图2b）。其中：坚硬岩组和较软岩组占比最大，涵盖研究区内大部分年代的地层，从前震旦系至新近系均有分布，主要集中于龙门山中央断裂上盘；软岩组与较坚硬岩组分布占比相当，主要分布在龙门山后山断裂两侧及龙门山前主边界断裂的下盘区域。较坚硬岩以石英砂岩、砂岩及灰岩等为主，软岩组则主要为第四系河湖相松散砾石-黏土沉积。③ 地表形态数据：地形坡度可反映地表形态，是评估地震滑坡危险性的基础数据。本文采用全球SRTM数据提取地形坡度，如图2c所示。研究区地形坡度分布在0°—89°，大部分区域坡度值介于30—50°。④ 其它地质环境数据：主要指影响岩体强度的地质环境因子，包括地形、水文及地质因子。⑤ 同震滑坡编目：来源于震前震后高分遥感影像解译及野外地质调查（许冲等，2013）。研究区同震滑坡（图2d）用于评估模型精度。
![]()
图 2 研究使用的主要数据源（a） 地震动图；（b） 工程岩组；（c） 地形坡度；（d） 同震滑坡Figure 2. Data sources used in this study（a） Ground motion maps；（b） Engineering rock mass；（c） Topographic slopes；（d） Co-seismic landslides2. 研究方法
2.1 纽马克位移分析法
纽马克位移分析法（Newmark，1965）认为坝体失稳取决于地震引起的变形，而非最小稳定系数。地震引起的变形是震前滑体临界加速度和地震动加速度共同作用的结果，当地震加速度大于滑体临界加速度时，滑体将沿最危险的结构面滑动。对地震动加速度中超过临界加速度的部分二次积分可获得滑体的累积位移值，其大小反映了地震对滑体的扰动程度。
临界加速度是震前边坡能够抵抗的最大地震动加速度，与边坡的岩体强度和几何形态有关，可通过滑体的极限平衡方程式求得，即
$$ {a_{\rm{c}}} ＝ （ {F_{ \rm{s}}} － 1 ） g\sin a ，$$ (1) 式中，ac为滑体临界加速度，a为滑动面倾角，F s为静态安全系数，表示为滑体抗滑力与下滑力的比值，可根据滑体的岩体力学参数和地形坡度计算获得，即
$$ {F_{ \rm{s}}} ＝ \frac{{c'}}{{\gamma t\sin a}} ＋ \frac{{\tan \varphi '}}{{\tan a}} － \frac{{m{\gamma _{\rm{w}}}\tan \varphi '}}{{\gamma \tan a}} ， $$ (2) 式中：c′和φ′分别为岩体的有效黏聚力和有效内摩擦角；γ和γw分别为岩体重度和地下水重度；m为潜在滑体中饱和部分占滑体厚度的比值；t为潜在滑体厚度。
纽马克位移分析法需要完整的地震加速度时程记录，当该记录缺乏时，可采用简化纽马克经验位移模型。其中，基于PGA的经验位移公式是目前国内外普遍采用的一种简化纽马克经验位移方程（Jibson，2007），即
$$ \lg D_{\rm{N}} ＝ 0.215 ＋ \lg \left[ {{{\left( {1 － \frac{{{a_{\rm{c}}}}}{{{\rm{PGA}}}}} \right)}^{2.341}} {\text{×}} {{\left( {\frac{{{a_{\rm{c}}}}}{{{\rm{PGA}}}}} \right)}^{ - 1.438}}} \right] ，$$ (3) 式中，DN为滑体累积位移，单位为cm；PGA单位为g；ac为滑体临界加速度，单位为g。已知PGA和临界加速度时，通过式（3）可求得特定地震动条件下边坡的累积位移分布。
2.2 静态安全系数和临界加速度
滑坡形成很大程度上取决于岩体结构面破坏所形成的滑动面。因此，可将岩体结构面所对应的内摩擦角和内聚力作为岩体有效内摩擦角和有效内聚力。根据划分的工程岩组，参考相关规范，赋予岩组不同的有效内摩擦角和有效内聚力（刘甲美，2015）。由于本文目的在于分析岩体强度修正在地震滑坡危险性评价中的适用性，因此，岩体参数的赋值主要参考已有研究工作（马思远等，2019），如表1所示。滑动面倾角一般与岩体结构面的分布有关，常用边坡坡度角代替。滑体重度γ和厚度t受岩组类别影响，不同岩组对应不同的重度和厚度。目前，这两个参数主要采用经验赋值，常取固定常数。本文将滑体重度和厚度的乘积作为常量（γt＝60 kN·m−2，其中滑体重度为20 kN·m−3，滑体厚度为3 m）（Jibson，2007）。滑体饱和度m受降雨影响显著，在干旱与雨季时节差异明显。对于大区域范围，滑体饱和度很难准确测得。因此，本文采用不同的滑体饱和度参数（m＝0，0.5，1），分别计算地震作用下边坡的累积位移，评估滑体在不同饱和度下的地震滑坡危险性。
表 1 研究区工程地质岩组结构面强度经验赋值Table 1. Empirical value of the structural surface strength of the engineering geological rocks in the studied area工程地质岩组 有效内摩擦角/° 有效黏聚力/MPa 坚硬岩组 40 0.035 较坚硬岩组 35 0.028 较软岩组 30 0.025 软岩组 20 0.015 图3a为当m＝0时计算获得的研究区静态安全系数分布图，值越大表明边坡越稳定，当F s＜1时，边坡下滑力大于抗滑力，则认为边坡处于变形破坏中。事实上，在震前，边坡处于静态稳定状态，即F s＞1。而在实际计算中，岩体力学参数来自于经验赋值，并不能反映岩体的实际强度，因此，在地形陡峭区域，存在F s＜1的情况，与实际情况不符。为解决此问题，Jibson （2007）通过迭代不断提高岩体力学参数的取值，直到坡度小于60°的区域所对应的F s＞1。这种处理方法会导致坡度较大的区域被赋予较高的岩体力学参数值，而这部分区域多属于较坚硬岩和坚硬岩组，易低估该区域的地震滑坡危险性。统计本文计算的静态安全系数表明，研究区仅有0.25%的区域对应于F s＜1，且多分布在高陡边坡区域，间接说明本文岩体力学参数赋值方法具有一定的可信度。最终参考已有研究，当F s＜1时，将F s统一修改为1.01，以避免采用迭代法导致的岩体力学参数赋值过高的问题（Dreyfus et al，2013）。
![]()
图 3 研究区斜坡静态安全系数（a）和临界加速度（b）分布Figure 3. Distribution of static factor of safety （a） and critical acceleration （b） in study area图3b为基于图3a采用式（1）获得的临界加速度分布图，临界加速度的大小反映了边坡所能承受的最大地震动加速度。由式（1）和式（2）可知，临界加速度的大小主要取决于岩体的物理力学参数和地形坡度。相同地形坡度下，岩体的力学性质越差，临界加速度越小，边坡越易受地震扰动形成滑坡。在同一岩组中，由于岩组物理力学参数赋值单一，因此临界加速度的大小主要取决于地形坡度，坡度越大，临界加速度越小，边坡越易形成滑坡。现有岩体物理力学参数是一种基于工程岩体分类的经验参数，一定程度上忽视了岩体所处地质环境因子的影响。由于岩体的力学性质与成岩条件、结构面发育、风化程度等密切相关，同一类岩体在不同地质环境条件下，其物理力学差异巨大，不考虑地质环境因子的影响将降低岩体物理力学参数赋值的可靠性。因此，为获得更加可靠的岩体力学参数，须探讨岩体强度在不同地质环境下的空间差异性。
2.3 基于层次分析法修正的临界加速度
相对于准确的实测单点岩体强度信息，区域岩体强度的空间差异性更适合于地震滑坡危险性分析。考虑到岩体强度与所处的地质环境相关，选择地质、地形、水文相关因子作为评价指标，采用层次分析法（analytic hierarchy process，缩写为AHP）建立岩体强度修正模型。AHP是一种基于专家经验知识的多层次多因子的定权方法（郭金玉等，2008），通过量化指标（表2）比较两两因子，构建判别矩阵，确定各因子权重，最终确定岩体强度修正系数。为确保判别矩阵的合理性，通常在确定权重前进行一致性检验，即计算一致性指标值（consistency index，缩写为CI），
${\rm{CI}} ＝ （ {{\lambda _{\max }} － n} ） / （ {n － 1} ） $ ，其中n代表判别矩阵的阶数，λmax代表判别矩阵的最大特征值或主特征值。当n≤3时，CI＝0表示判别矩阵具有完全的一致性；反之，CI值越大，判别矩阵的一致性越差，当CI＜0.1时，表示判别矩阵通过一致性检验。综合文献资料和滑坡因子的敏感性分析（Pourghasemi et al，2018），本文选择高程、距水系距离和距断层距离作为评价指标。表 2 判别矩阵定量标度及其描述Table 2. Scale of judgment matrix and its description标度值bij 相对重要性描述 1 bi与bj 同样重要 3 bi比bj 稍微重要 5 bi比bj 明显重要 7 bi比bj 强烈重要 9 bi比bj 极端重要 2，4，6，8 上述相邻的判断中值 倒数 bij＝bji 1） 高程。高程影响岩石的风化程度。位于不同高程的岩石，受太阳直射、温差变化作用明显，影响岩石风化进而产生裂缝。历史地震滑坡编目和高程分布的结果显示高程是影响地震滑坡分布的重要因子（许冲等，2010），因此，本文选择高程作为岩体强度的影响因子。根据研究区的高程分布，采用0.5 km作为分级间隔将高程划分为9级，如图4a所示。
![]()
图 4 岩体强度的主要评价指标（a） 高程；（b） 距水系距离；（c） 距断层距离Figure 4. Main evaluation indicators for rock mass strength（a） Elevation；（b） Distance to the river；（c） Distance to the fault2） 距水系距离。水对应岩体水理性质，是影响岩体强度的重要因子。一方面，水体容易软化岩体结构面，降低其有效强度，使得岩体在外力作用下更易发生破坏；另一方面，地下水径流冲刷、孔隙水压力增大等易导致岩体形成软弱结构面或破坏已有结构面，极易在外界因素变化下形成滑坡（Kamp et al，2008）。根据研究区的水系分布，本文采用2 km分级间隔将距水系距离划分为9级，如图4b所示。
3） 距断层距离。断层是构造运动中广泛发育的一种构造形态（张咸恭等，2000），断层的广泛分布破坏了岩层的连续性和完整性。断层带上的岩石往往较破碎，而远离断层区域，构造运动影响减弱，岩石完整性较好。岩体完整性影响岩体强度，对于同类岩体，完整岩体的强度显然高于破碎岩体。因此，本文将距断层距离作为评价岩体完整性的指标，根据研究区断层分布，以2 km分级间隔将距断层距离划分为9级，如图4 所示。
根据表2中的量化指标，通过两两比较来评价上述地质因子的重要性，建立判别矩阵（Kayastha et al，2013；刘丽娜等，2014），并据此计算各评价指标权重，显示本文构建的判别矩阵具有较好的一致性（表3）。评价指标权重结果表明，距断层距离是影响岩体强度的主要因素，其次是高程和距水系距离。
表 3 评价指标权重和对应的判别矩阵Table 3. Evaluation index weight and corresponding judgment matrix评价指标 距断层距离 高程 距水系距离 权重 一致性检验 距断层距离 1 3 7 0.669 4 CI＝0.003 5＜0.1 高程 1/3 1 3 0.242 6 距水系距离 1/7 1/3 1 0.087 9 综合各地质环境因子分级值及权重信息，利用式（4）计算在不同地质环境因子影响下的岩体强度指数。指数越高，地质环境因子对岩体的物理性质影响越大，岩体强度越低。然而该方法只能获得岩体强度受地质环境因子影响的相对差异性，并不能获得岩体准确的物理力学参数。因此，本文在岩体强度参数经验赋值的基础上，适当修正岩体力学参数。考虑到岩体强度参数经验赋值代表的是岩体综合强度（也称平均强度），而在不同地质环境因子综合作用下，岩体实际强度高于或低于综合强度。故本文将基于AHP获得的岩体强度指数归一化到 ［ 0.5，1.5 ］ ，计算岩体强度修正系数fm ［ 式（5） ］ 。由于临界加速度与岩体强度存在明显的正相关，同等坡度下，岩体强度越大，临界加速度越大。为简化操作，本文将对岩体强度的修正变换为式（6）的对临界加速度的修正。
$$ {I_{\rm{m}}} ＝ \sum\limits_{i ＝ 1}^3 {{W_i}{X_i}} ， $$ (4) $$ {f_{\rm{m}}} ＝ 0.5 ＋ \frac{{{I_{\rm{M}}} － {I_{\rm{m}}}}}{{{I_{\rm{M}}} － {I_{\rm{N}}}}} ， $$ (5) $$ {a_{{\rm{c}}{\rm{m}}}} ＝ {f_{\rm{m}}} {a_{\rm{c}}} ， $$ (6) 式中：Im为岩体强度指数；Wi为第i个地质因子的权重；Xi为因子分级；fm为修正系数；IM和IN为Im的最大值和最小值；ac和acm分别为临界加速度和修正后的临界加速度。
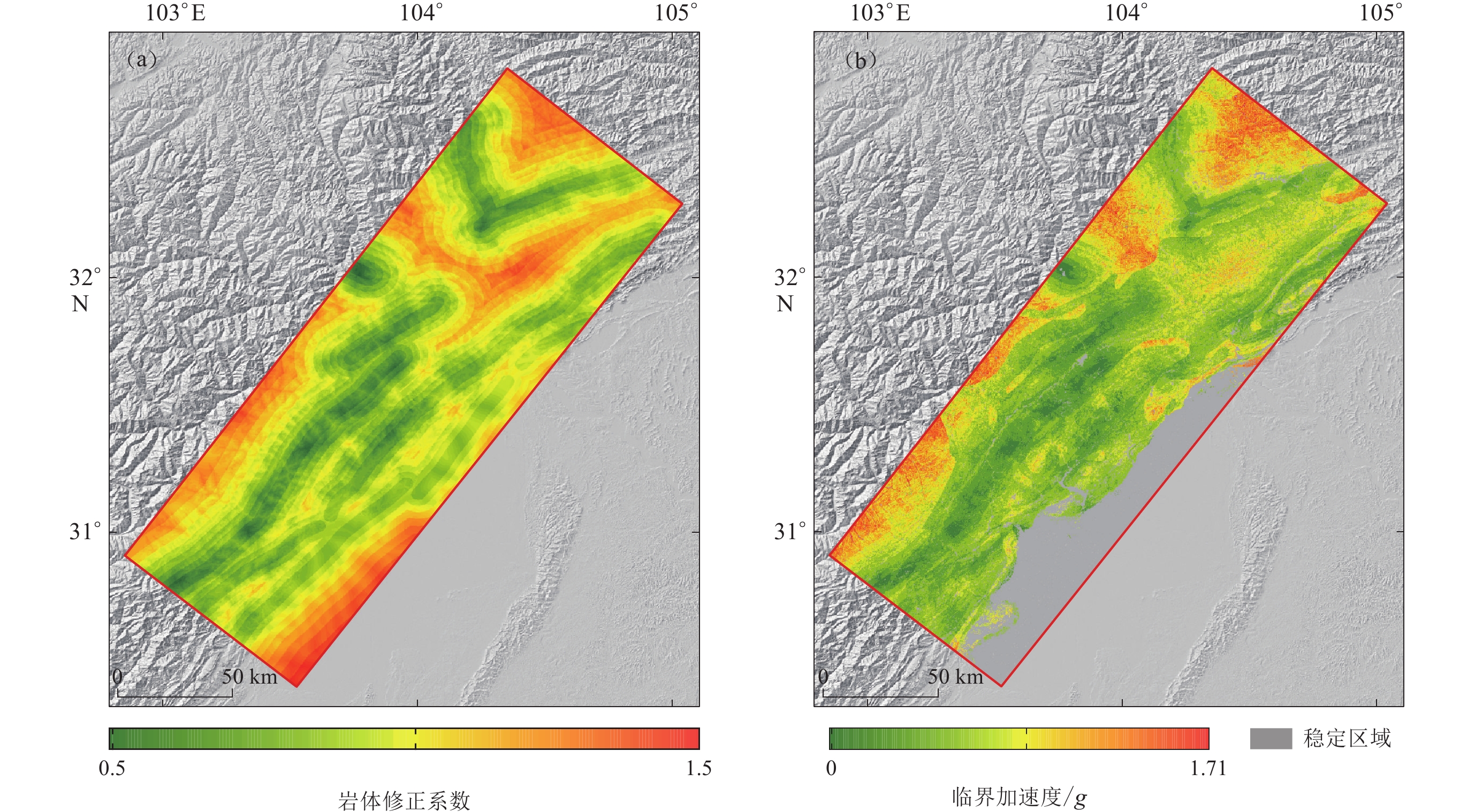
图5a显示了基于式（5）获得的岩体强度修正系数分布。修正值大小反映了场点岩体的实际强度与综合强度的比值，修正值大于1代表岩体的综合强度低于实际强度，修正值小于1表示岩体综合强度高于实际强度。由图5a可以看出，岩体的物理力学性质受地质环境因子影响剧烈，在整个研究区均存在不同程度的修正。例如，受构造运动影响，断层两侧的岩体强度修正系数均处于低值，岩体的实际强度低于经验值，显然经验值高估了岩体强度。受地形和水文因素影响，同一类岩组的岩体强度在不同区域存在差异性。利用图5a修正图2b的临界加速度，修正后的临界加速度的空间分布（图5b）与工程岩组的相关性明显减弱。整体而言，修正后的临界加速度更能有效地反映边坡的实际稳定性。
![]()
图 5 研究区岩体强度修正系数（a）和修正后的临界加速度（b）Figure 5. Distribution of the modified factor of rock mass strength （a） and the modified critical acceleration （b）3. 结果及精度评定
3.1 地震滑坡危险性评价
地震动参数是反映地震扰动程度的重要指标。强震过后，即时地震动参数的快速获取是评估地震滑坡危险性的重要前提，但是国内至今尚未有开放共享的即时地震动参数信息。本文利用美国地质调查局官网发布的地震动图提取的汶川地震的PGA作为主要地震动参数，采用简化纽马克经验位移公式（式（3））并借助地理空间信息系统（ArcGIS）的空间数据分析工具，评价地震滑坡危险性。
滑体在不同饱和度下基于传统临界加速度和修正后的临界加速度获得的边坡累积位移分布如图6a和b所示。为对比二者差异，采用统一色标显示。整体上看，滑体在同一饱和度下，基于不同的临界加速度获得的边坡累积位移分布趋势一致。高位移区主要分布在发震断层两侧，集中于高陡边坡区域。通常，滑坡多发生在坡度25°—50°的范围（姚鑫等，2009）。此外，发震断层两侧是高PGA分布区域，对应的地震扰动作用更明显，因此断层两侧高陡区域是高位移的集中分布区域；而低位移区主要分布在坚硬岩和地势相对平缓区域，多远离发震断层。在场地方面，研究区内存在多条构造断裂带及复杂的地貌形态，导致岩体强度的空间差异性大。基于传统临界加速度的边坡累积位移并未反映出这种差异性，而基于修正后的加速度的边坡累积位移能够很好地反映这种空间差异性。滑体在饱和度分别为0，0.5，1下的边坡累积位移的整体分布同样符合上述分析。此外，滑体受地下水影响，导致边坡累积位移高值区面积随着饱和度的增大而逐渐扩大，表明地下水对地震滑坡的影响不可忽略。
![]()
图 6 基于不同临界加速度获得的边坡累积位移分布及其差异性（a） 传统临界加速度；（b） 修正临界加速度；（c） 不同临界加速度的边坡位移差分Figure 6. Distribution and differences of cumulative displacement of slopes calculated using different critical accelerations（a） Critical acceleration；（b） Modfied critical acceleration；（c） Cumulative displacement difference不同临界加速度下的边坡累积位移分布差值如图6c所示。为显示空间差异，仅取 ［ −5，5 ］ 的差值区间。其中，正值代表本文方法获得的边坡累积位移值高于传统方法；负值则为低于传统方法获得的边坡累积位移值。由图6c可知，本文方法的边坡累积位移与传统方法的边坡累积位移存在较大差异。在研究区东北区域，两者差值多小于0，即基于传统临界加速度的边坡累积位移高于本文方法。分析地质环境显示出，该区域距龙门山中央断裂和后山断裂均较远，岩体受地质构造影响弱，岩体完整性好，本文综合不同地质环境因素作用增强修正区域岩体强度。对于其它区域，尤其是断层附近区域，本文折减修正了原有岩体强度，这也可以解释图6c的评估结果出现空间分布差异的原因。而滑体在不同饱和度下，受地下水的影响，这种空间分布差异性随滑体饱和度m的升高而逐渐增大，当m＝1时，这种差异性最大。
3.2 精度评价
为定量评估基于修正后临界加速度的边坡累积位移分布的可靠性，利用汶川MW7.9地震诱发的同震滑坡来验证精度。采用阈值（临界位移）法将边坡累积位移划分为危险区和稳定区，利用滑坡预测正确率（landslide prediction accuracy，缩写为LPA）和危险区比例（hazard area ratio，缩写为HAR）（马思远等，2019）评价边坡累积位移分布的准确性，LPA和HAR计算方法为
$$ {\rm{LPA}}＝\frac{{{{S}}_{ {\rm{L}}}^{ D_{\rm{N}} ＞ T}}}{{{{{S}}_{ {\rm{L}}}}}} ， $$ (7) $$ {\rm{HAR}}＝\frac{{{{S}}_{ {\rm{S}}}^{ D_{\rm{N}}＞ T}}}{{{{{S}}_{ {\rm{S}}}}}} ， $$ (8) 式中：SL和SS分别为滑坡源区面积和研究区总面积；
${{{S}}_{ {\rm{L}}}^{ D_{\rm{N}}＞ T}}$ 和${{{S}}_{ {\rm{S}}}^{ D_{\rm{N}} ＞ T}}$ 分别为滑坡源区内和研究区的边坡累积位移值DN超过临界位移T时的面积。LPA值越大，代表划分的危险区域内发育的同震滑坡越多，地震滑坡危险区划越准确。当研究区大范围被划分为危险区时，LPA会出现虚高现象，故引入HAR值，HAR代表危险区占研究区的比例。对于相同的HAR，LPA越高，地震滑坡危险性区划越准确；同样，对于相同的LPA，HAR越低，地震滑坡危险区划越可靠。临界位移是划分地震滑坡危险区的重要参数，目前尚未有统一的赋值标准，多采用经验阈值。地震滑坡危险性主要取决于边坡累积位移的相对大小而非绝对大小，因此临界位移的赋值须根据实际的累积位移分布确定。为消除临界位移赋值对精度评价的影响，本文采用多组临界位移（取为0.01，0.5，1，2，3，4，5 cm），分别计算不同临界位移下的LPA和HAR，结果如表4所示。随着临界位移的增加，两种方法划分的地震滑坡危险区均不断减小，即较高的临界位移易低估研究区的地震滑坡危险性，反之，易高估地震滑坡危险性。整体而言，当不考虑地下水影响时（m＝0），本文方法划分的地震滑坡危险区均略大于传统方法，HAR相差在2%—4%。但本文方法对应的LPA均远高于传统方法，且大部分相差在10%以上，差值最高在T＝2 cm （12.29%），而相应的HAR仅相差3.91%。仅在临界位移值为T＝0.01 cm的情况下，两者的LPA差值为1.45%，HAR差值为2%。综合不同临界位移值计算获得的HAR和LPA值，本文方法在HAR略高于传统方法的情形下，能获得远高于传统方法的LPA。值得指出的是在临界位移为0.01时，传统方法与本文方法的计算结果均对应有较高的LPA，分别为88.56%和90.01%，进一步验证了纽马克位移模型在地震滑坡危险性评价中的适用性。此外，为对比分析滑体在不同饱和度下地震滑坡的危险性，分别计算不同饱和度下（m＝0，0.5，1）边坡的累积位移。结果表明，无论是基于传统的临界加速度还是基于修正后的临界加速度计算获得的边坡累积位移，所划分的地震滑坡危险区面积均随着滑体饱和度的增加而增加。换言之，随着孔隙水压力的增大，地震滑坡危险性的区划范围在不断扩大，间接说明了地震期间伴随的强降雨会增加地震次生灾害。因此，在实际地震滑坡危险性评估中，地下水对岩体强度的弱化影响不可忽视。
表 4 不同临界位移对应的地震滑坡危险性评价Table 4. The hazard assessment of seismic landslide corresponding to different threshold坡体饱和度 临界位移T/cm 传统方法计算获得的边坡累积位移DN 本文方法计算获得的边坡累积位移DNc LPA HAR LPA HAR m＝0 0.01 88.56% 43.13% 90.01% 45.13% 0.5 62.90% 23.55% 72.15% 27.31% 1 50.94% 17.40% 62.36% 21.56% 2 36.32% 11.05% 48.61% 14.96% 3 27.84% 7.92% 39.20% 11.15% 4 22.30% 6.08% 32.51% 8.75% 5 18.55% 4.90% 27.51% 7.11% m＝0.5 0.01 93.01% 51.29% 93.47% 52.31% 0.5 78.62% 34.47% 83.40% 37.26% 1 70.43% 28.79% 77.21% 31.93% 2 58.33% 21.65% 67.28% 25.20% 3 49.75% 17.25% 59.49% 20.82% 4 43.36% 14.34% 53.36% 17.71% 5 38.52% 12.27% 48.26% 15.39% m＝1 0.01 95.46% 59.80% 95.55% 60.17% 0.5 89.47% 46.72% 91.06% 48.41% 1 85.15% 41.98% 88.03% 44.04% 2 78.00% 35.81% 82.68% 38.27% 3 72.08% 31.54% 77.83% 34.23% 4 67.19% 28.29% 73.54% 31.06% 5 63.08% 25.74% 69.71% 28.51% 显然，对不同岩组采用统一的临界位移忽视了不同岩体之间力学性质的差异性，而忽视这种差异势必会影响地震滑坡危险性评估的可靠性。已有研究表明，完整坚硬的岩组对应的临界位移一般小于破碎的软岩；统一的临界位移取值，往往会低估完整的坚硬岩组或高估破碎软岩所对应的地震滑坡危险性，因此有必要对不同的岩组采用不同的临界位移值划分地震滑坡危险区域。李鑫（2018）对比分析了地震滑坡实际调查点与简化纽马克模型的累积位移，发现在特定区域不同烈度情况下，坚硬岩组的临界位移合理取值区间在1.3—2.2 cm，较坚硬岩组的取值区间在1.7—3 cm，软岩组的取值区间在1.8—4 cm。因此，本文分别将坚硬岩组、较坚硬岩组、较软岩组、软岩组的临界位移值设置为1.6 cm，2 cm，2.5 cm和3 cm，分别计算不同岩组对应的LPA和HAR值，结果列于表5。对于不同的岩组，本文方法对应的LAP均高于传统方法，差异在2.28%—17.41%，大部分在5%以上。相应的，本文方法预测的危险区域面积均高于传统方法预测的危险区域面积，差异在0.08%—15.21%，大部分处于3%以内。整体而言，本文方法划分的地震滑坡危险区优于传统方法划分的地震滑坡危险区。
表 5 不同岩组对应的地震滑坡危险性评价Table 5. The hazard assessment of seismic landslide corresponding to different rock groups坡体饱和度 岩组 传统方法计算获得的边坡累积位移DN 本文方法计算获得的边坡累积位移DNc LPA HAR LPA HAR m＝0 软岩 45.45% 0.50% 52.27% 0.59% 较软岩 44.80% 15.62% 51.68% 19.21% 较硬岩 42.23% 26.24% 59.64% 41.45% 坚硬岩 10.64% 1.18% 19.75% 2.46% m＝0.5 软岩 52.27% 0.67% 54.55% 0.81% 较软岩 65.88% 31.80% 70.30% 35.15% 较硬岩 68.12% 49.26% 79.07% 61.38% 坚硬岩 28.69% 4.02% 39.68% 6.15% m＝1 软岩 61.36% 1.04% 63.64% 1.12% 较软岩 82.65% 54.50% 84.56% 56.76% 较硬岩 86.60% 72.34% 91.42% 78.46% 坚硬岩 56.48% 11.62% 63.92% 13.93% 4. 讨论与结论
本文基于工程地质图并参考工程规范标准获取边坡的岩体力学参数，结合地形坡度及地震动参数信息，采用简化纽马克位移模型评估地震滑坡危险性，利用同震滑坡验证评估精度。结果表明，简化纽马克位移分析方法可用于地震滑坡危险性快速评估，危险区分布整体上与地震滑坡分布较为一致，相应的危险区内分布大量的同震滑坡。准确的震前岩体强度参数和震后即时地震动参数是获取可靠评估结果的前提条件（Godt et al，2008；Jibson，2011；Dreyfus et al，2013）。
目前，岩体强度参数主要是基于工程地质图，根据岩性和地层年代对工程岩组进行分类，参考工程规范及实测数据，赋予岩组统一的岩体力学参数。因此，对于同一类岩组，其对应的岩体仅代表岩组的综合强度，并不能反映复杂地质背景条件下的空间差异性，这也导致划分的地震滑坡危险区在场地尺度方面表现欠佳（王涛等，2015；李鑫等，2018）。为了解决这个问题，本文基于岩体强度的空间差异性，通过分析断层距、高程和水系距离三个因素对岩体强度的影响，建立一种复杂地质条件下的岩体强度修正模型，并将模型应用于基于纽马克位移分析方法的地震滑坡危险性评估。结果表明，相比于传统简化的岩体物理力学参数，利用修正后的岩体强度信息获得的地震滑坡危险性评价结果与同震滑坡分布更加一致。这也意味着提高岩体强度参数赋值的准确性可以获得更加可靠的评估结果。
作为纽马克模型另一个重要输入参数，地震动参数的快速获取是开展地震滑坡危险性评价的重要前提。但是，国内至今在震后尚无法立即获取开放共享的地震动特征参数。而汶川地震后，美国地质调查局在10分钟内即发布了汶川地震相应的地震动参数。本文正是基于美国地质调查局发布的地震动峰值加速度评估汶川地震滑坡危险性。因此，建立适用于我国地质背景的地震动参数共享平台，是震后快速开展地震滑坡危险性评估的重要保障。此外，在传统纽马克经验位移模型中，模型的输入参数仅考虑水平向地震动加速度，忽视了垂直向地震动加速度对地震滑坡的影响，造成了地震滑坡危险性低估（Ingles et al，2006）。因此，综合考虑不同方向的地震动加速度对边坡稳定性的扰动，值得深入分析和探讨。
-
![]()
图 1 研究区断层分布及地震动图
Figure 1. Distribution of fault and ground motion map in the study area
![]()
图 2 研究使用的主要数据源
（a） 地震动图；（b） 工程岩组；（c） 地形坡度；（d） 同震滑坡
Figure 2. Data sources used in this study
（a） Ground motion maps；（b） Engineering rock mass；（c） Topographic slopes；（d） Co-seismic landslides
![]()
图 3 研究区斜坡静态安全系数（a）和临界加速度（b）分布
Figure 3. Distribution of static factor of safety （a） and critical acceleration （b） in study area
![]()
图 4 岩体强度的主要评价指标
（a） 高程；（b） 距水系距离；（c） 距断层距离
Figure 4. Main evaluation indicators for rock mass strength
（a） Elevation；（b） Distance to the river；（c） Distance to the fault
![]()
图 5 研究区岩体强度修正系数（a）和修正后的临界加速度（b）
Figure 5. Distribution of the modified factor of rock mass strength （a） and the modified critical acceleration （b）
![]()
图 6 基于不同临界加速度获得的边坡累积位移分布及其差异性
（a） 传统临界加速度；（b） 修正临界加速度；（c） 不同临界加速度的边坡位移差分
Figure 6. Distribution and differences of cumulative displacement of slopes calculated using different critical accelerations
（a） Critical acceleration；（b） Modfied critical acceleration；（c） Cumulative displacement difference
表 1 研究区工程地质岩组结构面强度经验赋值
Table 1 Empirical value of the structural surface strength of the engineering geological rocks in the studied area
工程地质岩组 有效内摩擦角/° 有效黏聚力/MPa 坚硬岩组 40 0.035 较坚硬岩组 35 0.028 较软岩组 30 0.025 软岩组 20 0.015 
下载: 导出CSV
表 2 判别矩阵定量标度及其描述
Table 2 Scale of judgment matrix and its description
标度值bij 相对重要性描述 1 bi与bj 同样重要 3 bi比bj 稍微重要 5 bi比bj 明显重要 7 bi比bj 强烈重要 9 bi比bj 极端重要 2，4，6，8 上述相邻的判断中值 倒数 bij＝bji
下载: 导出CSV
表 3 评价指标权重和对应的判别矩阵
Table 3 Evaluation index weight and corresponding judgment matrix
评价指标 距断层距离 高程 距水系距离 权重 一致性检验 距断层距离 1 3 7 0.669 4 CI＝0.003 5＜0.1 高程 1/3 1 3 0.242 6 距水系距离 1/7 1/3 1 0.087 9
下载: 导出CSV
表 4 不同临界位移对应的地震滑坡危险性评价
Table 4 The hazard assessment of seismic landslide corresponding to different threshold
坡体饱和度 临界位移T/cm 传统方法计算获得的边坡累积位移DN 本文方法计算获得的边坡累积位移DNc LPA HAR LPA HAR m＝0 0.01 88.56% 43.13% 90.01% 45.13% 0.5 62.90% 23.55% 72.15% 27.31% 1 50.94% 17.40% 62.36% 21.56% 2 36.32% 11.05% 48.61% 14.96% 3 27.84% 7.92% 39.20% 11.15% 4 22.30% 6.08% 32.51% 8.75% 5 18.55% 4.90% 27.51% 7.11% m＝0.5 0.01 93.01% 51.29% 93.47% 52.31% 0.5 78.62% 34.47% 83.40% 37.26% 1 70.43% 28.79% 77.21% 31.93% 2 58.33% 21.65% 67.28% 25.20% 3 49.75% 17.25% 59.49% 20.82% 4 43.36% 14.34% 53.36% 17.71% 5 38.52% 12.27% 48.26% 15.39% m＝1 0.01 95.46% 59.80% 95.55% 60.17% 0.5 89.47% 46.72% 91.06% 48.41% 1 85.15% 41.98% 88.03% 44.04% 2 78.00% 35.81% 82.68% 38.27% 3 72.08% 31.54% 77.83% 34.23% 4 67.19% 28.29% 73.54% 31.06% 5 63.08% 25.74% 69.71% 28.51%
下载: 导出CSV
表 5 不同岩组对应的地震滑坡危险性评价
Table 5 The hazard assessment of seismic landslide corresponding to different rock groups
坡体饱和度 岩组 传统方法计算获得的边坡累积位移DN 本文方法计算获得的边坡累积位移DNc LPA HAR LPA HAR m＝0 软岩 45.45% 0.50% 52.27% 0.59% 较软岩 44.80% 15.62% 51.68% 19.21% 较硬岩 42.23% 26.24% 59.64% 41.45% 坚硬岩 10.64% 1.18% 19.75% 2.46% m＝0.5 软岩 52.27% 0.67% 54.55% 0.81% 较软岩 65.88% 31.80% 70.30% 35.15% 较硬岩 68.12% 49.26% 79.07% 61.38% 坚硬岩 28.69% 4.02% 39.68% 6.15% m＝1 软岩 61.36% 1.04% 63.64% 1.12% 较软岩 82.65% 54.50% 84.56% 56.76% 较硬岩 86.60% 72.34% 91.42% 78.46% 坚硬岩 56.48% 11.62% 63.92% 13.93%
下载: 导出CSV
-
陈晓利,单新建,张凌,刘春国,韩娜娜,兰剑. 2019. 地震诱发滑坡的快速评估方法研究:以2017年MS7.0级九寨沟地震为例[J]. 地学前缘,26(2):312–320. Chen X L,Shan X J,Zhang L,Liu C G,Han N N,Lan J. 2019. Quick assessment of earthquake-triggered landslide hazards:A case study of the 2017 MS7.0 Jiuzhaigou earthquake[J]. Earth Science Frontiers,26(2):312–320 (in Chinese).
郭金玉,张忠彬,孙庆云. 2008. 层次分析法的研究与应用[J]. 中国安全科学学报,18(5):148–153. doi: 10.3969/j.issn.1003-3033.2008.05.025 Guo J Y,Zhang Z B,Sun Q Y. 2008. Study and applications of analytic hierarchy process[J]. China Safety Science Journal,18(5):148–153 (in Chinese).
黄润秋,李为乐. 2008. “5.12”汶川大地震触发地质灾害的发育分布规律研究[J]. 岩石力学与工程学报,27(12):2585–2592. doi: 10.3321/j.issn:1000-6915.2008.12.028 Huang R Q,Li W L. 2008. Research on development and distribution rules of geohazards induced by Wenchuan earthquake on 12th May,2008[J]. Chinese Journal of Rock Mechanics and Engineering,27(12):2585–2592 (in Chinese).
黄润秋. 2011. 汶川地震地质灾害后效应分析[J]. 工程地质学报,19(2):145–151. doi: 10.3969/j.issn.1004-9665.2011.02.001 Huang R Q. 2011. After effect of geohazards induced by the Wenchuan earthquake[J]. Journal of Engineering Geology,19(2):145–151 (in Chinese).
李鑫. 2018. 基于汶川地震资料的地震滑坡危险性快速评估技术研究[D]. 北京: 中国地震局地球物理研究所: 29–46. Li X. 2018. Study on Seismic Landslide Hazard Rapid Assessment Based on the Inventory of Landslides Triggered by Wenchuan Earthquake[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 29–46 （in Chinese）.
李鑫,迟明杰,李小军. 2018. 基于简化纽马克位移模型的地震滑坡岩土体强度参数研究[J]. 地震学报,40(6):820–830. doi: 10.11939/jass.20180026 Li X,Chi M J,Li X J. 2018. Rock-soil strength parameters of earthquake-triggered landslides based on simplified Newmark displacement model[J]. Acta Seismologica Sinica,40(6):820–830 (in Chinese).
李雪婧,高孟潭,徐伟进. 2019. 基于Newmark模型的概率地震滑坡危险性分析方法研究:以甘肃天水地区为例[J]. 地震学报,41(6):795–807. doi: 10.11939/jass.20180075 Li X J,Gao M T,Xu W J. 2019. Probabilistic seismic slope displacement hazard analysis based on Newmark displacement model:Take the area of Tianshui,Gansu Province,China as an example[J]. Acta Seismologica Sinica,41(6):795–807 (in Chinese).
刘甲美. 2015. 概率地震滑坡危险性区划方法及应用[D]. 北京: 中国地震局地球物理研究所: 29–39. Liu J M. 2015. Probabilistic Seismic Landslide Hazard Zonation Method and its Application[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 29–39 （in Chinese）.
刘甲美,高孟潭,陈鲲. 2015. 地形效应影响下地震动参数与斜坡稳定性的相关性研究[J]. 地震学报,37(5):865–874. doi: 10.11939/jass.2015.05.014 Liu J M,Gao M T,Chen K. 2015. On the correlation of ground motion parameters with slope stability incorporating topographic effects[J]. Acta Seismologica Sinica,37(5):865–874 (in Chinese).
刘丽娜,许冲,徐锡伟,陈剑. 2014. GIS支持下基于AHP方法的2013年芦山地震区滑坡危险性评价[J]. 灾害学,29(4):183–191. doi: 10.3969/j.issn.1000-811X.2014.04.034 Liu L N,Xu C,Xu X W,Chen J. 2014. GIS-based landslide hazard evaluation using AHP method in the 2013 Lushan earthquake region[J]. Journal of Catastrophology,29(4):183–191 (in Chinese).
马思远,许冲,王涛,刘甲美. 2019. 应用2类Newmark简易模型进行2008年汶川地震滑坡评估[J]. 地震地质,41(3):774–788. doi: 10.3969/j.issn.0253-4967.2019.03.015 Ma S Y,Xu C,Wang T,Liu J M. 2019. Application of two simplified Newmark models to the assessment of landslides triggered by the 2008 Wenchuan earthquake[J]. Seismology and Geology,41(3):774–788 (in Chinese).
王进,郭靖,王卫东,方理刚. 2012. 权重线性组合与逻辑回归模型在滑坡易发性区划中的应用与比较[J]. 中南大学学报(自然科学版),43(5):1932–1939. Wang J,Guo J,Wang W D,Fang L G. 2012. Application and comparison of weighted linear combination model and logistic regression model in landslide susceptibility mapping[J]. Journal of Central South University (Science and Technology)
,43(5):1932–1939 (in Chinese). 王涛. 2010. 汶川地震重灾区地质灾害危险性评估研究[D]. 北京: 中国地质科学院: 27–40. Wang T. 2010. Study on Seismic Landslide Hazard Assessment in Wenchuan Earthquake Severly Afflicted Area[D]. Beijing: Chinese Academy of Geological Sciences 27–40（in Chinese）.
王涛,吴树仁,石菊松,辛鹏. 2013. 基于简化Newmark位移模型的区域地震滑坡危险性快速评估:以汶川MS8.0级地震为例[J]. 工程地质学报,21(1):16–24. doi: 10.3969/j.issn.1004-9665.2013.01.003 Wang T,Wu S R,Shi J S,Xin P. 2013. Case study on rapid assessment of regional seismic landslide hazard based on simplified Newmark displacement model:Wenchuan MS8.0 earthquake[J]. Journal of Engineering Geology,21(1):16–24 (in Chinese).
王涛,吴树仁,石菊松,辛鹏. 2015. 地震滑坡危险性概念和基于力学模型的评估方法探讨[J]. 工程地质学报,23(1):93–104. Wang T,Wu S R,Shi J S,Xin P. 2015. Concepts and mechanical assessment method for seismic landslide hazard:A review[J]. Journal of Engineering Geology,23(1):93–104 (in Chinese).
许冲,戴福初,姚鑫,陈剑,涂新斌,曹琰波,肖建章. 2010. 基于GIS的汶川地震滑坡灾害影响因子确定性系数分析[J]. 岩石力学与工程学报,29(增刊):2972–2981. Xu C,Dai F C,Yao X,Chen J,Tu X B,Cao Y B,Xiao J Z. 2010. GIS based certainty factor analysis of landslide triggering factors in Wenchuan earthquake[J]. Chinese Journal of Rock Mechanics and Engineering,29(S1):2972–2981 (in Chinese).
许冲,徐锡伟,吴熙彦,戴福初,姚鑫,姚琪. 2013. 2008年汶川地震滑坡详细编目及其空间分布规律分析[J]. 工程地质学报,21(1):25–44. doi: 10.3969/j.issn.1004-9665.2013.01.004 Xu C,Xu X W,Wu X Y,Dai F C,Yao X,Yao Q. 2013. Detailed catalog of landslides triggered by the 2008 Wenchuan earthquake and statistical analyses of their spatial distribution[J]. Journal of Engineering Geology,21(1):25–44 (in Chinese).
姚鑫,许冲,戴福初,张永双. 2009. 四川汶川MS8级地震引发的滑坡与地层岩性、坡度的相关性[J]. 地质通报,28(8):1156–1162. doi: 10.3969/j.issn.1671-2552.2009.08.019 Yao X,Xu C,Dai F C,Zhang Y S. 2009. Contribution of strata lithology and slope gradient to landslides triggered by Wenchuan MS8 earthquake,Sichuan,China[J]. Geological Bulletin of China,28(8):1156–1162 (in Chinese).
张咸恭, 王思敬, 张倬元. 2000. 中国工程地质学[M]. 北京: 科学出版社: 45–48. Zhang X G, Wang S J, Zhang Z Y. 2000. Engineering Geology of China[M]. Beijing: Science Press: 45–48 （in Chinese）.
中华人民共和国建设部. 2004. GB 50021—2001 岩土工程勘察规范[S]. 北京: 中国建筑工业出版社: 20–28. Ministry of Construction of the People’s Republic of China. 2004. GB 50021−2001 Code for Investigation of Geotechnical Engineering[S]. Beijing: China Architecture & Building Press: 20–28 （in Chinese）.
中华人民共和国住房和城乡建设部. 2015. GB/T 50218—2014 工程岩体分级标准[S]. 北京: 中国计划出版社: 3–14. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. 2015. GB/T 50218–2014 Standard for Engineering Classification Rock Mass[S]. Beijing: China Planning Press : 3–14（in Chinese）.
Chen S,Miao Z L,Wu L X,He Y G. 2020. Application of an incomplete landslide inventory and one class classifier to earthquake-induced landslide susceptibility mapping[J]. IEEE J Sel Top Appl Earth Obs Remote Sens,13:1649–1660. doi: 10.1109/JSTARS.2020.2985088
Dreyfus D,Rathje E M,Jibson R W. 2013. The influence of different simplified sliding-block models and input parameters on regional predictions of seismic landslides triggered by the Northridge earthquake[J]. Eng Geol,163:41–54. doi: 10.1016/j.enggeo.2013.05.015
Fan X M,Scaringi G,Korup O,West A J,Van Westen C J,Tanyas H,Hovius N,Hales T C,Jibson R W,Allstadt K E,Zhang L M,Evans S G,Xu C,Li G,Pei X J,Xu Q,Huang R Q. 2019. Earthquake-induced chains of geologic hazards:Patterns,mechanisms,and impacts[J]. Rev Geophys,57(2):421–503. doi: 10.1029/2018RG000626
Godt J W, Sener B, Verdin K L, Wald D J, Earle P S, Harp E L, Jibson R W. 2008. Rapid assessment of earthquake-induced landsliding[C]//Proceedings of the First World Landslide Forum. Tokyo: Association for Disaster Prevention Research: 219–222.
Guzzetti F,Reichenbach P,Ardizzone F,Cardinali M,Galli M. 2006. Estimating the quality of landslide susceptibility models[J]. Geomorphology,81(1/2):166–184.
Ingles J,Darrozes J,Soula J C. 2006. Effects of the vertical component of ground shaking on earthquake-induced landslide displacements using generalized Newmark analysis[J]. Eng Geol,86(2/3):134–147.
Intrieri E,Carla T,Gigli G. 2019. Forecasting the time of failure of landslides at slope-scale:A literature review[J]. Earth-Sci Rvi,193:333–349. doi: 10.1016/j.earscirev.2019.03.019
Jibson R W. 1993. Predicting earthquake-induced landslide displacements using Newmark's sliding block analysis[J]. Transp Res Rec,1411:9–17.
Jibson R W. 2007. Regression models for estimating coseismic landslide displacement[J]. Eng Geol,91(2/3/4):209–218.
Jibson R W. 2011. Methods for assessing the stability of slopes during earthquakes:A retrospective[J]. Eng Geol,122(1/2):43–50.
Jibson R W,Harp E L,Michael J A. 2000. A method for producing digital probabilistic seismic landslide hazard maps[J]. Eng Geol,58(3/4):271–289.
Kamp U,Growley B J,Khattak G A,Owen L A. 2008. GIS-based landslide susceptibility mapping for the 2005 Kashmir earthquake region[J]. Geomorphology,101(4):631–642. doi: 10.1016/j.geomorph.2008.03.003
Kayastha P,Dhital M R,De Smedt F. 2013. Application of the analytical hierarchy process (AHP) for landslide susceptibility mapping:A case study from the Tinau watershed,west Nepal[J]. Comput Geosci,52:398–408. doi: 10.1016/j.cageo.2012.11.003
Newmark N M. 1965. Effects of earthquakes on dams and embankments[J]. Géotechnique,15(2):139–160.
Pourghasemi H R,Yansari Z T,Panagos P,Pradhan B. 2018. Analysis and evaluation of landslide susceptibility:A review on articles published during 2005−2016 (periods of 2005−2012 and 2013−2016)[J]. Arab J Geosci,11(9):193. doi: 10.1007/s12517-018-3531-5
Reichenbach P,Rossi M,Malamud B D,Mihir M,Guzzetti F. 2018. A review of statistically-based landslide susceptibility models[J]. Earth-Sci Rev,180:60–91. doi: 10.1016/j.earscirev.2018.03.001
Tsai H Y,Tsai C C,Chang W C. 2019. Slope unit-based approach for assessing regional seismic landslide displacement for deep and shallow failure[J]. Eng Geol,248:124–139. doi: 10.1016/j.enggeo.2018.11.015
Xu C,Xu X W,Dai F C,Wu Z D,He H L,Shi F,Wu X Y,Xu S N. 2013. Application of an incomplete landslide inventory,logistic regression model and its validation for landslide susceptibility mapping related to the May 12,2008 Wenchuan earthquake of China[J]. Nat Hazards,68(2):883–900. doi: 10.1007/s11069-013-0661-7
Zhou B G,Zhang Y M. 1994. Some characteristics of earthquake-induced landslide in southwestern China[J]. Northwest Seismol J,16(1):95–103.
-
期刊类型引用(2)
1. 罗华. 地震滑坡地质灾害危险性评价及生态修复策略研究. 环境科学与管理. 2024(08): 180-184 . 
百度学术
2. Liye Feng，Wenwen Qi，Chong Xu，Wentao Yang，Zhiqiang Yang，Zikang Xiao，Zhaoning Chen，Tao Li，Xiaoyi Shao，Huiran Gao，Zhiwen Xue. Landslide Research from the Perspectives of Qinling Mountains in China: A Critical Review. Journal of Earth Science. 2024(05): 1546-1567 . 必应学术
其他类型引用(3)
计量
- 文章访问数: 367
- HTML全文浏览量: 159
- PDF下载量: 48
- 被引次数: 5
