Evaluating seismometer orientation of ChinArray-Ⅰ using teleseismic P-wave and Rayleigh-wave polarization
-
摘要:
利用远震P波和瑞雷面波偏振特征的两种独立分析方法,对2011—2013年间在南北地震带南段布设的中国地震科学探测台阵一期台站的方位偏差进行了评估。研究使用了震中距30°—90°范围内696次远震的P波数据和震中距10°—170°范围内1 928次地震的瑞雷面波数据。结果显示:两种偏振分析方法所得台站的水平方位角偏差具有较好的一致性。在全部352个台站中,除4个台站由于可用数据较少而未进行评估外,281个台站的南北向分量与地理北向偏差小于10°,21个台站的方位偏差在10°—20°之间,其余台站则出现故障或偏差较大。所获结果与前人基于远震P波的结果类似,但存在7个台站的方位偏差与其结果差异超过5°,进一步的分析表明这些台站在不同时段水平方位角偏差发生过改变,需要分时段进行评估。同时,研究发现仪器不同分量的增益故障会影响仪器水平方位角的偏差估计,可与噪声功率谱结合开展协同评估。
-
关键词:
- 中国地震科学探测台阵 /
- 地震计方位 /
- 远震P波 /
- 瑞雷面波 /
- 偏振分析
Abstract:The accurate estimation of seismometer orientation is considered essential for seismological studies that depend on three-component seismic records. It is necessary to align the north-south horizontal component with the geographic north during station deployment to achieve accurate recording and analysis of seismic waveforms. Orientation deviation is influenced by a variety of factors. Ocean-bottom seismometers cannot achieve alignment with geographic directions due to limitations of the deployment method. Local magnetic anomalies or incorrect corrections for magnetic declination corrections can cause the magnetic compass fail to align to geographic north when seismometers are deployed on land. Ground subsidence and instrument movement during the operation stage can additionally cause orientation deviations. It is therefore considered an important step in enhancing the accuracy of subsequent research to employ seismological methods to estimate the orientation deviation during instrument deployment.
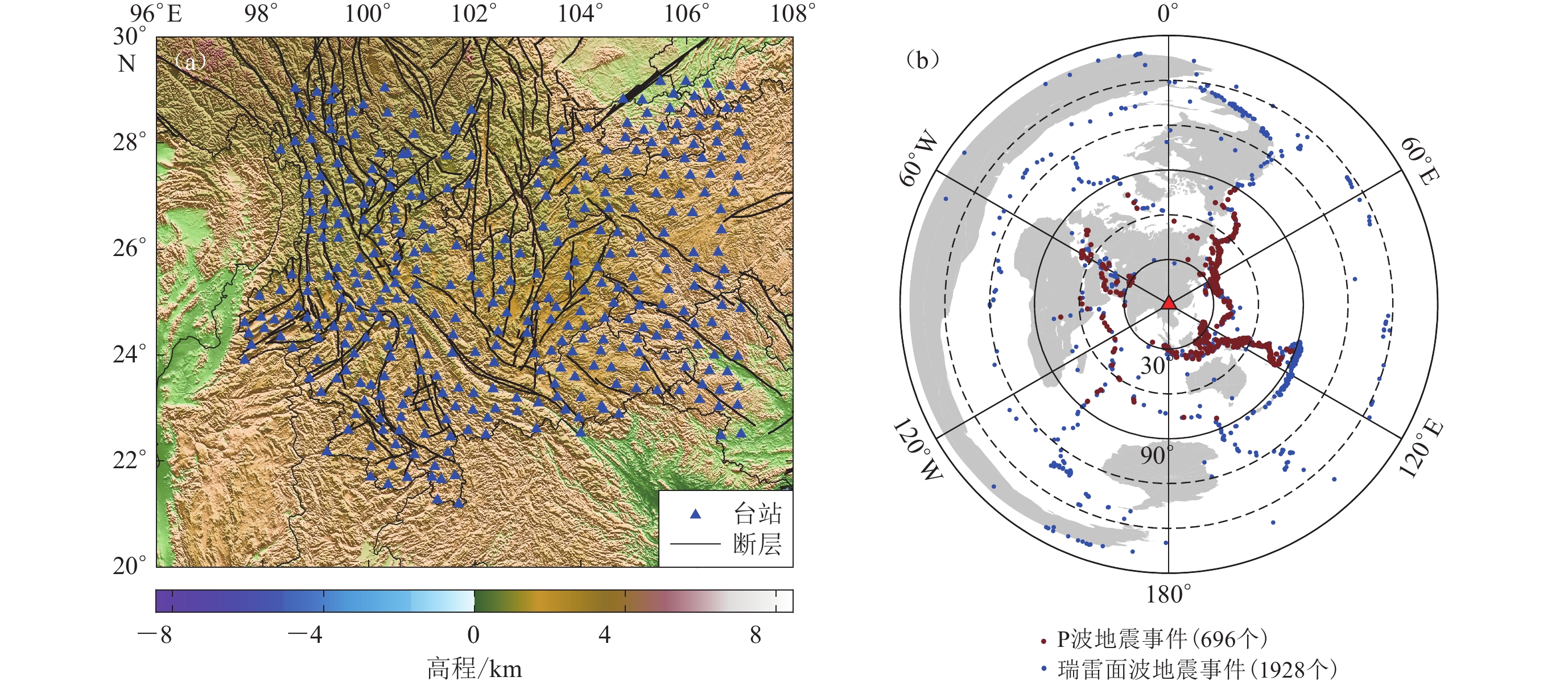
Because of the large surface deformation and high seismicity in Yunnan Province, many seismic studies have been carried out in this area using data recorded by China Earthquake Administration (CEA) permanent stations. However, the large distances between the stations of the permanent seismic stations can lead to the phenomenon of low resolution of the research results on a small scale. In order to conduct an in-deep study of the seismicity and deep structure of the region, 350 broadband transportable array were deployed in Yunnan and the surrounding areas of the southern section of the North-South Seismic Belt during 2011 to 2013, known as the ChinArray phase Ⅰ . Due to changes in the observation environment, the positions of two stations were shifted by a few kilometers in the middle of the deployment period during the observation period, so that a total of 352 stations were observed in the study area.
We estimate the seismometer orientations of ChinArray phase Ⅰ . Two independent polarization analysis methods, teleseismic P-wave and Rayleigh surface wave, are used for the study, and the two methods relies on the polarization characteristics of seismic waveforms. We selected P waves from 696 teleseismic events located in the epicentral distances range of 30 to 90 degrees, and Rayleigh waves from 1 928 events located within the range of 10 to 170 degrees of epicentral distances, and used both waveform data for orientation estimation, respectively.
By comparing the two methods, we found that the results were very consistent. The comparison shows that out of 348 stations that were measurable, 343 of them have an average difference of less than 10 degrees between the results obtained using the two methods, and only five stations have a difference of more than 10 degrees. There are some errors in the different measurement methods, considering that the means of orientation deviations for each station obtained from P-waves and surface-waves are similar, and that P-waves have a smaller overall dispersion, the P-wave measurement results were utilized in this thesis for a statistical analysis of the orientation deviation of the ChinArray phase Ⅰ . The statistical results indicated that orientation deviation measurements for 281 stations were less than 10 degrees, 21 stations have seismometer orientation deviations between 10 to 20 degrees, and the remaining stations encountered instrument failure or greater deviations. The results of this study are similar to previous analyses of teleseismic P-waves, but deviations greater than 5 degrees were observed at seven stations. It was further determined that the primary cause of these deviations was changes in the orientations of instruments at some stations during deployment, affecting five stations. For the other two stations, we analyze the noise level of the stations based on the power spectrum analysis method of probability density to detect the observation quality of the stations during the observation period, and find that the relevant anomalous measurements are due to the gain failures of the horizontal components.
In the current methodologies, the error range for measurements obtained from P-waves is typically smaller, while surface-waves measurement are relatively discrete. Surface wave-based measurements possess a higher temporal resolution when it comes to resolving time variations of orientations. High-quality Rayleigh surface-wave signals are easier to obtain than teleseismic P-wave, but the local subsurface structures lead to large error values. A broader range of epicentral distances can be chosen when we use surface waves to achieve better orientation coverage and stable results.
The results in this paper and a number of previous studies show that both teleseismic P-wave and Rayleigh surface-wave polarization methods can provide effective estimates of orientation deviation in seismometer placement after reliable data quality control. And the methods and outcomes of this research provide orientation correction information for the ChinArray phaseⅠand contribute to the data quality assessment of other transportable stations.
-
引言
准确估计地震计的布设方位角对基于三分量记录的地震学研究具有重要作用。现代三分量地震计通过一个垂直分量和南北、东西两个水平分量来记录地表的三维运动信息。在台站布设时,需要将南北向的水平分量北与地理北进行对准,实现对地震波形的准确记录和分析。众多地震学研究方法,如震源机制反演、剪切波分裂、接收函数和面波偏振分析等都需要根据地震位置将地震计水平分量记录旋转到沿地震和台站对应的大圆路径的径向(R)和切向(T)分量上,因此准确的三分量地震观测记录对地震学研究是十分重要的。地震计自身的三分量之间的正交性通常十分精确,而地震计的南北向北分量与地理北之间的偏差是影响旋转准确性的主要因素,如果这个偏差较大,通过坐标旋转得到的结果会存在较大的系统偏差,因此对地震计布设方位角的准确估计十分必要。
地震计布设的水平方位角偏差(以下简称方位偏差)一般用南北向北分量与地理北的偏差角度来表征。方位偏差受多种因素的影响,例如:受布设方式限制,海底地震仪(ocean bottom seismometer,缩写为OBS)的水平分量无法实现与地理方向对齐,需要额外处理确定其方位(Zha et al,2013;Xu et al,2020);在陆地上布设台站时,常用磁罗盘确定地理北,在进行磁偏角校正后,将地震计方向与地理北进行对准。但局部磁异常或错误磁偏角校正会导致地理北估计有偏差,寻北仪设备精度不高会直接导致仪器南北分量未对准。同时安装过程中的极性输入或使用定向杆或标尺将地理北与仪器南北分量对齐时也存在人为误差,这些都会引起地震计方位偏差(Ringler et al,2013;龙剑锋等,2016)。此外,在仪器运行期间的地面沉降、仪器移动等问题也会引起方位偏差,这在流动观测中尤为常见。因此,采用地震学方法对仪器布设期间的方位偏差进行估计是提升后续研究准确性的重要步骤。
研究人员提出了多种方法用以估计地震计的方位偏差。早期研究利用气枪信号来测量OBS水平分量的实际方向,通过在OBS周边环形区域进行气枪信号激发,测量OBS记录中信号振幅随方位的变化来确定其水平方位(Anderson et al,1987)。相关方法成本较高且适用性较差,因此后续研究中多使用仪器记录到的天然地震中的地震波形,利用不同震相波形的偏振特征估计地震计的方位偏差(Niu,Li,2011;Stachnik et al,2012;Wang et al,2016)。
面波信号是地震记录中信噪比较高的信号,依据瑞雷面波主要在径向和垂向方向偏振且二者相位差为90°的特性,可以对仪器的方位偏差进行估计(Baker,Stevens,2004;Stachnik et al,2012)。相关方法使用的面波信号可源于浅源地震、数值模拟以及噪声互相关函数。利用GeoScope和国际加速度计部署(International Deployment of Accelerometers,缩写为IDA)台网记录的145次浅源地震面波信号的椭圆率,Laske (1995)利用非线性反演方法对面波相速度以及台站方位偏差进行了分析,发现所用台站中至少有4个的方位偏差可能超过3°。利用周期60—250 s的长周期面波信号对更多台站的分析表明,部分台站的方位偏差大于12°,对相速度测量产生了较大影响(Laske,Masters,1996)。Ekström和Busby (2008)基于全球矩心矩张量(centroid moment tensor,缩写为CMT)分析的震源机制解,计算了400多次MW5.5以上地震的理论地震图,通过对比理论地震图以及美国数字地震台网USArray台阵的一些固定台站记录到的地震信号来估算地震计方位偏差。对周期50—150 s的面波信号的分析表明超过10%的台站方位偏差大于7°,并且面波结果与更长周期的体波结果比较一致。Stachnik等(2012)将Baker和Stevens (2004)面波方位角估算方法用于测量OBS及陆地地震计的方位角,他们提出的方法不依赖反演方法且方便快捷,被广泛应用到了台站方位偏差估计中(Rueda,Mezcua,2015;Doran,Laske,2017;Xu et al,2020;Büyükakpınar et al,2021)。为降低对天然地震的依赖,增加可测量路径,Zha等(2013)基于类似方法,利用多分量噪声互相关函数中的瑞雷面波估算OBS的方位偏差,获得了稳定的测量结果。
远震P波信号也可用来估计地震计的方位偏差。Schulte-Pelkum等(2001)利用15—100 s的长周期P波质点运动研究上地幔各向异性时,发现仪器方位偏差会对结果有较大干扰,而在所用的267个全球地震台网(Global Seismic Network,缩写为GSN)台站中,有多个地震计偏差在10° 以上。Niu和Li (2011)利用5—50 s的远震P波通过多事件信噪比加权方法对中国数字地震台网803个宽频带台站的方位偏差进行了估计,发现其中270个台站的地震计方位偏差大于8°,并且个别台站存在极性反转现象。黄静等(2015)估算了北京遥测地震台网10个台站的方位角,并与寻北仪的测量结果进行比较,发现部分仪器的方位偏差大于10°。Wang等(2016)估算了NECsaids台阵仪器的方位偏差,并对误差来源进行了分析。基于P波信号的方位偏差估计方法在多个地区得到了应用(陈继锋等,2016;Son et al,2022;Zeng et al,2021)。
近年来,研究人员也联合使用多种手段对地震计方位偏差进行测量。Ensing和van Wijk (2019)利用远震P波以及背景噪声互相关中的瑞雷信号分析了新西兰12个地震台的方位偏差;Xu等(2020)分别提取了远震P波、地震信号和背景噪声中的瑞雷面波,并对渤海布设的28个海底地震计方位进行了测量。利用不同类型的地震波信号进行独立测量有利于结果的交叉验证和对比分析,在多个区域台网的质量分析评估中得到了应用(Ojo et al,2019;Büyükakpınar et al,2021)。
中国地震科学探测台阵项目在南北地震带南段布设了350个流动台站,观测期为2011年3月—2013年12月(图1a)。Zeng等(2021)利用远震P波偏振方法对这些台站的方位偏差进行了估计并讨论了地震计未对准对接收函数H-κ叠加法、莫霍面Ps反射波约束地壳各向异性及从背景噪声中提取多分量格林函数的影响。上述接收函数等方法只应用了P波偏振分析方法,而P波波形窗口位置及长度、滤波参数以及波形相关系数等质量控制标准的选取均会影响最终的估计结果(Scholz et al,2017;Xu et al,2020)。引入多种判别方法对结果进行比较也有助于获取更加可靠的结果。因此本文拟使用P波和瑞雷面波两种极化分析方法,对该台阵的地震计方位偏差进行对比分析,并对台阵运行期间台站方位偏差的变化以及仪器本身故障所导致的估计偏差进行详细分析,以期通过这两种方法的联合分析,得到中国地震科学探测台阵一期更加精确的地震计方位偏差。
1. 数据和方法
青藏高原东南缘地区存在强烈的地壳形变和地震活动,为了对该地区的地震活动性、深部结构等进行研究,中国地震局地球物理研究所联合国内单位,在南北地震带南段的云南及周边区域布设了宽频带流动地震台阵,观测时间为2011年3月—2013年12月。该台阵平均台间距约30 km,由350个台站组成,每个台站使用的地震计均为宽频带Güralp CMG-3ESP或CMG-40T,数据采集器为Reftek-130B,流动台网命名为X1 (图1a)。受观测环境变化影响,观测期内两个台站X1.51051和X1.53201的位置在布设中期进行了几千米的移动,因此在研究区内共有352个观测点。
本文使用远震P波以及瑞雷面波的偏振特性来对地震计方位偏差进行估计。图1b显示了文中使用的地震事件的分布,可以看出,这些事件在方位和距离上都具备较好的分布,有利于获取稳定的方位偏差测量结果。
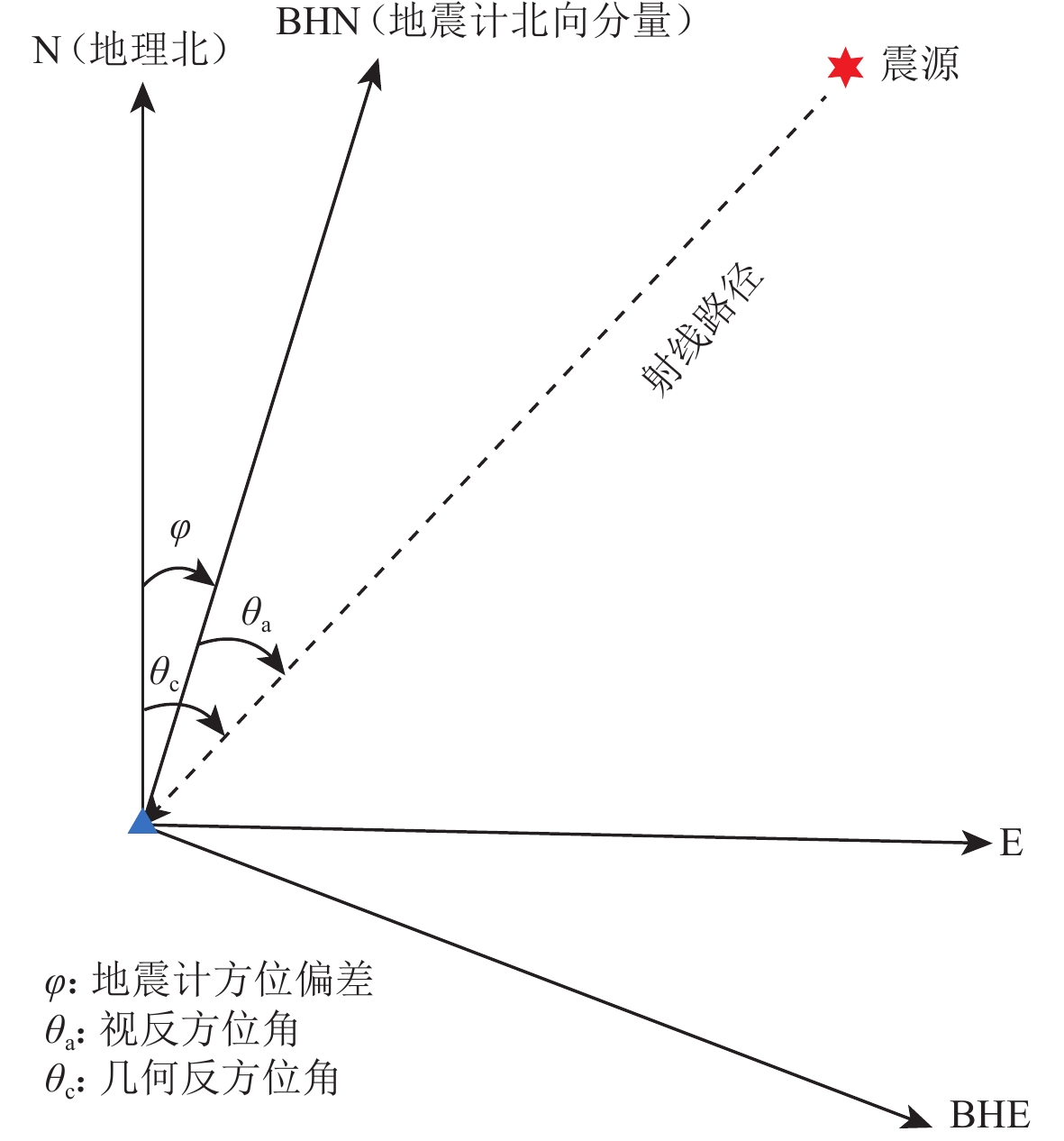
本文采用的方位偏差估计方法都是基于地震波波形的偏振特征,其基本原理如图2所示。图中三角形和六角星分别表示台站和地震的位置,N指示地理北方向,BHN表示地震计北向分量的实际摆放方向。依据地震和台站的位置可得到二者之间的大圆路径,将其与地理北之间的夹角θc作为几何反方位角。几何反方位角θc仅与二者的空间位置有关,与地震计的摆放方向无关。利用地震计记录到的地震波波形(本文中为远震P波及瑞雷面波)的偏振性质,可以获得大圆路径与地震计摆放方向BHN之间的夹角θa,作为视反方位角。视反方位角θa与地震及台站的空间位置无关,完全由波形的偏振特征决定。当地震计摆放正确时,几何反方位角和视反方位角相等,当地震计摆放存在偏差时,二者相应地存在差值。将这两个角度之间的差值定义为地震计方位偏差φ (φ=θc-θa),并定义其顺时针方向为正。实际测量时,由单个地震记录所获得的偏差存在一定误差,因此需要对多个地震所获得的结果进行统计分析以获得稳定的偏差角度测量值。本文主要使用远震P波偏振及瑞雷面波偏振进行视反方位角测量,详述如下。
1.1 P波偏振分析法
在均匀各向同性层状介质中传播时,P波的偏振是线性的,其质点运动轨迹集中于包含震源和地震计的垂直平面内。P波的运动集中于垂直分量和径向分量,而在切向分量中不存在(Lay,Wallace,1995)。如果BHN分量与地理北对准,基于P波质点运动的原理,计算得到的视反方位角θa应与几何反方位角θc一致;若两者未对准,对于给定的地震事件,选择不同的方位角,将其在台站上记录到的P波旋转至径向和切向,当切向中的分量最小时,就可以得到从这个地震所获取的视反方位角,进而获取地震计的偏差角度φ (图2)。在利用P波偏振分析进行方位角测量时,一般使用震中距在30°—90° 之间的远震事件。震中距小于30° 时,远震P波中会出现P波三重震相,波形较为复杂,并且相应波形受岩石圈横向不均匀性的影响较大;而震中距大于90° 的地震,其远震记录中会包含沿核幔边界传播的绕射波,波形受到干扰(黄建平等,2012;眭怡等,2018)。在30°—90° 之间的远震事件的P波波形相对简单,有利于最终获取稳定的测量结果。
对信号清晰的远震P波记录的BHN和BHE分量进行旋转,获取其径向和切向分量。当切向分量最小时所对应的方位角可作为该地震所对应的最佳视反方位角,进而获取偏差角度φ。实际的远震P波记录中包含噪声,当噪声较大时,会对单个地震事件得到的φ值产生较大的影响。Niu和Li (2011)提出了多地震事件信噪比加权叠加法来获取稳定的结果。该方法选取单个台站记录到的一组地震,以信噪比 (signal-noise-ratio,缩写为SNR)为权重,通过求取该组地震切向分量的加权最小值来获取最佳偏差角度φ。其切向上的加权能量ET (φ)可表示为:
$$ {E_{\mathrm{T}}} ( \varphi ) = \frac{{{\displaystyle\sum\limits_{i = 1}^N {{\omega _i}E_{\mathrm{T}}^i ( \varphi ) } } }}{{\displaystyle\sum\limits_{i = 1}^N {{\omega _i}} }} \text{,} $$ (1) 式中:N是所使用的地震事件总数;$ {E}_{{\mathrm{T}}}^{i} $(φ)代表了第i次地震事件切向分量的能量;ωi表示加权权重,一般取为两个水平分量P波信噪比的平均值。将可能的反方位角在0°—180° 范围内以1°的增量进行遍历,当ET (φ)达到最小值$ {E}_{{\mathrm{T}}}^{{\mathrm{min}}} $时,可获取最终的方位偏差。由于象限的对称性,满足条件的φ值有φ和φ+180°两个,对垂直分量和径向分量进行互相关,取互相关为正时的φ值为最终结果。利用Niu 和Li (2011)提出的方法:
$$ \frac{E_{\mathrm{T}} ( \varphi ) }{E^{\rm{noi}}}\text{≤}1+\frac{k}{n-k}f_{k\text{,} n-1} ( 1-\alpha ) \text{,} $$ (2) 式中,Enoi为直达P波之前的两个水平分量噪声的平均值,参数k=1,n取为每秒1个自由度,α=0.05表示95%的置信区间(Silver,Chan,1991),f为统计中的F分布。相应地改进公式(2)可提升对噪声较高的记录的误差估计准确度(Niu,Li,2011)。在利用多个事件进行偏差估计后,我们也将单次地震所对应的测量结果进行输出以辅助后续分析。
在对ChinArray一期的地震计方位角进行估计时,本文选取了台阵观测期间距离台阵中心30°—90°之间MW5.0以上的远震事件,以确保P波信号具有较强的能量且波形相对简单。依据全国地震情报中心(National Earthquake Information Center,缩写为NEIC)的全球地震目录,本文选取了符合要求的696次地震,并利用IASPEI91模型(Kennett,1991)计算了P波的理论走时,截取了352个台站上对应的约182万个P波三分量波形。为确保测量稳定性,选取P波理论走时前50 s至后200 s的波形,去除均值和线性趋势,进行5—50 s带通滤波,并计算了P波信号的信噪比SNR。其中信号部分取P波前1 s至后5 s,噪声部分取P波到时前30 s至前5 s,信噪比SNR定义为噪声与P波信号在对应时窗内均方根的比值。
为进一步确保结果的可靠性,本文首先选取BHZ分量计算垂直分量的信噪比,并对信噪比大于4的波形,选择信号质量较好的一个波形手动拾取远震P波走时,进而利用互相关方法对其余波形的P波进行对齐,以获取较为一致的P波走时。利用更新后的P波走时,重新计算各个分量的SNR,并选择两个水平分量信噪比之和大于5 (SNRBHE+SNRBHN>5)的记录用于后续分析。最终用于方位角测定的远震事件为696个(图1b)。经过信噪比筛选,共保留了来自696个远震事件的8万4 318个高信噪比P波波形,并按照台站进行归并。受台站观测质量和观测时段的影响,有4个台站最终可用的远震数量少于10个,因此未进行分析。利用Niu和Li (2011)提出的多事件加权方法对其余348个台站进行了方位偏差测量。
1.2 瑞雷面波偏振分析法
本文也使用基于瑞雷面波偏振的方法估计地震计的方位偏差,并与基于P波的结果进行对比。在均匀各向同性层状介质中,与P波类似,瑞雷面波能量也集中在垂向和径向,在切向上不存在。瑞雷面波的质点运动一般表现为逆进椭圆,其垂向和径向的波形具有90° 的相位差(Tanimoto,Rivera,2005)。当旋转到正确的反方位角时,将径向分量作希尔伯特(Hilbert)变换使其相位移动90°,这样在瑞雷面波窗口内,变换后的波形与垂向波形具有最高的相关系数(Baker,Stevens,2004)。基于这种偏振特征,可以对台站记录到的瑞雷面波信号进行不同角度旋转获得最佳视反方位角。与基于P波的方法类似,该方法也需要遍历方位角获取θa,二者区别仅在于P波的最佳角度是在切向能量最小时获得,而瑞雷面波的最佳角度在互相关系数最高时获得。本文中对方位角从0°—360° 以1° 增量进行遍历。
旋转变换后的两个水平分量间的相关系数定义如下(Baker,Stevens,2004):
$$ {C_{{\textit{z}}\bar r}} = \frac{{{S_{{\textit{z}}\bar r}}}}{{\sqrt {{S_{{\textit{z}}{\textit{z}}}}{S_{ r\bar r}}} }} \text{,} $$ (3) $$ S_{ jk}=\sum\limits_{\tau=1}^Nx_j ( \tau ) x_k ( \tau ) \qquad\ 当j=z时表示垂直分量\text{,} $$ (4) 式中:${C_{{\textit{z}}\bar r}} $表示两个分量的互相关系数,在$ [ $−1,1$ ] $之间取值,表征分量间波形的相似性。由于在进行方位旋转时,$S_{{\textit{z}}\bar r} $和${S_{{r}\bar r}} $会同步变化,而Szz为一常数,因此$C_{{\textit{z}}\bar r} $随方位角的变化相对平缓,会降低θa判别的分辨率。Stachnik等(2012)提出利用比值$C_{{\textit{z}}\bar r} ^{*}$来优化测量,
$$ C_{{\textit{z}}\bar r} ^{*} = \frac{{{S_{{\textit{z}}\bar r}}}}{{{S_{{\textit{z}}{\textit{z}}}}}} \text{.} $$ (4) 由于Szz为一常数,$C_{{\textit{z}}\bar r} ^{*}$的值主要由$ S_{{\textit{z}}\bar r} $决定。在移除伴随变化的$S_{ r \bar r }$之后,$C_{{\textit{z}}\bar r} ^{*}$相比$ C_{{\textit{z}}\bar r} $对角度的分辨能力更好。但由于$C_{{\textit{z}} \bar r} ^{*}$可能的取值范围较大,因此在进行方位角测量时,需要联合两个参数来进行分析,即利用$C_{{\textit{z}}\bar r} $来对波形的相似性进行判别,去除相似性较低的低质量信号,而利用$C_{{\textit{z}}\bar r}^{*}$的峰值来获取最佳的视反方位角(Stachnik et al,2012;Doran,Laske,2017)。相关方法事实上综合利用了瑞雷面波的相位和振幅信息,并且与P波基于能量的方法不同,不需要进行180° 的相位判断校正(Scholz et al,2017)。
基于面波偏振测量的视反方位角在0°—360° 之间,在进行多事件的统计平均时往往使用角度均值来代替算数均值,以避免角度周期带来的均值偏差,其中角度均值(circular mean)定义为:
$$ \bar{\varphi }=\mathrm{arctan}\left(\frac{{\sum\limits _{i=1}^{N}} \mathrm{sin}{\varPhi }_{i}}{{\sum\limits_{i=1}^{N} }\mathrm{cos}{\varPhi }_{i}}\right)\frac{180^\circ }{\text{π}}\text{,} $$ (5) 式中,Φi表示转换为弧度的单次方位偏差测量值,N表示参与测量的地震事件个数,$ \bar \varphi $最终根据其正负转换至0°—360° 区间。
与线性标准差类似,可定义角度的标准差为(Berens,2009):
$$ {\sigma }_{\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{c}\_\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}=\frac{\sqrt{2 ( 1-R ) }18{0}^\circ }{\text{π}}\text{,} $$ (6) 其中
$$ R = \frac{1}{N}\sqrt {{{\left( {\sum\limits_{i= 1}^N {\cos {\varphi _i}} } \right)}^2} + {{\left( {\sum\limits_{i = 1}^N {\sin {\varphi _i}} } \right)}^2}}. $$ (7) 由瑞雷面波获得的偏差角度的离散度往往较大,在获取最终均值时需要对测量值进行必要筛选。Stachnik等(2012)采用初始统计结果中位于均值95%置信区间内的数据进行二次统计分析以获得稳定测量结果。Scholz等(2017)将高信噪比数据所获得的视反方位角进行平均,并剔除与均值偏差大于25° 的测量值后进行重新计算,发现相应处理对均值影响很小,且可大大减小测量的标准差。相应方法均借鉴了统计分析中的稳健均值和稳健标准差计算思想。本文使用稳健平均方法,去除初次平均一倍标准差之外的单次测量。在进行误差估计时,假定测量结果为高斯分布,将两倍标准差作为其95%置信区间,以保持与P波分析方法一致(Niu,Li,2011)。
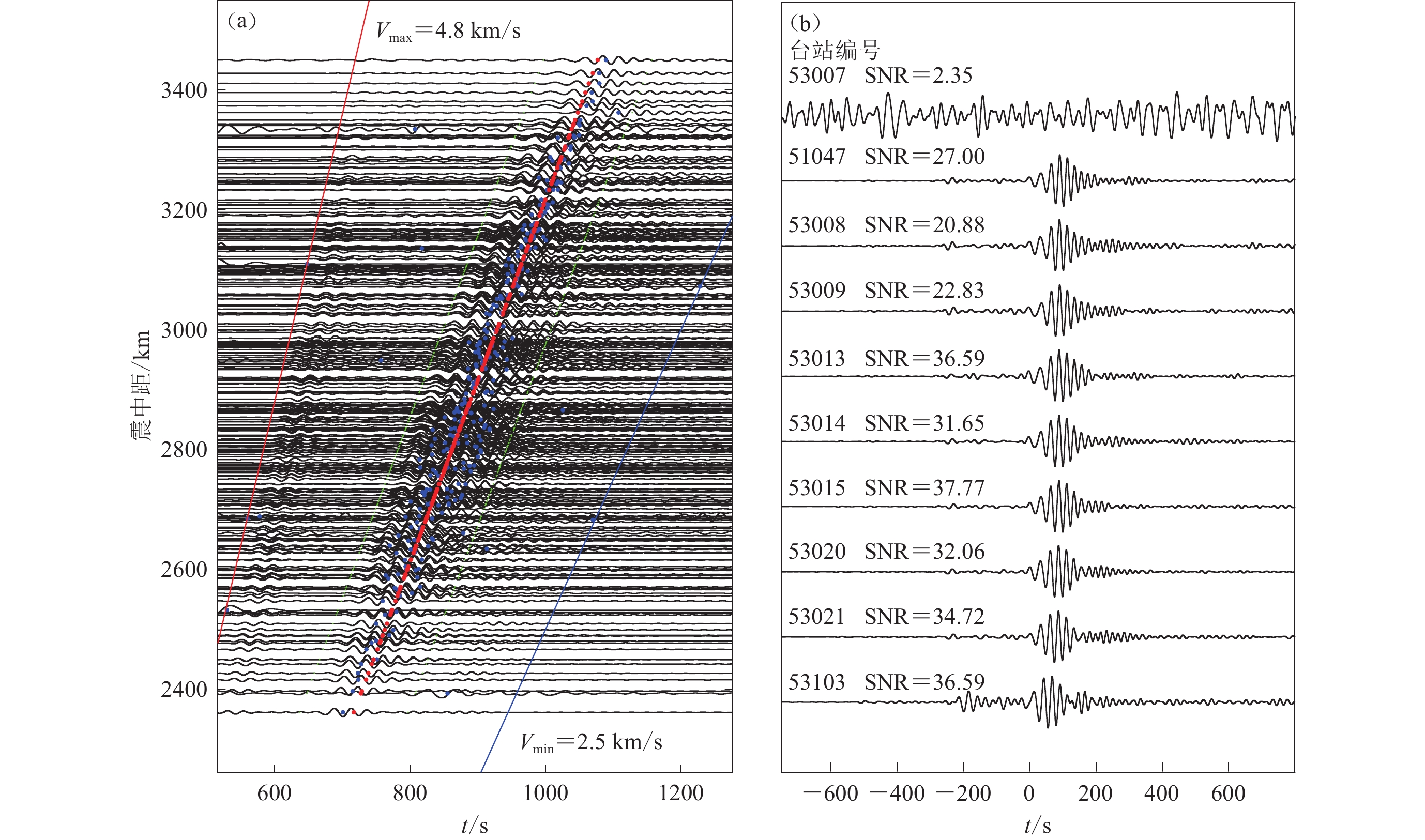
在瑞雷面波偏振分析中使用的地震事件震中距处于10°—170° 之间,震级大于MW5.0。由于面波沿地表传播,其传播速度受介质横向不均匀性影响较大,因此本文采用逐级筛选的策略对瑞雷面波信号进行质量控制。首先依据震中距以及相速度Vmin=2.5 km/s和Vmax= 4.8 km/s对瑞雷面波的窗口区间进行初次选取,如图3a所示。由于所使用的震中距范围较大,利用单一相速度选择的时间窗口长度较长,为了选取准确的面波窗口,降低其它震相的干扰,将垂直分量的波形进行20—60 s带通滤波,并计算整个时窗内波形的包络,将包络的最大值作为对应的面波能量峰值。从图3a中可以看出,绝大部分的峰值(蓝点)与面波信号具有很好的对应,受到观测质量及干扰信号的影响,也有少部分峰值偏离实际的面波信号。由于ChinArray的台站位置集中,台站间距较小,因此可以根据峰值到时与震中距之间的关系,利用线性拟合获得面波信号在整个台阵传播的视速度,并依据该视速度获取面波信号在各个台站上的峰值到时,如图3a中红点所示。可以看出,经过线性拟合得到的峰值到时与面波波形更加符合。以各个台站的峰值到时为中心,选择−80 s至80 s的时间窗口作为瑞雷面波的信号窗口,−240 s至−80 s作为噪声的时间窗口,计算面波的信噪比。由于面波信号一般较强,因此最终只保留面波信噪比大于20的波形用于后续的测量分析。图3b显示了一个震源深度约20 km的MW5.7地震的部分波形。可以看出,利用上述筛选策略,可较为准确地获取可靠面波信号窗口,并对信噪比较低的记录进行自动剔除,从而保证后续方位角测量的稳定性。最终,本文选择了1 928个地震事件用于瑞雷面波偏振分析(图1b中的蓝色圆点)。
![]() 图 3 面波信号筛选策略(a) 多个台站记录到的2012年1月17日MW5.7地震的垂直分量波形。红线和蓝线分别表示选取的面波相速度最大值和最小值对应的走时,蓝点表示各个波形在此视窗内的包络最大值,红点表示线性拟合后所得的峰值位置,绿线表示由此峰值优化选取后的面波视窗。所有波形经过20—60 s带通滤波;(b) 部分面波波形及相应信噪比Figure 3. Schematic on optimal surface wave selection procedure(a) The vertical records of a MW5.7 earthquake on January 17,2012. The red and blue lines represent the arrival times at each station using the default min/max phase velocity,and the blue dots are the envelope peaks of each band-passed (20−60 s) waveform. Red dots show the envelope peaks after linear fit and the green lines mark the final selected surface wave signal window at each station; (b) Examples of the surface waveforms and corresponding SNRs
图 3 面波信号筛选策略(a) 多个台站记录到的2012年1月17日MW5.7地震的垂直分量波形。红线和蓝线分别表示选取的面波相速度最大值和最小值对应的走时,蓝点表示各个波形在此视窗内的包络最大值,红点表示线性拟合后所得的峰值位置,绿线表示由此峰值优化选取后的面波视窗。所有波形经过20—60 s带通滤波;(b) 部分面波波形及相应信噪比Figure 3. Schematic on optimal surface wave selection procedure(a) The vertical records of a MW5.7 earthquake on January 17,2012. The red and blue lines represent the arrival times at each station using the default min/max phase velocity,and the blue dots are the envelope peaks of each band-passed (20−60 s) waveform. Red dots show the envelope peaks after linear fit and the green lines mark the final selected surface wave signal window at each station; (b) Examples of the surface waveforms and corresponding SNRs1.3 基于两种方法的偏振分析示例
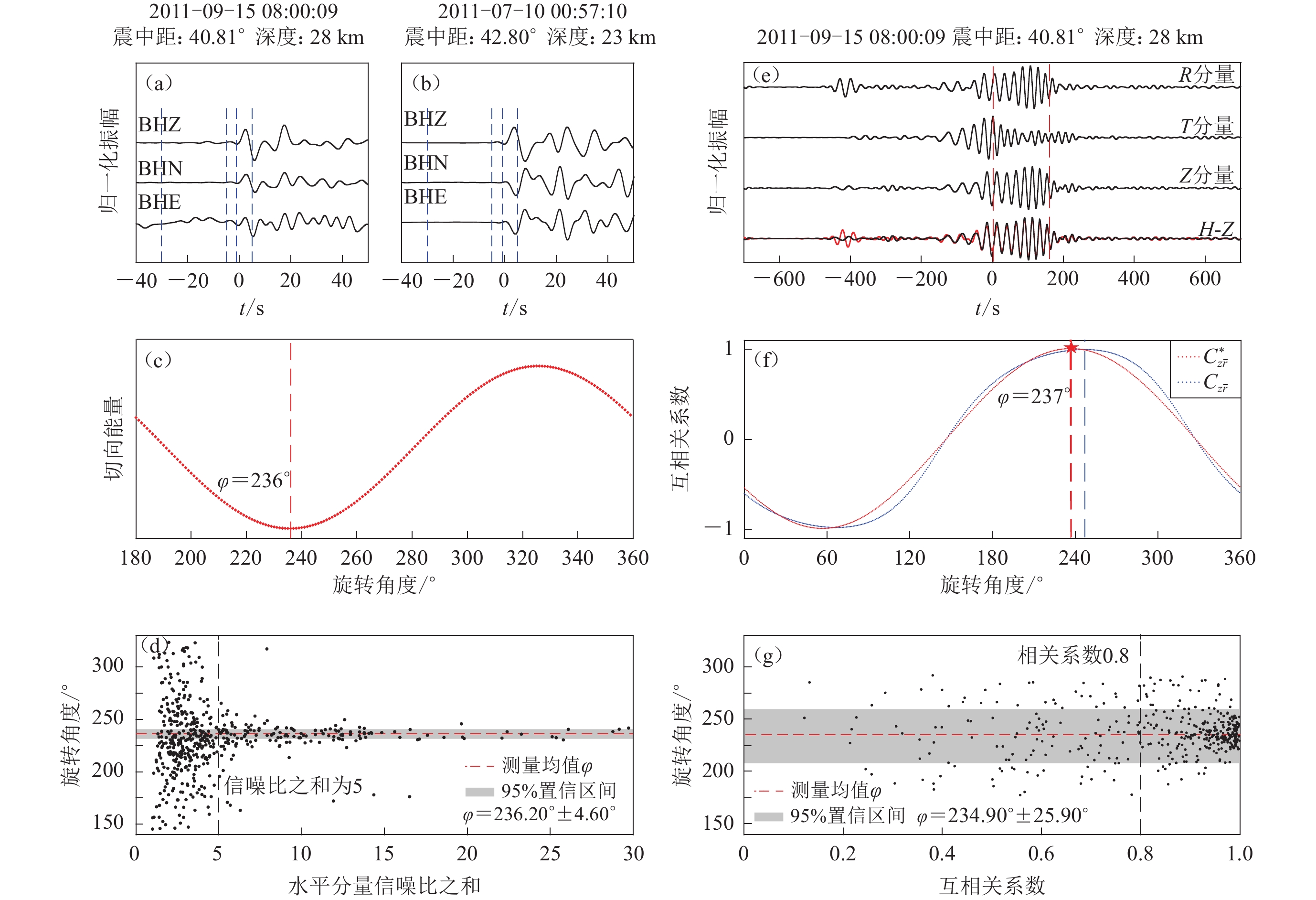
图4以台站X1.53035.01为例,显示了两种方法的方位偏差测量结果。该台站共记录到515个远震事件,其中水平分量信噪比之和大于5的事件为95个。图4a和图4b分别显示了其记录到的两次远震P波波形,其中图4a中的蓝色虚线表示计算信噪比的信号和噪声窗口。图4c显示了利用多事件加权叠加分析方法对95个事件的波形进行叠加处理获得的ET (φ)随角度的分布。可见,当偏差角度φ接近236°时,ET (φ)取得最小值,此时的角度φ为地震计北分量与地理北沿顺时针方向的夹角。为展示信噪比对最终结果的影响,本文也将所有515个远震事件的信噪比和测量结果绘制成图4d,可见:当两个水平分量的信噪比之和小于5时,由单个事件所获得的偏差角度分布较为离散;随着信噪比的提高,偏差角度测量结果趋于稳定,这与Niu和Li (2011)以及Wang等(2016)所得到的结果类似。最终由P波偏振分析结果可知,该地震计的北分量与地理北向偏差较大,接近指向西南方向,角度为236.20°±4.60°。
![]() 图 4 P波(左列)和瑞雷面波(右列)偏振分析估算的台站X1.53035.01的方位角(a,b) 两个地震事件的三分量波形,蓝色虚线标识计算信噪比和偏差角度所使用的噪声和信号窗口;(c) 台站记录到所有地震事件加权后的切向能量与方位角变化的关系;(d) 记录到的每个地震事件得到的偏差角度与水平分量信噪比之和的分布关系;(e) 一个远震事件在取得最佳视反方位角时的三分量波形,红色垂直虚线表示瑞雷波的时间窗;(f) 两个相关系数$C_{{\textit{z}}\bar r} $和$C_{{\textit{z}}\bar r }^{*} $随偏差角度的变化;(g) 所有事件的单次偏差角度与最佳互相关系数的分布Figure 4. An example of orientation estimation for station X1.53035.01 using P-wave (left column) and Rayleigh-wave (right column) polarization analysis(a,b) The waveforms from two seismic events,the blue dashed lines indicate the time windows of noise and signal for SNR calculation and orientation deviation estimation,respectively;(c) Variation of the SNR-weighted-transverse energy concerning the orientation deviation between the north component and the north;(d) Distribution of the orientation deviation and the sum of horizontal component SNR obtained for each recorded seismic event;(e) The three-component seismic waveforms rotated to R,T,Z components using the optimal apparent back-azimuth,and the red vertical dashed lines mark the Rayleigh wave time window;(f) Variations of $C_{{\textit{z}}\bar r} $ and $C_{{\textit{z}}\bar r }^{*} $ concerning the orientation deviation;(g) The distribution of the orientation deviations and the corresponding best cross-correlation coefficients for multiple seismic events
图 4 P波(左列)和瑞雷面波(右列)偏振分析估算的台站X1.53035.01的方位角(a,b) 两个地震事件的三分量波形,蓝色虚线标识计算信噪比和偏差角度所使用的噪声和信号窗口;(c) 台站记录到所有地震事件加权后的切向能量与方位角变化的关系;(d) 记录到的每个地震事件得到的偏差角度与水平分量信噪比之和的分布关系;(e) 一个远震事件在取得最佳视反方位角时的三分量波形,红色垂直虚线表示瑞雷波的时间窗;(f) 两个相关系数$C_{{\textit{z}}\bar r} $和$C_{{\textit{z}}\bar r }^{*} $随偏差角度的变化;(g) 所有事件的单次偏差角度与最佳互相关系数的分布Figure 4. An example of orientation estimation for station X1.53035.01 using P-wave (left column) and Rayleigh-wave (right column) polarization analysis(a,b) The waveforms from two seismic events,the blue dashed lines indicate the time windows of noise and signal for SNR calculation and orientation deviation estimation,respectively;(c) Variation of the SNR-weighted-transverse energy concerning the orientation deviation between the north component and the north;(d) Distribution of the orientation deviation and the sum of horizontal component SNR obtained for each recorded seismic event;(e) The three-component seismic waveforms rotated to R,T,Z components using the optimal apparent back-azimuth,and the red vertical dashed lines mark the Rayleigh wave time window;(f) Variations of $C_{{\textit{z}}\bar r} $ and $C_{{\textit{z}}\bar r }^{*} $ concerning the orientation deviation;(g) The distribution of the orientation deviations and the corresponding best cross-correlation coefficients for multiple seismic events瑞雷面波偏振方法依赖于Z分量与R分量希尔伯特变换之间的相似性。图4e显示了震中距为40.81° 的一个远震面波在取得最佳视反方位角时的波形,由上到下分别为R,T,Z三个分量。红色为对应R分量进行希尔伯特变换之后的波形,将其与Z分量波形进行对比可以看出,在取得最佳视反方位角时,两者具有较高的相似性,相关系数达到0.99。由该面波信号所得的偏差角度φ的测量结果如图4f所示,其中红色曲线为依据最大值归一化的${C}_{{\textit{z}}\bar{r}}^{*}$,蓝色曲线表示相应的$C_{{\textit{z}}\bar r} $。可以看出,$C_{{\textit{z}}\bar r} $在峰值附近变化较为平缓,而${C}_{{\textit{z}}{\bar r}}^{*}$则相对更易获得峰值点位置,由该地震测量得到的偏差角度为237°,与P波得到的结果一致。图4g显示了该台站记录到的845个远震面波事件的单次测量值以及对应的互相关系数$C_{{\textit{z}}\bar r} $。本文选取了$C_{{\textit{z}}\bar r} $大于0.8的496个事件的测量结果估算其偏差方向,最终得到地震计的偏差角度为234.90°±25.90°。由图4可以看出,虽然利用了不同的偏振分析方法,但在进行有效质量控制之后,不同方法可以获得较为一致的方位偏差估计。
2. 地震计方位偏差测量结果
2.1 P波偏振分析法与瑞雷面波偏振分析法结果对比
远震P波和瑞雷面波均可对地震计的方位偏差进行估计,图5展示了两个台站的测量结果,其中台站X1.51011.01偏差角度较小,而台站X1.51017.01的BHN分量向东偏差了15° 左右。
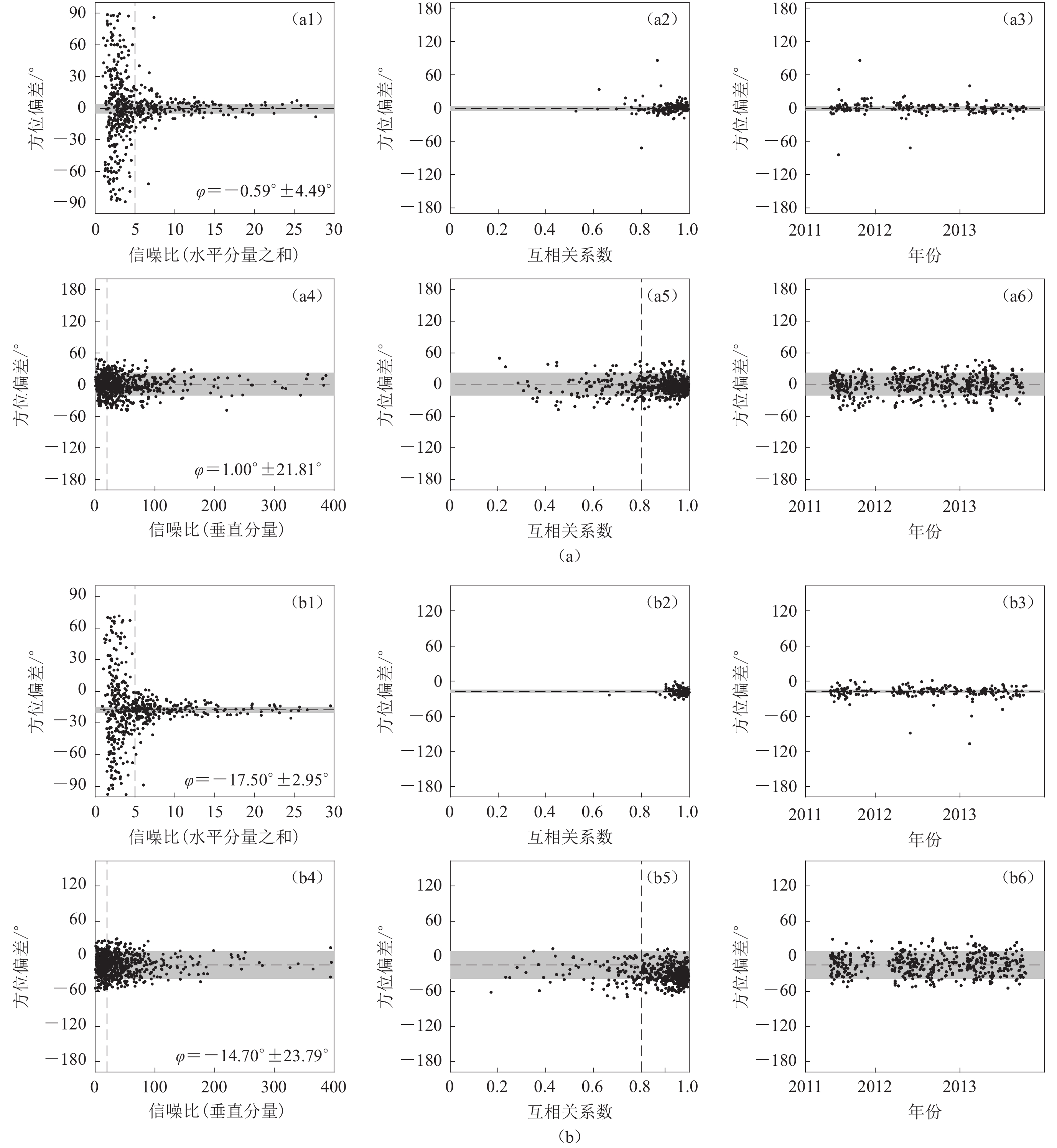
两个台站均使用多次地震来进行测量和统计分析,其中X1.51011.01使用了442次有效远震的P波记录和790次地震的瑞雷面波记录。而台站X1.51017.01使用了130次有效远震的P波记录和765次地震的瑞雷面波记录。从图5可以看出,对信噪比较低的P波波形,其测量角度离散度较大(图5a1,b1),而随着信噪比的增加,多个事件测量的结果趋于稳定。图5a2和b2也显示了水平分量信噪比之和大于5的波形在取得最佳视反方位角时对应的相关系数,可以看出信噪比较高波形的相关系数较为集中,多数在0.7以上。在整个观测时间段内,由单次地震的远震P波得到的偏差角度也较为稳定(图5a3,b3)。瑞雷面波的测量结果也显示了类似特征。面波方法依赖相关系数$C_{{\textit{z}}\bar r} $来进行质量控制,只有$C_{{\textit{z}}\bar r} $大于0.8时才可作为后续的测量样本进行统计分析(图5a5,b5)。对单次地震事件面波信号在不同时期的测量结果如图5a6和b6所示。分别对比图5a3,a6,b3和b6可以看出,对于筛选后的P波和瑞雷面波,由单个面波事件测量值的离散度相对P波较大,但二者的平均趋势类似。同时,在不同时间发生的地震,最终得到的结果也具有较好的一致性,表明两个台站在运行期间没有经历过明显的方位角变动(图5a3,a6,b3,b6)。最终X1.51011.01台站两种方法的结果分别为−0.59°±4.49°和1.00°±21.81°,偏差角度均在1°以内;台站X1.51017.01则为−17.50°±2.95° 和−14.70°±23.79°,偏差角度均在15°上下。两个台站应用两种不同偏振分析方法均得到类似的估计结果,表明两种方法对于较小以及较大的方位偏差均可以进行有效的测量分析。
图6对两种方法所得到的方位偏差结果进行了对比,为便于比较,将P波和瑞雷面波的测量偏差角度均转换至−180°—180°。对比结果显示在348个可测量的台站中,343个台站使用两种方法所得的平均结果差异在10° 以内,仅有5个台站(图6a中红点)差异超过10°,两种方法差异的分布如图6b所示。差异较大的5个台站由P波和瑞雷面波所得的北分量方向在图6c中分别以红色和蓝色的箭头表示,其中X1.52048.01台站的方位偏差达到约为69°,X1.52040.01台站的方位偏差约为45°,这些差异比较大的台站与台站仪器本身的故障有关,详见后文分析。
![]() 图 6 两种偏振分析方法的结果对比(a) 两种偏振分析方法所得结果对比。右侧图分别显示了两种结果两倍均方差的分布;(b) 两种结果均值差异分布;(c) 出现不同问题的台站分布Figure 6. Comparisons of the orientation estimation results from the two polarization approaches(a) Orientation estimation from the two independent estimation methods. The right figures show the distribution of twice stand deviation for 95% confidence level for the two methods;(b) Distribution of the difference in mean of orientation deviation between the two methods; (c) Distribution of the stations with abnormal orientation estimations,and all these stations have problems
图 6 两种偏振分析方法的结果对比(a) 两种偏振分析方法所得结果对比。右侧图分别显示了两种结果两倍均方差的分布;(b) 两种结果均值差异分布;(c) 出现不同问题的台站分布Figure 6. Comparisons of the orientation estimation results from the two polarization approaches(a) Orientation estimation from the two independent estimation methods. The right figures show the distribution of twice stand deviation for 95% confidence level for the two methods;(b) Distribution of the difference in mean of orientation deviation between the two methods; (c) Distribution of the stations with abnormal orientation estimations,and all these stations have problems不同测量方法均会存在一定的误差,即便地震计摆放完全正确也会存在非零的测量均值。参考之前的研究,本文将测量的方位偏差值超过10° 的台站视为地震计方位存在问题的台站(Davis,2003;Niu,Li,2011;Scholz et al,2017;Zeng et al,2021)。由于P波和面波所得的均值类似,而P波的总体离散度较小,本文利用P波的测量结果对中国科学探测台阵一期台阵的方位偏差情况进行了统计。统计结果表明,共有281个台站测量值小于10°,21个台站的地震计方位偏差在10°—20° 之间,46个台站出现了仪器故障或偏差大于20° 的现象。
2.2 台阵运行期间仪器方位角的变化
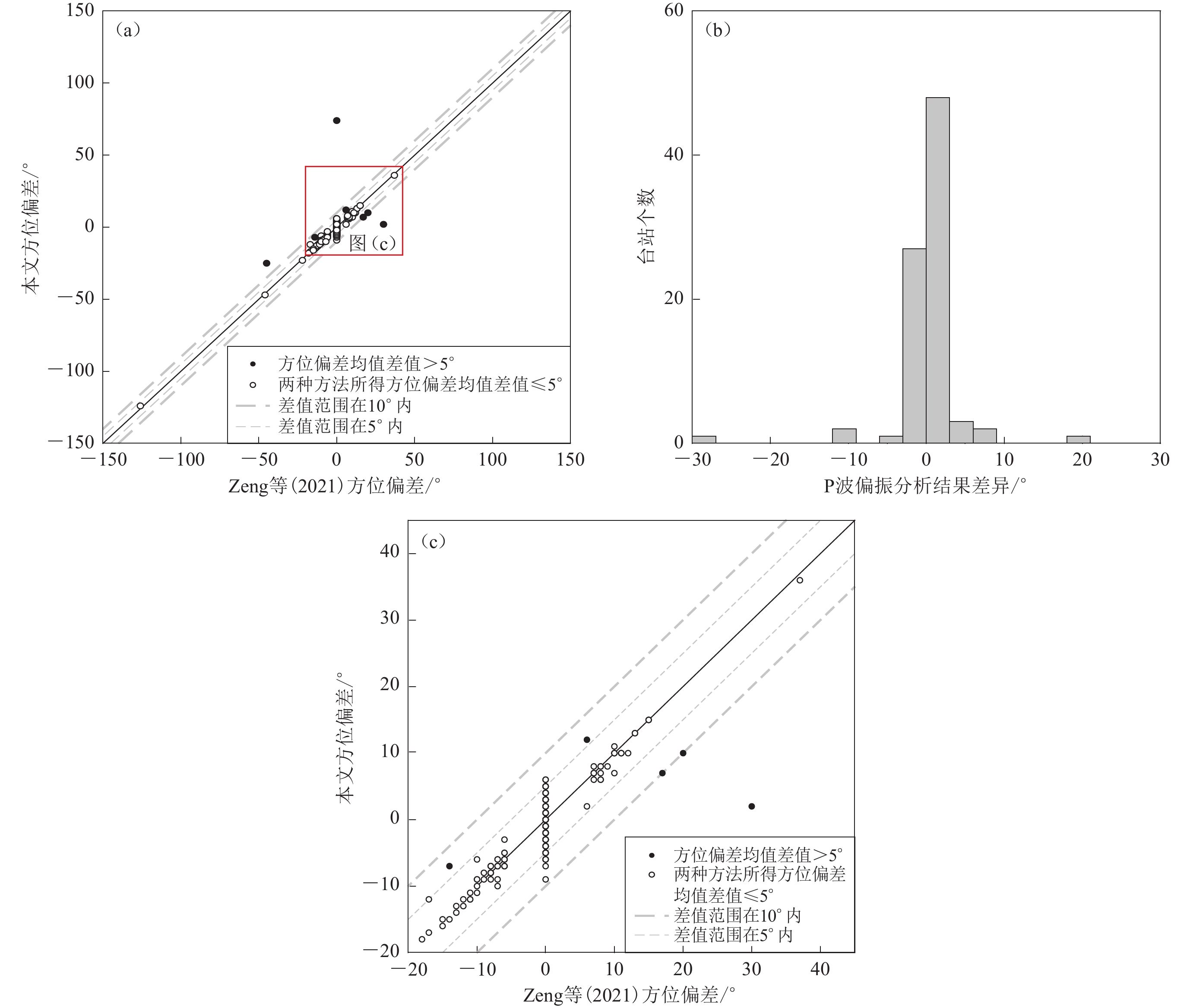
Zeng等(2021)利用P波偏振方法对ChinArray一期的台站方位偏差进行了估计,发现有94个地震计的方位偏差大于5°。本文采用的P波分析方法与其相同,因此与其给出的94个台站的偏差结果进行了对比,如图7所示。由于采用类似的方法和处理策略,其中88个台站的测量结果差异在5° 以内,占总数的93.6%,一致性较高,但也有6个台站与其结果差异大于5° (图7a,b)。对Zeng等(2021)认为方位角未出现偏差的台站,我们将其偏差视为0°,与本文利用P波偏振得到的方位偏差结果进行了比较,如图7c所示。可以看出,多数的差异均在5°—10° 之间,表明本文与Zeng等(2021)的结果具有较好的一致性。只有X1.52048.01台站差值达到约70°,与台站仪器本身的故障有关,详见后文分析。
![]() 图 7 本文与Zeng等(2021)地震计方位偏差测量结果的对比(a) 本文结果与Zeng等(2021)得到的方位偏差结果对比;(b) 本文结果与Zeng等(2021)中94个异常台站测量结果的差异分布统计图;(c) 对应图(a)中坐标−20°—45°范围内的放大部分,并将Zeng等(2021)中未列出的台站偏差视为0°,对Zeng等(2021)测量结果小于5° 的台站只表示出差值大于10° 的台站Figure 7. Comparison of orientation deviation measurement results from Zeng et al (2021) with those from this study(a) Comparison of deviations from P-wave analyses;(b) Histogram of the difference between the two studies for the 94 abnormal stations listed in Zeng et al (2021);(c) Zoom in of the −20°−45° range in Fig. (a),and consider the station deviations as 0 degrees not listed in Zeng et al (2021),the solid dots mark the difference greater than 10 degrees if the results are less than 5 degrees
图 7 本文与Zeng等(2021)地震计方位偏差测量结果的对比(a) 本文结果与Zeng等(2021)得到的方位偏差结果对比;(b) 本文结果与Zeng等(2021)中94个异常台站测量结果的差异分布统计图;(c) 对应图(a)中坐标−20°—45°范围内的放大部分,并将Zeng等(2021)中未列出的台站偏差视为0°,对Zeng等(2021)测量结果小于5° 的台站只表示出差值大于10° 的台站Figure 7. Comparison of orientation deviation measurement results from Zeng et al (2021) with those from this study(a) Comparison of deviations from P-wave analyses;(b) Histogram of the difference between the two studies for the 94 abnormal stations listed in Zeng et al (2021);(c) Zoom in of the −20°−45° range in Fig. (a),and consider the station deviations as 0 degrees not listed in Zeng et al (2021),the solid dots mark the difference greater than 10 degrees if the results are less than 5 degrees对于P波和瑞雷波偏振分析结果中存在的少数较大差异台站,以及我们P波分析结果和Zeng等(2021)结果之间存在较大差异的台站,我们对观测资料、处理过程进行了仔细分析,发现主要缘于台站运行期间方位角发生了变化以及仪器增益故障方面的原因,以下分别举例进行分析。
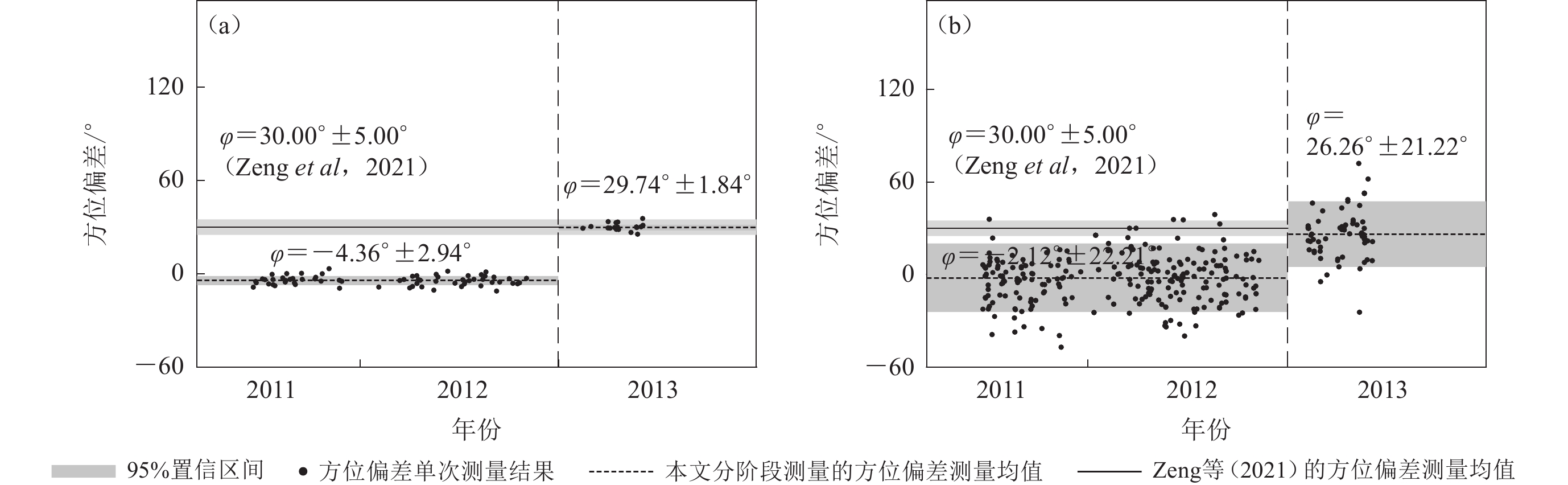
我们对两者结果偏差较大的7个台站进行了对比分析,发现其主要原因是部署期间部分台站的仪器方位角在不同阶段存在变化,涉及到的台站有5个。利用在不同时间段内记录到的信噪比较高的波形记录,可以对方位角随时间的变化进行评估。图8显示了X1.51008.01台站使用P波偏振分析和瑞雷面波偏振分析估算的不同时间段的方位角。从图中可以看出,两种方法结果一致性较好,均明确地展现了方位偏差的分时段变化。从观测期至2012年11月,该台站方位角与正北方向偏差不大,而在此之后有了较为明显的近30° 的偏差,与Zeng等(2021)给出的测量结果一致。该台站可能在观测后期存在仪器方位偏差的变动。在利用加权多事件方法对一组地震进行联合处理时,相应的分时段特征有可能在加权平均中被掩盖,从而得到相对平均的结果。同时,不同的数据预处理和筛选策略可能会对部分时段的地震事件进行移除,这可能是引起测量差异的主要原因。
本文分析了与Zeng等(2021)偏差比较大的7个台站的分时段测量结果(表1)。从表1中可以看出,相比全时段使用P波偏振的结果,相应分时段的估计误差多数减小。在利用相应方法开展方位角测量时,需要对具有较大误差分布的结果进行细致分析,同时利用单个事件的输出结果进行检查。利用一组事件内的多次测量结果,或者Wang等(2016)单事件测量,多事件平均的测量方法,可对台站运行期间仪器的方位角变化进行分析。
表 1 不同时间段得到的方位偏差测量结果比较Table 1. Comparison of orientation estimation results at different time periods台站名 本文P波偏振分析法测量结果/° Zeng等(2021)的P波偏振
分析法测量结果/°本文瑞雷波偏振分析法测量结果/° X1.51 008.01 −4.36±2.94
(2 011-06-18—2 012-11-02)
29.74±1.84
(2 013-02-14—2 013-06-15)30.00±5.00
(—2 013-03-29)−2.12±22.21
(2 011-06-18—2 012-11-07)
26.26±21.22
(2 013-02-06—2 013-06-05)X1.51 019.01 −5.00±11.30
(2 011-06-22—2 012-12-17)
−15.69±6.36
(2 013-01-31—2 013-10-01)−14.00±3.00
(—2 012-10-16)2.72±21.83
(2 011-06-21—2 012-12-17)
−14.57±23.83
(2 013-01-05—2 013-10-06)X1.51 059.01 −2.37±4.29
(2 011-07-06—2 011-09-16)
10.43±13.00
(2 012-01-01—2 013-09-15)17.00±6.00
(2 011-12-21—2 012-10-21)
10.00±5.00
(—2 013-04-10)−0.80±20.99
(2 011-07-06—2 011-12-30)
7.28±19.39
(2 012-01-09—2 013-09-28)X1.53 103.01 1.60±9.37
(2 011-10-18—2 012-08-14)
−44.29±7.22
(2 012-09-03—2 013-05-26)−45.00±3.00
(—2 012-08-27)−10.92±20.35
(2 011-10-14—2 012-08-31)
−52.28±19.76
(2 012-09-03—2 013-05-29)X1.53 148.01 6.60±6.00
(2 011-09-02—2 013-04-21)
1.60±15.00
(2 013-09-04—2 013-11-12)
只包含7个地震事件<5
(—2 013-09-02)
20.00±6.00
(2 013-09-02—)8.08±18.82
(2 011-07-29—2 013-04-23)
2.02±29.76
(2 013-09-04—2 013-11-12)X1.52 028.01 12.00±17.00
单个地震事件计算的方位角分布
分散,方位偏差随几何反方位角的分布
存在线性关系,有效地震数少6.00±5.00
存在波形被干扰的现象3.70±38.60
方位偏差随几何反方位角的
分布中,存在线性关系X1.52 048.01 74.00±16.00
单个地震事件计算的方位角分布分散,
有效地震数少重新标记到时
反方位偏差小于5°5.20±93.00
方位偏差随几何反方位角的分布
存在明显的线性关系2.3 仪器增益故障引起的方位偏差测量
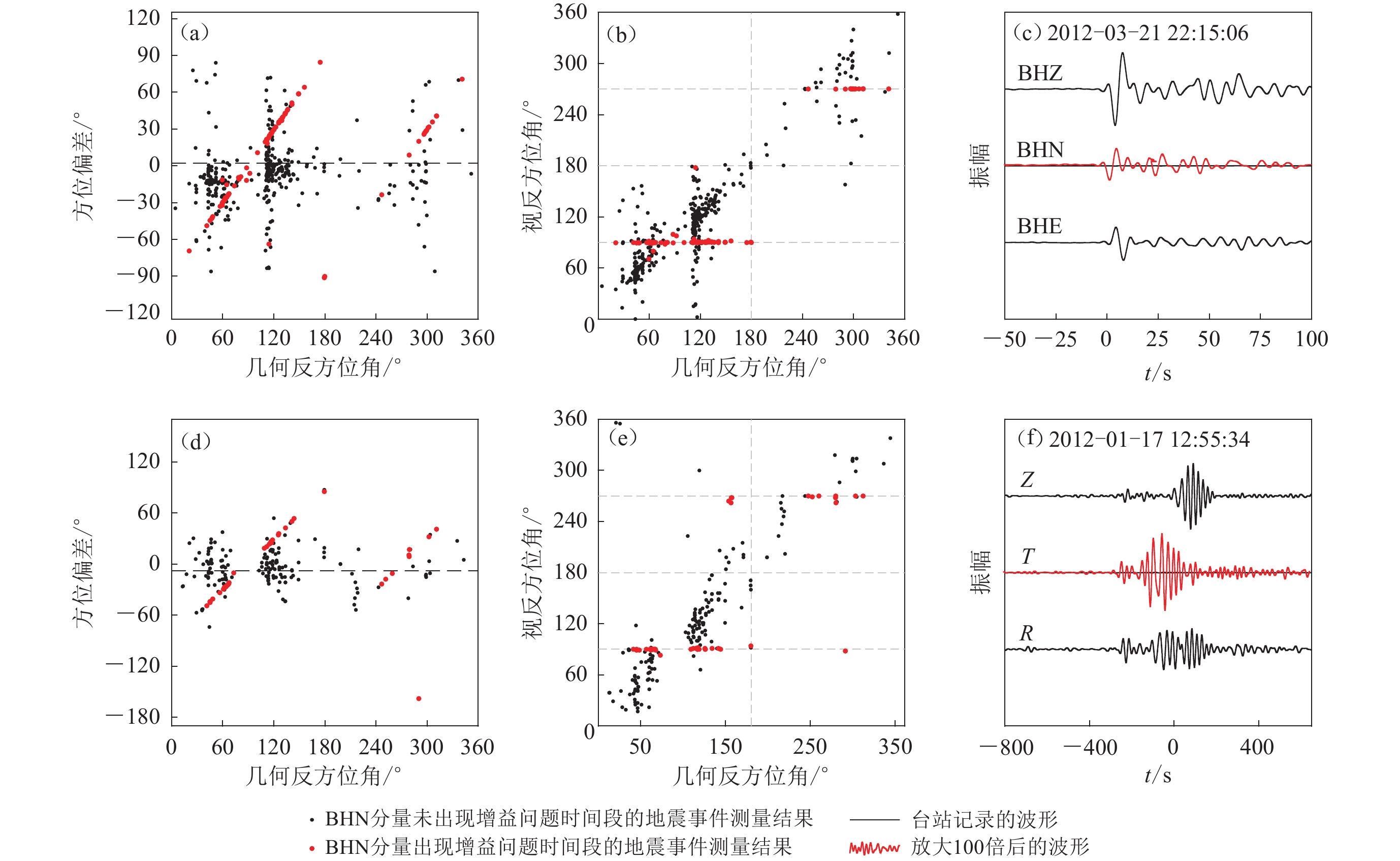
受地震波传播路径以及台站下方结构的影响,由单个地震测量得到的方位偏差往往存在一些误差,一般需要对来自于不同方位的地震测量结果进行平均以获取稳定的结果。在对来自不同方位地震测量结果的分析中,本文发现部分台站单个事件测量结果随几何反方位角的分布有特定的形态,瑞雷波偏振分析结果显示,X1.52048.01台站误差远高于其它台站,且在运行的整个时间段单个事件测量结果与几何反方位角呈线性关系,但P波偏振分析中使用的地震数较少,这种分布不明显。我们选取Zeng等(2021)认为方位偏差小于5° 的X1.53012台站作为示例,如图9所示。从图中可以看出,部分测量方位偏差与几何反方位角存在较为明显的线性关系(图9a,d中红点所示)。为进一步分析其原因,将由各个地震所得到的最佳视反方位角进行了绘制,如图9b,e所示。其中一部分的视反方位角与几何反方位角具有一致性,表明该台站的方位偏差不大。但同时,一部分事件测量得到的视反方位角为恒定的数值。而且,对于几何反方位角在0°—180° 的事件,视反方位角约为90°,几何反方位角在180°—360° 时,对应的视反方位角稳定在270°。我们选取了两个地震的波形进行检查,发现在同一个地震记录中,该台站的北分量波形振幅远小于东分量。当对波形振幅放大100倍之后,才可以观察到较为合理的地震波波形(图9c,f),这表明该分量增益存在故障。
![]() 图 9 增益故障台站X1.53012.01示例图(a)−(c)为P波偏振法分析的结果,图(d)−(f)为瑞雷波偏振分析的结果。(a) 单个地震事件计算的方位偏差与几何反方位角的分布;(b) 地震事件的视反方位角与几何反方位角的分布;(c) 该台站记录到某一个地震事件的三分量波形;图(d)−(f)与图(a)−(c)对应Figure 9. An example of a gain failure station X1.53012.01Figs. (a)−(c) and Figs. (d)−(f) represents the results obtained through P-wave polarization analysis and Rayleigh-wave polarization analysis. (a) The distribution relationship between back-azimuth and their orientation deviation of the individual event;(b) The relationship between BAZ and apparent back-azimuth;(c) The three-component waveforms from a certain earthquake event. Figs. (d)−(f) are corresponding to Figs. (a)−(c)
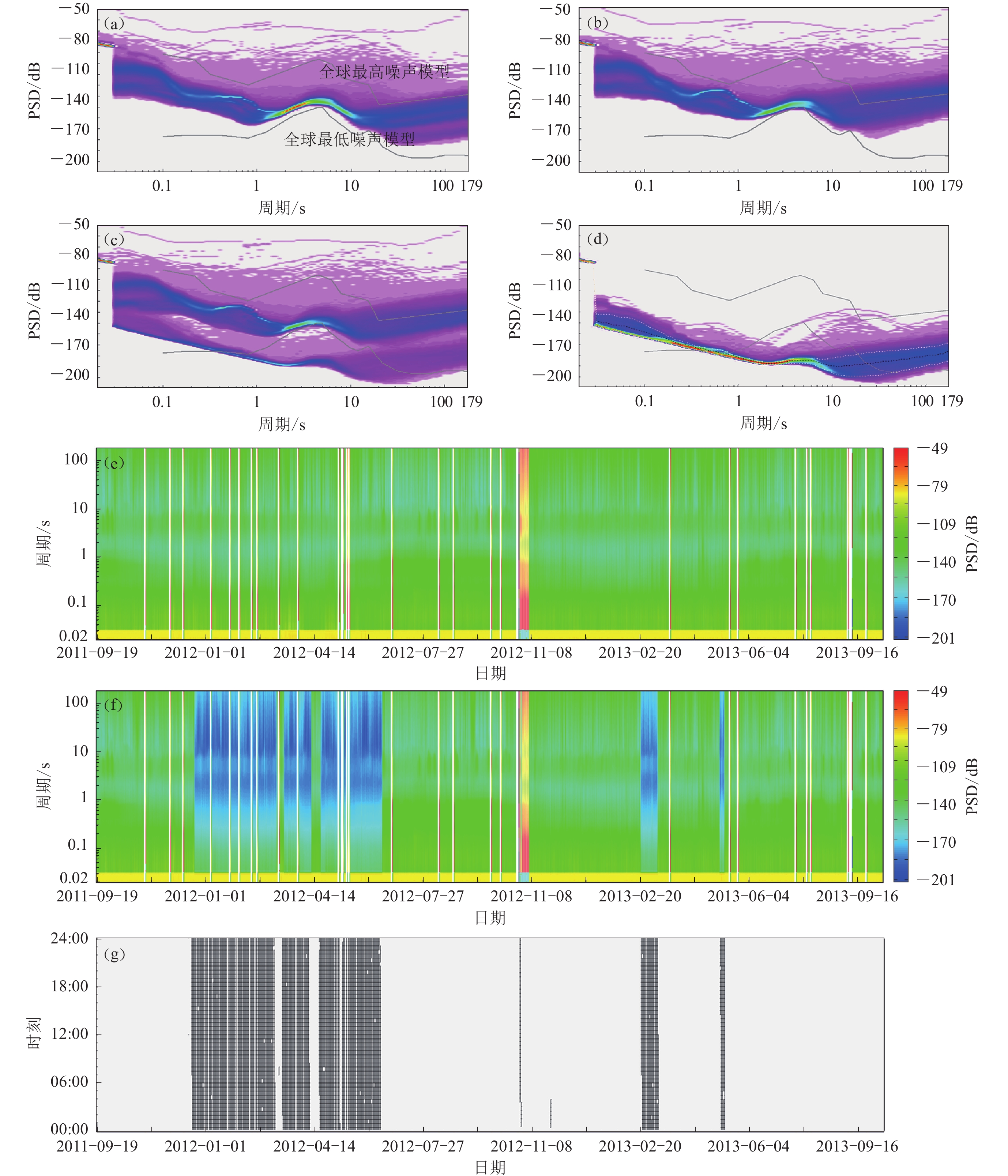
图 9 增益故障台站X1.53012.01示例图(a)−(c)为P波偏振法分析的结果,图(d)−(f)为瑞雷波偏振分析的结果。(a) 单个地震事件计算的方位偏差与几何反方位角的分布;(b) 地震事件的视反方位角与几何反方位角的分布;(c) 该台站记录到某一个地震事件的三分量波形;图(d)−(f)与图(a)−(c)对应Figure 9. An example of a gain failure station X1.53012.01Figs. (a)−(c) and Figs. (d)−(f) represents the results obtained through P-wave polarization analysis and Rayleigh-wave polarization analysis. (a) The distribution relationship between back-azimuth and their orientation deviation of the individual event;(b) The relationship between BAZ and apparent back-azimuth;(c) The three-component waveforms from a certain earthquake event. Figs. (d)−(f) are corresponding to Figs. (a)−(c)由于远震发生的时间无法控制,本文基于概率密度的功率谱分析方法对该台站的噪声水平进行了评估分析,该方法利用功率谱来表征台站的噪声水平,并用基于概率密度的方法对结果进行展现,可以表征台站在观测期内的观测质量(McNamara,Buland,2004;王芳等,2019)。从图10中可以看出,三个分量中,东分量和垂直分量的功率谱密度峰值均位于全球最高和最低噪声模型之间,而北分量则分为明显的两支,其中一支明显低于全球低噪声模型,表明仪器观测存在一定问题。利用PQLX软件,我们对该功率谱异常区间内的数据进行了分析,其对应的观测时段如图10g所示,对应时段的功率谱统计如图10d所示,每周的平均功率谱值随时间的演化如图10e,f所示。由图10可以看出,该台站的北分量在观测期间记录到的数值大小发生过阶段性的改变,在2012年1—5月以及2013年2月前后,其噪声功率谱有30 dB的显著下降。而在对应的时段,东分量的噪声功率谱一直处于正常状态。本文依据图10g中的时间段对图9中存在线性关系的测量值进行了对比,发现对应测量均源于在对应时间段内发生的地震,这表明相关的异常测量值是由于北分量的增益异常导致的。
![]() 图 10 X1.53012.01台站基于概率密度函数(PDF)的噪声功率谱密度(PSD)分析的仪器增益判别(a−c) 2011—2013年BHZ,BHE,BHN三个分量的噪声功率谱概率密度图;(d) BHN分量中偏低分支对应数据的独立概率密度统计图;(e,f) BHE和BHN分量每周平均功率谱随时间的演化;(g) 图(c)中低于全球最低噪声模型部分对应的数据观测时段Figure 10. The noise power spectral density (PSD) analysis based on probability density function (PDF) of the station X1.53012.01 for gain discrimination of seismometers(a−c) The PDF-PSD images using records during 2011−2013 for BHZ,BHE,BHN components,respectively;(d) The PDF-PSD image calculated using the corresponding records related to the anormal branch in Fig. (c) for the BHN component;(e,f) The time variation of weekly averaged PSD for BHE and BHN components,respectively;(g) Date and time distribution of the records related to the anormal branch of the BHN component
图 10 X1.53012.01台站基于概率密度函数(PDF)的噪声功率谱密度(PSD)分析的仪器增益判别(a−c) 2011—2013年BHZ,BHE,BHN三个分量的噪声功率谱概率密度图;(d) BHN分量中偏低分支对应数据的独立概率密度统计图;(e,f) BHE和BHN分量每周平均功率谱随时间的演化;(g) 图(c)中低于全球最低噪声模型部分对应的数据观测时段Figure 10. The noise power spectral density (PSD) analysis based on probability density function (PDF) of the station X1.53012.01 for gain discrimination of seismometers(a−c) The PDF-PSD images using records during 2011−2013 for BHZ,BHE,BHN components,respectively;(d) The PDF-PSD image calculated using the corresponding records related to the anormal branch in Fig. (c) for the BHN component;(e,f) The time variation of weekly averaged PSD for BHE and BHN components,respectively;(g) Date and time distribution of the records related to the anormal branch of the BHN component通常制造商对地震仪的规范表明三分量地震仪每个分量的增益在1%以内(Ekström, Busby,2008),而图10表明单个分量的增益可能由于仪器故障比另外两个分量低数个量级。基于P波的切向能量ET (φ)最小原理以及基于相关系数$C_{{\textit{z}}\bar r}^{*} $的判断都以两个水平分量增益相近为前提。当某一个水平分量增益远远小于另外一个水平分量时,无论地震来自于哪个方位,其所能取得的ET (φ)所对应的方位都会来自于另外一个正交分量所在方向。以图9为例,由于增益故障,所有地震均会将北分量作为P波的切向分量以获得最佳的视反方位角。依据右手坐标系,当地震的几何反方位角位于0°—180° 时,其最佳视反方位角θa为90°;当地震的几何反方位角位于180°—360° 时,θa为270°。此时,多个地震取得的θa在图9b中呈现为两条直线,而方位偏差φ会表现为倾斜的直线,且其与最终真实的方位偏差的交点在横轴上分别接近90°和270°。
由于相应问题源于同一台站不同分量之间增益的差异,而在同一分量上的增益相对稳定,相应波形较难在质量控制阶段进行剔除。在进行信噪比计算时均使用同一分量的不同信号窗口,无法体现分量之间的差异。相应的地震波形在进行放大之后也可呈现较为正常的状态(图9c,f),在计算$ C_{{\textit{z}}\bar r}^{*} $时,增益较小的分量同时抵消,也可对不同分量之间的增益差异进行评估。但相关故障会引起θa及φ呈现出与几何反方位角的线性关系,该特点可用于分析判断仪器的方位偏差是否与仪器的增益故障有关。
3. 讨论与结论
远震P波和瑞雷面波方法是两种常用的地震计方位偏差估计方法,本文以及多种研究表明,在进行可靠的数据质量控制后,这两种方法均可以对地震计摆放的方位偏差进行有效的估计。相比远震P波,可用的高质量瑞雷面波信号更容易取得。但为减少局部结构对面波测量结果的影响,在面波测量中多使用周期20 s以上的长周期信号,其所对应的${C}_{{\textit{z}} \bar{r}}^{*}$变化相对平缓,利用其对应峰值取得的测量偏差值离散度较高,导致误差值较大。同时,相比体波信号,面波本身在传播中也更容易受到介质横向不均匀性的影响,其在台站的入射方位更容易偏离大圆路径。在使用面波进行测量时,可选择较宽泛范围的震中距以获得较好的方位覆盖,从而取得稳定结果。联合两种方法进行独立测量和比较,也是获得可靠结果的重要方法。
多个地震的测量有助于获取稳定的平均结果,但也有可能存在系统性的偏差。如Wang等(2016)讨论了由台站下方倾斜界面引起的P波方位角的系统偏差,Büyükakpınar等(2021)也发现倾斜速度界面会对结果有系统性的影响。由于南北地震带南段的地下结构相对复杂,本文未对相应影响进行分析。对地震位置、台站下方结构以及地震分布的细致分析尚需更多的研究。
相比固定台站,流动台站受观测环境和观测条件的限制,往往较难选取与固定台站等同的高质量台基进行仪器布设,观测期间的运行维护难度也高于固定台站。因此对流动台站观测质量的判别十分重要。从本文研究结果来看,利用远震波形进行方位偏差测量时,对不同时期发生的地震事件的单独测量结果进行系统分析十分必要,相应结果可以用于观测期间方位角可能变化的细致评估。在现有方法中,P波测量得到的误差范围较小,面波测量值则相对离散。观测期内,可用于P波测量的远震为696次,而可用于面波偏振分析的则达到1 928次。在分辨方位角时间变化方面,基于面波的测量具有更高的时间分辨率。而基于噪声互相关函数中的面波信号,则可进一步提升方位角评估的时间分辨率,并可利用多个台站对其进行平均以获取稳定的结果,相关方法值得进一步尝试,并关注噪声源特征对测量结果的影响(Zha et al,2013;赵玲云等,2021)。基于概率密度函数的噪声功率谱密度是监测台阵观测质量的重要方法,结合噪声强度的变化,以及基于功率谱密度的水平和垂直分量的谱比测量,也可以对不同分量之间的谱比异常进行更细致的判断(王芳等,2019;Bahavar et al,2020)。综合这些质量评估手段,可以对台站观测噪声水平、方位偏差等多种质量参数进行协同分析,丰富对观测数据的质量评估手段。
由于多种测量方法均存在一定的误差,本文最终选择方位偏差10° 作为地震计偏差较大的标准。从对ChinArray一期的评估结果来看,281个台站的方位偏差小于10°,21个台站在10°—20° 之间,46个台站在运行阶段出现过仪器故障或偏差大于20°。野外的复杂观测环境,观测期间的异常情况以及台站布设的流程均是影响仪器方位偏差的重要因素。随着中国地震台阵观测台阵的持续开展,光纤寻北仪、浅井观测等新型观测技术得到了广泛应用。这些观测技术的进步与本文所使用的质量控制分析手段的应用,有助于进一步评估和改善大规模野外流动观测的观测质量,实现对海量地震观测数据的深入挖掘和应用。
中国地震局地球物理研究所地震科学数据中心(DOI:10.11998.SeisDmc/SN;郑秀芬等,2009)为本文提供了地震波形数据,本文部分图件使用GMT绘制(Wessel et al,2019),作者在此一并表示感谢。
-
图 4 P波(左列)和瑞雷面波(右列)偏振分析估算的台站X1.53035.01的方位角
(a,b) 两个地震事件的三分量波形,蓝色虚线标识计算信噪比和偏差角度所使用的噪声和信号窗口;(c) 台站记录到所有地震事件加权后的切向能量与方位角变化的关系;(d) 记录到的每个地震事件得到的偏差角度与水平分量信噪比之和的分布关系;(e) 一个远震事件在取得最佳视反方位角时的三分量波形,红色垂直虚线表示瑞雷波的时间窗;(f) 两个相关系数$C_{{\textit{z}}\bar r} $和$C_{{\textit{z}}\bar r }^{*} $随偏差角度的变化;(g) 所有事件的单次偏差角度与最佳互相关系数的分布
Figure 4. An example of orientation estimation for station X1.53035.01 using P-wave (left column) and Rayleigh-wave (right column) polarization analysis
(a,b) The waveforms from two seismic events,the blue dashed lines indicate the time windows of noise and signal for SNR calculation and orientation deviation estimation,respectively;(c) Variation of the SNR-weighted-transverse energy concerning the orientation deviation between the north component and the north;(d) Distribution of the orientation deviation and the sum of horizontal component SNR obtained for each recorded seismic event;(e) The three-component seismic waveforms rotated to R,T,Z components using the optimal apparent back-azimuth,and the red vertical dashed lines mark the Rayleigh wave time window;(f) Variations of $C_{{\textit{z}}\bar r} $ and $C_{{\textit{z}}\bar r }^{*} $ concerning the orientation deviation;(g) The distribution of the orientation deviations and the corresponding best cross-correlation coefficients for multiple seismic events
图 3 面波信号筛选策略
(a) 多个台站记录到的2012年1月17日MW5.7地震的垂直分量波形。红线和蓝线分别表示选取的面波相速度最大值和最小值对应的走时,蓝点表示各个波形在此视窗内的包络最大值,红点表示线性拟合后所得的峰值位置,绿线表示由此峰值优化选取后的面波视窗。所有波形经过20—60 s带通滤波;(b) 部分面波波形及相应信噪比
Figure 3. Schematic on optimal surface wave selection procedure
(a) The vertical records of a MW5.7 earthquake on January 17,2012. The red and blue lines represent the arrival times at each station using the default min/max phase velocity,and the blue dots are the envelope peaks of each band-passed (20−60 s) waveform. Red dots show the envelope peaks after linear fit and the green lines mark the final selected surface wave signal window at each station; (b) Examples of the surface waveforms and corresponding SNRs
图 6 两种偏振分析方法的结果对比
(a) 两种偏振分析方法所得结果对比。右侧图分别显示了两种结果两倍均方差的分布;(b) 两种结果均值差异分布;(c) 出现不同问题的台站分布
Figure 6. Comparisons of the orientation estimation results from the two polarization approaches
(a) Orientation estimation from the two independent estimation methods. The right figures show the distribution of twice stand deviation for 95% confidence level for the two methods;(b) Distribution of the difference in mean of orientation deviation between the two methods; (c) Distribution of the stations with abnormal orientation estimations,and all these stations have problems
图 7 本文与Zeng等(2021)地震计方位偏差测量结果的对比
(a) 本文结果与Zeng等(2021)得到的方位偏差结果对比;(b) 本文结果与Zeng等(2021)中94个异常台站测量结果的差异分布统计图;(c) 对应图(a)中坐标−20°—45°范围内的放大部分,并将Zeng等(2021)中未列出的台站偏差视为0°,对Zeng等(2021)测量结果小于5° 的台站只表示出差值大于10° 的台站
Figure 7. Comparison of orientation deviation measurement results from Zeng et al (2021) with those from this study
(a) Comparison of deviations from P-wave analyses;(b) Histogram of the difference between the two studies for the 94 abnormal stations listed in Zeng et al (2021);(c) Zoom in of the −20°−45° range in Fig. (a),and consider the station deviations as 0 degrees not listed in Zeng et al (2021),the solid dots mark the difference greater than 10 degrees if the results are less than 5 degrees
图 9 增益故障台站X1.53012.01示例
图(a)−(c)为P波偏振法分析的结果,图(d)−(f)为瑞雷波偏振分析的结果。(a) 单个地震事件计算的方位偏差与几何反方位角的分布;(b) 地震事件的视反方位角与几何反方位角的分布;(c) 该台站记录到某一个地震事件的三分量波形;图(d)−(f)与图(a)−(c)对应
Figure 9. An example of a gain failure station X1.53012.01
Figs. (a)−(c) and Figs. (d)−(f) represents the results obtained through P-wave polarization analysis and Rayleigh-wave polarization analysis. (a) The distribution relationship between back-azimuth and their orientation deviation of the individual event;(b) The relationship between BAZ and apparent back-azimuth;(c) The three-component waveforms from a certain earthquake event. Figs. (d)−(f) are corresponding to Figs. (a)−(c)
图 10 X1.53012.01台站基于概率密度函数(PDF)的噪声功率谱密度(PSD)分析的仪器增益判别
(a−c) 2011—2013年BHZ,BHE,BHN三个分量的噪声功率谱概率密度图;(d) BHN分量中偏低分支对应数据的独立概率密度统计图;(e,f) BHE和BHN分量每周平均功率谱随时间的演化;(g) 图(c)中低于全球最低噪声模型部分对应的数据观测时段
Figure 10. The noise power spectral density (PSD) analysis based on probability density function (PDF) of the station X1.53012.01 for gain discrimination of seismometers
(a−c) The PDF-PSD images using records during 2011−2013 for BHZ,BHE,BHN components,respectively;(d) The PDF-PSD image calculated using the corresponding records related to the anormal branch in Fig. (c) for the BHN component;(e,f) The time variation of weekly averaged PSD for BHE and BHN components,respectively;(g) Date and time distribution of the records related to the anormal branch of the BHN component
表 1 不同时间段得到的方位偏差测量结果比较
Table 1 Comparison of orientation estimation results at different time periods
台站名 本文P波偏振分析法测量结果/° Zeng等(2021)的P波偏振
分析法测量结果/°本文瑞雷波偏振分析法测量结果/° X1.51 008.01 −4.36±2.94
(2 011-06-18—2 012-11-02)
29.74±1.84
(2 013-02-14—2 013-06-15)30.00±5.00
(—2 013-03-29)−2.12±22.21
(2 011-06-18—2 012-11-07)
26.26±21.22
(2 013-02-06—2 013-06-05)X1.51 019.01 −5.00±11.30
(2 011-06-22—2 012-12-17)
−15.69±6.36
(2 013-01-31—2 013-10-01)−14.00±3.00
(—2 012-10-16)2.72±21.83
(2 011-06-21—2 012-12-17)
−14.57±23.83
(2 013-01-05—2 013-10-06)X1.51 059.01 −2.37±4.29
(2 011-07-06—2 011-09-16)
10.43±13.00
(2 012-01-01—2 013-09-15)17.00±6.00
(2 011-12-21—2 012-10-21)
10.00±5.00
(—2 013-04-10)−0.80±20.99
(2 011-07-06—2 011-12-30)
7.28±19.39
(2 012-01-09—2 013-09-28)X1.53 103.01 1.60±9.37
(2 011-10-18—2 012-08-14)
−44.29±7.22
(2 012-09-03—2 013-05-26)−45.00±3.00
(—2 012-08-27)−10.92±20.35
(2 011-10-14—2 012-08-31)
−52.28±19.76
(2 012-09-03—2 013-05-29)X1.53 148.01 6.60±6.00
(2 011-09-02—2 013-04-21)
1.60±15.00
(2 013-09-04—2 013-11-12)
只包含7个地震事件<5
(—2 013-09-02)
20.00±6.00
(2 013-09-02—)8.08±18.82
(2 011-07-29—2 013-04-23)
2.02±29.76
(2 013-09-04—2 013-11-12)X1.52 028.01 12.00±17.00
单个地震事件计算的方位角分布
分散,方位偏差随几何反方位角的分布
存在线性关系,有效地震数少6.00±5.00
存在波形被干扰的现象3.70±38.60
方位偏差随几何反方位角的
分布中,存在线性关系X1.52 048.01 74.00±16.00
单个地震事件计算的方位角分布分散,
有效地震数少重新标记到时
反方位偏差小于5°5.20±93.00
方位偏差随几何反方位角的分布
存在明显的线性关系 -
陈继锋,李亮,李少睿,刘白云,陈晓龙. 2016. 甘肃省测震台网地震台站地震计方位角检验与校正[J]. 地震工程学报,38(3):460–465. doi: 10.3969/j.issn.1000-0844.2016.03.018 Chen J F,Li L,Li S R,Liu B Y,Chen X L. 2016. Check and correction of seismometer azimuth for Gansu Seismic Network stations[J]. China Earthquake Engineering Journal,38(3):460–465 (in Chinese).
黄静,房立华,王长在,郭永霞. 2015. 采用P波分析法校正北京遥测地震台网地震计方位角[J]. 地震地磁观测与研究,36(4):47–53. Huang J,Fang L H,Wang C Z,Guo Y X. 2015. Application of P waveform analysis in the seismometer azimuth correction of Beijing Seismic Telemetry Network[J]. Seismological and Geomagnetic Observation and Research,36(4):47–53 (in Chinese).
黄建平,李振春,孔雪,国强,严君. 2012. 基于PWD的绕射波波场分离成像方法综述[J]. 地球物理学进展,27(6):2499–2510. doi: 10.6038/j.issn.1004-2903.2012.06.025 Huang J P,Li Z C,Kong X,Guo Q,Yan J. 2012. The review of the wave field separation method about reflection and diffraction based on the PWD[J]. Progress in Geophysics,27(6):2499–2510 (in Chinese).
龙剑锋,张学应,骆佳骥,赵希磊. 2016. 偏振分析算法测定井下地震计方位角偏差[J]. 地震地磁观测与研究,37(1):86–90. Long J F,Zhang X Y,Luo J J,Zhao X L. 2016. To measure the azimuth deviation of the bore-hole seismograph using polarization analysis method[J]. Seismological and Geomagnetic Observation and Research,37(1):86–90 (in Chinese).
眭怡,吴庆举,张瑞青. 2018. 基于三重震相拟合的华南地区上地幔P波与S波速度结构[J]. 地球物理学报,61(8):3237–3250. doi: 10.6038/cjg2018L0507 Sui Y,Wu Q J,Zhang R Q. 2018. P- and S-wave velocity structures of upper mantle beneath South China derived from seismic triplications[J]. Chinese Journal of Geophysics,61(8):3237–3250 (in Chinese).
王芳,王伟涛,龙剑锋,牟磊育,傅磊. 2019. 中国大陆地区宽频带地震台网台基噪声特征[J]. 地震学报,41(5):569–584. doi: 10.11939/jass.20190031 Wang F,Wang W T,Long J F,Mu L Y,Fu L. 2019. Seismic noise characteristics of broad-band seismic networks in Chinese mainland[J]. Acta Seismologica Sinica,41(5):569–584 (in Chinese).
赵玲云,王伟涛,王芳,李娜. 2021. 噪声源的时空分布及其对噪声互相关函数的影响:以ChinArray二期数据为例[J]. 地球物理学报,64(12):4327–4340. doi: 10.6038/cjg2021O0054 Zhao L Y,Wang W T,Wang F,Li N. 2021. The distribution of noise source both in space and time and its influence on noise cross-correlation functions[J]. Chinese Journal of Geophysics,64(12):4327–4340 (in Chinese).
郑秀芬,欧阳飚,张东宁,姚志祥,梁建宏,郑洁. 2009. “国家数字测震台网数据备份中心”技术系统建设及其对汶川大地震研究的数据支撑[J]. 地球物理学报,52(5):1412–1417. Zheng X F,Ouyang B,Zhang D N,Yao Z X,Liang J H,Zheng J. 2009. Technical system construction of Data Backup Centre for China Seismograph Network and the data support to researches on the Wenchuan earthquake[J]. Chinese Journal of Geophysics,52(5):1412–1417 (in Chinese).
Anderson P N,Duennebier F K,Cessaro R K. 1987. Ocean borehole horizontal seismic sensor orientation determined from explosive charges[J]. J Geophys Res:Solid Earth,92(B5):3573–3579. doi: 10.1029/JB092iB05p03573
Bahavar M,Spica Z J,Sánchez-Sesma F J,Trabant C,Zandieh A,Toro G. 2020. Horizontal-to-vertical spectral ratio (HVSR) IRIS station toolbox[J]. Seismol Res Lett,91(6):3539–3549. doi: 10.1785/0220200047
Baker G E,Stevens J L. 2004. Backazimuth estimation reliability using surface wave polarization[J]. Geophys Res Lett,31(9):L09611.
Berens P. 2009. CircStat:A MATLAB toolbox for circular statistics[J]. J Stat Softw,31(10):1–21.
Büyükakpınar P,Aktar M,Petersen G M,Köseoğlu A. 2021. Orientations of broadband stations of the KOERI seismic network (Turkey) from two independent methods:P- and Rayleigh-wave polarization[J]. Seismol Res Lett,92(3):1512–1521. doi: 10.1785/0220200362
Davis P M. 2003. Azimuthal variation in seismic anisotropy of the southern California uppermost mantle[J]. J Geophys Res: Solid Earth,108(B1):2052.
Doran A K,Laske G. 2017. Ocean-bottom seismometer instrument orientations via automated Rayleigh-wave arrival-angle measurements[J]. Bull Seismol Soc Am,107(2):691–708. doi: 10.1785/0120160165
Ekström G,Busby R W. 2008. Measurements of seismometer orientation at USArray transportable array and backbone stations[J]. Seismol Res Lett,79(4):554–561. doi: 10.1785/gssrl.79.4.554
Ensing J X,van Wijk K. 2019. Estimating the orientation of borehole seismometers from ambient seismic noise[J]. Bull Seismol Soc Am,109(1):424–432. doi: 10.1785/0120180118
Kennett B L N. 1991. IASPEI 1991 seismological tables[J]. Terra Nova,3(2):122. doi: 10.1111/j.1365-3121.1991.tb00863.x
Laske G. 1995. Global observation of off-great-circle propagation of long-period surface waves[J]. Geophys J Int,123(1):245–259. doi: 10.1111/j.1365-246X.1995.tb06673.x
Laske G,Masters G. 1996. Constraints on global phase velocity maps from long-period polarization data[J]. J Geophys Res: Solid Earth,101(B7):16059–16075. doi: 10.1029/96JB00526
Lay T,Wallace T C. 1995. Modern Global Seismology[M]. San Diego:Academic Press:7−8.
McNamara D E,Buland R P. 2004. Ambient noise levels in the continental United States[J]. Bull Seismol Soc Am,94(4):1517–1527. doi: 10.1785/012003001
Niu F L,Li J. 2011. Component azimuths of the CEArray stations estimated from P-wave particle motion[J]. Earthquake Science,24(1):3–13. doi: 10.1007/s11589-011-0764-8
Ojo A O,Zhao L,Wang X. 2019. Estimations of sensor misorientation for broadband seismic stations in and around Africa[J]. Seismol Res Lett,90(6):2188–2204. doi: 10.1785/0220190103
Ringler A T,Hutt C R,Persefield K,Gee L S. 2013. Seismic station installation orientation errors at ANSS and IRIS/USGS stations[J]. Seismol Res Lett,84(6):926–931. doi: 10.1785/0220130072
Rueda J,Mezcua J. 2015. Orientation analysis of the Spanish Broadband National Network using Rayleigh-wave polarization[J]. Seismol Res Lett,86(3):929–940. doi: 10.1785/0220140149
Scholz J R,Barruol G,Fontaine F R,Sigloch K,Crawford W C,Deen M. 2017. Orienting ocean-bottom seismometers from P-wave and Rayleigh wave polarizations[J]. Geophys J Int,208(3):1277–1289. doi: 10.1093/gji/ggw426
Schulte-Pelkum V,Masters G,Shearer P M. 2001. Upper mantle anisotropy from long-period P polarization[J]. J Geophys Res:Solid Earth,106(B10):21917–21934. doi: 10.1029/2001JB000346
Silver P G,Chan W W. 1991. Shear wave splitting and subcontinental mantle deformation[J]. J Geophys Res:Solid Earth,96(B10):16429–16454. doi: 10.1029/91JB00899
Son Y O,Seo M S,Kim Y H. 2022. Measurement of seismometer misorientation based on P-wave polarization:Application to permanent seismic network in South Korea[J]. Geosci J,26(2):235–247. doi: 10.1007/s12303-021-0031-5
Stachnik J C,Sheehan A F,Zietlow D W,Yang Z,Collins J,Ferris A. 2012. Determination of New Zealand ocean bottom seismometer orientation via Rayleigh-wave polarization[J]. Seismol Res Lett,83(4):704–713. doi: 10.1785/0220110128
Tanimoto T,Rivera L. 2005. Prograde Rayleigh wave particle motion[J]. Geophys J Int,162(2):399–405. doi: 10.1111/j.1365-246X.2005.02481.x
Wang X,Chen Q F,Li J,Wei S J. 2016. Seismic sensor misorientation measurement using P-wave particle motion:An application to the NECsaids array[J]. Seismol Res Lett,87(4):901–911. doi: 10.1785/0220160005
Wessel P,Luis J F,Uieda L,Scharroo R,Wobbe F,Smith W H F,Tian D. 2019. The Generic Mapping Tools Version 6[J]. Geochem Geophys Geosyst,20(11):5556–5564. doi: 10.1029/2019GC008515
Xu W W,Yuan S Y,Wang W T,Luo X H,Li L. 2020. Comparing orientation analysis methods for a shallow-water ocean-bottom seismometer array in the Bohai Sea,China[J]. Bull Seismol Soc Am,110(6):3174–3184. doi: 10.1785/0120200174
Zeng S J,Zheng Y,Niu F L,Ai S X. 2021. Measurements of seismometer orientation of the first phase ChinArray and their implications on vector-recording-based seismic studies[J]. Bull Seismol Soc Am,111(1):36–49. doi: 10.1785/0120200129
Zha Y,Webb S C, Menke W. 2013. Determining the orientations of ocean bottom seismometers using ambient noise correlation[J]. Geophys Res Lett,40(14):3585–3590. doi: 10.1002/grl.50698




 下载:
下载: