Thermal-gravity equilibrium adjustment mechanism of Zhenbei-Huangyan seamount chain
-
摘要: 珍贝—黄岩海山链作为我国南海的残留扩张中心, 对其研究具有重要的科学意义. 本文运用均衡学方法, 通过重力异常数据反演了过珍贝—黄岩海山链剖面的地壳界面变化, 同时计算了岩石圈热结构状态, 在此基础上建立了珍贝—黄岩海山链的岩石圈地温结构模型. 通过均衡分析方法, 对剖面上测点的海底地形数据进行了热均衡和重力均衡分析, 得到了热均衡和重力均衡形变量. 结果表明, 在珍贝—黄岩海山链高热流区域, 热均衡作用可以产生最大约0.55 km的形变, 其重力均衡形变范围为0.77—1.89 km. 热均衡通过改变海底地形和地壳物质密度不断作用于重力均衡, 重力又反过来作用于热均衡, 形成了热均衡-重力均衡动态调节机制.Abstract: During the processing of isostatic gravity anomaly analysis, it was pointed that the isostatic correction of the South China Sea was not completely, especially in Zhenbei-Huangyan seamount chain. No reasonable explanation for this phenomenon has been proposed until now, and seamounts compensation mechanism remains unresolved. It is feasible and necessary to conduct the dynamic equilibrium research in this region. We combine the thermal and gravimetric method to evaluate crustal density structure so as to establish the litho-spheric thermal structure of Zhenbei-Huangyan seamount chain based on the observed free-air gravity anomaly data. And then we analyze the thermal equilibrium and the gravity equilibrium effects based on the submarine topography data by adopting the standardized equilibrium technology. The results show that in the high heat flow region of Zhenbei-Huangyan seamount chain, the deformation induced by the thermal equilibrium is up to 0.55 km and the deformation due to the gravity is from 0.77 to 1.89 km. As a long-term adjustment factor, the thermal equilibrium constantly affects the gravity equilibrium by changing submarine topography and crustal material density, and gravity acts on geothermal equilibrium in turn at the same time, so the dynamic adjustment mechanism generates.
-
引言
珍贝—黄岩海山链是海底扩张后期岩浆活动的产物,被认为是残留扩张中心,对其进行均衡动态研究具有重要的科学意义. 利用重力和地形资料研究地壳均衡在我国起步较晚,最早为雷受旻(1984)等利用艾利(Ariy)模式计算了我国南海地区的均衡异常,此后冯锐等(1987)在我国东部等海区作了实验均衡改正. 均衡改正计算随着地壳均衡学的发展经历了局部补偿、 区域补偿、 实验均衡模式和动态均衡模式等4个阶段. 张训华(1996)对采用局部补偿模式(艾利模式)计算的南海均衡异常分析时发现,整个海区以正异常为主,珍贝—黄岩海山链出现了低均衡重力异常,将以正异常为主的南海海域分成南北两部分,似乎均衡改正不完全. 对于这种现象目前尚未能作出合理解释,南海的补偿机制仍没有解决.
本文以珍贝—黄岩海山链为例,结合地热与重力数据,提出了热-重力均衡动态补偿模式. 该模式原理为: 热地幔物质对上覆低密度地壳加热,基于热胀冷缩原理,上覆低密度地壳岩石圈产生形变. 由于受到水平方向上岩石圈的挤压作用,所产生的水平方向的膨胀作用不明显,主要表现在垂直方向上. 受热膨胀作用的影响,地壳物质向上运移,产生海底地形高程和物质密度变化. 热均衡作用通过改变地壳物质密度和海底地形高程间接作用于重力均衡. 当南海中存在地幔对流或地幔热柱时,热动力充足,地壳物质在垂直方向上运移频率和幅度变大,重力均衡状态被打破,进而产生火山喷发、 海啸、 海底地震等现象. 当地幔对流或地幔热柱位置发生迁移之后,地幔热动力不足,地壳物质冷却产生热沉降,此时重力均衡成为均衡主导作用,地壳物质向下运移,逐渐达到重力均衡状态. 为了探讨热均衡和重力均衡产生的影响,本文分别计算热均衡形变量以及无热均衡作用影响下的重力均衡形变量,并将二者进行对比,进而得到动态热均衡和重力均衡对地壳物质垂直方向上位移的影响程度.
1. 地质背景和重力异常场特征
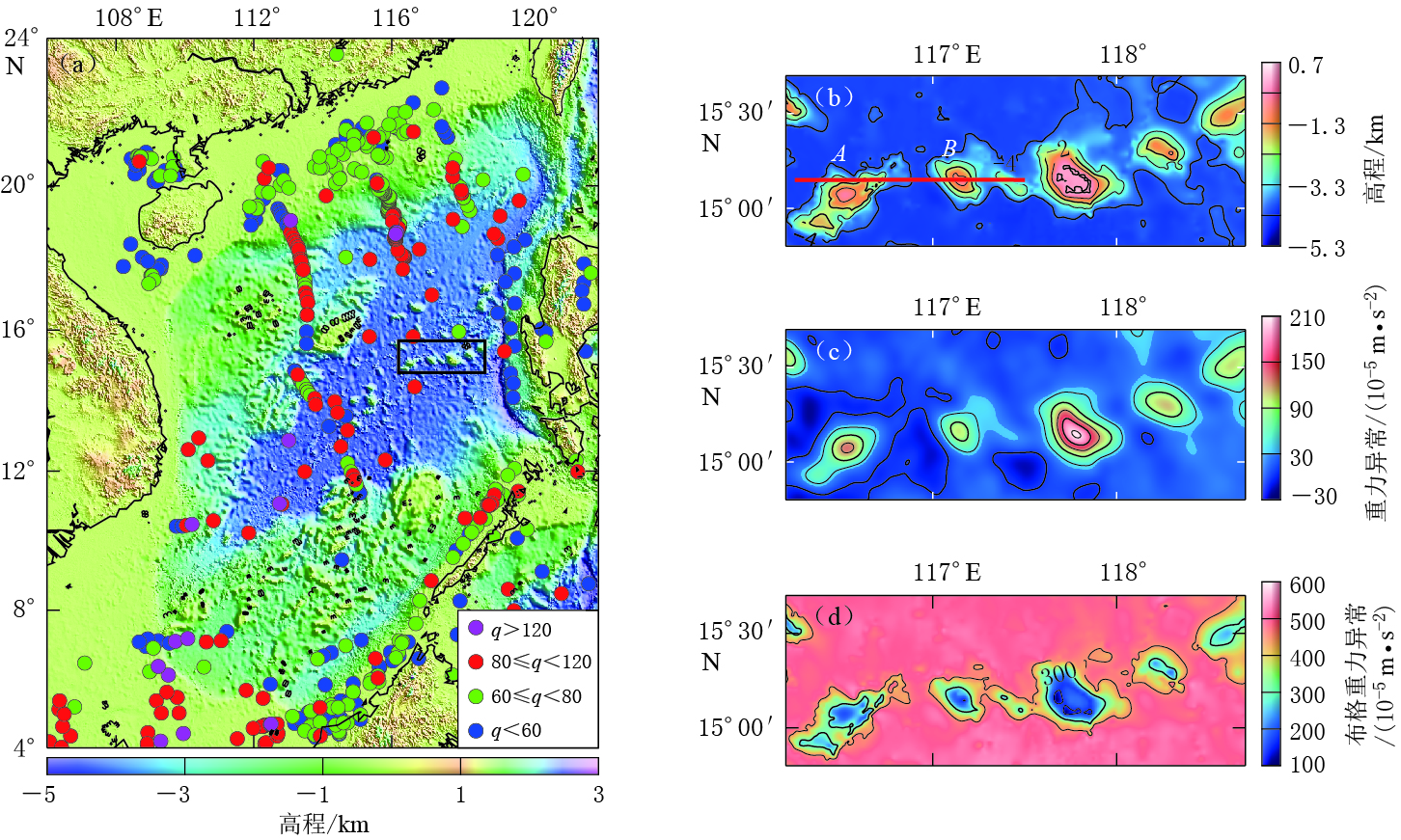
南海是新生代形成的洋盆(姚伯初,1996),位于欧亚、 印度、 太平洋三大板块交汇处,大陆与海洋、 地壳与地幔的物质交换尤其活跃(张健等,2001; 闫贫,刘海龄,2005),是研究被动大陆边缘及边缘海演化的理想场所(杨金玉等,2001). 南海在形成演化过程中发生海底扩张(周蒂等,2005),扩张中心岩浆大规模产出. 扩张期后,扩张中心冷却,经过强烈的热沉降作用,形成了海山(闫贫,刘海龄,2005). 珍贝—黄岩海山链被认为是南海中央海盆的残留扩张中心,是南海扩张期后晚中新世火山活动的产物(王叶剑等,2009). 图 1a给出了南海海底地形及热流分布. 可以看出南海北部热流值较低,大致为60—80 mW/m2,部分地区热流值小于60 mW/m2. 南海海盆为热盆,盆内热流值大致为80—120 mW/m2,部分地区热流值大于120 mW/m2(张健,石耀霖,2004). 由于珍贝—黄岩海山链处热流测点少,据周围地区观测值及热模拟推算,该处热流值大致为120—160 mW/m2,其中160 mW/m2为海山处没有完全冷却时的值(张健,汪集旸,2000).
根据水深及海底地貌地形特征,南海海盆可以划分为西北海盆、 中央海盆和西南海盆等3个次海盆(Taylor,Hayes, 1980,1983). 其中,中央海盆南北长约900 km、 东西宽约450 km,呈扁菱形状. 其海底由南向北依次分布着珍贝—黄岩海山链、 涨中海山、 宪南海山、 宪北海山、 玳瑁海山. 沿15°N分布的珍贝—黄岩海山链由黄岩海山、 珍贝海山等组成,其东西长约250 km,南北宽约40—60 km,分布在14°49′N—15°42′N、 116°12′E—118°42′E 海域(图 1b),是该区规模最大的长条状东西向链状海山(林巍等,2013). 如图 1c所示,珍贝—黄岩海山链重力异常呈东西向长条串珠状展布. 组成海山链的每个海山表现为孤立的重力高值异常圈闭,分别对应(90—210)×10-5 m/s2 的重力高值异常区. 布格重力异常(图 1d)显示,珍贝—黄岩海山链对应着孤立的重力低值异常圈闭,海底平原布格重力异常均在400×10-5 m/s2以上,海山分别对应着(100—300)×10-5 m/s2的重力低值异常区.
![]() 图 1 研究区地质与地球物理特征图(a) 南海海底地形及热流q (单位: mW/m2)测点图, 黑色框为本文研究区域; (b) 珍贝—黄岩海 山链海底地形图, 图中AB为过珍贝—黄岩海山链的地震剖面; (c) 珍贝—黄岩海山链 自由空间重力异常图; (d) 珍贝—黄岩海山链布格重力异常图Figure 1. Geological and geophysical characteristics of the research areas(a) Bathymetric chart and heat-flow q (in unit of mW/m2) observation point distribution, the black rectangle gives the studied area in this study; (b) Topography of the Zhenbei-Huangyan seamount chain, where AB is a seismic profile across Zhenbei-Huangyan seamount chain; (c) The free air gravity anomaly of the Zhenbei-Huangyan seamount chain; (d) The Bouguer gravity anomaly of the Zhenbei-Huangyan seamount chain
图 1 研究区地质与地球物理特征图(a) 南海海底地形及热流q (单位: mW/m2)测点图, 黑色框为本文研究区域; (b) 珍贝—黄岩海 山链海底地形图, 图中AB为过珍贝—黄岩海山链的地震剖面; (c) 珍贝—黄岩海山链 自由空间重力异常图; (d) 珍贝—黄岩海山链布格重力异常图Figure 1. Geological and geophysical characteristics of the research areas(a) Bathymetric chart and heat-flow q (in unit of mW/m2) observation point distribution, the black rectangle gives the studied area in this study; (b) Topography of the Zhenbei-Huangyan seamount chain, where AB is a seismic profile across Zhenbei-Huangyan seamount chain; (c) The free air gravity anomaly of the Zhenbei-Huangyan seamount chain; (d) The Bouguer gravity anomaly of the Zhenbei-Huangyan seamount chain2. 均衡计算方法
2.1 热均衡形变量
岩石圈热状态和结构存在差异性. 南海扩张时期,由于岩石圈拉张减薄产生热物质上涌; 扩张期后,基于热胀冷缩原理,岩石圈经过强烈的热沉降作用,冷却收缩,地表下沉(何丽娟,2002; 陈石等,2011),从而产生热均衡调整. 在不考虑岩石圈厚度不准确、 南海海盆地表热流测量误差(张健,汪集旸,2000)以及地壳横向密度分布不均匀等影响因素(S and well,Smith,1997; Smith,S and well, 1997)的情况下,按照海洋地区热均衡研究理论(Hasterok,Chapman, 2007a,b),岩石圈分层地热模型热均衡表示为

式中,Ai为第i层生热率,ki为第i层热导率,Δzi为第i层厚度,qi-1为第i层顶部热流,Ti-1为第i层顶部的温度.
本文的计算模型中设定地表至上地幔岩石圈的热过程中热传导占主导机制,而在地幔中热对流占主导作用,因此,岩石圈底部的热状态用等熵关系式来表达:

式中: z为计算深度; Ta为岩石圈温度,取1 573 K; 地幔绝热梯度约为0.3 K/km(Turcotte,Schubert,2002).
实验结果表明,岩石热导率随温度和压力变化(Hofmeister,1999).通常在等压条件下,岩石热导率随温度升高而减小.本文按照McKenzie等(2005)的研究结果给出了温度、 压力的变化与岩石圈热导率k的经验公式为

式中,kh为岩石圈随温度变化的热导率,b=5.3,c=1.5×10-3,d0=1.753×10-2,d1=-1.036 5 ×10-4,d2= 2.245 1×10-7,d3=-3.407 1×10-4(Hofmeister,1999). 温度变化产生的热均衡形变量ΔεT的表达式为

式中: α为岩石热膨胀系数,α=3.0×10-5 K-1; T(z)为计算区域的地温结构,Tref(z)为标准化参考地温结构; zmax为岩石圈厚度. 由于全球岩石圈厚度为60—120 km,而本文研究区域位于南海海盆内部,属于岩石圈最薄弱的地区,故zmax取60 km.
2.2 重力均衡形变量
重力均衡理论认为,由于地形负载和其横向密度分布存在差异性,均衡面以上的地壳物质会在重力作用下产生均衡调整. 由于研究区域位于海域,需要考虑海水压力影响,海洋地区重力均衡形变量Δεw(图 2)根据重力均衡理论可建立如下关系:

式中: ρ ′ c为标准参考区的地壳平均密度,取2.78 g/cm3;h′c为标准参考区的地壳平均厚度,取30 km; ρc为计算区的地壳平均密度;hc为计算区的地壳平均 厚度;ρm为均衡面以上的地幔物质密度,取3.3 g/cm3; hm为均衡面以上的地幔物质厚度; ρw为海水密度,取1.03 g/cm3; ε为海底地形高程. 地幔物质厚度hm与重力均衡形变量Δεw之间的关系为

结合式(5)、(6)化简得到重力均衡形变量Δεw为

式中,地壳平均密度ρc和地壳平均厚度hc可根据地震数据由地震纵波速度与岩石密度之间的非线性经验公式 加德纳公式计算求得,即

![]() 图 2 海洋地壳组分均衡调整模式示意图(引自McKenzie等, 2005)图中LOC为补偿深度, MSL为平均海平面Figure 2. Schematic diagram of parameters used in gravitational correction of the ocean area (after McKenzie et al, 2005)LOC is the compensation depth, MSL is the mean sea level
图 2 海洋地壳组分均衡调整模式示意图(引自McKenzie等, 2005)图中LOC为补偿深度, MSL为平均海平面Figure 2. Schematic diagram of parameters used in gravitational correction of the ocean area (after McKenzie et al, 2005)LOC is the compensation depth, MSL is the mean sea level由于中央海盆位于南海海盆中部,海底地形低,上部承载水压大,岩石充水饱和性好,因而用加德纳公式计算的地壳密度误差相对较低. 在后面的计算中,测点的地壳平均密度差为0.1 g/cm3时,重力均衡差为100 m,在允许的误差范围之内.
3. 数据及计算结果分析
本文海底地形及自由空间重力异常数据引自美国加州大学圣迭戈分校斯克里普斯海洋研究所(http://topex.ucsd.edu/),数据精度均为1′×1′. 海底地形模型基于V17. 1,重力模型基于V22. 1. 地震数据引自2011年5—6月,在“南海深海过程演变”项目支持下,中国科学院南海海洋研究所、 国家海洋局第二海洋研究所、 广东省地震局、 广州海洋地质调查局等单位合作的三维海底地震仪探测实验结果(丘学林等,2012; 王建等,2014).
3.1 热均衡计算结果
依据第2节的方法原理,在给定地表热流值的情况下,根据式(1)—(3)计算了珍贝—黄岩海山链的理论岩石圈温度与热流曲线,岩石圈厚度取60 km. 整个细化的模型分为4层,具体参数见表 1. 图 3a给出了地表热流值为80—160 mW/m2的9条曲线,计算间隔为10 mW/m2. 等熵关系依据式(2)计算. 另外,根据式(4)计算了由于温度变化产生的理论热均衡形变量ΔεT. 南海海盆属于热盆,热流值较高,其内部绝大多数热流观测值均大于80 mW/m2. 海盆周边存在多期火山活动的区域实测热流值,高达340 mW/m2(Wu et al,1999). 研究表明,中央海盆在15 Ma停止扩张,岩浆物质逐渐冷却,产生热沉降,作为南海残留扩张中心的珍贝—黄岩海山链处热流值随之降低. 在不确定地表热流值的情况下,以深海平原的平均热流值80 mW/m2为均衡参考量(Wu et al,1999),将地表热流值为80—160 mW/m2所产生的热均衡形变量绘制成曲线,如图 3b所示. 当珍贝—黄岩海山链处热流值高达160 mW/m2时,由于热膨胀效应产生的地形形变量为 0.55 km. 若以全球平均热流值60 mW/m2为均衡参考量时,由于热膨胀效应产生的地形形变量则会更大.
表 1 热均衡模型的材料参数(引自张健和石耀霖, 2004)Table 1. Material parameters of the thermal equilibrium model (after Zhang and Shi, 2004)分层 生热率A/(μW·m-3) 比热容c/(J·(kg·℃)-1) 热导率k/(W·(m·℃)-1) 大洋沉积层 1.280 900 0.85 洋壳层2 1.300 900 2.93 洋壳层3 0.400 900 2.30 岩石圈上地幔 0.024 1000 3.30 ![]() 图 3 热均衡计算结果(a) 给定地表热流值情况下岩石圈热结构图; (b) 热均衡产生的垂直形变量ΔεT随地表热流值q变化图Figure 3. The computing result of the thermal equilibrium(a) Theory thermal structure of the lithosphere on the condition that a surface heat flow value is given; (b) Variation of vertical deformation ΔεT caused by thermal equilibrium with surface heat flow q
图 3 热均衡计算结果(a) 给定地表热流值情况下岩石圈热结构图; (b) 热均衡产生的垂直形变量ΔεT随地表热流值q变化图Figure 3. The computing result of the thermal equilibrium(a) Theory thermal structure of the lithosphere on the condition that a surface heat flow value is given; (b) Variation of vertical deformation ΔεT caused by thermal equilibrium with surface heat flow q3.2 重力均衡计算结果
为了获得相对准确的测点平均地壳厚度与地壳密度,本文首先采用Parker界面反演法,用布格重力异常反演出南海的莫霍面深度(郝天珧等,2008),并与地震数据计算得到的莫霍面深度进行对比得到测线上的莫霍面深度(图 4中最下面黑粗线),发现珍贝—黄岩海山链处的莫霍面深度为12—14 km,而其周边海盆地壳厚度仅为8—10 km.
![]() Figure 4. D seismic section across Zhenbei-Huangyan seamount chain modified from Qiu et al (2012) and Wang et al (2014)
Figure 4. D seismic section across Zhenbei-Huangyan seamount chain modified from Qiu et al (2012) and Wang et al (2014)图 4给出了过珍贝—黄岩海山链的三维地震速度剖面. 图中共有13个地震测点,由于测线边缘地区接收信息较少,其结果精度较低,因而在计算时去掉1,12,13号测点,保留2—11号测点. 用地震速度与岩石密度的经验公式(加德纳公式),将测点的地震速度数据换算成密度. 表 2给出了计算重力均衡所需要的模型参数.
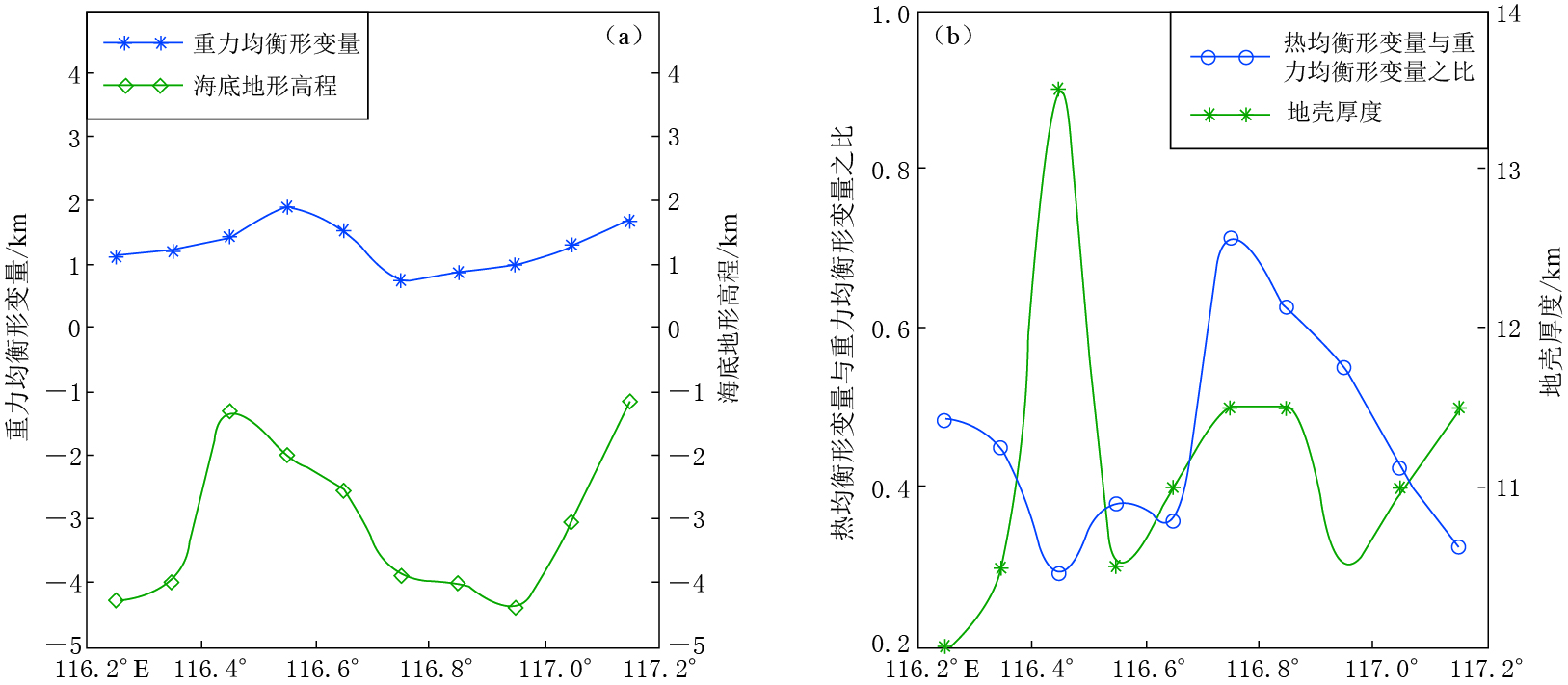
表 2 过珍贝—黄岩海山链的地震剖面上各观测点参数Table 2. Model parameters of the observation points on the seicmic section across Zhenbei Huangyan seamount chain测点 海底地形高程/km 地壳厚度/km 平均地壳密度/(g·cm-3) 2 -4.28 10 2.731 3 -4.01 10.5 2.754 4 -1.31 13.5 2.703 5 -2.00 10.5 2.766 6 -2.55 11 2.734 7 -3.88 11.5 2.718 8 -4.01 11.5 2.697 9 -4.39 10.5 2.723 10 -3.06 11 2.710 11 -1.15 11.5 2.676 对于海洋重力均衡的计算,标准参数的选取对结果影响比较大.为了确保结果的准确性和真实性,本文调研了南海海盆及其周边区域大量的地震剖面,以及由地震剖面反演出的密度剖面. 根据调研的地震剖面选取标准参考地壳厚度为30 km,大于海盆内部的地壳厚度,小于陆壳厚度;参考平均地壳密度为2.78 g/cm3(Chen et al,2009). 基于标准化参量,利用艾利模型计算了重力均衡量,结果如图 5所示. 图 5a为重力均衡形变量与海底地形对照图.可以看出,海底地形高程与重力均衡形变量具有一定的相关性,地形相对较高的,其均衡修正值也相对较大.珍贝、黄岩两座海山处均衡修正量最大,可达1.6—1.89 km; 两座海山之间的位置均衡修正量最小,仅为0.77 km.
![]() 图 5 重力均衡计算结果(a) 重力均衡形变量与海底地形高程对比图; (b) 热均衡形变量与重力均衡形变量之比与地壳厚度对比图Figure 5. The computing result of the gravity equlibrium(a) Comparison between vertical deformation caused by gravity equlibrium (blue line) and the seabed terrain elevation (green line); (b) Comparison between the ratio of thermal equlibrium to gravity equlibrium (blue line) and crustal thickness (green line)
图 5 重力均衡计算结果(a) 重力均衡形变量与海底地形高程对比图; (b) 热均衡形变量与重力均衡形变量之比与地壳厚度对比图Figure 5. The computing result of the gravity equlibrium(a) Comparison between vertical deformation caused by gravity equlibrium (blue line) and the seabed terrain elevation (green line); (b) Comparison between the ratio of thermal equlibrium to gravity equlibrium (blue line) and crustal thickness (green line)由于珍贝—黄岩海山链是南海残留扩张中心,扩张期岩浆热液活动比较频繁,对于没有热流测点的情况,按照3.1节所述,本文赋予整条测线地表热流值为160 mW/m2,该值对应的热均衡量为0.55 km. 利用热均衡与重力均衡的比值作为衡量热均衡与重力均衡对于物质垂向变形的影响结果,如图 5b所示. 可以看出,测线上各测点的比值均小于1,热均衡量相对于重力均衡的作用要小一些. 而在珍贝、 黄岩两座海山处,地壳厚度最厚,热均衡与重力均衡的比值达到最小,仅为0.3; 海山之间的部分,地壳厚度相对较薄,热均衡与重力均衡的比值大于0.7,基本上达到对等的水平. 除黄岩海山处的测点之外,从曲线总体趋势上看,热均衡形变量与重力均衡形变量之比与地壳厚度呈负相关关系,说明热均衡对地壳薄的地区影响更大. 但黄岩海山处没有表现出明显的负相关关系,究其原因,可能与地震测点的疏密程度及莫霍面的反演精度有关.
通过热均衡与重力均衡对比分析,发现热均衡作为主动均衡因素,重力均衡作为被动均衡因素,虽然热均衡量对于重力均衡量相对小一些,但作为同一个数量级的均衡调节因素,热均衡作用不容忽视.
4. 讨论与结论
由于在南海的形成演化过程中发生海底扩张,其扩张中心岩浆大规模产出,周围岩石圈受热膨胀; 扩张期后,扩张中心冷却,经过强烈的热沉降作用,岩石圈收缩,地表下降. 基于热胀冷缩原理,岩石圈受热产生的地形形变,与由于受自身重力作用产生的地形形变作为持续的动态调整关系,促使地表向更均衡的方向发展. 本文通过热均衡与重力均衡的计算发现:
1)珍贝—黄岩海山链由于热均衡作用最大可产生约0.55 km的形变,并且在地壳越薄弱、 构造活动越活跃、 地表热流值越高的地区,热均衡产生的效果越明显. 与热均衡形变量相比,重力均衡量值相对较大,最大可产生1.89 km的形变. 珍贝、 黄岩两座海山之间的重力均衡修正量只有0.77 km,与海底地形存在较好的对应关系.
2)由于海盆中地壳厚度薄、 密度大、 热流值高,其重力均衡改正量相对较小,热均衡改正量相对较大. 而陆壳内地壳厚度厚,密度相对更小,重力均衡改正量大,热均衡改正量相对较小,因而产生了陆地均衡改正相对完全而海洋均衡改正相对不完全的现象,热均衡对海洋重力均衡的影响比对陆地大.
3)采用重力学与地热学交叉融合的方法,克服了单一方法在地球物理学应用中的多解性和局限性. 在前人提出的问题上进一步研究,找出了南海重力均衡改正不完全的原因,推动了地壳均衡模式中动态均衡补偿模式的发展.
4)提出了热-重力均衡动态补偿模式. 基于热胀冷缩原理,岩石圈受热膨胀产生向上的地形形变,重力作用则基于万有引力,产生向下的形变调整,热均衡通过改变海底地形和物质密度不断作用于重力均衡,重力均衡又反过来作用于热均衡,从而形成了热-重力均衡动态调节机制.
由于南海深海盆地区地球物理资料较少,珍贝—黄岩海山链处没有实测热流值,文中所用的热流值根据南海整体热流值分布和南海构造活动推算而得,因而对于本文数据的准确性只能等将来获得实测数据后进行验证; 另外,由于受仪器设备和测量成本的限制,该地区地震测线的长度较短,测点的密集程度相对较低,获得比较精细的地层速度-密度结构十分必要. 在未来的工作中,作者将对考虑热因素的重力均衡进行计算,以获取更为精确的重力均衡补偿结果来充实南海地区的地球物理资料. 此外,还希望能获得更多的实测数据来进行计算验证,不断修正计算结果,以完善均衡理论.
-
图 1 研究区地质与地球物理特征图
(a) 南海海底地形及热流q (单位: mW/m2)测点图, 黑色框为本文研究区域; (b) 珍贝—黄岩海 山链海底地形图, 图中AB为过珍贝—黄岩海山链的地震剖面; (c) 珍贝—黄岩海山链 自由空间重力异常图; (d) 珍贝—黄岩海山链布格重力异常图
Figure 1. Geological and geophysical characteristics of the research areas
(a) Bathymetric chart and heat-flow q (in unit of mW/m2) observation point distribution, the black rectangle gives the studied area in this study; (b) Topography of the Zhenbei-Huangyan seamount chain, where AB is a seismic profile across Zhenbei-Huangyan seamount chain; (c) The free air gravity anomaly of the Zhenbei-Huangyan seamount chain; (d) The Bouguer gravity anomaly of the Zhenbei-Huangyan seamount chain
图 2 海洋地壳组分均衡调整模式示意图(引自McKenzie等, 2005)
图中LOC为补偿深度, MSL为平均海平面
Figure 2. Schematic diagram of parameters used in gravitational correction of the ocean area (after McKenzie et al, 2005)
LOC is the compensation depth, MSL is the mean sea level
图 3 热均衡计算结果
(a) 给定地表热流值情况下岩石圈热结构图; (b) 热均衡产生的垂直形变量ΔεT随地表热流值q变化图
Figure 3. The computing result of the thermal equilibrium
(a) Theory thermal structure of the lithosphere on the condition that a surface heat flow value is given; (b) Variation of vertical deformation ΔεT caused by thermal equilibrium with surface heat flow q
图 4 过珍贝—黄岩海山链的三维地震速度剖面[根据丘学林等(2012)和王建等(2014)修改]
Figure 4. D seismic section across Zhenbei-Huangyan seamount chain modified from Qiu et al (2012) and Wang et al (2014)
图 5 重力均衡计算结果
(a) 重力均衡形变量与海底地形高程对比图; (b) 热均衡形变量与重力均衡形变量之比与地壳厚度对比图
Figure 5. The computing result of the gravity equlibrium
(a) Comparison between vertical deformation caused by gravity equlibrium (blue line) and the seabed terrain elevation (green line); (b) Comparison between the ratio of thermal equlibrium to gravity equlibrium (blue line) and crustal thickness (green line)
表 1 热均衡模型的材料参数(引自张健和石耀霖, 2004)
Table 1 Material parameters of the thermal equilibrium model (after Zhang and Shi, 2004)
分层 生热率A/(μW·m-3) 比热容c/(J·(kg·℃)-1) 热导率k/(W·(m·℃)-1) 大洋沉积层 1.280 900 0.85 洋壳层2 1.300 900 2.93 洋壳层3 0.400 900 2.30 岩石圈上地幔 0.024 1000 3.30 表 2 过珍贝—黄岩海山链的地震剖面上各观测点参数
Table 2 Model parameters of the observation points on the seicmic section across Zhenbei Huangyan seamount chain
测点 海底地形高程/km 地壳厚度/km 平均地壳密度/(g·cm-3) 2 -4.28 10 2.731 3 -4.01 10.5 2.754 4 -1.31 13.5 2.703 5 -2.00 10.5 2.766 6 -2.55 11 2.734 7 -3.88 11.5 2.718 8 -4.01 11.5 2.697 9 -4.39 10.5 2.723 10 -3.06 11 2.710 11 -1.15 11.5 2.676 -
张训华. 1996. 地壳均衡与均衡重力异常[J]. 海洋地质动态, (8): 1-4. Zhang X H. 1996. The isostasy and isostatic gravity anomaly[J]. Marine Geology Letters, (8): 1-4 (in Chinese).
Taylor B, Hayes D E. 1980. The tectonic evolution of the South China Sea basin[G]//The Tectonic and Geologic Evolution of Southeast Asian Seas and Islands. New York: American Geophysical Union: 89-104.
Taylor B, Hayes D E. 1983. Origin and history of the South China Sea basin[G]//The Tectonic and Geologic Evolution of Southeast Asian Seas and Islands. New York: American Geophysical Union: 23-56.
Turcotte D L, Schubert G. 2002. Geodynamics[M]. 2nd ed. Cambridge: Cambridge University Press: 1-456.
-
期刊类型引用(1)
1. 冯旭亮, 王鹏飞, 宋立军, 袁炳强. 深水区盆地基底重力异常提取——以南薇西盆地为例. 地球物理学进展. 2019(04): 1600-1608 .  百度学术
百度学术
其他类型引用(1)




 下载:
下载: