First arrival time picking algorithm of micro-seismic based on improved STA/LTA and adaptive VMD
-
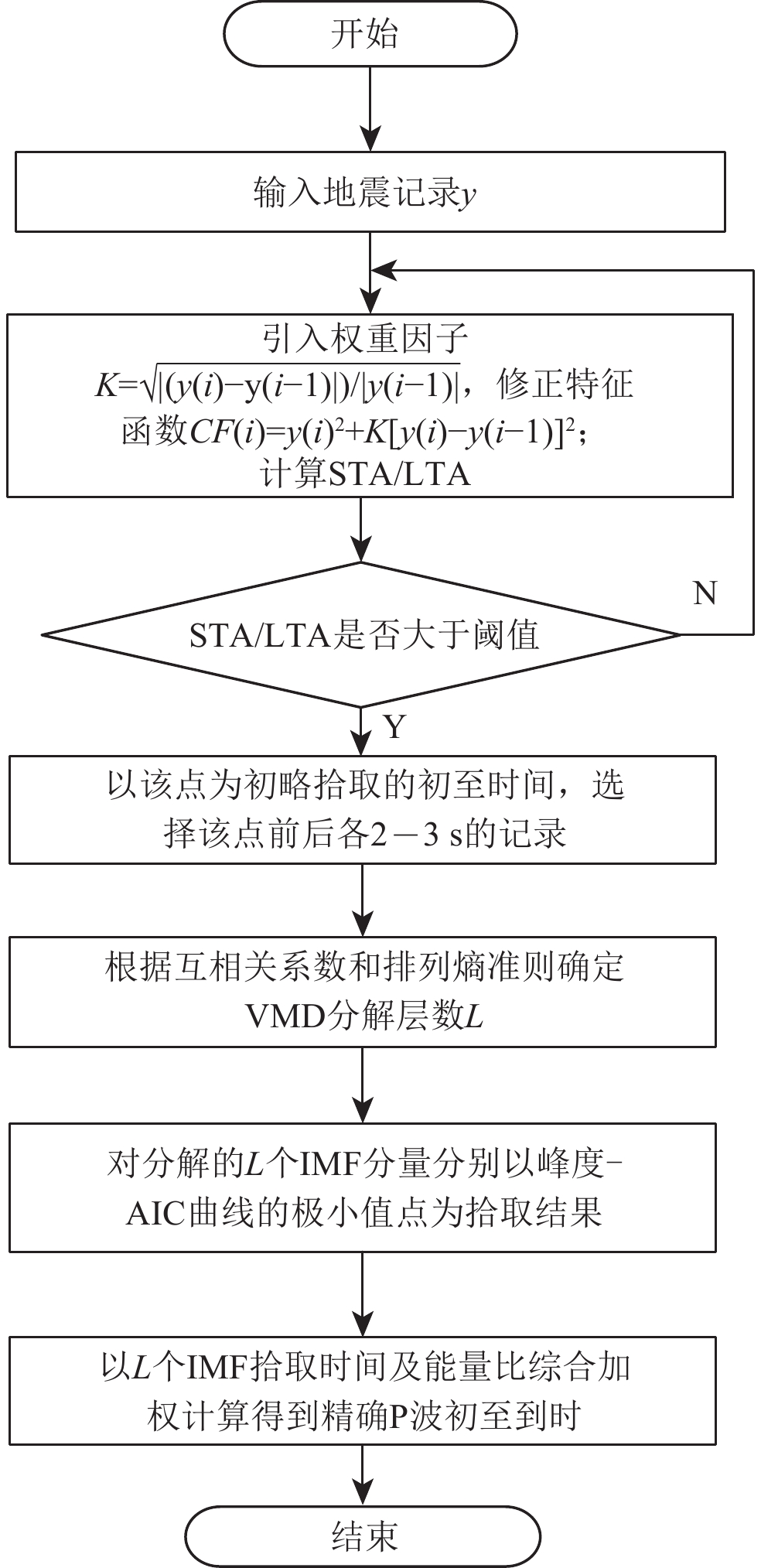
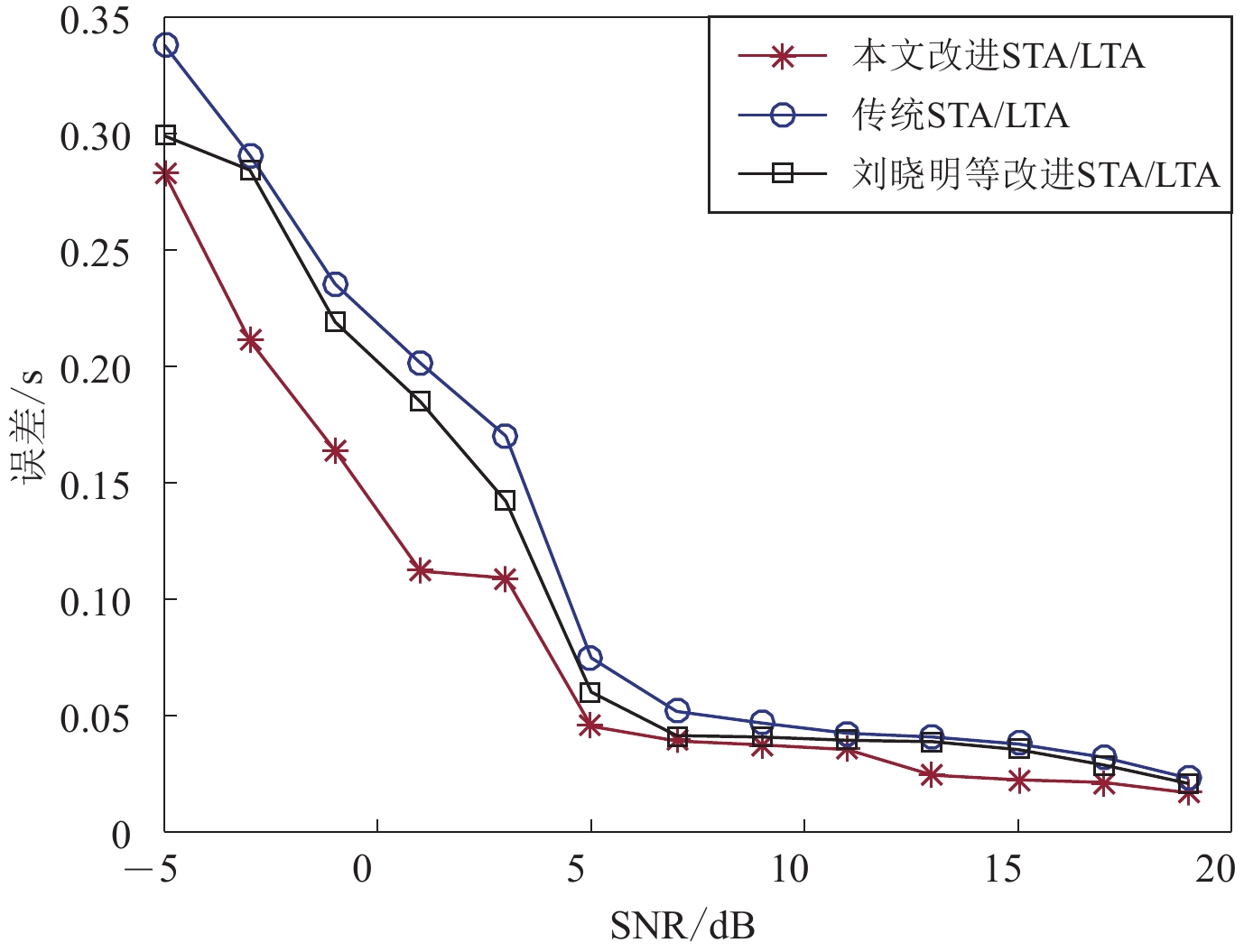
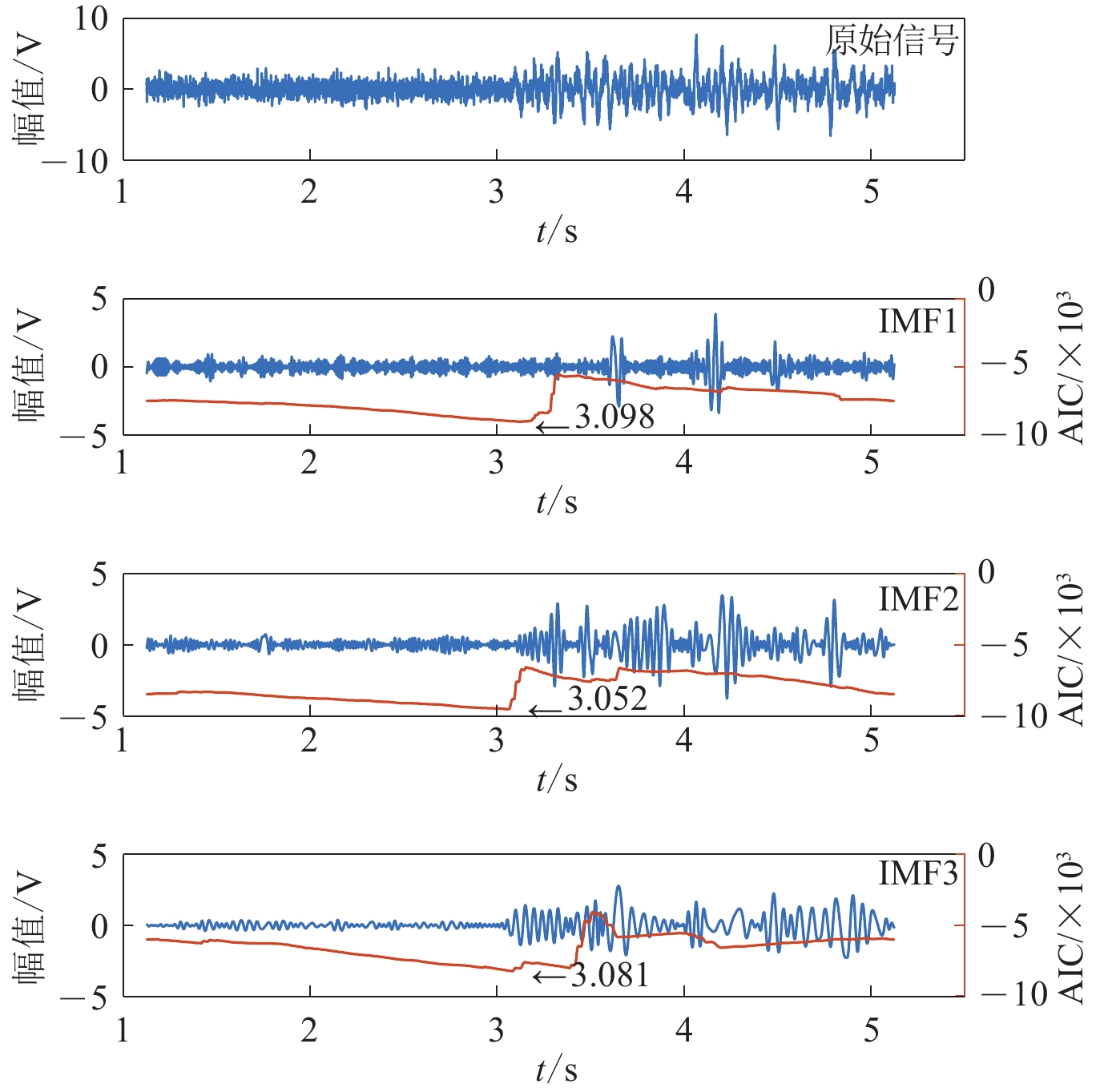
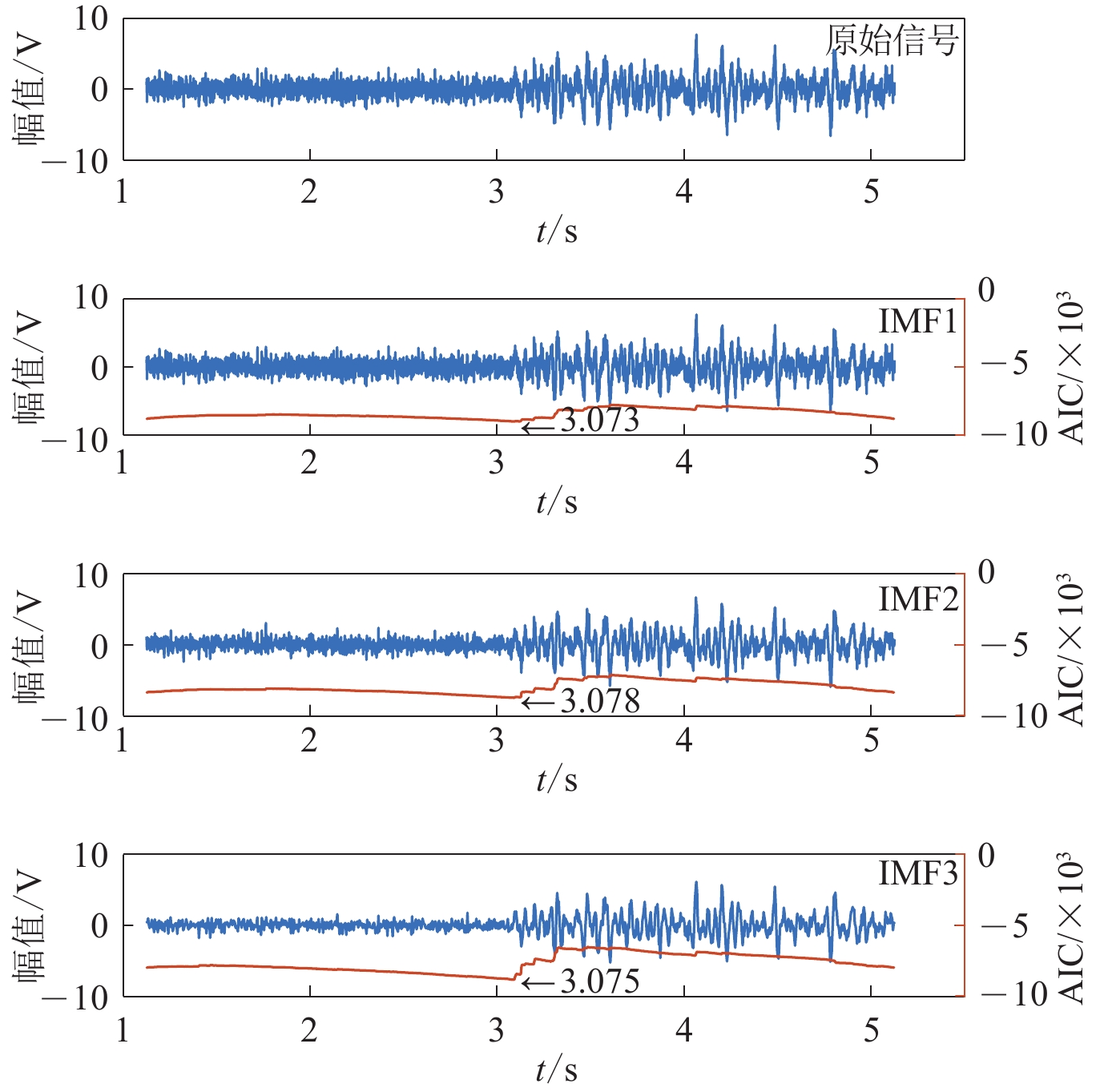
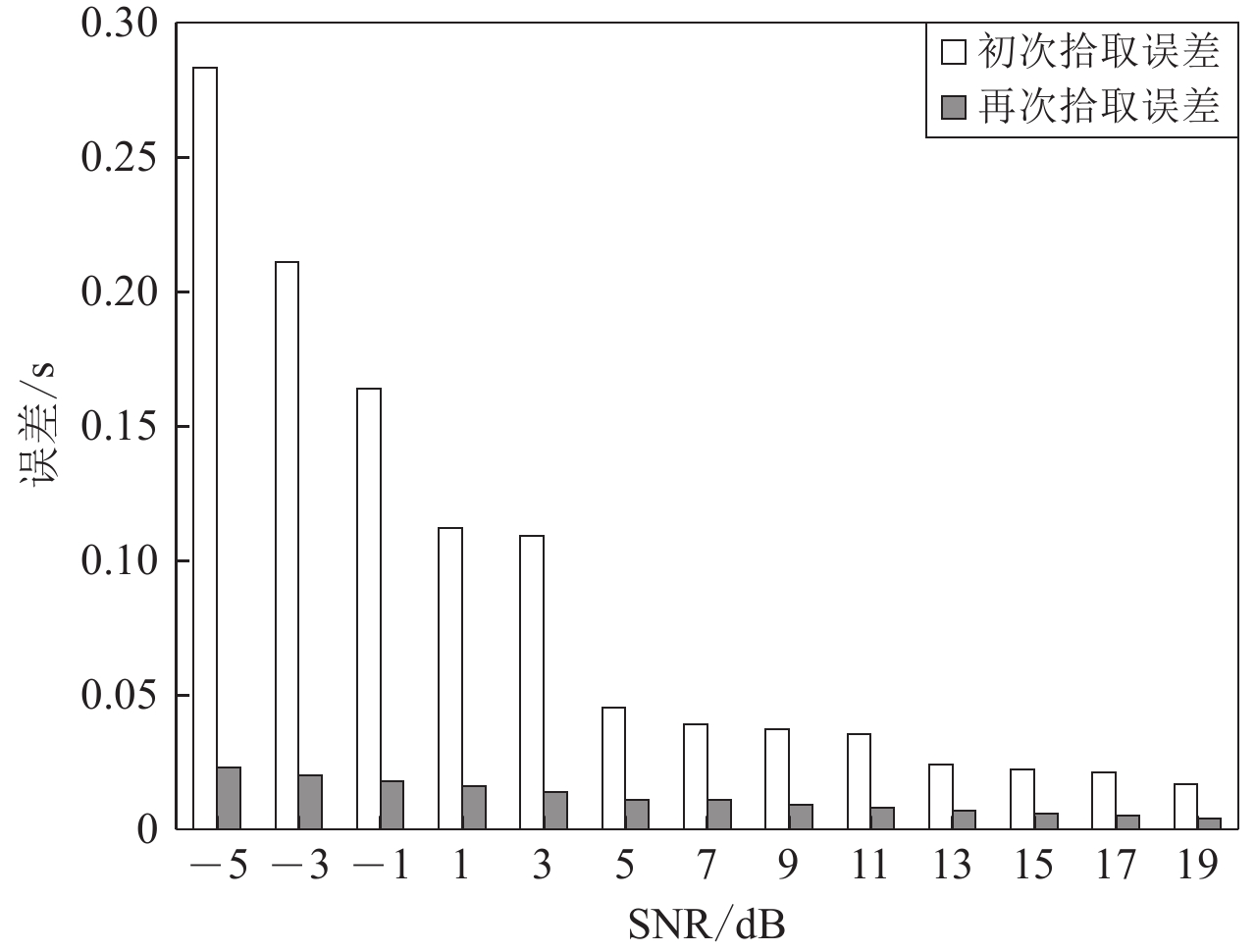
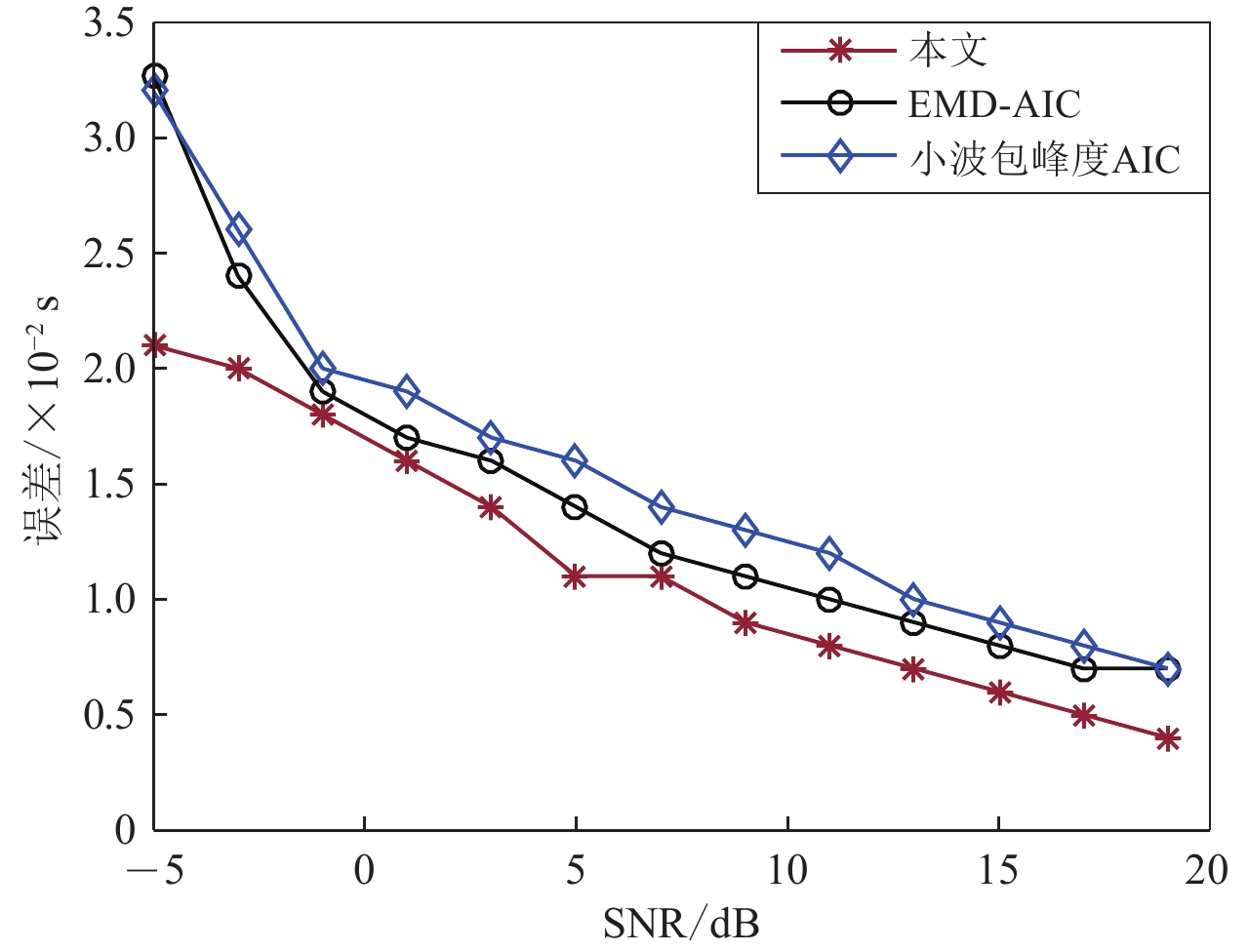
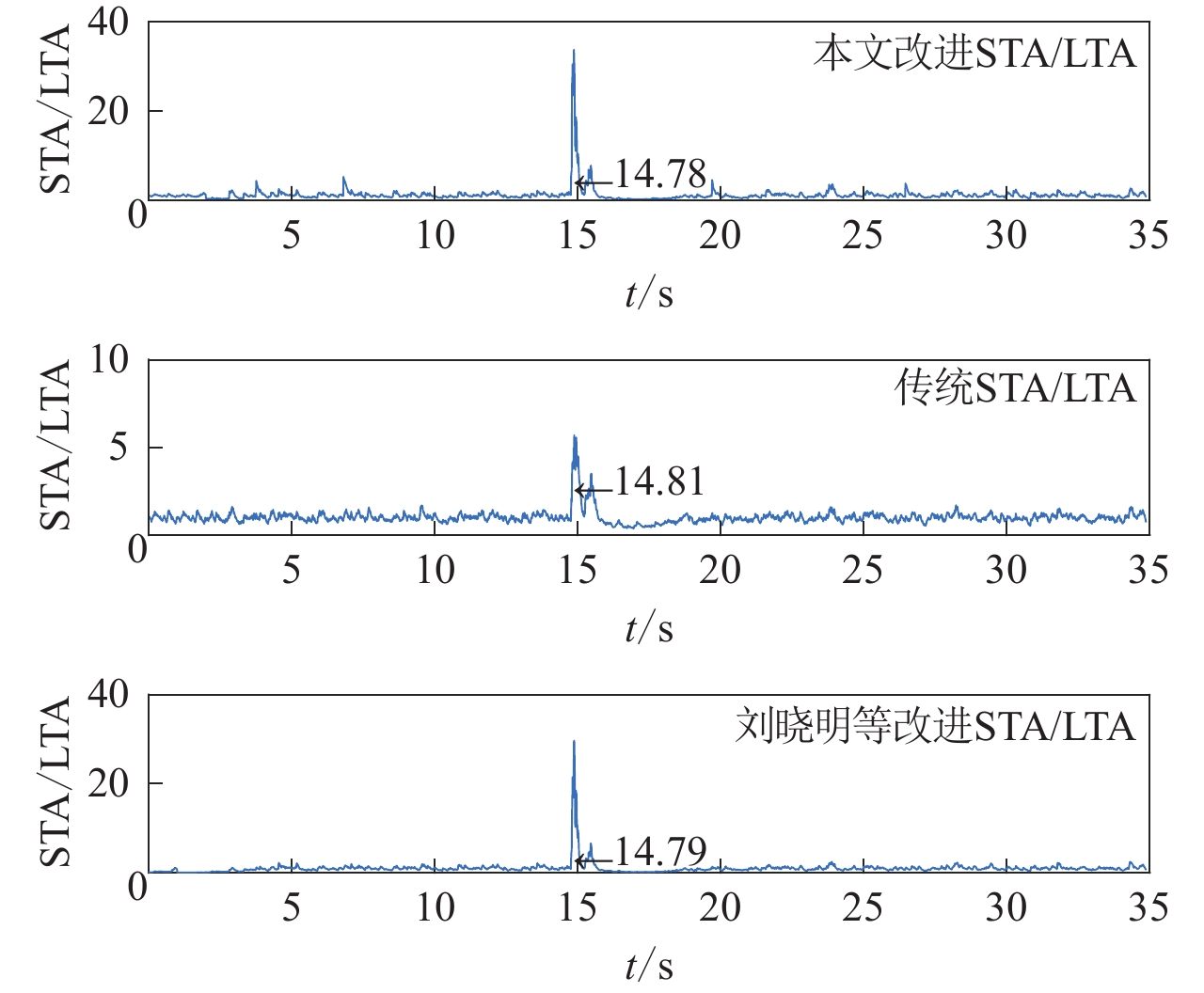
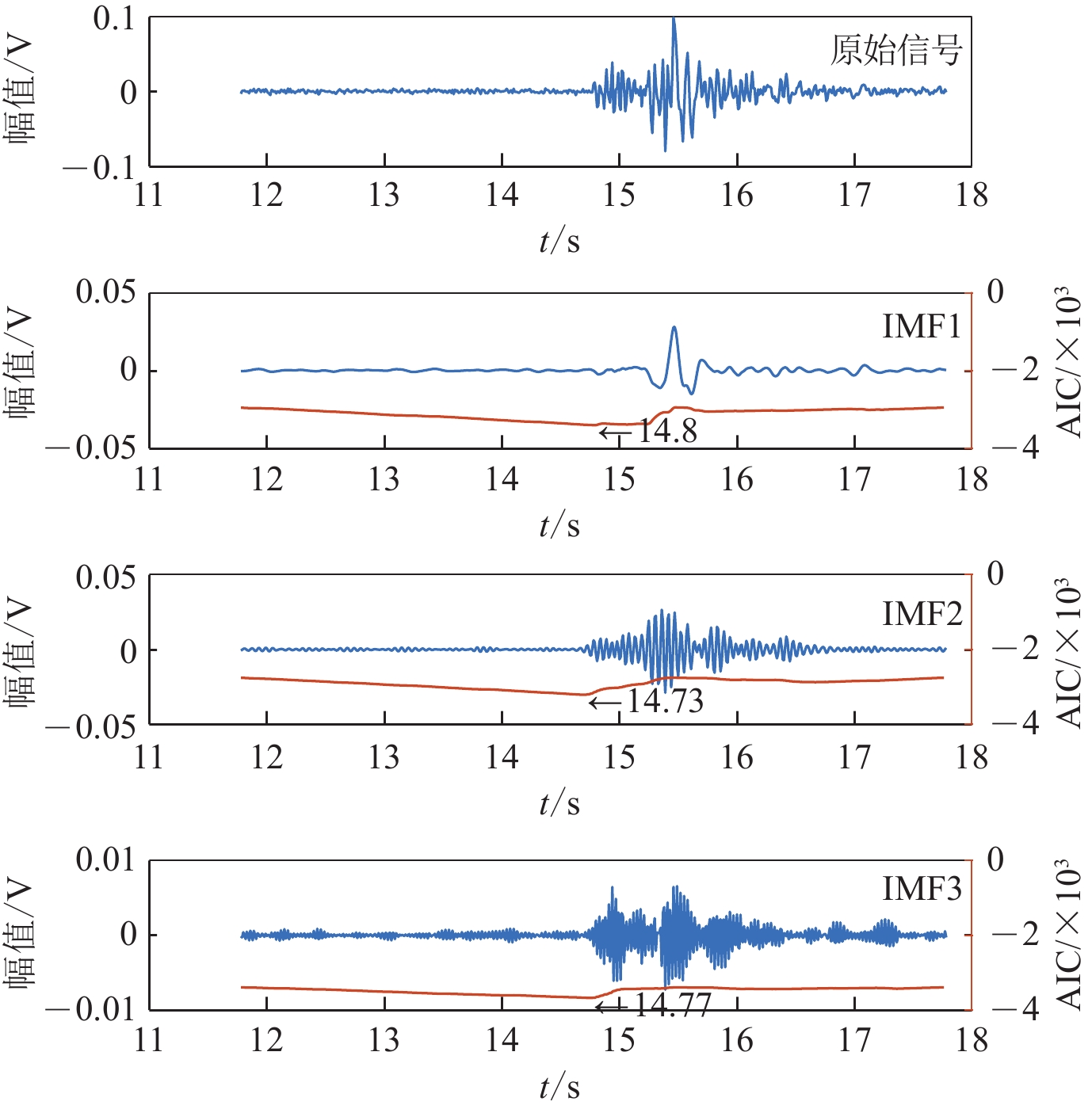
摘要: 针对低信噪比条件下微震初至拾取准确度低的问题，基于信号幅度变化引入权重因子，对传统长短时窗比值（STA/LTA）算法进行改进，提高初次拾取精度。为了进一步降低拾取误差，对变分模态分解（VMD）算法进行优化，基于互相关系数和排列熵准则自适应确定VMD分解层数，对初次拾取结果前后2—3 s的记录进行优化VMD，并计算分解后各本征模函数（IMF）的峰度赤池信息准则值，得到各IMF的到时，以各IMF的拾取结果及能量比综合加权得到二次拾取到时。仿真实验表明：改进后的STA/LTA在较低信噪比下可降低初次拾取误差约0.01 s以上；相比经验模态分解（EMD)和小波包分解，自适应VMD分解后能再次降低误差，最终与人工拾取结果平均误差在0.023 s以内。实际微震信号初至拾取结果表明，本算法能快速有效地识别初至P波，与人工拾取结果相比误差小，准确率高。Abstract: Accurate and reliable picking of the first arrival time is one of the critical steps in micro-seismic monitoring. Aiming at the problem of low accuracy of first arrival picking for micro-seisms under low signal-to-noise ratio, the traditional short term averaging/long term averaging algorithm is improved by introducing weight factor according to the change of signal amplitude to improve the accuracy of initial pickup. In order to further reduce the pickup error, variational mode decomposition （VMD） is optimized based on cross-correlation coefficient and permutation entropy criterion, and decomposition layers are determined adaptively. Then, the signals of 2−3 s before and after the initial pickup are decomposed by VMD, and the Kurtosis-Akaike information criterion （AIC） values of the decomposed intrinsic mode functions （IMF） are calculated to get the arrival time of each IMF, and the secondary arrival time is obtained by comprehensively weighting the picking results and energy ratios of each IMF. Simulation results show that the improved STA/LTA can reduce the initial picking error by more than 0.01 s at low SNR; compared with empirical mode decomposition （EMD） and wavelet packet decomposition, the adaptive VMD decomposition can reduce the picking error again, and the finalaverage picking error is less than 0.023 s. The first arrival time picking results of real micro-seismic signals show that the proposed algorithm can identify the first break of P-wave quickly and effectively, and the error is smaller than that of manual picking, which shows that the algorithm is effective and the picking accuracy is high.
-
Keywords:
- STA/LTA /
- variational mode decomposition /
- first arrival picking /
- micro-seismic /
- AIC
-
引言
地震前兆观测作为地震预测的最基础工作，必须建立覆盖面积地区的地震台网，进行长期的地震前兆数据观测，从中捕获有意义的前兆信息。当今地震成因理论认为，地震是地应力变化而导致的（牛安福等，2011），因此，地应力观测是开展地震预测研究不可或缺的手段之一，其中钻孔应变观测技术由于可以其有效地减少地表干扰，且观测精度高，可获得地壳变化的多种信息（邱泽华，2004）。
钻孔应变观测技术在我国的应用已有50多年。1966年邢台地震后，一些地质工作者提倡使用地应力方法进行地震预测试验，曾取得了重要的进展，由此开始研制各种钻孔应变仪器，钻孔应变仪的研制对震前地壳变化研究具有重要意义。YRY四分量钻孔应变仪是将应变器放在钻孔中观测地应变，其精度高，高频响应可达100 Hz，分辨率可达10−9量级，能够清晰地记录到应变固体潮汐（牛安福等，2011）。
在2008年汶川MS8.0地震和2013年芦山MS7.0地震前，姑咱台钻孔应变仪记录到了很多压性脉冲和潮汐畸变，研究人员经过分析处理，认为这些畸变信号属于地震前兆异常（邱泽华等，2009，2015；刘琦，张晶，2011；池顺良等，2014；刘琦等，2014），然而在前兆观测数据中是否存在人工难以辨识的微弱异常还难以确定。为此，本文在上述研究的基础上，拟利用芦山地震前数天的短周期信号进行时频分析，提取震前出现的微弱异常信号，对微弱异常与地震前兆的相关性予以进一步分析。
1. 姑咱台钻孔应变数据
姑咱地震台位于四川省甘孜藏族自治州康定县姑咱镇，为国家级台站，隶属于四川省地震局康定地震中心站（池顺良等，2013）。
姑咱台YRY四分量钻孔应变仪于2006年10月28日安装（刘琦等，2014），包括4个分量，1路方位为北偏东51°，记为北南分量，2—4路方位依次顺时针加45°，分别为东西分量、北东分量、北西分量（池顺良等，2013）。图1给出了姑咱台2008年1月1日—2014年11月25日共6年11个月的四分量钻孔应变记录曲线，数据采样率为每分钟一次。曲线上较为明显的畸变异常包括远震带来的同震效应、外界环境干扰以及地震前兆异常．由图1可见，排除掉仪器自身的干扰，该仪器可以记录到清晰的固体潮背景（廖盈春，2007）。2012年10月前后和2013年4月16—20日，钻孔应变仪分别记录到了明显的畸变信号，而且这些畸变信号满足自检关系，说明仪器状态良好，且能够排除远震和环境干扰所带来的影响，因此可以认为这些应变异常反映的是地下真实受力所产生的应变变化（刘琦等，2014）。
![]()
图 1 2008年1月1日—2014年11月25日姑咱台钻孔应变四分量观测曲线Figure 1. Observation curves of four-component borehole strain at the station Guzan during the period from 1 January 2008 to 25 November 2014上述应变异常在仪器记录的前兆观测序列中呈现显著变化，但由于钻孔应变观测数据量大，且包含多种异常，在前兆数据中是否存在人工难以辨识的微弱异常尚难以确定。为此，本文引入信号处理的方法，首先将四分量钻孔应变前兆观测序列分别进行一阶差分变换，进而增强异常信号的短周期成分（邱泽华等，2009），随后采用时频分析法对所提取到的北南分量异常信号在高频部分的具体变化予以分析，其余分量的处理结果将在其后补充说明。
2. 利用小波变换分析芦山地震前高频应变异常变化
对地震前兆信号进行小波变换，就是将该信号按某一小波函数簇展开，即将信号表示为一系列不同尺度和不同时移的小波函数的线性组合，其中每一项的系数称为小波系数，利用小波系数的位置和尺度可以很好地探测到地震前兆信号的时频变化（崔锦泰，1995）。
2.1 局部小波变换原理
时频分析法兼具时域和频域的分辨率，适用于非平稳地震信号的分析（钱世锷，2005）。本文引入时频分析法中的连续小波变换方法用于信号处理。 设h（t）为有限离散时间序列，其小波变换可定义为
$ C(a{\text{，}}\!\!\! b){\text{＝}} \frac{1}{{\sqrt a }}\int_{ {\text{－}} \infty }^\infty {h(t){\psi ^ * }\left(\frac{{t {\text{－}} b}}{a}\right)} {\rm{d}}t{\text{，}} $
(1) 式中：t为观测时间，单位为分钟；a为尺度因子；b为平移因子；ψ（t）为基本小波。
若将时间序列h（t）整体进行小波变换，在变换过程中小波基的支撑长度与所选择的尺度成正比。为确保所分析序列的频率分辨率，须选择足够大的尺度进行分析，此时小波基的支撑长度会大于所分析序列的长度，处理结果会使相邻时段信号的频谱产生相互影响（崔锦泰，1995）。
若将时间序列h（t）进行局部化处理，按天进行连续小波变换，则h（t）的小波变换为
$ S(a{\text{，}}\!\!\!b) {\text{＝}} \frac{1}{{\sqrt a }}\left[\int_1^k {{s_1}(t){\psi ^ * }\left(\frac{{t {\text{－}} b}}{a}\right)} {\rm{d}}t {\text{＋}} \!\!\int_{k {\text{＋}}1}^{2k} {{s_2}(t){\psi ^ * }\left(\frac{{t {\text{－}} b}}{a}\right)} {\rm{d}}t {\text{＋}} \cdots {\text{＋}} \int_{k(n {\text{－}} 1) {\text{＋}}1}^{kn} {{s_n}(t){\psi ^ * }\left(\frac{{t {\text{－}} b}}{a}\right)} {\rm{d}}t\right]{\text{，}}\!\!\!\!\!\!\!\!\!\! $
(2) 局部累加求和可得
$ S(a{\text{，}}\!\!\! b) {\text{＝}} \frac{1}{{\sqrt a }}\sum\limits_{{{i}} {\text{＝}} {\rm{1}}}^n {\int_{k(i {\text{－}} 1) {\text{＋}} 1}^{ki} {{s_n}(t){\psi ^ * }\left(\frac{{t{\text{－}} b}}{a}\right)} {\rm{d}}t}{\text{，}} $
(3) 式中，k为时间序列中每天的采样点数，n为分析天数，sn（t）为每天的时间序列，S（a， b）为相应的局部小波变换结果。这样既可使时间序列h（t）每天的处理结果相互独立且完整，又可以确保地震前兆信号频谱结果的真实性。
基本小波必须满足容许性条件
$ \int_{ {\text{－}} \infty }^\infty {\frac{{\left| {\psi^2 {{\left(\omega \right)}}} \right|}}{\omega }} {\rm{d}}\omega {\text{＜}}{\text{＋}} \infty {\text{.}} $
(4) 小波变换的基本小波具有多种形式，本文选用的是分析非平稳信号常用的cmor3-3小波。
2.2 震前钻孔应变数据连续小波变换及频率分布对比分析
刘琦等（2014）利用S变换对2013年芦山MS7.0地震前后的钻孔应变数据进行大尺度时间范围的整体分析以及小尺度时间的对比分析，分别给出了芦山地震前后应变异常变化的宏观和局部认识。为了对芦山地震的高频应变异常进行更细致的分析，本文尝试采用连续小波变换方法，对每一天的小波变换结果进行对比，以期挖掘更多信息。
参考刘琦等（2014）关于芦山地震可靠异常全部出现在周期小于10分钟的高频段内的结果，本文选取2013年4月1—20日的北南分量钻孔应变分钟值的差分数据按天进行连续小波变换。以4月17日为例，图2给出了该日一阶差分应变数据的小波变换结果。由于一阶差分变换可以减弱观测数据中日、月引潮力等低频影响（徐伟民等，2015），着重体现应变观测数据的高频变化，因此基于一阶差分数据进行小波变换，可以增强应变信号的短周期成分。为了进一步分析应变信号的高频段，图2b在图2a的基础上仅给出了周期小于28分钟（0.6—8.3 mHz）的数据处理结果。可以看出，与图2a相比，图2b中的高频段信号清晰完整，有利于提取钻孔应变信号的高频异常。
![]()
图 2 2013年4月17日一阶差分应变数据的小波变换结果（a） 差分数据的频段为0—8.3 mHz；（b） 差分数据为高频段0.6—8.3 mHzFigure 2. Wavelet transform results of the first-order differential strain data on 17 April 2013（a） Frequency band is 0−8.3 mHz；（b） High frequency band is 0.6−8.3 mHz图3给出了2013年4月1—20日北南分量钻孔应变分钟值差分数据的局部小波变换结果，可以看到，4月2日，6日，9日和11日这4天中，在周期小于28分钟的频段内出现较强能量，且图中4月16—19日这4天的可靠异常在该频段内具有显著能量。因此4月1—20日这个时段所出现的两种异常能量较明显地反映了芦山地震前应变从弱到强的变化过程。
![]()
图 3 2013年4月1—20日应变差分数据的局部小波变换结果Figure 3. Local wavelet transform results of the strain differential data from April 1 to April 20，2013图4给出了4月2日，6日，9日和11日弱应变异常时段与4月19日显著异常时段的频率分布对比结果。为了能够直观地分析比较两种异常的频率分布，图中已对频率所对应的小波系数进行了归一化处理。可以看出：频率峰值在5.9 mHz附近时，4月2日，11日与4月19日出现的应变异常具有相似性；频率峰值在7.2 mHz附近时，4月6日与4月19日出现的应变异常具有相似性。经计算得出两种异常在两个峰值频率附近的相关系数分别为0.82和0.85，因此提取到的弱应变异常与显著异常在研究频段内具有很强的相关性。
![]()
图 4 2013年4月2，6，9，11日弱异常时段与4月19日高频异常时段归一化频率的分布对比结果虚线表示异常时段在5.9 mHz和7.2 mHz两个异常频率峰值点的对应情况Figure 4. Comparison of the normalized frequency distribution of the weak abnormal time interval on 2，6，9 and 11 April 2013 with that of the high-frequency abnormal time interval on 19 April 2013The dashed lines indicate the correspondence at the abnormal peak frequency 5.9 mHz and 7.2 mHz2.3 无震日变化统计分析及同震时段分析
为了能够较完整地研究芦山地震前的应变变化，对2012年1月1日—2012年8月31日的钻孔应变数据进行去趋势处理，结果如图5所示。图5a给出了钻孔应变北南分量的观测曲线，该时段的畸变信号包括外界干扰和同震效应。
![]()
图 5 2012年1月1日—2012年8月31日姑咱台钻孔应变北南分量观测曲线处理结果（a） 完整时段；（b） 平稳时段；（c） 日变化统计Figure 5. Observation curves of the NS component of borehole strain recorded at the station Guzan from 1 January 2012 to 31 August 2012（a） In the whole time interval; （b） In the stationary time interval；（c） Daily variation statistics为了统计出日变化曲线，将观测序列进行差分处理，然后设定差分序列的阈值为差分序列平均值±3倍标准差，并剔除观测序列中异常点所处的时间点，最终处理结果如图5b所示。图5b中的观测曲线已经排除外界干扰，并在该曲线中提取每天同一时刻求和进行算数平均，将该平均值作为该时刻的统计平均，最后得到平稳时段观测曲线的统计平均结果，如图5c所示。信号的统计时长为24小时，从图中能够看出统计信号平稳光滑，可以作为2012年1月1日—2012年8月31日时段的无震日变化曲线。
图6选取包含2013年4月19日前兆异常时段和3次同震时段（北京时间2013年4月16日18点44分伊朗与巴基斯坦交界MS7.7地震、4月17日6时55分巴布亚新几内亚MS6.7地震、4月19日11时5分千岛群岛MS7.0地震）的频率分布对比结果，可见，与4月19日前兆异常时段相比，4月16日和4月19日两次同震时段内，周期小于10分钟的频段内几乎无能量出现，而4月17日的同震时段在该频段内出现了较强的能量。由于4月17日同震在3次远震中震级最小、震中距最大，因此推断该同震对本时段的异常现象无法造成干扰（刘琦等，2014）。从图6中还可以看出，3次远震在5.9 mHz和7.2 mHz这两个异常频率点的贡献并不大，因此可以排除远震对周期小于10分钟的信号会造成影响。
![]()
图 6 2013年4月19日高频异常时段与3次同震时段归一化频率分布对比结果虚线表示异常时段在5.9 mHz和7.2 mHz两个异常频率峰值点的对应情况Figure 6. Comparison of the normalized frequency distributions of high-frequency anomalies in three coseismic time intevals with that of high-frequency anomaly interval on April 19，2013The dashed lines indicate the correspondence at the abnormal peak frequency 5.9 mHz and 7.2 mHz为了进一步分析对比无震时段与高频异常的频率分布，将统计出的无震背景信号进行差分处理并进行局部小波变换。图7给出了无震时段以及5次异常时段的归一化小波系数对比结果，可见，无震时段信号的能量集中在0.6—4.1 mHz频段，对5.9 mHz和7.2 mHz这两个异常频率峰值点几乎无贡献，经计算得到统计出的无震时段与显著应变异常时段在研究频段内的相关系数仅为−0.007，因此可以排除无震信号也存在这两个异常频率的可能性。
![]()
图 7 无震时段以及5次高频异常时段归一化频率分布对比结果虚线表示异常时段在5.9 mHz和7.2 mHz两个异常频率峰值点的对应情况Figure 7. Comparison of the normalized frequency distribution in the aseismic time interval with that in five high-frequency abnormal time intervalsThe dashed lines indicate the correspondence at the abnormal peak frequency of 5.9 mHz and 7.2 mHz以上仅给出了北南分量钻孔应变异常在高频段的具体变化。为了进一步补充说明异常频率的可能性，图8给出了东西、北东分量应变异常时段的频率（5—8.3 mHz）分布对比结果。可以看出，对于东西、北东两分量的频率分布情况，峰值频率在5.9 mHz附近时，4月2日与4月19日的应变异常在该频率成分上具有相似性；峰值频率在7.2 mHz附近时，4月6日与4月19日在该频率成分上具有相似性，与北南分量的处理结果基本一致。表1具体给出了三分量应变观测在两个峰值频率附近的相关系数计算结果。由表1中的统计结果可以看出，三分量的异常时段在5.9 mHz和7.2 mHz频率附近分别呈现出较强的相关性，并且排除了无震和远震的干扰，因此可以认为这两个异常频率点有可能与芦山MS7.0地震相关。
![]()
图 8 钻孔应变观测东西（a）、北东分量（b）弱异常时段与可靠异常时段频率分布对比结果虚线表示异常时段在5.9 mHz和7.2 mHz两个异常频率峰值点的对应情况Figure 8. Comparison of the normalized frequency distribution of EW- （a） and NE-components （b） in weak abnormal intervals with that in the reliable abnormal time intervalsThe dashed lines indicate the correspondence at the abnormal peak frequency 5.9 mHz and 7.2 mHz表 1 异常频率下三分量应变观测相关系数统计Table 1. Correlative coefficients for three-component strain at the abnormal peak frequencies峰值频率/mHz 相关系数 北南分量 东西分量 北东分量 5.9 0.82 0.64 0.85 7.2 0.85 0.79 0.81 3. 讨论与结论
本文利用局部小波变换方法对芦山地震前数天姑咱台四分量钻孔应变仪记录到的三分量应变异常变化进行了时频分析，提取到了震前更早的弱应变异常，通过同一高频段内与显著应变异常的对比，初步认为研究频段内出现的两个异常频率峰值可能与芦山地震相关，随后对震前平静时段进行统计分析，结果显示远震以及无震时段信号的高频部分对这两个异常频率点的贡献不大，且经计算得出这两个异常频率点全部出现在周期小于10分钟的可靠异常频段内，与刘琦等（2014）的结果一致，因此有可能反映了震前异常信号在高频段内会有特定频点的能量突增。
需要说明的是，本文只是针对芦山地震一个震例分析说明了局部小波变换方法运用的思路与结果，在具体运用中，针对不同前兆数据的特征还存在一些有待研究的问题，例如选择相对合理的小波基等，而对于其前兆异常分析仍较肤浅，是否存在地震前兆异常信号特有的频率范围，目前尚无法确定，今后还需要更多的震例统计分析来充分验证上述异常信号频率来源的可靠性。
-
![]()
图 1 基于改进STA/LTA及优化VMD的微震初至拾取算法流程图
Figure 1. The flow chart of the first break picking of micro-seismic based on imp-roved STA/LTA and adaptive VMD
![]()
图 2 基于雷克子波和卷积模型的理论和模拟地震记录
Figure 2. Theoretical and simulated seismogram based on Ricker wavelet and convolution model
![]()
图 4 不同SNR下三种STA/LTA算法拾取误差曲线
Figure 4. Picking up error curves of three STA/LTA algorithms under different SNRs
![]()
图 5 优化VMD峰度AIC为3.07 s时的初至拾取结果
Figure 5. First arrival picking based on improved VMD when Kurtosis-AIC is 3.07 s
![]()
图 7 基于小波包峰度AIC的初至拾取
Figure 7. First arrival picking based on wavelet packet Kurtosis-AIC
![]()
图 10 广西平果2013年7月4日ML1.3爆破的一条实际微震记录
Figure 10. Real micro-seismic record of some coal mine with ML1.3 at Pingguo，Guangxi on July 4th 2013
![]()
图 11 本文改进STA/LTA初次拾取结果
Figure 11. First picking results of improved STA/LTA in this paper
![]()
图 12 本文改进STA/LTA及优化VMD峰度AIC拾取结果
Figure 12. First arrival picking by improved STA/LTA and adaptive VMD Kurtosis-AIC
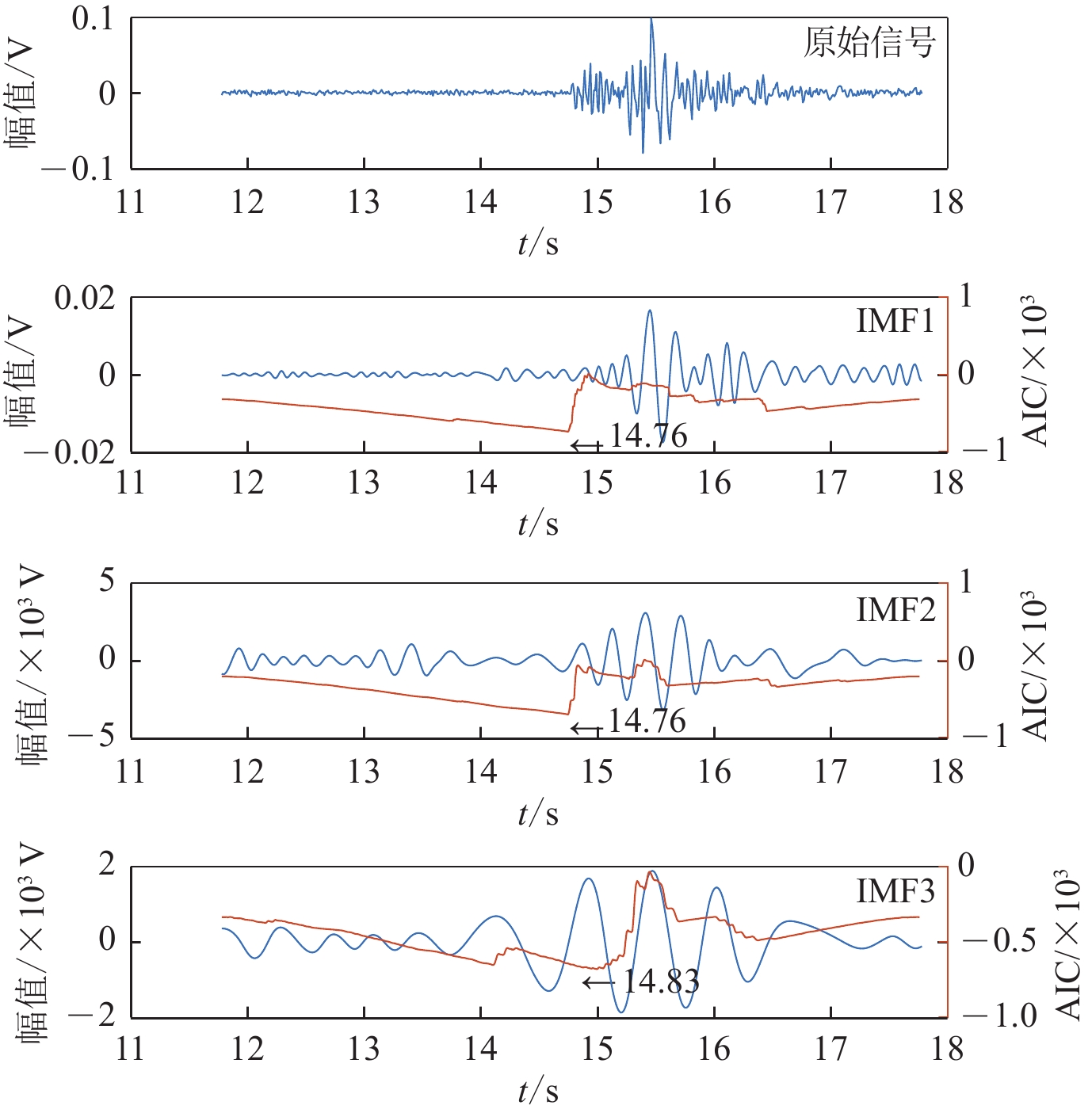
表 1 实际微震记录初至拾取结果
Table 1 First arrival picking of real micro-seismics
拾取方法 误差 30 ms 误差 20 ms 误差 10 ms 记录条数 占比 记录条数 占比 记录条数 占比 本文 1 117 98.2% 1 090 95.9% 1 031 90.7% EMD-AIC 1 090 95.9% 1 052 92.5% 980 86.2% 小波包峰度AIC 1 075 94.5% 1 037 91.2% 968 85.1% 
下载: 导出CSV
-
贾瑞生,谭云亮,孙红梅,洪永发. 2015. 低信噪比微震P波震相初至自动拾取方法[J]. 煤炭学报,40(8):1845–1852. Jia R S,Tan Y L,Sun H M,Hong Y F. 2015. Method of automatic detection on micro-seismic P-arrival time under low signal-to-noise ratio[J]. Journal of China Coal Society,40(8):1845–1852 (in Chinese).
李伟,江晓林,陈海波,金珠鹏,刘志军,李兴伟,林井祥. 2018. 基于EEMD_Hankel_SVD的矿山微震信号降噪方法[J]. 煤炭学报,43(7):1910–1917. Li W,Jiang X L,Chen H B,Jin Z P,Liu Z J,Li X W,Lin J X. 2018. Denosing method of mine microseismic signal based on EEMD_Hankel_SVD[J]. Journal of China Coal Society,43(7):1910–1917 (in Chinese).
刘晗,张建中. 2014. 微震信号自动检测的STA/LTA算法及其改进分析[J]. 地球物理学进展,29(4):1708–1714. doi: 10.6038/pg20140429 Liu H,Zhang J Z. 2014. STA/LTA algorithm analysis and improvement of microseismic signal automatic detection[J]. Progress in Geophysics,29(4):1708–1714 (in Chinese).
刘晓明,赵君杰,王运敏,彭平安. 2017. 基于改进的STA/LTA方法的微地震P波自动拾取技术[J]. 东北大学学报(自然科学版),38(5):740–745. Liu X M,Zhao J J,Wang Y M,Peng P A. 2017. Automatic picking of microseismic events P-wave arrivals based on improved method of STA/LTA[J]. Journal of Northeastern University (Natural Science)
,38(5):740–745 (in Chinese). 唐贵基,王晓龙. 2015. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报,49(5):73–81. doi: 10.7652/xjtuxb201505012 Tang G J,Wang X L. 2015. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi’an Jiaotong University,49(5):73–81 (in Chinese).
田优平,赵爱华. 2016. 基于小波包和峰度赤池信息量准则的P波震相自动识别方法[J]. 地震学报,38(1):71–85. doi: 10.11939/jass.2016.01.007 Tian Y P,Zhao A H. 2016. Automatic identification of P-phase based on wavelet packet and kurtosis-AIC method[J]. Acta Seismologica Sinica,38(1):71–85 (in Chinese).
王志坚,常雪,王俊元,杜文华,段能全,党长营. 2018. 排列熵优化改进变模态分解算法诊断齿轮箱故障[J]. 农业工程学报,34(23):59–66. doi: 10.11975/j.issn.1002-6819.2018.23.007 Wang Z J,Chang X,Wang J Y,Du W H,Duan N Q,Dang C Y. 2018. Gearbox fault diagnosis based on permutation entropy optimized variational mode decomposition[J]. Transactions of the Chinese Society of Agricultural Engineering,34(23):59–66 (in Chinese).
赵大鹏,刘希强,刘尧兴,王志铄,赵晖,张亚琳. 2013. 高阶统计量及AIC方法在区域地震事件和直达P波初动识别中的应用[J]. 地震地磁观测与研究,34(5/6):61–69. Zhao D P,Liu X Q,Liu Y X,Wang Z S,Zhao H,Zhang Y L. 2013. Detection of regional seismic events by high order statistics method and automatic identification of direct P-wave first motion by AIC method[J]. Seismological and Geomagnetic Observation and Research,34(5/6):61–69 (in Chinese).
郑近德,程军圣,杨宇. 2013. 改进的EEMD算法及其应用研究[J]. 振动与冲击,32(21):21–26. doi: 10.3969/j.issn.1000-3835.2013.21.004 Zheng J D,Cheng J S,Yang Y. 2013. Modified EEMD algorithm and its applications[J]. Journal of Vibration and Shock,32(21):21–26 (in Chinese).
郑小霞,周国旺,任浩翰,符杨. 2017. 基于变分模态分解和排列熵的滚动轴承故障诊断[J]. 振动与冲击,36(22):22–28. Zheng X X,Zhou G W,Ren H H,Fu Y. 2017. A rolling bearing fault diagnosis method based on variational mode decomposition and permutation entropy[J]. Journal of Vibration and Shock,36(22):22–28 (in Chinese).
朱权洁,姜福兴,魏全德,王博,刘金海,刘晓辉. 2018. 煤层水力压裂微震信号P波初至的自动拾取方法[J]. 岩石力学与工程学报,37(10):2319–2333. Zhu Q J,Jiang F X,Wei Q D,Wang B,Liu J H,Liu X H. 2018. An automatic method determining arrival times of microseismic P-phase in Hydraulic fracturing of coal seam[J]. Chinese Journal of Rock Mechanics and Engineering,37(10):2319–2333 (in Chinese).
Bandt C,Pompe B. 2002. Permutation entropy:A natural complexity measure for time series[J]. Phys Rev Lett,88(17):174102. doi: 10.1103/PhysRevLett.88.174102
Charles M,Ge M C. 2018. Enhancing manual P-phase arrival detection and automatic onset time picking in a noisy microseismic data in underground mines[J]. Int J Min Sci Technol,28(4):691–699. doi: 10.1016/j.ijmst.2017.05.024
Dragomiretskiy K,Zosso D. 2014. Variational mode decomposition[J]. IEEE Trans Signal Proc,62(3):531–544. doi: 10.1109/TSP.2013.2288675
Gaci S. 2014. The use of wavelet-based denoising techniques to enhance the first-arrival picking on seismic traces[J]. IEEE Trans Geosci Remote Sens,52(8):4558–4563. doi: 10.1109/TGRS.2013.2282422
Kirbas I,Peker M. 2017. Signal detection based on empirical mode decomposition and Teager-Kaiser energy operator and its application to P and S wave arrival time detection in seismic signal analysis[J]. Neural Comput Appl,28(10):3035–3045. doi: 10.1007/s00521-016-2333-5
Li F Y,Zhang B,Verma S,Marfurt K J. 2018. Seismic signal denoising using thresholded variational mode decomposition[J]. Explora Geophys,49(4):450–461. doi: 10.1071/EG17004
Li X B,Shang X Y,Wang Z W,Dong L J,Weng L. 2016. Identifying P-phase arrivals with noise:An improved Kurtosis method based on DWT and STA/LTA[J]. J Appl Geophys,133:50–61. doi: 10.1016/j.jappgeo.2016.07.022
Li X B, Shang X Y, Morales-Esteban A, Wang Z W. 2017. Identifying P phase arrival of weak events: The Akaike information criterion picking application based on the empirical mode decomposition[J] Comput Geosci, 100: 57–66.
Liu M Z,Yang J X,Cao Y P,Fu W N,Cao Y L. 2017. A new method for arrival time determination of impact signal based on HHT and AIC[J]. Mech Syst Signal Proc,86:177–187. doi: 10.1016/j.ymssp.2016.10.003
Shang X Y,Li X B,Morales-Esteban A,Dong L J. 2018. Enhancing micro-seismic P-phase arrival picking:EMD-cosine function-based denoising with an application to the AIC picker[J]. J Appl Geophys,150:325–337. doi: 10.1016/j.jappgeo.2017.09.012
Xue Y J,Cao J X,Wang D X,Du H K,Yao Y. 2016. Application of the variational-mode decomposition for seismic time-frequency analysis[J]. IEEE J Select Top Appl Earth Observ Remote Sens,9(8):3821–3831. doi: 10.1109/JSTARS.2016.2529702
-
期刊类型引用(8)
1. 李潇，岳龙，徐清风，臧艺博，韩帮杰，王哲，李炜. 青岛地区钻孔倾斜仪地铁干扰定量分析. 地震工程学报. 2025(02): 383-392 . 
百度学术
2. 张山元，曾庆堂，段胜朝，番绍辉，李圣. 腾冲台YRY-4分量钻孔应变仪资料可靠性及同震响应特征浅析. 防灾减灾学报. 2024(02): 51-56+68 . 百度学术
3. 李晨阳，池成全. 机器学习在地震观测异常数据提取中的应用. 海南师范大学学报(自然科学版). 2024(03): 348-356 . 百度学术
4. 孙刚，王运生，余正良，赵方彬，唐涛，吴昊宸. 石棉M_S4.5级地震斜坡动力响应规律. 科学技术与工程. 2023(29): 12399-12405 . 百度学术
5. 冯凯宇，窦立婷，李晨，任力伟，成诚，丁学文. 四分量钻孔应变干扰特征时频域研究. 山西地震. 2022(01): 21-27 . 百度学术
6. 杨志鹏，陈秀清，张御阳，颜欢，陈碧洪，阮祥. 基于MATLAB的定点形变观测数据时频分析软件设计及应用研究. 震灾防御技术. 2022(01): 172-180 . 百度学术
7. 杨志鹏，陈秀清，余洋洋，张御阳，巫萌飞，徐建明，赵晶，张正伟. 基于小波分解与同步挤压变换的西昌小庙台形变典型干扰的时频响应特征研究. 地震工程学报. 2022(05): 1192-1206 . 百度学术
8. 金刚，王运生，何先龙，史丙新，周宇航. 基于连续小波变换的斜坡动力响应特征分析——以四川长宁M_s6.0级地震为例. 中国地质灾害与防治学报. 2021(02): 1-8 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 701
- HTML全文浏览量: 308
- PDF下载量: 122
- 被引次数: 12
