Two-dimensional soil and topographic amplification effects of a partially filled circular-arc alluvial valley under plane SH waves
-
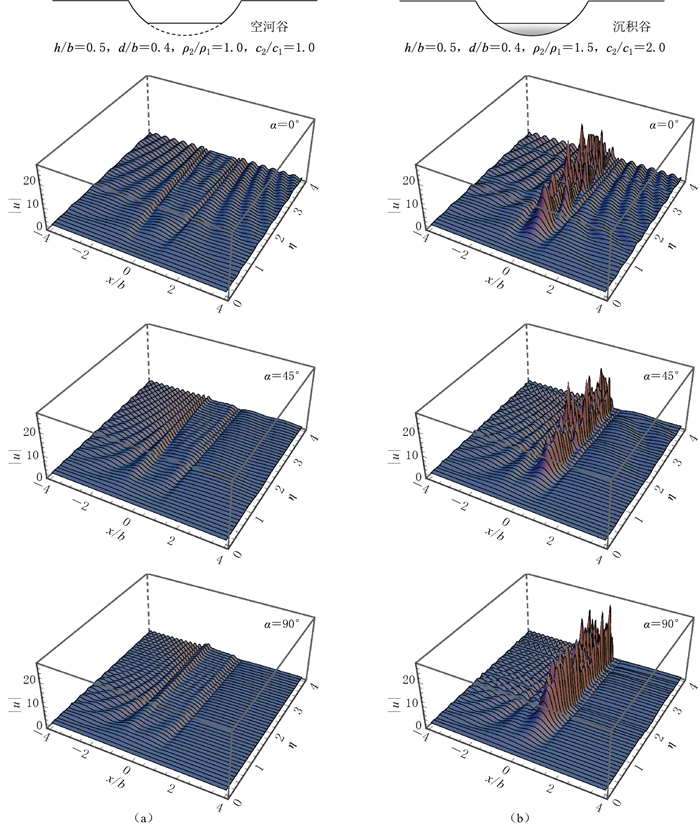
摘要: 场地效应通常包含土层放大效应和地形放大效应，为了揭示二者的相对贡献，本文构造了平面SH波作用下部分充填沉积谷的解析模型，借助于区域分解策略，在波函数展开法的框架下，提出了超定方程组解法，得到了部分充填圆弧形沉积谷对平面SH波散射的波函数级数解，而且级数解的收敛测试表明了超定方程组解法的必要性.通过与文献结果进行对比，验证了本文方法的正确性.通过调整解析模型中两个子区域内的材料参数，计算了沉积谷引起的场地放大效应和相应的空河谷引起的地形放大效应.对二维土层与地形效应进行对比分析，结果显示，在沉积谷内二维土层放大效应通常强于地形放大效应，而地形放大效应决定了沉积谷外的地面运动放大形态.针对最大地面运动，进行了沉积谷和相应空河谷的参数分析，进一步描述了二维土层放大效应，研究结果表明二维土层放大效应引起的最大地面运动通常远远大于地形放大效应引起的最大地面运动，并且二维土层效应通常随着土层与基岩的阻抗比的增大而增大，但不是一维土层放大效应与二维地形放大效应的简单线性叠加.Abstract: Site amplification consists of two-dimensional (2D) soil layer amplification effects and topographic amplification effects. The objective of this study is to investigate the relative contribution of soil amplification and topographic amplification. To that end, the wavefunction series solution for the scattering of plane SH waves by a partially filled circular-arc alluvial valley is proposed. The wavefunction series solution is obtained by a novel method of over-determined system of equations in the framework of the wavefunction expansion technique with the aid of a region-matching strategy. The convergence tests are conducted to reveal the necessity of the proposed over-determined system of equations method. The validity of the proposed solution is verified by comparison with previous results. By adjusting the material parameters of the two sub-regions in the analytical model, both of the surface motions of the alluvial valley and the empty canyon are calculated. The site amplification patterns of the alluvial valley are compared with the topographic amplification patterns of the empty canyon with the same geometry, the results show that the soil amplification effects are usually larger than the topographic amplification effects within the alluvial valley, while the topographic effects dominate the amplification pattern of ground motions outside the alluvial valley. Afterwards, a parametric study in terms of the maximum surface motion is carried out to determine the relative importance of soil and topographic contributions in a more comprehensive manner and to further characterize the 2D soil layer amplification effects. It is evident that the maximum soil layer amplification generally far outweighs the maximum topographic amplification. The 2D soil amplification increases with the impedance contrast between the soil layer and the underlying bedrock but is not a simple linear superposition of 1D soil amplification and 2D topographic amplification.
-
-
![]()
图 1 部分充填圆弧形沉积谷的二维模型
Figure 1. 2D model of the partially filled circular-arc alluvial valley
![]()
图 2 不同W/N值下沉积谷附近地表 5个不同位置处的位移幅值|u|
Figure 2. Surface displacement amplitudes |u| at five points in and around an alluvial valley for different values of W/N
![]()
图 3 不同N值下沉积谷附近地表 5个不同位置处的位移幅值|u|
Figure 3. Surface displacement amplitudes |u| at five points in and around an alluvial valley for different values of N
![]()
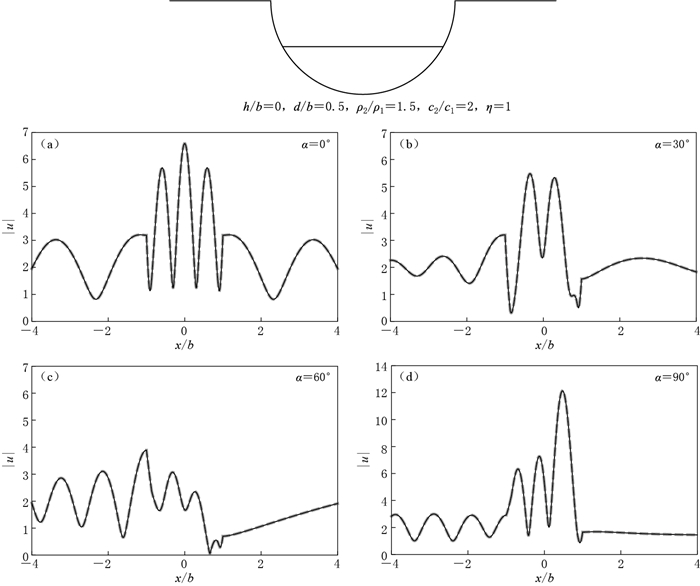
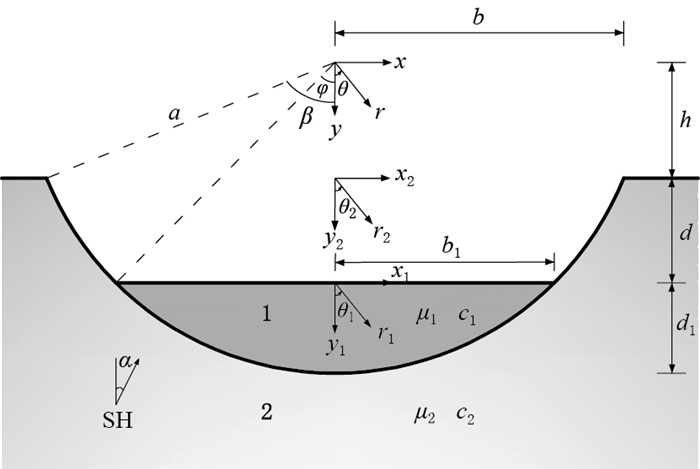
图 4 入射角α=0° (a), 30° (b), 60° (c)和90° (d)时本文方法计算的位移幅值|u|结果(实线)与Tsaur和Chang (2008)结果(虚线)的比较(h/b=0, d/b=0.5, ρ2/ρ1=1.5, c2/c1=2, η=1)
Figure 4. The comparison of surface displacement amplitudes |u| between our predictions (solid line) and those of Tsaur and Chang (2008) (dashed line) for incident angles α=0° (a), 30° (b), 60° (c) and 90° (d) (h/b=0, d/b=0.5, ρ2/ρ1=1.5, c2/c1=2 at η=1)
![]()
图 5 空河谷(ρ2/ρ1=1, c2/c1=1, 实线)和沉积谷(ρ2/ρ1=1.5, c2/c1=2, 虚线)在入射角度α=0° (a), 30° (b), 60° (c), 90° (d)的条件下地表位移幅值|u|的比较(h/b=0.5, d/b=0.4, η=1)
Figure 5. The comparison of surface displacement amplitudes |u| between an empty canyon (ρ2/ρ1=1, c2/c1=1, solid line) and an alluvial valley (ρ2/ρ1=1.5, c2/c1=2, dotted line) when incident angles α=0° (a), 30° (b), 60° (c) and 90° (d) (h/b=0.5, d/b=0.4, η=1)
![]()
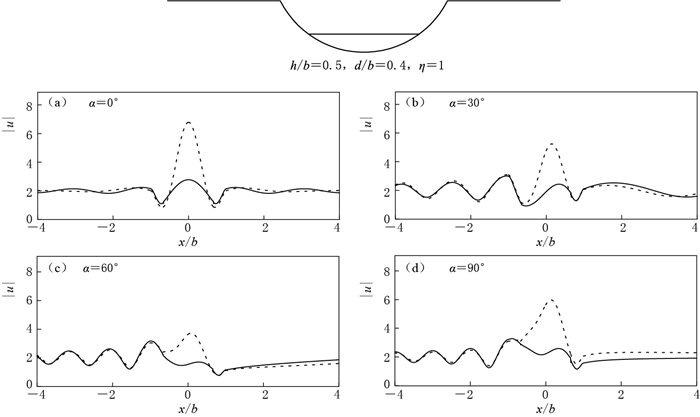
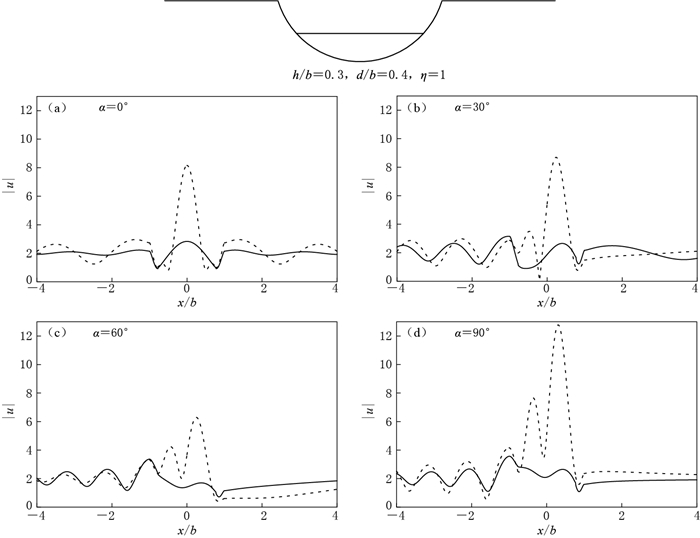
图 6 空河谷(ρ2/ρ1=1, c2/c1=1, 实线)和沉积谷(ρ2/ρ1=1.5, c2/c1=2, 虚线)在入射角度α=0° (a), 30° (b), 60° (c), 90° (d)条件下地表位移幅值|u|的比较(h/b=0.3, d/b=0.4, η=1)
Figure 6. The comparison of surface displacement amplitudes |u| between an empty canyon (ρ2/ρ1=1, c2/c1=1, solid line) and an alluvial valley (ρ2/ρ1=1.5, c2/c1=2, dotted line) when incident angles α=0° (a), 30° (b), 60° (c) and 90° (d) (h/b=0.3, d/b=0.4, η=1)
![]()
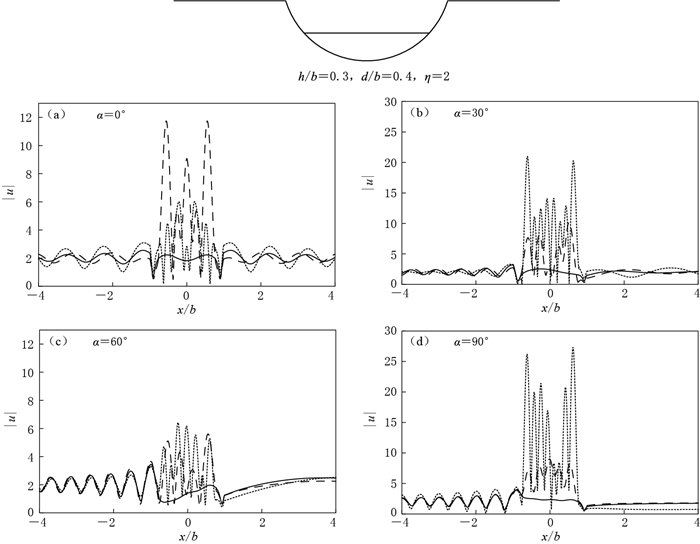
图 7 参数为h/b=0.3, d/b=0.4, η=2时空河谷(ρ2/ρ1=1, c2/c1=1, 实线)和沉积谷(ρ2/ρ1=1.5, c2/c1=2, 充填硬土，虚线；ρ2/ρ1=1.5, c2/c1=3, 充填软土，点线)在入射角度α = 0° (a), 30° (b), 60° (c), 90° (d)条件下地表位移幅值|u|的比较
Figure 7. The comparison of surface displacement amplitudes |u| for h/b=0.3, d/b=0.4 at η=2 and different incident angles α=0° (a), 30° (b), 60° (c) and 90° (d) between an empty canyon (ρ2/ρ1=1, c2/c1=1, solid line) and two alluvial valleys (ρ2/ρ1=1.5, c2/c1=2, dashed line; ρ2/ρ1=1.5, c2/c1=3, dotted line)
![]()
图 8 入射角度α=0°, 45°, 90°条件下截断空河谷(a)和沉积谷(b)的地表位移幅值|u|随着无量纲距离x/b和无量纲频率η的变化情况
Figure 8. 3D plot of surface displacement amplitudes |u| versus x/b and η for a truncated canyon (a) and an alluvial valley (b) at different incident angles α=0°, 45° and 90°
![]()
图 9 入射角度α=0° (a), 45° (b), 90° (c)时两个沉积谷和一个相同形状的截断空河谷的最大地表位移幅值|u|max随无量纲频率η的变化情况
Figure 9. Maximum surface displacement amplitudes |u|max versus η for two alluvial valleys and a truncated canyon with the same geometry at incident angles α=0° (a), 45° (b) and 90° (c)
![]()
图 10 典型的较深(a)、中等深度(b)和较浅(c)沉积谷的形状示意图
Figure 10. The sketches of the shapes of typical deep (a), medium deep (b) and shallow (c) alluvial valleys
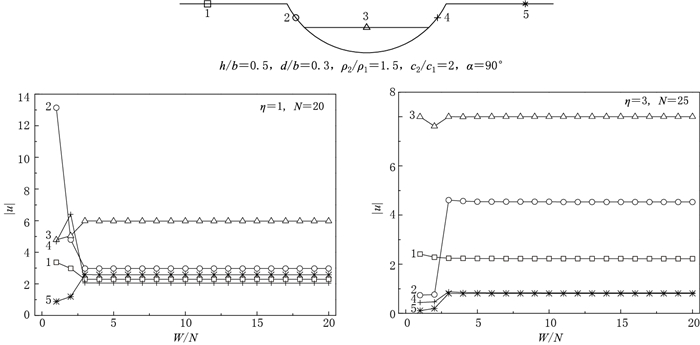
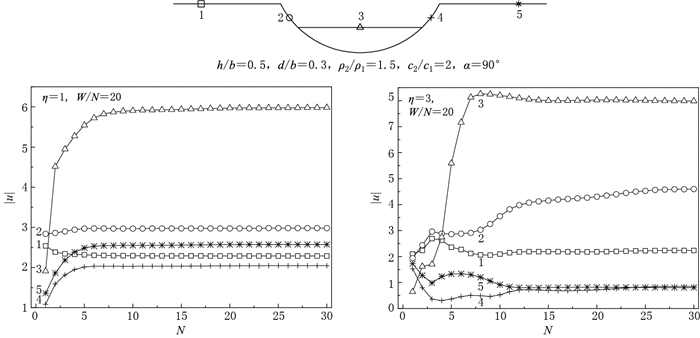
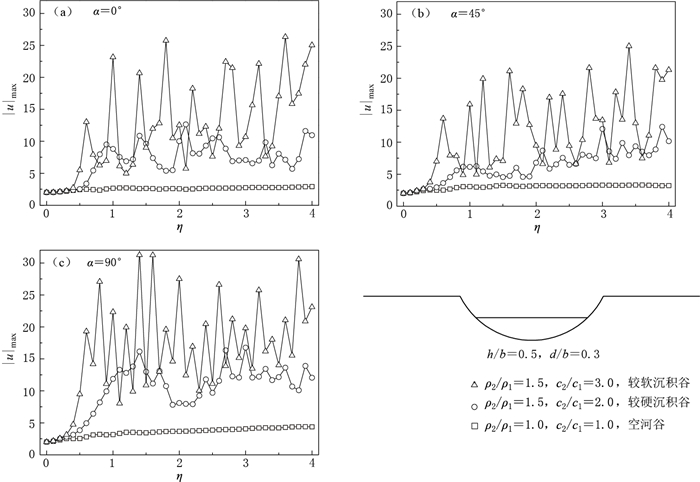
表 1 截断空河谷和沉积谷在η=1时的最大地表位移幅值|u|max
Table 1 Maximum surface displacement amplitudes for truncated canyons and alluvial valleys at η=1
h/b d/b ρ2/ρ1=1.0, c2/c1=1.0 ρ2/ρ1=1.5, c2/c1=2.0 ρ2/ρ1=1.5, c2/c1=3.0 α=0° α=45° α=90° α=0° α=45° α=90° α=0° α=45° α=90° 0.1 0.1 2.21 2.43 2.46 8.73 5.78 10.44 6.76 5.92 23.94 0.1 0.3 2.74 3.20 3.69 6.46 4.82 19.79 6.59 8.01 16.93 0.1 0.5 2.87 3.44 4.11 6.40 6.85 13.30 5.77 5.24 7.91 0.1 0.7 2.54 3.48 3.81 5.15 3.98 5.59 11.98 10.91 17.48 0.5 0.1 2.20 2.42 2.42 5.16 3.83 12.65 11.54 7.23 13.32 0.5 0.3 2.66 3.06 3.16 8.81 6.15 11.87 23.17 15.91 22.35 0.5 0.5 2.75 3.11 3.36 3.45 3.05 3.28 5.41 3.07 5.17 1.0 0.1 2.18 2.37 2.38 7.01 6.92 10.26 8.81 6.57 8.55 1.0 0.3 2.50 2.82 2.90 3.19 2.76 3.16 4.89 3.29 4.82 
下载: 导出CSV
表 2 截断空河谷和沉积谷在η=4时的最大地表位移幅值|u|max
Table 2 Maximum surface displacement amplitudes for truncated canyons and alluvial valleys at η=4
h/b d/b ρ2/ρ1=1.0, c2/c1=1.0 ρ2/ρ1=1.5, c2/c1=2.0 ρ2/ρ1=1.5, c2/c1=3.0 α=0° α=45° α=90° α=0° α=45° α=90° α=0° α=45° α=90° 0.1 0.1 2.64 3.53 4.38 6.15 8.18 19.98 18.32 15.08 17.15 0.1 0.3 2.50 3.98 4.44 12.01 15.27 12.44 13.42 9.89 14.41 0.1 0.5 2.85 3.63 4.31 5.87 8.62 12.24 18.89 13.18 18.33 0.1 0.7 3.01 3.76 4.13 6.63 13.00 16.38 21.39 21.42 25.86 0.5 0.1 2.56 3.16 3.78 6.54 8.95 9.27 6.70 10.26 18.43 0.5 0.3 2.92 3.22 4.38 10.93 10.13 12.01 25.09 21.39 23.19 0.5 0.5 3.09 3.16 4.23 10.54 10.41 9.68 22.36 10.86 30.48 1.0 0.1 2.65 2.97 2.98 7.31 6.38 7.76 10.23 11.88 13.89 1.0 0.3 2.82 2.88 3.42 8.32 10.97 9.31 9.33 14.72 11.16
下载: 导出CSV
-
巴振宁, 梁建文. 2014.瑞雷波斜入射下层状半空间中沉积谷地周围的三维散射研究[J].地震学报, 36(4): 571-583. http://www.dzxb.org/Magazine/Show?id=28985 Ba Z N, Liang J W. 2014. 3D scattering by an alluvial valley embedded in a layered half-space for obliquely incident Rayleigh waves[J]. Acta Seismologica Sinica, 36(4): 571-583 (in Chinese). http://www.dzxb.org/Magazine/Show?id=28985
刘中宪, 黄磊. 2015.含软夹层层状沉积谷地对P、SV和Rayleigh波的散射[J].地震工程与工程振动, 35(1): 105-117. http://www.cqvip.com/QK/95364X/201501/664249574.html Liu Z X, Huang L. 2015. P, SV and Rayleigh waves scattering in layered alluvial valleys with soft interlayer[J]. Earthquake Engineering and Engineering Vibration, 35(1): 105-117 (in Chinese). http://www.cqvip.com/QK/95364X/201501/664249574.html
杨彩红, 梁建文, 张郁山. 2006.多层沉积凹陷地形对平面SH波散射问题的解析解[J].岩土力学, 27(12): 2191-2196. doi: 10.3969/j.issn.1000-7598.2006.12.020 Yang C H, Liang J W, Zhang Y S. 2006. Analytical solution of scattering of plane SH waves around a canyon with multi-layered alluvia[J]. Rock and Soil Mechanics, 27(12): 2191-2196 (in Chinese). doi: 10.3969/j.issn.1000-7598.2006.12.020
袁晓铭, 李雨润, 孙锐. 2002.圆弧状沉积盆地与软土单覆盖层出平面地表运动对比[J].地震工程与工程振动, 22(4): 16-21. http://d.wanfangdata.com.cn/Periodical/dzgcygczd200204003 Yuan X M, Li Y R, Sun R. 2002. Comparison of out-of-plane surface ground motion between a circular-arc alluvial valley and a single overburden soft layer[J]. Earthquake Engineering and Engineering Vibration, 22(4): 16-21 (in Chinese). http://d.wanfangdata.com.cn/Periodical/dzgcygczd200204003
Abramowitz M, Stegun I A. 1964. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables[M]. New York: Dover: 363.
Assimaki D, Gazetas G. 2004. Soil and topographic amplification on canyon banks and the 1999 Athens earthquake[J]. J Earthq Eng, 8(1): 1-43. doi: 10.1142/S1363246904001250
Assimaki D, Gazetas G, Kausel E. 2005a. Effects of local soil conditions on the topographic aggravation of seismic motion: Parametric investigation and recorded field evidence from the 1999 Athens earthquake[J]. Bull Seismol Soc Am, 95(3): 1059-1089. doi: 10.1785/0120040055
Assimaki D, Kausel E, Gazetas G. 2005b. Soil-dependent topographic effects: A case study from the 1999 Athens earthquake[J]. Earthquake Spectra, 21(4): 929-966. doi: 10.1193/1.2068135
Assimaki D, Kausel E. 2007. Modified topographic amplification factors for a single-faced slope due to kinematic soil-structure interaction[J]. J Geotech Geoenviron Eng, 133(11): 1414-1431. doi: 10.1061/(ASCE)1090-0241(2007)133:11(1414)
Baise L G, Glaser S D, Dreger D. 2003. Site response at Treasure and Yerba Buena Islands, California[J]. J Geotech Geoenviron Eng, 129(6): 415-426. https://core.ac.uk/display/9084226
Bielak J, Xu J F, Ghattas O. 1999. Earthquake ground motion and structural response in alluvial valleys[J]. J Geotech Geoenviron Eng, 125(5): 413-423. doi: 10.1061/(ASCE)1090-0241(1999)125:5(413)
Cao H, Lee V W. 1989. Scattering of plane SH waves by circular cylindrical canyons with variable depth-to-width ratio[J]. Eur Earthq Eng, 3(2): 29-37. https://www.researchgate.net/publication/270979438_Scattering_of_plane_SH_waves_by_circular_cylindrical_canyons_with_variable_depth-to-width_ratio
Chaillat S, Bonnet M, Semblat J F. 2009. A new fast multi-domain BEM to model seismic wave propagation and amplification in 3-D geological structures[J]. Geophys J Int, 177(2): 509-531. doi: 10.1111/gji.2009.177.issue-2
Gao Y, Zhang N, Li D, Liu H, Cai Y, Wu Y. 2012. Effects of topographic amplification induced by a U-shaped canyon on seismic waves[J]. Bull Seismol Soc Am, 102(4): 1748-1763. doi: 10.1785/0120110306
Gao Y, Zhang N. 2013. Scattering of cylindrical SH waves induced by a symmetrical V-shaped canyon: Near-source topographic effects[J]. Geophys J Int, 193(2): 874-885. doi: 10.1093/gji/ggs119
Gatmiri B, Arson C. 2008. Seismic site effects by an optimized 2D BE/FE method Ⅱ. Quantification of site effects in two-dimensional sedimentary valleys[J]. Soil Dyn Earthquake Eng, 28(8): 646-661. doi: 10.1016/j.soildyn.2007.09.002
Gatmiri B, Arson C, Nguyen K V. 2008. Seismic site effects by an optimized 2D BE/FE method Ⅰ. Theory, numerical optimization and application to topographical irregularities[J]. Soil Dyn Earthquake Eng, 28(8): 632-645. doi: 10.1016/j.soildyn.2007.09.001
Gazetas G, Kallou P V, Psarropoulos P N. 2002. Topography and soil effects in the MS5.9 Parnitha (Athens) earthquake: The case of Adámes[J]. Natural Hazards, 27(1/2): 133-169. doi: 10.1023/A:1019937106428
Gelagoti F, Kourkoulis R, Anastasopoulos I, Tazoh T, Gazetas G. 2010. Seismic wave propagation in a very soft alluvial valley: Sensitivity to ground-motion details and soil nonlinearity, and generation of a parasitic vertical component[J]. Bull Seismol Soc Am, 100(6): 3035-3054. doi: 10.1785/0120100002
Gelagoti F, Kourkoulis R, Anastasopoulos I, Gazetas G. 2012. Nonlinear dimensional analysis of trapezoidal valleys subjected to vertically propagating SV waves[J]. Bull Seismol Soc Am, 102(3): 999-1017. doi: 10.1785/0120110182
Harrington R F. 1967. Matrix methods for field problems[J]. Proc IEEE, 55(2): 136-149. doi: 10.1109/PROC.1967.5433
Lanzo G, Pagliaroli A. 2009. Numerical modeling of site effects at San Giuliano di Puglia (Southern Italy) during the 2002 Molise seismic sequence[J]. J Geotech Geoenviron Eng, 135(9): 1295-1313. doi: 10.1061/(ASCE)GT.1943-5606.0000055
Lee V W, Wu X. 1994. Application of the weighted residual method to diffraction by 2-D canyons of arbitrary shape: Ⅰ. Incident SH waves[J]. Soil Dyn Earthq Eng, 13(5): 355-364. doi: 10.1016/0267-7261(94)90026-4
Lee V W, Chen S, Hsu I R. 1999. Antiplane diffraction from canyon above subsurface unlined tunnel[J]. J Eng Mech, 125(6): 668-675. doi: 10.1061/(ASCE)0733-9399(1999)125:6(668)
Lee V W, Luo H, Liang J W. 2006. Antiplane (SH) waves diffraction by a semicircular cylindrical hill revisited: An improved analytic wave series solution[J]. J Eng Mech, 132(10): 1106-1114. doi: 10.1061/(ASCE)0733-9399(2006)132:10(1106)
Luo H. 2008. Diffraction of SH-Waves By Surface or Sub-Surface Topographies With Application to Soil-Structure Interaction on Shallow Foundations[D]. Los Angeles: University of Southern California: 2-5.
Psarropoulos P N, Tazoh T, Gazetas G, Apostolou M. 2007. Linear and nonlinear valley amplification effects on seismic ground motion[J]. Soils Found, 47(5): 857-871. doi: 10.3208/sandf.47.857
Sánchez-Sesma F J. 1987. Site effects on strong ground motion[J]. Soil Dyn Earthquake Eng, 6(2): 124-132. doi: 10.1016/0267-7261(87)90022-4
Seed H B, Idriss I M. 1969. Influence of soil conditions on ground motions during earthquakes[J]. J Soil Mech Found Div, 95(1): 99-138. http://cedb.asce.org/CEDBsearch/record.jsp?dockey=0016200
Semblat J F, Kham M, Parara E, Bard P Y, Pitilakis K, Makra K, Raptakis D. 2005. Seismic wave amplification: Basin geometry vs soil layering[J]. Soil Dyn Earthquake Eng, 25(7/10): 529-538. https://hal.archives-ouvertes.fr/hal-00107884/document
Semblat J F, Lokmane N, Driad-Lebeau L, Bonnet G. 2010. Local amplification of deep mining induced vibrations part. 2: Simulation of ground motion in a coal basin[J]. Soil Dyn Earthquake Eng, 30(10): 947-957. doi: 10.1016/j.soildyn.2010.04.006
Semblat J F. 2011. Modeling seismic wave propagation and amplification in 1D/2D/3D linear and nonlinear unbounded media[J]. Int J Geomech, 11(6): 440-448. doi: 10.1061/(ASCE)GM.1943-5622.0000023
Todorovska M I, Lee V W. 1991. Surface motion of shallow circular alluvial valleys for incident plane SH waves-analytical solution[J]. Soil Dyn Earthquake Eng, 10(4): 192-200. doi: 10.1016/0267-7261(91)90033-V
Trifunac M D. 1971. Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves[J]. Bull Seismol Soc Am, 61(6): 1755-1770. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.529.9298
Trifunac M D. 1972. Scattering of plane SH waves by a semi-cylindrical canyon[J]. Earthquake Eng Struct Dyn, 1(3): 267-281. doi: 10.1002/(ISSN)1096-9845
Tsaur D H, Chang K H. 2008. SH-waves scattering from a partially filled semi-circular alluvial valley[J]. Geophys J Int, 173(1): 157-167. doi: 10.1111/gji.2008.173.issue-1
Tsaur D H, Chang K H. 2009. Scattering of SH waves by truncated semicircular canyon[J]. J Eng Mech, 135(8): 862-870. doi: 10.1061/(ASCE)0733-9399(2009)135:8(862)
Yuan X M, Men F L. 1992. Scattering of plane SH waves by a semi-cylindrical hill[J]. Earthquake Eng Struct Dyn, 21(12): 1091-1098. doi: 10.1002/(ISSN)1096-9845
Yuan X M, Liao Z P. 1994. Scattering of plane SH waves by a cylindrical canyon of circular-arc cross-section[J]. Soil Dyn Earthquake Eng, 13(6): 407-412. doi: 10.1016/0267-7261(94)90011-6
Yuan X M, Liao Z P. 1995. Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section[J]. Earthquake Eng Struct Dyn, 24(10): 1303-1313. doi: 10.1002/(ISSN)1096-9845
Zhang N, Gao Y F, Cai Y Q, Li D Y, Wu Y X. 2012a. Scattering of SH waves induced by a non-symmetrical V-shaped canyon[J]. Geophys J Int, 191(1): 243-256. doi: 10.1111/gji.2012.191.issue-1
Zhang N, Gao Y F, Li D Y, Wu Y X, Zhang F. 2012b. Scattering of SH waves induced by a symmetrical V-shaped canyon: A unified analytical solution[J]. Earthquake Eng Eng Vib, 11(4): 445-460. doi: 10.1007/s11803-012-0135-z
Zhang N, Gao Y F, Yang J, Xu C J. 2015. An analytical solution to the scattering of cylindrical SH waves by a partially filled semi-circular alluvial valley: Near-source site effects[J]. Earthquake Eng Eng Vib, 14(2): 189-201. doi: 10.1007/s11803-015-0016-3
Zhang N, Gao Y F, Pak R Y S. 2017. Soil and topographic effects on ground motion of a surficially inhomogeneous semi-cylindrical canyon under oblique incident SH waves[J]. Soil Dyn Earthquake Eng, 95(1): 17-28. doi: 10.1080/13632460409350479?scroll=top&needAccess=true
计量
- 文章访问数: 703
- HTML全文浏览量: 304
- PDF下载量: 25
