Effects of rock damage on seismic source characteristics of underground nuclear explosions
-
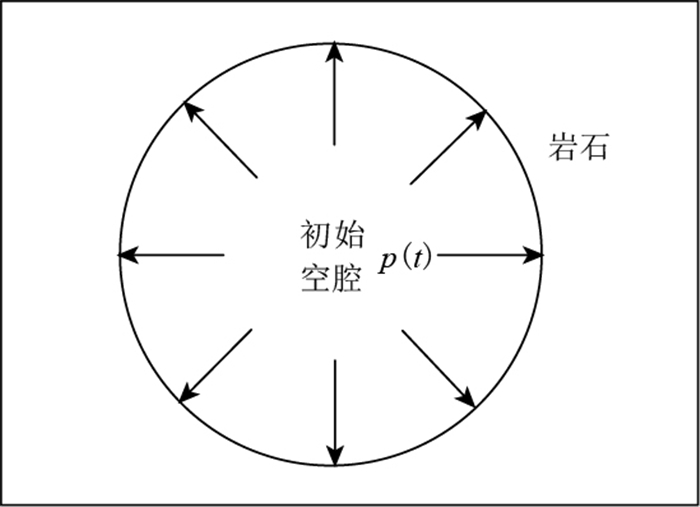
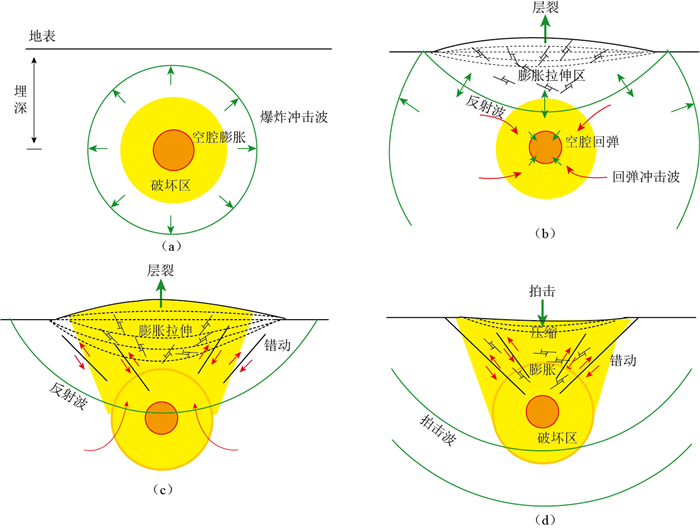
摘要: 本文在考虑动态力源扰动的情况下,对岩石损伤对地震波辐射的影响及其震源表示进行了理论推导,证明了当有动态力源存在时,Ben-Zion和Ampuero于2009年给出的结果只是岩石非弹性响应对震源及相应地震波场的贡献,而非其全部.在此基础上,应用相关结果对岩石损伤破坏对地下核爆炸震源成分的影响进行了分析,给出了地下核爆炸情况下补偿线性偶极子源和构造应力释放与岩石损伤破坏之间的关系.结果表明,地下核爆炸补偿线性偶极子源主要来自于地表反射拉伸波和空腔回弹冲击波等造成的爆心上方锥形区域中的岩石破坏,而构造应力释放则主要来自于整个岩石破坏区内的构造应力松弛.Abstract: In this paper we readdress the effects of rock damage on seismic radiation and its source representation taking account of the existence of dynamic force disturbances in the source. We proved that, when dynamic force distur-bances exist, the result given by Ben-Zion and Ampuero in 2009 is not for the whole seismic wave field but for the contribution by the nonelasticity. Furthermore, based on the theoretical formulations obtained in this paper, we analyzed effects of rock damage upon source characterizations of underground nuclear explosions and relationships between rock damages and their non-isotropic secondary sources including the compensated linear vector dipole (CLVD) and tectonic stress release. The results show that, the CLVD of an underground explosion mainly comes from rock damages within a cone area above the explosion itself which is induced by surface reflected tensional shock waves and cavity rebound, while the tectonic stress release may be caused by stress relaxation within whole damaged area of the explosion.
-
Keywords:
- rock damage /
- seismic source /
- underground nuclear explosion /
- CLVD /
- tectonic stress release
-
引言
重庆地区位于四川盆地东南缘,华南地震区的长江中游地震带内(图1)。重庆区域内的断裂主要以基底断裂为主,如华蓥山断裂、长寿—遵义断裂、七曜山—金佛山断裂、彭水断裂和城口断裂,这些基底断裂对重庆的地震活动具有明显的控制作用。此外,四川盆地与其周缘的龙门山、米仓山—大巴山、七曜山—金佛山、大娄山及大凉山形成了典型的盆山体系。这些盆山构造非常复杂,并且对盆地内油气的分布有较大的控制作用。四川盆地油气资源丰富,其东南缘的地震活动可能与所在地区的盐岩和油气的存在相关,几个典型的注水诱发地震序列的震源集中在三叠系以下的沉积岩地层中(雷兴林等,2014)。特殊的地质构造和地理位置造成了重庆地区地震强度不高、震源浅的特点(丁仁杰,李克昌,2004)。2010年以来重庆及周边地区共发生6次MS4.5以上地震,分别为2010年重庆荣昌MS4.7地震、2013年重庆石柱MS4.5地震、2013年湖北巴东MS5.1地震、2014年湖北秭归MS4.7地震、2016年重庆荣昌MS4.8地震和2017年重庆武隆MS5.0地震。这些地震的震源深度均较浅,其中荣昌MS4.7地震震源深度仅1.85 km左右(王小龙等,2012),最深的武隆MS5.0地震震源深度也仅10 km左右(李翠平等,2019)。
地震的孕育与介质性质及结构密切相关,重庆地区的地震震源较浅,因此有必要深入研究重庆地区的浅层速度结构。并且地壳的浅层速度结构可为盆地基底、微小震定位和地壳上地幔深部结构成像提供重要的研究基础,亦可为地震工程场地评估和防震减灾提供重要参考。
目前,地壳浅层S波速度结构研究主要有地震勘探和天然源等方法。地震勘探虽然具有信噪比高、精度高的特点,但是探测成本较高、对环境具有一定的破坏性。天然源则是利用背景噪声和天然地震事件等数据研究浅层结构,该方法利用地震台站的地震波形资料,节约了成本。例如,基于背景噪声瑞雷面波频散曲线研究地表至浅层数百米深度的S波速度结构(张宝龙等,2016;王娟娟等,2018)。
此外,接收函数直达P波垂向与径向的幅度比与浅层S波速度有关(Ammon,1991)。近年来,基于接收函数直达P波振幅约束浅层结构的新方法取得了新进展。Julià (2007)经过半空间接收函数公式推导,得出了接收函数直达P波的理论振幅公式,证明直达P波垂向与径向的幅度比与射线参数和浅层S波速度有关;并认为随着接收函数有限频率的增加,入射波的波长变短,S波速度值对应的深度范围变浅。钱银苹等(2018)基于接收函数直达P波理论振幅公式进行了数值实验,结果表明该公式能够对近地表S波速度结构进行有效约束,之后又基于不同速度模型对近地表S波速度对应的深度进行了数值试验,最后将该方法应用到青藏高原东北缘。王旭等(2019)同样针对该公式进行了理论模拟,并利用不同频率的接收函数直达P波振幅计算了青藏高原东北缘流动地震台阵下方的浅层S波速度结构。
本文将采用接收函数直达P波约束浅层S波速度的方法研究重庆及周边地区台站下方浅层S波速度结构,探讨该区域浅层速度结构与地质构造的关系,为研究区孕震环境提供科学依据。
1. 数据与方法
1.1 数据资料获取
本文收集整理了重庆台网及邻区固定台站自2011年1月至2018年10月观测到的远震波形记录,选取了MS≥5.5、震中距为30°—90°的远震波形(图2)。对所选波形作如下处理:① 截取P波到时前20 s和后80 s的远震波形数据;② 将截取后的N,E,Z分量波形旋转至R,T,Z分量;③ 选取多个高斯滤波因子α (共6个滤波因子:1.0,1.5,2.5,3,4,5,分别对应不同的通带频率,也即不同深度信息),利用时间域反褶积方法,计算P波接收函数。经过自动及人工挑选,平均每个滤波因子可挑选出震相清晰的接收函数1万2 500多条。图3为华蓥山断裂附近的ROC台6个滤波因子的R向接收函数。
1.2 台站下方浅层S波速度及误差分析
在P波初动附近(±2 s)提取径向接收函数和垂向接收函数的波峰极大值,用垂向分量最大振幅值对径向最大振幅值作归一处理(Ammon,1990),得到的结果即为接收函数直达P波绝对幅度的观测值。
根据入射P波引起的自由表面位移方程(Aki,Richards,2002)可计算直达P波绝对幅度的理论值,即
$$ \frac{{r}_{0}}{{{\textit{z}}}_{0}}=\frac{2p{\eta }_{{v}_{{\rm{S}}0}}}{{\dfrac{1}{v^2_{{\rm{S}}0}}}-2{p}^{2}} \text{,} $$ (1) 式中,
${\eta }_{{v}_{{\rm{S0}}}}=\sqrt {v^2_{\rm{S0}} - 2p^2}$ 为S波的垂直慢度,p为水平慢度(射线参数),$ {{v}}_{\rm{S}0} $ 为浅层S波速度。式(1)表示在低频时震相振幅与平均速度之间的关系(钱银苹等,2018)。绝对幅度的理论值与观测值之间的差异用Misfit (
$ {{v}}_{{\rm{S}}0} $ )表示,即$$ \mathrm{M}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{i}\mathrm{t} ( {v}_{{\rm{S}}0} ) =\sqrt{{\sum\limits _{i}{ ( {A}^{{\rm{obs}}}-{A}_{i}^{{\rm{syn}}} ) }^{2}}}\;\;\text{,} $$ (2) 式中,
$ {A}^{\mathrm{o}\mathrm{b}\mathrm{s}} $ 为绝对幅度的观测值,$ {A}_{i}^{\mathrm{s}\mathrm{y}\mathrm{n}} $ 为不同$ {{v}}_{{\rm{S}}0} $ 计算的理论值。Misfit最小值所对应的${{v}}_{\rm{S}0}$ 即为vS0的最优值,每条接收函数可确定一个$ {{v}}_{{{\rm{S}}}0} $ 。实际处理中,对于一个台站,按1°的震中距叠加接收函数,利用叠加的接收函数确定
$ {{v}}_{\rm{S}0} $ ,它们的平均值即为这个台站的浅层S波速度。因每叠加1°,接收函数都可以确定一个vS值,为了评估计算结果的质量,以均方误差ε来表示计算误差。当误差大于0.4时,舍弃该台站的结果。图4为ROC台滤波因子为5时确定的
$ {{v}}_{{\rm{S}}0} $ 值,计算结果为(2.68±0.13) km/s。2. 结果
根据上述流程,对重庆及邻区固定台站的不同高斯滤波因子(1.0,1.5,2.5,3,4,5)的接收函数进行了处理,共得到6个不同频率接收函数的浅层S波速度。本文参考了钱银苹等(2018)利用数值试验估计出的不同频率S波速度对应的深度范围,其中:α为1时表示10—11 km深度;α为1.5时表示7 km左右深度;α为2.5时表示4—5 km深度;α为3和4时表示3—4 km深度;α为5时表示2—3 km深度。根据不同滤波因子的接收函数计算的重庆及邻区台站的vS,绘制了S波速度分布图(图5)。从图中可以看出,重庆境内长江沿线的近地表S波速度在2—3 km左右深度处较低(图5a)。七曜山—金佛山断裂为四川盆地的东南边界,在2—3 km深度处四川盆地的S波低速异常与四川盆地沉积特征相符。华蓥山断裂附近台站(ROC,HYS,XHA)的S波速度结构与断裂两侧的台站下方相比表现为高速异常,与王小龙等(2013)周期5 s的相速度结果一致。城口断裂以北的大巴山地区(CHK,HCB,WUX,SHL,SXH)S波速度较高。彭水台网(GOT,LUJ,LAX,XIT,ANZ)S波速度较低,应为水库渗透影响,导致该地区速度出现相对低值。而水库西北方的武隆地区呈现明显高速,速度为2.9 km/s。α=2.5—4表示3—5 km左右深度,该深度范围与α=5对应深度的速度分布特征较一致,台站的速度变化小于0.2 km/s,并且速度值随深度增大。α=1.5和1对应的深度范围,研究区的S波速度进一步增大。武隆、仙女山、涪陵地区高值区范围增大,该区S波平均速度约为3.33 km/s,而四川盆地在α=1.5和1时对应的深度范围仍为明显的低速异常,说明8—10 km左右深度,四川盆地仍为沉积层。
3. 讨论
3.1 重庆及周边浅层S波速度结构
除彭水台网外,重庆浅层S波速度结构与盆山构造明显相关,盆地内低速异常与沉积层特征对应,大巴山、大娄山区域则表现相对高速特征。王小龙等(2013)及王小龙(2017)利用地震背景噪声成像技术反演三峡库区5—40 s的瑞雷面波相速度分布模型及三维剪切波速度模型,结果也显示四川盆地周边的龙门山、米仓山、大巴山、七曜山和大娄山等地质构造与地壳S波速度结构具有明显的对应关系。α=1.5和1对应的深度范围,四川盆地仍为明显的低速异常,说明8—10 km左右深度,四川盆地仍为沉积层;宋晓东等(2015)通过对面波层析成像的三维S波速度模型的研究认为,四川盆地内部上地壳绝大部分都表现为低速,反映出盆地内存在很厚的沉积层;李建有等(2018)利用低频和高频接收函数的两步反演地壳S波速度结构,认为四川盆地4—10 km呈现相对低速区,S波速度介于2.8—3.2 km/s之间,基本反映了四川盆地绝大部分为沉积岩或新生代松软覆盖层的低速分布特征(范军等,2015);华蓥山断裂S波速度(HYS,ROC,XHA)均较其两侧沉积层速度高,反映了四川盆地沉积层中间薄两侧厚的特点;四川盆地的深地震反射剖面显示四川盆地上地壳以沉积层为主,从西北向东南逐渐变薄,在龙门山前沉积层厚度超过15 km,在华蓥山下沉积层减薄到8 km并发生了褶皱变形,形成了华蓥山薄皮褶皱冲断带(王海燕等,2017),与本文计算的S波特征相符。华蓥山以东的川东地区(XIM,FUP,LIJ,HOT,WAZ,SHG,LOH,SHZ,YAL,WUX,JIP)的浅层S波速度表现为低速异常。川东地区是华蓥山与七曜山之间的褶皱变形区,浅层发育一系列NE-NNE向的隔档式褶皱,并且该区发育以寒武系和三叠系膏盐岩为主的多套滑脱层,挤压变形后形成多套滑脱层构造,滑脱构造下覆寒武系底达8 km左右(王志勇等,2018)。
3.2 孕震环境
本文讨论2010年以来重庆5次显著地震,分别为2010年重庆荣昌MS4.7地震(图5a)、2013年重庆石柱MS4.5地震(图5c)、2016年垫江MS4.4地震(图5a)、2016年重庆荣昌MS4.8地震(图5b)和2017年重庆武隆MS5.0地震(图5f)。5次地震的震中位置来自国家地震台网中心正式测定和精定位,震源深度来自CAP方法和精定位。
2010年9月10日荣昌MS4.7地震震源机制解最佳深度为2.93 km (王志伟等,2018),2016年12月27日MS4.8地震最佳拟合深度为3.8 km,同样为浅源地震。α=4和5对应深度处ROC台S波速度分别为2.69 km/s和2.68 km/s,与重庆地区平均速度2.66 km/s较一致,没有明显的高低速特征。许多研究表明荣昌地区地震活动与天然气开采过程中的注水密切相关,注水引起的流体压力扩散导致断层带孔隙压力增加,使得断层带强度降低,触发断层活动(王志伟等,2018),而震源深度与主要储藏层及注水井有关(王小龙等,2012)。
2016年垫江MS4.4地震的波形具有明显的浅源特征,CAP方法反演出的震源深度约为1—2 km (黄世源等,2020)。地震位于川东滑脱构造地区,黄世源等(2020)认为在区域应力作用下,震源区沉积盖层内部的软弱地层受挤压变形,导致地层内斜交的裂隙发生切层失稳滑动,从而诱发了垫江MS4.4地震,而震中附近(XIM台)较低速度的S波为该地震的发生提供了条件。
石柱MS4.5柱地震Rg面波发育明显,震源深度约为4 km (王同军等,2015),地震同样发生在低速异常的川东构造区内,与垫江MS4.4地震不同的是,石柱MS4.5地震震中附近有方斗山断裂。
武隆MS5.0地震发生在七曜山—金佛山断裂与彭水断裂之间,震源深度约为10 km (李翠平等,2019)(图5f),震源区附近S波速度显示出明显的横向不均匀分布特征,武隆地区S波速度明显高于川东滑脱构造区和彭水台网。其中α=1—1.5对应的深度范围,WUL台出现明显的高速异常,S波速度为3.22—3.44 km/s。武隆MS5.0地震发生在高低速交界部位的有利于积累应变的高速体一侧,许多研究表明地壳高低速过渡区域可能是中强地震孕育和发生的关键部位。
4. 结论
本文基于重庆台网及邻区固定台站自2011年1月至2018年10月观测到的远震波形记录,利用接收函数直达P波振幅约束浅层结构的方法计算了重庆及周边地区台站下方浅层S波速度结构,该方法不依赖初始模型,不需要反演,能有效抑制速度结果的不唯一性。最终形成以下几点认识:
重庆浅层S波速度结构与盆山构造明显相关,盆地内低速异常与沉积层特征对应,大巴山、大娄山区域均表现为相对高速特征;华蓥山断裂S波速度均较其两侧沉积层速度高,表现出四川盆地沉积层中间薄两侧厚的特点;华蓥山以东的川东地区的浅层S波速度表现为低速异常,该区存在多套滑脱层构造。
此外,本文还讨论了2010年以来重庆5次显著地震的孕震环境:川东滑脱构造地区的垫江MS4.4地震和石柱MS4.5地震两个浅源地震与该区明显的低速异常有关;荣昌MS4.7和MS4.8地震震源区没有明显的高低速特征,可能与天然气开采过程中的注水相关;武隆MS5.0地震发生在高低速交界部位的有利于积累应变的高速体的一侧。
审稿人提出了建设性的建议,作者在此表示衷心的感谢. -
-
何永锋, 赵克常, 张献兵. 2010.地下核爆炸的主要非爆炸源机制[J].地球物理进展, 25(3): 789-794. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201003009.htm He Y F, Zhao K C, Zhang X B. 2010. Primary non-explosive source mechanisms for underground nuclear explosions[J]. Progress in Geophysics, 25(3): 789-794 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201003009.htm
何永锋, 赵克常, 张献兵, 马裕然, 王洋. 2012.地下核爆炸地震波二次源特征[J].地球物理学报, 55(5): 1742-1748. doi: 10.6038/j.issn.0001-5733.2012.05.031 He Y F, Zhao K C, Zhang X B, Ma Y R, Wang Y. 2012. The characteristic of the waveform from the second source induced by underground explosion[J]. Chinese Journal of Geophysics, 55(5): 1742-1748 (in Chinese). doi: 10.6038/j.issn.0001-5733.2012.05.031
徐恒垒, 靳平, 朱号锋, 李欣. 2017. 2013、2016年两次朝鲜核试验P波和面波信号幅值比差异的观测与分析[J].地球物理学报, 60(7): 2652-2662. doi: 10.6038/cjg20170713 Xu H L, Jin P, Zhu H F, Li X. 2017. Observations and analyses of the amplitude-ratio differences among P waves and surface waves between 2013 and 2016 nuclear tests of North Korea[J]. Chinese Journal of Geophysics, 60(7): 2652-2662 (in Chinese). doi: 10.6038/cjg20170713
Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods[M]. San Francisco: W.H.Freeman: 57-60.
Aki K, Reasenberg P, DeFazio T, Tsai Y B. 1969. Near-field and far-field seismic evidences for triggering of an earthquake by the BENHAM explosion[J]. Bull Seismol Soc Am, 59(6): 2197-2207. https://pubs.geoscienceworld.org/bssa/article-lookup/59/6/2197
Aki K, Tsai Y B. 1972. Mechanism of Love-wave excitation by explosive sources[J]. J Geophys Res, 77(8): 1452-1475. doi: 10.1029/JB077i008p01452
Archambeau C B. 1972. The theory of stress wave radiation from explosions in prestressed media[J]. Geophys J Int, 29(3): 329-366. doi: 10.1111/j.1365-246X.1972.tb06163.x
Ben-Zion Y, Ampuero J P. 2009. Seismic radiation from regions sustaining material damage[J]. Geophys J Int, 178(3): 1351-1356. doi: 10.1111/gji.2009.178.issue-3
Brune J N, Pomeroy P W. 1963. Surface wave radiation patterns for underground nuclear explosions and small-magnitude earthquakes[J]. J Geophys Res, 68(17): 5005-5028. doi: 10.1029/JZ068i017p05005
Bukchin B G, Mostinsky A Z, Egorkin A A, Levshin A L, Ritzwoller M H. 2001. Isotropic and nonisotropic components of earthquakes and nuclear explosions on the Lop Nor Test Site, China[J]. Pure Appl Geophys, 158(8): 1497-1515. doi: 10.1007/PL00001231
Byerlee J D. 1978. Friction of rocks[J]. Pure Appl Geophys, 116(4/5): 615-626. https://www.researchgate.net/publication/226604677_Friction_of_Rocks
Denny M D, Johnson L R. 1991. The explosion seismic source function: Models and scaling laws reviewed[G]//Explosion Source Phenomenology, Geophys Monogr Ser, Vol.65. Washington D C: The American Geophysical Union: 1-24.
Fisk M D. 2006. Source spectral modeling of regional P/S discriminants at nuclear test sites in China and the former Soviet Union[J]. Bull Seismol Soc Am, 96(6): 2348-2367. doi: 10.1785/0120060023
Fisk M D. 2007. Corner frequency scaling of regional seismic phases for underground nuclear explosions at the Nevada Test Site[J]. Bull Seismol Soc Am, 97(3): 977-988. doi: 10.1785/0120060186
Jin P, Xu H L, Wang H C, Pan C Z, Xu X, Wang X L. 2017. Secondary seismic sources behind amplitude ratios between the first 2016 and 2013 North Korean nuclear tests[J]. Geophys J Int, 211(1): 322-334. doi: 10.1093/gji/ggx289.
Johnson L R, Sammis C G. 2001. Effects of rock damage on seismic waves generated by explosions[J]. Pure Appl Geophys, 158(11): 1869-1908. doi: 10.1007/PL00001136
Knopoff L, Randall M J. 1970. The compensated linear vector dipole: A possible mechanism for deep earthquakes[J]. J Geophys Res, 75(26): 4957-4963. doi: 10.1029/JB075i026p04957
Lambert D G, Flinn E A, Archambeau C B. 1972. A comparative study of the elastic wave radiation from earthquakes and underground explosions[J]. Geophys J Int, 29(4): 403-432. doi: 10.1111/j.1365-246X.1972.tb06168.x
Massé R P. 1981. Review of seismic source models for underground nuclear explosions[J]. Bull Seismol Soc Am, 71(4): 1249-1268. https://pubs.geoscienceworld.org/bssa/article-lookup/71/4/1249
Mueller R A, Murphy J R. 1971. Seismic characteristics of underground nuclear detonations, Part Ⅰ. Seismic spectrum scaling[J]. Bull Seismol Soc Am, 61(6): 1675-1692. http://bssa.geoscienceworld.org/content/61/6/1675
Murphy J R, Stevens J L, Kohl B C, Bennett T J. 2014. Reply to "Comment on 'Advanced seismic analyses of the source characteristics of the 2006 and 2009 North Korean nuclear tests' by J. R. Murphy, J. L. Stevens, B. C. Kohl, and T. J. Bennett" by H. J. Patton and F. V. Pabian[J]. Bull Seismol Soc Am, 104(4): 2111-2115. doi: 10.1785/0120140057
Patton H J, Pabian F V. 2014. Comment on "Advanced seismic analyses of the source characteristics of the 2006 and 2009 North Korean nuclear tests" by J. R. Murphy, J. L. Stevens, B. C. Kohl, and T. J. Bennett[J]. Bull Seismol Soc Am, 104(4): 2104-2110. doi: 10.1785/0120130262
Patton H J, Taylor S R. 2011. The apparent explosion moment: Inferences of volumetric moment due to source medium damage by underground nuclear explosions[J]. J Geophys Res, 116(B3): B03310. doi: 10.1029/2010JB007937.
Randall M J. 1966. Seismic radiation from a sudden phase transition[J]. J Geophys Res, 71(22): 5297-5302. doi: 10.1029/JZ071i022p05297
Stevens J L, Thompson T W. 2015. 3D numerical modeling of tectonic strain release from explosions[J]. Bull Seismol Soc Am, 105(2A): 612-621. doi: 10.1785/0120140125
Taylor S R, Patton H J. 2013. Can teleseismic mb be affected by rock damage around explosions?[J]. Geophys Res Lett, 40(1): 100-104. doi: 10.1029/2012GL054526
Vavryuk V, Kim S G. 2014. Nonisotropic radiation of the 2013 North Korean nuclear explosion[J]. Geophys Res Lett, 41(20): 7048-7056. doi: 10.1002/2014GL061265





 下载:
下载: