Coseismic response of water level in Xin10 well caused by MS6.7 Akto, Xinjiang, earthquake
-
摘要: 本文根据新10井数字化高频采样水位仪记录到的2016年11月25日新疆阿克陶MS6.7地震所引起的水震波，对比分析了该井水位与地表垂向运动的相关性特征，并对二者与井-含水层系统水文参数的关系进行了深入探讨.分析结果显示：①与地震波信号相似，新疆阿克陶MS6.7地震引起的新10井水震波存在两个显著的周期，即6—10 s和15—30 s；②新10井水震波响应幅度与地表垂向运动幅度整体呈正相关，且在高频阶段(频率大于0.08 Hz)二者的振幅比随着频率的减小而增大，表明该井水位对周期大于12 s的信号放大效能较高；③利用水震波与地震波的振幅比估算新10井观测含水层渗透系数的量级为10-2 cm/s，且在地震波作用过程中含水层的水文参数也存在波动.本研究表明，井水位的同震响应机理较为复杂，在分析水位同震响应特征时，高采样率的水位数据是获得可靠结果与认识的基础.
-
关键词:
- 新疆阿克陶MS6.7地震 /
- 水震波 /
- 地震波 /
- 同震响应机理
Abstract: A hydroseismogram induced by the Akto MS6.7 earthquake in Xinjiang on November 25, 2016 was recorded by digital high frequency sampling level gauge. We comparatively analyzed the correlation characteristics between the water level and the vertical ground motion, and the relationship between the above two and the hydrological parameters of well-aquifer system was carried out by a thorough discussion. The results suggested that: ① similar to the seismic signal, there are two significant periods, 6--10 s and 15--30 s in the hydroseismogram of Xin10 well induced by the Akto MS6.7 earthquake. ② overall, the response amplitude of hydroseismogram in Xin10 well was positively correlated to the amplitude of vertical ground motion, and the amplitude ratio of the two increased with the reduction in frequency at high frequency (greater than 0.08 Hz), which indicated that the water level of Xin10 well could enlarge signals with period more than 12 s more effectively. ③ permeability coefficient of Xin10 well-aquifer system was estimated at about 10-2 cm/s by using the amplitude ratio of the hydroseismogram and seismic waves, and the hydrogeological parameters in aquifer also fluctuated during the process of seismic wave action. The results in this paper also showed that the coseismic response mechanism of well water level is more complicated, and high sampling rate of water level data is the guarantee to obtain reliable results and knowledge in coseismic response of water level analysis. -
引言
我国是一个多震国家，尤其是近年来我国进入了地震高发期（胡敏章等，2019）。地震在带来直接灾害的同时，还会激发大量的次生地质灾害。特别是在山地区域，由地震激发的山体滑坡、泥石流等地质灾害将造成重大的生命财产损失，例如2008年汶川MS8.0地震就激发了海量的地震滑坡，造成重大人员伤亡和严重的房屋建筑损毁（Yuan et al，2010，2013）。在所有这些地震滑坡中，土质滑坡占据了不小的比例。因此，研究土坡地震响应规律对科学防震减灾具有重要的理论和实用价值，而开展对土坡地震响应研究工作的核心之一便是地震动参数的选取问题。
王秀英等（2010）研究了地震动参数与汶川地震诱发山体滑坡之间的关系，认为峰值加速度（peak ground acceleration，缩写为PGA）与诱发崩滑之间存在明显的正相关性；张郁山和赵凤新（2011）在地震动峰值位移（peak ground displacement，缩写为PGD）对单自由度体系非线性动力反应的影响研究中得出了地震动峰值位移对体系弹塑性速度及位移的影响；李小军（2013）进一步分析了新一代中国地震动参数区划图中考虑场地条件的地震动参数调整结果和变化特征；杜修力等（2015，2018）对地震动峰值位移对高拱坝和地下结构地震反应的响应影响作出了相应的研究，探寻了高拱坝和地下结构的地震响应与地震动峰值位移的变化关系；而陈冲等（2017）研究了地震动峰值加速度作用下含水边坡稳定性关系，认为在含水情况下，随输入峰值加速度的增大，滑动面向坡内大幅移动，由浅层破坏转变为深层破坏；张江伟等（2018）对地震动参数对土坡地震响应的影响权重进行了研究，得出地震动各参数对坡体变形位移的影响相关性。纵观目前地震动参数对边坡响应的影响规律的研究，可以看出，针对地震动峰值特征参数影响土坡地震响应的对比性研究较少。本文拟针对地震动峰值加速度（PGA）、峰值速度（PGV）和峰值位移（PGD）三个地震动峰值特征参数来研究其对土坡响应的影响规律。为此，随机选取100条含有不同PGA，PGV和PGD的实际地震动纪录，研究三个峰值特征参数对边坡动力响应的影响规律和相关性，以期为土坡地震响应研究中地震动参数选取问题提供参考依据。
1. 地震动选取
随机选取100条来自太平洋地震研究中心数据库中不同地震的原始记录，通过对每条地震动进行基线校正、积分来获取其PGA，PGV以及PGD。经统计，100条地震动的PGA的范围为0.004 1—1.225 9 g，PGV的范围为0.378—112.376 cm/s，PGD的变化范围为0.035 3—35.674 5 cm。对三种地震动峰值参数对边坡的地震响应的表现情况进行对比研究。图1-3给出了前三条地震动M1—M3的加速度、速度、位移时程曲线。
![]()
图 1 地震动M1的加速度 （a）、速度 （b）、位移 （c） 时程曲线Figure 1. Acceleration （a），velocity （b），displacement （c） time history curves of ground motion M1![]()
图 2 地震动M2的加速度 （a）、速度 （b）、位移 （c） 时程曲线Figure 2. Acceleration （a），velocity （b），displacement （c） time history curves of ground motion M2![]()
图 3 地震动M3的加速度 （a）、速度 （b）、位移 （c） 时程曲线Figure 3. Acceleration （a），velocity （b），displacement （c） time history curves of ground motion M32. 研究方法及模型建立
2.1 研究方法
在模拟、计算土坡的动力响应时，采用动力平衡方程，即
$${\boldsymbol{M}}\ddot {\boldsymbol{u}} {\text{＋}} {\boldsymbol{C}}\dot {\boldsymbol{u}} {\text{＋}} {\boldsymbol{Ku}} {\text{＝}} {\boldsymbol{F}}{\text{（}}t{\text{）}}{\text{，}}$$ (1) 式中，M为结构的质量矩阵，C为结构的阻尼矩阵，K为结构的刚度矩阵，
${\ddot{\boldsymbol u}}$ 为结构的加速度列阵，${\dot{\boldsymbol u}}$ 为结构的速度列阵，u为结构的位移列阵，F（t）为结构的节点荷载列阵。对于求解地震作用下的动力问题，动力荷载就是地震荷载，于是求解边坡地震动力稳定性问题的基本力学运动方程可写为
$$ {\boldsymbol{M}}\ddot {\boldsymbol{u}} {\text{＋}} {\boldsymbol{C}}\dot {\boldsymbol{u}} {\text{＋}} {\boldsymbol{Ku}} {\text{＝}} - {\boldsymbol{M}}{\ddot {\boldsymbol{u}}_g}{\text{（}}t{\text{）}}{\text{.}} $$ (2) 地震是一种随时间变化的复杂荷载，边坡岩土体在地震作用下往往会进入弹塑性状态，这时便无法得到解析解，解析方法也不再适用，但通过数值计算可以得到结构动力反应的数值解。在有限元模拟软件ABAQUS中分为隐式和显式两种算法，其中隐式算法是以Newmark-β法为基础，而显式模块则采用中心差分法来解决动力学问题，这些方法的中心思想是假定结构在每一个微小时间步内呈现线弹性反应，然后通过在时域内逐步积分求解。本文采用隐式算法。
2.2 模型建立
建立如图4所示的土质边坡模型，长为170 m，宽为70 m，边坡坡角为37°，模型坡高30 m，坡顶后缘长80 m。从坡顶至坡脚均匀设置P1，P2，P3，P4，P5 5个观测点（图4）用于记录边坡在地震动作用下各峰值特征参数的变化情况。假定模型材料为均质材料，表1为边坡土体的物理、力学参数。本构模型为理想的弹塑性本构模型，土坡地震模拟计算中采用摩尔-库仑强度准则，式（3），（4）为摩尔-库仑强度准则的相关公式。模型底部采用静态边界条件，侧面设置粘弹性边界，阻尼采用瑞雷阻尼形式（胡聿贤，2006）。
表 1 边坡土体参数Table 1. Parameters for soil slop参数 密度
/（kg·m−3）弹性模量
/MPa泊松比 黏聚力
/kPa内摩擦角
/°数值 2070 90.8 0.3 13.99 25 $$ \left\{ \begin{array}{l} {\tau _{{n}}} {\text{＝}} \dfrac{1}{2}{\text{（}}{\sigma _1} {\text{－}} {\sigma _3}{\text{）}}\cos \phi{\text{，}} \\ {\sigma _n} {\text{＝}} \dfrac{1}{2}{\text{（}}{\sigma _1} {\text{＋}} {\sigma _3}{\text{）}} {\text{＋}} \dfrac{1}{2}{\text{（}}{\sigma _1} {\text{－}} {\sigma _3}{\text{）}}\sin \phi {\text{，}} \end{array} \right. $$ (3) $$ f {\text{＝}} \frac{1}{2}{\text{（}}{\sigma _1} {\text{－}} {\sigma _3}{\text{）}} {\text{＋}} \frac{1}{2}{\text{（}}{\sigma _1} {\text{＋}} {\sigma _3}{\text{）}}\sin \phi {\text{－}} C\cos \phi {\text{＝}} 0{\text{，}} $$ (4) 式中，σn和τn分别为滑移面上的正应力和切应力，σ1为最大主应力，σ3为最小主应力，C为土的黏聚力，
$\phi$ 为内摩擦角，f为屈服函数。3. 结果分析
将所选取的地震动原始数据进行基线矫正处理后作为模拟实验的数据进行数值模拟分析。由于篇幅限制，本文仅列出土坡在地震动M1，M2，M3作用下的变形云图（图5）。
![]()
图 5 土坡在地震动M1 （a），M2 （b），M3 （c）作用下的变形云图Figure 5. Deformation nephograms of soil slope under ground motion of M1 （a），M2 （b），M3 （c）收集并计算P1至P5各点地震响应结果，选取每条地震动所对应观测点的最终变形位移作为模拟实验的代表数据，结合每条地震动数据中所包含的特征参数信息绘制散点图，通过图像可以直观地显示出地震动各峰值特征参数对边坡地震响应的影响规律。
3.1 地震动峰值特征参数的影响规律
收集分析P1至P5 5个观测点在不同地震动作用下的最大位移数据，研究其与PGA，PGV，PGD三个地震动峰值参数的变化规律，图6—10所示为各参数与边坡5个观测点最大位移的变化规律。
![]()
图 6 P1点变形位移随PGA （a），PGV （b），PGD （c）的变化Figure 6. Variation of P1 displacement with PGA （a），PGV （b），PGD （c）![]()
图 7 P2点变形位移随PGA （a），PGV （b），PGD （c）的变化Figure 7. Variation of P2 displacement with PGA （a），PGV （b），PGD （c）![]()
图 8 P3点变形位移随PGA （a），PGV （b），PGD （c）的变化Figure 8. Variation of P3 displacement with PGA （a），PGV （b），PGD （c）![]()
图 9 P4点变形位移随PGA （a），PGV （b），PGD （c）的变化Figure 9. Variation of P4 displacement with PGA （a），PGV （b），PGD （c）![]()
图 10 P5点变形位移随PGA （a），PGV （b），PGD （c）的变化Figure 10. Variation of P5 displacement with PGA （a），PGV （b），PGD （c）由图6—10可以看出，各峰值特征参数与土坡变形都有较好的相关性，随着PGA，PGV，PGD的增大，坡体变形位移响应也相应增大，各峰值特征参数对于边坡变形的图像都呈现正相关的趋势。分别比较PGA，PGV，PGD三个地震动峰值特征参数与土坡同一点的位移变化曲线可以得出：PGV与土坡变形的线性关系最为明显，说明其能更好地反映土坡在地震作用下的变形响应规律；PGA，PGD与土坡变形的线性关系稍弱，但仍具有较好的正相关性。通过对图像进行线性拟合，PGV与土坡变形的相关系数最高，对比PGA，PGD的线性关系，PGD的相关系数更高，其相关性稍优于PGA。
而对比同一个地震动峰值参数对于不同边坡观测点位移的图像可以看出，各峰值参数对不同观测点的变化规律图像都比较一致。
3.2 参数优化选择
不同的地震动强度指标反应出的边坡地震响应程度有所不同，在边坡稳定性评价中，如何选择合理的强度指标是能否突出反应边坡地震响应程度的关键。
上节内容就PGA，PGV和PGD三个地震动峰值特征参数对土坡地震响应的影响程度进行了分析。为了进一步进行参数优化选择，作者对比分析了各土坡地震响应与地震动峰值特征参数的相关性，表2显示了土坡地震位移响应与PGA，PGV，PGD的相关系数ρ。相关性系数ρ的计算方法如式（5）所示，将第n条地震动的某一地震动强度指标值记为In，采用有限元法计算边坡模型在第n条地震动输入下的边坡最大地震响应值Rn，重复上述步骤，得到所有地震动记录的Rn及其对应的In，将所有地震动的计算结果绘制在R-I坐标系中，并通过式（5）计算得到R与I之间的相关系数ρ，即
表 2 地震动峰值特征参数和边坡地震响应的相关系数Table 2. The correlation coefficients between peak ground motion characteristic parameters and slope seismic responses监测点位移 相关系数 ρ PGA PGV PGD P1位移 0.873 0.984 0.925 P2位移 0.874 0.978 0.922 P3位移 0.863 0.982 0.926 P4位移 0.861 0.980 0.928 P5位移 0.869 0.982 0.931 $$\rho {\text{＝}} \frac{{\displaystyle\sum\limits_{{{n}} {\text{＝}} 1}^{100} {{\text{（}}{R_n} {\text{－}} \overline R }{\text{）}}{\text{（}}{I_n} {\text{－}} {\overline {I\;}}{\text{）}}}}{{\sqrt {\displaystyle\sum\limits_{{{n}} {\text{＝}} 1}^{100} {{\text{（}}{R_n} {\text{－}} \overline R } {{\text{）}}^2}} \sqrt {\displaystyle\sum\limits_{{{n}} {\text{＝}} 1}^{100} {{{{\text{（}}{I_n} {\text{－}} {\overline {I\;}}{\text{）}}}^2}} } }}{\text{.}}$$ (5) 由表2中地震动峰值特征参数与边坡地震响应的相关性计算结果可以得出：PGV与边坡各监测点响应的相关性最高，相关系数介于0.978—0.984，平均值为0.981；而PGD的相关性略小于PGV，相关系数介于0.922—0.931，平均值为0.926；在三个地震动峰值特征参数中，PGA的相关性最小，相关系数介于0.861—0.874，平均值为0.868。对比结果显示，PGV可以作为最优参数进行考虑，但是其它参数仍可作为辅助参数进行综合对比研究。
4. 讨论与结论
通过计算分析土坡在100条随机地震动作用下的响应，探讨了PGA，PGV和PGD三个峰值特征参数土坡变形的影响规律和相关性，能够得出以下结论：① 对于土坡坡面的变形位移响应，与其相关性最高的特征参数为PGV，其次是PGD，最后是PGA，且三者与土坡变形位移都具有较好的正相关性；② PGA由于其获取的便利性以及工程运用的广泛性，可以作为描述地震动强弱的合理参数；③ PGD能够直接反应地震幅度对结构所造成的影响。综上所述，在关于土坡地震响应的研究中，可以选择PGV作为研究参数进行分析，也可以结合其它两个特征参数对分析结果进行综合考量。
值得指出的是，本文工作基于二维均质土坡模型展开，尚存在一定的局限性。在今后的研究中，可以针对三维模型分析或是进行动力试验，以便更好地为实际工程服务。
新疆维吾尔自治区地震局监测中心提供了水磨沟台的地震波形数据，审稿专家提出了修改建议，作者在此一并表示衷心的感谢. -
![]()
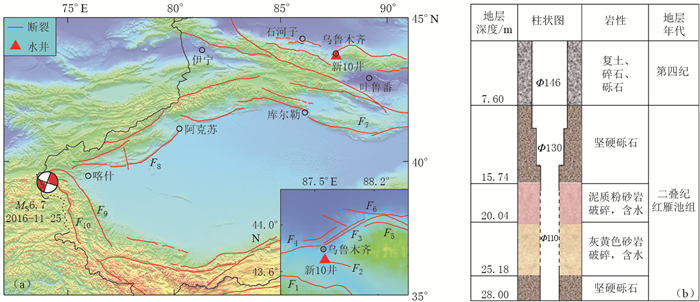
图 1 新10井构造环境(a)及其井孔结构(b)图
F1：柴窝堡盆地南缘断裂；F2：红雁池断裂；F3：雅玛克里断裂；F4：西山断裂；F5：二道沟断裂；F6：阜康断裂; F7：兴地断裂；F8：柯坪断裂；F9：西昆仑北缘断裂；F10：布伦口断裂
Figure 1. Geotectonic environment (a) and borehole structure (b) of Xin10 well
F1: Southern margin fault of Chaiwopu basin; F2: Hongyanchi fault; F3: Yama-Kerrey fault; F4: Xishan fault; F5: Erdaogou fault; F6: Fukang fault; F7: Xingdi fault; F8: Kalpin fault; F9: Northern margin fault of West Kunlun; F10: Bulunkou fault
![]()
图 2 新10井水震波(左)与水磨沟台地震波(右)的形态(a, b)及时频特征(c, d)对比
Figure 2. Waveforms (a, b) and time-frequency characteristics (c, d) of hydroseismogram in the Xin10 well (left) and those of the seismic waves in Shuimogou station (right)
![]()
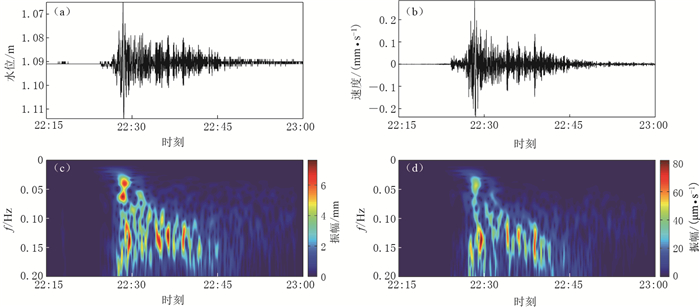
图 3 时间域水位与地表运动速度垂向分量的幅度对比
(a)水位与垂向速度散点图; (b)不同周期τ的水位幅值变化; (c)不同周期τ的垂向速度变化; (d)不同周期τ的水位与垂向速度振幅比m
Figure 3. Amplitude comparison between water level and vertical component of ground motion velocity in time domain
(a) Scatter diagram of water level versus vertical velocity; (b) Amplitude of water level in different periods τ; (c) Vertical velocity changes in different periods τ; (d) Amplitude ratio m of water level to vertical velocity in different periods τ
![]()
图 4 水位(a)与地表运动速度垂向分量(b)的频谱对比
Figure 4. Spectrum comparison between water level (a) and vertical component of ground motion velocity (b)
![]()
图 5 频率域水位与地表运动速度垂向分量的散点图(a)及其振幅比m (b)
Figure 5. Scatter diagram (a) and amplitude ratio m (b) of water level to vertical component of ground motion velocity in frequency domain
![]()
图 6 水震波变化幅值比R (a)和放大因子比R′ (b)
Figure 6. Amplitude ratio R of water level changes (a) and amplification factor ratio R′ (b) of hydroseismogram
![]()
图 7 不同渗透系数K下新10井水震波放大因子的理论值和实测值
(a)水位对含水层孔隙压力波动的放大因子A; (b)水位对地表垂向位移的放大因子A′
Figure 7. Theoretical values and measured values of amplification factor for the Xin10 well under different permeability coefficients K
(a) Amplification factor A of water level fluctuation to aquifer pore pressure; (b) Amplification factor A′ of water level to vertical displacement of ground surface
-
刘序俨, 郑小菁, 王林, 季颖锋. 2009.承压井水位观测系统对体应变的响应机制分析[J].地球物理学报, 52(12): 3147-3157. doi: 10.3969/j.issn.0001-5733.2009.12.025. Liu X Y, Zheng X J, Wang L, Ji Y F. 2009. Response analysis of the well-water-level system in confined aquifer[J]. Chinese Journal of Geophysics, 52(12): 3147-3157. doi: 10.3969/j.issn.0001-5733.2009.12.025 (in Chinese).
舒优良, 张世民, 黄辅琼. 2006.印尼8.7级和8.5级两次强震周至深井的震时效应研究[J].地震地磁观测与研究, 27(2): 16-22. http://www.cnki.com.cn/Article/CJFDTotal-FZJS200502015.htm Shu Y L, Zhang S M, Huang F Q. 2006. A study on earthquake-time effect of Zhouzhi deep borehole on two strong earthquakes: Magnitude 8.7 and magnitude 8.5 in Indonesia[J]. Seismological and Geomagnetic Observation and Research, 27(2): 16-22 (in Chinese). doi: 10.1007/s11589-009-0149-4
舒优良, 张世民, 黄辅琼. 2014.汶川8.0级地震周至深井水震波的记录特征[J].震灾防御技术, 9(增刊): 572-580. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=zzfy2014s1002&dbname=CJFD&dbcode=CJFQ Shu Y L, Zhang S M, Huang F Q. 2014. Characteristics of water level depth vibration of Zhouzhi deep well during Wenchuan M8.0 earthquake[J]. Technology for Earthquake Disaster Prevention, 9(S): 572-580 (in Chinese). https://www.sciencedirect.com/science/article/pii/S0040195116304905
Barbour A J. 2015. Pore pressure sensitivities to dynamic strains: Observations in active tectonic regions[J]. J Geophys Res, 120(8): 5863-5883. doi: 10.1002/2015JB012201
Blanchard F B, Byerly P. 1935. A study of a well gauge as a seismograph[J]. Bull Seismol Soc Am, 25(40): 313-321. http://bssa.geoscienceworld.org/content/25/4/313
Brodsky E E, Roeloffs E A, Woodcock D, Gall I, Manga M. 2003. A mechanism for sustained groundwater pressure changes induced by distant earthquakes[J]. J Geophys Res, 108(B8): 2390. doi: 10.1029/2002JB002321.
Cooper Jr H H, Bredehoeft J D, Papadopulos I S, Bennett R R. 1965. The response of well-aquifer systems to seismic waves[J]. J Geophys Res, 70(16): 3915-3926. doi: 10.1029/JZ070i016p03915.
Eaton J P, Takasaki K J. 1959. Seismological interpretation of earthquake-induced water-level fluctuations in wells[J]. Bull Seismol Soc Am, 49(3): 227-245. http://bssa.geoscienceworld.org/content/49/3/227
Elkhoury J E, Brodsky E E, Agnew D C. 2006. Seismic waves increase permeability[J]. Nature, 441(7097): 1135-1138. doi: 10.1038/nature04798.
Elkhoury J E, Niemeijer A, Brodsky E E, Marone C. 2011. Laboratory observations of permeability enhancement by fluid pressure oscillation of in situ fractured rock[J]. J Geophys Res, 116(B2): B02311. doi: 10.1029/2010JB007759.
He A H, Fan X F, Zhao G, Liu Y, Singh R P, Hu Y L. 2017. Co-seismic response of water level in the Jingle well (China) associated with the Gorkha Nepal (MW7.8) earthquake[J]. Tectonophysics, 714/715: 82-89. doi: 10.1016/j.tecto.2016.08.019.
Hsieh P A, Bredehoeft J D, Farr J M. 1987. Determination of aquifer transmissivity from earth tide analysis[J]. Water Resour Res, 23(10): 1824-1832. doi: 10.1029/WR023i010p01824
Liu L B, Roeloffs E, Zheng X Y. 1989. Seismically induced water level fluctuations in the Wali well, Beijing, China[J]. J Geophys Res, 94(B7): 9453-9462. doi: 10.1029/JB094iB07p09453.
Ma Y C, Huang F Q. 2017. Coseismic water level changes induced by two distant earthquakes in multiple wells of the Chinese mainland[J]. Tectonophysics, 694: 57-68. doi: 10.1016/j.tecto.2016.11.040
Manga M, Beresnev I, Brodsky E E, Elkhoury J E, Elsworth D, Ingebritsen S E, Mays D C, Wang C Y. 2012. Changes in permeability caused by transient stresses: Field observations, experiments, and mechanisms[J]. Rev Geophys, 50(2): RG2004. doi: 10.1029/2011RG000382.
Manga M, Wang C Y, Shirzaei M. 2016. Increased stream discharge after the 3 September 2016 MW5.8 Pawnee, Oklahoma earthquake[J]. Geophys Res Lett, 43(22): 11588-11594. doi: 10.1002/2016GL071268.
Mays D C. 2010. Contrasting clogging in granular media filters, soils, and dead-end membranes[J]. J Environ Eng, 136(5): 475-480. doi: 10.1061/(ASCE)EE.1943-7870.0000173.
Montgomery D R, Manga M. 2003. Streamflow and water well responses to earthquakes[J]. Science, 300: 2047-2049. doi: 10.1126/science.1082980.
Pride S R, Berryman J G, Harris J M. 2004. Seismic attenuation due to wave-induced flow[J]. J Geophys Res, 109(B1): B01201. doi: 10.1029/2003JB002639.
Rexin E E, Oliver J, Prentiss D. 1962. Seismically-induced fluctuations of the water level in the Nunn-Bush Well in Milwaukee[J]. Bull Seismol Soc Am, 52(1): 17-25. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/52/1/17/101282/seismically-induced-fluctuations-of-the-water?redirectedFrom=fulltext
Shalev E, Kurzon I, Doan M L, Lyakhovsky V. 2015. Water-level oscillations caused by volumetric and deviatoric dynamic strains[J]. Geophys J Int, 204(2): 841-851. http://adsabs.harvard.edu/abs/2016GeoJI.204..841S
Shi Z, Wang G, Manga M, Wang C Y. 2015. Continental-scale water-level response to a large earthquake[J]. Geofluids, 15(1/2): 310-320. doi: 10.1111/gfl.12099/abstract
Shih D C F, Wu Y M, Chang C H. 2013. Significant coherence for groundwater and Rayleigh waves: Evidence in spectral response of groundwater level in Taiwan using 2011 Tohoku earthquake, Japan[J]. J Hydrol, 486: 57-70. doi: 10.1016/j.jhydrol.2013.01.013
Stockwell R G, Mansinha L, Lowe R P. 1996. Localization of the complex spectrum: The S transform[J]. IEEE Trans Signal Process, 44(4): 998-1001. doi: 10.1109/78.492555
Sun X L, Wang G C, Yang X H. 2015. Coseismic response of water level in Changping well, China, to the MW9.0 Tohoku earthquake[J]. J Hydrol, 531: 1028-1039. doi: 10.1016/j.jhydrol.2015.11.005
Wang C Y, Wang C H, Manga M. 2004. Coseismic release of water from mountains: Evidence from the 1999 (MW7.5) Chi-Chi, Taiwan, earthquake[J]. Geology, 32(9): 769-772. doi: 10.1130/G20753.1.
Weingarten M, Ge S M. 2014. Insights into water level response to seismic waves: A 24 year high-fidelity record of global seismicity at Devils Hole[J]. Geophys Res Lett, 41(1): 74-80. doi: 10.1002/2013GL058418
Yan R, Woith H, Wang R J. 2014. Groundwater level changes induced by the 2011 Tohoku earthquake in China mainland[J]. Geophys J Int, 199(1): 533-548. doi: 10.1093/gji/ggu196
Yan R, Wang G C, Shi Z M. 2016. Sensitivity of hydraulic properties to dynamic strain within a fault damage zone[J]. J Hydrol, 543: 721-728. doi: 10.1016/j.jhydrol.2016.10.043
Zhang Y, Fu L Y, Huang F Q, Chen X Z. 2015. Coseismic water-level changes in a well induced by teleseismic waves from three large earthquakes[J]. Tectonophysics, 651: 232-241. https://www.sciencedirect.com/science/article/pii/S004019511500195X
-
期刊类型引用(1)
1. 禹海涛，李晶，王祺. 软土隧道基于地震响应的输入地震动排序. 地震学报. 2022(01): 123-131 . 
本站查看
其他类型引用(3)
下载:
计量
- 文章访问数: 1412
- HTML全文浏览量: 665
- PDF下载量: 45
- 被引次数: 4
